Load Nowcasting: Predicting Actuals with Limited Data
Abstract
1. Introduction and Motivation
2. The Nowcasting Problem
2.1. Formal Problem Description
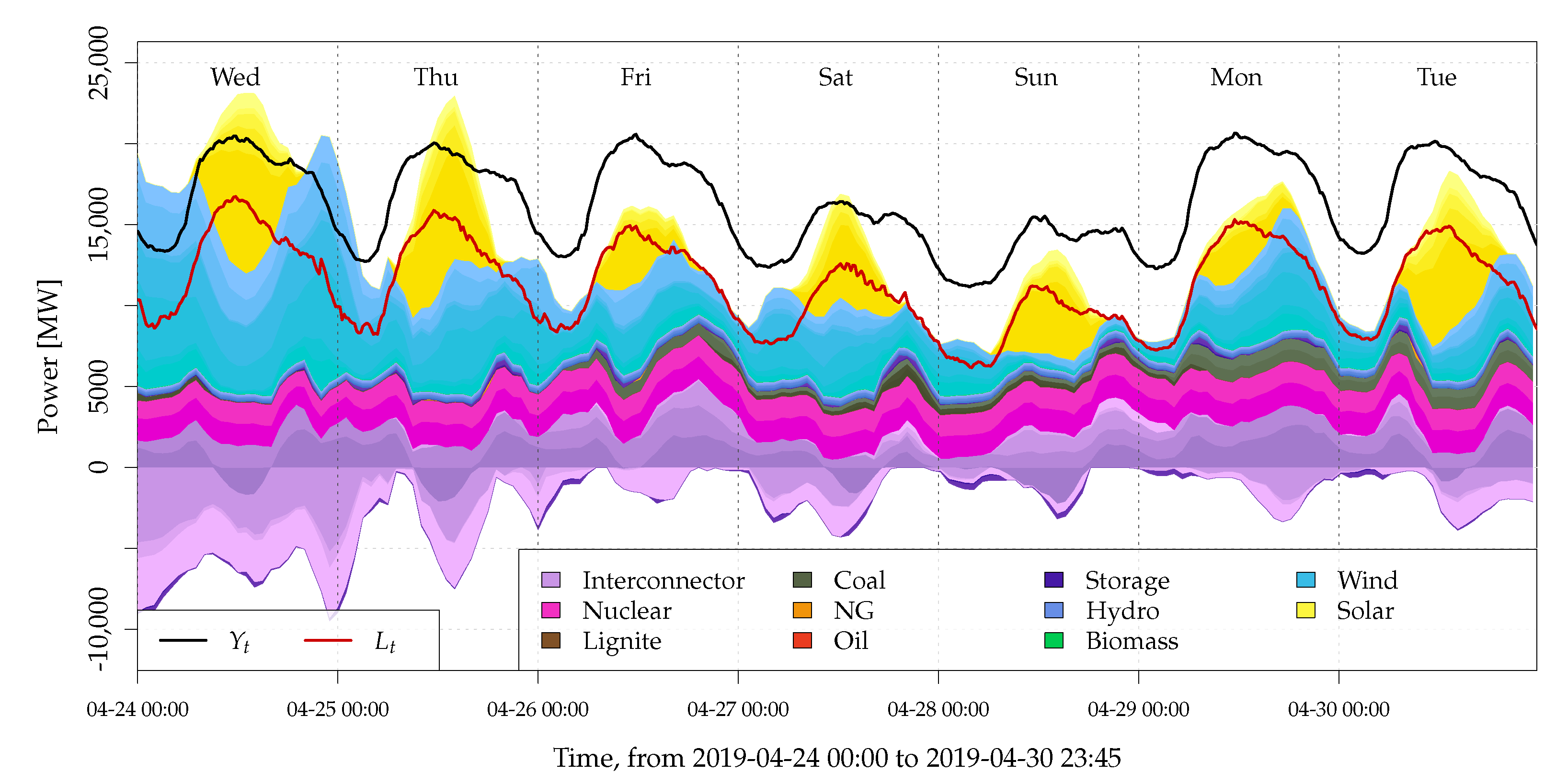
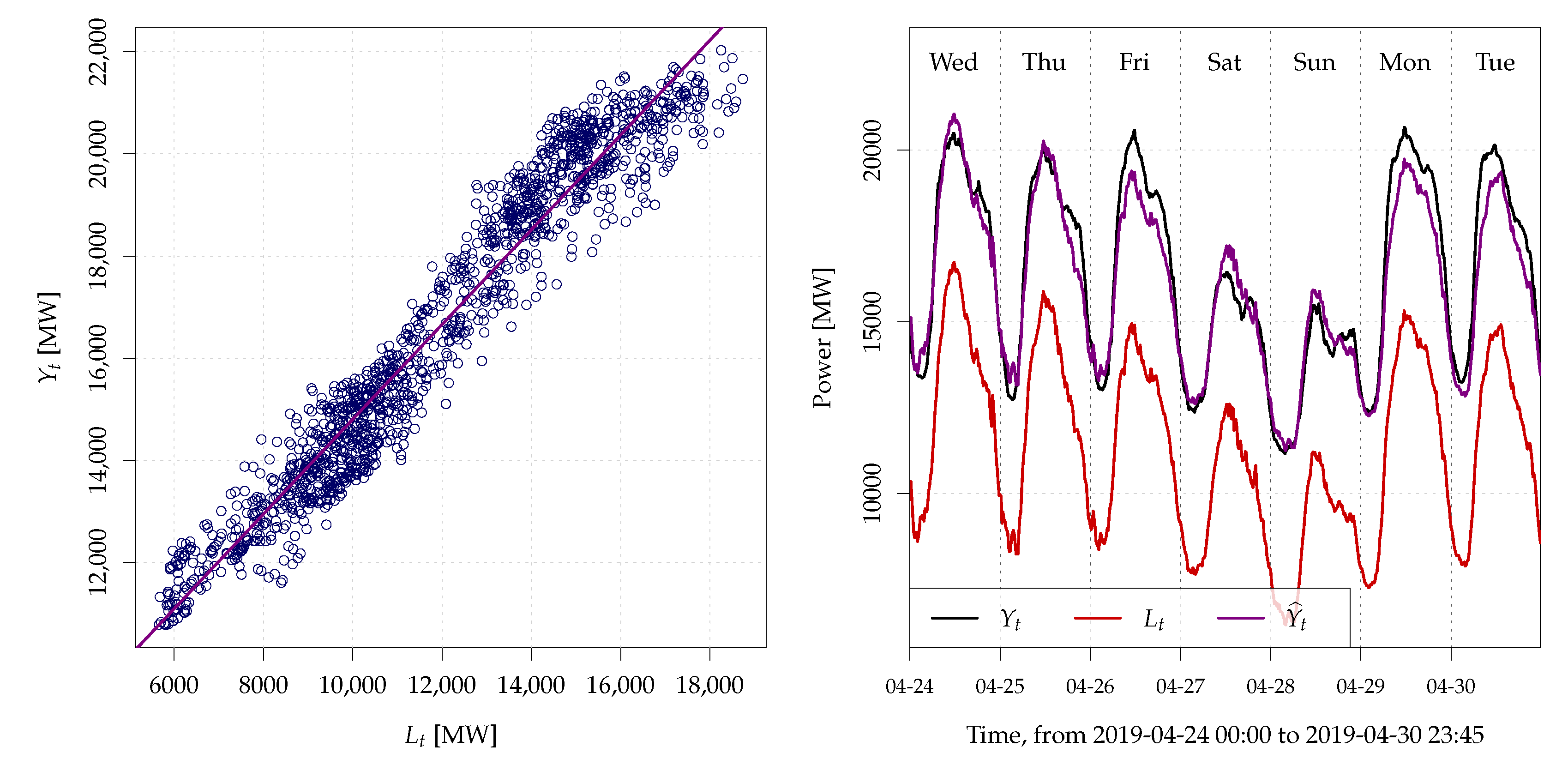
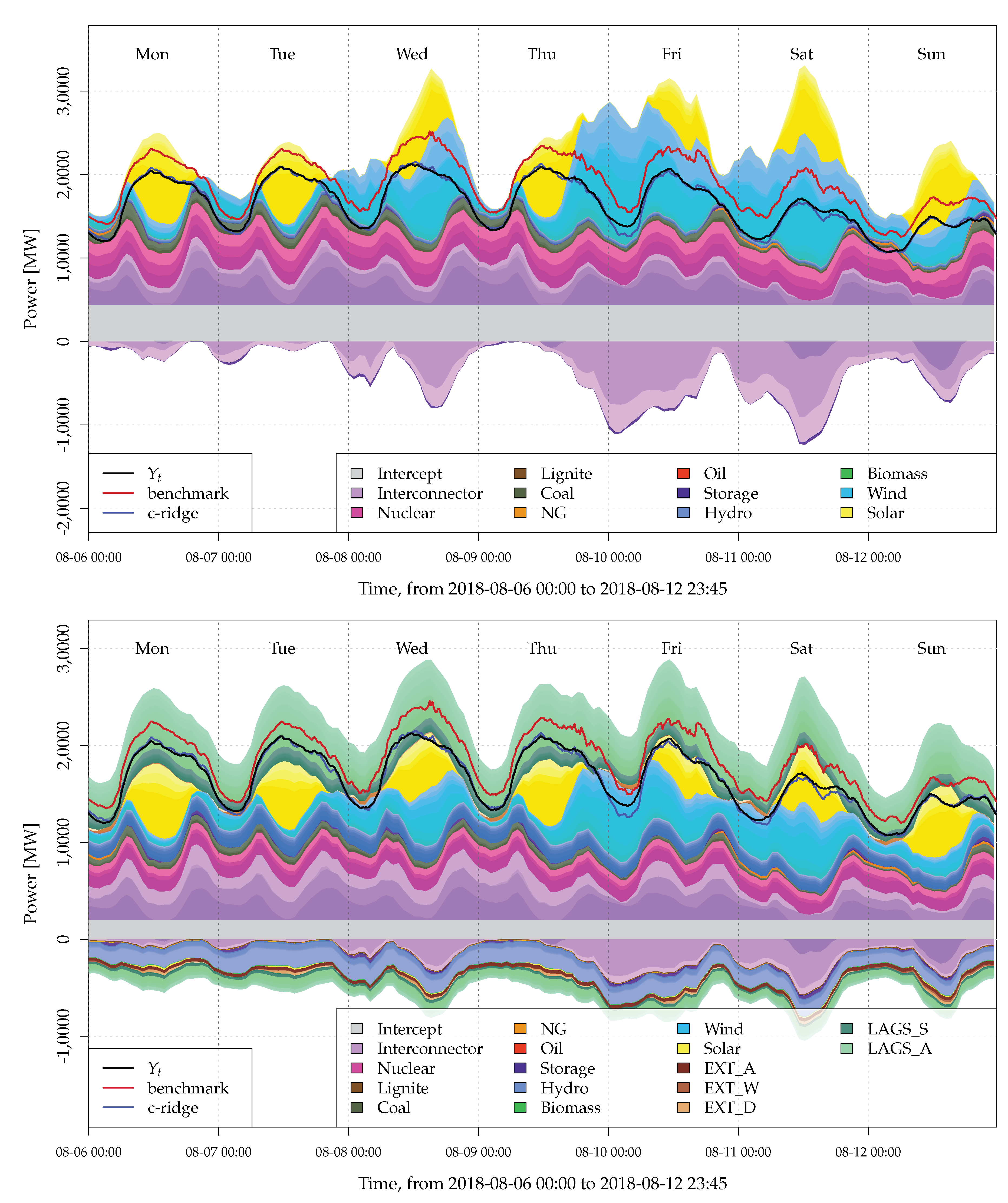
2.2. Data and Problem Illustration
3. Nowcasting Models
3.1. Benchmark Model
3.2. Proposed Nowcasting Model
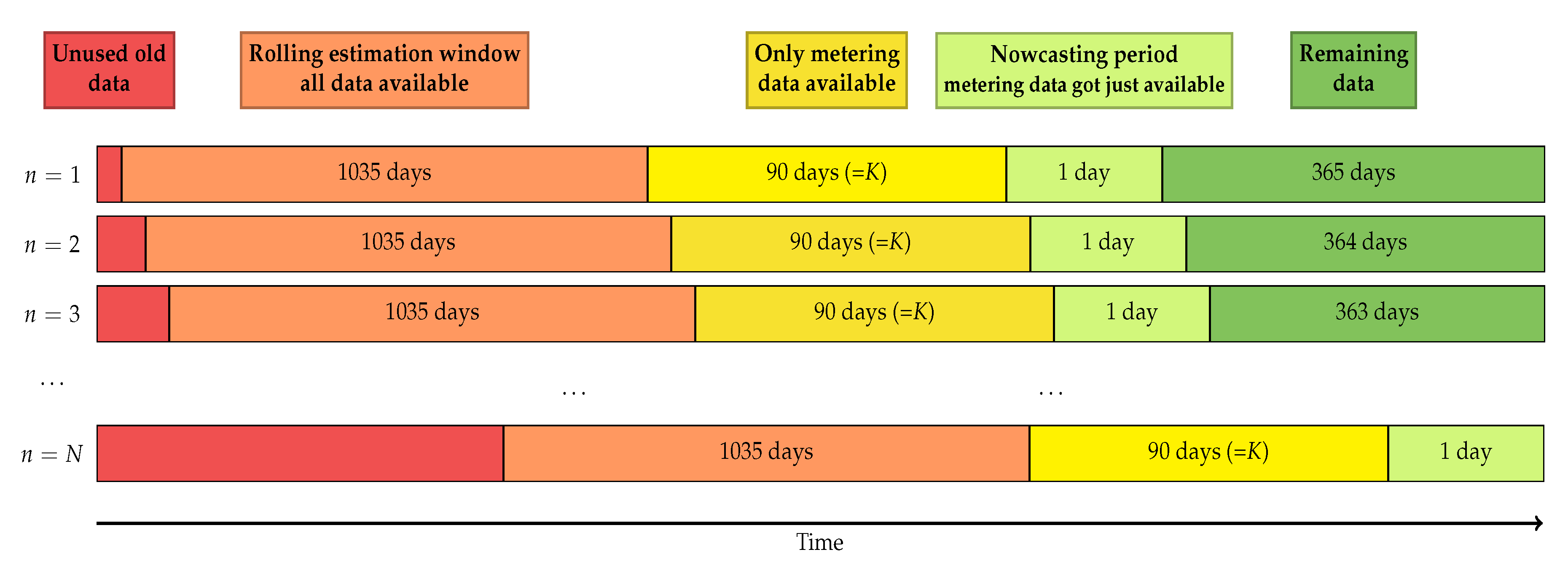
3.3. Estimation of Proposed Nowcasting Model
4. Nowcasting Study
- (i)
- All available data from the past 37 months (three years plus one month):99,360 observations of , denoted as 3years
- (ii)
- All available data from the past 25 months (two years plus one month):64,320 observations of , denoted as 2years
- (iii)
- All available data from the past 13 months (one year plus one month):29,280 observations of , denoted as 1year
- (iv)
- Data of the past year, 120 days centered around the nowcasting day of the past year:11,520 observations of , denoted as 4months
- (v)
- Data of the past year, 60 days centered around the nowcasting day of the past year:observations of , denoted as 2months
- (vi)
- Data of the past year, 30 days centered around the nowcasting day of the past year:observations of , denoted as 1month
5. Results
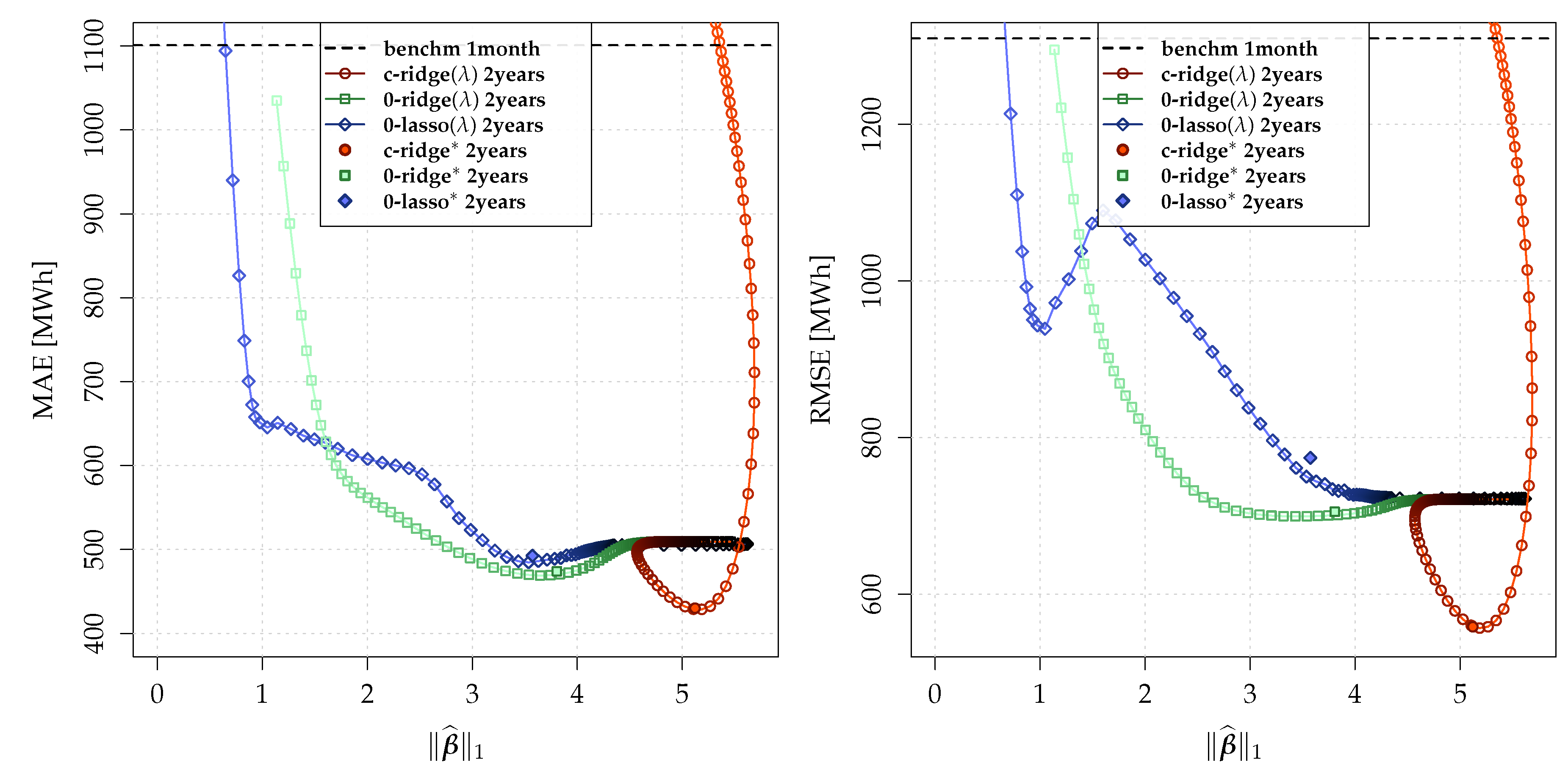
5.1. Nowcasting Performance
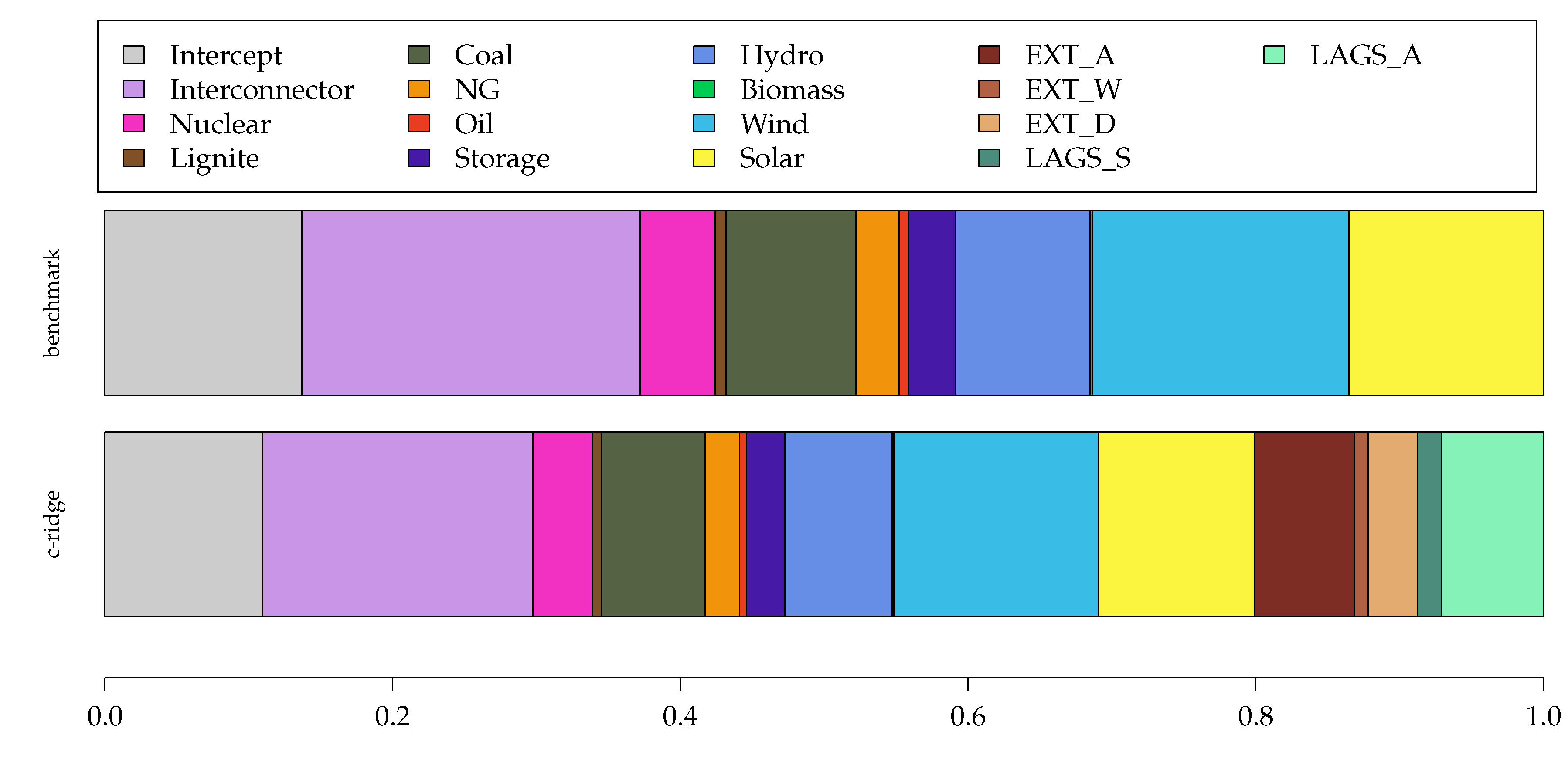
5.2. Model Interpretation
6. Summary and Conclusions
Funding
Conflicts of Interest
References
- Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast. 2016, 32, 914–938. [Google Scholar] [CrossRef]
- Schumacher, M.; Hirth, L.; How Much Electricity Do We Consume? A Guide to German and European Electricity Consumption and Generation Data (2015). FEEM Working Paper No. 88.2015. Available online: https://ssrn.com/abstract=2715986orhttp://dx.doi.org/10.2139/ssrn.2715986 (accessed on 20 December 2019).
- Hirth, L.; Mühlenpfordt, J.; Bulkeley, M. The ENTSO-E Transparency Platform—A review of Europe’s most ambitious electricity data platform. Appl. Energy 2018, 225, 1054–1067. [Google Scholar] [CrossRef]
- Gerbec, D.; Gubina, F.; Toros, Z. Actual load profiles of consumers without real time metering. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 12–16 June 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 2578–2582. [Google Scholar]
- Banbura, M.; Giannone, D.; Reichlin, L. Nowcasting. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1717887 (accessed on 20 December 2019).
- Sun, J.; Xue, M.; Wilson, J.W.; Zawadzki, I.; Ballard, S.P.; Onvlee-Hooimeyer, J.; Joe, P.; Barker, D.M.; Li, P.W.; Golding, B.; et al. Use of NWP for nowcasting convective precipitation: Recent progress and challenges. Bull. Am. Meteorol. Soc. 2014, 95, 409–426. [Google Scholar] [CrossRef]
- Xingjian, S.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.c. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Dutchess, NY, USA, 2015; pp. 802–810. [Google Scholar]
- Sanfilippo, A. Solar Nowcasting. In Solar Resources Mapping; Springer: Cham, Switzerland, 2019; pp. 353–367. [Google Scholar]
- Sala, S.; Amendola, A.; Leva, S.; Mussetta, M.; Niccolai, A.; Ogliari, E. Comparison of Data-Driven Techniques for Nowcasting Applied to an Industrial-Scale Photovoltaic Plant. Energies 2019, 12, 4520. [Google Scholar] [CrossRef]
- Gaillard, P.; Goude, Y.; Nedellec, R. Additive models and robust aggregation for GEFCom2014 probabilistic electric load and electricity price forecasting. Int. J. Forecast. 2016, 32, 1038–1050. [Google Scholar] [CrossRef]
- Ziel, F. Modeling public holidays in load forecasting: A German case study. J. Mod. Power Syst. Clean Energy 2018, 6, 191–207. [Google Scholar] [CrossRef]
- Ziel, F. Quantile regression for the qualifying match of GEFCom2017 probabilistic load forecasting. Int. J. Forecast. 2019, 35, 1400–1408. [Google Scholar] [CrossRef]
- Kanda, I.; Veguillas, J.Q. Data preprocessing and quantile regression for probabilistic load forecasting in the GEFCom2017 final match. Int. J. Forecast. 2019, 35, 1460–1468. [Google Scholar] [CrossRef]
- Haben, S.; Giasemidis, G.; Ziel, F.; Arora, S. Short term load forecasting and the effect of temperature at the low voltage level. Int. J. Forecast. 2019, 35, 1469–1484. [Google Scholar] [CrossRef]
- Ziel, F.; Liu, B. Lasso estimation for GEFCom2014 probabilistic electric load forecasting. Int. J. Forecast. 2016, 32, 1029–1037. [Google Scholar] [CrossRef]
- Dudek, G. Pattern-based local linear regression models for short-term load forecasting. Electr. Power Syst. Res. 2016, 130, 139–147. [Google Scholar] [CrossRef]
- Takeda, H.; Tamura, Y.; Sato, S. Using the ensemble Kalman filter for electricity load forecasting and analysis. Energy 2016, 104, 184–198. [Google Scholar] [CrossRef]
- Wang, Y.; Gan, D.; Zhang, N.; Xie, L.; Kang, C. Feature selection for probabilistic load forecasting via sparse penalized quantile regression. J. Modern Power Syst. Clean Energy 2019, 7, 1200–1209. [Google Scholar] [CrossRef]
- Uniejewski, B.; Nowotarski, J.; Weron, R. Automated variable selection and shrinkage for day-ahead electricity price forecasting. Energies 2016, 9, 621. [Google Scholar] [CrossRef]
- Ambach, D.; Croonenbroeck, C. Space-time short-to medium-term wind speed forecasting. Stat. Methods Appl. 2016, 25, 5–20. [Google Scholar] [CrossRef]
- Liu, W.; Dou, Z.; Wang, W.; Liu, Y.; Zou, H.; Zhang, B.; Hou, S. Short-term load forecasting based on elastic net improved GMDH and difference degree weighting optimization. Appl. Sci. 2018, 8, 1603. [Google Scholar] [CrossRef]
- Kath, C.; Ziel, F. The value of forecasts: Quantifying the economic gains of accurate quarter-hourly electricity price forecasts. Energy Econ. 2018, 76, 411–423. [Google Scholar] [CrossRef]
- Narajewski, M.; Ziel, F. Econometric modelling and forecasting of intraday electricity prices. J. Commod. Mark. 2019, 100107. [Google Scholar] [CrossRef]
- Pirbazari, A.M.; Chakravorty, A.; Rong, C. Evaluating feature selection methods for short-term load forecasting. In Proceedings of the 2019 IEEE International Conference on Big Data and Smart Computing (BigComp), Kyoto, Japan, 27 February–2 March 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–8. [Google Scholar]
- Muniain, P.; Ziel, F. Probabilistic forecasting in day-ahead electricity markets: Simulating peak and off-peak prices. Int. J. Forecast. 2020. [Google Scholar] [CrossRef]
- Gneiting, T. Making and evaluating point forecasts. J. Am. Stat. Assoc. 2011, 106, 746–762. [Google Scholar] [CrossRef]

| Models → | benchm | c-ridge | 0-ridge | 0-lasso | c-ridge | 0-ridge | 0-lasso | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Period↓ | MAE | Imp. | MAE | Imp. | MAE | Imp. | MAE | Imp. | MAE | Imp. | MAE | Imp. | MAE | Imp. |
| 3years | 1302.7 | −18.3 | 453.6 | 58.8 | 483.6 | 56.1 | 509.5 | 53.7 | 452.1 | 58.9 | 481.4 | 56.3 | 507.0 | 53.9 |
| 2years | 1328.8 | −20.7 | 430.0 | 60.9 | 474.1 | 56.9 | 487.8 | 55.7 | 428.7 | 61.1 | 469.0 | 57.4 | 484.7 | 56.0 |
| 1year | 1290.5 | −17.2 | 653.9 | 40.6 | 588.7 | 46.5 | 591.0 | 46.3 | 630.5 | 42.7 | 581.7 | 47.2 | 588.8 | 46.5 |
| 4months | 1130.2 | −2.7 | 934.3 | 15.1 | 549.5 | 50.1 | 583.8 | 47.0 | 923.2 | 16.1 | 538.3 | 51.1 | 578.6 | 47.4 |
| 2months | 1097.9 | 0.3 | 944.5 | 14.2 | 602.4 | 45.3 | 626.6 | 43.1 | 919.6 | 16.5 | 593.8 | 46.1 | 617.2 | 43.9 |
| 1month | 1100.9 | 0.0 | 918.0 | 16.6 | 607.1 | 44.9 | 635.0 | 42.3 | 913.1 | 17.1 | 604.1 | 45.1 | 629.3 | 42.8 |
| Models → | benchm | c-ridge | 0-ridge | 0-lasso | c-ridge | 0-ridge | 0-lasso | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Period↓ | RMSE | Imp. | RMSE | Imp. | RMSE | Imp. | RMSE | Imp. | RMSE | Imp. | RMSE | Imp. | RMSE | Imp. |
| 3years | 1556.0 | −18.8 | 578.9 | 55.8 | 710.0 | 45.8 | 868.5 | 33.7 | 582.2 | 55.5 | 713.0 | 45.6 | 825.0 | 37.0 |
| 2years | 1562.4 | −19.3 | 560.4 | 57.2 | 705.1 | 46.2 | 759.5 | 42.0 | 556.8 | 57.5 | 699.5 | 46.6 | 721.9 | 44.9 |
| 1year | 1460.6 | −11.5 | 1051.3 | 19.7 | 858.9 | 34.4 | 940.9 | 28.2 | 919.9 | 29.8 | 817.2 | 37.6 | 923.3 | 29.5 |
| 4months | 1332.9 | −1.8 | 1185.3 | 9.5 | 776.6 | 40.7 | 960.9 | 26.6 | 1102.3 | 15.8 | 754.6 | 42.4 | 880.6 | 32.8 |
| 2months | 1299.5 | 0.8 | 1274.3 | 2.7 | 877.1 | 33.0 | 975.9 | 25.5 | 1121.3 | 14.4 | 828.2 | 36.8 | 966.9 | 26.2 |
| 1month | 1309.7 | 0.0 | 1147.9 | 12.4 | 850.3 | 35.1 | 917.6 | 29.9 | 1150.5 | 12.2 | 858.2 | 34.5 | 914.5 | 30.2 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ziel, F. Load Nowcasting: Predicting Actuals with Limited Data. Energies 2020, 13, 1443. https://doi.org/10.3390/en13061443
Ziel F. Load Nowcasting: Predicting Actuals with Limited Data. Energies. 2020; 13(6):1443. https://doi.org/10.3390/en13061443
Chicago/Turabian StyleZiel, Florian. 2020. "Load Nowcasting: Predicting Actuals with Limited Data" Energies 13, no. 6: 1443. https://doi.org/10.3390/en13061443
APA StyleZiel, F. (2020). Load Nowcasting: Predicting Actuals with Limited Data. Energies, 13(6), 1443. https://doi.org/10.3390/en13061443





