Towards Developing an Automated Faults Characterisation Framework for Rotating Machines. Part 1: Rotor-Related Faults
Abstract
1. Introduction
2. Theoretical Background of the Modified Faults Diagnosis Architecture
2.1. Coherent Composite Spectrum (CCS)
2.2. Feature Extraction
2.3. Dimensionality Reduction
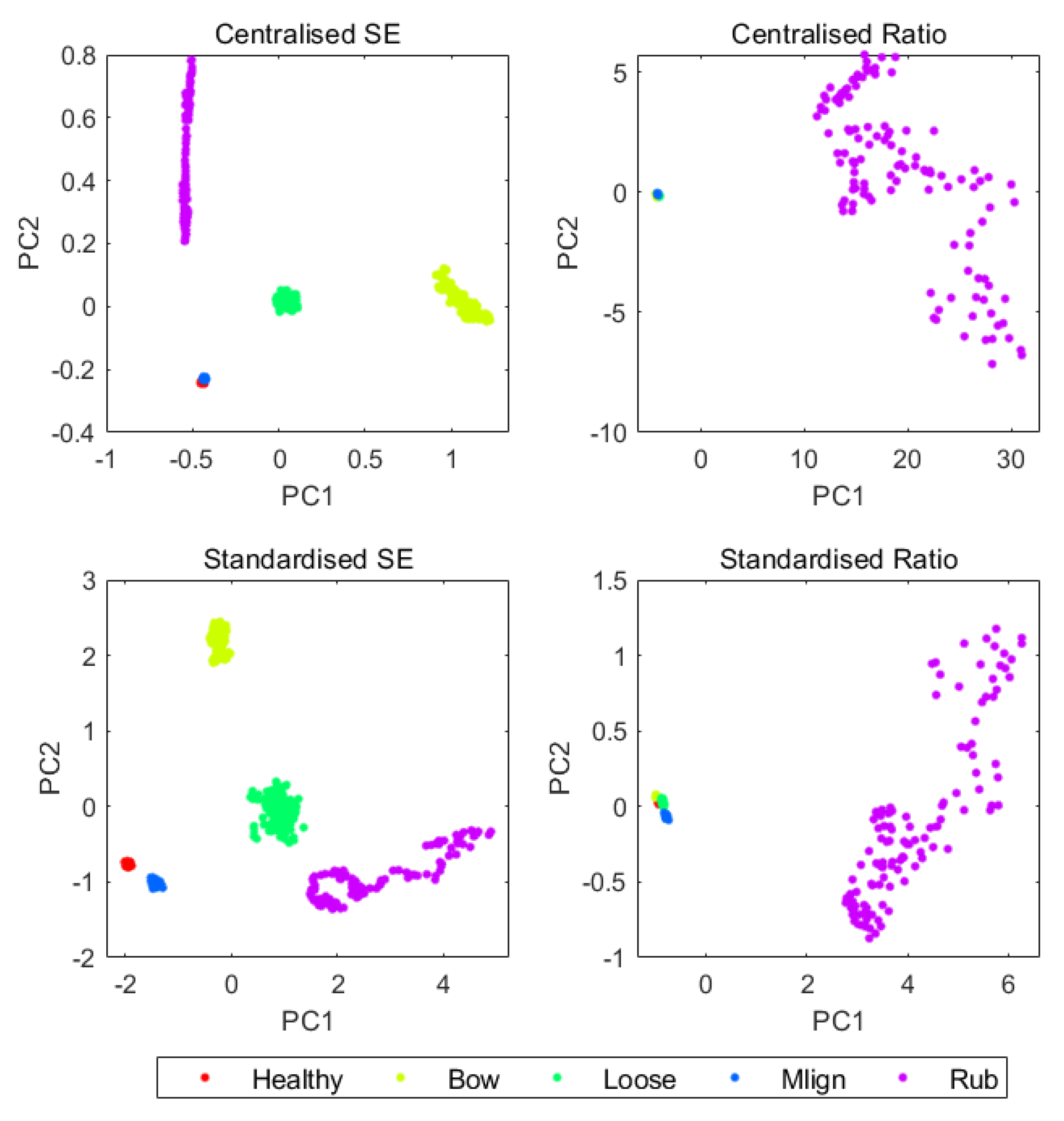
2.3.1. Data Centralisation and Standardisation
2.3.2. Singular Value Decomposition (SVD)
2.4. Supervised Learning
2.4.1. k-Nearest Neighbours (k-NN)
2.4.2. Naïve Bayes Classifier
2.4.3. Support Vector Machine (SVM)
2.4.4. Artificial Neural Network (ANN)
2.4.5. K-Fold Cross-Validation
3. Experimental Organisation and Data Source
3.1. The Rig
3.2. Dynamic Characteristics
3.3. Simulation of Faults
4. Data Arrangement and Signal Processing Parameters
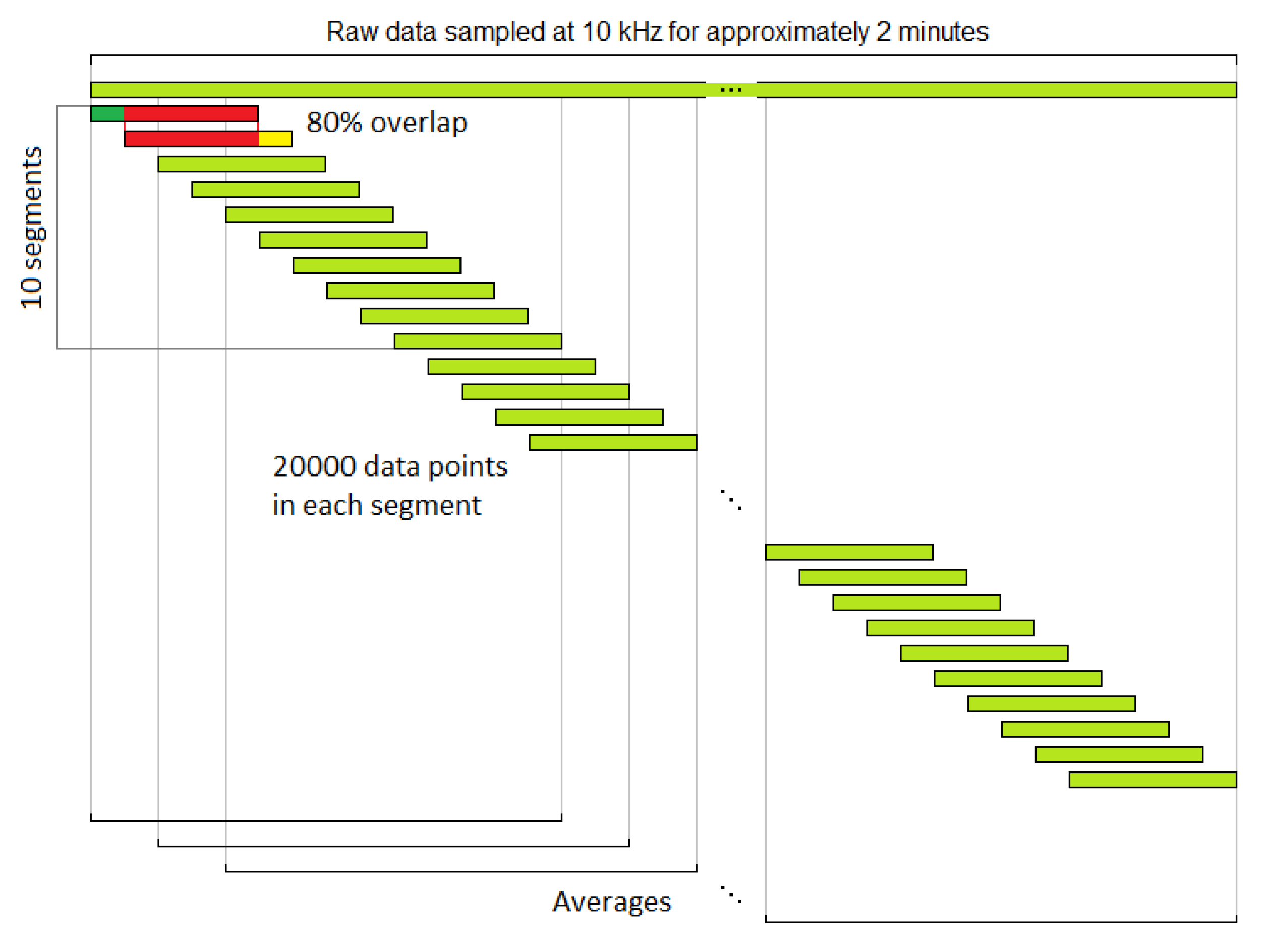
4.1. Data Arrangement for CCS Data Fusion
4.2. Data Arrangement for Dimensionality Reduction
5. Data Analysis and Discussion of Results
5.1. Accuracy Comparison
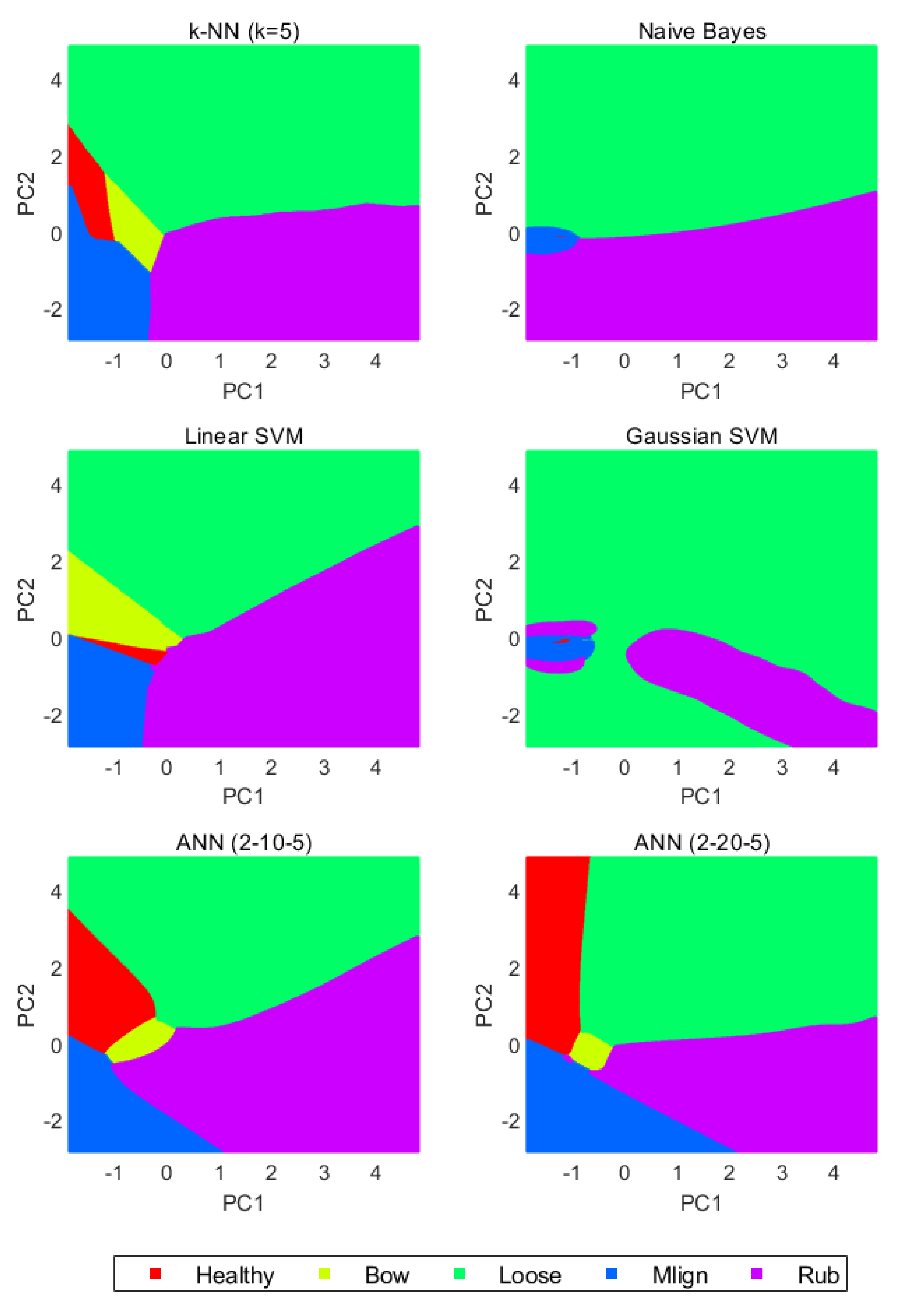
5.2. Visualised Decision Rules
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Yunusa-Kaltungo, A.; Sinha, J. Condition Monitoring: A Simple and Practical Approach; LAP Lambert Academic Publishing: Saarbrücken, Germany, 2012. [Google Scholar]
- Kostek, R.; Landowski, B.; Muślewski, Ł. Simulation of rolling bearing vibration in diagnostics. J. Vibroengin. 2015, 17, 4268–4278. [Google Scholar]
- Saidi, L.; Ali, J.B.; Fnaiech, F. Application of higher order spectral features and support vector machines for bearing faults classification. ISA Trans. 2015, 54, 193–206. [Google Scholar] [CrossRef] [PubMed]
- Liang, B.; Iwnicki, S.D.; Zhao, Y. Application of power spectrum, cepstrum, higher order spectrum and neural network analyses for induction motor fault diagnosis. Mech. Syst. Signal Process. 2013, 39, 342–360. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K.; Nembhard, A.D. Use of composite higher order spectra for faults diagnosis of rotating machines with different foundation flexibilities. Measurement 2015, 70, 47–61. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K. Faults diagnosis in rotating machines using higher order spectra. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014; American Society of Mechanical Engineers Digital Collection; ASME: New York, NY, USA, 2014. [Google Scholar]
- Arthur, N.; Penman, J. Induction machine condition monitoring with higher order spectra. IEEE Trans. Ind. Electron. 2000, 47, 1031–1041. [Google Scholar] [CrossRef]
- Chow, T.W.; Tan, H.Z. HOS-based nonparametric and parametric methodologies for machine fault detection. IEEE Trans. Ind. Electron. 2000, 47, 1051–1059. [Google Scholar] [CrossRef]
- McCormick, A.C.; Nandi, A.K. Bispectral and trispectral features for machine condition diagnosis. IEEE Proc. Vis. Image Signal Process. 1999, 146, 229–234. [Google Scholar] [CrossRef]
- Yang, D.M.; Stronach, A.F.; MacConnell, P.; Penman, J. Third-order spectral techniques for the diagnosis of motor bearing condition using artificial neural networks. Mech. Syst. Signal Process. 2002, 16, 391–411. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K. Combined bispectrum and trispectrum for faults diagnosis in rotating machines. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2014, 228, 419–428. [Google Scholar]
- Luo, S.; Cheng, J.; Zeng, M.; Yang, Y. An intelligent fault diagnosis model for rotating machinery based on multi-scale higher order singular spectrum analysis and GA-VPMCD. Measurement 2016, 87, 38–50. [Google Scholar] [CrossRef]
- Saidi, L.; Henao, H.; Fnaiech, F.; Capolino, G.A.; Cirrincione, G. Application of higher order spectral analysis for rotor broken bar detection in induction machines. In Proceedings of the 8th IEEE Symposium on Diagnostics for Electrical Machines, Power Electronics & Drives, Bologna, Italy, 5–8 September 2011; pp. 31–38. [Google Scholar]
- Yunusa-Kaltungo, A.; Sinha, J.K.; Elbhbah, K. HOS analysis of measured vibration data on rotating machines with different simulated faults. In Proceedings of the Advances in Condition Monitoring of Machinery in Non-Stationary Operations, Lyon, France, 15–17 December 2014; Springer: Berlin/Heidelberg, Germany, 2016; pp. 81–89. [Google Scholar]
- Saidi, L.; Ali, J.B.; Fnaiech, F. Bi-spectrum based-EMD applied to the non-stationary vibration signals for bearing faults diagnosis. ISA Trans. 2014, 53, 1650–1660. [Google Scholar] [CrossRef] [PubMed]
- Yunusa-Kaltungo, A.; Sinha, J.K. Generic vibration-based faults identification approach for identical rotating machines installed on different foundations, VIRM 11-Vibrations in Rotating. Machinery 2016, 11, 499–510. [Google Scholar]
- de la Rosa, J.J.; Muñoz, A.M. Higher-order cumulants and spectral kurtosis for early detection of subterranean termites. Mech. Syst. Signal Process. 2008, 22, 279–294. [Google Scholar] [CrossRef]
- Saidi, L.; Fnaiech, F. Bearing defects decision making using higher order spectra features and support vector machines. In Proceedings of the IEEE 14th International Conference on Sciences and Techniques of Automatic Control & Computer Engineering-STA’2013, Sousse, Tunisia, 20–22 December 2013; pp. 419–424. [Google Scholar]
- McCormick, A.C. Cyclostationary and Higher-order Statistical Signal Processing Algorithms for Machine Condition Monitoring. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 1998. [Google Scholar]
- Howard, I.M. Higher-order spectral techniques for machine vibration condition monitoring. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 1997, 211, 211–219. [Google Scholar] [CrossRef]
- Collis, W.B.; White, P.R.; Hammond, J.K. Higher-order spectra: The bispectrum and trispectrum. Mech. Syst. Signal Pr. 1998, 12, 375–394. [Google Scholar] [CrossRef]
- Rivola, A.; White, P.R. Use of higher order spectra in condition monitoring: Simulation and experiments. In Proceedings of the 1999 ASME Design Engineering Technical Conferences, Las Vegas, NV, USA, 12–15 September 1999; Paper No. DETC99/VIB-8332; ASME: New York, NY, USA, 1999. [Google Scholar]
- Yunusa-Kaltungo, A.; Sinha, J.K. A comparison of signal processing tools: Higher order spectra versus higher order coherences. J. Vib. Eng. Technol. 2015, 3, 461–472. [Google Scholar]
- Elbhbah, K.; Sinha, J.K. Vibration-based condition monitoring of rotating machines using a machine composite spectrum. J. Sound Vib. 2013, 332, 2831–2845. [Google Scholar] [CrossRef]
- Sinha, J.K.; Elbhbah, K. A future possibility of vibration based condition monitoring of rotating machines. Mech. Syst. Signal Process. 2013, 34, 231–240. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K.; Elbhbah, K. An improved data fusion technique for faults diagnosis in rotating machines. Measurement 2014, 58, 27–32. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K.; Nembhard, A.D. A novel fault diagnosis technique for enhancing maintenance and reliability of rotating machines. Struct. Health Monit. 2015, 14, 604–621. [Google Scholar] [CrossRef]
- Nembhard, A.D.; Sinha, J.K. Unified Multi-speed analysis (UMA) for the condition monitoring of aero-engines. Mech. Syst. Signal Process. 2015, 64, 84–99. [Google Scholar] [CrossRef]
- Jolliffe, I. Principal Component Analysis; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Nagbe, K.; Cugliari, J.; Jacques, J. Short-Term Electricity Demand Forecasting Using a Functional State Space Model. Energies 2018, 11, 1120. [Google Scholar] [CrossRef]
- Shen, Y.; Abubakar, M.; Liu, H.; Hussain, F. Power Quality Disturbance Monitoring and Classification Based on Improved PCA and Convolution Neural Network for Wind-Grid Distribution Systems. Energies 2019, 12, 1280. [Google Scholar] [CrossRef]
- Papaioannou, G.P.; Dikaiakos, C.; Dramountanis, A.; Papaioannou, P.G. Analysis and Modeling for Short- to Medium-Term Load Forecasting Using a Hybrid Manifold Learning Principal Component Model and Comparison with Classical Statistical Models (SARIMAX, Exponential Smoothing) and Artificial Intelligence Models (ANN, SVM): The Case of Greek Electricity Market. Energies 2016, 9, 635. [Google Scholar]
- AbuBaker, M. Data Mining Applications in Understanding Electricity Consumers’ Behavior: A Case Study of Tulkarm District, Palestine. Energies 2019, 12, 4287. [Google Scholar] [CrossRef]
- Fei, W.; Moses, P. Fault Current Tracing and Identification via Machine Learning Considering Distributed Energy Resources in Distribution Networks. Energies 2019, 12, 4333. [Google Scholar] [CrossRef]
- Zeng, B.; Guo, J.; Zhu, W.; Xiao, Z.; Yuan, F.; Huang, S. A Transformer Fault Diagnosis Model Based On Hybrid Grey Wolf Optimizer and LS-SVM. Energies 2019, 12, 4170. [Google Scholar] [CrossRef]
- Feng, S.; Chen, J.; Tang, Y. Identification of Low Frequency Oscillations Based on Multidimensional Features and ReliefF-mRMR. Energies 2019, 12, 2762. [Google Scholar] [CrossRef]
- Xiao, C.; Liu, Z.; Zhang, T.; Zhang, L. On Fault Prediction for Wind Turbine Pitch System Using Radar Chart and Support Vector Machine Approach. Energies 2019, 12, 2693. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Pająk, M.; Muślewski, Ł.; Landowski, B.; Grządziela, A. Fuzzy identification of the reliability state of the mine detecting ship propulsion system. Pol. Marit. Res. 2019, 26, 55–64. [Google Scholar] [CrossRef]
- Russell, S.J.; Norvig, P. Artificial Intelligence: A Modern Approach; Pearson Education Limited: Kuala Lumpur, Malaysia, 2016. [Google Scholar]
- Yunusa-Kaltungo, A.; Kermani, M.M.; Labib, A. Investigation of critical failures using root cause analysis methods: Case study of ASH cement PLC. Eng. Fail. Anal. 2017, 73, 25–45. [Google Scholar] [CrossRef]
- Reynolds, P.; Pavic, A. Quality assurance procedures for the modal testing of building floor structures. Exp. Tech. 2000, 24, 36–41. [Google Scholar] [CrossRef]
- Ewins, D.J. Basics and state-of-the-art of modal testing. Sadhana 2000, 25, 207–220. [Google Scholar] [CrossRef][Green Version]
- Ewins, D.J. Modal Testing: Theory, Practice and Application, 2nd ed.; Research Studies Press: Hertfordshire, UK, 2000. [Google Scholar]
- Wang, J.; Xu, M.; Zhang, C.; Huang, B.; Gu, F. Online Bearing Clearance Monitoring Based on an Accurate Vibration Analysis. Energies 2020, 13, 389. [Google Scholar] [CrossRef]
- Aggarwal, A.; Strangas, E.G. Review of Detection Methods of Static Eccentricity for Interior Permanent Magnet Synchronous Machine. Energies 2019, 12, 4105. [Google Scholar] [CrossRef]
- Li, X.; Elasha, F.; Shanbr, S.; Mba, D. Remaining Useful Life Prediction of Rolling Element Bearings Using Supervised Machine Learning. Energies 2019, 12, 2705. [Google Scholar] [CrossRef]
- Salomon, C.P.; Ferreira, C.; Sant’Ana, W.C.; Lambert-Torres, G.; Borges da Silva, L.E.; Bonaldi, E.L.; de Oliveira, L.E.L.; Torres, B.S. A Study of Fault Diagnosis Based on Electrical Signature Analysis for Synchronous Generators Predictive Maintenance in Bulk Electric Systems. Energies 2019, 12, 1506. [Google Scholar] [CrossRef]
- Shi, R.; Zhang, X. VSG-Based Dynamic Frequency Support Control for Autonomous PV–Diesel Microgrids. Energies 2018, 11, 1814. [Google Scholar] [CrossRef]
- Caruso, M.; Di Tommaso, A.O.; Marignetti, F.; Miceli, R.; Ricco Galluzzo, G. A General Mathematical Formulation for Winding Layout Arrangement of Electrical Machines. Energies 2018, 11, 446. [Google Scholar] [CrossRef]





| Case | Description | Abbreviation | Severity and Location |
|---|---|---|---|
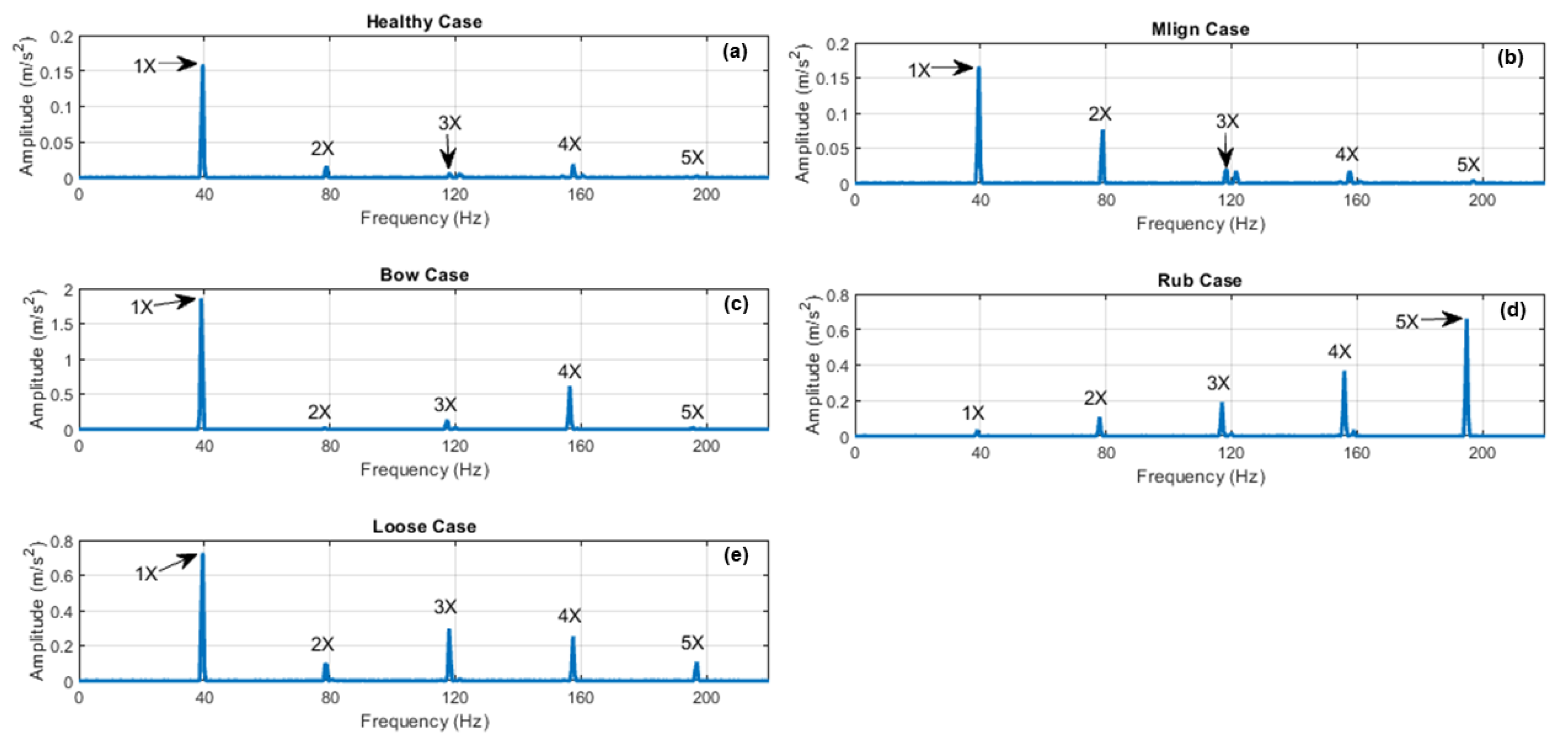
| 1 | Healthy with residual misalignment | Healthy | The reference case likely contains some residual misalignment at the couplings, due to manufacturing and assembly imperfections |
| 2 | Rotor bow | Bow | 3.4 mm run-out was created at the centre of the 1000 mm shaft. |
| 3 | Rotor misalignment | Mlign | 0.8 mm mild steel shim beneath RHS of bearing 1 foundation |
| 4 | Bearing looseness | Loose | Loosening some of the bearing 3 threaded bar nuts |
| 5 | Rotor rub | Rub | Partial rub using two Perspex blades (TDC and BDC of 1000 mm shaft), 275 mm from bearing 1 |
| Speed | 20Hz | 30Hz | 40Hz | |||
|---|---|---|---|---|---|---|
| Case Code | Raw Data | Averages | Raw Data | Averages | Raw Data | Averages |
| Healthy | 1,272,000 | 153 | 1,279,000 | 153 | 1,110,000 | 132 |
| Bow | 1,266,000 | 152 | 1,271,000 | 152 | 1,266,000 | 152 |
| Loose | 1,058,000 | 126 | 1,248,000 | 150 | 1,261,000 | 151 |
| Mlign | 996,000 | 118 | 927,000 | 109 | 928,000 | 110 |
| Rub | 1,259,000 | 151 | 1,271,000 | 152 | 994,000 | 118 |
| Total | - | 700 | - | 716 | - | 663 |
| Speed | Feature Extracted | PC1 | PC2 | PC3 | PC4 | PC5 | PC 1&2 |
|---|---|---|---|---|---|---|---|
| 20 Hz | Centralised SE | 98.8046 | 0.9327 | 0.1915 | 0.0697 | 0.0015 | 99.7373 |
| Centralised ratio | 83.4228 | 11.3585 | 4.6620 | 0.5567 | N/A | 94.7813 | |
| Standardised SE | 47.3572 | 35.6890 | 13.2328 | 3.3719 | 0.3492 | 83.0462 | |
| Standardised ratio | 45.8536 | 26.7937 | 22.3915 | 4.9611 | N/A | 72.6473 | |
| 30 Hz | Centralised SE | 80.2678 | 14.5710 | 4.8346 | 0.3196 | 0.0069 | 94.8389 |
| Centralised ratio | 86.4172 | 10.9302 | 2.3409 | 0.3117 | N/A | 97.3474 | |
| Standardised SE | 50.2902 | 32.7920 | 14.7593 | 2.1318 | 0.0267 | 83.0822 | |
| Standardised ratio | 57.7854 | 24.8192 | 15.9871 | 1.4083 | N/A | 82.6047 | |
| 40 Hz | Centralised SE | 85.3494 | 13.2058 | 0.7743 | 0.6089 | 0.0616 | 98.5552 |
| Centralised ratio | 97.3550 | 2.3694 | 0.2433 | 0.0323 | N/A | 99.7244 | |
| Standardised SE | 55.1189 | 31.6004 | 10.7211 | 1.8511 | 0.7085 | 86.7193 | |
| Standardised ratio | 97.5927 | 1.5837 | 0.6559 | 0.1677 | N/A | 99.1764 |
| Speed | Feature Extracted | k-NN k = 5 | Naïve Bayes | Linear SVM | Gaussian SVM | ANN 2-10-5 | ANN 2-20-5 |
|---|---|---|---|---|---|---|---|
| 20Hz | Centralised SE | 98.14 | 98.29 | 98.4 | 98.1 | 97.7 | 97.9 |
| Centralised Ratio | 98.71 | 98.57 | 98.9 | 99.3 | 99.0 | 99.3 | |
| Standardised SE | 93.43 | 85.43 | 94.0 | 94.4 | 93.3 | 94.0 | |
| Standardised Ratio | 88.57 | 84.71 | 88.0 | 88.7 | 89.7 | 90.1 | |
| 30Hz | Centralised SE | 94.13 | 94.41 | 96.1 | 94.7 | 94.1 | 95.9 |
| Centralised Ratio | 96.79 | 96.51 | 97.9 | 98.6 | 83.5 | 83.9 | |
| Standardised SE | 99.16 | 98.46 | 98.9 | 99.4 | 98.3 | 98.6 | |
| Standardised Ratio | 100 | 100 | 100 | 100 | 100 | 100 | |
| 40Hz | Centralised SE | 98.19 | 97.89 | 98.0 | 98.5 | 96.8 | 98.0 |
| Centralised Ratio | 100 | 95.17 | 99.4 | 99.7 | 87.9 | 98.0 | |
| Standardised SE | 100 | 100 | 100 | 100 | 100 | 100 | |
| Standardised Ratio | 100 | 100 | 100 | 100 | 99.8 | 96.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yunusa-Kaltungo, A.; Cao, R. Towards Developing an Automated Faults Characterisation Framework for Rotating Machines. Part 1: Rotor-Related Faults. Energies 2020, 13, 1394. https://doi.org/10.3390/en13061394
Yunusa-Kaltungo A, Cao R. Towards Developing an Automated Faults Characterisation Framework for Rotating Machines. Part 1: Rotor-Related Faults. Energies. 2020; 13(6):1394. https://doi.org/10.3390/en13061394
Chicago/Turabian StyleYunusa-Kaltungo, Akilu, and Ruifeng Cao. 2020. "Towards Developing an Automated Faults Characterisation Framework for Rotating Machines. Part 1: Rotor-Related Faults" Energies 13, no. 6: 1394. https://doi.org/10.3390/en13061394
APA StyleYunusa-Kaltungo, A., & Cao, R. (2020). Towards Developing an Automated Faults Characterisation Framework for Rotating Machines. Part 1: Rotor-Related Faults. Energies, 13(6), 1394. https://doi.org/10.3390/en13061394






