Abstract
The magnetizing inductance of the medium frequency transformer (MFT) impacts the performance of the isolated dc-dc power converters. The ferrite material is considered for high power transformers but it requires an assembly of type “I” cores resulting in a multi air gap structure of the magnetic core. The authors claim that the multiple air gaps are randomly distributed and that the average air gap length is unpredictable at the industrial design stage. As a consequence, the required effective magnetic permeability and the magnetizing inductance are difficult to achieve within reasonable error margins. This article presents the measurements of the equivalent B(H) and the equivalent magnetic permeability of two three-phase MFT prototypes. The measured equivalent B(H) is used in an FEM simulation and compared against a no load test of a 100 kW isolated dc-dc converter showing a good fit within a 10% error. Further analysis leads to the demonstration that the equivalent magnetic permeability and the average air gap length are nonlinear functions of the number of air gaps. The proposed exponential scaling function enables rapid estimation of the magnetizing inductance based on the ferrite material datasheet only.
1. Introduction
The medium frequency transformer (MFT) is one of the key components in the isolated dc-dc converters [1,2,3,4] related to: smart grids [5], photovoltaic power plants [6], wind power plants [7], and electric vehicle charging [8,9]. The three-phase topology is considered for high power applications where the high power density and high efficiency are required. In [10,11], an analytical approach was proposed to compare multi-phase dc-dc topologies. In [12], the single-phase and three-phase topologies were compared. A 10 kVA 1 kHz three-phase MFT prototype was reported in [13], and a 2 kVA 100 kHz three-phase MFT was reported in [14]. A 5 MW three-phase converter was presented in [15] but using three single-phase MFTs. The general circuit diagram of the three-phase isolated dc-dc converter is composed of two voltage source converters (VSC), and an MFT is presented in Figure 1.
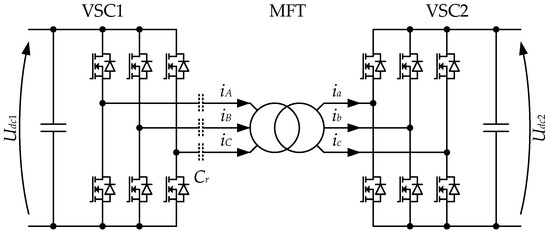
Figure 1.
Three-phase isolated dc-dc converter circuit diagram; Cr is the optional resonant capacitor.
The performance of the converter highly depends on the MFT and its equivalent circuit parameters. The leakage inductance has a significant influence on the operation of the converter and the specified value is usually well achieved in the MFT development process. In the LLC resonant dc-dc (LLC) converter [1,16,17], the magnetizing inductance has a significant effect on the zero voltage switching (ZVS) [18,19,20], but it may be difficult to achieve within reasonable error margins [21]. The maximum value of the magnetizing inductance should take into account the drain-source capacitance Cds of the MOSFET (or other power semiconductor switch). It should ensure the magnetizing current sufficient to charge and discharge the Cds during the dead time of a VSC leg. In the dual active bridge (DAB) converter [2,22], the magnetizing inductance should not increase the VSC current and it should be considered at low operating power.
The operating frequency of the 100 kilowatt class isolated dc-dc converters is considered in the range from few kilohertz to tens of kilohertz [23,24,25]. The voltage and current fundamentals and harmonics influence the design of the MFT magnetic core and windings. The choice of MFT magnetic core material should be done according to the material properties and cost. The performance factor, which is defined as a product of the frequency and flux density at a specified core loss density, is used to compare different types of core materials [26,27]. The amorphous and especially nanocrystalline materials are preferred in the low and medium frequencies due to the high flux density [28,29]. On the other hand, the main advantage of ferrite cores is their low power loss, which makes them an attractive material for the construction of medium and high frequency transformers [30,31]. The ferrite also offers low cost in terms of material and transformer assembly. In [32], the ferrite core MFT was considered for an optimized dc-dc converter operating at a few kHz. Finally, the ferrite seems as a good candidate for the short term industrialization of the high power three-phase MFT. However, the construction of a ferrite magnetic core for high power MFT requires an assembly of type “I” cores since the C-cores or E-cores do not exist for large transformers. This results in a multi air gap structure of the magnetic core.
The influence of the air gap on the transformer magnetic properties in LLC converters was analysed in [33,34]. It was assumed that the air gap length was known and controlled in the MFT design process. The considered air gaps had relatively large size in order to reduce the slope of the B(H) curve and to minimize the influence of magnetic saturation on the magnetizing inductance value. The influence of the air gap length on the equivalent magnetic permeability, magnetic reluctance and magnetizing inductance in ferrite core transformers was analysed in [35,36,37,38]. The influence on the core and winding power loss was studied in [39,40,41]. All the analysed cases considered a single and uniform air gap of a known length. The analysis of a single but non-uniform air gap in toroidal cores was presented in [42,43]. The influence of the number of uniform air gaps with a controlled size on the magnetic properties and transients in a current transducer was considered in [44].
In the transformer core structure characterized by a construction periodicity (ferromagnetic material—air gap, ferromagnetic material—diamagnetic material, etc.), it is possible to utilize the homogenization technique or multiscale methods in the description of magnetic properties (reluctance of homogenized core, equivalent magnetic permeability, equivalent B(H), etc.). The use of the homogenization technique in the finite element method (FEM) analysis of step-lap joints in steel sheet transformers was proposed in [45]. The homogenization technique was further developed in 2D FEM of steel sheet cores [46,47,48] and amorphous cores [49]. The multiscale methods were proposed in the analysis of the magnetic properties of transformer cores in [50]. In order to increase the accuracy of magnetic computations, a higher order FEM [51] and a step-wise method were proposed [52].
In all the presented references, it was assumed that the air gap length or the diamagnetic material dimensions were known. However, during the core assembly, the core experiences different mechanical constraints, which are required to ensure its integrity. This impacts the magnetic properties [53] and changes the core structure near the air gaps. In many cases, these changes are difficult to determine, especially once the core is assembled.
According to the authors’ knowledge, a study of multiple air gaps in the ferrite core transformers, enabling an efficient MFT design for the isolated dc-dc converters, has not been reported. In this article, it is proposed the analysis of the number of air gaps on the equivalent B(H) and the equivalent magnetic permeability. It is considered that different MFTs have a similar probability distribution of the average air gap length. The authors propose an experimental approach to the determination of the equivalent B(H), implying that the physical phenomena as: nonlinearity, fringing effect, structure dissymmetry, technological aspects, etc. are taken into account.
The novel aspects of this work includes:
- Determination of the equivalent B(H) and the equivalent magnetic permeability in a three-phase multi air gap ferrite core MFT.
- Demonstration that the equivalent magnetic permeability and the average air gap length of the multi air gap ferrite core MFT are nonlinear functions of the number of air gaps.
- Proposal of an exponential scaling function, enabling a rapid estimation of the magnetizing inductance based on the ferrite material datasheet only.
The multi air gap medium frequency transformer prototype is presented in Section 2. The measurement of the magnetic flux in the function of the magnetizing current and the calculation of the equivalent B(H) and the equivalent magnetic permeability are presented in Section 3. The finite element simulation of the MFT no load test, using the measured equivalent B(H), is presented in Section 4. The FEM simulation result is compared with an experimental measurement on a 100 kW 1.2 kV 20 kHz dc-dc converter in Section 5. The results are analysed and discussed in Section 6, where the influence of the number of air gaps on the equivalent permeability and the average air gap length are presented. A scaling function enabling a rapid estimation of the magnetizing inductance is proposed.
2. High Power Medium Frequency Transformer
2.1. MFT Prototypes
The authors have developed two three-phase MFT prototypes for a 100 kW 1.2 kV 20 kHz dc-dc converter. The dc-dc converter is presented in details in [54]. The three-phase structure is still novel in the MFT applications with very little demonstrators. The specifications of two MFT prototypes T1 and T2 are presented in Table 1. The MFT T1 can operate in delta and star vector groups whereas the T2 in star only. The winding of both transformers is made of the same litz wire composed of 3870 strands of 0.1 mm diameter.

Table 1.
Specification of the medium frequency transformer prototypes for the nominal operating conditions.
The MFT T2 is presented in Figure 2 and its design is detailed in [55]. In particular, a significant difference between the calculated and measured magnetizing inductance is highlighted. This shows the important influence of the parasitic air gaps on the magnetizing inductance.

Figure 2.
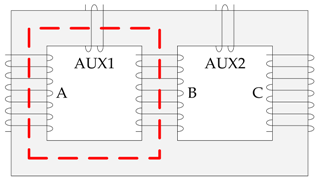
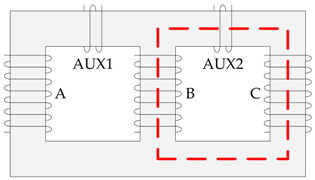
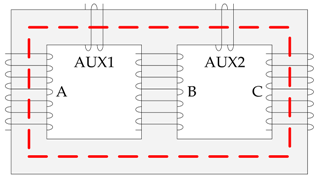
Medium frequency transformer prototype T2 showing primary winding terminals: 1*-1, 2*-2, 3*-3, secondary winding terminals: 4*-4, 5*-5, 6*-6, three columns A, B, C, and additional auxiliary coils AUX1 and AUX2 for flux measurement (blue wire around the yoke).
2.2. Magnetic Core
The magnetic core of the MFT prototypes is made of MnZn ferrite 3C90 from Ferroxcube. The core is assembled with I-cores measuring 25 mm × 25 mm × 100 mm each. The core assembly is presented in Figure 3. In this core design, the I-cores are not interleaved. It can be seen that the core involves multiple parasitic air gaps. Moreover, due to manufacturing tolerances, the I-core is not an ideal rectangular cuboid and its dimensions vary from one sample to another. This causes the non-uniform parasitic air gaps in the core. There are at least two types of parasitic air gaps: perpendicular and longitudinal to the axis of the magnetic flux path. The authors claim that the parasitic air gap size is unpredictable at the industrial design stage and that it cannot be modelled precisely. In Appendix A, some example views of the ferrite core assembly are presented. It can be seen that the air gap length varies from almost zero to about 0.5 mm. Consequently, the use of material datasheet in the calculation of effective magnetizing inductance leads to significant errors. However, the magnetizing inductance or the equivalent B(H) can be measured on the transformer prototype. Such a measurement can be helpful in a new transformer design with a similar core assembly.
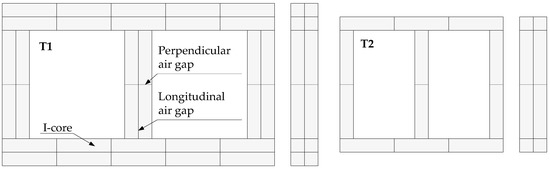
Figure 3.
Medium frequency transformer core assembly composed of elementary I-cores: T1 (left) and T2 (right).
3. Equivalent B(H) Measurement
3.1. Measurement Setup
The nonlinear magnetic properties of core material are represented by the magnetic permeability, which relates the magnetic flux density B with the magnetic field strength H. The nonlinear magnetic properties of a transformer core can be described by the current-dependent flux linkage characteristics Ψ(i) using the experimental approach. From the flux linkage characteristics, the B(H) curve can be determined under certain simplifying assumptions. The measurement of Ψ(i) hysteretic characteristics for inherently asymmetric three-phase transformer with three columns was proposed in [56]. In this approach to determine Ψ(i) characteristics for each winding, only two phases are excited in a special manner.
A dedicated static B(H) measurement setup was developed as presented in Figure 4. It is composed of a high current AC power supply, oscilloscope and probes. The primary and secondary windings of each phase were connected in series in order to achieve a high magnetomotive force (MMF). The windings of two columns were connected in anti-parallel so that their MMFs add together. Two additional auxiliary coils (AUX1 and AUX2) were placed on the yoke allowing the measurement of the magnetic flux in the core (see the blue wire in Figure 2) and minimizing the magnetic coupling in the air. The voltage of the remaining winding (so-called zero-coil) is measured in order to verify that the magnetic flux coupled with this winding is close to zero.
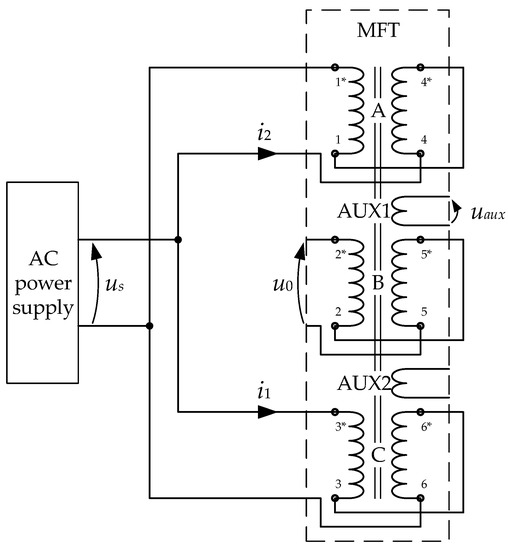
Figure 4.
Circuit diagram of the equivalent B(H) measurement setup where the windings C and A are supplied.
For each MFT prototype, three measurements were performed according to the winding configurations presented in Table 2. The frequency of the power supply in the static B(H) measurement setup was set to 100 Hz. This value was considered in order to minimize the effect of eddy currents (considering a high frequency material as ferrite) and to achieve good performance of the available power supply.

Table 2.
Winding configurations of the equivalent B(H) mearement circuits.
The waveforms of the magnetic flux density B(t) and the magnetic field strength H(t) were calculated with:
where i1 and i2 are the current of the first and second excitation winding respectively, Nexc is the number of turns of each excitation winding, lm is the average magnetic circuit length (visualized in Table 2), uaux is the voltage of the auxiliary coil placed on the yoke, T is the period of the excitation voltage, Φ is the core magnetic flux, Naux is the number of turns of the auxiliary coil, and Ac is the average cross-section of the core.
3.2. Measurement Results
The measured waveforms for the example case where the C and A windings of T2 are supplied are presented in Figure 5a. The measurement was performed with the transformer temperature equal to ambient at 25 °C. It can be observed that the supply voltage is close to sinusoidal. The currents in two excitation windings show the core saturation. Their amplitudes are slightly different due to a difference in winding impedance. The amplitude of the zero-coil voltage is relatively low.
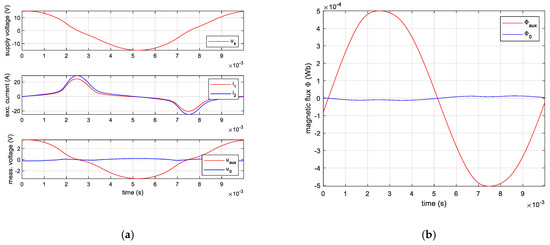
Figure 5.
Waveforms of the T2 supplied with C and A windings: (a) measured supply voltage us, excitation currents i1 (C) and i2 (A), auxiliary coil voltage uaux (AUX1) and zero coil voltage u0 (B); (b) magnetic flux of the auxiliary coil Φaux (AUX1) and magnetic flux of the zero coil Φ0 (B).
Figure 5b presents the waveforms of the magnetic flux calculated according to (2). The Φaux correspond to the main magnetic flux in two side columns and two yokes. The Φ0 corresponds to the magnetic flux in the central column. It is observed that the magnetic flux in the central column is below 5% of the main flux so it seems fair to neglect it.
Thanks to (1) and (3), the magnetic field strength H and the magnetic flux density B are calculated. In Figure 6, the resulting B(H) is plotted for the positive values of H. The B(H) is separated into the upward and downward curves, which are then interpolated with piecewise linear functions in order to facilitate the data analysis. The anhysteretic B(H) curve is calculated as the average of the interpolated upward and downward curves and further filtered to achieve a smooth curve adequate for further processing. Moreover, the coercive field Hc and remanent flux density Br can be captured.
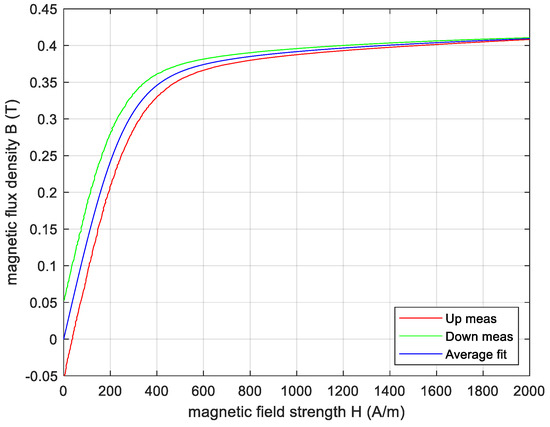
Figure 6.
Measured equivalent B(H) of the T2 supplied with C and A windings: upward curve (red), downward curve (green) and interpolated anhysteretic curve (blue).
3.3. Synthesis of Equivalent B(H) Measurement
The measurement process presented in the previous section was repeated for the MFT T1 and T2 for the cases with the supply of windings: A and B, B and C, and C and A, according to Table 2. The measured equivalent anhysteretic B(H) and relative permeability µr(H) are presented in Figure 7. The 3C90 datasheet curves [57] are plotted for comparison. As expected, a significant difference between the datasheet and the measurement is observed. There is a difference between T1 and T2 since they have a different core assembly, T1 having more parasitic air gaps than T2 (see Figure 3). For each MFT, the equivalent B(H) differs slightly for different measurement circuits. This proves that the parasitic air gaps are randomly distributed in the core assembly. For each transformer, the authors arbitrarily select the solid line curve (CA) as the reference B(H) for the whole core.
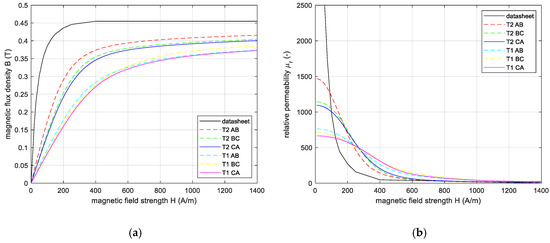
Figure 7.
Synthesis of equivalent B(H) measurement: (a) equivalent anhysteretic B(H); (b) equivalent relative permeability µr; curves based on 3C90 datasheet (black) and measurement: T2 supply of A and B windings (red), T2 supply of B and C windings (green), T2 supply of C and A windings (blue)—the same as in Figure 6, T1 supply of A and B windings (cyan), T1 supply of B and C windings (yellow), T1 supply of C and A windings (magenta).
4. Finite Element Simulation
4.1. Finite Element Model
A 3D MFT T2 model was developed in Ansys Maxwell. A simplified transformer geometry was considered. The model was divided into three computational domains as shown in Figure 8. The Ω1 domain is the volume of the windings, the Ω2 domain is the volume of the core, and the Ω3 domain consists of the air surrounding the MFT. In this model, it is assumed that the magnetic core is homogenized. It means that the core components: ferrite, air gaps and also glue, impregnation resin, etc. form a homogenous material. In a similar manner, the winding is also homogenized.
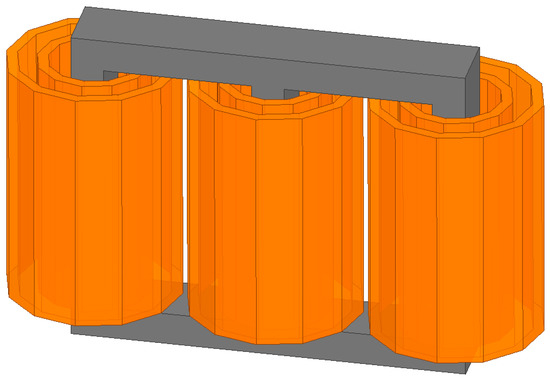
Figure 8.
3D MFT model divided into three computational domains: Ω1 volume of the windings (orange), Ω2 volume of the homogenized core (grey) and Ω3 air surrounding the MFT (white).
The Maxwell’s equations for the defined domains have the form:
where is the electrical conductivity tensor:
The permeability tensor, which for nonlinear properties describes the relation between dB and dH in the constitutive equation, can be expressed as:
where is the magnetic permeability tensor:
It was assumed that the ferrite core has isotropic electrical and magnetic properties. Hence, the electrical conductivity and magnetic permeability tensors have the form:
where σc = 0.25 S/m (at 25 °C) and μc = dB/dH are defined in the previous section (Figure 7b, curve T2 CA). In Ansys Maxwell, the material conductivity enables the calculation of eddy current effects. However, it can be noticed that the ferrite conductivity is low so the eddy current effects do not have a significant impact on the magnetic field and core power loss.
4.2. Magnetic Simulations
In order to perform a magnetic transient simulation, the finite element model was coupled with an equivalent circuit model. A no load test was considered, as presented in Figure 9. The coupling between the finite element model and the equivalent circuit model is done through the nonlinear inductances L1, L2 and L3, which correspond to the primary winding. The voltage sources model the VSC square output voltage, and Rp is the primary winding resistance.
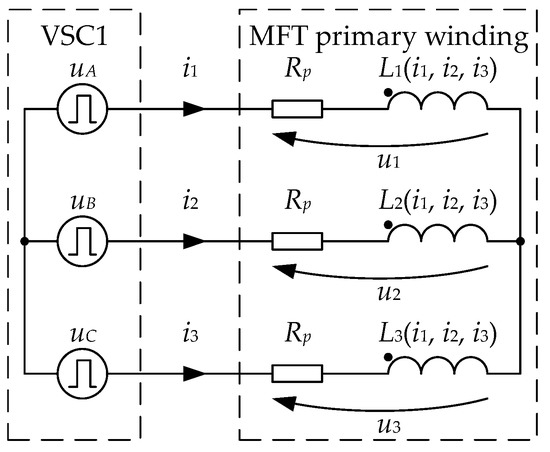
Figure 9.
MFT no load test equivalent circuit model coupled with the finite element model through the nonlinear inductances L1, L2 and L3.
The magnetic transient simulation result is presented in Figure 10. The MFT phase voltage is presented, being a typical VSC output voltage waveform. The MFT primary current is presented in steady-state. This result will be further used to validate the measured equivalent B(H).
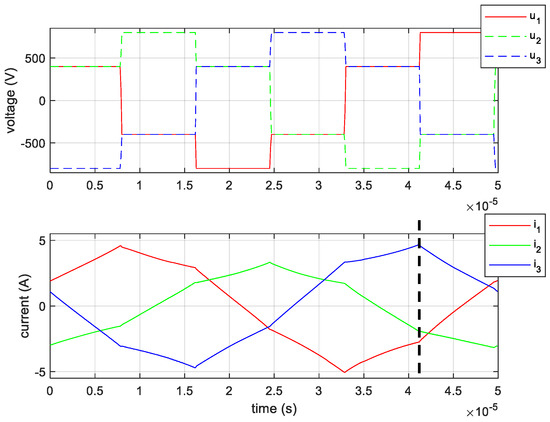
Figure 10.
MFT no load test magnetic transient simulation result: primary phase voltage (top) and primary current (bottom); the dashed vertical line indicates the time instant for the magnetostatic simulation.
In Figure 11, the magnetostatic simulation result corresponding to the time instant defined by the dashed line in Figure 10 is presented. The magnitude of the flux density is plotted on the core surface and the maximum value of 0.27 T is observed, as expected. In Figure 12, the magnetic field strength and the magnetic flux density are plotted along the path defined by the dashed line in Figure 11. The different values of quotient B/(µ0H) in the central and the right column can be observed due to the nonlinearity of the B(H) curve.
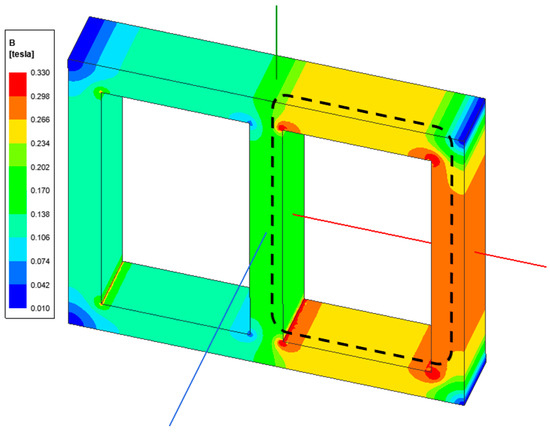
Figure 11.
Magnetic flux density B magnitude on the core surface with the current excitation i1 = −2.76 A, i2 = −1.93 A, i3 = 4.69 A; the dashed line indicates the magnetic flux path in the centre of the core.
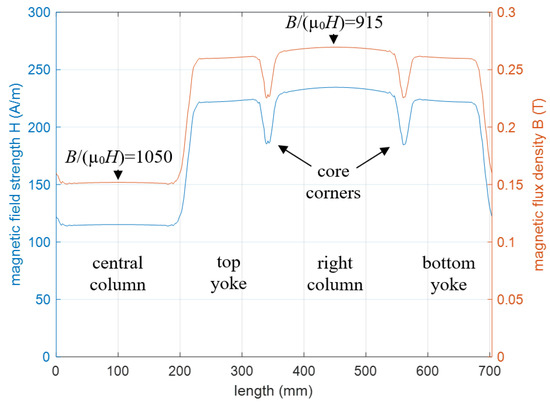
Figure 12.
Magnetic field strength H and magnetic flux density B along the path in the centre of the core passing through the central column, top yoke, right column, and bottom yoke; the values of static permeability B/(µ0H) are presented.
5. Experimental Verifications
5.1. Converter Test Bench
The power converter test bench was developed for the 100 kW dc-dc converter, as presented in Figure 13. A MFT no load test was considered in order to evaluate the magnetizing inductance. In the no load test, the VSC1 operates normally with 1200 Vdc input voltage and the AC terminals of the VSC2 are disconnected. The circuit diagram of the experimental setup is equivalent to the one used in the simulation that is presented in Figure 9. The test was performed at an ambient temperature of 25 °C. The MFT temperature was measured nearly equal to the ambient as the test lasts for a few minutes only.

Figure 13.
100 kW three-phase isolated dc-dc converter test bench implementation.
5.2. No Load Test Experimental Results
The measured waveform of the MFT T2 no load current is presented in Figure 14. The simulated no load current from the previous section is plotted for the comparison. Generally, quite a good fit between the simulation and the measurement is observed. Some minor differences are discussed hereafter.
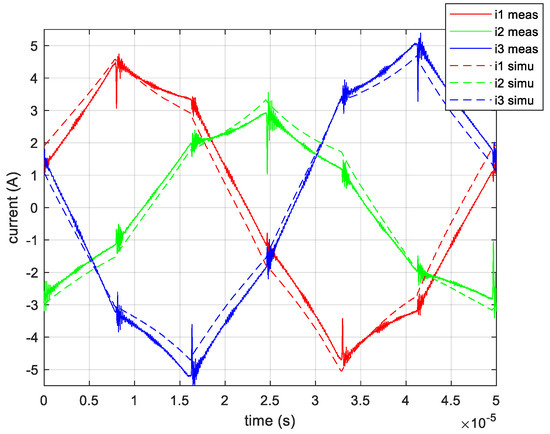
Figure 14.
MFT T2 no load test primary current: experimental result (solid line), magnetic transient simulation result (dashed line).
There are some high frequency oscillations present in the measurement. They are due to the parasitic capacitance of the windings that have not been modelled. This could be improved by adding the winding self and mutual capacitances into the model. However, the simulation time would increase significantly.
There are some differences in the current amplitude of different phases. As it has been presented in Figure 7, the B(H) is not strictly the same for the whole core. Since in the simulation, the authors have assumed a single equivalent B(H), then it seems normal to observe some differences in the measured currents.
Moreover, there might be some differences due to the fact that the simulation model assumes the anhysteretic B(H). In Figure 6, one can see that the measured equivalent B(H) is hysteretic, thus it may influence the shape of the current waveform, in particular, the corresponding ascending and descending slopes of the current.
Finally, the RMS current error is within 10% and the authors consider this acceptable. If the datasheet B(H) was used (Figure 7), then the RMS current error would reach approximately 500%. This experimental result proves the validity of the measured equivalent B(H).
6. Scaling of Relative Permeability
The approach presented in the previous paragraphs has limited usage in the MFT design process since it is based on the measurement on a physical device. This limits the practical usage to post-manufacturing analysis or to a new design of a similar transformer. In this section, an approach based on a simple count of perpendicular parasitic air gaps is proposed.
In the MFT design process from scratch, when evaluating the performance of isolated dc-dc converters, one is usually interested in the magnetizing inductance at the nominal B(H) operating point. This is usually below the B(H) saturation, so the anhysteretic curve from Figure 7 can be linearized as presented in Figure 15.
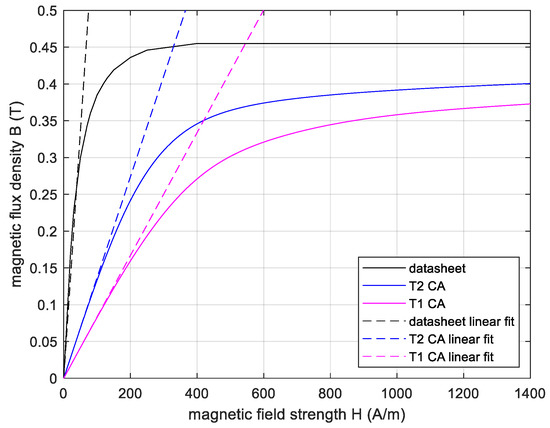
Figure 15.
Equivalent anhysteretic B(H): datasheet and measurement (solid line), linear interpolation (dashed line).
From Figure 3, we can count the number of perpendicular parasitic air gaps along the magnetic path. This equals to 10 and 14 for T2 and T1 respectively. The core used for the datasheet measurement had zero air gaps. The value of datasheet linearized relative permeability, which equals µr0 = 5300, is read from Figure 15. Thus, the equivalent relative permeability ratio Kµ of the multi air gap core can be calculated with:
where µr is the equivalent relative permeability defined in Figure 15 for T1 or T2. The equivalent relative permeability ratio is plotted in Figure 16 as a function of a number of parasitic air gaps.
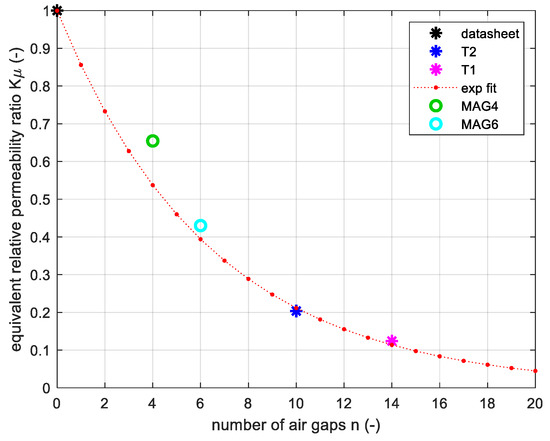
Figure 16.
Equivalent relative permeability ratio Kµ in the function of a number of parasitic air gaps n: datasheet, T2 and T1 measurement (stars), exponential interpolation (red dashed line), and single-phase multi air gap transformer MAG4 and MAG6 measurement (circles).
In addition, an exponential interpolation is proposed allowing to estimate the equivalent relative permeability for any high power ferrite core MFT with a similar core assembly. The exponential interpolation function is defined as:
where n is the number of perpendicular parasitic air gaps along the magnetic flux path.
This function was validated with the experimental B(H) measurement on two single-phase multi air gap (MAG) transformers presented in Appendix B. The MAG4 transformer has four air gaps and MAG6 has six air gaps. Both use the same I-cores as T1 and T2. The resulting ratios are displayed in Figure 16 and it can be seen that for MAG4 the ratio is slightly higher than the exponential interpolation. This is normal because for this transformer the I-cores were carefully selected to minimize the parasitic air gaps and the core assembly is simpler compared to the three-phase MFT. However, a general trend of the equivalent relative permeability ratio is clearly observed even if the four MFT prototypes involve different technologies and different manufacturers.
Furthermore, a simple reluctance model of the magnetic core neglecting the fringing effect is considered according to [35]. The total magnetic circuit reluctance can be related to the sum of the I-core and air gap reluctances as:
where lm is the average magnetic circuit length, lI is the length of the I-core, la is the average air gap length, and Ac is the average cross-section of the core. Assuming that the average magnetic circuit length lm is equal to n∙lI, then it can be found the relative average air gap length la/lm defined as:
Considering an ideal core assembly, where the average air gap length la equals n times the known individual air gap length lg, the relative average air gap length la/lm is a linear function of n:
In Figure 17, these linear functions are presented for four transformers T2, T1, MAG4, and MAG6. It was verified that the individual air gap length lg changes between prototypes. However, considering the proposed exponential interpolation (11), the effective relative average air gap length is a nonlinear function of n as presented in Figure 17. This is due to the fact that the I-core is not an ideal rectangular cuboid and its dimensions vary from one sample to another. As a consequence, the mechanical assembly of the core gets more difficult when a large number of I-cores is assembled.
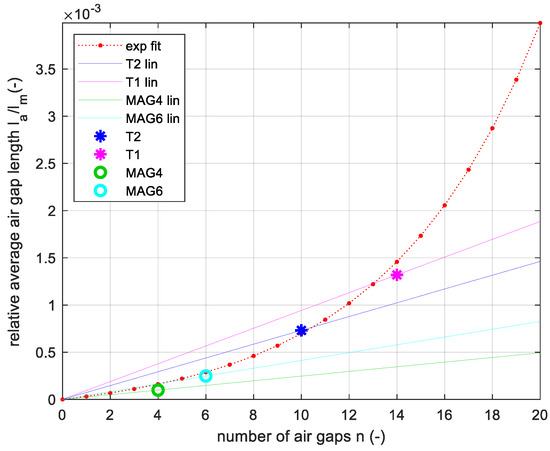
Figure 17.
Relative average air gap length la/lm in the function of a number of parasitic air gaps n: T2, T1, MAG4 and MAG6 measurement (stars/circle), the corresponding idealized reluctance model (solid lines), and the relative average air gap length calculated based on the proposed exponential interpolation (red dashed line).
The proposed approach can be used in scaling the datasheet B(H) for a finite element simulation, in the rapid estimation of transformer magnetizing inductance or in evaluating the size of the average air gap length. The magnetizing inductance can be estimated based on the magnetic reluctance model according to:
where N is the primary/secondary number of turns. It shall be mentioned that the proposed estimation is meant to provide an order of magnitude of the magnetizing inductance. This shall be sufficient when evaluating the performance of isolated dc-dc converters. However, the proposed scaling function could be further validated with a large number of MFT prototypes with different types of I-cores and a different number of parasitic air gaps.
7. Conclusions
The analysis of the effective permeability and average air gap length in multi air gap ferrite core three-phase medium frequency transformer was presented. The calculation of the magnetizing inductance in multi air gap ferrite core MFT based on core material datasheet leads to significant errors. This may impact the design of isolated dc-dc converters as the magnetizing inductance influences their performance.
The measurement of the equivalent B(H) and the equivalent permeability for two three-phase MFT prototypes was presented. The measured equivalent B(H) was used in a finite element simulation, giving good results when compared to a 100 kW dc-dc converter no load operation. The use of the anhysteretic B(H) gives satisfactory results within 10% error compared to the experiment.
This article demonstrates that the equivalent magnetic permeability and the average air gap length of the multi air gap ferrite core MFT are nonlinear functions of the number of air gaps. An empirical scaling function is proposed for the rapid estimation of the magnetizing inductance in the multi air gap MFT. In fact, the relative average air gap length increases with the number of parasitic air gaps due to the increasing difficulty in mechanical assembly of the core. The proposed scaling function can be used in the design of isolated dc-dc converters using 25 mm × 25 mm × 100 mm I-cores or similar, based on the core material datasheet and a number of parasitic air gaps.
The measured or scaled equivalent B(H) can also be used in the equivalent circuit simulation instead of finite element simulation. This would allow more convenient simulations as well including the winding capacitance. The measured B(H) can be further utilized in the simulations taking into account the hysteresis. This work shall be further extended taking into account the influence of the temperature since the ferrite relative permeability depends on the temperature. The proposed scaling function could be further validated with a large number of MFT prototypes with different types of I-cores and a different number of parasitic air gaps in order to determine the uncertainty range. The experimental validation of the influence of the magnetizing inductance on the performance of three-phase isolated dc-dc converters is recommended.
Author Contributions
Conceptualization, P.D. and A.W.; methodology, P.D., A.W. and M.M.; software, P.D.; validation, P.D.; formal analysis, P.D., A.W. and M.M.; investigation, P.D., A.W. and M.M.; resources, P.D., A.W. and M.M.; data curation, P.D.; writing—original draft preparation, P.D., A.W. and M.M; writing—review and editing, P.D., A.W., M.M. and F.S.; visualization, P.D., A.W. and M.M; supervision, A.W., M.M., B.L., M.M.-G.; project administration, B.L. and M.M.-G.; funding acquisition, M.M.-G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a grant overseen by the French National Research Agency (ANR) as part of the “Investissements d’Avenir” Program (ANE-ITE-002-01) and the LINTE2 Laboratory at the Gdansk University of Technology.
Acknowledgments
The authors would like to thank Caroline Stackler, Martin Guillet and Alexis Fouineau for their valuable support in writing this article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In Figure A1, two example views of the ferrite core assembly are presented where the perpendicular and longitudinal parasitic air gaps can be observed up to about 0.5 mm. In each assembly, 4 randomly selected I-cores are aligned along a calliper on a flat surface. The I-cores are assembled tight together so that even if there is an air gap on the visible surface then there is somewhere a direct contact between the neighbour I-cores. In the 3-phase MFT core assembly, composed of tens of I-cores, the air gaps are even larger due to the cumulating I-core misalignments.

Figure A1.
Two assemblies of 4 randomly selected 3C90 ferrite I-cores showing the perpendicular parasitic air gap and the longitudinal parasitic air gap measuring up to about 0.5 mm.
Appendix B
The core assemblies of the single-phase multi air gap MFTs are presented in Figure A2. The MAG4 has 4 and the MAG6 has 6 perpendicular parasitic air gaps along the magnetic flux path. The MAG4 is detailed in [58].
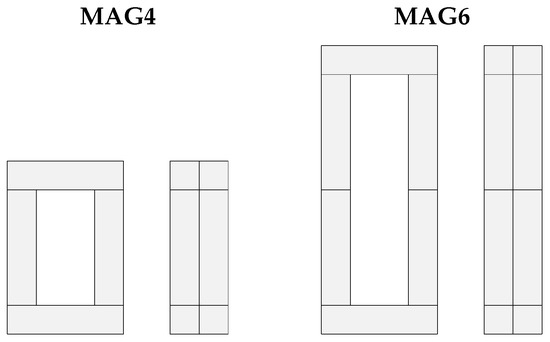
Figure A2.
Single-phase multi air gap MFT core assembly: MFT4 with 4 air gaps (left) and MFT6 with 6 air gaps (right).
References
- Yang, B.; Lee, F.C.; Zhang, A.J. Guisong Huang LLC resonant converter for front end DC/DC conversion. In Proceedings of the APEC. Seventeenth Annual IEEE Applied Power Electronics Conference and Exposition (Cat. No.02CH37335), Dallas, TX, USA, 10–14 March 2002; Volume 2, pp. 1108–1112. [Google Scholar]
- De Doncker, R.W.A.A.; Divan, D.M.; Kheraluwala, M.H. A three-phase soft-switched high-power-density DC/DC converter for high-power applications. IEEE Trans. Ind. Appl. 1991, 27, 63–73. [Google Scholar] [CrossRef]
- Schwarz, F.C.; Klaassens, J.B. A Controllable 45-kW Current Source for DC Machines. IEEE Trans. Ind. Appl. 1979, IA-15, 437–444. [Google Scholar] [CrossRef]
- Mweene, L.H.; Wright, C.A.; Schlecht, M.F. A 1 kW 500 kHz front-end converter for a distributed power supply system. IEEE Trans. Power Electron. 1991, 6, 398–407. [Google Scholar] [CrossRef]
- Adamowicz, M. Power Electronics Building Blocks for implementing Smart MV/LV Distribution Transformers for Smart Grid. Acta Energetica 2014, 4, 6–13. [Google Scholar] [CrossRef]
- Walker, G.R.; Sernia, P.C. Cascaded DC-DC converter connection of photovoltaic modules. IEEE Trans. Power Electron. 2004, 19, 1130–1139. [Google Scholar] [CrossRef]
- Dincan, C.G.; Kjaer, P.; Chen, Y.-H.; Sarrá-Macia, E.; Munk-Nielsen, S.; Bak, C.L.; Vaisambhayana, S. Design of a High-Power Resonant Converter for DC Wind Turbines. IEEE Trans. Power Electron. 2019, 34, 6136–6154. [Google Scholar] [CrossRef]
- Du, Y.; Lukic, S.; Jacobson, B.; Huang, A. Review of high power isolated bi-directional DC-DC converters for PHEV/EV DC charging infrastructure. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 553–560. [Google Scholar]
- Ruffo, R.; Khalilian, M.; Cirimele, V.; Guglielmi, P.; Cesano, M. Theoretical and experimental comparison of two interoperable dynamic wireless power transfer systems for electric vehicles. In Proceedings of the 2017 IEEE Southern Power Electronics Conference (SPEC), Puerto Varas, Chile, 4–7 December 2017; pp. 1–6. [Google Scholar]
- Garcia-Bediaga, A.; Villar, I.; Rujas, A.; Etxeberria-Otadui, I.; Rufer, A. Analytical Models of Multiphase Isolated Medium-Frequency DC–DC Converters. IEEE Trans. Power Electron. 2017, 32, 2508–2520. [Google Scholar] [CrossRef]
- Lagier, T. Convertisseurs Continu-Continu Pour Les Réseaux d’électricité à Courant Continu. Doctoral Thesis, INPT, Toulouse, France, 2016. [Google Scholar]
- Xue, J.; Wang, F.; Boroyevich, D.; Shen, Z. Single-phase vs. three-phase high density power transformers. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 4368–4375. [Google Scholar]
- Lee, Y.; Vakil, G.; Watson, A.J.; Wheeler, P.W. Geometry optimization and characterization of three-phase medium frequency transformer for 10 kVA Isolated DC-DC converter. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 511–518. [Google Scholar]
- Noah, M.; Kimura, S.; Endo, S.; Yamamoto, M.; Imaoka, J.; Umetani, K.; Martinez, W. A novel three-phase LLC resonant converter with integrated magnetics for lower turn-off losses and higher power density. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 322–329. [Google Scholar]
- Soltau, N.; Stagge, H.; De Doncker, R.W.; Apeldoorn, O. Development and demonstration of a medium-voltage high-power DC-DC converter for DC distribution systems. In Proceedings of the 2014 IEEE 5th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Galway, Ireland, 24–27 June 2014; pp. 1–8. [Google Scholar]
- Kim, E.-S.; Oh, J.-S. High-Efficiency Bidirectional LLC Resonant Converter with Primary Auxiliary Windings. Energies 2019, 12, 4692. [Google Scholar] [CrossRef]
- Bouvier, Y.E.; Serrano, D.; Borović, U.; Moreno, G.; Vasić, M.; Oliver, J.A.; Alou, P.; Cobos, J.A.; Carmena, J. ZVS Auxiliary Circuit for a 10 kW Unregulated LLC Full-Bridge Operating at Resonant Frequency for Aircraft Application. Energies 2019, 12, 1850. [Google Scholar] [CrossRef]
- Morel, F.; Stackler, C.; Ladoux, P.; Fouineau, A.; Wallart, F.; Evans, N.; Dworakowski, P. Power electronic traction transformers in 25 kV/50 Hz systems: Optimisation of DC/DC Isolated Converters with 3.3 kV SiC MOSFETs. In Proceedings of the PCIM Europe 2019; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 7–9 May 2019; pp. 1–8. [Google Scholar]
- Dujic, D.; Steinke, G.K.; Bellini, M.; Rahimo, M.; Storasta, L.; Steinke, J.K. Characterization of 6.5 kV IGBTs for High-Power Medium-Frequency Soft-Switched Applications. IEEE Trans. Power Electron. 2014, 29, 906–919. [Google Scholar] [CrossRef]
- Huber, J.E.; Rothmund, D.; Wang, L.; Kolar, J.W. Full-ZVS modulation for all-SiC ISOP-type isolated front end (IFE) solid-state transformer. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–8. [Google Scholar]
- Mogorovic, M.; Dujic, D. Medium Frequency Transformer Design and Optimization. In Proceedings of the PCIM Europe 2017; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 16–18 May 2017; pp. 1–8. [Google Scholar]
- Everts, J. Design and Optimization of an Efficient (96.1%) and Compact (2 kW/dm3) Bidirectional Isolated Single-Phase Dual Active Bridge AC-DC Converter. Energies 2016, 9, 799. [Google Scholar] [CrossRef]
- Mogorovic, M.; Dujic, D. 100 kW, 10 kHz Medium-Frequency Transformer Design Optimization and Experimental Verification. IEEE Trans. Power Electron. 2019, 34, 1696–1708. [Google Scholar] [CrossRef]
- Villar, I.; Mir, L.; Etxeberria-Otadui, I.; Colmenero, J.; Agirre, X.; Nieva, T. Optimal design and experimental validation of a Medium-Frequency 400 kVA power transformer for railway traction applications. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 684–690. [Google Scholar]
- Ortiz, G.; Biela, J.; Bortis, D.; Kolar, J.W. 1 Megawatt, 20 kHz, isolated, bidirectional 12 kV to 1.2 kV DC-DC converter for renewable energy applications. In Proceedings of the 2010 International Power Electronics Conference—ECCE ASIA, Sapporo, Japan, 21–24 June 2010; pp. 3212–3219. [Google Scholar]
- Villar, I.; Garcia-Bediaga, A.; Viscarret, U.; Etxeberria-Otadui, I.; Rufer, A. Proposal and validation of medium-frequency power transformer design methodology. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 3792–3799. [Google Scholar]
- Hurley, W.G.; Merkin, T.; Duffy, M. The Performance Factor for Magnetic Materials Revisited: The Effect of Core Losses on the Selection of Core Size in Transformers. IEEE Power Electron. Mag. 2018, 5, 26–34. [Google Scholar] [CrossRef]
- Ruiz-Robles, D.; Ortíz-Marín, J.; Venegas-Rebollar, V.; Moreno-Goytia, E.; Granados-Lieberman, D.; Rodríguez-Rodriguez, J. Nanocrystalline and Silicon Steel Medium-Frequency Transformers Applied to DC-DC Converters: Analysis and Experimental Comparison. Energies 2019, 12, 2062. [Google Scholar] [CrossRef]
- Ruiz-Robles, D.; Venegas-Rebollar, V.; Anaya-Ruiz, A.; Moreno-Goytia, E.L.; Rodríguez-Rodríguez, J.R. Design and Prototyping Medium-Frequency Transformers Featuring a Nanocrystalline Core for DC–DC Converters. Energies 2018, 11, 2081. [Google Scholar] [CrossRef]
- Bahmani, M.A. Design considerations of medium-frequency power transformers in HVDC applications. In Proceedings of the 2017 Twelfth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 11–13 April 2017; pp. 1–6. [Google Scholar]
- Stojadinović, M.; Biela, J. Modelling and Design of a Medium Frequency Transformer for High Power DC-DC Converters. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018 -ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 1103–1110. [Google Scholar]
- Stackler, C.; Morel, F.; Ladoux, P.; Fouineau, A.; Wallart, F.; Evans, N. Optimal sizing of a power electronic traction transformer for railway applications. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 1380–1387. [Google Scholar]
- Keuck, L.; Schafmeister, F.; Boecker, J.; Jungwirth, H.; Schmidhuber, M. Computer-Aided Design and Optimization of an Integrated Transformer with Distributed Air Gap and Leakage Path for LLC Resonant Converter. In Proceedings of the PCIM Europe 2019; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 7–9 May 2019; pp. 1–8. [Google Scholar]
- Noah, M.; Endo, S.; Kimura, S.; Yamamoto, M.; Imaoka, J.; Umetani, K.; Hiraki, E. An investigation into a slight-variation of the transformer effective permeability in LLC resonant converter. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017. [Google Scholar]
- Ayachit, A.; Kazimierczuk, M.K. Sensitivity of effective relative permeability for gapped magnetic cores with fringing effect. IET Circuits Devices Syst. 2017, 11, 209–215. [Google Scholar] [CrossRef]
- Salas, R.A.; Pleite, J. Simulation of the Saturation and Air-Gap Effects in a POT Ferrite Core With a 2-D Finite Element Model. IEEE Trans. Magn. 2011, 47, 4135–4138. [Google Scholar] [CrossRef]
- Balakrishnan, A.; Joines, W.T.; Wilson, T.G. Air-gap reluctance and inductance calculations for magnetic circuits using a Schwarz-Christoffel transformation. IEEE Trans. Power Electron. 1997, 12, 654–663. [Google Scholar] [CrossRef]
- Stenglein, E.; Albach, M. A Novel Approach to Calculate the Reluctance of Air-Gaps in Ferrite Cores. In Proceedings of the PCIM Europe 2017; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 16–18 May 2017; pp. 1–8. [Google Scholar]
- Ayachit, A.; Kazimierczuk, M.K. Steinmetz Equation for Gapped Magnetic Cores. IEEE Magn. Lett. 2016, 7, 1–4. [Google Scholar] [CrossRef]
- Komma, T.; Gueldner, H. The effect of different air-gap positions on the winding losses of modern planar ferrite cores in switch mode power supplies. In Proceedings of the Automation and Motion 2008 International Symposium on Power Electronics, Electrical Drives, Ischia, Italy, 11–13 June 2008; pp. 632–637. [Google Scholar]
- Albach, M.; Rossmanith, H. The influence of air gap size and winding position on the proximity losses in high frequency transformers. In Proceedings of the 2001 IEEE 32nd Annual Power Electronics Specialists Conference (IEEE Cat. No.01CH37230), Vancouver, BC, Canada, 17–21 June 2001; Volume 3, pp. 1485–1490. [Google Scholar]
- Zurek, S. FEM Simulation of Effect of Non-Uniform Air Gap on Apparent Permeability of Cut Cores. IEEE Trans. Magn. 2012, 48, 1520–1523. [Google Scholar] [CrossRef]
- Stenglein, E.; Kuebrich, D.; Albach, M. Analytical calculation of the current depending inductance of a stepped air gap inductor. In Proceedings of the 2016 18th European Conference on Power Electronics and Applications (EPE’16 ECCE Europe), Karlsruhe, Germany, 5–9 September 2016; pp. 1–10. [Google Scholar]
- Lesniewska, E.; Jalmuzny, W. Influence of the number of core air gaps on transient state parameters of TPZ class protective current transformers. IET Sci. Meas. Technol. 2009, 3, 105–112. [Google Scholar] [CrossRef]
- Nakata, T.; Takahashi, N.; Kawase, Y. Magnetic performance of step-lap joints in distribution transformer cores. IEEE Trans. Magn. 1982, 18, 1055–1057. [Google Scholar] [CrossRef]
- Pietruszka, M.; Napieralska-Juszczak, E. Lamination of T-joints in the transformer core. IEEE Trans. Magn. 1996, 32, 1180–1183. [Google Scholar] [CrossRef]
- Hihat, N.; Napieralska-Juszczak, E.; Lecointe, J.-P.; Sykulski, J.K.; Komeza, K. Equivalent Permeability of Step-Lap Joints of Transformer Cores: Computational and Experimental Considerations. IEEE Trans. Magn. 2011, 47, 244–251. [Google Scholar] [CrossRef]
- Gyselinck, J.; Melkebeek, J. Two-dimensional finite element modelling of overlap joints in transformer cores. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2001, 20, 253–268. [Google Scholar] [CrossRef]
- Shin, P.S.; Lee, J. Magnetic field analysis of amorphous core transformer using homogenization technique. IEEE Trans. Magn. 1997, 33, 1808–1811. [Google Scholar] [CrossRef]
- Hollaus, K.; Schöbinger, M. Multiscale finite element method for perturbation of laminated structures. In Proceedings of the 2017 International Conference on Electromagnetics in Advanced Applications (ICEAA), Verona, Italy, 11–15 September 2017; pp. 1262–1263. [Google Scholar]
- Hauck, A.; Ertl, M.; Schöberl, J.; Kaltenbacher, M. Accurate magnetostatic simulation of step-lap joints in transformer cores using anisotropic higher order FEM. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2013, 32, 1581–1595. [Google Scholar] [CrossRef]
- Da Luz, M.V.F.; Dular, P.; Leite, J.V.; Kuo-Peng, P. Modeling of Transformer Core Joints via a Subproblem FEM and a Homogenization Technique. IEEE Trans. Magn. 2014, 50, 1009–1012. [Google Scholar] [CrossRef]
- Penin, R.; Parent, G.; Lecointe, J.-P.; Brudny, J.-F.; Belgrand, T. Impact of Mechanical Deformations of Transformer Corners on Core Losses. IEEE Trans. Magn. 2015, 51, 1–5. [Google Scholar] [CrossRef]
- Lagier, T.; Chédot, L.; Ghossein, L.; Wallart, F.; Lefebvre, B.; Dworakowski, P.; Mermet-Guyennet, M.; Buttay, C. A 100 kW 1.2 kV 20 kHz DC-DC converter prototype based on the Dual Active Bridge topology. In Proceedings of the 2018 IEEE International Conference on Industrial Technology (ICIT), Lyon, France, 20–22 February 2018; pp. 559–564. [Google Scholar]
- Dworakowski, P.; Wilk, A.; Michna, M.; Lefebvre, B.; Lagier, T. 3-phase medium frequency transformer for a 100 kW 1.2 kV 20 kHz Dual Active Bridge converter. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; Volume 1, pp. 4071–4076. [Google Scholar]
- Fuchs, E.F.; You, Y. Measurement of λ-1 characteristics of asymmetric three-phase transformers and their applications. IEEE Power Eng. Rev. 2002, 22, 69–70. [Google Scholar] [CrossRef]
- Ferroxcube 3C90 Material Specification. Available online: https://www.ferroxcube.com/upload/media/product/file/MDS/3c90.pdf (accessed on 19 January 2020).
- Wilk, A.; Michna, M.; Dworakowski, P.; Lefebvre, B. Influence of air gap size on magnetizing current and power losses in ferrite core transformers—Experimental investigations. In Proceedings of the EPNC 2018 Twenty-Fifth Symposium on Electromagnetic Phenomena in Nonlinear Circuits, Arras, France, 26–29 June 2018. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).