Synthesis Gas Composition Prediction for Underground Coal Gasification Using a Thermochemical Equilibrium Modeling Approach
Abstract
1. Introduction
2. Materials and Methods
- -
- reactions are considered not to vary in time and space (steady-state batch reactions),
- -
- reactions are fast enough to reach an equilibrium state (infinite residence time),
- -
- homogeneous mixing with uniform pressure and temperature are assumed, although different hydrodynamics are observed in practice,
- -
- kinetic and potential energies are neglected,
- -
- ideal gas behavior of the gas phase,
- -
- pyrolysis is considered as a single step reaction producing gas,
- -
- the reactor is considered adiabatic,
- -
- the produced gas does not contain any oxygen, and
- -
- solely major species compose the produced synthesis gas (e.g., CO, CO2, H2, CH4, N2 and H2O).
- -
- temperature of the products is equal to the gasification temperature,
- -
- oxygen is completely consumed,
- -
- the final synthesis gas mixture is in equilibrium and homogeneous,
- -
- all involved chemical reactions can reach an equilibrium state,
- -
- coal is composed of C, H, O, N and S,
- -
- solid gasification products include only char, which is entirely composed of carbon, and,
- -
- ash and tars are not considered in the simulations.
Minimisation Problem of the Thermodynamic Equilibrium
3. Results and Discussion
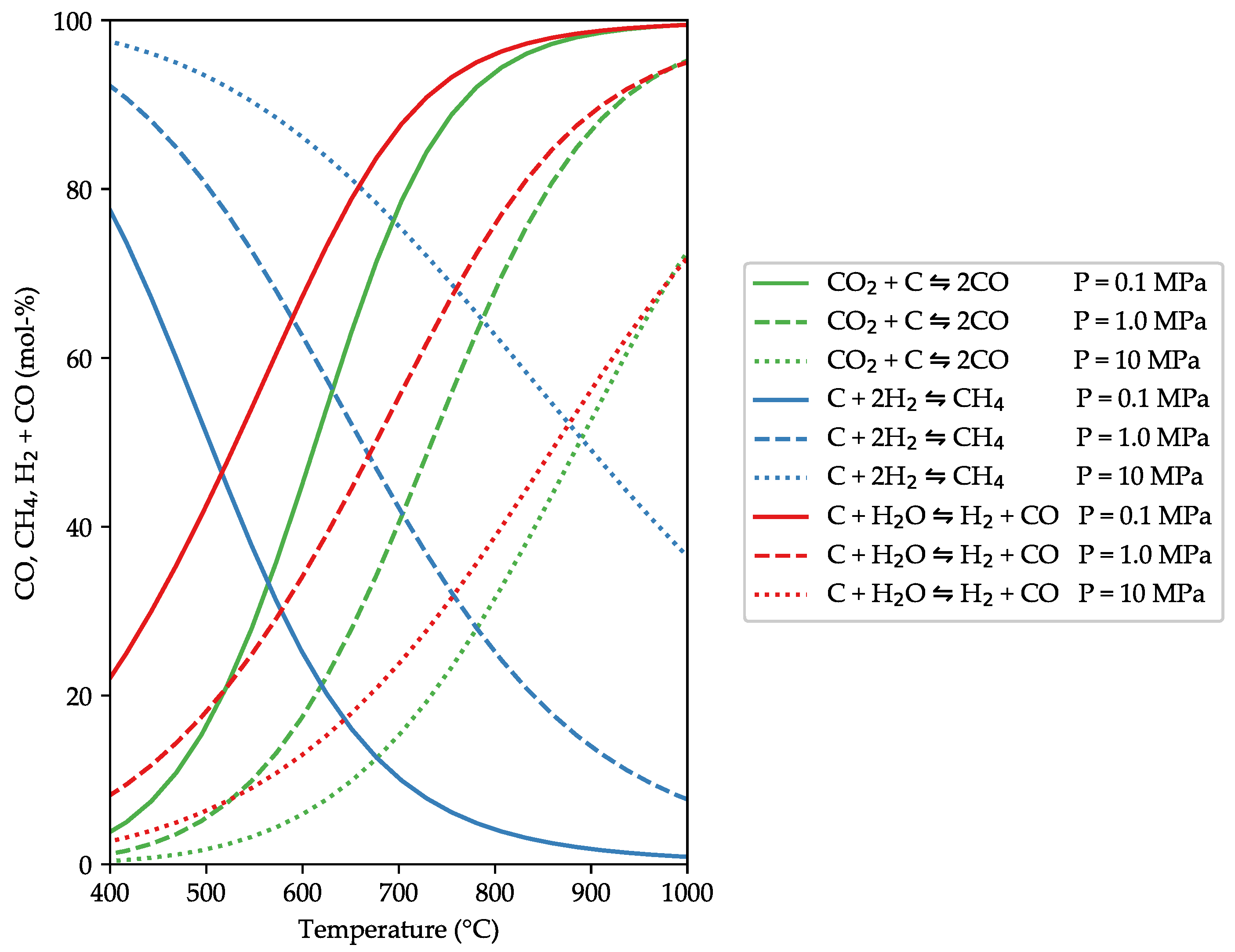
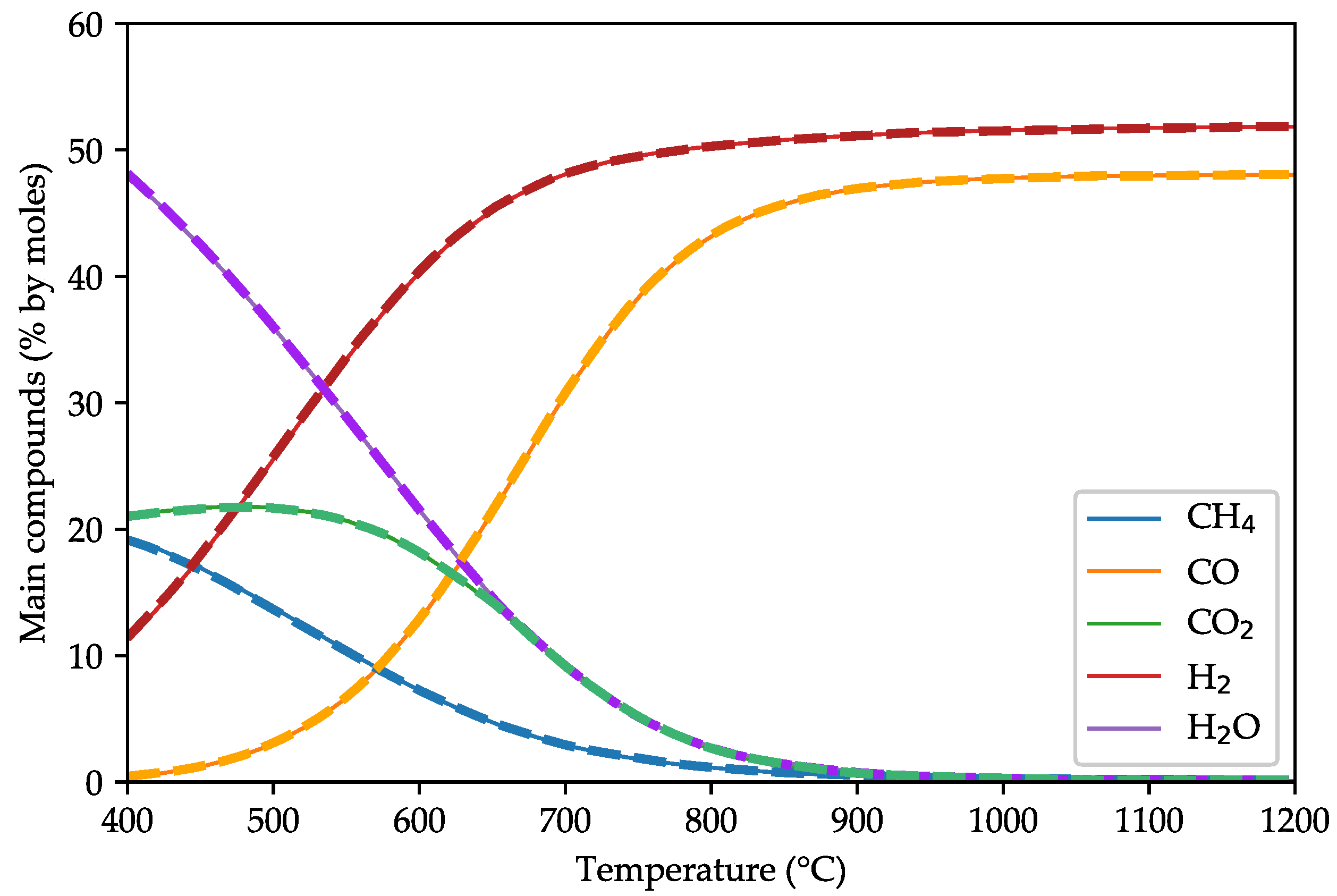
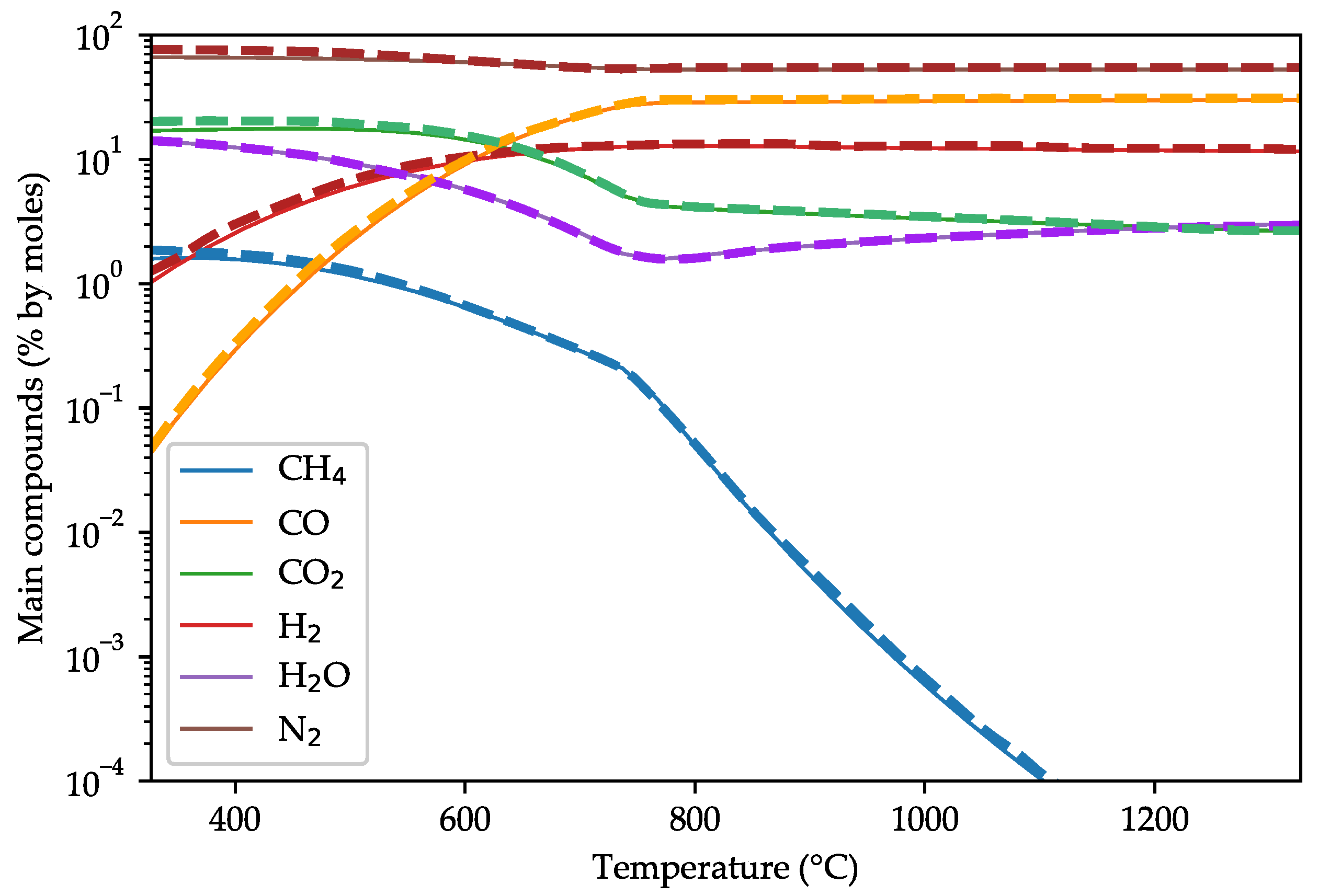
3.1. Model Validation against Other Equilibrium Models
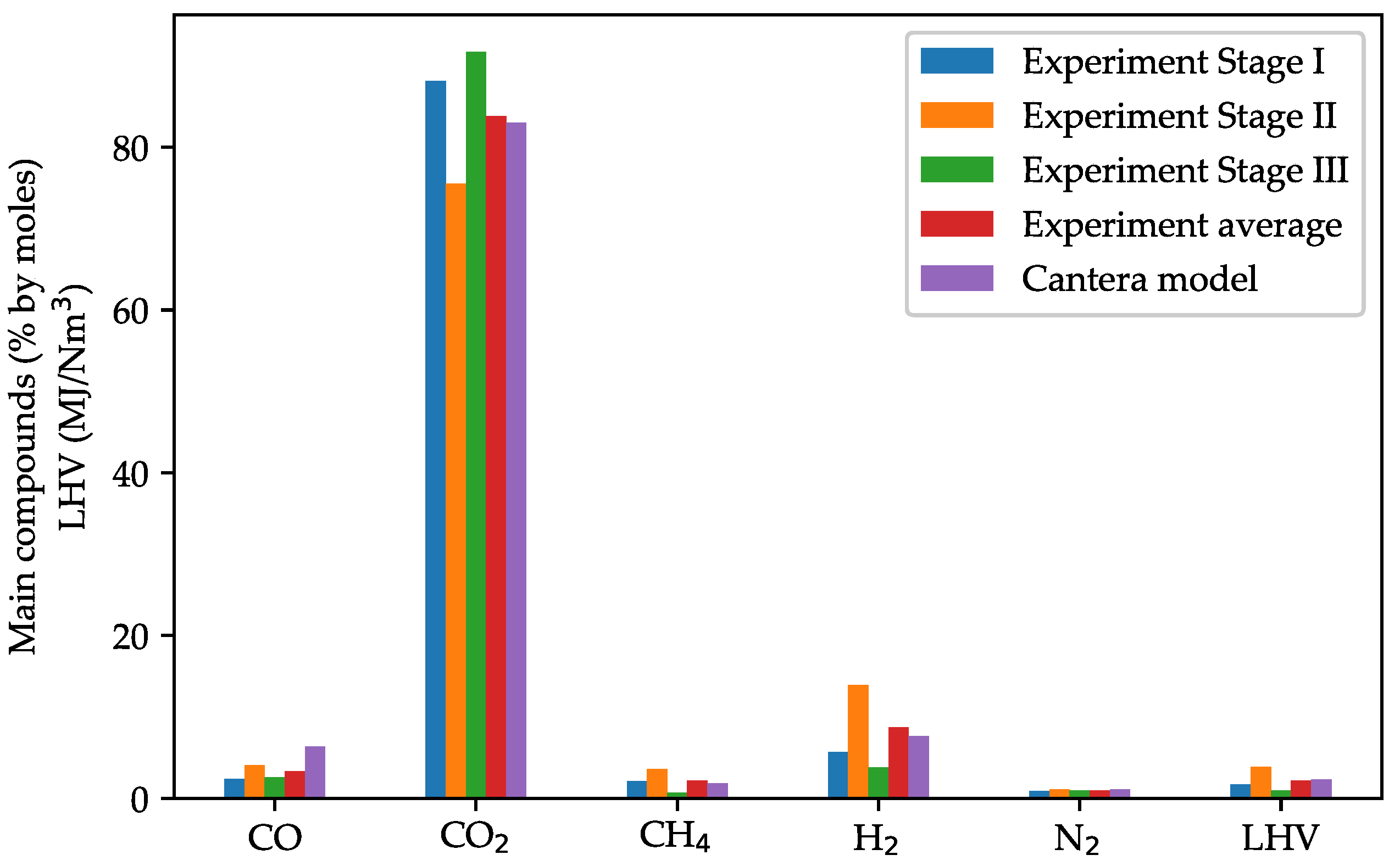
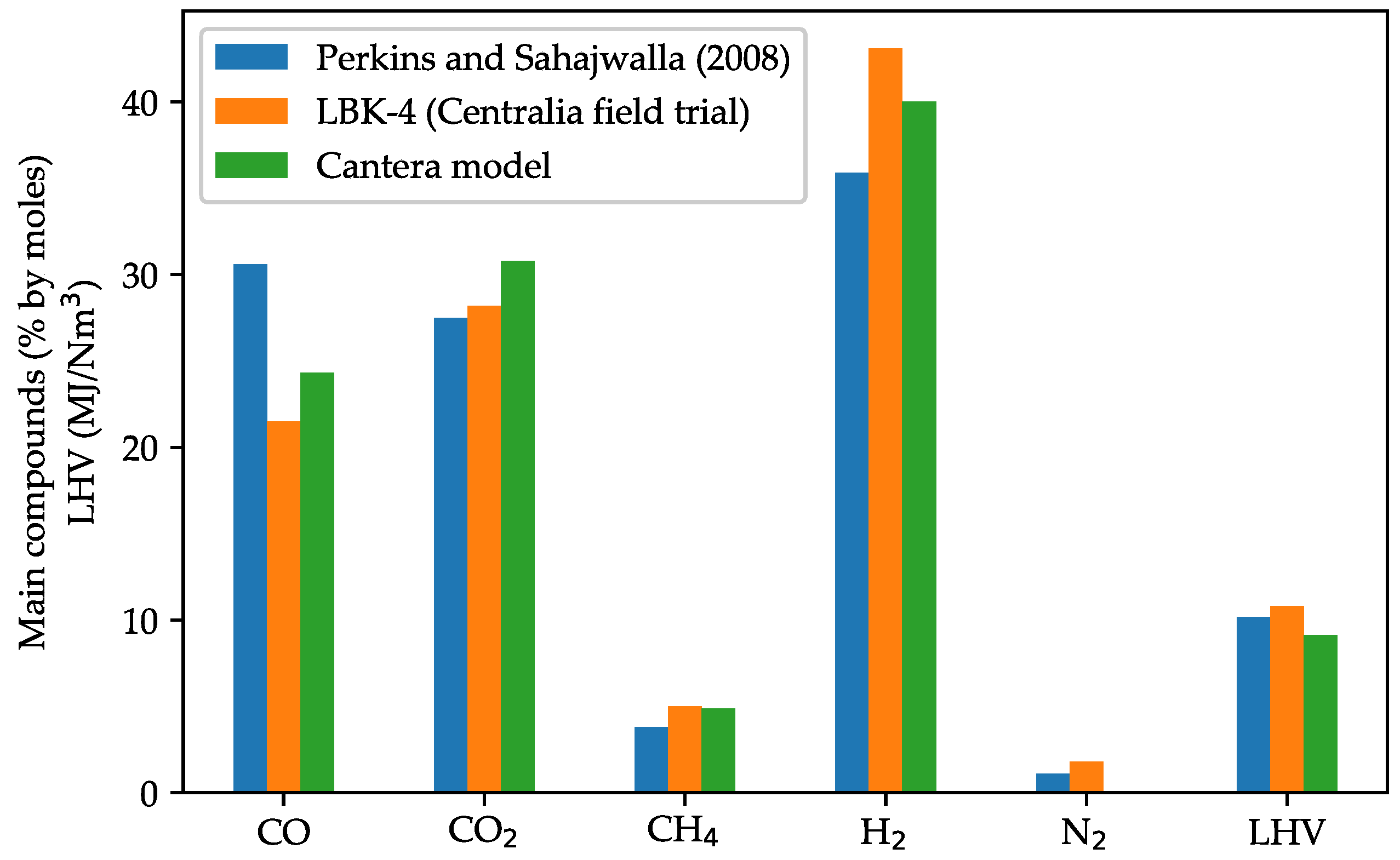
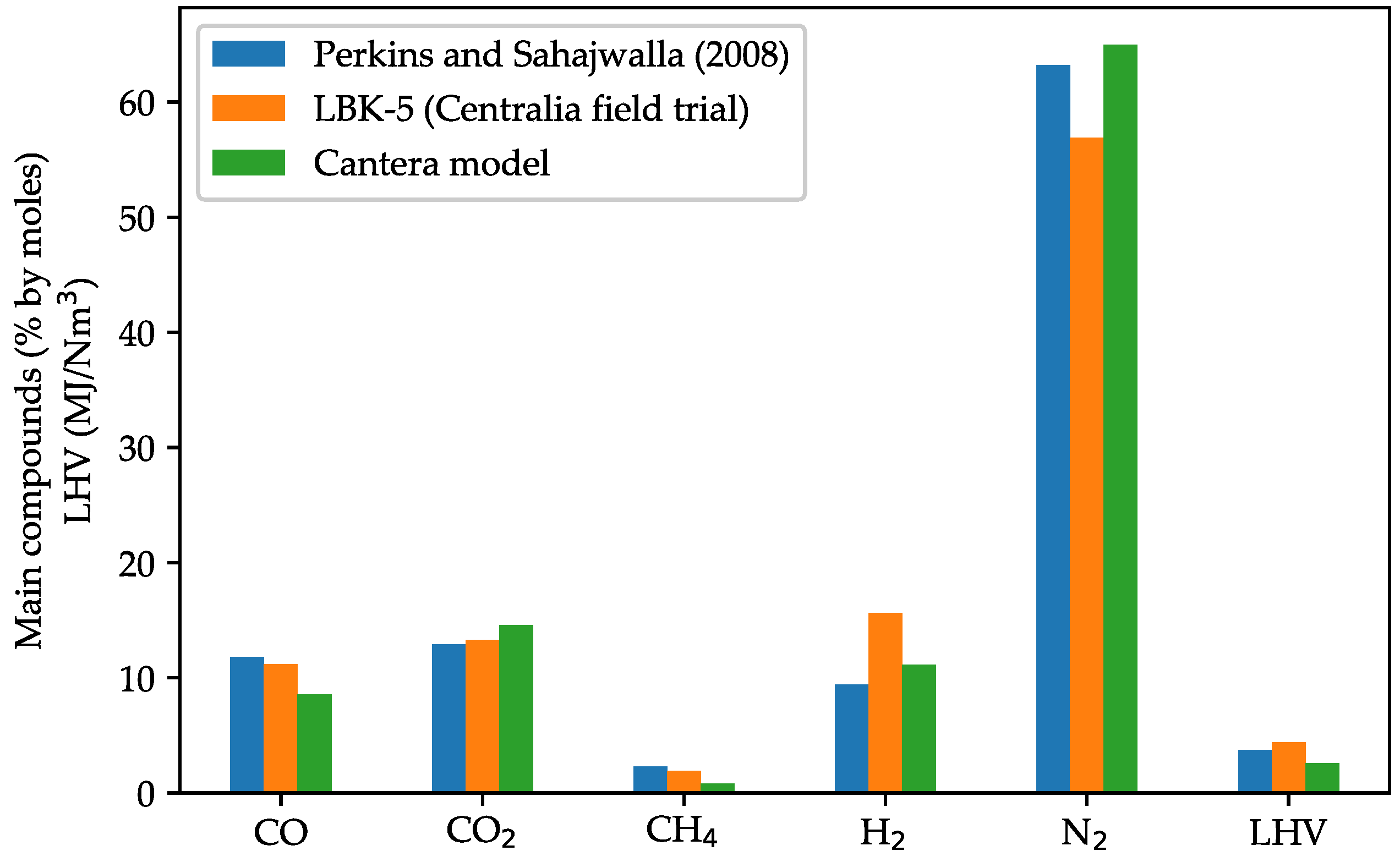
3.2. Model Validation against UCG Experimental Data
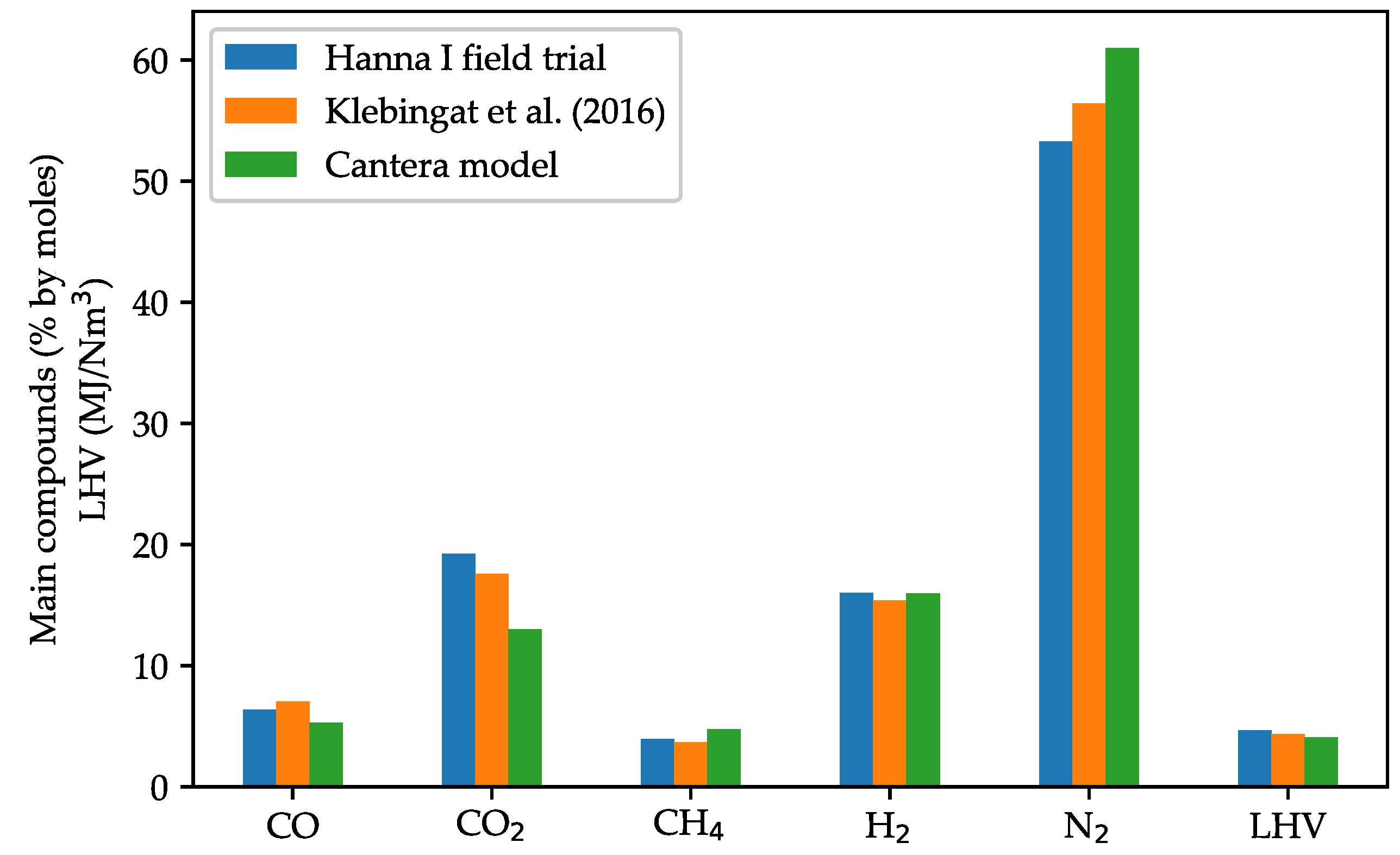
3.3. Model Validation against UCG Field Trials
4. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Blinderman, M.; Klimenko, A. Introduction to Underground Coal Gasification and Combustion; Woodhead Publishing: Cambridge, UK, 2017. [Google Scholar] [CrossRef]
- Bhutto, A.W.; Bazmi, A.A.; Zahedi, G. Underground coal gasification: From fundamentals to applications. Prog. Energy Combust. Sci. 2013, 39, 189–214. [Google Scholar] [CrossRef]
- Nakaten, N.; Kötting, P.; Azzam, R.; Kempka, T. Underground Coal Gasification and CO2 Storage Support Bulgaria’s Low Carbon Energy Supply. Energy Procedia 2013, 40, 212–221. [Google Scholar] [CrossRef]
- Couch, G. Underground Coal Gasification; CCC/151; IEA Clean Coal Centre: London, UK, 2009; p. 129. [Google Scholar]
- Durucan, S.; Korre, A.; Shi, J.Q.; Idiens, M.; Stańczyk, K.; Kapusta, K.; Rogut-Dabrowska, A.; Kempka, T.; Wolf, K.H.; Younger, P.; et al. TOPS: Technology Options for Coupled Underground Coal Gasification and CO2 Capture and Storage. Energy Procedia 2014, 63, 5827–5835. [Google Scholar] [CrossRef]
- Kempka, T.; Fernández-Steeger, T.; Li, D.Y.; Schulten, M.; Schlüter, R.; Krooss, B.M. Carbon dioxide sorption capacities of coal gasification residues. Environ. Sci. Technol. 2011, 45, 1719–1723. [Google Scholar] [CrossRef] [PubMed]
- Nakaten, N.C.; Kempka, T. Techno-Economic Comparison of Onshore and Offshore Underground Coal Gasification End-Product Competitiveness. Energies 2019, 12, 3252. [Google Scholar] [CrossRef]
- Adhikary, D.; Khanal, M.; Jayasundara, C.; Balusu, R. Deficiencies in 2D Simulation: A Comparative Study of 2D Versus 3D Simulation of Multi-seam Longwall Mining. Rock Mech. Rock Eng. 2016, 49, 2181–2185. [Google Scholar] [CrossRef]
- Nitao, J.J.; Camp, D.W.; Buscheck, T.A.; White, J.A.; Burton, G.C.; Wagoner, J.L.; Chen, M. Progress on a New Integrated 3-D UCG Simulator and its Initial Application. In Proceedings of the International Pittsburgh Coal Conference, Pittsburgh, PA, USA, 12–15 September 2011; p. 13. [Google Scholar]
- Nourozieh, H.; Kariznovi, M.; Chen, Z.; Abedi, J. Simulation Study of Underground Coal Gasification in Alberta Reservoirs: Geological Structure and Process Modeling. Energy Fuels 2010, 24, 3540–3550. [Google Scholar] [CrossRef]
- Khan, M.; Mmbaga, J.; Shirazi, A.; Trivedi, J.; Liu, Q.; Gupta, R. Modelling Underground Coal Gasification—A Review. Energies 2015, 8, 12603–12668. [Google Scholar] [CrossRef]
- Puig-Arnavat, M.; Bruno, J.C.; Coronas, A. Review and analysis of biomass gasification models. Renew. Sustain. Energy Rev. 2010, 14, 2841–2851. [Google Scholar] [CrossRef]
- Ferreira, S.; Monteiro, E.; Brito, P.; Vilarinho, C. A Holistic Review on Biomass Gasification Modified Equilibrium Models. Energies 2019, 12, 160. [Google Scholar] [CrossRef]
- Rodrigues, R.; Muniz, A.R.; Marcilio, N.R. Evaluation of Biomass and Coal Co—Gasification of Brazilian Feedstock Using a Chemical Equilibrium Model. Braz. J. Chem. Eng. 2016, 33, 401–414. [Google Scholar] [CrossRef]
- Shabbar, S.; Janajreh, I. Thermodynamic equilibrium analysis of coal gasification using Gibbs energy minimization method. Energy Convers. Manag. 2013, 65, 755–763. [Google Scholar] [CrossRef]
- Baratieri, M.; Baggio, P.; Fiori, L.; Grigiante, M. Biomass as an energy source: Thermodynamic constraints on the performance of the conversion process. Bioresour. Technol. 2008, 99, 7063–7073. [Google Scholar] [CrossRef]
- Li, X.; Grace, J.R.; Watkinson, A.P.; Lim, C.J.; Ergüdenler, A. Equilibrium modeling of gasification: A free energy minimization approach and its application to a circulating fluidized bed coal gasifier. Fuel 2001, 80, 195–207. [Google Scholar] [CrossRef]
- George, J.; Arun, P.; Muraleedharan, C. Stoichiometric Equilibrium Model Based Assessment of Hydrogen Generation through Biomass Gasification. Procedia Technol. 2016, 25, 982–989. [Google Scholar] [CrossRef]
- Perkins, G. Underground coal gasification – Part II: Fundamental phenomena and modeling. Prog. Energy Combust. Sci. 2018, 67, 234–274. [Google Scholar] [CrossRef]
- Basu, P. Biomass Gasification and Pyrolysis: Practical Design and Theory; Elsevier: West Chester, OH, USA, 2010; pp. 133–153. [Google Scholar] [CrossRef]
- Johnson, J. Fundamentals of Coal Gasification. In Chem. Coal Util; Elliot, M., Ed.; John Wiley and Sons: Hoboken, NJ, USA, 1981. [Google Scholar]
- Gambarotta, A.; Morini, M.; Zubani, A. A non-stoichiometric equilibrium model for the simulation of the biomass gasification process. Appl. Energy 2018, 227, 119–127. [Google Scholar] [CrossRef]
- Cempa-Balewicz, M.; Jacek Ła̧czny, M.; Smoliński, A.; Iwaszenko, S. Equilibrium Model of Steam Gasification of Coal. J. Sustain. Min. 2013, 12, 21–28. [Google Scholar] [CrossRef]
- Żogała, A. Equilibrium Simulations of Coal Gasification—Factors Affecting Syngas Composition. J. Sustain. Min. 2014, 13, 30–38. [Google Scholar] [CrossRef]
- Eri, Q.; Wu, W.; Zhao, X. Numerical Investigation of the Air-Steam Biomass Gasification Process Based on Thermodynamic Equilibrium Model. Energies 2017, 10, 2163. [Google Scholar] [CrossRef]
- Zagorščak, R.; An, N.; Palange, R.; Green, M.; Krishnan, M.; Thomas, H.R. Underground coal gasification—A numerical approach to study the formation of syngas and its reactive transport in the surrounding strata. Fuel 2019, 253, 349–360. [Google Scholar] [CrossRef]
- Samdani, G.; Anuradda, G.; Preeti, A.; Sapru, R.K.; Lohar, B.L.; Mahajani, S. Kinetics of heterogeneous reactions with coal in context of underground coal gasification. Fuel 2017, 199, 102–114. [Google Scholar] [CrossRef]
- Hwang, M.; Song, E.; Song, J. One-dimensional modeling of an entrained coal gasification process using kinetic parameters. Energies 2016, 9, 99. [Google Scholar] [CrossRef]
- Perkins, G.; Sahajwalla, V. A Mathematical Model for the Chemical Reaction of a Semi-infinite Block of Coal in Underground Coal Gasification. Energy Fuels 2005, 19, 1679–1692. [Google Scholar] [CrossRef]
- Várhegyi, G.; Antal, M.J.; Jakab, E.; Szabó, P. Kinetic modeling of biomass pyrolysis. J. Anal. Appl. Pyrolysis 1997, 42, 73–87. [Google Scholar] [CrossRef]
- Guo, B.; Li, D.; Cheng, C.; Zi-an, L.; Shen, Y. Simulation of biomass gasification with a hybrid neural network model. Bioresour. Technol. 2001, 76, 77–83. [Google Scholar] [CrossRef]
- Psichogios, D.C.; Ungar, L.H. A Hybrid Neural Network-First Principles Approach to Process Modeling. AIChE J. 1992, 38, 1499–1511. [Google Scholar] [CrossRef]
- Renzi, M.; Riolfi, C.; Baratieri, M. Influence of the Syngas Feed on the Combustion Process and Performance of a Micro Gas Turbine with Steam Injection. Energy Procedia 2017, 105, 1665–1670. [Google Scholar] [CrossRef]
- Andrianopoulos, E.; Korre, A.; Durucan, S. Chemical process modelling of underground coal gasification and evaluation of produced gas quality for end use. Energy Procedia 2015, 76, 444–453. [Google Scholar] [CrossRef]
- Stańczyk, K.; Świa̧drowski, J.; Kapusta, K.; Howaniec, N.; Cybulski, K.; Rogut, J.; Smoliński, A.; Wiatowski, M.; Kotyrba, A.; Krause, E.; et al. Hydrogen-Oriented Underground Coal Gasification for Europe (HUGE); RFCS Publications, European Commission: Brussels, Belgium, 2012; p. 160. [Google Scholar] [CrossRef]
- Gregg, D.W.; Edgar, T.F. Underground Coal Gasification-Journal Review. AIChE J. 1978, 24, 753–781. [Google Scholar] [CrossRef]
- Klebingat, S.; Kempka, T.; Schulten, M.; Azzam, R.; Fernandez-Steeger, T.M. Innovative thermodynamic underground coal gasification model for coupled synthesis gas quality and tar production analyses. Fuel 2016, 183, 680–686. [Google Scholar] [CrossRef]
- Żogała, A. Critical Analysis of Underground Coal Gasification Models. Part II: Kinetic and Computational Fluid Dynamics Models. J. Sustain. Min. 2014, 50, 29–37. [Google Scholar] [CrossRef]
- Dufaux, A.; Gaveau, B.; Létolle, R.; Mostade, M.; Noël, M.; Pirard, J.P. Modelling of the underground coal gasification process at Thulin on the basis of thermodynamic equilibria and isotopic measurements. Fuel 1990, 69, 624–632. [Google Scholar] [CrossRef]
- Kerinin, E.V.; Shifrin, E.I. Mathematical Model of Coal Combustion and Gasification in a Passage of an Underground Gas Generator. Combust. Explos. Shock Waves 1993, 29, 148–154. [Google Scholar] [CrossRef]
- Cena, R.J. A simple UCG field performance and economic model. In Proceedings of the 13th Annual Underground Coal Conversion Symposium DOE/METC/-88/6095 (CONF-8708106), Laramie, WY, USA, 24–27 August 1987; pp. 391–403. [Google Scholar]
- Smith, G.P.; Golden, D.M.; Frenklach, M.; Moriarty, N.W.; Eiteneer, B.; Goldenberg, M.; Bowman, C.T.; Hanson, R.K.; Song, S.; Gardiner, W.C.; et al. GRI-MECH 3.0. 2000. Available online: http://combustion.berkeley.edu/gri-mech/version30/text30.html (accessed on 14 January 2020).
- Burton, E.; Friedmann, J.; Upadhye, R. Best Practices in Underground Coal Gasification; Contract No. W-7405-Eng-48; Lawrence Livermore Natl. Lab.: Livermore, CA, USA, 2006. [Google Scholar]
- Goodwin, D.G.; Malaya, N.; Moffat, H.; Speth, R. Cantera: An Object-Oriented Software Toolkit for Chemical Kinetics, Thermodynamics, and Transport Processes; Version 2.1.0; Caltech: Pasadena, CA, USA, 2013. [Google Scholar]
- Kacur, J.; Durdan, M.; Laciak, M.; Flegner, P. Impact analysis of the oxidant in the process of underground coal gasification. Measurements 2014, 51, 147–155. [Google Scholar] [CrossRef]
- La Villetta, M.; Costa, M.; Massarotti, N. Modelling approaches to biomass gasification: A review with emphasis on the stoichiometric method. Renew. Sustain. Energy Rev. 2017, 74, 71–88. [Google Scholar] [CrossRef]
- Klebingat, S.; Kempka, T.; Schulten, M.; Azzam, R.; Fernández-Steeger, M.T. Optimization of synthesis gas heating values and tar by-product yield in underground coal gasification. Fuel 2018, 229, 248–261. [Google Scholar] [CrossRef]
- Smith, W.R.; Missen, R.W. Chemical Reaction Equilibrium Analysis: Theory and Algorithms; Wiley: New York, NY, USA, 1982; p. 364. [Google Scholar]
- Wong, F.; Gottlieb, J.; Lussier, L.S. Chemical Equilibrium Analysis of Combustion Products at Constant Volume; DRDC-VALCARTIER-TR-2003-375—Technical Report; Defence Research and Development Canada: Ottawa, ON, Canada, 2003; p. 251. [Google Scholar]
- Meyer, M. A New EOS Module for the Atmosphere Modelling Code PHOENIX. Ph.D. Thesis, University of Hamburg, Hamburg, Germany, 2017. Available online: http://ediss.sub.uni-hamburg.de/volltexte/2017/8643/ (accessed on 14 January 2020).
- Wong, F.C.H. Chemical Equilibrium Analysis of Combustion Products at Constant Volume. 2001. Available online: http://hdl.handle.net/1807/15258 (accessed on 14 January 2020).
- Wiatowski, M.; Kapusta, K.; Stańczyk, K.; Stańczyk, K. Efficiency assessment of underground gasification of ortho- and meta-lignite: High-pressure ex situ experimental simulations. Fuel 2019, 236, 221–227. [Google Scholar] [CrossRef]
- Perkins, G.; Sahajwalla, V. Steady-State Model for Estimating Gas Production from Underground Coal Gasification. Energy Fuels 2008, 22, 3902–3914. [Google Scholar] [CrossRef]
- Krantz, W.B.; Camp, D.W.; Gunn, R.D. A Water-Influx Model for UCG. In Proceedings of the Sixth Underground Coal Conversion Symposium, Shangri-La, OK, USA, 13–17 July 1980; pp. 21–31. [Google Scholar]
- Wiatowski, M.; Kapusta, K.; Ludwik-Pardała, M.; Stańczyk, K. Ex-situ experimental simulation of hard coal underground gasification at elevated pressure. Fuel 2016, 184. [Google Scholar] [CrossRef]
- Laciak, M.; Kostúr, K.; Durdán, M.; Kačur, J.; Flegner, P. The analysis of the underground coal gasification in experimental equipment. Energy 2016, 114, 332–343. [Google Scholar] [CrossRef]
- Kapusta, K.; Wiatowski, M.; Stańczyk, K. An experimental ex-situ study of the suitability of a high moisture ortho-lignite for underground coal gasification (UCG) process. Fuel 2016, 179. [Google Scholar] [CrossRef]
- Hill, R.; Thorsness, C. Summary Report on Large Block Experiments in Underground Coal Gasification, Tono Basin, Washington: Volume 1. Experimental Description and Data Analysis; Report No. UCRL-53305, Technical Report; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1982. [Google Scholar]
- Bartke, T.C.; Fischer, D.D.; King, S.B.; Boyd, R.M.; Humphrey, A.E. Vol. 2 Hanna I, Wyoming UCG Data Base - General Information and Executive Summary; Technical Report; Morgantown Energy Technology Center and United States, Department of Energy, Office of Scientific and Technical Information: Laramie, WY, USA, 1985. [Google Scholar]
- Morgantown Energy Technology Center and United States. Department of Energy. Office of Scientific and Technical Information. Hanna, Wyoming Underground Coal Gasification Data Base. Volume 1. General Information and Executive Summary. In Hanna, Wyoming Underground Coal Gasification Data Base; DE85013695; Morgantown Energy Technology Center: Morgantown, WV, USA, 1985; p. 53. [Google Scholar]
- Kangas, P.; Hannula, I.; Koukkari, P.; Hupa, M. Modelling super-equilibrium in biomass gasification with the constrained Gibbs energy method. Fuel 2014, 129, 86–94. [Google Scholar] [CrossRef]
| Reaction Name | Stoichiometry | Standard Heat of Reaction, Δ (kJ/mol) |
|---|---|---|
| Pyrolysis | Coal ⟶ Char, ash, tar, CO, CO2, H2, H2O, CH4 | ∼0 |
| Oxidation | −393.0 | |
| Boudouard | +172.5 | |
| Methanation | −75.0 | |
| Steam Gasification | +131.0 | |
| Water-Gas Shift | −41.0 | |
| Carbon Monoxide Oxidation | −283.0 | |
| Methane-Steam Reforming | +206.0 |
| Phase | Group | Compounds |
|---|---|---|
| Solid | Carbon | |
| Gas | Inorganic carbon compounds | , , |
| Hydrogen compounds | H, , O, , , , , , | |
| Nitrogen compounds | N, , , , , , , | |
| , , , , , , | ||
| , , , | ||
| Sulfur compounds | S, , , , , | |
| Hydrocarbons | , , , , , , , , | |
| , , , , , , | ||
| Other organic compounds | , , , , | |
| , , , |
| Type | Case | Ultimate Analysis (% by mass, af *) | References | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| C | H | O | N | S | Moisture | Chemical formula (mol/mol C) | Oxidizer | SR ** | |||
| Pine sawdust | Pyrolysis test | 45.20 | 5.40 | 39.00 | 0.10 | 0.00 | 9.40 | - | - | [16] | |
| Subbituminous coal | Highvale, CA | 66.05 | 3.81 | 18.70 | 0.80 | 0.20 | 10.39 | Air | 0.4 | [17] | |
| Ortho-lignite | Oltenia, ROU | 57.67 | 4.59 | 19.95 | 1.56 | 2.83 | 13.39 | Oxygen | 0.35 | [52] | |
| Subbituminous coal | LBK-4, Centralia, USA | 76.00 | 4.70 | 18.70 | 0.10 | 0.40 | 0.00 | Steam | 0.3 | [53] | |
| Subbituminous coal | LBK-5, Centralia, USA | 76.00 | 4.70 | 18.70 | 0.10 | 0.40 | 0.00 | Air | 0.3 | [53] | |
| Subbituminous coal | Hanna I, Hanna, USA | 74.33 | 6.03 | 16.68 | 1.94 | 1.02 | 0.00 | Air | 0.12 | [37] | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otto, C.; Kempka, T. Synthesis Gas Composition Prediction for Underground Coal Gasification Using a Thermochemical Equilibrium Modeling Approach. Energies 2020, 13, 1171. https://doi.org/10.3390/en13051171
Otto C, Kempka T. Synthesis Gas Composition Prediction for Underground Coal Gasification Using a Thermochemical Equilibrium Modeling Approach. Energies. 2020; 13(5):1171. https://doi.org/10.3390/en13051171
Chicago/Turabian StyleOtto, Christopher, and Thomas Kempka. 2020. "Synthesis Gas Composition Prediction for Underground Coal Gasification Using a Thermochemical Equilibrium Modeling Approach" Energies 13, no. 5: 1171. https://doi.org/10.3390/en13051171
APA StyleOtto, C., & Kempka, T. (2020). Synthesis Gas Composition Prediction for Underground Coal Gasification Using a Thermochemical Equilibrium Modeling Approach. Energies, 13(5), 1171. https://doi.org/10.3390/en13051171





