1. Introduction
Logistics and transportation activities are one of the fundamental pillars for economic development worldwide. The contribution of transportation to the gross domestic product (GDP) has remained significant over the last decade. According to the U.S. Bureau of Transportation Statistics [
1], the average annual growth in transportation-related demand from 1999 to 2016 was about 10%. In 2016, this demand accounted for
% of the GDP. Similarly, the contribution of transportation to the GDP of Europe is about 5% [
2]. Across the globe, both freight transportation and passenger-mobility activities have been on the rise. Between 1995 and 2015, freight transportation activities in the USA increased about
%, while the increase in the passenger transportation activities in the same period was about
%. In the EU-28, the increase in freight and passenger transportation was about 24% each. However, there is a series of negative externalities associated with this economic boom. The transportation field is one of the major contributors to global energy consumption, being responsible for almost 29% of the global energy consumption by sector, and producing up to 24% of global CO
emissions [
3]. Furthermore, according to the United Nations Department of Economics and Social Affairs, these numbers will only get worse, since the world population is forecasted to be
billion by 2100 [
4].
Air pollutants from passenger and freight transportation are mainly a consequence of fuel combustion, which has a direct impact on the environment. It also plays a role in the formation of pollutants which may be harmful to human beings [
5]. As social awareness about the environmental risks of our modern economies is increasing, sustainability is gaining momentum, and energy efficiency is receiving considerable attention from practitioners and academics. Energy use and emissions largely depend on several factors, including technologies, fuels, vehicle operation, demand, demographics, and road design. According to Juan et al. [
6] and Fan et al. [
7], available optimization measures can be generally categorized into: (i) improvement of energy efficiency; (ii) renewable energy and electrification; and (iii) optimal configuration of transportation modes. The field of Operations Research (OR) is also making important contributions to pollutant reduction and sustainable transportation management [
8]. Bektaş et al. [
5] provided an excellent review of OR methods for green freight transportation, with a particular focus on maritime and road transportation. Mathematical programming optimization, metaheuristic algorithms, and simulation techniques are among the most popular OR methods in the transportation sector [
9]. This paper reviews recent articles on energy-related transportation challenges associated with four major transportation modes: freight road, passenger rail, maritime, and air. The article also analyzes how optimization methods—of both exact and approximate nature—are being used to deal with the aforementioned challenges. Exact methods, which include linear and integer programming, aim at formulating and solving a problem with an objective function (such as minimization of cost or maximization of revenue) within a series of constraints. These methods are able to find globally optimal solutions. However, when the problem is computationally NP-hard [
10], they can only solve small-sized instances or, alternatively, need extremely long computing times to provide a solution. On the other hand, metaheuristic algorithms [
11] are able to provide near-optimal solutions to complex transportation problems in short computing times. Those algorithms are gaining more importance in the transportation literature because of the increasing complexity and size of real-life transportation systems.
In this paper, we focus on heuristic-based approaches that are used to solve energy-related transportation problems in freight road, passenger rail, maritime, and air transportation. Our focus is on those problems that have an explicit energy consideration, such as minimization of fuel costs or minimization of air pollution. In particular, the main research questions of this work can be summarized as follows: (i) For each transportation mode, what energy-related optimization problems have been more frequently studied in the existing literature? (ii) What are the common characteristics and trends emerging from the existing literature on energy-related optimization (iii) What are some of the most promising research lines in the area of energy-related transportation? To the best of our knowledge, these questions have not been answered before and, therefore, constitute a gap in the existing literature and might open some research lines.
The rest of the paper is structured as follows.
Section 2 describes the review methodology.
Section 3 comments on the growing demand of energy required to support modern transportation systems.
Section 4 reviews energy-related optimization problems in freight road transportation along with the solution methods employed to solve those problems.
Section 5,
Section 6 and
Section 7 complete a similar review for passenger rail, maritime, and air transportation modes, respectively.
Section 8 discusses results in terms of energy savings and reduction of CO
emissions. Finally,
Section 9 highlights the main findings of this work and provides an overview of open research lines.
2. Research Methodology
Several surveys have been published on the use of optimization techniques to improve fuel consumption in transportation systems. Some of these surveys refer to maritime transportation [
12], some to gas transportation [
13], and others to train transportation [
14] or road transportation [
5]. Notice, however, that one of the original contributions of our survey is that it provides a more holistic perspective by reviewing different transportation modes and extracting insights from this cross-modal analysis. Hence, this section depicts the methodology employed for conducting our literature review. Literature reviews are commonly used as a fundamental tool to manage the diversity of knowledge within academia, and to enable academics to assess current intellectual domains and specify research questions in order to spread knowledge as far as possible [
15]. Generally, structured reviews are conducted using an iterative procedure, which consists of defining appropriate keywords, searching the literature, and conducting the analysis [
16]. This systematic approach helps reduce the subjectivity bias inherent in these processes and ensures that all decisions are made transparently—i.e., without the subjectivity of any individual researcher and with the agreement of the entire work team. This search, by nature, generates many references which need to be explored for further analysis [
17]. In the present paper, we follow the systematic review proposed by Tranfield et al. [
15], which was later adapted by Evangelista et al. [
18]. The main steps of our procedure are described next.
2.1. Research Protocol
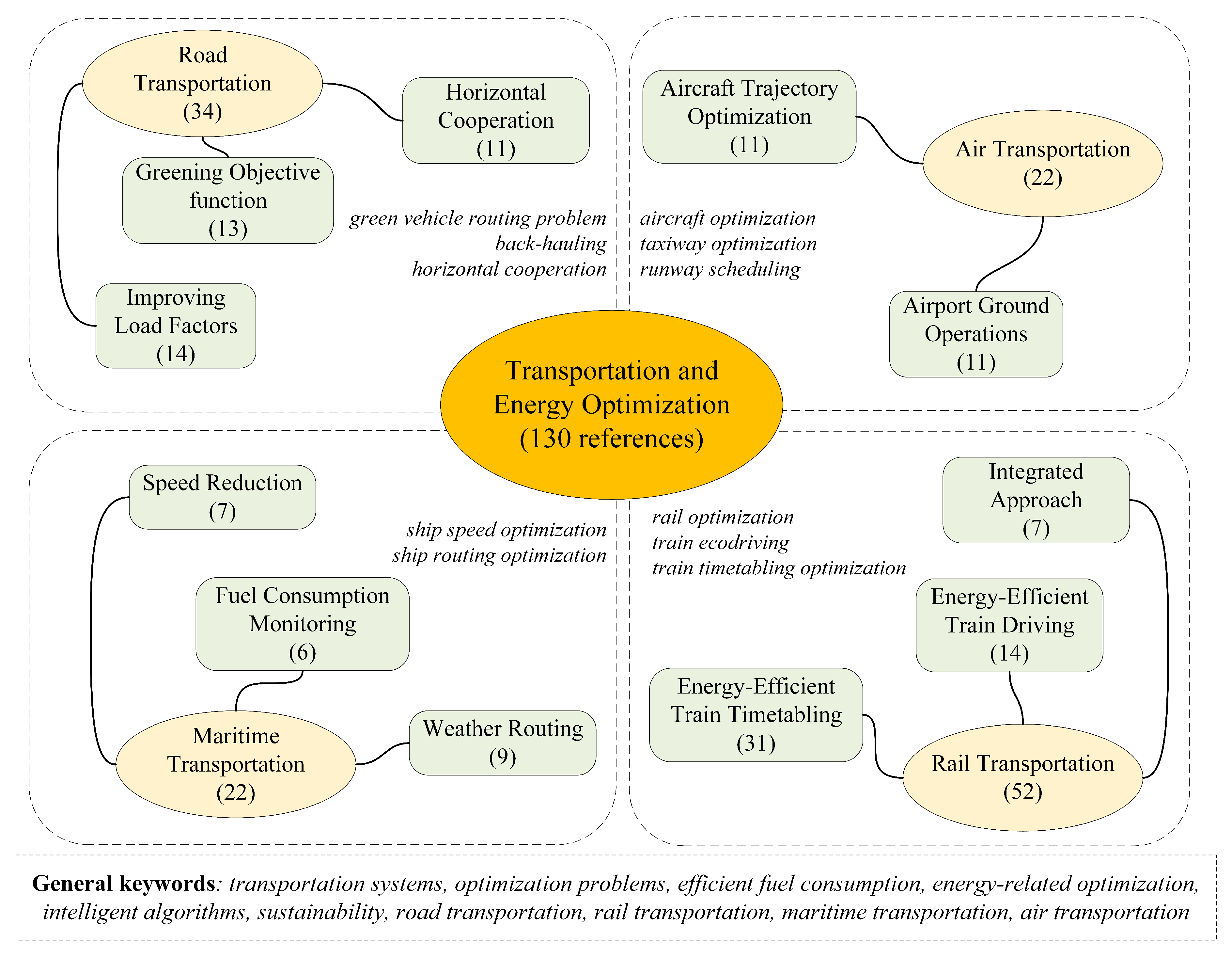
Traditionally, the research protocol is the soul of the methodological approach because it establishes the connections between the research questions and the expected findings. Thereby, we can state a three-fold objective for this phase: (i) to define the main research goals; (ii) to select the database(s) and the keywords; and (iii) to design the search process. Accordingly, we decided to base the review protocol on the following two questions: (i) In the context of energy-related transportation problems, what optimization techniques have been implemented so far in the literature? (ii) How have exact methods and metaheuristics been used in NP-hard problems of different sizes? While posing these questions, the authors also considered the diversity in transportation modes. To fulfill the aforementioned goals, relevant keywords were identified. According to the authors’ expertise on the topics (i.e., optimization and simulation techniques, as well as smart transportation and green logistics), a list of keywords was proposed by each author. From this list, the following keywords were finally selected: transportation systems, optimization problems, efficient fuel consumption, energy-related optimization, intelligent algorithms, sustainability, road transportation, rail transit systems, maritime transportation, and air transportation.
Then, we analyzed publications included in journals indexed within the Science Citation Index (SCI) and the Social Science Citation Index (SSCI), which are considered two of the main sources of information in academia [
19], as well as an indicator of scientific productivity and quality [
20]. According to Newbert [
21], the SCI/SSCI databases contain “more than 8000 high-quality, peer-reviewed journals cover-to-cover, providing users with complete bibliographic data, full-length author abstracts, and cited references from the world’s most influential research”. In addition, inclusion/exclusion criteria were implemented. The first one refers to the inclusion of those papers that are related to transportation (in any form or mode) and efficient fuel consumption. The second one concerns the consideration of works that actually apply optimization techniques. Finally, the third criterion ensures the inclusion of those articles that explore the application of simulation and machine learning in the optimization of transportation problems.
2.2. Implementation of the Research Protocol
The second phase allowed us to obtain the final sample of papers to be analyzed. Firstly, the combinations of keywords and related search criteria were applied, and 574 peer-reviewed articles were collected from the aforementioned databases. After filtering them according to the inclusion/exclusion criteria, the last step involved the classification of the references. Moreover, to process a large amount of information, we debugged the references by applying a filter to the articles according to their abstract descriptions. This step allowed us to check whether the article was strongly related to our research or not [
22]. Finally, the last step consisted of a full reading of the selected works, which included 175 academic papers. After sifting through those works according to their suitability to each transportation mode, 130 papers were selected to be presented in the current survey.
2.3. Analysis and Results
In this last phase, the selected journal articles were analyzed. Each paper was assigned to one of the main transportation modes. Then, each paper was classified based on its main approach for increasing efficiency in the use of energy. Finally, the optimization technique used in the paper was investigated. As a result of the survey, an overview of the four main transportation modes is presented. Moreover, some insights as well as several lines of future research are suggested at the end of this paper.
Figure 1 provides a conceptual map of how the review process has been performed. It also offers a graphical presentation of the relationships among transportation modes, references, and keywords.
3. Energy Requirements in Modern Transportation Systems
Over the past few decades, the movement of goods has grown dramatically due to several reasons. Advancements in communication technologies allow customers to search and locate, quickly and safely, the items that they demand [
23]. This facilitates the movement of items from one continent to another. In addition, due to the globalization effect, preferences of customers are getting more homogeneous, which allows companies to produce in one region and move the items to another continent [
24]. This movement of items has also been promoted by international trade regulations. Furthermore, the ever shortening life cycles of products calls for the introduction of new products and their transportation all over the world [
25]. Finally, the continuous improvement in transportation means (e.g., better infrastructure systems, more energy-efficient and faster trains, faster ships, better highways, etc.) [
26] makes it easier and cheaper to transport goods from one place to another. As a consequence, energy use in transportation activities is growing quickly. Several organizations track the trends of the energy sector.
Table 1 summarizes the main reports from official entities, companies, and non-governmental organizations (NGOs) that pay a special attention to the transportation sector. Generally speaking, they draw a similar perspective for a base scenario at two levels: (i) primacy energy consumption in the two big sectors (industrial and transportation); and (ii) supply of energy (oil, coal, electricity, renewable, etc.). However, there are differences in the alternative scenarios they project. These alternatives are formulated on the basis of disruptive geopolitical or economic events, i.e., economic growth or recession, and on the effects of energy prices and different public policies related to energy regulations.
In particular, the World Energy Outlook report [
27], which is provided by the International Energy Agency, examines future trends for the global energy sector. With respect to transportation, the agency predicts gradual implementation of the avoid, shift, and improve policies [
33]. The U.S. Energy Information Administration also publishes a yearly report about the energy sector. It contains projections to 2050 [
28]. In that report, the World Energy Projection System Plus [
34] is used. Some noteworthy energy-related companies also develop their own reports. That is the case of British Petroleum (BP) [
29] or Exxon Mobil [
30]. Their reports identify major challenges for the transition to low emission models. Similarly, reports from NGOs [
31,
32] center their efforts in the role that the energy sector plays on climate change. According to the recent data collected by the U.S. Energy Information Administration (
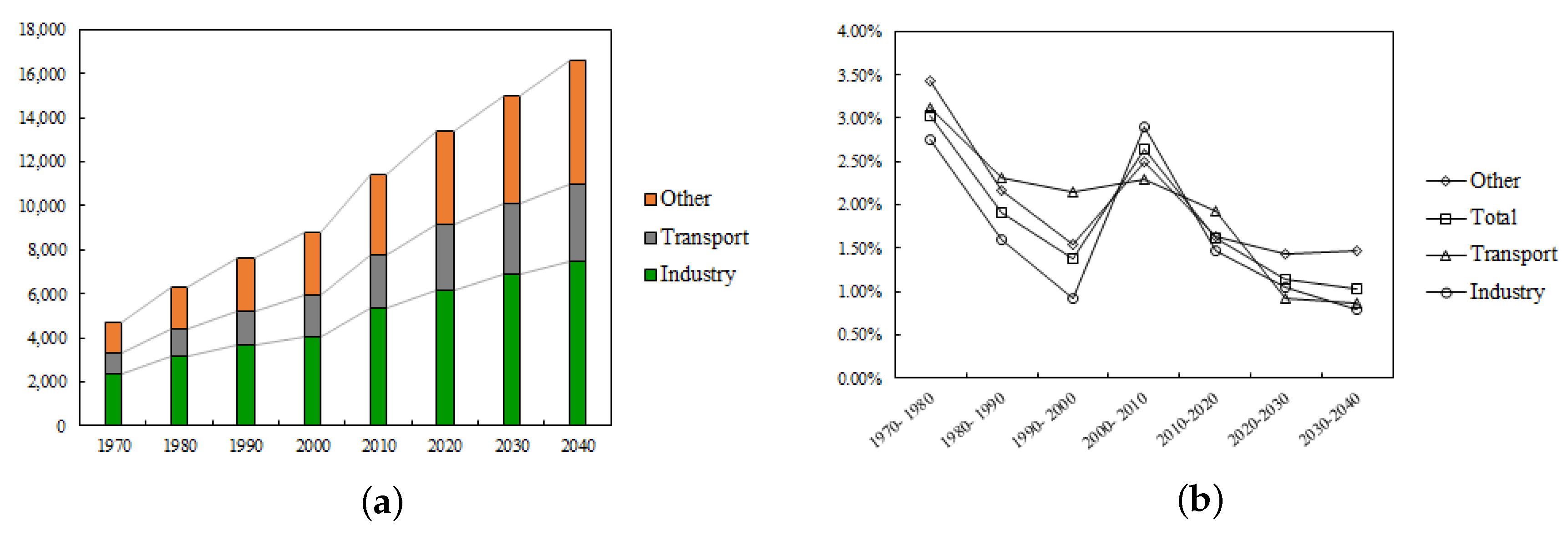
Figure 2), which are published in the International Energy Outlook [
28], energy consumption worldwide increased by
% at a compound annual growth rate during the period 1970–2020. Two different trends can be distinguished: the growth rate reached 3% during the period 1970–1980 while a slower growth of about
% was observed in the following periods. It is remarkable that predictions for 2020–2030 and 2030–2040 forecast decelerated rates around
% and
%, respectively. However, there is an exception during the period 2000–2010, in which a peak of
% appears. This is basically due to the strong development of e-commerce during the first decade of the 21st century. Thus, the cumulative growth in energy consumption has gone from 5000 billion toe in 1970 to almost three times that in 2020.
Figure 2 also presents energy consumption in the largest energy-related sectors: industrial, transportation, building, and non-combusted use of fuels (basically as feed stocks for petrochemicals), where building and non-combusted use of fuels are labeled as ‘other’. We observe that in the 1970s there was a clear dominance by the industry sector (with a share greater than 50%). However, in the next periods, that mixture tends to be homogenized with one third to each end user consumption sector. In this respect,
Table 2, based on data from the International Energy Agency [
27], shows the energy consumption share by the end user in 2016. Significant differences arise depending on the region. For example, in China,
% of energy consumption is devoted to the transportation sector, while, in the U.S., this number is
%, 25% above the Chinese share and 10% higher than the world average.
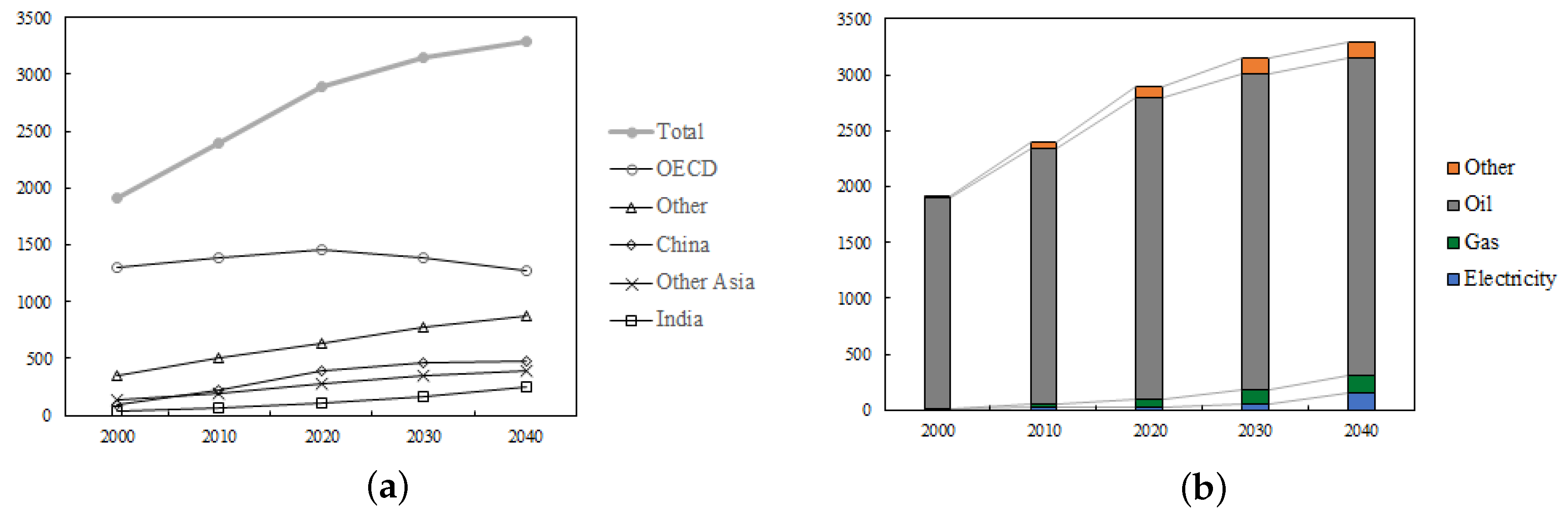
From the previous analysis, one can conclude that the volume of energy requested by the transportation sector is experiencing a rising trend. The demand for transport services grows quite quickly (
Figure 3a). However, the increase in energy efficiency limits the rise of energy consumption. In fact, according to the BP Statistical Review of World Economy [
29], the demand for transportation services in the period 2000–2020 almost doubles its initial value, whereas the energy consumption upturn is just 50% higher. Actually, the compounded annual growth rate is
% during the period 2000–2010, and it is expected to decrease down to
% during 2010–2020, with further reductions down to
% and
% during the periods 2020–2030 and 2030–2040, respectively. Furthermore, the growth in transportation-related energy consumption is concentrated in Asia, which accounts for 80% of the net increase. According to
Figure 3b, the demand for transportation energy is mainly dominated by oil, despite the increasing use of natural gas, electricity, and bio-fuels. Similarly, the share of oil within transportation will decline to around 85% by 2040, down from the current 94%. Natural gas, electricity, and bio-fuels together account for more than half of the increase in energy used in transportation, each providing around 5% of the demand by 2040.
With respect to electric vehicles, their popularity continues to grow rapidly. Most of them are in the form of passenger cars, light-duty trucks, and public buses [
6]. According to the projections developed by the U.S. Energy Information Administration [
28] and BP [
29], by 2040, there will be 350 million electric vehicles on the roads (309 million in the form of passenger cars). This result shows that the number of electric vehicles will constitute around 15% of all cars and 12% of light-duty vehicles. The development of autonomous cars also increases the expected use of electric passenger cars [
35]. As a result, by 2040, electricity is expected to power around 25% of passenger vehicle-km.
4. Road Transportation
The transportation sector has been traditionally split into two branches: passenger transportation and freight transportation.
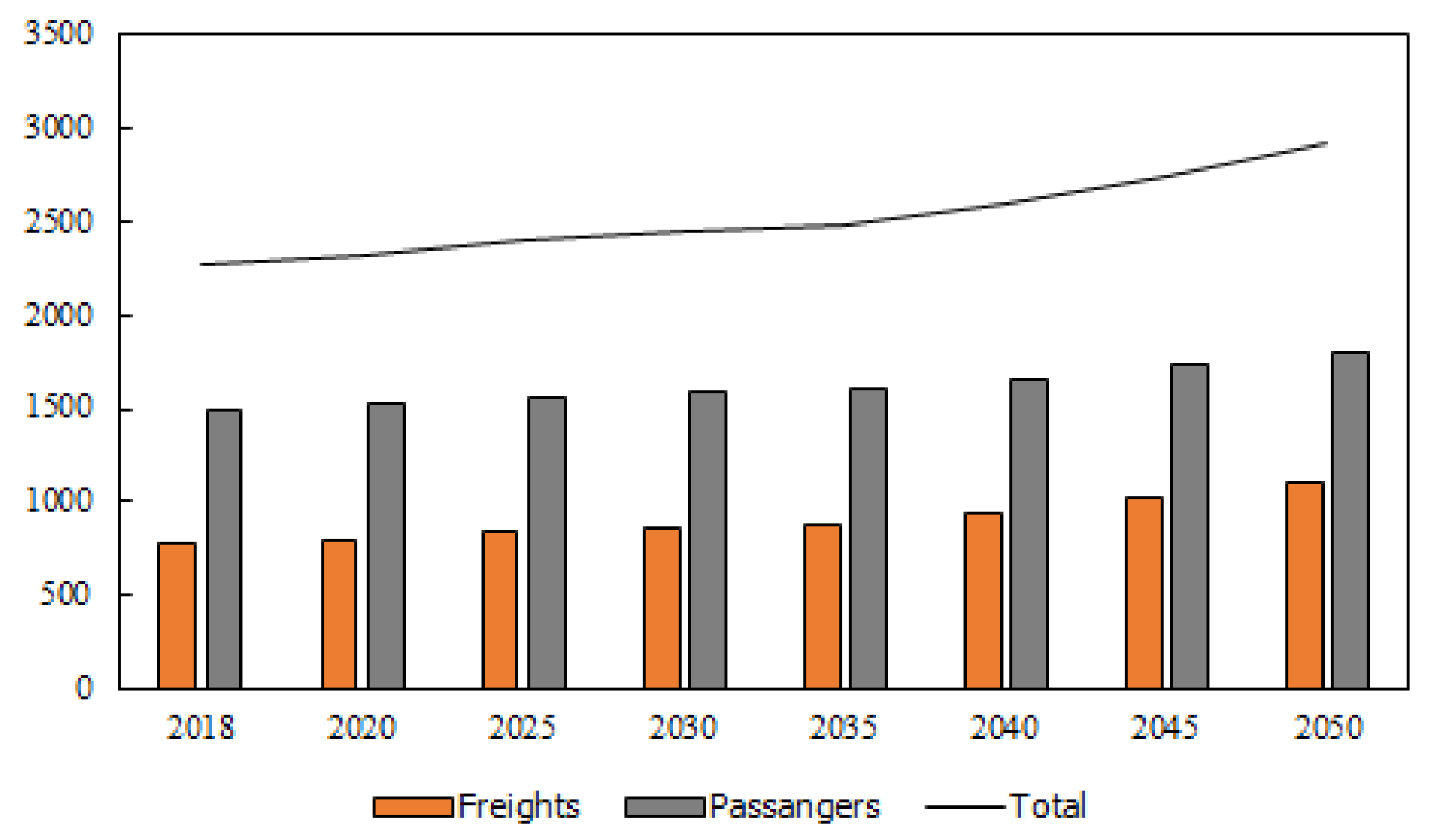
Figure 4, based on a report from the U.S. Energy Information Administration [
28], shows the distribution of energy consumption among freight and passenger transportation, including private cars.
According to this information, the upward trend in energy consumption is primarily due to the rise experienced in freight mobility. During the period 2018–2050, the compound annual growth rate in energy consumption associated with freight transportation (%) will approximately double the one associated with passenger transportation (%). Although those two transportation branches are relevant for the economic and social development of our world, it is freight transportation that dominates the scientific literature on road transportation.
Different strategies are used for energy optimization in road freight transportation:
The remainder of this section analyzes how optimization methods—of both exact and approximate nature—have been employed to promote each of these energy-saving strategies. To clarify the rest of this section,
Table 3 describes the energy optimization strategies in freight road transportation.
4.1. Strategies Based on Greening the Objective Function
There are two seminal papers that propose mathematical formulations for a pair of energy-related VRPs: the energy minimizing VRP and the pollution routing problem. The former was proposed by Kara et al. [
43], and the objective is to minimize a distance-weighted load function so that energy consumption is reduced. The pollution routing problem proposed by Bektaş and Laporte [
42] considers the driver, the fuel consumption, and the CO
emission costs simultaneously.
Once the previous problems were assumed by academics and practitioners, the scientific literature grew in that direction, proposing different variations and solution approaches. That is the case of Fukasawa et al. [
44] for the energy minimization problem, and Eshtehadi et al. [
45] for the pollution routing problem. The former authors proposed two mixed integer linear programming models: an arc-load formulation and a set partitioning formulation. The first one is solved by a branch-and-cut algorithm, while the second one is solved by a branch-cut-and-price algorithm. Finally, they showed how their proposed methodologies can outperform some previously published results. Similarly, the latter authors extended the energy minimization problem by incorporating demand and traveling time uncertainties into the original problem. Their solution approach uses worst-case analysis techniques and chance-constraint techniques.
Nevertheless, exact methods are uncommon when optimizing large-scale energy-related road transportation problems. The reason is that the VRP is an
NP-hard combinatorial optimization problem. Hence, as the size of the problem grows, it becomes increasingly difficult for exact methods to provide an optimal solution in reasonably low computing times. Actually, it is not uncommon to observe that exact methods have difficulties even in problems with a relatively small set of customers [
46]. In fact, the recent literature has focused on developing metaheuristics for solving realistic versions of the aforementioned problems. The literature is particularly rich in proposals based on single-solution metaheuristics, such as simulated annealing or tabu search, as well as on population-based metaheuristics (see Talbi [
47] for a classification of metaheuristics).
Koç and Karaoglan [
48] proposed a simulated annealing approach to solve a VRP with alternative fuel vehicles. The focus here is on the limited range of the vehicles, as well as on the scarce availability of refueling stations. Likewise, in a recent work developed by Hooshmand and MirHassani [
49], simulated annealing is chosen for solving a very similar problem with electric vehicles. Their heuristic algorithm follows a two-step approach. First, the problem is decomposed into clustering and routing stages. Then, the simulated annealing improves the solution obtained in the first stage. Huang et al. [
50] combined the previous algorithm with a tabu search metaheuristic for solving a problem similar to the one proposed by Kara et al. [
43]. The solution procedure is based on
k-means clustering, local search, and tabu list guided searching in order to improve the simulated annealing results. Tabu search was also employed by Kirci [
51]. Here, the problem is in line with the pollution routing problem with several extensions for modeling CO
emissions in a time-dependent vehicle routing context. In relation to the energy-minimizing problem, Ehmke et al. [
52] developed a tabu search algorithm and showed that significant savings in emissions are obtained in suburbs with heterogeneous demands.
Ant colony algorithms were proposed by Androutsopoulos and Zografos [
53], where routing and path-finding decisions are simultaneously addressed. Xiao and Konak [
54] developed a genetic algorithm. They took into account the time-varying traffic congestion because of its huge impact on emissions and on fuel consumption. The heuristic is combined with a dynamic programming procedure, which leads to efficient solutions for large instances. More recently, to better estimate CO
emissions, de Oliveira da Costa et al. [
55] applied the same metaheuristics using real road speed and gradient data.
4.2. Strategies Based on Improving Load Factors
The VRP with back-hauls allows the integration of deliveries and pick-ups in the same route, e.g., once all deliveries have been made (also known as line-hauls), vehicles may start collecting goods (back-hauls) [
40]. This practice leads to a reduction in routing costs, as well as savings in fuel consumption. The number of articles that apply exact methods is limited. Nevertheless, there are still some relevant works. For example, Granada-Echeverri et al. [
56] developed a mixed integer programming model. The idea is that the line-haul and back-haul routes are considered as two sub-problems. Then, tie arcs connecting these routes are defined to generate a solution for the VRP with back-hauls. The exact method proposed by Davis et al. [
57] also consists of a two-phase methodology to solve a real-life problem regarding food collection and delivery.
Most of the research covering VRPs with back-hauls develops heuristic-based solution approaches. From those, tabu search algorithms [
58], or methods that combine them with other heuristics, are the most recurrent solution methods. That is the case of Küçükoğlu and Öztürk [
59], who proposed an advanced hybrid metaheuristic algorithm to solve the VRP with back-hauls and time windows. It combines a tabu search algorithm with a simulated annealing procedure. The resulting approach is executed in a three-step process. In the first step, an initial solution is obtained running a nearest-neighbor heuristic. In the second step, the tabu search generates different neighborhoods. Finally, the simulated annealing, based on an acceptance criterion, selects a solution from these neighborhoods. Time windows were also taken into account by Reil et al. [
60], who assumed three-dimensional loading constraints in a two-fold approach. The first step, which focuses on the packing of goods, solves a
strip packing problem for each customer by using a tabu search heuristic. This results in a VRP with back-hauls, which is again solved in the second step with the tabu search. Likewise, Lai et al. [
61] solved a real case of an Italian carrier, for which an integer linear programming formulation and an adaptive guidance metaheuristic are proposed. The adaptive-guidance procedure is the result of combining a tabu search and the well-known savings heuristic proposed by Clarke and Wright [
62]. Extensions of the savings heuristics are also prominent in the literature. Some studies have proposed biased-randomized algorithms to cope with different variants of the VRP with back-hauls [
63,
64], e.g., clustered and mixed back-hauls as well as heterogeneous fleets of vehicles. The idea behind these algorithms lays on introducing some ‘oriented’ (non-uniform) random search when running the savings heuristic, while maintaining the logic behind it.
Population-based heuristics have also been proposed in the literature for dealing with the VRP with back-hauls. For example, Paraphantakul et al. [
65] proposed an ant colony system for a real case in Thailand. The particularities of that real problem motivated the use of this flexible algorithm. Küçükoğlu and Öztürk [
66] also developed an evolutionary algorithm for a real-life problem. Their proposed methodology was tested with several benchmarks, showing its efficiency. The algorithm is shown to outperform some of the best-known solutions for most of the instances.
4.3. Strategies Based on Horizontal Cooperation
In the case of horizontal cooperation, companies form a coalition for performing their logistics activities. This way, they can benefit from mutual cooperation. These benefits, which are described in [
67], include: (i) a significant reduction in transportation cost; (ii) a noticeable improvement in transport reliability; and (iii) a clear reduction of CO
emissions. Similar to the strategy for improving the load factors, problems dealing with more than one company are difficult to solve by using exact methods alone. Nevertheless, some horizontal cooperation approaches employ the ideas behind the multi-depot VRP (i.e., the classical VRP considering more than one depot). In these approaches, each depot is assumed to be owned by a company. Therefore, if the horizontal cooperation agreement successfully determines the allocation criteria and/or compensation mechanisms, it can be transformed into a multi-depot VRP setting. Contardo and Martinelli [
68] proposed a vehicle-flow and a set-partitioning formulation. The proposal by Bektaş [
69] is based on Benders decomposition, while Fernández et al. [
70] used a classical branch-and-cut algorithm for the multi-depot VRP.
The literature on the use of metaheuristics in horizontal cooperation is abundant. Pérez-Bernabeu et al. [
71] focused on the energy savings that can be achieved when applying horizontal cooperation policies. They implemented an iterated local search algorithm in order to obtain high quality solutions for the cooperative scenario. In fact, savings in energy consumption may reach up to 92% in a favorable scattered topology. Simheuristics, an extension of metaheuristics to deal with stochastic combinatorial optimization problems [
72], were proposed by Quintero-Araujo et al. [
73] and Quintero-Araujo et al. [
74]. The former compared a non-collaborative scenario against a collaborative one. The results illustrate the benefits of using horizontal cooperation in realistic urban environments. The latter tested a similar approach in a real case, which concerns the distribution of goods in convenience stores. Simulation was also applied by Serrano-Hernandez et al. [
75] for investigating the effect of different trust-related issues when forming a coalition. Several real-life case studies have also been illustrated. The proposals by Ballot and Fontane [
76] and Pan et al. [
77] are examples that both take place in France. The former work, based on retail chains, highlights potential savings of at least 25% in CO
emissions when cooperation occurs. The latter work, which is based on the food sector, pointd in the same direction but with a special focus on the relevant role that small and medium enterprises can play in horizontal cooperation. Both works use a solution approach that is based on the iterative local search metaheuristic framework.
4.4. Mixed Strategies
When different strategies are combined, further energy savings can be obtained. However, this increases the complexity of the resulting problems and makes the use of exact methods almost impossible. The combination of a
green objective function with load factor strategies is a recurrent topic in the literature. In Pradenas et al. [
78], a VRP with back-hauling and time windows is considered. Here, the objective function is the one proposed in [
43], and a scatter search algorithm is introduced for solving the problem. Likewise, Zachariadis et al. [
79] analyzed a similar problem based on the VRP with energy considerations. These authors also take into account both pick-ups and deliveries.
The combination of horizontal cooperation and back-hauling has a noticeable impact on the industry. A company with line-hauls can easily share their vehicles with a company with back-hauls, resulting in significant savings in costs and fuel consumption. This is the case, for instance, of the work developed by Bailey et al. [
80], where a greedy heuristic and a tabu search are selected to solve the cooperative problem. Additionally, the model was tested with real-life data from the transportation sector, resulting in a costs reduction of about 25% and leading to significant reductions in CO
emissions as well. Another example was provided by Juan et al. [
81], who compared a cooperative setting with a non-cooperative one. Similar to the previous works, the cooperative scenario is modeled as a multi-depot VRP. The solution approach consists of an iterated local search algorithm, resulting in savings of up to 25%.
Table 4 summarizes the relevant literature discussed in road freight transportation.
5. Rail Transit Systems
Research in this area has been motivated by the accelerated urbanization in several regions (e.g., China and Europe), which dramatically increased traffic congestion in these areas. This scenario has led to the offering of urban rail-transit systems as a transport mode with the ability to provide services for rising demand. Railways only account for about 2% of the total energy consumed by the transportation sector [
83]. However, with rising demand and frequent service, especially in the case of metro systems, there are opportunities to minimize the use of energy in rail transportation. Reducing fuel consumption has several benefits, including reducing CO
emissions and decreasing operating costs. Therefore, several approaches have been offered in the literature that would help with energy savings in rail operations. González-Gil et al. [
84] reviewed operator-related activities, while Scheepmaker et al. [
85] and Yang et al. [
14] reviewed energy-efficient train speed control and timetable optimization as two operational ways to preserve energy. In fact, it was shown by Yang et al. [
14] that 80% of the urban rail train energy is consumed by the traction system of the train, which is directly related to train operation strategies. Motivated by this finding, the current section also reviews efforts in the literature related to the mitigation of operational energy consumption via optimization approaches. We focus on two well-known approaches that help reduce fuel consumption in train operations: (i) train speed control (eco-driving) (
Section 5.1); and (ii) timetable optimization (
Section 5.2). We further discuss their integration in
Section 5.3.
5.1. Energy-Efficient Train Driving
Energy-efficient train driving, which is also referred to as “train speed control” or “eco-driving”, is the most popular approach to preserve energy in rail operations, mainly because of its ability to yield higher increments of efficiency [
86]. The goal is to obtain the optimal driving regimes (such as maximum acceleration, cruising, coasting, and maximum braking) along with a sequence of these driving regimes and guidelines about the switching points between them. The seminal study on energy-efficient driving dates back to the 1960s [
87]. Since then, it has attracted much attention in the literature. The work done in this area has actually proved to be very useful in practice. More specifically, energy-efficient train control has been shown to reduce energy consumption by 20– 30% when it is applied in driver advisory systems, which provide specific speed advice to train operators [
88].
The rich literature on energy-efficient train driving can be classified into several groups according to a number of factors. Scheepmaker et al. [
85] provided a very comprehensive classification based on: the consideration of continuous traction control or discrete settings, the utilization of regenerative energy, and the solution methods employed to solve the resulting optimization problems. Other survey papers in this area include those of Yang et al. [
14] focusing on urban rail transit, Gao and Yang [
89] focusing on modeling and optimization techniques, and Yin et al. [
90] focusing on automatic train operations (ATO) systems. One distinction factor is whether trains use continuous traction control or discrete traction throttle settings. Other factors that are considered in the model include on-board storage systems, train mass variations, unexpected delays, and driver’s behavior (if manual driving is used). Finally, a distinction can be made among different studies according to the solution method employed.
One common solution approach is as follows: (i) obtain the necessary conditions for optimality using the Pontryagin’s maximum principle [
91]; and (ii) solve these optimality conditions by employing numerical algorithms to obtain the optimal switching points between the regimes. This approach is named the indirect exact method, since it solves the necessary optimality conditions indirectly. Scheepmaker et al. [
85] provided a detailed review of those papers that employ this approach. An alternative approach to solve the optimal control problem is to convert it into a nonlinear optimization model and solve the resulting model using nonlinear programming methods. Betts [
92] provided the foundations of this approach. Wang et al. [
93,
94,
95] followed a similar approach.
Due to their flexibility in modeling complex scenarios, heuristic approaches are the most widely used methods in energy-efficient train speed control [
83]. Various heuristic approaches, in six different categories, are reviewed next:
Genetic Algorithms (GAs): GAs constitute the most widely used metaheuristic method according to an analysis conducted by Fernández et al. [
83]. Chang and Sim [
96] were among the first authors to propose a GA to solve the energy-efficient train driving problem. The goal is to create a coast control lookup table, which would dictate the operation of an ATO system by providing feedback on when to power-up, coast, or brake. The optimization problem minimizes the overall energy consumption by also taking into account the punctuality and rider discomfort as penalty functions. Han et al. [
97] considered a similar problem, where the goal is to identify the minimum energy-consuming schedule for a train which is driven in automatic operation mode along a non-constant gradient and with speed limits. The author also proposed a GA and compared it (in terms of energy consumption) to the exact algorithm in [
98]. The algorithms were tested on Seoul’s metro subway system. The results show a better performance of the GA in terms of energy consumption. Wong and Ho [
99] proposed a GA for a dynamic, real-time, and coasting-control problem. They compared the GA to three exact methods and provided a comprehensive discussion about the pros and cons of each method. Lechelle and Mouneimne [
100] developed a GA that minimizes energy consumption while adhering to some additional constraints regarding the train and track characteristics as well as operational constraints. The GA, which was applied to a tramway network of Rouen (France), shows about 7% energy savings compared to the current approach used by the system. Ma et al. [
101] also proposed a GA to minimize energy consumption, but with the additional consideration of running time, which is introduced as a penalty cost to the optimization problem. The algorithm was tested on an urban train system, and shown to reduce energy consumption by almost 11%. Sicre et al. [
102] combined a GA with fuzzy parameters for energy-efficient manual driving. The fuzzy parameters help to capture the uncertainty in manual driving operations. The objective of the GA is to find a solution with a target running time and minimal energy requirements. The algorithm was implemented on a real Spanish high-speed train line, and shown to provide an improvement of about
% over the traditional manual-driving method. Chevrier et al. [
103] proposed a bi-objective evolutionary algorithm that yields a set of solutions optimizing both the running time and energy consumption. The compromise between the running time and energy consumption is summarized using a Pareto curve. The algorithm was tested on two case studies, where significant energy savings were achieved as a result. Considering a train as a continuous rigid particle chain, Lin et al. [
104] devise da multi-point combinatorial optimization problem with the consideration of multi-point coasting control. A GA is used to solve this problem using data from the Shanghai metro.
Numerical Simulations: Domínguez et al. [
105] developed a comprehensive simulation model of the Madrid’s metro system to determine the optimal speed profiles. The simulation model yields a Pareto curve, which helps to determine the most energy-efficient speed profile given the running time of the train. The approach was shown to yield about 13% energy savings, and resulted in the redesign of the current ATO speed profiles. Domínguez et al. [
106] further extended this study to consider regenerative breaking in the substations. Energy savings from
% to
% are reported. Dominguez et al. [
107] considered the possibility of storing the regenerated energy and feeding it back to the train by means of an on-board energy-saving device. The new model shows about 20% energy savings compared to the current practice.
Ant Colony Optimization: Ke et al. [
108] considered a block-layout design between successive stations for mass rapid transit systems. The energy saving problem is formulated as a combinatorial optimization problem, which is then solved by ant colony optimization. Ke et al. [
109] further extended the previous algorithm to consider a moving-block system metro line, which can perform online optimization with further energy savings of up to
% compared to the former algorithm.
Tabu Search: Motivated by the inaccuracy in speed tracking of ATO drivers, Liu et al. [
110] proposed two tabu search algorithms for the energy-efficient train problem. The resulting algorithms were tested on two case studies conducted with the Beijing subway. The first case study shows about
% energy reduction, while the second case study shows
% energy reduction. The main advantage of both algorithms is their speed, i.e., they both provide a good solution within 1 s, which makes them suitable for online control of trains.
Artificial Neural Networks: Chuang et al. [
111] proposed an artificial neural network for the energy-efficient driving problem with two objectives: minimizing energy usage and traveling time of passengers. A two-layer network was tested on the Kaohsiung (Taiwan Island) transit system and shown to provide energy savings with a small increase in the passengers’ travel time.
Particle Swarm Optimization (PSO): Domínguez et al. [
112] presented a multi-objective PSO algorithm, which considers both the running time and the energy consumption as objectives. This algorithm, which is based on the accurate simulation of the ATO and train motion, leads to a Pareto curve that compromises between the running time and the energy consumption. The algorithm is shown to provide better computational time compared to a non-dominated sorting GA. Considering the two main uncertainties in a train operation, i.e., the train load and the delays in the line, Fernández-Rodríguez et al. [
113] developed a model that designs robust and efficient speed profiles that can be integrated into an ATO system. The model also takes into account the running time and energy consumption as objectives. The proposed procedure has the following steps: in the first step, a Pareto curve of all possible speed profiles that are robust to passenger load variations is obtained; and, in the second step, a PSO algorithm, which also takes into account energy efficiency and possible delays, is used to select the speed profiles from the robust Pareto frontier. This procedure was tested on a case study, showing that the inclusion of the delay factor provides energy savings of up to 14%.
Finally, some studies compare different heuristic approaches and exact approaches. For example, Lu et al. [
114] compared a GA, an ant colony optimization algorithm, and dynamic programming over a variety of instances. The results favor the ant colony algorithm over the GA because the latter is not able to converge to good solutions in instances with large trip times. Dynamic programming provides better quality solutions, but suffers from the computational time involved. The authors recommended the use of multiple algorithms to solve the energy-efficient train optimization problem in order to obtain higher quality solutions.
5.2. Energy-Efficient Train Timetabling
Scheepmaker et al. [
85] defined timetabling optimization as the scheduling of trains on a railway network that allows as much energy-efficient driving as possible. The goal is to determine the running time of a train (or multiple trains) between two stations in such a way that the total energy consumption is minimum. When multiple trains are considered, regenerative braking—which allows the energy generated by a train during braking to be transferred to another train—provides an additional opportunity for saving energy. Accordingly, Yang et al. [
14] defined the goal of the timetable optimization as “finding the optimal timetable such that the regenerative energy can be furthest used to accelerate other trains”. Regenerative braking is especially helpful in urban rail networks, which consume more energy than other rail networks. In this section, we discuss energy-efficient timetable optimization methods with a particular goal of utilizing regenerative braking as much as possible.
Timetable optimization and energy-efficient driving are directly related to each other. More specifically, the outcome of the timetable optimization method is fed into the energy-efficient driving method as running times. The energy-efficient driving method then provides the acceleration and braking times to the timetable optimization method. The timetable optimization problem has mostly been modeled as an integer programming model or a mixed integer programming model. Due to the complexity of these models, heuristic approaches (e.g., genetic algorithms and simulated annealing algorithms) have been heavily utilized in the literature. In the remainder of this section, we briefly review the employed heuristic algorithms:
Genetic Algorithms: Albrecht [
115] was among the first to present a GA to solve a model that reduces power peaks and energy consumption to control the running time of trains with given headway and synchronization times. Controlling power peaks is directly related to better utilizing the regenerative energy. This situation is explained in the following lines: if the power peak is not controlled, then the voltage of the overhead contact line (that transfers the energy) reaches its maximum level and the regenerative braking is replaced by mechanical braking (which causes the energy to be lost as heat energy). Chen et al. [
116] considered the scheduling of multiple trains, so that the total traction power load can be evenly used and, hence, peak power consumption can be reduced. The experiments illustrate that GA does a good job in providing an optimal solution with reduced maximum traction power. There are also papers that examine direct approaches to the better utilization of regenerative energy. Nasri et al. [
117] optimized the scheduling of multiple trains in order to better utilize the regenerative energy by taking into account the effect of headway and reserve times on the amount of energy consumption. The proposed GA is shown to reduce the energy consumption up to 14%. Fournier et al. [
118] developed a model to modify the dwell time of metro trains, so that accelerations and braking are better synchronized and regenerative energy is utilized. The model is solved with a hybrid algorithm (that combines linear programming with a GA), showing up to 6% energy savings. Yang et al. [
119] formulated an integer programming model that maximizes the overlap time between successive trains with headway time and dwell time control, such that accelerating and braking synchronization is better achieved. They used a GA to solve this model and tested the algorithm on six case studies using data from the Beijing subway in China. The results show a 22% increase in the overlap time during the peak hours, and about 15% increase in the overlap time during the off-peak hours. Yang et al. [
120] further extended their previous model to also minimize passenger waiting times and coordinate up and down trains at the same station, so that regenerative energy is better utilized. A two-objective integer programming model is developed and solved with a GA, which is shown to save energy by
% and reduce passenger waiting times by
%. Yang et al. [
121] further extendrf their previous works by considering more realistic situations. For example, up and down trains located in the same electric supply interval are considered, and the operation time is extended to one day. They developed an integer programming model whose goal is to fully utilize the regenerative energy while taking into account the aforementioned considerations. A GA, combined with an allocation algorithm, is devised to solve this model. The resulting algorithm is shown to improve the utilization of regenerative energy by
% and to reduce total energy consumption by
%. Li and Yang [
122] considered stochastic delay times and running times. They proposed a stochastic cooperative scheduling approach with the goal of maximizing the utilization of regenerative energy. Again, a GA is shown to provide energy savings of about 15%. More recently, Yang et al. [
123] presented a multi-objective timetable optimization approach that integrates energy consumption, passenger waiting time, and robustness (defined as eliminating the effect of delays). The resulting model is solved with a non-dominated sorting GA, which was tested on a real-life dataset obtained from the Beijing metro. The results show that this approach can decrease total energy consumption by
%, while improving the passenger waiting time by
% and robustness by
%.
Simulated Annealing: Zhao et al. [
124] formulated an optimization model with two objectives, overlapping time (as a measure of regenerative braking energy utilization) and total passenger time. They designed a simulated annealing algorithm to solve the optimal timetable. Experiments, which were conducted with real-life data from Hong Kong, show that the resulting algorithm reduces the overlapping time by
%, as well as the total passenger time by
%. Le et al. [
125] developed a nonlinear integer programming model to maximize the utilization of regenerative braking energy. A simulated annealing algorithm is used to solve the model, which is shown to provide improvements between 4% and 12% in the utilization of regenerative braking energy.
Swarm Intelligence Algorithms: Liu et al. [
126] presented a timetable optimization problem that maximizes the use of regenerative braking energy by considering dwell time and headway time as decision variables. They proposed an improved artificial bee colony optimization algorithm and compared its performance with the CPLEX solver and a GA.
5.3. Integrated Approaches
Observing the benefits of eco-driving and timetable optimization approaches, several researchers have looked at the integration of these two approaches as a way to achieve further energy savings. Considering the complexity of each individual approach, the integrated approach turned out to be more sophisticated. Su et al. [
127] provided examples of numerical algorithms to solve the integrated problem. However, most papers consider the use of heuristic approaches—such as GAs and simulation annealing algorithms—to solve the so-called integrated problem. Yong et al. [
128] formulated a two-level hierarchical model. The first model decides the appropriate coasting points and number of inter-station runs of an urban rail train, while the second model decides on the travel time of a train in the inter-station runs by minimizing its energy consumption. This two-level optimization model is solved by a GA, which is shown to offer energy savings of about
%. Yang et al. [
129] formulated an integer programming model to reduce energy consumption and total travel time. The optimal timetable and speed profile are determined by solving an adaptive GA. The experimental results show that energy consumption can be reduced by
%, while achieving a reduction in travel times of about
%. Focusing on net energy consumption (which is defined as the difference between the tractive energy consumption and the utilization of regenerative energy), Li and Lo [
130] formulated an optimization problem to optimize both timetable and speed profile. They used a GA to solve this optimization model. Moreover, the integrated approach was compared to the timetable optimization model by Yang et al. [
119] and to an energy-efficient driving method by Su et al. [
131]. It is shown that the integrated approach improves about
% over the energy-efficient driving method and about
% over the timetabling method. More recently, Su et al. [
132] analyzed the integrated train problem with some additional considerations, including passenger demand, headway, cycle time, turn back time, and trip time. Dynamic programming is used to solve a multi-step decision problem that is formulated to find the optimal driving strategy. Then, a simulated annealing algorithm—based on the results of a dynamic programming approach—is used to solve the timetable optimization model. The resulting approach balances the traction energy and the use of regenerative energy so that the net energy consumption is minimized. The algorithm was tested using real-world data from Beijing. The results show that the net energy consumption can be reduced by up to
% compared to an approach that only performs a regenerative energy optimization.
Finally, there are studies that combine two heuristic approaches to obtain an improved timetable. For example, Huang et al. [
133] used a GA combined with a PSO algorithm to solve an integrated problem that optimizes the trajectories of trains, dwelling time of trains, and the timetable, in order to better use the regenerative braking energy. Again, a GA is utilized to optimize the energy-efficient operation of a single train. Then, PSO is used to find an optimal timetable for multiple trains that minimizes the overall energy consumption. The proposed approach is shown to reduce the total energy consumption by
%.
Table 5 provides a summary of the literature on passenger railroad transportation. As can be gleaned from the table, GAs constitute the solution method of choice for both eco-driving and timetable optimization. The combination of these two strategies (i.e., integrated approach) calls for more sophisticated methods such as the integration of two heuristic approaches.
6. Maritime Transportation
Maritime transportation is a critical element of international trade. Specifically, 80% of the total world merchandise trade in 2015 was achieved by maritime transportation [
134]. However, there is a counterpart: the maritime sector is a major contributor to the greenhouse effect. In fact, the International Maritime Organization reports that in 2012 maritime transport already emitted
% of the world’s total CO
emissions [
135]. This number is expected to increase around 150–250% by 2050 [
136] due to the rising demand for this mode of transportation. Considering the global energy crisis and the necessity of energy conservation and emissions reduction, it has become a fundamental challenge for the development of maritime technology to achieve energy efficiency [
137]. According to Rehmatulla et al. [
138], several solutions exist for reaching energy efficiency: (i) the use of energy efficient technologies; (ii) the utilization of renewable energy sources; (iii) the use of fuels with lower carbon content (such as biofuels); and (iv) the implementation of emission-reduction technologies. However, while these alternatives may be the best option for newly-built ships, their application in most existing ships could not always be possible due to the long payback period [
139,
140]. For these cases, some academics have proposed energy-saving methods based on operational optimization measures and energy-efficient management strategies. In this regard, Crist [
141] summarized the potential measures for saving fuel in-service ships. Other researchers, such as Wang et al. [
135] and Tian-yun [
142], state that the efficiency of ships mostly depends on environmental factors—such as wind speed and direction and on water speed and depth. According to other experts, ‘speed reduction’, ’reduction in fuel consumption’, and ’routing based on weather’ are three important factors that need to be considered [
143,
144]. Hence, the combined effects of the previous factors have to be considered when evaluating energy-efficiency measures.
Table 6 summarizes the relevant literature in maritime transportation.
6.1. General Speed Reduction
Speed is considered an important variable in shipping transportation [
146], and it is a key aspect for the world trade volume growth. In fact, high speed vessels are shown to help the delivery of goods on time, and also help to reduce the inventory costs [
146]. However, their effectiveness has been questioned from an environmental perspective [
147]. Most of the research in this area assumes fixed and deterministic ship speed [
12]. However, this unrealistic assumption has been challenged by some authors. For example, Wang et al. [
135] acknowledged the influence of environmental factors on speed and its inherent uncertainty. Therefore, to mitigate and predict it, they proposed a dynamic optimization method. The resulting algorithm is shown to achieve real-time energy efficiency. Notice that accurate demand prediction has been a big concern among academics. In this regard, the wavelet neural network method has been the most widely used approach due to its good predictive performance [
140,
145]. In another study, Fagerholt et al. [
148] reconsidered the optimal speed problem but with additional time-window constraints. The authors originally devised a nonlinear program. The novelty of this work is the approach in discretizing the demand, which allows the authors to solve this problem as a shortest path problem. This approach is shown to work well and provide significant energy savings.
6.2. Weather Routing
Weather routing of a ship concerns the identification of an optimal path for a ship based on the weather factor and the characteristics of the ship [
146]. Traditionally, the impact of weather in ship routing has been ignored and the ultimate goal has focused either on profit maximization or on the minimization of fuel consumption with additional considerations—e.g., the need for matching supply and demand at different ports that need to be visited [
149]. However, some researchers—for example, Padhy et al. [
150] and Wen et al. [
151]—emphasized the importance of taking into account weather and the wave factors while routing ships.
According to Meng et al. [
152], the majority of the literature focus on the so-called environmental routing problem (ERP), which aims to find an optimal route for a ship given the existing environmental conditions. One shortcoming of the traditional ERP is its ignorance of the ever changing weather conditions. In this regard, Wang et al. [
135] developed a dynamic model that is capable of taking into account real-time environmental conditions. Studies with a similar approach include those by Azaron and Kianfar [
153] and Shao et al. [
154]. Both studies use dynamic programming methods to capture the dynamic aspect of the problem. Rehmatulla et al. [
138] devised a multi-objective optimization model with objectives including fuel consumption, safety factors, and estimated time of arrival of a ship. This model is also able to take into account sophisticated weather forecasts. The authors also showed the applicability of a multi-objective GA approach for this problem.
6.3. Fuel Consumption Monitoring
Fuel consumption is found to be influenced by a number of factors, including the sailing speed, the weight of the ship, the cargo, the capacity of the bunker, and the weather conditions [
152]. Therefore, developing fuel management strategies is fundamental for determining the adequate amount of fuel in order to improve the performance of the fleet [
146]. However, it is surprising that only a few studies look at the relationship between environmental factors and ship fuel consumption. Two notable studies were presented by Wang and Meng [
155] and Brouer et al. [
156]. Meng et al. [
152] approached this problem in a more systemic way and developed an approach to investigate the relationship between fuel usage and several other factors, including weather conditions, sea conditions, sailing speed, etc. More recently, De et al. [
149] devised a robust mathematical model that, in addition, considers sustainability and disruption aspects. The resulting model is solved with a variable neighborhood search algorithm.
7. Air Transportation
The attention to air transportation has been increasing steadily over the last years. According to the International Civil Aviation Organization, three billion passengers traveled worldwide in 2013, while this number is expected to more than double by 2035 [
157]. This tremendous increase in passengers poses several challenges to the air transportation industry. One of the challenges is the need for capacity extensions to match supply and demand. This situation forces the airports to better utilize their resources and conduct their operations more efficiently [
158]. Several types of optimization problems arise in the aviation sector. A recent taxonomy of those problems was provided by Ng et al. [
159], who divided the air-side operations into three main categories: (i) airspace and air traffic flow management (subcategories: aircraft collision avoidance and flight path optimization); (ii) aircraft operation in the terminal maneuvering area (subcategories: aircraft sequencing/scheduling and fleet scheduling); and (iii) surface traffic operation (subcategories: aircraft maintenance routing, airport ground service scheduling, taxiway optimization, and aircraft gate assignment). The objectives of these problems fall into five major categories [
159]: (i) economic objectives that focus on cost minimization, profit maximization, or revenue maximization; (ii) customer satisfaction related objectives that deal with reliability, disruption management, failure prevention, etc.; (iii) operational efficiency with a focus on delay minimization, airborne and air traffic balance, turnaround maximization, airport resource management, etc; (iv) safety-related objectives that study collision avoidance, weather uncertainty, etc; and (v) environmental objectives that look at carbon emissions, noise, and energy consumption. Most of the literature is focused around the first four objectives, while the research on the fifth one is rather recent and limited.
Energy efficiency can be gained in a number of ways, including the innovative design of an aircraft, the utilization of sustainable alternative fuels, or the optimization of operational procedures. Although technological advancements and alternative fuel usage are heavily implemented to gain energy efficiency, designing more efficient operational procedures can achieve the same objective at a much lower cost (i.e., without investing in new technologies). Furthermore, designing new technology or new types of fuels is time-consuming, and observing their benefits could take a long time frame. On the contrary, operational improvements can be implemented in a short time frame, and their benefits can be enjoyed readily. We refer the reader to the work of Evans [
160] for a comprehensive discussion around new technologies and new types of fuels for greener air transport.
Energy-efficient operations are usually represented in an aviation model with concerns about fuel consumption. Most of the time, optimization problems are multi-objective and ‘fuel consumption minimization’ appears as one of the objectives. Therefore, heuristic methods are largely employed to solve these problems. There are some studies whose results imply less fuel burn, even though the energy efficiency is not their main focus [
161]. In this section, however, we only analyze studies that explicitly consider fuel consumption as the objective function or as one of the constraints of the model.
Table 7 provides a summary of the literature in this area.
7.1. Aircraft Trajectory Optimization
Air trajectory optimization (ATOp) is one of the well-studied problems in air transportation. The goal is to determine the entire trajectory to be flown by an aircraft, while adhering to potential constraints during the climb phase, cruising phase, and descent phase of the flight [
171]. Hammad et al. [
172] provided a survey on ATOp problems with a focus on sustainability considerations. Fuel cost minimization is at the heart of the ATOp problem, and many of the reviewed papers consider fuel usage as the most frequent economic objective considered. Which solution method is employed to solve an ATOp problem depends on how the optimization model is formulated. Problems with a single objective are solved by both mathematical programming models and heuristic methods. Among the most frequently used heuristics are GAs and simulated annealing algorithms. Problems with multiple objectives are solved using methods including lexicographic optimization [
173] and non-dominated genetic sorting algorithms [
163].
Pervier et al. [
162] used a GA to minimize the fuel burnt and nitrogen emissions. Celis et al. [
163] illustrated the applicability of GAs in solving the aircraft trajectory optimization problem using three case studies. The optimization problems under consideration include objective functions of fuel cost minimization, total flight time minimization, and nitrogen emission minimization. Hasegawa et al. [
174] considered trajectory optimization with several realistic constraints. Pursuing the minimization of fuel cost, a GA algorithm is used to solve the problem. The effectiveness of the algorithm is illustrated in a study concerning a real airport, where a more efficient trajectory is obtained. Focusing on the cruising phase of a flight trajectory, Patrón and Botez [
175] presented an in-cruise optimization model that aims at minimizing the flight cost. A GA is implemented to solve this problem, achieving a cost reduction of about 5%. Zhang et al. [
164] also studied the flight trajectory optimization problem with environmental considerations, with the goal of minimizing the consumed energy and pollutants such as carbon-dioxide and nitrogen. They used a GA to solve this problem. The novelty lies in the approach that is applied to discretize the dynamics equations on the vertical and lateral motion planes.
Bouttier et al. [
165] developed a noisy simulated annealing algorithm for aircraft trajectory optimization. It takes into account uncertainties in environmental conditions and air traffic control operations. Finally, Ho-Huu et al. [
166] utilized the multi-objective evolutionary algorithm based on decomposition, which integrates the fuel consumption and noise as components of the objective function.
7.2. Airport Ground Operations
The literature on airport ground operations encompasses several problems, including taxiway optimization (the ground movement problem), the aircraft gate assignment problem, the airport ground service scheduling problem, the runway scheduling problem, and the aircraft maintenance routing problem. Those problems are related to each other. Some papers look at individual problems, while others simultaneously consider two or more problems as their results affect each other.
Taxiway Optimization: This is also referred to as the ground movement problem, and is mostly focused on minimizing total taxi time of one or more aircrafts on the airport surface [
176]. Ravizza et al. [
167] were the first to study the trade-off between taxi time and fuel consumption during taxiing. A bi-objective optimization problem is developed, which simultaneously minimizes the taxi time and fuel consumption. A routing and scheduling problem, called the
k-quickest path problem with time windows, is solved with a population-based algorithm, which allows the analysis of the trade-off between taxi time and fuel consumption. This algorithm performed well with real-life data from the Zurich airport. The primary result is that this trade-off is very sensitive to how the fuel-based objective function is modeled. With the goal of speeding up the approach of Ravizza et al. [
167], Weiszer et al. [
177] proposed a multi-component optimization problem that combines the ground movement problem and the speed profile optimization problem. Two objective functions are considered: minimization of total taxi time and minimization of fuel consumption. The goal of the ground movement problem is to route aircrafts from one destination to another in a fuel efficient manner, while adhering to the constraints of other aircrafts around them. The speed profile optimization problem, on the other hand, aims at finding the optimal speed profiles in four different phases (acceleration, traveling at constant speed, braking, and rapid braking), while minimizing taxiing time and fuel burn simultaneously. Tianci et al. [
168] decomposed the ground movement problem and the speed profile optimization problem, so that the results on the former can be fully utilized. An approach utilizing PSO is presented. The resulting heuristic is shown to generate fast and efficient solutions. Chen et al. [
178] introduced a decision-making framework that integrates the efficient speed profiles generated in [
179] into a routing and scheduling framework. The goal here is to minimize the total time and the fuel burnt. The resulting framework was tested using data from the Zurich and Manchester airports, showing a 9% and 50% reduction in time and fuel consumption, respectively.
Runway Scheduling: Runway scheduling encompasses two problems: ‘the aircraft landing problem (ALP)’ and ‘the aircraft take-off problem’. The goal is to determine the sequence of landing or taking-off aircrafts on a runway or multiple runways, while optimizing certain objectives subject to given constraints [
180]. Focusing on the ALP, Mesgarpour et al. [
169] considered a multi-objective optimization model with the goal of minimizing average delay, maximizing runway throughput, and minimizing fuel cost. Since the resulting problem is
NP-hard, the authors suggested the use of a heuristic method. Later, Mesgarpour [
181] compared the performance of dynamic programming, iterated descent, and simulated annealing algorithms for the static ALP, using data from the Heathrow airport. The optimization model minimizes extra fuel cost arising from trying to achieve the desired landing schedule, as well as costs related to violations of time windows regarding landing times. It also tries to maximize runway throughput. All three algorithms are found to perform well, but the iterated descent algorithm is found to be computationally faster. The iterated descent is also the preferred approach for the dynamic version of the problem. Recently, Rodríguez-Díaz et al. [
182] proposed a multi-objective ALP with the goal of maximizing runway capacity and also minimizing the fuel consumption and noise levels. The Pareto frontier is explored via the
-constraints method. Using real-life data, a
% reduction in fuel consumption was achieved.
Integrated Approach: Since airport ground operations are related to each other, it is important to consider an integrated approach, which takes into account multiple sub-problems and the interactions among them. The sub-problems are difficult to solve already, making their combination an even more challenging problem. Therefore, heuristics have been utilized in the literature for the integrated problems. For example, Weiszer et al. [
170] considered three airport ground operations simultaneously: the ground movement problem, the runway scheduling problem, and the airport-buses scheduling problem. They proposed an integrated optimization problem, which seeks to minimize the total time, fuel consumption, and bus scheduling cost. The resulting problem is solved with a GA. Weiszer et al. [
183] further enriched this model by incorporating preferences of the decision maker to a multi-objective optimization model, thus facilitating the generation of the Pareto frontier.
8. Discussion
With the expected increase in transportation activities, optimization of energy consumption becomes more and more relevant [
184]. As shown in this review, many authors have already started to propose energy-related optimization models and algorithms in the field of freight road, passenger train, maritime, and air transportation. Some of these models and solution approaches have been able to produce results that could have a noticeable impact on current and future real-life transportation activities. For instance, in the area of freight road transportation, savings up to 25% in CO
emissions have been obtained when considering horizontal cooperation concepts in realistic environments [
76]. Similar savings in cost reduction have also been achieved when combining back-haul with horizontal cooperation strategies [
80]. Likewise, in the field of passenger rail transportation, reductions between 20% and 30% in energy consumption have been obtained by optimizing speed in trains [
88]. In addition, other works related to timetable optimization have achieved reductions of about 2% in total energy consumption, while improving the passenger waiting time by almost 16% [
123]. Similarly, in the area of maritime transportation, some works have obtained significant energy savings for the optimal speed problem [
148], while others have formulated weather-dependent and multi-objective versions of the environmental routing problem [
135,
138]. Finally, in the field of air transportation, potential savings in flight cost of up to 5% have been shown in the aircraft trajectory optimization problem [
175], while savings in fuel consumption between 9% and 50% have been achieved for the taxiway optimization problem [
178].
Although it is not easy to predict the exact level of reduction in energy consumption, our review shows that optimization algorithms can make a significant contribution to achieve this goal. Many factors have a substantial impact on final savings. Additionally, these factors are different depending on the transportation mode under study, the particularities of the problem itself, the sophistication of the optimization method employed, etc.
Table 8 shows a set of scientific articles that consider minimization of energy consumption using OR methodologies. In particular, the following information is provided: the paper reference, the associated transportation mode, the mathematical model related to the energy optimization process, and the energy savings (in percentage) achieved via the solving procedure. The table also illustrates to what extent optimization methods can help to reduce energy consumption in different transportation modes. According to the selected studies, feasible achievable savings range from 15% to 30%, with some extreme cases.
In all the considered transportation modes, similar trends can be observed: (i) the incorporation of richer and more realistic optimization problems, including time windows in transportation deliveries as well as other real-life conditions (disruptions, speed limits, etc.); (ii) the consideration of multiple objectives, including transportation cost, CO emissions, waiting times, etc.; and (iii) the need to deal with disruptions, variations in demands, dynamic traffic conditions, etc.
The aforementioned trends also open uncountable research opportunities, mainly due to the complexity of modern transportation systems, which include multi-modal as well as integrated freight and passenger transportation networks working under uncertainty and dynamic scenarios. These opportunities are further discussed in
Section 9.
9. Conclusions and Future Work
This paper reviews existing work on energy-related optimization in the field of transportation with a focus on some of the most popular energy-related optimization challenges in road, train, maritime, and air transportation. The focus is on exact and approximated approaches that have successfully contributed to the reduction of emissions as well as energy consumption. In particular, and in response to our first research question, the work identifies those energy-related optimization problems that have been more frequently studied in the existing literature, i.e., vehicle routing problems with green objective functions, back-hauls, and horizontal cooperation strategies in freight road systems; energy-efficient driving and timetabling in passenger rail systems; speed optimization, weather-based routing, and fuel consumption in maritime systems; and aircraft trajectory optimization as well as airport ground operations in air transportation systems. In addition, and in response to our second research question, some common characteristics and trends can be observed in all these transportation modes. Among the identified characteristics are the growing use of richer and more realistic models, the consideration of multi-objective problems, and the increasing inclusion of realistic conditions, which include dynamic and uncertainty components. The trends include: (i) the shift from a monetary-efficient economy (i.e., with the main goal of minimizing the monetary cost of transportation operations) towards a multi-objective economy, where dimensions such as the environmental and social impact (i.e., sustainability) of transportation activities will also have to be considered; and (ii) due to the different number of transportation modes available and the increasing sources of energy (both renewable and carbon-based), more options are offered to decision makers in the supply chain, including combinations of the available alternatives. Hence, energy mix and transportation-mode mix opportunities will emerge. This shift towards a multi-objective, multi-modal, and multi-source economy makes the use of optimization methods more necessary than ever. In addition, due to the increasing complexity and large-scale nature of most modern transportation networks, heuristic-based algorithms are becoming the predominant methodology in most realistic applications.
The paper also states the need for even more powerful approaches that can effectively cope with energy-related optimization problems under uncertainty and dynamic scenarios, or even under the pressure of providing reasonably good transportation plans in real time. In particular, and related to our third research question, many energy-related optimization research opportunities are still to be explored. New hybrid methods and algorithms are required to deal with the increasing complexity of transportation systems. For instance, the increased cost of renewable fuel may vary greatly. Therefore, flexible optimization algorithms that can capture these changes and recommend the most efficient combination of transportation modes are needed. Uncertainty and dynamism in these costs need to be considered as well. Algorithms combining metaheuristics with simulation and machine learning methods can provide the required flexibility. Simulation allows us to mimic the behavior of a process or system and gain more insight about it. Simulation models are capable of representing real-life uncertainty (such as uncertainty in customers’ demand and/or traveling times) via the use of probability distributions. They also allow us to model complex relationships in large-scale transportation systems. The increase in computing power and the wide availability of simulation software have sped up the use of simulation techniques during the last years [
9]. One drawback of simulation, however, is that it is not an optimization method itself. Therefore, it cannot be used to solve the energy-related optimization problems discussed in this survey. Fortunately, simulation can be combined with heuristic algorithms to deal with stochastic optimization problems. This hybridization is known as
simheuristics, and it has already been used to solve transportation-related problems under uncertainty [
72,
185]. Examples of simheuristics applications in the area of transportation can be found in the works of Gonzalez-Martin et al. [
186], Gruler et al. [
187], and Guimarans et al. [
188]. However, the application of simheuristics to solve energy-related optimization problems in rail, maritime, and air transportation remains as an area to be explored by researchers and practitioners. Another emerging hybrid methodology involves integrating metaheuristics with machine learning algorithms to solve energy-related transportation problems with dynamic elements—such as dynamic traffic conditions. One such approach is called
learnheuristics [
189,
190]. Another extension of optimization methods refers to the use of ‘agile’ algorithms that are able to provide real-time solutions as the dynamic systems evolve over time. One such example is the work of Fikar et al. [
191], who used a fast discrete-event-based heuristic to solve a complex transportation problem with synchronization issues.