1. Introduction
The emergence and development of greenhouses have overturned the cultivation patterns of traditional agriculture, allowing plant growth to occur beyond the limitations of the natural environment by creating a growing microclimate isolated from the external conditions [
1]. This all-season production with high efficiency makes it possible to secure the food supply for the ever-increasing population and ensure the sustainable development of human society [
2]. However, the high cultivation output of greenhouse agriculture requires significant energy consumption and high capital [
3]. For heating purpose, large amounts of fossil fuel, natural gas, liquefied petroleum gas, and various expensive heating devices are required in greenhouses, especially during cold seasons; fossil fuel accounts for more than 50% of the total energy consumption, which, in principle, is disadvantageous for sustainable development [
4,
5]. Thus, greenhouse agriculture requires a choice between efficient and costly production. In recent years, the worldwide application of Chinese solar greenhouses has offered an unprecedented opportunity to break the impasse [
6,
7]. Unlike conventional greenhouses, Chinese solar greenhouses provide a suitable environment for various crops throughout the year without the requirement of auxiliary lighting and heating, even in areas at latitudes near 40° and when the outside air temperature falls below −10 °C [
8].
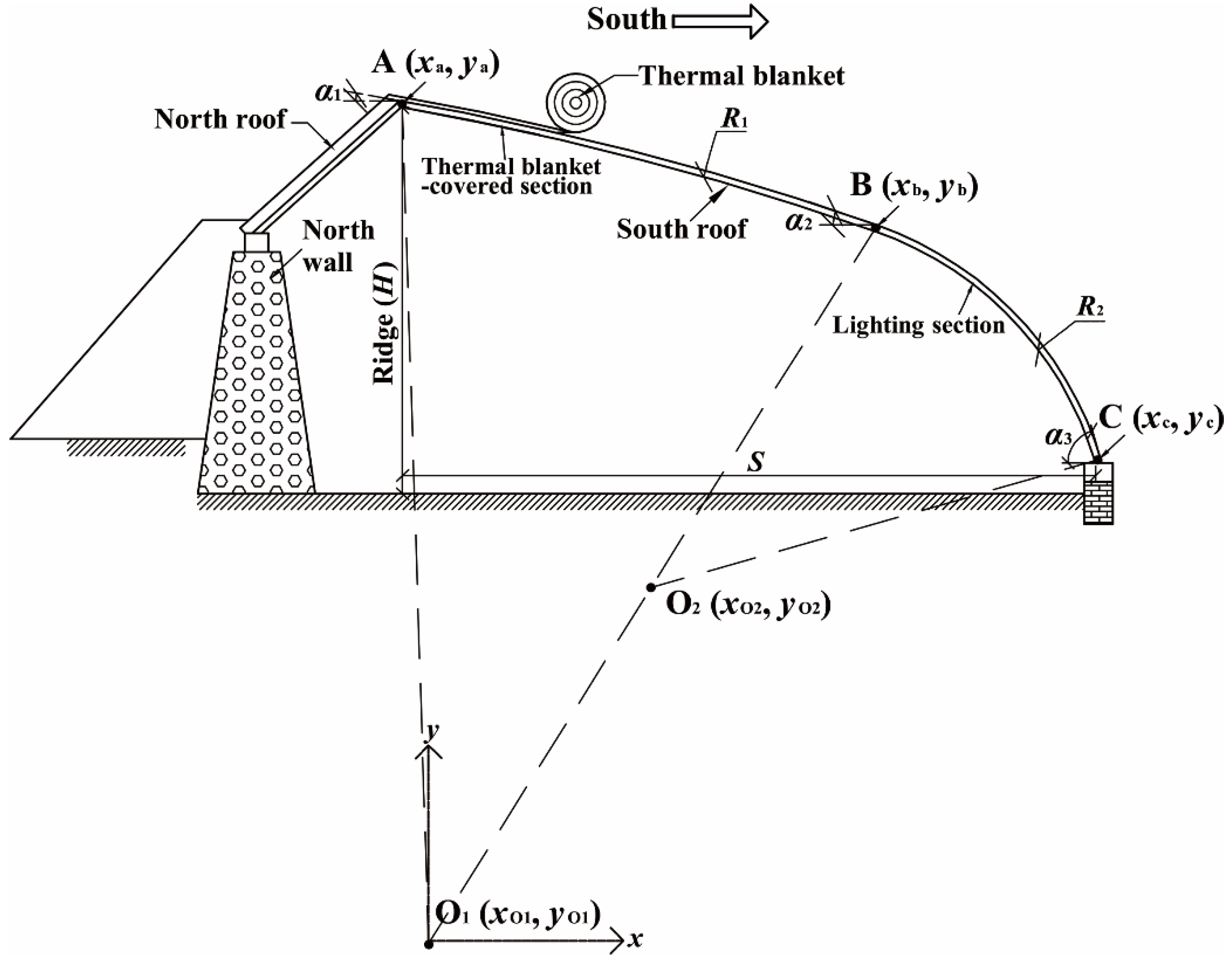
The smooth operation of a Chinese solar greenhouse under such a harsh environment is achieved owing to its unique building envelope, which is designed to make full use of solar energy [
9]. The building envelope of a solar greenhouse is mainly composed of the south roof, north roof, and north wall. The ground under a solar greenhouse also plays an important role in the greenhouse operating system. Generally, the south roof is made of plastic light-passing materials characterized by selective transmittance, and, during nighttime, it is covered with a thermal blanket for insulation. The selective transmittance of the roof materials results in the greenhouse effect. In other words, during the daytime, the south roof is transparent to short-wave solar radiation, performing the lighting function, and opaque to long-wave radiation, performing the heat preservation function [
10,
11]. Further, during the daytime, the external solar radiation enters the solar greenhouse through the south lighting roof, and a part of it provides energy for the photosynthesis process in crops with dynamic growth indexes (plant height, stem diameter, and leaf area), and the rest falls on the various internal surfaces [
12]. The falling solar radiation rises the internal surface temperature, and then warms the inside air via convection; meanwhile, the north wall and the ground, two large building components with high thermal capacity, continuously transfer the solar energy to their interiors from the warming surfaces, and then store it as heat [
13,
14]. During the nighttime, there is no longer solar energy supply, and the temperature difference between the inside and outside drives the dissipation of the heat energy in the solar greenhouse to the outside environment, which will result in a decrease in the inside air temperature. Meanwhile, the north wall and the ground release the solar energy stored during the daytime to the greenhouse space to compensate for the greenhouse’s heat loss caused by the temperature difference with the outside environment, effectively stabilizing the nocturnal air temperature fluctuation. These processes occurring within the solar greenhouse induce a comfortable temperature environment for off-season crops planting. Therefore, in solar greenhouse cultivation, the spatial distribution of solar radiation directly influences the crop photosynthesis, and the solar radiation allocation in each component affects the construction of the greenhouse’s thermal environment; these two parts constitute the solar greenhouse light environment. It was determined that a favorable light environment is the foundation of a desirable growth environment for crops and is key in the solar greenhouse design.
Although the nocturnal operation of a conventional greenhouse is driven by heating systems, the light environment in the daytime not only functions in crop photosynthesis but also regulates the inside air temperature by the greenhouse effect. The diurnal light environment is very important for the conventional greenhouse energy balance and determines the nocturnal heating demand [
15]. Considerable studies have been carried out on the light environment of conventional greenhouses and attempted to reduce the greenhouse running cost by combining the diurnal natural lighting and the nocturnal auxiliary heating. Sethi [
11] analyzed the lighting performance of the five most commonly used greenhouse types and tried to select the optimum orientation for lowering the heating load by maximizing the received solar radiation. The investigation was done by developing a mathematical model for computing the hourly transmitted total solar radiation, and the monthly total solar radiation incident on the greenhouse cover was used to estimate the greenhouse’s solar radiation availability. Their results suggested that a greenhouse with an east-west orientation should be used in the northern hemisphere. Similarly, Çakır and Şahin [
16] calculated the amount of external solar beam radiation reaching greenhouse covers with different shapes. A comparison among seasonal total solar energy gaining rates was made to assess whether the greenhouses were usable in the cold season in Turkey. However, the solar radiation captured by a greenhouse is more important than the solar radiation falling on the greenhouse cover for evaluating the greenhouse’s lighting performance. Because the solar beam radiation evolution follows the law of the solar trajectory, Gupta et al. [
17] investigated the ratio of the transmitted beam radiation falling on each component inside the greenhouse to the total beam radiation entering the greenhouse under clear sunny conditions through a three-dimensional shadow analysis in Auto-CAD. A total solar fraction has been defined to determine the amount of solar energy loss from the transparent sections of the greenhouses. El-Maghlany et al. [
18] studied the abilities to capture solar radiation of greenhouses having elliptic curved surface with different aspect ratios. The entering solar radiation was calculated from an integral considering the nonuniform transmittance along the curved surface, and the captured solar radiation was derived from the ratio of the greenhouse’s cover surface to its cultivated land area. Furthermore, to decrease the solar energy loss through the transparent components in a conventional greenhouse, the installation of an opaque wall was suggested, which made the design of the conventional greenhouse similar to that of a solar greenhouse. It was found that the north wall’s insulation can significantly reduce the heating demand of a single span greenhouse in Iran [
5,
19].
Compared with conventional greenhouses, which have an entirely transparent envelope, the Chinese solar greenhouse is opaque, except for the south roof (for lighting) (
Figure 1). The interior solar radiation consists of beam, diffuse, and reflective radiations [
20]. With the shadow generated by the opaque components, the solar greenhouse acquires a more complex light distribution, and the solar radiation reflection between various surfaces changes the allocation of the entering solar radiation, which ultimately affects the energy balance of the solar greenhouse system. Therefore, studying the light environment inside solar greenhouses to attain a precise view of the solar radiation allocation and spatial distribution is essential. In past decades, both onsite measurements and model simulations were conducted to evaluate the light environment in solar greenhouses. In Xingyang (34°36′ N and 113°21′ E), China, Wang et al. [
21] investigated the characteristics of the light environment in a sinking solar greenhouse by field measurements. The experimental results indicated that the transmittance of the south roof was minimum in the morning and evening and was maximum at around noon. In Yongning (38°18′ N and 106°15′ E), China, a measurement-base study by Zhang et al. [
22] revealed that the solar radiation intensity in the southern part was always higher than that in the northern part of a solar greenhouse. However, the onsite measurement of the environmental factors is time-consuming, and it is unrealizable for a solar greenhouse during the design phase. Several calculation models for solar greenhouses’ light environment have been established to determine the solar radiation capture, allocation, and distribution. To increase greenhouse space utilization, the south roof is curved in most Chinese solar greenhouses [
23]. Xuan [
24] developed the south roof equation in a solar greenhouse and studied the amount of solar radiation entering the greenhouse through the south roof with different curvatures. The results showed that there was no significant difference in the total entering solar radiation among south roofs with different curvatures. Chen et al. [
25] developed a model to calculate the total solar radiation collected by the south roof over the entire typical winter season for off-season vegetable production. In their work, the nonuniform transmittance caused by the varied slope along the south roof was considered. Further, their model was used to determine the optimal orientation of a solar greenhouse. In the study of the solar radiation distribution inside a solar greenhouse, many scholars have simplified both the greenhouse shape and evolution progress of the interior light environment. Considering clear sunny conditions, Han et al. [
26] predicted the spatial distribution of the solar radiation within a solar greenhouse by using simulations coded with the VB programming language. To simplify the calculation, the curved south roof was represented by a tilted surface, and an average value of the lighting roof transmittance was adopted; the interior beam radiation and diffuse radiation were estimated based on the shadowing effect of the greenhouse enclosure structure. Ma et al. [
27] established a solar greenhouse light environment model that neglects the interior solar radiation reflection, for which an analytical equation of the south roof in a solar greenhouse was developed, and a varying roof transmittance was considered based on an empirical formula deduced from the measured data of a PVC film in Beijing. Yang and Ma [
28] investigated the effects of different roof inclination angles on the indoor light environment of solar greenhouse by using the mathematic model established by Ma et al. [
27]. Their results suggested that 32° was the optimal inclination angle of roof that was conductive to solar radiation accumulation in a solar greenhouse. Xu et al. [
29] established a relatively perfect solar radiation model for solar greenhouse based on the previous models. The model was developed with a consideration of the influence of the sunrays’ incident angle on the beam transmittance and can be applied to sunny weather conditions. Obviously, these models are suitable only for sunny weather in certain regions. Moreover, the simplified interior solar radiation evolution cannot accurately describe the light environment of a solar greenhouse; most important, it is hard to find the lighting environment models that consider the light demands of crops to guide the solar greenhouse planting.
To fill these gaps, a solar greenhouse light environment model suitable for regions at different weather conditions and different geographical latitudes was developed in this study. With this model, the effects of both the shape parameters of the south roof and the optical properties of the lighting materials on the lighting roof transmittance were analyzed quantitatively; the interior solar radiation evolution was accurately described considering the dynamic beam radiation, diffuse radiation, and multi-reflection. Based on the model, we conducted a case study of a solar greenhouse located in the Hexi Corridor, China, where solar greenhouses offer a remarkable opportunity for utilizing solar energy to produce vegetables year round on once unproductive lands. The solar radiation allocation is obtained to determine the solar radiation availability for the north wall and the entire solar greenhouse; the spatial distribution of the solar radiation is obtained to evaluate the light conditions for growing crops in the greenhouse. The model established in this study is expected to guide the optimization of both the light environment regulation and the crop planting for a solar greenhouse, thereby increasing the energy utilization and promoting production efficiency.
3. Experimental Validation of the Solar Greenhouse Light Environment Model
For the validation of the reliability of the established solar greenhouse light environment model, both onsite field measurements and model simulations were conducted in a Chinese solar greenhouse of the Hexi Corridor, which was constructed at the national Gobi ecological agricultural industry park in Dongdong Village, Jiuquan City, Gansu Province, China (98°30′ E, 39°42′ N, altitude 1666 m). The experimental site is rich in solar radiation with cumulative solar radiation of >6.1 GJ/m
2·yr
−1 and 2800–3300 h of annual sunshine, which ensures a sufficient energy-supply for the operation of solar greenhouses [
8]. The experimental solar greenhouse was built in 2019, and a middle-fruit-type tomato crop growing started in September 2019. The greenhouse was constructed facing the due south (
γG = 0°) and was 80 m long with an east-west orientation. It had a span of 10 m with the horizontal projection of the south roof (
S) occupying 8.7 m and had a ridge height
H of 4.9 m. The south roof was composed of two circular-arcs. The slope angles
α1,
α2, and
α3 at end points of each circular-arc were 10°, 19°, and 79°, respectively. A layer of clear polyolefin (PO) film was used as the roof lighting material. The north roof had a slope angle of 42°; it was constructed using steel sandwich panels with a 0.15 m-thick layer of polystyrene in the middle, and its inner surface was blackwashed. The north wall was a gravel-layered wall with a vertical height of 3.3 m and a slope angle of 82°. This type of north wall is specifically designed for the Gobi region, and can efficiently improve the greenhouse temperature environment with its good heat storage/release performance [
14]. The internal and external views of the experimental greenhouse are depicted in
Figure 4.
We now consider the optical properties of the building materials that affect the solar radiation evolution inside a solar greenhouse. In the experimental solar greenhouse, regarding the inner surfaces of the north wall and north roof were covered with black light-absorbing film; the ground was moist dark-colored cultural substrates, which made of blend of pumice, expanded shale, compost, and sand; on the plant canopy layer, nearly 10% of the solar radiation was reflected, and the rest was absorbed and used for plant transpiration and photosynthesis, the following surface solar radiation absorbances were adopted:
ρw =
ρnr =
ρg =
ρc = 0.9 [
33,
41].
For the roof lighting material, the solar radiation absorbance of PO film was zero due to its small thickness (0.001 m); the beam radiation transmittance
τb on the lighting roof was not uniform and varied with time and the diffuse radiation transmittance
τd was constant according to these transmission characteristics. During the validation,
τb and
τd of PO film could be calculated based on the material’s refractive index (
Z taken as 1.535 [
35]) by using Equations (15)–(18). Input parameters used in the model validation are shown in
Table 1.
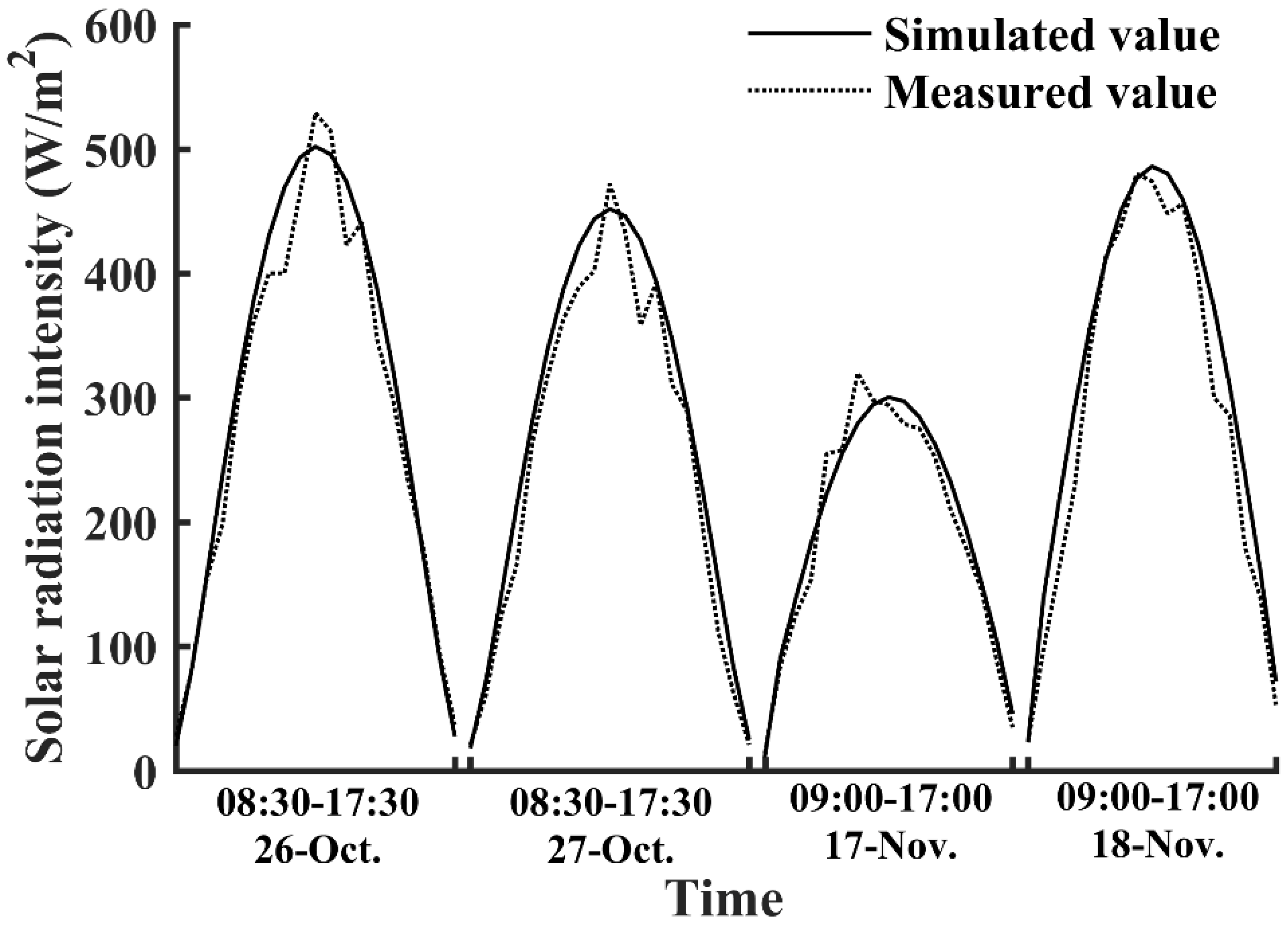
The solar radiation inside the greenhouse was measured and recorded using a PC-2B solar radiation recorder (Jinzhou Sunshine, Jinzhou, China), which has an accuracy of ±0.5%. The measurement point was set at a height of 1.3 m at the center of the greenhouse. The data were recorded at 30 min intervals, and the field measurement was performed from 1 October 2019 to 31 December 2019. During the validation, the measured and simulated data were compared under both clear sunny conditions and cloudy conditions. From the outdoor meteorological data collected from the China Meteorological Administration data center, it was found that 26 October had a typical sunny weather with a zero cloud cover CC throughout the day and that 27 October had a slightly cloudy weather with a CC equal to 1; then, a commonly cloudy weather with a CC of 7 was observed in 17 November, which was followed by a slightly cloudy day with a CC of 2. These four days have suitable weather conditions to validate the established light environment model.
Based on the design parameters of the experimental greenhouse and the weather data of the selected days, the solar greenhouse light environment model was implemented within the MATLAB environment. In the simulation period, the lowest daily average temperature on 26 and 27 October was above zero. Therefore, the thermal blanket was kept rolled-up, and the horizontal length of the thermal blanket-covered section was kept at 0.8 m during these days. The lowest daily average temperature on 17 and 18 November was −9.8 °C, and the opening and closing times of thermal blanket in these days were obtained using a mathematic model established by Chen et al. [
25], with the lighting times from 09:30 to 17:00; the moving end finally stopped at a point with the horizontal length of 0.8 m. Using Equation (24), (27), and (29), the time-dependent beam radiation, diffuse radiation, and reflective radiation at the measured point (the center of the greenhouse at a height of 1.3 m) were calculated, respectively. The summation of these three solar radiations (Equation (30)) was taken as the simulated results of the solar radiation intensity at the measurement point.
A comparison of the simulation and measurement results of the dynamic solar radiation intensity in the experimental greenhouse is presented in
Figure 5. The figure shows that the model captured the key solar radiation variations. Under the typical sunny condition (26 October), it was observed that the unregular peaks appeared around the midday on the measured solar radiation variation curve when compared with the simulated solar radiation variation curve, which were caused by the shading of the roof frame. Furthermore, the mean percentage error (MPE), mean bias error (MBE), root mean square error (RMSE), and determination coefficient (R
2) were calculated to validate the established model. In clear sunny weather, the MPE, MBE, and RMSE were 1.67%, 13.59 W/m
2, and 28.09 W/m
2, respectively; in cloudy weather, the MPE, MBE, and RMSE were 10.30%, 17.75 W/m
2, and 28.53 W/m
2, respectively. Overall, the determination coefficient R
2 for this model was 0.9756. These results validate the established solar greenhouse light environment model. Han et al. [
26] established an estimation model of solar radiation within solar greenhouses considering only the evolution of the beam and diffuse parts of the solar radiation entering a solar greenhouse and neglecting the interior reflection. They reported that, in clear sunny weather condition, the model had an MPE, MBE, and R
2 of 8.8%, 35 W/m
2, 0.6112, respectively. The solar radiation model in solar greenhouse established by Xu et al. [
29] took the influence of the sunrays’ incident angle on the beam transmittance into account. The model had an MBE of 68.48 W/m
2, and an RMBE of 79.18 W/m
2.
4. Model Applications in Solar Greenhouse Planting and Light Environment Regulation
4.1. Seasonal Spatial Distribution of the Solar Radiation in the Solar Greenhouse That Determines the Greenhouse Planting
Because there is no auxiliary lighting and heating, solar greenhouse cultivation still partially depends on the natural environment. In particular, the seasonal variation of the climate conditions significantly influences the crop planting in the solar greenhouse. Light in a solar greenhouse is weaker than on the outside and is determined by the periodic external solar radiation variations with a cycle of a year; it is also affected by the greenhouse envelope, which can be reflected by the spatial distribution of the solar radiation.
The calculation model established in this study can be applied to simulate and predict the light environment of a solar greenhouse accurately and conveniently. In this section, a case study based on the established solar greenhouse light environment model is conducted to investigate the annual dynamic spatial distribution of the solar radiation of a solar greenhouse in Jiuquan city, with the aim of guiding the planning of crops planting and thereby exploiting the maximum possible entering solar energy. The studied solar greenhouse has the same design parameters as the experimental solar greenhouse described in
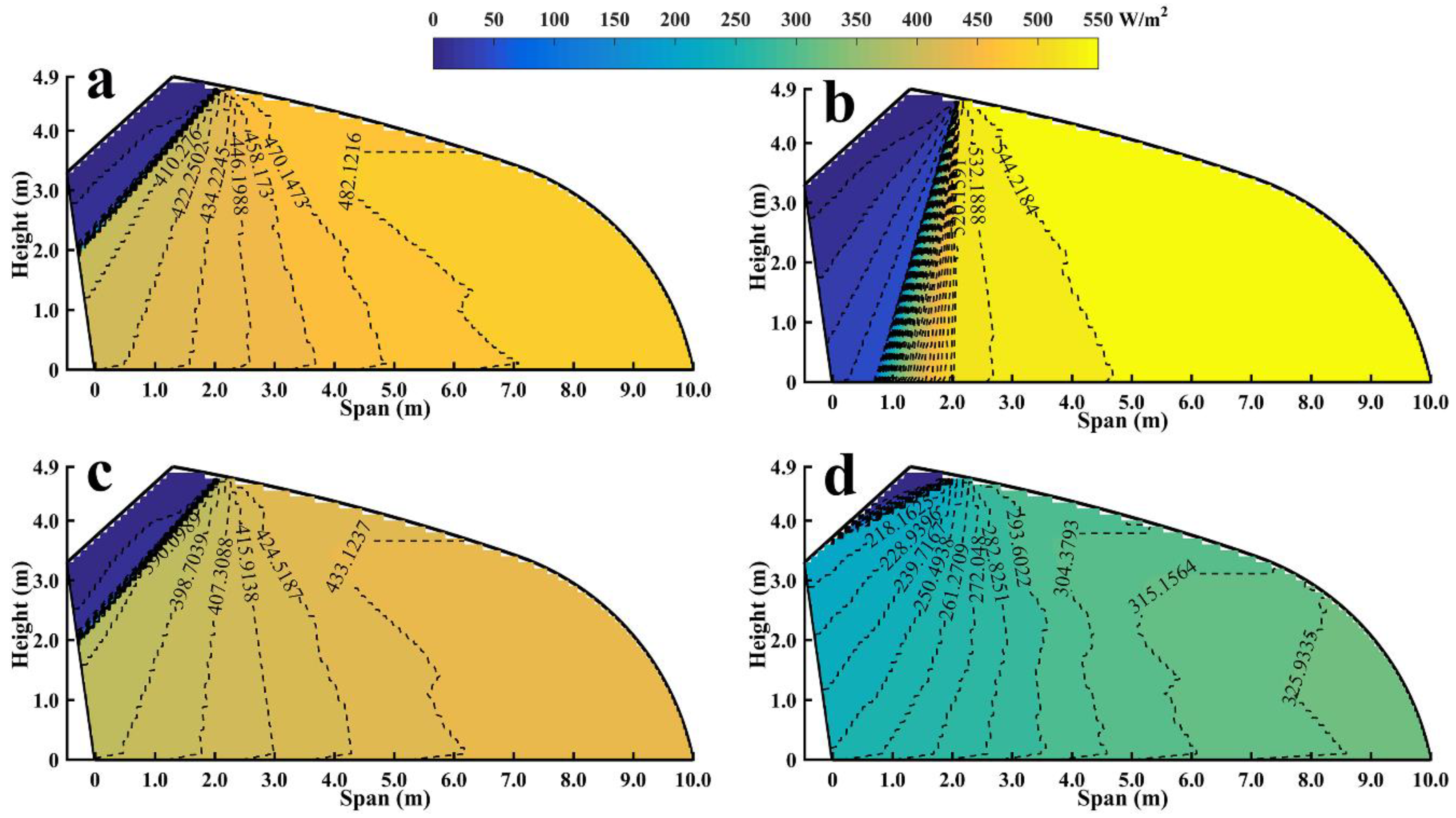
Section 3. Four typical solar terms, namely the vernal equinox (20 March), summer solstice (21 June), autumn equinox (23 September), and winter solstice (22 December), are selected to represent the external solar radiation variation in a year. The summer solstice has the maximum daily total solar radiation of a year, while the winter solstice has the minimum daily total solar radiation in the northern hemisphere. The simulated spatial distribution of the average solar radiation intensity during the lighting hours for the studied solar greenhouse is presented in
Figure 6.
It can be observed that a shadow exists in the region near the north roof and north wall for all four solar terms; the largest and smallest shadow areas appeared in the summer and winter solstices, respectively. The shadow results from the opaque north roof and the thermal blanket covering the south roof, both of which act as shields against solar beam radiation. The change in the shadow area is expected owing to the solar altitude variation in the northern hemisphere. In the summer solstice, on the 2.0 m-height horizontal plane representing the commonly highest crop canopy, the projected shadow occupies a width of 1.6 m in which the average solar radiation intensity is only 38.42 W/m2 (3472 lux), which is significantly lower than that in the region with no shadow and is particularly disadvantageous for crops growth. For the region with no shadow, a high-intensity light region appears near the south roof with a solar radiation intensity reaching 482.12, 544.22, 433.12, and 325.93 W/m2, in the four solar terms from spring to winter, respectively. Then, the solar radiation intensity distributions exhibit an obviously decrease from the greenhouse center to the side near the north wall on the cross-section, falling to 410.28, 520.16, 390.10, and 218.16 W/m2, respectively. Along the vertical direction, a small solar radiation intensity variation in vernal equinox, summer solstice, and autumn equinox are observed; whereas in the winter solstice, a relatively large variation is observed within an approximately 2.5 m from the north wall; in this case, the solar radiation in the upper space is 53.9 W/m2 lower than that in the bottom on average. This is mainly caused by the nonuniform beam radiation intensity and beam transmittance along the south roof.
After converting the solar radiation intensity into illuminance using Equation (32), the average illuminance within the space required for crops growth is found to range between 42,000 and 50,000 lux in the entire greenhouse span in the vernal equinox, between 54,000 and 57,200 lux within 8.0 m from the bottom of the south roof in the summer solstice, between 40,000 and 45,000 lux and 22,000 and 33,500 lux in the entire span in the autumn equinox and winter solstice, respectively.
Every crop has an appropriate illuminance range: the minimum value is defined as light compensation point and the maximum is light saturation point. When the light intensity is lower than the light compensation point, the crop photosynthesis is weak and the organics could hardly be accumulated within the crop body. When the light intensity is higher than the light saturation point, it will destroy the chlorophyll and chloroplast membrane and will result in photoinhibition [
42]. When the light intensity is within the appropriate range that the crop demands, crop can growths healthily. For a given solar greenhouse, its annual spatial dynamics of solar radiation can be used to determine the reasonable crop varieties and planting seasons based on the lighting demands of different crops, thereby optimizing the solar greenhouse planting pattern and enhancing the production efficiency. Regarding the studied solar greenhouse located in the Hexi corridor, some recommendations can be made for its crop planting: the light-demanding crops requiring an illuminance in the range of 42,000–57,200 lux, such as tomatoes or watermelons [
43,
44], can be planted in spring and summer; the low light-tolerating crops that require an illuminance in the range of 25,000–40,000 lux, such as cucumbers or peppers can be planted in autumn and winters [
45,
46]; and the crops that require a moderate illuminance and a long sunshine exposure, such as zucchinis that need 40,000–50,000 lux of illuminance and 8–11 h of light per day [
47], should be planted in spring and autumn. Additionally, when the solar greenhouse is utilized in summer, some supplementary lighting measures should be taken to improve the light environment in the low light region near the north wall.
4.2. Optimizing the Regulation of the Solar Greenhouse Light Environment
4.2.1. Effect of the Interior Multi-Reflection on the Light Environment of the Solar Greenhouse
The purpose of this section is to determine the effect of the interior multi-reflection on the solar radiation allocation and spatial distribution in the solar greenhouse quantitatively by using the established model. Because the winter solstice (December 22) has the minimum total solar daily radiation of a year in the northern hemisphere, the interior light environment of this day can be used to effectively and objectively evaluate the light performance of a solar greenhouse. Therefore, the model simulations would be performed with and without multi-reflection in the studied solar greenhouse in Jiuquan on a sunny winter solstice day (CC = 0). The adopted surface solar radiation absorbances are ρw = ρnr = ρg = 0.9. The opening time of the thermal blanket is 1.1 h after the sunrise, and the closing time is 0.5 h before the sunset, during which the horizontal length of the thermal blanket covered-south roof is kept at 0.8 m.
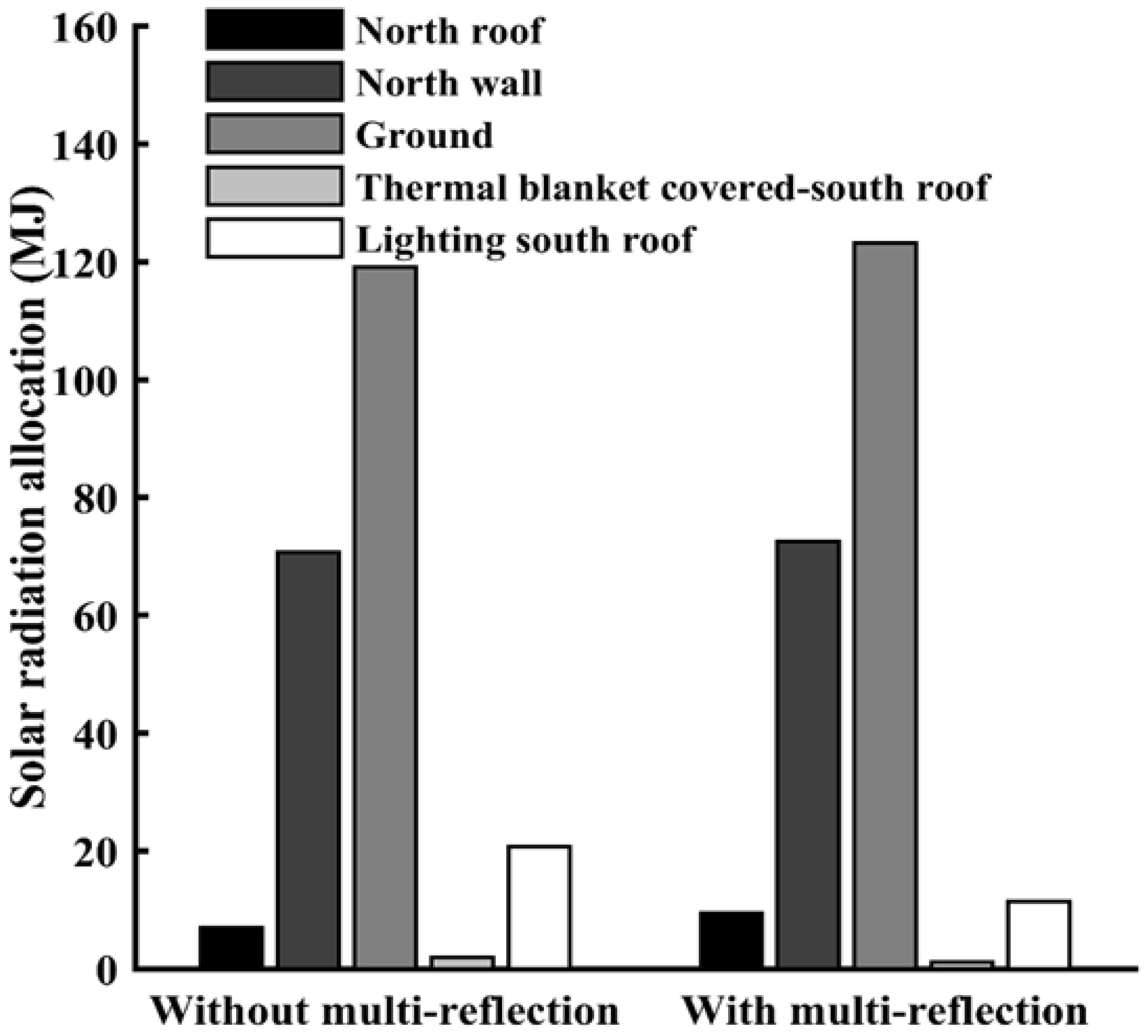
A comparison of the solar energy allocation in the solar greenhouse with the interior multi-reflection neglected and considered is presented in
Figure 7. As already reported in
Section 2.3, the cumulative solar radiations entering the greenhouse through the south roof for these two cases are equal in one day: 223.93 MJ for a one-meter length along the east-west orientation, according to Equation (22). From
Figure 7, it is observed that, during the lighting hours (09:50–17:20), the cumulative solar radiation (
SRA) allocated to the inner surfaces of the north roof, north wall, ground, and south roof are 7.00, 70.72, 119.08, and 22.79 MJ, respectively when neglecting reflection. However, when considering multi-reflection, those values are 9.44, 72.52, 123.19, and 12.60 MJ, respectively. Except for that of the south roof, all
SRAs are larger than in the first case and increase by 34.9% for the north roof, 2.5% for the north wall, and 3.5% for the ground. The south roof is divided into the lighting section and the thermal blanket-covered section, in which the diffuse part and reflective part of the solar radiations falling on the thermal blanket-covered section are either reflected back to the interior or absorbed by the blanket close to the transparent lighting film, without being transmitted outsides and directly lost.
Therefore, solar radiation energy is lost through the south roof only in the lighting section, with daily cumulative values of 20.77 and 11.47 MJ with and without multi-reflection, respectively; thus, the interior multi-reflection results in a 44.8% lower daily cumulative value. Consequently, the total solar radiation availability of the solar greenhouse can be obtained by Equation (34), which gives 206.27 and 196.81 MJ/m with and without multi-reflection, respectively.
It can be determined that the total solar radiation availability of the solar greenhouse is underrated when neglecting the effects of the interior multi-reflection, which will result in increased energy consumption budget and thus unnecessary waste. Therefore, it is strongly recommended that the interior solar radiation multi-reflection be considered for the solar greenhouse design.
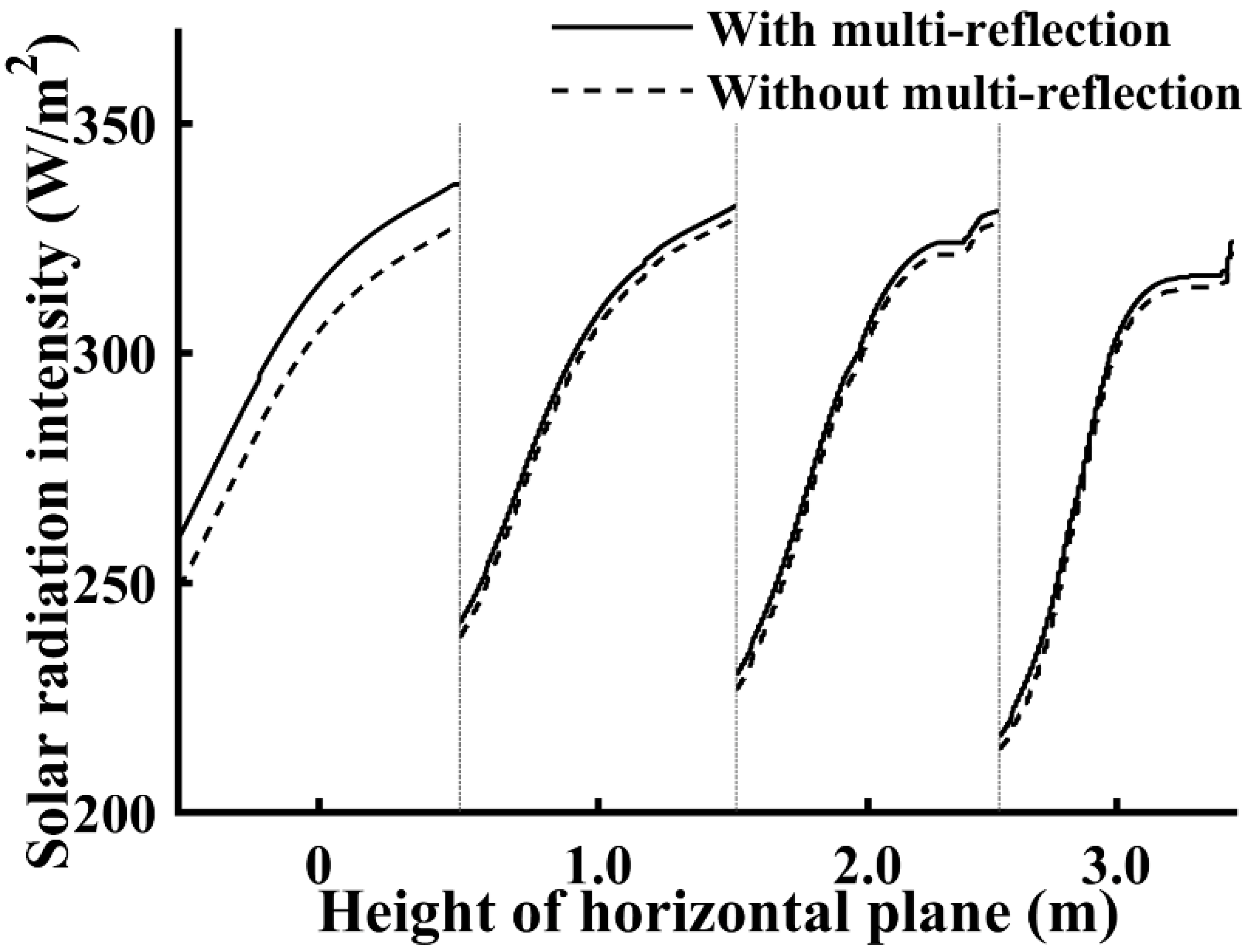
The spatial distributions of the solar radiation on the solar greenhouse cross-section obtained with and without interior solar radiation multi-reflection are shown in
Figure 8, with the average solar radiation intensity distribution on each horizontal plane with a height of 0, 1.0, 2.0, and 3.0 m presented. With multi-reflection, the solar radiation intensity along the horizontal planes comprising the solar greenhouse space is higher; the most obvious difference between the two cases is observed in the 0 m-height plane, i.e., the ground surface. The average solar radiation intensity differences between the two cases on the four planes with the heights of 0, 1.0, 2.0, and 3.0 m are 10.28, 2.96, 3.02, and 3.06 W/m
2, respectively, and the maximum solar radiation intensity differences are 11.91, 3.39, 3.76, and 4.80 W/m
2, respectively, which appear approximately 1.5 m from the north wall’s inner surface. It appears that the multi-reflection slightly alleviates the low light environment in the north-side region of the greenhouse. However, it must be noted that, in the studied solar greenhouse, both the north wall and north roof have a black colored inner surface (
Figure 4), so the north wall and north roof have a low reflectance:
rw =
rnr = 0.1; therefore, the reflection within the greenhouse space is very weak. Next, we determine whether a more satisfactory light environment can be achieved by enhancing the interior reflections.
Inside a solar greenhouse, reflections occur between the inner surfaces of the north wall, north roof, south roof, and the ground surface (including the crop canopy), and it is important to consider the function of each component. The north wall and the ground under the solar greenhouse play important roles in storing the entering solar energy and releasing it to inside during nighttime when then inside air temperature is low. The north roof functions as a thermal insulation component with lower thermal conductivity and density; that is, little solar radiation absorbed by the inner surface of the north roof is stored and cannot be used for improving the nocturnal thermal environment. Therefore, the interior reflection can be enhanced by increasing the reflectance of the inner surface of the north roof without affecting the regenerative elements.
4.2.2. Inner Surface Reflectance of the North Roof
As mentioned in
Section 2.4.3, the surface reflectance depends mainly on the surface color. In a solar greenhouse, the inner surface reflectance of the north roof can be increased by whitewashing its inner surface. Then, a new value of the reflectance of the north roof
rnr = 0.9 is considered in the evolution of the greenhouse light environment. To investigate the influence of the inner surface reflectance on the light environment of the solar greenhouse, simulation analyses were conducted for the experimental solar greenhouse and an optimized solar greenhouse by using the established light environment model. The two solar greenhouses have the same design parameters except for the inner surface color of the north roof. The simulation is carried out under a sunny winter solstice day (
CC = 0).
The results of the solar radiation energy allocation in the solar greenhouse are presented in
Figure 9, allowing the comparison between the experimental greenhouse, which has a north roof with low inner surface reflectance (
rnr = 0.1), and the optimized greenhouse, which has a north roof with high inner surface reflectance (
rnr = 0.9). It can be observed that the two solar greenhouses do not exhibit significant differences in solar radiation allocation. For the solar greenhouse with the optimized north roof, during the lighting hours, the cumulative solar radiation (
SRA) allocated to the inner surfaces of the north roof, north wall, ground, and the thermal blanket-covered section and the lighting section of the south roof are 1.06, 73.47, 127.92, 1.33, and 13.76 MJ, respectively; here, the solar radiation energy lost through the lighting section of the south roof increases by 20.0% owing to the enhanced interior reflection. Then, the total solar radiation availability of the optimized solar greenhouse obtained by Equation (34) has a value of 203.51 MJ/m, which is 1.3% lower than that of the experimental solar greenhouse with a north roof with low inner surface reflectance. Nevertheless, it must be noted that the solar radiation availability for the two regenerative components, i.e., the north wall and ground, are increased by 1.3 and 3.8%, respectively. This indicates that enhancing the interior reflection by increasing the inner surface reflectance of the north roof optimizes the interior solar energy allocation, and therefore has some positive effect on the development of the interior thermal environment.
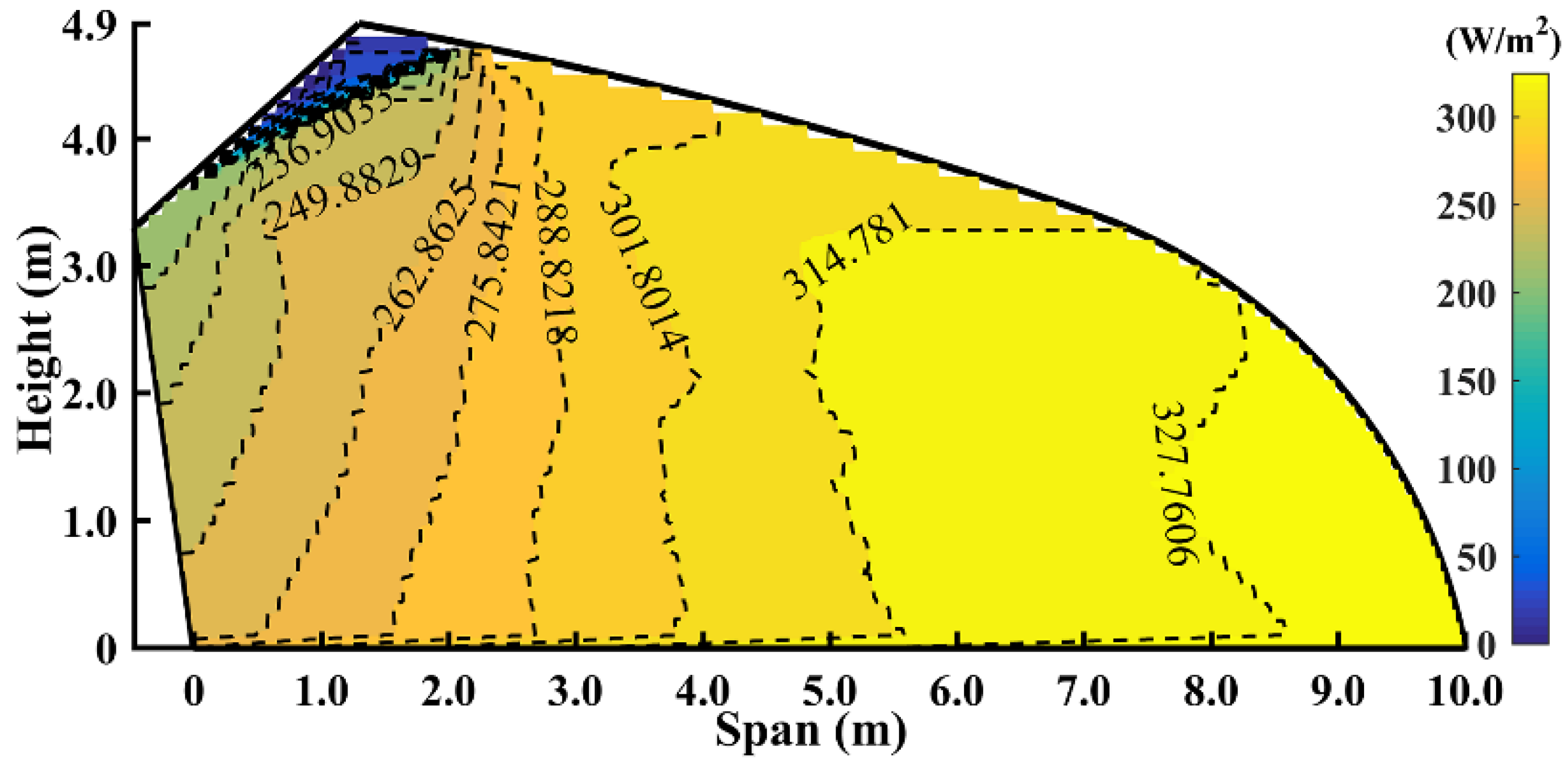
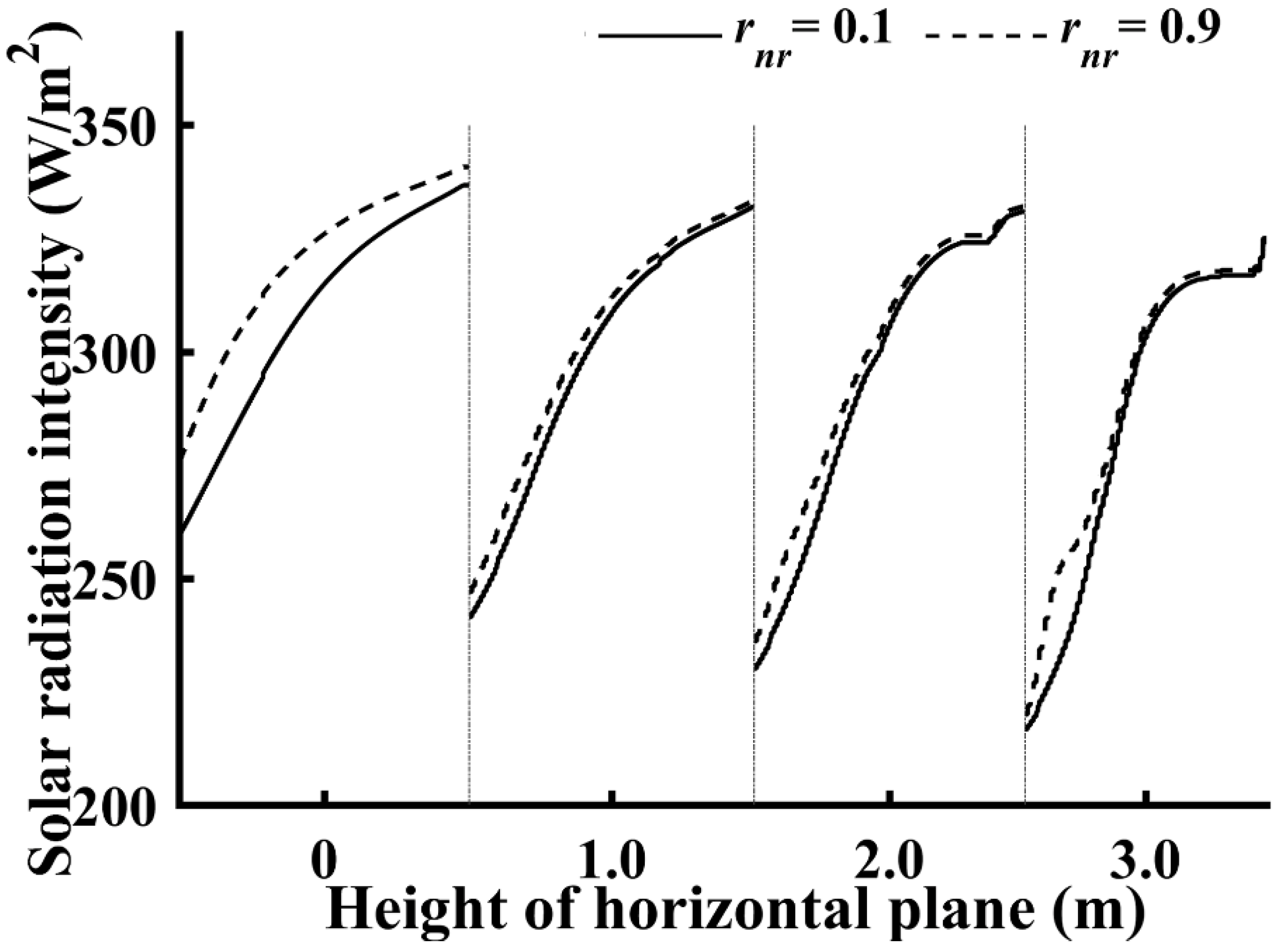
Next, the spatial distributions of the solar radiation for the two solar greenhouses with different north roofs are compared. The spatial distributions of the average solar radiation intensity of the greenhouses with common and optimized north roofs are illustrated in
Figure 6d and
Figure 10, respectively. The average distributions of the solar radiation intensity on the four horizontal planes at the heights of 0, 1.0, 2.0, and 3.0 m, respectively, are highlighted in
Figure 11.
From
Figure 10, it is evident that the solar radiation intensity in the solar greenhouse with a north roof with high inner surface reflectance is generally larger than the experimental solar greenhouse, particularly in the innermost regions near the north wall. This induces a smaller solar radiation intensity amplitude from north to south in the optimized solar greenhouse, as clearly depicted in
Figure 11. Considering the entire horizontal plane, the average difference in the solar radiation intensity between the two solar greenhouses is 11.85 W/m
2 for the 0 m-height plane, 3.95 W/m
2 for the 1.0 m-height plane, 4.54 W/m
2 for the 2.0 m-height plane, and 5.54 W/m
2 for the 3.0 m-height plane, which correspond to increases of 3.8, 1.3, 1.5, and 2.0%, respectively, for the light environment quality inside the solar greenhouse. When considering only the region within 3.0 m from the north wall, the average differences of the solar radiation intensity between the two solar greenhouses are 18.96 W/m
2 for the 0 m-height plane, 6.78 W/m
2 for the 1.0 m-height plane, 8.84 W/m
2 for the 2.0 m height-plane, and 11.98 W/m
2 for the 3.0 m-height plane, which correspond to increases of 6.8, 2.6, 3.5, and 5.0%, respectively, for the light environment quality in the north side of the solar greenhouse. Therefore, it can be determined that the north roof with high inner surface reflectance has a function of supplementary lighting, and its application can improve the light environment in the low light region near the north wall and relieves the light distribution gap between the south and north for a solar greenhouse, thereby providing better light conditions for crops.
4.2.3. Thermal Blanket-Covered Length on the South Roof during the Lighting Hours
In Chinese solar greenhouses design, the enhancement of the heat storage and release of the north wall has been considered the most feasible improvement in the thermal environment [
48]. However, as reported in
Section 4.2.2, the enhancements of the solar radiation availability for the north wall by increasing the inner surface reflectance of the north roof are limited. This is because the beam radiation contributes the most to the total solar radiation allocated to the north wall. In reality, the solar radiation availability of the heat-store/release component (the north wall) is mainly affected by the shadow areas projected by both the north roof and the thermal blanket-covered south roof. As previously mentioned, the north roof has a fixed length while the length of the thermal blanket on the south roof varies with time. According to the common solar greenhouse design standard, a horizontal length of the thermal blanket on the south roof should be set to 0.8 m during the lighting hours [
38]; however, the thermal blanket length sometimes becomes larger and reaches even 1.5 m in current practical applications [
49]. Based on the established solar greenhouse light environment model, the projection regions can be obtained.
Consider a rolled-up thermal blanket on the south roof following the solar greenhouse design standard.
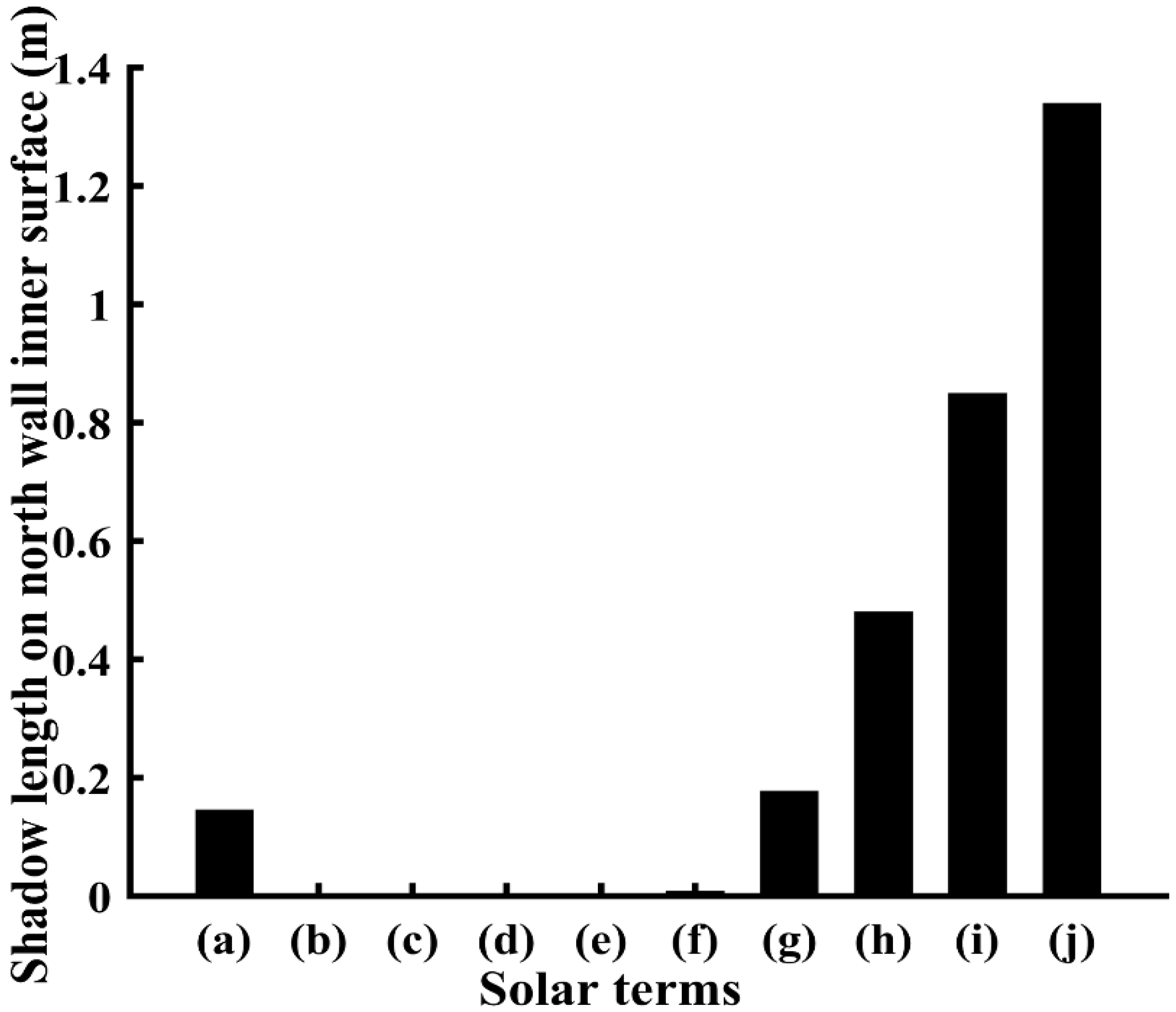
Figure 12 illustrates the length variation of the shadow projected on the north wall’s inner surface from 8 November (beginning of winter) to 20 March (vernal equinox), which is the typical cold time in Jiuquan when off-season vegetables are produced; the lengths projected by the north roof and the thermal blanket-covered south roof are also highlighted, respectively. The value of the shadow length on a day is selected as the average projection length between 11:00 to 15:00, because there is a one-hour time difference between the times in the experimental site (98°30′ E) and the Nation Time Service Center site (120° E). It can be observed that, during the simulation period, the projected shadow length is close to zero for just about two months around the winter solstice owing to the small solar altitude at this time of year in the northern hemisphere. Therefore, the entire inner surface of the north wall can accept the solar beam radiation in the two months’ time. However, after 20 January, the shadow length projected on the wall’s inner surface increases with time; especially in the the middle of February, the shadow area has already represented more than a fourth of the wall’s entire inner surface and continues to increase rapidly. Moreover, it can be observed that the shadow is mostly generated by the thermal blanket-covered south roof. It is important to note that, according to the past ten years’ data provided by the China Meteorological Administration data center, the outside minimum average temperature in January and February in the studied area is below −10 °C. Therefore, for a solar greenhouse, the heat storage/release capacity of the north wall, which depends on the solar radiation availability, will be critical in ensuring a safe nocturnal environment for crop growth owing to the intermittent nature of solar energy. However, such a wide range of shadows significantly reduces the potential amount of solar energy stored in the north wall, which will lead to inadequate energy supply for the solar greenhouse heating during the nighttime, thereby threatening the crop growth.
To solve this problem, the parking position of the thermal blanket during the lighting hours was optimized in this study because the thermal blanket is the main section generating the shadow on the north wall, and, therefore, it is not necessary to change the north roof structure adding manufacturing difficulties. For the optimization, the rolled-up blanket is installed at a high enough height, allowing the length of the thermal blanket-covered south roof to equal to zero, which allows more beam radiation to enter the greenhouse in lighting hours, increasing the heat storage of the north wall during the period lasting from 15 January to 20 March.
To demonstrate the effectiveness of the optimization measure, a simulation was carried out based on the already optimized solar greenhouse described in
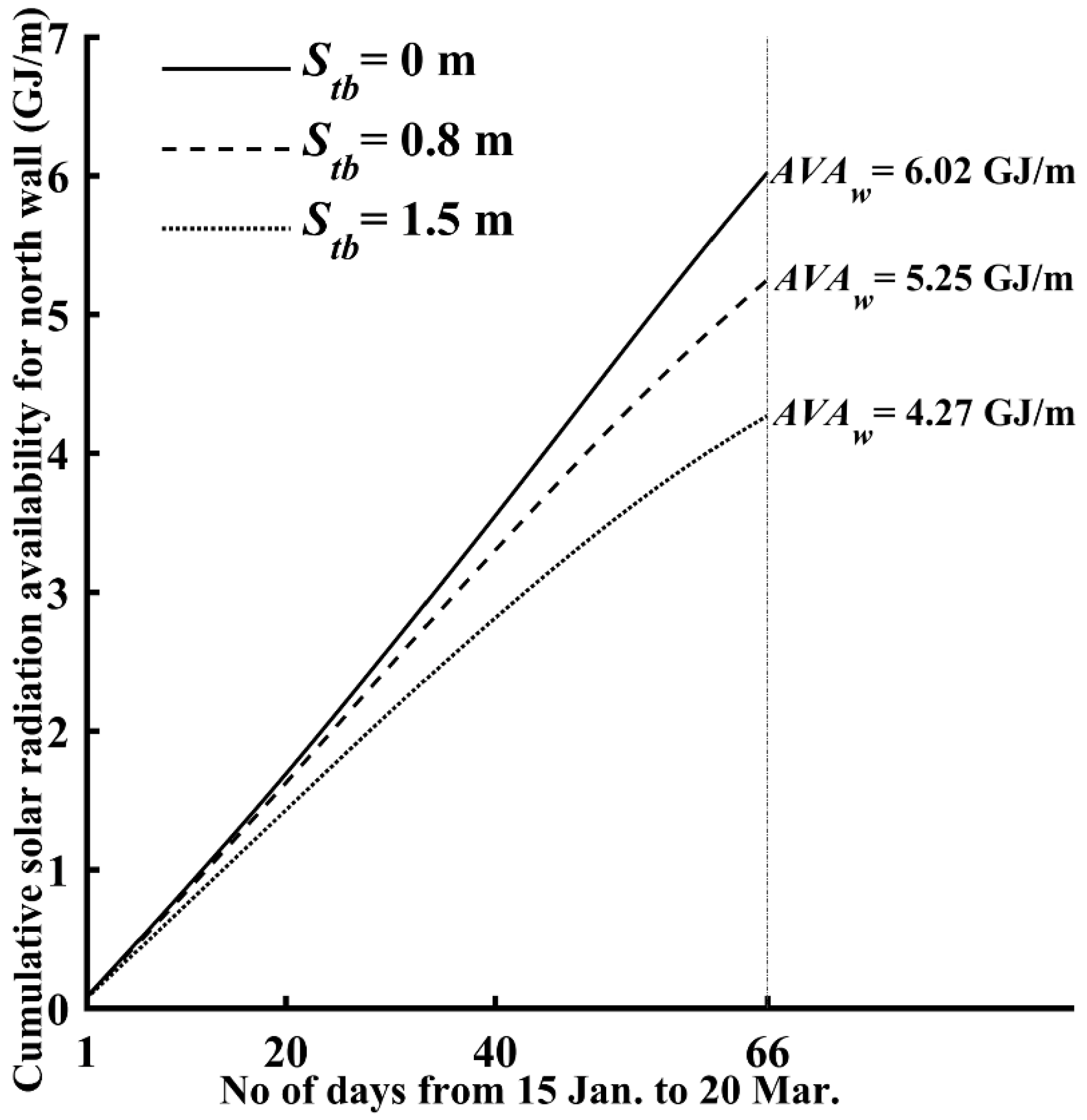
Section 4.2.2 with different thermal blanket parking positions, by using the established light environment model. The calculation time is between 15 January and 20 March, and clear sunny weather is assumed for all days. In
Figure 13, the cumulative solar radiation availability for the north wall day by day in the solar greenhouse with the optimized thermal blanket parking position are shown and compared with the simulated results in the greenhouses with a 0.8 m and a 1.5 m thermal blanket-covered in the lighting hours. The comparison indicates that the application of the optimization measure significantly increases the solar radiation availability for the north wall. In the entire calculation period, when compared to the 0.8 m and 1.5 m thermal blankets for the lighting hours, the covered blanket length of zero increases the north wall’s solar radiation availability by 0.77 and 1.75 GJ/m, respectively, for a one-meter section along the east-west orientation, corresponding to an improvement of 14.7 and 41.1%, respectively. Accordingly, it is strongly recommended to park the rolled-up thermal blanket high enough on the roof during the lighting hours; this will maximize the north wall’s solar radiation availability and enhance its heat storage/release capacity.
5. Conclusions
Solar radiation is the sole energy source for Chinese solar greenhouse agriculture. The allocation of solar radiation in the solar greenhouse system directly affects the greenhouse thermal environment development, whereas the spatial distribution of solar radiation reflects the light conditions on which crop growth depends. Therefore, the light environment is a key indicator for evaluating a solar greenhouse’s performance. For this purpose, a solar greenhouse light environment model was established and validated in this study, considering greenhouse structures, materials, and interior solar radiation progresses. With the established model, the solar greenhouse light environment was dynamically simulated in terms of solar beam radiation, diffuse radiation, and multi-reflection, with target date/time, geographic location, weather conditions, solar greenhouse’s orientation and shape parameters, and optical properties of the building materials as the inputs, based on the law of the solar trajectory, the radiation angular distribution coefficient method, and the multiple diffuse reflection method. By using this model, the solar radiation allocation, the spatial distribution of the solar radiation, and the solar radiation availability in a solar greenhouse can be determined quantitatively. The following conclusions may be drawn:
- (1)
The solar greenhouse light environment model established in this study is valid because the simulated and measured results are consistent for different weather conditions. The MPE was calculated to be 1.67% for clear sunny weather and 10.30% for cloudy weather, and a satisfactory determination coefficient R2 of 0.9756 between the simulated and measured results was obtained for the established model.
- (2)
The varying slope angle along the curved south roof results in a nonuniform beam radiation intensity and beam transmittance on the south roof. This leads to a significantly complex light environment inside the solar greenhouse. Generally, the spatial distribution of solar radiation exhibits a decrease in both south-to-north and bottom-to-top directions within a solar greenhouse.
- (3)
The seasonal spatial distribution of the solar radiation in a solar greenhouse is quantitatively investigated with the established model. The results suggest that the solar greenhouse can be used to plant crops that require an illuminance in the range of 42,000–57,200 lux in spring and summer and crops that require an illuminance in the range of 25,000–40,000 lux in autumn and winter.
- (4)
Increasing the inner surface reflectance of the north wall by whitewashing enhanced the interior refection. The north roof with high inner surface reflectance is a supplementary lighting component, which helps effectively improve the light environment of the low light region, with average increases in the solar radiation intensity of 18.96 W/m2 (6.8%), 6.78 W/m2 (2.6%), 8.84 W/m2 (3.5%), and 11.98 W/m2 (5.0%) for the 0, 1.0, 2.0, and 3.0 m height-planes, respectively, in the region within 3.0 m from the north wall.
- (5)
Between 15 January and 20 March, the thermal blanket covered-south roof with a length of zero in the lighting hours increases the cumulative solar radiation availability for the north wall by 0.77 and 1.75 GJ/m along a one-meter section along the east-west orientation; this is 14.7 and 41.1% higher than when the thermal blanket occupies a horizontal length of 0.8 and 1.5 m, respectively, on the south roof.
Although the validation and application of the established solar greenhouse light environment model were performed in the Jiuquan city of the Hexi Corridor, the model is applicable and convenient for Chinese solar greenhouses in different regions with different climates and geographical features. With the established model, the dynamic light environment in a solar greenhouse can be predicted quantitatively to optimize the greenhouse lighting regulation and planting pattern. Additionally, the model provides precise boundary conditions for the energy balance and thermal environment development of a solar greenhouse system. It is expected that the solar greenhouse light environment model established in this study will be used to create desirable growth environments for crops and enhance the production efficiency.