Abstract
The stability of Modular multilevel converter (MMC) itself is the premise of analyzing the stability of MMC cascading with other cells, so this paper addressed the small-signal stability of MMC with dc voltage control mode which is the common operation mode of grid-side MMC in high-voltage direct current (HVDC) systems. First, the small signal model of MMC with open-loop control mode and dc voltage control mode while considering the dc voltage controller and current controller are established with the harmonic state-space (HSS) modeling method. Subsequently, eigenvalues and participation factors are analyzed to estimate the stability of MMC system and the influence of controller parameters, especially the proportional coefficients of dual-loop controllers, which can improve the design efficiency of control system. Finally, time-domain simulations in MATLAB/Simulink are provided to verify the accuracy of HSS small signal model and the effectiveness of the theoretical stability analysis.
1. Introduction
Modular multilevel converter (MMC) topology was first introduced in 2003 [1,2] and it has been widely used in high voltage and high power applications, due to its advantages of modularity, scalability, and power controllability. The stability of MMC itself is a significant premise to study the stability of MMC cascading with other cells, e.g., wind farm, PV inverters, weak grid, and so on. While the key is the modeling of MMC itself. However, MMC is characterized by the obvious internal dynamics in sub-module capacitor voltages and arm currents [3,4], which makes its modeling considerably more complicated than the conventional two/three-level voltage source converters (VSCs). Most of the initial researches [5,6,7,8] used the average model, which neglected these internal harmonic characteristics in the modeling process and only obtained the simplified mathematical equations of MMC in fundamental frequency.
Many scholars recently have done deep studies about the modeling of MMC to achieve high accuracy of small signal model of MMC. The state-space model of MMC based on dynamic phasors contains the internal dynamics, which is often used to model a nonlinear time-varying system as a linear time-invariant system [9,10,11,12]. The small signal state-space model of MMC with dual-loop controllers and circulating current suppression controller in dq coordinate frame was established in [13]. However, only the second harmonic components of submodule capacitor voltages were considered and harmonics of other variables, e.g., arm currents, were neglected. Another state-space model of MMC that was based on dynamic phasors was built in dq coordinate frame [14,15], but this modeling method needs to take park transformations at different frequencies which makes the modeling process complicated. Additionally, this model only contained the internal harmonics but ignored the external harmonics, which would exist on the ac side and dc side of MMC and produce influence on the internal harmonics. Reference [16] raised a dynamic phasor model method of MMC that was only applied to open-loop control. However, it required listing all of the relationships among the considered harmonic frequencies in advance; therefore, this method is not suitable for extending to higher harmonic frequencies. Additionally, it also neglected the external harmonics. The idea of multiple harmonic linearization was used in [17] to obtain the small signal model of MMC with single current loop. However, this modeling process neglected the harmonics of dc side. Moreover, this small signal model did not have enough equations to solve the value of state variables, so it is only suitable for deriving the relative relationships, such as the output impedance of MMC. Therefore, it is necessary to propose a small signal modeling method of MMC, which takes the dynamic characteristics of both internal and external harmonics into account and establishes a complete model of MMC while considering the inner and outer control loops. The harmonic state-space (HSS) modeling method could characterize the frequency coupling mechanism of harmonics, and it has been successfully used in two/three-level VSCs [18,19,20,21]. The HSS method is also applicable to model the ac side impedance of MMC [22], showing a satisfactory result. However, this small-signal impedance model only contributes to the stability analysis of the interconnected systems [23]. Thus, it could not be used as a tool to estimate the stability of MMC itself.
In the MMC-based HVDC system, grid-side MMC often adopts dc voltage control mode. Therefore, this paper develops a precise small signal model of MMC under dc voltage control mode based on the HSS method in frequency domain, while considering both internal and external harmonic dynamics, as well as the interactions. Additionally, the stability of the system and the influence of controller parameters are then analyzed with the pacification factor method and eigenvalue analysis method.
This paper follows the steps below, which are shown in Figure 1, in order to analyze the stability of MMC system. First, a model of MMC main circuit and control system are established; Second, the MMC state-space equation in time-domain is established. Next, the state-space equations are transformed into linear time-invariant form in frequency-domain. Finally, MMC dynamic response, root locus, and stability based on small signal state-space equation are analyzed.
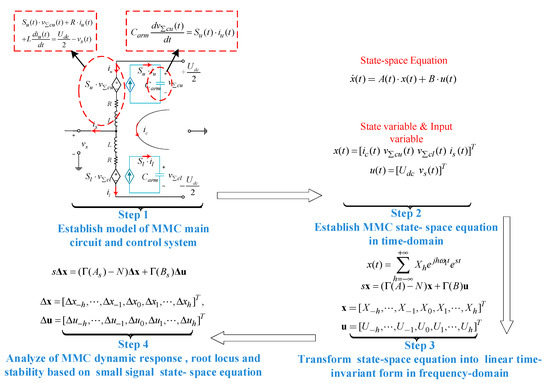
Figure 1.
Basic structure of modular multilevel converter (MMC).
When compared with the traditional state-space equation, the signal x(t) is expressed as an exponentially modulated periodic (EMP) signal to represent harmonic of different orders in the tome domain in Step 3 of Figure 1. On the other hand, because the MMC control system and electrical system are coupled with each other and control loops are coupled with each other, the Toeplitz matrix Γ(A) is applied to express the coupling of state variables with different frequencies in Step 3. Therefore, as compared with the traditional state-space model, the MMC small signal model that is based on harmonic state-space in this paper makes the analysis of dynamic characteristics, steady-state characteristics, and stability of MMC more accurate.
The rest of this paper is organized, as follows. Section 2 introduces the basic topology and operation theory of MMC and it derives the state-space equations in time domain. Section 3 builds the steady-state model and the small signal model of MMC based on the HSS method in open-loop control mode and dc-voltage control mode, respectively. Section 4 uses the eigenvalues and participation factors of the established HSS small signal model to analyze the stability of a dc-voltage controlled MMC system and the influence of controller parameters on the stability of the system. Section 5 provides a case study of dc voltage-mode controlled MMC, and the simulation result verifies the validity of theoretical analyses. Section 6 concludes the work of this paper.
2. Basic Theory of MMC
Figure 2 shows the basic structure of MMC. The converter consists of three phases, and each phase consists of one upper arm and one lower arm connected in series between two dc terminals. Each arm has N series-connected half-bridge submodules (SM) and one arm inductor L, the equivalent parasitic resistance of which is R. CSM is capacitance of submodule capacitors, whose nominal voltages are all Udc/N.
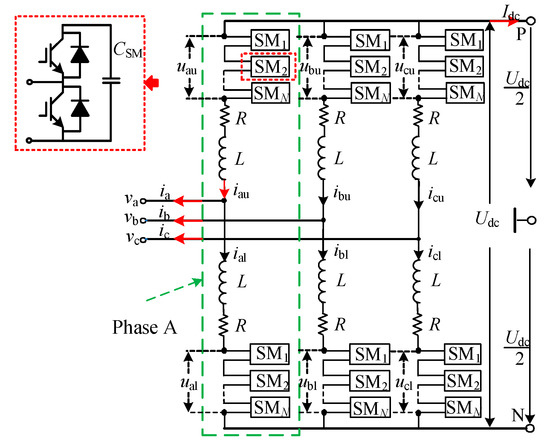
Figure 2.
Basic structure of MMC.
Figure 3 shows the control block diagram of MMC. The control system of MMC is divided into outer loop and inner loop, where outer loop is dc voltage control loop and inner loop is current control loop.
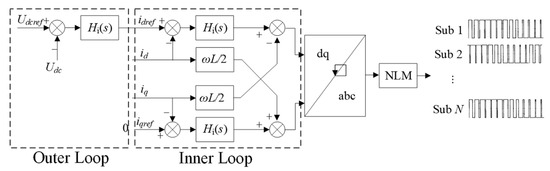
Figure 3.
Control block diagram of MMC.
In outer control loop, the difference of dc voltage reference value and actual dc voltage value goes through a PI controller and generates current reference value in d axis. Inner control loop adopts the basic dq decoupling control strategy, as shown in Figure 3, where idref and iqref are d-axis and q-axis current reference values, respectively. idref is given by the outer dc voltage control loop and iqref is 0. The differences between the current reference values and actual current values go through PI controllers, dq inverse transformation, and nearest level approximation modulation (NLM) and modulation function in abc reference frame are finally generated.
When the MMC operates in steady state, while assuming that capacitance voltages of all submodules are perfectly balanced, the average equivalent circuit of one phase could be constructed, as in Figure 4 [8]. Additionally, Carm is the equivalent capacitance of one arm, where Carm = CSM/N. The switching functions of upper and lower arms are Su and Sl respectively. vs is the ac side phase voltage of the converter, and Vdc is the dc terminal voltage. v∑cu and v∑cl are the sum of the capacitor voltages of the upper and lower arms, respectively.
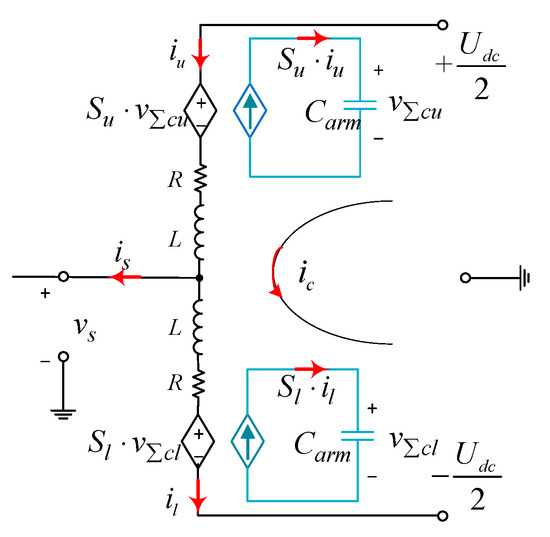
Figure 4.
The average equivalent circuit of one phase of MMC.
In Figure 4, the average switching functions of upper arm Su and lower arm Sl are defined as:
where m(t) is the modulation function of this phase: m(t) = 2vs(t)/Udc.
While applying Kirchhoff’s law to this one-phase circuit of MMC, the equations of the upper and lower arms can be derived as:
The dynamic performance of the submodule capacitors can be obtained as:
The arm currents of upper and lower arms can be represented as:
where is is ac side phase current of the converter and ic = (iu + il)/2, which refers to the circulating current flowing through the upper and lower arms of the converter at the same time.
Note that the dc component of ic is Ic0, and then the dc side current Idc can be expressed as:
Substituting (7) and (8) into (3)–(6), the state-space equations of one-phase of MMC can be expressed as:
where
The above state-space equation of MMC indicates a nonlinear time periodic (NLTP) system. The detailed derivation process of converting this system into a linear time-invariant (LTI) system with the HSS method will be shown in the following section.
3. Small Signal Modeling of MMC Based on HSS
3.1. HSS-Based Large Signal Model of MMC Power Stage
Any time-varying periodic signal y(t) can be described as the form of Fourier series expansion:
where ω1 = 2π/T1 and T1 is the fundamental period of the periodic signal, and h is the harmonic order.
Specially, the state variable x(t) is written as an exponentially modulated periodic (EMP) signal to represent the transient evolution of the harmonics:
where s = σ + jω is used to modulate the Fourier coefficient for extracting the transient response of harmonic components [18].
Based on the transformations (14) and (15), the NLTP state-space model in (10) of single phase of MMC in time-domain can be expressed as a LTI HSS model in the frequency-domain [19,20,21]:
where
where Xn, Un are, respectively, the nth Fourier coefficient of state variable x(t) and input variable u(t), and n = −h, … −1, 0, 1, …, h.
where Icn is the nth Fourier coefficient of ic(t), and V∑cun is the nth Fourier coefficient of v∑cuo(t). Other parameters have similar meanings, which are not explained repeatedly here.
Γ(A) and N in (16) are expressed as:
Γ(A) is a Toeplitz matrix form of A, as shown in (19), which consists of the Fourier series of the matrix A, where An is the nth Fourier coefficient of A (n = −h, …, −1, 0, 1, …, h). O in (19) is zero matrix. I in (20) is the identity matrix, which has the same order as A.
When n = 0,
When n ≠ 0,
Γ(B) in (16) is a Toeplitz matrix form of B, being similar to (19), which consists of the Fourier series of the matrix B, where Bn is the nth Fourier coefficient of B.
When n = 0,
When n ≠ 0,
Equation (16) represents the steady-state model of single phase of MMC that is based on the HSS method, which is linearized from (10) and is a LTI system. Therefore, the stability of MMC can be analyzed with the classical control theory. This HSS model can not only obtain the information of the 0–hth harmonics, but also reflect the interactions between the harmonics.
Letting the left side of (16) to be zero, the steady-state solution of HSS model of MMC can be calculated by:
where the frequency-domain values of state variables can be obtained. Referring to (14), the time-domain values of ico(t), v∑cuo(t), v∑clo(t), and iso(t) can be solved.
3.2. HSS-Based Small Signal Model of MMC with Open-loop Control
Based on Equations (3)–(6), the small-signal model of MMC around an operation trajectory (characterized by mo(t), v∑cuo(t), v∑clo(t), iso(t)) can be derived as:
In open-loop control mode, the modulation signal m(t) is directly given, so it could serve as an input variable in the state-space model. While combining Equations (26)–(29), the small signal model of MMC in open-loop control mode, which is also the model of power stage of MMC, can be represented as:
where
where ico(t), v∑cuo(t), v∑clo(t), and iso(t) represent the steady operation point of MMC, which can be solved from Equation (25).
By converting Equation (30) into a HSS equation, the small signal model of MMC with open-loop control mode can be expressed as:
where
Γ(As) is the Toeplitz matrix form of As, and Γ(Bs) is the Toeplitz matrix form of Bs. The elements in (35), such as Δxn, Δun, Asn, and Bsn are the nth Fourier coefficients of Δx(t), Δu(t), As(t), Bs(t), and n = −h, …, −1, 0, 1, …, h.
3.3. HSS-Based Small Signal Model of MMC with DC-Voltage Control
DC-voltage control is commonly used in an MMC-based HVDC system to maintain the dc bus voltage. Figure 5 shows the control structure, which contains outer dc-voltage control loop, inner current control loop, and phase-locked loop (PLL), where Udc and Udcref are the dc side voltage of MMC and its reference value, respectively. Isd, Isq are the values of MMC ac side current in dq coordinate system. Vsd, Vsq are the values of MMC ac side voltage in dq coordinate system, and Md, Mq are the values of modulation signal in dq coordinate system. ω1 is the fundamental angular frequency of 314.1 rad/s, and θ is the output phase angle of PLL. H1(s), H2(s), and H3(s) are the PI controllers of dc voltage control, current control, and PLL control, respectively. kid is the decoupling coefficient. The effect of small signal disturbance on PLL can be neglected when the converter is integrated with a strong enough ac grid [24]. Therefore, the small signal model of MMC in this paper does not take the effect of PLL into account.

Figure 5.
DC-voltage control structure of MMC.
3.3.1. Small Signal Model of Inner Current Control Loop
The inner current control loop contains two PI controller. Two additional state variables xi1, xi2 are introduced to simplify the integral operation:
where kp2 and ki2 are proportional coefficients and integral coefficients of the PI controllers in current control loop respectively.
Then the output small signal insertion indexes ΔMd1, ΔMq1 in dq coordinate system of the inner loop are:
The ΔMd1, ΔMq1 in dq coordinate system need to be transformed into Δmi(t) in abc coordinate system, where Δmi(t) is the control signal of phase A that is produced by the inner loop. Firstly, according to the dq transformation matrix, Isd and Isq can be expressed as:
where the Park transformation matrix Tdq is:
From Equation (38), the relationships between Isd, Isq, the amplitude I, and the phase angle φ of phase A current are:
Combining Equations (14), (36) and (40), Equation (36) in time-domain can be represented in the frequency-domain:
According to inverse Park transformation matrix, Δmi(t) could be calculated as:
where the inverse Park transformation matrix Tdq−1 is:
According to the complex form of Fourier expansion, the ±1st coefficients of Δmi(t) are:
Substituting (37) and (41) into (44) the ±1st coefficients of Δmi(t) are:
3.3.2. Small Signal Model of Outer DC-Voltage Control Loop
As shown in Figure 5, the difference between the actual value of the dc voltage and the reference value would pass through the outer loop PI controller and then the inner loop PI controller, producing small signal insertion index ΔMd2 in d axis. Two additional state variables xv1, xv2 are introduced to achieve the integral operation of dc components for two integral components:
where kp1 and ki1 are the proportional and integral coefficients of the PI controllers in outer DC voltage control loop, respectively. Afterwards, the output control signal ΔMd2 is:
According to inverse Park transformation matrix, the control signal Δmv(t) of phase A in abc coordinate system can be obtained from
According to the complex form of Fourier expansion, the ±1st coefficients of Δmv(t) are:
Assume the equivalent impedance on the dc side is ZL. According to Equation (9), ΔUdc is
Substituting (47) and (50) into (49), the ±1st coefficients of Δmv(t) can be represented, as follows:
3.3.3. Small Signal Model of DC-Voltage Controlled MMC
The models of control system and open-loop system need to be integrated into one state-space equation in order to establish the small signal model of the entire closed-loop system of MMC.
The state variables of the closed-loop system of MMC include four state variables of power stage (Δic, Δv∑cu, Δv∑cl, Δis) and four state variables of control system (Δxi1, Δxi2, Δxv1, Δxv2):
The input variables of the closed-loop system of MMC are the same as the input variables of the power stage of MMC:
By combining the equations of control system (36), (45), (46) and (51) with the HSS model of power stage in (34), the HSS model of the entire closed-loop system can be expressed as:
where:
Additionally, N is the same as (20).
The variables Δxi1, Δxi2, Δxv1, Δxv2, and ΔUdcref in (55) are all dc components. When these variables are transformed into Fourier series, they only have values at the frequency of 0 Hz, and the components of other frequencies are zero.
The control signals Δmi+1, Δmi−1, Δmv+1, and Δmv−1 in (56) are added to the system matrix Ac, and they are only related to the matrix components A0O, A0P, A0N, A−1O, A−1N, A1O, and A1P. The other matrix components A0, A+1, A−1, A+2, A−2 … are only dependent on the main circuit of MMC. Subsequently, the specific expressions of these matrix are presented in the Appendix A.
Similarly, for the input matrix Bc, as shown in (57), the controlling signals Δmv+1 and Δmv−1 need to be added into the matrix, and they are only related to the matrix components B0O, B+1O, and B−1O. The specific expressions are also presented in the Appendix A.
In general case, circulating current mainly contains dc and second harmonic components and the capacitor voltages mainly contains dc, fundamental, second and third harmonic components. Therefore, the harmonic order considered in the HSS model is h = 3.
4. Stability Analysis Based on the HSS-Based Small Signal Model
Table 1 shows the main parameters of the studied MMC. It is worth mentioning that the number of modules in one arm is 20 to reduce the simulation time. Figure 5 shows the MMC operates in dc voltage control mode. Firstly, the outer loop controller parameters are set as kp1 = 0.87 and ki1 = 10, the inner loop controller parameters are set as kp2 = 0.019 and ki2 = 0.057. It needs to be noted that, since the four state variables of control system Δxi1, Δxi2, Δxv1, and Δxv2 only have values at the frequency of 0 Hz, they do not have significance at other frequencies (−3ω1, −2ω1, −1ω1, 1ω1, 2ω1, 3ω1). Thus, there are always 24 eigenvalues at the origin (0, j0), having no effect on the stability analysis of the system. After calculation, it is confirmed that in addition to these 24 eigenvalues, there is another eigenvalue that is located at the origin. Therefore, these 25 eigenvalues will not be discussed in this paper. Additionally, other eigenvalues are plotted as shown in Figure 6. It can be seen that all eigenvalues are on the left half plane of the complex plane, which indicated that the MMC system is stable with these controller parameters.

Table 1.
The main parameters of MMC in calculation and simulation.
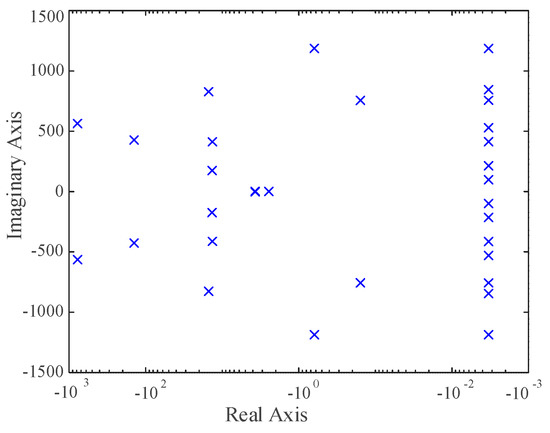
Figure 6.
Calculated eigenvalues of the system matrix when kp1 = 0.87, ki1 = 10, kp2 = 0.019, and ki2 = 0.057.
The concept of oscillation mode is introduced, that is, a real root or a pair of conjugate complex roots represent one oscillation mode of the system in order to further analyze the eigenvalues. Additionally, the participation factor analysis is introduced to analyze the interaction between state variables and oscillation modes. The participation factor of the kth state variable in the ith oscillation mode of the system can be calculated by [25]:
where Φki is the element in the kth row and ith column of the right eigenvector matrix, and Ψik is the element in the ith row and kth column of the left eigenvector matrix.
Table 2 lists the oscillation modes of the MMC systems and their main participating state variables, according to the value of the participation factors.

Table 2.
The oscillation modes of the MMC systems and their main participating state variables.
Eigenvalue loci when kp1 and kp2 changes are shown in Figure 7a,b, respectively, to analyze the effect of the controller parameters on the stability of MMC. When increasing the parameter kp1 of outer voltage loop with other parameters unchanged, as shown in Figure 7a, oscillation modes 2, 3, 6, 7, 8, 10, 11 remain unchanged, which means that these eigenvalues are not affected by the change of kp1 and most of other oscillation modes move to the right. As kp1 gradually increases, oscillation modes 4, 12, 14, 15 move horizontally to the right whose imaginary parts are nearly unchanged. Additionally, when kp1 is 1.57, oscillation mode 14 firstly moves to the right half plane, which causes the instability of the system. For example, when kp1 = 2.87, the eigenvalues of oscillation mode 14 are (4.196 ± j176.9). The corresponding oscillation period is 2π/176.9 = 0.0355 s.
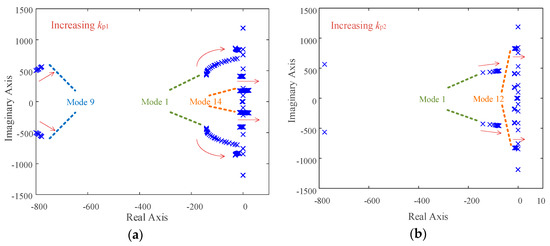
Figure 7.
Eigenvalue loci (a) when kp1 is increasing. (b) When kp2 is increasing.
Based on the analysis of participation factor, the oscillation mode 14 is strongly related to the dc component of the submodule capacitor voltage. It indicates that the instability is due to the change of proportional coefficient kp1 of the outer dc voltage controller, which affects the dc component of submodule capacitor voltage, in turn causing oscillation mode 14 to move to the right half plane and causes instability.
Only the eigenvalues whose imaginary parts remain unchanged could cross into the right half plane, even if kp1 continues to increase. This indicates that with the dc-voltage control mode, the change of controller parameter kp1 will not change the unstable oscillation frequency of the MMC system.
When increasing the proportional coefficient kp2 of inner current control loop with other parameters unchanged, as shown in Figure 7b, oscillation modes 2, 3, 6, 7, 8, 10, 11 remain unchanged, which means that these eigenvalues will not be affected by the change of kp2, and most of other oscillation modes move to the right. As kp2 gradually increases, oscillation modes 5, 12, 13, and 15 move horizontally to the right, whose imaginary parts are nearly unchanged. Additionally, when kp2 is 0.042, oscillation mode 12 firstly moves to the right half plane, which causes the instability of the system. For example, when kp2 = 0.16, eigenvalues of oscillation mode 12 are (0.107 ± j756.8). The corresponding oscillation period is 2π/756.8 = 0.0083 s.
The oscillating modes 12 is related to the third frequency component of the ac side current based on the analysis of participation factors. It indicates that the instability is due to the change of proportional coefficient kp2 of inner current controller, which affects the third frequency component of the ac side current, in turn causing the oscillation mode 12 to move to the right half plane and cause instability.
Even if kp2 continues to increase, only the eigenvalues whose imaginary parts remain unchanged could cross into the right half plane, which indicated that with the dc-voltage control mode, the change of controller parameter kp2 will also not change the unstable oscillation frequency of the MMC system.
5. Simulation Verifications
The small signal model of MMC that is based on HSS method is built in m. file in MATLAB and the considered order is set to be 3 in the model. Time-domain simulations are carried out in the MTLAB/Simulink and parameters adopted are as shown in Table 1 to validate the theoretical analysis.
5.1. Open-Loop Control Mode
When MMC operates in open-loop control mode and the reference of m(t) has a step change from 0.885sin(ω1t + φ) to 0.87sin(ω1t + φ) at 3 s, the transient response of ic(t) is presented in Figure 8a and the zoom-in view is shown in Figure 8b, showing good agreement between the small-signal model and the simulation results.
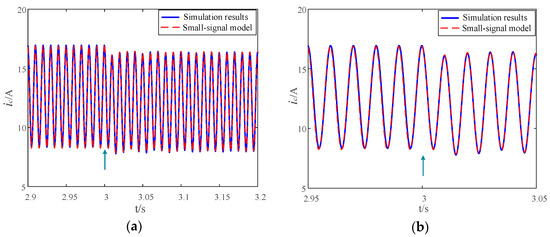
Figure 8.
Step response comparison of ic(t) with open-loop control mode. (a) Zoom-out view of ic(t). (b) Zoom-in view of ic(t).
Figure 9 shows the harmonic components of Δic(t) with open-loop control mode, which indicated that fundamental component’s change of m(t) would result in both dc and second harmonic components’ changes of ic(t), which proves that the small-signal model that is presented in this paper could reflect the internal harmonic interactions of MMC.

Figure 9.
Harmonic components of Δic(t) with open loop control mode.
5.2. DC-Voltage Control Mode
When MMC operates in dc-voltage control mode and the dc voltage reference value Udcref has a step change from 700 V to 735 V at 3 s, the transient response of ic(t) is presented in Figure 10a, and the transient response of v∑cu(t) is presented in Figure 10b, all showing good agreement between the small-signal model and simulation results, thus verifying the accuracy of the modeling presented in this paper.
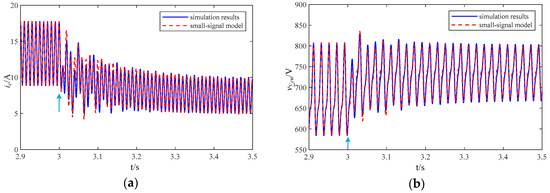
Figure 10.
Step response comparison of (a) ic(t) with dc voltage control mode. (b) v∑cu(t) with dc voltage control mode.
The outer loop controller parameter kp1 is first changed to 2.87 o verify the predicted oscillation period with different parameters, while other parameters remain unchanged in the simulation model. Figure 11 shows the simulation waveform of ic(t) with kp1 = 2.87. It can be seen that the MMC system is unstable and the measured oscillation period of ic(t) is approximately 0.032 s, which is almost consistent with the predicted oscillation period 2π/176.9 = 0.0355 s in Section 4.
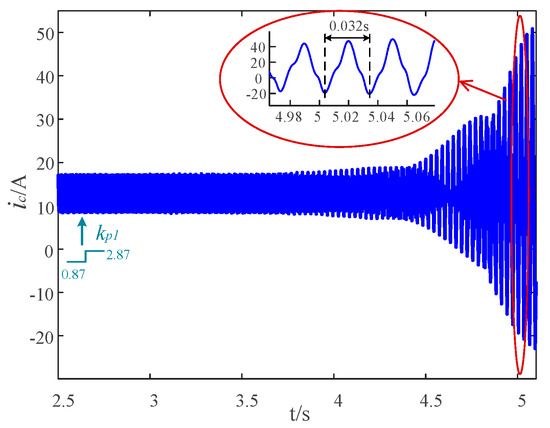
Figure 11.
Simulation waveform of ic(t) with kp1 = 2.87 while other parameters remain unchanged.
Subsequently, the inner loop controller parameter kp2 is changed to 0.162, while other parameters in the simulation model remain unchanged. Figure 12 shows the simulation waveform of ic(t) with kp2 = 0.162. It can be seen that the MMC system is unstable, and the measured oscillation period of ic(t) is about 0.009 s, which is almost consistent with the predicted oscillation period 2π/756.8 = 0.0083 s in Section 4.
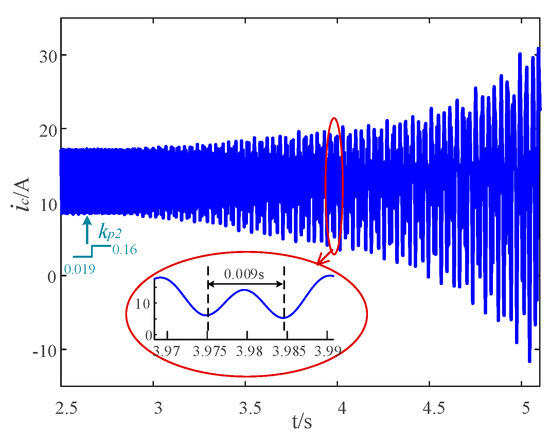
Figure 12.
Simulation waveform of ic(t) with kp2 = 0.162 while other parameters remain unchanged.
6. Conclusions
An accurate and complete small signal model of MMC with dc voltage control mode that is based on the HSS modeling method is derived, which considers the internal and external harmonic interactions, thus achieving higher accuracy. Subsequently, through the analysis of the eigenvalues, participation factors, and the calculation of oscillation frequencies under different controller parameters, the effect of controller parameters on the stability of MMC is studied and the following conclusions can be drawn. Besides, the time-domain simulation built in MATLAB/Simulink verifies the accuracy of the HSS-based MMC model and validity of stability analysis.
- (1)
- When MMC operates with dc-voltage control mode, either too large outer loop proportional coefficient kp1 or inner loop proportional coefficient kp2 might cause the system unstable.
- (2)
- The too large proportional coefficient kp1 of outer dc voltage control loop will cause an oscillation mode with certain frequency, while the too large proportional coefficient kp2 of inner current control loop will cause another oscillation mode with another certain frequency.
Author Contributions
Methodology, N.M. and S.Y.; Software, N.M., S.Y. and Y.L.; Formal analysis, Z.L. and P.L.; Validation, Z.L. and P.L.; Writing—original draft, S.Y. and Z.L.; Writing—review & editing, N.M., Y.W., B.Y. and Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Science and Technology Projects of SGCC, grant number 4000-201956494A-0-0-00.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
A0 is determined by the main circuit of MMC and does not involve the closed-loop control part, which is:
A0O represents the relationship between sΔx0 and Δx0. According to (46) and (50), ΔUdc, sΔxv1 are related to ΔIc0, and sΔxv2 is related to both ΔIc0 and Δxv1. Thus A0O could be noted as:
A0N, A0P represent the relationship between sΔx−1 and Δx−1, sΔx+1 and Δx+1 respectively. According to (45), the first part of Δmi+1 is related toΔIs+1 and the first part of Δmi−1 is related to ΔIs−1. Therefore, A0N and A0P are noted as:
A+1 is determined by the main circuit of MMC and does not involve the closed-loop control part, which is:
A+1N represents the relationship between sΔx0 and Δx−1. According to (41), sΔxi1 and sΔxi2 are both related to ΔIs−1. Thus A+1N could be noted as:
A+1O represents the relationship between sΔx+1 and Δx0. According to (45) and (51), the second part of Δmi+1 is related to Δxi1 and the third part of Δmi+1 is related to Δxi2; the second, third and fourth part of Δmv+1 are related to ΔIc0, Δxv1, Δxv2 respectively. The specific expression of A+1O is presented as:
A−1 is determined by the main circuit of MMC and does not involve the closed-loop control part, which is:
A−1P represents the relationship between sΔx0 and Δx+1. According to (41), sΔxi1 and sΔxi2 are both related to ΔIs+1. Thus A−1P could be noted as:
A−1O represents the relationship between sΔx−1 and Δx0. According to (45) and (51), the second part of Δmi−1 is related to Δxi1 and the third part of Δmi−1 is related to Δxi2; the second, third and fourth part of Δmv−1 are related to ΔIc0, Δxv1, Δxv2 respectively. The specific expression of A−1O is:
A+2 is determined by the main circuit of MMC and does not involve the closed-loop control part, which is:
A−2 is determined by the main circuit of MMC and does not involve the closed-loop control part, which is:
B0 and B±h are determined by the main circuit of MMC and does not involve the closed-loop control part, which are:
B0O represents the relationship between sΔx0 and Δu0. According to (46), sΔxv1 and sΔxv2 are related to ΔUdcref. Thus B0O could be noted as:
B+1O represents the relationship between sΔx+1 and ΔUdcref. According to (51), the first part of Δmv+1 is related to ΔUdcref. Thus B+1O could be noted as:
B−1O represents the relationship between sΔx−1 and ΔUdcref. According to (51), the first part of Δmv−1 is related to ΔUdcref. Thus B−1O could be noted as:
References
- Lesnicar, A.; Marquardt, R. An innovative modular multilevel converter topology suitable for a wide power range. In Proceedings of the Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; Volume 3, p. 6. [Google Scholar]
- Lesnicar, A.; Marquardt, R. A new modular voltage source inverter topology. In Proceedings of the European Conference on Power Electronics and Applications, Toulouse, France, 2–4 September 2003. [Google Scholar]
- Harnefors, L.; Antonopoulos, A.; Norrga, S.; Angquist, L.; Nee, H. Dynamic analysis of modular multilevel converters. IEEE Trans. Ind. Electron. 2013, 60, 2526–2537. [Google Scholar] [CrossRef]
- Ilves, K.; Antonopoulos, A.; Norrga, S.; Nee, H. Steady-state analysis of interaction between harmonic components of arm and line quantities of modular multilevel converters. IEEE Trans. Power Electron. 2012, 27, 57–68. [Google Scholar] [CrossRef]
- Peralta, J.; Saad, H.; Dennetiere, S.; Mahseredjian, J.; Nguefeu, S. Detailed and averaged models for a 401-level MMC–HVDC system. IEEE Trans. Power Deliv. 2012, 27, 1501–1508. [Google Scholar] [CrossRef]
- Saeedifard, M.; Iravani, R. Dynamic performance of a modular multilevel back-to-back HVDC system. IEEE Trans. Power Deliv. 2010, 25, 2903–2912. [Google Scholar] [CrossRef]
- Xu, J.; Gole, A.M.; Zhao, C. The use of averaged-value model of modular multilevel converter in DC grid. IEEE Trans. Power Deliv. 2015, 30, 519–528. [Google Scholar] [CrossRef]
- Ludois, D.C.; Venkataramanan, G. Simplified terminal behavioral model for a modular multilevel converter. IEEE Trans. Power Electron. 2014, 29, 1622–1631. [Google Scholar] [CrossRef]
- Rowe, H.E. Some general properties of nonlinear elements. II. Small signal theory. Proc. IRE 1958, 46, 850–860. [Google Scholar] [CrossRef]
- Middlebrook, R.D. Small-signal modeling of pulse-width modulated switched-mode power converters. Proc. IEEE 1988, 4, 343–354. [Google Scholar] [CrossRef]
- Witulski, A.F.; Hernandez, A.F.; Erickson, R.W. Small signal equivalent circuit modeling of resonant converters. IEEE Trans. Power Electron. 1991, 6, 11–27. [Google Scholar] [CrossRef]
- Coelho, E.A.A.; Cortizo, P.C.; Garcia, P.F.D. Small-signal stability for parallel-connected inverters in stand-alone AC supply systems. IEEE Trans. Ind. Appl. 2002, 38, 533–542. [Google Scholar] [CrossRef]
- Diaz, G.B.; Suul, J.A.; D’Arco, S. Small-signal state-space modeling of modular multilevel converters for system stability analysis. In Proceedings of the Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 5822–5829. [Google Scholar]
- Li, T.; Gole, A.M.; Zhao, C. Harmonic instability in MMC-HVDC converters resulting from internal dynamics. IEEE Trans. Power Deliv. 2016, 31, 1738–1747. [Google Scholar] [CrossRef]
- Jamshidi Far, A.; Jovcic, D. Small-signal dynamic DQ model of modular multilevel converter for system studies. IEEE Trans. Power Deliv. 2016, 31, 191–199. [Google Scholar] [CrossRef]
- Lu, X.; Lin, W.; Wen, J.; Yao, W. Dynamic phasor modelling and operating characteristic analysis of half-bridge MMC. In Proceedings of the International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 2615–2621. [Google Scholar]
- Sun, J.; Liu, H. Sequence impedance modeling of modular multilevel converters. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1427–1443. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F. Harmonic stability in power electronic-based power systems: Concept, modeling, and analysis. IEEE Trans. Smar. Grid 2019, 10, 2858–2870. [Google Scholar] [CrossRef]
- Love, G.N.; Wood, A.R. Harmonic state space model of power electronics. In Proceedings of the International Conference on Harmonics and Quality of Power, Wollongong, Australia, 28 September–1 October 2008; pp. 1–6. [Google Scholar]
- Orillaza, J.R.C.; Wood, A.R. Harmonic state-space model of a controlled TCR. IEEE Trans. Power Deliv. 2013, 28, 197–205. [Google Scholar] [CrossRef]
- Kwon, J.; Wang, X.; Blaabjerg, F.; Bak, C.L.; Sularea, V.; Busca, C. Harmonic interaction analysis in a grid-connected converter using harmonic state-space (HSS) modeling. IEEE Trans. Power Electron. 2017, 32, 6823–6835. [Google Scholar] [CrossRef]
- Lyu, J.; Zhang, X.; Cai, X.; Molinas, M. Harmonic state-space based small-signal impedance modeling of a modular multilevel converter with consideration of internal harmonic dynamics. IEEE Trans. Power Electron. 2019, 34, 2134–2148. [Google Scholar] [CrossRef]
- Sun, J. Impedance-based stability criterion for grid-connected inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Xiong, L.; Liu, X.; Zhao, C.; Zhuo, F. A fast and robust real-time detection algorithm of decaying DC transient and harmonic components in three-phase systems. IEEE Trans. Power Electron. 2020, 35, 3332–3336. [Google Scholar] [CrossRef]
- Kundur, P.S. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).