Quantification of the Energy Storage Contribution to Security of Supply through the F-Factor Methodology
Abstract
1. Introduction
- Presentation of F-factors as a methodology for the quantification of the security contribution of ES.
- Demonstration of the mathematical formulation for the optimization problem that is solved for the evaluation of the F-factor metric.
- Sensitivity analysis of the security contribution of ES as a function of multiple quantities such as energy storage power capability, efficiency, energy capacity and characteristics of load patterns.
2. Literature Review
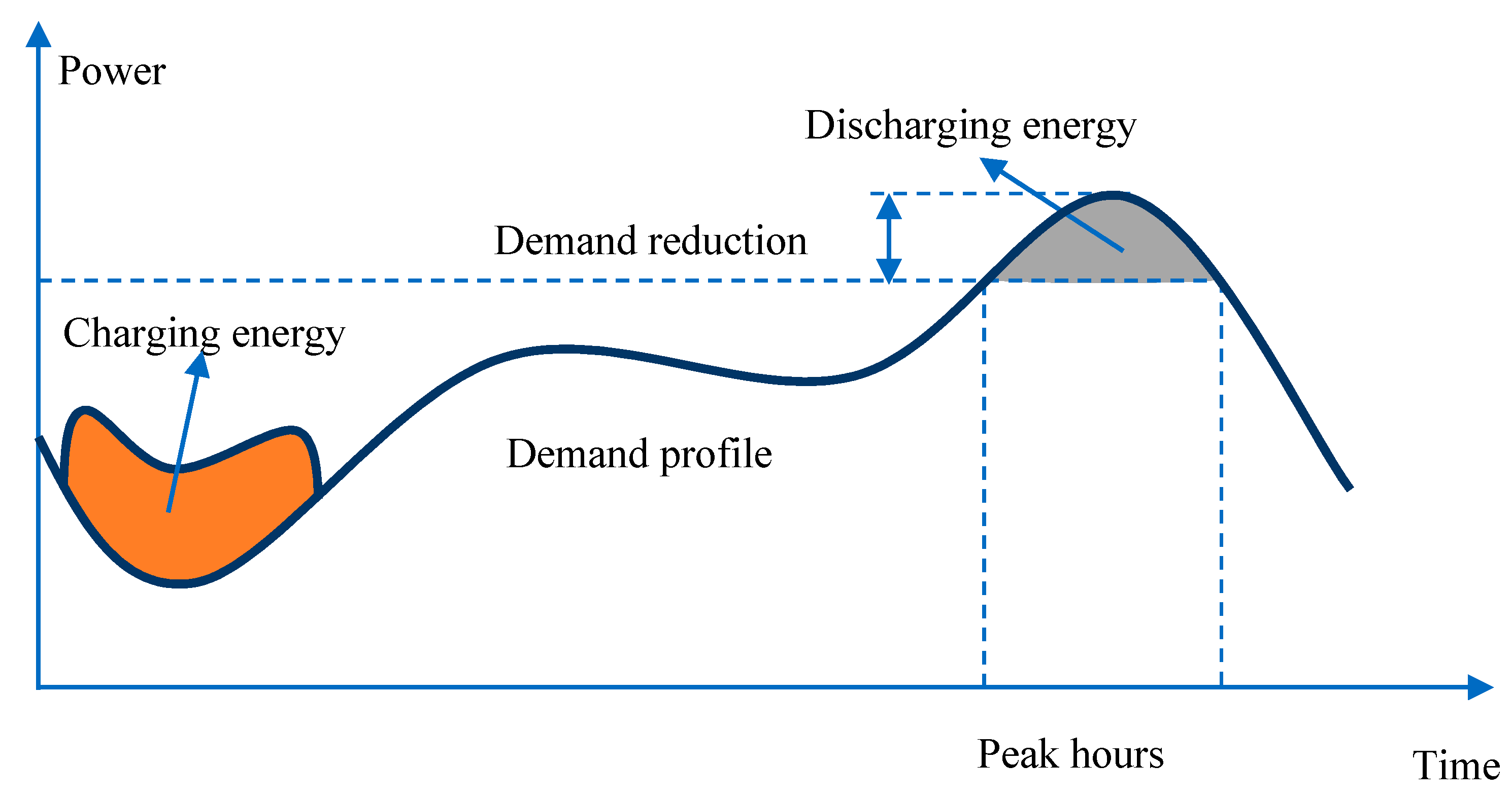
3. The F-Factor Methodology
3.1. Definition of the Metric
3.2. Optimization Problem
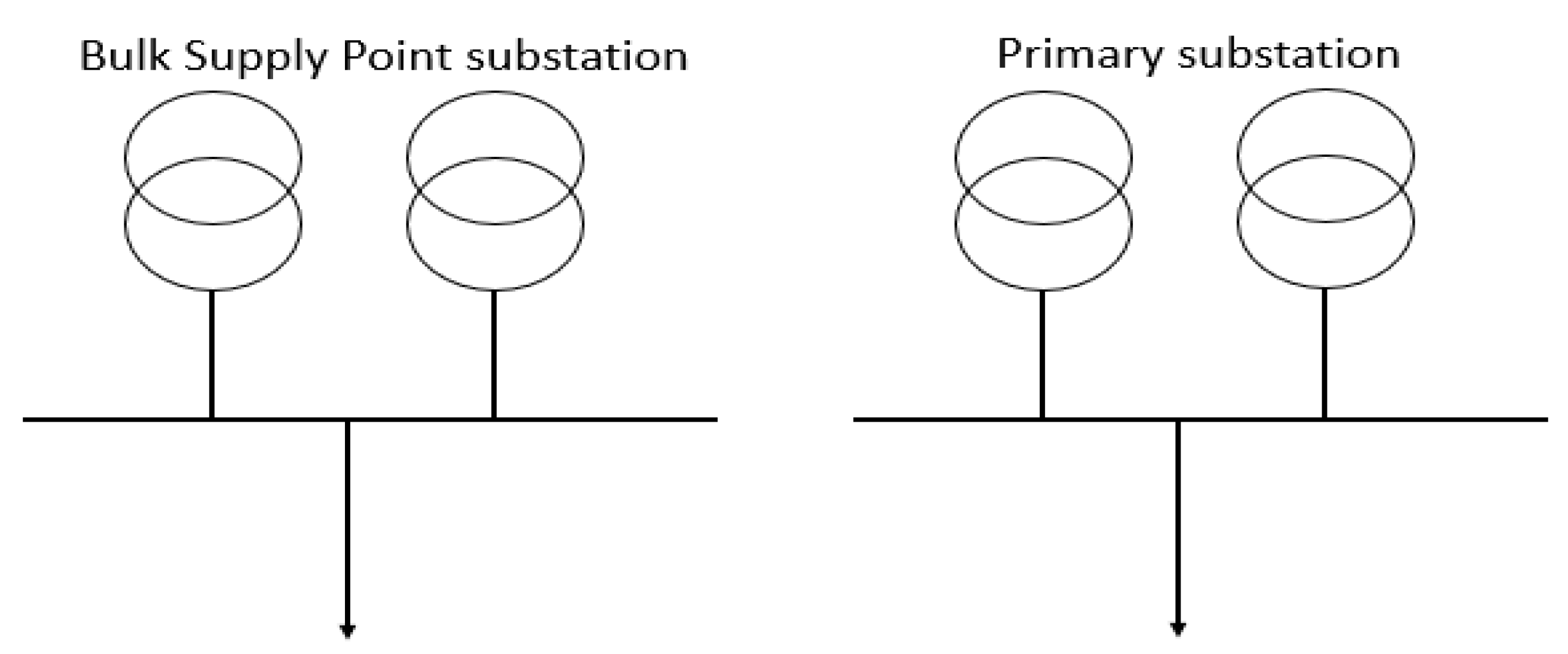
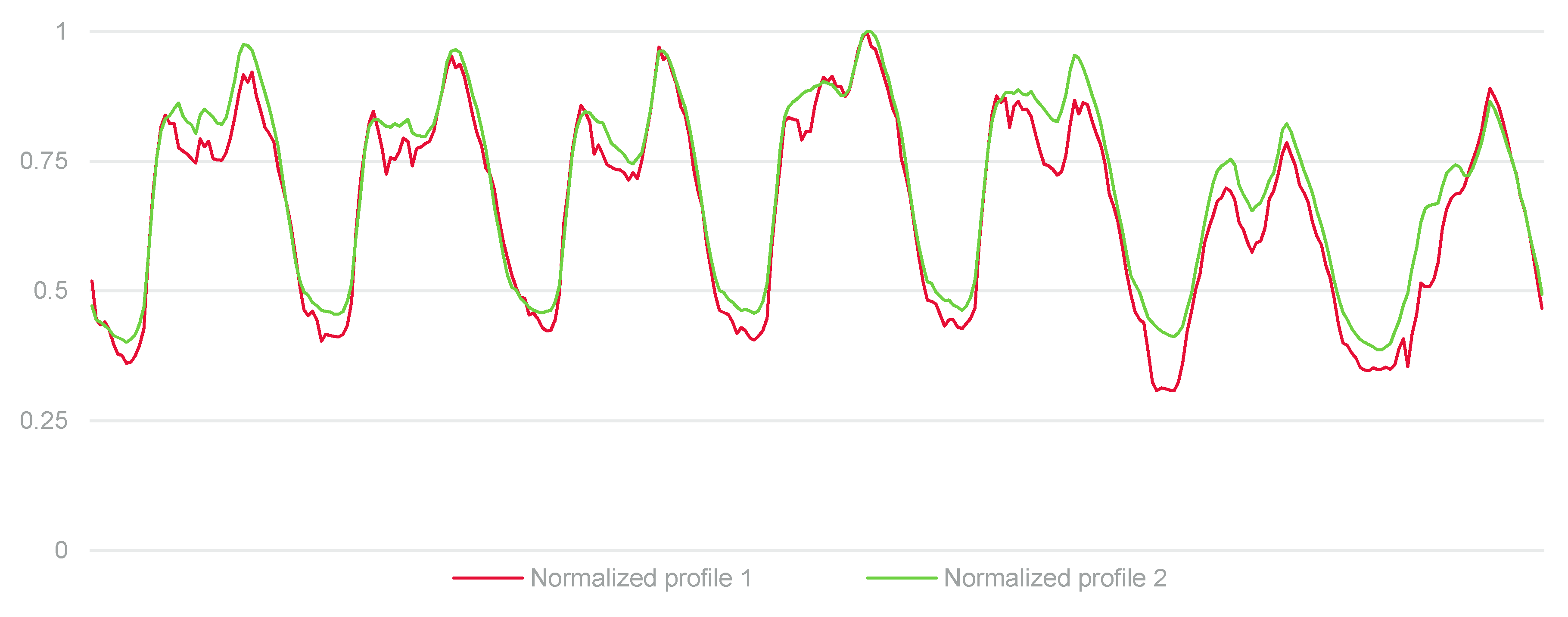
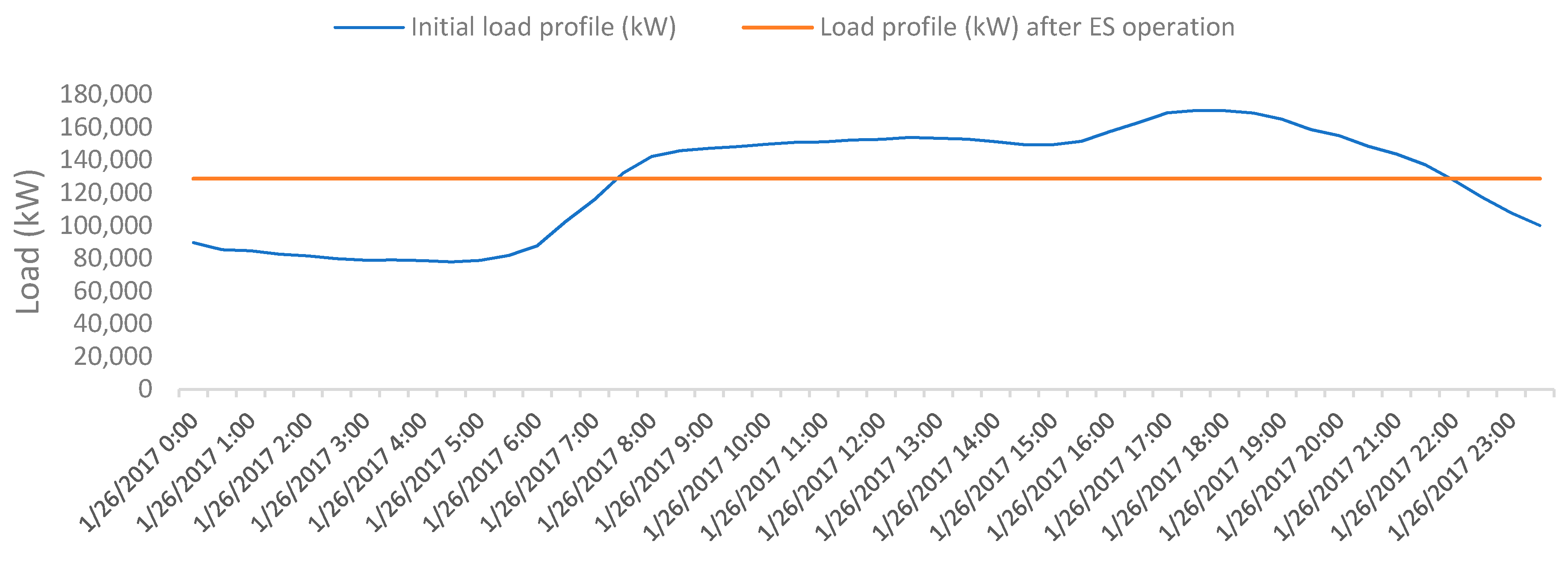
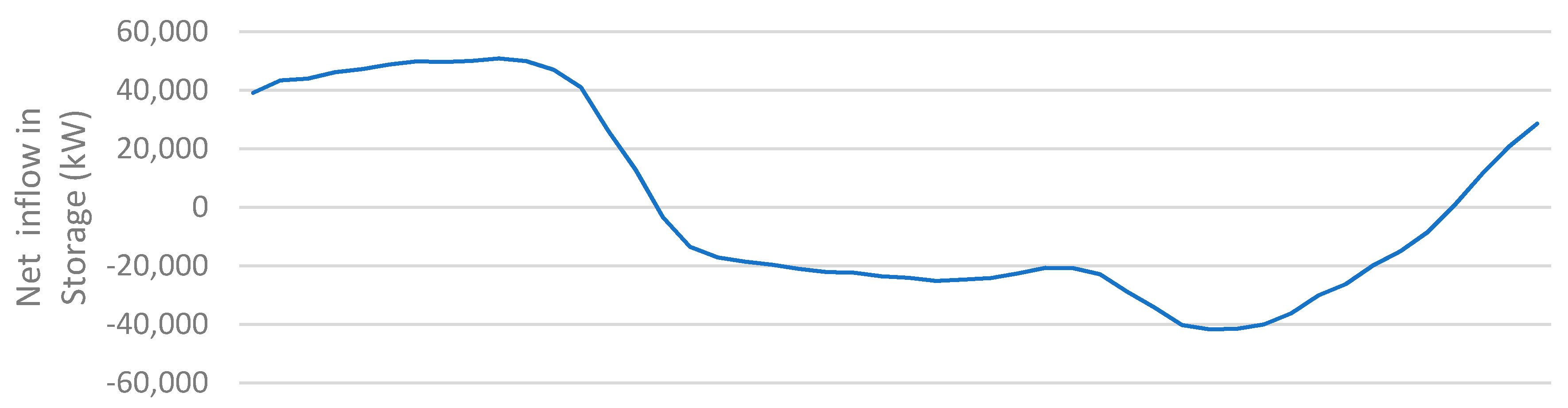
4. Case Study: Evaluation of the ES Security Contribution via F-factors
5. Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Giannelos, S.; Konstantelos, I.; Strbac, G. Option value of dynamic line rating and storage. In Proceedings of the 2018 IEEE International Energy Conference (ENERGYCON), Limassol, Cyprus, 3–7 June 2018; pp. 1–6. [Google Scholar]
- Giannelos, S.; Konstantelos, I.; Strbac, G. Option Value of Demand-Side Response Schemes Under Decision-Dependent Uncertainty. IEEE Trans. Power Syst. 2018, 33, 5103–5113. [Google Scholar] [CrossRef]
- Pudjianto, D.; Aunedi, M.; Djapic, P.; Strbac, G. Whole-Systems Assessment of the Value of Energy Storage in Low-Carbon Electricity Systems. IEEE Trans. Smart Grid 2014, 5, 1098–1109. [Google Scholar] [CrossRef]
- Moreno, R.; Moreira, R.; Strbac, G. A MILP model for optimizing multi-service portfolios of distributed energy storage. Appl. Energy 2015, 137, 554–566. [Google Scholar] [CrossRef]
- Nieto, A.; Vita, V.; Maris, T.I. Power quality improvement in power grids with the integration of energy storage systems. Int. J. Eng. Res. Technol. 2016, 5, 438–443. [Google Scholar]
- Papadaskalopoulos, D.; Pudjianto, D.; Strbac, G. Decentralized Coordination of Microgrids With Flexible Demand and Energy Storage. IEEE Trans. Sustain. Energy 2014, 5, 1406–1414. [Google Scholar] [CrossRef]
- Agamah, S.; Ekonomou, L. Energy storage system scheduling for peak demand reduction using evolutionary combinatorial optimization. Sustain. Energy Technol. Assess. 2017, 23, 73–82. [Google Scholar]
- Strbac, G.; Konstantelos, I.; Djapic, P. Analysis of Integrated Energy Storage Contribution to Security of Supply: Report for Smarter Network Storage Project. Available online: http://innovation.ukpowernetworks.co.uk/innovation/en/Projects/tier-2-projects/Smarter-Network-Storage-(SNS)/Project-Documents/SNS_P2_6_SDRC9.6v1.pdf (accessed on 30 January 2020).
- Konstantelos, I.; Djapic, P.; Strbac, G.; Papadopoulos, P.; Laguna, A. Contribution of Energy Storage and Demand-Side Response to Security of Distribution Network. In Proceedings of the CIRED, Glasgow, Scotland, 12–15 June 2017. [Google Scholar]
- Agamah, S.; Ekonomou, L. A heuristic combinatorial optimization algorithm for load-levelling and peak demand reduction using energy storage systems. Electr. Power Compon. Syst. 2018, 45, 2093–2103. [Google Scholar] [CrossRef]
- Strbac, G.; Aunedi, M.; Konstantelos, I.; Moreira, R.; Teng, F.; Moreno, R.; Pudjianto, D.; Laguna, A.; Papadopoulos, P. Opportunities for Energy Storage: Assessing Whole-System Economic Benefits of Energy Storage in Future Electricity Systems. IEEE Power Energy Mag. 2017, 15, 32–41. [Google Scholar] [CrossRef]
- Strbac, G.; Konstantelos, I.; Pollitt, M.; Green, R. Report for the UK National Infrastructure Commission: Delivering Future-Proof Energy Infrastructure. Available online: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/507256/Future-proof_energy_infrastructure_Imp_Cam_Feb_2016.pdf (accessed on 30 January 2020).
- National Grid, Future Energy Scenarios 2016. Available online: http://fes.nationalgrid.com/ (accessed on 30 January 2020).
- European Smart Grids Task Force. Regulatory Recommendations for the Deployment of Flexibility; European Smart Grids Task Force: Brussels, Belgium, 2015; Available online: https://ec.europa.eu/energy/sites/ener/files/documents/EG3%20Final%20-%20January%202015.pdf (accessed on 30 January 2020).
- Electricity Networks Association. Engineering Recommendation P2/6: Security of Supply; Electricity Networks Association: London, UK, 2006; Available online: http://www.dcode.org.uk/assets/uploads/ENA_ER_P2_Issue_6__2006_-1.pdf (accessed on 30 January 2020).
- Milligan, M.; Porter, K. Determining the capacity value of wind: An updated survey of methods and implementation. In Proceedings of the Wind-Power, Houston, TX, USA, 1–4 June 2008. [Google Scholar]
- Keane, A.; Milligan, M.; Dent, C.J.; Hasche, B.; D’Annunzio, C.; Dragoon, K.; Holttinen, H.; Samaan, N.; Soder, L.; O’Malley, M. Capacity Value of Wind Power. IEEE Trans. Power Syst. 2010, 26, 564–572. [Google Scholar] [CrossRef]
- Amelin, M. Comparison of Capacity Credit Calculation Methods for Conventional Power Plants and Wind Power. IEEE Trans. Power Syst. 2009, 24, 685–691. [Google Scholar] [CrossRef]
- Public Service Electric and Gas Company, Electric Power Research Institute. An Assessment of Energy Storage Systems Suitable for Use by Electric Utilities; Final Report; Public Service Electric and Gas Co.: Newark, NJ, USA, 1979. [Google Scholar]
- Sioshansi, R.; Madaeni, S.H.; Denholm, P. A dynamic programming approach to estimate the capacity value of energy storage. IEEE Trans. Power Syst. 2014, 29, 395–403. [Google Scholar] [CrossRef]
- Konstantelos, I.; Strbac, G. Capacity value of energy storage in distribution networks. J. Energy Storage 2018, 18, 389–401. [Google Scholar] [CrossRef]
- Nolan, S.; O’Malley, M.; Hummon, M.; Kiliccote, S.; Ma, O. A methodology for estimating the capacity value of demand response. In Proceedings of the 2014 IEEE PES General Meeting|Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar]
- Earle, R.; Kahn, E.P.; Macan, E. Measuring the Capacity Impacts of Demand Response. Electr. J. 2009, 22, 47–58. [Google Scholar] [CrossRef]
- Abdullah, M.A.; Muttaqi, K.M.; Agalgaonkar, A.P.; Sutanto, D. Estimating the capacity value of energy storage integrated in wind power generation. In Proceedings of the 2013 IEEE Power and Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013. [Google Scholar]
- National Renewable Energy Laboratory (NREL). The Value of Energy Storage for Grid Applications; Technical Report; NREL: Boulder, CO, USA, 2013.
- Tuohy, A.; O’Malley, M. Impact of pumped storage on power systems with increasing wind penetration. In Proceedings of the IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–8. [Google Scholar]
- Tuohy, A.; O’Malley, M. Pumped storage in systems with very high wind penetration. Energy Policy 2011, 39, 1965–1974. [Google Scholar] [CrossRef]
- Zhou, Y.; Mancarella, P.; Mutale, J. A framework for capacity credit assessment of electrical energy storage and demand response. IET Gener. Transm. Distrib. 2016, 10, 2267–2276. [Google Scholar] [CrossRef]
- Da Silva, A.M.L.; Cassula, A.M.; Nascimento, L.C.; Freire, J.C.; Sacramento, C.E.; Guimarães, A.C.R. Chronological Monte Carlo-Based Assessment of Distribution System Reliability. In Proceedings of the 2006 International Conference on Probabilistic Methods Applied to Power Systems, Stockholm, Sweden, 11–15 June 2006; pp. 1–7. [Google Scholar]
- Black, M.; Strbac, G. Value of Bulk Energy Storage for Managing Wind Power Fluctuations. IEEE Trans. Energy Convers. 2007, 22, 197–205. [Google Scholar] [CrossRef]
- Thatte, A.A.; Xie, L. Towards a Unified Operational Value Index of Energy Storage in Smart Grid Environment. IEEE Trans. Smart Grid 2012, 3, 1418–1426. [Google Scholar] [CrossRef]
- Denholm, P.; Sioshansi, R. The value of compressed air energy storage with wind in transmission-constrained electric power systems. Energy Policy 2009, 37, 3149–3158. [Google Scholar] [CrossRef]
- Drury, E.; Denholm, P.; Sioshansi, R. The Value of Compressed Air Energy Storage in Energy and Reserve Markets. Energy 2011, 36, 4959–4973. [Google Scholar] [CrossRef]
- Dong, J.; Gao, F.; Guan, X.; Zhai, Q.; Wu, J. Storage Sizing With Peak-Shaving Policy for Wind Farm Based on Cyclic Markov Chain Model. IEEE Trans. Sustain. Energy 2017, 8, 978–989. [Google Scholar] [CrossRef]
- Mahmud, K.; Hossain, M.J.; Town, G.E. Peak-Load Reduction by Coordinated Response of Photovoltaics, Battery Storage, and Electric Vehicles. IEEE Access 2018, 6, 29353–29365. [Google Scholar] [CrossRef]
- Agamah, S.U.; Ekonomou, L. Peak demand shaving and load-levelling using a combination of bin packing and subset sum algorithms for electrical energy storage system scheduling. IET Sci. Meas. Technol. 2016, 10, 477–484. [Google Scholar] [CrossRef]
- Allan, R.; Strbac, G.; Djapic, P.; Jarrett, K. Developing the P2/6 Methodology; University of Manchester: Manchester, UK, 2004. Available online: https://webarchive.nationalarchives.gov.uk/20100919182336/http://www.ensg.gov.uk/assets/methodology.pdf (accessed on 30 January 2020).
- Energy Networks Association, Engineering Report 130, Working Group. Substation Demand Profiles, London. 2018. Available online: http://www.energynetworks.org/assets/files/news/publications/Reports/ENA%20HVWG%20Report%20Final.pdf (accessed on 30 January 2020).
- Koller, M.; Borsche, T.; Ulbig, A.; Andersson, G. Defining a degradation cost function for optimal control of a battery energy storage system. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013; pp. 1–6. [Google Scholar]
- Castronuovo, E.D.; Lopes, J. On the Optimization of the Daily Operation of a Wind-Hydro Power Plant. IEEE Trans. Power Syst. 2004, 19, 1599–1606. [Google Scholar] [CrossRef]
- Swider, D.J. Compressed Air Energy Storage in an Electricity System With Significant Wind Power Generation. IEEE Trans. Energy Convers. 2007, 22, 95–102. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, J.; De La Muela, R.M.R.; Santos, L.M.; Gonzalez, A.M. Stochastic Joint Optimization of Wind Generation and Pumped-Storage Units in an Electricity Market. IEEE Trans. Power Syst. 2008, 23, 460–468. [Google Scholar] [CrossRef]
- Brown, P.; Lopes, J.A.P.; Matos, M. Optimization of Pumped Storage Capacity in an Isolated Power System With Large Renewable Penetration. IEEE Trans. Power Syst. 2008, 23, 523–531. [Google Scholar] [CrossRef]
- Zhang, N.; Kang, C.; Kirschen, D.S.; Xia, Q.; Xi, W.; Huang, J.; Zhang, Q. Planning Pumped Storage Capacity for Wind Power Integration. IEEE Trans. Sustain. Energy 2012, 4, 393–401. [Google Scholar] [CrossRef]
- Giannelos, S.; Konstantelos, I.; Strbac, G. Option Value of Soft Open Points in Distribution Networks. 2015, pp. 1–6. Available online: https://core.ac.uk/download/pdf/77010954.pdf (accessed on 30 January 2020).
- Abdeltawab, H.H.; Mohamed, Y.A.-R.I. Robust Energy Management of a Hybrid Wind and Flywheel Energy Storage System Considering Flywheel Power Losses Minimization and Grid-Code Constraints. IEEE Trans. Ind. Electron. 2016, 63, 4242–4254. [Google Scholar] [CrossRef]
| at 10% of Peak | at 20% of Peak | at 30% of Peak | at 50% of Peak | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Efficiency | Efficiency | Efficiency | Efficiency | |||||||||
| 100% | 80% | 60% | 100% | 80% | 60% | 100% | 80% | 60% | 100% | 80% | 60% | |
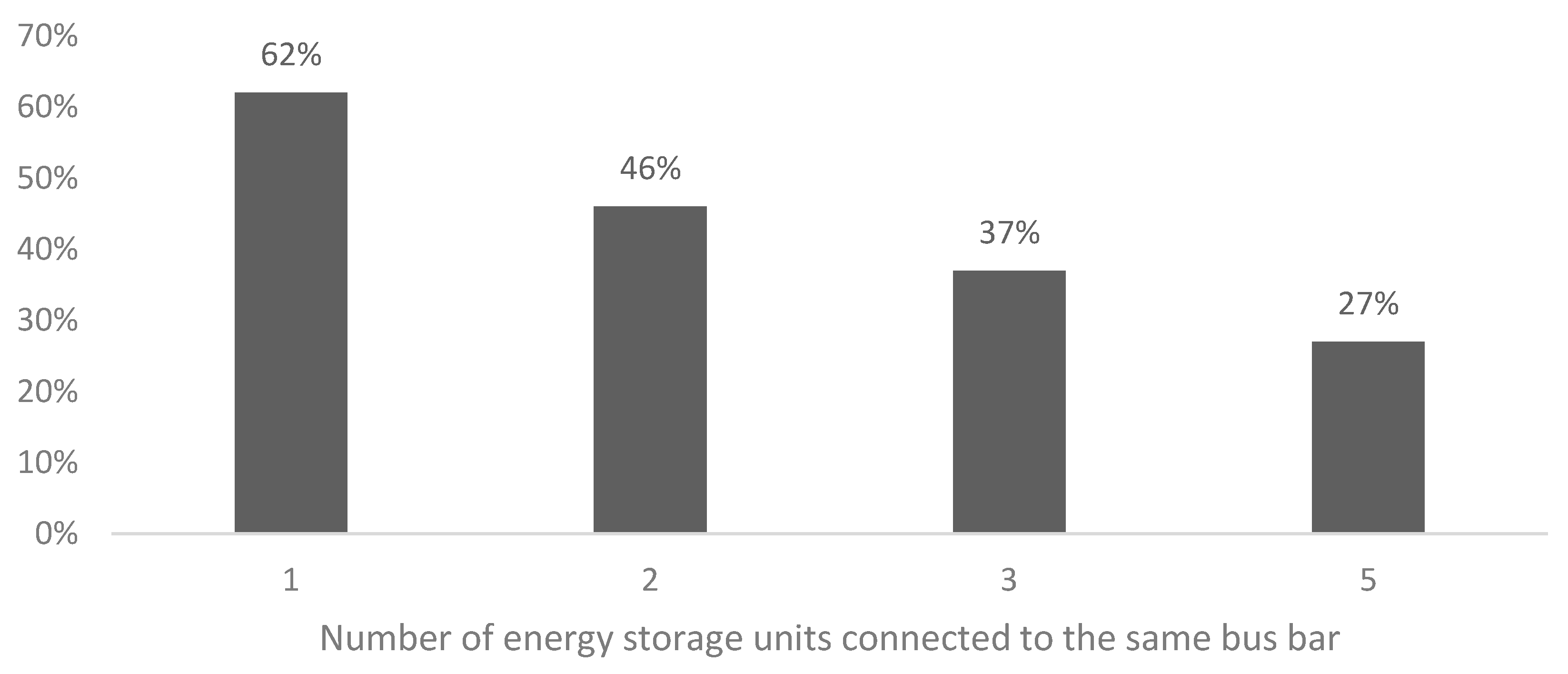
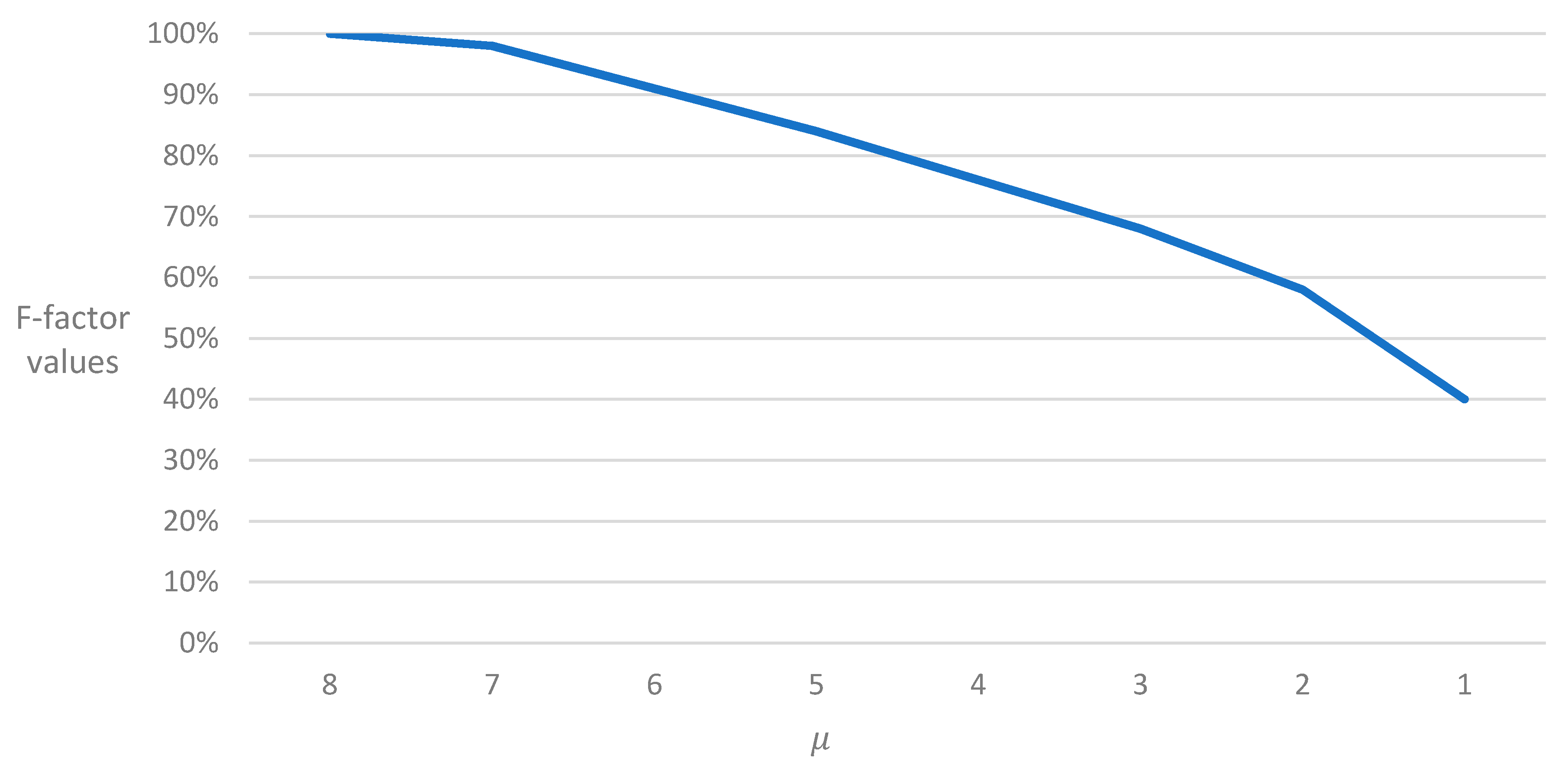
| 1 h | 62% | 62% | 62% | 46% | 46% | 46% | 37% | 37% | 37% | 27% | 27% | 27% |
| 2 h | 92% | 92% | 92% | 61% | 61% | 61% | 49% | 49% | 49% | 37% | 37% | 37% |
| 3 h | 100% | 100% | 100% | 73% | 73% | 73% | 59% | 59% | 59% | 45% | 45% | 45% |
| 4 h | 100% | 100% | 100% | 84% | 84% | 84% | 67% | 67% | 67% | 52% | 50% (52%) | 46% (52%) |
| 5 h | 100% | 100% | 100% | 93% | 93% | 93% | 74% | 74% | 73% (74%) | 54% (59%) | 50% (58%) | 46% (55%) |
| 6 h | 100% | 100% | 100% | 100% | 100% | 96% (100%) | 82% | 82% | 73% (82%) | 54% (62%) | 50% (59%) | 46% (56%) |
| 7 h | 100% | 100% | 100% | 100% | 100% | 96% (100%) | 89% | 82% (89%) | 73% (89%) | 54% (63%) | 50% (60%) | 46% (57%) |
| 8 h | 100% | 100% | 100% | 100% | 100% | 96% (100%) | 90% (96%) | 82% (96%) | 73% (92%) | 54% (64%) | 50% (61%) | 46% (57%) |
| at 10% of Peak | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Efficiency | Efficiency | Efficiency | Efficiency | |||||||||
| 100% | 80% | 60% | 100% | 80% | 60% | 100% | 80% | 60% | 100% | 80% | 60% | |
| 1 h | 49% | 49% | 49% | 40% | 40% | 40% | 34% | 34% | 34% | 25% | 25% | 25% |
| 2 h | 80% | 80% | 80% | 58% | 58% | 58% | 45% | 45% | 45% | 33% | 33% | 33% |
| 3 h | 100% | 100% | 100% | 68% | 68% | 68% | 53% | 53% | 53% | 41% | 41% | 41% |
| 4 h | 100% | 100% | 100% | 76% | 76% | 76% | 61% | 61% | 61% | 48% | 45% (48%) | 41% (46%) |
| 5 h | 100% | 100% | 100% | 84% | 84% | 84% | 68% | 68% | 66% (68%) | 49%(53%) | 45% (51%) | 41% (49%) |
| 6 h | 100% | 100% | 100% | 91% | 91% | 87% (91%) | 75% | 75% | 66% (75%) | 49% (56%) | 45% (53%) | 41% (49%) |
| 7 h | 100% | 100% | 100% | 98% | 98% | 87% (98%) | 82% | 75% (82%) | 66% (78%) | 49% (57%) | 45% (53%) | 41% (49%) |
| 8 h | 100% | 100% | 100% | 100% | 98% (100%) | 87% (100%) | 82% (88%) | 75% (85%) | 66% (79%) | 49% (57%) | 45% (53%) | 41% (49%) |
| Efficiency | Efficiency | Efficiency | Efficiency | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100% | 80% | 60% | 100% | 80% | 60% | 100% | 80% | 60% | 100% | 80% | 60% | |
| 1 h | 47% | 47% | 47% | 34% | 34% | 34% | 29% | 29% | 29% | 22% | 22% | 22% |
| 2 h | 69% | 69% | 69% | 51% | 51% | 51% | 39% | 39% | 39% | 29% | 29% | 29% |
| 3 h | 87% | 87% | 87% | 59% | 59% | 59% | 46% | 46% | 46% | 35% | 35% | 35% |
| 4 h | 100% | 100% | 100% | 66% | 66% | 66% | 53% | 53% | 53% | 40% | 40% | 40% |
| 5 h | 100% | 100% | 100% | 73% | 73% | 73% | 59% | 59% | 59% | 45% | 45% | 45% |
| 6 h | 100% | 100% | 100% | 80% | 80% | 80% | 64% | 64% | 64% | 49% | 49% | 46% (49%) |
| 7 h | 100% | 100% | 100% | 86% | 86% | 86% | 68% | 68% | 68% | 53% | 50% (53%) | 46% (53%) |
| 8 h | 100% | 100% | 100% | 92% | 91% | 91% | 73% | 73% | 73% | 54% (57%) | 50% (57%) | 46% (55%) |
| Efficiency | Efficiency | Efficiency | Efficiency | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100% | 80% | 60% | 100% | 80% | 60% | 100% | 80% | 60% | 100% | 80% | 60% | |
| 1 h | 34% | 34% | 34% | 28% | 28% | 28% | 25% | 25% | 25% | 21% | 21% | 21% |
| 2 h | 56% | 56% | 56% | 45% | 45% | 45% | 38% | 37% | 37% | 27% | 27% | 27% |
| 3 h | 75% | 75% | 75% | 56% | 56% | 56% | 43% | 43% | 43% | 32% | 32% | 32% |
| 4 h | 90% | 90% | 90% | 62% | 62% | 62% | 48% | 48% | 48% | 36% | 36% | 36% |
| 5 h | 100% | 100% | 100% | 68% | 68% | 68% | 53% | 53% | 53% | 41% | 41% | 41% |
| 6 h | 100% | 100% | 100% | 73% | 73% | 73% | 58% | 58% | 58% | 45% | 45% | 41% (45%) |
| 7 h | 100% | 100% | 100% | 77% | 77% | 77% | 62% | 62% | 62% | 49% | 45% (49%) | 41% (47%) |
| 8 h | 100% | 100% | 100% | 82% | 82% | 82% | 67% | 67% | 67% | 49% (53%) | 45% (51%) | 41% (49%) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giannelos, S.; Djapic, P.; Pudjianto, D.; Strbac, G. Quantification of the Energy Storage Contribution to Security of Supply through the F-Factor Methodology. Energies 2020, 13, 826. https://doi.org/10.3390/en13040826
Giannelos S, Djapic P, Pudjianto D, Strbac G. Quantification of the Energy Storage Contribution to Security of Supply through the F-Factor Methodology. Energies. 2020; 13(4):826. https://doi.org/10.3390/en13040826
Chicago/Turabian StyleGiannelos, Spyros, Predrag Djapic, Danny Pudjianto, and Goran Strbac. 2020. "Quantification of the Energy Storage Contribution to Security of Supply through the F-Factor Methodology" Energies 13, no. 4: 826. https://doi.org/10.3390/en13040826
APA StyleGiannelos, S., Djapic, P., Pudjianto, D., & Strbac, G. (2020). Quantification of the Energy Storage Contribution to Security of Supply through the F-Factor Methodology. Energies, 13(4), 826. https://doi.org/10.3390/en13040826





