1. Importance of a Dynamic Emission Factor in Sector-Coupled Energy Systems
Sector-coupled energy systems have a great potential for the development of renewable district heating systems [
1]. A sector-coupled energy system in general connects the different energy sectors, which are electricity, heat and mobility, with the aim of increasing the share of renewable energies in all energy sectors. The principle of sector-coupling is described in detail in [
2]. To properly analyze dependencies and synergies of the different energy sectors in future renewable energy systems, Smart Energy System approaches, as defined in [
3], are needed. Therefore, holistic models containing all parts of the energy system with a focus on the national energy system, like the energy system model EnergyPLAN, have been developed [
3,
4]. With such models, optimal solutions for the complex, sector-coupled energy system considering all synergies can be found. For design decisions on a municipal level, models with a higher degree of detail in the individual districts have been introduced to both derive individual energy concepts and support the local planning process. Consequently, the national energy system itself is often not considered anymore in detail, as it means a considerable effort to model the entire energy system for each decision on district level. To overcome this a system boundary for the urban energy system model needs to be set and parameters like costs and emission of the energy carriers crossing the system boundary need to be defined. The analysis of the transition from the current energy system to a system entirely based on 100% renewable energy system demands for an appropriate consideration of greenhouse gas emission of the energy commodities that are imported into the local system. In the future, electricity is probably the most important commodity crossing the system boundary of local energy systems. The emission attributed to one energy unit is time-dependent due to the volatile share of renewable electricity within the total electricity generation [
5,
6,
7]. Hence, the climate impact of electricity usage strongly fluctuates over time, requiring operational strategies of dispatchable distributed energy resources to be as important as the chosen components themselves. However, many local energy system models use a constant emission factor for grid-sourced electricity.
In this article, the term emission factor refers to the greenhouse gas emission in the equivalent of carbon dioxide (CO2) attributed to one kilowatt-hour electricity from the upstream electricity grid. A constant emission factor means a fixed value regardless of the time, at which electricity is sourced from the grid. A dynamic emission factor implies that individual emission factors are used for each point in time, depending on the upstream power grid.
There is a wide range of available tools for planning and optimizing sector-coupled district energy systems, with many different emphases and specializations. Some approaches consider a flexible energy system design due to uncertainties, like [
8] focusing on long term uncertainties, and [
9] concentrating on demand uncertainties. Others use a multi-objective optimization, which often considers costs, emission and in some cases a third objective, like security, share of renewable energies within the system (e.g., [
4]), exergy efficiency (e.g., [
10]), or just costs and exergy [
11]. There are approaches focusing on the flexible design of a special technology within district energy systems, such as the sizing of combined heat and power (CHP), or co-generation plants (e.g., [
12,
13,
14]), respectively. Other studies include the refurbishment of buildings [
15]. Falke et al. also take the emission of the components’ manufacturing through life cycle assessment into account [
16]. In terms of CO
2 emissions, all mentioned models are using a constant emission factor for grid-sourced electricity, or do not explicitly state that a dynamic emission factor is used. Only one article was found, which explicitly mentions that a dynamic emission factor was used as input parameter for grid-sourced electricity [
17].
To study the impact of varying the emission factor of grid-sourced electricity, Worner et al. analyzed the potential emission savings of an emission oriented control of a heat pump in a two-story single-family house with dynamic emission factors for grid-sourced electricity [
6]. So far, there is no publication discussing the impact of different ways to consider the emission factor of grid-sourced electricity on design decisions in investment and unit commitment optimization models within future energy scenarios in a sector-coupled urban district energy system. The current work analyzes and quantifies the impact of the time-dependent characteristic of the emission factor of grid-sourced electricity in such energy system models for designing Smart Energy Systems. The concept of a local emission factor is introduced—an approach for designing renewable and system-beneficial district energy systems by using a dynamic emission factor as a design parameter. The aim is to significantly improve local energy system models without adding unnecessary complexity, while providing a remedy for neglecting the national electricity system.
2. Introduction of the Applied Optimization Method and Case Study
First, the general model and the mathematical background of the applied method of an investment and unit commitment model are described. Secondly, the structure, the scenario data, the concept of a local emission factor and the parameters of the case study are presented.
2.1. General Model Description
The aim of the techno-economic optimization model is to find the best trade-off solution between costs and emissions for designing a system-beneficial generation site of an urban district energy supply facility. The problem statement for this energy system investment and unit commitment optimization is:
Given are the heat and electricity demand of an urban district, energy converter and storage options and energy commodity sources. The heat and electricity demand are represented by aggregated load profiles, which include grid losses for distribution in case of the heat demand. The technical parameters, such as conversion factors and energy losses, and the economic parameters, such as capital and operation costs, are given for each energy converter and storage unit. The commodity sources are natural gas and electricity from the upstream electricity system. Both are characterized by energy-specific costs and an emission factor. The optimization problem is concerned with deciding on how to dimension and how to commit the energy converter and storage units, while minimizing the costs and meeting a given emission limit and finding the solution with minimum emissions. The optimization model is characterized by a linear mathematical formulation (linear problem (LP)), a time-resolution of one hour and an optimization period of one year. The model includes the energy sectors of electricity and heat, so it is a multi-energy system (MES) or a sector-coupled energy system.
The following sections introduce the mathematical background of the energy system model. The detailed structure and components of the optimization model is given in
Section 2.3.1.
2.2. Mathematical Model Description
The python open-source optimization library oemof-solph is selected as modeling framework [
18]. Oemof-solph is embedded in the oemof cosmos, which contains many additional tools for energy system analysis including optimization methods.
2.2.1. Objective Function and Global Constraints
In the following sections, the interpretation and use of the generic variables and constraints of oemof-solph are provided. This is derived from the oemof documentation [
19]. The designation of the variables is partially adjusted to clarify their use.
Two objective functions are used for the optimization of the energy system. The first function is the sum of all costs:
where
is the sum of all variable costs within the energy system
and
is the sum of all investment decisions and fixed costs
The pair of indices
represents a flow
going from node
i to node
o. In this energy system model, a flow is considered to be a power flow of an energy commodity and has the unit kW. Every power flow has a time index
t. A node is one of the oemof node instances. The node classes
bus,
source,
sink,
transformer and
storage are used in this energy system model and are explained in
Section 2.2.2. The time step width is represented by
. The variable costs in
are given by
. The specific investments costs in
are calculated by the annuity method:
with
as capital expenditure per installed capacity in
,
as fixed operating costs in
,
is the weighted average cost of capital, and
is the lifetime of the transformer or storage unit to which the flow is related.
Each power flow has an upper bound, which represents the nominal or maximum power of the flow. The maximum can be defined individually for each time step
t, which becomes important for air-source heat pumps:
If
is defined as an investment flow, the maximum power
is the investment flow
. All investment flows are constrained by:
The second objective function is the sum of all emissions
in
:
where the energy-specific emission factors are given by
in
. In case of a cost-optimization the total emission is constrained by an emission limit
:
2.2.2. Node Constraints
The constraints of the nodes of the energy system are derived from the oemof documentation [
19]. The index
n is used as index for the instances of a specific node class. The following paragraphs introduce the oemof-solph node classes.
A
bus (node index
n) is characterized by a balance equation. At each time step the sum of inflows is equal to the sum of outflows:
An energy converter unit is modeled by a
transformer. The in- and outflows of a transformer are related by conversion factors
:
The node class
storage is modeled using the following constraints:
In Equation (
11), the stored energy
of each storage
n of the initial storage level
and the energy at the last time step
are set equal in order to maintain the energy conservation law. The energy balance of each time step is described by Equation (
12). The stored energy of time step
t is the result of the stored energy in time step
multiplied by the specific energy loss factor
minus the efficiency weighted power outflow
plus the efficiency weighted power inflow
.
The node classes Source and Sink do not create any additional constraints. Both represent nodes with one outflow or one inflow, respectively.
2.3. Case Study
The approach of using different methods for the consideration of the emissions of grid-sourced electricity is tested and analyzed within a case study. The town Heide in the German state Schleswig–Holstein (geographical coordinates 54.1951764 9.1019015) is considered for the case study. The region is characterized by a high number of wind power plants, which need to be curtailed on a regular basis due to congestions in the electricity grid [
20].
2.3.1. Structure of the Energy System
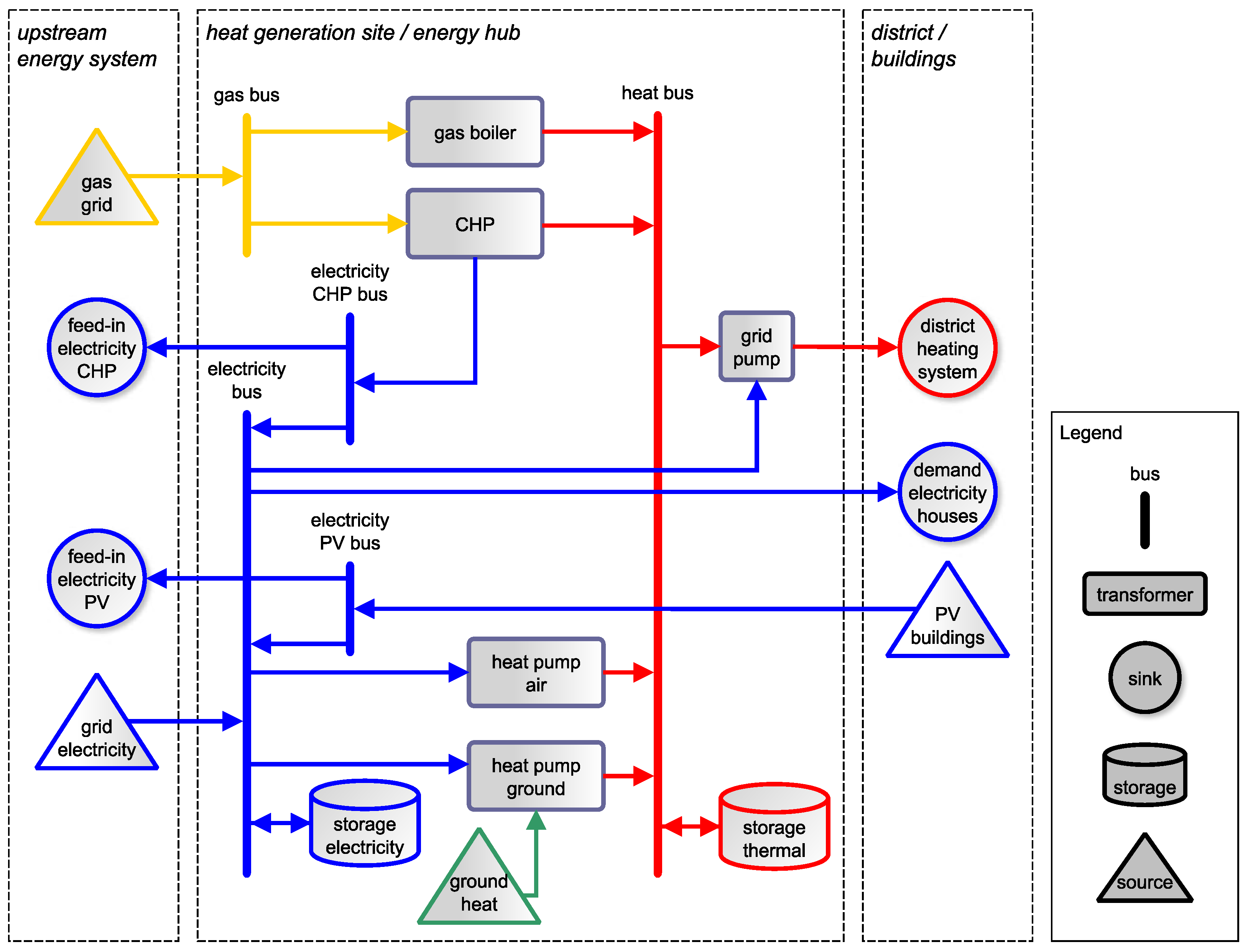
The energy system of the case study is shown in
Figure 1. The energy system configuration represents the generation site of a generic urban district energy system that supplies both heat via a district heating system and electricity. The options for generating heat are a gas boiler, a gas-fired combined heat and power plant, an air-source heat pump and a ground-source heat pump. Several ground heat collectors for brine heat pumps can be integrated in parks and green areas. Solar thermal heat generation is not considered due to limited open spaces in many urban areas. Biomass fired boilers are not considered to be heat supply option in this analysis too, as wood-based heating is not a transferable solution to all urban areas due to limited regional resources (e.g., the federal state Schleswig–Holstein of Germany has a very low forest coverage of 10.7%. Wood-based biomass from the state itself can only cover around 3% of the end-energy heat demand [
21].) Heat can be stored in a hot water storage. The generation site supplies the heat and electricity demand of a district heating system, to which the buildings of the district are connected. The heat demand is given by a time series of an hourly resolution including the losses of the heating grid. The electricity sector consists of three buses, the “electricity CHP bus”, the “electricity pv bus” and the “electricity bus”. Electricity can be fed into the grid from the combined heat and power plant (CHP) and the photovoltaic system (PV). The storage option of electricity is a lithium-ion-battery, since this battery technology has a very good cost-performance ratio and could also be very relevant in the future due to potentials in reducing production costs [
22]. The sources of electricity for supplying the buildings and the heat generation facilities are the electricity grid and the PV on the roofs of the houses. Both electrical and heat demand are given by an aggregated time series for all buildings of the district (see
Section 2.3.4). Within the model, all energy converters, the storage technologies, and the solar energy source, are implemented as investment objects, which means that the installed capacity is a decision variable of the optimization problem (see Equations (
3) and (
6)).
2.3.2. Emission Scenarios of Grid-Sourced Electricity
The different ways of evaluating the emission of grid-sourced electricity is the focus of this study. In this context, the terms constant and dynamic emission factors are further specified, and the scenarios for the emission factor are introduced.
As constant emission factors, the average values of the dynamic emission factors are used. The emission factors are further differentiated according to their reference system: a national emission factor refers to the emission factor of the national power grid, while a local emission factor takes local congestions within the electricity grid and the resulting curtailment of renewable energies into account.
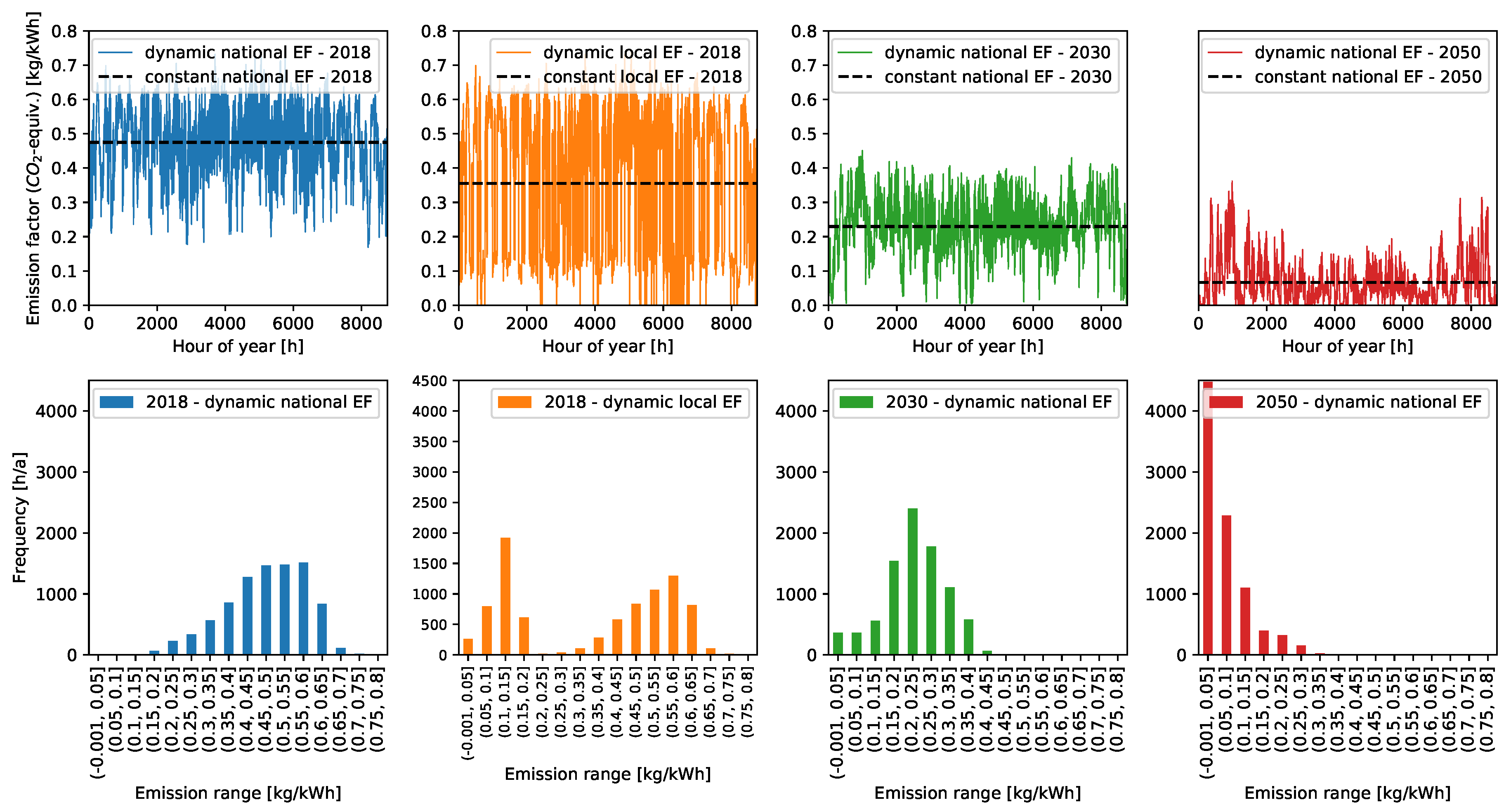
Section 2.3.3 provides detailed information about the local emission factor. It is assumed that using a dynamic emission factor for grid-sourced electricity has a remarkable impact on the design of urban heat and electricity supply systems, and that this is crucial for designing renewable and system-beneficial urban energy systems. Therefore, the design approach is tested with four different emission series for grid-sourced electricity: the national emission factor of Germany of 2018, a local emission factor considering the local excess of renewable energies, and the national average emission factor of a future scenario for the national power supply system in 2030 and 2050 (see
Figure 2).
In
Figure 2, the charts at the top show the seasonal course of time of the emission factor scenarios. The charts at the bottom summarize the frequency distribution of the emission factor in number of hours per year. The scenario “local emission factor—2018” is explained in detail in
Section 2.3.3. The results of a multi-energy systems optimization based on a trend scenario for Germany applying the International Energy Agency (IEA) allocation method is used as future emission parameters for the years 2030 and 2050 [
7]. Each emission scenario is compared with a design approach using the average value as a constant emission factor for grid-sourced electricity. The average emission factor is shown as “constant emission factor”. During the transition of the electricity system from a fossil-based to a renewable energy system, the frequency of low emission intensities must increase to meet the Paris’ climate goals (compare
Figure 2 charts from left to right).
2.3.3. Concept and Generation of Local Emission Factor
The emission series “dynamic local emission factor—2018”, shown in
Figure 2, is the result of a manipulation of the national emission series of 2018. For this purpose, historical data of feed-in management (i.e., curtailment of renewable energy generation due to grid congestions) has been analyzed. Within Germany, northern regions like Schleswig–Holstein tend to have more surplus energy generation due to a high capacity of wind power plants [
20,
23,
24], relatively sparsely populated regions as well as low amount of energy-intensive industries. Contrarily, regions in the south-west of Germany are more densely populated with fewer corresponding renewable generation capacities installed. Hence, there are transmission lines, especially in northern Lower Saxony, that are congested during high wind power generation, which is frequently addressed through curtailment of wind power plants north of the congestion. This is documented in reports of the Federal Network Agency [
20]. In 2018, the excess of renewable energies in Schleswig–Holstein slightly decreased by 15% compared to 2017, but still accounts of 2860 GWh [
23]. In the same year, the share of wind energy of the total excess is 94% [
23]. Therefore, it is assumed that increasing the electricity procurement from the district energy system during times of feed-in management on the surplus power side of the congestion avoids curtailment of wind or solar energy feed-in. Consequently, the local emission factor of grid-sourced electricity is expected to be zero or to be reduced compared to the national average.
Two types of congestions are considered. First, local feed-in management in the medium voltage grid of the investigated municipality. Information and historical data about local curtailment measures are public and can be received from the distribution grid operator (DSO) [
24]. In this case, it is assumed that an increase in power demand of heat generation site directly reduces the local excess of renewable energy. During that period, the emission factor is reduced to zero. Secondly, congestions caused by thermal overloading within the transmission network were taken into account. In that case, it is more difficult to establish a causal link between an increase of power at the specific local district and the reduction of the congestion in the transmission grid, because power flows in the meshed transmission network can differ between load states. Building on the aforementioned insights that systematic congestions exist and can be cured by a power reduction north of the congestion, a methodology for emission factor reduction is proposed. For this, curtailment at HV/MV transformer stations in Schleswig–Holstein, which are located on the same side of the bottleneck (north auf Hamburg) are taken into account. The relevant data can be obtained by the local transmission system operator (TSO) [
25]. If there is feed-in management at one of these transformer stations, it is assumed that the local emission factor of grid-sourced electricity can be reduced. Due to uncertainties in causality, the local emission factor is set to 30% of the actual national emission factor instead of zero, as it is assumed for feed-in management at the HV/MV transformer station of the district.
2.3.4. Parameters of Case Study
This section shortly discusses the relevant parameters for the model. The detailed parameter set of the case study can be found in
Appendix A.
The commodity prices for electricity and gas are conform to the current purchase prices of heating network operators in Germany (see
Appendix A.2). The emission factors in CO
2-equivalent of the consumed commodities are provided in
Table A5 and explained in detail in
Section 2.3.2 and
Section 2.3.3 in case of electricity. For the feed-in of electricity in the upstream power system, no emission credits are assumed (see
Table A5). The investment costs of the energy converter and storage technologies are based on actual manufacturer data (see
Appendix A.1). Both the efficiency and maximum power output of the air-source heat pump results from preceding calculations depending on the outside temperature and district heating supply temperature.
The case study is based on a district with a diverse mixture of building types. The heat demand series are obtained from a detailed building simulation of the different building types using the software TRNSYS [
26]. Single load profiles are aggregated by taking the simultaneity factor of the demand profiles of multiple buildings into account. The total heat demand is calculated by adding the district heating grid losses to the aggregated demand. For single-family residences, row houses and multi-family houses, the German guideline VDI 4655 is used as source of the electricity demand profiles [
27]. For the variety of commercial buildings present in the district, electricity profiles from [
28] are applied. To prevent unrealistically high peaks of power in the aggregated load profiles, simultaneity effects of adding single load profiles together are included by applying a time shift randomly drawn from a normal distribution to the load profile of each building. All energy profiles are individually scaled to the real annual energy demand of the corresponding building, which is based on data provided by the local utility company. Therefore, the heat and electricity demand is modeled with high accuracy (see
Appendix A.3). The detailed parameter set of the case study can be found in the appendix (
Appendix A).
3. Results of the Case Study
The following sections present the results of the comparison of dynamic and constant emission factors for grid-sourced electricity in investment and unit commitment models of urban energy systems. An optimization period of one year with a time-resolution of one hour is chosen. Four different emission scenarios are analyzed. First, for each emission scenario the Pareto front of total costs and total emission is presented. The second section compares the design decisions of the optimization models. The last section provides a detailed insight in the results of the unit commitment and evaluates the effectiveness of the approach to design renewable and system-beneficial district energy systems.
3.1. Total Costs and Total Emission
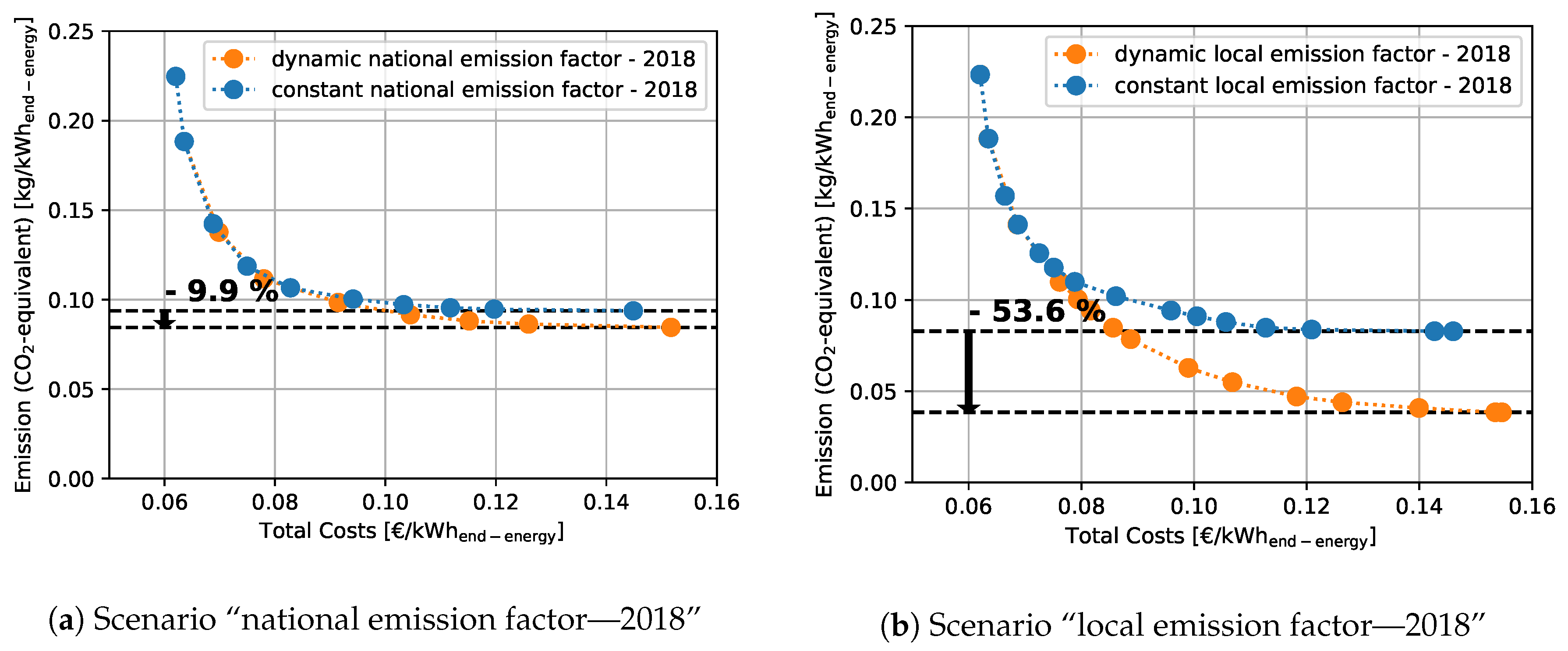
Figure 3 illustrates the Pareto-fronts of the bi-objective optimization of costs and emission for the scenarios of 2018. Each point on the Pareto front represents a so-called Pareto-optimal solution of the optimization calculation [
29]. An improvement of one objective can only be achieved by the deterioration of the other objective. The set of optimal solutions is called Pareto front [
29]. The total costs include all costs of the energy system model, i.e., investment costs and operation costs (see
Section 2.2.1). The total costs refer to the total amount of end-energy of heat and electricity supplied to the buildings. The total emission is the sum of all emission attributed to the energy commodities, which are imported into the local energy system. The total emission value is related to the total amount of end-energy. In
Figure 3a, the national emission factor of 2018 is used as parameter, and, in
Figure 3b, the local emission factor is applied. In all emission scenarios and energy systems settings, the emission can be reduced drastically with only moderate additional costs (left hand side of Pareto front). These are the optimizations with high emission limits. Here, the difference between dynamic and constant emission scenarios is small and reaches zero in the most cost-efficient case without any emission limit. By applying lower emission limits (from left to right), the difference of a dynamic and a constant emission factor increases. Hereby, the calculations with a dynamic emission factor perform better. By using a dynamic emission factor, lower emissions with fewer costs can be achieved. With a dynamic emission factor, the best emission value is 9.9% lower in case of the national emission factor, and 53.6% lower in case of the local emission factor for the historical data of 2018.
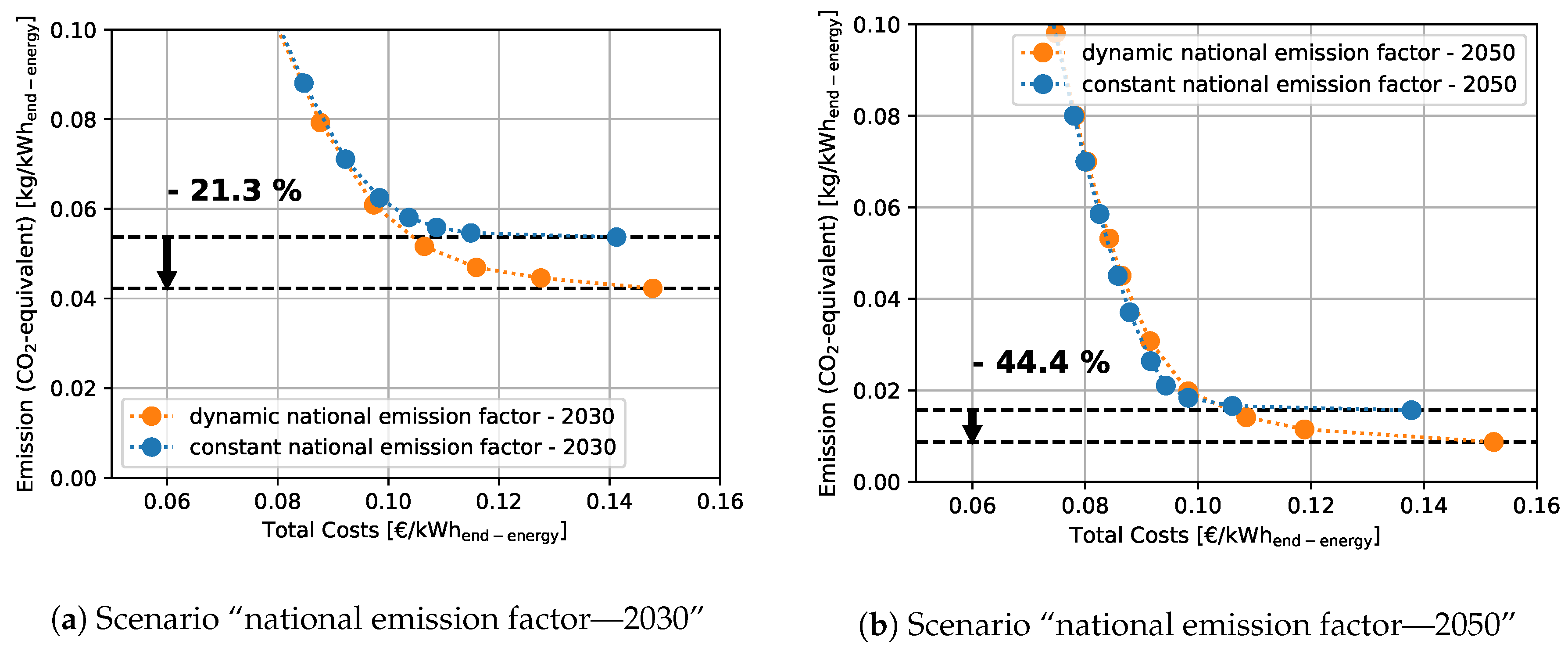
Figure 4 presents the Pareto-fronts of future scenarios of the German energy system of the years 2030 and 2050 based on scenario calculations of Böing and Regett [
7]. In emission scenario 2030, the deviation between constant and dynamic emission factors at minimum emission is 21.3% and reaches 44.4% in 2050 (see
Figure 4). Lower total emission can be achieved due to a lower overall average emission factor of the electricity system (compare
Figure 2). In contrast to the results of the emission scenarios 2018 and 2030, in the scenario of 2050, the optimization with a constant emission factor performs better total emission values at costs lower than approximately 0.1 €/kWh (see
Figure 4b). At approximately
€/kWh, the Pareto-fronts intersect and the model with a dynamic emission factor achieves lower emission. Generally, the total cost for achieving the same total emission limit decrease in future energy scenarios with a high share of renewable energies in the upstream electricity system.
3.2. Energy System Design Decisions
In
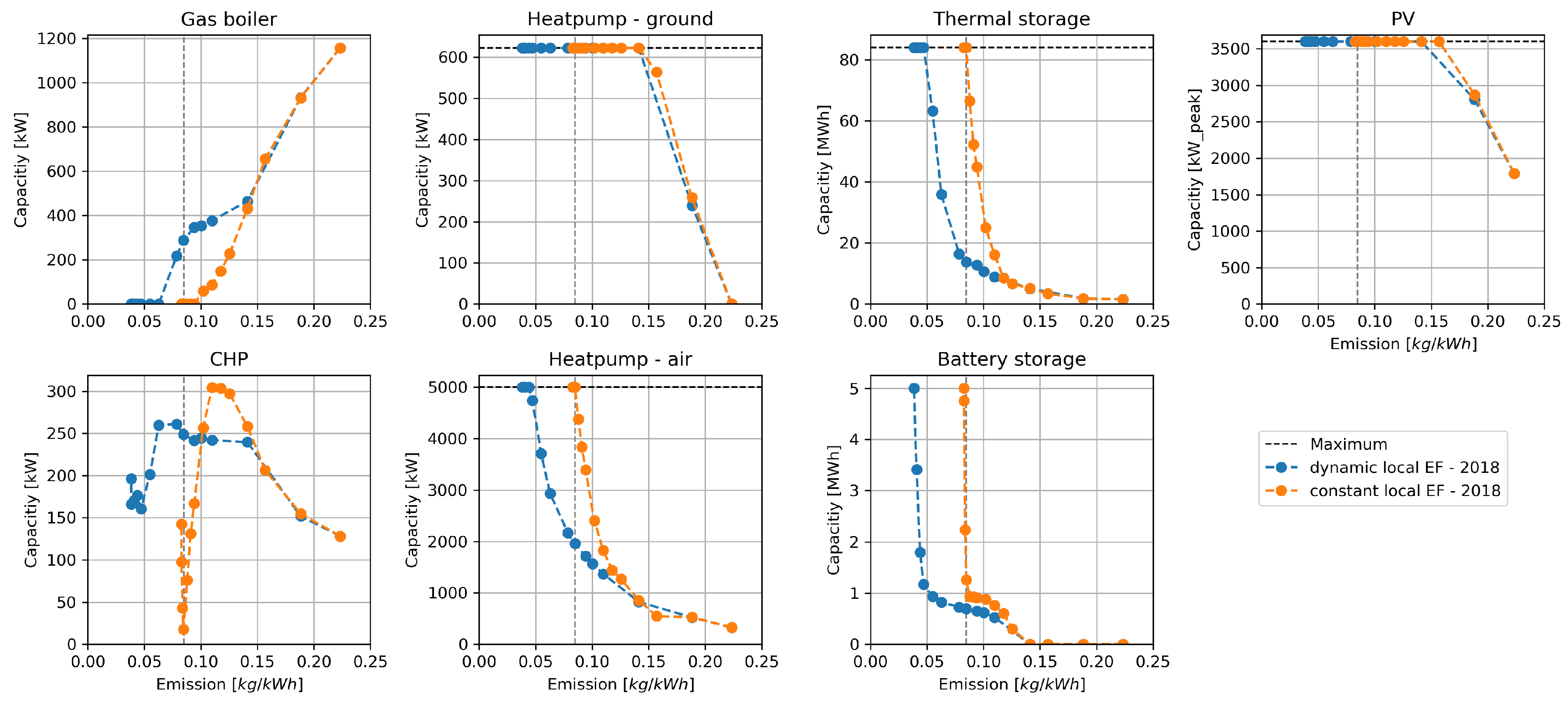
Figure 5, the results of the investment decisions of “local emission factor—2018” depending on the emission limit are given.
The grey dashed vertical line in
Figure 5 marks a comparative example at an emission limit of 0.0848 kg/kWh. This is almost the emission optimum of 0.0828 kg/kWh of the model with constant emission factors. In this example, the heat generation at constant emission is constituted of only power-to-heat applications (orange plot). The maximum capacity of the air-source and ground-source heat pump is installed. In the case of a dynamic emission factor, the fossil gas boiler and CHP are built up and the maximum capacity of the ground-source heat pump is installed. The capacity of the air-source heat pump is lower compared to the constant emission scenario with a capacity of 1958 kW. The thermal storage capacity reaches the maximum possible capacity of 84 MWh at constant emission factors, whereas the result is far lower with a capacity of 13.8 MWh at dynamic emission factors.
Altogether, the order of investment decisions is the same for dynamic and constant emission factors while decreasing the emission limit. By applying emission limits from 0.2 kg/kWh to 0.15 kg/kWh, the capacities of photovoltaics systems (PVs) and the ground-source heat pump are increased until the maximum capacity. The capacity of the air-source heat pump as well as the capacity of the thermal storage are extended. The same happens with the CHP capacity, while the gas boiler capacity drops. When emission limits lower than 0.15 kg/kWh are used, the installed capacities of dynamic and constant emission factors diverge. In case of a constant emission factor, the gas boiler capacity decreases at higher emission limits compared to a dynamic emission factor. As the emission limits further decrease, the thermal storage, the air-source heat pump and the battery storage capacities increase. In that range, the capacities of thermal storage, air-source heat pump, and battery storage, are higher with a constant compared to a dynamic emission factor. The capacity of the CHP of the constant emission model is higher at total emission from 0.1 to 0.15 kg/kWh and lower at total emission below 0.1 kg/kWh as the model with a dynamic emission factor. Altogether, in case of a dynamic emission factor lower capacities of energy converter and storage technologies need to be installed to achieve the same emission limit. Except for small differences in the CHP capacities, the final design decisions at the emission-optimal configuration of dynamic and constant emission factors are the same.
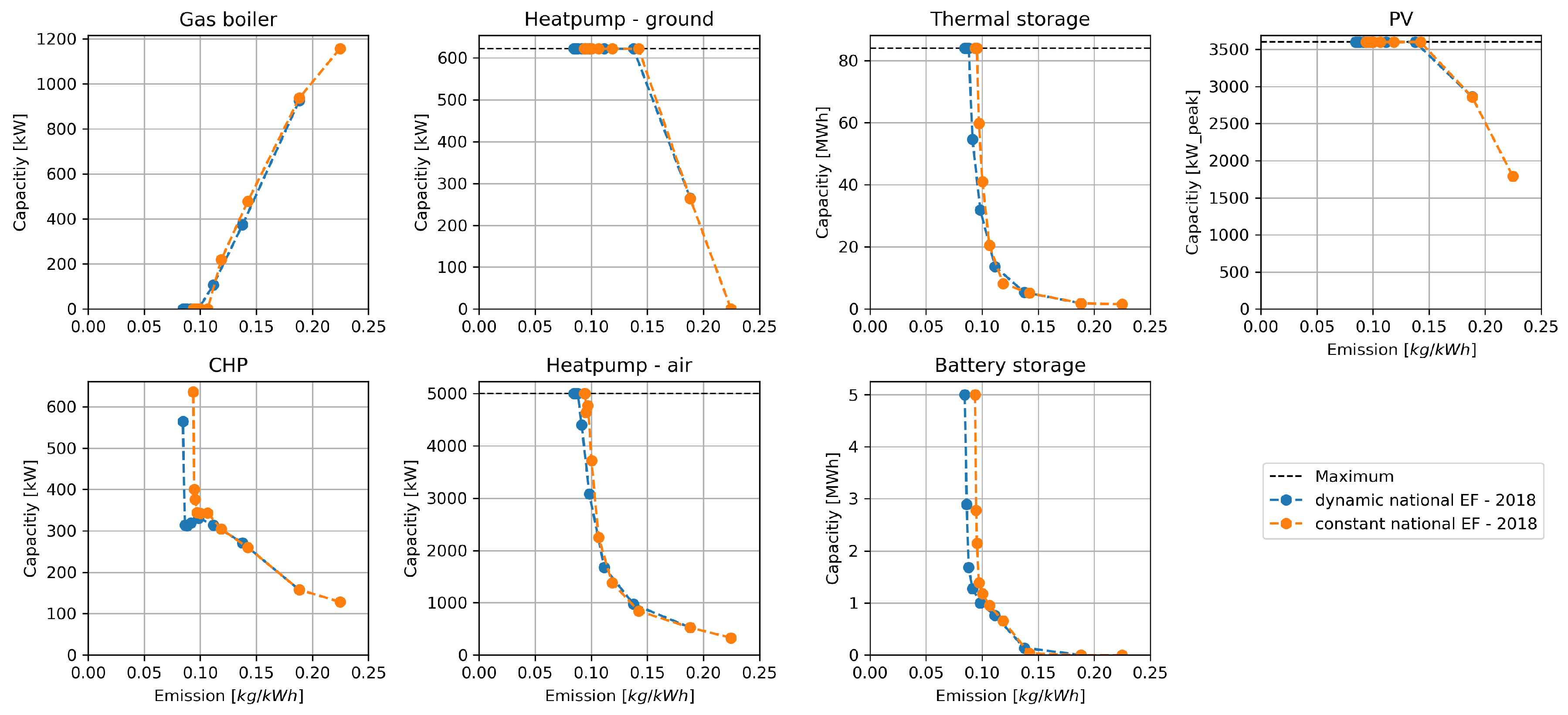
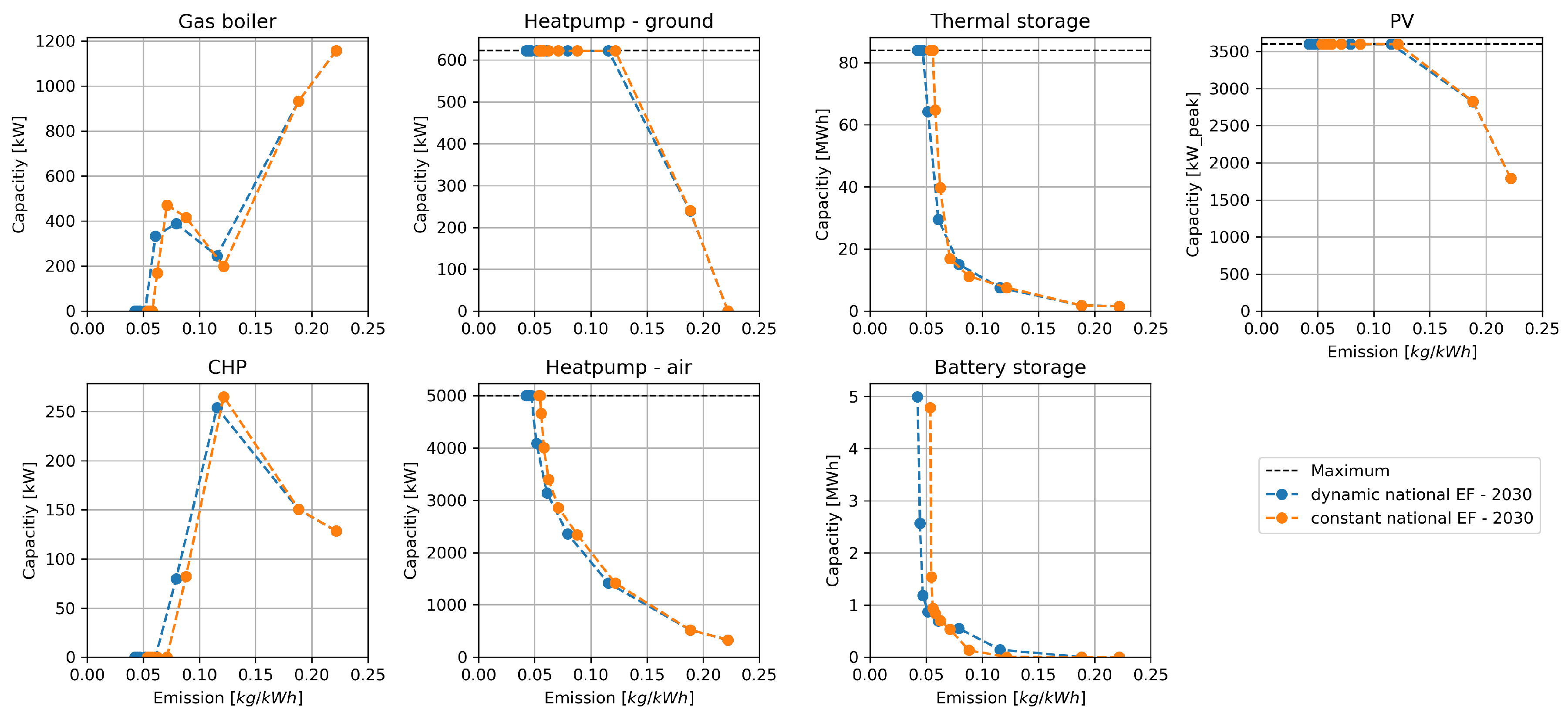
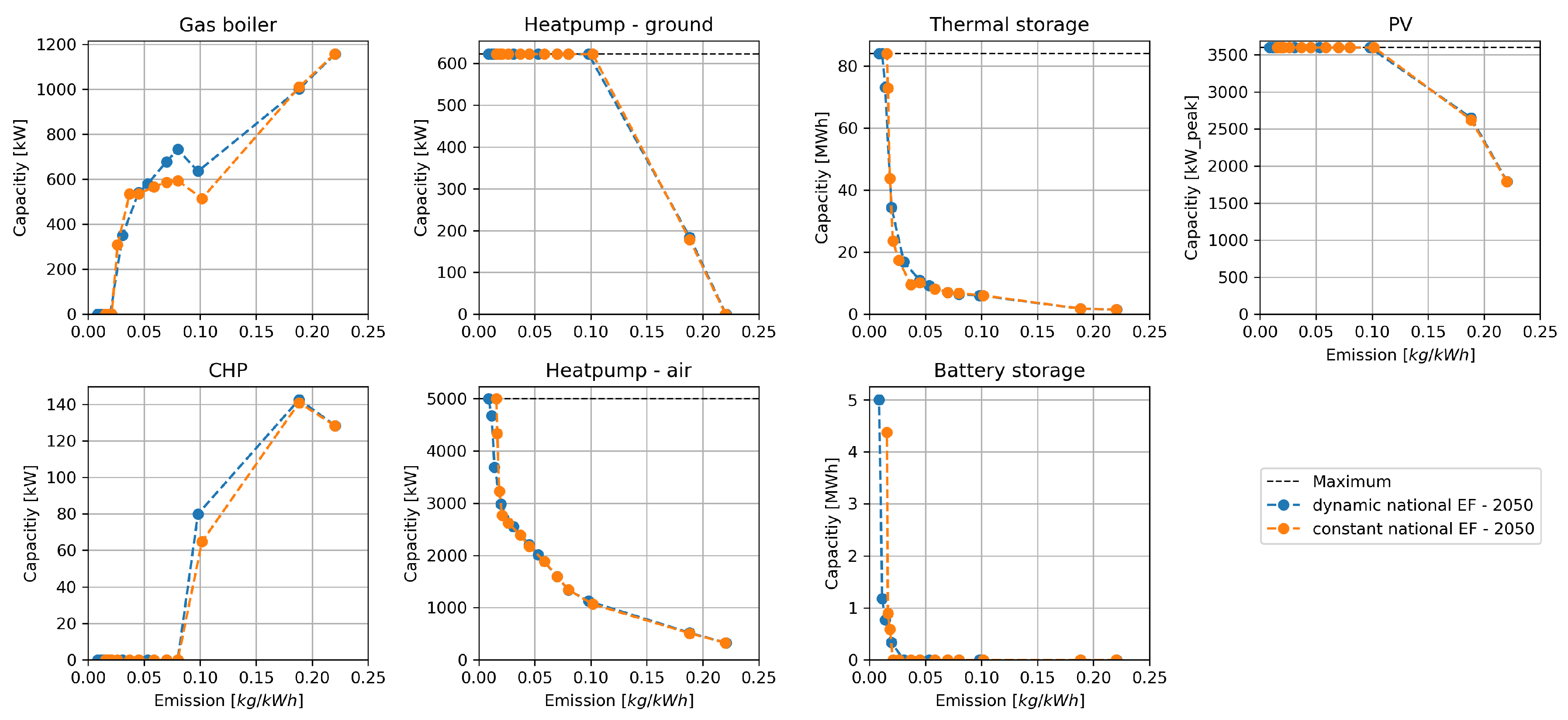
Figure 6 shows the design decisions of the scenario “national emission factor—2018”. The design decisions for the emission scenarios “national emission factor—2030" and "national emission factor—2050" are displayed in
Figure 7 and
Figure 8.
In all scenarios, the investment optimization results in a similar expansion of converter and storage units. The results mostly depend on the emission limit as well as the emission intensity of the grid-sourced electricity. Differences can be seen at the CHP and gas boiler. In the scenarios “local emission factor—2018” and “national emission factor—2018” (
Figure 5 and
Figure 6), the CHP is part of the emission-optimal energy system. This is not the case in the future scenarios of 2030 and 2050 (
Figure 7 and
Figure 8). The main difference between the scenarios is that the graphs shift from the right to left side of the diagrams starting from emission scenario 2018 and moving towards 2050. This means that the expansion of renewable units and storages (PV, ground-source heat pump, air-source heat pump, thermal storage and battery storage) and the decline of fossil fueled units (CHP and gas boiler) are only necessary at lower emission limits in the scenarios of 2030 and 2050, e.g., the thermal storage has a capacity of around 40 MWh in scenario “national emission factor—2018” at a total emission limit of 0.1 kg/kWh (
Figure 6), and a capacity of around 10 MWh at the same emission limit in the scenario “national emission factor—2030” (
Figure 7).
Regarding the differences between constant and dynamic emission factors, the deviation in the design decision of the converter and storage units of the scenarios “national emission factor—2018”, “national emission factor—2030”, and “national emission factor—2050”, are less compared to the scenario “local emission factor—2018” (compare
Figure 5). In the scenario of 2050, the gas boiler and CHP capacity show differences at an emission limit of around 0.10 kg/kWh. The scenario “local emission factor—2018” shows the biggest differences between constant and dynamic emission factors.
3.3. Unit Commitment and System-Beneficial Design
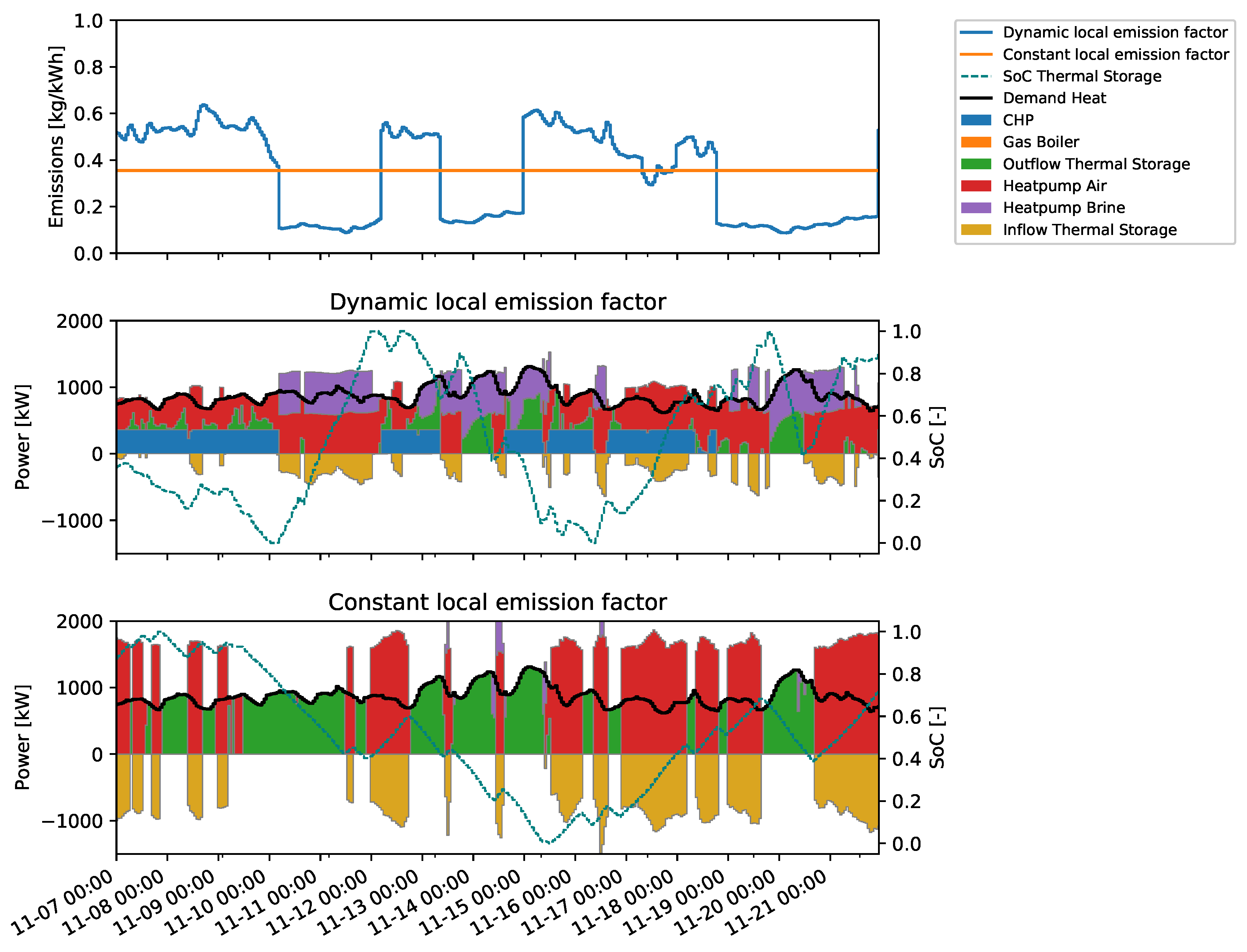
The following section gives an insight into the detailed results of the unit commitment based on the emission scenario “dynamic local emission factor—2018”. In this example, the differences in the unit commitment are analyzed and the effectiveness of the approach using a dynamic local emission factor is evaluated.
Figure 9 compares the results at an emission limit of 84.8 g/kWh for an exemplary period of two weeks in November.
The first chart at the top of
Figure 9 shows the input parameter of the emission factor. The installed capacities of heat generation and storage units of this example can be found in
Figure 5. The two lower graphs of
Figure 9 illustrate the different unit commitment profiles. The model with a dynamic emission factor has information about the times of low emission intensity of grid-sourced electricity (subplot in the middle). During these times, the total heat pump capacity is used, and the thermal storage is charged. At times of high emission intensities, the CHP generates electricity for the heat pumps and the thermal storage is discharged. The unit commitment differs, if a constant emission factor is used. The commitment of the storage is not dependent on the emission factor but solely on the COP of the air-source heat pump and the availability of solar power for driving the heat pumps. Since the model with a constant emission factor has less options for achieving the same emission limit, more capacities of storage and heat pumps need to be installed to satisfy the emission limit. Energy needs to be shifted from times with high outside temperature, implying a high COP of the air-source heat pump, to times with low outside temperature and a high heat demand.
Figure 10 summarizes the emission intensity for each heat generation option of the two models with dynamic and constant emission factors. The triangles describe the theoretical minimum and maximum emission factor per one kilowatt-hour heat, when electricity from the upstream grid is used. These limits are recalculated from the parameter set and show the range of options of the optimization model (see
Section 2.3.4 and
Appendix A). Heat generated by the gas boiler causes 0.263 kg/kWh constantly and is determined by the efficiency of the gas boiler and the composition of natural gas. The emission factor of the air-source heat pump is dependent on the outside temperature and the emission factor of the electricity grid. Here, the minimum and maximum values of the air-source heat pump of the dynamic model have a wider range as compared to the model with a constant emission factor. Likewise, the emission factor of the ground-source heat pump is constant in the model with a constant emission factor, because the supply temperature of the district heating grid and the ground temperature are constant. In
Figure 10, the emission factor of the CHP for generating heat is calculated by ascribing the actual emission factor of the upstream electricity system to the electricity output of the CHP, e.g., if the emission factor of the electricity grid is zero, all emission of the gas combustion are attributed to the heat output of the CHP. Consequently, the emission attributed to one kilowatt-hour heat from the CHP can become less than zero at times of a high emission factor of the electricity grid. The emission factor of the CHP for generating heat is fixed at a value of 0.209 kg/kWh in the case of a constant emission factor. As a result, the capacity investment is zero.
The red dots in
Figure 10 indicate the emission factor of the heat generation units during operation. For the heat pumps (HP), only the times when electricity is sourced from the grid are plotted. The plots of the CHP show all times of operation. The black boxes mark the second and third quartile. The lower whisker covers the first quartile and the top whisker marks the fourth quartile. When the air-source heat pump is running and electricity is consumed from the grid, the emission factor of the electricity grid is lower than 0.1 kg/kWh at more than 75% of time in the model with a dynamic emission factor. In the model with a constant emission factor, the only way of optimizing the emission factor of the air-source heat pump is to use it at times of high outside temperature. Since the yearly heat demand profile and the profile of the outside temperature are opposite, there are less options for a low emission factor for generating heat. In the model with a dynamic emission factor, the CHP runs mainly at times of a high emission factor within the electricity grid (compare
Figure 10). Hereby, the CHP can contribute to emission saving within the district energy system.
For the assessment of the effects on the upstream electricity system, the absolute grid-support coefficient (
) for the generation case according to Klein et al. is used as quantitative measure [
30]. The absolute
is defined by the weighted and normalized sum of grid-sourced electricity.
values greater than one indicate grid-adverse unit commitment while values lower than one indicate grid-supportive behavior (see [
30] for more details). The emission factor is used as grid-based reference quantity and the generation case of the GSC is calculated. The GSC calculations for the optimization with an emission limit of 84.8 g/kWh result in 0.321 for a dynamic emission factor, and 0.973 for a constant emission factor. That means, the procurement of electricity is well oriented to the reference quantity emission factor in the dynamic emission factor model, whereas the constant emission factor model shows a grid-neutral relation.
Table 1 summarizes the results of key values of the comparison.
The average emission factor (Av. EF) refers to the average emission of the actual grid-sourced electricity of the model results. The average emission value of grid-sourced electricity of the model with a dynamic emission factor is 113.7 g/kWh, and is much lower than the scenario “constant local emission factor” with an average value of 354.2 g/kWh. The total costs of energy are 24% lower in the model with a dynamic emission factor compared to a constant emission factor. Especially the investment costs show a significant deviation of 2.19 ct/kWh, which equals 26.4%. The operation costs differ by 17.6%.
4. Discussion of Method and Results
First, the parameters and the general methodological approach are reflected. Second, the results of the optimization, the outcome of the comparison of dynamic and constant emission factors and the benefits of the local emission factor concept for designing renewable and system-beneficial urban energy system are discussed.
4.1. Parameters and Methodology
The case study is one specific example of analyzing the impact of the assessment of grid-sourced electricity on the design decisions in an investment optimization with specific parameters, e.g., the potential of renewable energies within the district, the position within the national electricity system, the technology and cost data set, which might change in the next decades. However, the energy system set-up and characteristics of this district represent a typical mixed existing building stock. The technology options for a district heating facility considered in this analysis gain a broad transferability. The option of building air-source heat pumps is given in every district. The existence of a gas network for supplying a gas boiler and a CHP is also standard in many cities. Many districts also have a certain amount of open space for the construction of geothermal probes, and there is the option of using roof areas to install PV, even though the quantitative potentials may vary from district to district. Within the study, the use of excess energy due to a congested grid in the area of the town Heide is considered. As congestions depend on the local grid situation, the results cannot be generalized. However, in the course of the ongoing energy transition, congested grids will become more likely due to the volatile generation characteristics. The problem of a significant amount of excess energy from renewable energies also applies to other countries, like Denmark [
31], Ireland, China, Italy and Spain [
32]. Altogether, for such use cases, this case study demonstrates the relevance of the ecological assessment of grid-sourced electricity in the actual and future sector-coupled urban energy systems. It is shown that a dynamic assessment leads to different design decisions, especially in the local emission factor scenario, and far-reaching differences in the unit commitment, which can be shown by the example of
Section 3.3. In all emission scenarios, a dynamic assessment of grid-sourced electricity makes the achievement of lower total emission of the urban energy system possible.
In the parameter set, German aspects of the regulatory framework are omitted. This is an additional bonus for feeding electricity from the CHP into the upstream power system. Also, fees which occur by using the buildings’ electricity generation of PV in the central energy hub, e.g., the EEG apportionment, network charges and additional taxes on electricity. The regulatory framework undergoes permanent modifications and differs from country to country. This means, the parameter set is reduced to essential techno-economic relations, which are valid in many countries. Therefore, the results gain a broader transferability.
Since an optimization model with one year optimization period was used, the feasibility of the unit commitment results needs to be interpreted with respect to the perfect-foresight optimization approach. In that sense, this work demonstrates the potential of using an emission driven unit commitment within the control strategy of district energy systems. Still, it does not answer the question of how to implement this control strategy in existing and future energy supply sites, but gives a motivation and quantifies its limits. However, the results show similar outcomes as other studies like [
6], where an emission reduction potential of 12% by applying an emission oriented control of a heat pump in a two-story single-family house for 2017 in Germany was calculated [
6].
4.2. Energy System Design
Generally, the results of the different emission scenarios do not vary in the qualitative design decisions, and the order of building up energy converter and storage technologies are independent of whether a dynamic or constant emission factor is applied. However, quantitative specific emission limits lead to different design decisions, e.g., an emission limit of 0.1 kg/kWh results in different design decisions in the emission scenario 2018 and 2050 regarding the thermal storage. The deviation in the design decisions of dynamic and constant emission factors is greatest in scenario “local emission factor—2018” and smallest in scenario “national emission factor—2050”. The wider the distribution of the emission factor, the bigger is the impact whether a constant instead of a time resolved emission factor is used (compare
Figure 2).
Although the methodology and the scenario data are slightly different, the qualitative results of the installed generation units are similar to [
16]. By decreasing the emission limit the natural gas boiler capacities need to decrease gradually. In the cost optimum without emission limit, PV is already installed and increases with stronger emission limits until installation limit [
16]. CHP is a useful option to decrease the emission in the short term, while it cannot contribute to resolving the issue of CO
2 emission in the long run, if fossil gas is used.
The emission scenario “local emission factor—2018” considers the curtailment of renewable electricity generation due to two different reasons: the curtailment of renewable electricity generation directly within the same distribution grid the district is located in, and curtailment of neighboring HV/MV transformer station. In the second case, the local emission factor is assumed to be 30% of the national emission factor, because there is an uncertainty whether an increase in power in the district always reduces the congestion in the transmission grid. On a qualitative level, the approach of lowering the emission factor at times of congestions in an emission constraint optimization leads to incentives for using renewable excess energy. Fluctuating renewable energies pose a challenge to balancing supply and demand at all time, which demands system-beneficial appliances. This means that performing an emission optimization with a dynamic local emission factor at the same time implies a system-beneficial design and unit commitment of the local energy system. Consequently, the concept of a dynamic local emission factor is an approach for achieving both renewable and system-beneficial district energy systems.
5. Conclusions and Outlook
The effect of different considerations—dynamic or constant—of the emission factor of grid-sourced electricity in energy system optimization models at urban scale is investigated and the concept of a local emission factor is introduced. In a multi-objective optimization with costs and emission as objective functions, the application of a dynamic local emission factor achieves up to 53.6% lower emission. This is shown by the scenario “local emission factor” of the case study. Vice versa, at the same emission limit for the urban energy system, huge cost benefits of more than 30% can be achieved. This demonstrates the importance of an adequate consideration of the emission factor of grid-sourced electricity within an energy system with a high share of renewable energies. In future scenarios for the national energy system with a high share of renewable energies in the electricity system, the absolute deviation of dynamic and constant emission factors decreases in the emission-optimal system design, whereas relatively, the deviation increases from 21.3% in 2030 to 44.4% in 2050. Looking at the design decisions in detail, a dynamic emission factor leads to lower investment capacities in case of equal total emission through an emission optimized unit commitment. However, the dimensioning of the transformer and storage units converges towards the same configuration in the emission-optimal system configuration independent of dynamic or constant emission factors.
In that process, the concept of local emission factor, in which the emission factor is reduced at times of local and regional feed-in management due to local and regional congestions within the electricity grid, is a promising solution for building up renewable, sector-coupled and system-beneficial urban energy systems. Combining the objectives, emission and grid-supportiveness within one parameter is a powerful approach for designing future local energy systems. Hereby, the degree of detail in local energy system models can be kept, and still obtain the important interconnections to the overall energy system in order to realize a Smart Energy System approach according to Lund et al. [
3]. In future works, the relation of increasing the electrical load at district level to avoid curtailment of renewable energy generation in neighboring districts needs to be analyzed more accurately for improving the quantification within this work. Therefore, a general methodology for the generation of local emission factors needs to be developed to analyze and design urban and regional energy systems in different transformation scenarios of the overall energy system.