Stochastic 3D Carbon Cloth GDL Reconstruction and Transport Prediction
Abstract
1. Introduction
2. Methodology
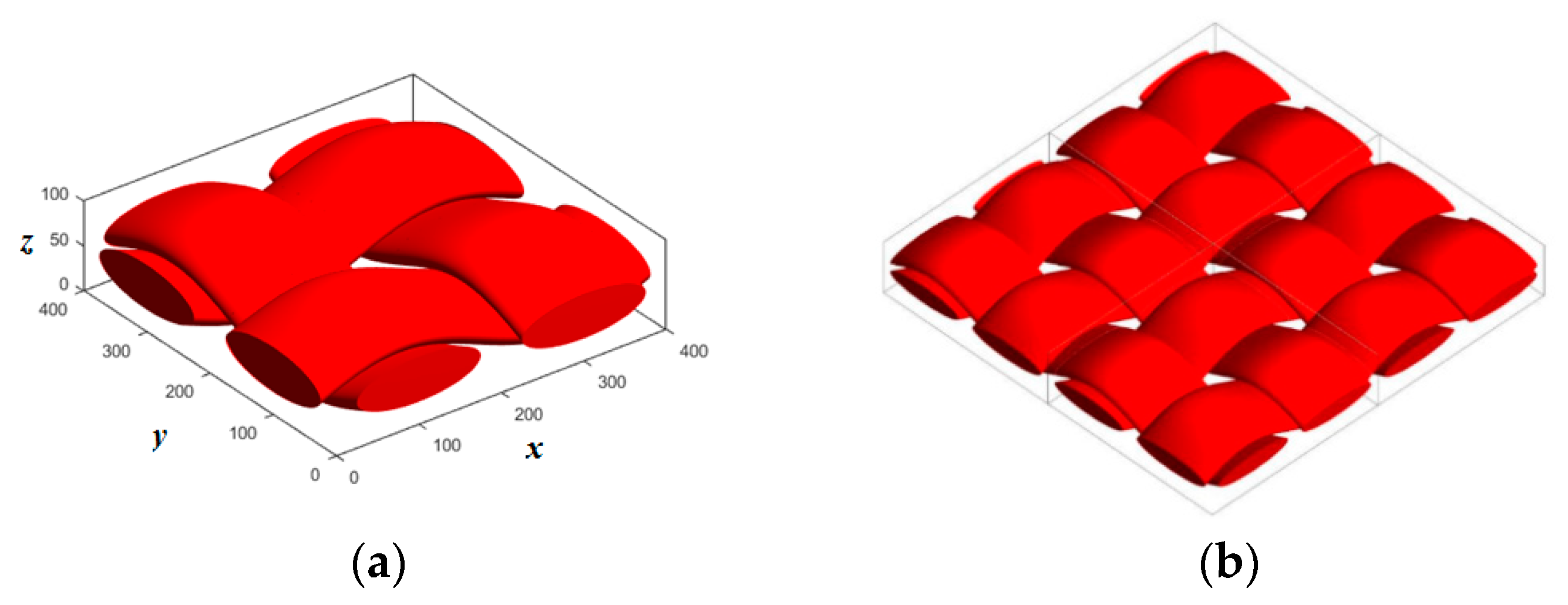
2.1. The Microstructure Reconstruction Model of Carbon Cloth GDL
- (i)
- Carbon cloth fibers are divided into two pairs of mutually orthogonal bundles.
- (ii)
- Each bundle has an elliptic cross-section.
- (iii)
- A bundle consists of many fibers, which distributed homogeneously.
- (iv)
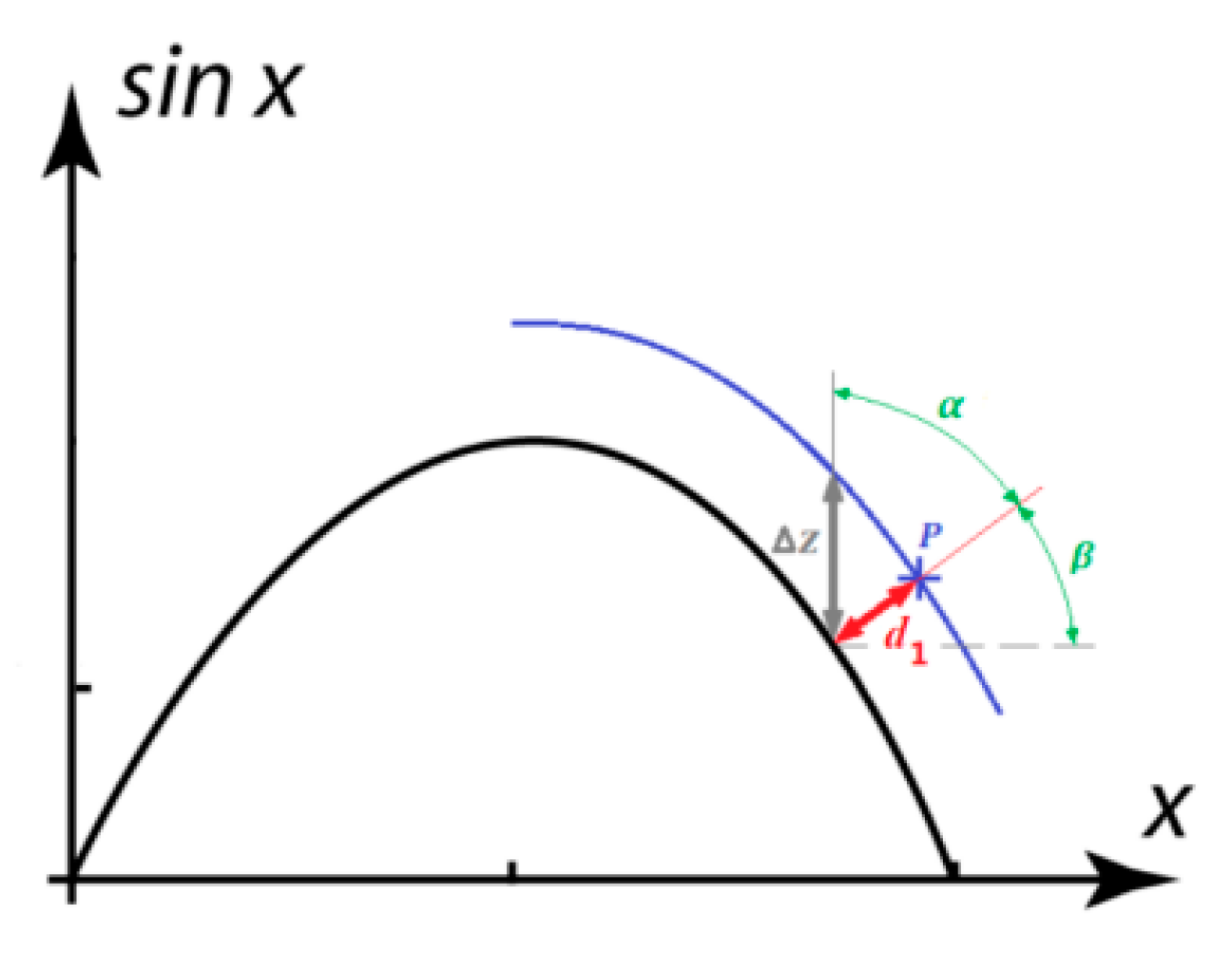
- A fiber is considered as a cylinder with a sinusoidal directrix.
- (i)
- Generating an elliptic bundle of cylinder fibers with a given radius.
- (ii)
- Merging two elliptic bundles into a 2D slice.
- (iii)
- Generating of all 2D slices by changing the centers of fiber sections along the sinusoidal directrix. There were two directrixes inside each slice and one was shifted relative to the other by half the wavelength.
- (iv)
- Creating the orthogonal fibers in a similar way and then assembly of the two pairs of fibers.
2.2. The Bunched Fiber Model of Carbon Cloth GDL
2.3. The Single Fiber Model of Carbon Cloth GDL
2.4. Determination of the Anisotropic Permeability and Tortuosity
2.4.1. Calculation of Permeability
2.4.2. Calculation of Tortuosity
3. Results and Discussion
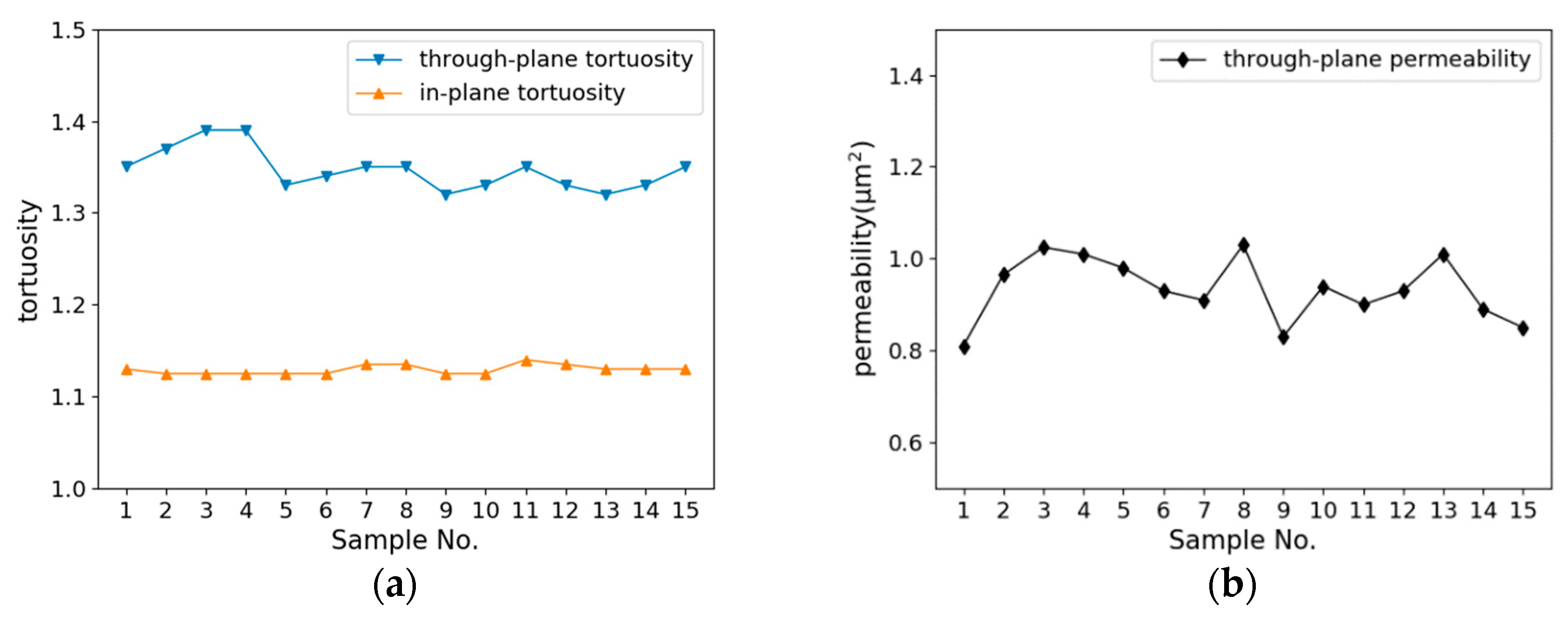
3.1. Calculation Permeability and Tortuosity of the Single Fiber Carbon Cloth Model
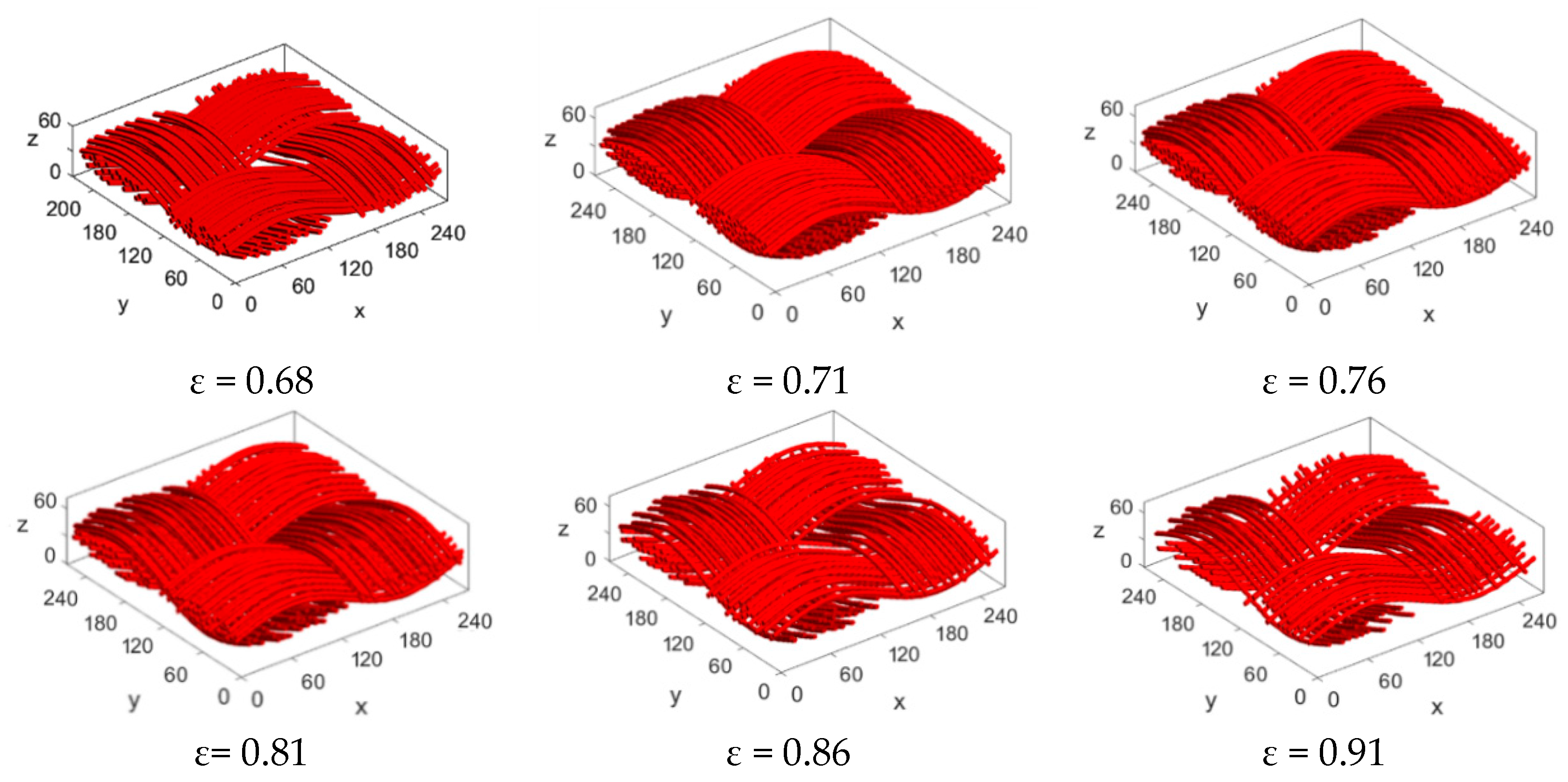
3.2. Calculation of Permeability and Tortuosity for Carbon Cloth Models with the Same Fiber Radius but Different Porosity
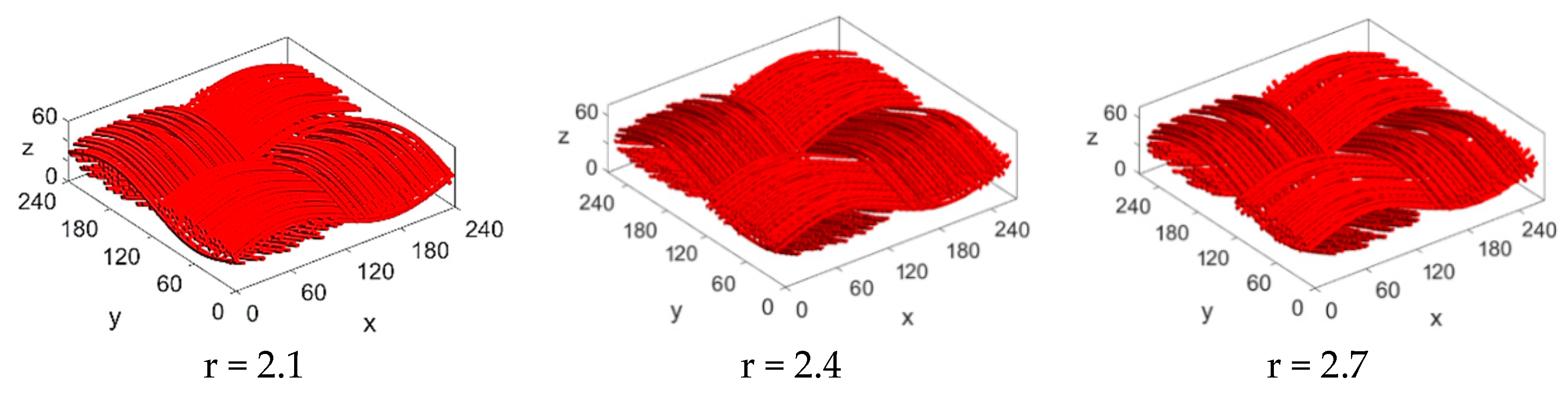
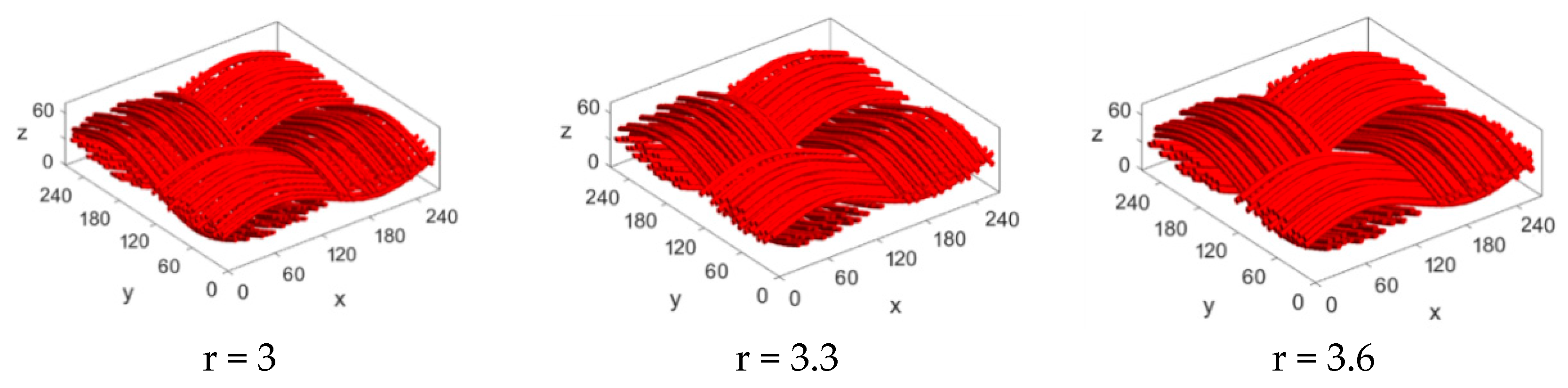
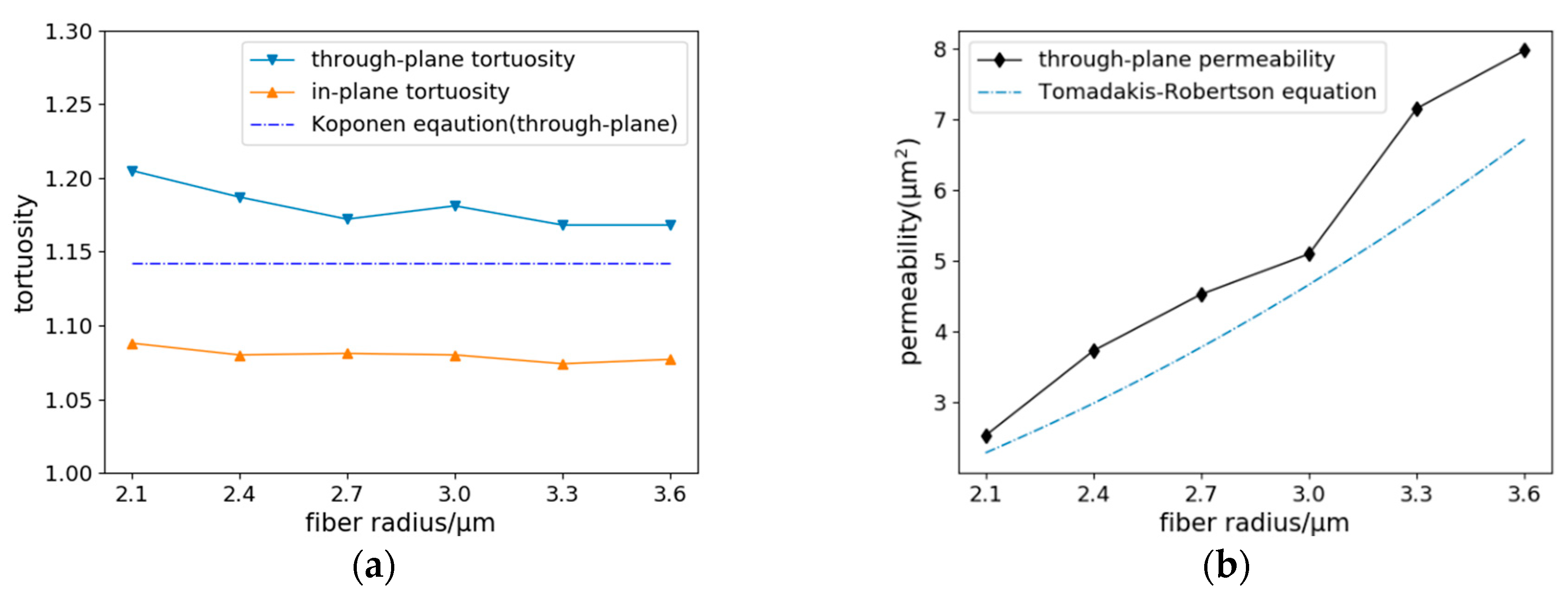
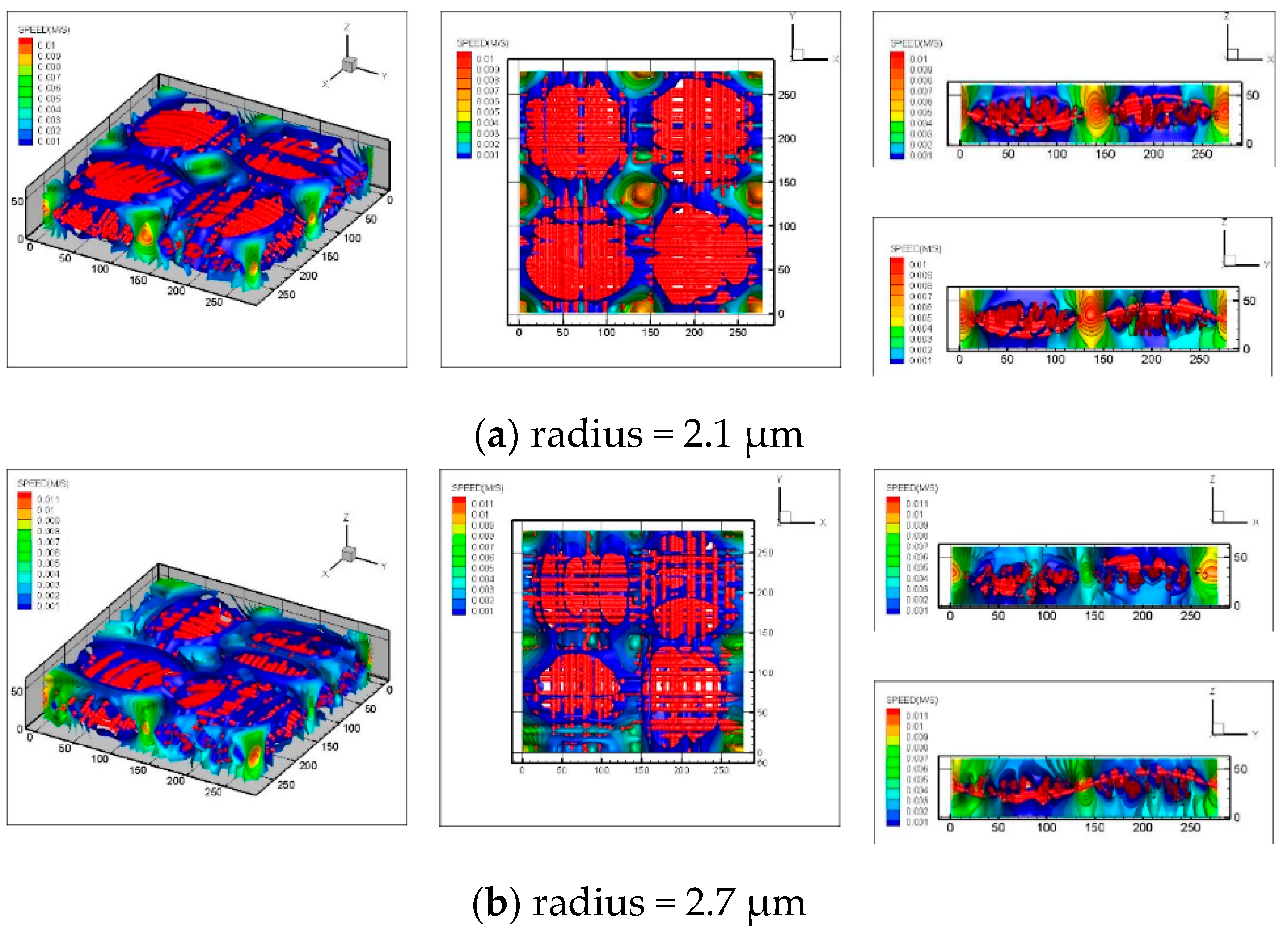
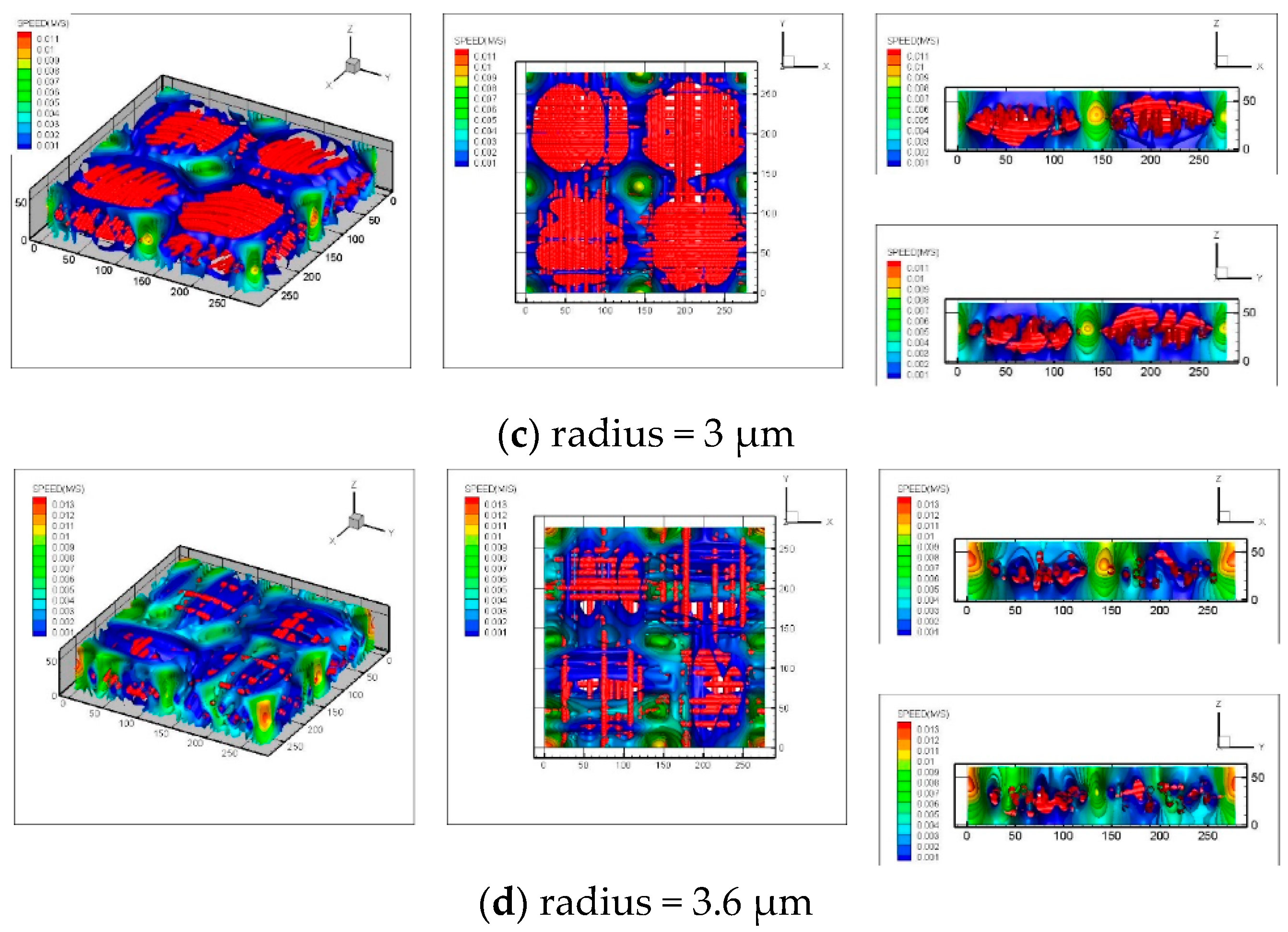
3.3. Calculation of Permeability and Tortuosity for Carbon Cloth Models with the Same Porosity but Different Fiber Radius
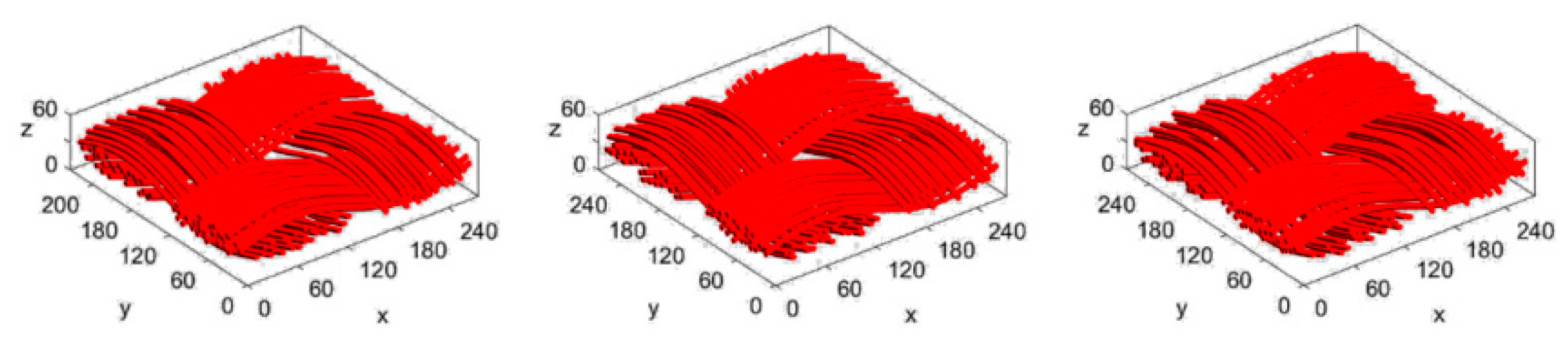
3.4. Velocity Distribution
4. Conclusions
- In the GDL model, the fiber radius and fiber distribution are taken as input parameters and all the input parameters are adjustable. The initial model porosity is 0.68 and the initial fiber radius is 3 μm. The model predictions are validated with the tortuosity along both through-plane and in-plane directions and the permeability along through-plane direction.
- Different structural parameters can be changed individually to analyze its influence on the transmission characteristics of the structure. By changing the porosity and fiber radius, respectively, it is found that with the increase of porosity, the tortuosity in the through-plane direction gradually decreases and in the in-plane direction stays nearly constant. When the porosity is in the range of 0.68–0.86, the permeability in the through-plane direction basically conforms to the calculation results of the empirical equation and increases gradually as the porosity increases. When the fiber radius is changed, as the radius becomes larger, the tortuosity in the through-plane direction slightly decreases while the permeability correspondingly increases.
Author Contributions
Funding
Conflicts of Interest
References
- Fadzillah, D.; Rosli, M.; Talib, M.; Kamarudin, S.; Daud, W. Review on microstructure modelling of a gas diffusion layer for proton exchange membrane fuel cells. Renew. Sustain. Energy Rev. 2017, 77, 1001–1009. [Google Scholar] [CrossRef]
- El-Kharouf, A.; Mason, T.J.; Brett, D.J.; Pollet, B.G. Ex-situ characterisation of gas diffusion layers for proton exchange membrane fuel cells. J. Power Sources 2012, 218, 393–404. [Google Scholar] [CrossRef]
- Park, S.; Popov, B.N. Effect of a GDL based on carbon paper or carbon cloth on PEM fuel cell performance. Fuel 2011, 90, 436–440. [Google Scholar] [CrossRef]
- Inoue, G.; Yoshimoto, T.; Matsukuma, Y.; Minemoto, M. Development of simulated gas diffusion layer of polymer electrolyte fuel cells and evaluation of its structure. J. Power Sources 2008, 175, 145–158. [Google Scholar] [CrossRef]
- Schulz, V.P.; Becker, J.; Wiegmann, A.; Mukherjee, P.P.; Wang, C.-Y. Modeling of Two-Phase Behavior in the Gas Diffusion Medium of PEFCs via Full Morphology Approach. J. Electrochem. Soc. 2007, 154, B419–B426. [Google Scholar] [CrossRef]
- Mukherjee, P.P.; Kang, Q.; Wang, C.-Y. Pore-scale modeling of two-phase transport in polymer electrolyte fuel cells—progress and perspective. Energy Environ. Sci. 2011, 4, 346–369. [Google Scholar] [CrossRef]
- Oostrom, M.; Lenhard, R. Comparison of relative permeability-saturation-pressure parametric models for infiltration and redistribution of a light nonaqueous-phase liquid in sandy porous media. Adv. Water Resour. 1998, 21, 145–157. [Google Scholar] [CrossRef]
- Wang, Z.H.; Wang, C.Y.; Chen, K.S. Two-phase flow and transport in the air cathode of proton exchange membrane fuel cells. J. Power Sources 2001, 94, 40–50. [Google Scholar] [CrossRef]
- Hinebaugh, J.; Bazylak, A. Stochastic modeling of polymer electrolyte membrane fuel cell gas diffusion layers—Part 1: Physical characterization. Int. J. Hydrog. Energy 2017, 42, 15861–15871. [Google Scholar] [CrossRef]
- Hinebaugh, J.; Gostick, J.; Bazylak, A. Stochastic modeling of polymer electrolyte membrane fuel cell gas diffusion layers—Part 2: A comprehensive substrate model with pore size distribution and heterogeneity effects. Int. J. Hydrog. Energy 2017, 42, 15872–15886. [Google Scholar] [CrossRef]
- Shojaeefard, M.; Molaeimanesh, G.; Nazemian, M.; Moqaddari, M. A review on microstructure reconstruction of PEM fuel cells porous electrodes for pore scale simulation. Int. J. Hydrog. Energy 2016, 41, 20276–20293. [Google Scholar] [CrossRef]
- Becker, J.; Flückiger, R.; Reum, M.; Büchi, F.N.; Marone, F.; Stampanoni, M. Determination of Material Properties of Gas Diffusion Layers: Experiments and Simulations Using Phase Contrast Tomographic Microscopy. J. Electrochem. Soc. 2009, 156, B1175. [Google Scholar] [CrossRef]
- Thiedmann, R.; Fleischer, F.; Hartnig, C.; Lehnert, W.; Schmidt, V. Stochastic 3D Modeling of the GDL Structure in PEMFCs Based on Thin Section Detection. J. Electrochem. Soc. 2008, 155, B391. [Google Scholar] [CrossRef]
- Koido, T.; Furusawa, T.; Moriyama, K. An approach to modeling two-phase transport in the gas diffusion layer of a proton exchange membrane fuel cell. J. Power Sources 2008, 175, 127–136. [Google Scholar] [CrossRef]
- Ostadi, H.; Rama, P.; Liu, Y.; Chen, R.; Zhang, X.; Jiang, K. Nanotomography based study of gas diffusion layers. Microelectron. Eng. 2010, 87, 1640–1642. [Google Scholar] [CrossRef][Green Version]
- Ostadi, H.; Rama, P.; Liu, Y.; Chen, R.; Zhang, X.; Jiang, K. Influence of threshold variation on determining the properties of a polymer electrolyte fuel cell gas diffusion layer in X-ray nano-tomography. Chem. Eng. Sci. 2010, 65, 2213–2217. [Google Scholar] [CrossRef]
- Rama, P.; Liu, Y.; Chen, R.; Ostadi, H.; Jiang, K.; Zhang, X.; Gao, Y.; Grassini, P.; Brivio, D. Determination of the anisotropic permeability of a carbon cloth gas diffusion layer through X-ray computer micro-tomography and single-phase lattice Boltzmann simulation. Int. J. Numer. Methods Fluids 2011, 67, 518–530. [Google Scholar] [CrossRef]
- Rama, P.; Liu, Y.; Chen, R.; Ostadi, H.; Jiang, K.; Gao, Y.; Zhang, X.; Brivio, D.; Grassini, P. A Numerical Study of Structural Change and Anisotropic Permeability in Compressed Carbon Cloth Polymer Electrolyte Fuel Cell Gas Diffusion Layers. Fuel Cells 2011, 11, 274–285. [Google Scholar] [CrossRef]
- García-Salaberri, P.A.; Hwang, G.; Vera, M.; Weber, A.Z.; Gostick, J.T. Effective diffusivity in partially-saturated carbon-fiber gas diffusion layers: Effect of through-plane saturation distribution. Int. J. Heat Mass Transf. 2015, 86, 319–333. [Google Scholar] [CrossRef]
- García-Salaberri, P.A.; Gostick, J.T.; Hwang, G.; Weber, A.Z.; Vera, M. Effective diffusivity in partially-saturated carbon-fiber gas diffusion layers: Effect of local saturation and application to macroscopic continuum models. J. Power Sources 2015, 296, 440–453. [Google Scholar] [CrossRef]
- Schladitz, K.; Peters, S.; Reinel-Bitzer, D.; Wiegmann, A.; Ohser, J. Design of acoustic trim based on geometric modeling and flow simulation for non-woven. Comput. Mater. Sci. 2006, 38, 56–66. [Google Scholar] [CrossRef]
- Froning, D.; Yu, J.; Gaiselmann, G.; Reimer, U.; Manke, I.; Schmidt, V.; Lehnert, W. Impact of compression on gas transport in non-woven gas diffusion layers of high temperature polymer electrolyte fuel cells. J. Power Sources 2016, 318, 26–34. [Google Scholar] [CrossRef]
- Froning, D.; Yu, J.; Reimer, U.; Lehnert, W. Stochastic Analysis of the Gas Flow at the Gas Diffusion Layer/Channel Interface of a High-Temperature Polymer Electrolyte Fuel Cell. Appl. Sci. 2018, 8, 2536. [Google Scholar] [CrossRef]
- Salomov, U.R.; Chiavazzo, E.; Asinari, P. Pore-scale modeling of fluid flow through gas diffusion and catalyst layers for high temperature proton exchange membrane (HT-PEM) fuel cells. Comput. Math. Appl. 2014, 67, 393–411. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, X.; Rama, P.; Chen, R.; Ostadi, H.; Jiang, K. An Improved MRT Lattice Boltzmann Model for Calculating Anisotropic Permeability of Compressed and Uncompressed Carbon Cloth Gas Diffusion Layers Based on X-Ray Computed Micro-Tomography. J. Fuel Cell Sci. Technol. 2012, 9, 041010. [Google Scholar] [CrossRef]
- Gao, Y.; Montana, A.; Chen, F. Evaluation of porosity and thickness on effective diffusivity in gas diffusion layer. J. Power Sources 2017, 342, 252–265. [Google Scholar] [CrossRef]
- Tomadakis, M.M.; Robertson, T.J. Viscous Permeability of Random Fiber Structures: Comparison of Electrical and Diffusional Estimates with Experimental and Analytical Results. J. Compos. Mater. 2005, 39, 163–188. [Google Scholar] [CrossRef]
- Koponen, A.; Kataja, M.; Timonen, J. Tortuous flow in porous media. Phys. Rev. E 1996, 54, 406–410. [Google Scholar] [CrossRef]




| Model | Porosity | Fiber Radius/μm | Ellipse Size/μm | Thickness/μm |
|---|---|---|---|---|
| Single fiber model of carbon cloth GDL | 0.68 | 3 | Semi-major/semi-minor axis 60/12 | 60 |
| Through-Plane Tortuosity | In-Plane Tortuosity | Through-Plane Tortuosity (Koponen Equation) | Through-Plane Permeability (μm2) | Through-Plane Permeability (μm2) (Tamadakis and Robertson Equation) |
|---|---|---|---|---|
| 1.347 | 1.129 | 1.254 | 0.934 | 1.077 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Jin, T.; Wu, X. Stochastic 3D Carbon Cloth GDL Reconstruction and Transport Prediction. Energies 2020, 13, 572. https://doi.org/10.3390/en13030572
Gao Y, Jin T, Wu X. Stochastic 3D Carbon Cloth GDL Reconstruction and Transport Prediction. Energies. 2020; 13(3):572. https://doi.org/10.3390/en13030572
Chicago/Turabian StyleGao, Yuan, Teng Jin, and Xiaoyan Wu. 2020. "Stochastic 3D Carbon Cloth GDL Reconstruction and Transport Prediction" Energies 13, no. 3: 572. https://doi.org/10.3390/en13030572
APA StyleGao, Y., Jin, T., & Wu, X. (2020). Stochastic 3D Carbon Cloth GDL Reconstruction and Transport Prediction. Energies, 13(3), 572. https://doi.org/10.3390/en13030572





