A Fuzzy Control Strategy Using the Load Forecast for Air Conditioning System
Abstract
1. Introduction
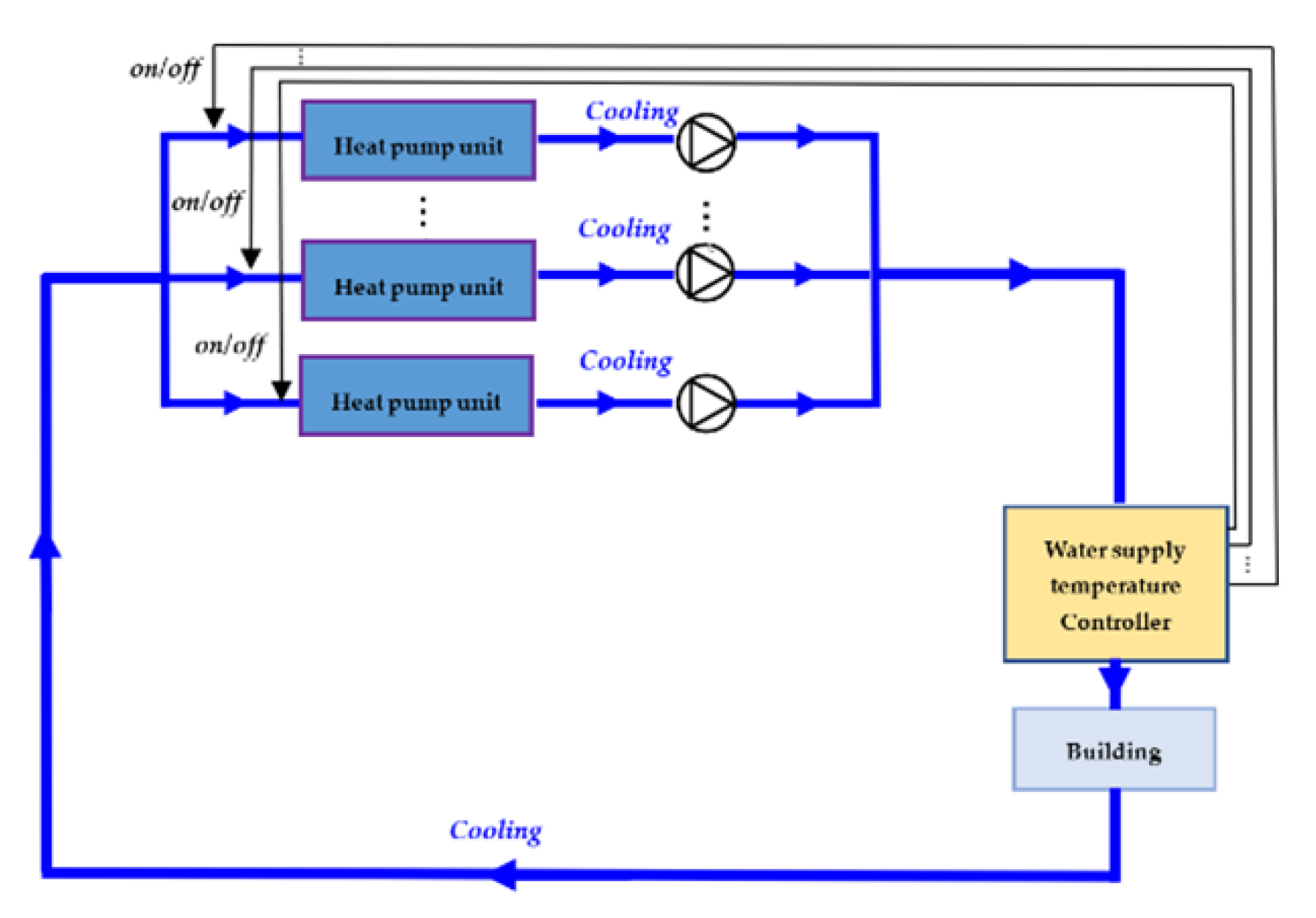
2. Case Description
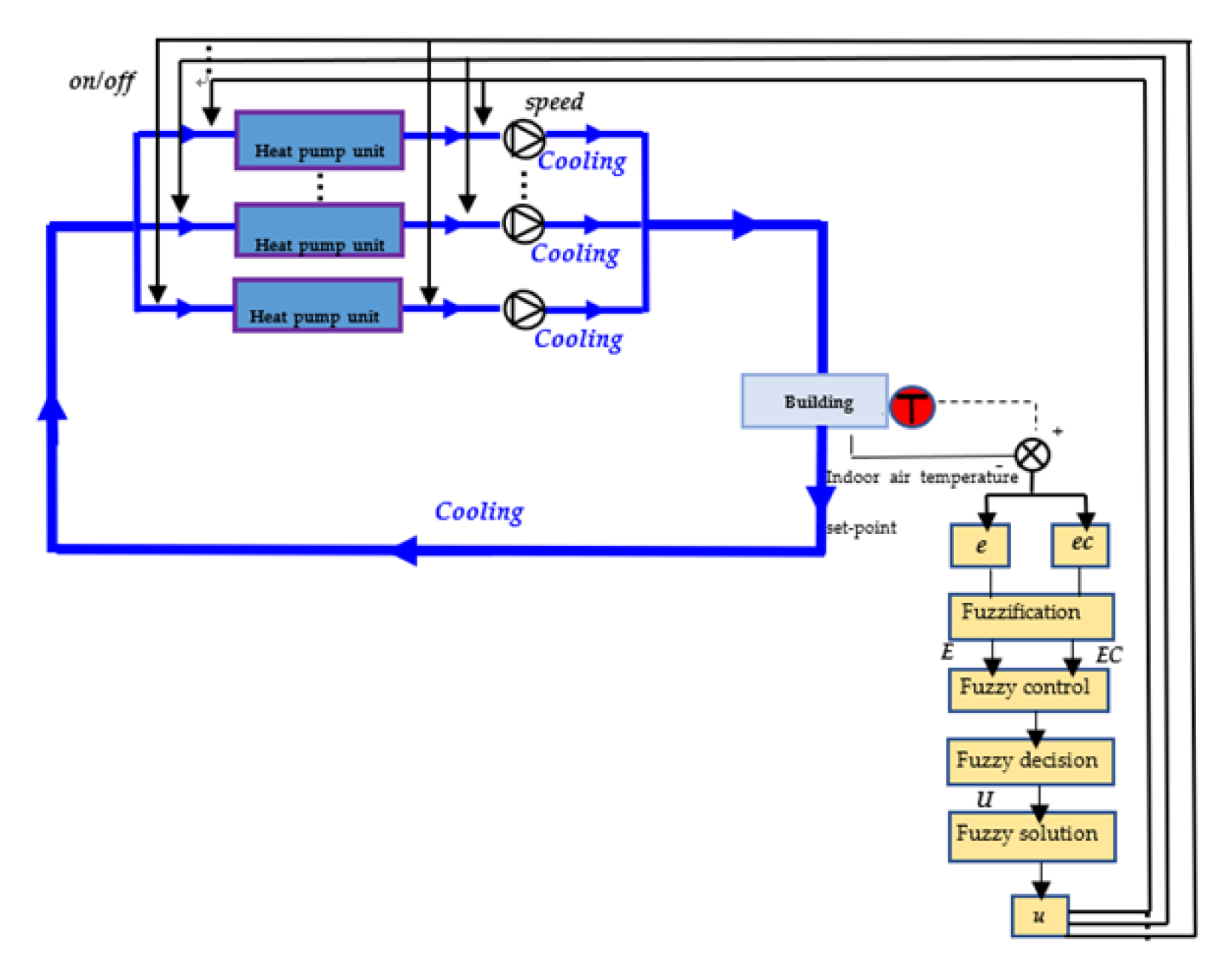
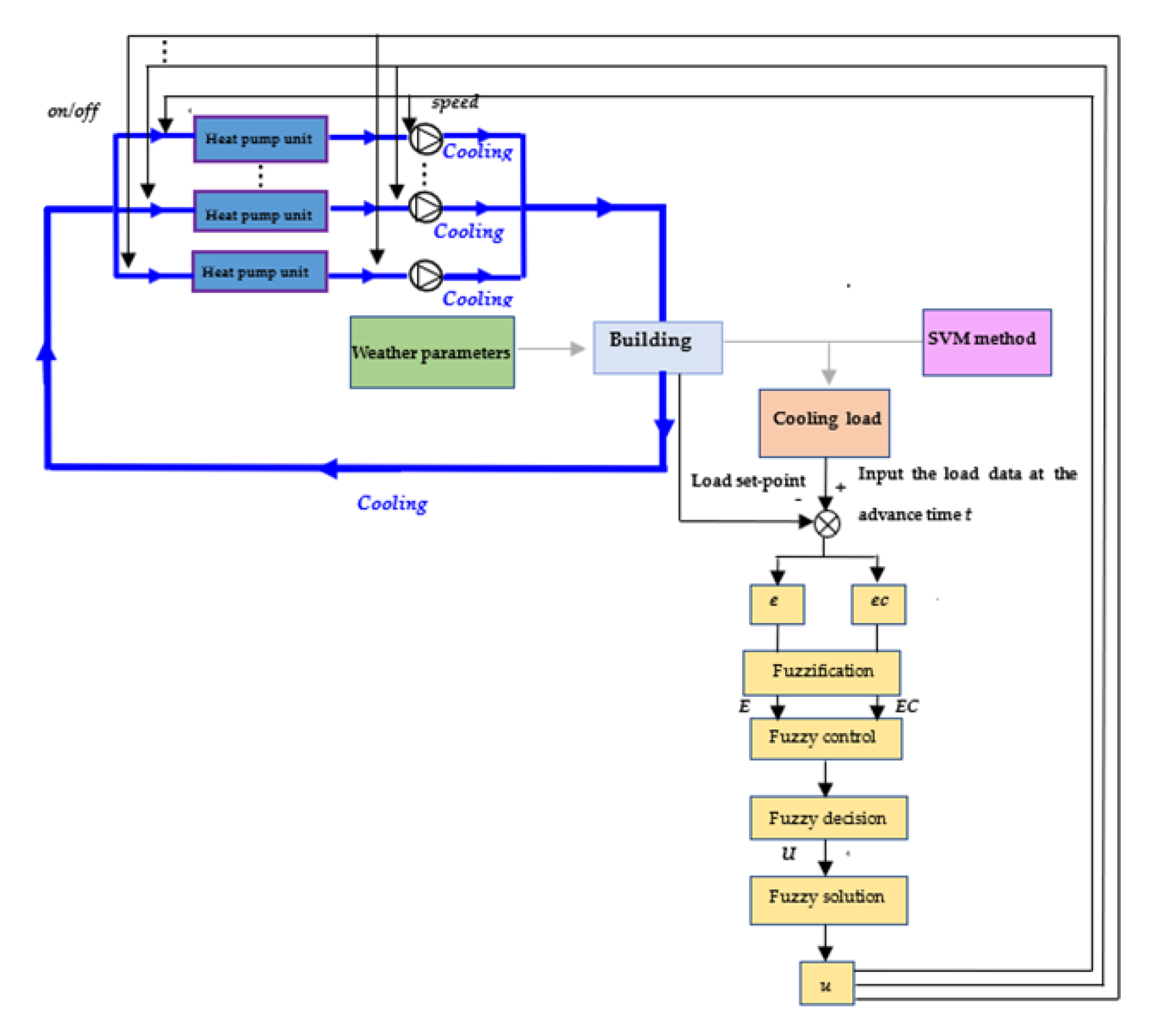
3. LFF Control Strategy
4. The Method of Control Optimizations
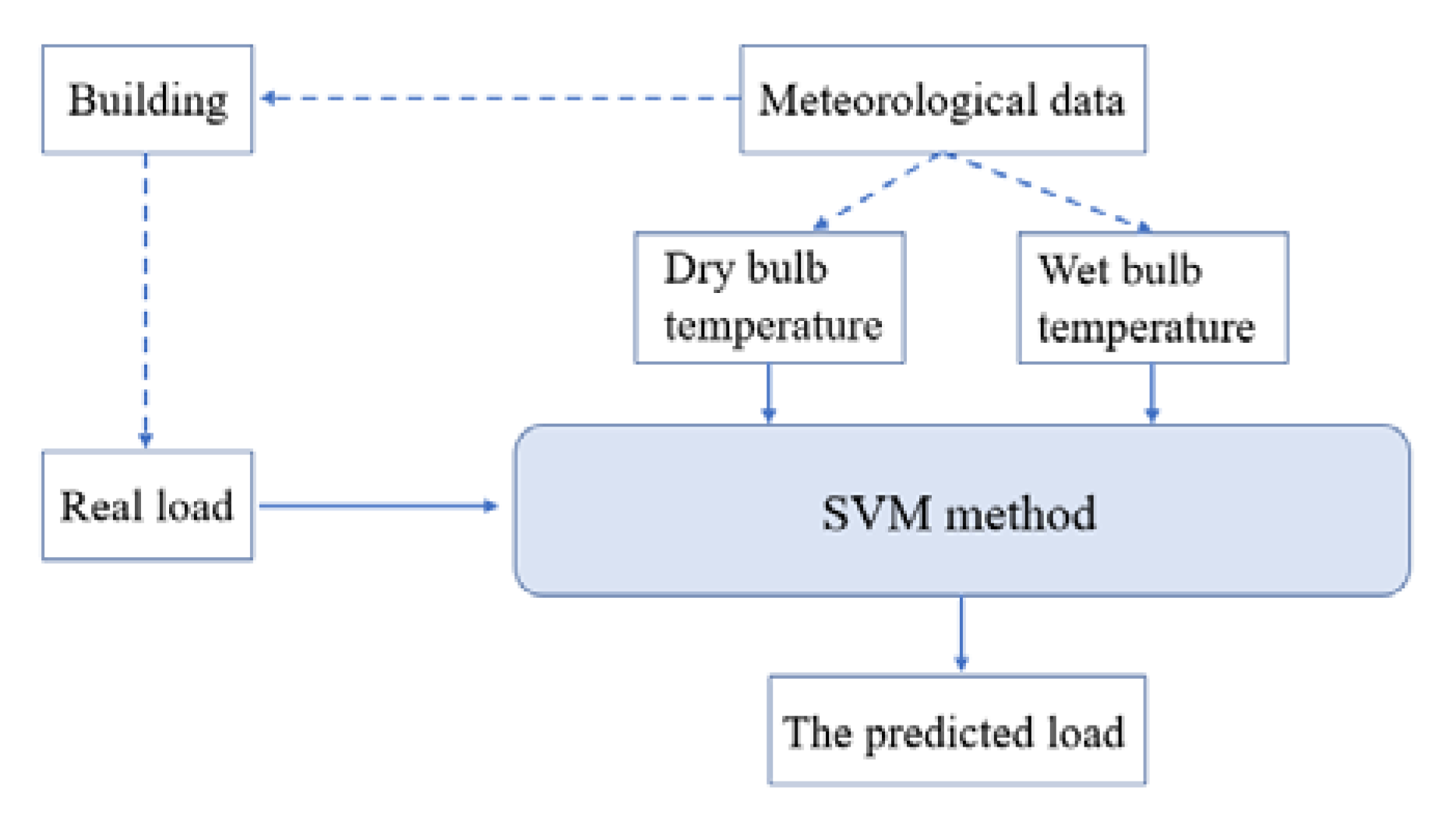
4.1. The Load Forecast Model Based on SVM
- The objective function of the support vector machine is established from the training samples. The load calculated by the simulation and the corresponding dry bulb temperature (T, , , ) and wet bulb temperature (W, ) of the typical meteorological year are used as training samples to establish the support vector machine objective function, where , and represent the dry bulb temperatures of 1 h, 2 h, and 3 h in advance and represents the wet bulb temperature 1 h earlier.
- The optimal combination of key parameters of the SVM is determined via MATLAB program calculations. The best combination of key parameters of the SVM is Best c = 14.4149, g = 0.7136.
- The optimal combination parameters are substituted into the SVM model to obtain its decision regression model to obtain the predicted load. The annual (8760 h) maximum instantaneous cooling load obtained by the SVM method is 68.6 kW.
4.2. The Calculation of Time Delay
4.3. Fuzzy Control Scheme
4.4. Optimization of Pumps and Units Control
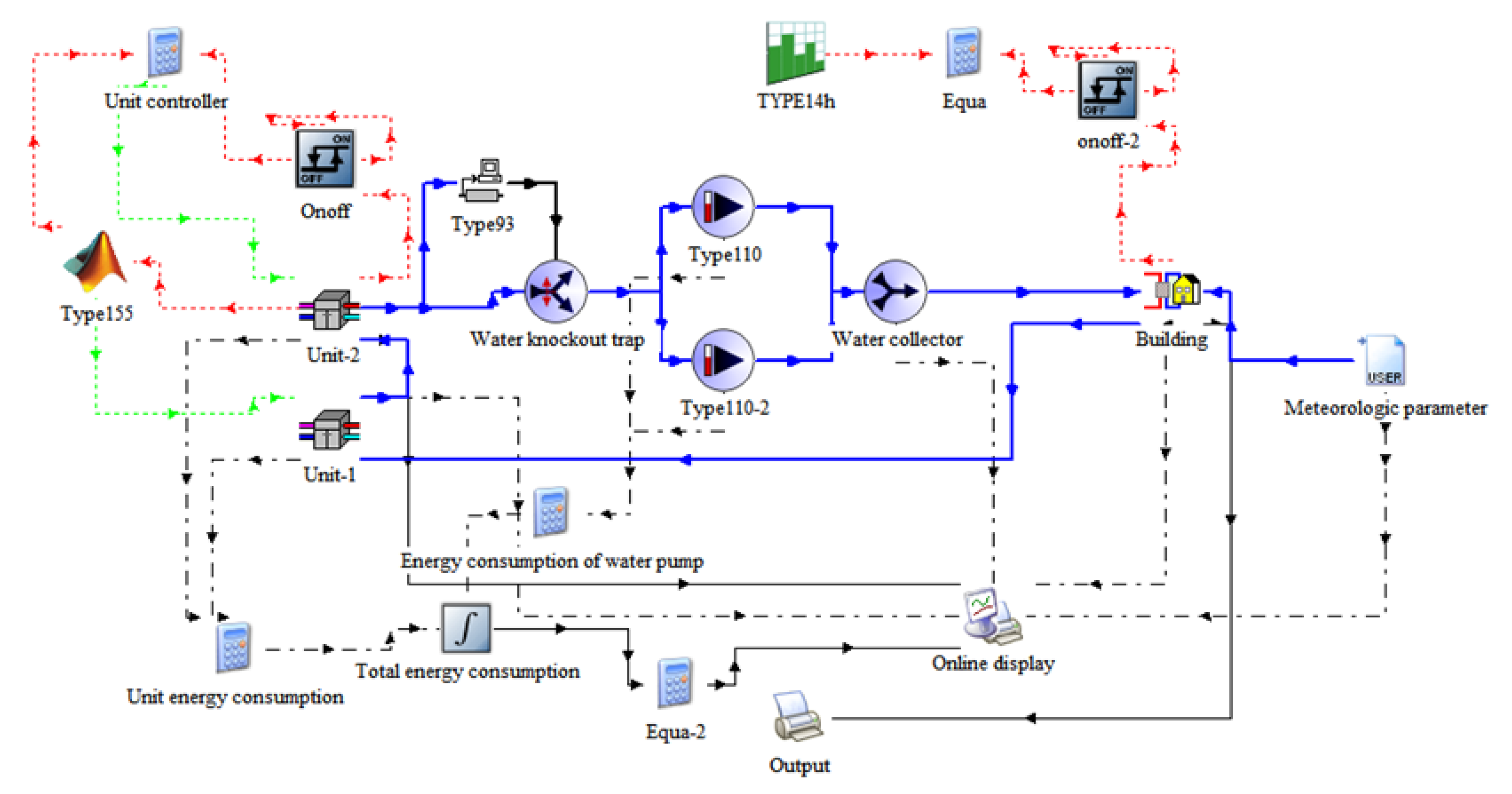
5. TRNSYS Simulation Platform
5.1. Establishment of the Simulation Platform
5.2. Verification of Simulation Platform
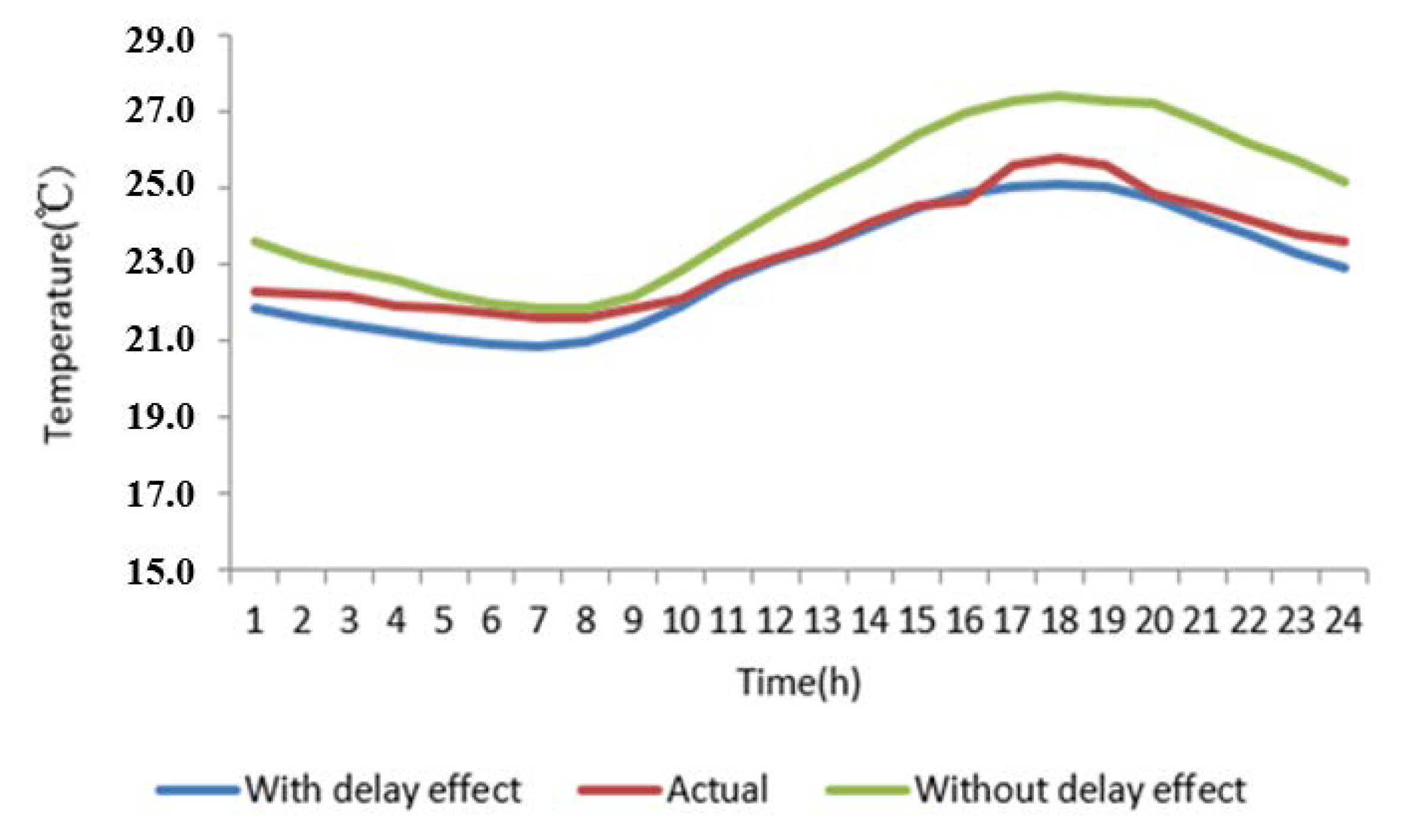
5.2.1. Indoor Temperature Validation Test
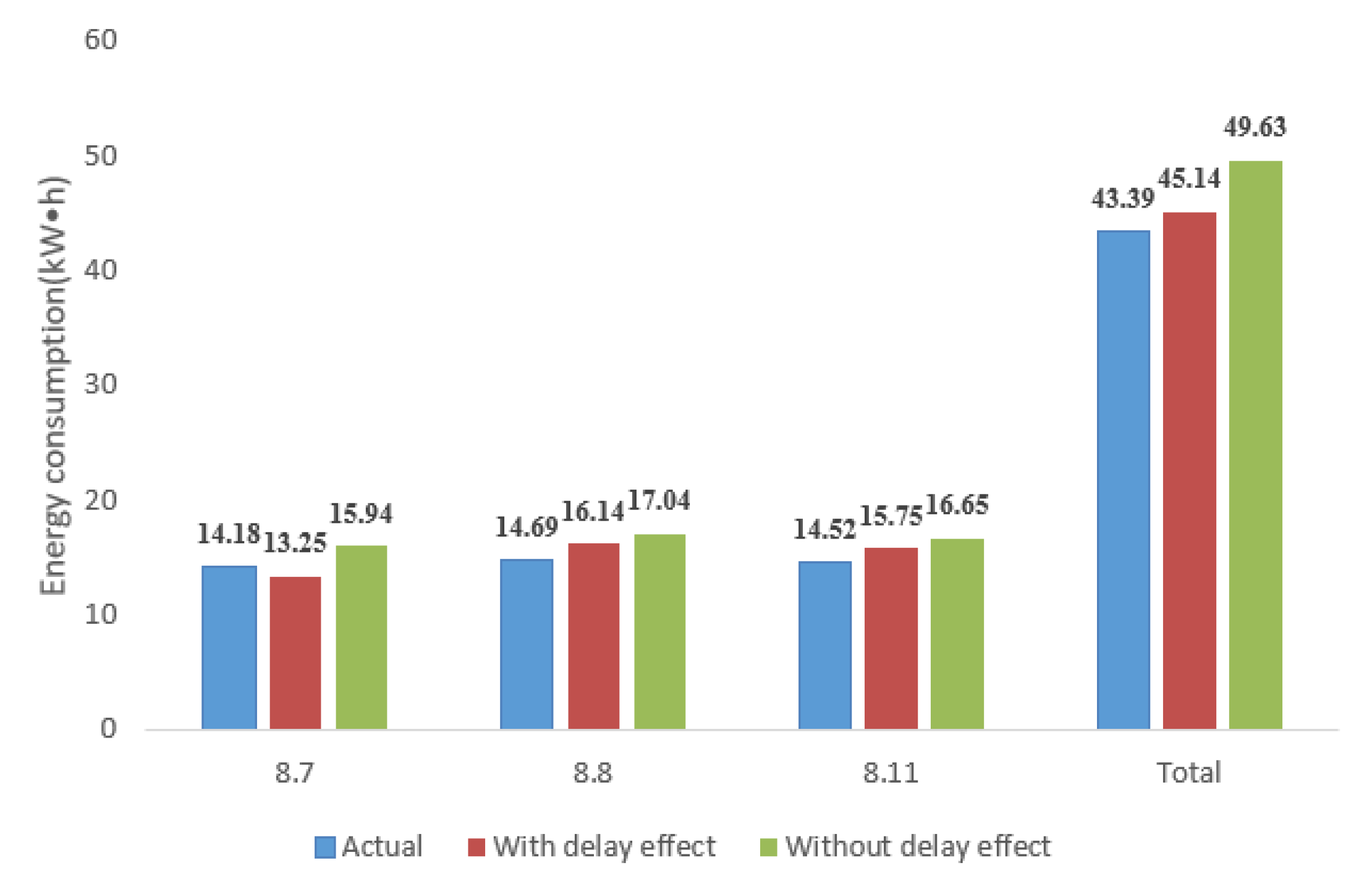
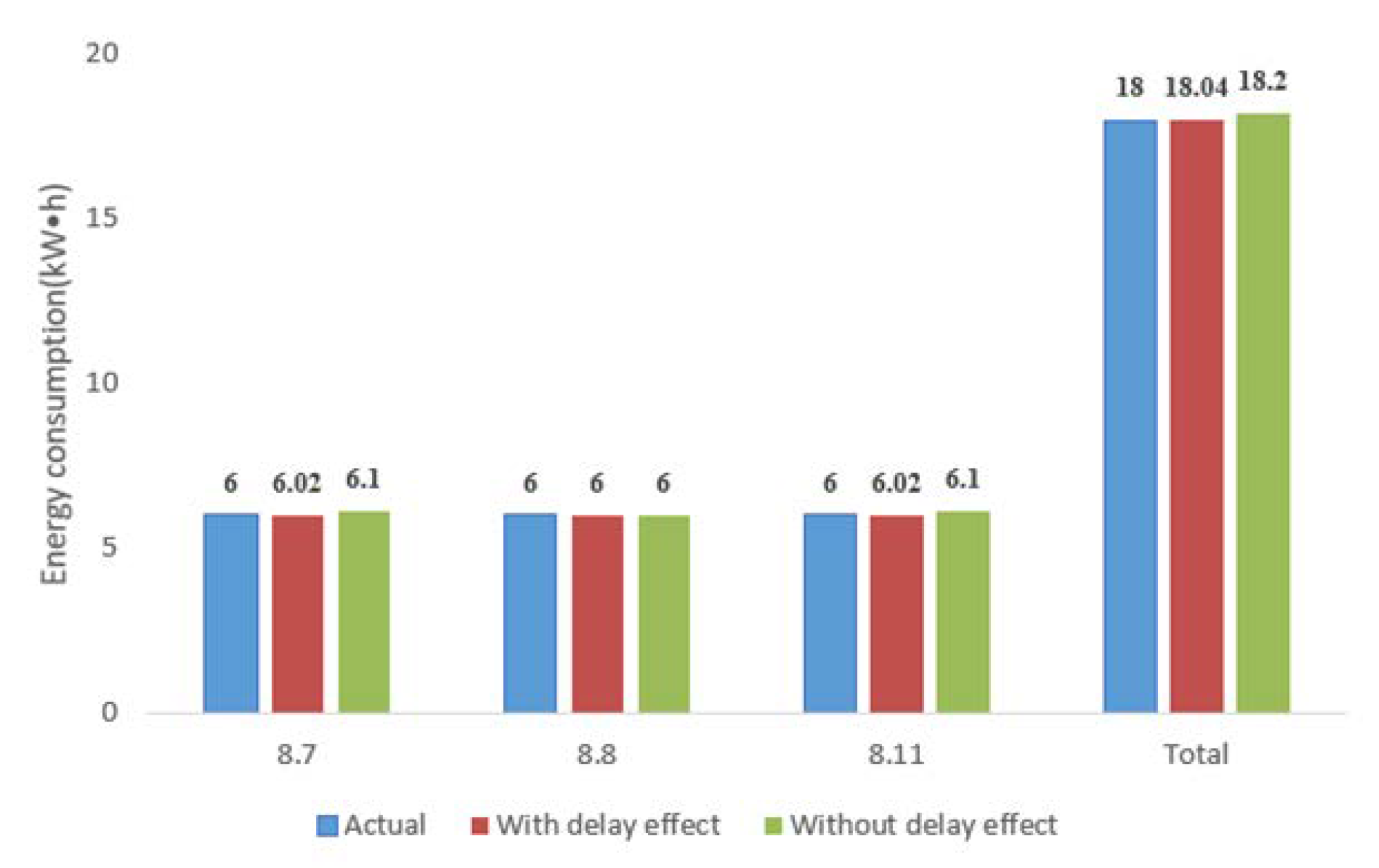
5.2.2. Heat Pump Unit and Pump Energy Consumption Validation Test
6. Results and Discussion
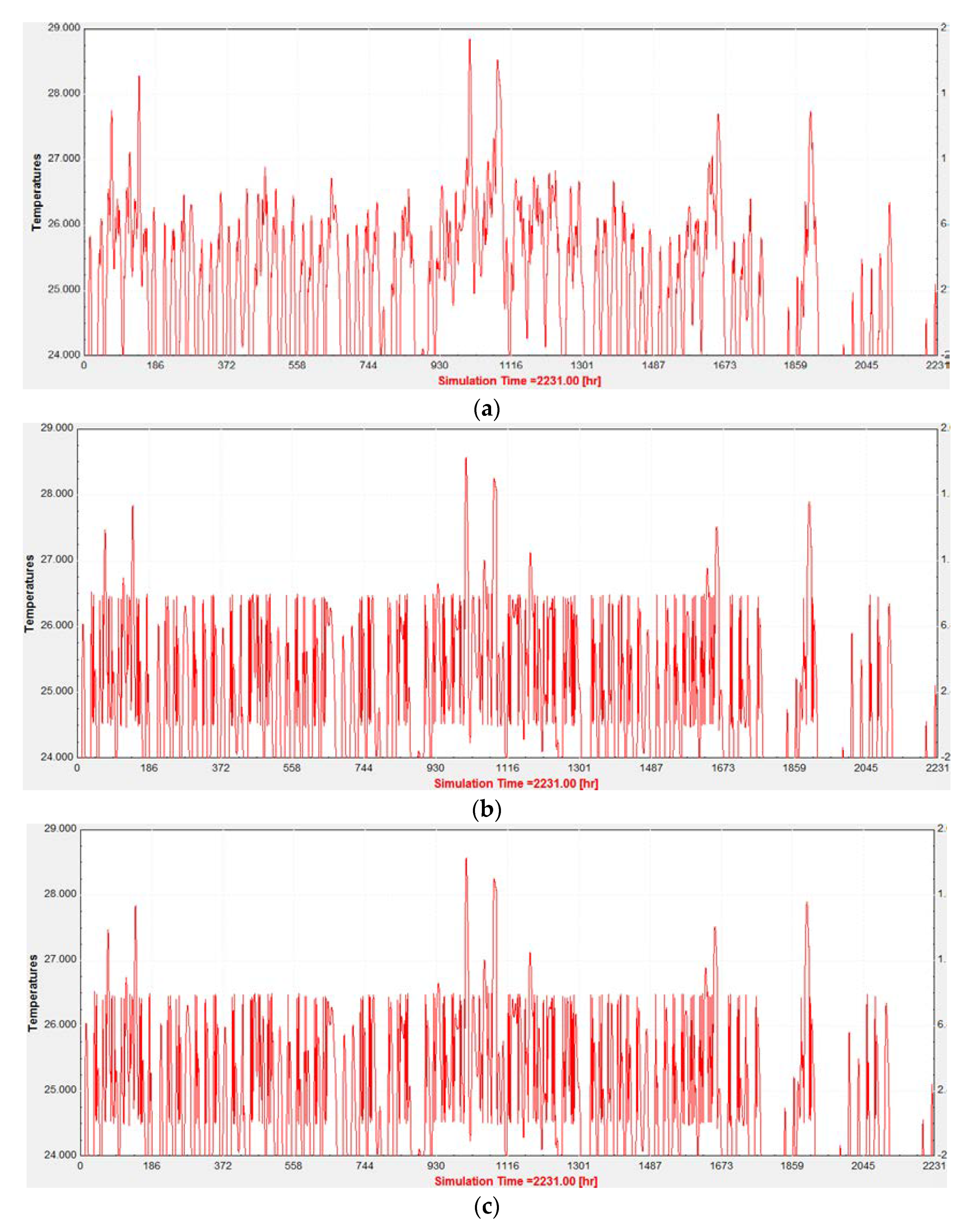
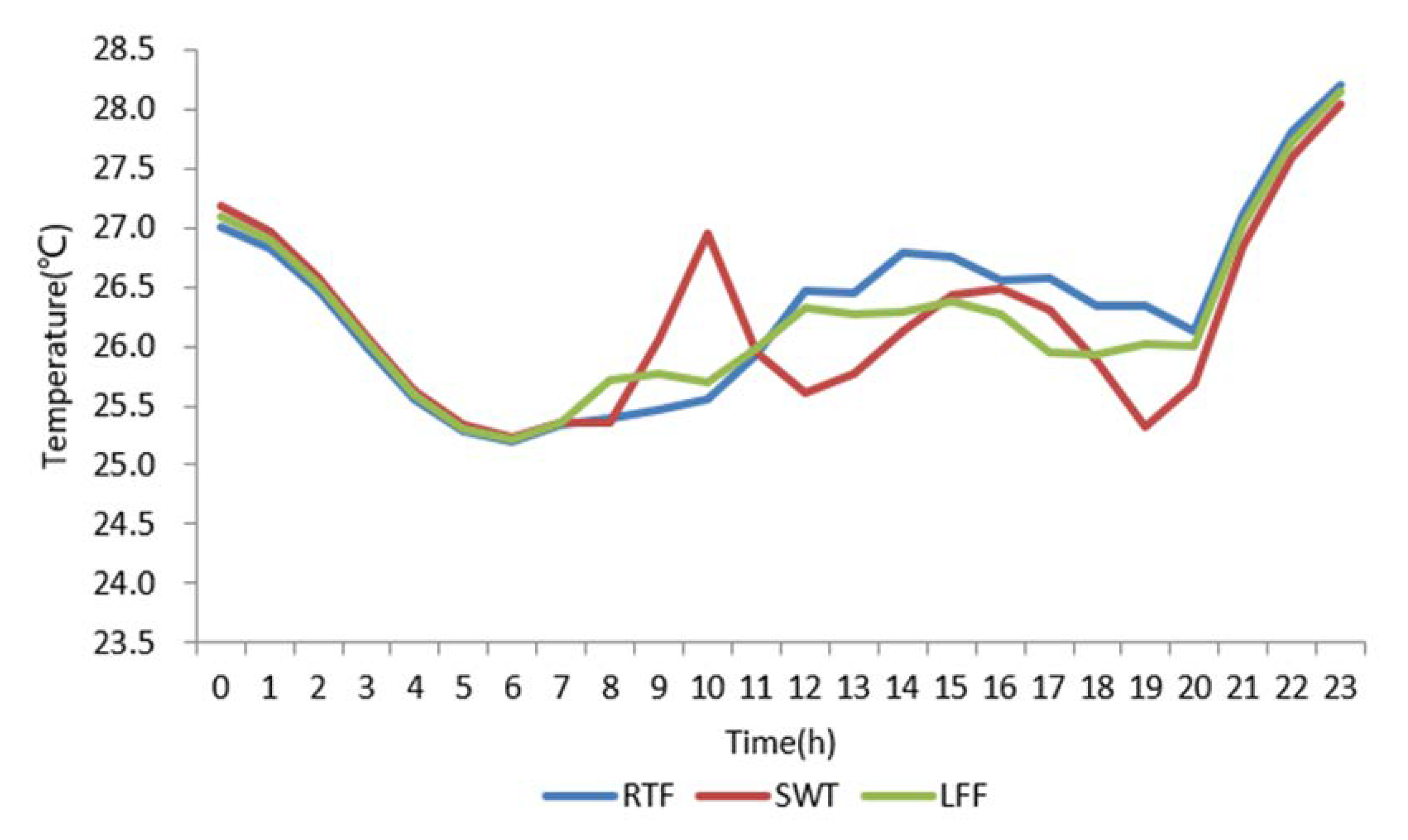
6.1. Simulation Results of Indoor Temperature
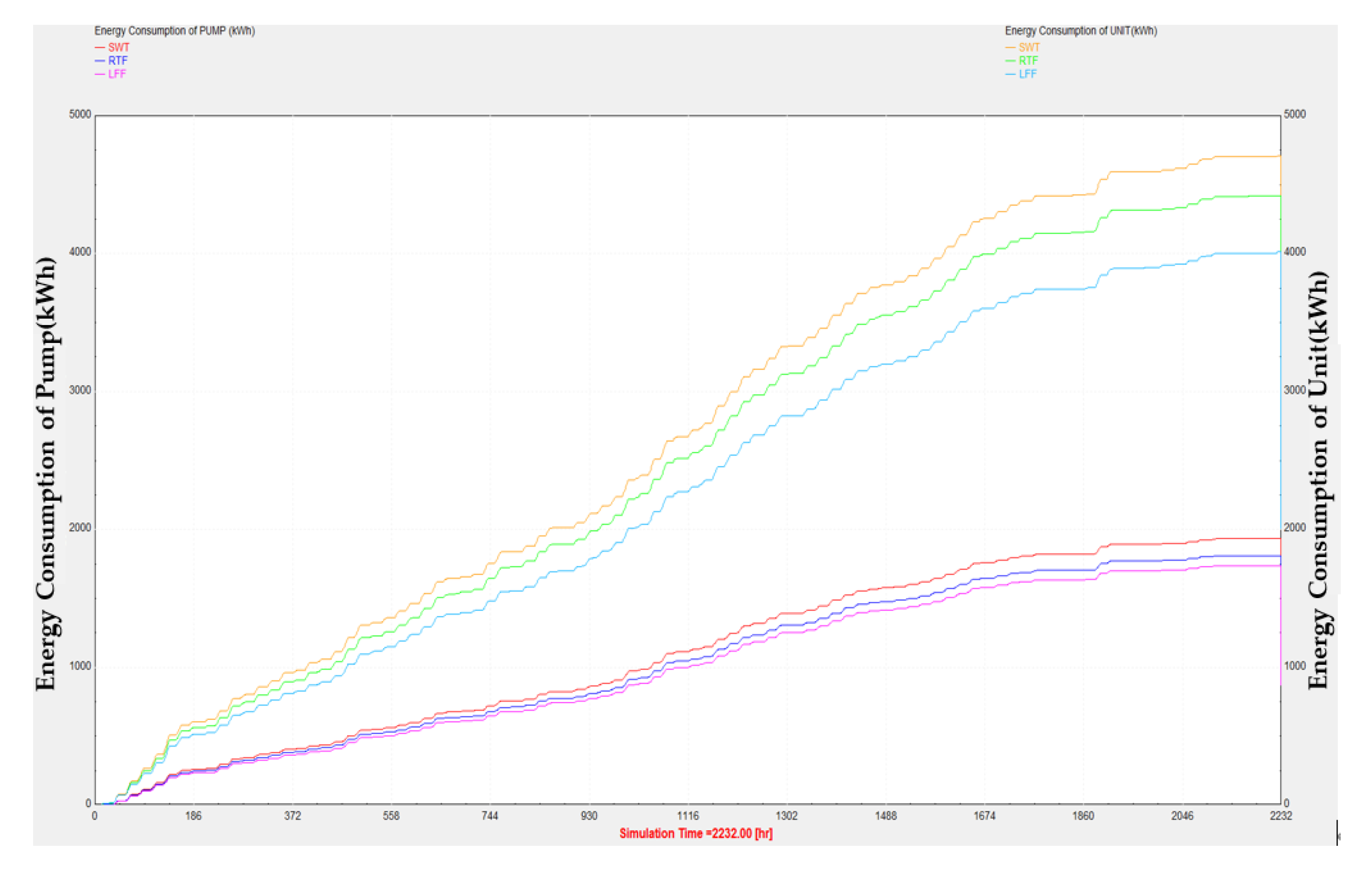
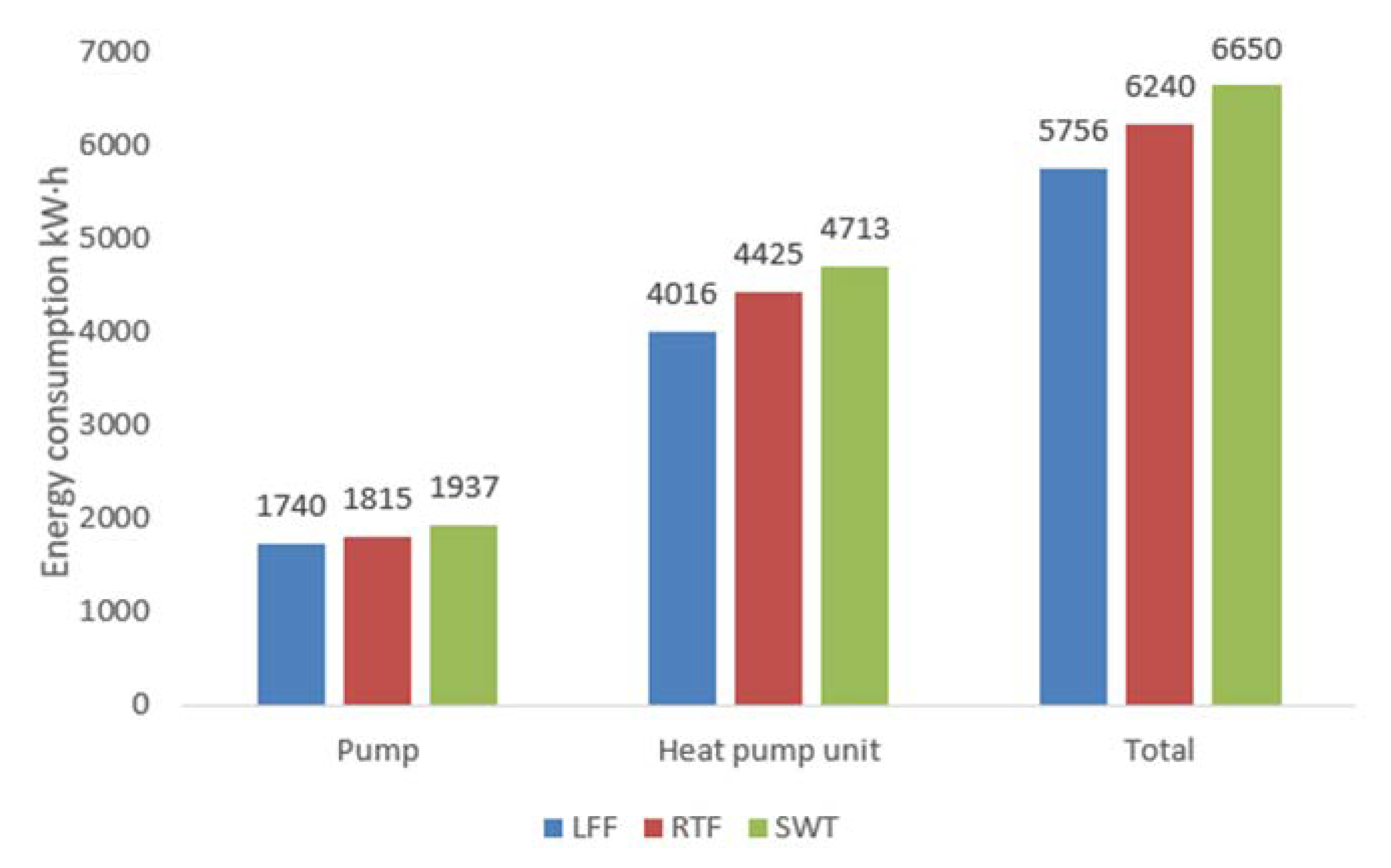
6.2. Simulation Results of Energy Consumption
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| LFF | load forecast fuzzy |
| RTF | room temperature fuzzy |
| SWT | supply water temperature |
| SVM | Support Vector Machines |
| SVR | Support Vector Regression |
| C | error cost |
| γ | kernel parameter |
| the number of the terminal of the branch I of the air conditioning system | |
| the ratio of the flow rate of each branch pipe to the total flow | |
| Dn | the inner diameter of the chilled water outlet pipe |
| the delay time of each main pipe | |
| NB | negative large |
| NS | negative small |
| PS | positive small |
| PB | positive large |
| Ak | fuzzy set |
| EC | the change rate of the load versus time |
| ω | weight vectors |
| nonlinear mapping function | |
| threshold | |
| (xm, ym) | a pair of input and output vectors |
| n | number of samples |
| upper training error | |
| lower training error | |
| M | the total number of the terminal of the air conditioning system |
| he inner diameter of each section of the main pipe | |
| he real-time flow rate of the chilled water outlet. | |
| the length of each main pipe | |
| NM | medium |
| Z | zero |
| PM | medium |
| μ | a membership function |
| E | the difference between the input load and the set load |
| U | Pump speed control |
References
- Costa, A.; Keane, M.M.; Torrens, J.I.; Corry, E. Building operation and energy performance: Monitoring, analysis and optimisation toolkit. Appl. Energy 2013, 101, 310–316. [Google Scholar] [CrossRef]
- Lam, J.C.; Wan, K.K.; Tsang, C.L.; Yang, L. Building energy efficiency in different cli-mates. Energy Convers Manag. 2008, 49, 2354–2366. [Google Scholar] [CrossRef]
- Du, Z.M.; Jin, X.Q.; Fang, X.; Fan, B. A dual-benchmark based energy analysis method to evaluate control strategies for building HVAC systems. Appl. Energy 2016, 183, 700–714. [Google Scholar] [CrossRef]
- Peng, Y.; Rysanek, A.; Nagy, Z. Using machine learning techniques for occupancy-prediction-based cooling control in office buildings. Appl. Energy 2018, 211, 1343–1358. [Google Scholar] [CrossRef]
- Yordanova, S.; Merazchiev, D.; Jain, L. A Two-Variable Fuzzy Control Design with Application to an Air-Conditioning System. Fuzzy Syst. IEEE Trans. 2015, 23, 474–481. [Google Scholar] [CrossRef]
- Wang, S.W.; Tang, R. Supply-based feedback control strategy of air-conditioning systems for direct load control of buildings responding to urgent requests of smart grids. Appl. Energy 2017, 201, 419–432. [Google Scholar] [CrossRef]
- Krstic, M. Input Delay Compensation for Forward Complete and Strict-Feedforward Nonlinear Systems. IEEE Trans. Autom. Control 2010, 55, 287–303. [Google Scholar] [CrossRef]
- Mossolly, M.; Ghali, K.; Ghaddar, N. Optimal control strategy for a multi-zone air conditioning system using a genetic algorithm. Energy 2009, 34, 58–66. [Google Scholar] [CrossRef]
- Powell, K.M.; Sriprasad, A.; Cole, W.J.; Edgar, T.F. Heating, cooling, and electrical load forecasting for a large-scale district energy system. Energy 2014, 74, 877–885. [Google Scholar] [CrossRef]
- Wei, B.; Tang, J.; Wei, Z. Dynamic simulation to the operation of central air conditioning system. Ind. Electron. Appl. 2010, 100, 861–867. [Google Scholar]
- Chan, I.Y.T. Simulation and evaluation of control strategies for air conditioning system using TRNSYS. Int. J. Prison. Health 2012, 8, 92–99. [Google Scholar]
- Li, Q.; Zheng, C.; Shirazi, A.; Mousa, O.B.; Moscia, F.; Scottc, J.A.; Taylor, R.A. Design and analysis of a medium-temperature, concentrated solar thermal collector for air-conditioning applications. Appl. Energy 2017, 190, 1159–1173. [Google Scholar] [CrossRef]
- Xue, X.; Wang, S.; Yan, C.; Cui, B. A fast chiller power demand response control strategy for buildings connected to smart grid. Appl. Energy 2015, 137, 77–87. [Google Scholar] [CrossRef]
- Shirazi, A.; Pintaldi, S.; White, S.D.; Morrison, G.L.; Rosengarten, G.; Tylor, R.A. Solar-assisted absorption air-conditioning systems in buildings: Control strategies and operational modes. Appl. Therm. Eng. 2016, 92, 246–260. [Google Scholar] [CrossRef]
- Fiorentini, M.; Wall, J.; Ma, Z.; Braslavsky, J.H.; Cooper, P. Hybrid model predictive control of a residential HVAC system with on-site thermal energy generation and storage. Appl. Energy 2017, 187, 465–479. [Google Scholar] [CrossRef]
- Attaran, S.M.; Yusof, R.; Selamat, H. A novel optimization algorithm based on epsilon constraint-RBF neural network for tuning PID controller in decoupled HVAC system. Appl. Therm. Eng. 2016, 99, 613–624. [Google Scholar] [CrossRef]
- Lygouras, J.N.; Botsaris, P.N.; Vourvoulakis, J.; Kodogiannis, V. Fuzzy logic controller implementation for a solar air-conditioning system. Appl. Energy 2007, 84, 1305–1318. [Google Scholar] [CrossRef]
- Wang, J.J.; An, D.W.; Jing, Y.Y. Genetic optimization algorithm of PID decoupling control for VAV air-conditioning system. J. Tianjin Univ. 2009, 15, 308–314. [Google Scholar] [CrossRef]
- Xia, Y.; Deng, S.; Chen, M.Y. Inherent operational characteristics and operational stability of a variable speed direct expansion air conditioning system. Appl. Therm. Eng. 2016, 73, 268–277. [Google Scholar] [CrossRef]
- Li, X.; Chen, J.; Chen, Z.; Liu, W.; Hu, W. A new method for controlling refrigerant flow in automobile air conditioning. Appl. Therm. Eng. 2004, 24, 1073–1085. [Google Scholar] [CrossRef]
- Li, S. Optimum Control Strategy and Performance Simulation of a Constant Temperature and Humidity Air-conditioning System. J. Refrig. 2012, 33, 22–27. [Google Scholar]
- Yu, X.; Wang, R.Z.; Zhai, X.Q. Year round experimental study on a constant temperature and humidity air-conditioning system driven by ground source heat pump. Energy 2011, 36, 1309–1318. [Google Scholar] [CrossRef]
- Liu, X.; Liu, J.; Lu, Z.; Xing, K.; Mai, Y. Diversity of energy-saving control strategy for a parallel chilled water pump based on variable differential pressure control in an air-conditioning system. Energy 2015, 88, 718–733. [Google Scholar]
- Liu, X.F.; Liu, J.P.; Lu, J.D.; Liu, L.; Zou, W. Research on operating characteristics of direct-return chilled water system controlled by variable temperature difference. Energy 2012, 40, 236–249. [Google Scholar] [CrossRef]
- Wang, S.; Gao, D.C.; Sun, Y.; Xiao, F. An online adaptive optimal control strategy for complex building chilled water systems involving intermediate heat exchangers. Appl. Therm. Eng. 2013, 50, 614–628. [Google Scholar] [CrossRef]
- Chiou, C.B.; Chiou, C.H.; Chu, C.M.; Lin, S.L. The application of fuzzy control on energy saving for multi-unit room air-conditioners. Appl. Therm. Eng. 2009, 29, 310–316. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V.N. Support vector networks. Mach. Learn. 1995, 20, 273–295. [Google Scholar] [CrossRef]
- Selakov, A.; Cvijetinović, D.; Milović, L. Hybrid PSO-SVM method for short-term load forecasting during periods with significant temperature variations in city of Burbank. Appl. Soft Comput. 2014, 16, 80–88. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Support Vector Regression. Neural Inf. Process. Lett. Rev. 2007, 11, 203–224. [Google Scholar]
- Fu, Y.; Li, Z.; Zhang, H. Using Support vector machine to predict next-day electricity load of public buildings with sub-metering devices. Procedia Eng. 2015, 121, 1016–1022. [Google Scholar] [CrossRef]
- Shrivastava, N.A.; Khosravi, A.; Panigrahi, B.K. Prediction Interval Estimation of Electricity Prices Using PSO-Tuned Support Vector Machines. IEEE Trans. Ind. Inform. 2015, 11, 322–331. [Google Scholar] [CrossRef]
- Ebtehaj, I.; Bonakdari, H.; Shamshirband, S. A combined support vector machine-wavelet transform model for prediction of sediment transport in sewer. Flow Meas. Instrum. 2016, 47, 19–27. [Google Scholar] [CrossRef]
- Li, Y.M.; Wu, J.Y.; Shiochi, S. Experimental validation of the simulation module of the water-cooled variable refrigerant flow system under cooling operation. Appl. Energy 2010, 87, 1513–1521. [Google Scholar] [CrossRef]
- Hien, L.V.; Trinh, H. Stability Analysis and Control of Two-Dimensional Fuzzy Systems with Directional Time-Varying Delays. IEEE Trans. Fuzzy Syst. 2018, 26, 1550–1564. [Google Scholar] [CrossRef]
- Ozkop, E.; Altas, I.H.; Okumus, H.I.; Sharaf, A.M. A fuzzy logic sliding mode controlled electronic differential for a direct wheel drive EV. Int. J. Electron. 2015, 102, 1919–1942. [Google Scholar] [CrossRef]


| 1 | 5.30 | 32 | 1/12 | 0.12 | 44.24 |
| 2 | 7.24 | 40 | 1/12 | 0.15 | 47.22 |
| 3 | 4.41 | 50 | 1/12 | 0.15 | 29.96 |
| 4 | 7.32 | 50 | 1/12 | 0.20 | 37.30 |
| 5 | 8.01 | 50 | 1/12 | 0.25 | 32.65 |
| 6 | 5.45 | 65 | 1/12 | 0.17 | 31.29 |
| 7 | 6.80 | 65 | 1/12 | 0.20 | 33.46 |
| 8 | 4.69 | 65 | 1/12 | 0.23 | 20.19 |
| 9 | 8.52 | 65 | 1/12 | 0.26 | 32.61 |
| 10 | 7.21 | 80 | 1/12 | 0.19 | 37.62 |
| 11 | 4.69 | 80 | 1/12 | 0.21 | 22.25 |
| 12 | 16.4 | 80 | 1/12 | 0.23 | 71.30 |
| Total | 440 | ||||
| u | Pump Control Method |
|---|---|
| 0.0–0.2 | Both pumps are off and the pump control signal is 0 |
| 0.2–0.5 | One pump control signal is 0, the other pump control signal is 0.5 + u |
| 0.5–1.0 | One pump control signal is 1 and the other control signal is 2u − 1 |
| u | Heat Units Control Method |
|---|---|
| 0.00–0.50 | One unit start-stop time ratio is 1, another unit start-stop time ratio is 0 |
| 0.50–0.66 | One unit start-stop time ratio is 1, another unit start-stop time ratio is 0.17 |
| 0.66–0.75 | One unit start-stop time ratio is 1, another unit start-stop time ratio is 0.33 |
| 0.75–0.80 | One unit start-stop time ratio is 1, another unit start-stop time ratio is 0.50 |
| 0.80–1.00 | Start and stop time rate of both units is 1 |
| Contrast Item | Unit Energy Consumption (kW·h)/Energy Saving Rate (%) | Pump Energy Consumption (kW·h)/Energy Saving Rate (%) | Total Energy Consumption (kW·h)/Energy Saving Rate (%) |
|---|---|---|---|
| LFF | 4016 | 1740 | 5756 |
| SWT | 4713/14.5% | 1937/10.2% | 6650/13.4% |
| RTF | 4425/9.2% | 1815/4.1% | 6240/7.8% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Shan, Y. A Fuzzy Control Strategy Using the Load Forecast for Air Conditioning System. Energies 2020, 13, 530. https://doi.org/10.3390/en13030530
Zhao J, Shan Y. A Fuzzy Control Strategy Using the Load Forecast for Air Conditioning System. Energies. 2020; 13(3):530. https://doi.org/10.3390/en13030530
Chicago/Turabian StyleZhao, Jing, and Yu Shan. 2020. "A Fuzzy Control Strategy Using the Load Forecast for Air Conditioning System" Energies 13, no. 3: 530. https://doi.org/10.3390/en13030530
APA StyleZhao, J., & Shan, Y. (2020). A Fuzzy Control Strategy Using the Load Forecast for Air Conditioning System. Energies, 13(3), 530. https://doi.org/10.3390/en13030530






