Numerical Simulations of the Flow of a Dense Suspension Exhibiting Yield-Stress and Shear-Thinning Effects
Abstract
1. Introduction
2. Mathematical Framework
2.1. Governing Equations
2.1.1. Conservation of Mass
2.1.2. Conservation of Linear Momentum
2.2. Constitutive Equation for the Stress Tensor
2.3. Expanded Form of the Governing Equations
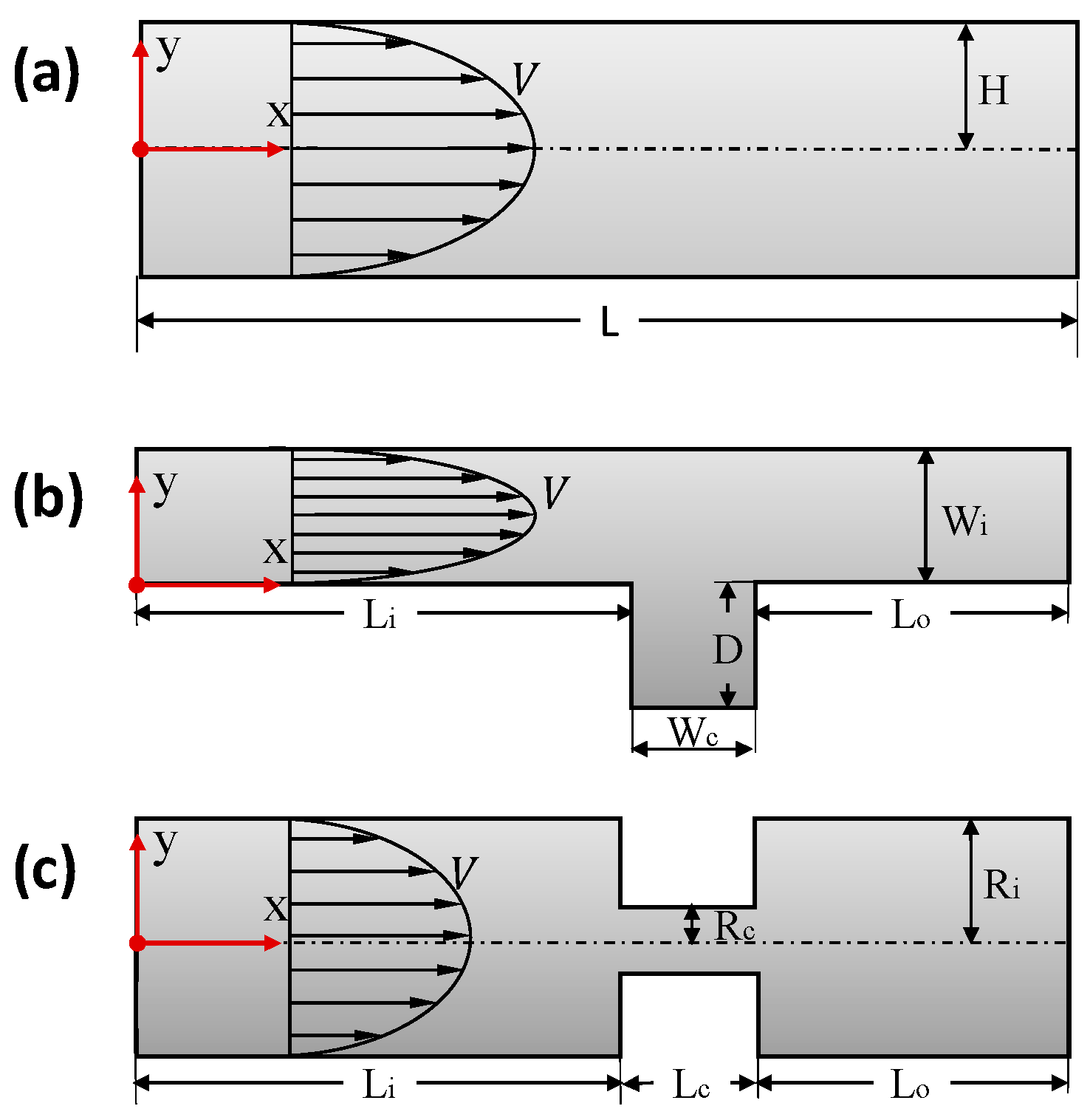
3. Problem Description
4. Results and Discussion
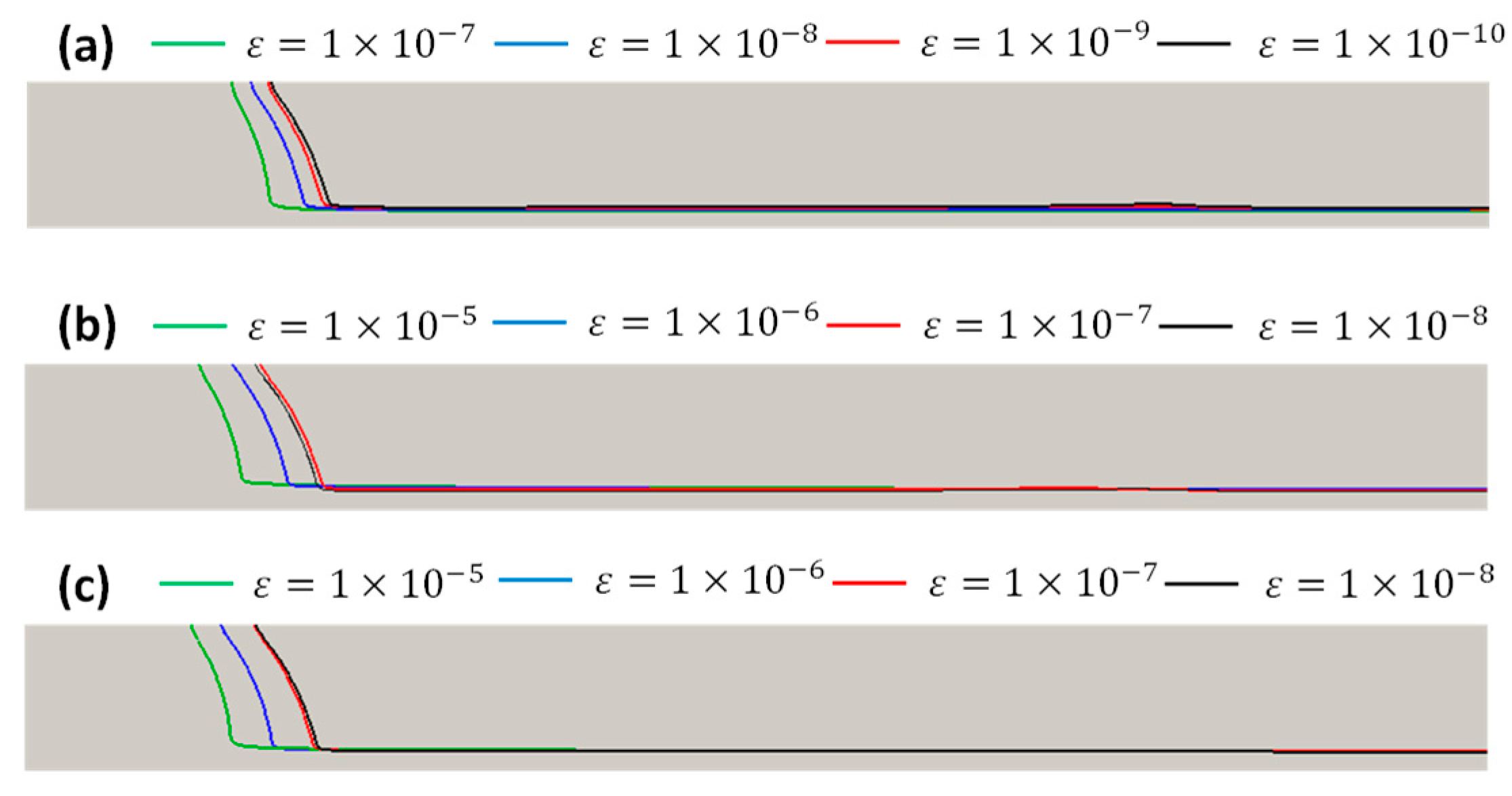
4.1. Convergence Properties of the Regularization Methods
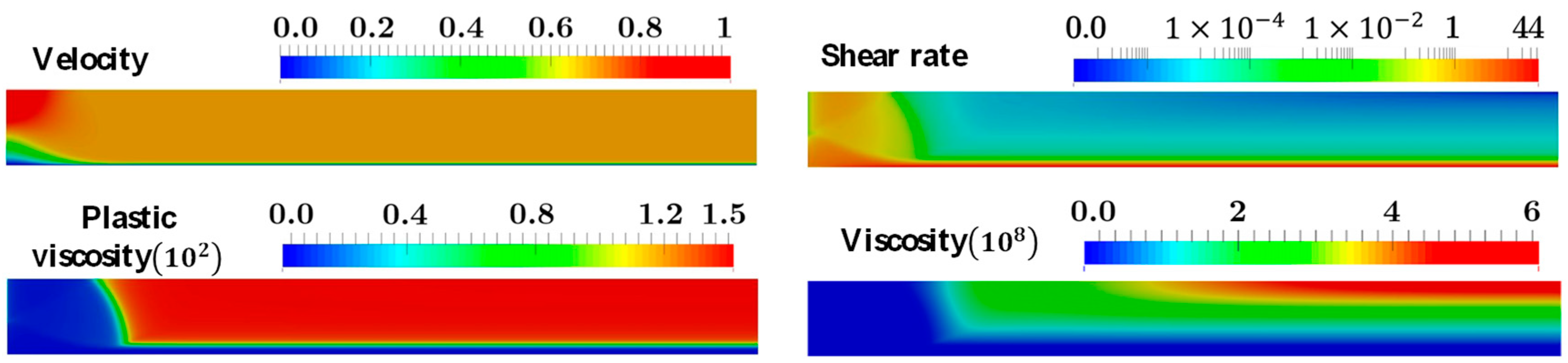
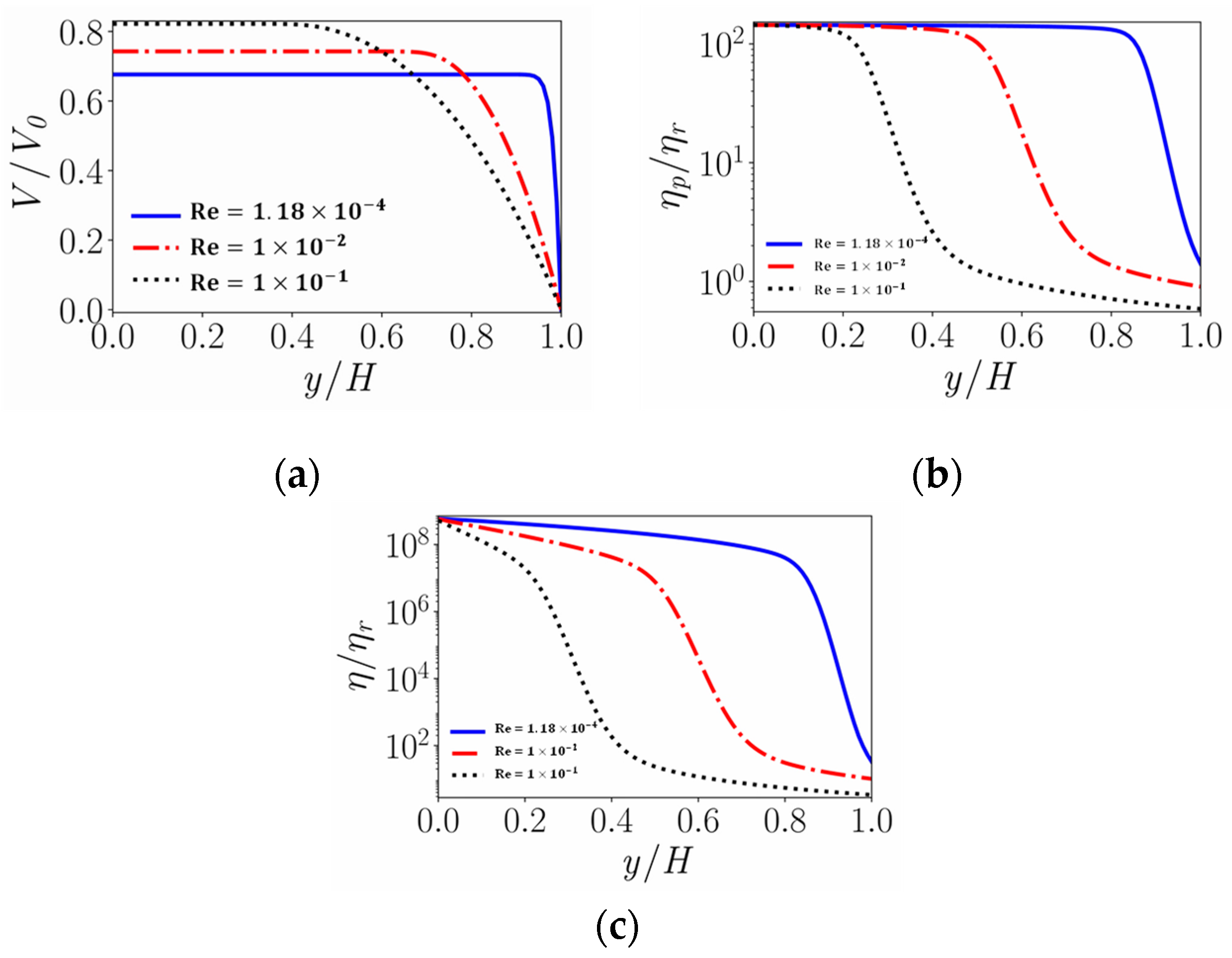
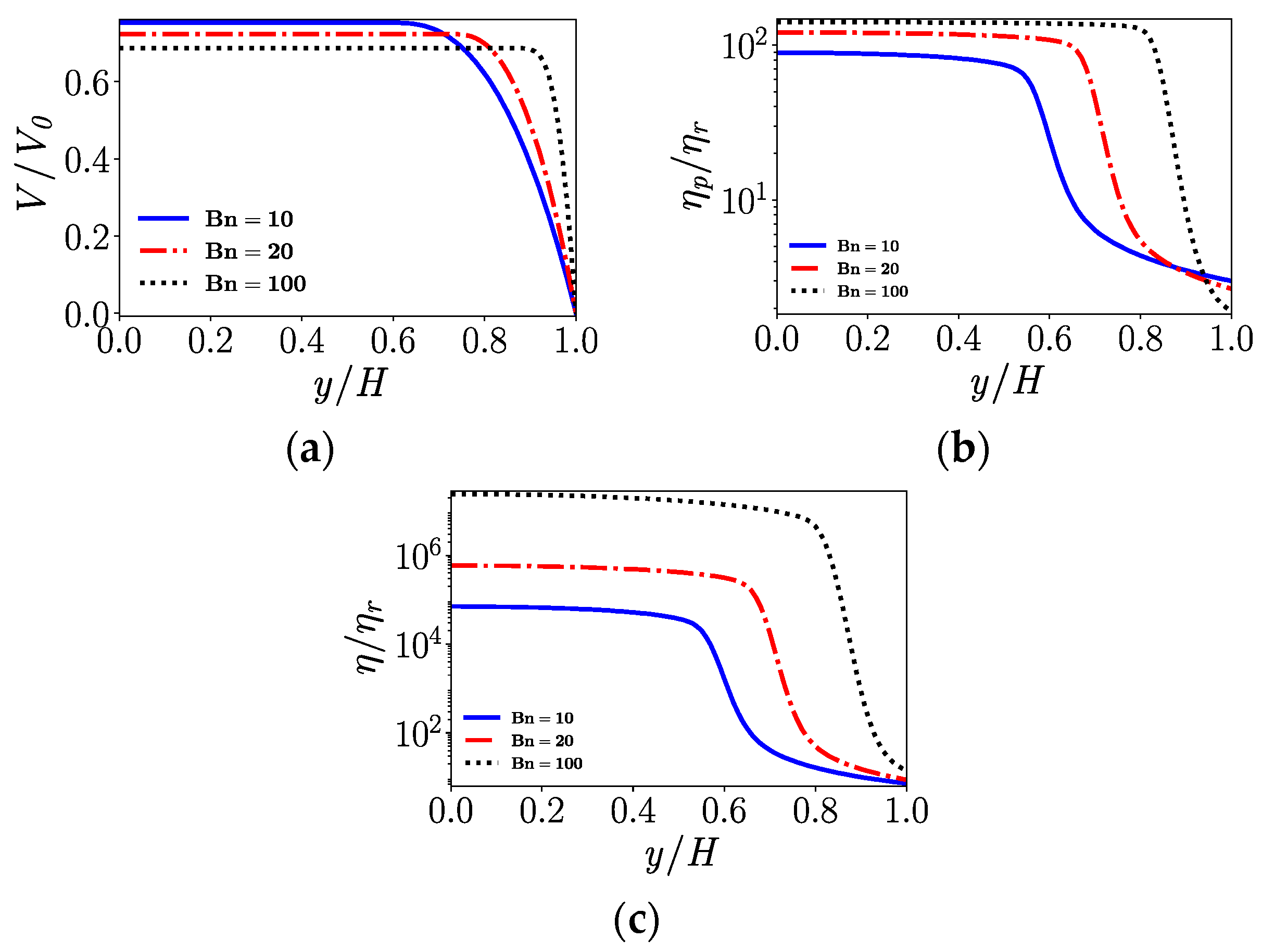
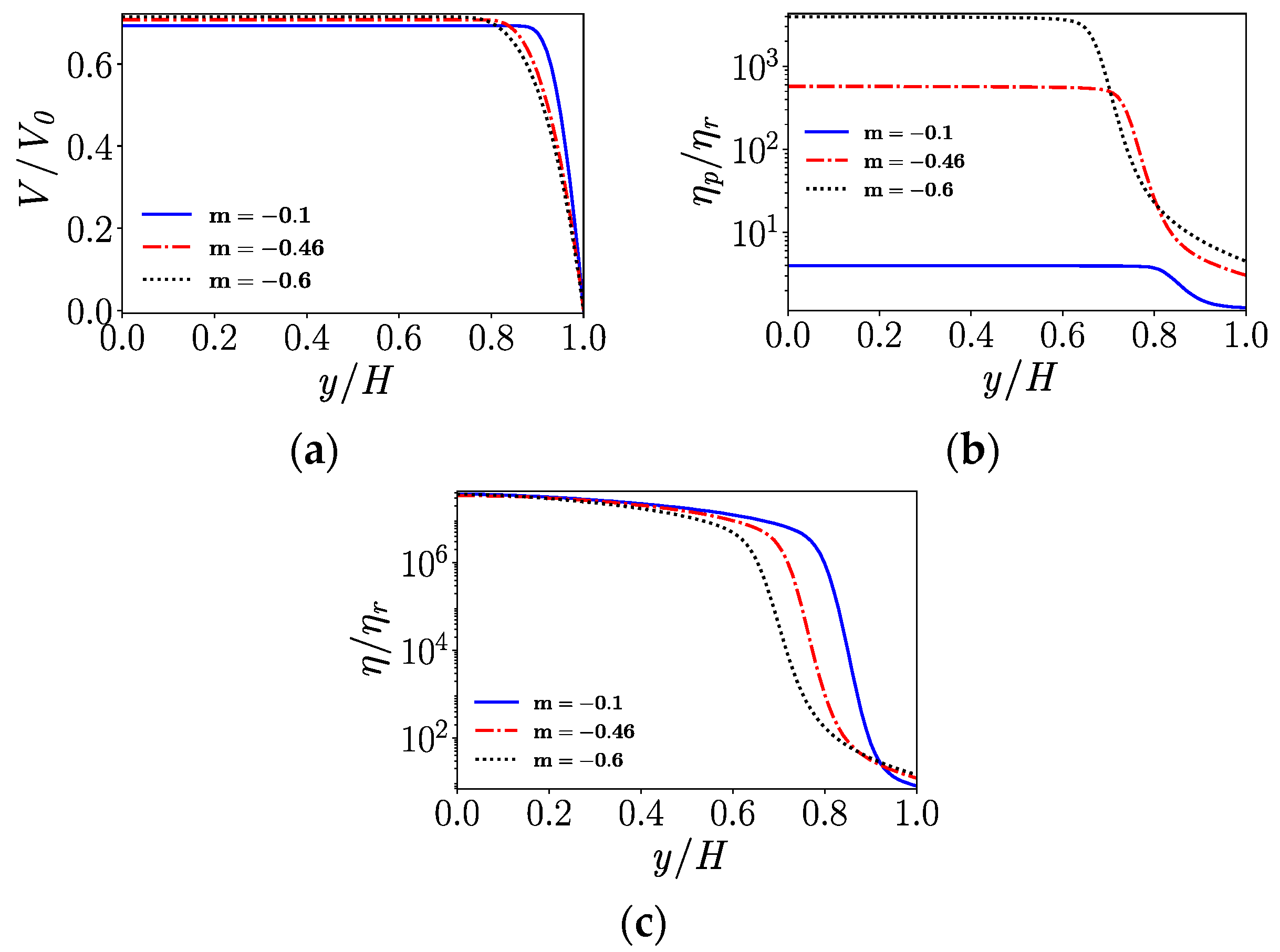
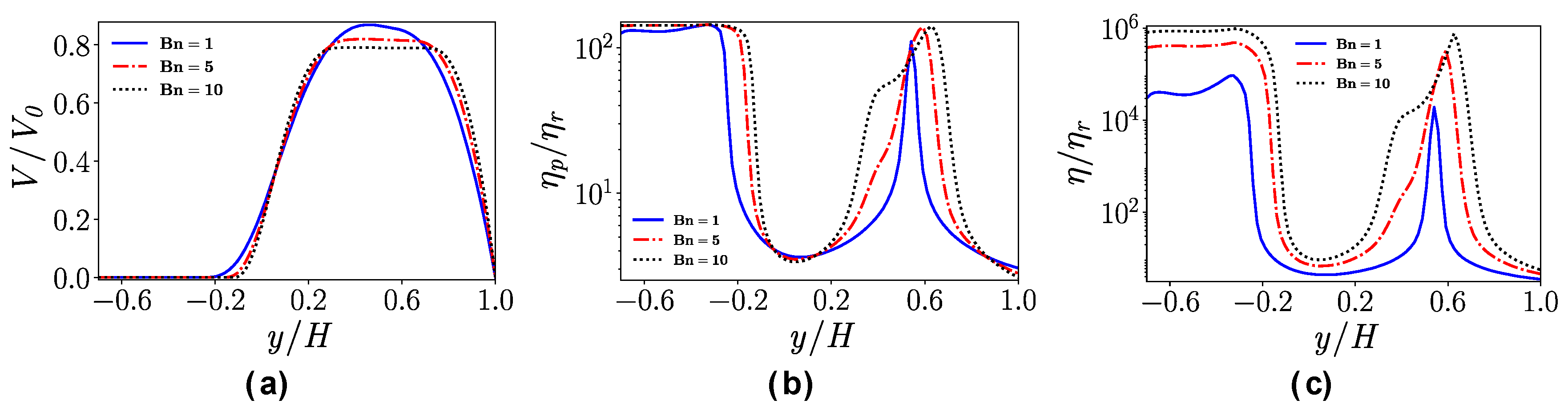
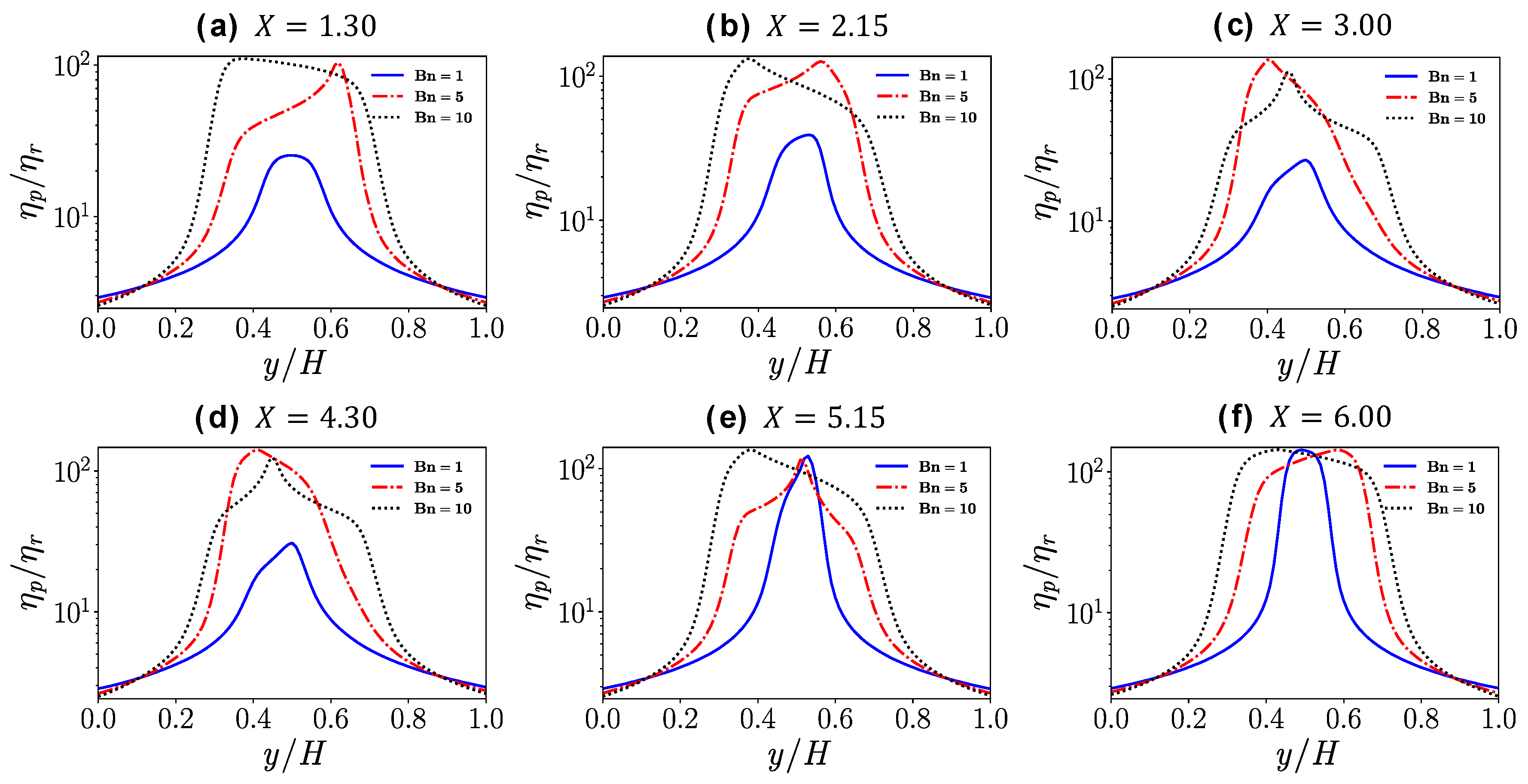
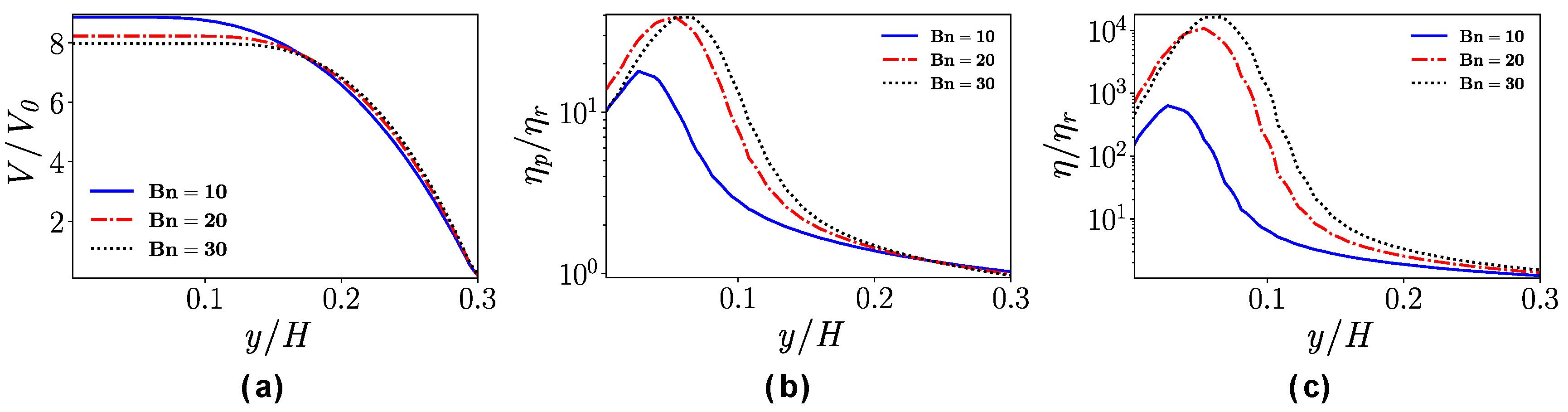
4.2. Flow in a Straight Channel
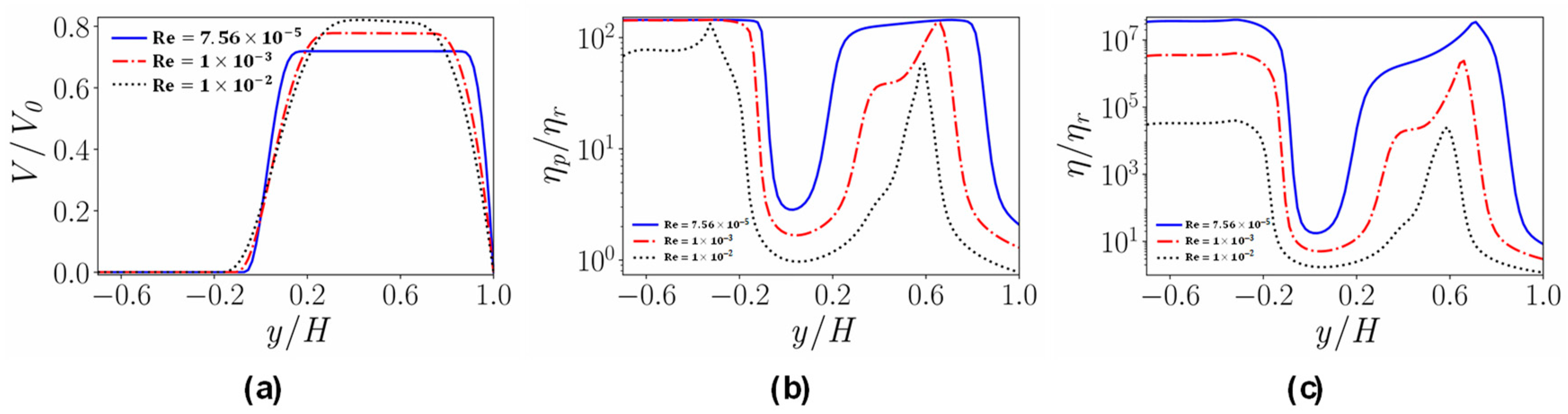
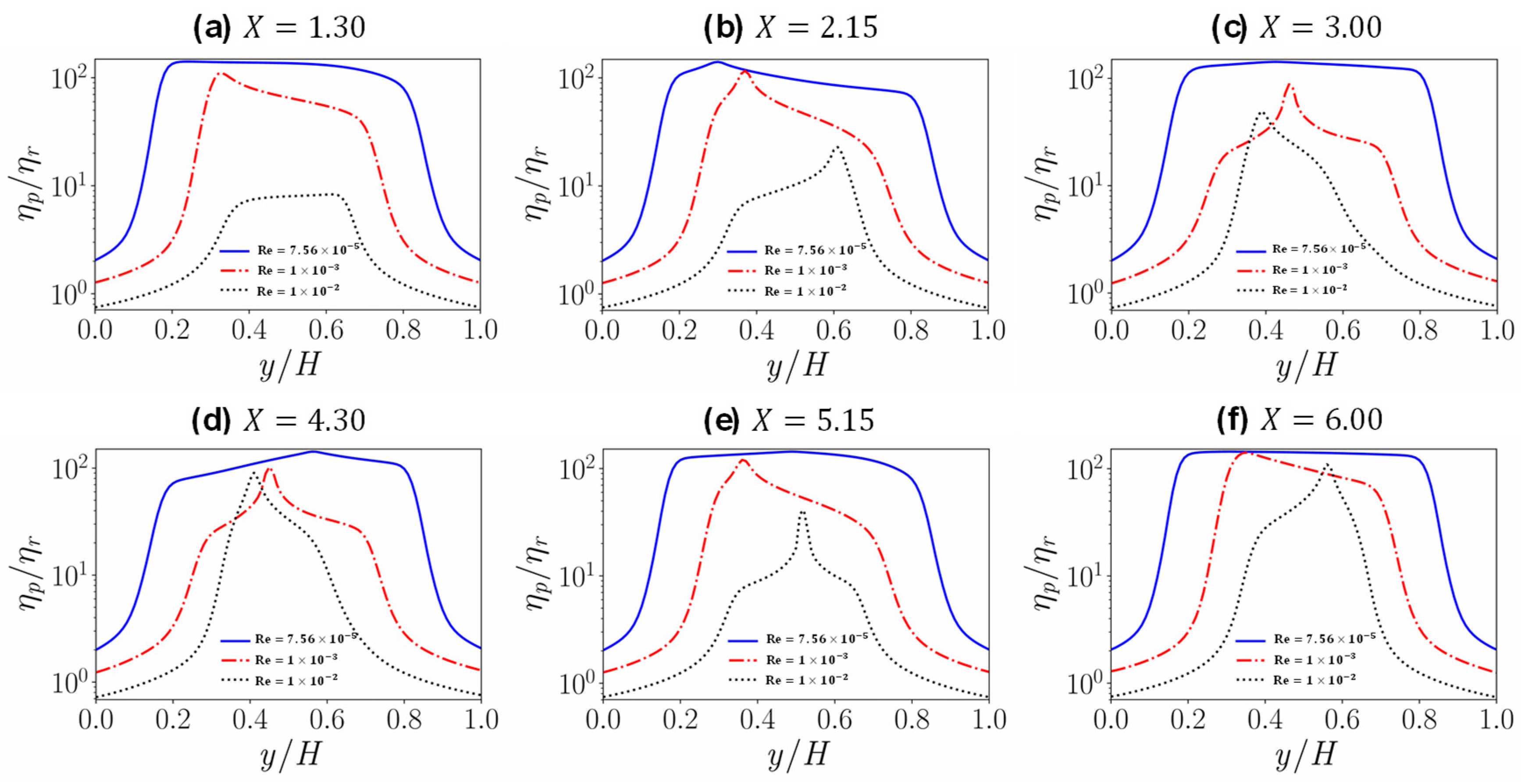
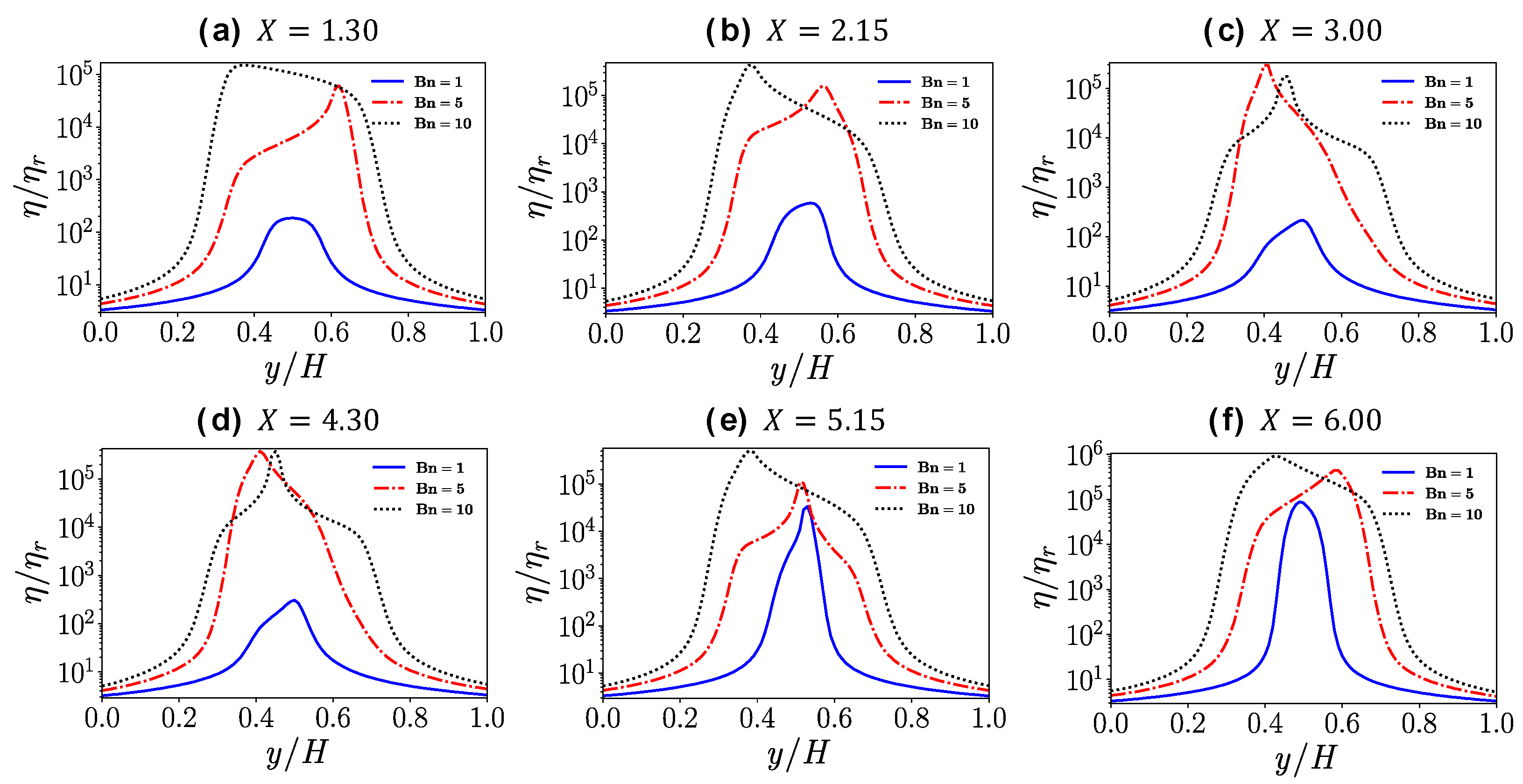
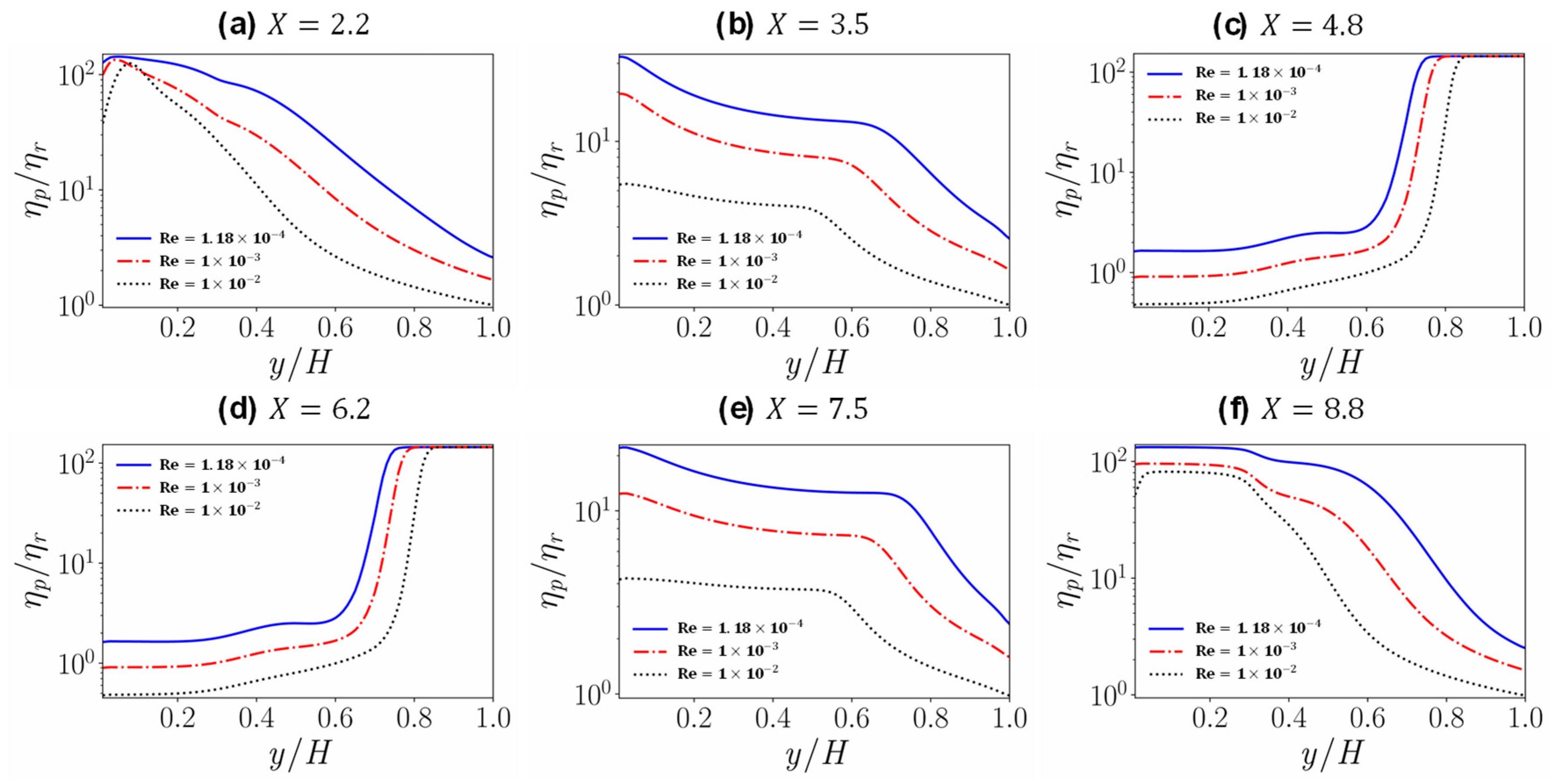
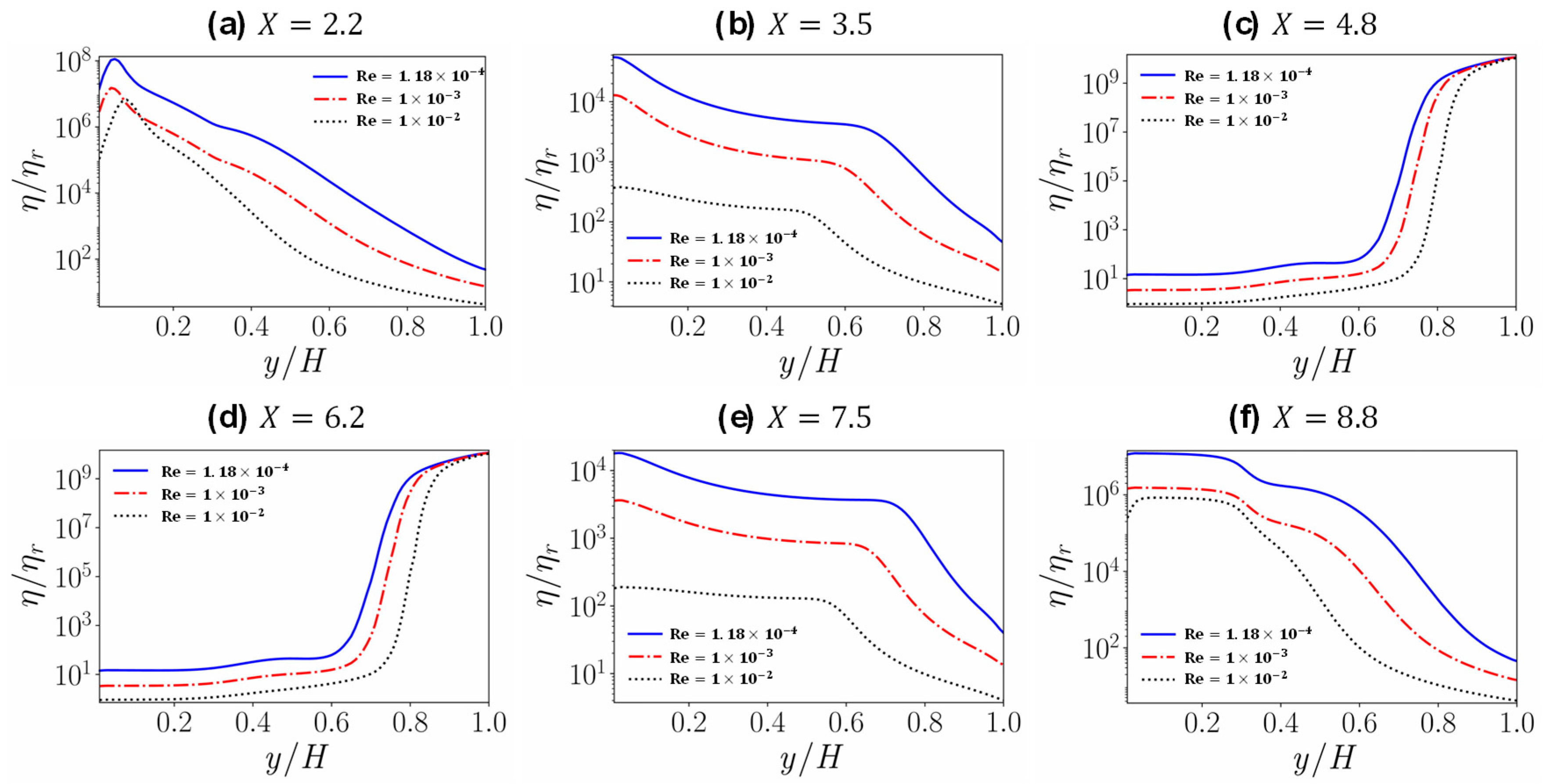
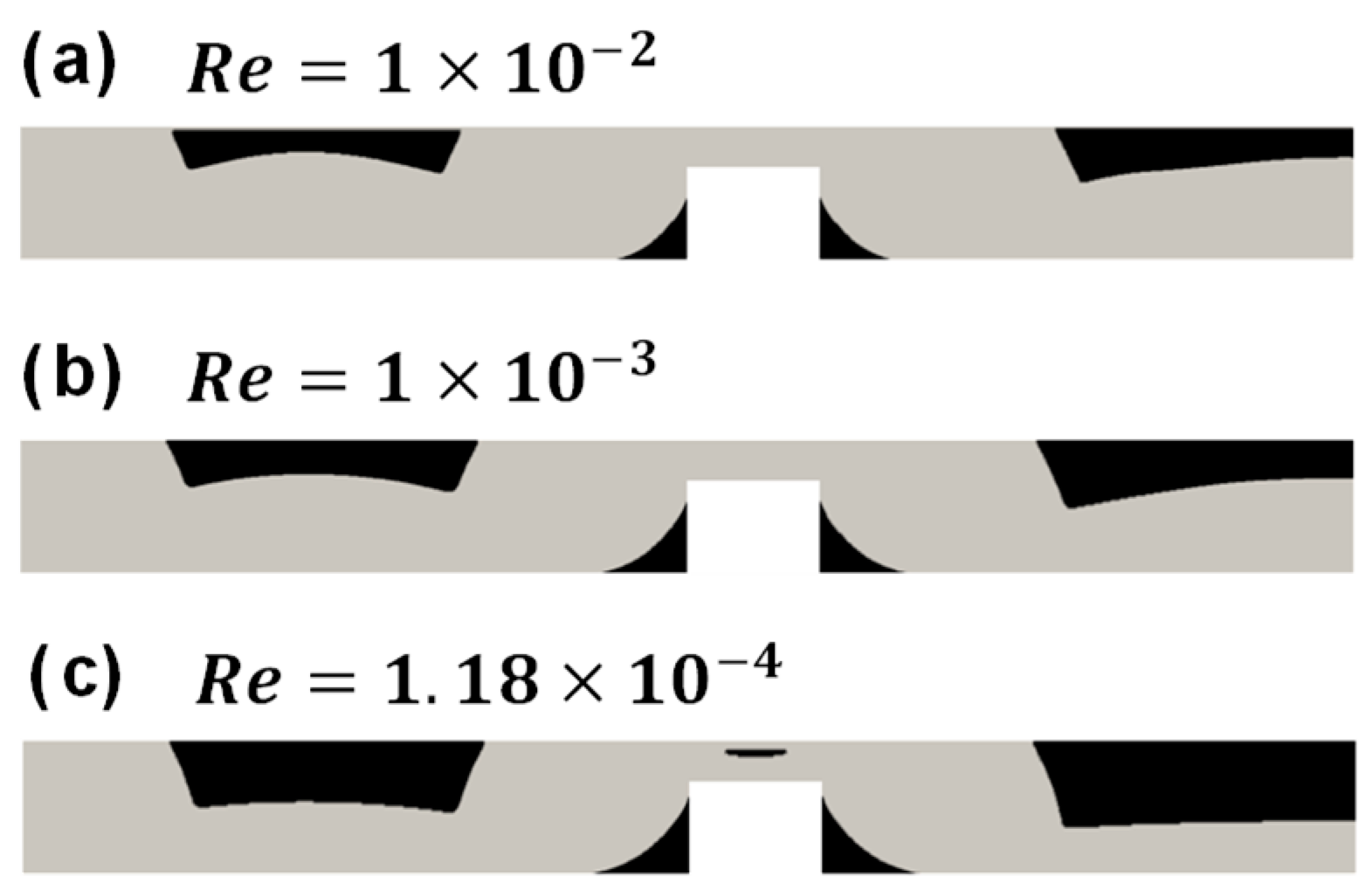
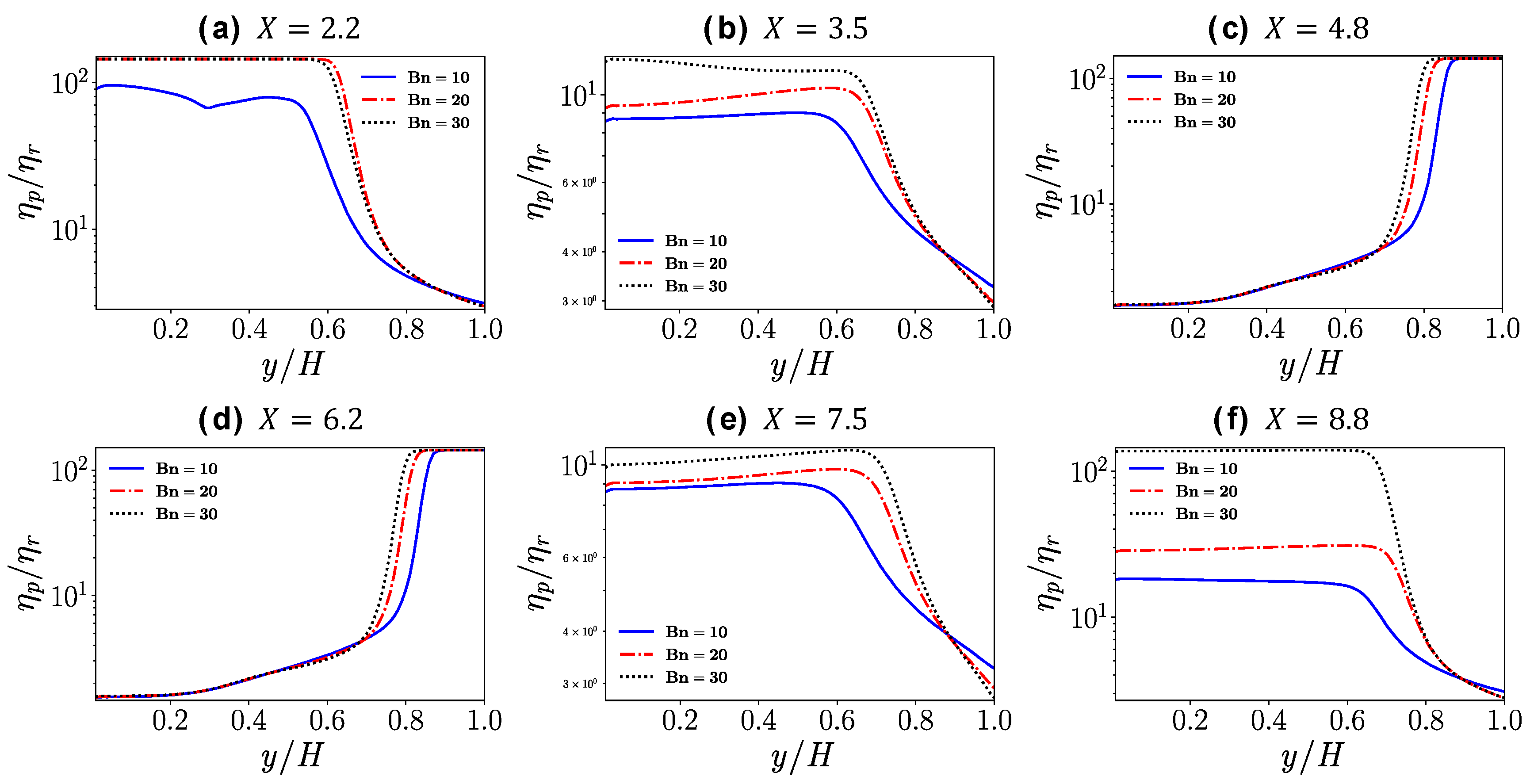
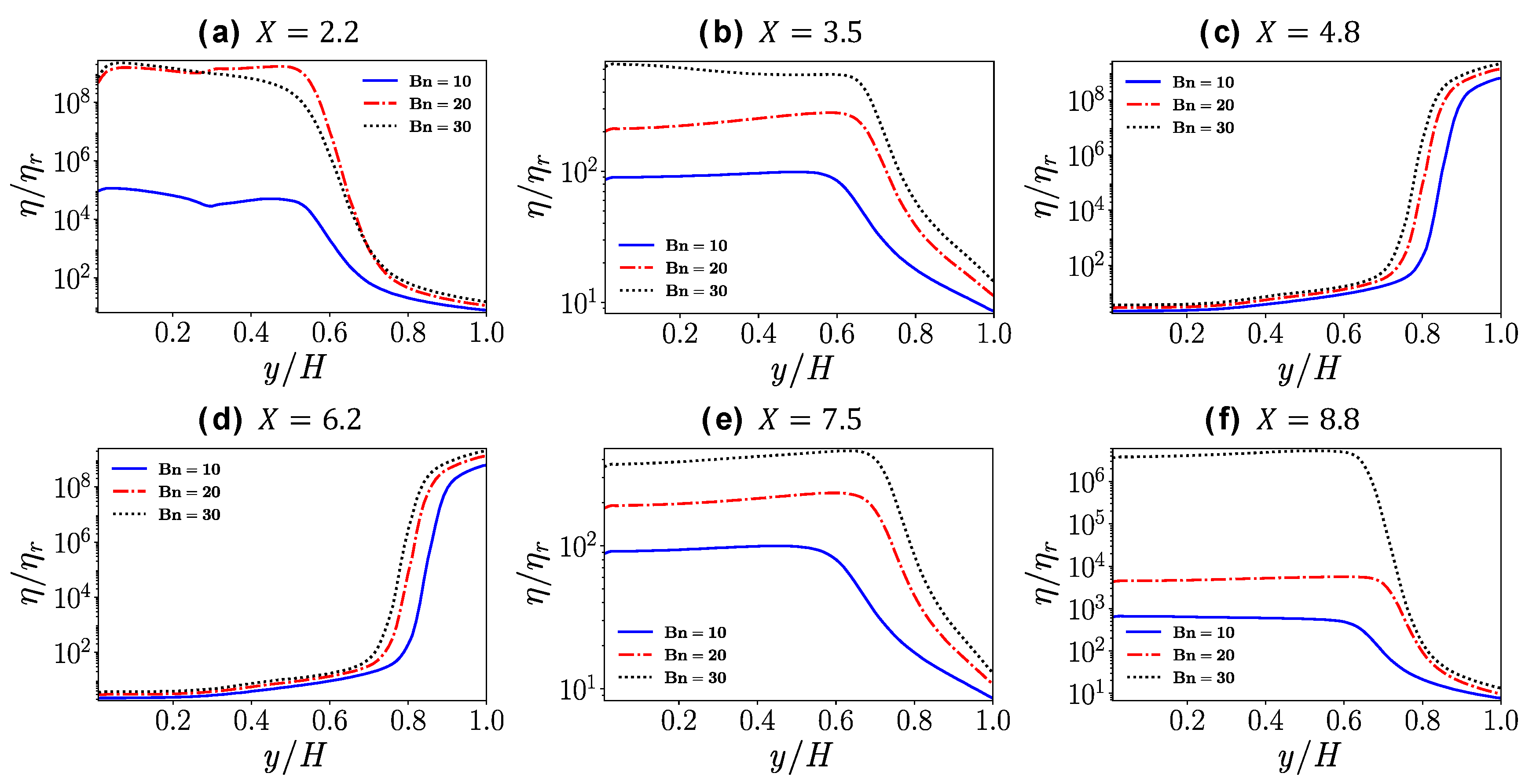
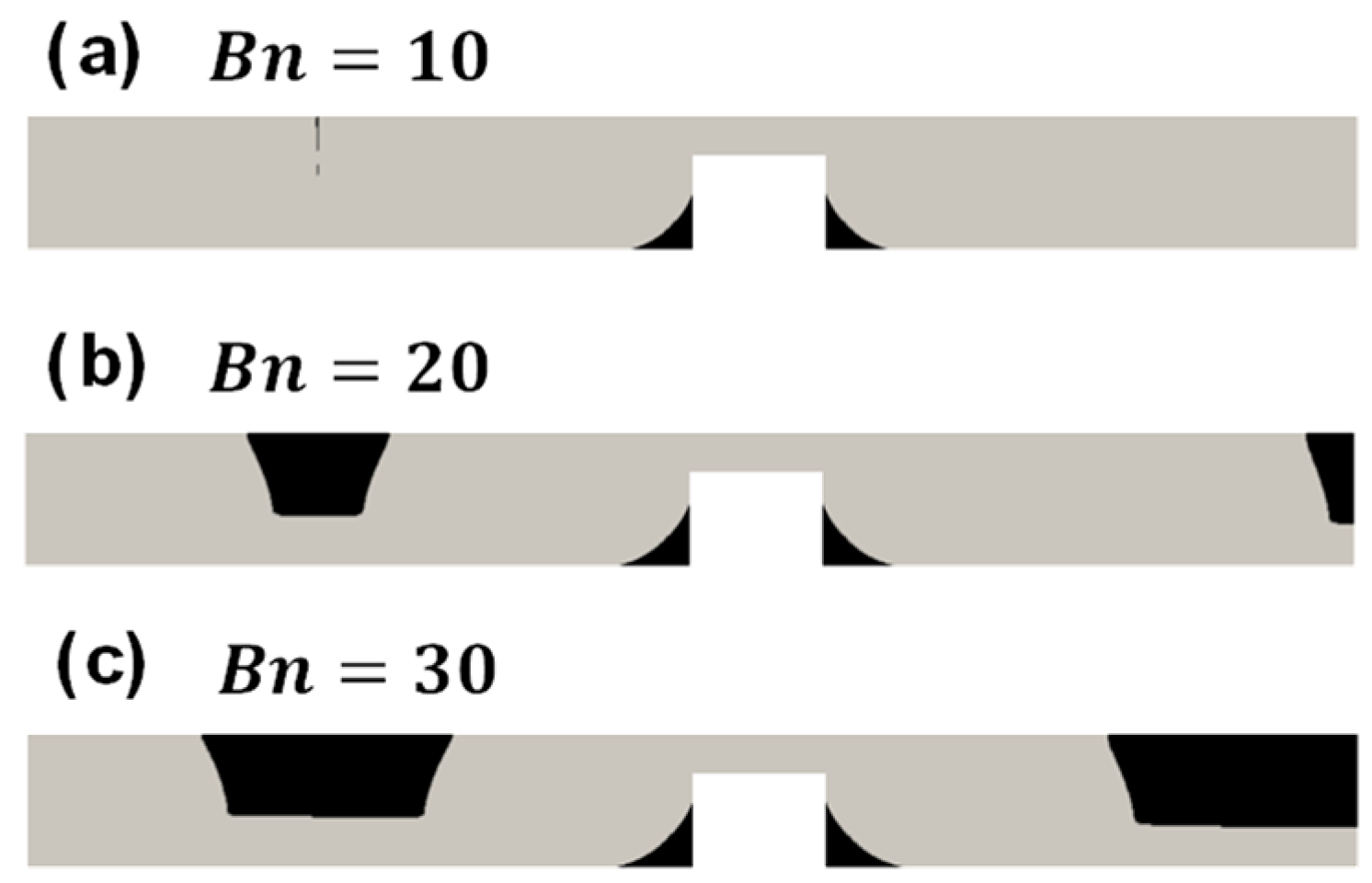
4.3. Flow in a Channel with a Crevice
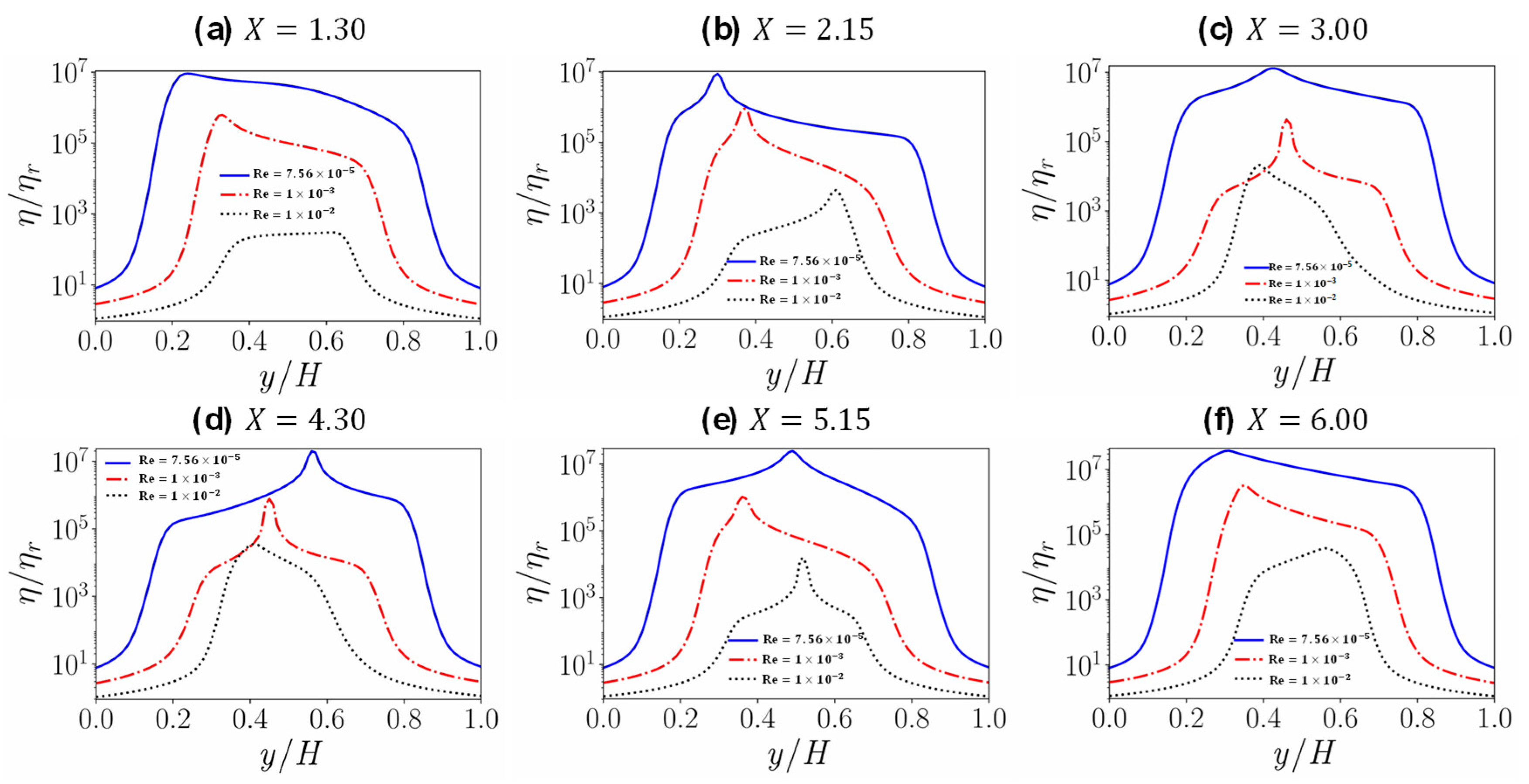
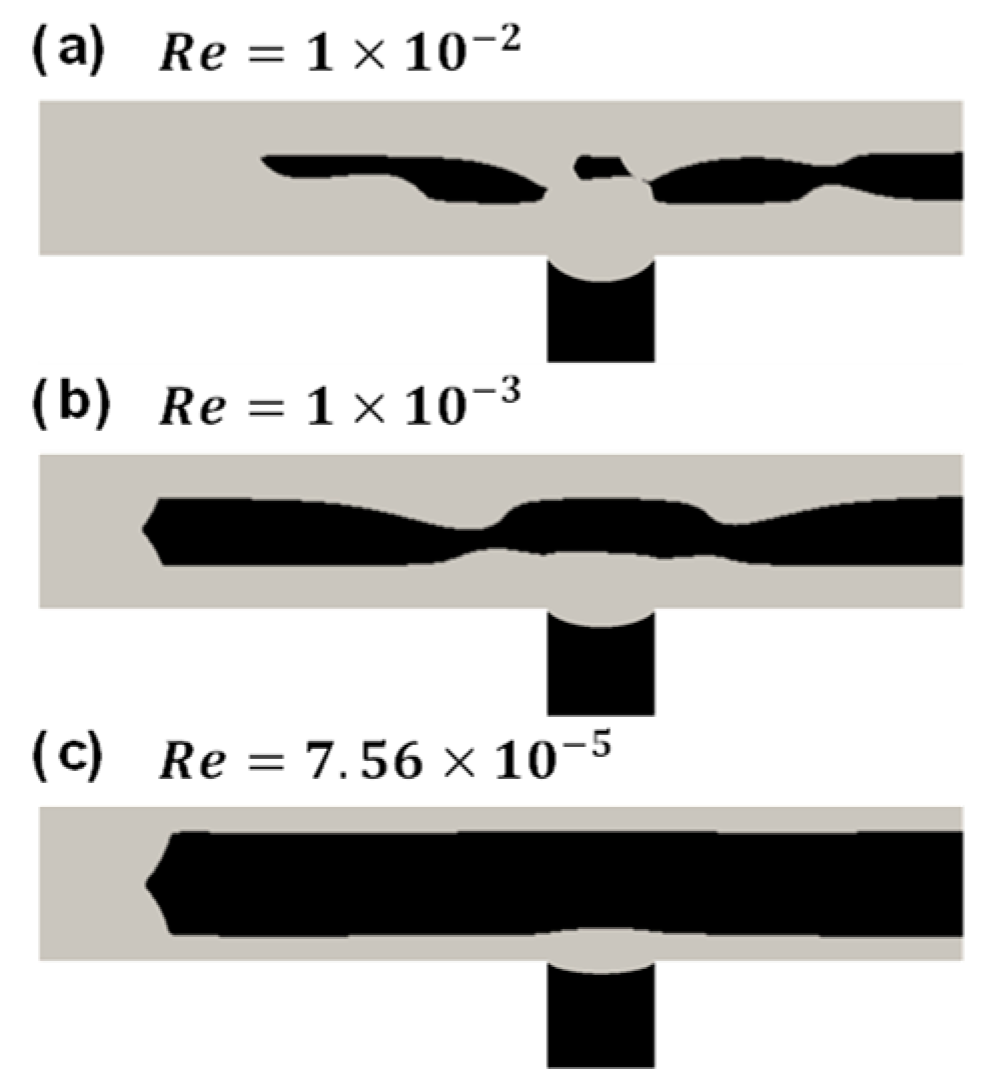
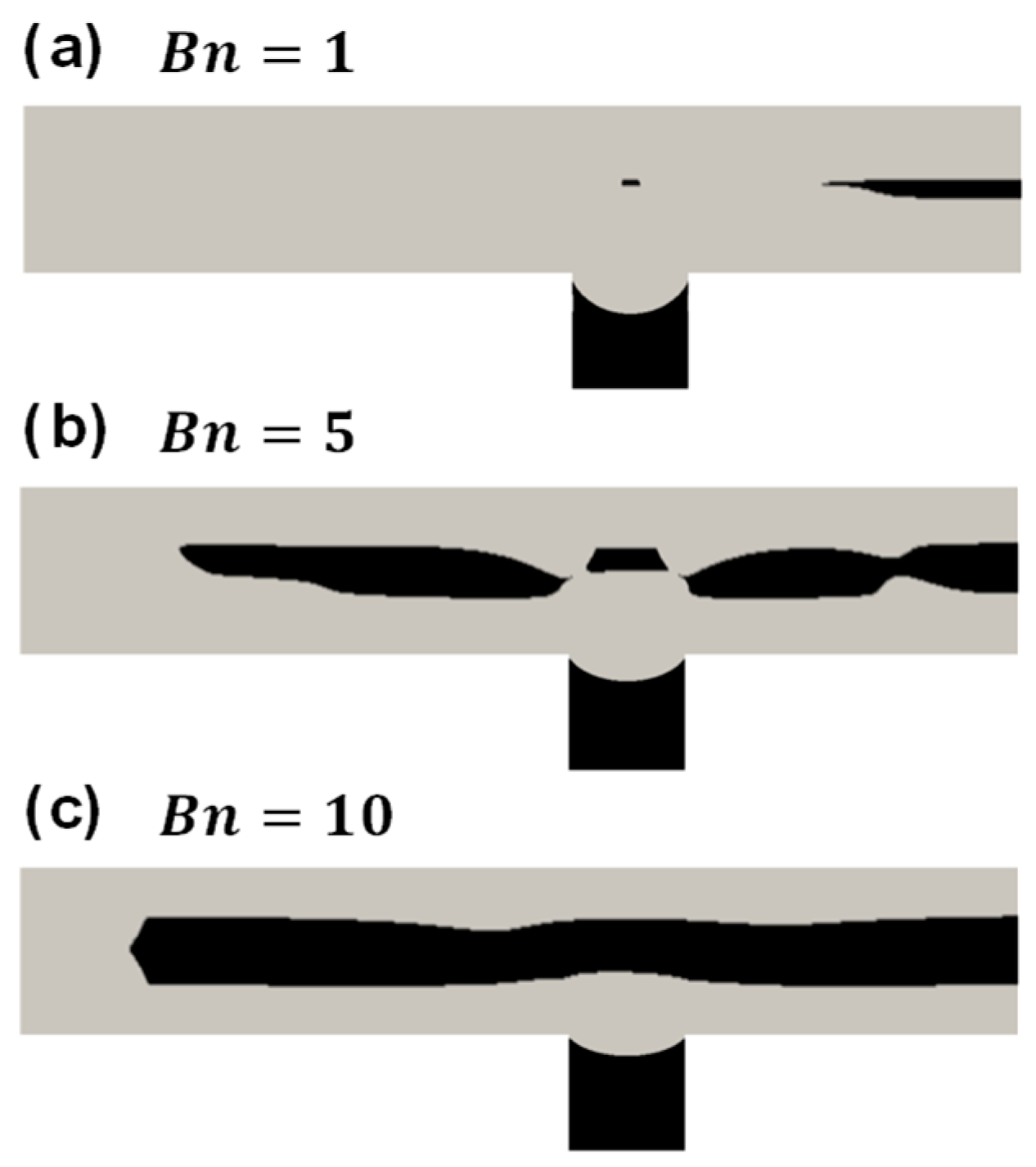
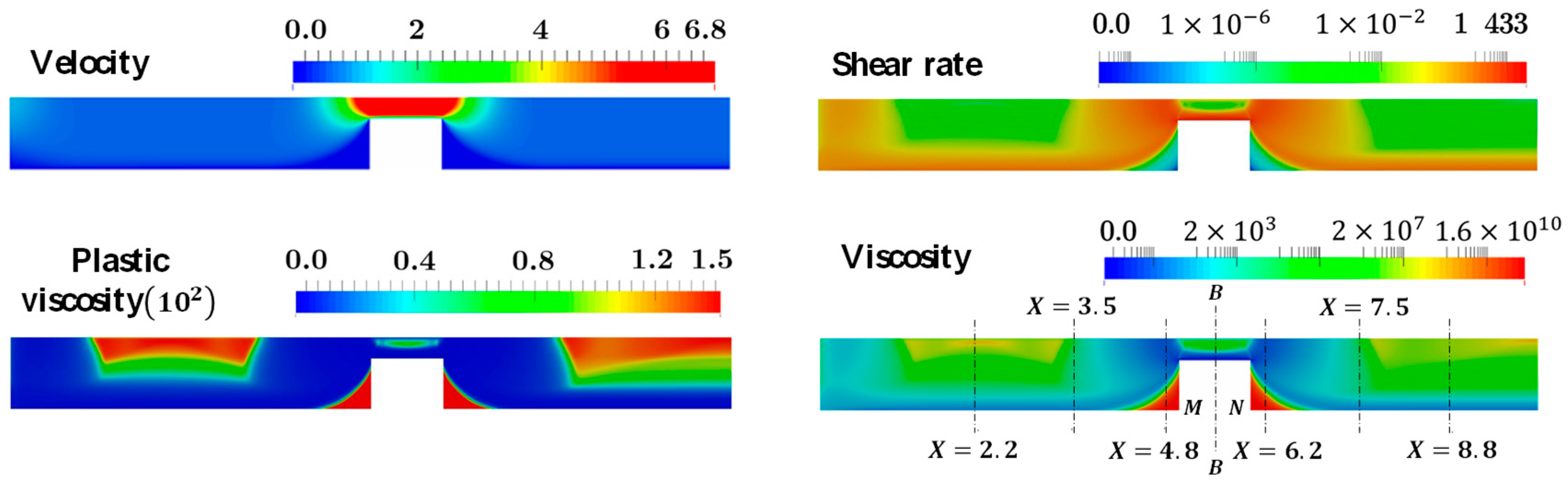
4.4. Flow in a Pipe with a Contraction
5. Conclusions
- Three representative regularization methods are used to look at the convergence properties on the determination of the yield surface; these methods are (1) the Simple model; (2) the Papanastasiou model and (3) the Bercovier and Engelman model. The yield surface could be described reasonably with a proper choice of the regularization parameter, , depending on the regularization method and the flow conditions. However, the maximum value of required to represent the yield surface is much lower for the Simple model than for the Papanastasiou and the Bercovier and Engelman models.
- In the straight channel, for flows with low Reynolds number and high Bingham number, a plug region near the center line where the stress is below the yield stress will form. For shear-thinning fluids, the viscosity parameter n has a similar influence on the velocity profiles as the Bingham number.
- In the case of the channel with a crevice, even though some vorticial structures seem to propagate inside the crevice due to the free shear layer near the interface of the main channel and the crevice, the fluid in the deeper portion of the crevice still has high apparent viscosity because of the existence of the yield stress, forming an unyielded region. Furthermore, near the crevice the flow near the interface of the main channel and the crevice is disturbed a little; this results in a reduction of the plastic viscosity and the apparent viscosity.
- For the pipe with a contraction, near the neck, the unyielded region reduces significantly due to the enhanced flow disturbance; while the shear rate is nearly zero at the bottom corner of the contraction segment, resulting in a very small yielded region.
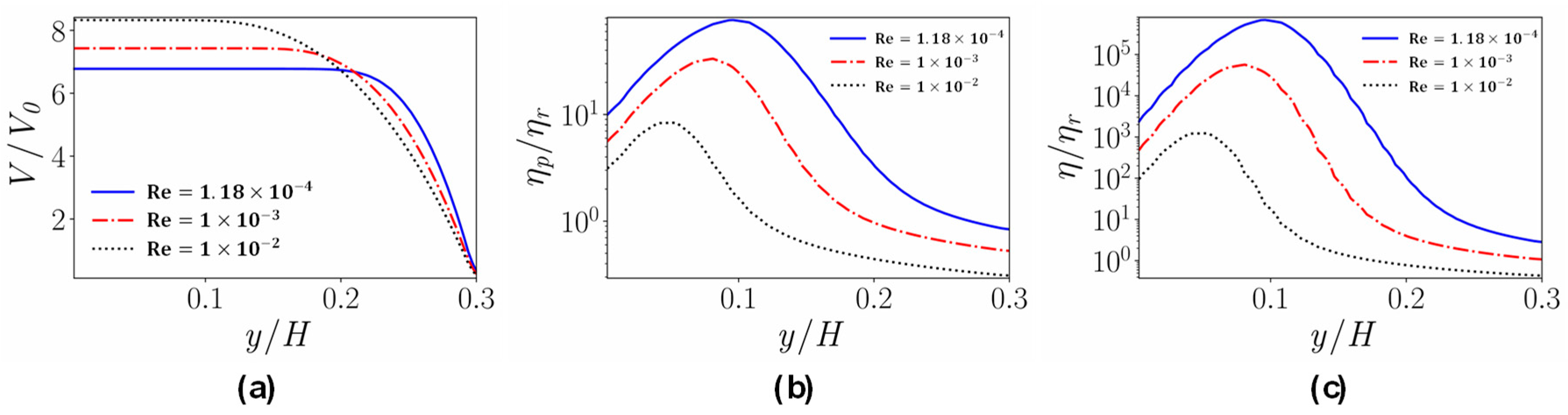
- For the Bingham numbers considered in this work, further increasing the Reynolds number leads to the disappearance of the yield region. The yield phenomenon can still be observed if both the Reynolds number and the Bingham number are increased; this is an important issue and a problem more demanding in computational time; we plan to study this in the near future.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| b | body force vector (N) |
| ratio of the yield stress to the viscous stress | |
| Bingham number | |
| Related to the symmetric part of velocity gradient () | |
| divergence operator | |
| gradient operator | |
| H | reference length |
| material parameter | |
| material parameter | |
| pressure (Pa) | |
| Generalized Reynolds number | |
| generalized Reynolds number | |
| time | |
| stress tensor (Pa) | |
| yield stress (Pa) | |
| viscous stress (Pa) | |
| velocity vector (m/s) | |
| dimensionless velocity vector | |
| dimensionless Cartesian coordinates | |
| position vector (m) | |
| dimensionless position vector | |
| Greek symbols | |
| density of fluid (kg/m3) | |
| dynamic viscosity (Pa∙s) | |
| plastic viscosity (Pa∙s) | |
| regularization parameter | |
| shear rate () | |
| dimensionless time | |
| yield stress (Pa) | |
References
- Ferry, J.D.; Ferry, J.D. Viscoelastic Properties of Polymers; John Wiley & Sons: Hoboken, NJ, USA, 1980. [Google Scholar]
- Natan, B.; Rahimi, S. The status of gel propellants in year 2000. Int. J. Energ. Mater. Chem. Propuls. 2009, 5, 172–194. [Google Scholar] [CrossRef]
- Bonn, D.; Denn, M.M. Yield stress fluids slowly yield to analysis. Science 2009, 324, 1401–1402. [Google Scholar] [CrossRef] [PubMed]
- Putz, A.M.V.; Burghelea, T.I. The solid–fluid transition in a yield stress shear thinning physical gel. Rheol. Acta 2009, 48, 673–689. [Google Scholar] [CrossRef]
- Barnes, H.A. Thixotropy—A review. J. Nonnewton. Fluid Mech. 1999, 81, 133–178. [Google Scholar] [CrossRef]
- Stickel, J.J.; Powell, R.L. Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech. 2005, 37, 129–149. [Google Scholar] [CrossRef]
- Barnes, H.A.; Walters, K. The yield stress myth? Rheol. Acta 1985, 24, 323–326. [Google Scholar] [CrossRef]
- Coussot, P.; Nguyen, Q.D.; Huynh, H.T.; Bonn, D. Avalanche behavior in yield stress fluids. Phys. Rev. Lett. 2002, 88, 175501. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; De Kee, D. Slotted-plate device to measure the yield stress of suspensions: Finite element analysis. Ind. Eng. Chem. Res. 2002, 41, 6375–6382. [Google Scholar] [CrossRef]
- Qian, Y.; Kawashima, S. Distinguishing dynamic and static yield stress of fresh cement mortars through thixotropy. Cem. Concr. Compos. 2018, 86, 288–296. [Google Scholar] [CrossRef]
- Malkin, A.; Kulichikhin, V.; Ilyin, S. A modern look on yield stress fluids. Rheol. Acta 2017, 56, 177–188. [Google Scholar] [CrossRef]
- Coussot, P. Yield stress fluid flows: A review of experimental data. J. Nonnewton. Fluid Mech. 2014, 211, 31–49. [Google Scholar] [CrossRef]
- Gomes, A.F.C.; Marinho, J.L.G.; Santos, J.P.L. Numerical simulation of drilling fluid behavior in different depths of an oil well. Braz. J. Pet. Gas 2019, 13, 309–322. [Google Scholar] [CrossRef]
- Saeid, N.H.; Busahmin, B.S. Numerical investigations of drilling mud flow characteristics in vertical well. An Int. J. (ESTIJ) 2017, 6, 2250–3498. [Google Scholar]
- Subramanian, R.; Azar, J.J. Experimental study on friction pressure drop for nonnewtonian drilling fluids in pipe and annular flow. Soc. Pet. Eng. Int. Oil Gas Conf. Exhib. China 2000 IOGCEC 2000 2000. [Google Scholar] [CrossRef]
- Ovarlez, G.; Mahaut, F.; Deboeuf, S.; Lenoir, N.; Hormozi, S.; Chateau, X. Flows of suspensions of particles in yield stress fluids. J. Rheol. 2015, 59, 1449–1486. [Google Scholar] [CrossRef]
- Saasen, A.; Ytrehus, J.D. Viscosity models for drilling fluids—Herschel-bulkley parameters and their use. Energies 2020, 13, 5271. [Google Scholar] [CrossRef]
- Soo, S.L. Multiphase Fluid Dynamics; Science Press: Beijing, China, 1990. [Google Scholar]
- Rajagopal, K.R.; Tao, L. Mechanics of Mixtures; World Scientific: Singapore, 1995; Volume 35. [Google Scholar]
- Johnson, G.; Massoudi, M.; Rajagopal, K.R. Flow of a fluid infused with solid particles through a pipe. Int. J. Eng. Sci. 1991, 29, 649–661. [Google Scholar] [CrossRef]
- Massoudi, M. A mixture theory formulation for hydraulic or pneumatic transport of solid particles. Int. J. Eng. Sci. 2010, 48, 1440–1461. [Google Scholar] [CrossRef]
- Phillips, R.J.; Armstrong, R.C.; Brown, R.A.; Graham, A.L.; Abbott, J.R. A constitutive equation for concentrated suspensions that accounts for shear-induced particle migration. Phys. Fluids A 1992, 4, 30–40. [Google Scholar] [CrossRef]
- Zhou, Z.; Wu, W.-T.; Massoudi, M. Fully developed flow of a drilling fluid between two rotating cylinders. Appl. Math. Comput. 2016, 281, 266–277. [Google Scholar] [CrossRef]
- Tao, C.; Kutchko, B.G.; Rosenbaum, E.; Wu, W.T.; Massoudi, M. Steady flow of a cement slurry. Energies 2019, 12, 2604. [Google Scholar] [CrossRef]
- Peker, S.M.; Helvaci, S.S. Solid-liquid Two Phase Flow; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Slattery, J.C. Advanced Transport Phenomena; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Li, Y.; Wu, W.-T.; Liu, X.; Massoudi, M. The effects of particle concentration and various fluxes on the flow of a fluid-solid suspension. Appl. Math. Comput. 2019, 358, 151–160. [Google Scholar] [CrossRef]
- Massoudi, M.; Vaidya, A. On some generalizations of the second grade fluid model. Nonlinear Anal. Real World Appl. 2008, 9, 1169–1183. [Google Scholar] [CrossRef]
- Roscoe, R. Suspensions, flow properties of disperse systems. In Flow Properties of Disperse Systems; Hermans, J.J., Ed.; North Holland Publishing Company: Amsterdam, The Netherlands, 1953. [Google Scholar]
- Tabuteau, H.; Coussot, P.; de Bruyn, J.R. Drag force on a sphere in steady motion through a yield-stress fluid. J. Rheol. 2007, 51, 125–137. [Google Scholar] [CrossRef]
- Coussot, P.; Tocquer, L.; Lanos, C.; Ovarlez, G. Macroscopic vs. local rheology of yield stress fluids. J. NonNewton Fluid Mech. 2009, 158, 85–90. [Google Scholar] [CrossRef]
- Cao, Q.-L.; Massoudi, M.; Liao, W.-H.; Feng, F.; Wu, W.-T. Flow characteristics of water-HPC gel in converging tubes and tapered injectors. Energies 2019, 12, 1643. [Google Scholar] [CrossRef]
- Mas, R.; Magnin, A. Experimental validation of steady shear and dynamic viscosity relation for yield stress fluids. Rheol. Acta 1997, 36, 49–55. [Google Scholar] [CrossRef]
- Denn, M.M.; Bonn, D. Issues in the flow of yield-stress liquids. Rheol. Acta 2011, 50, 307–315. [Google Scholar] [CrossRef]
- White, J.L. A plastic-viscoelastic constitutive equation to represent the rheological behavior of concentrated suspensions of small particles in polymer melts. J. NonNewton Fluid Mech. 1979, 5, 177–190. [Google Scholar] [CrossRef]
- Prager, W. Introduction to Mechanics of Continua; Courier Corporation: North Chelmsford, MA, USA, 2004. [Google Scholar]
- Putz, A.; Frigaard, I.A.; Martinez, D.M. On the lubrication paradox and the use of regularisation methods for lubrication flows. J. NonNewton Fluid Mech. 2009, 163, 62–77. [Google Scholar] [CrossRef]
- Frigaard, I.A.; Nouar, C. On the usage of viscosity regularisation methods for visco-plastic fluid flow computation. J. NonNewton Fluid Mech. 2005, 127, 1–26. [Google Scholar] [CrossRef]
- Allouche, M.; Frigaard, I.A.; Sona, G. Static wall layers in the displacement of two visco-plastic fluids in a plane channel. J. Fluid Mech. 2000, 424, 243–277. [Google Scholar] [CrossRef]
- Bercovier, M.; Engelman, M. A finite-element method for incompressible non-Newtonian flows. J. Comput. Phys. 1980, 36, 313–326. [Google Scholar] [CrossRef]
- Papanastasiou, T.C. Flows of materials with yield. J. Rheol. 1987, 31, 385–404. [Google Scholar] [CrossRef]
- Von Kampen, J.; Madlener, K.; Ciezki, H.K. Characteristic flow and spray properties of gelled fuels with regard to the impinging jet injector type. In Proceedings of the 42nd AIAA Joint Propulsion Conference, Sacramento, California, USA, 9–12 July 2006; Volume 4, pp. 2639–2650. [Google Scholar]
- Abdali, S.S.; Mitsoulis, E.; Markatos, N.C. Entry and exit flows of Bingham fluids. J. Rheol. 1992, 36, 389–407. [Google Scholar] [CrossRef]
- Mitsoulis, E.; Tsamopoulos, J. Numerical simulations of complex yield-stress fluid flows. Rheol. Acta 2017, 56, 231–258. [Google Scholar] [CrossRef]
- Alexandrou, A.N.; McGilvreay, T.M.; Burgos, G. Steady herschel-bulkley fluid flow in three-dimensional expansions. J. NonNewton Fluid Mech. 2001, 100, 77–96. [Google Scholar] [CrossRef]
- Neofytou, P.; Drikakis, D. Non-Newtonian flow instability in a channel with a sudden expansion. J. NonNewton Fluid Mech. 2003, 111, 127–150. [Google Scholar] [CrossRef]



| Boundary Type | Boundary Conditions | |
|---|---|---|
| Pressure | Velocity | |
| Wall | Zero gradient | Fixed value (0) |
| Inlet | Zero gradient | Fixed value |
| Outlet | Fixed value (0) | Zero gradient |
| Label | Grid Number | Mean Plastic Viscosity at Exit (102) |
|---|---|---|
| Grid A | 25,000 | 2.12074 |
| Grid B | 43,956 | 2.04562 |
| Grid C | 69,104 | 2.00631 |
| Grid D | 100,000 | 1.99802 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.-G.; Feng, F.; Wu, W.-T.; Massoudi, M. Numerical Simulations of the Flow of a Dense Suspension Exhibiting Yield-Stress and Shear-Thinning Effects. Energies 2020, 13, 6635. https://doi.org/10.3390/en13246635
Li M-G, Feng F, Wu W-T, Massoudi M. Numerical Simulations of the Flow of a Dense Suspension Exhibiting Yield-Stress and Shear-Thinning Effects. Energies. 2020; 13(24):6635. https://doi.org/10.3390/en13246635
Chicago/Turabian StyleLi, Meng-Ge, Feng Feng, Wei-Tao Wu, and Mehrdad Massoudi. 2020. "Numerical Simulations of the Flow of a Dense Suspension Exhibiting Yield-Stress and Shear-Thinning Effects" Energies 13, no. 24: 6635. https://doi.org/10.3390/en13246635
APA StyleLi, M.-G., Feng, F., Wu, W.-T., & Massoudi, M. (2020). Numerical Simulations of the Flow of a Dense Suspension Exhibiting Yield-Stress and Shear-Thinning Effects. Energies, 13(24), 6635. https://doi.org/10.3390/en13246635






