Local Heat Transfer Analysis in a Single Microchannel with Boiling DI-Water and Correlations with Impedance Local Sensors
Abstract
1. Introduction
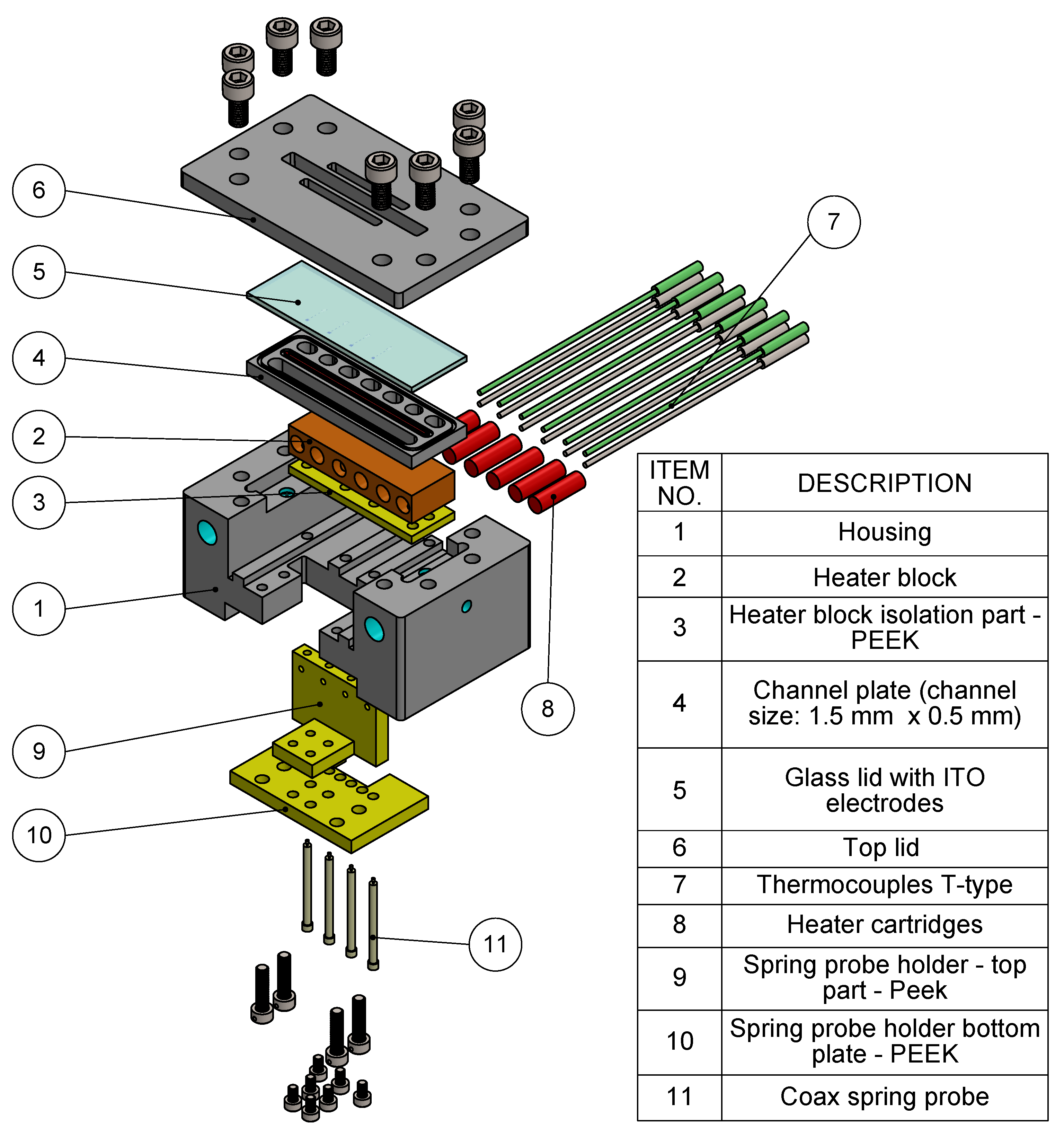
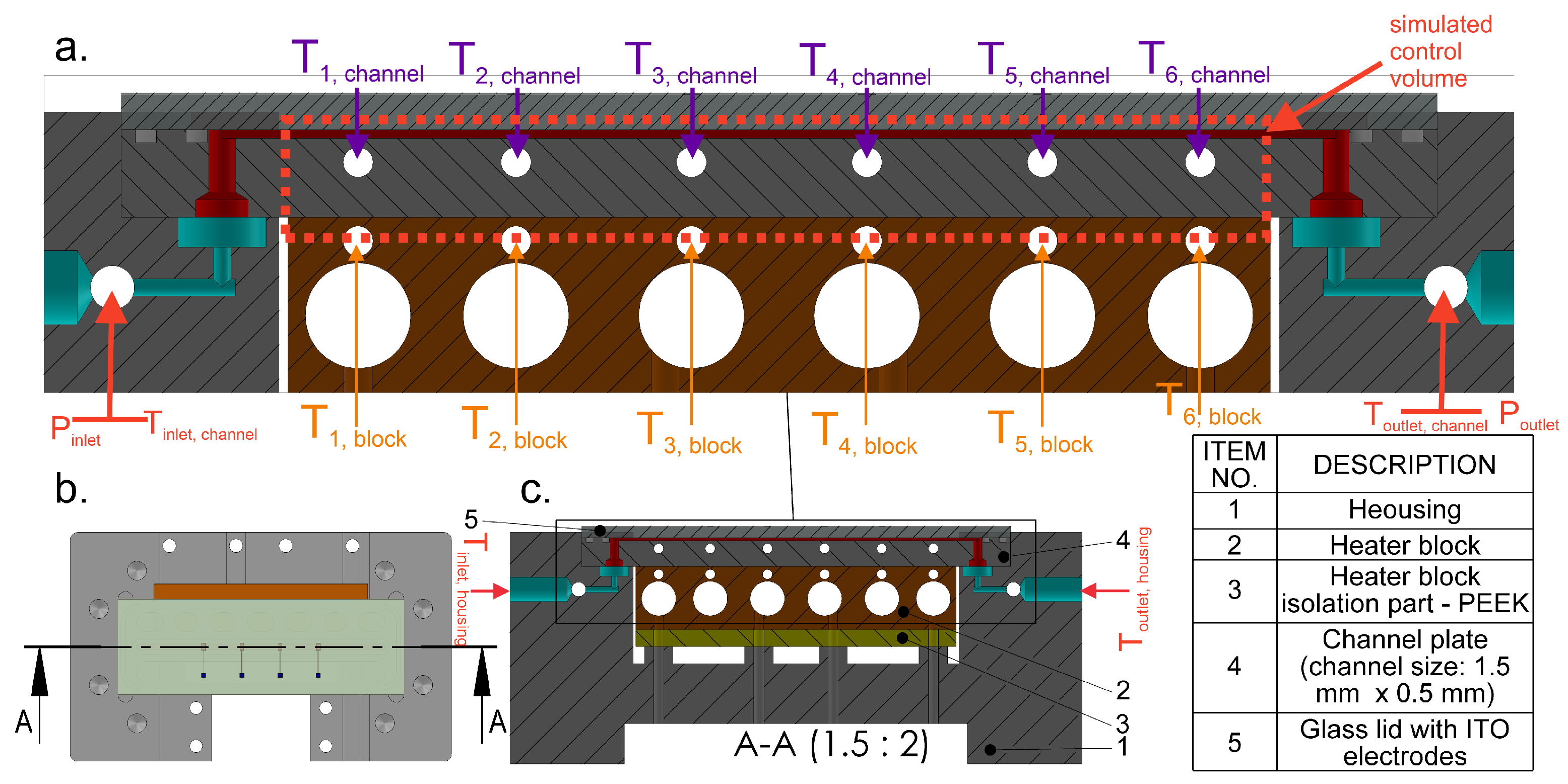
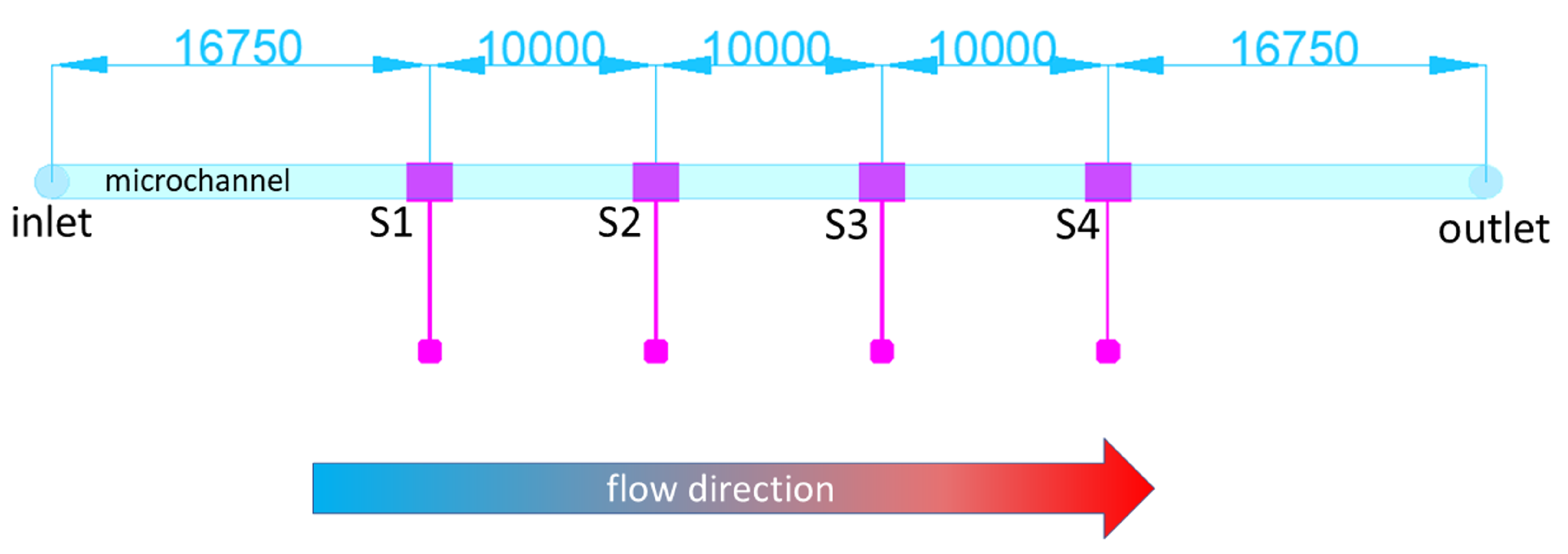
2. Experimental Setup
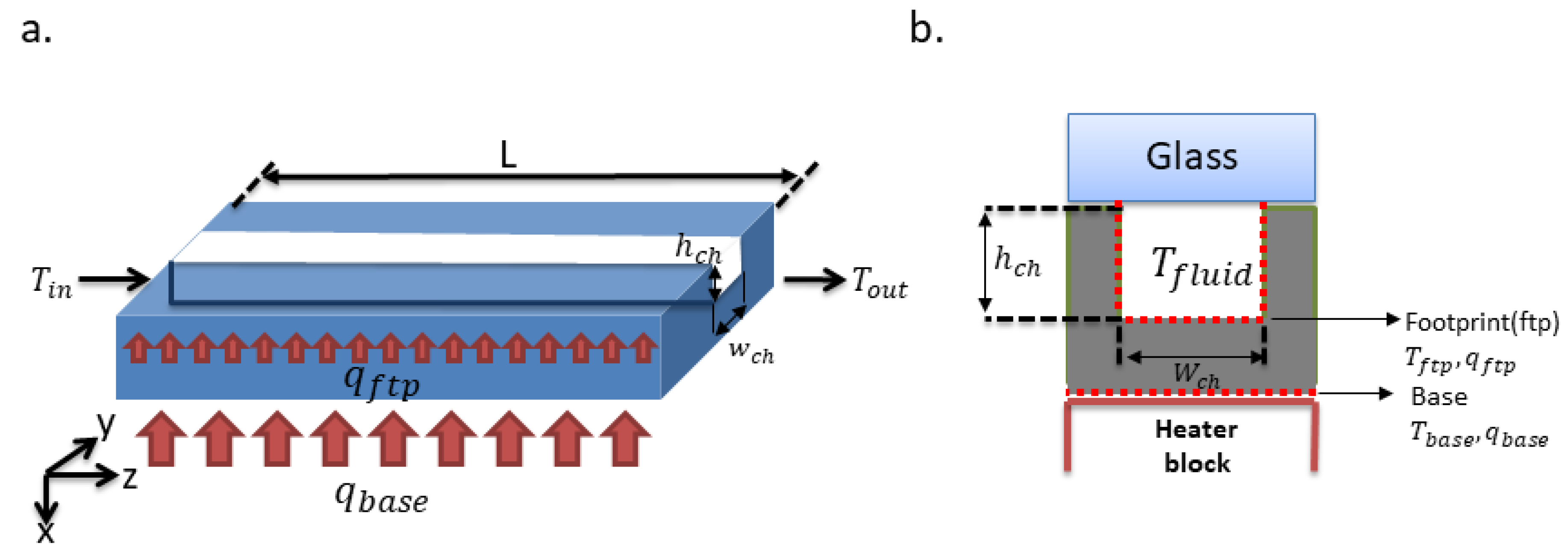
3. Data Reduction
4. Results and Discussions
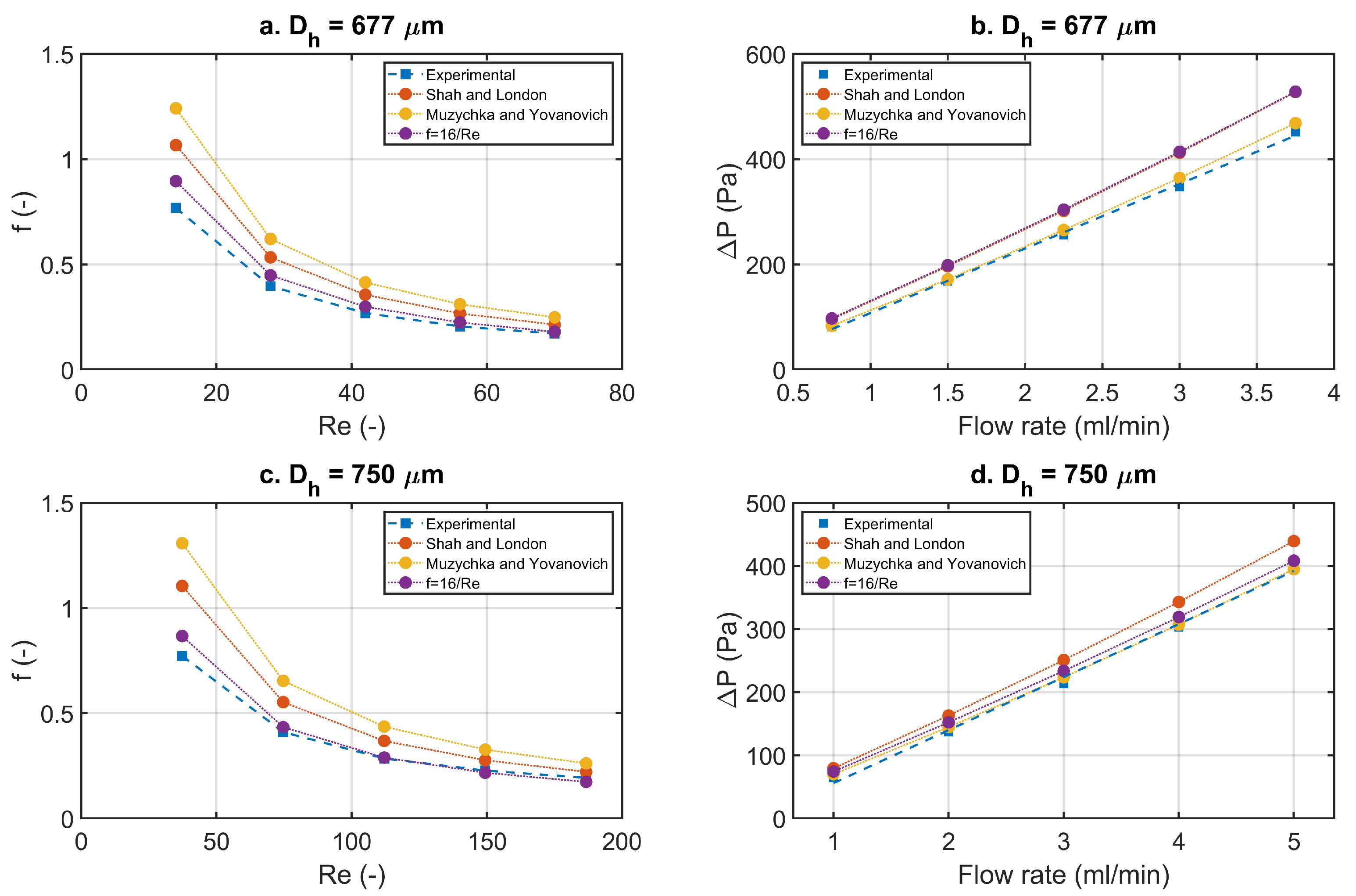
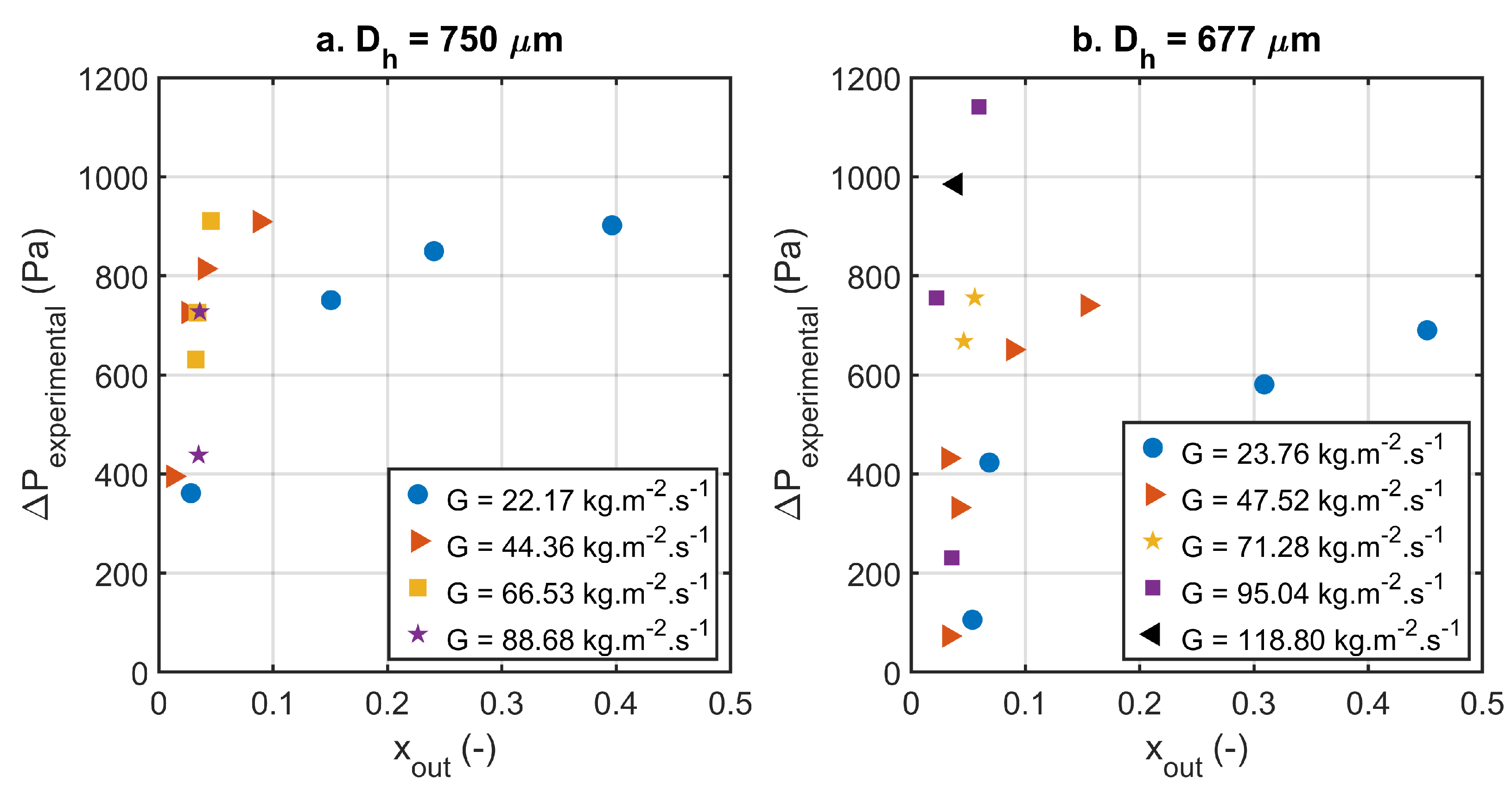
4.1. Single Phase Pressure Drop Validation
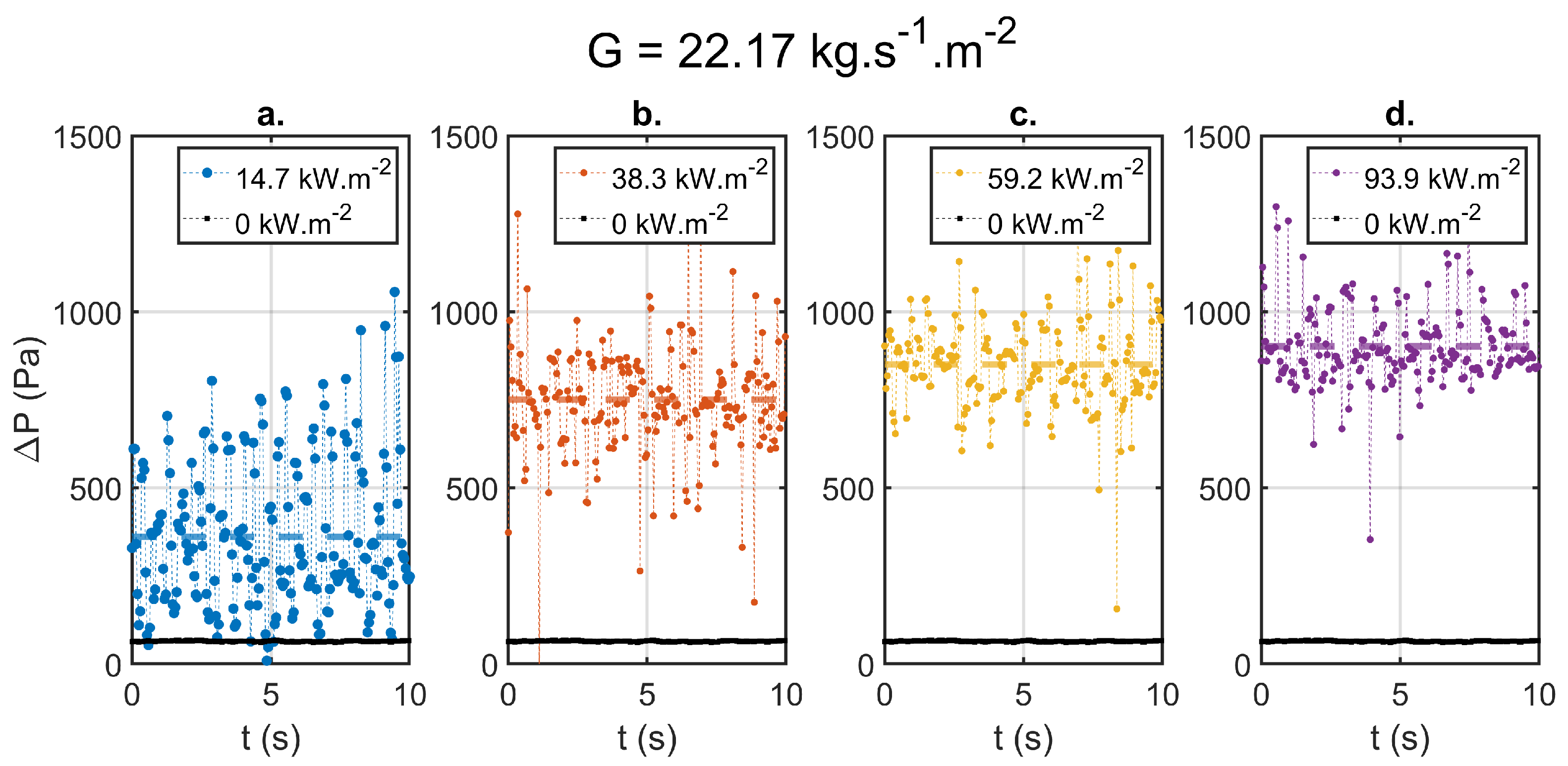
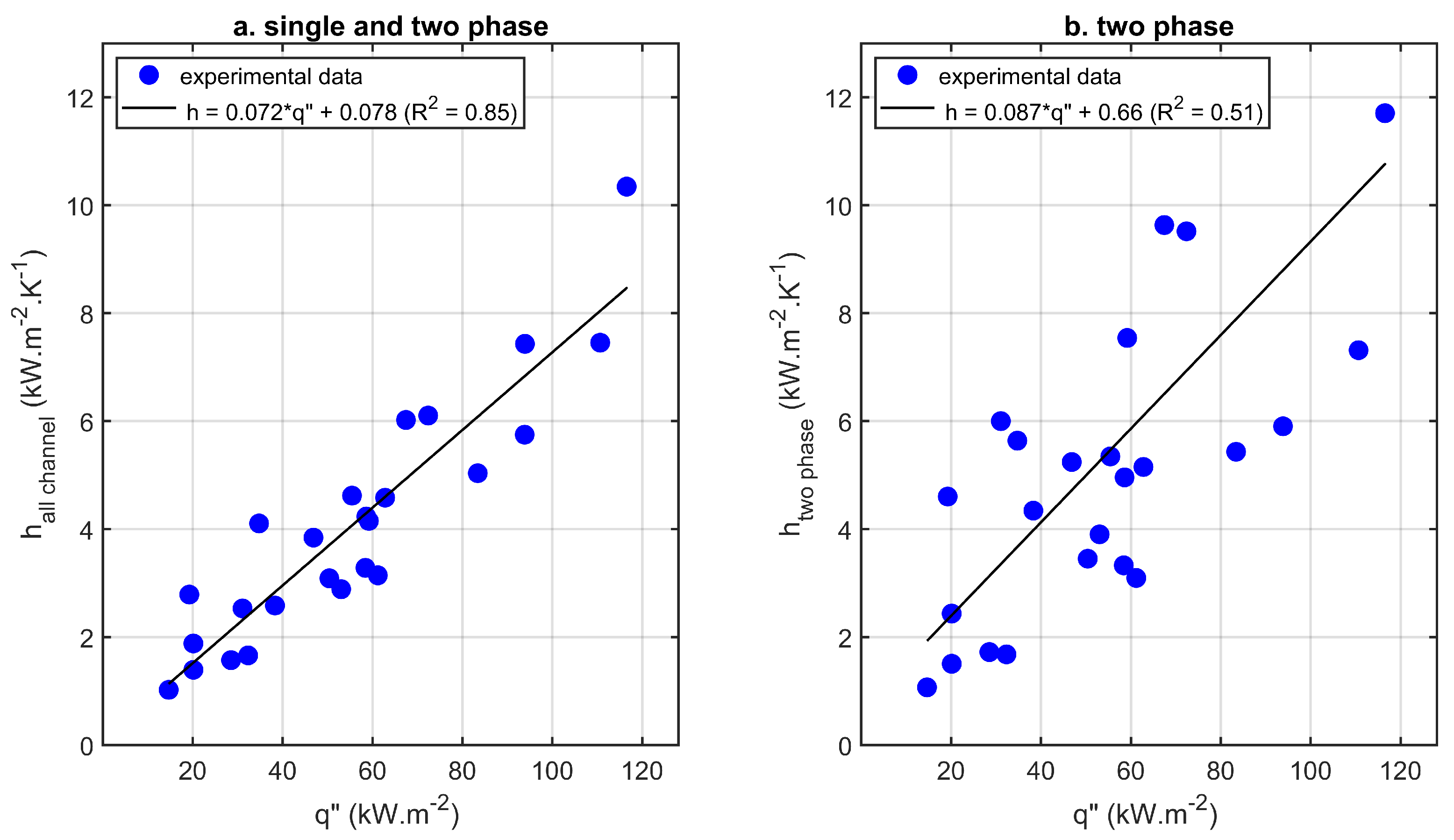
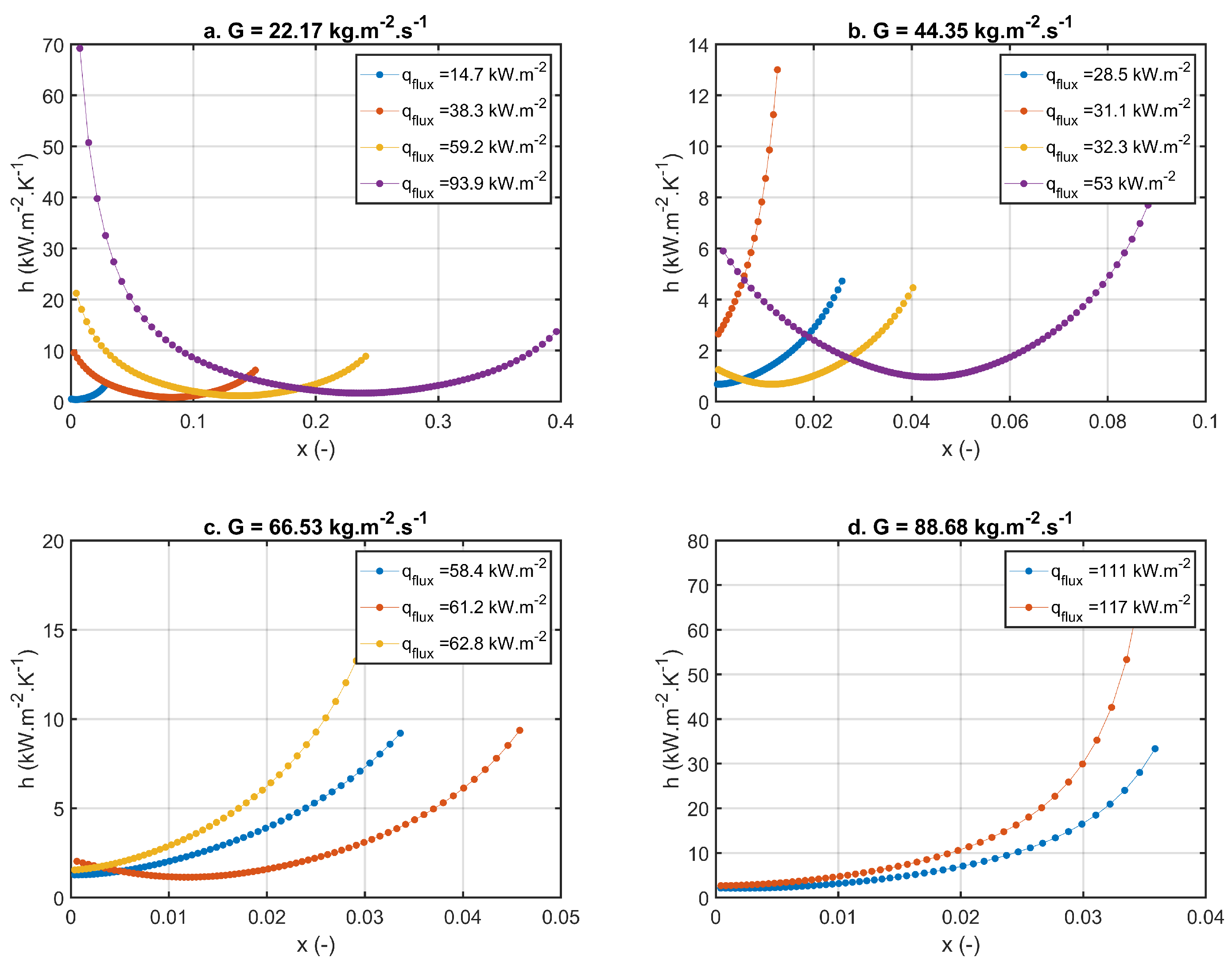
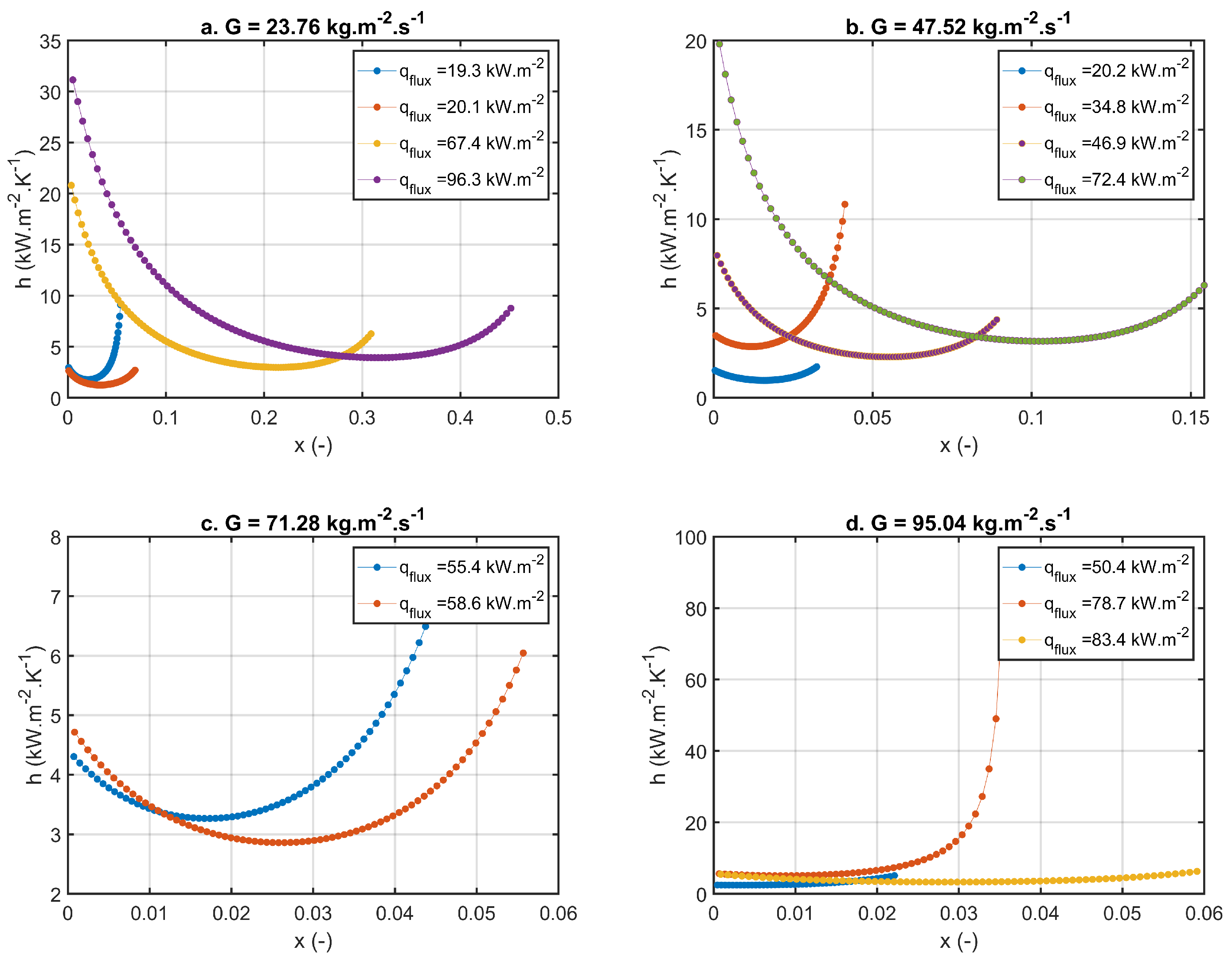
4.2. Two Phase Experimental Results
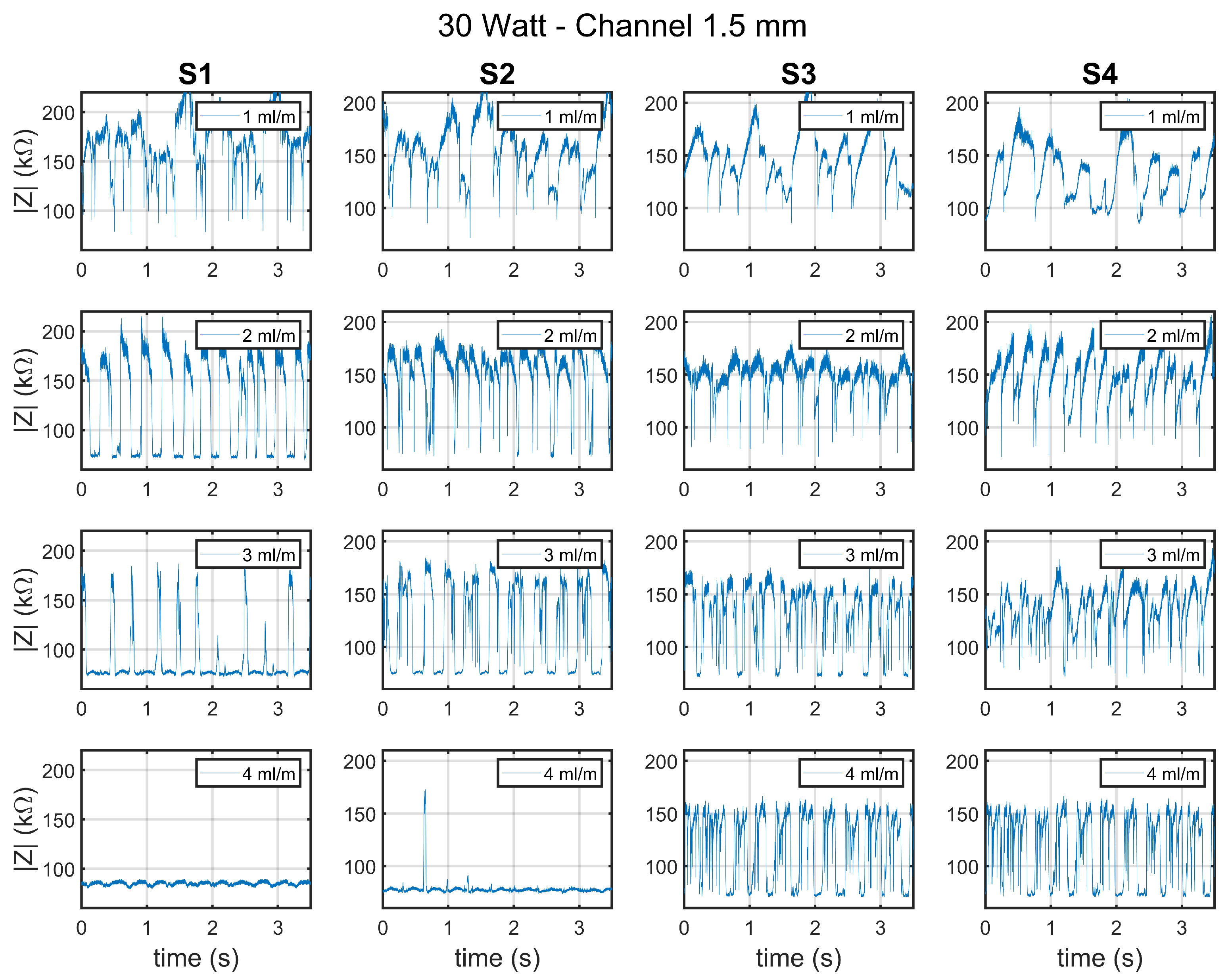
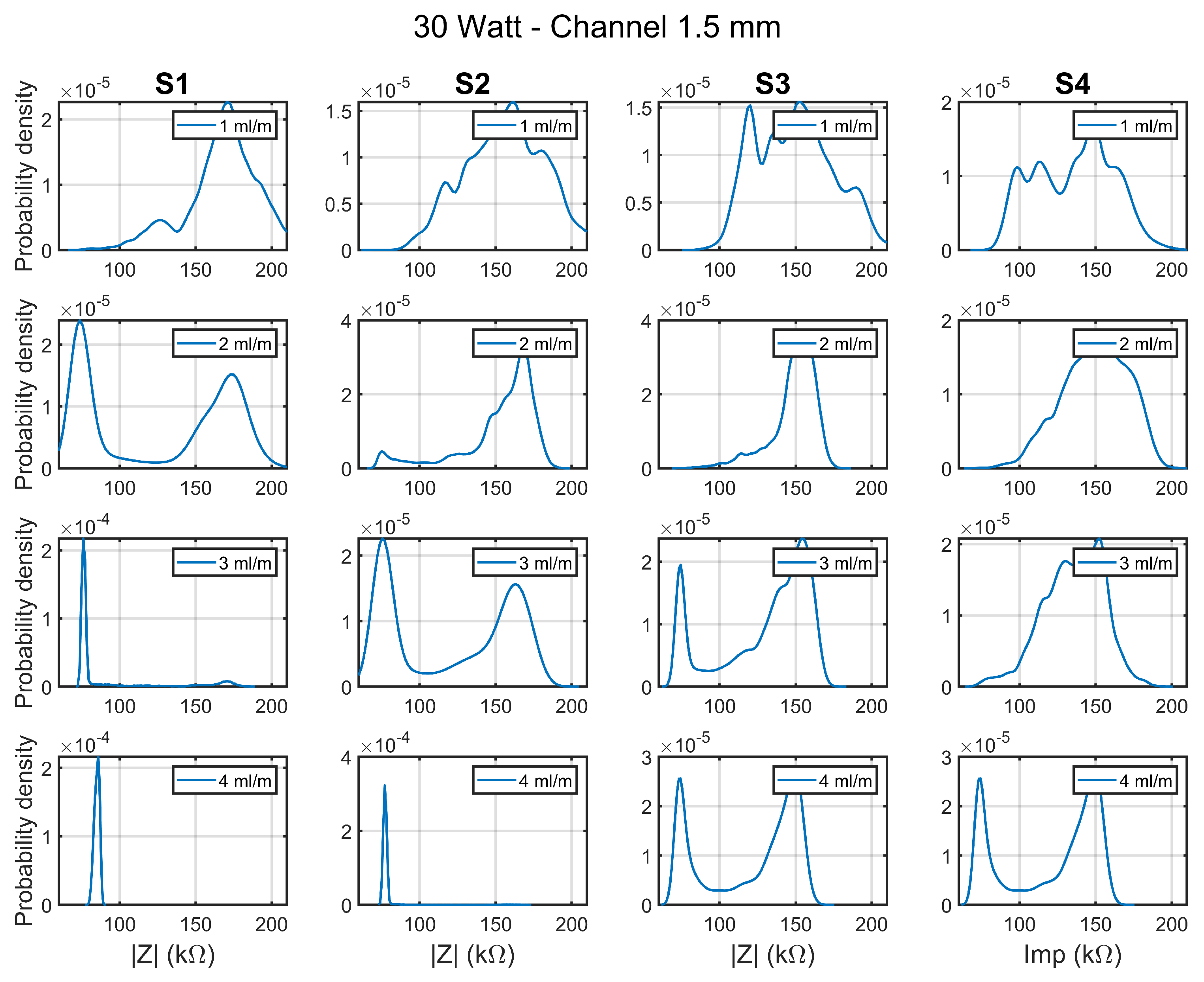
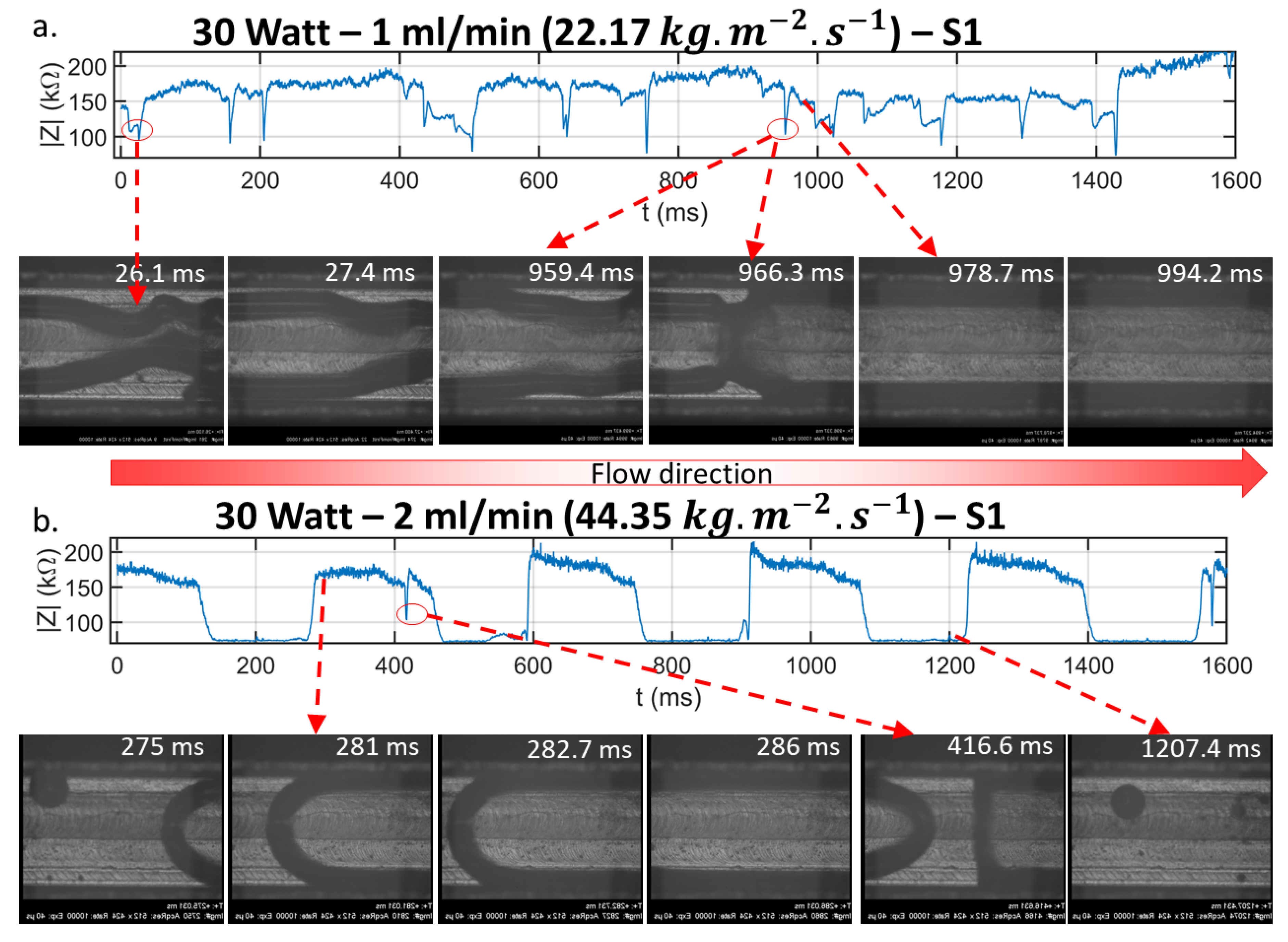
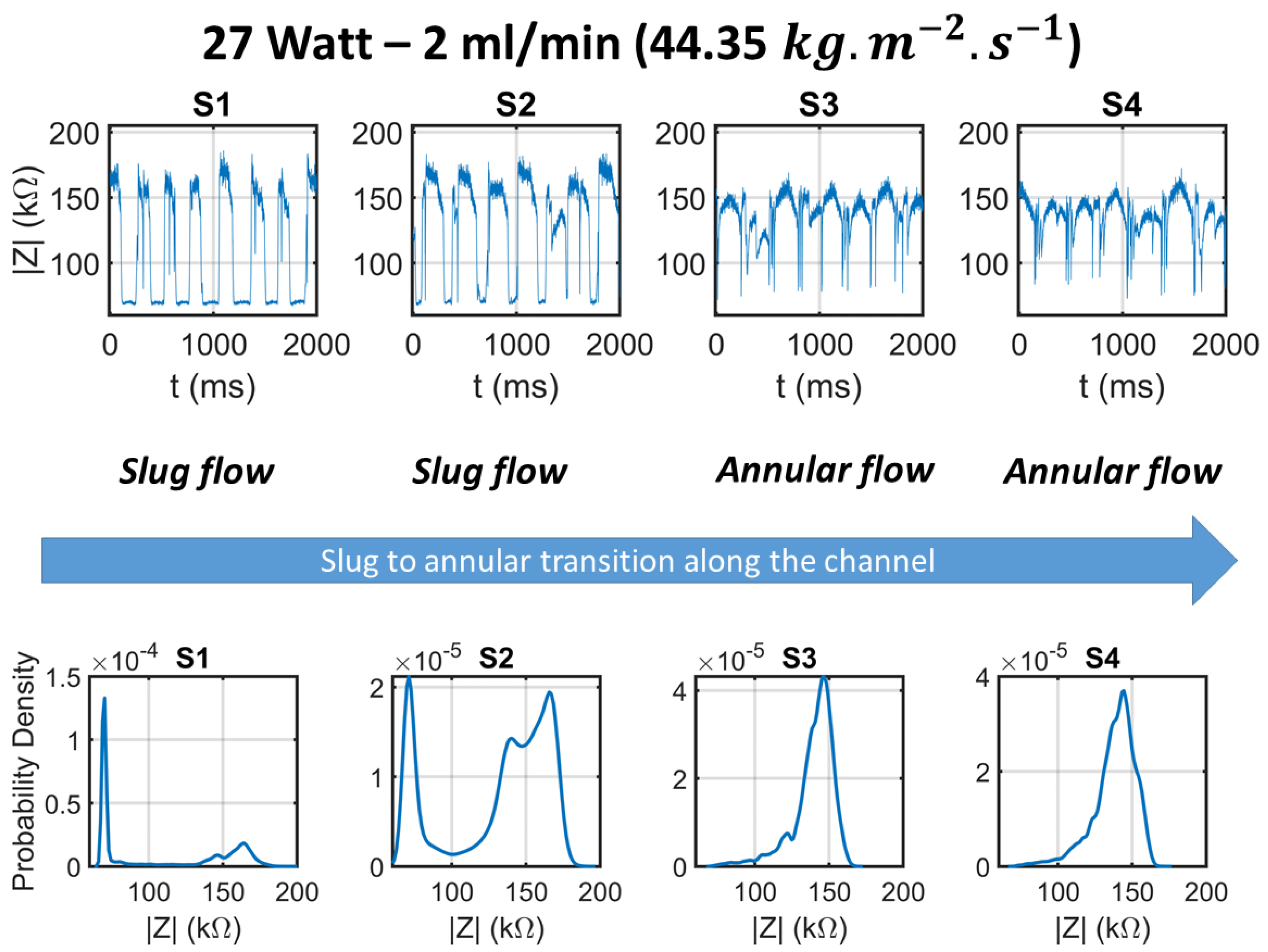
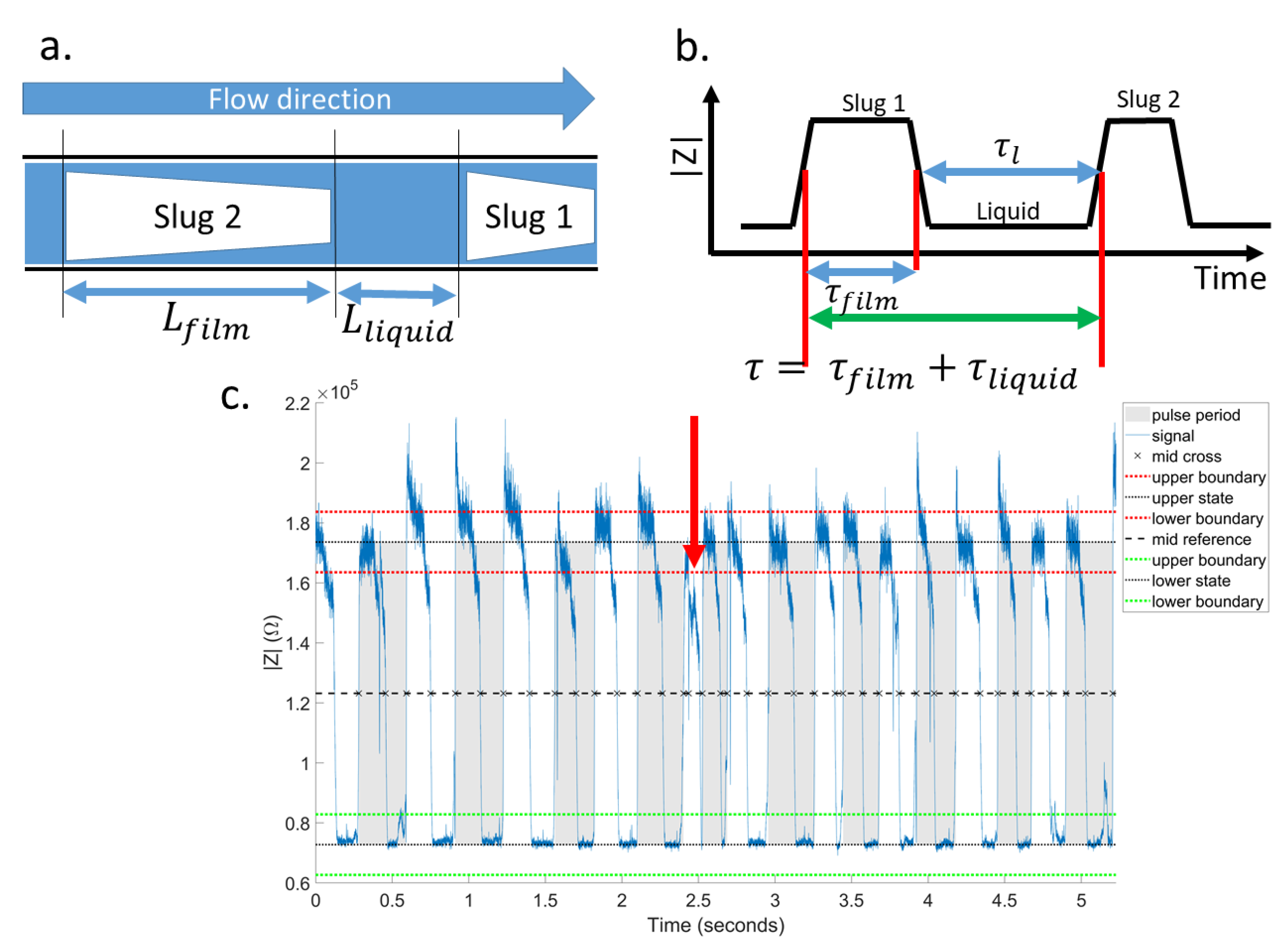
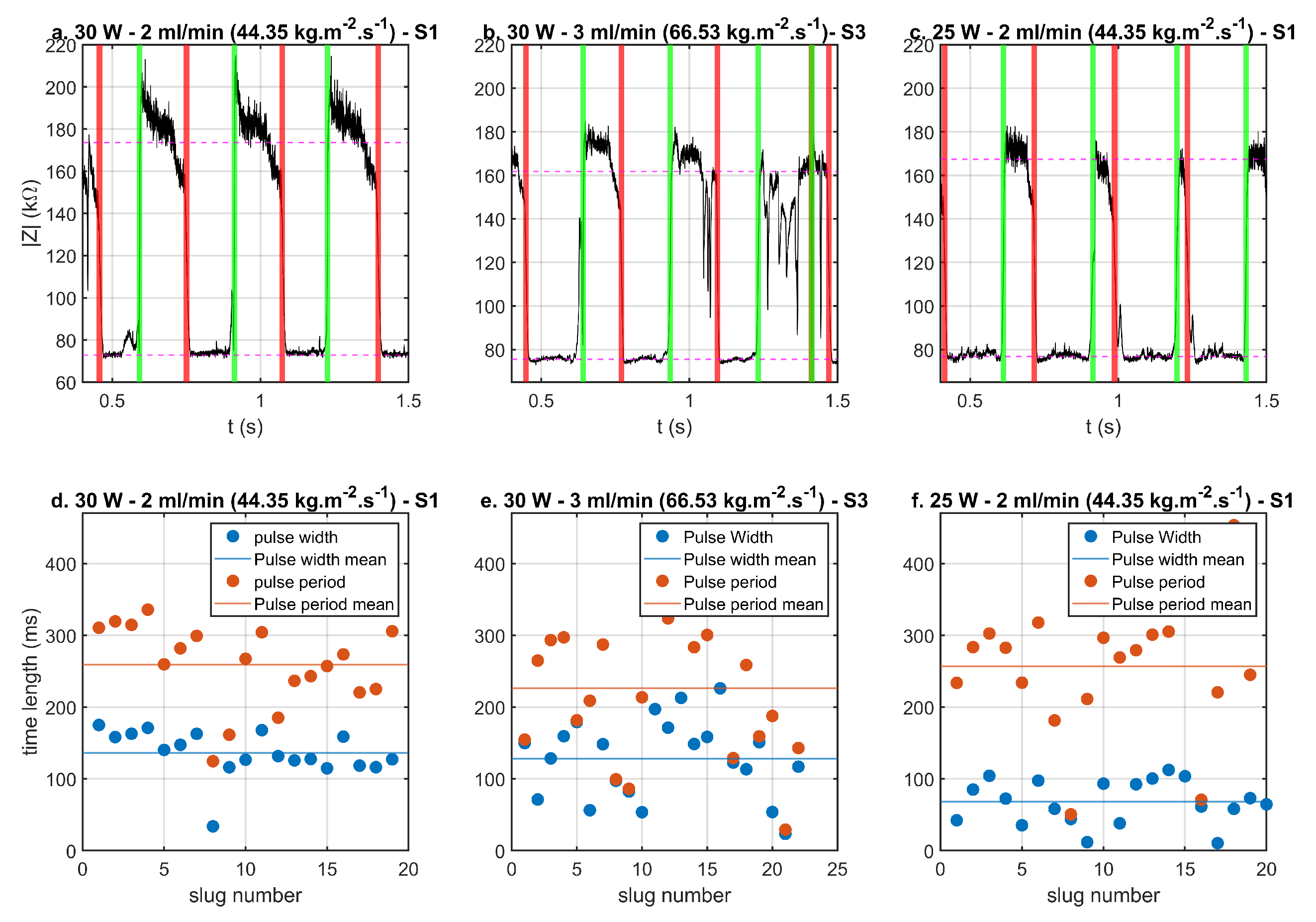
4.3. Local Electrical Sensing
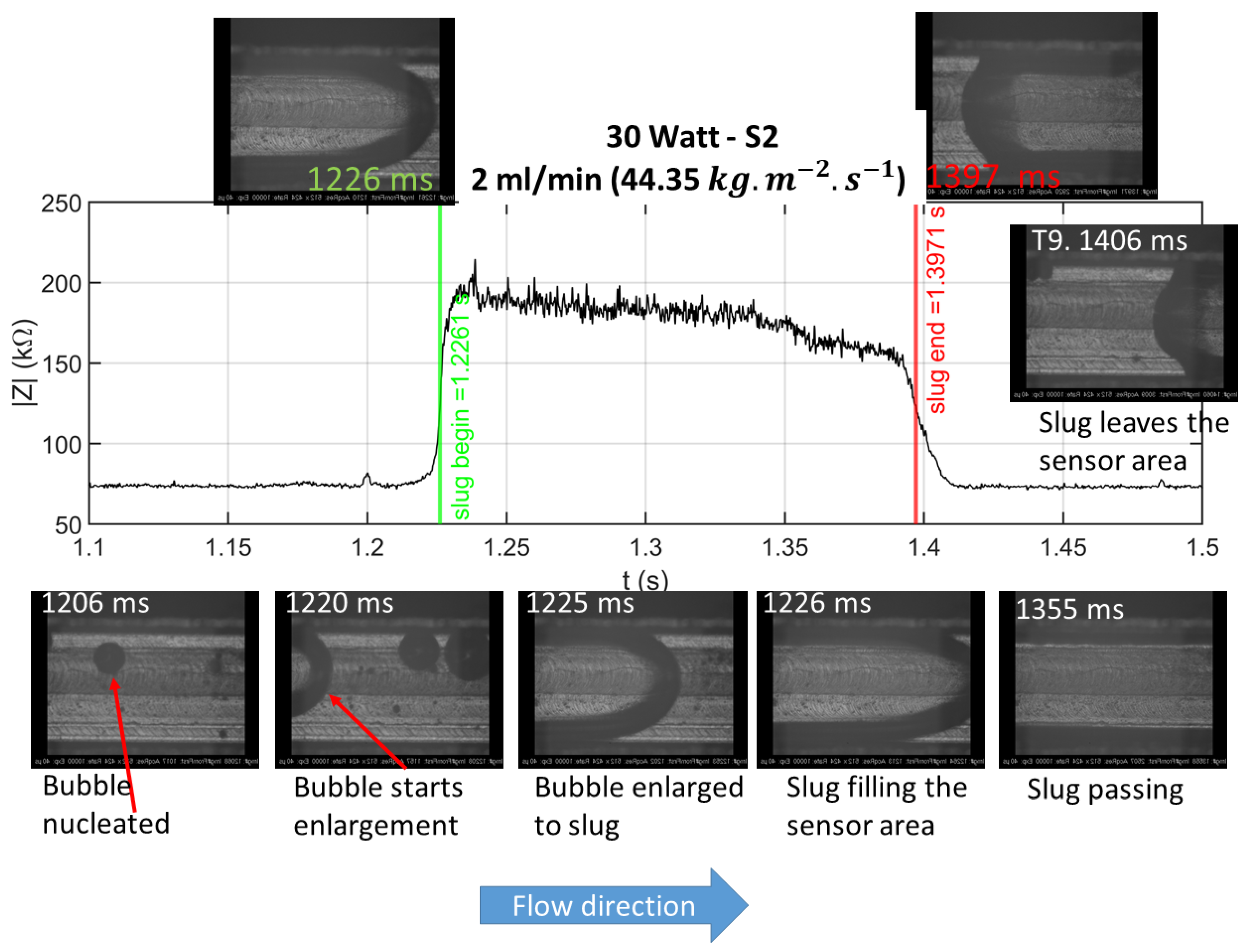
Slug Flow Analysis Using Impedance Sensors
5. Summary
- It was found that the flow regime in the channels varied considerably between the selected experimental conditions.
- Two different regimes were identified for the value of the heat transfer coefficient with respect to the vapor quality within the investigated mass and heat flux conditions: At the onset of evaporation (0 < x < 0.05), the heat transfer coefficient increases with the vapour quality. At intermediate vapor quality ranges (0.05 < x < 0.5), the heat transfer coefficient shows a “U” shape profile. Since the dry-out did not occur in any of the experiments, the heat transfer coefficient did not decrease to a value typical for gas systems.
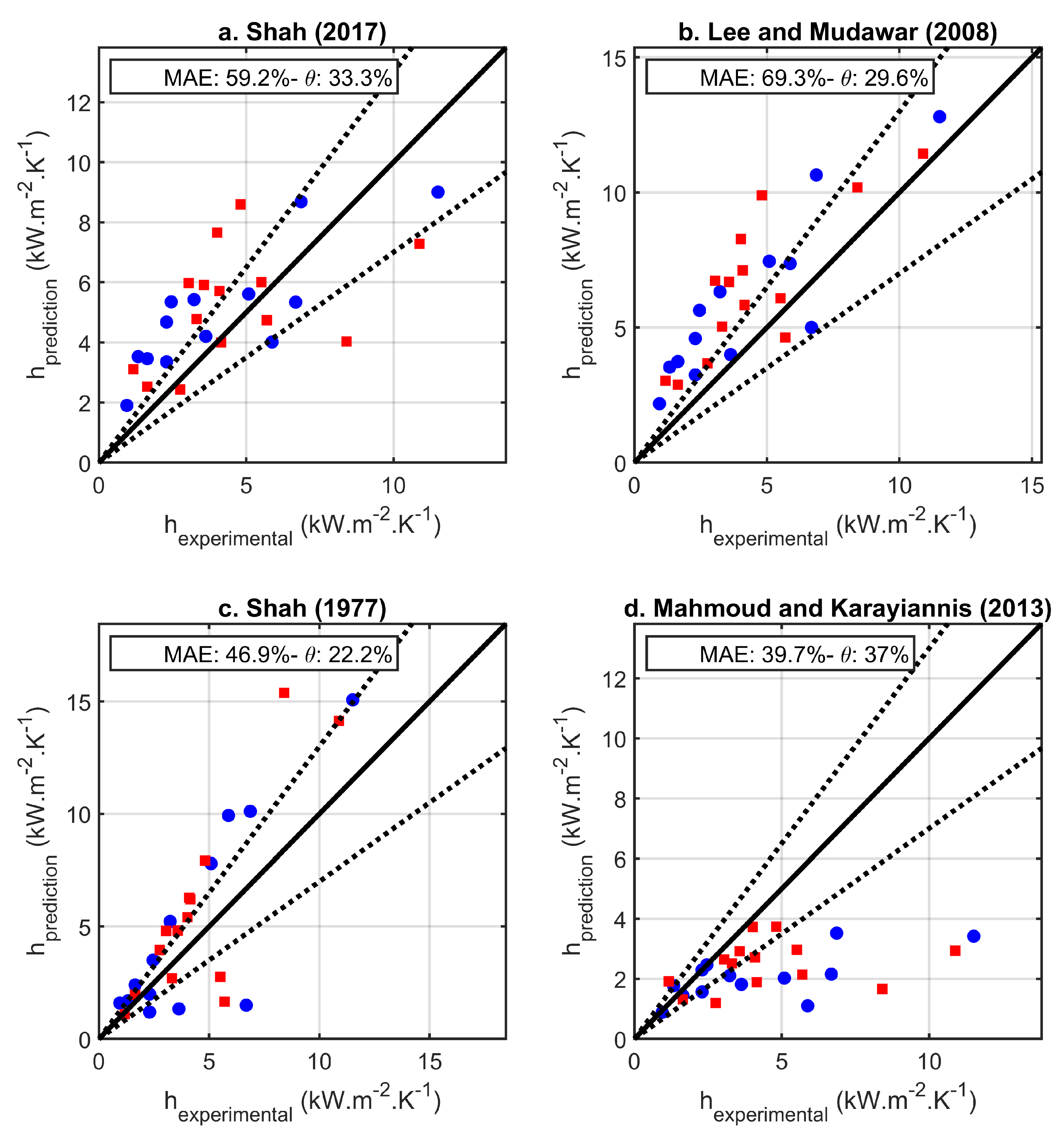
- For the heat transfer coefficient, a similar comparison was done using four correlations. It was found that most correlations predicted the correct values for some points but failed in other regimes. The correlation published by Mahmoud and Karayianis [48] showed the best predictive performance over the whole range of experiments. There are relatively big mean absolute error values observed between experimental results and prediction of the selected correlations. We conclude that this is due to the relative unstable and different flow conditions.
- It was affirmed that it is possible to find local information regarding the flow regime using impedance sensors as we presented previously in [35]. In most conditions, slug flow and annular flow regimes were observed in the channel. In the instances when bubbly flow was found, it transformed into slug flow. The application of such sensing system was highlighted in mechanistic models based on flow regime such as the model presented by Falsetti et al. [33].
- The slug passing frequency and duty cycle are critical and usable information that was obtained and cross checked with the synchronized videos. Thus for the case when slug flow is the dominant regime in the channel, the information gleaned form the impedance spectroscopy, namely residence time and bubble frequency at the sensor location is very useful.
- Since it has been found that the flow regime is of paramount importance regarding the heat transfer, the information gained from impedance spectroscopy is a useful tool to use the correct correlations for a given set of experimental conditions.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | cross-section area | () |
| heat capacity | () | |
| hydraulic diameter | () | |
| f | friction factor | (-) |
| G | mass flux | () |
| h | heat transfer coefficient | () |
| latent heat of vaporization | () | |
| channel height | () | |
| I | electrical current | () |
| k | thermal conductivity | () |
| K | pressure loss coefficient | (-) |
| L | channel length | () |
| heat flux | () | |
| power | () | |
| t | time | () |
| T | temperature | () |
| V | electrical voltage | () |
| channel width | () | |
| x | vapor quality, | (-) |
| void fraction | (-) | |
| channel aspect ratio | (-) | |
| liquid film thickness | () | |
| dynamic viscosity | () | |
| density | () | |
| time period | () | |
| two phase multiplier | (-) | |
| Dimensionless numbers | ||
| Boiling number | ||
| Bond number | ||
| C | Chisholm parameter | |
| Martinelli parameter | ||
| Froude number, | ||
| Nusselt number | ||
| Peclet number, | ||
| Prandtl number, | ||
| Reynolds number, | ||
| Webber number, | ||
| Subscripts | ||
| acceleration | ||
| ambient | ||
| base | ||
| channel | ||
| expansion | ||
| effective | ||
| fluid | ||
| footprint | ||
| v | vapor | |
| inlet | ||
| l | liquid | |
| local | ||
| heat loss | ||
| outlet | ||
| saturation | ||
| single phase | ||
| two phase | ||
| w | wall | |
| sudden contraction | ||
| sudden expansion | ||
| corner | ||
Appendix A. Single Phase Pressure Drop
Appendix B. Boiling Heat Transfer Coefficient Correlations
References
- Kandlikar, S.G. History, Advances, and Challenges in Liquid Flow and Flow Boiling Heat Transfer in Microchannels: A Critical Review. J. Heat Transf. 2012, 134. [Google Scholar] [CrossRef]
- Karayiannis, T.; Mahmoud, M. Flow boiling in microchannels: Fundamentals and applications. Appl. Therm. Eng. 2017, 115, 1372–1397. [Google Scholar] [CrossRef]
- Huang, H.; Thome, J.R. An experimental study on flow boiling pressure drop in multi-microchannel evaporators with different refrigerants. Exp. Therm. Fluid Sci. 2017, 80, 391–407. [Google Scholar] [CrossRef]
- Bigham, S.; Moghaddam, S. Physics of the Microchannel Flow Boiling Process and Comparison with the Existing Theories. J. Heat Transf. 2017, 139, 111503. [Google Scholar] [CrossRef]
- Harirchian, T.; Garimella, S.V. A comprehensive flow regime map for microchannel flow boiling with quantitative transition criteria. Int. J. Heat Mass Transf. 2010, 53, 2694–2702. [Google Scholar] [CrossRef]
- Al-Zaidi, A.H.; Mahmoud, M.M.; Karayiannis, T.G. Flow boiling of HFE-7100 in microchannels: Experimental study and comparison with correlations. Int. J. Heat Mass Transf. 2019, 140, 100–128. [Google Scholar] [CrossRef]
- Bigham, S.; Moghaddam, S. Microscale study of mechanisms of heat transfer during flow boiling in a microchannel. Int. J. Heat Mass Transf. 2015, 88, 111–121. [Google Scholar] [CrossRef]
- Magnini, M.; Thome, J. An updated three-zone heat transfer model for slug flow boiling in microchannels. Int. J. Multiph. Flow 2017, 91, 296–314. [Google Scholar] [CrossRef]
- Kandlikar, S.G. Scale effects on flow boiling heat transfer in microchannels: A fundamental perspective. Int. J. Therm. Sci. 2010, 49, 1073–1085. [Google Scholar] [CrossRef]
- Li, W.; Yang, F.; Alam, T.; Qu, X.; Peng, B.; Khan, J.; Li, C. Enhanced flow boiling in microchannels using auxiliary channels and multiple micronozzles (I): Characterizations of flow boiling heat transfer. Int. J. Heat Mass Transf. 2018, 116, 208–217. [Google Scholar] [CrossRef]
- Li, W.; Wang, Z.; Yang, F.; Alam, T.; Jiang, M.; Qu, X.; Kong, F.; Khan, A.S.; Liu, M.; Alwazzan, M.; et al. Supercapillary Architecture Activated Two-Phase Boundary Layer Structures for Highly Stable and Efficient Flow Boiling Heat Transfer. Adv. Mater. 2019, 32, 1905117. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Alam, T.; Yang, F.; Qu, X.; Peng, B.; Khan, J.; Li, C. Enhanced flow boiling in microchannels using auxiliary channels and multiple micronozzles II: Enhanced CHF and reduced pressure drop. Int. J. Heat Mass Transf. 2017, 115, 264–272. [Google Scholar] [CrossRef]
- Prajapati, Y.K.; Pathak, M.; Khan, M.K. Bubble dynamics and flow boiling characteristics in three different microchannel configurations. Int. J. Therm. Sci. 2017, 112, 371–382. [Google Scholar] [CrossRef]
- Ozdemir, M.R.; Mahmoud, M.M.; Karayiannis, T.G. Flow Boiling of Water in a Rectangular Metallic Microchannel. Heat Transf. Eng. 2020, 1–25. [Google Scholar] [CrossRef]
- Mahmoud, M.M.; Karayiannis, T.G. Flow Boiling in Mini to Microdiameter Channels. In Encyclopedia of Two-Phase Heat Transfer and Flow IV; World Scientific: Singapore, 2018; pp. 233–301. [Google Scholar] [CrossRef]
- Cheng, L.; Xia, G. Fundamental issues, mechanisms and models of flow boiling heat transfer in microscale channels. Int. J. Heat Mass Transf. 2017, 108, 97–127. [Google Scholar] [CrossRef]
- Cheng, L.; Ribatski, G.; Thome, J.R. Two-phase flow patterns and flow-pattern maps: Fundamentals and applications. Appl. Mech. Rev. 2008, 61, 050802. [Google Scholar] [CrossRef]
- Cheng, L. Flow Boiling Heat Transfer with Models in Microchannels. In Microchannel Phase Change Transport Phenomena; Elsevier: Amsterdam, The Netherlands, 2016; pp. 141–191. [Google Scholar] [CrossRef]
- Kim, S.M.; Mudawar, I. Review of databases and predictive methods for heat transfer in condensing and boiling mini/micro-channel flows. Int. J. Heat Mass Transf. 2014, 77, 627–652. [Google Scholar] [CrossRef]
- Anwar, Z.; Palm, B.; Khodabandeh, R. Flow boiling heat transfer, pressure drop and dryout characteristics of R1234yf: Experimental results and predictions. Exp. Therm. Fluid Sci. 2015, 66, 137–149. [Google Scholar] [CrossRef]
- Zhuan, R.; Wang, W. Boiling heat transfer characteristics in a microchannel array heat sink with low mass flow rate. Appl. Therm. Eng. 2013, 51, 65–74. [Google Scholar] [CrossRef]
- Kim, S.M.; Mudawar, I. Universal Approach to Predicting Saturated Flow Boiling Heat Transfer in Mini Micro-Channels–Part II. Two-Phase Heat Transfer Coefficient. Int. J. Heat Mass Transf. 2013, 64, 1239–1256. [Google Scholar] [CrossRef]
- Qu, W.; Mudawar, I. Flow boiling heat transfer in two-phase micro-channel heat sinks––I. Experimental investigation and assessment of correlation methods. Int. J. Heat Mass Transf. 2003, 46, 2755–2771. [Google Scholar] [CrossRef]
- Mortada, S.; Zoughaib, A.; Arzano-Daurelle, C.; Clodic, D. Boiling heat transfer and pressure drop of R-134a and R-1234yf in minichannels for low mass fluxes. Int. J. Refrig. 2012, 35, 962–973. [Google Scholar] [CrossRef]
- Szczukiewicz, S.; Magnini, M.; Thome, J. Proposed models, ongoing experiments, and latest numerical simulations of microchannel two-phase flow boiling. Int. J. Multiph. Flow 2014, 59, 84–101. [Google Scholar] [CrossRef]
- Mukherjee, A. Contribution of Microlayer Evaporation During Flow Boiling Inside Microchannels. In Proceedings of the ASME 2008 6th International Conference on Nanochannels, Microchannels, and Minichannels (ASMEDC), Darmstadt, Germany, 23–25 June 2008. [Google Scholar] [CrossRef]
- Yin, L.; Jia, L.; Guan, P. Bubble confinement and deformation during flow boiling in microchannel. Int. Commun. Heat Mass Transf. 2016, 70, 47–52. [Google Scholar] [CrossRef]
- Thome, J.R.; Consolini, L. Mechanisms of Boiling in Micro-Channels: Critical Assessment. Heat Transf. Eng. 2010, 31, 288–297. [Google Scholar] [CrossRef]
- Huh, C.; Kim, M.H. Pressure Drop, Boiling Heat Transfer and Flow Patterns during Flow Boiling in a Single Microchannel. Heat Transf. Eng. 2007, 28, 730–737. [Google Scholar] [CrossRef]
- Cheng, L. Flow Patterns and Bubble Growth in Microchannels. In Microchannel Phase Change Transport Phenomena; Elsevier: Amsterdam, The Netherlands, 2016; pp. 91–140. [Google Scholar] [CrossRef]
- Jagirdar, M.; Lee, P.S. Study of transient heat transfer and synchronized flow visualizations during sub-cooled flow boiling in a small aspect ratio microchannel. Int. J. Multiph. Flow 2016, 83, 254–266. [Google Scholar] [CrossRef]
- Piasecka, M.; Strak, K.; Maciejewska, B. Calculations of Flow Boiling Heat Transfer in a Minichannel Based on Liquid Crystal and Infrared Thermography Data. Heat Transf. Eng. 2017, 38, 332–346. [Google Scholar] [CrossRef]
- Falsetti, C.; Magnini, M.; Thome, J. A new flow pattern-based boiling heat transfer model for micro-pin fin evaporators. Int. J. Heat Mass Transf. 2018, 122, 967–982. [Google Scholar] [CrossRef]
- Kandlikar, S.G. High Flux Heat Removal with Microchannels—A Roadmap of Challenges and Opportunities. Heat Transf. Eng. 2005, 26, 5–14. [Google Scholar] [CrossRef]
- Talebi, M.; Sadir, S.; Cobry, K.; Stroh, A.; Dittmeyer, R.; Woias, P. Investigation of water microchannel boiling flow regimes using electrical sensing elements along a single microchannel. Meas. Sci. Technol. 2019, 30, 125301. [Google Scholar] [CrossRef]
- Talebi, M.; Baeumker, E.; Cobry, K.; Sadir, S.; Stroh, A.; Woias, P. Investigation of Slug Flow in Microchannel Boiling by Impedimetric Sensing. In Proceedings of the 2019 IEEE SENSORS, Montreal, QC, Canada, 27–30 October 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Talebi, M.; Cobry, K.; Sadir, S.; Dittmeyer, R.; Woias, P. Flow Regime Detection of Boiling Flow in Microchannels Using Electrical Sensing Elements Validated by Videography. In Proceedings of the ASME 2018 16th International Conference on Nanochannels, Microchannels, and Minichannels. American Society of Mechanical Engineers, Dubrovnik, Croatia, 10–13 June 2018; p. V001T02A016. [Google Scholar]
- Pico Technology USB TC-08-Channel Thermocouple Data Logger Data Sheet, 9th ed.; Pico Technology Ltd.: St Neots, UK, 2019.
- Product Information mzr-7205 · High Performance Pump Series; HNP Mikrosysteme GmbH: Schwerin, Germany, 2019.
- Kenning, D.B.R.; Lewis, J.S.; Karayiannis, T.G. Pressure drop and heat transfer characteristics for single-phase developing flow of water in rectangular microchannels. J. Phys. Conf. Ser. 2012, 395, 012085. [Google Scholar] [CrossRef]
- Zohuri, B. Compact Heat Exchangers; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Shah, R.; London, A. Laminar Flow Forced Convection in Ducts; Elsevier: Amsterdam, The Netherlands, 1978. [Google Scholar] [CrossRef]
- Muzychka, Y.S.; Yovanovich, M.M. Pressure Drop in Laminar Developing Flow in Noncircular Ducts: A Scaling and Modeling Approach. J. Fluids Eng. 2009, 131. [Google Scholar] [CrossRef]
- Da Silva Lima, R.J.; Quibén, J.M.; Thome, J.R. Flow boiling in horizontal smooth tubes: New heat transfer results for R-134a at three saturation temperatures. Appl. Therm. Eng. 2009, 29, 1289–1298. [Google Scholar] [CrossRef]
- Shah, M. A General Correlation for Heat Transfer during Subcooled Boiling in Pipes and Annuli. In Proceedings of the ASHRAE Semiannual Meeting, Chicago, IL, USA, 13–17 February 1977; pp. 202–217. [Google Scholar]
- Shah, M.M. New correlation for heat transfer during subcooled boiling in plain channels and annuli. Int. J. Therm. Sci. 2017, 112, 358–370. [Google Scholar] [CrossRef]
- Lee, J.; Mudawar, I. Fluid flow and heat transfer characteristics of low temperature two-phase micro-channel heat sinks – Part 2. Subcooled boiling pressure drop and heat transfer. Int. J. Heat Mass Transf. 2008, 51, 4327–4341. [Google Scholar] [CrossRef]
- Mahmoud, M.M.; Karayiannis, T.G. Heat transfer correlation for flow boiling in small to micro tubes. Int. J. Heat Mass Transf. 2013, 66, 553–574. [Google Scholar] [CrossRef]
- Sempértegui-Tapia, D.F.; Ribatski, G. Flow boiling heat transfer of R134a and low GWP refrigerants in a horizontal micro-scale channel. Int. J. Heat Mass Transf. 2017, 108, 2417–2432. [Google Scholar] [CrossRef]
- Talebi, M.; Woias, P.; Cobry, K. Analysis of impedance data from bubble flow in a glass/SU8 microfluidic device with on-channel sensors. Sens. Actuators Phys. 2018, 279, 543–552. [Google Scholar] [CrossRef]
- Talebi, M.; Cobry, K.; Zhou, Z.; Sadir, S.; Dittmeyer, R.; Woias, P. Investigation of boiling phenomena in microchannels using impedance spectroscopy technique correlated with videography. In Proceedings of the MikroSystemTechnik (Congress 2017), Munich, Germany, 23–25 October 2017; pp. 1–4. [Google Scholar]
- Thome, J.; Dupont, V.; Jacobi, A. Heat transfer model for evaporation in microchannels. Part I: Presentation of the model. Int. J. Heat Mass Transf. 2004, 47, 3375–3385. [Google Scholar] [CrossRef]
- Rosa, E.S.; Flora, B.F.; Souza, M.A.S.F. Design and performance prediction of an impedance void meter applied to the petroleum industry. Meas. Sci. Technol. 2012, 23, 055304. [Google Scholar] [CrossRef]
- Muzychka, Y.S.; Yovanovich, M.M. Laminar Forced Convection Heat Transfer in the Combined Entry Region of Non-Circular Ducts. J. Heat Transf. 2004, 126, 54–61. [Google Scholar] [CrossRef]
- Lim, T.W.; You, S.S.; Choi, J.H.; Kim, H.S. Experimental Investigation of Heat Transfer in Two-phase Flow Boiling. Exp. Heat Transf. 2014, 28, 23–36. [Google Scholar] [CrossRef]


| Property | Unit | Value or Range | Uncertainty |
|---|---|---|---|
| Channel hydraulic diameter | 750 & 1050 | ||
| Flow rate | 0.5–4 | ||
| Temperature | 60–140 | ±0.5 | |
| Total heaters applied power | 7–30 | ||
| measurement excitation freq. | 50 | less than 0.01% = 5 Hz | |
| measurement sampling freq. | 13.7 | ||
| Reynolds number @ 90 | - | 25–206 | |
| differential pressure sensing | 0–350 | 0.35 | |
| absolute inlet pressure sensing | 0 to 40,000 | 40 | |
| input power | 7–33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Talebi, M.; Sadir, S.; Kraut, M.; Dittmeyer, R.; Woias, P. Local Heat Transfer Analysis in a Single Microchannel with Boiling DI-Water and Correlations with Impedance Local Sensors. Energies 2020, 13, 6473. https://doi.org/10.3390/en13236473
Talebi M, Sadir S, Kraut M, Dittmeyer R, Woias P. Local Heat Transfer Analysis in a Single Microchannel with Boiling DI-Water and Correlations with Impedance Local Sensors. Energies. 2020; 13(23):6473. https://doi.org/10.3390/en13236473
Chicago/Turabian StyleTalebi, Mohammadmahdi, Sahba Sadir, Manfred Kraut, Roland Dittmeyer, and Peter Woias. 2020. "Local Heat Transfer Analysis in a Single Microchannel with Boiling DI-Water and Correlations with Impedance Local Sensors" Energies 13, no. 23: 6473. https://doi.org/10.3390/en13236473
APA StyleTalebi, M., Sadir, S., Kraut, M., Dittmeyer, R., & Woias, P. (2020). Local Heat Transfer Analysis in a Single Microchannel with Boiling DI-Water and Correlations with Impedance Local Sensors. Energies, 13(23), 6473. https://doi.org/10.3390/en13236473






