Modeling of Limestone Dissolution for Flue Gas Desulfurization with Novel Implications
Abstract
1. Introduction
2. Materials and Methods
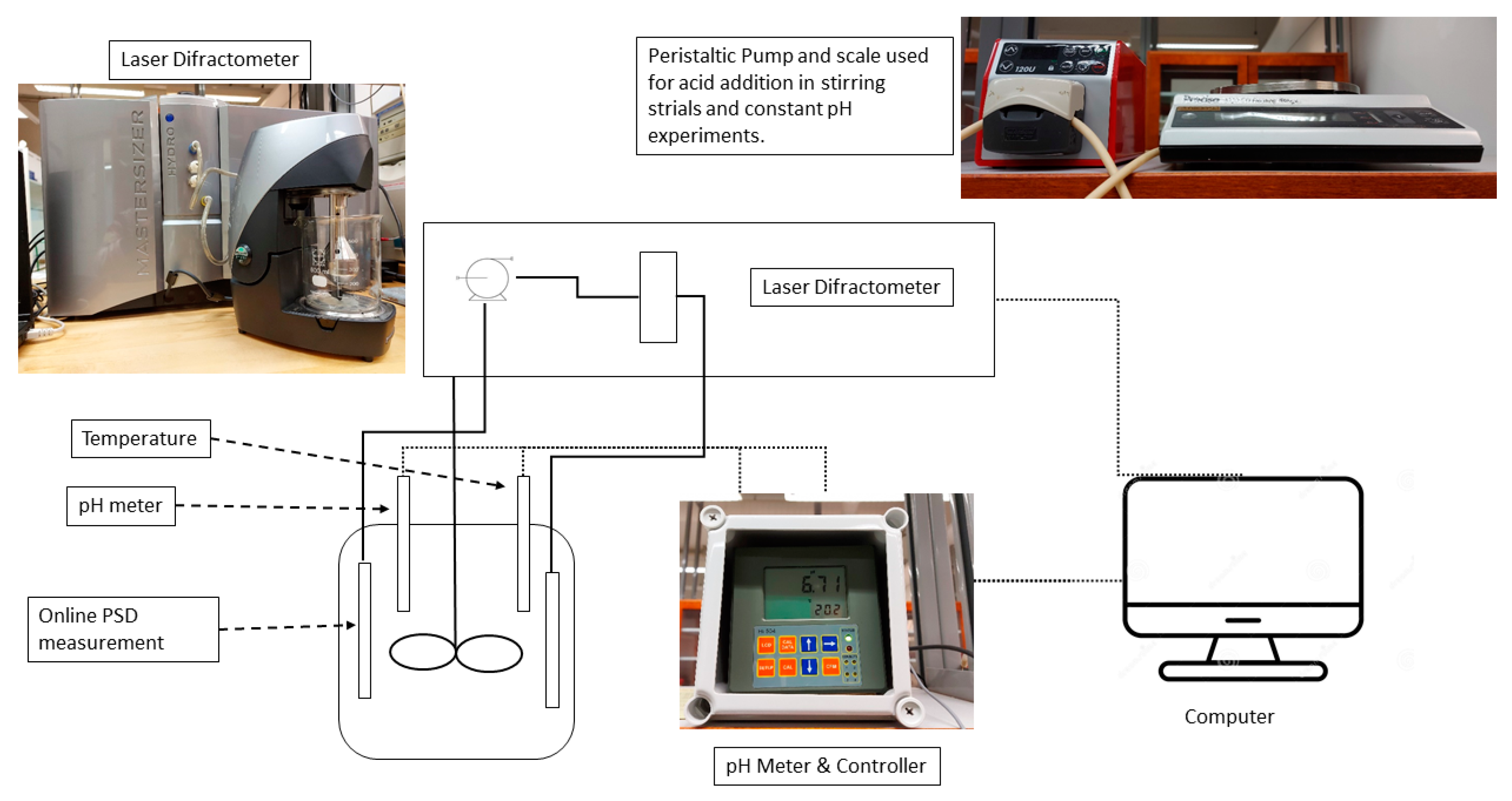
2.1. Experimental Procedure
2.2. Mathematical Modeling
3. Results
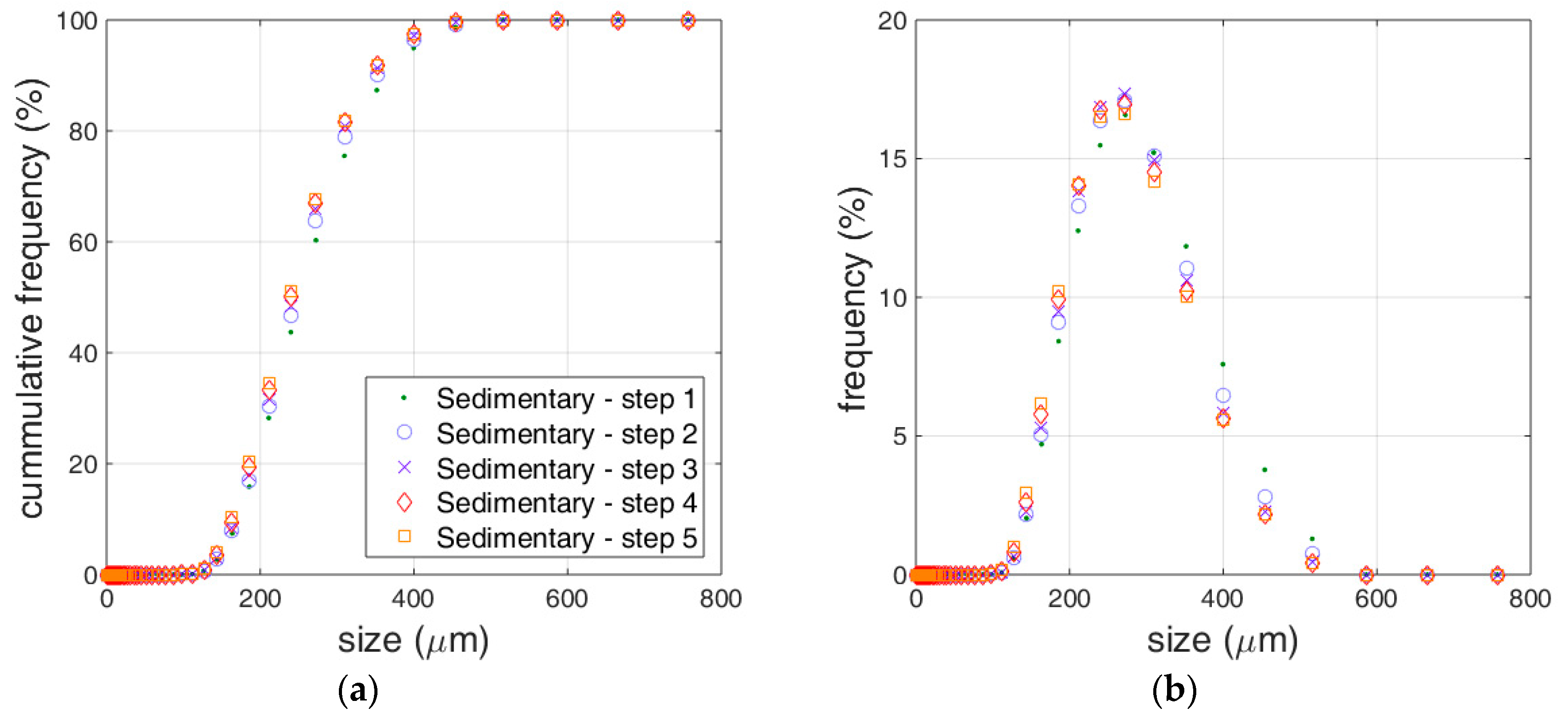
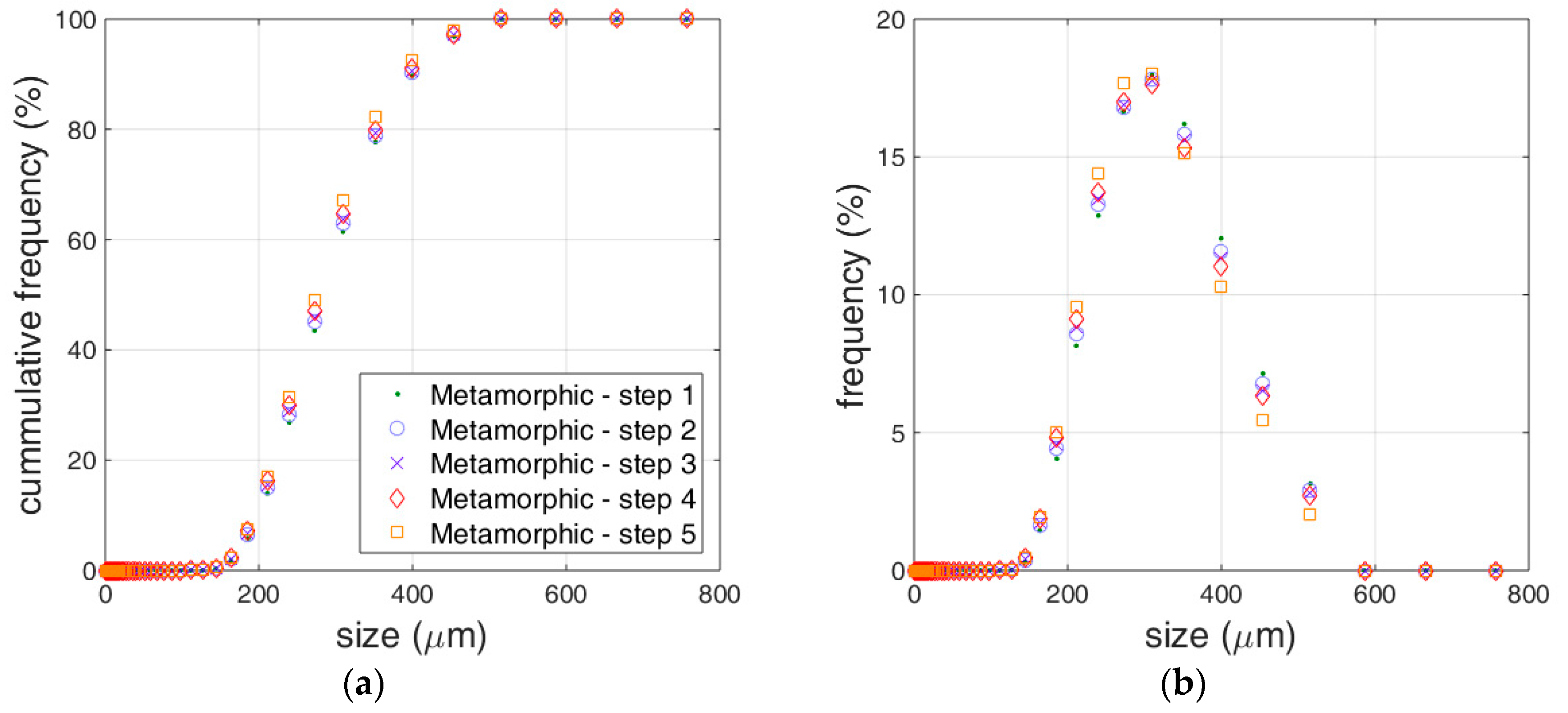
3.1. Limestone Analysis
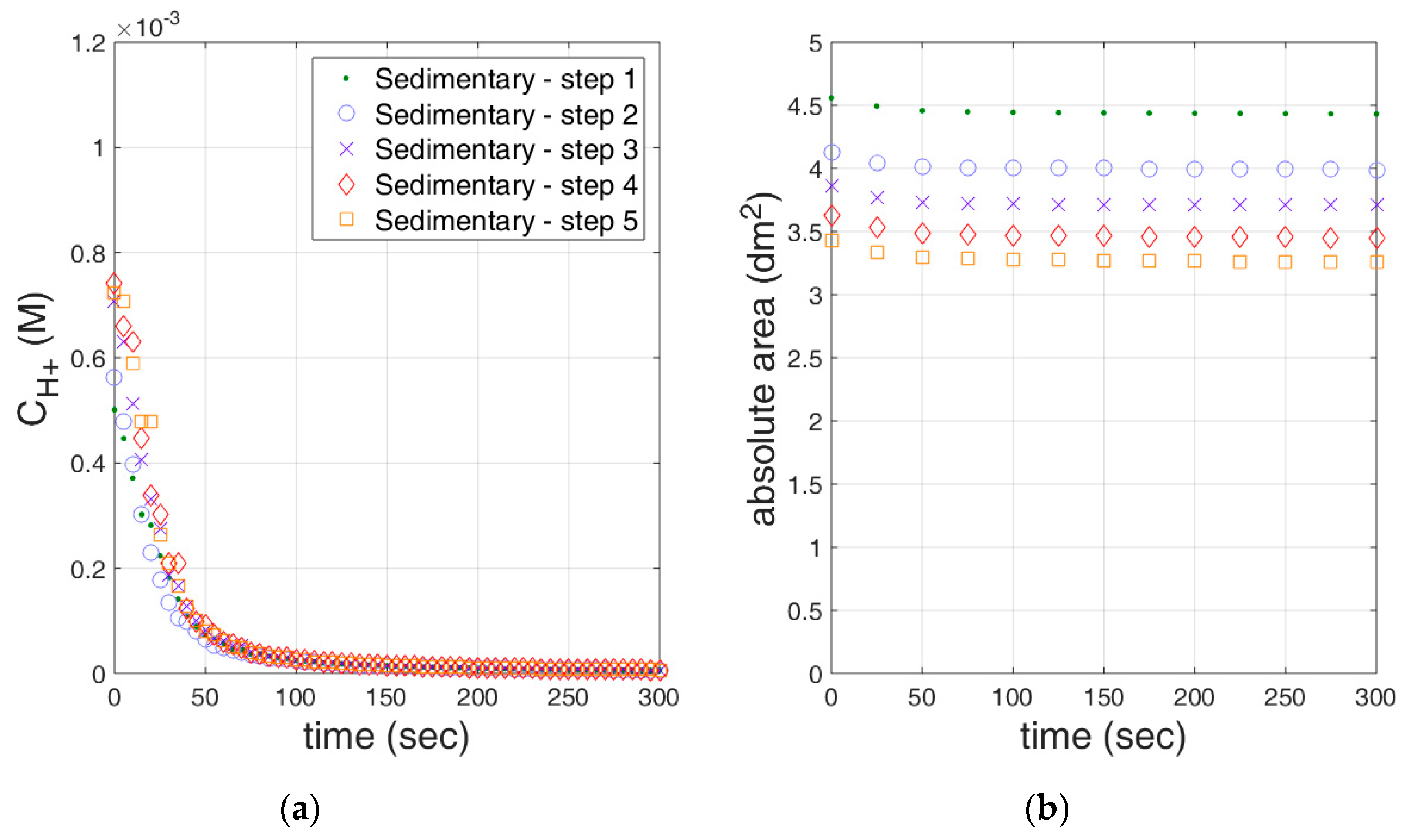
3.2. Reactivity Estimation of Limestone
| Quantity | Symbol | Units | Min Value | Median Value | Max Value | Reference |
|---|---|---|---|---|---|---|
| Reynolds number (agitated tank) | Re | none | 42,000 | This Work | ||
| Convective mass transfer coefficient | 10−3 dm/s | 0.01 | 2 | 12 | [2,43] | |
| Limestone particle size | dp | 10−6 m | 150 | 320 | 500 | This Work |
| Solid calcite concentration | g/L | 2 | 3 | 5 | This Work | |
| Calcite absolute contact area | A | dm2 | 3 | 4 | 5 | This Work |
| Conductivity (local) | σ | mS/cm2 | 0.4 | 100 | 105 | [46] |
| Hydron concentration | mol/L | 10−6 | 6 × 10−6 | 2 × 10−3 | This Work | |
| Hydron surface activity coefficient | none | 0 | 0.2 | 1 | [2,47,48] | |
| Hydron ion diffusivity in water | 10−5 cm2 s−1 | 9.3 | [2,46] | |||
| Hydroxide anion diffusivity in water | 10−5 cm2 s−1 | 5.273 | [46] | |||
| Hydrogen Carbonate ion diffusivity in water | 10−5 cm2 s−1 | 1.185 | [46] | |||
| Carbonate ion diffusivity in water | 10−5 cm2 s−1 | 0.923 | [46] | |||
| Calcium ion diffusivity in water | 10−5 cm2 s−1 | 0.79 | 0.792 | 0.84 | [2,46] | |
| Magnesium ion diffusivity in water | 10−5 cm2 s−1 | 0.706 | [46] | |||
| Boundary layer thickness (mass transfer) | δ | 10−5 m | 1 | 2.4 | 5 | [5,43] |
| Diffusive mass transfer coefficient | 10−3 dm/s | 0.14 | 2.8 | 9.3 | This Work [2] | |
| Effective reactivity parameter | M−2 dm−2 s−1 | 105 | 106 | 107 | This work [2,41] | |
| First Damköhler number | none | 104 | 106 | 109 | This work | |
| Second Damköhler number | none | 30 | 300 | 3000 | This work |
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Latin Symbols | Significance | Units |
| Polynomial multiplicative factor | dimensionless | |
| A | Absolute contact area | dm2 |
| Particles’ superficial area | dm2 | |
| Polynomial multiplicative factor | dimensionless | |
| Substitute variable | dimensionless | |
| Polynomial multiplicative factor | dimensionless | |
| Hydrogen ion concentration | M | |
| Initial Hydrogen ion concentration | M | |
| Undissolved limestone concentration | g/L (or M) | |
| Shape factor | dimensionless | |
| dp | Limestone particle size | µm |
| D | Average ionic diffusivity | cm2 s−1 |
| Hydrogen ion diffusivity in water | cm2 s−1 | |
| Hydroxide anion diffusivity in water | cm2 s−1 | |
| Hydrogen carbonate ion diffusivity in water | cm2 s−1 | |
| Carbonate ion diffusivity in water | cm2 s−1 | |
| Calcium ion diffusivity in water | cm2 s−1 | |
| Magnesium ion diffusivity in water | cm2 s−1 | |
| First Damköhler number | dimensionless | |
| Second Damköhler number | dimensionless | |
| Reaction rate constant | M−2 dm−2 s−1 | |
| Model rate parameter | M−1 dm−2 s−1 | |
| Interfacial mass transfer coefficient | dm/s | |
| Convective mass transfer coefficient | dm/s | |
| Diffusive mass transfer coefficient | dm/s | |
| Lumped rate parameter | M−1 dm−2 s−1 | |
| Reactivity parameter | M−2 dm−2 s−1 | |
| Effective reactivity parameter | M−2 dm−2 s−1 | |
| Agitation rate | rpm | |
| Substitute variable | dimensionless | |
| Characteristic length of the particle | dm | |
| Re | Reynolds number (agitated tank) | dimensionless |
| Particle volume | dm3 | |
| Substitute variable | dimensionless | |
| Conversion | dimensionless | |
| Substitute parameter | dimensionless | |
| Greek symbols | Significance | Units |
| Agitator impeller diameter | m | |
| Substitute variable | dimensionless | |
| δ | Mass transfer boundary layer thickness | m |
| Hydrogen surface activity coefficient | dimensionless | |
| Dynamic viscosity | Pa.s | |
| Mass density | Kg/m3 | |
| σ | Local conductivity | mS/cm2 |
References
- Levich, V.G. Physicochemical Hydrodynamics; Prentice Hall: Upper Saddle River, NJ, USA, 1962; ISBN 0-13-674440-0. [Google Scholar]
- Letterman, R.D. Calcium Carbonate Dissolution Rate in Limestone Contactors | Project Summary: Calcium Carbonate Dissolution Rate in Limestone Contactors; U.S. Environmental Protection Agency: Washington, DC, USA, 1995.
- Hattori, Y.; Haruna, Y.; Otsuka, M. Dissolution process analysis using model-free Noyes-Whitney integral equation. Colloids Surf. B Biointerfaces 2013, 102, 227–231. [Google Scholar] [CrossRef] [PubMed]
- Aris, R. On shape factors for irregular particles—I: The steady state problem. Diffusion and reaction. Chem. Eng. Sci. 1957, 6, 262–268. [Google Scholar] [CrossRef]
- Lund, K.; Fogler, H.S.; McCune, C.C.; Ault, J.W. Acidization—II. The dissolution of calcite in hydrochloric acid. Chem. Eng. Sci. 1975, 30, 825–835. [Google Scholar] [CrossRef]
- Gray, F.; Anabaraonye, B.; Shah, S.; Boek, E.; Crawshaw, J. Chemical mechanisms of dissolution of calcite by HCl in porous media: Simulations and experiment. Adv. Water Resour. 2018, 121, 369–387. [Google Scholar] [CrossRef]
- Mahulkar, A.V.; Gogate, P.R.; Pandit, A.B. Matching Chemistry with Chemical Engineering for Optimum Design and Performance of Pharmaceutical Processing. In Pharmaceutical Process Chemistry; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2010; pp. 443–467. ISBN 978-3-527-63367-8. [Google Scholar]
- Kartashev, A.L.; Kartasheva, M.A.; Terekhin, A.A. Mathematical Models of Dynamics Multiphase Flows in Complex Geometric Shape Channels. Procedia Eng. 2017, 206, 121–127. [Google Scholar] [CrossRef]
- Carletti, C.; Montante, G.; De Blasio, C.; Paglianti, A. Liquid mixing dynamics in slurry stirred tanks based on electrical resistance tomography. Chem. Eng. Sci. 2016, 152, 478–487. [Google Scholar] [CrossRef]
- De Blasio, C.; Carletti, C.; Lundell, A.; Visuri, V.-V.; Kokkonen, T.; Westerlund, T.; Fabritius, T.; Järvinen, M. Employing a step-wise titration method under semi-slow reaction regime for evaluating the reactivity of limestone and dolomite in acidic environment. Miner. Eng. 2016, 86, 43–58. [Google Scholar] [CrossRef]
- De Blasio, C.; Carletti, C.; Westerlund, T.; Järvinen, M. On modeling the dissolution of sedimentary rocks in acidic environments. An overview of selected mathematical methods with presentation of a case study. J. Math. Chem. 2013, 51, 2120–2143. [Google Scholar] [CrossRef]
- Organization of the Petroleum Exporting Countries, OPEC. World Oil Outlook 2040; OPEC: Vienna, Austria, 2018; ISBN 978-3-9503936-6-8. [Google Scholar]
- World Bank World—Total Population 2008–2018. Available online: https://www.statista.com/statistics/805044/total-population-worldwide/ (accessed on 24 December 2019).
- De Blasio, C. Introduction. In Fundamentals of Biofuels Engineering and Technology; Springer International Publishing: Basel, Switzerland, 2019; pp. 3–12. [Google Scholar]
- Dudley, B. Proven coal reserves leading countries 2018. In BP Statistical Review of World Energy; Pureprint Group Limited: Uckfield, UK, 2019; p. 42. Available online: https://www.bp.com/content/dam/bp/business-sites/en/global/corporate/pdfs/energy-economics/statistical-review/bp-stats-review-2020-full-report.pdf (accessed on 22 November 2020).
- ECN, The Netherlands Phyllis2—Database for Biomass and Waste. Available online: https://www.ecn.nl/phyllis2/ (accessed on 22 August 2018).
- Huang, J.; Wang, H.; Zhong, Y.; Huang, J.; Fu, X.; Wang, L.; Teng, W. Growth and physiological response of an endangered tree, Horsfieldia hainanensis merr., to simulated sulfuric and nitric acid rain in southern China. Plant Physiol. Biochem. 2019, 144, 118–126. [Google Scholar] [CrossRef]
- Srivastava, R.K.; Jozewicz, W.; Singer, C. SO2 scrubbing technologies: A review. Environ. Prog. 2001, 20, 219–228. [Google Scholar] [CrossRef]
- Carletti, C.; De Blasio, C.; Mäkilä, E.; Salonen, J.; Westerlund, T. Optimization of a Wet Flue Gas Desulfurization Scrubber through Mathematical Modeling of Limestone Dissolution Experiments. Ind. Eng. Chem. Res. 2015, 54, 9783–9797. [Google Scholar] [CrossRef]
- De Blasio, C.; Carletti, C.; Salonen, J.; Björklund-Sänkiaho, M. Ultrasonic Power to Enhance Limestone Dissolution in the Wet Flue Gas Desulfurization Process. Modeling and Results from Stepwise Titration Experiments. ChemEngineering 2018, 2, 53. [Google Scholar] [CrossRef]
- Carletti, C.; De Blasio, C.; Miceli, M.; Pirone, R.; Westerlund, T. Ultrasonic enhanced limestone dissolution: Experimental and mathematical modeling. Chem. Eng. Process. Process Intensif. 2017, 118, 26–36. [Google Scholar] [CrossRef]
- Molerus, O.; Latzel, W. Suspension of solid particles in agitated vessels—II. Archimedes numbers > 40, reliable prediction of minimum stirrer angular velocities. Chem. Eng. Sci. 1987, 42, 1431–1437. [Google Scholar] [CrossRef]
- Plummer, L.N.; Wigley, T.M.L.; Parkhurst, D.L. The kinetics of calcite dissolution in CO2—water systems at 5 degrees to 60 degrees C and 0.0 to 1.0 atm CO2. Am. J. Sci. 1978, 278, 179–216. [Google Scholar] [CrossRef]
- Ahlbeck, J.; Engman, T.; Fältén, S.; Vihma, M. Measuring the reactivity of limestone for wet flue-gas desulfurization. Chem. Eng. Sci. 1995, 50, 1081–1089. [Google Scholar] [CrossRef]
- Levenspiel, O. Chemical Reaction Engineering, 3rd ed.; Wiley: Hoboken, NJ, USA, 1998; ISBN 0-471-25424-X. [Google Scholar]
- Salmi, T.; Grénman, H.; Wärnå, J.; Murzin, D.Y. New modelling approach to liquid-solid reaction kinetics: From ideal particles to real particles. Chem. Eng. Res. Des. 2013, 91, 1876–1889. [Google Scholar] [CrossRef]
- Russo, V.; Salmi, T.; Carletti, C.; Murzin, D.Y.; Westerlund, T.; Tesser, R.; Grénman, H. Application of an Extended Shrinking Film Model to Limestone Dissolution. Ind. Eng. Chem. Res. 2017, 56, 13254–13261. [Google Scholar] [CrossRef]
- Salmi, T.; Grénman, H.; Wärnå, J.; Murzin, D.Y. Revisiting shrinking particle and product layer models for fluid-solid reactions—From ideal surfaces to real surfaces. Chem. Eng. Process. Process Intensif. 2011, 50, 1076–1084. [Google Scholar] [CrossRef]
- Salmi, T.; Grénman, H.; Bernas, H.; Wärnå, J.; Murzin, D.Y. Mechanistic modelling of kinetics and mass transfer for a Solid-liquid system: Leaching of zinc with ferric iron. Chem. Eng. Sci. 2010, 65, 4460–4471. [Google Scholar] [CrossRef]
- Carletti, C.; Grénman, H.; De Blasio, C.; Mäkilä, E.; Salonen, J.; Murzin, D.Y.; Salmi, T.; Westerlund, T. Revisiting the dissolution kinetics of limestone—Experimental analysis and modeling. J. Chem. Technol. Biotechnol. 2015, 91, 1517–1531. [Google Scholar] [CrossRef]
- Otsuki, A.; Hayagan, N.L. Zeta potential of inorganic fine particle—Na-bentonite binder mixture systems. Electrophoresis 2020, 41, 1405–1412. [Google Scholar] [CrossRef] [PubMed]
- Al Mahrouqi, D.; Vinogradov, J.; Jackson, M.D. Zeta potential of artificial and natural calcite in aqueous solution. Adv. Colloid Interface Sci. 2017, 240, 60–76. [Google Scholar] [CrossRef] [PubMed]
- Rezaei Gomari, S.; Amrouche, F.; Santos, R.G.; Greenwell, H.C.; Cubillas, P. A New Framework to Quantify the Wetting Behaviour of Carbonate Rock Surfaces Based on the Relationship between Zeta Potential and Contact Angle. Energies 2020, 13, 993. [Google Scholar] [CrossRef]
- Derkani, M.H.; Fletcher, A.J.; Fedorov, M.; Abdallah, W.; Sauerer, B.; Anderson, J.; Zhang, Z.J. Mechanisms of Surface Charge Modification of Carbonates in Aqueous Electrolyte Solutions. Colloids Interfaces 2019, 3, 62. [Google Scholar] [CrossRef]
- Väisänen, M.; Hölttä, P. Structural and metamorphic evolution of the Turku migmatite complex, southwestern Finland. Geol. Surv. Finl. 2002, 71, 177–218. [Google Scholar] [CrossRef]
- Bang, J.-H.; Song, K.; Park, S.; Jeon, C.; Lee, S.-W.; Kim, W. Effects of CO2 Bubble Size, CO2 Flow Rate and Calcium Source on the Size and Specific Surface Area of CaCO3 Particles. Energies 2015, 8, 12304–12313. [Google Scholar] [CrossRef]
- Yuan, K.; Starchenko, V.; Lee, S.S.; De Andrade, V.; Gursoy, D.; Sturchio, N.C.; Fenter, P. Mapping Three-dimensional Dissolution Rates of Calcite Microcrystals: Effects of Surface Curvature and Dissolved Metal Ions. ACS Earth Space Chem. 2019, 3, 833–843. [Google Scholar] [CrossRef]
- Davis, K.J.; Dove, P.M.; Yoreo, J.J.D. The Role of Mg2+ as an Impurity in Calcite Growth. Science 2000, 290, 1134–1137. [Google Scholar] [CrossRef]
- Rhodes, M. Introduction to Particle Technology, 2nd ed.; Wiley: Hoboken, NJ, USA, 2008; ISBN 978-0-470-01427-1. [Google Scholar]
- Shiraki, R.; Rock, P.A.; Casey, W.H. Dissolution Kinetics of Calcite in 0.1 M NaCl Solution at Room Temperature: An Atomic Force Microscopic (AFM) Study. Aquat. Geochem. 2000, 6, 87–108. [Google Scholar] [CrossRef]
- Sjöberg, E.L.; Rickard, D.T. Calcite dissolution kinetics: Surface speciation and the origin of the variable pH dependence. Chem. Geol. 1984, 42, 119–136. [Google Scholar] [CrossRef]
- Fogler, H.S. Elements of Chemical Reaction Engineering, 5th ed.; Prentice Hall: Boston, MA, USA, 2016; ISBN 978-0-13-388751-8. [Google Scholar]
- Blasio, C.D.; Mäkilä, E.; Westerlund, T. Use of carbonate rocks for flue gas desulfurization: Reactive dissolution of limestone particles. Appl. Energy 2012, 90, 175–181. [Google Scholar] [CrossRef]
- Nascimento, D.R.; Oliveira, B.R.; Saide, V.G.P.; Magalhães, S.C.; Scheid, C.M.; Calçada, L.A. Effects of particle-size distribution and solid additives in the apparent viscosity of drilling fluids. J. Pet. Sci. Eng. 2019, 182, 106275. [Google Scholar] [CrossRef]
- Yamauchi, V.; Tanaka, K.; Hattori, K.; Kondo, M.; Ukawa, N. Remineralization of desalinated water by limestone dissolution filter. Desalination 1987, 66, 365–383. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics: A Ready-Reference Book of Chemical and Physical Data; CRC Press: Boca Raton, FL, USA, 2017; ISBN 978-1-4987-5428-6. [Google Scholar]
- Steefel, C.I.; Maher, K. Fluid-Rock Interaction: A Reactive Transport Approach. Rev. Mineral. Geochem. 2009, 70, 485–532. [Google Scholar] [CrossRef]
- Brand, A.S.; Feng, P.; Bullard, J.W. Calcite dissolution rate spectra measured by in situ digital holographic microscopy. Geochim. Cosmochim. Acta 2017, 213, 317–329. [Google Scholar] [CrossRef]
- Fischer, C.; Arvidson, R.S.; Lüttge, A. How predictable are dissolution rates of crystalline material? Geochim. Cosmochim. Acta 2012, 98, 177–185. [Google Scholar] [CrossRef]


| Rate Determining Steps | Reactions |
|---|---|
| Absorption of gaseous SO2 in liquid water | |
| Oxidation of (liquid phase) | |
| Solid limestone is dissolving in acidic environment (pH 5.5, industrial process) | |
| Crystallization of gypsum |
| Sample | ρ (kg/m3) | CaCO3 wt % | CaO wt % | Al2O3 wt % | SiO2 wt % | MgO wt % |
|---|---|---|---|---|---|---|
| Metamorphic Limestone | 2720 | 98.5 | 54.5 | 0.13 | 0.5 | 0.59 |
| Sedimentary Limestone | 2703 | 99.1 | 55.2 | 0.01 | 0.05 | 0.32 |
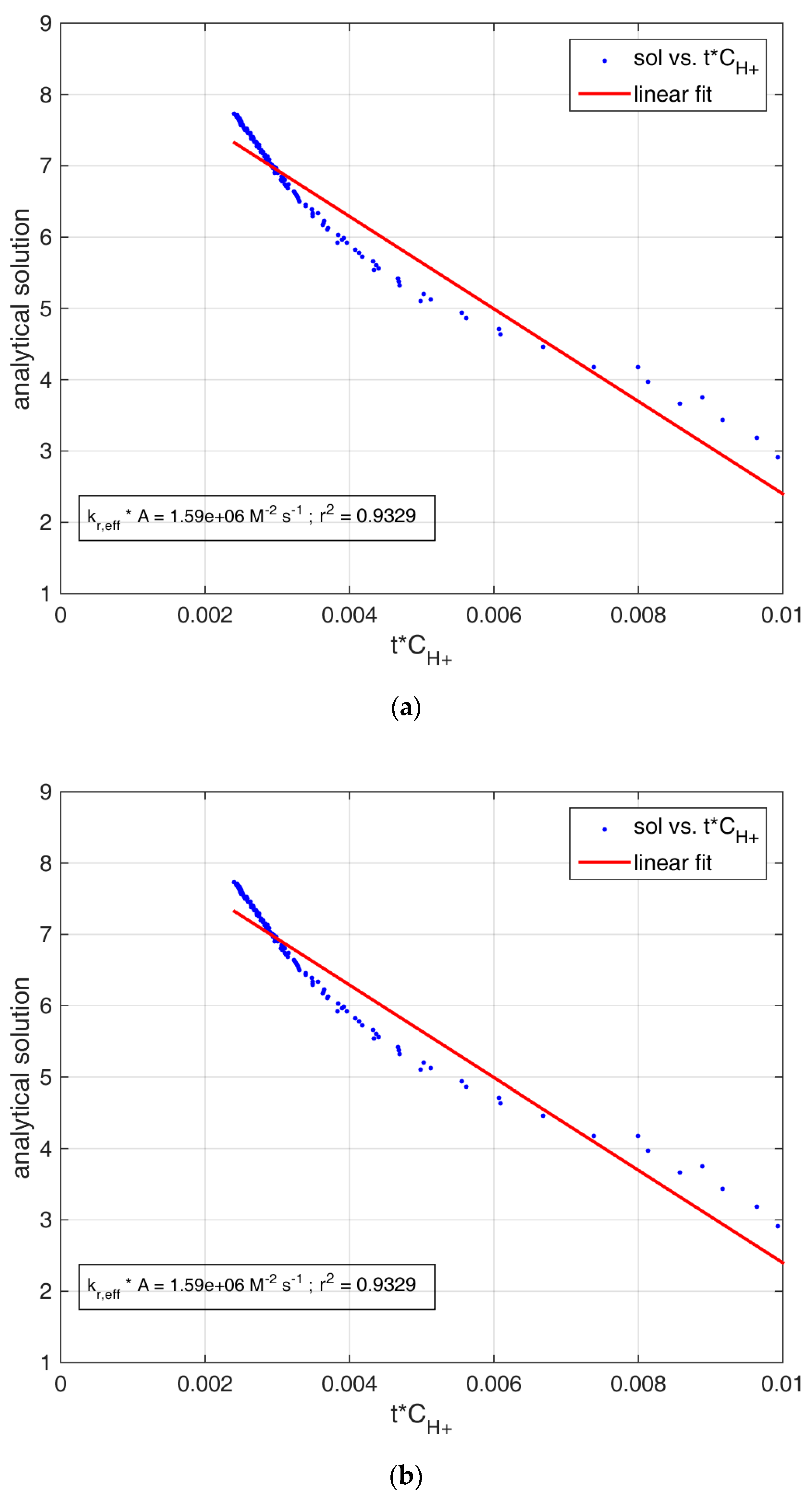
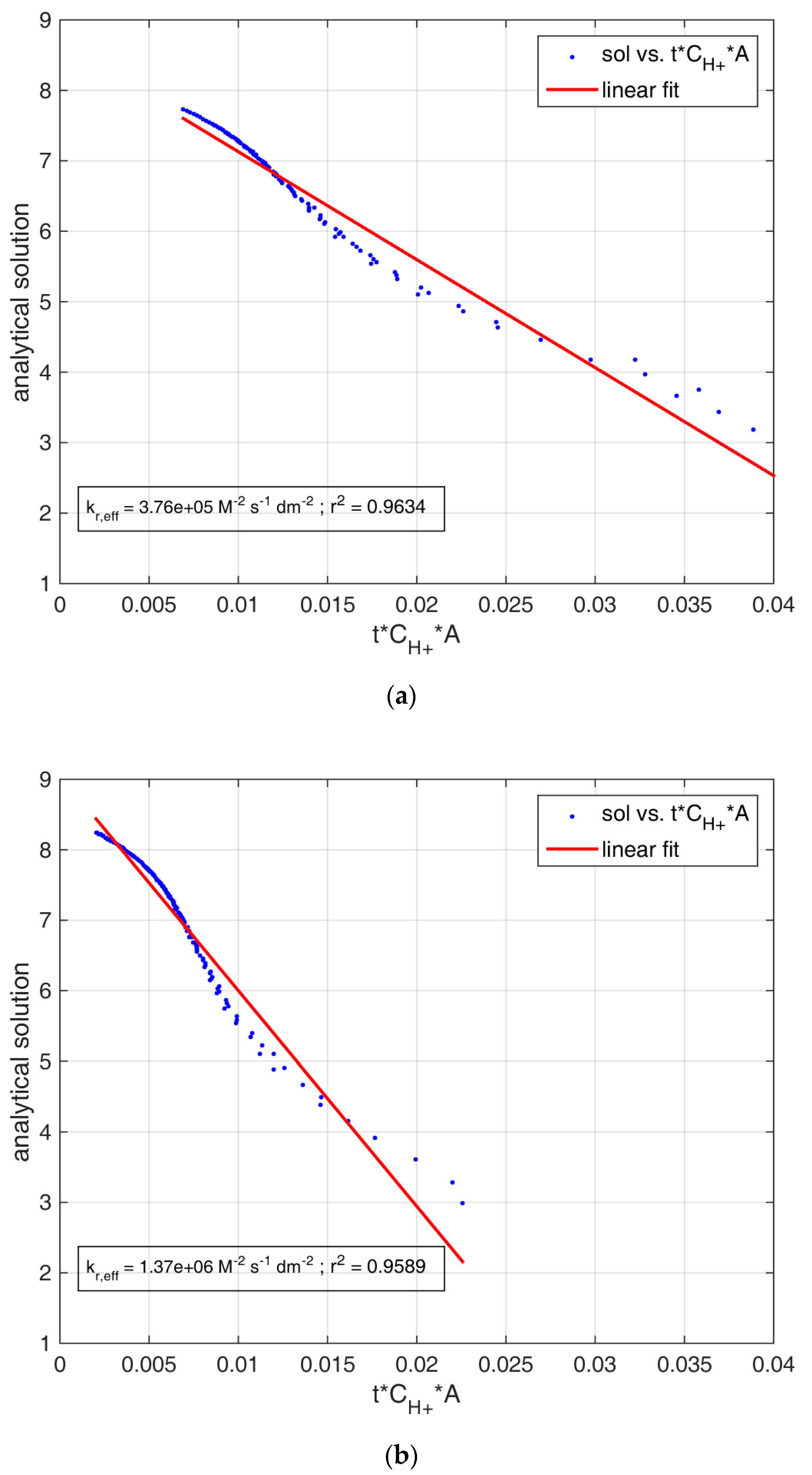
| Experiment | kr,eff A (107 M−2 s−1) | Goodness of Fit (r2) | Averaged Contact Area (dm2) | kr,eff (107 M−2 dm−2 s−1) | Goodness of Fit (r2) |
|---|---|---|---|---|---|
| Metamorphic_step1 | 0.159 ± 0.008 | 0.9329 | 3.76 ± 0.33 | 0.038 ± 0.001 | 0.9634 |
| Metamorphic_step2 | 0.129 ± 0.009 | 0.8835 | 3.78 ± 0.31 | 0.031 ± 0.002 | 0.9216 |
| Metamorphic_step3 | 0.112 ± 0.008 | 0.8683 | 3.72 ± 0.38 | 0.027 ± 0.002 | 0.9126 |
| Metamorphic_step4 | 0.132 ± 0.010 | 0.8719 | 3.80 ± 0.28 | 0.032 ± 0.002 | 0.9085 |
| Metamorphic_step5 | 0.109 ± 0.008 | 0.8512 | 3.74 ± 0.36 | 0.026 ± 0.002 | 0.8935 |
| Sedimentary_step1 | 0.636 ± 0.034 | 0.9020 | 3.45 ± 0.70 | 0.137 ± 0.005 | 0.9589 |
| Sedimentary_step2 | 1.018 ± 0.057 | 0.9124 | 3.74 ± 0.35 | 0.223 ± 0.008 | 0.9619 |
| Sedimentary_step3 | 0.409 ± 0.032 | 0.8527 | 3.78 ± 0.30 | 0.097 ± 0.006 | 0.9109 |
| Sedimentary_step4 | 0.327 ± 0.030 | 0.8035 | 3.75 ± 0.34 | 0.079 ± 0.006 | 0.8730 |
| Sedimentary_step5 | 0.428 ± 0.035 | 0.8329 | 3.74 ± 0.36 | 0.101 ± 0.006 | 0.9062 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Blasio, C.; Salierno, G.; Sinatra, D.; Cassanello, M. Modeling of Limestone Dissolution for Flue Gas Desulfurization with Novel Implications. Energies 2020, 13, 6164. https://doi.org/10.3390/en13236164
De Blasio C, Salierno G, Sinatra D, Cassanello M. Modeling of Limestone Dissolution for Flue Gas Desulfurization with Novel Implications. Energies. 2020; 13(23):6164. https://doi.org/10.3390/en13236164
Chicago/Turabian StyleDe Blasio, Cataldo, Gabriel Salierno, Donatella Sinatra, and Miryan Cassanello. 2020. "Modeling of Limestone Dissolution for Flue Gas Desulfurization with Novel Implications" Energies 13, no. 23: 6164. https://doi.org/10.3390/en13236164
APA StyleDe Blasio, C., Salierno, G., Sinatra, D., & Cassanello, M. (2020). Modeling of Limestone Dissolution for Flue Gas Desulfurization with Novel Implications. Energies, 13(23), 6164. https://doi.org/10.3390/en13236164








