Intelligent Systems for Power Load Forecasting: A Study Review

1. Introduction

The electrical load is the power that needs to be supplied to consumers. It is also referred to as power consumption or demand power. The electrical load fluctuates, and it is not always possible to store the generated power efficiently and in an optimal manner. Thus, it is necessary to keep the generated power to meet the demand power at a specific time [1]. Electrical load forecasting is used by electric power generation companies to estimate the total power needed to supply customers. It helps electrical power facilities make important decisions, decreasing power production costs, and increasing the power facility’s accuracy. The electrical load is determined by two main parameters—Electrical Power (MW, kW) or Electrical Energy (MWh, kWh). Many studies have focused on power load forecasting with the primary goal of finding a reliable and precise model for power load forecasting. These studies used a different number and types of input features related to consumer behaviour and features that directly affect the electrical load. Among the environmental and weather conditions, these input variables are calendar data, type of days (working days or holidays), temperature, wind speed, air pressure, humidity, previous load, etc. The goal is to find the relation between the inputs into the system or input variables and the system outputs or power load. The power load is changing randomly over the day and has different values-from time to another in the same day and season to another year season. For example—in the summer, the air temperature increases. Most consumers use air condition, which causes increasing the consumed power. For a reliable and accurate forecasting system, the model should be tested and valid for all day and year seasons. The critical type of power load forecasting is in the short-term, which uses for scheduling the electricity flow to users [2]. Demand power is forecasted in advance as short-term, mid-term and long-term. The power systems need tight control functions to produce good quality power so that the power quality parameters [EN 50160] can be immediately corrected. The power load forecasted in the short-term plays a very significant role in electric utility. For these reasons, we focused on reviewing past studies on short-term forecasting below. This study presents five sections: Section 1 with the introduction, Section 2 includes the motivation of this study, Section 3 explains the power load forecasting, Section 4 presents the previous studies of load forecasting, and Section 5 and Section 6 with a discussion and conclusion.

2. Motivation of This Study

As a result of the growing and continuous use of renewable energy sources, being clean and free electrical power sources, forecasting models are being developed worldwide in order to incorporate the renewable energy sources for supplying the demand power as much as possible. The most significant challenge for power load predicting is to create a reliable and precise model to estimate demand electrical power values because it is impossible to store the generated power. The generated power must be fed to supply the load in an optimal way that will keep balancing the power grid as can be seen in Figure 1. For this purpose, this study aims to be a review of the previous studies focusing on the design of power demand forecasting models. This study can help researchers and students, who can get an accessible brief overview on power forecasting. The electrical power which is generated from renewable energy sources depends on weather conditions that fluctuate randomly, thus making the electrical power generation values uncontrollable. From the perspective of the economy and the power quality, the power load must consider the generated power from renewable energy sources. Hence comes the need to study and design intelligent control models to operate and control the power flow from sources to consumers in an efficient manner. A smart control model includes several stages or models, where one of the important models is a forecasting power load model. This study has been motivated to provide a brief description of power load forecasting systems.

3. Power Load Forecasting

The future power load value must be forecasted so that it is known in advance in order to minimize possible costs and to keep power quality satisfactory. The electrical power load fluctuates naturally depending on several conditions, such as temperature, humidity, pressure, time, season, etc. These important input variables must be taken into account when designing power load forecasting systems. Short term load forecasting (STLF) says what the future value of the power load will be. The control system of the utility power will use the forecasted power to decide the number of working generators units. For example, if the forecasted load is high, a new generator unit should start, which will supply the equivalent increase of the electrical load. On the contrary, if the forecasted load is low, some generator units should be cut off. The electrical power is generated according to the power needed to supply the specific load or demand power, which means the production power should be as equal to the consumption power as possible, having taken into account the power quality parameters. So, for the utility reliability and to ensure the regular power supply to customers according to power quality levels, the future power should be forecasted. Based on the available research, the power load forecasting methods can divided into three types below:

• Short-term load forecasting-used to predict the load power from one hour to one week.
• Mid-term load forecasting-used to predict load power from one week to one year.
• Long-term forecasting-used to forecast the load power for periods between one and up to 50 years [3,4].

In general, the mean absolute percentage error (MAPE) and root mean square error (RMSE) are used when evaluating the forecasting accuracy of designed models for power load forecasting field as in the following equation. MAPE demonstrates the average relative error between the actual power load value and the predicted power load value. RMSE calculates the square root of the sum of the squared differences between the actual power load value and the predicted value from the model output.

$$\mathrm{MAPE}=\frac{100}{n}\sum _{i=1}^n\left(\frac{A_i-F_i}{A_i}\right)$$

(1)

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}\sum _{i=1}^n{(A_i-F_i)}^2}$$

(2)

where $A_i$ is the actual value of the electrical load, $F_i$ is forecast value of electrical load, n is the number of evaluated forecast values.

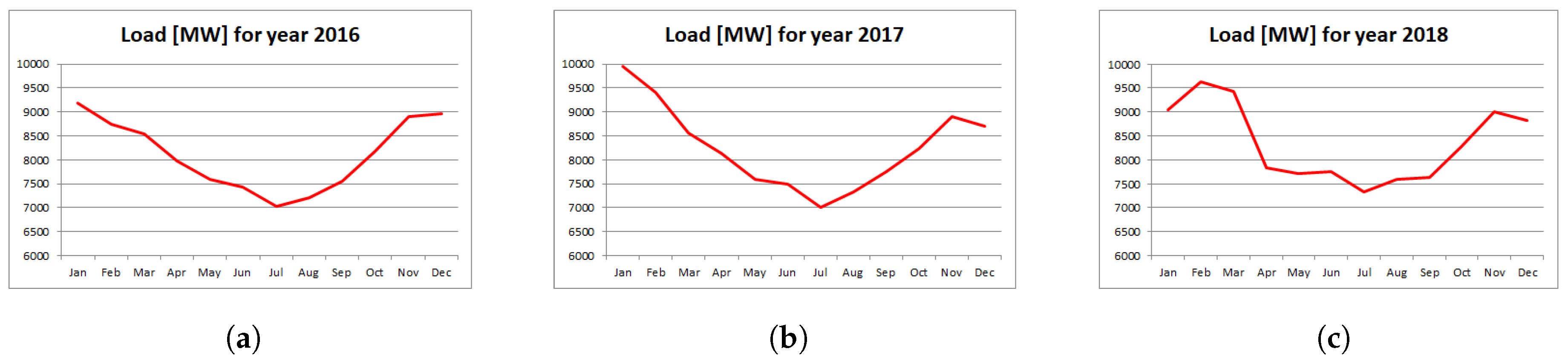
Power Load Profile

The power demand differs over the time of day. It depends on human activities and many other factors, such as the time of day, season, weather condition, days of the week. A power load curve is a plot of variation values of the consumed power over time. The load curve reflects the behaviour of consumers as they use different home appliances, such as TVs, microwaves, washing machines, etc. The power load curve can be plotted either for one day, known as the daily power load curve, weekly for one week, monthly for one month or yearly for one year. In most cities worldwide, the residential daily power load starts at 6:00 a.m. and ends at 6:00 p.m., while reaching its maximum value in the afternoon. The significant information of the power load to control the run of the certain number of power generators can be obtained from daily load curves. Figure 2a–c, give the power load of the Czech Republic for the entire years 2016, 2017 and 2018, respectively, provided by CEOS, a.s. (https://www.ceps.cz/en/homepage). The graphs showed the power load reached: minimum values from April till September, and maximum values approximately from January to April and from September to December.

4. Previous Studies of Load Forecasting

Among the many published papers using and combining various types of techniques with the purpose to design models for power and electrical load forecasting, we focused on five groups of techniques: ANN, SVR, DT, LR, and FS. The load forecasting models seek to determine relations between the power load and many factors affecting it, such as air temperature, humidity, types of days, previous load, etc.

4.1. Artificial Neural Network (ANN)

In this section, the applied neural network for power load forecasting, either ANN alone or with other pre-processing techniques, is discussed. In 2009, Xiao et al. used a back propagation neural network with rough sets for power demand forecasting. The system was compared with standard BP and in general the performance of BP with rough sets was better than standard BP [5]. Din and Marnerides applied the Feed Forward Neural Network (FFN) and Recurrent Neural Network (RNN) with deep learning for short period power load forecasting, using a dataset collected from New England for the period from 2007 to 2012. The model was tested for two cases: the first case time domain features were used, while in the second case both features from time and frequency domains were used. The evaluated system using MAPE, RMSE and MAE errors, which rendered lower rates in the second case than in the first one, and the accuracy of the model were improved in the second case [6]. An applied ANN with wavelet decomposition was designed by Reddy and Jung; the experiment results showed the efficiency performance of the proposed system, which exceeded ANN [7]. Electrical load forecasting using advanced wavelets with neural networks was proposed by Rana and Koprinska. The proposed system consists of four steps: load data decomposed into high and low frequencies using wavelet transform, feature chosen based mutual information, training NN for each component and testing the trained model. The model was evaluated for two data sets from Australia and Spain. The mean absolute percentage errors were 0.268% and 1.716% for the Australian and Spanish data sets respectively. In addition, the articles conclude that the system out-performed the other existing models [8]. Mordjaoui et al. proposed using a dynamic Neural network to forecast the electricity load. The proposed system was designed and tested using a dataset of the French Transmission System Operator. The simulation results proved the validation of the designed method [9]. The idea for using loads of identical days as the input variable of the combination from wavelet transform with a neural network to predict future values of the load was proposed by Chen et al. [10]. Zheng et al. designed an intelligent model for demand power forecasting, k-means for cluster data wavelet transform to decompose the data and finally NN to forecast the final value of the power load [11]. Niu et al. used a Hybrid Monte Carlo technique for training a Bayesian neural network (BNN) for the purpose of designing a power load forecasting model. The designed system was compared with BNN trained using a La-place algorithm and ANN trained using a Backpropagation technique using MAPE and RMSE criteria. The experiment’s result proved the validity of the designed method for load forecasting [12]. Combining the K-means clustering with ANN for load forecasting was made by Jahan et al. The experiments used k-means and k-medoids for clustering the original data into groups then measuring the distance between each sample and each cluster as new features which were fed into ANN. The results of ANN proved better than a decision tree when comparing the results using the MAPE criterion [13]. Khwaja et al. proposed using a bagged neural network (BNN) for load forecasting. The idea of BNN is dividing the data set into random parts, then training the neural network for each part, the average of the outputs representing the output of the model. The outcome of the proposed idea reduced the forecasting error when compared with standard ANN and other existing approaches [14]. Wang et al. proposed BPNN for power load forecasting. The idea was to optimize the network weights using a genetic algorithm faster than standard BPNN. The results showed that the proposed optimization algorithm improved the learning speed and the accuracy of the learning process [15]. Ekici applied an extreme learning machine (ELM), regularized ELM (RELM) and ANN for electrical load forecasting, and comparing their performance. The outcome of the experiments confirmed that the RELM learned much faster than ANN and the forecasting accuracy of RELM was better than standard ELM [16]. A hybrid model for short load forecasting was studied by Zhang et al. [17]. The model has been constructed from improved empirical mode decomposition, an autoregressive integrated moving average (ARIMA) and wavelet neural network optimized by the fruit fly optimization algorithm. The MAPE of the model’s forecasting results was improved and is about 0.82% higher than other compared systems. In the USA, Ashfaq et al. designed a one day-ahead system for power load forecasting. The designed system constructed in three stages: pre-processing, in this stage removing unwanted samples, the forecasting stage using ANN, and the optimization stage for minimizing the forecasting errors. The forecasting accuracy of the system improved in comparison with other models [18]. Yi Liang et al. introduced a hybrid system for electricity forecasting. The model is constructed as follows: empirical mode decomposition, minimal redundancy maximal relevance, neural network for regression with the fruit fly optimization algorithm. The simulation results of the model proved the validity of the system in STLF [19]. In Spain, a short-term load forecasting model was designed using three stages: SOM maps used for pattern recognition, k-means for clustering the patterns, and ANN to predict the power load. The methodology has been trained and tested using a data set from the Iberdrola company. The system has a small error when compared with others [20]. Short-term weekday power load forecasting was proposed in [21]. The paper compared ANN with different learning algorithms. The best results were obtained when using a Generalized Neural Network with wavelet transform that was trained using an adaptive genetic algorithm and fuzzy system. In Canada, El-Hendawi and Wang designed a method for short-term demand power forecasting. The method combined the full wavelet packet transform with neural networks. The designed system decreases the forecasting error by 20% when compared with standard neural networks [22].

4.2. Support Vector Regression (SVR)

SVM is a powerful tool for classification and regression purposes. SVM was applied and used by several researchers in the area of power load forecasting, whether alone or combined with other techniques to improve the forecasting accuracy. Liang et al. designed a prediction system to predict demand power using a wavelet transform with least squares SVM (LSSVM) with the optimization factors of LSSVM using a cuckoo search; the results of designed system were compared with other various methods of SVM, which proved the efficiency of the introduced model [23]. Ren et al. proposed an annual power load forecasting system of based SVM, which was optimized by particle swarm optimization. The proposed approach was trained and tested using data of the city of Beijing city for the years from 1978 till 2010. The simulation results proved the validity of the model for load prediction, where the MSE error was about 2.53% [24]. Liu et al. have designed an intelligent system for short-term load forecasting using wavelet least square SVM (W-LSSVM) combined with the DWT and inconsistency rate model (DWT-IR) for feature selection. The system was evaluated using RMSE and MAPE, which was about 0.019 and 1.83% respectively. It proved the activity of the model and out-performed other existing methods when the results were compared [25]. Niu at al. have designed a power load prediction method, which combined an ant colony optimization (ACO) with a support vector machine (SVM), ACO used for feature selection and SVM for load regression. The proposed system was suitable for short-term load forecasting and surpassed other existing methods [26]. The use of the large-scale linear programming support vector regression (LP-SVR) for STLF was studied by Perea et al. The studied model was compared against bagged regression tree, Feed Forward ANN and Large-Scale Support Vector Regression (LSSVR). The MAPE error of the LP-SVR approach was about 1.58% lower than from the other compared models [27]. Sreekumar et al. applied and tested a tree model of SVM for short-term power demand forecasting. Standard SVM, SVM optimized using Genetic Algorithm (SVRGA), and SVM optimized using a Particle Swarm Optimization Algorithm (SVRPSO). The outcome accuracy of the proposed mode when estimated for SVM, SVRGA and SVRPSO was about 97.67%, 97.82% and 97.89% respectively. The article concluded that the three models were highly active for STLF, but SVRPSO, and SVRGA consumed more time than standard SVM [28]. A data set from Hubei SVM for short-term power load prediction was studied by Ye et al. The performance of the proposed approach was compared with traditional models: BPNN and the time series method. The MAPE error for SVM was about 1.91%, for BPNN it was 4.06% and for the time series it was about 4.47%. The capacity of SVM in STLF was better than others according to the simulation results [29]. A combination of singular spectrum analysis (SSA), a support vector machine (SVM) and Cuckoo search (CS), was applied for power forecasting by Zhang et al. Results of the proposed approach were compared with other studies, which confirmed the capability of the hybrid model in load forecasting [30]. A hybrid intelligent system was designed for STLF in [31]. The previous temperature and the wavelet coefficients of the previous load are used as input variables where the Gram–Schmidt (GS) was used for feature selection and SVR was used to predict the consumed power. The system was applied for both weekdays and weekend days. The hybrid system produced the best prediction accuracy when compared with others. Dai et al. have designed a daily peak power load forecasting system. The load was decomposed using the complete ensemble empirical mode decomposition with adaptive noise, and modified grey wolf optimization and support vector machine used to forecast the final result of the load. The performance of the model was compared with various SVMs and ANN. The simulation results confirmed the ability and reliability of the designed system [32]. The empirical mode decomposition (EMD) method and the support vector machine with the particle swarm optimization (PSO) algorithm were designed in [33]. The experiment was carried out in three forecasting parts, followed by a summation of the results of these parts as the final forecasting result. The experiment outcome demonstrated that the proposed example was effective when compared with other existing formations of SVM.

4.3. Decision Trees (DT)

There are a huge number of studies which used various kinds of decision trees to estimate the demand power. Using a random forest decision tree for demand power forecasting was designed by Dudek. The proposed method was tested on a dataset from Poland. The performance of the system was highly accurate when compared with the results of other current methods [34]. The REPTree Decision Tree for power load forecasting is applied and tested by Hambali et al. The designed system was compared with standard and other decision trees which proved the validity of the proposed system for predicting the power load [35]. Li et al. have designed a decision tree to estimate future demand power for short-term periods. The input features were weather data and power load, while the current load was used as the output of the system. The outcome of the experiments showed the validation of DT for power load forecasting [36]. The use of generalized minimum redundancy and maximum relevance (G-mRMR) for feature selection and random forest for short-term demand power forecasting is studied in [37]. Results showed that the G-mRMR can capture important features for STLF, plus the forecasting results were better than other tested existing patterns. In Tunisia, one day ahead of one-hour step for short-term power demand prediction using a random forest technique was studied in [38]. The article concluded that the designed system was fast and did not need any improvement in the approach. In 2018, Moon et al. designed two stages to predict daily power load: a moving average method and random forest, and the predicted result was evaluated using time-series cross-validation. The results of the proposed model outperformed others when comparing the results, which proves the validity of the proposed model [39]. In Spain four models of regression trees (bagging, random forest, conditional forest and boosting) have been designed and tested for power load prediction using the data set of a campus university in Cartagena [40]. The temperature, calendar information and types of days are used as predictors to improve the performance of the model. The designed system has been tested for special and regular days. In southern China, Liu et al. used the day’s average humidity, average temperature, humidity average of the first three days, temperature average of first three days and historical load at same moment of the first days. The used factors were input variables to predict the load using a Gradient Boosting Decision Tree. The forecasting accuracy was evaluated and compared with other current systems. The compared result proved the validity of the designed method for load prediction [41].

4.4. Linear Regression (LR)

Linear regression for STLF and its various types have been used and studied by many researchers. Aprillia et al. have constructed a system for power load prediction as follows: a whale optimization algorithm to detect and choose the appropriate level of the wavelet decomposition, discrete wavelet transform to decompose data into detail and approximation signals and a multiple linear regression technique to predict the final result of the load. The proposed scheme was tested for weekdays and holiday days for all seasons and produced a low forecasting error when compared with different models [42]. Amral et al. have designed multiple linear regression for load forecasting. The experiments were made for both the dry and rainy seasons. The MAPE error between the actual and forecasted values was about 3.52% and 4.34% for the dry and rainy days respectively [43]. Saber and Rezaul Alam applied multiple linear regression on a big data set to find the relation between weather conditions and demand power. Multi-core parallel processing is used to deal with big data. The MAPE error of the system was about 3.99% and the implementation time was faster than the other existing models like ANN [44]. Improving the accuracy of the STLF based combining clustering K-nearest neighbour (K-NN) and K-means with multivariate linear regression was studied in [45]. The used input variables are: Max and Min temperature and the previous power load. The MAPE of the combined model was about 3.345%, i.e., better than multi-linear regression.

4.5. Fuzzy Sets (FSs)

There are many studies which used and designed fuzzy models for power load forecasting. The main and basic idea is converting the input crisp values into fuzzy values or membership degree (fuzzification), such as air temperature, wind speed and so on. The same procedure is used for the target output (power load). Next, the fuzzy inputs pass the inference engine which include several fuzzy rules (if - then) to make decisions. The last stage is defuzzification to convert the output of the inference engine from a fuzzy to crisp value, which will represent the forecasted power load. Fuzzy sets and their different configurations have been used successfully by several researchers for load forecasting fields. For example, the use of fuzzy logic and an adaptive neuro fuzzy inference system (ANFIS) for short-term load forecasting has been applied by cevik and cunka. The system has been tested and compared with other systems where the MAPE error was about 2.1% and 1.85% for fuzzy logic and ANFIS respectively, which confirmed the validity of the proposed model [46]. Short period load forecasting using fuzzy control in Jordan has been designed by Mamlook et al. They used the previous day load, previous week load, previous day temperature, forecasted temperature, weather and index day, which is classified as a weekend or workday. The results confirmed the validity of the system for demand power forecasting [47]. A new type of reduction (TR) based on an artificial neural network (ANN) of an interval type two fuzzy logic system (IT2FLS) for power load prediction was proposed by Khosravi and Nahavandi. The paper compared the result of the planned system with 5 conventional TR. The numerical results show that the performance of the designed model outperformed IT2FLS with traditional TR [48]. Khosravi et al. applied IT2FLS for short-term load forecasting. The input variables used are: lagged power demands, meteorology data and calendar information, where the genetic algorithm was used for training the system. The simulation results proved the validity of the IT2FLS for STLF problem, which out-performed the type 1 fuzzy system and ANN [49]. Power demand prediction using a fuzzy logic system was applied by Manoj and Shah, where the temperature, similar previous day load and time are used as input variables. The forecasted and the real load were compared, where the error ranged between about +2.69% and −1.88% [50]. An extreme learning machine (ELM) algorithm for training IT2FLS of the purpose of designing a power load forecasting model was designed by Hassan et al. The data set used in this experiment is taken from the Australian National Electricity Market and Ontario Electricity Market. The performance of the proposed system was compared with the performance of ANN, ANFIS and IT2FS, which was trained using a KF algorithm. The Empirical results showed and confirmed that the designed model works better for load forecasting and it out-performed the other compared systems [51]. Another study in Indonesia by Dharma et al. used IT2FLS to design a model for load forecasting. The system tested using the data sets of 2005 and 2006, where the MAPE error was about 1.0335% and 1.5683% for the years 2005 and 2006 respectively. This study also concluded that IT2FLS can solve load forecasting problems better than standard fuzzy logic [52]. Analysing demand power prediction using a fuzzy logic system was introduced in [53]. The input variables used are temperature, humidity and wind speed while the power load was used as the target output. The model was tested for different numbers of days: holidays and working days. In 2016, Danladi et al. designed a model for demand power forecasting based on fuzzy sets. The model used three parameters as inputs: temperature, time and previous day load. The MAPE of the model was about 6.17%, as well observed that the most significant weather parameters affecting the power load was the temperature [54]. A fuzzy model for hourly load forecasting for different days has been designed by Ganguly et al. Time and day type (workday, weekend or holiday) were used as input variables [55]. The results of the suggested model were satisfactory. They also concluded that the model could not deal with any sudden changes in the load. In Iran, Malekzadeh et al. used a data set measured from Iran and a locally applied linear model tree for training the Takagi-Sugeno-Kang neuro fuzzy model. The model has been used to analyse short-term power load forecasting. The local linear model tree helps to set up the parameters and build a flexible neuro fuzzy [56].

5. Discussion

Table 1. The results of MAPE of comparison for 6 forecasting models.

Model	MAPE	Year	Place
ANN (AWNN) [8]	0.268%	2016	Australia and Spain
SVM (CEEMDAN-MGWO-SVM) [32]	0.1961%	2018	China
DT (RF) [34]	1.166%	2015	Poland
LR (WOA-DWT-MLR) [42]	1.2955%	2019	New England and Taiwan
FS (IT2FS) [52]	1.0335%	2011	Indonesia
SOM-K-means-ANN [20]	2.71%	2014	Spain

shows the approximate comparison results of the six short-term power load forecasting systems presented in this article. These systems used different types of input variables and forms. The results were compared using MAPE criteria and other variables such as the place and date of the study. The best results in [32] Complete Ensemble Empirical Mode Decomposition with Adaptive Noise and Support Vector Machine Optimized by Modified Grey Wolf Optimization Algorithm (CEEMDAN-MGWO-SVM), which achieved the smallest value of MAPE (0.1961%). The MAPE in [8] was about 0.268% for the Australian data set, the model used advanced wavelet transform with neural networks. The forecasting result of Inerval type 2 fuzzy system (IT2FS) was about 1.0335% [52]. The random forest decision tree was 1.166% [34], the multiple linear regression (WOA-DWT-MLR) was about 1.2955% [42], and lastly, the combination of SOM map, k-Means and ANN (SOM-K-means-ANN), the load was forecasted in three clusters, with the best result obtained from cluster 3, which was 2.71% [20].

Power load is an important variable of the power control flow process. Power load forecasting is a significant task when designing smart control models. This study can help researchers to identify factors that directly affect the power load as well as help to choose a suitable model for power load prediction.

6. Conclusions

The major contribution of this study is to review the knowledge of the demand power and previous studies in power load forecasting systems that can help scholars and experts in this field. Normally, power load is affected by different factors such as weather conditions and human behaviour. An important weather variable is temperature, as the load increases due to the used air conditioning in the summer and heating devices in winter. To control and operate the power grid system economically while keeping power quality at standard levels, we should know and forecast the demand power needed to supply the load. Therefore, the forecasting process plays a key role in these issues. As a result, to control and operate power systems in an optimal way, the generated power should agree with a specific standard of power quality parameters such as EN 50160. Estimating the future power value needed to supply the customers is an important task, which provides load prediction for power generation scheduling and making control decisions. Many studies have been introduced over the last decade concerning STLF as accurate demand power forecasting models play a key role in minimizing the costs of power production. Short-term power load forecasting is considered to be an important part when designing a smart control system. This review deals with short-term power load forecasting for the past decade. As can be seen, a large number of studies have used a neural network model, support vector machine and fuzzy sets, while a smaller number of studies have used decision tree and linear regression. In general, the expert systems based on SVR, neural networks and fuzzy sets rendered better results in the field of power load forecasting than the others models, such as decision tree and linear regression.