A Distribution System State Estimator Based on an Extended Kalman Filter Enhanced with a Prior Evaluation of Power Injections at Unmonitored Buses
Abstract
1. Introduction
- The algorithm conceived to estimate the inputs to the prediction step of the filter. Such a sequence of data is obtained by disaggregating the active and reactive power injection variations measured at the substation;
- A deeper analysis of the relative impact of an increasing number of PMUs and SMs on state estimation performance when such measurements are used in the update step of the EKF.
2. Related Work
3. Models Description
3.1. System Model
- The intrinsic voltage phase and RMS amplitude fluctuations at the slack bus in normal operating conditions (first two entries);
- The errors resulting from the linearization of the power injection equations (remaining entries).
3.2. Measurement Model
- and are the long vectors including the active and reactive power injections as functions of the state. In practice, the i-th elements of such functions are given by (2).
- comprises both the slack bus RMS voltage and the RMS voltage values measured by M PMUs deployed at buses . Similarly, is the vector of voltage angles measured directly by the same PMUs.
- Finally, vectors and comprise the RMS values and the angles, respectively, of the phasors of the current flowing through one of the lines connected to the M buses where the PMUs are installed.
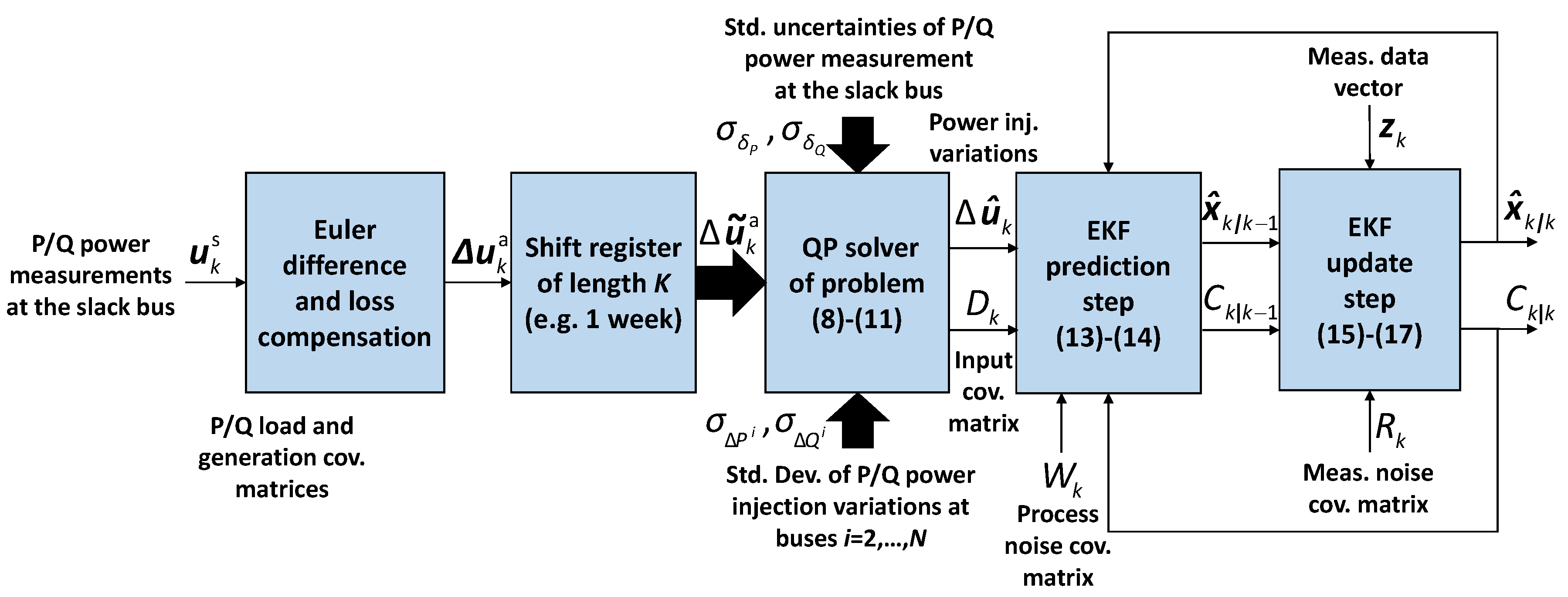
4. State Estimation Algorithm
4.1. Prior Estimation of Power Injection Variations
- K be the number of samples collected in the observation interval and arranged into vector ;
- be the column vector of the corresponding uncertainty contributions;
- be the -long column vector obtained by stacking elements and for and (namely the active and reactive power injection variations at all the buses different from the slack bus in the observation interval ).
- Linear constraint (9) withis the underdetermined linear system that has to be solved to find the inputs to the EKF. In each equation, the sum at time of the active or reactive power injection variations, respectively, at all buses different from the slack bus is set equal to sum of the aggregate value returned by (7) and the unknown uncertainty contribution . The uncertainty contributions should be estimated as well. However, since they can be reasonably assumed to be small and their impact on (9) should be kept as small as possible, the minimization of their mean square value is indeed the objective function of the optimization problem (8).
- Constraint (10) relies on the assumption that the mean value of variables is zero and provides a lower bound to the variances of the uncertainty contributions affecting the aggregate active and reactive power variations, respectively. Therefore, it provides a lower bound to the objective function as well. Indeed, the variance values estimated over the observation interval cannot be smaller than the square of the combined standard uncertainties (denoted with and ) of the power injection variations measured at the slack bus.
- Finally, the equality constraint (11) forces the sample variances of the unknown active and reactive bus power injections variations to be equal to given values denoted as and , respectively, for . Such values can be found a priori, for example, from past pseudo-measurements. Again, (11) relies on the realistic assumption that the mean values of the power injection variations over time are null.
4.2. EKF Implementation
5. Case Study Description
6. State Estimation Results
6.1. QP Settings for EKF Input Evaluation
6.2. Process Noise (EKF Only)
6.3. Power Injection Measurements
- The first scenario refers to the classic case in which just historical a priori information on power injections (i.e., pseudo-measurements only) is available. In this case, the unknown delays and the time misalignment between the collected data strongly affect measurement uncertainty, which consequently is as large as load inherent variability (scenario 1).
- The second scenario relies on the assumption that power injection measurements rely not only on pseudo-measurements, but also on the data collected by the SMs every 15 minutes. Such data are assumed to be aligned in time with a delay of a few seconds before being aggregated (scenario 2). In this case, we assume that the weight of SMs measurements on the total relative variance of power injection measurement data is about 33% at all buses (scenario 2).
- The third scenario is similar to the second one, but a deeper penetration of SMs is envisioned. Therefore, the weight of SMs measurements on the total relative variance of power injection data reaches about 67% (scenario 3).
- Finally, the fourth scenario relies on the assumption that all power measurements are collected from customers’ SMs and are properly aligned in time before being aggregated. Of course, in this case, the traditional pseudo-measurements are no longer used (scenario 4).
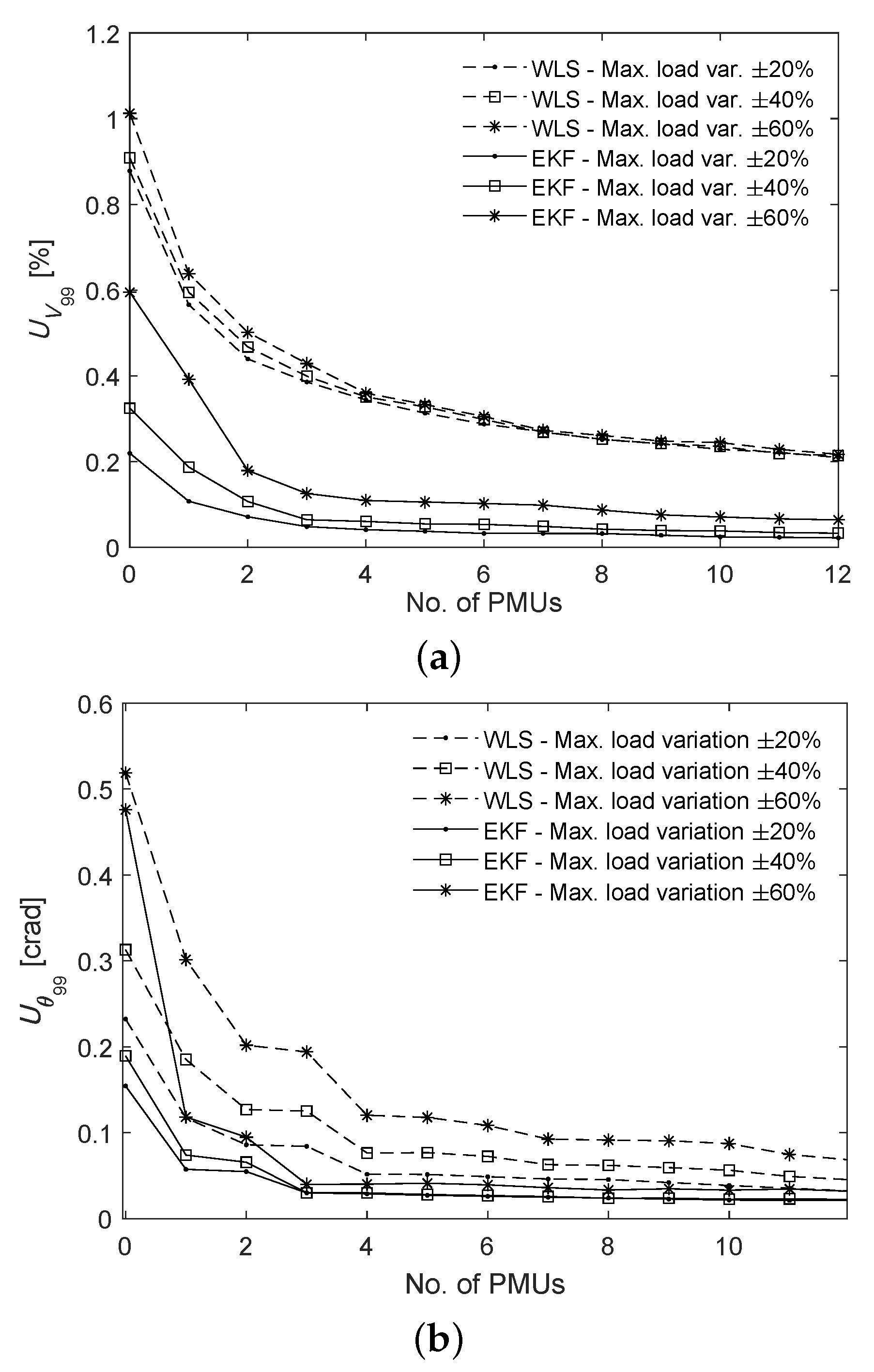
6.4. PMU-Based Measurements
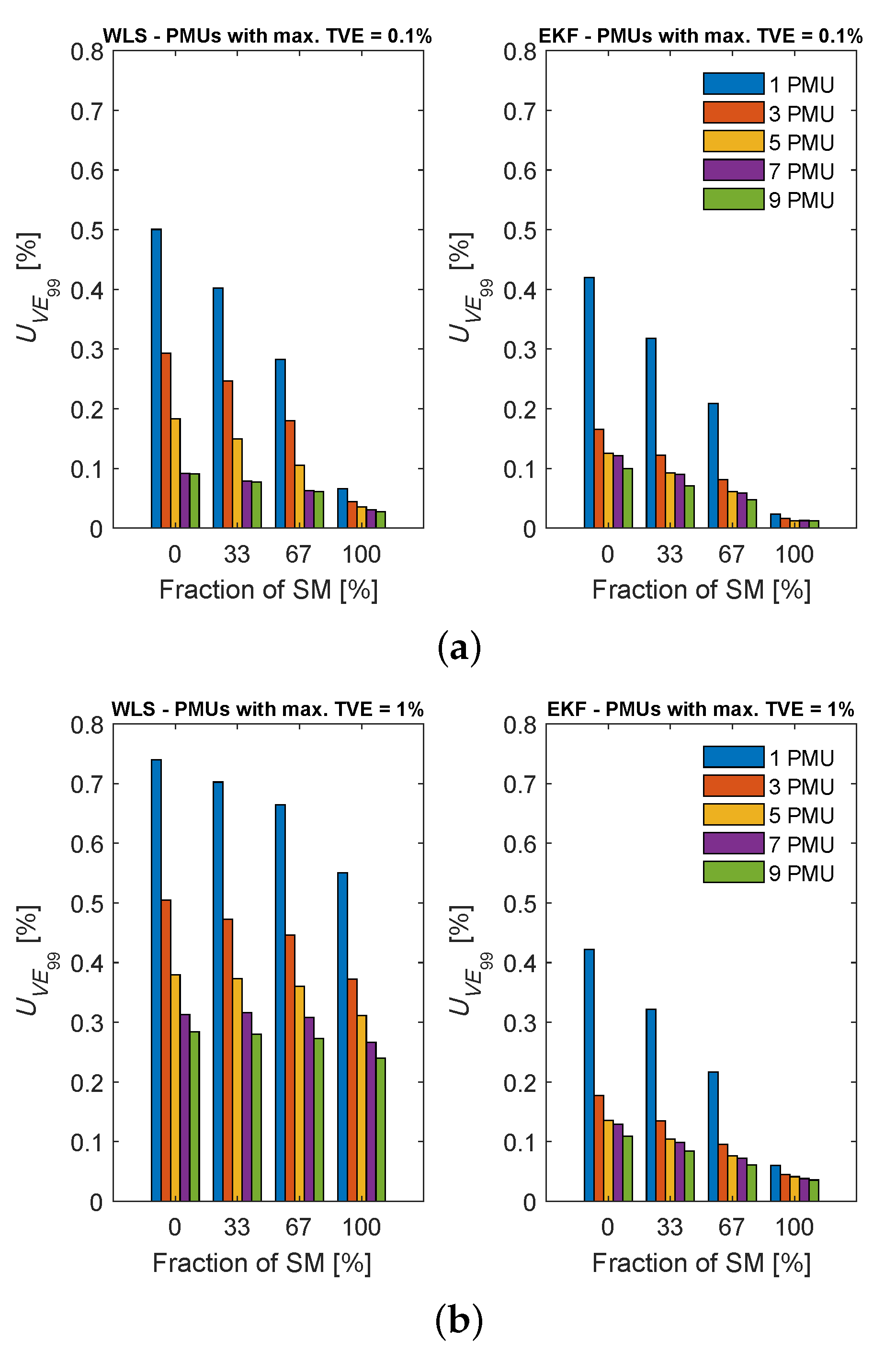
6.5. Performance Analysis
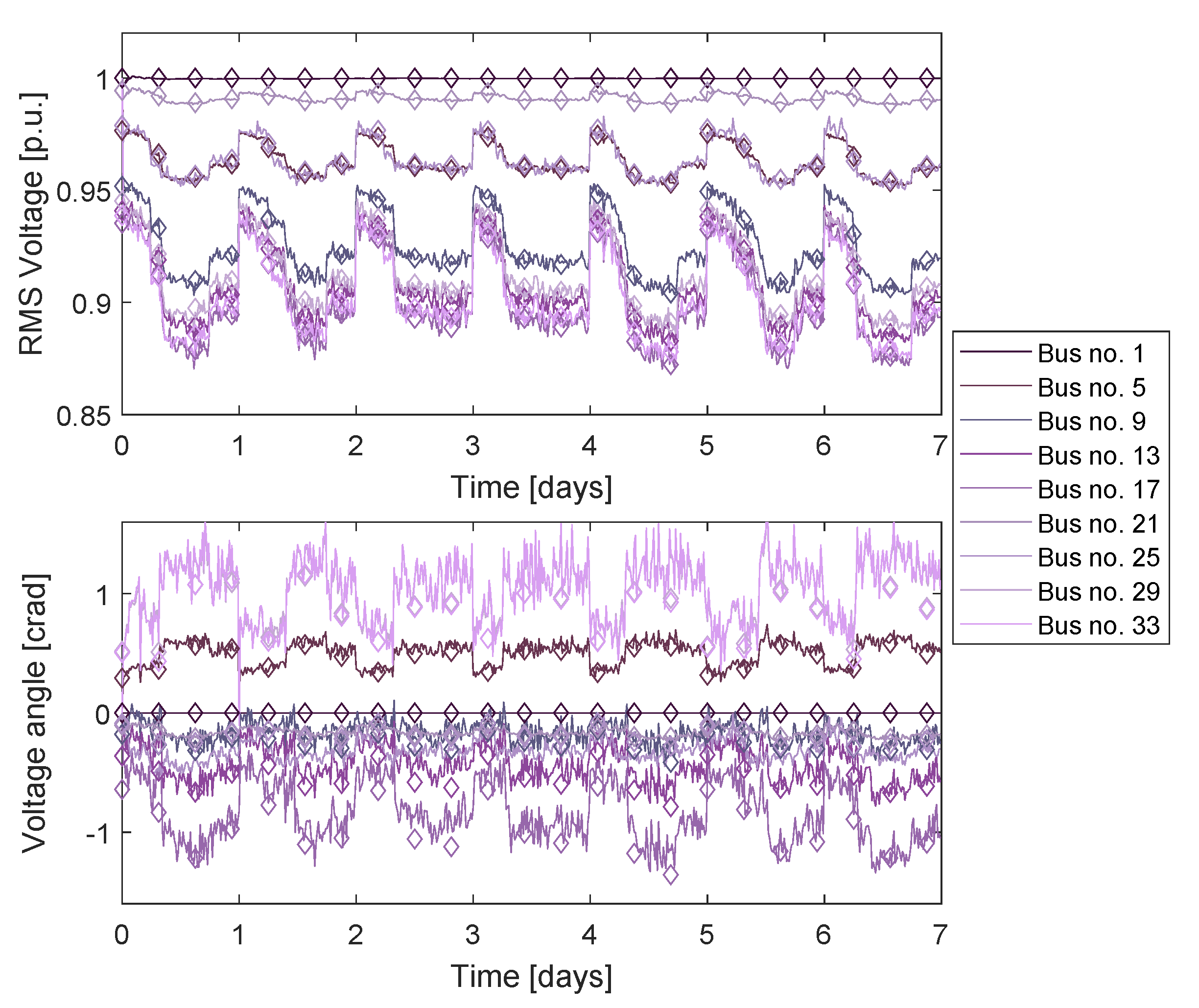
- The initial EKF transient is quite short (just a few samples). This is most probably due to the good initialization of the EKF;
- The estimated state tracks the pseudo-periodic voltage pattern resulting from the time-varying load conditions shown in Figure 3 very well;
- State estimation accuracy is clearly high, since the differences between estimated and actual values at a given time are very small.
7. Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AMI | Advanced Metering Infrastructure |
| DSO | Distribution System Operator |
| DSSE | Distribution System State Estimation |
| EKF | Extended Kalman Filter |
| GMM | Gaussian Mixture Model |
| QP | Quadratic Programming |
| PMU | Phasor Measurement Unit |
| PSO | Particle Swarm Optimization |
| RMS | Root Mean Square |
| SE | State Estimation |
| SM | Smart Meter |
| TVE | Total Vector Error |
| UTC | Coordinated Universal Time |
| WLS | Weighted Least Squares |
Appendix A. Load Aggregation Algorithm
- The sum of all the average load profiles included in the i-th subset is approximately equal to the nominal power injection at the corresponding bus, i.e., .
- The relative sample variance of the power at the i-th bus is approximately equal to a given fraction of , i.e., .
Appendix B. PMU Placement Algorithm
- For each PMU configuration , the state of the system under given load conditions (i.e., with known maximum variability) is estimated by the EKF or the WLS algorithm times, with large enough to ensure a reasonably accurate estimate of the state covariance matrix, i.e., in the order of a few hundred.
- If the sequences of estimation errors are realizations of ergodic processes (as it should be when either the EKF or the WLS estimator is used), the state covariance matrix associated with the m-th PMU configuration can be estimated directly from the steady-state estimation error sequences. In the EKF case, tends also to coincide with the solution of the linearized matrix Riccati equation.
- Once all covariance matrices for are computed, the PMU configuration is selected as follows, i.e.,where operators returns the eigenvalues of the argument.
- Afterward, configuration is removed from set , i.e., , and the algorithm starts over.
References
- Landi, C.; Del Prete, G.; Gallo, D.; Luiso, M. The use of real-time instruments for smart power systems. In Proceedings of the 2012 IEEE International Energy Conference and Exhibition (ENERGYCON), Florence, Italy, 9–12 September 2012; pp. 884–889. [Google Scholar]
- Muscas, C.; Pau, M.; Pegoraro, P.A.; Sulis, S. Smart electric energy measurements in power distribution grids. IEEE Instrum. Meas. Mag. 2015, 18, 17–21. [Google Scholar] [CrossRef]
- Soares, T.; Bezerra, U.H.; Tostes, M.E.L. Full-Observable Three-Phase State Estimation Algorithm Applied to Electric Distribution Grids. Energies 2019, 12, 1327. [Google Scholar] [CrossRef]
- Abur, A.; Exposito, A. Power System State Estimation (Theory and Implementation); Marcel Dekker: New York, NY, USA, 2004. [Google Scholar]
- Wang, D.; Guan, X.; Lie, T.; Gu, Y.; Shen, C.; Xu, Z. Extended Distributed State Estimation: A Detection Method against Tolerable False Data Injection Attacks in Smart Grids. Energies 2014, 7, 1517–1538. [Google Scholar] [CrossRef]
- Albu, M.; Kyriakides, E.; Dumitrescu, A.M.; Florea, I.M. Analysis of distribution grids: State estimation using model uncertainties. In Proceedings of the 2011 IEEE International Workshop on Applied Measurements for Power Systems (AMPS), Aachen, Germany, 28–30 September 2011; pp. 68–73. [Google Scholar]
- Muscas, C.; Pau, M.; Pegoraro, P.A.; Sulis, S.; Ponci, F.; Monti, A. Multiarea Distribution System State Estimation. IEEE Trans. Instrum. Meas. 2015, 64, 1140–1148. [Google Scholar] [CrossRef]
- Manousakis, N.; Korres, G.; Georgilakis, P. Taxonomy of PMU Placement Methodologies. IEEE Trans. Power Syst. 2012, 27, 1070–1077. [Google Scholar] [CrossRef]
- Babu, R.; Bhattacharyya, B. Strategic placements of PMUs for power network observability considering redundancy measurement. Measurement 2019, 134, 606–623. [Google Scholar] [CrossRef]
- Pokhrel, B.; Bak-Jensen, B.; Pillai, J. Integrated Approach for Network Observability and State Estimation in Active Distribution Grid. Energies 2019, 12, 2230. [Google Scholar] [CrossRef]
- Arboleya, P. State Estimation in Low Voltage Networks Using Smart Meters: Statistical Analysis of the Errors. In Proceedings of the 2018 IEEE Power Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- Nuqui, R.F.; Phadke, A.G. Phasor measurement unit placement techniques for complete and incomplete observability. IEEE Trans. Power Deliv. 2005, 20, 2381–2388. [Google Scholar] [CrossRef]
- Abur, A. Impact of phasor measurements on state estimation. In Proceedings of the International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 5–8 November 2009; pp. I-3–I-7. [Google Scholar]
- Liu, J.; Tang, J.; Ponci, F.; Monti, A.; Muscas, C.; Pegoraro, P. Trade-Offs in PMU Deployment for State Estimation in Active Distribution Grids. IEEE Trans. Smart Grid 2012, 3, 915–924. [Google Scholar] [CrossRef]
- Pití, A.; Verticale, G.; Rottondi, C.; Capone, A.; Lo Schiavo, L. The Role of Smart Meters in Enabling Real-Time Energy Services for Households: The Italian Case. Energies 2017, 10, 199. [Google Scholar] [CrossRef]
- Phadke, A.G.; Bi, T. Phasor measurement units, WAMS, and their applications in protection and control of power systems. J. Mod. Power Syst. Clean Energy 2018, 6, 619–629. [Google Scholar] [CrossRef]
- Tosato, P.; Macii, D.; Luiso, M.; Brunelli, D.; Gallo, D.; Landi, C. A Tuned Lightweight Estimation Algorithm for Low-Cost Phasor Measurement Units. IEEE Trans. Instrum. Meas. 2018, 67, 1047–1057. [Google Scholar] [CrossRef]
- von Meier, A.; Stewart, E.; McEachern, A.; Andersen, M.; Mehrmanesh, L. Precision Micro-Synchrophasors for Distribution Systems: A Summary of Applications. IEEE Trans. Smart Grid 2017, 8, 2926–2936. [Google Scholar] [CrossRef]
- Borghetti, A.; Nucci, C.A.; Paolone, M.; Ciappi, G.; Solari, A. Synchronized Phasors Monitoring During the Islanding Maneuver of an Active Distribution Network. IEEE Trans. Smart Grid 2011, 2, 82–91. [Google Scholar] [CrossRef]
- Cavraro, G.; Arghandeh, R.; Barchi, G.; von Meier, A. Distribution network topology detection with time-series measurements. In Proceedings of the 2015 IEEE Power Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 18–20 February 2015. [Google Scholar]
- Pignati, M.; Zanni, L.; Romano, P.; Cherkaoui, R.; Paolone, M. Fault Detection and Faulted Line Identification in Active Distribution Networks Using Synchrophasors-Based Real-Time State Estimation. IEEE Trans. Power Deliv. 2017, 32, 381–392. [Google Scholar] [CrossRef]
- Kettner, A.M.; Paolone, M. Sequential Discrete Kalman Filter for Real-Time State Estimation in Power Distribution Systems: Theory and Implementation. IEEE Trans. Instrum. Meas. 2017, 66, 2358–2370. [Google Scholar] [CrossRef]
- Todescato, M.; Carli, R.; Schenato, L.; Barchi, G. Smart Grid State Estimation with PMUs Time Synchronization Errors. Energies 2020, 13, 5148. [Google Scholar] [CrossRef]
- Hernández, C.; Maya-Ortiz, P. Comparison between WLS and Kalman filter method for power system static state estimation. In Proceedings of the International Symposium on Smart Electric Distribution Systems and Technologies (EDST), Vienna, Austria, 8–11 September 2015; pp. 47–52. [Google Scholar]
- Sarri, S.; Paolone, M.; Cherkaoui, R.; Borghetti, A.; Napolitano, F.; Nucci, C. State estimation of Active Distribution Networks: Comparison between WLS and iterated Kalman-filter algorithm integrating PMUs. In Proceedings of the of the IEEE PES International Conference and Exhibition Innovative Smart Grid Technologies (ISGT Europe), Berlin, Germany, 14–17 October 2012; pp. 1–8. [Google Scholar]
- Macii, D.; Aziz, Z.; Fontanelli, D. Uncertainty Analysis of Distribution System State Estimation based on Extended Kalman Filtering and Phasor Measurement Units. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Auckland, New Zealand, 20–23 May 2019; pp. 1–6. [Google Scholar]
- Huang, Y.; Werner, S.; Huang, J.; Kashyap, N.; Gupta, V. State Estimation in Electric Power Grids: Meeting New Challenges Presented by the Requirements of the Future Grid. IEEE Signal Process. Mag. 2012, 29, 33–43. [Google Scholar] [CrossRef]
- Chakrabarti, S.; Kyriakides, E. PMU Measurement Uncertainty Considerations in WLS State Estimation. IEEE Trans. Power Syst. 2009, 24, 1062–1071. [Google Scholar] [CrossRef]
- Macii, D.; Barchi, G.; Petri, D. Uncertainty sensitivity analysis of WLS-based grid state estimators. In Proceedings of the IEEE International Workshop on Applied Measurements for Power Systems Proceedings (AMPS), Aachen, Germany, 24–26 September 2014. [Google Scholar]
- Tungadio, D.H.; Jordaan, J.A.; Siti, M.W. Power system state estimation solution using modified models of PSO algorithm: Comparative study. Measurement 2016, 92, 508–523. [Google Scholar] [CrossRef]
- Manoharan, Y.; Ramya, K.; Manoharan, H.; Manoharan, A. State approximation in power system by using quasi derived originating procedure. Measurement 2019, 146, 924–929. [Google Scholar]
- Zhao, J.; Gómez-Expósito, A.; Netto, M.; Mili, L.; Abur, A.; Terzija, V.; Kamwa, I.; Pal, B.; Singh, A.K.; Qi, J.; et al. Power System Dynamic State Estimation: Motivations, Definitions, Methodologies, and Future Work. IEEE Trans. Power Syst. 2019, 34, 3188–3198. [Google Scholar] [CrossRef]
- da Silva, A.M.L.; Filho, M.B.D.C.; de Queiroz, J.F. State forecasting in electric power systems. IEEE Proc. C Gener. Transm. Distrib. 1983, 130, 237–244. [Google Scholar]
- Alves da Silva, A.P.; Leite da Silva, A.M.; Stacchini de Souza, J.C.; Do Coutto Filho, M.B. State forecasting based on artificial neural networks. In Proceedings of the 11th Power Systems Computation Conference (PSCC), Avignon, France, 30 August–3 September 1993; Volume I, pp. 461–468. [Google Scholar]
- Saikia, A.; Mehta, R.K. Power system static state estimation using Kalman filter algorithm. Int. J. Simul. Multidiscip. Des. Optim. 2016, 7, A7. [Google Scholar] [CrossRef]
- Blood, E.A.; Krogh, B.H.; Ilic, M.D. Electric power system static state estimation through Kalman filtering and load forecasting. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, Pennsylvania, 20–24 July 2008; pp. 1–6. [Google Scholar]
- Zhao, J.; Zhang, G.; Dong, Z.Y.; La Scala, M. Robust Forecasting Aided Power System State Estimation Considering State Correlations. IEEE Trans. Smart Grid 2018, 9, 2658–2666. [Google Scholar] [CrossRef]
- Sinha, A.K.; Mondal, J.K. Dynamic state estimator using ANN based bus load prediction. IEEE Trans. Power Syst. 1999, 14, 1219–1225. [Google Scholar] [CrossRef]
- Della Giustina, D.; Pau, M.; Pegoraro, P.; Ponci, F.; Sulis, S. Electrical distribution system state estimation: Measurement issues and challenges. IEEE Instrum. Meas. Mag. 2014, 17, 36–42. [Google Scholar] [CrossRef]
- Macii, D.; Barchi, G.; Schenato, L. On the Role of Phasor Measurement Units for Distribution System State Estimation. In Proceedings of the of IEEE Workshop on Environmental, Energy, and Structural Monitoring Systems, Naples, Italy, 17–18 September 2014; pp. 1–6. [Google Scholar]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Application to Tracking and Navigation—Theory, Algorithm and Software; John Wiley and Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- Brodén, D.A.; Paridari, K.; Nordström, L. Matlab applications to generate synthetic electricity load profiles of office buildings and detached houses. In Proceedings of the IEEE Innovative Smart Grid Technologies—Asia (ISGT-Asia), Auckland, New Zealand, 4–7 December 2017; pp. 1–6. [Google Scholar]
- Zimmerman, R.D.; Murillo-Sanchez, C.E.; Thomas, R.J. MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef]
- Sandels, C.; Widén, J.; Nordström, L. Forecasting household consumer electricity load profiles with a combined physical and behavioral approach. Appl. Energy 2014, 131, 267–278. [Google Scholar] [CrossRef]
- Sandels, C.; Brodén, D.; Widén, J.; Nordström, L.; Andersson, E. Modeling office building consumer load with a combined physical and behavioral approach: Simulation and validation. Appl. Energy 2016, 162, 472–485. [Google Scholar] [CrossRef]
- Singh, R.; Pal, B.; Jabr, R. Statistical Representation of Distribution System Loads Using Gaussian Mixture Model. IEEE Trans. Power Syst. 2010, 25, 29–37. [Google Scholar] [CrossRef]
- Cataliotti, A.; Cosentino, V.; Guaiana, S.; Nuccio, S.; Cara, D.D.; Panzavecchia, N.; Tinè, G. Measurement uncertainty impact on simplified load flow analysis in MV smart grids. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Montevideo, Uruguay, 12–15 May 2018; pp. 1–6. [Google Scholar]
- Pegoraro, P.; Sulis, S. On the uncertainty evaluation in distribution system state estimation. In Proceedings of the IEEE International Conference on Smart Measurements for Future Grids (SMFG), Bologna, Italy, 14–16 November 2011; pp. 59–63. [Google Scholar]
- Ni, F.; Nguyen, P.H.; Cobben, J.F.G.; van den Brom, H.E.; Zhao, D. Uncertainty analysis of aggregated smart meter data for state estimation. In Proceedings of the 2016 IEEE International Workshop on Applied Measurements for Power Systems (AMPS), Aachen, Germany, 28–30 September 2016; pp. 1–6. [Google Scholar]
- Carstens, H.; Xia, X.; Yadavalli, S. Measurement uncertainty in energy monitoring: Present state of the art. Renew. Sustain. Energy Rev. 2018, 82, 2791–2805. [Google Scholar] [CrossRef]
- BIPM; IEC; IFCC; ILAC; ISO; IUPAC; IUPAP; OIML. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. 2008. Available online: https://www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_E.pdf (accessed on 26 October 2020).
- IEEE/IEC International Standard—Measuring Relays and Protection Equipment—Part 118-1: Synchrophasor for Power Systems—Measurements. IEC/IEEE 60255-118-1:2018. 2018, pp. 1–78. Available online: https://standards.ieee.org/standard/60255-118-1-2018.html (accessed on 26 October 2020).
- Frigo, G.; Derviškadić, A.; Colangelo, D.; Braun, J.; Paolone, M. Characterization of uncertainty contributions in a high-accuracy PMU validation system. Measurement 2019, 146, 72–86. [Google Scholar] [CrossRef]
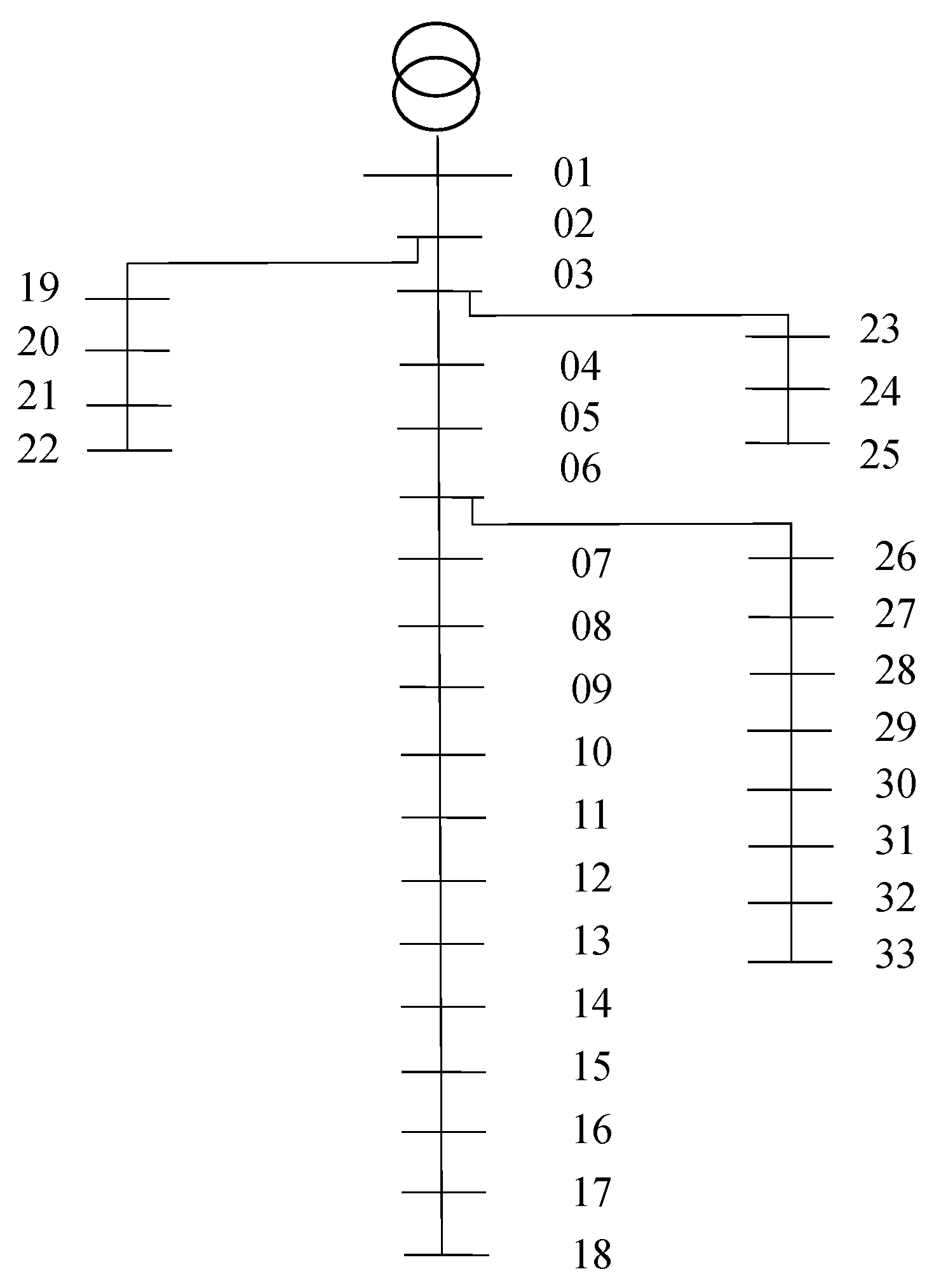


| Bus | Line | From | To | ||||
|---|---|---|---|---|---|---|---|
| 1 | – | – | 1 | 1 | 2 | 0.092 | 0.047 |
| 2 | 100 | 60 | 2 | 2 | 3 | 0.493 | 0.251 |
| 3 | 90 | 40 | 3 | 3 | 4 | 0.366 | 0.186 |
| 4 | 120 | 80 | 4 | 4 | 5 | 0.381 | 0.194 |
| 5 | 60 | 30 | 5 | 5 | 6 | 0.819 | 0.707 |
| 6 | 60 | 20 | 6 | 6 | 7 | 0.187 | 0.619 |
| 7 | 200 | 100 | 7 | 7 | 8 | 0.711 | 0.235 |
| 8 | 200 | 100 | 8 | 8 | 9 | 1.030 | 0.740 |
| 9 | 60 | 20 | 9 | 9 | 10 | 1.044 | 0.740 |
| 10 | 60 | 20 | 10 | 10 | 11 | 0.197 | 0.065 |
| 11 | 45 | 30 | 11 | 11 | 12 | 0.374 | 0.130 |
| 12 | 60 | 35 | 12 | 12 | 13 | 1.468 | 1.16 |
| 13 | 60 | 35 | 13 | 13 | 14 | 0.542 | 0.713 |
| 14 | 120 | 80 | 14 | 14 | 15 | 0.591 | 0.526 |
| 15 | 60 | 10 | 15 | 15 | 16 | 0.746 | 0.545 |
| 16 | 60 | 20 | 16 | 16 | 17 | 1.289 | 1.721 |
| 17 | 60 | 20 | 17 | 17 | 18 | 0.732 | 0.574 |
| 18 | 90 | 40 | 18 | 2 | 19 | 0.164 | 0.157 |
| 19 | 90 | 40 | 19 | 19 | 20 | 1.504 | 1.355 |
| 20 | 90 | 40 | 20 | 20 | 21 | 0.410 | 0.478 |
| 21 | 90 | 40 | 21 | 21 | 22 | 0.709 | 0.937 |
| 22 | 90 | 40 | 22 | 3 | 23 | 0.451 | 0.308 |
| 23 | 90 | 50 | 23 | 23 | 24 | 0.898 | 0.709 |
| 24 | 420 | 200 | 24 | 24 | 25 | 0.896 | 0.701 |
| 25 | 420 | 200 | 25 | 6 | 26 | 0.203 | 0.103 |
| 26 | 60 | 25 | 26 | 26 | 27 | 0.284 | 0.145 |
| 27 | 60 | 25 | 27 | 27 | 28 | 1.059 | 0.934 |
| 28 | 60 | 20 | 28 | 28 | 29 | 0.804 | 0.701 |
| 29 | 120 | 70 | 29 | 29 | 30 | 0.508 | 0.259 |
| 30 | 200 | 600 | 30 | 30 | 31 | 0.974 | 0.963 |
| 31 | 150 | 70 | 31 | 31 | 32 | 0.311 | 0.362 |
| 32 | 210 | 100 | 32 | 32 | 33 | 0.341 | 0.530 |
| 33 | 60 | 40 | – | – | – | – | – |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Macii, D.; Fontanelli, D.; Barchi, G. A Distribution System State Estimator Based on an Extended Kalman Filter Enhanced with a Prior Evaluation of Power Injections at Unmonitored Buses. Energies 2020, 13, 6054. https://doi.org/10.3390/en13226054
Macii D, Fontanelli D, Barchi G. A Distribution System State Estimator Based on an Extended Kalman Filter Enhanced with a Prior Evaluation of Power Injections at Unmonitored Buses. Energies. 2020; 13(22):6054. https://doi.org/10.3390/en13226054
Chicago/Turabian StyleMacii, David, Daniele Fontanelli, and Grazia Barchi. 2020. "A Distribution System State Estimator Based on an Extended Kalman Filter Enhanced with a Prior Evaluation of Power Injections at Unmonitored Buses" Energies 13, no. 22: 6054. https://doi.org/10.3390/en13226054
APA StyleMacii, D., Fontanelli, D., & Barchi, G. (2020). A Distribution System State Estimator Based on an Extended Kalman Filter Enhanced with a Prior Evaluation of Power Injections at Unmonitored Buses. Energies, 13(22), 6054. https://doi.org/10.3390/en13226054







