Study and Simulation of a Wind Hydro Isolated Microgrid
Abstract
1. Introduction
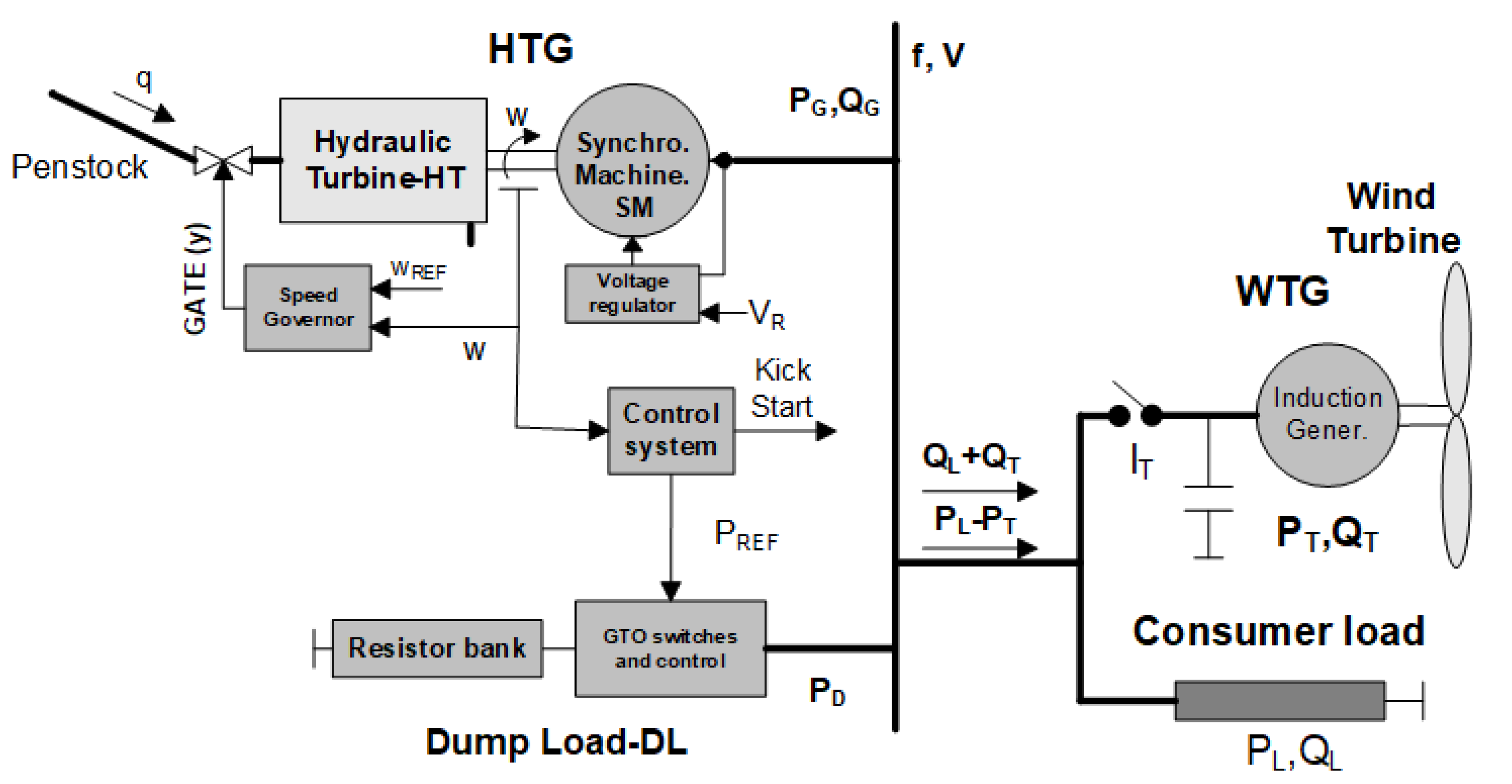
2. WHIM Modeling
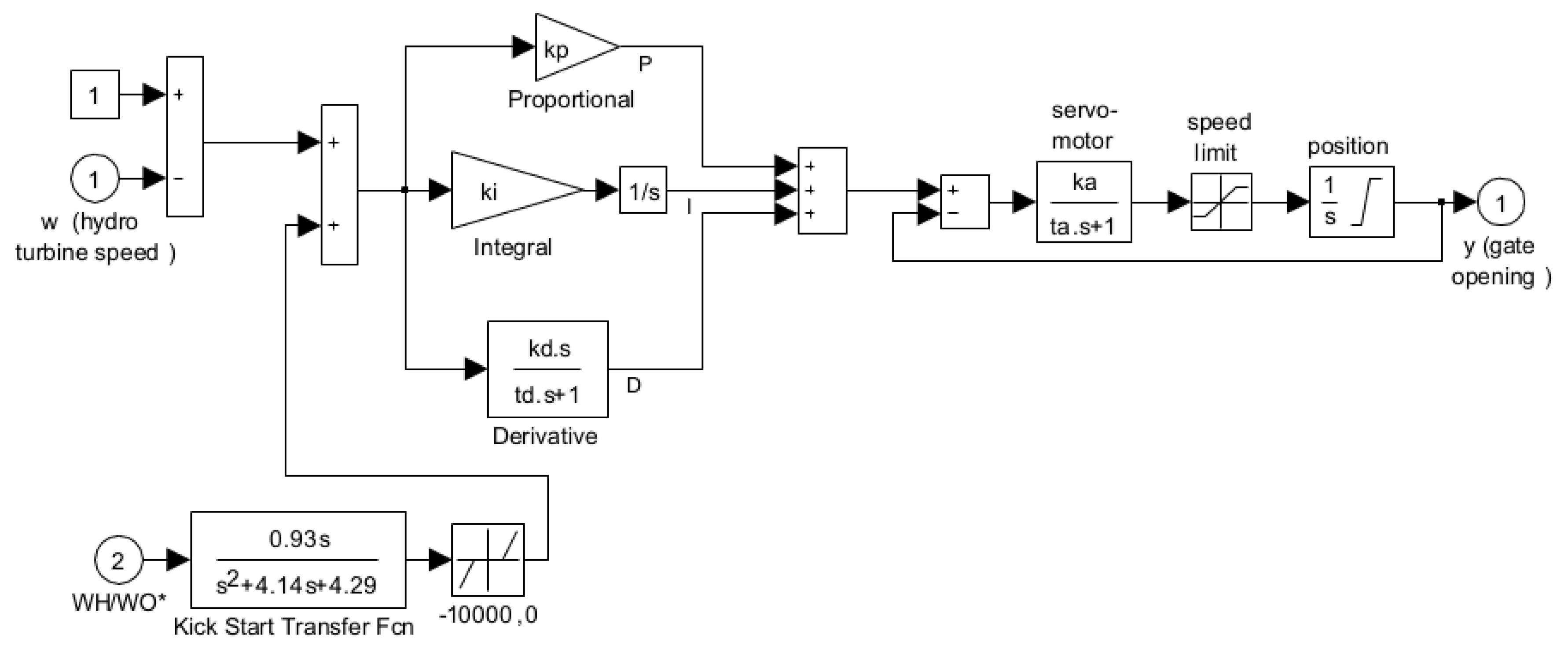
2.1. The HTG Model
2.2. The WTG Model
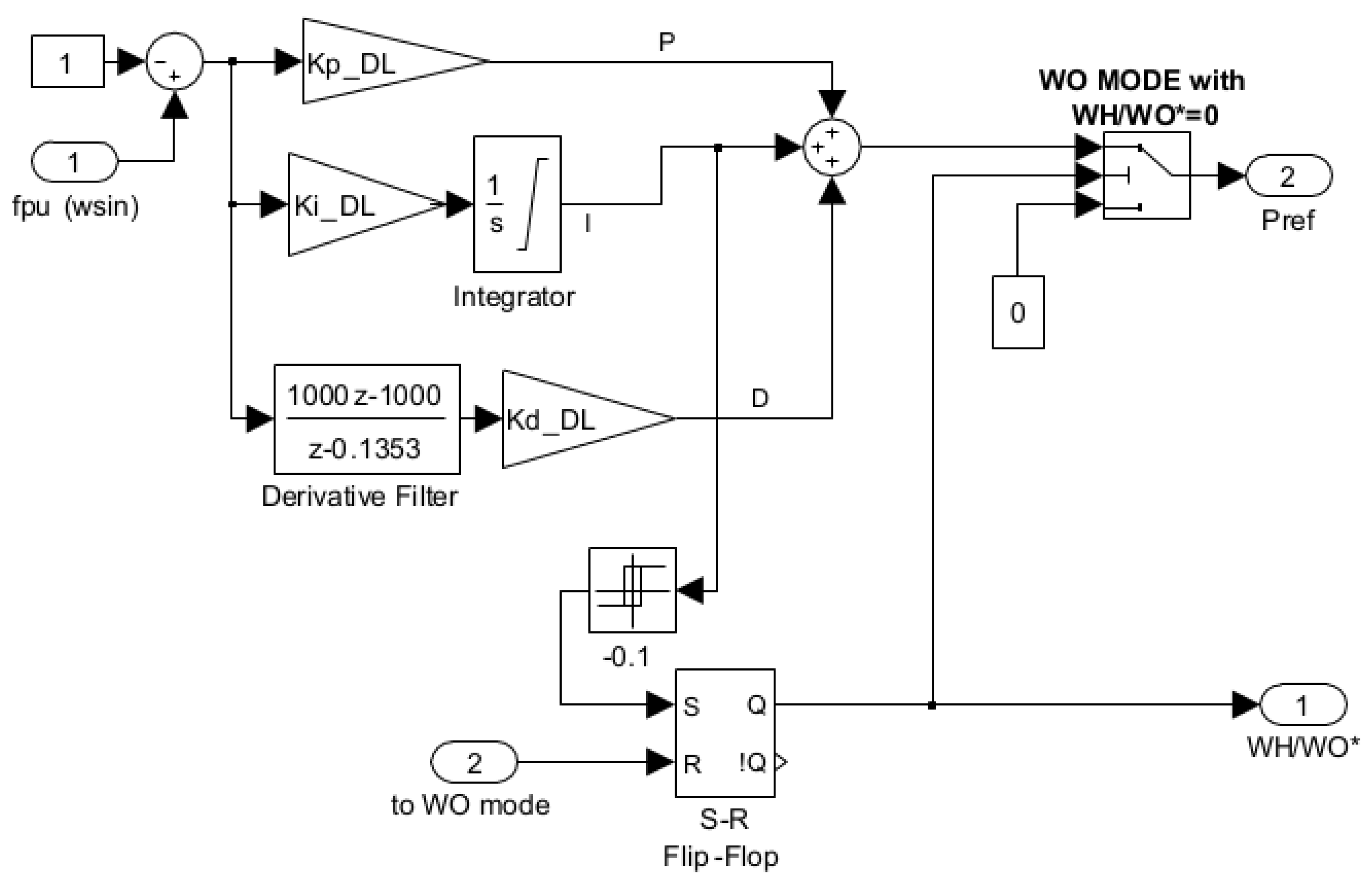
2.3. The DL Model
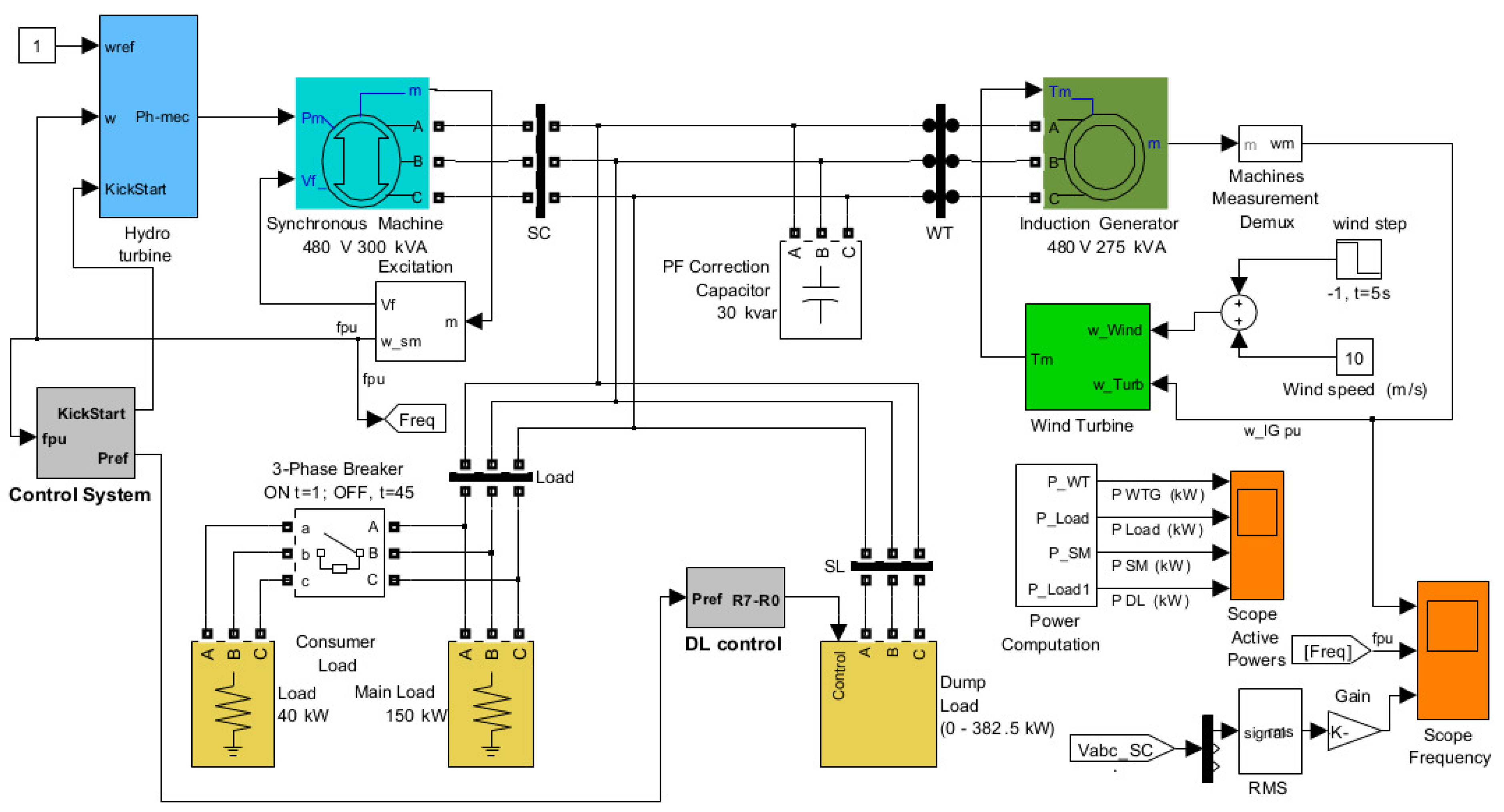
3. Simulation Schematics
4. Simulation Results
4.1. Simulations in WO Mode
4.2. WO to WH Mode Transition
4.3. The WH Mode Simulation
4.4. Hydraulic Variables
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. System Configuration
Appendix A.1. Isolated Microgrid
Appendix A.2. Hydro Turbine Generator
Appendix A.3. Wind Turbine Generator
Appendix A.4. Dump Load
References
- Lasseter, R. Microgrids. In Proceedings of the IEEE PES Winter Meeting; IEEE: New York, NY, USA, 2002; Volume 1, pp. 305–308. [Google Scholar]
- Basak, P.; Chowdhury, S.; Halder nee Dey, S.; Chowdhury, S.P. A Literature Review on Integration of Distributed Energy Resources in the Perspective of Control, Protection and Stability of Microgrid. Renew. Sustain. Energy 2012, 16, 5545–5556. [Google Scholar] [CrossRef]
- Piagi, P.; Lasseter, R.H. Autonomous Control of Microgrids. In PES Meeting, Montreal; IEEE: New York, NY, USA, 2006. [Google Scholar]
- Sebastián, R.; García-Loro, F. Review on Wind Diesel Systems Dynamic Simulation. In IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society; IEEE: New York, NY, USA, 2019; pp. 2489–2494. [Google Scholar]
- Sebastián, R.; Peña-Alzola, R. Flywheel Energy Storage and Dump Load to Control the Active Power Excess in a Wind Diesel Power System. Energies 2020, 13, 2029. [Google Scholar] [CrossRef]
- Sebastián, R. Battery Energy Storage for Increasing Stability and Reliability of an Isolated Wind Diesel Power System. IET Renew. Power Gener. 2017, 11, 296–303. [Google Scholar] [CrossRef]
- Bø, T.I.; Johansen, T.A. Battery Power Smoothing Control in a Marine Electric Power Plant Using Nonlinear Model Predictive Control. IEEE Trans. Control. Syst. Technol. 2016, 25, 1449–1456. [Google Scholar] [CrossRef]
- Taghizadeh, M.; Mardaneh, M.; Sha Sadeghi, M. Frequency Control of a New Topology in Proton Exchange Membrane Fuel Cell/Wind Turbine/Photovoltaic/Ultra-Capacitor/Battery Energy Storage System Based Isolated Networks by a Novel Intelligent Controller. J. Renew. Sustain. Energy 2014, 6, 053121. [Google Scholar] [CrossRef]
- Hasmaini, M.; Hazlie, M.; Bakar, A.H.; Ping, H.W. A Review on Islanding Operation and Control for Distribution Network Connected with Small Hydro Power Plant. Renew. Sustain. Energy Rev. 2011, 15, 3952–3962. [Google Scholar]
- Paish, O. Small Hydro Power: Technology and Current Status. Renew. Sustain. Energy Rev. 2002, 6, 537–556. [Google Scholar] [CrossRef]
- Doolla, S.; Bhatti, T.; Bansal, R. Load Frequency Control of an Isolated Small Hydro Power Plant Using Multi-pipe Scheme. Electr. Power Components Syst. 2011, 39, 46–63. [Google Scholar] [CrossRef]
- Sebastián, R.; Quesada, J. Modeling and Simulation of an Isolated Wind Hydro Power System. In IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society; IEEE: New York, NY, USA, 2016; pp. 4169–4174. [Google Scholar]
- Sebastián, R. Application of a Battery Energy Storage for Frequency Regulation and Peak Shaving in a Wind Diesel Power System. IET Gener. Transm. Distrib. 2016, 10, 764–770. [Google Scholar] [CrossRef]
- Lukasievicz, T.; Oliveira, R.; Torrico, C. A Control Approach and Supplementary Controllers for a Stand-Alone System with Predominance of Wind Generation. Energies 2018, 11, 411. [Google Scholar] [CrossRef]
- Sebastián, R.; Peña-Alzola, R. Flywheel Energy Storage Systems: Review and Simulation for an Isolated Wind Power System. Renew. Sustain. Energy Rev. 2012, 16, 6803–6813. [Google Scholar] [CrossRef]
- Mendis, N.; Muttaqi, K.M.; Perera, S. Management of Battery-Supercapacitor Hybrid Energy Storage and Synchronous Condenser for Isolated Operation of PMSG Based Variable-Speed Wind Turbine Generating Systems. IEEE Trans. Smart Grid 2014, 5, 944–953. [Google Scholar] [CrossRef]
- Sarasúa, J.; Martínez-Lucas, G.; Platero, C.; Sánchez-Fernández, J. Dual Frequency Regulation in Pumping Mode in a Wind–Hydro Isolated System. Energies 2018, 11, 2865. [Google Scholar] [CrossRef]
- Sarasúa, J.; Martínez-Lucas, G.; Lafof, M. Analysis of Alternative Frequency Control Schemes for Increasing Renewable Energy Penetration in El Hierro Island Power System. Int. J. Electr. Power Energy Syst. 2019, 113, 807–823. [Google Scholar] [CrossRef]
- Briongos, F.; Platero, C.A.; Sánchez-Fernández, J.A.; Nicolet, C. Evaluation of the Operating Efficiency of a Hybrid Wind–Hydro Powerplant. Sustainability 2020, 12, 668. [Google Scholar] [CrossRef]
- Mover, W.G.P.; Supply, E. Hydraulic Turbine and Turbine Control Models for System Dynamic Studies. IEEE Trans. Power Syst. 1992, 7, 167–179. [Google Scholar]
- Kothari, D.P.; Nagrath, I.J. Modern Power System Analysis; Tata McGraw-Hill Education: New York, NY, USA, 2003. [Google Scholar]
- Rodríguez-Amenedo, J.L.; Burgos-Díaz, J.C.; Arnalte-Gómez, S. Sistemas Eólicos de Producción de Energía Eléctrica; Rueda: Madrid, Spain, 2003; ISBN 9788472071391. [Google Scholar]
- Gagnon, R.; Saulnier, B.; Sybille, G.; Giroux, P. Modeling of a Generic High-Penetration No-Storage Wind-Diesel System Using Matlab Power System Blockset. In Proceedings of the 2002 Global Windpower Conference, Paris, France, 2–5 April 2002. [Google Scholar]
- Knudsen, H.; Nielsen, J.N. Introduction to the Modeling of Wind Turbines. In Wind Power in Power Systems; Wiley: Chicester, UK, 2005; pp. 525–585. [Google Scholar]
- MathWorks, Model-Based Simulation and Design. Available online: https://mathworks.com/products/simulink.html (accessed on 27 September 2020).
- Platero, C.A.; Nicolet, C.; Sánchez, J.A.; Kawkabani, B. Increasing Wind Power Penetration in Autonomous Power Systems Through No-Flow Operation of Pelton Turbines. Renew. Energy 2014, 68, 515–523. [Google Scholar] [CrossRef]
- Margaris, I.D.; Papathanassiou, S.A.; Hatziargyriou, N.D.; Hansen, A.D.; Sorensen, P. Frequency Control in Autonomous Power Systems with High Wind Power Penetration. IEEE Trans. Sustain. Energy 2012, 3, 189–199. [Google Scholar] [CrossRef]



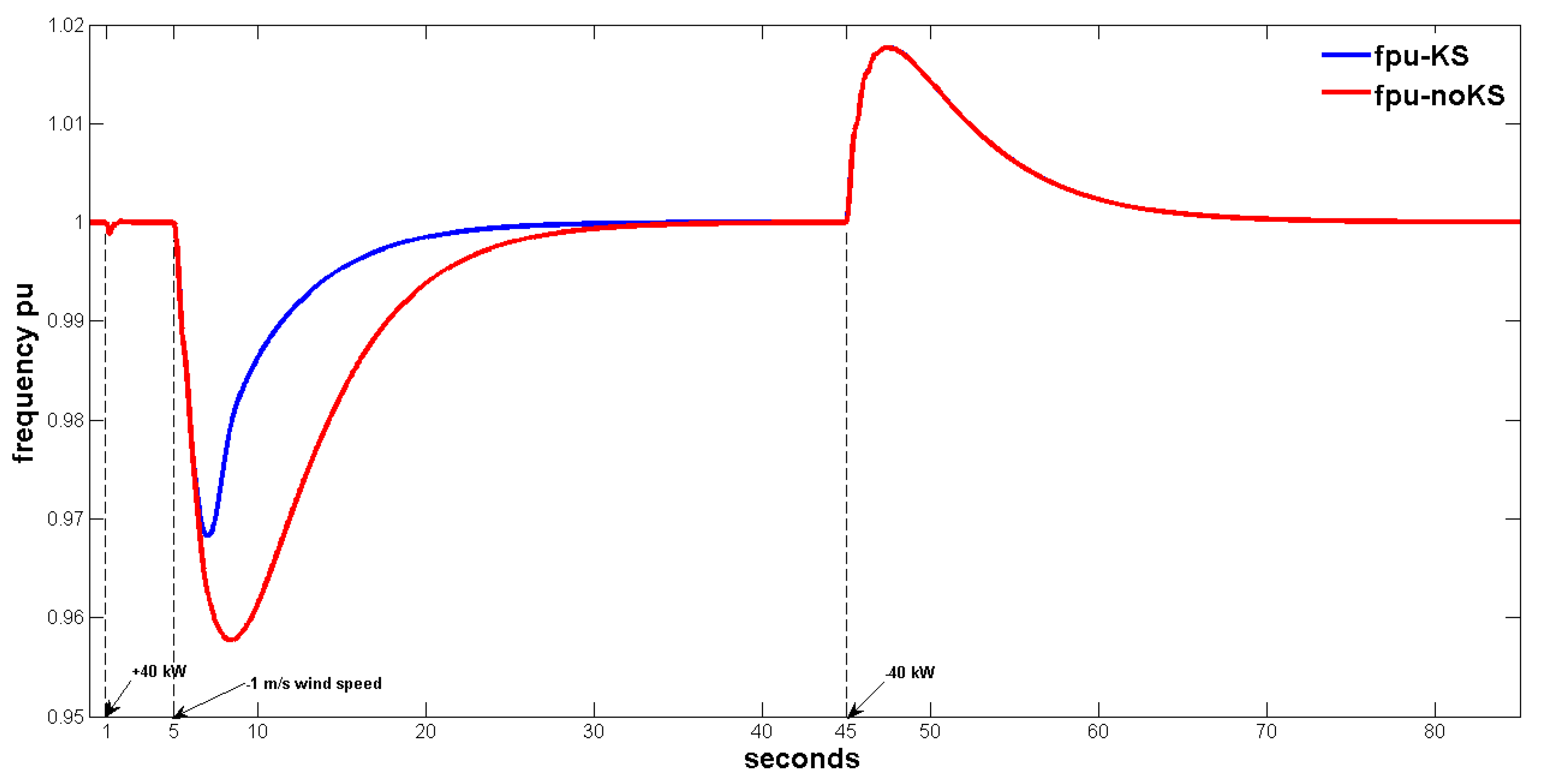

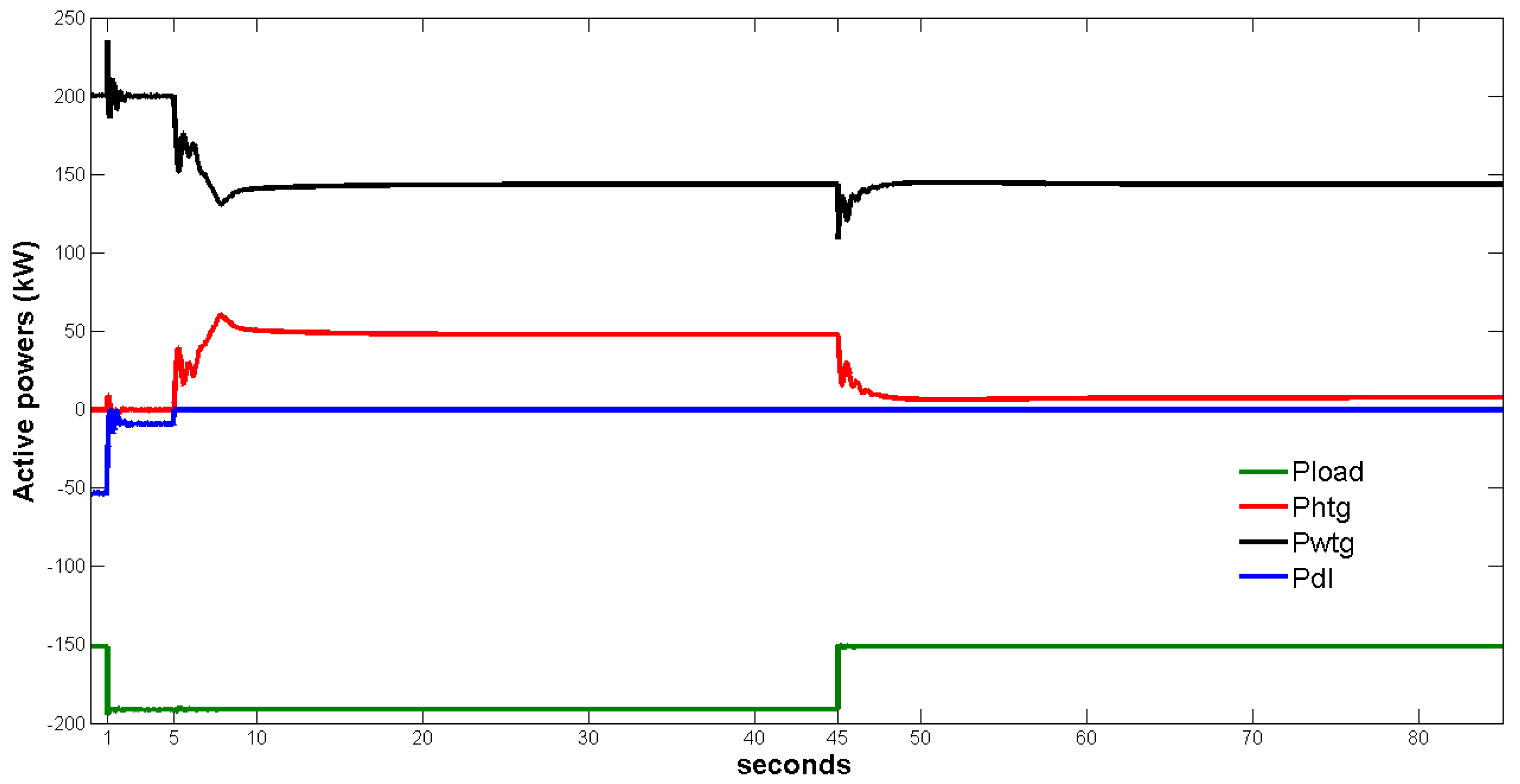
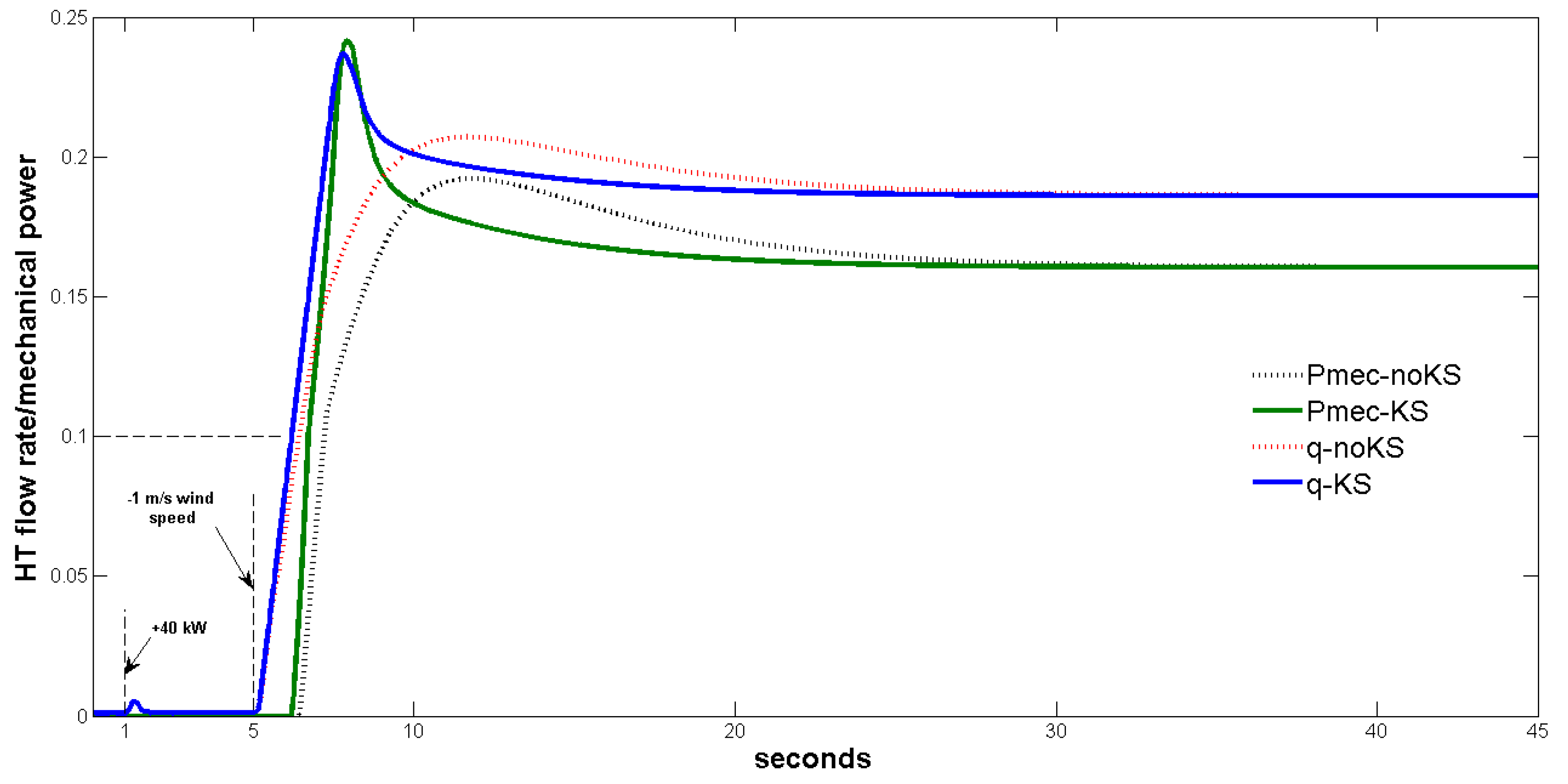
| Variable\Case | WO | WO2WH KS | WO2WH no-KS | WH |
|---|---|---|---|---|
| f | [0.9988, 1] | [0.9683, 1] | [0.9577, 1] | [1, 1.0177] |
| f [%] | −0.12 | −3.17 | −4.23 | +1.77 |
| V | [0.9908, 1.0018] | [0.9817, 1.0146] | [0.9758, 1.0195] | [0.9898, 1.0235] |
| V [%] | 1.1 | 3.29 | 4.37 | 3.37 |
| [s] | 0.975 | 26.487 | 32.8440 | 30.892 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sebastián, R.; Nevado, A. Study and Simulation of a Wind Hydro Isolated Microgrid. Energies 2020, 13, 5937. https://doi.org/10.3390/en13225937
Sebastián R, Nevado A. Study and Simulation of a Wind Hydro Isolated Microgrid. Energies. 2020; 13(22):5937. https://doi.org/10.3390/en13225937
Chicago/Turabian StyleSebastián, Rafael, and Antonio Nevado. 2020. "Study and Simulation of a Wind Hydro Isolated Microgrid" Energies 13, no. 22: 5937. https://doi.org/10.3390/en13225937
APA StyleSebastián, R., & Nevado, A. (2020). Study and Simulation of a Wind Hydro Isolated Microgrid. Energies, 13(22), 5937. https://doi.org/10.3390/en13225937





