1. Introduction
Operation and maintenance activities make up a large portion of the levelized cost of energy for offshore wind power. Operators spend this money because the cost of failure is larger and comprises the cost of repairs, loss of productivity and loss of remaining fatigue life caused in the time the asset still operates while the structure is in a condition of exceeded design parameters. These exceeded design parameters could either be caused by damage, such as a crack, or environmental parameters, such as excessive scour. Detecting the exceedance of design parameters quickly can save a lot of money, identifying the type of damage and assessing its severity can provide considerable further benefits. For example, it was found in a cost-benefit analysis that implementing structural health monitoring on offshore wind support structures significantly reduced the operational expense [
1,
2].
The idea of modal analysis is that a damage or some other change to the structure causes a measurable change in the modal parameters. An example of where it can be particularly important to detect damage is after a seismic event, which can cause significant change in the structure’s dynamic response. This is a problem facing offshore wind as it expands to locations with seismic activity [
3,
4]. While a single earthquake can cause notable damage, there are often repeated, sequential incidents which are even more impactful [
5]. The action of earthquakes on offshore structures is also very complex, involving seismic waves and non-linear structural responses [
6], so using measured data can provide valuable insights into these situations [
7]. Damage detection of structures can either be in an experimental modal analysis, where a load is applied, or operational modal analysis (OMA), where operational loads provide excitation to the structure [
8]. In OMA, the excitation energy comes from operational loads. The operational excitation should be uniform in terms of frequency domain, and therefore, any non-uniformity in the measured response is due to the structure itself. This assumption of frequency domain uniformity is generally not consistent with wind energy but can be approximately satisfied enough to discern structural modes [
9].
Vibration based damage detection has been developed since the 1970s, and a broad range of detection methods have been derived, however, choosing a method for offshore wind structures should be done with the limitations in mind. With many newer constructions, ‘virgin state’ modal data is collected, so there is an ‘intact’ condition to compare to. This comparison can be done either on derived modal parameters [
10,
11,
12] or directly on the measured signal [
13,
14], although the latter is challenging due to the signal’s direct dependence on environmental conditions.
A limitation, however, is that, due to the expense and challenge of recording data from offshore wind turbines, usually only a handful of sensors are placed. For vibration approaches, these sensors are usually accelerometers [
15,
16] but can sometimes be fiber Bragg grating [
17,
18]. This small number of sensors makes methods such as curvature-based methods [
19], or the Rayleigh quotient-based methods [
20], impractical, despite their promise. Thus, any method used must work with only a few sensors. There have been studies aimed at using a combination of data sources to assist in damage detection; an example is Cevasco et.al. investigated the potential for damage detection using typical SCADA (Supervisory Control And Data Acquisition) data and found that the approach showed promise given the right machine learning models were used [
21]. Additionally, a data fusion approach was proposed in another paper, which combined accelerometer with inclinometers and found that doing so greatly improved the effectiveness in damage detection [
22].
However, if only a few accelerometer signals are recorded, then damage detection can be dependent on the ability to discern certain modes of the structure and hence calculate mode-based metrics. Some suitable approaches include eigenfrequencies, modal assurance criterion (MAC) and modal flexibility. Some methods, such as multiple damage location assurance criteria (MDLAC) [
23] compare numerically calculated modes to measured modes, to identify a damage, one would then take the case which maximized the MDLAC value. Following such an approach, of comparing to a numerical model, necessitates a good numerical model. The modal parameters can be attained with solving the eigenvalue problem.
Although real data can be used for lifetime extension [
24], there are very limited data on already failed structures. The lifetime of the structure is dependent on complex, stochastic loading [
25] and there is also significant interdependence between failure modes, for example corrosion, in particular pitting corrosion, plays a role in both the initiation and propagation of cracks [
26]. To overcome the lack of existing cases of identified structural damage, in exploring damage detection approaches, researchers have used numerical models of offshore jacket structures with a simulated damage and calculated damage metrics. These structures have predominantly been oil and gas platforms, but some include wind energy structures. The aims have typically been evaluation of the metric and its suitability for a generic structure. Some researchers did so with the aim of evaluating effectiveness given measurement noise; for example, Malekzehtab et al. used mode shapes and natural frequency in an objective function, combined with a penalty term to avoid false positives [
27]. Liu et al found, in a Monte-Carlo simulation, that using modal flexibility in a damage detection problem could still be successful with 3% noise [
28]. Other researchers aimed for a method robust to environmental factors. Wang et al. used Modal Strain Energy Decomposition to detect damage with temperature variations [
29], while others used a residual strain energy-based approach [
11,
12]. Neural networks have also been employed for damage detection, for example [
14,
30], both of which found this to achieve even higher accuracy than other methods.
This paper can be of significant value for those looking to conduct modal-analysis based work on offshore wind jacket structures, as it gives a detailed view of the response of these structures to several potential damages and changes in parameters. By having several damage effects presented in a single paper, this can act as a reference for either mode-based damage detection or further study. This work differs from other studies in this area in four ways. (1) This paper uses a more detailed model to investigate damages which can not only capture their effects in a more realistic way, but also allows for the investigation of other aspects. (2) Other works have typically not included the mass and moment of inertia for the rotor nacelle assembly (RNA), however, this aspect is important for wind turbines, as it makes the modal properties not rotationally symmetric around the tower and makes a substantial difference to the mode shapes—it is found that for jacket structure, the orientation of RNA must be considered. (3) A broader range of ‘damages’ are simulated including global scour, corrosion and marine growth, as well as a sensitivity study to various soil parameters. By having this broad range applied to the same structure and in one paper allows for a clear reference. (4) Mode switching is a known and troublesome phenomenon in the mode-based damage detection of pseudo-symmetrical structures; this paper explores ways of overcoming it.
In terms of damage identification, there are four levels: damage detection, damage localization, damage severity assessment and damage consequence/progression [
31]. Simply knowing that a damage has occurred—damage detection—can be of great benefit for an offshore wind jacket structure, as inspection teams can be sent to investigate. Further benefit can be gained through knowing where damage has occurred, as time and resources can be saved in planning the repair of the damage. Quantification of damage can provide more benefit still, allowing judgements to be made about the criticality of the damage and how it affects future operation. To achieve all four levels, it is required to have both direct sensing and dedicated models [
32]; this can be very expensive. A more cost-effective approach is to use a detailed model which was used for the design of the structure to conduct virtual sensing. By using Operational Modal Analysis (OMA), combined with a numerical solution to the eigenvalue problem, information can be obtained on both the current state of the structure as well as how it might respond to damage.
This paper aims to show what information can be gained from a numerical, structural model and what lessons can be learned and applied to OMA in the hopes of achieving the four damage detection levels.
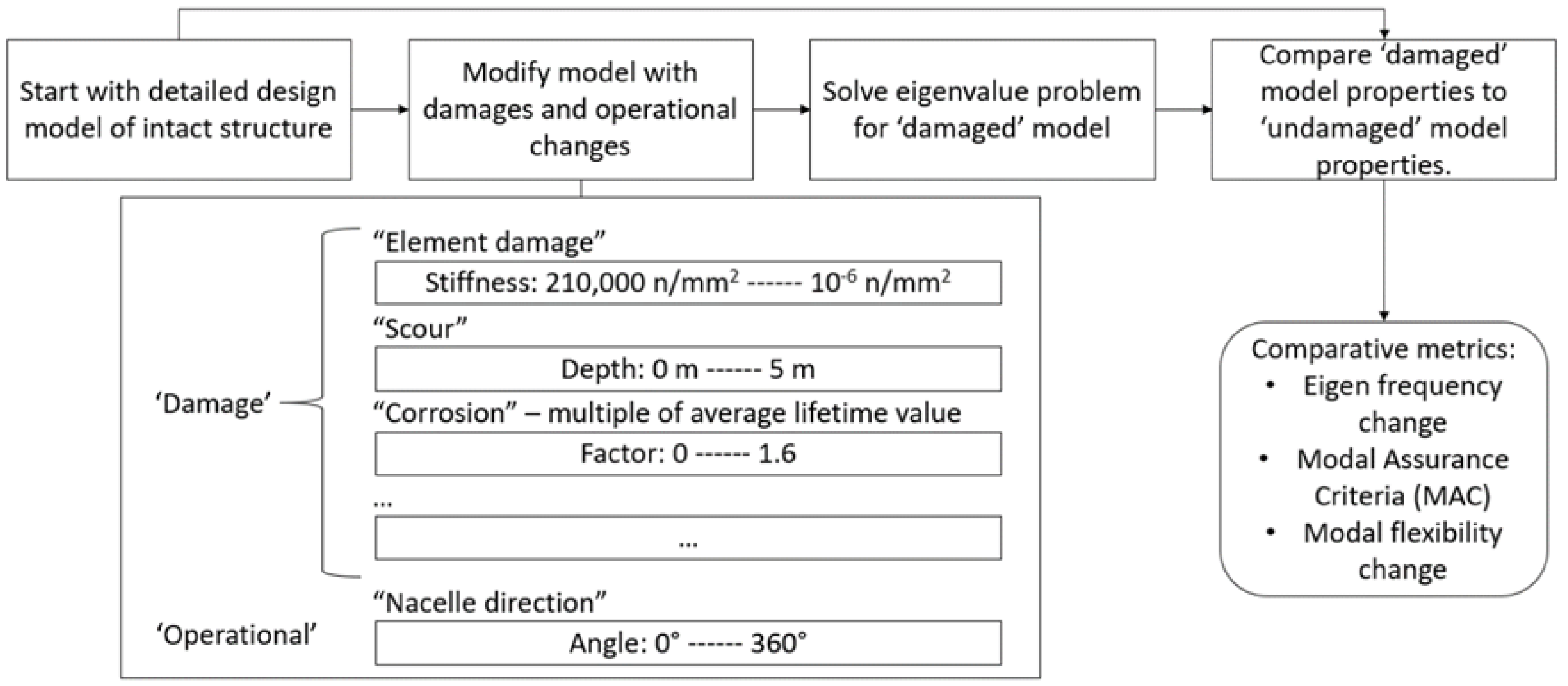
The approach followed in this paper is presented diagrammatically in
Figure 1. The process followed is to alter a detailed design model with simulated damages, solve the eigenvalue problem for that model and compare the modal properties to the unaltered model. ‘Damages’ include element damage, global scour and corrosion. The operational condition altered is the nacelle direction.
A limitation of this paper is that there are no laboratory tests or operational data for comparison. This is unfortunate, but unavoidable. The real structure from which the model was based is not damaged, so no damaged operational data is available. Additionally, because so many parameters are investigated in this paper, and the model incorporates so many details, a laboratory model of all of this would be unfeasible. There are other published publications in this field with the same limitation, for a few examples: [
11,
15,
33].
The paper begins with the damage quantification approach in
Section 2, which presents the metrics used and the equations for calculating them. In
Section 3, the structure evaluated in this case study is presented along with information about the numerical model used. The types of damage replicated in the numerical model and the method for implementing them are given in
Section 4. Results are presented in
Section 5 and
Section 6; the results in
Section 5 are presented separately, because they are useful for understanding
Section 6, which is the outcomes from each damage case. Finally, a discussion is given in
Section 7 and a conclusion in
Section 8.
3. Case Study Structure and Model
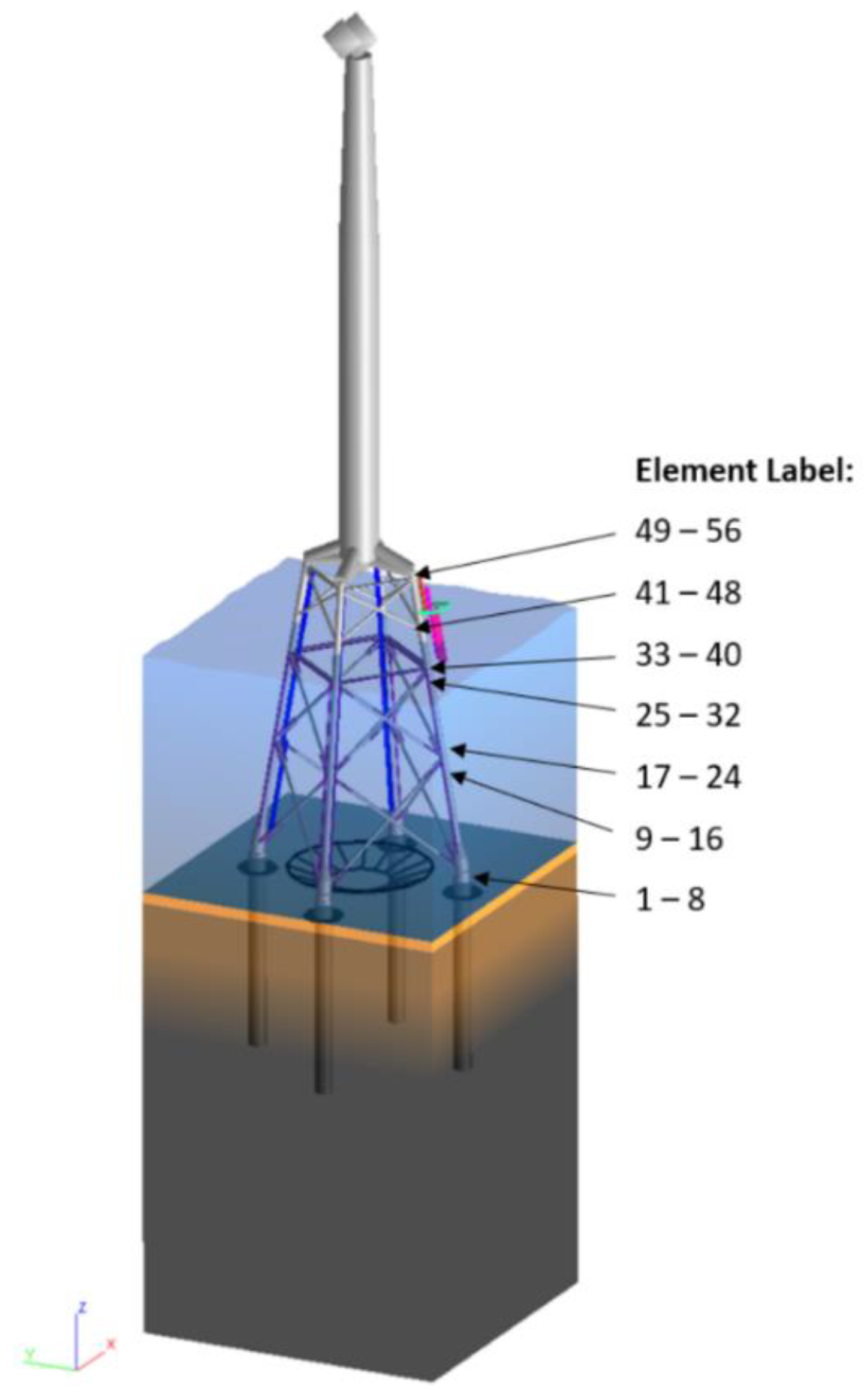
The structure being evaluated is a four-legged jacket structure from the Wikinger wind farm, which is owned by Iberdrola. These jackets are situated in the Baltic Sea with a 39–42 m water depth. Their footprint is 23 m by 23 m, and the jacket is 62 m tall. The turbine is a 5 MW, Adwen AD 5–135 turbines [
36]. The structure is fixed to the seabed using 40 m long pile foundations at each leg [
37]. The 67 m long blades are not modelled; however, the structure is modelled with the moment of inertia and mass to represent the blades and nacelle.
Ramboll’s in-house software package, ROSAP (Ramboll Offshore Structural Analysis Package), is used to conduct the eigen value analysis. Ramboll have developed this over the past 30+ years. Version 53 is used in this case [
38]. The ROSAP package, and the module ROSA, has been used for the design of the majority of offshore wind turbine foundations worldwide [
39].
ROSA (Ramboll Offshore Structural Analysis) is design software which uses beam elements for frames, truss structures and piping systems. The transition piece is modelled as a ‘super element’ where the complex shape is analyzed in ANSYS and the results are used as an element in this model. The soil structure interaction is conducted considering each soil layer and in accordance with API (American Petroleum Institute) standards [
40].
Only the first five mode shapes and corresponding eigenfrequencies are investigated in this paper and the reasons for this come from the rationalization that the aim is to reflect practical measurement of operational global dynamics. While a coupled dynamics analysis will result in modes from sources such as the blades [
41], this eigen analysis only gives structural modes, and so, the first five modes are major structural modes. The reason for not using higher modes is that in practice, in an OMA situation for offshore wind structures, lower modes can more reliably be detected and the most significant are first and second order fore-aft and side-side modes [
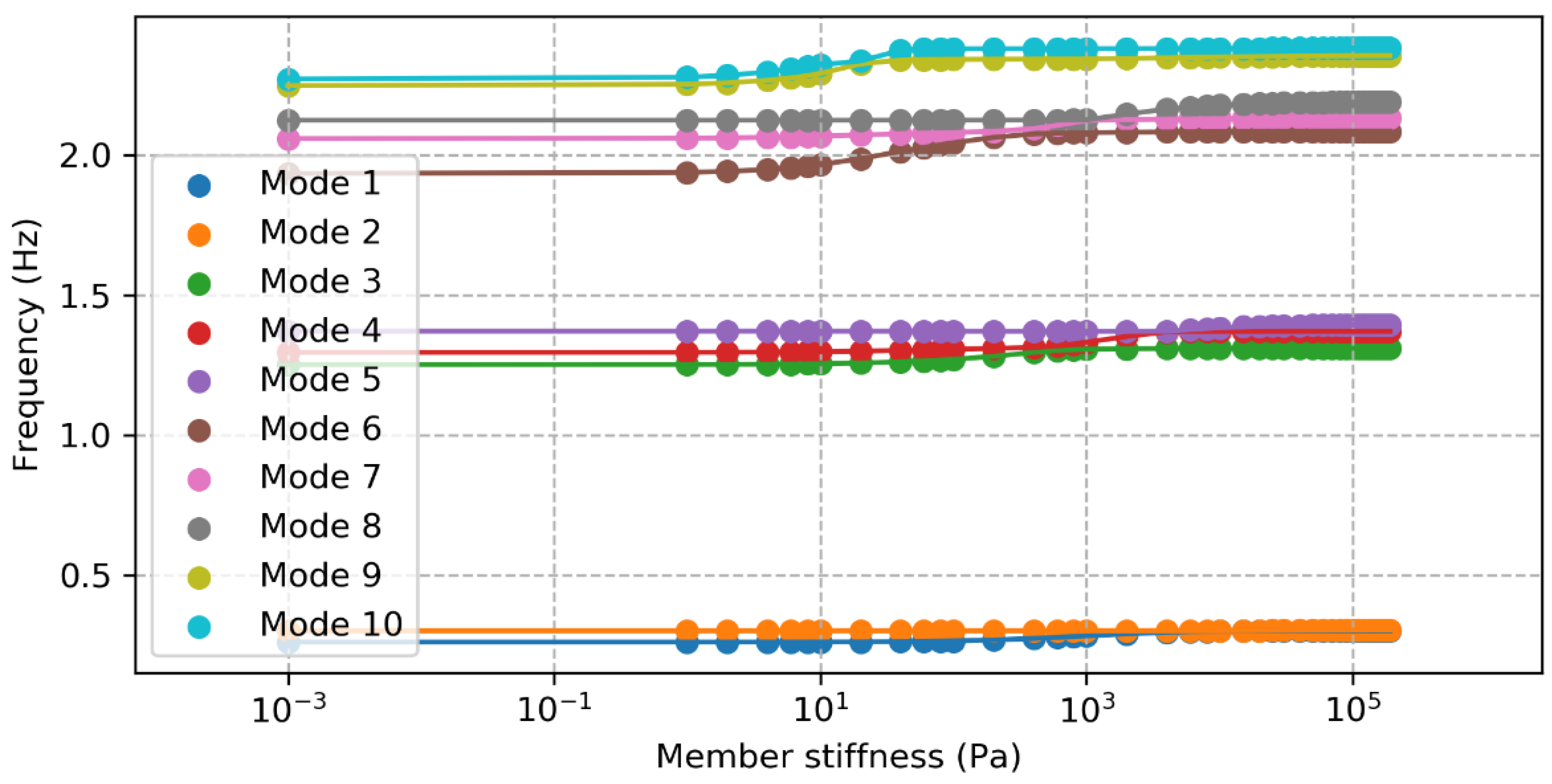
16]. In this structure, the frequency of the sixth mode is much higher than the fifth, and so even with significant damage the frequencies do not change enough for a mode 6 or higher to be mistaken for mode 5 or lower. An example demonstrating the difference in eigenfrequencies can be seen in
Figure 2, which shows the eigenfrequencies of the first 10 modes as a leg element is damaged. This demonstration shows that even after a large change in the structure, the sixth eigenfrequency is still much higher than the fifth.
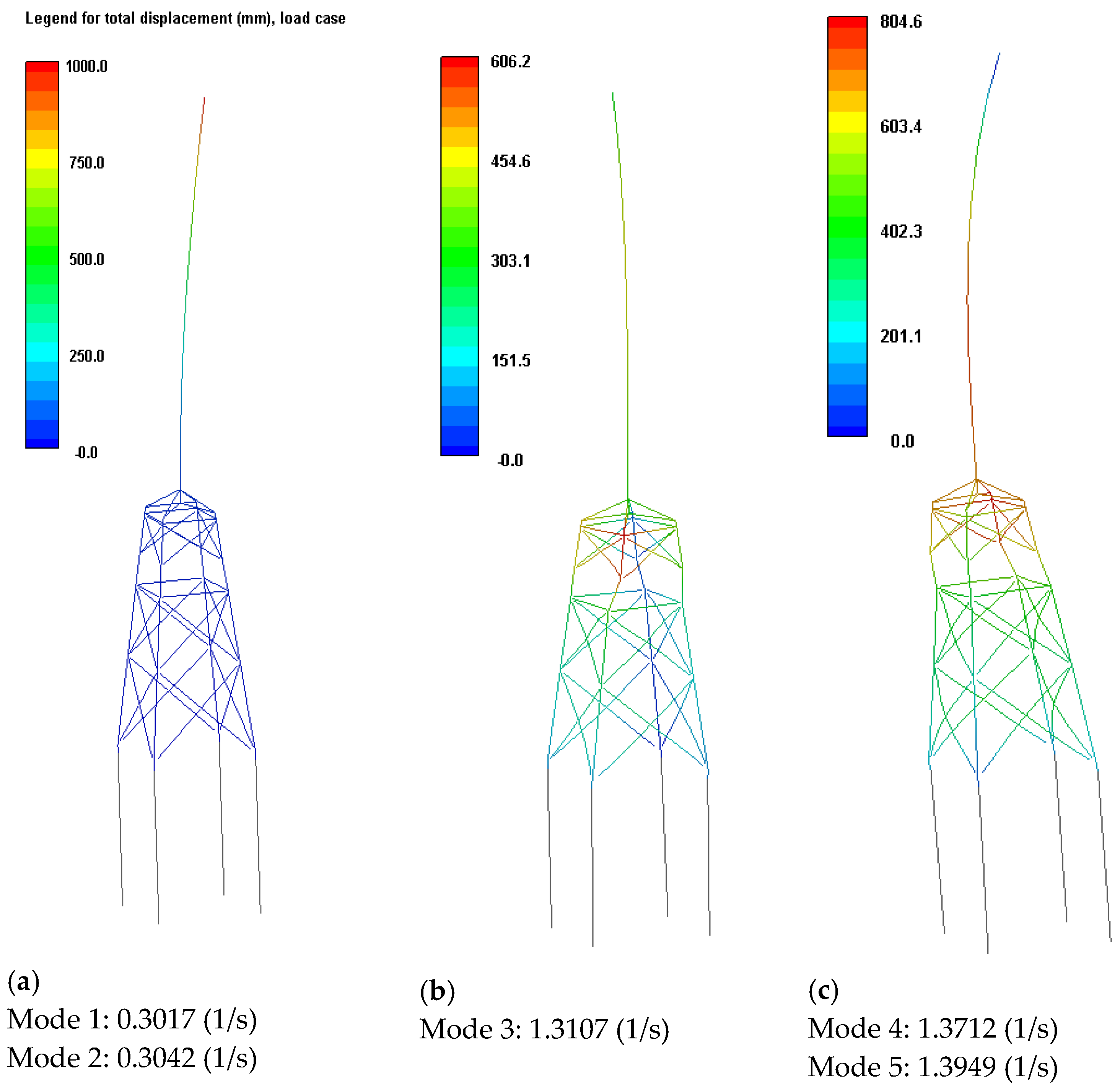
Of the five modes calculated, the first two are both tower modes which are tower fore-aft and side-side. The third mode is a torsional mode while the fourth and fifth are both tower-swaying modes. Plots of these modes along with their respective frequencies, are shown in
Figure 3, with modes 1 and 2, as well as modes 4 and 5 shown together. A representation of the structural model is shown in
Figure 4.
Fundamentally, ROSA works in the same way as any beam-element based structural model which solves the eigenvalue problem and so these results can be reproduced with other, similar software.
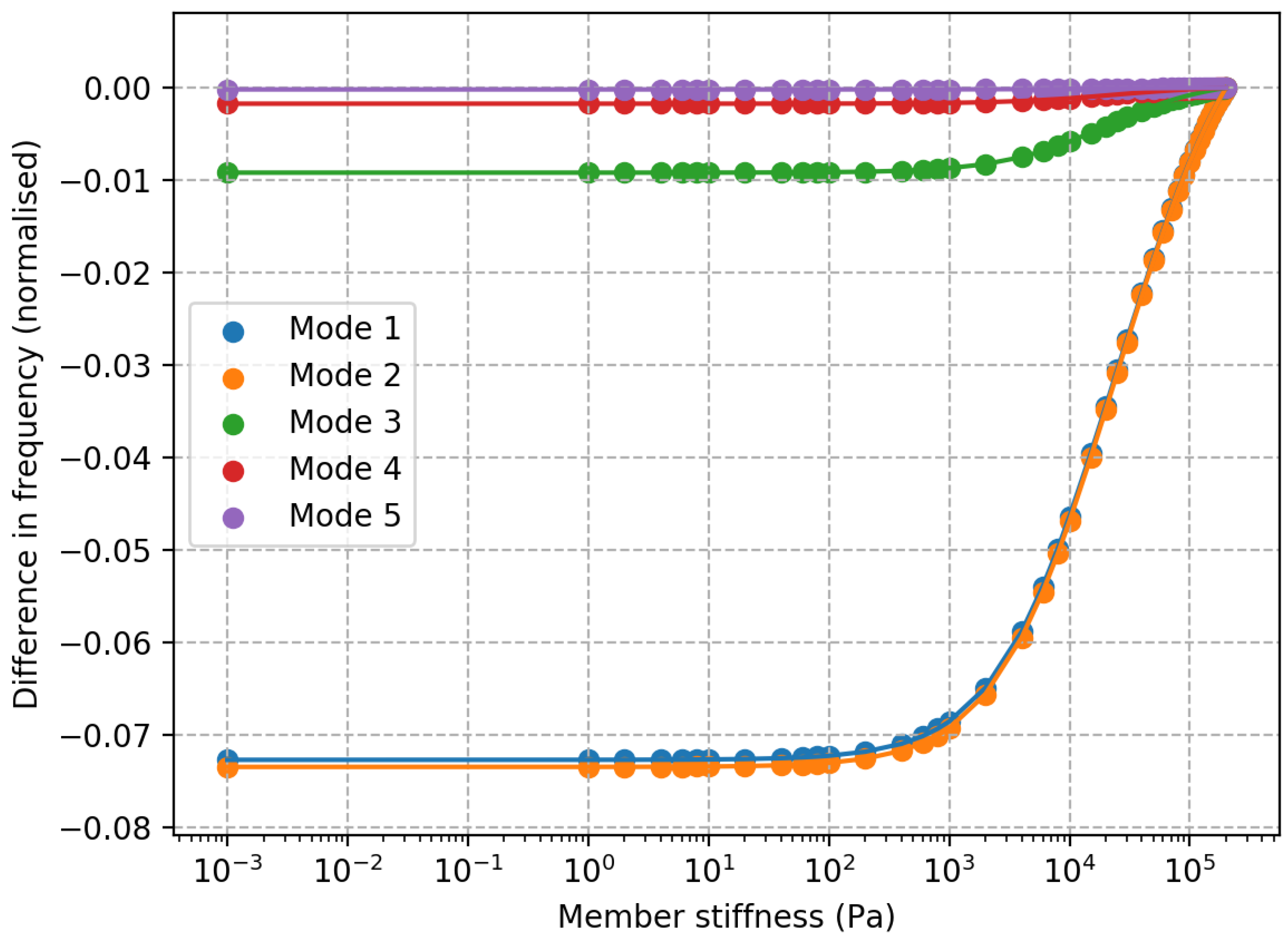
A wide range of relevant parameters are included in ROSA, and can be adjusted by the user in ‘cards’ within the text-based input file. Some of these parameters include element and joint stiffness; corrosion; scour, both global and local in addition to a range of other items. The parameters changed are discussed in more detail in the following section.
There are several failure mechanisms which are time dependent and expected to occur, such as marine growth, scour, corrosion and some others [
42,
43]. The model includes these at the level which they are generally expected, or an average amount over the lifetime of the structure. In cases when one of these parameters is varied, they might be given as a multiple of this expected value or as a measurable value, as appropriate. For example, corrosion is defined as a profile with respect to depth, and so, this is varied as multiplied by a factor, however, global scour can be quantified with just scour depth and so this value is given.
5. Detectability Considerations
5.1. Dependence on Nacelle Direction of Modal Properties in Intact Condition
The turbine blades and nacelle have a large mass and moment of inertia and, as a result, their position relative to the rest of the structure has a significant impact on the modal parameters of the structure, which is particularly apparent, due to the structure’s lack of rotational symmetry. Therefore, it is necessary to investigate the effect from changing nacelle yaw direction.
The nacelle and blades are modelled here as point masses with pre-assigned moment of inertia values. To model the nacelle yawing from the original reference direction, the point masses are moved around the tower by 1 degree each iteration, and the moment of inertia components are transformed correspondingly. This process of changing the direction is then repeated for a ‘damaged’ case, with joint loss at the middle of a leg element.
To determine the response of the structure with the nacelle yawed away from the original direction and compare it back to the original reference direction, the mode shapes are then transformed back to the original reference direction and compared to the ‘intact’ case at the original direction; the transformation is conducted using elementary coordinate rotation as shown in Equation (8) [
51], which is applied for both translation and rotation values. An alternative approach is to compare ‘damaged’ at
degrees to ‘intact’ at
degrees where
is each change from the reference. The first method is used here rather than the second as this would make future comparison to operational data more convenient since the directional values in operational data are effectively continuous. This method also allows them to use more of the data rather than only comparing subsets.
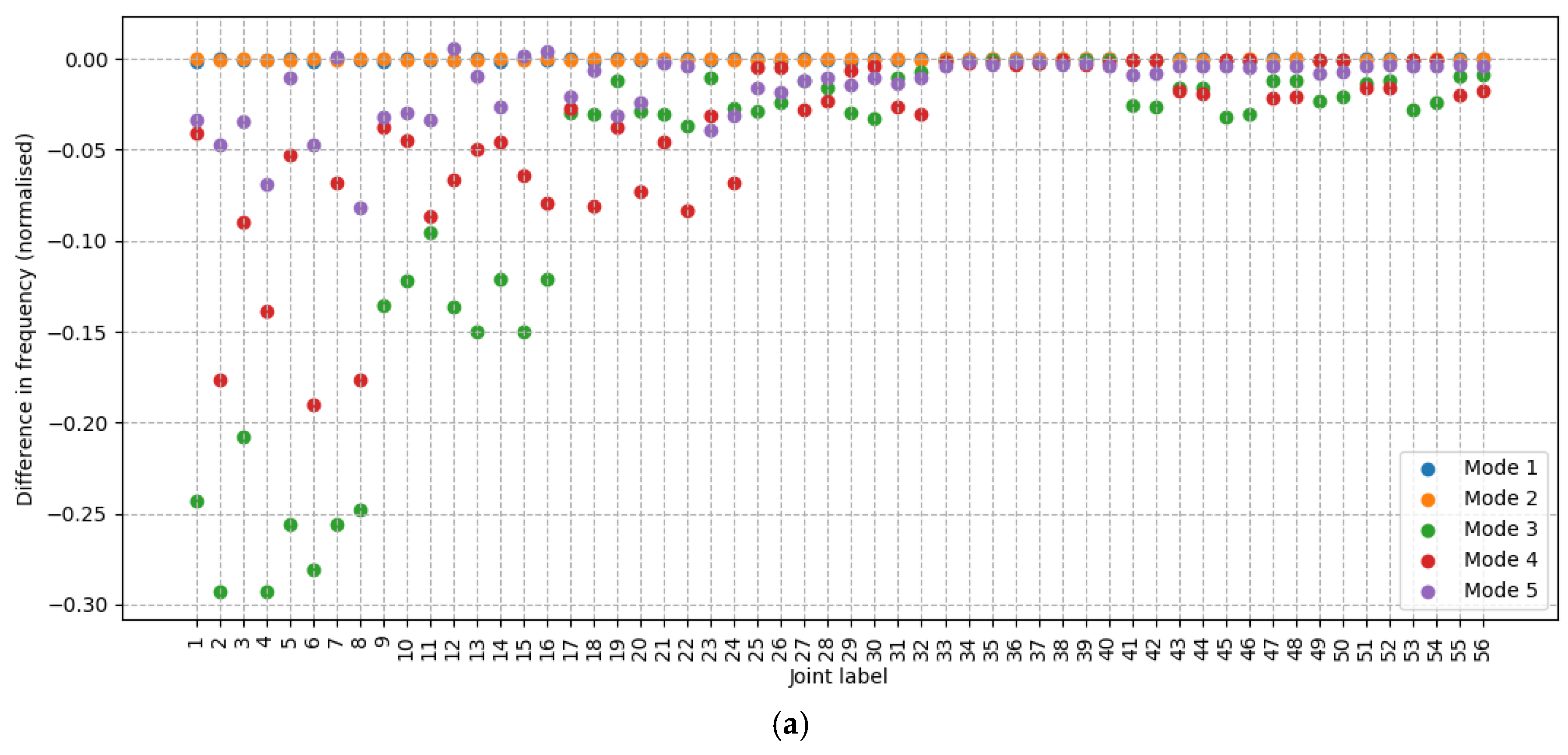
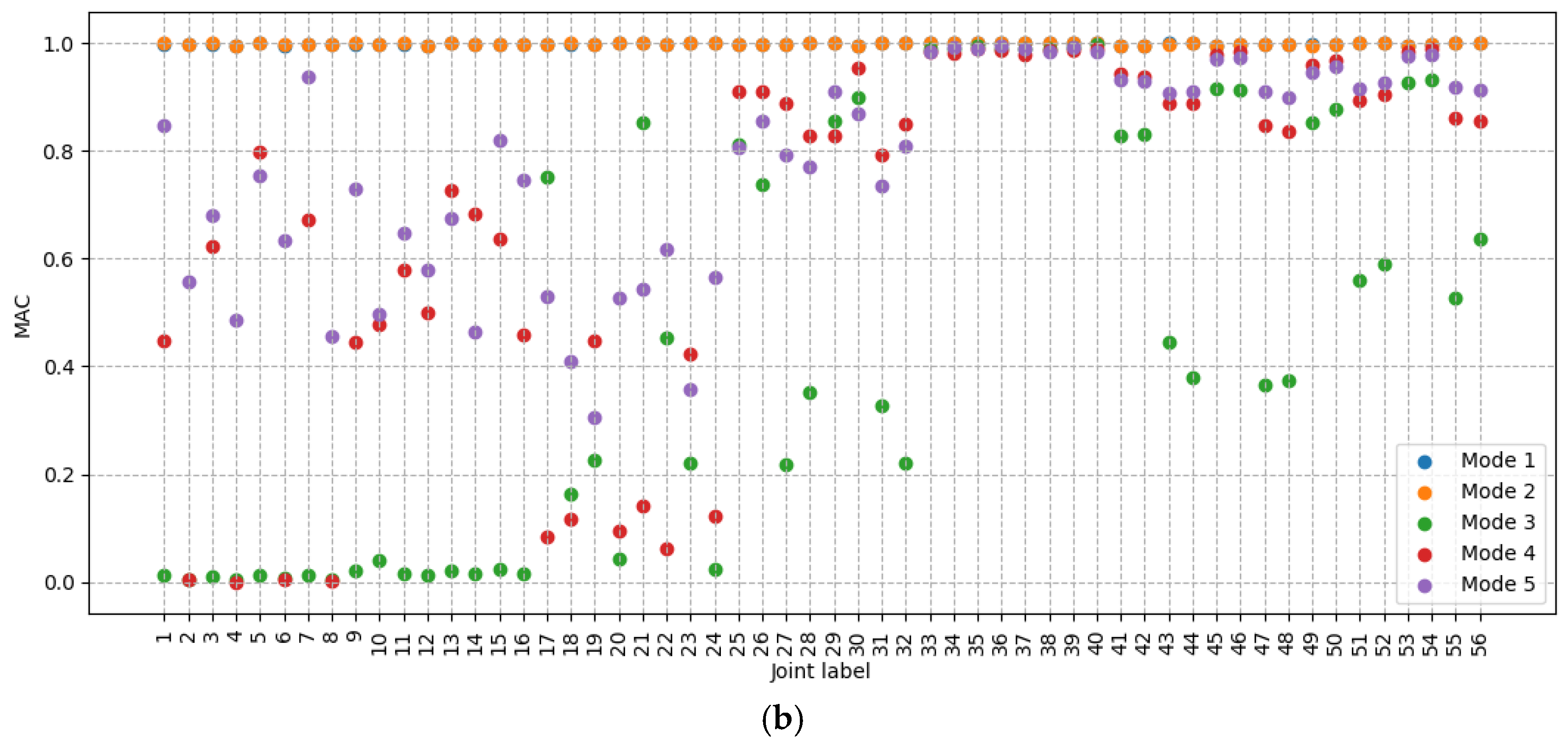
As the turbine direction yaws to make a complete rotation, the natural frequency does not change by an amount that exceeds a 4% threshold, where it would be considered detectible. The maximum change in frequency calculated using the ROSA model, normalized by the original frequencies, for the first five modes are: 0.002, 0.009, 0.002, 0.022, 0.024, respectively. However, the mode shapes, as quantified by the MAC values, change considerably.
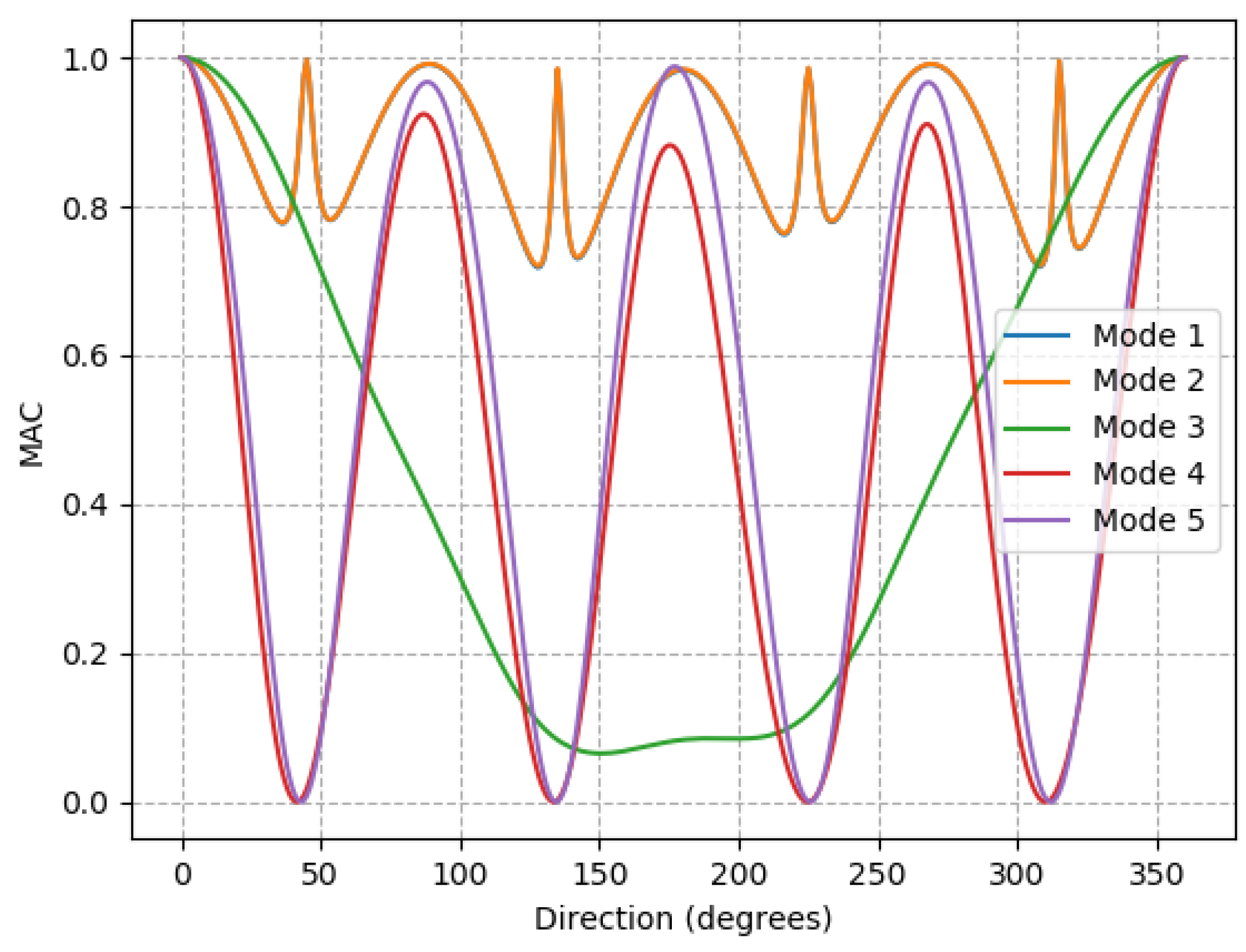
Figure 5 shows the MAC values for the first five mode shapes, as calculated after the shapes have been transformed back to the original reference. MAC is calculated in comparison to 0 degrees case.
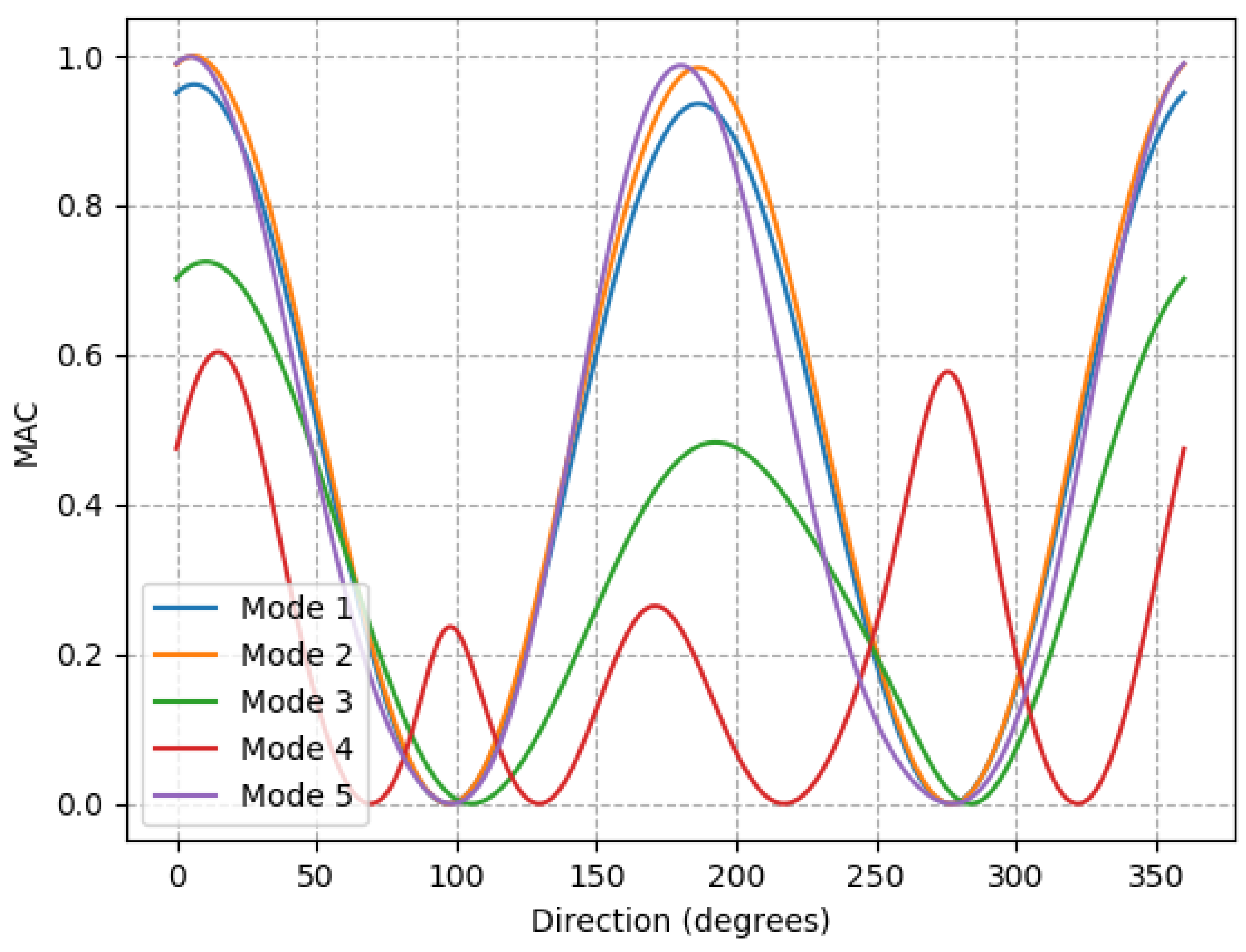
The first two modes are the tower fore-aft and side-side modes. In the first two modes, the tower always oscillates roughly in the direction of the jacket legs. There is an edge-case exception to this which is when the nacelle is pointed equally between two jacket legs, which is the case for 45 degrees, 135 degrees, 225 degrees and 315 degrees. In cases when the nacelle is pointed equally between jacket legs, there appears to be a transition as the direction of the first two modes swap with each other. The MAC value for 45 degrees, 135 degrees, 225 degrees and 315 degrees is 1, because of the transformation approach. Without the mode shape being transformed, the MAC values in the leg directions are 0.5 as the MAC changes between 1 and 0.
Mode 3 is a torsional mode with the otherwise vertical axis of oscillation offset slightly in the direction of the nacelle. As the nacelle turns, the axis about which mode 3 oscillates also moves.
Modes 4 and 5 are tower swaying modes and their direction rotates at the rate of the nacelle yaw, but in the opposite direction (in a sense of clockwise/counterclockwise about the tower centerline). At 0 degrees of yaw, mode 5 is in line with the nacelle and 4 is perpendicular. At 45 degrees of yaw, mode 4 is in line with the nacelle yaw and mode 5 is perpendicular.
The change in mode vectors resulting from RNA yaw is important to be aware of, because without accounting for it, even an intact structure would appear damaged using MAC. However, being aware of this, MAC can be used effectively to detect and identify damage.
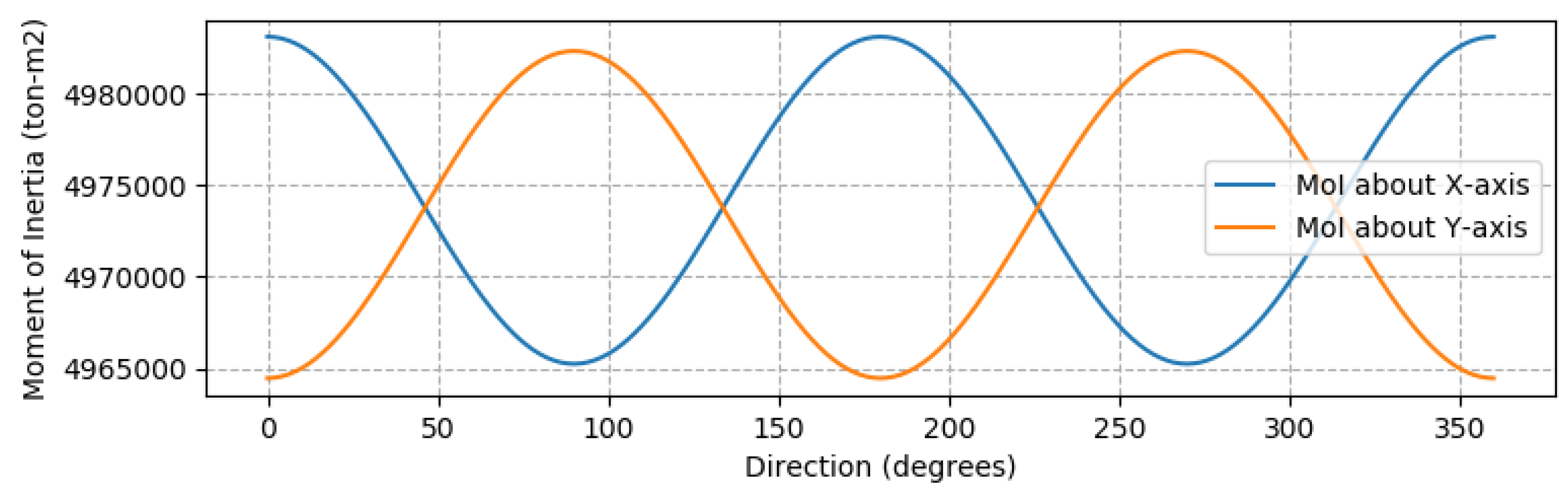
Figure 6 shows the dynamic moment of inertia of the structure calculated by the model. This shows a smooth change in moment of inertia with nacelle direction which gives some indication that the model is performing as expected. We also see that the spikes in the first and second modes seen in
Figure 5 correspond to directions when the x-axis and Y-axis moment of inertia are equal; this is where the change in oscillating direction occurs.
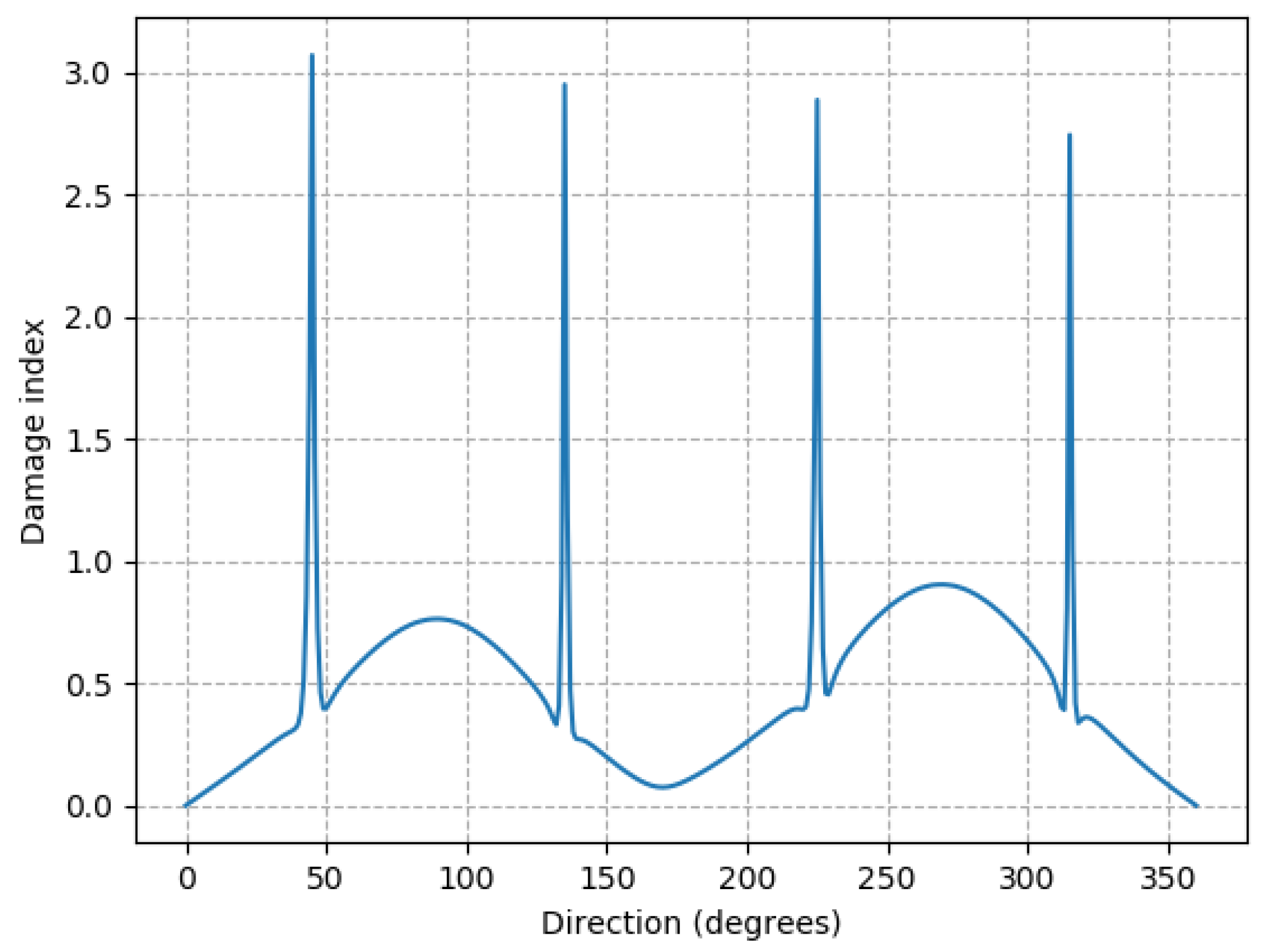
The ‘damage index’ value calculated using modal flexibility varies less with direction, except for the four peaks. This damage index is not quantifying a damage in this case, there is no damage, it is showing the effect on this metric of an operational behavior-it is a difference in the flexibility of the structure, due to this operational behavior. Besides the peaks, the values are all under 0.9, which, by itself, does not mean much but can be used as a reference when quantifying damage cases. The seemingly anomalous results in this plot are the peaks at 45 degrees, 135 degrees, 225 degrees and 315 degrees. The modal flexibility, and hence damage index seen in
Figure 7 is more affected by lower modes and these peaks correspond with the rapid change in MAC seen in
Figure 5, which are changes in mode shape between the first and second modes. It is possible that these four peaks are an artefact of the numerical solution process, and might not be seen in measurements of a real structure, so this aspect should be taken with caution.
5.2. Choice of Damage Metric
The MAC is a comparative value between two observations. If an observation is made at two points in time, there is not necessarily any time history linking these two observations, instead, there are a set of modes to be compared with another set of modes. This raises the question of how that pairing should be done to best represent the change. This is particularly important in the case of mode switching, where the labelling of modes can change, due to changes in frequency. This is important for the task of damage identification, as well as potentially in sensor placement when determining which mode shapes need to be identified. Although each numerical model represents a discreet state, gradually induced change in the model can help give an indication of whether a comparison makes logical sense.
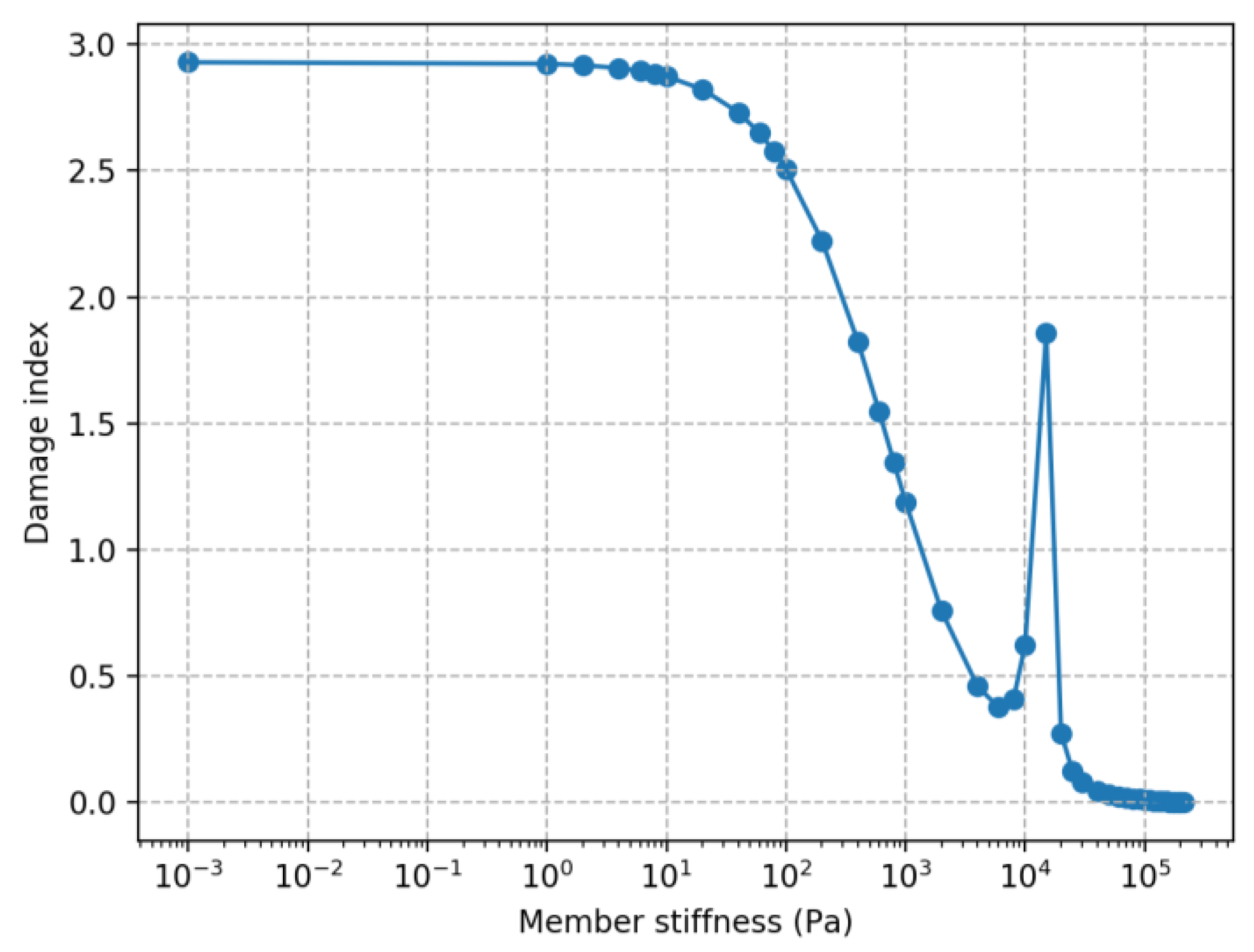
To illustrate the problem, as well as a potential solution to the problem, a leg element is gradually damaged, meaning the stiffness at a joint is gradually reduced. This is also useful from the perspective of damage identification to determine when a damage becomes detectible. In this case, the leg element is halfway up the structure.
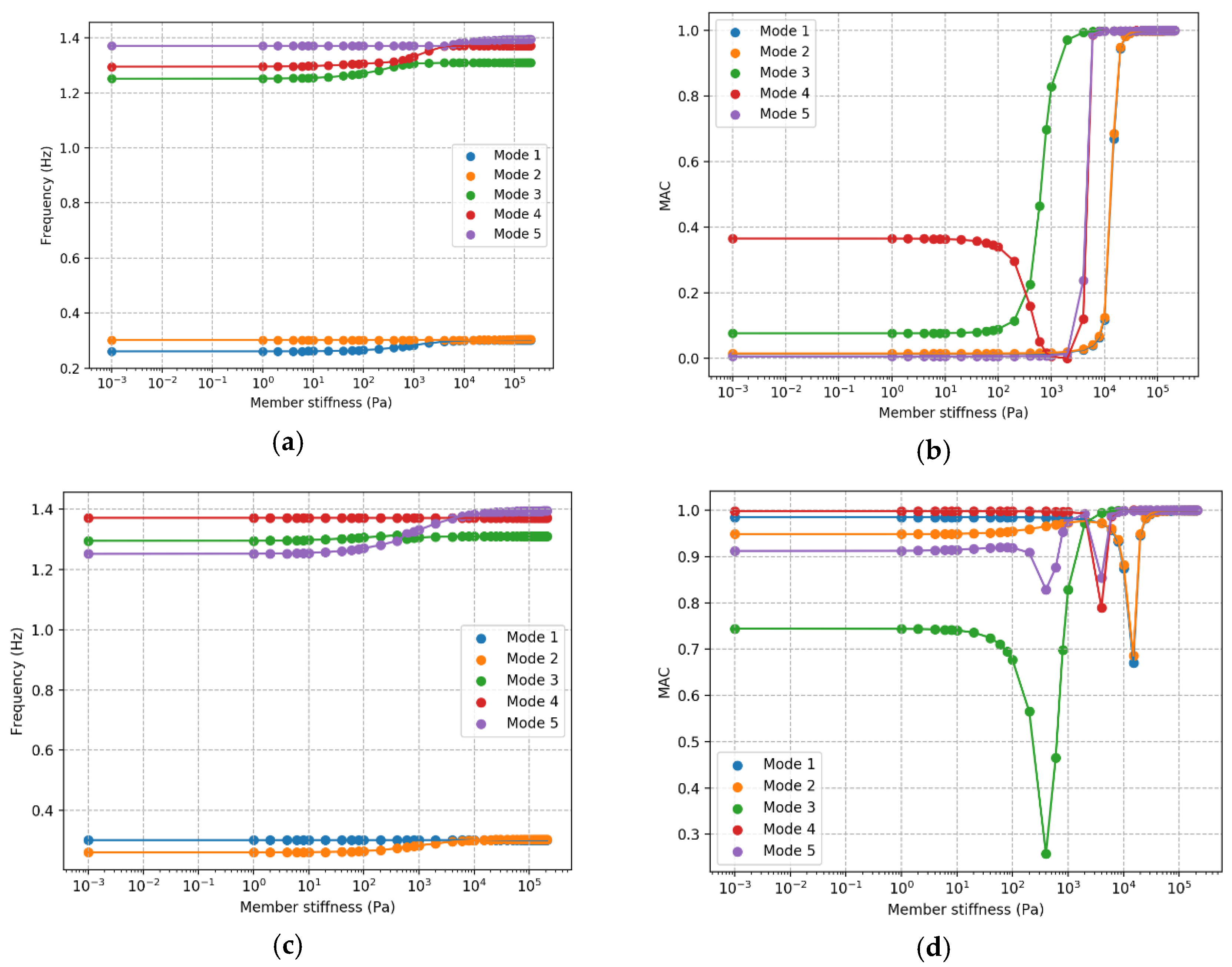
Figure 8a,c show the mode frequencies as simulated damage is gradually induced.
Figure 8a shows comparisons made where the order is based on frequency order, as is the established approach. Choosing the modes to compare based on the order of frequencies is not always the correct approach. Some of the modes have a gradual reduction in frequency, but the reduction stops when it becomes the same as the next mode down, but then the frequency of the next mode down continues the downwards trend–when one frequency passes another, the comparison changes.
Figure 8c shows comparisons made where the sum MAC value is maximized using the Hungarian algorithm. With this approach, one frequency can go below the other without the comparison changing. The implication when comparing frequency is that rather than determining the frequency for mode 1 changes by 14% from start to finish, instead mode 2 changes 14% and mode 5 changes 10%.
The effect of this change is even more apparent looking at MAC values.
Figure 8b,d show the MAC values calculated with these two approaches. If the comparison is made based on frequency order, then all modes have points where they become completely inconsistent with the undamaged mode. If the comparison is made based on maximizing the sum of MAC, then these drops happen only briefly before the MAC returns to a relatively high value. The drops occur when two frequencies approach equality. If there is a mode shape that is so close to being consistent with an intact mode shape, such as a MAC of greater than 0.9, then that is a strong argument that this pairing is what should be considered. This also gives more information for determining which damage has occurred, since, if all MAC values are roughly 0, then this may also be the case for many types of damage.
The damage index calculated through the modal flexibility does not have this same question of which modes to compare as all modes are combined before damaged and intact are compared. The damage index calculated for this gradual implementation of damage is shown in
Figure 9. This figure shows a peak at the same time modes 1 and 2 have a sharp reduction at 2 × 10
4, but not any of the other similar sharp reductions. While the MAC returned to a relatively high value, the damage index continued to increase as more damage was implemented, therefore, the damage index is a better choice for quantifying the level of damage.
7. Discussion
The results of this study reveal several findings about the behavior of this jacket structure and about the potential for damage detection based on these measurement values. Some consideration should be made as to the applicability of these results to other cases. In terms of similar models of similar jacket structures, it should be expected that comparable results would be achieved. It should also be expected that this is a good approximation of the real system, as this study was conducted using the design model to which the system was built. However, if a more complex model is used, such as one which explicitly models the blades, the results may differ, due to the more complex dynamic behavior. Measurement results from a real wind turbine may be different still, and so it would be important to understand this difference for any case of interest.
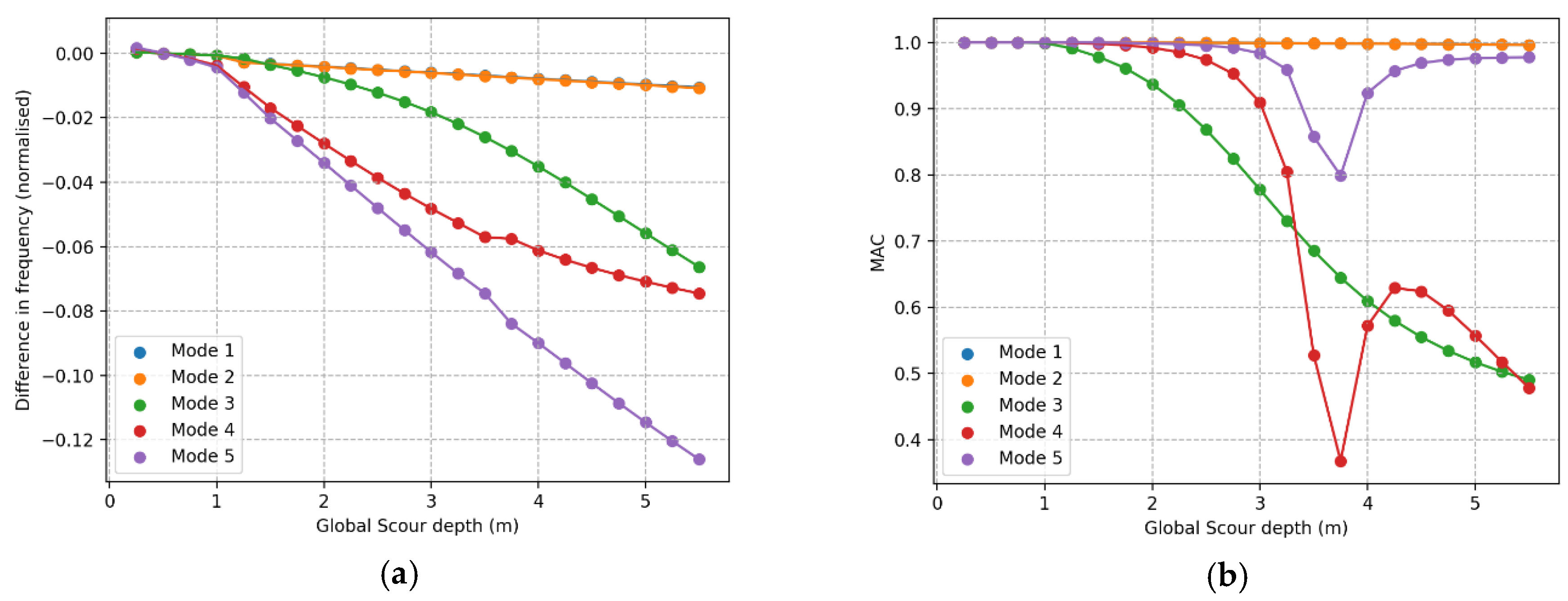
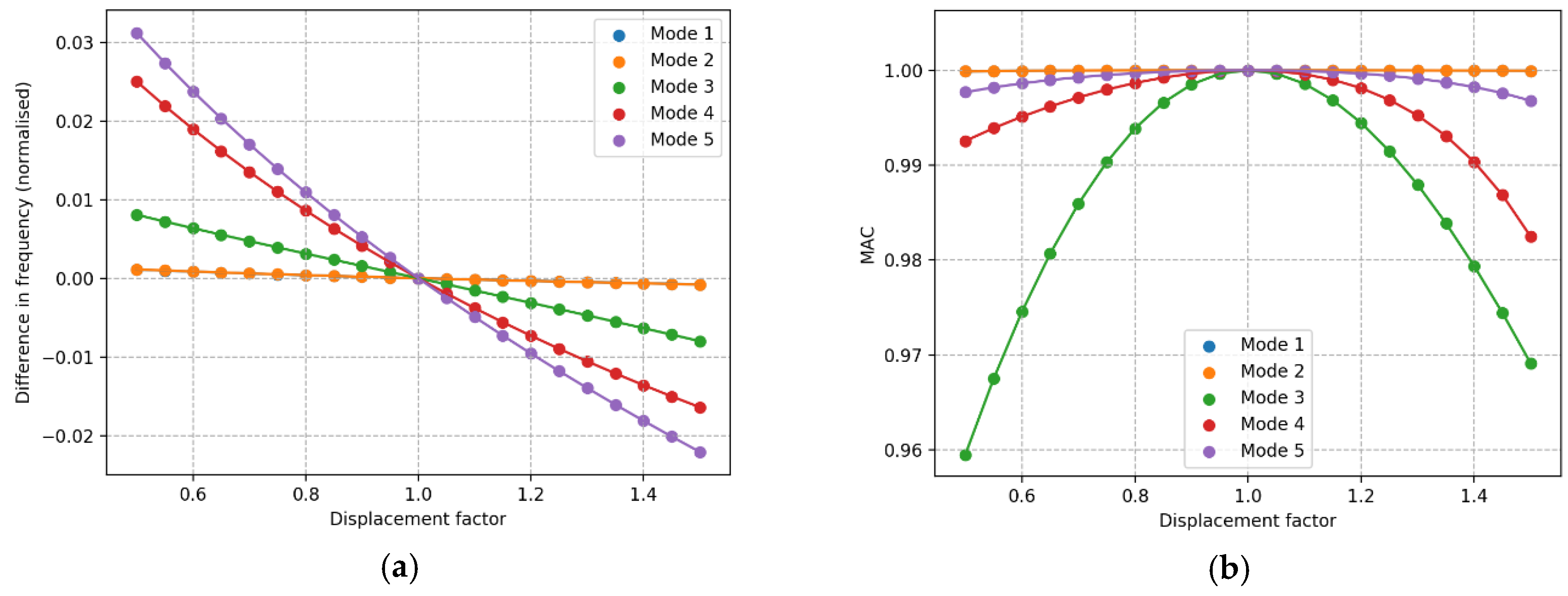
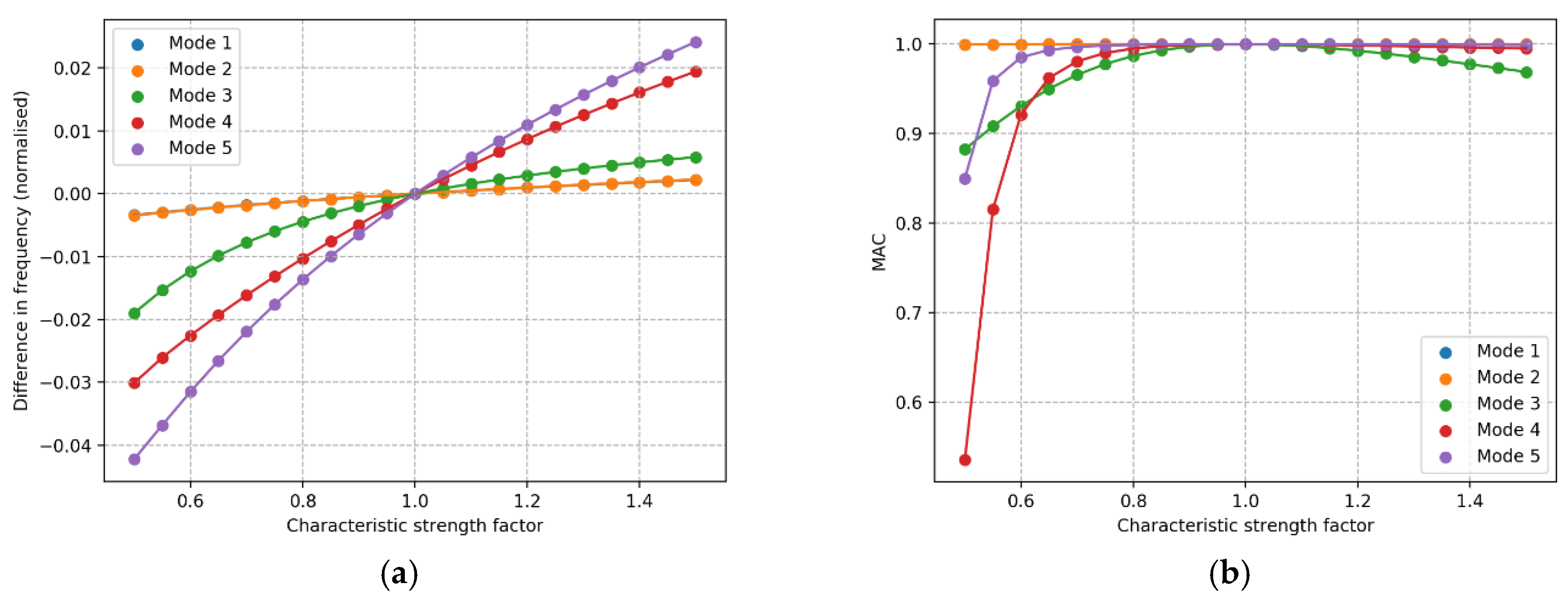
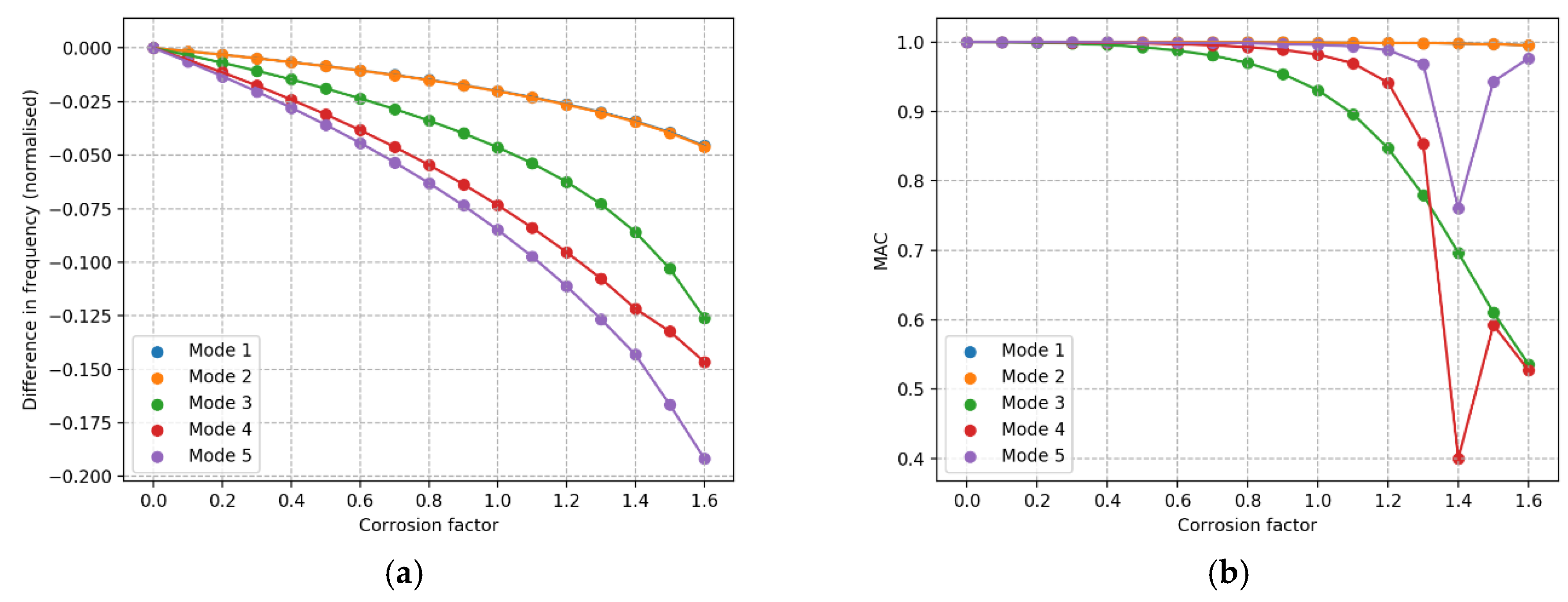
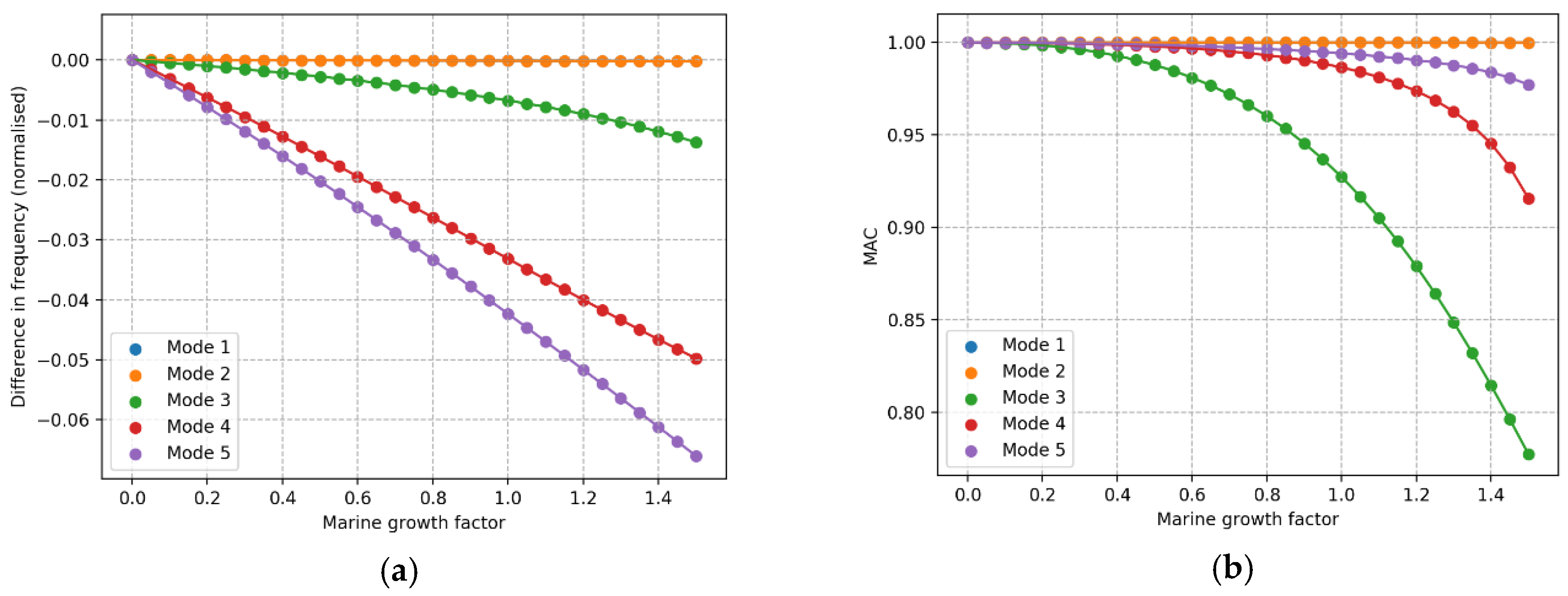
There is a consistent order in normalized change in frequency and MAC values for effects that are global on the structure, which is that all factors investigated that are not a damage to a specific structural element. The order in terms of largest change to smallest is consistently fifth, fourth, third, second, first for normalized change in frequency and for MAC, within moderate changes, the order is third, fourth, fifth, with negligible change in first and second. This order is of course dependent on how the comparison is chosen, but the conclusion is that based on the order of frequency change or MAC values, these effects cannot be distinguished. To distinguish between these effects, this can potentially be done based on the quantity of the changes with respect to each other, as well as using time history observing the development of the change.
Damages to the structural member joints have a nonsymmetric effect and therefore, the observed change in modal parameters is closely related to the nacelle direction. As a result of this directionality, the side of the structure on which the damage has occurred is identifiable. The level of effect the joint damage has can also be characterized by the height of the damage and, therefore, it should be possible to locate joint damage with reasonable accuracy.
It is useful to calculate several metrics when trying to detect and identify damage. This gives more information about what change has occurred and can make the situation easier to understand. In calculations that require comparison of specific modes, it is useful to make this selection both with the order of the frequency and by maximizing the total MAC value, as it appears that neither approach is always the better choice. The damage metric calculated with the modal flexibility can be hard to interpret on its own as the value indicating ‘damage’ changes between damage types. For example, the damage index is 1.2 with 6 m of scour, 0.35 with a marine growth factor of 1.45 and 2 at a corrosion factor of 1.6, while just changing the direction of the nacelle the value can go up to 0.3. By itself, it can only show if there is a change in the structure, but it can be useful if combined with other information.
When the frequencies of two modes intersect, there is a sharp change in the shape of these two modes which is observed in the MAC values. When this happens with lower modes, the change is also observed in the modal flexibility.
8. Conclusions
This paper presented the simulated dynamic response of an offshore wind turbine jacket structure and how it changes in response to a range of situations. These situations include: (1) operational changes, the turbine nacelle yaw; (2) damage, including cracks on structural joints; and (3) exceeding design parameters for corrosion, scour, marine growth and tower bolt tension. This can serve as a useful reference for future work, as these situations were investigated on a single structure using a highly detailed design model. The structural response, and hence damage detection feasibility, based on a numerical model of damages, has been investigated. For the range of conditions, an eigenvalue solution was conducted to determine the modal properties and sensitivity studies to a range of parameter changes was conducted. There is a greater level of detail in the model used for this study than in other, similar studies. An example of the increased level of detail is including the blades and nacelle through representing them as a moment of inertia and mass including the mass and moment of inertia of the nacelle and blades. Including the cracks on structural elements, other types of damage are simulated such as scour, marine growth and corrosion. The metrics calculated are global metrics to reflect real-world limitations, these metrics are normalized frequency changes, MAC and a value derived from modal flexibility.
It was found the nacelle direction substantially alters the mode shapes and, hence, the MAC values, although the frequencies are not significantly altered. Therefore, any damage detection algorithm using mode shapes should include knowledge of the nacelle yaw direction. This also impacts how cracks in joint elements appear in terms of MAC value; the result is that, at some nacelle yaw directions, it may be hard to detect damage, but this potentially aids in locating the damage.
If there is a significant enough change in the modal properties caused by the damage, then the frequency of one mode can move below the frequency of another, this mode-switching is an issue encountered for semi-symmetric structures. Two methods for dealing with this were used and assessed, which include using the Hungarian algorithm to maximize the sum of MAC values, as well as using a modal stiffness-based damage metric. Both approaches were shown to be effective, although the Hungarian algorithm was only effective up to a limited level of change in some parameters.
There are several observations that would aid in the localization of cracks through changes in global dynamics. One of these observations confirms what is already known, which is that for cracks on elements, the severity on the structural dynamics is a function of height in the structure; lower elements change mode shape and frequency more than higher ones. This, combined with the directionality of the nacelle, can make localization of the damaged member joint possible using global metrics.
Effects which apply to the structure evenly, such as corrosion or global scour, there is a common order in which the MAC and frequencies are changed. The result of this is that these types of features may be difficult to discern from each other through modal properties alone.