On Applications of Elements Modelled by Fractional Derivatives in Circuit Theory
Abstract
1. Introduction
2. FO Transmission Lines
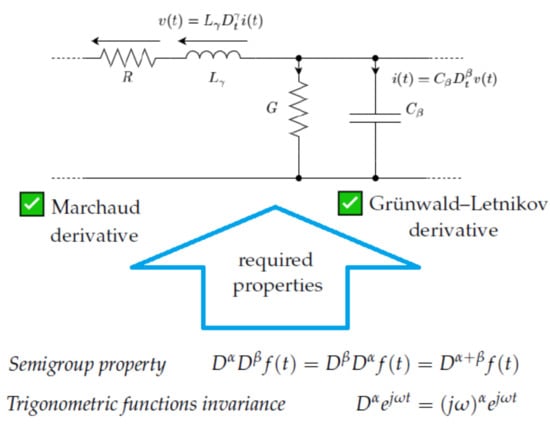
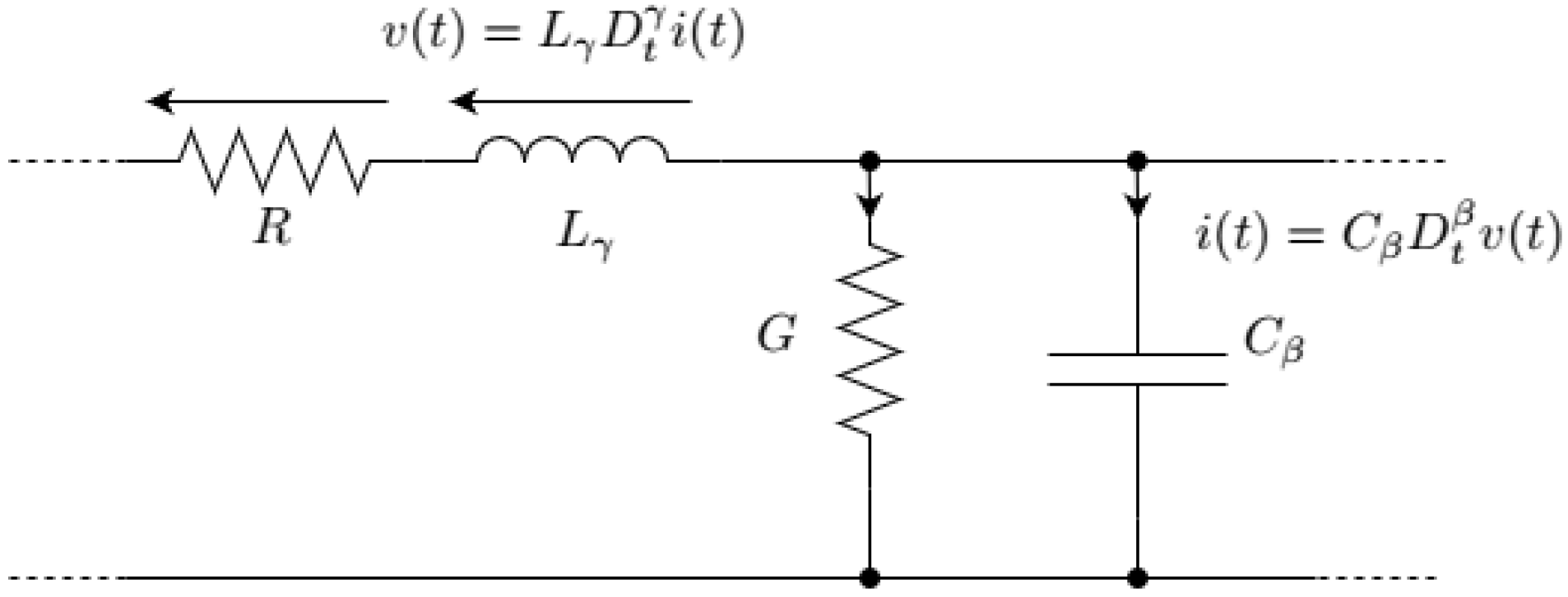
3. FO Derivative Properties Necessary for Applications in Circuit Theory
- Identity
- Compatibility with IO derivative
- Compatibility with IO integral
- Linearity
- Semigroup property (also called the index law)
- Trigonometric functions invariancewhere . The domain of the complex power function is chosen so that it contains the complex right half-plane . Hence,It may be concluded from (7) and (8) that the phasor analysis can generally be applied whenwhere is a certain constant depending on and . However, the specific condition (16) seems to be a much more natural one to be postulated. One should note that it is required for the analysis of circuits with zero initial conditions for which the substitution in the Laplace domain provides the solution in the phasor domain.
4. FO Derivatives
- Atangana–Koca–Caputo [58]
4.1. Riemann–Liouville
4.2. Caputo
4.3. Liouville–Caputo
4.4. Liouville
4.5. Marchaud
4.6. Two-Sided Fractional Ortigueira–Machado Derivative
4.7. Grünwald–Letnikov
5. Nonclassical Derivatives
- Caputo–Fabrizio (with the base point set at 0)where is a certain normalizing factor.
- Atangana–Baleanu (with the base point set at 0)where denotes the (one-parameter) Mittag–Leffler function and is a certain normalizing factor.
- Atangana–Koca–Caputo for (with the base point set at 0)where denotes the two-parameter Mittag–Leffler function and is a certain normalizing factor.
- Conformable derivative
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ortigueira, M.D. An introduction to the fractional continuous-time linear systems: The 21st century systems. IEEE Circuits Syst. Mag. 2008, 8, 19–26. [Google Scholar] [CrossRef]
- Elwakil, A.S. Fractional-order circuits and systems: An emerging interdisciplinary research area. IEEE Circuits Syst. Mag. 2010, 10, 40–50. [Google Scholar] [CrossRef]
- Freeborn, T.J. A Survey of Fractional-Order Circuit Models for Biology and Biomedicine. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 416–424. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: New York, NY, USA, 1993. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier Science: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; Chapman and Hall/CRC: Boca Raton, FL, USA, 2015. [Google Scholar]
- Al-daloo, M.; Soltan, A.; Yakovlev, A. Overview study of on-chip interconnect modeling approaches and its trend. In Proceedings of the 2018 7th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 7–9 May 2018; pp. 1–5. [Google Scholar]
- Al-Daloo, M.; Soltan, A.; Yakovlev, A. Advance Interconnect Circuit Modeling Design Using Fractional-Order Elements. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2020, 39, 2722–2734. [Google Scholar] [CrossRef]
- Shang, Y.; Fei, W.; Yu, H. A fractional-order RLGC model for Terahertz transmission line. In Proceedings of the 2013 IEEE MTT-S International Microwave Symposium Digest (MTT), Seattle, WA, USA, 2–7 June 2013; pp. 1–3. [Google Scholar] [CrossRef]
- Shang, Y.; Yu, H.; Fei, W. Design and Analysis of CMOS-Based Terahertz Integrated Circuits by Causal Fractional-Order RLGC Transmission Line Model. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 355–366. [Google Scholar] [CrossRef]
- Aydin, O.; Samanci, B.; Ozoguz, I.S. Characterization of Microstip Transmission Lines Using Fractional-order Circuit Model. Balk. J. Electr. Comput. Eng. 2018, 6, 266–270. [Google Scholar] [CrossRef][Green Version]
- Chang, Y.-Y.; Yu, S.-H. A compact fractional-order model for Terahertz composite right/left handed transmission line. In Proceedings of the 2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS), Beijing, China, 16–23 August 2014; pp. 1–4. [Google Scholar]
- Yang, C.; Yu, H.; Shang, Y.; Fei, W. Characterization of CMOS Metamaterial Transmission Line by Compact Fractional-Order Equivalent Circuit Model. IEEE Trans. Electron Devices 2015, 62, 3012–3018. [Google Scholar] [CrossRef]
- Shi, L.; Qiu, L.; Huang, X.; Zhang, F.; Wang, D.; Zhou, L.; Gao, J. Characterization of Si-BCB transmission line at millimeter-wave frequency by compact fractional-order equivalent circuit model. Int. J. Microw. Comput. Aided Eng. 2019, 29, e21685. [Google Scholar] [CrossRef]
- de Oliveira, E.C.; Machado, J.A.T. A review of definitions for fractional derivatives and integral. Math. Probl. Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Teodoro, G.S.; Machado, J.T.; de Oliveira, E.C. A review of definitions of fractional derivatives and other operators. J. Comput. Phys. 2019, 388, 195–208. [Google Scholar] [CrossRef]
- Sikora, R.; Pawłowski, S. Fractional derivatives and the laws of electrical engineering. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2018, 37, 1384–1391. [Google Scholar] [CrossRef]
- Sikora, R.; Pawłowski, S. On certain aspects of application of fractional derivatives in the electromagnetism. Prz. Elektrotechniczny 2018, 94, 101–104. [Google Scholar]
- Latawiec, K.J.; Stanisławski, R.; Łukaniszyn, M.; Czuczwara, W.; Rydel, M. Fractional-order modeling of electric circuits: Modern empiricism vs. classical science. In Proceedings of the 2017 Progress in Applied Electrical Engineering (PAEE), Koscielisko, Poland, 25–30 June 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, B. Comparative Study of Riemann–Liouville and Caputo Derivative Definitions in Time-Domain Analysis of Fractional-order Capacitor. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 2184–2188. [Google Scholar] [CrossRef]
- Gulgowski, J.; Stefański, T.P.; Trofimowicz, D. On Applications of Fractional Derivatives in Circuit Theory. In Proceedings of the 2020 27th International Conference on Mixed Design of Integrated Circuits and System (MIXDES), Wroclaw, Poland, 25–27 June 2020; pp. 160–163. [Google Scholar]
- Gómez-Aguilar, J.F.; Dumitru, B. Fractional Transmission Line with Losses. Z. Naturforschung A 2014, 69, 539–546. [Google Scholar] [CrossRef]
- Cvetićanin, S.M.; Zorica, D.; Rapaić, M.R. Generalized time-fractional telegrapher’s equation in transmission line modeling. Nonlinear Dyn. 2017, 88, 1453–1472. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Tenreiro Machado, J. What is a Fractional Derivative? J. Comput. Phys. 2015, 293, 4–13. [Google Scholar] [CrossRef]
- Gulgowski, J.; Stefanski, T.P. On Applications of Fractional Derivatives in Electromagnetic Theory. 2020; submitted for publication in conference proceedings. [Google Scholar]
- Weisstein, E.W. “Telegraph Equation”. From MathWorld—A Wolfram Web Resource. 2020. Available online: https://mathworld.wolfram.com/TelegraphEquation.html (accessed on 30 August 2020).
- Atangana, A.; Gómez-Aguilar, J.F. Decolonisation of fractional calculus rules: Breaking commutativity and associativity to capture more natural phenomena. Eur. Phys. J. Plus 2018, 133, 166. [Google Scholar] [CrossRef]
- Atangana, A.; Gómez-Aguilar, J. Fractional derivatives with no-index law property: Application to chaos and statistics. Chaos Solitons Fractals 2018, 114, 516–535. [Google Scholar] [CrossRef]
- Zahra, W.; Hikal, M.; Bahnasy, T.A. Solutions of fractional order electrical circuits via Laplace transform and nonstandard finite difference method. J. Egypt. Math. Soc. 2017, 25, 252–261. [Google Scholar] [CrossRef]
- Sene, N. Fractional input stability for electrical circuits described by the Riemann–Liouville and the Caputo fractional derivatives. AIMS Math. 2019, 4, 147–165. [Google Scholar] [CrossRef]
- Chen, L.; Wu, X.; Xu, L.; Lopes, A.M.; Tenreiro Machado, J.; Wu, R.; Ge, S. Analysis of a rectangular prism n-units RLC fractional-order circuit network. Alex. Eng. J. 2020. [Google Scholar] [CrossRef]
- Alsaedi, A.; Nieto, J.J.; Venktesh, V. Fractional electrical circuits. Adv. Mech. Eng. 2015, 7, 1687814015618127. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.; Yépez-Martínez, H.; Escobar-Jiménez, R.; Astorga-Zaragoza, C.; Reyes-Reyes, J. Analytical and numerical solutions of electrical circuits described by fractional derivatives. Appl. Math. Model. 2016, 40, 9079–9094. [Google Scholar] [CrossRef]
- Lopes, A.; Tenreiro Machado, J. Fractional-order model of a nonlinear inductor. Bull. Pol. Acad. Sci. Tech. Sci. 2019, 67, 61–67. [Google Scholar] [CrossRef]
- Stefanski, T.P.; Gulgowski, J. Electromagnetic-based derivation of fractional-order circuit theory. Commun. Nonlinear Sci. Numer. Simul. 2019, 79, 104897. [Google Scholar] [CrossRef]
- Moreles, M.A.; Lainez, R. Mathematical modeling of fractional order circuit elements and bioimpedance applications. Commun. Nonlinear Sci. Numer. Simul. 2017, 46, 81–88. [Google Scholar] [CrossRef]
- Kaczorek, T. Selected Problems of Fractional Systems Theory; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Kaczorek, T. Positive fractional linear electrical circuits. In Photonics Applications in Astronomy, Communications, Industry, and High-Energy Physics Experiments 2013; Romaniuk, R.S., Ed.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2013; Volume 8903, pp. 481–494. [Google Scholar] [CrossRef]
- Kaczorek, T.; Rogowski, K. Fractional Linear Systems and Electrical Circuits; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Gómez, F.; Rosales, J.; Guía, M. RLC electrical circuit of non-integer order. Cent. Eur. J. Phys. 2013, 11, 1361–1365. [Google Scholar] [CrossRef]
- Banchuin, R.; Chaisricharoen, R. The analysis of active circuit in fractional domain. In Proceedings of the 2018 International ECTI Northern Section Conference on Electrical, Electronics, Computer and Telecommunications Engineering (ECTI-NCON), Chiang Rai, Thailand, 25–28 February 2018; pp. 21–24. [Google Scholar]
- Rosales, J.; Filoteo, J.; Gonzalez, A. A comparative analysis of the RC circuit with local and non-local fractional derivatives. Rev. Mex. Fis. 2018, 64, 647–654. [Google Scholar] [CrossRef]
- Puşcaşu, S.V.; Bibic, S.M.; Rebenciuc, M.; Toma, A.; Nicolescu, D. Aspects of Fractional Calculus in RLC Circuits. In Proceedings of the 2018 International Symposium on Fundamentals of Electrical Engineering (ISFEE), Bucharest, Romania, 1–3 November 2018; pp. 1–5. [Google Scholar]
- Shah, P.V.; Patel, A.D.; Salehbhai, I.A.; Shukla, A.K. Analytic Solution for the Electric Circuit Model in Fractional Order. Abstr. Appl. Anal. 2014, 2014, 343814. [Google Scholar] [CrossRef]
- Sene, N.; Gómez-Aguilar, J. Analytical solutions of electrical circuits considering certain generalized fractional derivatives. Eur. Phys. J. Plus 2019, 134, 1–14. [Google Scholar] [CrossRef]
- Magesh, N.; Saravanan, A. Generalized Differential Transform Method for Solving RLC Electric Circuit of Non-Integer Order. Nonlinear Eng. 2018, 7, 127–135. [Google Scholar] [CrossRef]
- Sowa, M.; Majka, Ł. Ferromagnetic core coil hysteresis modeling using fractional derivatives. Nonlinear Dyn. 2020, 101, 775–793. [Google Scholar] [CrossRef]
- Guía, M.; Gómez, F.; Rosales, J. Analysis on the time and frequency domain for the RC electric circuit of fractional order. Cent. Eur. J. Phys. 2013, 11, 1366–1371. [Google Scholar] [CrossRef]
- Abro, K.A.; Atangana, A. Mathematical analysis of memristor through fractal-fractional differential operators: A numerical study. Math. Methods Appl. Sci. 2020, 43, 6378–6395. [Google Scholar] [CrossRef]
- Abro, K.; Memon, A.; Memon, A. Functionality of circuit via modern fractional differentiations. Analog. Integr. Circuits Signal Process. 2019, 99, 11–21. [Google Scholar] [CrossRef]
- R-Smith, N.A.; Brančík, L. Nonuniform lossy transmission lines with fractional-order elements using NILT method. In Proceedings of the 2017 Progress in Electromagnetics Research Symposium-Fall (PIERS-FALL), Singapore, 19–22 November 2017; pp. 2540–2547. [Google Scholar]
- Jakubowska-Ciszek, A.; Walczak, J. Analysis of the transient state in a parallel circuit of the class RLβCα. Appl. Math. Comput. 2018, 319, 287–300. [Google Scholar]
- Kaczorek, T. Minimum Energy Control of Fractional Positive Electrical Circuits with Bounded Inputs. Circuits Syst. Signal Process. 2016, 35, 1815–1829. [Google Scholar] [CrossRef]
- Kaczorek, T. Positive Linear Systems Consisting of n Subsystems With Different Fractional Orders. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 58, 1203–1210. [Google Scholar] [CrossRef]
- Kaczorek, T. An Extension of the Cayley-Hamilton Theorem to Different Orders Fractional Linear Systems and Its Application to Electrical Circuits. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 1169–1171. [Google Scholar] [CrossRef]
- Kaczorek, T. Singular fractional linear systems and electrical circuits. Int. J. Appl. Math. Comput. Sci. 2011, 21, 379–384. [Google Scholar] [CrossRef]
- Hristov, J. Electrical Circuits of Non-integer Order: Introduction to an Emerging Interdisciplinary Area with Examples. In Analysis and Simulation of Electrical and Computer Systems; Mazur, D., Gołębiowski, M., Korkosz, M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 251–273. [Google Scholar]
- Gomez-Aguilar, J.F. Fundamental solutions to electrical circuits of non-integer order via fractional derivatives with and without singular kernels. Eur. Phys. J. Plus 2018, 133. [Google Scholar] [CrossRef]
- Sene, N. Stability analysis of electrical RLC circuit described by the Caputo-Liouville generalized fractional derivative. Alex. Eng. J. 2020, 59, 2083–2090. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.; Escobar-Jiménez, R.; Olivares-Peregrino, V.; Taneco-Hernández, M.; Guerrero-Ramírez, G. Electrical circuits RC and RL involving fractional operators with bi-order. Adv. Mech. Eng. 2017, 9, 1687814017707132. [Google Scholar] [CrossRef]
- Morales-Delgado, V.; Gómez-Aguilar, J.; Taneco-Hernandez, M. Analytical solutions of electrical circuits described by fractional conformable derivatives in Liouville-Caputo sense. AEU Int. J. Electron. Commun. 2018, 85, 108–117. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.; Morales-Delgado, V.; Taneco-Hernández, M.; Baleanu, D.; Escobar-Jiménez, R.; Al Qurashi, M. Analytical Solutions of the Electrical RLC Circuit via Liouville-Caputo Operators with Local and Non-Local Kernels. Entropy 2016, 18, 402. [Google Scholar] [CrossRef]
- Tenreiro Machado, J.; Lopes, A.M. Fractional-order modeling of a diode. Commun. Nonlinear Sci. Numer. Simul. 2019, 70, 343–353. [Google Scholar] [CrossRef]
- Sowa, M. Harmonic Balance Methodology for Circuits with Fractional and Nonlinear Elements. Circuits Syst. Signal Process. 2018, 37, 4695–4727. [Google Scholar] [CrossRef]
- Stefański, T.P.; Gulgowski, J. Fractional Order Circuit Elements Derived from Electromagnetism. In Proceedings of the 2019 MIXDES—26th International Conference “Mixed Design of Integrated Circuits and Systems”, Rzeszów, Poland, 27–29 June 2019; pp. 310–315. [Google Scholar]
- Stefański, T.P.; Trofimowicz, D.; Gulgowski, J. Simulation of Signal Propagation Along Fractional-Order Transmission Lines. In Proceedings of the 2020 27th International Conference on Mixed Design of Integrated Circuits and System (MIXDES), Wroclaw, Poland, 25–27 June 2020; pp. 164–167. [Google Scholar]
- Martynyuk, V.; Ortigueira, M. Fractional model of an electrochemical capacitor. Signal Process. 2015, 107, 355–360. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.; Córdova-Fraga, T.; Escalante-Martínez, J.; Calderón-Ramón, C.; Escobar-Jiménez, R. Electrical circuits described by a fractional derivative with regular Kernel. Rev. Mex. Fís. 2016, 62, 144–154. [Google Scholar] [CrossRef]
- Abro, K.A.; Atangana, A. Numerical Study and Chaotic Analysis of Meminductor and Memcapacitor Through Fractal-Fractional Differential Operator. Arab. J. Sci. Eng. 2020. [Google Scholar] [CrossRef]
- Abro, K.A.; Memon, A.A.; Uqaili, M.A. A comparative mathematical analysis of RL and RC electrical circuits via Atangana-Baleanu and Caputo-Fabrizio fractional derivatives. Eur. Phys. J. Plus 2018, 133, 1–9. [Google Scholar] [CrossRef]
- Atangana, A.; Alkahtani, B.S.T. Extension of the resistance, inductance, capacitance electrical circuit to fractional derivative without singular kernel. Adv. Mech. Eng. 2015, 7, 1–6. [Google Scholar] [CrossRef]
- Atangana, A.; Nieto, J.J. Numerical solution for the model of RLC circuit via the fractional derivative without singular kernel. Adv. Mech. Eng. 2015, 7, 1–7. [Google Scholar] [CrossRef]
- Alizadeh, D.B.S.; Rezapour, S. Analyzing transient response of the parallel RCL circuit by using the Caputo-Fabrizio fractional derivative. Adv. Differ. Equ. 2020, 55, 1–19. [Google Scholar] [CrossRef]
- Sheikh, N.A.; Ching, D.L.C.; Ullah, S.; Khan, I. Mathematical and Statistical Analysis of Rl and RC Fractional-Order Circuits. Fractals 2020, 28, 1–7. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Atangana, A.; Morales-Delgado, V.F. Electrical circuits RC, LC, and RL described by Atangana-Baleanu fractional derivatives. Int. J. Circuit Theory Appl. 2017, 45, 1514–1533. [Google Scholar] [CrossRef]
- Martínez, L.; Rosales, J.; Carreño, C.; Lozano, J. Electrical circuits described by fractional conformable derivative. Int. J. Circuit Theory Appl. 2018, 46, 1091–1100. [Google Scholar] [CrossRef]
- Bhalekar, S.; Patil, M. Can we split fractional derivative while analyzing fractional differential equations? Commun. Nonlinear Sci. Numer. Simul. 2019, 76, 12–24. [Google Scholar] [CrossRef]
- Garrappa, R.; Kaslik, E.; Popolizio, M. Evaluation of Fractional Integrals and Derivatives of Elementary Functions: Overview and Tutorial. Mathematics 2019, 7, 407. [Google Scholar] [CrossRef]
- Shchedrin, G.; Smith, N.C.; Gladkina, A.; Carr, L.D. Exact results for a fractional derivative of elementary functions. SciPost Phys. 2017, 4, 29. [Google Scholar] [CrossRef]
- Ferrari, F. Weyl and Marchaud derivatives: A forgotten history. Mathematics 2018, 6, 6. [Google Scholar] [CrossRef]
- Rogosin, S.; Dubatovskaya, M. Letnikov vs. Marchaud: A survey on two prominent constructions of fractional derivatives. Mathematics 2018, 6, 3. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.T. Fractional Derivatives: The Perspective of System Theory. Mathematics 2019, 7, 150. [Google Scholar] [CrossRef]
- Ortigueira, M.D. Two-sided and regularised Riesz-Feller derivatives. Math. Methods Appl. Sci. 2019. [Google Scholar] [CrossRef]
- Ortigueira, M.D. Fractional Calculus for Scientists and Engineers; Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Tarasov, V.E. No nonlocality. No fractional derivative. Commun. Nonlinear Sci. Numer. Simul. 2018, 62, 157–163. [Google Scholar] [CrossRef]
- Tarasov, V.E. No violation of the Leibniz rule. No fractional derivative. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 2945–2948. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Tenreiro Machado, J. A critical analysis of the Caputo–Fabrizio operator. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 608–611. [Google Scholar] [CrossRef]
- Cresson, J.; Szafrańska, A. Comments on various extensions of the Riemann—Liouville fractional derivatives: About the Leibniz and chain rule properties. Commun. Nonlinear Sci. Numer. Simul. 2020, 82, 104903. [Google Scholar] [CrossRef]
- Stynes, M. Fractional-order derivatives defined by continuous kernels are too restrictive. Appl. Math. Lett. 2018, 85, 22–26. [Google Scholar] [CrossRef]
- Diethelm, K.; Garrappa, R.; Giusti, A.; Stynes, M. Why fractional derivatives with nonsingular kernels should not be used. Fract. Calc. Appl. Anal. 2020, 23, 610–634. [Google Scholar] [CrossRef]
- Sabatier, J. Fractional-Order Derivatives Defined by Continuous Kernels: Are They Really Too Restrictive? Fractal Fract. 2020, 4, 40. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gulgowski, J.; Stefański, T.P.; Trofimowicz, D. On Applications of Elements Modelled by Fractional Derivatives in Circuit Theory. Energies 2020, 13, 5768. https://doi.org/10.3390/en13215768
Gulgowski J, Stefański TP, Trofimowicz D. On Applications of Elements Modelled by Fractional Derivatives in Circuit Theory. Energies. 2020; 13(21):5768. https://doi.org/10.3390/en13215768
Chicago/Turabian StyleGulgowski, Jacek, Tomasz P. Stefański, and Damian Trofimowicz. 2020. "On Applications of Elements Modelled by Fractional Derivatives in Circuit Theory" Energies 13, no. 21: 5768. https://doi.org/10.3390/en13215768
APA StyleGulgowski, J., Stefański, T. P., & Trofimowicz, D. (2020). On Applications of Elements Modelled by Fractional Derivatives in Circuit Theory. Energies, 13(21), 5768. https://doi.org/10.3390/en13215768