Abstract
An integrated electrical and thermal residential renewable energy system consisting of solar thermal collectors, gas boiler, fuel cell combined heat and power, a photovoltaic system with battery, inverter, and thermal storage for a single-family house of Sonnenhaus standard is investigated with a model predictive controller (MPC). The main focus of this article is to define a multi-objective mathematical function, develop a coupled simulation framework for the nonlinear time-varying deterministic discrete-time problem of the energy system using TRNSYS and MATLAB. With the developed methodology, a sensitivity analysis of maximum optimization time, swarm (or population or mesh) size of a typical spring day and a typical summer day assuming a 100% accurate weather and load forecast with three different algorithms: particle swarm optimization (PSO), genetic algorithm (GA) and global pattern search (GPS) are analyzed. Finally, the obtained results are compared with a status quo controller. Results show that the PSO algorithm optimizer performs the best in this MPC for such a complex and time-consuming MPC model in both the spring day and the summer day. The obtained results show that the PSO with swarm size 50 in the selected typical spring day and the PSO with swarm size 40 in the selected summer day reduces the objective function’s fitness value from 413 to −177 within 6 h optimization time and from 1396 to 1090 in 4 h optimization time respectively.
1. Introduction
In the buildings sector, as shown in [1], 64% are residential buildings, and of the 19 million residential buildings in Germany, 15.7 million are single- and two-family houses. Just single and two-family houses have a demand of 39% of the total end energy consumption in the buildings sector [1]. This value equates to 10% of the whole of Germany’s emission (ca. 84 million tonnes of CO2 equivalent) emitted from single and two-family residential buildings of which around 325–400 TWh (75–85%) is consumed just for space heating demand and hot water demand in single and two-family houses [1]. According to [1], by 2030 there could be an extra of 28 million tonnes of CO2 equivalent emissions (difference from the goal of 70 million tonnes in 2030) in the buildings sector if the current emission reduction rate follows. Therefore, many advances in this sector are necessary. Hence, increasing the renewable energy utilization in residential buildings, especially for heating, is essential, which would apparently result in reduced primary energy consumption. In the Energiefortschrittbericht [2], Prognos 2020 [3], Energieeffizienz Strategie Gebäude [4] and several instances, the need for intelligent control of hybrid renewable energy systems (thermal and electrical) which promotes optimum integration of renewables in residential buildings along with decentral sector coupling is emphasized. Decentral sector coupling can be simply defined as a combination of different energy sectors (electricity, heating, cooling and transport) with locally installed energy generation units closer to the site of energy consumption.
With the need for decentralized integration of renewable power, the classical control systems have a very straight SISO (single input single output) control, which only has an overview of that particular component’s operation. However, when coupling different decentral electrical and thermal energy systems, along with the building and the occupants, the system becomes more sophisticated for the SISO control. In [5], the authors previously have simulated a similar system as this article, and the shortcomings of the SISO controllers, especially on the building heating control is shown, and the need for a more sophisticated advanced control strategy is displayed. Moreover, energy management becomes more efficient and effective when the adaptive system is applied (for example, predicting the demand for the building or the consumer and planning the energy production).
The model-free control strategies as described in [6] are easy to implement and are low of cost, but the results are limited. For a building control, for example, they use weather predictions without any building or historical data to control the heating system and the temperature setpoints. Another kind of control uses fuzzy logic to identify the controller logic using monitored data. The ability of such controllers is high, but user-experience for the definition of the logic is necessary and requires customization to each scenario. Finally, there are advanced controls that use a control system model or a digital twin of the system. According to [6], advanced controls are further divided into adaptive, optimal, and model-predictive control (MPC). Adaptive control is based on the adjustment of model parameters [7], and the optimal controller finds an optimal setting for the parameters which are being adjusted to an optimum of a control strategy [8]. MPC, on the other hand, does the optimal control by using the disturbance prediction and optimize a model to obtain a control signal that minimizes the errors between the desired and the simulated outputs. Different from the optimal controller, MPC control methods could also be non-optimal advanced control which makes a decision that is good for the current scenario even though it is not optimal (e.g., power-to-heat utilization for thermal demands when excess decentral electricity is available) [6,9]. The importance of building modelling in MPC irrespective of white, grey or black-box model is explained in [10].
The implementation of MPC at a component level like just in building heating or in an energy system component like heat pump alone is already achieved. For example, [11] implemented an MPC controller in a Swiss office building by customizing the MPC for that particular building and showed that customization of MPC results in a costly or un-economical solution. MPC was introduced in the energy storage system using weather forecast, and this was reviewed by Thieblemont et al. [6] and Zhun et al. [12]. However, the adaption of the MPC controller for the energy systems along with the storage and building all together into a single system controller and universalization of this controller is still open. In addition, the MPC controllers until now require customization for each particular case.
The initial studies of MPC in the building sector were investigating buildings alone as a simple RC (Resistance-Capacitance) model for ventilation and the first study applying TRNSYS was done by Zakula [13] introducing TRNSYS MPC for cooling of buildings with a heat pump. MATLAB for MPC, GenOpt software for Genetic algorithm optimizer and TRNSYS for HVAC and building were used in that study. That proved to be too complicated at that time. Pichler et al. [14], studied the predictive control in TRNSYS for auxiliary energy supply in an HVAC system. A similar system with solar thermal and absorption chiller has been studied in [15] with the GA algorithm in Python and a state-space model, which resulted in a 10% reduction in auxiliary use. In [16] the authors introduced a MATLAB-TRNSYS predictive controller, but for just the electrical consumption in an HVAC for the building and the objective there was reduction of cost. They reduced the costs by 10% with the use of MPC. A similar result for just the floor heating optimization in a building was achieved by [17]. They used just a linear MATLAB inbuilt algorithm. RC model MPC and TRNSYS-Genopt MPC for electric floor heating were compared in [18] and reported that circa 20% more peak power reduction is possible by using a complicated building model but though also incurs more computation time. In [19] an economic MPC in MATLAB with a state-space model from the physical equation model was developed. Thus, reducing the consumption and increasing the self-utilization by the Photovoltaic -Heat pump system. The ISO 12,790 simple RC model works well for calculating the yearly demand as time series for heating. However, as [20] showed, such grey-box models are not as accurate as whitebox TRNSYS models, and therefore for predictive control, those grey-box models are not as effective.
Liu et al. [21] achieved 24% energy reduction with a co-simulation based GA optimizer MPC with MATLAB and TRNSYS for a cooling HVAC system, with the objective being the reduction of electricity consumption. A similar economic MPC with electrical heating and a photovoltaic (PV) system was introduced in [22], but in contrary used a simple mathematical equation based model for all the system components. In [23,24], a smart home control system with PV and solar thermal was done with a state-space model with the use of a training data set in MATLAB with HYDSEL toolbox and Gurobi software. Ref. [25] developed a simple rule-based MILP (mixed-integer linear programming) predictive controller to reduce the heating power variance and peak power reduction in a fan coil HVAC system. This article follows a similar approach to [26], where Coffey et al. designed a framework to investigate MPC for building temperature setpoint scheduling with TRNSYS model and GenOpt optimization and a third software SimCon for simulation coupling. A similar MPC control of thermally activated building system with electrical heating and variable pricing is achieved in [27], where Labview is coupled with TRNSYS and artificial neural network (ANN) optimization is investigated with a set of training data. Apart from TRNSYS, there also instances, where EnergyPlus software is used for building simulation in a MPC and also other intelligent control approaches like ANN, fuzzy logic, etc.
Most of the previous literature sources have a single objective problem focused on a component level, either building or electricity storage or demand response load shifting, or just a single HVAC component like a heat pump. Most of the previous literature sources use a physical system based mathematical state-space model, for which the computation time is very short. In this case, it is a more complicated system model, and for this investigation, a highly accurate dynamic TRNSYS system model is opted, so as to have a detailed analysis. In addition, the optimization and organization layer is integrated into MATLAB [28] while the simulation layer with a white-box model is held in TRNSYS [29]. The advantage is that more algorithms can be tested, and this could possibly speed up the optimization by keeping the organization layer and optimization layer in MATLAB itself. Moreover, here the focus is to include them as a system and not focus on economic optimization but renewable energy fraction, high self-consumption and reduced grid export. For this, different optimization algorithms have to be studied with different building types and different energy systems.
With the decentralized energy systems trend in German residential buildings sector and the increasing hybrid renewable energy systems integration with auxiliary energy systems in thermal and electrical systems, the simple SISO controllers are not good enough. Thus, the need for complex controllers is currently existent. Although MPC is one of the attractive complex controller options, implementation of MPC require individual customization. The idea of this particular article is to develop a framework in MATLAB with the simulated model in TRNSYS, where an MPC Control can be done using different optimization algorithms. With the developed framework in this article, several parameters and boundary conditions and fine-tuning of MPC are planned to be studied for different building standards in the future. Furthermore, how the sensitivity of those optimization algorithms with regards to the changes in the building’s characteristics would be investigated. It is possible further to investigate ways of universalization of such hybrid energy system with different buildings. The adaptive demand forecast of occupants and the weather forecast accuracy are not included in the scope of this study but do play a part in intelligent buildings. The implementation of the MPC into a real system is also not in view of this article.
This article is categorized in the following way: As next in Section 2, the energy system and the building are described. The simulation model of the system is also shortly explained. Then in Section 3, the MPC is adapted to this specific energy system. More in detail, Section 4 lists down the methodology of the co-simulation in TRNSYS and MATLAB and the adaptation of the TRNSYS model with constraints and objective function calculation. In Section 4.5, the different algorithms and the implementation in MATLAB are illustrated. Finally, in Section 5, the results of the status quo and MPC controlled system with the selected optimization algorithm are showcased and compared. Lastly, in Section 6, the article is concluded, and future developments are enlisted.
2. Description of the System and Simulation Model
2.1. Intelligent Home Energy Management System
An integrated thermal and electrical system with multi-energy sources in a household optimized for self-utilization was developed as a part of the iHEM project (intelligent Home Energy Management). The goal of the project was to have an integrated home energy system with an intelligent control unit communicating to all the components through a superior management concept. The intent was to have a demonstrator where different concepts can be tested and can function as an example of such a futuristic household decentral energy system where the load and production energy are forecasted, and an optimum predictive operation strategy is developed. The system is eventually not only efficiently optimized but also prioritized for self-utilization with maximum possible renewable energy ratio. As shown in Figure 1, the energy system consists of electrical and thermal components with prioritized renewable sources: photovoltaic modules and solar thermal collectors. Then as an auxiliary, there is a gas boiler for thermal loads and electrical grid for feed-in of excess production and import of the deficient electricity. As a buffer, electrical and thermal storage are also taken into account. In addition, as a niche, a micro solid oxide fuel cell (SOFC) CHP is coupled to this complex system. Then finally, a power-to-heat process with an electrical heating element to increase the self-utilization of electricity is implemented. The demonstrator is built up at Ehingen, Germany (48.2° N) in the premises of Sailer GmbH. In the scope of the project, OFFIS developed a simple initial MPC in Python with the Nelder-Mead Algorithm with a simple mathematical system model, as shown in [30]. More about the project can be found at [31].
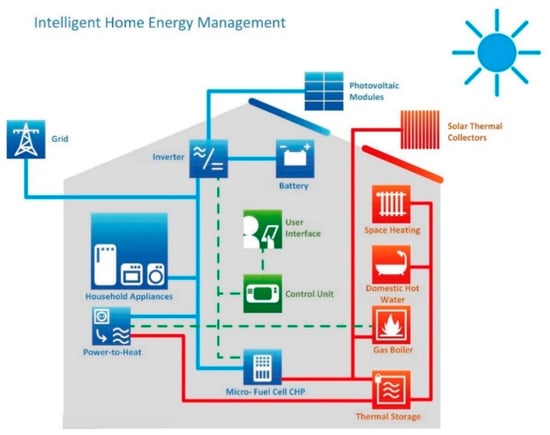
Figure 1.
Overview of the energy system built up as demonstrator during iHEM project [30].
Here for this article, the same iHEM energy system is modelled in TRNSYS as a detailed physical-mathematical dynamic system simulation model and is coupled to a Sonnenhaus standard single-family house (SFH) building model. Authors showed the shortcomings of SISO controllers for such a system in Sonnenhaus and gave a detailed description of the Sonnenhaus in their previous publication [5]. Simulation models of other different single-family houses and their different reflexes for a SISO controller are also showcased in [5].
2.2. Model Description in TRNSYS
2.2.1. Single-Family House According to Sonnenhaus Standard
An actual two-floor KfW55 building [32] as shown in Figure 2 with 183 m2 area with 63 m2 roof as a single zone adapted to a Sonnenhaus-standard characteristic is modelled. The building as per the Sonnenhaus standard is simulated using TRNBuild using SketchUp in TRNSYS software. The blinds are shut when the building temperature is above 24 °C and the windows are opened when above 26 °C. The building has 9 m2, 7.42 m2, 16 m2 and 1.6 m2 window area in the south, east, west and north respectively. More on the dimensions & characteristics of the building can be found in [32].
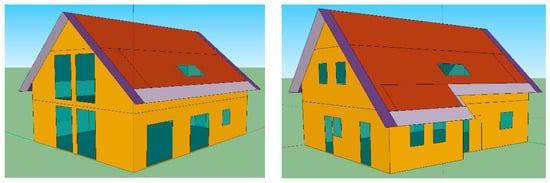
Figure 2.
The building envelope as modelled in SketchUp: East-North orientation in left and West-South view in the right.
The Sonnenhaus standard [33] is a voluntary certification standard like Passive house for energy efficiency in buildings which requires a minimum solar fraction of 50% for the thermal demand of the building (space heating and hot water demand) with direct solar thermal or also with a photovoltaic system. The Sonnenhaus standard permits annual primary energy consumption of maximum 15 kWh/m2a (max. 30 kWh/m2a with a fossil fuel auxiliary heater) and commonly without heat recovery units. The U-values for the building components are input, as shown in Table 1. The ventilation and infiltration were input according to DIN 18599.

Table 1.
Building parameters overview of the Sonnenhaus standard single-family house.
2.2.2. Thermal System
The simulations are carried out with historical weather data from 2018 of the demonstrator in Ehingen, Germany (48.8° N 9.7° E). As shown in Figure 3, a Focus AR Solar thermal collector [34] of 26 m2 at 55° slope with Type 539 is simulated. Type 340 model [35] is used to simulate the 2 m3 Sailer Hybrid Quattro storage tank [36] which consists of lance elements that enable to charge the thermal storage efficiently and maintain different temperature nodes inside the storage by stratification. The modelling approach of the thermal storage with a stratifier can be found at [37]. For the 7 kW gas boiler, type 700, a simple gas condensing boiler is used. There are also 3 electrical heating elements (1 kW on the top, 2 kW in the mid zone and 1 kW in the bottom zone) inside the tank, as shown in [38]. The heating elements are used to feed-in the excess electricity from the decentral production into the thermal storage if the thermal storage can accommodate more heat instead of exporting the electricity to the grid. With this, the self-utilization of the decentrally produced electricity is prioritized and grid export is kept low. The excess energy from the SOFC-CHP and PV is being fed into the storage tank if the temperature in the relative zone is less than 85 °C. The BlueGen [39] 2 kWel SOFC-CHP is modelled using a simple 2D characteristic model from the product data-sheet. The thermal energy from the fuel cell is fed to the thermal storage. The selection of a fuel cell CHP in a single-family house is debatable, nevertheless, it was used in the research project and therefore also used for this paper. A freshwater station, Sailer FriWasta [40] for the delivery of domestic hot water (DHW) is modelled and used. The DHW load according to VDI 4655 with 500 kWh per person and in total four persons in the household is being used in the simulation. The system is simulated with a timestep of 15 min in TRNSYS. More about the energy system, it’s simulation methods and the sizing optimization can be found at [41].
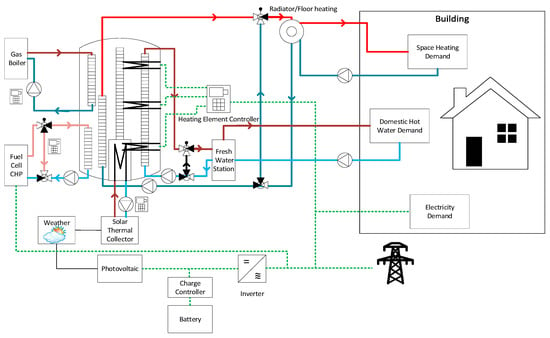
Figure 3.
Schematics of the energy system as simulated in TRNSYS.
A floor heating with a heating setpoint of 20 °C during the day hours and 16 °C during the night (22:00–6:00) is used. The floor heating inlet temperature is also varied perpendicular to the ambient temperature. The infiltration and ventilation systems were designed for each building, as mentioned in Table 1. Along with that, the simulation of window opening during the summer months is achieved via increasing the infiltration when the ambient temperature goes above 26 °C. The self-shading and shading via overhangs are also taken into account in the simulation.
2.2.3. Electrical System
With the same fuel cell CHP model, the fuel cell also delivers electricity. The whole system here is kept as a single-phase DC-AC (alternating current—direct current) system, and the fuel cell has an inverter inbuilt and directly contributes electricity to the AC side. Along with that, 2.94 kW PV (Type 94a) with a 35° slope facing south is connected, and Aleo Solar S19-295 PV module [42] data is input into the system, which also connects to a 6.74 kWh Lithium-ion BMZ 7.0 battery [43] with a StecaGrid SolUse 2503-48 2.6 kW charge controller. The DC side is then further connected to the Type 48c inverter model with the input data representing the 3.3 kW StecaGrid 3203x inverter [44]. The annual electricity demand as in VDI 4655 is taken as 4140 kWh for a four-person household. Using power-to-heat, the excess power is fed into the thermal storage via heating elements and the remaining is fed to the grid. The fuel cell in this system configuration does not charge the battery and excess power is sent either to the thermal store or to the grid, but so is the possibility in the real BlueGen SOFC-CHP.
3. Model Predictive Controller of the System
3.1. MPC Framework for This Problem
Though Building-HVAC (Heating, Ventilation and Air Conditioning) problem is nonlinear and time-varying, most frequently, a black box linearized time-invariant model is used to represent this system. However, with a TRNSYS-MATLAB white-box model, a time-varying deterministic discrete-time model is achievable. Though a continuous problem, the control inputs for such a problem even in real life are discrete. Thus, a constrained time-varying deterministic discrete-time model is used to represent a Building-HVAC problem here.
Figure 4 shows the process flow of the MPC system. The disturbances in this Building-HVAC problem are weather and occupancy. Then, the setpoint constraints such as the thermal heat power demand or the delivery temperature and electrical power demand in the residential building are fed into the MPC. The goal of the objective function is to maximize renewable energy fraction for the given time horizon while satisfying the given constraints of space heating (SH) as a soft constraint; DHW and electricity demand as hard constraints. The state of thermal storage with minimum hot water grade, warm water grade, and minimum fractional state of charge (FSOC) of the battery are defined as system constraints. The manipulated variable input, u, is the set of input to auxiliary energy system components which utilizes the forecast of the energy produced by renewable energy producers and the energy demand.
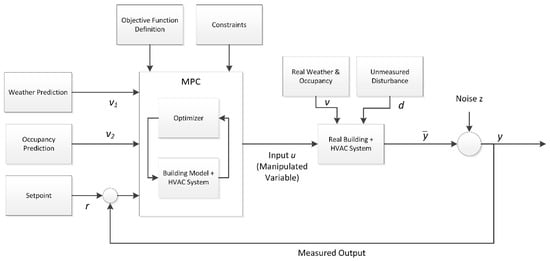
Figure 4.
MPC formulation schema for the decentral residential energy system problem.
With the weather and occupancy prediction, the MPC simulates the Building-HVAC system in a 24 h-TRNSYS model with two days pre-simulation to achieve the required setpoints satisfying the constraints. The optimizer uses this simulation model to find the objective function value and the optimizer uses the optimization algorithm in MATLAB environment to iterate and find the best case of the manipulated variable where the objective function value is the lowest. This best-case u is then passed over to the real system, in this case, a sequential simulation of the residential system. The initial control horizon is assumed to be 24 h with the prediction horizon also the same, and the minimum control timestep as 15 min.
3.2. Introduction to Optimization Simulation in MATLAB
In order to be able to interact directly with TRNSYS, it is necessary that the optimizer be nonlinear in nature, so as to understand the nonlinear behavior of the input-output system model. For this reason, non-gradient optimization algorithm: particle swarm optimization, genetic algorithm and global pattern search algorithm are selected to analyze the response of the optimizer for this system model. In the following subsections, the algorithms are described and, in the end, some considerations of how to integrate them into the MATLAB environment are presented.
3.2.1. PSO—Particle Swarm Optimization
The PSO is a metaheuristic algorithm that was first developed by [45] to solve nonlinear continuous problems. This algorithm is based on bird movement and their ability to adjust the flight trajectories avoiding collisions, and in comparison with other optimization algorithms, it has a simple concept and easily implemented. Since its first form, the PSO algorithm has been upgraded [45,46] and nowadays, it is widely used in optimization problems. Indeed, PSO is an algorithm based on social behavior, and it uses an individual population to optimize an objective function [47]. In particular, each particle searches for a solution by combining its local best position evaluation, as well as the best-evaluated particle of the group [47]. Basically, each particle is composed of three-dimensional vectors: the best position (Pi), velocity (Vi), and the current position (Xi). The implemented PSO algorithm can be seen in Algorithm 1.
| Algorithm 1: PSO algorithm |
| Input: Swarm size, stop criterion, objective function; Output: Best solution and best fitness
|
In summary, Algorithm 1 initializes the particles and its’ velocity randomly, calculates particle fitness, and iteratively recalculates the particle position in order to obtain a new, improved position [47]. The iterations continue until the stop criterion is reached. It is to be noted that the stop criterion can be either the maximum number of iteration or the fitness value tolerance of its best value.
3.2.2. GA—Genetic Algorithm
Similar to PSO, the GA is an evolutionary heuristic that uses the population concept to optimize the objective function by using probabilistic and deterministic rules [48]. In the case of GA, it was first presented by [49], as a natural evolution abstraction [50] that uses chromosomes, natural selection, recombination, mutation and inversion concepts to solve problems. Because of this, GA is capable of handling complex optimization problems, multi-objective functions, continuous and time-variant systems subject to noise or disturbances [51]. In order to execute GA, it is necessary to correctly represent the problem by using the correct objective function and input parameters [52] as seen in Algorithm 2.
As enlisted in Algorithm 2, GA, after initializing, selects the parents in order to reproduce and recombine, obtaining the next generation of individuals. In this algorithm, three basic operators are used: selection operator (step 3), which selects the most apt individuals; recombination operator (step 4), which is responsible for propagating the best characteristics to the next generation; and mutation operator (step 5), which diversifies next generations and avoids local minimums [48]. In summary, after defining the objective function, and initializing the population, a new population is generated by using the operators iteratively and evaluated until the stop criterion is reached [51].
| Algorithm 2: GA algorithm |
| Input: Population size, stop criterion, objective function; Output: Best solution and best fitness
|
3.2.3. GPS—Generalized Pattern Search
Proposed by [53], GPS is a direct search algorithm that depends only on the output function values. At first, its main purpose was to solve unconstrained nonlinear problems [54], but after it was extended to linear constrained systems [55]. Indeed, GPS is very effective in solving complex and non-smooth functions. The first step to run a GPS algorithm is to implement an objective function. From this function and an initial point, a control mesh is created in order to start the optimization and, iteratively, GPS creates a set of mesh trial points and search for a better fitness by actively varying the mesh size [56]. This allows refining the search based on new search conditions, which observes a convergence theory, as presented in Algorithm 3.
| Algorithm 3: GPS algorithm |
| Input: Population number, problem dimension, stop criterion, objective function, problem constraints; Output: Best solution and best fitness
|
As shown in Algorithm 3, an algorithm iteration is divided into two steps: SEARCH and POLL. In the first one, the objective function is evaluated on a finite subset of trial points on the mesh to find a new trial mesh point with a lower objective function value. In this step, any selection strategy can be used to obtain the new trial points, including none, as the SEARCH step is optional. In the second step, a local search is performed to find a new trial mesh point in the poll set. If the iteration does not result in a trial mesh point with better fitness, the mesh size parameter is decreased [57]. One consideration about GPS is that while evolutionary algorithms such as GA generate a population of individuals each iteration, GPS modifies the trial mesh point each step to search for the best fit. In other words, the GPS controls the individual’s position despite generating a population [58].
3.2.4. Algorithm Considerations
In order to use the laid-out algorithms as optimizers for model-based predictive controllers in MATLAB, it is important to highlight what must be done to make it functional. In summary, 3 points must be considered: objective function, parameter settings for best tune and initialization.
At first, a MATLAB function that can write data to the model and receive the result from the model is required. In this function, the input must be the parameters of TRNSYS, and the function ought to output the values of the objective function calculated from the model outputs.
Another point to be addressed is related to the algorithm’s initialization. Due to the characteristics of the presented algorithms, it is possible that they do not find the right solution, at first. Therefore, initializing the parameters based on the dynamic model helps to significantly improve the model behaviour. The main difficulty may not be directly linked to the ability of the algorithms to return a right solution, but to do so in an acceptable computational time, which is compatible with the process to be controlled.
A final consideration is the adjustment of the parameters. Although there are standardized parameters to be used for most applications using these algorithms, there is no guarantee that these parameters are the best for all cases, especially when the algorithms are applied to models that are more complex. Therefore, it is important to be careful when tuning the model parameters, which can prove to be the most laborious part in the design of MPC controllers with these optimization algorithms.
4. Methodology
In this section, the development of the MPC for this Building-HVAC system is explained. In Section 4.1, the setup of the simulation in TRNSYS to achieve a coupled TRNSYS-MATLAB simulation and the parameters of the simulation’s control strategy is explained. The art of constraints and their boundary conditions in Section 4.2 and the definition of the objective function as a mathematical function, how these boundary conditions influence the objective function are explained in Section 4.3. Finally, the process of simulation is shown in Section 4.4, and Section 4.5 explains the development of the optimizer algorithm.
4.1. Integration of MPC in TRNSYS
Figure 5 shows the manipulated auxiliary energy variable, storage state constraints and output variable (loads) in this problem. The manipulated variables are the values, which can be changed by the MPC optimizer with which the values of the objective function changes. The components in the energy system with the manipulated variable is shown in blue and enlisted in Table 2.
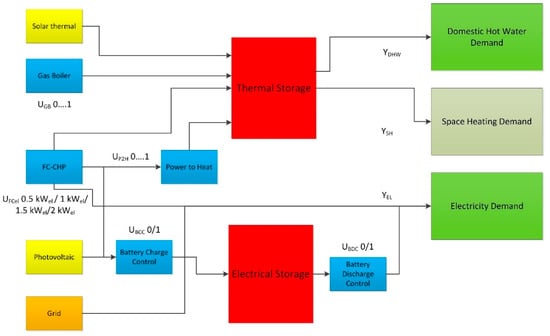
Figure 5.
The manipulated variables and the output variables of the iHEM energy system.

Table 2.
Boundary conditions for the respective manipulated variable.
The gas boiler maximum power control (UGB), fuel cell CHP electrical power setpoint (UFCel), power-to-heat maximum power control (UP2H), active battery charging control (UBCC) and active battery discharging control (UBDC) are the manipulated variables. The non-controllable and prioritized system elements are solar thermal and photovoltaics shown in yellow, and the non-preferred grid import or export is shown in orange. The important state variable component – thermal storage and electrical storage shown in red. The objective function also takes into consideration that the system state constraints and demand constraints are met. The demand constraints, as shown are DHW demand (YDHW), electricity demand (YEL) and space heating demand (YSH). The soft load constraint of space heating shown in light green and hard output constraints such as DHW demand and electricity demand are shown in green. In this first implementation, the space heating here is not controlled actively as they are included as a soft constraint, including an incurring penalty if the room setpoint is not achieved.
4.1.1. Gas Boiler
The control input of the gas boiler from the MPC is input for every 15 min (timestep) in terms of a continuous floating-point variable (0 to 1), and this is the gas boiler’s power input with a minimum turndown ratio of 0.10. If the temperature is less than the setpoint in the auxiliary volume zone and if the MPC input permits, the gas boiler and the respective pump for storage feed-in are activated.
4.1.2. Battery Control
For the battery control, an on-off binary signal (0 or 1) from the MPC for the battery discharging and battery charging in one-hour control timestep is accomplished. Thus, even when there is excess PV power generation, the MPC can decide if it wants to prioritize battery charging or supply the power-to-heat or to feed into the grid and vice versa decide if it has to allow the local controller to discharge the battery now or prolong until later. This control can support different scenarios in achieving better target values of different parameters. One example is as status quo, when battery FSOC is less than a value say, 0.50, the produced DC power is prioritized to charge the battery first even if there is a load demand. Then in the morning hours, the battery is fully charged, and from midday when there is no internal load, the electricity grid is fed in with excess electricity, and this makes the grid unstable. To counter this, in the future, the feed-in tariff would come up with variable pricing thus reducing the incentive when the grid is unstable (demand > supply). In this system, the power-to-heat can be given preference with such a battery control.
4.1.3. FC-CHP Control
FC-CHP manipulated variable (UFCel) is a simple discrete integer control input for the electrical power setpoint. As here a SOFC-CHP, which requires 30 h to switch on and up to 30 min to reach the new setpoint, is considered, a full shutdown of the FC-CHP is not aforethought. The MPC control time step is defined as 3 h, and the UFCel can vary between 500 W, 1000 W, 1500 W and 2000 W
4.1.4. Power-to-Heat Control
The power-to-heat control (UP2H) for the MPC is considered as a continuous floating variable (0 to 1), and MPC just gives one manipulated input value. This manipulated variable is then used locally by TRNSYS to control the three heating elements (HE). Firstly, the temperature sensors in the storage at the respective node are checked if there is a potential available heat storage space for power-to-heat. If the temperature sensor returns temperature more than 85 °C, then that particular heating element is forbidden to be switched on. The priority is first given to the middle heating element, then the top and at last the bottom. For example, if the MPC gives an input value of 0.8 and all three temperature nodes are below 85 °C. The middle heating element with 2 kW capacity (0.5 ratio) would be directed with 2 kW electricity and from the rest 0.25 (1 kW) can be fed into the top heating element, and the remaining 0.05 (0.2 kW) can be fed to the bottom HE. Now the same 0.8 UP2H with the top HE node above 85 °C, would result in 2 kW supplied to HE middle and 1 kW to HE bottom and the rest 0.2 kW unused. All the unused electricity after the battery control, load supply and power-to-heat supply will be exported into the grid.
4.2. Constraints
4.2.1. Load and Weather Forecast
In this article, the historical weather data and the historical load profile are taken as input. However, in reality, the weather forecast from weather providers and load forecast from machine learning are made available to the system. These forecasts, however, come with an uncertainty. To not make it more complicated, here the historical data with a 100% prediction accuracy is assumed.
4.2.2. Setpoint Constraints
These constraints are a category of various setpoints required by each component of the energy system. These constraints are defined in the TRNSYS environment and then used by the system simulation. This array mainly consists of the setpoint temperature for the space heating inlet, room temperature setpoint and domestic hot water delivery setpoint in the demand side and the setpoint temperature for the gas boiler in the energy input side.
4.2.3. Control Input Constraints
These are the system constraints, to which values can be given as input to the system according to the boundary conditions and the system configuration. In this case, with the mentioned manipulated variables and the HVAC system as in Section 4.1.
4.2.4. Output Constraints
The output constraints are the ones that cannot be directly controlled but must be satisfied for the system to function correctly and any solution, which does not satisfy these constraints, is a mere false solution. Therefore, these are included in the objective function and incur a high penalty when not satisfied. The space heating load is considered as soft constraint while the electrical and DHW loads are considered as hard constraints.
4.2.5. System Constraints
System constraints are intermediate state variables, and they tend to vary in accordance with the run time but nevertheless have to be controlled and have their own boundary conditions. For this problem, the auxiliary volume, the minimum state of charge of the battery and thermal storage temperatures are those system constraints, and these are actively controlled inside the TRNSYS system simulation. The required auxiliary volume in thermal storage and its setpoint temperature are also system constraints, which are regulated inside the TRNSYS environment.
4.3. Objective Function
The objective is to increase the usage of the non-controllable renewables, especially the use of solar thermal and photovoltaic. The secondary goal on the thermal side is to reduce the use of the gas boiler and at the same time not compromising the comfort in the space heating and always satisfying the DHW requirements, thereby effectively reducing the heat losses in the thermal storage. The secondary goal in terms of the electrical system is to increase self-utilization. Thus, actively controlling the production of the FC-CHP and aptly controlling the power-to-heat so as not to lose the storage space for the solar thermal. Moreover, in the electrical system, battery storage is also managed effectively by controlling the battery charging and discharging. Thus, an overall goal for the given time horizon as a maximization problem is to increase renewable energy and as a minimization problem is to reduce the usage of gas boiler input, grid import and reduce the grid export.
Abbreviations used in Equations (1) and (2) explained after Equation (7).
Therefore, as in Equation (1), the maximization objective function is defined as a sum of the renewable thermal fraction plus the renewable electricity fraction plus the decentral system self-utilization and an added penalty if the hard and soft output constraints are not satisfied. For the maximization problem, thermal renewable fraction contains a sum of the used thermal renewable energy inputs integrated over the day with respect to the DHW and SH load over the day. The renewable electricity fraction is calculated by the amount of electricity delivered by the PV and FC-CHP to the electrical load and the decentral system self-utilization is the utilization factor of the produced electricity internally. The self-utilization factor is reduced if more electricity that is produced decentrally is fed to the grid or vice versa, i.e., more grid import due to less decentral electricity production. A similar objective function with the same optimization goals as a minimization function is defined in Equation (2), where the focus is to reduce the grid export and to reduce the auxiliary energy usage for thermal and electrical demand.
The authors compared the simple minimization objective and simple maximization objective, but the results from such simple mathematical objective functions were not acquiring satisfactory results. Therefore, a combined complex minimization function with weighted multi-objective function incurring a penalty for the use of auxiliary energy and bonus for the use of the renewable function, as shown in Equation (3) was derived. Except for the gas boiler objective, all the other functions are squared, so as to increase the penalty or bonus value quadratically, thus giving more importance when the values are above a certain threshold.
The penalty function is shown in Equations (4)–(7). The space heating load penalty () is the most important and is a soft constraint, thus is defined as a quadratic penalty function [59] to penalize the constraint violation with increasing severity in case of a positive temperature difference between real room temperature and set room temperature. Similarly, the DHW penalty function is calculated for the simulation, but in a real implementation, this is unnecessary, but as for the simulation, it is used so that the objective function does not end up in an unfeasible optimized solution. Then a simple penalty function (with constant ϒ is also defined for electricity demand. The aim of this penalty is to reduce the grid import.
where = 30; = 1000; = 1000; = 500; = 1000; = 2000; = 9; = 15; = 15; = 700,
where:
| Electrical power produced by photovoltaics at the timestep (kW) | |
| Electrical power produced by fuel cell CHP at the timestep (kW) | |
| Electrical load at the timestep (kW) | |
| Electrical power delivered to the electrical load by the decentral power system at the timestep (kW) | |
| Electrical power supplied by the grid to satisfy the load at the timestep (kW) | |
| Excess electrical power produced in the decentral power system fed into the grid at the timestep (kW) | |
| Thermal heat demand of the space heating delivered at the timestep (kW) | |
| Thermal heat demand of the domestic hot water delivered at the timestep (kW) | |
| Thermal heat input of the gas boiler auxiliary production at the timestep (kW) | |
| Thermal heat input of the solar collector production at the timestep (kW) | |
| Thermal heat input produced by the fuel cell CHP as auxiliary production at the timestep (kW) | |
| Electrical power of the FC CHP & PV used in thermal auxiliary production at the timestep (kW) | |
| Room setpoint temperature (°C) | |
| Actual room temperature (°C) | |
| DHW setpoint temperature (°C) | |
| Actual DHW delivery temperature (°C) |
4.4. Coupling of TRNSYS and MATLAB
The process (as in Figure 6) starts with an input of the weather prediction for which the 24-h simulation model should simulate for the MPC optimization. This value should hypothetically come from the weather provider like for example the German weather agency, DWD. In the next step, the forecasted load demand (DHW, SH, electricity) for the next 24 h is input. The DHW forecast and electricity forecast should be done by machine learning or artificial intelligence. With the TRNSYS white-box model, the SH load is calculated during the simulation. The MPC then acquires the setpoint constraints, in this case, the temperature setpoints for the DHW load, the SH inlet temperature, room setpoint temperature and the setpoint temperature for the gas boiler. For the gas boiler as described in Section 4.1.1, the volume required in the auxiliary zone is calculated first, then the respective temperature sensor value is read and with the SH temperature setpoint and the DHW temperature setpoint the gas boiler setpoint is calculated. Along with these inputs to the 24-h simulation model, the simulations are also awaiting the control inputs from the MATLAB environment and MATLAB, in turn, requires the control input constraints. In addition, throughout the simulation, it is made sure the system constraints are not violated. Using the control inputs, the 24-h simulation model simulates the future responses of the system, and the simulation outputs are used to calculate the objective function, which is used by the optimizer. The optimizer uses the respective algorithm and functions as an input-output time-varying deterministic discrete-time model optimizer. The optimum solution is then hypothetically sent to the real building. Once the real weather, occupancy or the system response varies notably from the simulated solution, the control first prioritizes the real-time decision made by the onsite active controllers, and the MPC calculates a new solution through iteration with the currently available data.
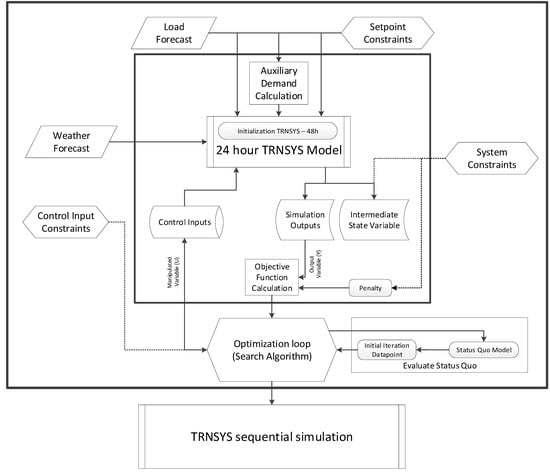
Figure 6.
Simulation framework of the coupled TRNSYS-MATLAB Building-HVAC MPC.
The optimizer initiates the simulation with a set of control inputs, and the initial iteration uses the previous day optimum solution as a starting point for the optimization. The 24-h simulation done in TRNSYS is always with a 48-h pre-simulation, and with the outputs of the simulations, the objective function is also calculated directly in the TRNSYS environment.
The calculated objective function for each iteration is used by the optimizer in MATLAB to find the best manipulated variable dataset. The manipulated variable dataset from the best iteration (optimum solution) is sent further to the real plant (in this article a sequential TRNSYS simulation) at the end of the current day for the next control horizon. The simulation is recurring, and for the second optimization day, the new initialization is done by taking the previous day optimum solution, which is also the initial iteration for the MATLAB optimizer. Finally, all the optimum solutions are taken together, and a sequential simulation is done, which is compared to a status quo simulation.
MATLAB is here the master simulation software, which calls TRNSYS by DOS command. TRNSYS deck file is edited by MATLAB for the respective start and stop time. The input parameters for the algorithm are set, and MATLAB sends the weather data, the load forecast and the control inputs to TRNSYS by printing the input values in a text file that is read in TRNSYS. TRNSYS runs the 24-h simulation once MATLAB runs the DOS command and TRNSYS outputs the objective function to MATLAB in the form of a text file for each iteration. The minimization of this objective function is the goal of the optimizer algorithm, which takes place in MATLAB.
4.5. Algorithm
To implement the optimization algorithm, some tests were performed in order to validate the algorithm itself and the whole process. At first, tests were performed with a model optimized for just one day, so that the tuning of the optimization algorithms parameters were tested and verified whether standardized parameters in the literature could be used as a reference for the type of model and optimization performed. In this sense, it was essential to start with a small amount of time, since these algorithms tend to make a large number of calls to the program that performs the simulation, and this takes a significant amount of time and tends to increase according to the model’s simulation time. These tests resulted in the implementation of the algorithm, as shown in Algorithm 4, which is an extension to the general case of days.
One can note that, in the presented algorithm, the optimizers were adjusted to return the same outputs with the same format. Thus, regardless of using PSO, GA or GPS, the format of the algorithm does not change. In addition, even though it is not possible to guarantee mathematically that the results are optimal, they have been tuned to result in the best possible outputs. Because of this, and considering the difficulty in finding the best tune for a complex model that tends to take several seconds to finalize a call, the final tuning took into consideration, as an evaluation criterion, the lesser amount of time that the optimizer took to return a value considered good enough to be applied. In summary, the global minimum is not the aim of this algorithm. As the control horizon is 24 h, the optimization time can utmost be 24 h, and the aim of this algorithm is to considerably reduce the objective function value, which is good enough in a lesser amount of time.
| Algorithm 4: Simulation Algorithm |
| Input: No. of days, simulation time, TRNSYS file path; Output: Optimum values, optimum objective function values
|
5. Results
In the scope of this paper, it is decided to run the optimization algorithm for a typical spring day, 14 March and a typical summer day, 25 May (as shown in Figure 7); compare the optimizer performance and the optimized key performance indicators (KPI). The spring day is selected such that there is considerably good solar radiation and yet cold enough such that building heating is also required. The summer day is selected such that the temperature and irradiation are not extreme, but a representative of an average summer day with warm temperatures and not so high irradiation.
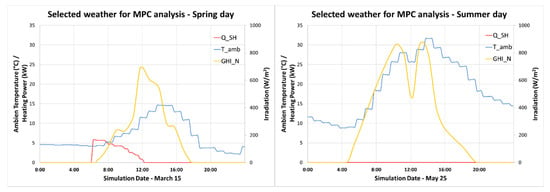
Figure 7.
Selected spring day (left) and summer day (right) for the MPC analysis.
For this problem, a time constraint is also necessary. Unlike the usual optimization problems, the time taken for one iteration of the TRNSYS model takes ca. 3–10 s. Thus, the compromise of not finding the global minimum must be made, so as not to run the optimization loop for an unrealistic duration of more than 24 h for a 24-h control horizon. The stability of the manipulated variables, the objective function value, its changing rate and satisfaction of the output variables are taken as the key criteria. As an initial point for the optimizer, the best fitness point of the variables from the previous horizon is taken for the actual horizon. And as a simplification in this article, ‘pre-optimized day’ fitness value, is taken from a 6h PSO optimization of the respective previous day and used for all the three algorithms. This is done such that all the three algorithms have the same initial conditions of the optimizer, with which a fair comparison can be carried out. The simulation is carried out with Intel i7-4790 CPU @ 3.6 GHz computer with all three algorithms executed in parallel and fitness evaluations for each algorithm executed sequentially.
In Table 3, the selected optimizer parameters of each algorithm for the simulated MPC is shown. Since GPS turned out to be a special case, due to its adaptive mesh, certain parameters had to be defined differently in comparison with the PSO and GA. The functional tolerance as 1 × 10−5 and maximum stall generations as 100 is defined for all cases. This means that if the objective function value for the evaluation function is less than the tolerance for the maximum stall generations, then the optimization stop criterion is reached. Maximum function evaluations and maximum iterations are calculated in accordance with the maximum optimization time. The maximum optimization time was initially taken as 12-h for all the three algorithms, but since GPS could not get to conclusive results by 12 h, the authors decided to extend the GPS optimization time until a comparative fitness value optimization is reached. More about this is discussed later in Section 5.1.3. In addition, for the PSO and GA algorithms, a sensitivity analysis is done with the swarm or population size. Thus, the selected size (20/30/40/50/75/100) is simulated for the summer & spring day to identify the best parameter value.

Table 3.
Optimizer parameters of each algorithm for the simulated MPC.
5.1. Optimizer Algorithm Results
5.1.1. Particle Swarm Optimization
As seen in Figure 8, the PSO results are quite promising. The swarm size of 20 and 50 are the best performing. In terms of the optimization speed and objective function value, PSO 75 seems to perform better, but PSO 50 seems to do a better job when the optimization time could be set more than 6 h.
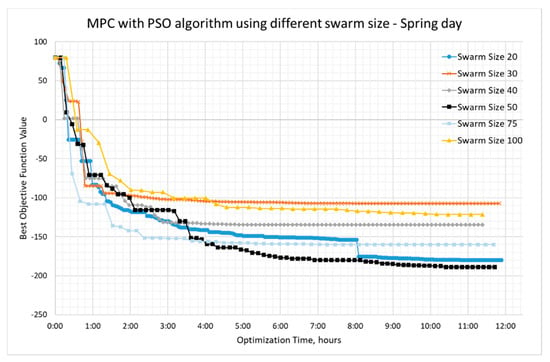
Figure 8.
PSO optimization results on the spring day with different swarm size.
For the summer day, as in Figure 9, the PSO algorithm also performs well, but the difference between the different swarm sizes is small. Although, it is to be noted that for the selected summer day, swarm size 50 was not the best functioning parameter and has a difference of ca. 100 in fitness value in comparison with the best functioning swarm size 40. It can also be noticed that the optimization is faster. This was expected because the control problem is much simpler than in spring due to the lack of SH demand and gas boiler production requirement.
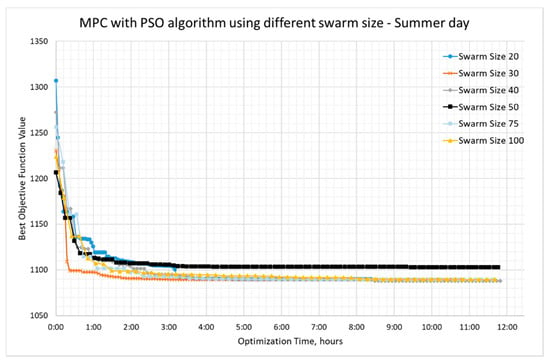
Figure 9.
PSO optimization results on the summer day with different swarm size.
5.1.2. Genetic Optimization
In contrary to PSO, GA performs better with increased population size on the spring day. As in Figure 10, the GA 100 and GA 40 have a clear dominance than the other values. However, the objective function does not reach a better-optimized value than the PSO 50, but GA is faster. Almost all of the variants reach a steady-state within 5 h. The GA 200 was also tried out, and the values as expected seem to reduce the performance.
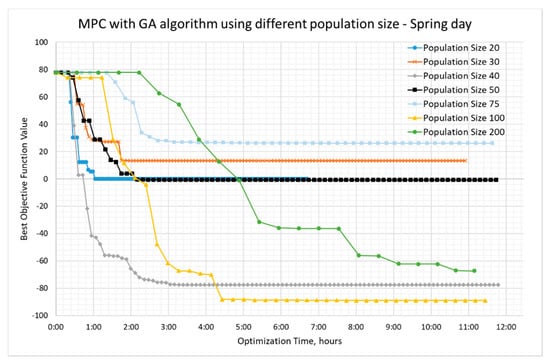
Figure 10.
GA optimization results on the spring day with different population size.
Reciprocating the sensitivity of the population size, also in summer day (Figure 11), population size 100 turned out to be good enough along with size 75.
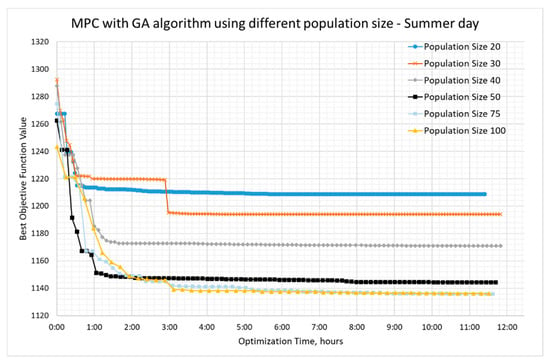
Figure 11.
GA optimization results on the summer day with different population size.
5.1.3. Global Pattern Search
GPS algorithm optimizer was simple to implement yet complicated enough to parametrize. Even though other control system problems seem to function quite well with GPS, this Building-HVAC problem has been not up to the expectation. As seen in Figure 12, within 12 h, all that the GPS optimizer could manage was to reduce the fitness value to −20. Thus, it was decided to continue further running the optimizer, and even after 24 h, the fitness could only be optimized to a value of −93.
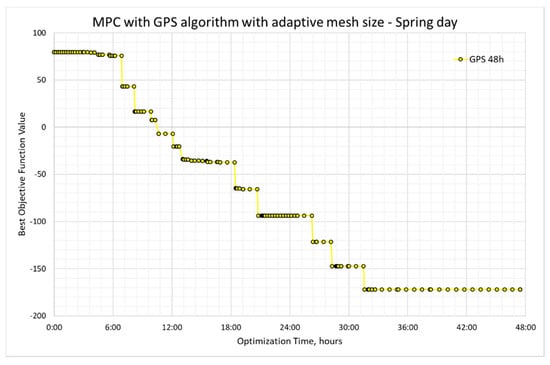
Figure 12.
GPS optimization results on the spring day with its adaptive mesh size.
To get a comparable fitness value to the PSO 50, the GPS optimizer had to be run for 48 h. Many extra parameters as mentioned in [60] such as different search function, contraction and expansion factor, complete search, complete poll, cache and scale mesh have been tried, and to its dismay, none of it was speeding up the optimizer and the problem according to the authors’ experiences seems to lie in the mesh size. The adaptive mesh size, which seems to be a benevolence for the other control problems, is a problem here. Even though the initial mesh size was input as 20, soon the adaptive mesh ends up to a size of less than 1, thus slowing down the whole optimization.
Furthermore, for the summer day, as shown in Figure 13, the optimization is achievable in 24 h, but the fitness values are still not as good as the other algorithms.
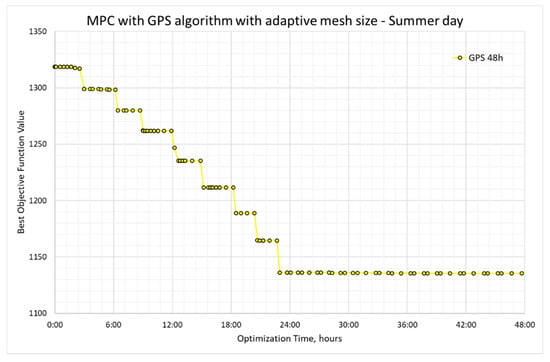
Figure 13.
GPS optimization results on the summer day with its adaptive mesh size.
5.2. Outcomes
5.2.1. Spring Day
For the optimizer results of all three algorithms, the manipulated variables are plotted in Figure 14. As the optimizers cannot afford to run the optimization for more than 24 h for a problem with a control horizon of 24 h, 24 h was taken for the GPS as the best point solution, to be compared with the other two algorithms. Despite that, the objective function, as shown in the bottom right graph, could only reach −93 which is identical to GA 100 but requires twice the optimization time. And the PSO 50, clearly comes out as the preferred algorithm where the optimizer reduces the objective function by 600.
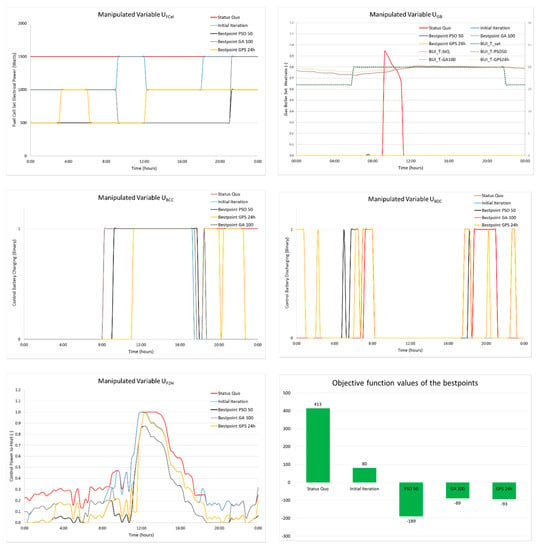
Figure 14.
Manipulated variables of the optimized fitness of each algorithm plotted with the initial iteration and the status quo on the spring day.
In the top left by UFCel, it is seen that the fuel cell electrical power setpoint is optimized from a constant 1500 Watts in the status quo case to a 500 W until 21:00 h by the PSO 50. On the right top, UGB is reduced to almost zero, thus achieving to meet the whole demand without any thermal auxiliary demand. Finally, in the bottom left, it can be seen that also the UP2H is reduced to a possible minimum, but also at the same time converts the excess PV power to heat during the day hours.
A better overview is acquired from Table 4. The QST is increased by 12% in comparison to the status quo, while QGB is reduced to almost zero despite the fact that power-to-heat is also reduced. Thus, the requirement of PFCel is cut down and thus improving the self-utilization and reducing the unnecessary power-to-heat. In addition, the battery (PBatt) is used more. Though the grid export is reduced, this comes under the expense of a little grid import. The reason for more PP2H, in the GPS and GA, is because of the increased PFCel production. This also explains why PGrid-Export and PGrid-Import have lesser values in GA and GPS than the PSO.

Table 4.
Key energy values from the best point of each optimized control on the spring day.
5.2.2. Summer Day
During the summer day, due to the fact that there is no SH demand and no requirement for the gas boiler energy input, the control problem is comparatively simplified. Nevertheless, the algorithms function similarly but faster. In addition, on the summer day, PSO performs better than GPS and GA.
As shown in Figure 15 on the bottom right, the objective function value does not vary much with regards to the status quo. However, there is a difficulty in finding which PSO configuration performs better. Just with the objective function values, PSO 40 functions better than the PSO 50, but when seeing the UFCel graph on the top left, and the UP2H on the bottom left, a significant difference in the PFCel can be seen. The FC-CHP production is set to 1500 W at the end of the day by PSO 40, whereas the PSO 50 maintains it at 1000 W. Due to this the power-to-heat also in increased. This could also be seen in Table 5, where due to the increased PFCel, the PV utilization is reduced, thus reducing the utilization factor and increasing the penalty for the power-to-heat use when using status quo controllers.
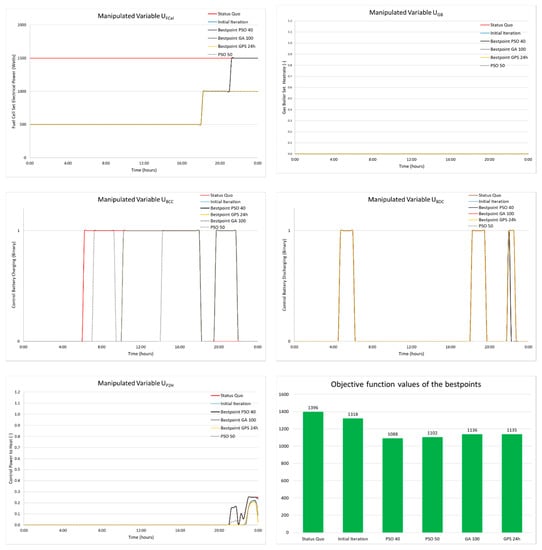
Figure 15.
Manipulated variables of the optimized fitness of each algorithm plotted with the initial iteration and the status quo on the summer day.

Table 5.
Key energy values from the best point of each optimized control on the summer day.
5.3. Comparison of the Results
As shown in Figure 16, the outcomes of the optimization with different algorithms in the selected typical summer day and spring day are quite identical. Particle swarm optimization does definitely stand out in comparison to the genetic algorithm and global pattern search algorithm. Yet the value of the swarm size in PSO optimizer could not be clearly configured with these results. Due to the random behavior of the PSO algorithm, the same PSO with same swarm size could return different results, but it is clear that even the worst-case PSO performs better than the best case of GA. This is an indication that PSO algorithm is better apt for this HVAC-Building problem than GA.
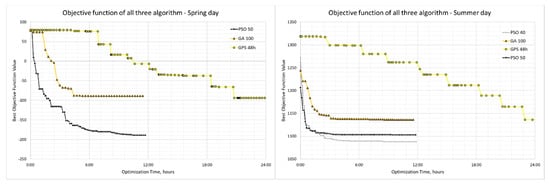
Figure 16.
Optimum solutions of all three algorithms on the selected spring day (on the left) and the summer day (on the right).
However, one can take away from these results that in the selected spring day, the PSO optimization with swarm size 50 does take 6 h for a high-quality optimization with fitness value improving from 413 in status quo to −177 and eventually increasing the solar thermal production by 12% and reducing the gas boiler production by 99%. Similarly, in the typical summer day, PSO optimization with swarm size 40 reduces the fitness value of the objective function from 1396 to 1090 in 4 h optimization time and eventually decreases the grid export power by 48% by reducing the fuel cell electricity production by 54%. The differences are more pronounced in the spring than the summer, due to the fact that the opportunity to optimize is quite low in summer compared to the spring. It is also expected that in winter the control problem might be similar to summer, except for the fact that there is no renewable energy and the optimizer would only have to optimize the use of auxiliary energy.
6. Conclusions
In this article, a hybrid thermal-electrical renewable energy system in a Sonnenhaus standard single-family house is investigated with a developed TRNSYS system model. This TRNSYS model is used as an input-output white-box system model, and an MPC simulation framework combining TRNSYS and MATLAB is developed. The MPC problem of this decentral residential energy system problem is schematized with a 24-h control horizon and a 15 min minimum control time step. As the energy system itself is complex, the formulation of the objective function, the definition of the constraints was also an important step. For the MPC optimizer, due to the complexity of the system, three different algorithms (particle swarm optimization, genetic algorithm and global pattern search) that are widely used in other control problems were selected to study the optimizer’s performance. The key performance indicators with the different optimizers are then compared in this article with a reference case without MPC for the same time period.
The results are quite promising and in terms of mathematical optimization, the PSO algorithm functions the best with such a system for the analyzed two days. The initial results show that the PSO with swarm size 50 does reduce the objective function from 413 in the status quo to −189 with 12 h maximum optimization time, while GA with population size 100 manages to reduce the fitness value to −89 within the same time. Surprisingly, GPS could not manage to give a good quality optimization within 12 h and in fact, needs 48 h on the spring day to achieve a comparable fitness value. The results are identical also during the summer with the PSO optimizer performing the best by reducing the fitness value from 1396 to 1088 with swarm size 40. Even though the fitness value reduction of the objective function is not so high, the optimization is faster during the summer day due to the fact that the control problem is comparatively more straightforward without the need for gas boiler and space heating. Moreover, the best swarm size of the PSO does incur different values for the analyzed summer day and spring day. Therefore, it is not possible here to conclude, which is the better swarm size configuration. The main focus of this article is to develop the MPC framework for such a decentral thermal-electrical system and establish a co-simulation with TRNSYS and MATLAB. The results here are preliminary, and it is too soon to conclude, as they are for the selected days and not for the whole year. Nonetheless, it is a promising indication that the PSO algorithm functions better than its counterparts (GA and GPS). One good evidence is that for both the spring and summer day, the worst-case configuration of the PSO functions better than the best configuration of GA and GPS. Moreover, the sensitivity of the swarm size in PSO, i.e., the difference between the fitness value of the best and worst swarm size configuration, is smaller than GA. Nevertheless, all three algorithms would be further investigated in the perspective of a full year and with different buildings and energy system configurations. In the future, the simulation model is planned to be investigated for its annual performance with an adapted fast six-day sequence dynamic testing procedure similar to [61].
One general limitation of the MPC is that it only finds a better objective function fitness value in the given maximum optimization time and this may not be the global optimum. In this particular case study, on 25 May (summer day), by the end of the day, FC-CHP electricity production and power-to-heat consumption is increased, which is certainly not the global optimum. As the cold start of the FC-CHP requires 30 h, in an ideal scenario, FC-CHP could be switched off for the whole summer, which is the best feasible practical solution. However, in this simulative study, this is not implemented, thus the second-best scenario would be to run the FC-CHP at minimum possible 500 W electricity generation all through the summer. Still, even this solution could not be acquired here. It can be certainly said, that the battery is under-utilized in this configuration with FC-CHP and although MPC facilitates the use of the battery, the full potential is still not utilized. MPC analysis to show what are the pros and cons of the MPC with respect to the status quo controller of the same energy system with and without the FC-CHP would throw more light into this complication and it is certainly worth analyzing in future studies to fine-tune MPC with regards to this.
To implement the MPC Strategy in real-time applications, the accuracy of the weather forecast and the demand forecast plays an important role. More than 95% accuracy is nowadays achievable for the day-ahead weather forecast with the current technology of adaptive regression models. Using the strategy of machine learning with adaptive artificial neural networks by coupling the localized historical weekday profile of the user demands, load forecast can be achieved. In this particular energy system, the weather and demand forecast inaccuracy on the minute-level could be decoupled with energy storage. In terms of electricity, there is always the backup of the electrical grid, even if the battery storage runs empty. In terms of thermal loads, the thermal storage has to take into account a factor of inaccuracy in load demands. For the DHW, as a rule of thumb, the auxiliary volume should always be able to supply the required hot water for a bathtub or a shower i.e., ca. 200 L. For the SH loads, a similar buffer could be achieved by having an auxiliary volume buffer for at least a minimum of 2 h of SH demand. By doing so, it is safe to say that even if the energy demand forecast were inaccurate, the effect would be minimal. The idea behind whitebox MPC is to have a forecast for the next day (00:00 to 24:00) at 12:00 of the current day and run the MPC optimization with a maximum of 12 h optimization time so as to have the optimum control inputs for the next day by 00:00. Once there is a deviation in the system state variables during the day, the MPC optimization with a shorter horizon from the current time till the end of the current day could be carried out, so as to acquire a feasible control action for the rest of the day. Meanwhile, the system could fall back to the onsite status quo control execution.
Whitebox model MPC is used here so as to have an in-depth analysis of the outcomes of the MPC with accurate thermal behaviour of the building and the energy system generation. When dealing with the inaccurate weather or load forecasts, to implement recurring MPC optimization routine with deviating outcomes, the computation time has to be lower. One possibility to achieve lower computation time is a cloud-based implementation of the white box MPC with high-performance processors. If an onsite embedded or IoT (Internet of Things) architecture based MPC with low computation time is preferred, a compromise has to be made in regard to the accuracy of the system model. Self-learning system identification methods, such state-space representation of the system (grey box model derivation from the white box) or stochastic MPC (parallel solution with probabilistic bounds for different weather and load forecast accuracy) can be achieved so as to make the computation faster.
Author Contributions
Conceptualization of the research, simulation of the energy system in TRNSYS, coordination, investigation, and visualization carried out by M.N. The methodology of the co-simulation was done by A.F.O.d.A.D. and M.N. The optimization algorithm development and implementation were carried out by A.F.O.d.A.D. and A.F.d.L. Supervision, administration, funding acquisition and manuscript review contributed by W.C. All authors have read and agreed to the published version of the manuscript.
Funding
The work described in this paper is partially part of the completed project Intelligentes Heimenergiemanagement (iHEM) funded under the Research Initiative Energiespeicher by the Bundesministerium für Wirtschaft und Energie under the Project Number—03ET1205A (2014–2017). The article processing charge was funded by the Baden-Württemberg Ministry of Science, Research and Culture and the University of Applied Sciences Ulm in the funding program Open Access Publishing.

Acknowledgments
Narayanan would like to acknowledge Gyula Gróf and his Department of Energy Engineering at Budapest University of Technology and Economics for their administrative support and Gerhard Mengedoht from THU for his help. Dantas would like to thank MEC (Ministry of Education and Culture), Brazil.
Conflicts of Interest
The authors declare no conflict of interest. Due to the project iHEM, the authors had to choose the certain energy system components for the study as used in the project. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Deutsche Energie Agentur. DENA Dena–Gebäudereport Kompakt 2019, Statistiken und Analysen zur Energieeffizienz im Gebäudebestand 2019; Deutsche Energie Agentur: Berlin, Germany, 2019. [Google Scholar]
- Bundesministerium für Wirtschaft und Energie (BMWi). Zweiter Fortschrittsbericht zur Energiewende, Die Energie der Zukunft 2019; Bundesministerium für Wirtschaft und Energie (BMWi): Berlin, Germany, 2019.
- Prognos, A.G.; Fraunhofer, I.S.I.; GWS; Iinas. Energiewirtschaftliche Projektionen und Folgeabschätzungen 2030/2050; Bundesministerium für Wirtschaft und Energie (BMWi): Cologne, Germany, 2020.
- Bundesministerium für Wirtschaft und Energie (BMWi). Energieeffizienzstrategie Gebäude, Wege zu Einem Nahezu klimaneutralen Gebäudebestand; Bundesministerium für Wirtschaft und Energie (BMWi): Berlin, Germany, 2015.
- Narayanan, M.; Mengedoht, G.; Commerell, W. Importance of buildings and their influence in control system: A simulation case study with different building standards from Germany. Int. J. Energy Environ. Eng. 2018, 9, 413–433. [Google Scholar] [CrossRef]
- Thieblemont, H.; Haghighat, F.; Ooka, R.; Moreau, A. Predictive Control Strategies based on Weather Forecast in Buildings with Energy Storage System: A Review of the State-of-the Art. Energy Build. 2017, 153, 485–500. [Google Scholar] [CrossRef]
- Aström, K.J.; Wittenmark, B. Adaptive Control: Second Edition. Available online: http://store.doverpublications.com/0486462781.html (accessed on 28 August 2017).
- Kirk, D.E. Optimal Control Theory: An Introduction. Available online: http://store.doverpublications.com/0486434842.html (accessed on 28 August 2017).
- Reynders, G.; Nuytten, T.; Saelens, D. Potential of structural thermal mass for demand-side management in dwellings. Build. Environ. 2013, 64, 187–199. [Google Scholar] [CrossRef]
- Prívara, S.; Cigler, J.; Váňa, Z.; Oldewurtel, F.; Sagerschnig, C.; Žáčeková, E. Building modeling as a crucial part for building predictive control. Energy Build. 2013, 56, 8–22. [Google Scholar] [CrossRef]
- Sturzenegger, D.; Gyalistras, D.; Morari, M.; Smith, R.S. Model Predictive Climate Control of a Swiss Office Building: Implementation, Results, and Cost–Benefit Analysis. IEEE Trans. Control Syst. Technol. 2016, 24, 1–12. [Google Scholar] [CrossRef]
- Yu, Z.J.; Huang, G.; Haghighat, F.; Li, H.; Zhang, G. Control strategies for integration of thermal energy storage into buildings: State-of-the-art review. Energy Build. 2015, 106, 203–215. [Google Scholar] [CrossRef]
- Zakula, T. Model Predictive Control for Energy Efficient Cooling and Dehumidification. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2013. [Google Scholar]
- Pichler, M.F.; Lerch, W.; Heinz, A.; Goertler, G.; Schranzhofer, H.; Rieberer, R. A novel linear predictive control approach for auxiliary energy supply to a solar thermal combistorage. Solar Energy 2014, 101, 203–219. [Google Scholar] [CrossRef]
- Pintaldi, S.; Li, J.; Sethuvenkatraman, S.; White, S.; Rosengarten, G. Model predictive control of a high efficiency solar thermal cooling system with thermal storage. Energy Build. 2019, 196, 214–226. [Google Scholar] [CrossRef]
- Alibabaei, N.; Fung, A.S.; Raahemifar, K. Development of Matlab-TRNSYS co-simulator for applying predictive strategy planning models on residential house HVAC system. Energy Build. 2016, 128, 81–98. [Google Scholar] [CrossRef]
- Görtler, G.; Beigelböck, B. Simulation einer prädiktiven Raumtemperaturregelung unter Verwendung einer idealen Wettervorhersage. Bauphysik 2010, 32, 405–413. [Google Scholar] [CrossRef]
- Zhang, K. Assessing simplified and detailed models for predictive control of space heating in homes. In Proceedings of the 9th International Conference on System Simulation in Buildings, Liege, Belgium, 10 December 2014; Volume 12. [Google Scholar]
- Kuboth, S.; Heberle, F.; König-Haagen, A.; Brüggemann, D. Economic model predictive control of combined thermal and electric residential building energy systems. Appl. Energy 2019, 240, 372–385. [Google Scholar] [CrossRef]
- Bruno, R.; Pizzuti, G.; Arcuri, N. The Prediction of Thermal Loads in Building by Means of the EN ISO 13790 Dynamic Model: A Comparison with TRNSYS. Energy Procedia 2016, 101, 192–199. [Google Scholar] [CrossRef]
- Liu, Y.; Pan, Y.; Huang, Z. Simulation-Based Receding-Horizon Supervisory Control of HVAC System. In Proceedings of the 13th Conference of International Building Performance Simulation Association, Chambery, France, 26–28 August 2013. [Google Scholar]
- Ostadijafari, M.; Dubey, A.; Liu, Y.; Shi, J.; Yu, N. Smart Building Energy Management using Nonlinear Economic Model Predictive Control. arXiv 2019, arXiv:1906.00362. [Google Scholar]
- Khakimova, A.; Shamshimova, A.; Sharipova, D.; Kusatayeva, A.; Ten, V.; Bemporad, A.; Familiant, Y.; Shintemirov, A.; Rubagotti, M. Hybrid model predictive control for optimal energy management of a smart house. In Proceedings of the 15th International Conference on Environment and Electrical Engineering (EEEIC), IEEE 2015, Rome, Italy, 10–13 June 2015; IEEE: Rome, Italy, 2015; pp. 513–518. [Google Scholar]
- Khakimova, A.; Kusatayeva, A.; Shamshimova, A.; Sharipova, D.; Bemporad, A.; Familiant, Y.; Shintemirov, A.; Ten, V.; Rubagotti, M. Optimal energy management of a small-size building via hybrid model predictive control. Energy Build. 2017, 140, 1–8. [Google Scholar] [CrossRef]
- Starcic, A.; Lesic, V.; Vasak, M. Predictive control for heating power variance and peak reduction in buildings. In Proceedings of the 42nd Annual Conference of the IEEE Industrial Electronics Society, IECON 2016, Florence, Italy, 24–27 October 2016; IEEE: Florence, Italy, 2016; pp. 7089–7094. [Google Scholar]
- Coffey, B.; Haghighat, F.; Morofsky, E.; Kutrowski, E. A software framework for model predictive control with GenOpt. Energy Build. 2010, 42, 1084–1092. [Google Scholar] [CrossRef]
- Jungwirth, J. Lastmanagement in Gebäuden: Entwicklung einer modellprädiktiven Regelung Mit Einem Adaptiven Gebäudemodell zur Flexibilisierung der Wärme- und Kälteversorgung von Gebäuden. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2014. [Google Scholar]
- MATLAB, version 9.8.0 (R2020a); The MathWorks Inc.: Natick, MA, USA, 2020.
- TRNSYS Transient System Simulation Tool–TRNSYS; Thermal Energy System Specialists LLC: Madison, WI, USA, 2019.
- Gerster, J.; Blank, M.; Stern, K.; Sonnenschein, M. Intelligentes Heimenergiemanagement–Nutzung der Synergiepotentiale bei der thermischen und elektrischen Objektversorgung durch modellbasierte und prädiktive Betriebsführungsstrategien. In Proceedings of the VDE-Kongress 2016-Internet der Dinge, Mannheim, Germany, 7–8 November 2016. [Google Scholar]
- Intelligentes Heimenergiemanagement- iHEM: Website. Available online: http://www.ihem.eu/ (accessed on 13 January 2017).
- Julia 1-3-Dammann-Haus. Available online: https://www.dammann-haus.de/julia-1-3.html?articles=julia-1-3 (accessed on 8 June 2018).
- Sonnenhauskriterien für Wohngebäude. Available online: http://www.sonnenhaus-institut.de/wp-content/uploads/1-Sonnenhauskriterien-2014.pdf (accessed on 29 August 2017).
- Sailer GmBH Sailer GmbH Ehingen–Focus AR Solar Collectors. Available online: http://www.sailergmbh.de/en/products/solar-collectors.html (accessed on 29 August 2017).
- Drück, H. Multiport Store Model for TRNSYS—Type 340; Institut für Thermodynamik und Wärmetecknik (ITW), Universität Stuttgart: Stuttgart, Germany, 2006. [Google Scholar]
- Sailer GmBH-Quattro Sailer GmbH Ehingen–Schichtenspeicher. Available online: http://www.sailergmbh.de/en/products/schichtenspeicher/schichtenspeicher.html (accessed on 13 January 2017).
- Narayanan, M.; Mengedoht, G.; Commerell, W. Design of simulation model for novel solar thermal storage tank. In Proceedings of the Simulation Technischer Systeme—Grundlagen und Methoden in Modellbildung und Simulation, Ulm, Germany, 9 March 2018. [Google Scholar]
- Narayanan, M.; Lindemann, G.; Mengedoht, G.; Commerell, W. Implementation of a Renewable Power to Heat Methodology using Raspberry Pi in an Energy System Demonstrator. In Proceedings of the 14th International Conference on Heat Engines and Environmental Protection, Mátrafüred, Hungary, 27–29 May 2019. [Google Scholar]
- Solid Power BlueGen Broschure. Available online: http://www.solidpower.com/fileadmin/user_upload/pages/Logos_materialien/SOLIDpower_BlueGEN_Brochure_UK_web.pdf (accessed on 23 May 2017).
- Sailer GmBH-FriWasta Sailer GmbH Ehingen–Frischwasserstation. Available online: http://www.sailergmbh.de/it/produkte/frischwasserstation.html (accessed on 30 August 2017).
- Narayanan, M.; Mengedoht, G.; Commerell, W. Simulation and design of an energy system with solar collectors, PV, fuel cell CHP and gas boiler at Ehingen, Germany. In Proceedings of the 13th International Conference on Heat Engines and Environmental Protection, Budapest, Hungary, 25–27 May 2017. [Google Scholar]
- Aleo Solar Aleo Solar S19 295-300W Datasheet. Available online: http://www.novisenergy.ch/pdf/aleo_S19_295_300W.PDF (accessed on 23 May 2017).
- BMZ Energiespeicher ESS 7.0|Energiespeicher|BMZ GmbH. Available online: https://ess.bmz-group.shop/de/products/Energiespeicher_ESS_7.0 (accessed on 26 May 2020).
- Steca Elektronik GmbH Coolcept3- StecaGrid 3203x Datasheet. Available online: http://www.steca.com/index.php?coolcept3-x-StecaGrid-3203x-5503x-en#productdownload (accessed on 9 February 2018).
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the International Conference on Evolutionary Computation Proceedings, IEEE World Congress on Computational Intelligence (Cat. No.98TH8360), 1998 IEEE, Anchorage, AK, USA, 4–9 May 1998. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization: An overview. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Hassan, R.; Cohanim, B.; de Weck, O.; Venter, G. A Comparison of Particle Swarm Optimization and the Genetic Algorithm. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference; Structures, Structural Dynamics, and Materials and Co-located Conferences; American Institute of Aeronautics and Astronautics, Austin, TX, USA, 18–21 April 2005. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992; ISBN 978-0-262-08213-6. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1996; ISBN 978-0-262-13316-6. [Google Scholar]
- Yang, X.-S. Engineering Optimization: An Introduction with Metaheuristic Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010; ISBN 978-0-470-64042-5. [Google Scholar]
- Beasley, D. An Overview of Genetic Algorithms: Part 1, Fundamentals. Univ. Comput. 1993, 15, 56–69. [Google Scholar]
- Torczon, V. On the Convergence of Pattern Search Algorithms. SIAM J. Optim. 1997, 7, 1–25. [Google Scholar] [CrossRef]
- Lewis, R.M.; Torczon, V. Pattern Search Algorithms for Bound Constrained Minimization. SIAM J. Optim. 1999, 9, 1082–1099. [Google Scholar] [CrossRef]
- Lewis, R.M.; Torczon, V. Pattern Search Methods for Linearly Constrained Minimization. SIAM J. Optim. 2000, 10, 917–941. [Google Scholar] [CrossRef]
- Booker, J.; Dennis, J.E.; Frank, P.D.; Serafini, B. A Rigorous Framework for Optimization Functions by Surrogates. Struct. Optim. 1999, 17, 1–13. [Google Scholar] [CrossRef]
- Audet, C.; Dennis, J.E. Analysis of Generalized Pattern Searches. SIAM J. Optim. 2002, 13, 889–903. [Google Scholar] [CrossRef]
- Tokan, F.; Güneş, F. Interference suppression by optimising the positions of selected elements using generalised pattern search algorithm. Antennas Propag. IET Microw. 2011, 5, 127–135. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. (Eds.) Penalty and Augmented Lagrangian Methods. In Numerical Optimization; Springer Series in Operations Research and Financial Engineering; Springer: New York, NY, USA, 2006; pp. 497–528. ISBN 978-0-387-40065-5. [Google Scholar]
- Global Optimization Toolbox Documentation. Available online: https://www.mathworks.com/help/gads/ (accessed on 14 August 2020).
- Menegon, D.; Persson, T.; Haberl, R.; Bales, C.; Haller, M. Direct characterisation of the annual performance of solar thermal and heat pump systems using a six-day whole system test. Renew. Energy 2020, 146, 1337–1353. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).