1. Introduction
With fast-growing advancements in smart systems, the real-time applications are handy candidates for utilizing the computing power in a cloud computing environment in order to maintain deadline constraints. Cloud computing is an economic-based paradigm consisting of distributed resources and providing services by collaborating in executing user applications. The cloud services are categorized into Infrastructure-as-a-Service (IaaS) that deals with providing computing such as VMs and storage resources as services, Platform-as-a-Service (PaaS) that offer deployment and development platforms as services, and Software-as-a-Service (SaaS) that facilitate users with web-based applications. The most common examples are IBM’s Blue Cloud (for IaaS), Google AppEngine and Microsoft Azure (for PaaS), and EC2 (for SaaS). These services are employed by using cloud deployment models, namely public, private, and hybrid established on the basis of organization preferences. The cloud compute and storage resources are selected and allocated on the basis of nature of user application. In addition, the cloud storage resources provide facilities such as accommodating data replication to satisfy data requirements of the data-intensive real-time systems that need to access, process and transfer data files stored in distributed data repositories [
1,
2]. Examples of such applications are self-driving vehicles, which depend on the data and computations under a complex network of interconnected devices such as GPS, surveillance cameras, radar, laser light, odometry, etc., to perceive the surroundings [
3,
4]. The cloud providers such as Amazon EC2 [
5] provide computing facilities (virtual machines) on a pay-as-you-go basis at the rate of 10 cents per hour. The lease prices vary depending on the virtual machines (VMs) specifications. The normal VM offers an approximate processing power of 1.2 GHz Opteron processor with a storage capacity of 160 GB disk space and 1.7 GB of memory [
5,
6,
7]. Such facilities pave the way for executing time-critical and IoT applications which demand high processing and storage capabilities [
8]. Stergioua et al. [
9] merged cloud computing with IoT to improve the functionality of the IoT. The IoT devices offload many tasks to the cloud environment from the smart systems because these devices have very limited processing and storage capabilities. Leveraging the capabilities of virtualization technology, VMs can be scaled up and down depending on the current system workloads [
10]. For executing VM code on smart platforms, smart virtual machines are proposed by Lee et al. [
11]. However, there is a lack of efficient resource scheduling and allocation strategies for deploying real-time applications with stringent QoS and data requirements in cloud computing environments. The scheduling policy for data-intensive real-time systems proposed in [
12] allocates HPC resources by considering that single copies of data-files are available on storage resources without taking into account the computation and transfer cost. The concept of real time scheduling is used in the deployment of smart environments [
13,
14,
15,
16,
17].
The Global Institute [
18] report on analyzing the economic impact of the IoT devices show that it will increase upto
$11 trillion by the year 2025. This increase is because the IoT devices and smart home appliances ranging from small sensors to large scale biometrics offload data and computation to the cloud computing environment on a regular basis [
19,
20]. For this purpose, the IT companies provide solutions such as Apple’s HomeKit [
21], Samsung’s SmartThings [
22], Amazon’s Alexa [
5], and Google’s Home [
23], etc. The smart systems are considered as data-intensive systems that are different from compute-intensive or eScience applications because of the storage, access, execution and management requirements of distributed datasets and hence, require different scheduling and allocation policies. These systems basically deal with the data and transport layers for replication and access of datasets. The data-intensive smart systems can be considered as a combination of data producers and consumers geographically distributed across multiple organizations. The producers are the entities that produce data and manage its distribution over multiple locations. The consumers can be the users or their applications which need this data produced by the producers for multiple purposes. The consumers investigate efficient ways out of many to access the data for executing applications on remote compute nodes.
The driving force of cloud computing is the virtual machine manager (VMM) that creates the virtual resources of the physical machines. The basic functionality of the VMM is to separate the virtual computing environment from the underlying physical infrastructure. In this research work, we implement the rate monotonic (RM) scheduling policy to allocate cloud computing resources for the real-time data-intensive periodic tasks. The scheduling problem is divided into three parts: the processing environment (cloud virtual machines), the nature of the real-time task (fixed priority system), and the optimization criteria (time- and cost-efficient allocation). The real-time task set is a collection of multiple tasks, each of which requires data for processing. The required data files are requested from the remotely located storage resources. The intelligent selection and assignment of cloud computing resources are investigated while the data files are replicated on decoupled storage resources and accessed by utilizing networks of varying capabilities. The proposed strategy evaluates all the storage locations for the replicas of the same data file and selects the one which has minimum data access and transfer cost. It submits the application to the computing resource that is closest to the selected storage location and can complete execution within minimum possible execution time. These files are fetched to the computing resources where tasks are executed, which add transfer time to the red tasks’ total execution time. In our proposed model, a user-specified budget is associated with each smart system request, and hence resources are selected not only on the basis of their high computational power, but also the cost associated with each and the storage resource are computed, as well as the ability to process jobs within tasks deadlines and scheduling preferences.
The major research contributions of our work are:
Creating a model for selecting appropriate cloud computing and storage resources to execute real-time data-intensive systems generated by smart devices where data is replicated on multiple storage resources,
Partitioning the task sets into groups based on common data-file demands such that the timing constraints of the original tasks set are not disturbed,
Analysing the economic perspective of data storage and processing by scheduling real-time smart systems on distributed nodes with different storage, execution, and data transfer costs and allocating heterogeneous cloud resources,
Allocating cloud computing resources to periodic real-time tasks such that the overall timing constraints of the smart devices remain intact,
Analysing cloud computing and IoT usability in the context of data-intensive smart systems.
Cloud computing is considered a promising platform for executing large-scale computing-intensive IoT and smart grid applications in a cost-efficient way due to the large pool of computing resources. These resources need intelligent scheduling and allocation of the tasks such that all tasks in a batch can be processed within the stipulated time span. The research community focuses on searching mechanisms for scheduling and allocating distributed cloud resources in a systematic way which can satisfy formulated objective function such as load balancing, makespan minimization, and cost-efficiency with respect to the user-defined QoS criteria [
3,
24,
25]. But, instead of the vast study in the cloud resource allocation domain, the existing literature is not mature in providing suitable scheduling mechanisms for real-time systems generated by smart devices due to the high deadline-miss ratio by a number of tasks in a batch [
26]. The problem becomes more challenging when such systems need data from external sources. A real-time system is characterized by the deadlines of the tasks. In such systems, deadline meeting is primarily important for utilizing maximum capabilities of the cloud resources, since most of the real-time systems such as sensors in smart systems or actuators in automated systems generate periodic tasks, which are sent to the processing units after regular intervals. Such systems need proper priority-based and non priority-based strategies for scheduling. In priority-based scheduling policy, the scheduling criteria is saved for the entire duration of task execution, while in non priority-based systems, the tasks have no precedence constraints and the scheduling criteria may change with the arrival of the next job of a task. The main advantage of priority-based policies is time-saving and its simple implementation. The priority-based scheduling is also known as static priority scheduling. The well-known static priority assignment algorithm is Rate Monotonic developed by Liu and Layland in 1973. The main features of this algorithm are its simple implementation at OS kernel level, predictability in real-time behavior like in smart systems, and its easy modification for implementing task priority inheritance protocol for the purpose of synchronization [
27].
In order to utilize the full potential of the cloud and IoT platforms, Suciu et al. [
28] proposed a conceptual framework for the deployment of IoT based smart microgrid applications. The developed framework has the capability of integrating real-time data generated by the ubiquitous sensing devices constituting the smart home with the cloud computing environment, but their system is prone to missing deadlines because they have not evaluated their system on each time instant according to the workload of the task. The dynamic algorithm for scheduling soft real-time systems on grid resources was proposed in [
29]. The proposed algorithm provides room for tasks with missed deadlines. Ye et al. [
30] proposed architecture of smart home-oriented cloud. They have suggested a layered cloud design that provides efficient services for digital appliances. The authors have considered the sensors sending data continuously without specifying any real-time constraints. Caron et al. [
1] consider task priorities for scheduling real-time tasks. The tasks are checked one by one. Shang et al. [
1] formulated a model which elaborates grid service reliability assessment for dependable and cost-efficient applications. They have derived a cost function based on genetic and particle swarm optimization techniques that calculate service expense of each utilized resource. Isard et al. [
4] considered scheduling problem of data-intensive tasks using the Hadoop structure. They have supposed coupled computing and data resources located at the same place and that the data is available for each task without transferring from remotely located resources. Therefore, they have not included the data transfer time in the task feasibility analysis. The proposed tasks are preemptable but no specific criterion is discussed for which task is to be preempted when an interruption occurs or when high priority tasks arrive. In ref. [
5], the authors have focused on submitting preemptable tasks to the federated grid. They have developed a schedule which maximizes the acceptance of incoming tasks, and minimizes user-defined QoS criteria violation. The authors have not emphasized the heterogeneity of resources. Poola et al. [
6] presented a mechanism for robust and fault-tolerant scheduling of scientific workflows on heterogeneous resources which concurrently optimizes makespan and execution cost. Ma et al. [
7] used a hybrid approach by combining the best features of genetic and greedy approaches for QoS-aware web service composition. They have focused on minimizing cost, but they have considered non-real-time tasks. A cost optimization technique for executing data-intensive tasks on distributed resources was developed by Mansouri et al. [
8]. Leveraging data storage and migration cost is addressed by using an optimal online algorithm, but their system is not suitable for executing real-time smart systems tasks. The proposed algorithm provides tasks scheduling and cloud resource allocation criteria for real-time tasks generated by smart systems considering resources heterogeneity, availability, data-intensive and timing constraints of the tasks.
The rest of the paper is structured as follows. In
Section 2, we throw light on discussing task, resource, and cost model. The proposed time- and cost-efficient scheduling algorithm is explained in
Section 3, while the performance of the proposed resource allocation strategy and details of the experimental setup is evaluated in
Section 4. The produced results are presented in
Section 5 and conclusions and future directions are provided in
Section 6.
2. Task, Resource and Cost Models
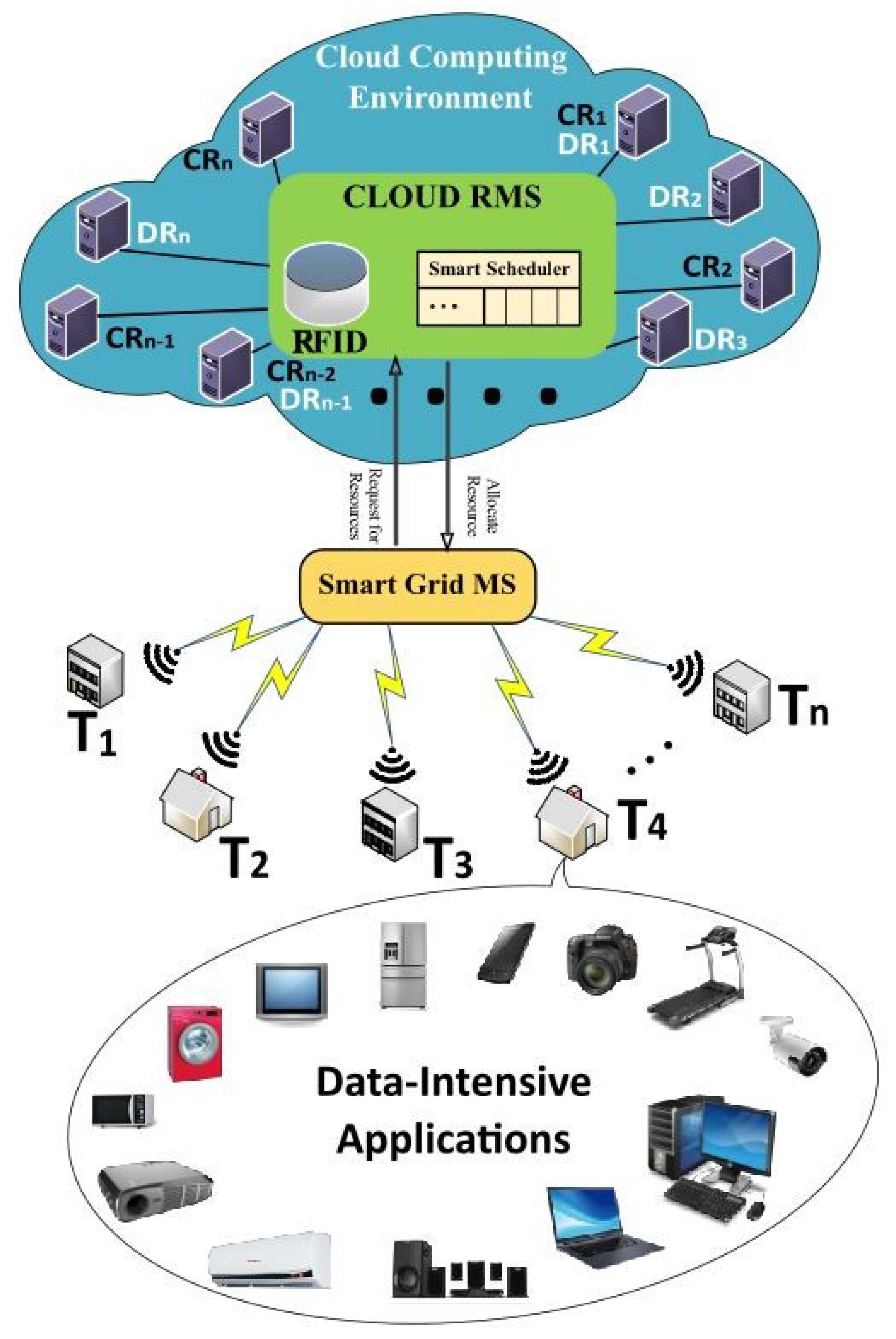
In this research, we consider scheduling feasibility of real-time periodic tasks in a cloud environment. Our model as shown in
Figure 1 is composed of smart devices which generate periodic tasks
. The tasks represent data-intensive applications that generate data on a regular basis and need computing resources for processing. The represented smart devices have limited memory, storage and processing capabilities. Each task needs data stored on some remote storage locations. The tasks constitute a task set
where the collection of task sets form a smart microgrid that sends data to a main smart hub known as Smart Grid Management System. The smart hub manages the received data and uploads the collected tasks to the cloud environment. The Cloud Resource Management System (Cloud RMS) handles task requests and manages cloud resources. The Cloud RMS has the responsibility to search suitable resources and required data files information from the Resource Files Information Directory (RFID) according to the task requirements and schedule tasks on cloud resources. The Cloud RMS also implements the scheduling policy. Our concerned cloud environment is comprised of both computational
and data storage resources
located remotely and connected by network links of different bandwidths. The resources are heterogeneous and characterized by power and cost constraints.
In this paper, we concentrate on two basic constraints; (a) the real-time tasks’ deadlines, and (b) user-specified budget. The presented model extends the RDTA model [
12] by introducing cost parameters, data files replication scenarios, and tasks’ grouping criteria.
2.1. Task and Resource Model
We consider batch processing of real-time periodic tasks, each of which can generate an infinite number of jobs. In periodic tasks set
, each
is defined by the quadruple:
where
shows the release time of the first job,
the required computation time,
the relative deadline of
which is the time difference between the absolute deadline and release time of a job, and
the period which is the time difference between the two successive jobs of a
.
In the above discussed model, a job i released at time instant needs to execute for units before the time . In our task model, we concentrate on a constrained deadline model which assumes that . Tasks preemption is not allowed and context switching overhead is subsumed into . We also assume that , which means that feasibility of the tasks is checked when the system is most loaded.
We consider computing resource set CR such that
. Each one is characterized by a computing power
such that
, where
, and measured in Millions of Instructions per Second (MIPS). The execution time of a
on resource
can be computed by
where
is the execution time of higher priority tasks than
. Mathematically,
where
set accumulates points or time instants on which task feasibility is analyzed. The
set is defined as follows.
Definition 1. is a set of positive and negative points for constituted by the relation such that and , where represents periods of higher priority tasks than . The point is said to be positive if is declared feasible (i.e., completes its execution at or before the deadline) at some point t by considering all associated time and data constraints. The point declares the infeasible when it misses the deadline. Each point in is called rate-monotonic scheduling point. From Definition (1), it is concluded that the set is the union of positive points set and negative points set where and . In other words, .
2.2. Data Files Model
In our task model, a tasks set consists of data-intensive real-time tasks where each task needs a set of data files for its execution. The set . The file is stored on data storage resource , where and . The is the set of total storage resources in the HPC environment. In other words, files in are stored on storage resources. We assume that the data files are replicated on more than one data storage resources.
The total execution time
of a task
is the sum of actual computation time
of
on computing resources
and the transfer time taken by the required
m data files in the set
by transferring from storage resources
to the computing resource
where task
k is executed. Mathematically,
where
=
is the transfer time of the file
.
The
represents the response time of the data storage resource
where the data file
is stored. The response time is the time when the request to fetch the file is made at the time when the request is entertained. Algebraically, the response time of data resource
is calculated as:
where
is the service time and
is the waiting time of the request respectively for accessing the file
. Also, the
denotes the size of the file
, and
shows the link bandwidth between data storage resource
and computing resource
. The proposed model selects that storage resource for file access for which
is minimum, i.e.,
.
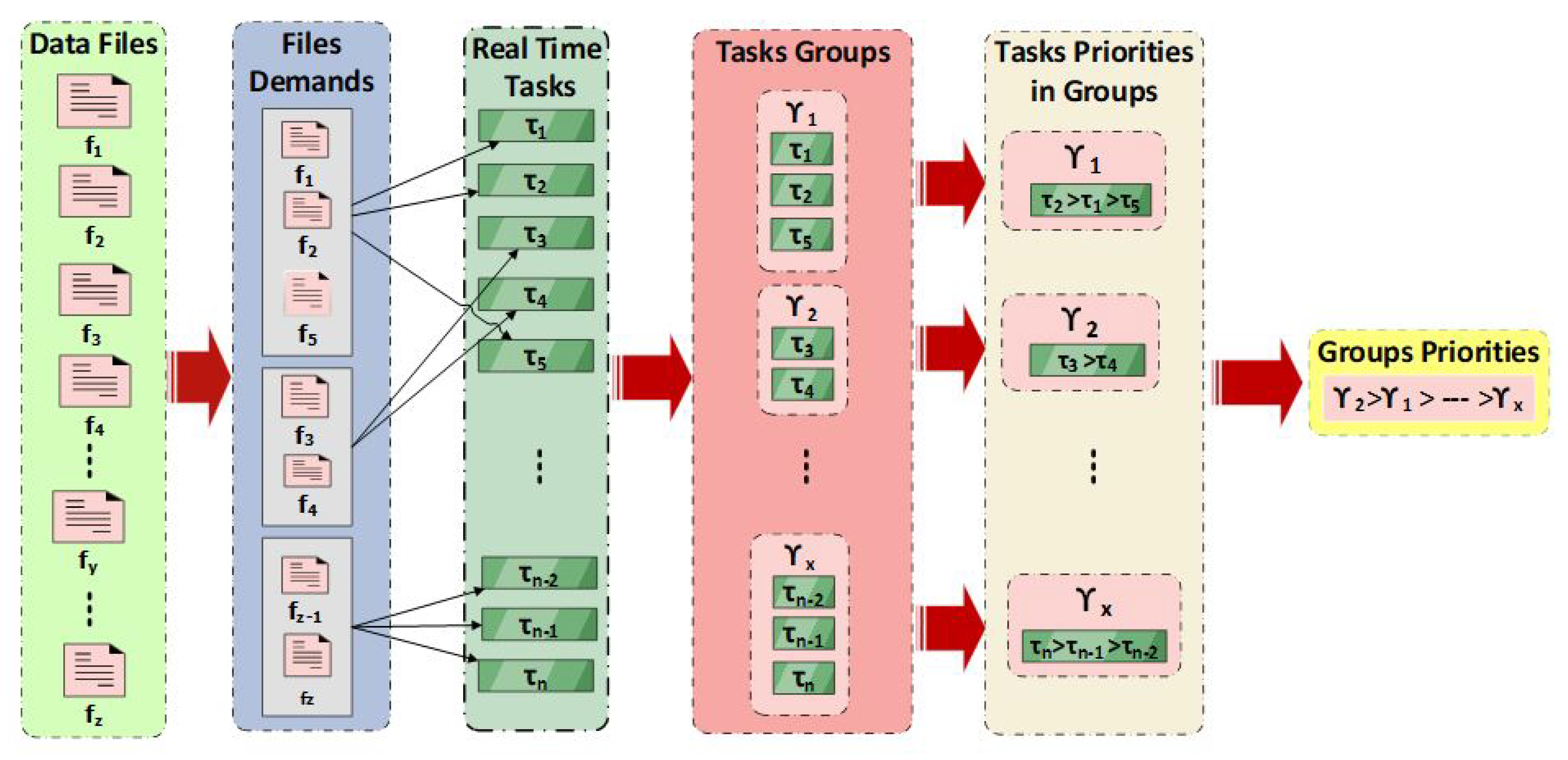
2.3. Task Grouping
The data-intensive real-time tasks in
T are grouped into
x number of groups on the basis of common data files demands. The tasks in a group represent a subset of
T or we can say each group is a set of tasks for easy understanding. The task grouping taxonomy is pictorially represented in
Figure 2.
Based on real-time task grouping criteria, the group of tasks, its cardinality, and priority assignment is defined in the following sections.
Definition 2. A group of real-time tasks is a subset of tasks, i.e., having common data files demands. Each group contains minimum one task which concludes that .
Definition 3. The cardinality of a task group defines the total number of tasks in a group. Let there be total x number of groups, then cardinality of the original tasks set can be defined as: The advantage of the task grouping mechanism is to reduce the total number of priority levels [25]. Additionally, for a higher priority task remains the member of for all lower priority tasks than in , since tasks in the same group are also sorted on the basis of RM priorities. In this way, the least number of points is tested on the set which decreases the execution time. From the above definitions, the following can be observed.
Observation 1. Let each task groupconstituted from task setcontains a single task in a worst case scenario and x represents the total number of groups in the system, thenwhere n represents.
Each real-time task in our task model has deadline d, which demonstrates the maximum allowed time for a task to complete its execution on a single computing resource. Let the maximum and minimum deadlines of the tasks in a group are denoted by and respectively. Here an interesting observation can be made.
Observation 2. of the taskssorted by RM priority assignment technique and following the implicit deadline model (period = deadline) is the period of the last task whileis the period of the first task in.
The relation follows:whereandrepresent periods of the last and the first task in, respectively. Proof. The RM technique sort the tasks based on priority assignment criteria: the lesser the period of the task, the higher the priority. This means that the last task has the lowest priority and first task has the highest priority among all tasks in . The is executed in the first and is executed in the last slot. In other words, which follows that . It also follows that and , which completes the proof. □
The authors in [
24] discussed that RM assigns static priorities to tasks and considered an optimal scheduling algorithm among static priority assignment scheduling algorithms. By optimal they mean that RM should schedule a task, if any other static priority assignment algorithm can schedule that task. Following are the general characteristics of the RM scheduling technique which play a role in proving its optimality.
- 1.
the system should consist of a fixed number of tasks;
- 2.
the tasks should have execution times known in advance;
- 3.
each task has a completion deadline equal to its period;
- 4.
tasks should be periodic which means that instances or jobs of a task should arrive after a fixed time interval;
- 5.
tasks should be independent;
- 6.
all tasks should arrive at time 0. This time instant is also known as the critical instant and the system is considered as the most overloaded at this instant.
Definition 4. The period of a task group is defined as the temporary period attached to the group of tasks which is the period of the last task in a group. In other words, is the group period because the tasks in a group are sorted using RM technique. For example, if a group accommodates tasks , then Since the groups are sorted on the basis of RM priorities, so which states that . Equation (8) states that all tasks in must complete execution at or before . It has been further evaluated that since the tasks in the same group are also sorted by RM priorities, so for a higher priority task remains the member of for all the lower priority tasks than . Definition 5. The group capacity can be defined as the total number of tasks in a group. Tasks in a group are added on the basis of common data files demand. The group capacity can be analyzed on the basis of resource utilization by a group of tasks called group utilization (GU) which is defined as the sum of the resource utilization of each task in the group. The computing resource utilization of each task is termed as task utilization (TU). Let n denotes the total number of tasks in a group , then GU and TU can be found as follows.where Theorem 1. Let be a group of n periodic tasks, where each task is characterized by . The group is said to be RM feasible if the following condition holds: The inequality (11) is called the Liu and Layland test reported in [24]. The expression is the threshold value of a group which means that a group can accommodate tasks as for as the remains lower than or equal to the threshold value. Equation (11) is checked repeatedly when a new task is added to the group. If adding a task changes the inequality to , then the incoming tasks are added to another group. The authors in [25] refer the test as the sufficient condition test. They claim that it is not necessary that the tasks in a group are not schedulable if Equation (11) does not hold. This means that utilization-based tests are sufficient, but not necessary. Let us explain by the following example task set taken from [26,29]. Example 1. Consider a task group where tasks follow RM ordering and having following characteristics and utilizations mentioned in Table 1 and Table 2 respectively. For the above tasks set Y, the and threshold = 0.756.
It shows that the aforementioned example task group
Y is not schedulable by using
test because it does not satisfy Equation (
11). However, the gantt chart in
Figure 3 shows the schedulability of these tasks within deadlines under RM technique. From the above discussion, it is clear that
test is sufficient only, so we use
test for checking group capacity only. For analyzing task or group feasibility, we use
test which is necessary and sufficient conditions test.
Theorem 2. A group of real-time tasks is schedulable if all tasks in are schedulable.
Theorem 3. The batch of real-time tasks called periodic tasks set represented by is deemed feasible if all task groups are schedulable.
2.4. Cost Model
Scheduling decisions by integrating cost parameters change the way computational resources are selected to fulfill the user criteria. The data-intensive real-time tasks are submitted to the broker which searches resources to process tasks within deadlines and user-specified budget constraints. The feasibility of tasks’ groups on computational resources is checked by considering data transfer time, transfer costs, computational cost, tasks’ deadlines, and computational power of the resources. The basic parameters considered for feasibility decisions in this research are:
- (a)
user-specified budget, and
- (b)
tasks deadlines.
Based on the above two parameters, the cloud computing and storage resources which can execute tasks within deadlines in a minimum cost by taking into account all data and processing constraints are selected.
By introducing cost model, Theorem 3 can be extended in Theorem 4 for checking schedulability of modified task set.
Theorem 4. The batch of real-time tasks called periodic tasks set represented by is deemed feasible with minimum cost if all task groups are schedulable by following all tasks constraints and holding inequality (12).where is the total cost incurred by the batch of tasks, and is the total user-specified budget. The cost of a resource can be expressed as execution cost per Millions of Instructions (MI), processing cost per unit time, processing cost per task, or simulation cost per unit time, etc. The cost for a single task is the sum of task execution cost and the data files transfer cost. 3. Time- and Cost-Efficient Scheduling Algorithm
The Algorithm 1 determines the schedulability of real-time independent tasks set consisting of tasks with different data files and timing constraints. The execution procedure of the tasks involves checking task group feasibility which cumulatively constitutes tasks set. The m number of tasks in a group are checked on r number of distributed computing resources where . Depending on the user budget and tasks scheduling preferences, the main objective of this algorithm is to execute distributed data-oriented applications by selecting computing and storage resources such that the tasks are processed with minimum total execution time and cost while tasks’ deadlines are respected. The proposed algorithm works in three parts: (a) task initial feasibility checking which predicts a task’s basic feasibility within a deadline by searching initial feasible computing resources, (b) task final feasibility and cost analysis which determines a task’s schedulability after considering all the associated constraints, and finally (c) task dispatching to the best suitable resources after fulfilling all the pre-requisites. The first two parts are the matching and mapping parts which create set of time- and cost-efficient computing–storage resources pairs. The third part is the dispatching part which ensures that the selected resources can process tasks within time and budget constraints. By cost we mean the sum of a task’s execution cost and data-files transfer cost. Similarly, the total execution time to be minimized is the sum of tasks actual execution time and the transfer time incurred by transferring data-files from the storage resources to the computing resources where the task is executed. The data-files are replicated on multiple storage resources and the resource which has the minimum transfer cost is selected for data-file transfer. The computing resource capability for executing a task is checked by analyzing task feasibility on points. As a result, the computing resource that can execute a task by maintaining the deadlines is initially selected from the list of available computing resources. The selected resource is called an initially feasible resource. The service requests are provisioned according to the described scheduling strategy; i.e., the total execution time of the task set and the incurred cost should be minimized. To ensure the fulfilment of the aforementioned two objectives, the set of storage resources are demonstrated which accommodate data-files needed for the task after identifying the initially feasible resources. A single file is assumed to be replicated on more than one storage resource, so the resource which has less transfer time and cost is selected. All such computing–storage resources pairs are further checked for calculating total execution time. The total execution time is the sum of all time factors. If the total time is within the task deadline and the total cost is within the user-specified budget, the compute–storage resources pair is declared feasible for assigning . After selecting all such pairs for all tasks in a group, the tasks are then dispatched to the qualified resources by the dispatcher and all required files are transferred. The tasks are scheduled and computations are carried out. In this way, if all tasks in a group are scheduled, then the group is said schedulable by the Algorithm 1. Furthermore, if all groups are scheduled, then the original task set T is declared schedulable with minimum time and cost. The resource allocation procedure completes when all the tasks are dispatched to the resources and the unmapped queue becomes empty. The pseudocode of the tasks mapping and dispatching procedures is given in Algorithm 1.
The purpose of Algorithm 2 is to find suitable compute–storage resource pairs for each data-file required by a task. For each task, sets of required data-files and initially feasible computing resources are passed from Algorithm 1 as input arguments to the file transfer time calculating function. For each data file, the storage resources are identified and the best data storage resource which qualifies the minimization criteria (transfer time and cost) are selected for retrieving data file. For each data file, all possible combinations of initially feasible compute–storage resource pairs are tried and finally, the right combination is returned with decreased transfer time and execution cost.
| Algorithm 1: Time- and cost-efficient assignment of real-time data-intensive group of tasks to the HPC resources |
![Energies 13 05706 i001 Energies 13 05706 i001]() |
| Algorithm 2: Selection of time- and cost-efficient compute–storage resource pairs for each data-file |
![Energies 13 05706 i002 Energies 13 05706 i002]() |
5. Results and Discussion
In this section, we evaluate the performance of our proposed algorithm by comparing it with two methodologies, RDTA [
12] and Greedy.
The makespan and cost minimization behavior of the proposed and the aforementioned two techniques was checked for the randomly generated task sets consisting of 100, 200, 300, 400, 500, 600, 700, 800, 900, and 1000 tasks. The plots reported in this paper are the average values of 300 runs of all the task sets. According to the task grouping criteria discussed in
Section 3, the task sets are grouped into 5, 7, 7, 4, 8, 5, 7, 9, 9, and 10 groups respectively. Each group accommodates different number of tasks based on applied grouping criteria. The task grouping details are given in
Table 4. The experiments were performed by checking system behavior on different number of computing resources. The number of computing resources was randomly generated within the range
. We assume that the data storage resource gives a response immediately when a request is made by a task for data file access and hence the response time is ignored. The time delay in preparing the computing resource is also taken as zero because in our system, the computational resource is supposed to be ready for task execution as soon as the task arrives at that resource.
It was observed that for small task sets, fewer number of computing resources was involved as compared to the larger task sets. It is also understandable that choosing the proper number of computing resources can contribute to maintaining tasks’ deadlines. If a lower number of computing resources is selected as compared to a large number of task sets, then it is likely that some tasks may not be RM feasible due to long waiting queues, which is crucial in real-time systems.
The main objective of this evaluation is to reduce the makespan and execution cost of the application while tasks deadlines are intact.
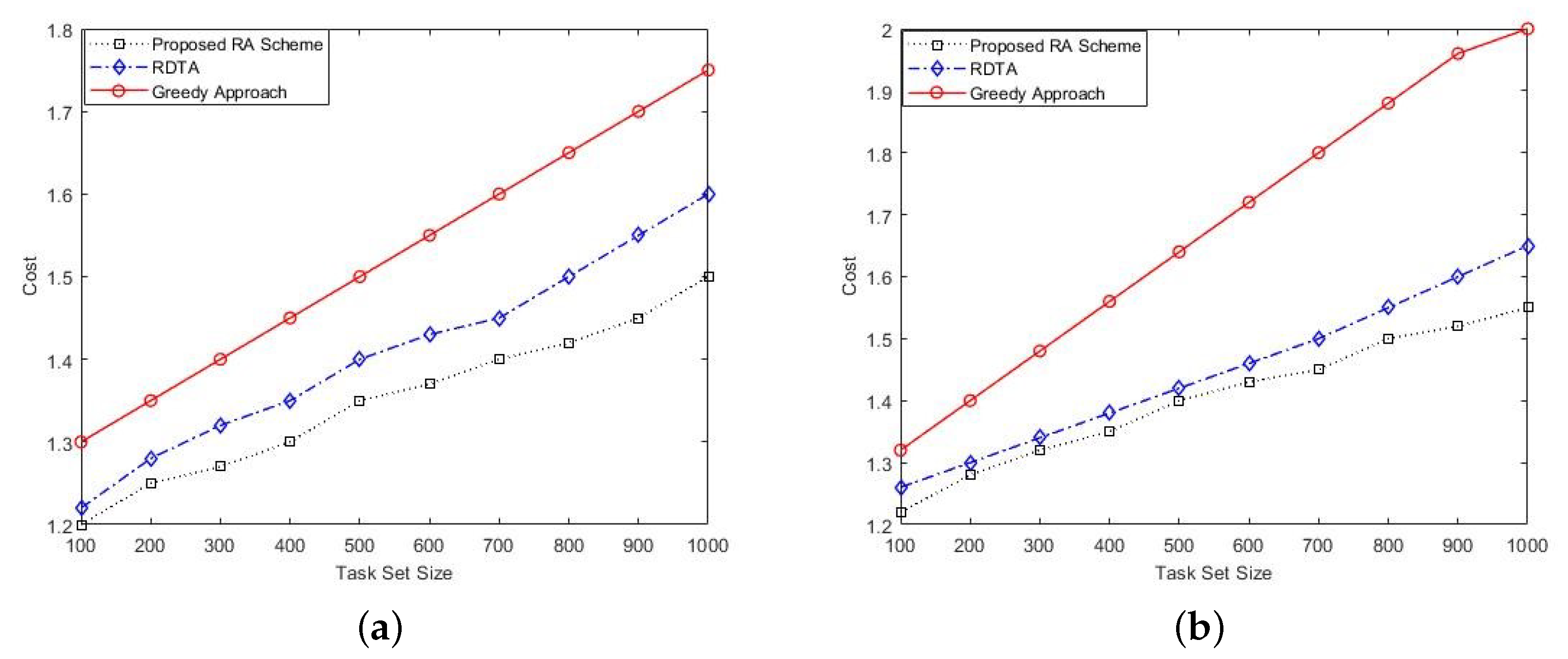
Figure 4a,b depicts the normalized values of the makespan. The variation in magnitude depends upon the total number of tasks per task set, number of data files demands, and the computation and deadline requirements of each task. The lower the makespan value, the better the performance of the RA scheme. The other performance measurement criterion is the execution cost minimization. From
Figure 5a,b, it is evident that decrease in makespan results in reduced processing cost.
It is known from
Figure 4a,b, that the proposed technique continues to make scheduling decision by analyzing tasks feasibility on searching
sets and checking each scheduling point until some positive point
is found. Although, the size of
set for task group
becomes large if the ratio between the periods of the first and the last task
in
is large which consumes time because large number of inequalities are tested, but this procedure enhances the chance of task feasibility because more
points become available for testing tasks schedulability. Furthermore, all the initial feasible computing resources are encountered and the resource having minimum cost for the task execution is selected for task processing. The RDTA approach merely deals with executing tasks within deadlines and hence does not consider the cost parameters, which are considerably high in that case. In the case of the Greedy technique, the graph is steeply higher because a feasible resource is selected at random without taking into account the low time and cost constraints. So, the resources with high computing power are selected when termed feasible.
To further investigate the effectiveness of the proposed technique, we have conducted more experiments with different system settings. It is also noticeable from
Figure 4a,b that the time taken by all tasks test also increases uniformly as the number of tasks increase because more tasks are tested. It is obvious that the makespan of some task sets is high although the computing resources were operated at full speed because they need data files from remote storage resources which increase the total completion time. The resources when operating on full capacities consume high energy, but currently energy efficiency is out of the scope of this research. The situations where makespan is low demonstrates that the data files are locally exist or perfected for some higher priority tasks and do not need re-fetching for the lower priority tasks, which adds zero file transfer time to the overall execution time. The plots show that as the task set size increases, the makespan of the Greedy and RDTA grow, as opposed to the proposed approach. This growth in case of Greedy approach is because of making a greedy selection for the data storage and computing resources among multiple choices for data files accessing and task execution. This selection does not intelligently consider the minimization criteria. The RDTA mechanism also encounters high execution time and hence cost as shown in
Figure 5a,b because the data file replication is not taken into account when making a choice for data files fetch among storage resources. In the case of the proposed approach, the ratio
results in a larger value which constitutes larger
set that provides more points for schedulability checking. This phenomenon provides more opportunities for task scheduling and hence results in large number of tasks meeting the deadlines constraints.
Table 4 shows the formation of task groups in our experimental evaluation on the basis of randomly generated data files demands. The task groups are created as for as the inequality
in Theorem 1 holds.
5.1. Effect of Data Files Transfer on Performance
One of the basic components of calculating execution time is the data files transfer time incurred by transferring data files from the remotely located storage resources to the decoupled computing resources if the required files are not locally available. In addition to the makespan and cost values, two more performance measures considered in the evaluation results are the percent share of the data transfer time and local data access.
In our experiments, the percent share of the data files transfer time in the makespan calculation is evaluated. The
Figure 6a,b plot the impact of the average data transfer time for the task sets. The lower value can put significant impact on reducing the overall makespan of the task set. As it is known from the task workload, the lower priority tasks scheduled on the same computing resource can utilize the same data files retrieved for the higher priority tasks in case the data requirements of the tasks are same. In that case, the data transfer time is zero. Additionally, the transfer time is also zero if the required file resides on the same node locally where the task is being executed. In this case, the more locally accessed files decrease the impact of remote data files transfer on the performance. It is less likely that the task is scheduled on the same computing resource for which all the required data files locally exist.
The above two factors can be correlated with the makespan calculation to indicate the impact of resource selection made by the RA scheme on achieving the decided objective. It is evident from
Figure 6a,b that the Greedy and RDTA schemes do not intelligently adapt for the data files locality of access procedure and hence contribute to high data transfer percentage. The percentage of locality of access rises with the increase in the task set size. In comparison to the RDTA and Greedy counterparts, there is a high chance for the lower priority tasks to reuse the pre-transferred data files by using the proposed RA scheme. In addition, it is more likely that the assigned tasks find the required data files locally. The Greedy approach exhibits degraded performance because there is a very less probability of finding appropriate computing resource for tasks assignment.
5.2. Impact on Resource Utilization
The utilization of the proposed RA scheme is measured on the basis of computing resources utilization in the HPC system. The resource utilization is directly related with the computation workload; when the task workload increases, the resource utilization also increases. The cumulative resource utilization can be calculated by the following equation.
where
represents the cumulative utilization of all computational resources spent on processing tasks workload, and
r represents the total number of computing resources engaged in processing tasks sets.
It is observed from
Figure 7 that the proposed RA scheme improves the resource utilization by keeping resources as busy as possible. The resource utilization is lower for the tasks sets having less number of tasks, but as soon as the number of tasks increases the resource utilization also increases. This means that the resource will be
utilized for the large task sets. This is an understandable phenomenon, because when the workload increases, more computational power is needed to complete tasks by their respective deadlines. If the computational power of the resources is relaxed for energy-efficient allocation, then it is very likely that some of the task groups may not be feasible. Moreover, this also will pertain to an unfair comparison. When the number of tasks increases, the proposed procedure pushes the system power to grow rapidly in order to accommodate more tasks to maintain the deadline constraints. This behavior results in high energy consumption but in this research we do not deal with the energy-efficient perspective.
Figure 7 reveals that implementing the proposed approach, the minimum system utilization is between
and
for small task sets but touches
when the task computational demands increase. The maximum system utilization approaches
by the other counterparts.
5.3. Failure Ratio
Failure ratio determines the ratio of tasks missed their deadlines, or the ratio of tasks which finished their execution after the deadlines. Mathematically,
The proposed algorithm is reactive in the context of deadlines missing by the tasks due to the efficient utilization of cloud resources, testing more and more points, and task grouping on the basis of similar data files demands which skip the re-fetching of the same data files from the storage resources on the same computing resource again and again, which adds transfer time overhead to the makespan calculation. It is also obvious that the RM technique gives higher priorities to the tasks with shorter periods. In our case, since we assume that periods of the tasks are equal to the deadlines, so tasks with short deadlines have higher priorities.
The proposed RA methodology incorporates the scheduling points test as feasibility criteria for determining initial feasible resources, which is slower in performance as compared to the other scheduling techniques. This performance gap is due to testing task feasibility on all scheduling points for all tasks in a task set to offer more opportunity for finding feasible points. The other techniques, such as the iterative one, have the advantage of skipping large number of scheduling points in the feasibility analysis and concludes the task’s feasibility very earlier. The proposed approach also does not consider the resources power consumption and the energy perspectives when operating with high power to execute more tasks within deadlines.