Abstract
This article presents the Reliability Assessment (RA) of renewable energy interfaced Electrical Distribution System (EDS) considering the electrical loss minimization (ELM). ELM aims at minimizing the detrimental effect of real power and reactive power losses in the EDS. Some techniques, including integration of Renewable Energy Source (RES), network reconfiguration, and expansion planning, have been suggested in the literature for achieving ELM. The optimal RES integration (also referred to as Distributed Generation (DG)) is one of the globally accepted techniques to achieve minimization of electrical losses. Therefore, first, the locations to accommodate these DGs are obtained by implementing two indexes, namely Index-1 for single DG and Index-2 for multiple DGs. Second, a Constriction Factor-based Particle Swarm Optimization (CF-PSO) technique is applied to obtain an optimal sizing(s) of the DGs for achieving the ELM. Third, the RA of the EDS is performed using the optimal location(s) and sizing(s) of the RESs (i.e., Solar photovoltaic (SPV) and Wind Turbine Generator (WTG)). Moreover, a Battery Storage System (BSS) is also incorporated optimally with the RESs to further achieve the ELM and to improve the system’s reliability. The result analysis is performed by considering the power output rating of WTG-GE’s V162-5.6MW (IECS), SPV-Sunpower’s SPR-P5-545-UPP, and BSS-Freqcon’s BESS-3000 (i.e., Battery Energy Storage System 3000), which are provided by the corresponding manufacturers. According to the outcomes of the study, the results are found to be coherent with those obtained using other techniques that are available in the literature. These results are considered for the RA of the EDS. RA is further analyzed considering the uncertainties in reliability data of WTG and SPV, including the failure rate and the repair time. The RA of optimally placed DGs is performed by considering the electrical loss minimization. It is inferred that the reliability of the EDS improves by contemplating suitable reliability data of optimally integrated DGs.
1. Introduction
1.1. Literature Survey
The incorporation of distributed power sources in the EDS can support the increasing load demands. To satisfy the increasing load demands, an extremely thorough comparison and assessment has been performed on exploring the potentiality of the distributed energy sources, including the wind and solar energies [,]. The EDS is the combination of electrical loads and Distributed Generation (DG) (especially, WTG and SPV) integrated with electrical storage system (namely BSS) []. In this regard, several comprehensive studies are available on sustainable energy production and management. The state policies, renewable energy plants, and the development of renewable energy sources including solar energy, wind energy, small hydroelectric energy, biomass energy, tidal energy, and geothermal energy have been analyzed for different states of India [,,]. As the energy crisis deepens day by day, the EDS accompanied by RESs is a better solution and also it acts as a complement to the central power grid system []. Therefore, a study on renewable energy potential has been performed for five countries, namely China, Iceland, India, Sweden, and the United States of America. The strengths, weaknesses, opportunities, and threats related to green energy generation and use have been reviewed for these countries using a SWOT analysis [,]. Sometimes an arrangement including the battery storage is needed due to high penetration of renewable resources into an electrical network to fulfill the load demands [,]. Thus, integration of BSS in the distribution system prevails as a better solution for obtaining a steady power output, especially from WTG and SPV owing to the uncertainties involved in the energy harvesting sources such as wind speed [], solar irradiation, and ambient temperature []. Therefore, it is a requisite to determine the siting(s) and sizing(s) of WTG, SPV, and BSS. The system reliability, stability, and power quality are thus, improved substantially. Therefore, to obtain improvements in system’s attributes, the multi-objective optimization methods for problems including operational cost, siting and sizing of distributed energy resources (DERs), Carbon Dioxide (CO) emission, total power loss, voltage deviation, demand-side management, charging-discharging of BSS, total harmonic distortion, and system reliability are also established [,,,,].
Improvement in network reliability is observed when congestion management algorithms are implemented to identify the transmission line congestion []. The DGs and BSSs are scheduled optimally to alleviate this transmission line congestion. A two-step optimization approach is used for solving the congestion problem []. In this optimization method, the optimum location and the size of the SPV array are observed, and then the BSS size with location is determined for accomplishing further reduction in electrical losses and voltage deviation. The authors in [] have proposed an index to obtain the optimal siting of DGs in EDS. This index is implemented to resolve the multiple problems, including total ELM, ENS, and voltage deviation. Another objective, namely loss of yearly energy minimization, is observed through the integration of DERs-based DGs and network reconfiguration []. Furthermore, a novel two-stage stochastic programming is proposed, and the uncertainty considerations together with the load variation are also studied especially for wind energy and solar power generation []. In this method, the total cost is reduced by incorporating BSS into the EDS and by considering the demand response programs in planning. Simultaneously, the enhancement of the power system reliability is achieved due to the obtained optimal BSS size and location. The reliability improvement and reduction in network losses are also observed using compound co-optimization strategic plan []. The reliability indices such as expected ENS, EIR, LOLE, and LOLP, are defined in the co-optimization strategy. Furthermore, a moth-flame optimization [], Olympic games ranking process [], firefly algorithm [], lightning search algorithm [], crow search optimization [], and an improved variant PSO [] techniques have been implemented and discussed in the literature so as to obtain the optimal site, optimal size, optimal parameters of DGs, and ELM.
The RA provides a better evaluation of any power system’s performance []. For assessing the power system’s reliability, some indices have been mentioned in the available literature. These indices are categorized into load-based and system-based indices. The indices values decrease if the ageing of the sub-components is considered []. Reliability is considered to be a primary requirement in the designing phase of EDS. Thus, the optimal siting and optimal sizing of RESs for further RA have also been considered. To fulfill the RA in EDS [], has introduced a restoration strategy for ENS calculation. The optimization of reliability indices has been considered in [,], and the improvement in the system’s reliability is observed.
1.2. Motivation
The complexity of the electrical power system relies in its ability to tackle the unexpected load variations. These load variations are managed by the electrical distribution system (EDS) for continuous electrical power supply to the loads. This system is categorized into radial and loop structured distribution systems. The use of radial DS (RDS) is preferred in this study as it is simple, cheap, and mostly applicable to sparsely distributed loads. Furthermore, to meet the rapid growth in demand as well as to promote sustainability, integration of renewable energy source (RES) in the distribution system is desideratum. The RESs, including Wind Turbine Generator (WTG) and Solar photovoltaic (SPV), provide minimal electrical losses, improves system bus voltages, possesses less operation costs, and more significantly, it emits less CO emissions. Thus, the optimization of these parameters would ultimately improves the reliability of the EDS. Reliability in an electrical power system is defined as the ability to provide adequate, stable, and reliable power for a particular distribution system. Therefore, the study on Reliability Assessment (RA) and performance analysis of RDS considering the optimal RES siting and sizing is crucial. It is also observed that the integration of renewable sources in EDS has considerable impacts on systems’ operation and planning strategy []. Some issues co-related to RES integration are explained as follows.
- Electrical loss minimization using system reconfiguration [].
- Electrical loss minimization [,],
- Reduction in investment during system capacity enhancement [],
- Improvement in bus voltage [],
- Mitigation of greenhouse gases [],
- Improvement in voltage stability [],
- Improvement in system’s reliability by considering the reliability indices [,,],
- Enhancement in system security [],
- Facilitate system restoration [],
- Reduction in harmonic distortion [],
- Optimal load management strategy [].
The mentioned issues have been analyzed individually that is without considering the effect on another issue(s). The concept of analyzing the effect of the mentioned issues motivates the authors for carrying out this research work. In the view of strong motivation, this work is concentrated on the reliability assessment of IEEE 33 bus distribution system by considering the effect of electrical loss minimization through optimal siting and sizing of distributed generation system.
1.3. Contribution
The available literature focus on optimal siting and sizing of DGs obtaining a better power system performance. Also, the DG integration of SPV, WTG, and BSS in the distribution system has not been discussed as of authors knowledge. The system RA is discussed individually without analyzing the impact of optimal DG integration. Thus, the two indexes have been implemented for obtaining the optimal location(s) of DG(s) in the selected EDS. Then, a Constriction Factor (CF)-based PSO technique for optimal sizing(s) of DG(s) is presented. Simultaneously, all the parameters considered in this study (as given in Table 1) are not discussed in the existing literature and thus, this work provides completeness in contribution. According to the outcomes of the study, the results are found coherent with those obtained using other techniques that are available in the literature. However, the results can be claimed to be even better since the proposed approach considers all the parameters given in Table 1, including the ELM and the reliability aspects. The comparative analysis for a reduction in electrical power loss and voltage deviation is performed by integrating the WTG, SPV, and BSS in IEEE 33 bus EDS. The results obtained are compared with the results in the literature, as described in Table 2. After obtaining the reduced power loss and improved bus voltages, the reliability assessment is accomplished. The performance analysis is done for the selected distribution system and then the system’s RA is carried out with and without the integration of DGs.

Table 1.
Published work.

Table 2.
Work related to IEEE 33 bus with multiple DGs.
Though the research on DG siting and sizing is abundant in the literature, the RA in the EDS still prevails as an emerging area of research. Thus, the work mainly focuses on the reliability assessment of an IEEE 33 bus system is carried out in the view of loss minimization technique of WTG, SPV, and BSS integration. For the accomplishment of the mentioned tasks, the research work is performed according to the framed flowchart as shown in Figure 1. Furthermore, the following contributions are highlighted in this work.
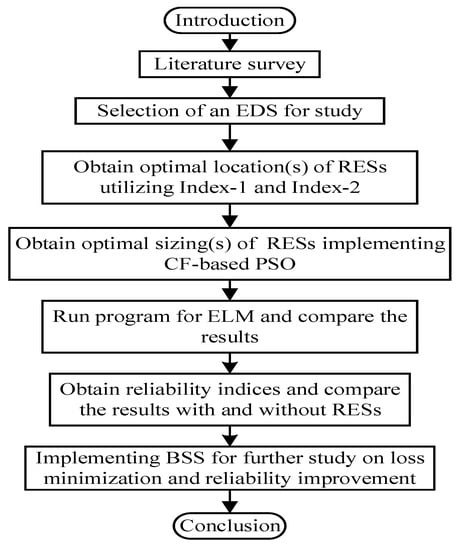
Figure 1.
Workflow of the research work.
- The optimal locations for SPV, WTG, and BSS is obtained by considering Index-1 and Index-2.
- Optimal sizes of SPV, WTG, and BSS are derived by employing CF-PSO technique.
- Distribution system performance, including minimization of loss and minimization of deviation in bus voltages, is analyzed with and without DGs.
- Comparison of CF-PSO technique with other nature-inspired optimization techniques for achieving a sound reliability assessment.
- A brief study is done on the inclusion of uncertainties in WTG and SPV reliability data such as failure rate () and time to repair (RT).
- Reliability assessment is done by evaluating the five indices namely EENS, AENS, SAIDI, SAIFI, and ASAI for Case 1, Case 2, and Case 3; where Case 1 is for integrating WTG only, Case 2 is for WTG+SPV, and Case 3 is for WTG+SPV+BSS (adding BSS optimally).
The work is further continued to accomplish the mentioned contributions as follows. The problem statement, objective function, and methodologies implemented, including Index-1, Index-2, and CF-based PSO techniques are delineated in Section 2. The basics of EDS reliability assessment is formulated and explained in Section 3. In Section 4, an overview of SPV, WTG, and BSS is explained using mathematical expressions. Furthermore, the results of several cases and scenarios are elucidated with supporting graphical depictions and tables in Section 5. Finally, the conclusions with future scopes are drawn in Section 6. The Appendix A of some important data and figure is provided at the end of the work.
1.4. Parameters Considered for the Study
The parameters considered for the study are described as follows.
- DG siting and DG sizing: The determination of bus voltages and the flow of powers is done by an Optimal Power Flow (OPF) method. The optimal siting of DGs is required for ELM during this power flow results. The performance of the power network is affected by an inappropriate location of DG. The IEEE 1547 standards for integration and operation of DG into EDSs are presented in [].
- Power loss: The occurrence of Active Power Loss (APL) is greater than Reactive Power Loss (RPL) in EDS. Hence, distribution companies should reduce these losses and this can be accomplished by means of reconfiguration of feeder, capacitor allocation, high voltage distribution system, grading of the conductor, DG placement, and many other methods.
- Bus voltage: It is expected to maintain bus voltages nearly 1 pu with an angle of . The power loss occurring in EDS during OPF creates a voltage drop at each bus of the system. Therefore, the DG integration technique is implemented for voltage profile (VP) improvement.
- DG type: The three DGs have been considered, which are categorized as WTG, SPV, and BSS. The classification of the several DG technologies is based on the generation of active power ‘P’ and reactive power ‘Q’, as illustrated in Figure 2.
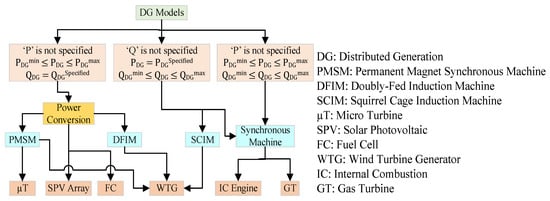 Figure 2. Models of several DG technologies.
Figure 2. Models of several DG technologies. - Reliability: The reliability indices considered for the distribution system reliability are as follows.
- -
- Expected Energy Not Supplied (EENS); MWh per year
- -
- Average Energy Not Supplied (AENS); MWh per customer per year
- -
- System Average Interruption Duration Index (SAIDI); hour per customer per year
- -
- System Average Interruption Frequency Index (SAIFI); failure per customer per year
- -
- Average System Availability Index (ASAI); pu
2. Problem Formulation, Objective Function (OF), and Methodology
The bus voltage and system reliability are the most affecting factors for the EDS when losses are considered. It becomes necessary to improve these two factors by implementing distributed generation (DG) into the EDS. DG siting is one of the favored techniques used in the EDS for the improvement of the system’s reliability and bus Voltage Profile (VP), including ELM. The DG location, DG size, DG power factor (pf), DG penetration, and DG type are required for the effective implementation of DGs in the EDS. Simultaneously, it is required to study the mathematical expressions, and modeling of related parameters and DGs integrated into the system. An overview of parameters considered for the ELM and mathematical modeling are elaborated in the upcoming subsections.
2.1. Optimal Location
Obtaining the optimal location of DGs is crucial part of EDS. To identify the optimal locations, two indexes are used. Index-1 is implemented only for placing the single DG and Index-2 is incorporated for placing more than one DGs in the EDS. Power loss is minimized by using Index-1 for placing 1DG (viz. Case 1). However, Index-2 provides minimum power loss for multiple DGs (viz. Case 2 and Case 3). These two indicators are represented by Equations (17) and (18), respectively [,]. It can be observed from the equation of Index-1 that the large index value depicts the weakest node of the system because the complex power injected at bus i is large. It implies that the single DG can be placed at this particular bus. On the other hand, Index-2 shows the voltage stability, which concludes that the reduced values of this index give the weakest bus of the EDS. Table 3 shows the values of both the indexes with corresponding five buses to arrange DG optimally in a given EDS. Therefore, DGs can be placed hierarchically at these buses.

Table 3.
Values of indexes with corresponding bus number [,].
In Figure 3, and are the magnitudes of the voltages at buses a and b, respectively. and are the phase angles of the voltages at buses a and b, respectively. and are the impedance and admittance of l-line, respectively. and are the resistance and reactance of a l-line. is the current in the l-line. The electrical power loss in the l-line is given by (1).
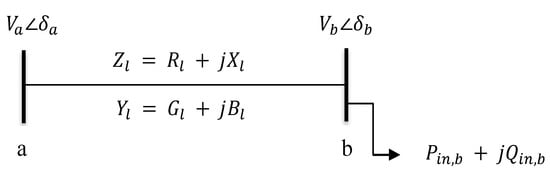
Figure 3.
General 2-bus system to formulate the line loss and load factor.
Then the bus voltage matrix is formed by using Equation (3) where [] is the network impedance matrix, [] is the bus injection matrix, and is the number of total buses in EDS.
By expanding Equation (3), the node voltages can be obtained by using Equations (4) and (5).
where i is 1,2,…,. , and are the element of impedance matrix that signify the row and column, row and column, and current injection at bus-i, respectively.
where and are active power and reactive power injected at bus-i, respectively. is the voltage at bus-i. Now, put (2) and (4) to (6) in (1) then the electrical loss of the line-l is derived as (7).
For an electrical system with number of branch/lines, the line loss is given by (8).
where is line loss, is apparent power injected at bus-i, l is 1 to .
where load factor (LF) is given by . is load factor of the line due to the bus injection (it is non-zero if line is in the path of bus else zero) as described in (11). For example, a 6-bus distribution is taken for explanation as shown in Figure 4 and a general branch loss formula is derived as (12).
where is branch/line loss matrix, is the load factor matrix, is complex power injection matrix. Equation (13) is reduced according to the Figure 4 where power injection at all the buses except the source bus are available.
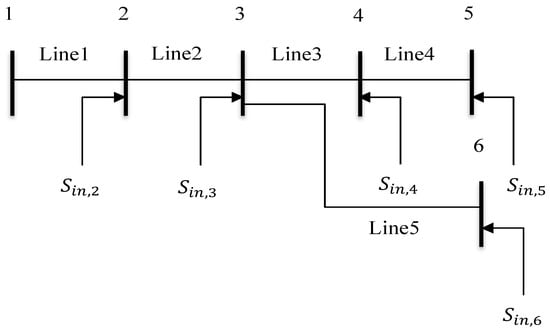
Figure 4.
6-bus EDS for Index-1 calculation.
The calculation of effective power injections is done as given in (16).
Equation (17) shows the final equation for the calculation of Index-1. The index is implemented for attaining the optimal position of one renewable energy source as DG. In Equation (15), || is fully dependent on LF values of all the branches (or lines) connected between bus and the source bus (main station). The closeness of the bus from the source bus can be observed in the as guided in Equation (10). If the bus is not near, the number of lines between bus and source bus is being plenty and the corresponding , , and parameters will account in the electrical loss component. Furthermore, if the node voltage is high, the value of will be small and vice-versa as observed in the derived equation. The equation of Index-1 is also accounted for the effective complex power supplied by the bus. The Index-1 will be high only when both the terms are high in (17). Thus, the value of Index-1 represents its main contribution in the total electrical loss and hence, in finding the optimal siting of one RES.
is the effective injection of complex power, which is the sum of injected powers from other buses connected to bus as shown in Figure 4.
where j is branch number, is sending bus voltage, and are the Active Power (AP) and Reactive Power (RP) at the receiving end bus, respectively. and are the resistance and reactance between sending and receiving end bus, respectively.
2.2. Power Balance
The AP and RP balance expressions are shown in Equations (19) and (20).
where = 0 and = 0 are the net AP and RP at i-bus, respectively. and represent DG AP and RP at i-bus, respectively. Active and reactive load demands are mentioned by and , respectively. is the bus voltage at j-bus, is the branch admittance between i, j-buses, and represent the phase angles of i-bus and j-bus voltages, respectively. (−) are the impedance angle of branch connected between i and j-buses.
2.3. Objective Function (OF)
In this research the OF is considered to be APL minimization in the EDS. The reliability indices are then evaluated by fixing the optimal location and size of the DGs. The OF of the problem is given in Equation (21).
2.3.1. Active Power Loss (APL)
The minimization of APL occurred in EDS is the OF considered. The primary aim of the OPF technique is to minimize the system APL as given as Equation (21).
where are the AP and RP at i and j-buses, respectively. = number of buses or nodes, and are defined as follows.
where , and , are the voltages and corresponding angles at and buses, respectively, = resistance of a branch between i and j-buses.
2.3.2. Reactive Power Loss (RPL)
The availability of RP ensures the AP transmission from source to load. Voltage stability margin or bus voltages are also dependent on this RP support. The RPL is obtained at different pf of DG using Equation (23).
where and are the RP generation and demand at the bus (including the slack bus), respectively. = RP demand at the bus.
2.3.3. Reliability Indices
The indices are assessed for divergent DG reliability data by fixing the site and size of DGs. Furthermore, the reliability improvement of distribution network has been accomplished by integrating one DG and multiple DGs in the EDS. Several reliability indices exist to observe the system’s reliability such as EENS, AENS, SAIDI, SAIFI, and ASAI which are also used in this study to analyze the reliability improvement. The indices of the network reliability are dependent function of failure rate () and repair time (RT) as given in Equation (24) [,,].
2.4. Constraints
The OF minimization is a primary task to obtain the optimal results. OF minimization is subjected to design the constraints so that the requirements of the EDS must be satisfied with DG operation. Thus, the constraints are discussed in the succeeding subsection [,].
2.4.1. Equality Constraints
These constraints follow the Kirchhoff’s current rule as the algebraic sum of powers in and powers out should be equal in an EDS [,]. Two of these constraints are described as follows.
where = AP generated by the generation units at bus, = AP demand at bus.
where = RP generated by the generation units at bus, = RP demand at bus.
2.4.2. Inequality Constraints
These constraints are associated with the limits applied to the system parameters for the operation of EDS. Some of these constraints are described as follows.
A. Power flow
To maintain the line capacity within limits, these constraints ensure the apparent power to be within limits at the ends of a line [,].
where = the highest permissible apparent powers () for lines i to j, = the actual transmitted from i to j.
B. DG capacity
These limits ensure the non-reversal of power flow. The power from the substation is provided to the EDS must be greater than the DG power. Also, the DG has the minimum and maximum power generation boundaries [].
where p = 1, 2,……, , (set to zero) and (from Equation (28)) are the lower and upper AP outputs of DG unit p, respectively. (set to zero) and (from Equation (29)) are the lower and upper RP outputs of DG unit p, respectively. = number of DGs present in the distribution network.
C. Bus voltage
The voltages at buses present in the EDS must be limited within minimum and maximum limits [,].
where and = the lower and upper boundaries of the bus voltage which are set to 95% and 105%, respectively.
D. Bus voltage
It refers as thermal capacity of the EDS lines. The current in the distribution lines must be within limits and should exceed the maximum current as given in Equation (33) [].
2.5. Constriction Factor-Based PSO (CF-PSO) Technique
PSO is a novel progression computational technique which is in the frame since 1995. The use of this method is seen in RP dispatch [], generation scheduling [], renewable source integrated power system [], and cost analysis []. In basic PSO method, the candidate solution is improved iteratively under any given constraint. The PSO algorithm is shown in Figure 5. Due to the reduction in computational time and requirement of less memory, PSO has overtaken many algorithms including the Genetic algorithm (GA) as PSO is mutation free. It searches the optimized value globally with the help of several particles present in a swarm based on specific constraints. As all particles have its local and global best values because of its own and global positions. This method updates the particle position and velocity as described in Equations (34) and (35).
where = particle velocity at iteration, W’ = particle inertial weight, = particle velocity at iteration, , = constants (0, 2.5), , = numbers generated randomly (0, 1), = the particle’s best position considering its own property, = the particle’s best position considering the whole population, , = particle position at and iterations, respectively. = constriction factor (CF) assures efficient convergence [,].
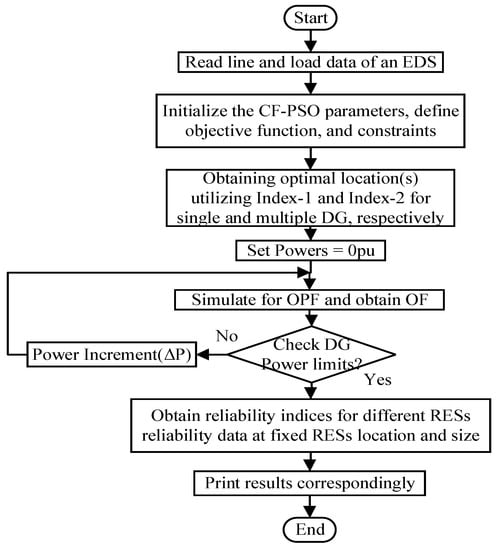
Figure 5.
Algorithm implemented for the research work.
Due to faster convergence to the global point, the basic PSO faces the difficulty of premature convergence. The particles have started oscillating around the optimal point without providing any type of restriction to the highest velocity of the particles available in swarm. Therefore, the optimal global solution is rare to obtain. The use of properly defined CF is briefly described for advance convergence of the PSO []. This can also be applied for the DG siting and DG size in the EDS. It reduces the computation time and requires little memory. Although this technique suffers from partial optimization, by altering its parameter during problem solving will produce an improved result [,,]. To obtain the improved result, a constriction factor (CF) is used and thus, the method is known as CF-based PSO technique. The parameters set for the CF-PSO are as follows. The values of initial weight, final weight, , , , , and CF are considered to be , , , , 0 to 1, 0 to 1, and , respectively. A flowchart is provided in Figure 5 to obtain the DG location, DG sizing and system reliability of the DGs in 33 bus EDS.
3. Reliability Assessment of Distribution System
The RA of an EDS is as important as contrasted to other components and parts of the EDS. The IEEE guide for EDS reliability is given by standard number 1366-2012 []. According to given standard, reliability of an EDS can be analyzed using some reliability indices. The reliability indices considered for EDS reliability assessment include EENS, AENS, SAIDI, SAIFI, and ASAI. These indices are mainly classified in two categories which are elaborated in Equations (39)–(46c).
3.1. Reliability Parameters at Load Point ‘p’
The reliability indices are the function of reliability parameters mentioned in Equations (36)–(38). The reliability parameters have been calculated at load point ’p’ as follows.
where = failure rate (average) of the element, n = number of elements in the EDS, = number of elements in the EDS, = duration of failure at load point due to failed element. The calculation equations of and are given in Appendix A.2.
3.2. System-Based Indices
These indices are further categorized in load-oriented indices and customer oriented indices as given in Equations (39)–(40) and Equations (41)–(46c), respectively.
3.2.1. Load-Oriented Indices
3.2.2. Customer Oriented Indices
These indices have allowed to enhance the EDS’s reliability related to the improvement of customer or load services. The two of the indices namely ECOST and IEAR are related to the cost reliability and thus, termed as reliability worth of the system.
where = expected interrupted cost at load point, = interrupted energy assessment rate at load point, = loss of expected energy, = system composite customer damage function ($ per kilowatt) as provided in Table A3 of Appendix A.
where CAIDI = Customer Average Interruption Duration Index.
Also, ASAI can be derived as follows.
where ASUI = Average Service Unavailability Index.
4. Modeling of WTG, SPV, and BSS
The reliability assessment of the IEEE 33 bus EDS is accomplished, considering the optimal siting(s) and sizing(s) of SPV, WTG, and BSS. In this regard, a brief modeling and specifications of these RESs are illustrated in Section 4.1, Section 4.2 and Section 4.3.
4.1. Wind Turbine Generator
The V162-5.6MW(IECS based on IEC IIB), a WTG, manufactured by General Electric Company is considered for its output power rating. The specifications of the WTG considered in this study are provided in Table 4. The mechanical power of WTG () is a function of generator rotor speed and wind speed as formulated in Equations (47)–(51) [].
where = air density, = area swept by the turbine rotor blades, = speed of the wind, is the non-linear function of the tip speed ratio () and pitch angle (), = generator rotor speed, GR = gear ratio, = rotor radius at the turbine blades, to and x are constants and computed in [].
where = output WTG power, = rated output WTG power, = rated wind speed.

Table 4.
Wind Turbine (V162-5.6 MW) specifications.
4.2. Solar Photovoltaic
The SPR-P5-545-UPP, a Solar PV Module, manufactured by Sunpower Company is considered for its output power rating. The specifications of the SPV module considered in this study are provided in Table 5. The SPV module is developed by implementing several cells. The power output for the SPV module can be derived as described by Equations (52)–(65) [,,].
where t = time instant, = AC output power, = maximum output power, = inverter efficiency, = fill factor actual, = short circuit current under operating conditions, = open circuit voltage under operating conditions, SR = solar radiation intensity (W/m), STC = standard test conditions, = temperature coefficient for current (A/C), = solar module temperature (C), = temperature coefficient for voltage (V/C), = fill factor ideal, = normalized series resistance of solar module, = normalized open circuit voltage, Q = an electron charge, N(≈1) = ideality factor, K = Boltzmann’s constant, = series resistance of SPV module, = ambient temperature of SPV module, = nominal operating cell temperature.

Table 5.
Bifacial Solar Panel (SPR-P5-545-UPP) specifications.
4.3. Battery Storage System
The BESS 3000, a Lithium-Ion Battery System, manufactured by Freqcon Company is considered for its output power rating. The specifications of the BSS considered in this study are provided in Table 6. The flowchart of BSS dispatch modeling is illustrated in Figure 6. Mathematical modeling is further defined. The BSS dispatch strategy starts functioning by monitoring the peak load hours. If the peak load is greater/less than the capacity of WTG and SPV, the BSS discharges/charges to support the distribution system; otherwise the BSS operates as a neutral device. Also, the BSS SOC will decide the charging or neutral operation during the off-peak hours. The battery model is derived with the help of Equations (66)–(68) assuming that no battery is self-discharging [].
where = DC charging/discharging power of the battery in Δt interval (W), = energy of battery (Wh), = AC power discharged/charged state of battery, = efficiency of the battery, = inverter power factor, = state of charge of the battery, = charging efficiency of the battery, = battery capacity (Ah), V = nominal voltage of the battery (V).

Table 6.
Battery Storage System (BESS 3000) specifications.
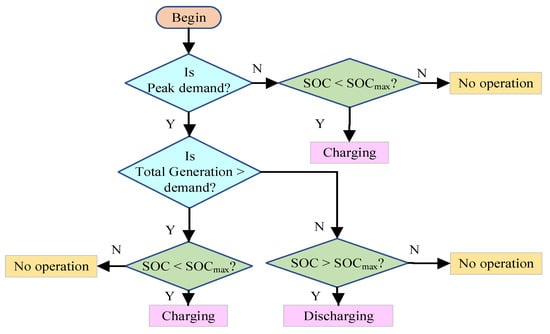
Figure 6.
General BSS dispatch strategy opted for battery operation.
5. Results and Discussion
The DG location, DG size, and EDS reliability are obtained and analyzed. The 33 bus EDS (Figure A1 of Appendix A.1) is considered in this study. The branch and load data for this EDS are adopted from []. It contains 33 buses and 32-branches with a total of 3.715 MW and 2.3 MVAr AP and RP loads, respectively. This EDS operates at 12.66 kV, 100 MVA base values. The APL and RPL for without DG case are obtained as 0.211009 MW and 0.143056 MVAr, respectively. The objective function (OF) minimization is done by implementing the CF-based PSO, as explained in Section 2. The following steps are followed to obtain the results.
- Step 1:
- Optimal siting(s) and sizing(s) of WTG, SPV, and BSS are evaluated considering electrical loss minimization (ELM). The technical ratings of WTG, SPV, and BSS have been illustrated in Table 4, Table 5 and Table 6, respectively. The BSS is assumed to be fully charged and produces its rated output power.
- Step 2:
- APL, RPL, and bus voltages are obtained by integrating WTG, WTG+SPV, and WTG+SPV+BSS (referred as Case 1, Case 2, and Case 3, respectively) in the EDS to analyze the results obtained in Step 1.
- Step 3:
- Reliability indices are estimated for EDS considering two different WTG and SPV reliability data, including and RT (for Scenario 1 to Scenario 6).
- Step 4:
- Furthermore, the reliability improvement is analyzed by adding BSS (considering 100% reliable) to the EDS in the presence of WTG and SPV. All related reliability data used are mentioned in Table A2 of the Appendix A.
5.1. DG Location and DG Rating
The bus number is obtained to allocate WTG, SPV, and BSS. The two indexes are implemented to obtain the locations as described in Section 2.1. It is observed from the analysis that Index-1 provides the location suitable for a single DG. This index examines the effective apparent power injection to the buses. The Load Factor value of line depends on whether the is in the path of the bus to the source node or not. The multiplication of Load Factor and injected apparent power provides the APL and RPL of line due to the bus injection. Thus, the maximum value of Index-1 at bus indicates the candidate bus to place one DG. The first six values of this index for respective buses are provided in Table 3.
The optimal siting for several DGs are found by implementing the Index-2. This index provides the hierarchy of weak buses in the EDS. It shows the sensitivity of the bus towards voltage collapse. The value of Index-2 must be greater than or equals to zero for ensuring the stable operation of the distribution system. The minimum value of this index depicts more sensitivity to the voltage collapse and thus, referred to as the weak bus. The optimal location(s) and size(s) of WTG, SPV, and BSS for three cases are obtained and reproduced in Table 7. The DGs are accommodated according to the locations obtained from the indexes, as mentioned in Section 2.1. The DG size and minimum APL are then evaluated, implementing CF-PSO as described in Section 2.

Table 7.
DG location and DG size obtained.
5.2. APL, RPL, and Bus Voltages
The accommodation of DG at an optimal location with optimal size reflects in VP improvement and minimization of APL and RPL. Most of the research has concentrated on APL minimization because of the dominance of losses in the EDS. In contrast, the RPL minimization for overall voltage improvement of all the 32 buses of the EDS has also been observed. The estimation of APL, RPL, and VP is considered before analyzing the system’s reliability. This is done to analyze the system’s reliability with the optimal DG size, DG location, minimum power loss, and better VP.
Several kinds of research are performed to obtain APL minimization, which is cited in Table 2 for single and multiple DGs, respectively. It is observed from Table 2 that the authors of the mentioned literature have not dealt with the cases considering various DGs combination. Therefore, it is vital to observe that the results obtained considering several types of DGs are compared with the conventional DGs []. The output results obtained for the APL are tabulated in Table 8. This table shows that the APL value is better for Case 1, and comparable for Case 2 and Case 3. The slight variations in APL for Case 2 and Case 3 are observed because the authors have considered the pf of WTG only. Furthermore, the bus voltage profile with one DG and multiple DGs is drawn in Figure 7. The voltages at all the buses vary according to the real power loss and reactive power loss in the distribution system. Therefore, the system requires real power support for active power loss minimization, which improves the bus voltages by compensating the losses. Furthermore, it is concluded from Table 8 that the active power loss minimization is not reduced significantly for Case 3 as compared to Case 2. Thus, there is a marginal improvement in bus voltage profile for Case 3 as compared to Case 2, which is depicted in Figure 7. Also, the improvement in bus voltages is observed when multiple DGs are placed. This VP is further improved at 0.85 and 0.82 pfs. This is because of increment in reactive power support at system buses. It is the point of interest to know about the two voltage peaks when the system is operated with single DG. The two voltage peaks appear at bus number 7 and 26 because these buses are directly connected to bus 6, at which single DG is placed optimally. Also, the size of the single DG is greater than the sum of the size of two DG and slightly lesser than the sum of the size of three DG, as obtained in Table 8. A comparison between present work and the best available method is made for ELM. Simultaneously, from Table 9 it can be inferred that the minimum bus voltage is improved and RPL is minimized with the implementation of multiple DGs at different pfs as illustrated. The graphical representation of APL and RPL for without DG, one DG, and multiple DGs are represented in Figure 8.

Table 8.
APL (MW) obtained considering WTG power factor.
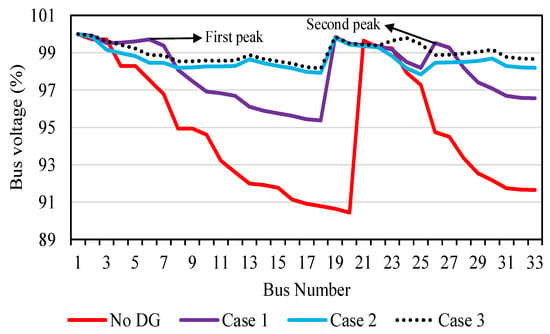
Figure 7.
Voltage profile for 33 bus system (WTG at 0.9 pf).

Table 9.
Minimum voltage, DG location, and RPL (MVAr) obtained.
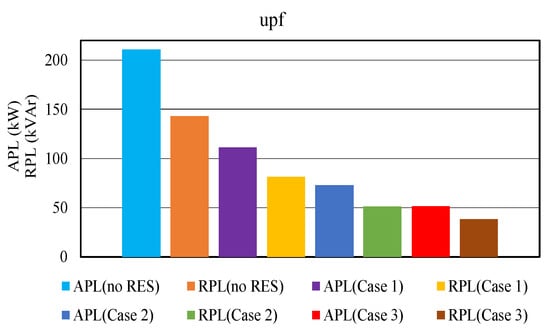
Figure 8.
Active and Reactive power losses (WTG at UPF).
5.3. Reliability Assessment
The indices obtained show the improvement in the system’s reliability. The indices are calculated for two different reliability data of DGs. It is observed that the indices are dependent on two reliability data, namely and RT of the system’s elements. The present work has considered different reliability data for DG only. The best reliability improvement is observed for 0.2 of and 12 h of RT. A detailed description of the DG reliability data effect on indices is given as per the following Scenarios.
- Scenario 1: 0.2 f/yr and 12 h (as provided in Table A2 of Appendix A.2)
- Scenario 2: 0.4 f/yr and 12 h
- Scenario 3: 0.6 f/yr and 12 h
- Scenario 4: 0.2 f/yr and 24 h
- Scenario 5: 0.2 f/yr and 48 h
- Scenario 6: No failure
Scenarios 1, 2, and 3 are considered by fixing the RT and varying . The appropriate case from the first three cases is then considered for variable RT to extract the best case from the top Five Scenarios. The values of these reliability data are fed manually in the optimization technique to get the values of indices for the system’s reliability improvement. Furthermore, the following key assumptions are considered to assess the reliability of the EDS.
- Circuit breakers, distribution lines, and potential transformers are available throughout with 100% reliability.
- The and RT of DG, Buses, feeders, and substations are given in Table A2.
- RT for each distribution branch = 10 h.
5.3.1. Effect on Load-Oriented Indices
The EENS and AENS are obtained and tabulated in Table 10 and Table 11 for all cases as illustrated in Figure 9a–d, respectively. It is important to note that the EENS and AENS decrease with the number of DGs, and these are also decreased with decreasing values of and RT. As the increasing number of DGs are integrated into an EDS, the supplied energy is improved in the EDS, and thus, the indices related to the energy not supplied are reduced. This reduction is more while integrating the DGs with lesser and RT values. The reducing EENS and AENS are desirable, and thus, the EDS reliability enhances with the integration of DGs with appropriate reliability data values.

Table 10.
EENS (MWh per year) evaluated for different Scenarios.

Table 11.
AENS (MWh per customer per year) evaluated for different Scenarios.
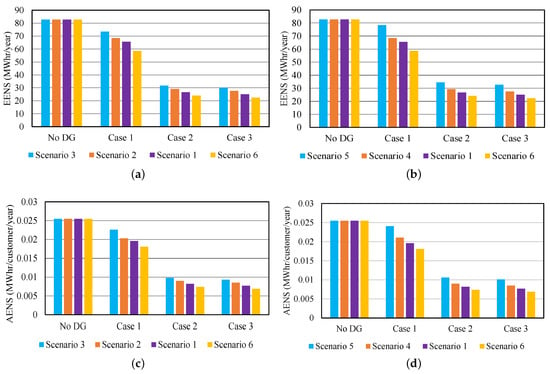
Figure 9.
Load-oriented indices for different DG reliability data (a) EENS at different , (b) EENS at different RT, (c) AENS at different , and (d) AENS at different RT.
5.3.2. Effect on System-Oriented Indices
The SAIDI, and SAIFI are obtained and tabulated in Table 12 and Table 13 for all cases considering all scenarios as shown in Figure 10a–d, respectively. The important point to be noted here that the SAIDI, and SAIFI, decreases with the increasing number of DGs; SAIDI is also decreased with the decreasing values of and RT. It is worthy to note that the SAIFI is not affected by the RT of the DG. It is because this index is independent of RT as shown in Equation (43). As the increasing number of DGs are incorporated into the EDS, the duration of the interruption and the number of interruptions occurred are reduced in the system. Thus, the SAIDI, and SAIFI are reduced. Customer Average Interruption Duration Index can be determined using the ratio of SAIDI, and SAIFI as shown in Equation (45). The reduction in the value of indices is more while integrating the DGs with lesser and RT values. Moreover, reducing SAIDI and SAIFI are desirable for EDS reliability enhancement.

Table 12.
SAIDI (hour per customer per year) evaluated for different Scenarios.

Table 13.
SAIFI (failure per customer per year) evaluated for different Scenarios.
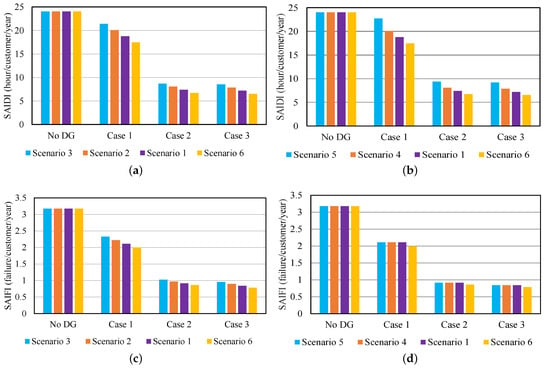
Figure 10.
System-oriented indices for different DG reliability data (a) SAIDI at different , (b) SAIDI at different RT, (c) SAIFI at different , and (d) SAIFI at different RT.
The ASAI is determined and tabulated in Table 14 for all cases considering six scenarios as illustrated in Figure 11a,b. The electrical power service availability for all loads increases with the integration of multiple DGs. This index is further increased when DGs have a lower and RT values. The increment in ASAI increases leads to the decrement in ASUI as given in Equations (46a) and (46c) which is desirable for the EDS reliability improvement.

Table 14.
ASAI (pu) evaluated for different Scenarios.
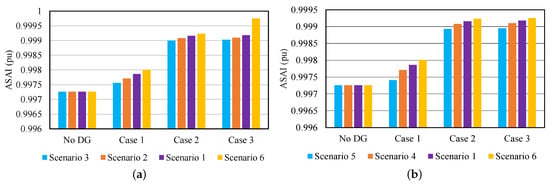
Figure 11.
System-oriented indices for different DG reliability data (a) ASAI at different , (b) ASAI at different RT.
6. Conclusions and Scope for Future Work
The optimal location(s) and size(s) of distributed generations derived for three cases ensure an enhancement in the electrical loss minimization and also, improves the bus voltage profile when compared to a system without distributed generations. While analyzing all the cases, it is observed that Case 3 has provided the best result. It was observed that the APL value is reduced at UPF by 0.00003 MW, 0.014472 MW, and 0.021307 MW for Case 1, Case 2, and Case 3, respectively when compared to []. The minimum value of bus voltage is improved by 6.42% for Case 3 at UPF when compared to No DG Case. The bus voltage profile was further improved at 0.85 and 0.82 power factors by 7.71% and 7.78%, respectively. After achieving the acceptable results, the reliability analysis is performed for the distributed generation integrated distribution system. It is concluded that the combination of Case 3 with Scenario 6 provides the best system’s reliability results. However, Scenario 6 being an ideal one, Case 3 with Scenario 1 is considered to yield better results for the improvement in the system’s reliability. This research analysis can be extended in the future for a greater number of standard distribution systems considering the following aspects.
- Reliability assessment of larger EDS.
- Inclusion of reliability data of subsystems.
- System reconfiguration.
- Considering CO emission.
- Economical aspects related to the system’s reliability, including net present value, Levelized cost of energy, and many other aspects.
- Security.
The future aspects can be dealt with large radial distribution systems, including IEEE 69 and 118 bus systems. Inclusion of reliability data in terms of electrical, mechanical, and structural subsystems which would be favorable in obtaining accurate reliability of the system. Distribution system reliability improvement can also be achieved by adjusting the number of branches which is termed as a system reconfiguration technique. Furthermore, the dependency of reliability analysis on CO emission, economics, system protection, and system security can also be considered for further research works.
Author Contributions
Conceptualization, Methodology, and Draft writing: S.K.; Software Implementation and Review: K.S.; Mathematical formulations: A.S.S.V.; Investigation, Results validation, and Data curation: R.M.E.; Supervision, Results validation, and Review: R.K.S.; Review and Editing: N.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors wholeheartedly thank the Department of Electrical Engineering, Indian Institute of Technology (Banaras Hindu University), Varanasi for providing the laboratory facilities and technical support to accomplish the research work promptly. The first author expresses his gratitude towards Govind Ballabh Pant Institute of Engineering and Technology, Pauri Garhwal, Uttarakhand, India for allowing him to pursue PhD from IIT(BHU) Varanasi, Uttar Pradesh, India.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
This work has used the following abbreviations:
| AENS | Average Energy Not Supplied (MWh per customer per year) |
| APL | Active Power Loss (MW) |
| ASAI | Average Service Availability Index (pu) |
| BSS | Battery Storage System |
| CF-PSO | Constriction Factor-based Particle Swarm Optimization |
| DG | Distributed Generation |
| DGen | Diesel Generator |
| EDS | Electrical Distribution System |
| EENS | Expected Energy Not Supplied (MWh per year) |
| EIR | Energy index of reliability (pu) |
| ELM | Electrical Loss Minimization |
| ENS | Energy Not Supplied (MWh) |
| GA | Genetic Algorithm |
| GE | General Electric |
| IEEE | Institution of Electrical and Electronics Engineers |
| LOLE | Loss of Load Expectation (hour) |
| LOLP | Loss of Load Probability (pu) |
| MOGA | Multi-objective Genetic Algorithm |
| MW | Megawatt |
| OPF | Optimal Power Flow |
| pf | Power Factor (pu) |
| RA | Reliability Assessment |
| RDS | Radial Distribution System |
| RES | Renewable Energy Source |
| RPL | Reactive Power Loss (MW) |
| SAIDI | System Average Interruption Duration Interruption (hour per customer per year) |
| SAIFI | System Average Interruption Frequency Interruption (failure per customer per year) |
| SPR | Surface Plasmon Resonance |
| SPV | Solar photovoltaic |
| WTG | Wind Turbine Generator |
| VP | Voltage Profile |
Appendix A
Appendix A.1
The IEEE 33 bus EDS as shown in Figure A1 has been selected for analysis. As mentioned in Section 5, it is inferred that the 33-bus distribution system is analyzed for obtaining the locations and sizes. The branch and load data have been taken from [].
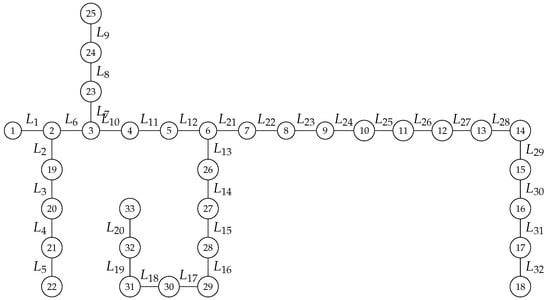
Figure A1.
The IEEE 33 bus EDS.
Appendix A.2

Table A1.
Load distribution for 33 bus [].
Table A1.
Load distribution for 33 bus [].
| Type of Load | |||||
|---|---|---|---|---|---|
| Bus Number (or Load Point) | Number of Loads | Mixed | Same Type of Loads | ||
| 2–5 | 148 | Industrial (I) | C | I | R |
| 6–9 | 10 | Commercial (C) | “ | “ | “ |
| 11, 12 | 132 | “ | “ | “ | “ |
| 13–15 | 110 | Residential (R) | “ | “ | “ |
| 16 | 2 | “ | “ | “ | “ |
| 17–20 | 118 | “ | “ | “ | “ |
| 21–26 | 126 | “ | “ | “ | “ |
| 27–31 | 108 | “ | “ | “ | “ |
| 32, 33 | 58 | “ | “ | “ | “ |

Table A2.
Reliability data for 33 bus [].
Table A2.
Reliability data for 33 bus [].
| Reliability Data for All Loads, Feeders, etc. | ||
|---|---|---|
| Bus, Feeder, etc. | (f/yr) | RT (h) |
| Load@4 | 0.321 | 11.04 |
| Load@(5, 7–12, 29, | 0.301 | 11.44 |
| 30, 14, 16, 18–22, 25–28) | ||
| Load@(13, 15) | 0.314 | 11.17 |
| Load@(17, 23, 24) | 0.208 | 1.75 |
| Load@(31–33) | 0.327 | 10.96 |
| substation | 0.1 | 5 |
| feeder (2, 3, 6) | 0.2 | 3 |
| DG | 0.2 | 12 |
From Table A2, average failure rate, and unavailability can be determined as given in Equations (A1) and (A2). The system reliability indices are thus evaluated for all six scenarios using the values of and .

Table A3.
Cost per kilowatt for Reliability worth estimation [].
Table A3.
Cost per kilowatt for Reliability worth estimation [].
| Type of Load | Interruption Duration (minutes) | Cost ($/kW) |
|---|---|---|
| 1 | 0.38 | |
| 20 | 2.97 | |
| Commercial | 60 | 8.55 |
| 240 | 31.32 | |
| 480 | 83.01 | |
| 1 | 1.63 | |
| 20 | 3.87 | |
| Industrial | 60 | 9.09 |
| 240 | 25.16 | |
| 480 | 55.81 | |
| 1 | 0 | |
| 20 | 0.09 | |
| Residential | 60 | 0.48 |
| 240 | 4.91 | |
| 480 | 15.69 |
References
- Raju, K.; Madurai Elavarasan, R.; Mihet-Popa, L. An Assessment of Onshore and Offshore Wind Energy Potential in India Using Moth Flame Optimization. Energies 2020, 13, 3063. [Google Scholar]
- Elavarasan, R.M. The motivation for renewable energy and its comparison with other energy sources: A review. Eur. J. Sustain. Dev. Res. 2019, 3, em0076. [Google Scholar] [CrossRef]
- Kumar, N.M.; Chopra, S.S.; Chand, A.A.; Elavarasan, R.M.; Shafiullah, G. Hybrid renewable energy microgrid for a residential community: A techno-economic and environmental perspective in the context of the SDG7. Sustainability 2020, 12, 3944. [Google Scholar] [CrossRef]
- Elavarasan, R.M.; Shafiullah, G.; Padmanaban, S.; Kumar, N.M.; Annam, A.; Vetrichelvan, A.M.; Mihet-Popa, L.; Holm-Nielsen, J.B. A comprehensive review on renewable energy development, Challenges, and policies of leading Indian states with an international perspective. IEEE Access 2020, 8, 74432–74457. [Google Scholar] [CrossRef]
- Elavarasan, R.M.; Shafiullah, G.; Manoj Kumar, N.; Padmanaban, S. A State-of-the-Art review on the drive of renewables in Gujarat, State of India: Present situation, barriers and future initiatives. Energies 2020, 13, 40. [Google Scholar] [CrossRef]
- Madurai Elavarasan, R.; Selvamanohar, L.; Raju, K.; Vijayaraghavan, R.R.; Subburaj, R.; Nurunnabi, M.; Khan, I.A.; Afridhis, S.; Hariharan, A.; Pugazhendhi, R. A Holistic Review of the Present and Future Drivers of the Renewable Energy Mix in Maharashtra, State of India. Sustainability 2020, 12, 6596. [Google Scholar] [CrossRef]
- Tan, X.; Li, Q.; Wang, H. Advances and trends of energy storage technology in microgrid. Int. J. Electr. Power Energy Syst. 2013, 44, 179–191. [Google Scholar] [CrossRef]
- Elavarasan, R.M.; Afridhis, S.; Vijayaraghavan, R.R.; Subramaniam, U.; Nurunnabi, M. SWOT analysis: A framework for comprehensive evaluation of drivers and barriers for renewable energy development in significant countries. Energy Rep. 2020, 6, 1838–1864. [Google Scholar]
- Elavarasan, R.M. Comprehensive review on India’s growth in renewable energy technologies in comparison with other prominent renewable energy based countries. J. Sol. Energy Eng. 2020, 142, 030801. [Google Scholar] [CrossRef]
- Sharma, S.; Bhattacharjee, S.; Bhattacharya, A. Grey wolf optimisation for optimal sizing of battery energy storage device to minimise operation cost of microgrid. IET Gener. Transm. Distrib. 2016, 10, 625–637. [Google Scholar] [CrossRef]
- Energy Storage System: Roadmap for India 2019–32. 2019. Available online: http://www.indiasmartgrid.org/reports/ISGF_Report_Energy_Storage_System_RoadmapforIndia_2019to2032_11July2019_Draft.pdf (accessed on 29 September 2020).
- Hassan, T.; Abbassi, R.; Jerbi, H.; Mehmood, K.; Tahir, M.F.; Cheema, K.M.; Elavarasan, R.M.; Ali, F.; Khan, I.A. A Novel Algorithm for MPPT of an Isolated PV System Using Push Pull Converter with Fuzzy Logic Controller. Energies 2020, 13, 4007. [Google Scholar] [CrossRef]
- Ebrahimi, H.; Marjani, S.R.; Talavat, V. Optimal planning in active distribution networks considering nonlinear loads using the MOPSO algorithm in the TOPSIS framework. Int. Trans. Electr. Energy Syst. 2020, 30, e12244. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Y.; Da, C.; Huang, Z.; Wang, M. Optimal allocation of distributed generation and electric vehicle charging stations based on intelligent algorithm and bi-level programming. Int. Trans. Electr. Energy Syst. 2020, 30, e12366. [Google Scholar] [CrossRef]
- da Silva Seta, F.; de Oliveira, L.W.; de Oliveira, E.J. Comprehensive approach for distribution system planning with uncertainties. IET Gener. Transm. Distrib. 2019, 13, 5467–5477. [Google Scholar] [CrossRef]
- Ahmadi, M.; Lotfy, M.E.; Howlader, A.M.; Yona, A.; Senjyu, T. Centralised multi-objective integration of wind farm and battery energy storage system in real-distribution network considering environmental, technical and economic perspective. IET Gener. Transm. Distrib. 2019, 13, 5207–5217. [Google Scholar] [CrossRef]
- Deb, G.; Chakraborty, K.; Deb, S. Spider monkey optimization technique–based allocation of distributed generation for demand side management. Int. Trans. Electr. Energy Syst. 2019, 29, e12009. [Google Scholar] [CrossRef]
- Dehnavi, E.; Aminifar, F.; Afsharnia, S. Congestion management through distributed generations and energy storage systems. Int. Trans. Electr. Energy Syst. 2019, 29, e12018. [Google Scholar] [CrossRef]
- Chedid, R.; Sawwas, A. Optimal placement and sizing of photovoltaics and battery storage in distribution networks. Energy Storage 2019, 1, e46. [Google Scholar] [CrossRef]
- Babu, K.B.; Maheswarapu, S. A solution to multi-objective optimal accommodation of distributed generation problem of power distribution networks: An analytical approach. Int. Trans. Electr. Energy Syst. 2019, 29. [Google Scholar] [CrossRef]
- Hesaroor, K.; Das, D. Annual energy loss reduction of distribution network through reconfiguration and renewable energy sources. Int. Trans. Electr. Energy Syst. 2019, 29, e12099. [Google Scholar] [CrossRef]
- BiazarGhadikolaei, M.; Shahabi, M.; Barforoushi, T. Expansion planning of energy storages in microgrid under uncertainties and demand response. Int. Trans. Electr. Energy Syst. 2019, 29, e12110. [Google Scholar] [CrossRef]
- Amir, V.; Azimian, M.; Razavizadeh, A.S. Reliability-constrained optimal design of multicarrier microgrid. Int. Trans. Electr. Energy Syst. 2019, 29, e12131. [Google Scholar] [CrossRef]
- RaguRaman, L.; Ravindran, M. MFLRS-RDF technique for optimal sizing and performance analysis of HRES. Int. J. Numer. Model. Electr. Netw. Devices Fields 2020, 33, e2675. [Google Scholar] [CrossRef]
- Gholami, M.; Zakariazadeh, A. Olympic ranking–based allocation of distributed generation units in distribution networks. Int. Trans. Electr. Energy Syst. 2020, 30, e12220. [Google Scholar] [CrossRef]
- Muhammad, M.A.; Mokhlis, H.; Amin, A.; Naidu, K.; Franco, J.F.; Wang, L.; Othman, M. Enhancement of simultaneous network reconfiguration and DG sizing via Hamming dataset approach and firefly algorithm. IET Gener. Transm. Distrib. 2019, 13, 5071–5082. [Google Scholar] [CrossRef]
- Manna, D.; Goswami, S.K. Optimum placement of distributed generation considering economics as well as operational issues. Int. Trans. Electr. Energy Syst. 2020, 30, e12246. [Google Scholar] [CrossRef]
- Pandey, A.K.; Kirmani, S. Optimal location and sizing of hybrid system by analytical crow search optimization algorithm. Int. Trans. Electr. Energy Syst. 2020, 30, e12327. [Google Scholar] [CrossRef]
- Kiani, A.T.; Nadeem, M.F.; Ahmed, A.; Khan, I.; Elavarasan, R.M.; Das, N. Optimal PV Parameter Estimation via Double Exponential Function-Based Dynamic Inertia Weight Particle Swarm Optimization. Energies 2020, 13, 4037. [Google Scholar] [CrossRef]
- Kumar, S.; Saket, R.; Dheer, D.K.; Holm-Nielsen, J.; Sanjeevikumar, P. Reliability enhancement of electrical power system including impacts of renewable energy sources: A comprehensive review. IET Gener. Transm. Distrib. 2020, 14, 1799–1815. [Google Scholar] [CrossRef]
- Samrout, M.; Yalaoui, F.; Châtelet, E.; Chebbo, N. New methods to minimize the preventive maintenance cost of series–parallel systems using ant colony optimization. Reliab. Eng. Syst. Saf. 2005, 89, 346–354. [Google Scholar] [CrossRef]
- Shahzad, M.; Ahmad, I.; Gawlik, W.; Palensky, P. Load concentration factor based analytical method for optimal placement of multiple distribution generators for loss minimization and voltage profile improvement. Energies 2016, 9, 287. [Google Scholar] [CrossRef]
- Parihar, S.S.; Malik, N. Optimal allocation of renewable DGs in a radial distribution system based on new voltage stability index. Int. Trans. Electr. Energy Syst. 2020, 30, e12295. [Google Scholar] [CrossRef]
- Hassan, A.A.; Fahmy, F.H.; Nafeh, A.E.S.A.; Abu-elmagd, M.A. Hybrid genetic multi objective/fuzzy algorithm for optimal sizing and allocation of renewable DG systems. Int. Trans. Electr. Energy Syst. 2016, 26, 2588–2617. [Google Scholar] [CrossRef]
- Atteya, I.I.; Ashour, H.; Fahmi, N.; Strickland, D. Radial distribution network reconfiguration for power losses reduction using a modified particle swarm optimisation. CIRED Open Access Proc. J. 2017, 2017, 2505–2508. [Google Scholar] [CrossRef]
- Wazir, A.; Arbab, N. Analysis and optimization of IEEE 33 bus radial distributed system using optimization algorithm. JETAE J. Emerg. Trends Appl. Eng. 2016, 1, 2518–4059. [Google Scholar]
- Paliwal, N.K.; Singh, A.K.; Singh, N.K.; Kumar, P. Optimal sizing and operation of battery storage for economic operation of hybrid power system using artificial bee colony algorithm. Int. Trans. Electr. Energy Syst. 2019, 29, e2685. [Google Scholar] [CrossRef]
- Saric, M.; Hivziefendic, J.; Konjic, T.; Ktena, A. Distributed generation allocation considering uncertainties. Int. Trans. Electr. Energy Syst. 2018, 28, e2585. [Google Scholar] [CrossRef]
- Baran, M.; Wu, F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- Chong, B.; Zhang, X.; Godfrey, K.; Yao, L.; Bazargan, M. Optimal location of unified power flow controller for congestion management. Eur. Trans. Electr. Power 2010, 20, 600–610. [Google Scholar] [CrossRef]
- Aghajani, A.; Kazemzadeh, R.; Ebrahimi, A. Optimal energy storage sizing and offering strategy for the presence of wind power plant with energy storage in the electricity market. Int. Trans. Electr. Energy Syst. 2018, 28, e2621. [Google Scholar] [CrossRef]
- Charfi, S.; Atieh, A.; Chaabene, M. Optimal sizing of a hybrid solar energy system using particle swarm optimization algorithm based on cost and pollution criteria. Environ. Prog. Sustain. Energy 2019, 38, e13055. [Google Scholar] [CrossRef]
- Wu, C.; Lou, Y.; Lou, P.; Xiao, H. DG location and capacity optimization considering several objectives with cloud theory adapted GA. Int. Trans. Electr. Energy Syst. 2014, 24, 1076–1088. [Google Scholar] [CrossRef]
- Duong, M.Q.; Pham, T.D.; Nguyen, T.T.; Doan, A.T.; Tran, H.V. Determination of optimal location and sizing of solar photovoltaic distribution generation units in radial distribution systems. Energies 2019, 12, 174. [Google Scholar] [CrossRef]
- Madurai Elavarasan, R.; Ghosh, A.; K Mallick, T.; Krishnamurthy, A.; Saravanan, M. Investigations on performance enhancement measures of the bidirectional converter in PV–wind interconnected microgrid system. Energies 2019, 12, 2672. [Google Scholar] [CrossRef]
- Natarajan, M.; Ramadoss, B.; Lakshmanarao, L. Optimal location and sizing of MW and MVAR based DG units to improve voltage stability margin in distribution system using a chaotic artificial bee colony algorithm. Int. Trans. Electr. Energy Syst. 2017, 27, e2287. [Google Scholar] [CrossRef]
- Nawaz, S.; Bansal, A.K.; Sharma, M.P. Allocation of DG and capacitor units for power loss reduction in radial distribution system. In Proceedings of the 2016 International Conference on Recent Advances and Innovations in Engineering (ICRAIE), Jaipur, India, 23–25 December 2016; pp. 1–6. [Google Scholar]
- Vita, V. Development of a decision-making algorithm for the optimum size and placement of distributed generation units in distribution networks. Energies 2017, 10, 1433. [Google Scholar] [CrossRef]
- Basso, T. IEEE 1547 and 2030 Standards for Distributed Energy Resources Interconnection and Interoperability with the Electricity Grid; Technical report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2014. [Google Scholar]
- Huang, W.; Zhang, N.; Yang, J.; Wang, Y.; Kang, C. Optimal configuration planning of multi-energy systems considering distributed renewable energy. IEEE Trans. Smart Grid 2017, 10, 1452–1464. [Google Scholar] [CrossRef]
- Bahramirad, S.; Daneshi, H. Optimal Sizing of Smart Grid Storage Management System in a Microgrid. In Proceedings of the 2012 IEEE PES Innovative Smart Grid Technologies, ISGT 2012, Washington DC, USA, 16–20 January 2012; pp. 1–6. [Google Scholar]
- Kumar, D.; Samantaray, S.; Kamwa, I.; Sahoo, N. Reliability-constrained based optimal placement and sizing of multiple distributed generators in power distribution network using cat swarm optimization. Electr. Power Compon. Syst. 2014, 42, 149–164. [Google Scholar] [CrossRef]
- Soliman, S.A.H.; Mantawy, A.A.H. Modern Optimization Techniques with Applications in Electric Power Systems; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- Bhumkittipich, K.; Phuangpornpitak, W. Optimal placement and sizing of distributed generation for power loss reduction using particle swarm optimization. Energy Procedia 2013, 34, 307–317. [Google Scholar] [CrossRef]
- Aman, M.; Jasmon, G.; Mokhlis, H.; Bakar, A. Optimal placement and sizing of a DG based on a new power stability index and line losses. Int. Trans. Electr. Energy Syst. 2012, 43, 1296–1304. [Google Scholar] [CrossRef]
- Shukla, T.; Singh, S.; Srinivasarao, V.; Naik, K. Optimal sizing of distributed generation placed on radial distribution systems. Electr. Power Compon. Syst. 2010, 38, 260–274. [Google Scholar] [CrossRef]
- Abdel-Aal, H.; Bassyouni, M.; Abdelkreem, M.; Abdel-Hamid, S.; Zohdy, K. Feasibility Study for a Solar-Energy Stand-Alone System:(SESAS). Smart Grid Renew. Energy 2012, 3, 204. [Google Scholar] [CrossRef][Green Version]
- Hamouda, Y.A. Wind energy in Egypt: Economic feasibility for Cairo. Renew. Sustain. Energy Rev. 2012, 16, 3312–3319. [Google Scholar] [CrossRef]
- Zhao, B.; Guo, C.; Cao, Y. A multiagent-based particle swarm optimization approach for optimal reactive power dispatch. IEEE Trans. Power Syst. 2005, 20, 1070–1078. [Google Scholar] [CrossRef]
- Kusiak, A.; Zhang, Z.; Xu, G. Minimization of wind farm operational cost based on data-driven models. IEEE Trans. Sustain. Energy 2013, 4, 756–764. [Google Scholar] [CrossRef]
- Wang, L.; Singh, C. Multicriteria design of hybrid power generation systems based on a modified particle swarm optimization algorithm. IEEE Trans. Energy Convers. 2009, 24, 163–172. [Google Scholar] [CrossRef]
- Ramezani, M.; Haghifam, M.R.; Singh, C.; Seifi, H.; Moghaddam, M.P. Determination of capacity benefit margin in multiarea power systems using particle swarm optimization. IEEE Trans. Power Syst. 2008, 24, 631–641. [Google Scholar] [CrossRef]
- Yang, H.; Xie, K.; Tai, H.M.; Chai, Y. Wind farm layout optimization and its application to power system reliability analysis. IEEE Trans. Power Syst. 2015, 31, 2135–2143. [Google Scholar] [CrossRef]
- Sunil Joseph, P.; DineshBalaji, C. Transmission loss minimization using optimization technique Based on PSO. 2011 IEEE Symp. Ind. Electron. Appl. 2013, 1, 1–5. [Google Scholar] [CrossRef]
- Clerc, M.; Kennedy, J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- El-Zonkoly, A. Optimal placement of multi-distributed generation units including different load models using particle swarm optimisation. IET Gener. Transm. Distrib. 2011, 5, 760–771. [Google Scholar] [CrossRef]
- Kansal, S.; Kumar, V.; Tyagi, B. Optimal placement of different type of DG sources in distribution networks. Int. J. Electr. Power Energy Syst. 2013, 53, 752–760. [Google Scholar] [CrossRef]
- Kansal, S.; Sai, B.; Tyagi, B.; Kumar, V. Optimal placement of distributed generation in distribution networks. Int. J. Eng. Sci. Technol. 2011, 3, 47–55. [Google Scholar] [CrossRef]
- Subcommittee, D. IEEE Guide for Electric Power Distribution Reliability Indices. Distribution 2012, 1997, 1–43. [Google Scholar]
- Heier, S. Grid Integration of Wind Energy: Onshore and Offshore Conversion Systems; John Wiley & Sons: Sussex, UK, 2014. [Google Scholar]
- Koutroulis, E.; Kolokotsa, D.; Potirakis, A.; Kalaitzakis, K. Methodology for optimal sizing of stand-alone photovoltaic/wind-generator systems using genetic algorithms. Sol. Energy 2006, 80, 1072–1088. [Google Scholar] [CrossRef]
- van Sark, W.G. Teaching the relation between solar cell efficiency and annual energy yield. Eur. J. Phys. 2007, 28, 415. [Google Scholar] [CrossRef]
- Singh, R.; Sharma, M.; Rawat, R.; Banerjee, C. An assessment of series resistance estimation techniques for different silicon based SPV modules. Renew. Sustain. Energy Rev. 2018, 98, 199–216. [Google Scholar] [CrossRef]
- Yang, J.; Sun, Y.; Xu, Y. Modeling impact of environmental factors on photovoltaic array performance. Int. J. Energy Environ. 2013, 4, 955–968. [Google Scholar]
- Gunawardana, A. Proper sizing of energy storage for grid connected photovoltaic system. Master’s Thesis, Department of Engineering Science Faculty of Engineering and Science, University of Agder, Kristiansand, Norway, 2014. [Google Scholar]
- Sultana, S.; Roy, P.K. Multi-objective quasi-oppositional teaching learning based optimization for optimal location of distributed generator in radial distribution systems. Int. J. Electr. Power Energy Syst. 2014, 63, 534–545. [Google Scholar] [CrossRef]
- Mahmoud, K.; Yorino, N.; Ahmed, A. Optimal distributed generation allocation in distribution systems for loss minimization. IEEE Trans. Power Syst. 2015, 31, 960–969. [Google Scholar] [CrossRef]
- Billington, R.; Allan, R.N. Reliability Evaluation of Power Systems; Springer: New York, NY, USA, 1996. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).