Glucose-Oxygen Biofuel Cell with Biotic and Abiotic Catalysts: Experimental Research and Mathematical Modeling
Abstract
1. Introduction
2. Materials and Methods
2.1. Cultivation of Microorganisms
2.2. Method for Preparing Electrodes
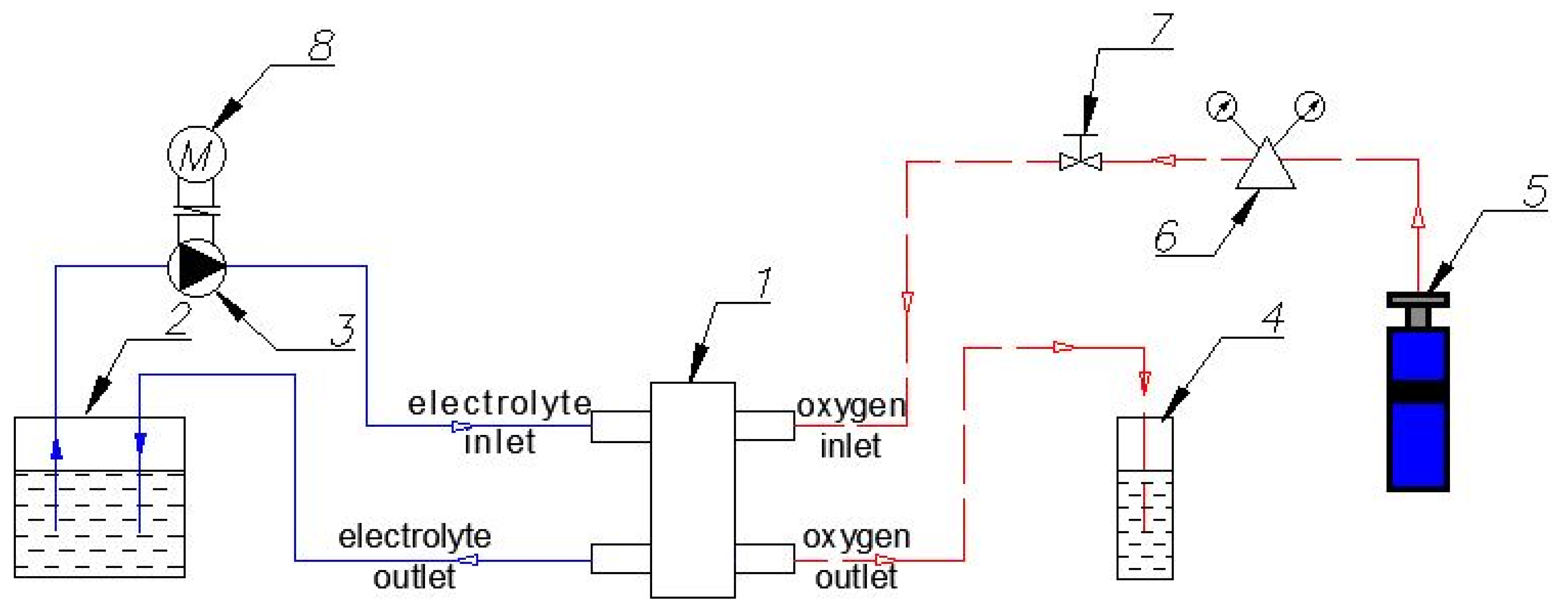
2.3. Experimental Campaign
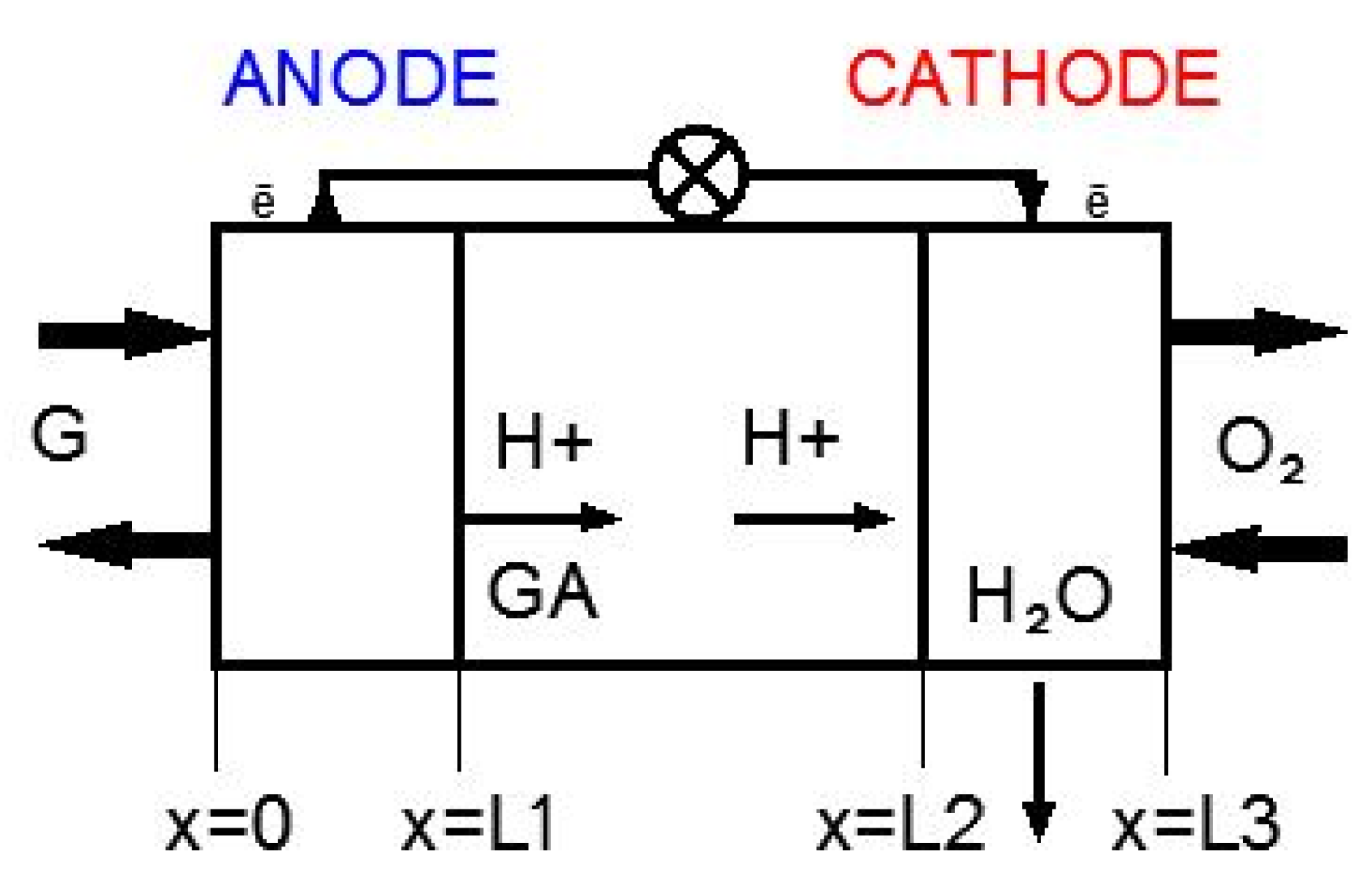
2.4. Mathematical Modeling
3. Results and Discussion
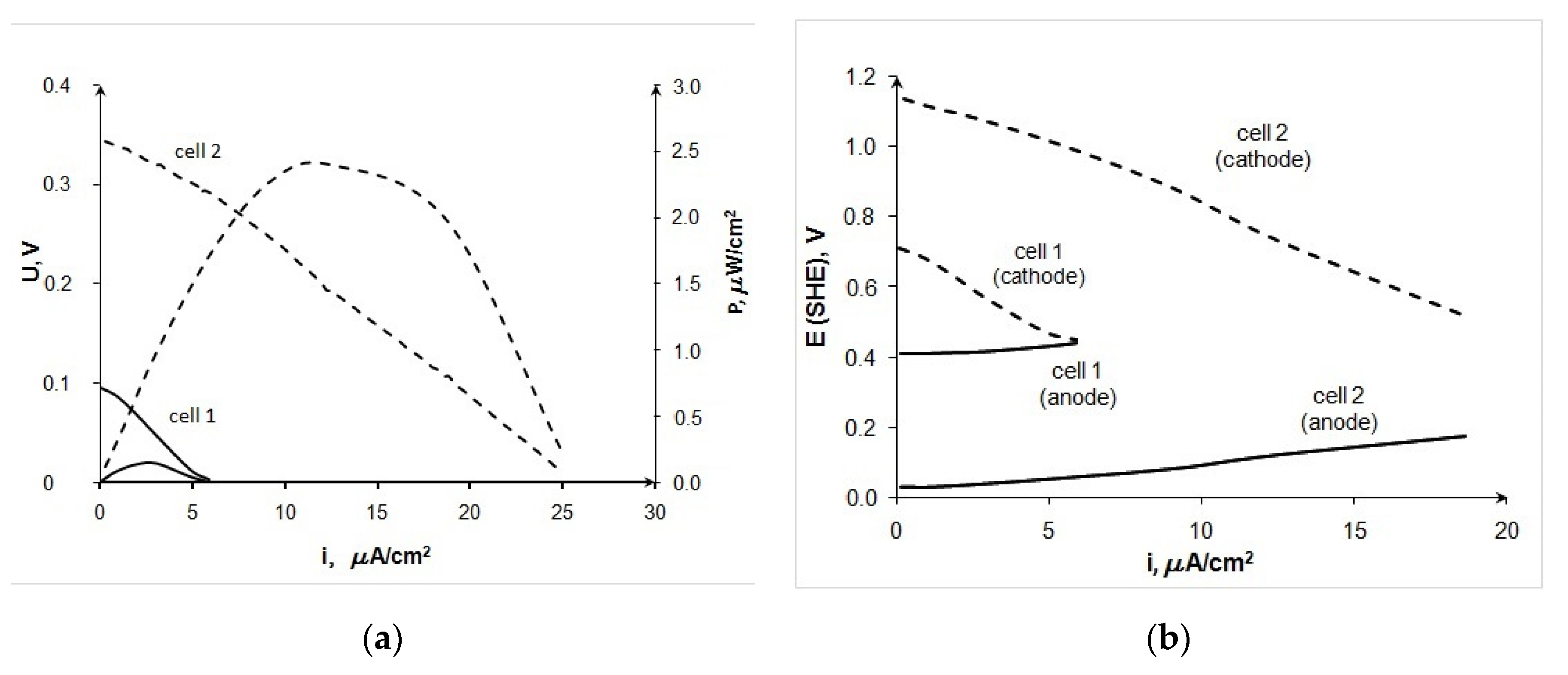
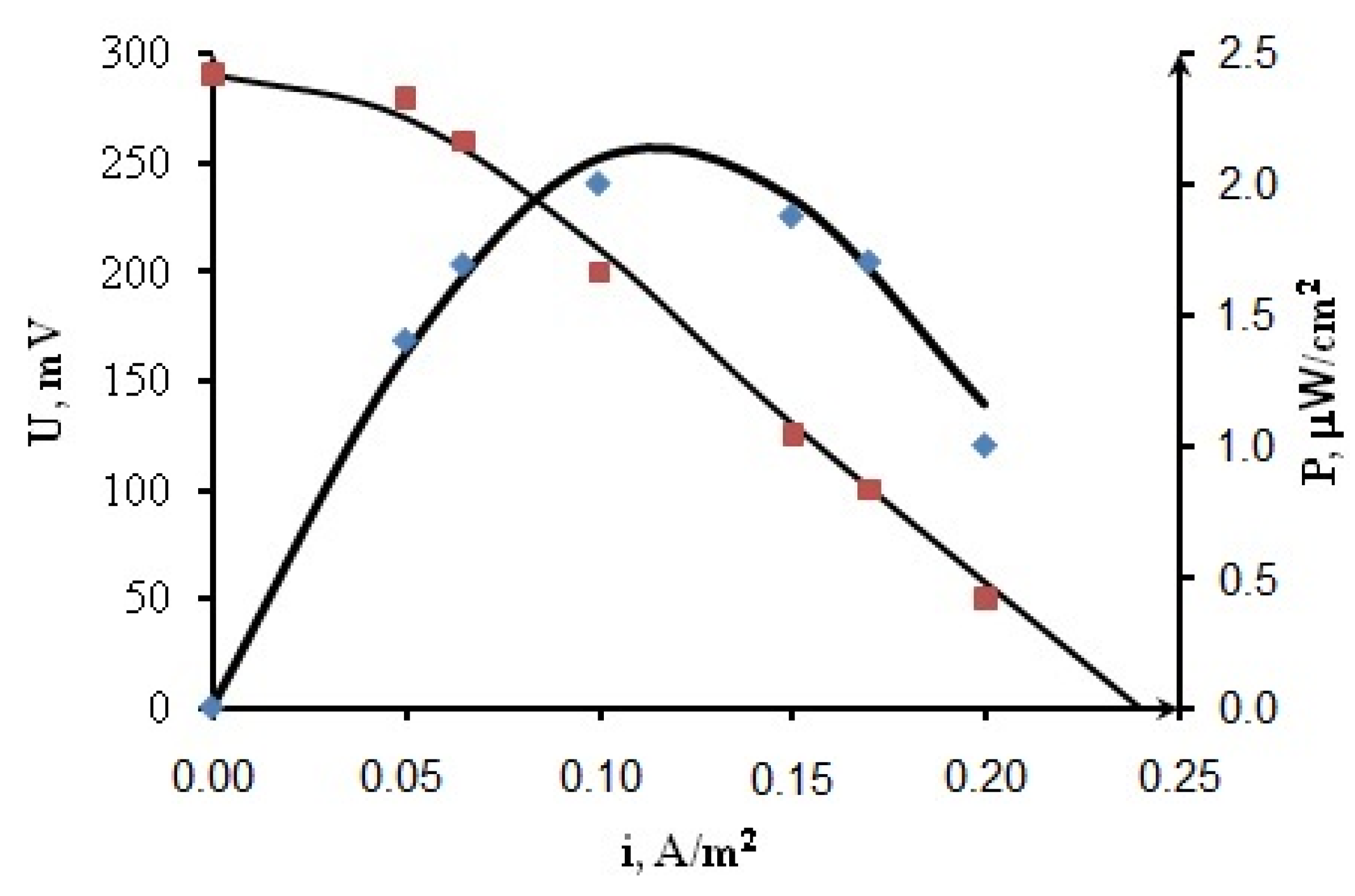
3.1. Experimental Results
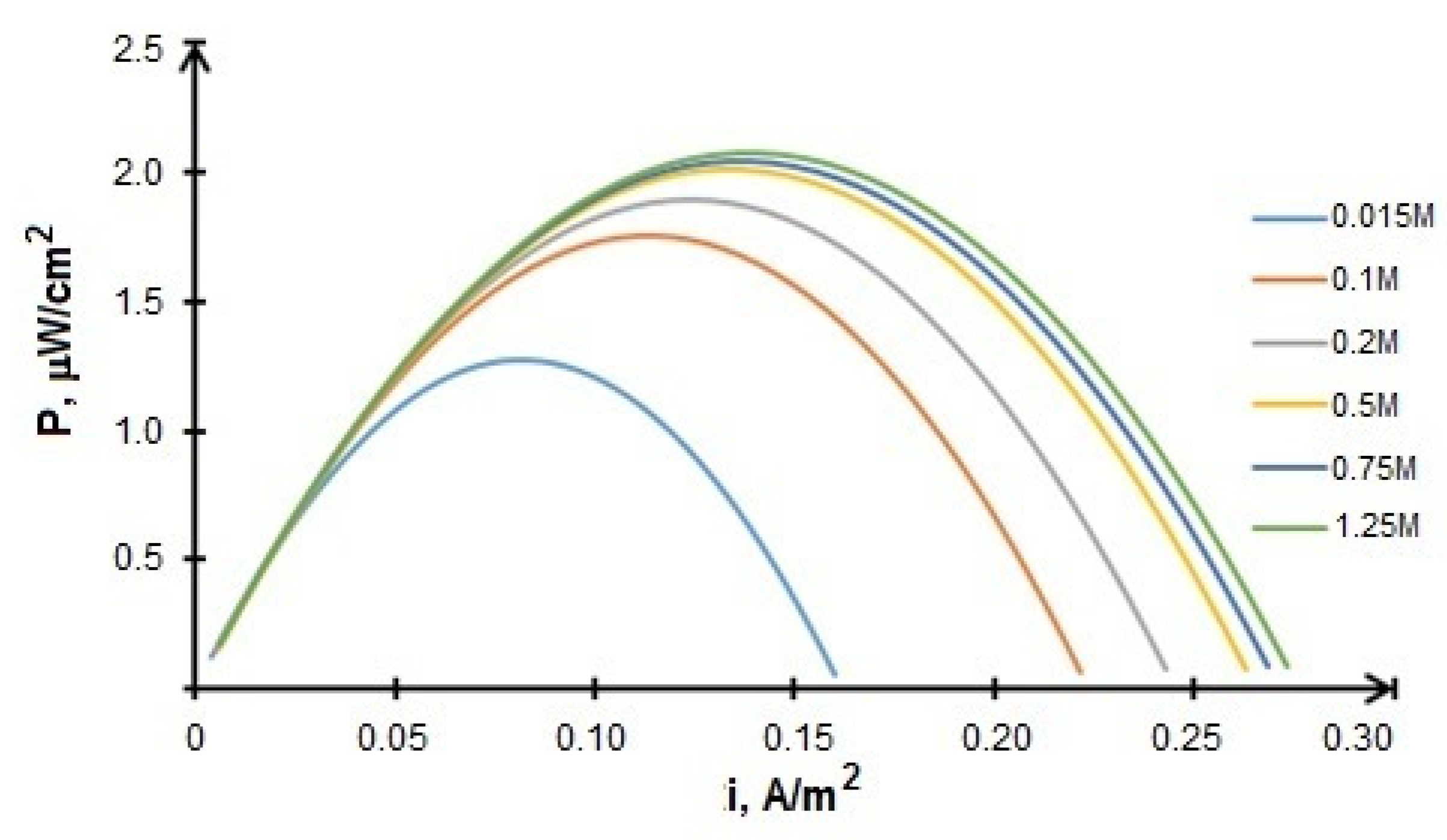
- BFC with the structure CoFe/C (cathode)—20Au/CNT (anode) has the highest characteristics among the tested FCs. The results are achieved with the acetate-phosphate buffer solution at pH 8 and can be further improved by increasing the glucose concentration from 0.2 to 0.5 M. The maximum power density of the system was 137 μW/cm2, which corresponds to the level of the best indicators for fuel cells without a membrane described in the literature [60,61].
- The overvoltage of the electrodes makes comparable contributions to the total voltage drop of the BFC at the application of the laccase-based cathode and Au/C anode in an electrolyte with pH 4.7. At pH 8, the BFC characteristics are limited by the overvoltage increase of the cathodic process. However, with the usage of Au/C anode, the growth of the cathodic overpotential at going from pH 4.7 to pH 8 is compensated by the anode overpotential decrease. This causes an increase in the maximum power density of BFC laccase-Au/CNTs from 2.3 μW/cm2 (pH 4.7) to 42.5 μW/cm2 (pH 8).
- The most effective approach to the formation of an anode based on biological material is the preliminary immobilization of the microorganisms on carbon material (CNT or TEG), followed by applying of CM+ BM mixture on GDL. The maximum power density of the BFC bioanode—CoFe cathode reached 2 µW/cm2 with using BM + CNT anode. The best results obtained at testing FCs with a biocathode and bioanode correspond to 2.75 μW/cm2 in the BFC laccase cathode—BM+TRG in an electrolyte with pH 8 at a glucose concentration of 0.5 M. These characteristics are higher than those obtained in the development of BFC with bioelectrodes [62]. The ratio of bacterial (nitrogen-fixing associate) and fungal cultures in the microbiological community was 75:25.
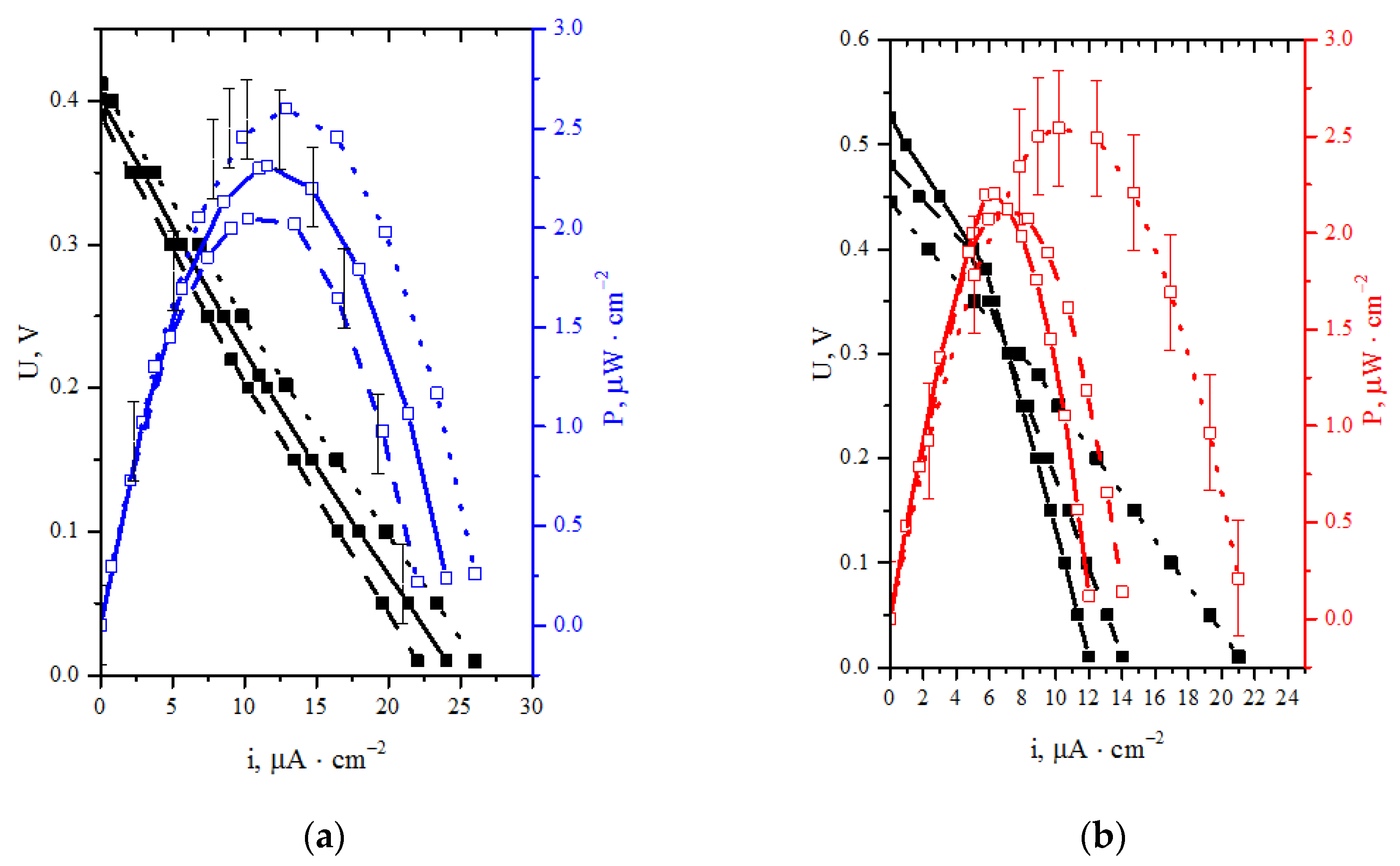
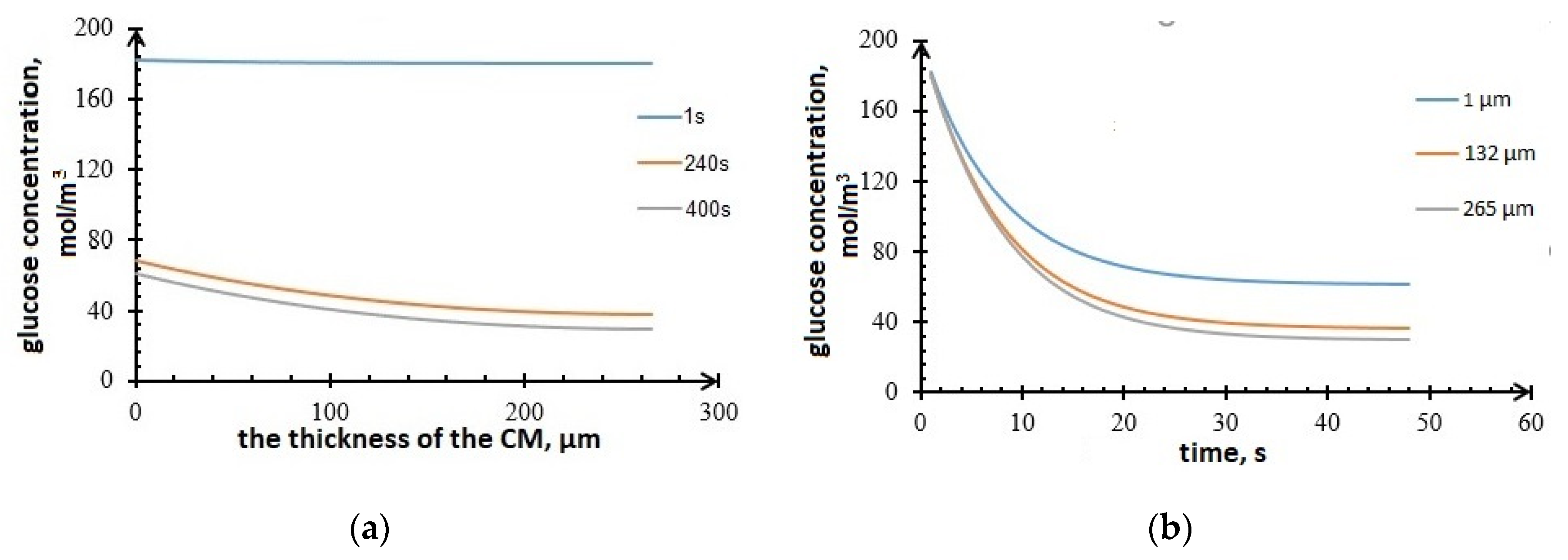
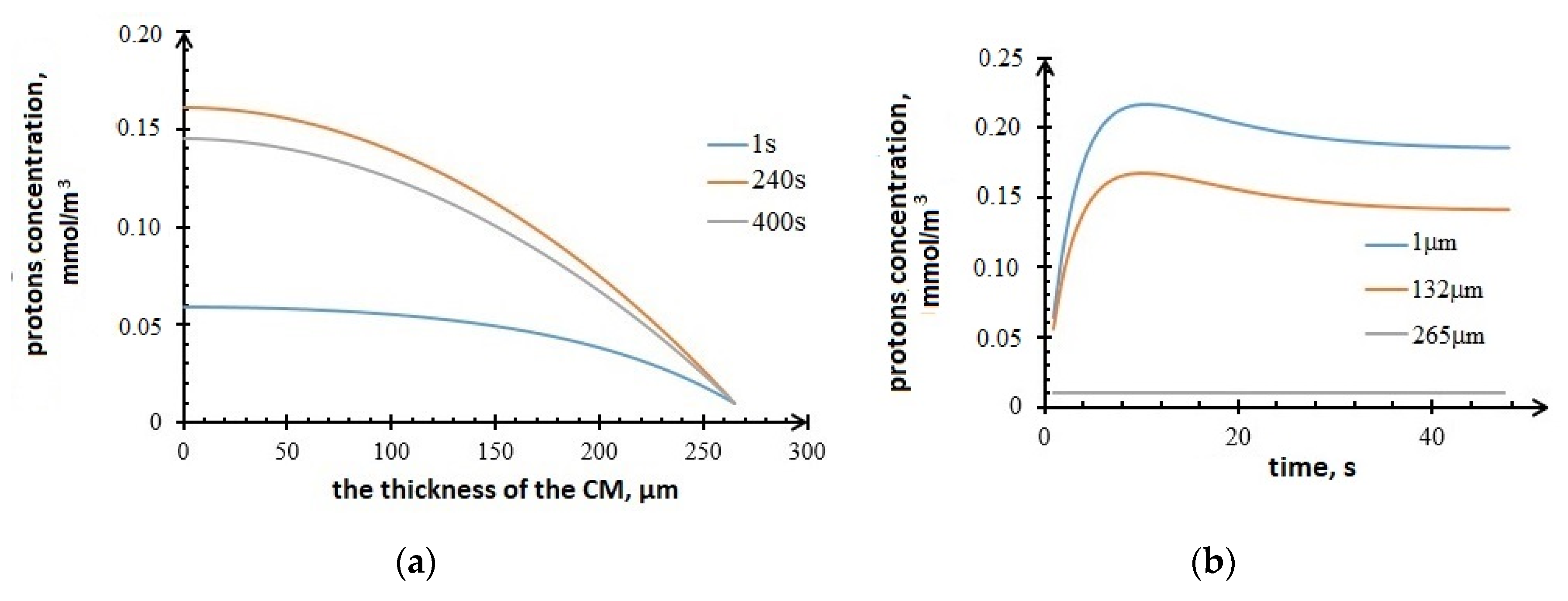
3.2. Results of Mathematical Modeling
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rozendal, R.A.; Hamelers, H.V.; Rabaey, K.; Keller, J.; Buisman, C.J. Towards practical implementation of bioelectrochemical wastewater treatment. Trends Biotechnol. 2008, 26, 450–459. [Google Scholar] [CrossRef] [PubMed]
- Sleutels, T.H.; Ter Heijne, A.; Buisman, C.J.; Hamelers, H.V. Bioelectrochemical systems: An outlook for practical applications. ChemSusChem 2012, 5, 1012–1019. [Google Scholar] [CrossRef] [PubMed]
- Leech, D.; Kavanagh, P.; Schuhmann, W. Enzymatic fuel cells: Recent progress. Electrochim. Acta 2012, 84, 223–234. [Google Scholar] [CrossRef]
- Opallo, M.; Dolinska, J. Glucose Electrooxidation. In Reference Module in Chemistry, Molecular Sciences and Chemical Engineering. Encyclopedia of Interfacial Chemistry. Surface Science and Electrochemistry; Wandelt, K., Ed.; Elsevier: Oxford, UK, 2018; pp. 633–642. [Google Scholar] [CrossRef]
- Retautas, D.; Marcinkevičiene, L.; Meskys, R.; Kulys, J. Mediatorless electron transfer in glucose dehydrogenase/laccase system adsorbed on carbon nanotubes. Electrochim. Acta 2015, 174, 940–944. [Google Scholar] [CrossRef]
- Ramašauskas, L.; Meškys, R.; Ratautas, D. Real-time glucose monitoring system containing enzymatic sensor and enzymatic reference electrodes. Biosens. Bioelectron. 2020, 164, 112338. [Google Scholar] [CrossRef]
- Persson, B.; Gorton, L.; Johansson, G.; Torstensson, A. Biofuel anode based on D-glucose dehydrogenase, nicotinamide adenine dinucleotide and a modified electrode. Enzym. Microb. Technol. 1985, 7, 549–552. [Google Scholar] [CrossRef]
- Yahiro, A.T.; Lee, S.M.; Kimble, D.O. Bioelectrochemistry: I. Enzyme utilizing bio-fuel cell studies. Biochim. Biophys. Acta 1964, 88, 375–383. [Google Scholar] [CrossRef]
- Laane, C.; Pronk, W.; Franssen, M.; Veeger, C. Use of a bioelectrochemical cell for the synthesis of (bio)chemicals. Enzym. Microb. Technol. 1984, 6, 165–168. [Google Scholar] [CrossRef]
- Kuznetsova, L.N.; Tarasevich, M.R.; Bogdanovskaya, V.A. Macrokinetics of processes in glucose oxidase-peroxidase bienzyme systems when assaying glucose by the H2O2 reduction current: Effect of the enzyme ratio on the steady-state potential and H2O2 reduction current in glucose solutions of different concentrations. Russ. J. Electrochem. 2000, 36, 716–720. [Google Scholar] [CrossRef]
- Khokhlachev, N.S.; Kalenov, S.V.; Zanina, O.S.; Tyupa, D.V.; Baurina, M.M.; Kuznetsov, A.Y. The role of stress agents as operating factors in formation and functioning of granular aerobic activated sludge at model domestic wastewater treatment. Bioprocess Biosyst. Eng. 2014, 37, 1771–1779. [Google Scholar] [CrossRef]
- Tyupa, D.V.; Kalenov, S.V.; Baurina, M.M.; Yakubovich, L.M.; Morozov, A.N.; Zakalyukin, R.M.; Sorokin, V.V.; Skladnev, D.A. Efficient continuous biosynthesis of silver nanoparticles by activated sludge micromycetes with enhanced tolerance to metal ion toxicity. Enzym. Microb. Technol. 2016, 95, 137–145. [Google Scholar] [CrossRef]
- Su, K.Z.; Yu, H.Q. Formation and characterization of aerobic granules in a sequencing batch reactor treating soybean-processing wastewater. Environ. Sci. Technol. 2005, 39, 2818–2827. [Google Scholar] [CrossRef] [PubMed]
- Rajendran, L.; Kirthiga, M.; Laborda, E. Mathematical modeling of nonlinear reaction–diffusion processes in enzymatic biofuel cells. Curr. Opin. Electrochem. 2017, 1, 121–132. [Google Scholar] [CrossRef]
- Bavarian, M.; Soroush, M.; Kevrekidis, I.G.; Benziger, J.B. Mathematical modeling, steady-state and dynamic behavior, and control of fuel cells: A review. Ind. Eng. Chem. Res. 2010, 49, 7922–7950. [Google Scholar] [CrossRef]
- Barton, S.C. 1D models for enzymatic biological fuel cells. Electrochem. Soc. Interface 2015, 24, 61–65. [Google Scholar] [CrossRef]
- Ivanov, I.; Vidaković-Koch, T.; Sundmacher, K. Recent advances in enzymatic fuel cells: Experiments and modeling. Energies 2010, 3, 803–846. [Google Scholar] [CrossRef]
- Gallaway, J.W.; Calabrese Barton, S.A. Kinetics of redox polymer-mediated enzyme electrodes. J. Am. Chem. Soc. 2008, 130, 8527–8536. [Google Scholar] [CrossRef]
- Tamaki, T.; Ito, T.; Yamaguchi, T. Modelling of reaction and diffusion processes in a high-surface-area biofuel cell electrode made of redox polymergrafted carbon. Fuel Cells 2009, 9, 37–43. [Google Scholar] [CrossRef]
- Rajendran, L.; Saravanakumar, K. Analytical expression of transient and steady-state catalytic current of mediated bioelectrocatalysis. Electrochim. Acta 2014, 147, 678–687. [Google Scholar] [CrossRef]
- Chan, D.S.; Dai, D.J.; Wu, H.S. Dynamic modeling of anode function in enzyme-based biofuel cells using high mediator concentration. Energies 2012, 5, 2524–2544. [Google Scholar] [CrossRef]
- Song, Y.; Penmatsa, V.; Wang, C. Modeling and simulation of enzymatic biofuel cells with three-dimensional microelectrodes. Energies 2014, 7, 4694–4709. [Google Scholar] [CrossRef]
- Bedekar, A.S.; Feng, J.J.; Krishnamoorthy, S.; Lim, K.G.; Palmore, G.T.R.; Sundaram, S. Oxygen limitation in microfluidic biofuel cells. Chem. Eng. Commun. 2007, 195, 256–266. [Google Scholar] [CrossRef]
- Kjeang, E.; Sinton, D.; Harrington, D.A. Strategic enzyme patterning for microfluidic biofuel cells. J. Power Sources 2006, 158, 1–12. [Google Scholar] [CrossRef]
- Osman, M.H.; Shah, A.A.; Wills, R.G.A.; Walsh, F.C. Mathematical modelling of an enzymatic fuel cell with an air-breath cathode. Electrochim. Acta 2013, 112, 386–393. [Google Scholar] [CrossRef]
- Do, T.Q.N.; Varničić, M.; Hanke-Rauschenbach, R.; Vidaković-Koch, T.; Sundmacher, K. Mathematical modeling of a porous enzymatic electrode with direct electron transfer mechanism. Electrochim. Acta 2014, 137, 616–626. [Google Scholar] [CrossRef]
- Sindhuja, M.; Kumar, N.S.; Sudha, V.; Harinipriya, S. Equivalent circuit modeling of microbial fuel cells using impedance spectroscopy. J. Energy Storage 2016, 7, 136–146. [Google Scholar] [CrossRef]
- Esfandyari, M.; Fanaei, M.A.; Gheshlaghi, R.; Mahdavi, M.A. Neural network and neuro-fuzzy modeling to investigate the power density and Columbic efficiency of microbial fuel cell. J. Taiwan Inst. Chem. Eng. 2015, 58, 84–91. [Google Scholar] [CrossRef]
- Ali, A.H.; Al-Mussawy, H.A.; Hussein, M.J.; Hamadi, N.J. Experimental and Theoretical Study on the Ability of Microbial Fuel Cell for Electricity Generation. Pollution 2018, 4, 359–368. [Google Scholar] [CrossRef]
- Hernandez-Flores, G.; Poggi-Varaldo, H.M.; Solorza-Feria, O.; Ponce Noyola, M.T.; Romero-Castanon, T.; Rinderknecht-Seijas, N. Tafel equation based model for the performance of a microbial fuel cell. Int. J. Hydrog. Energy 2015, 40, 17421–17432. [Google Scholar] [CrossRef]
- Cecconet, D.; Bolognesi, S.; Molognoni, D.; Callegari, A.; Capodaglio, G.A. Influence of reactor’s hydrodynamics on the performance of microbial fuel cells. J. Water Process Eng. 2018, 26, 281–288. [Google Scholar] [CrossRef]
- Zhang, X.C.; Halme, A. Modelling of a microbial fuel cell process. Biotechnol. Lett. 1995, 17, 809–814. [Google Scholar] [CrossRef]
- Lan, T.H.; Wang, C.T.; Sangeetha, T.; Yang, Y.C.; Garg, A. Constructed mathematical model for nanowire electron transfer in microbial fuel cells. J. Power Sources 2018, 402, 483–488. [Google Scholar] [CrossRef]
- Oliveira, V.B.; Simxes, M.; Melo, L.F.; Pinto, A.M.F.R. A 1D mathematical model for a microbial fuel cell. Energy 2013, 61, 463–471. [Google Scholar] [CrossRef]
- Drobotenko, M.I.; Svidlov, A.A. Mathematical modeling of processes in a microbial fuel cell taking into account their spatial heterogeneity. Ecol. Bull. Res. Cent. Black Sea Econ. Coop. 2017, 4, 81–85. [Google Scholar]
- Zeng, Y.; Choo, Y.F.; Kim, B.H.; Wu, P. Modelling and simulation of two-chamber microbial fuel cell. J. Power Sources 2010, 195, 79–89. [Google Scholar] [CrossRef]
- Mardanpour, M.M.; Yaghmaei, S.; Kalantar, M. Modeling of microfluidic microbial fuel cells using quantitative bacterial transport parameters. J. Power Sources 2017, 342, 1017–1031. [Google Scholar] [CrossRef]
- Sirinutsomboon, B. Modeling of a membraneless single-chamber microbial fuel cell with molasses as an energy source. Int. J. Energy Environ. Eng. 2014, 5, 93. [Google Scholar] [CrossRef]
- Bogdanovskaya, V.A.; Arkad’eva, I.N.; Osina, M.A. Bioelectrocatalytic oxygen reduction by laccase immobilized on various carbon carriers. Russ. J. Electrochem. 2017, 53, 1323–1333. [Google Scholar] [CrossRef]
- Arkadeva, I.N.; Bogdanovskaya, V.A.; Vasilenko, V.A.; Fokina, E.A.; Koltsova, E.M. Laccase spontaneous adsorption immobilization: Experimental studies and mathematical modeling at enzymatic fuel cell cathode construction. In IOP Conference Series: Earth and Environmental Science, Proceedings of the 2nd International Conference on Green Energy Technology (ICGET 2017), Rome, Italy, 18–20 July 2017; IOP Publishing Ltd.: Bristol, UK, 2017; Volume 83, pp. 127–134. [Google Scholar] [CrossRef]
- Arkadeva, I.; Fokina, E.; Bogdanovskaya, V.; Koltsova, E. Mathematical modeling of glucose electro-oxidation in a slight acid solution at the biofuel cell anode. In Proceedings of the 18th International Multidisciplinary Scientific GeoConference SGEM, Albena, Bulgaria, 2–8 July 2018; Volume 18, pp. 441–448. [Google Scholar] [CrossRef]
- Vasilenko, V.A.; Arkadeva, I.N.; Bogdanovskaya, V.A.; Fokina, E.A.; Koltsova, E.M. Research and mathematical modelling of direct bioelectrocatalytic oxygen reduction by laccase. Chem. Eng. Trans. 2018, 70, 1609–1614. [Google Scholar] [CrossRef]
- Koltsova, E.; Bogdanovskaya, V.; Vasilenko, V.; Kalenov, S.; Korchagin, O.; Fokina, E. Development of a bioanod, experimental studies and mathematical modelling of membraneless microbial fuel cell. Mater. Sci. Forum 2020, 995, 77–83. [Google Scholar] [CrossRef]
- Reshetilov, A.N.; Kitova, A.E.; Kolesov, V.V.; Yaropolov, A.I. Mediator-free bioelectrocatalytic oxidation of ethanol on an electrode from thermally expanded graphite modified by Gluconobacter oxydans membrane fractions. Electroanalysis 2015, 27, 1443–1448. [Google Scholar] [CrossRef]
- Vassilyev, Y.B.; Khazova, O.A.; Nikilaeva, N.N. Kinetics and mechanism of glucose electrooxidation on different electrode-catalysts: Part II. Effect of the nature of the electrode and the electrooxidation mechanism. J. Electroanal. Chem. 1985, 196, 127–144. [Google Scholar] [CrossRef]
- Bogdanovskaya, V.A.; Beketaeva, L.A.; Rybalka, K.V.; Efremov, B.N.; Zagudaeva, N.M.; Sakashita, M.; Iidzima, T.; Ismagilov, Z.R. Nanosize catalysts based on carbon materials promoted by cobalt tetra(para-methoxyphenyl) porphyrin pyropolymer for oxygen electroreduction. Russ. J. Electrochem. 2008, 44, 293–302. [Google Scholar] [CrossRef]
- Bogdanovskaya, V.A.; Tarasevich, M.R.; Lozovaya, O.V. Kinetics and mechanism of oxygen electroreduction on PtCoCr/C catalyst containing 20–40 wt % platinum. Russ. J. Electrochem. 2011, 47, 846–860. [Google Scholar] [CrossRef]
- Arkadeva, I.; Vasilenko, V.; Bogdanovskaya, V.; Sudarev, G.; Koltsova, E. Glucose-oxygen biofuel cell based on laccase cathode and gold-modified carbon black anode: Experimental research and mathematical modelling. In IOP Conference Series: Earth and Environmental Science, Proceedings of the 3rd International Conference on Green Energy and Environment Engineering (CGEEE 2020), Jeju Island, Korea, 22–24 July 2020; IOP Publishing Ltd.: Bristol, UK, 2020; in press. [Google Scholar]
- Shi, Q.; Diao, G.; Mu, S. The Electrocatalytic oxidation of glucose on the bimetallic Au-Ag particles-modified reduced graphene oxide electrodes in alkaline solutions. Electrochim. Acta 2014, 133, 335–346. [Google Scholar] [CrossRef]
- Newman, J.; Thomas-Alyea, K.E. Electrochemical Systems, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; p. 647. [Google Scholar]
- Kol’tsova, E.M.; Vasilenko, V.A.; Tarasov, V.V. Numerical methods for solving transport equations in fractal media. Russ. J. Phys. Chem. A 2000, 74, 848–850. [Google Scholar]
- Vasilenko, V.A.; Kolítsova, E.M.; Tarasov, V.V.; Gordeev, L.S. Methods of fractal geometry in investigation and simulation of mass transfer processes in liquid-liquid systems. Theor. Found. Chem. Eng. 2008, 42, 246–250. [Google Scholar] [CrossRef]
- Kato Marcus, A.; Torres, C.I.; Rittman, B.E. Conduction-based modeling of the biofilm anode of a microbial fuel cell. Biotechnol. Bioeng. 2007, 98, 1171–1182. [Google Scholar] [CrossRef]
- Torres, C.I.; Kato Marcus, A.; Parameshwaran, P.; Rittman, B.E. Kinetic experiments for evaluating the Nernst-Monod model for anode-respiring bacteria (ARB) in a biofilm anode. Environ. Sci. Technol. 2008, 42, 6593–6597. [Google Scholar] [CrossRef]
- Ahluwalia, R.K.; Arisetty, S.; Peng, J.K.; Subbaraman, R.; Wang, X.; Kariuki, N.; Myers, D.J.; Mukundan, R.; Borup, R.; Polevaya, O. Dynamics of particle growth and electrochemical surface area loss due to platinum dissolution. J. Electrochem. Soc. 2014, 161, F291–F304. [Google Scholar] [CrossRef]
- Hiraoka, F.; Kohno, Y.; Matsuzawa, K.; Mitsushima, S. A simulation study of Pt particle degradation during potential cycling using a dissolution/deposition method. Electrocatalysis 2015, 6, 10–108. [Google Scholar] [CrossRef]
- Darling, R.M.; Meyers, J.P. Kinetic model of platinum dissolution in PEMFCs. J. Electrochem. Soc. 2003, 150, A1523–A1527. [Google Scholar] [CrossRef]
- Arvay, A.; Ahmed, A.; Peng, X.-H.; Kannan, A.M. Convergence criteria establishment for 3D simulation of proton exchange membrane fuel cell. Int. J. Hydrog. Energy. 2012, 37, 2482–2489. [Google Scholar] [CrossRef]
- Robin, C.; Gerard, M.; Franco, A.A.; Schott, P. Multi-scale coupling between two dynamical models for PEMFC aging prediction. Int. J. Hydrog. Energy 2013, 38, 4675–4688. [Google Scholar] [CrossRef]
- Christwardana, M.; Kim, K.J.; Kwon, Y. Fabrication of mediatorless/membraneless glucose/oxygen based biofuel cell using biocatalysts including glucose oxidase and laccase enzymes. Sci. Rep. 2016, 6, 30128. [Google Scholar] [CrossRef]
- Santiago, Ó.; Navarro, E.; Raso, M.A.; Leo, T.J. Review of implantable and external abiotically catalysed glucose fuel cells and the differences between their membranes and catalysts. Appl. Energy 2016, 179, 497–522. [Google Scholar] [CrossRef]
- Bollella, P.; Fusco, G.; Stevar, D.; Gorton, L.; Ludwig, R.; Ma, S.; Boer, H. A glucose/oxygen enzymatic fuel cell based on gold nanoparticles modified graphene screen-printed electrode. Proof-of-concept in human saliva. Sens. Actuators B Chem. 2017, 256, 921–930. [Google Scholar] [CrossRef]




| Cathode-Anode Active Material | CG, M | OCV, mV | Pmax, (at U, mV), μW/cm2 | imax, μA/cm2 | Eanode (RHE), mV | Ecathode (RHE), mV |
|---|---|---|---|---|---|---|
| CNTN-Au/XC-72 * | 0.2 | 373 | 14.3 (168) | 236 | 561 | 934 |
| 0.2 | 371 | 14.5 (160) | 233 | 555 | 926 | |
| 0.2 | 366 | 14.2 (150) | 230 | 563 | 929 | |
| CoFe/C-Au/CNT * | 0.2 | 520 | 29.7 (241) | 350 | 494 | 1014 |
| 0.2 | 526 | 30.2 (245) | 354 | 495 | 1021 | |
| 0.2 | 514 | 29.5 (238) | 347 | 496 | 1010 | |
| 0.5 | 700 | 86 (308) | 623 | 312 | 1012 | |
| 0.5 | 704 | 90 (311) | 626 | 312 | 1016 | |
| 0.5 | 697 | 83 (305) | 619 | 310 | 1007 | |
| Laccase—Au/CNT ** | 0.2 pH4.7 | 342 | 2.1 (415) | 17 | 754.3 | 1096.3 |
| 0.2 pH4.7 | 339 | 1.6 (413) | 15 | 720.9 | 1059.4 | |
| 0.2 pH4.7 | 345 | 2.6 (417) | 20 | 677.5 | 1022.5 | |
| 0.5 pH4.7 | 401 | 2.3 (209) | 24 | 709.3 | 1110.3 | |
| 0.5 pH4.7 | 390 | 2.0 (220) | 22 | 690.2 | 1080.3 | |
| 0.5 pH4.7 | 412 | 2.6 (202) | 26 | 721.0 | 1133.0 | |
| 0.2 pH8 | 372 | 1.5 (337) | 25 | 554 | 926 | |
| 0.2 pH8 | 350 | 1.2 (350) | 23 | 520 | 870 | |
| 0.2 pH8 | 394 | 1.8 (324) | 27 | 588 | 982 | |
| 0.5 pH8 | 628 | 42.5 (192) | 488 | 281 | 909 | |
| 0.5 pH8 | 590 | 38.3 (210) | 500 | 250 | 870 | |
| 0.5 pH8 | 666 | 46.7(174) | 476 | 312 | 978 | |
| Laccase—BM+TEG ** | 0.5 pH4.7 | 526 | 2.20 (381) | 12 | 575.3 | 1101.3 |
| 0.5 pH4.7 | 480 | 1.90 (401) | 14 | 550.3 | 1070.4 | |
| 0.5 pH4.7 | 445 | 2.50 (280) | 21 | 670 | 1123 | |
| CoFe/C-BM+CNT ** | 0.2 pH8 | 291 | 1.99 (208) | 24 | 726 | 1017 |
| 0.2 pH8 | 293 | 2.03 (212) | 27 | 727 | 1020 | |
| 0.2 pH8 | 291 | 1.96 (205) | 22 | 723 | 1014 |
| Parameter | Symbol, Dimension | Value | References |
|---|---|---|---|
| Cell operating temperature | T, K | 298 | given |
| pH | 8 | given | |
| Initial glucose concentration | [G]0, mol/m3 | 200 | given |
| Open circuit voltage | Voc, V | 0.291 | given |
| Anode applied potential | Ea,anode V | 0.726 | given |
| Cathode applied potential | Ea,cathode V | 0.1017 | given |
| Monod constant | KG, mol/m3 | 19 | [38] |
| Active biomass density | ρb, kgBM/m3AL | 116 | calculated from experiment |
| Active biomass specific growth rate | μb, 1/sγ | 2.78 × 10−5 | fitted |
| Biomass decay rate constant | bb, 1/sγ | 1 × 10−6 | fitted |
| Active biomass volume fraction | Xb | 0.6 | assumed |
| Active biomass growth yield, ratio of dry biomass to consumed oxygen | Yb, kgdrybiomass / kgCOD | 0.01 | measured by Koch’s micromethod |
| COD for glucose | γCOD, kgCOD/molglucose | 192 × 10−3 | calculated from stoichiometry |
| Charge transfer coefficient | α | 0.5 | assumed |
| Faraday constant | F, C/mol | 96,485 | |
| Universal gas constant | R, J/(mol·K) | 8.314 | |
| Oxygen electroreduction reaction rate constant | kc, 1/sγ | 1.43 × 10−13 | fitted |
| Oxygen mass transfer coefficient | β, m/s | 0.1 | fitted |
| Ion-conducting phase conductivity | κl, A/(V·m) | 0.55 | [21] |
| Electron-conducting phase conductivity | κs, A/(V·m) | 0.46 | [21] |
| Microbial phase conductivity | κb, A/(V·m) | 5 × 10−2 | [38] |
| Volume fraction of the liquid phase on the electrode | ε | 0.8 | [21] |
| Anode CM porosity | γa | 0.9 | assumed |
| Cathode CM porosity | γc | 0.75 | assumed |
| Glucose diffusion coefficient in electrolyte | DG, m2/s | 5 × 10−12 | Initial [21] |
| Protons diffusion coefficient in electrolyte | DH+, m2/s | 1 × 10−9 | [21] |
| Oxygen diffusion coefficient in electrolyte | DO2, m2/s | 2 × 10−9 | [25] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasilenko, V.; Arkadeva, I.; Bogdanovskaya, V.; Sudarev, G.; Kalenov, S.; Vocciante, M.; Koltsova, E. Glucose-Oxygen Biofuel Cell with Biotic and Abiotic Catalysts: Experimental Research and Mathematical Modeling. Energies 2020, 13, 5630. https://doi.org/10.3390/en13215630
Vasilenko V, Arkadeva I, Bogdanovskaya V, Sudarev G, Kalenov S, Vocciante M, Koltsova E. Glucose-Oxygen Biofuel Cell with Biotic and Abiotic Catalysts: Experimental Research and Mathematical Modeling. Energies. 2020; 13(21):5630. https://doi.org/10.3390/en13215630
Chicago/Turabian StyleVasilenko, Violetta, Irina Arkadeva, Vera Bogdanovskaya, George Sudarev, Sergei Kalenov, Marco Vocciante, and Eleonora Koltsova. 2020. "Glucose-Oxygen Biofuel Cell with Biotic and Abiotic Catalysts: Experimental Research and Mathematical Modeling" Energies 13, no. 21: 5630. https://doi.org/10.3390/en13215630
APA StyleVasilenko, V., Arkadeva, I., Bogdanovskaya, V., Sudarev, G., Kalenov, S., Vocciante, M., & Koltsova, E. (2020). Glucose-Oxygen Biofuel Cell with Biotic and Abiotic Catalysts: Experimental Research and Mathematical Modeling. Energies, 13(21), 5630. https://doi.org/10.3390/en13215630








