Effects of Cyber Attacks on AC and High-Voltage DC Interconnected Power Systems with Emulated Inertia
Abstract
1. Introduction
1.1. Related Work
1.2. Contributions and Paper Organization
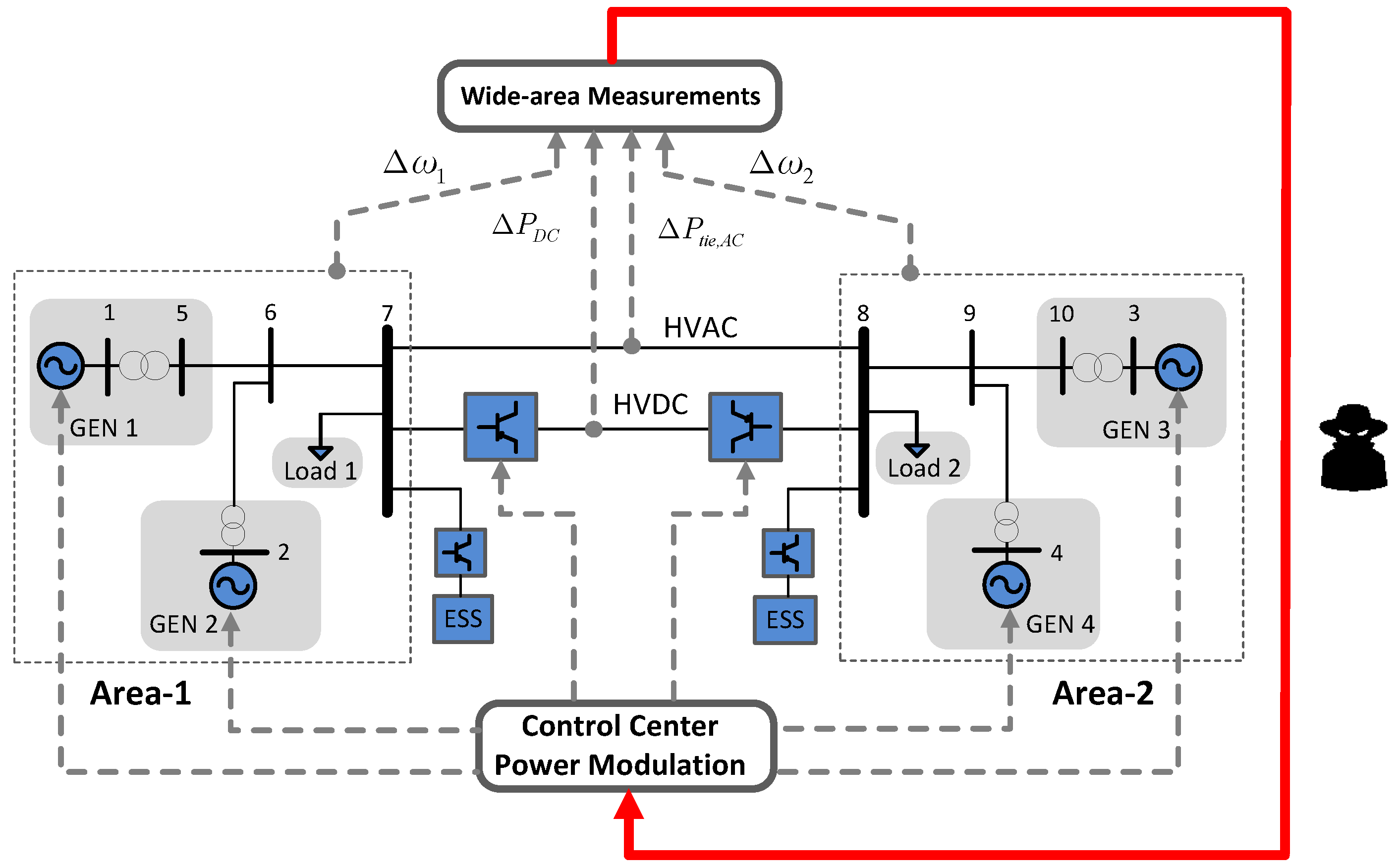
2. LFC Modeling in the Hybrid AC/DC System with Virtual Inertia
2.1. The Conventional LFC Structure
2.2. LFC for AC/HVDC Interconnected System
2.3. LFC for AC/HVDC System with Emulated Inertia by ESS
2.4. LFC System Model in the State-Space Form
3. DoS Attacks on the AC/DC Multi-Area LFC System with Virtual Inertia
3.1. The Test LFC System under DoS Attacks
3.2. Stability of the Test LFC System under DoS Attacks
4. FDI Attacks on the AC/DC Multi-Area LFC System with Virtual Inertia
4.1. The Test LFC Sytem under FDI Attacks: Basics
4.2. A Type of Stealthy FDI Attack on the Test LFC System: Zero-Dynamics Attack
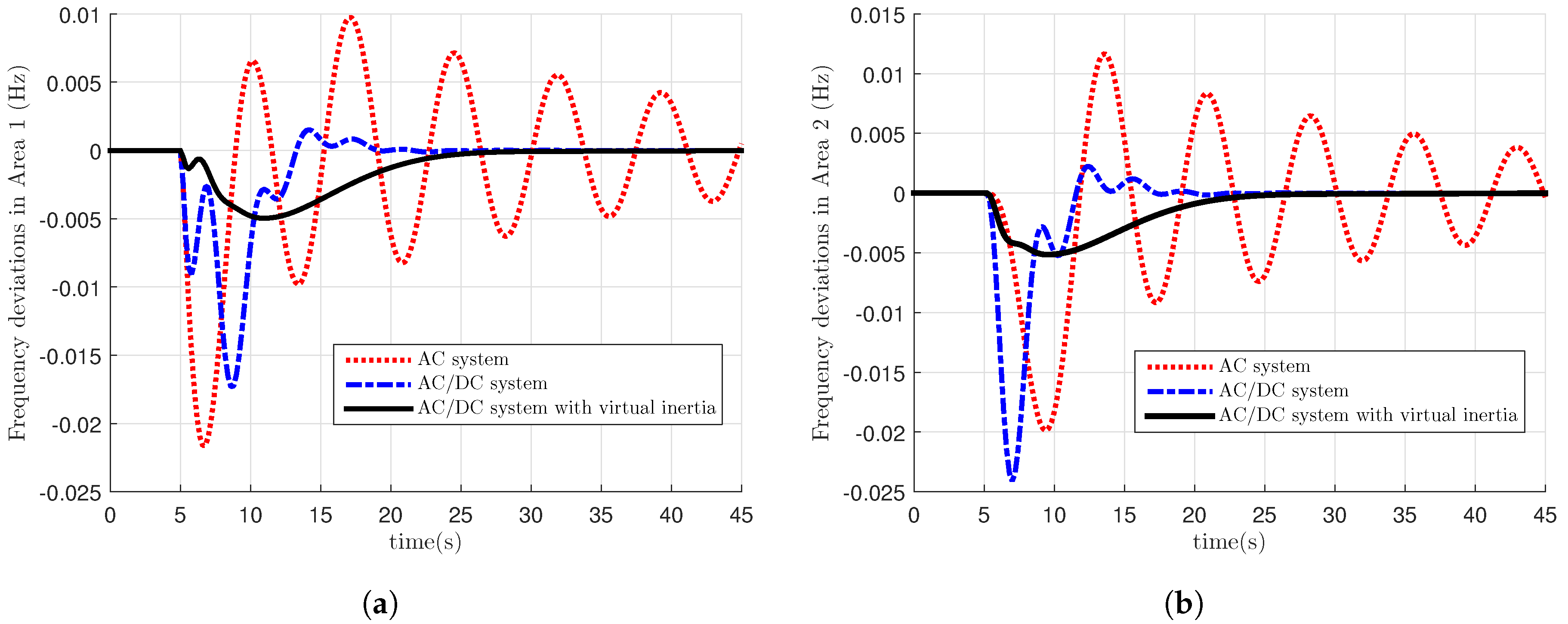
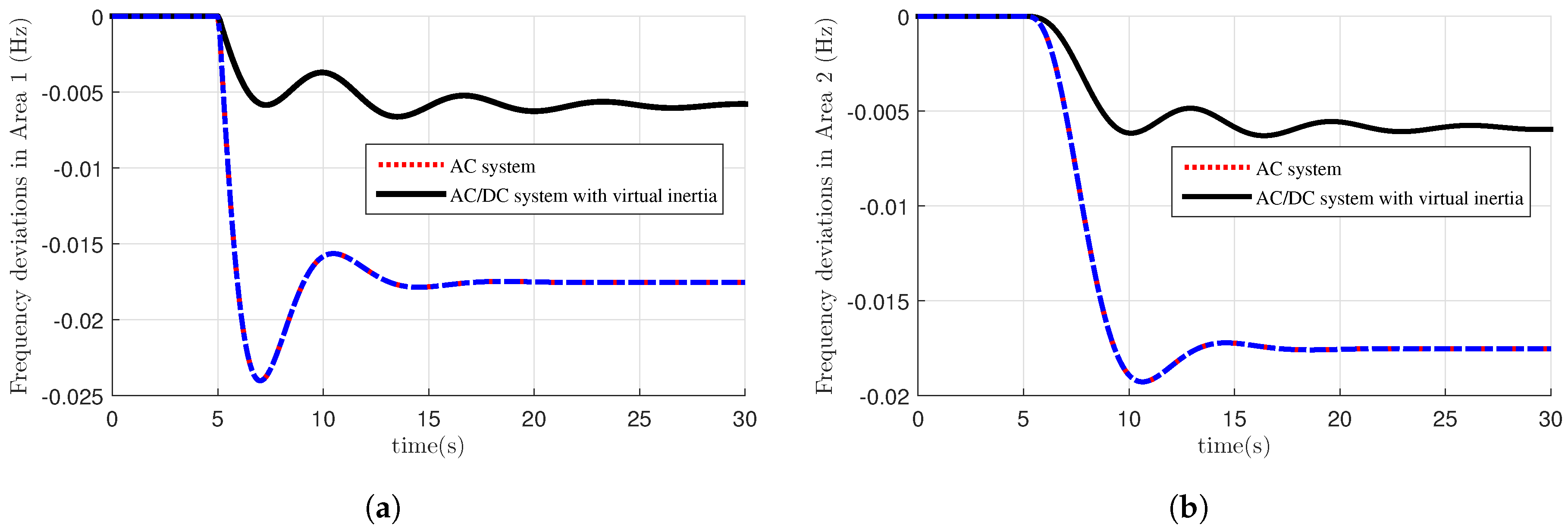
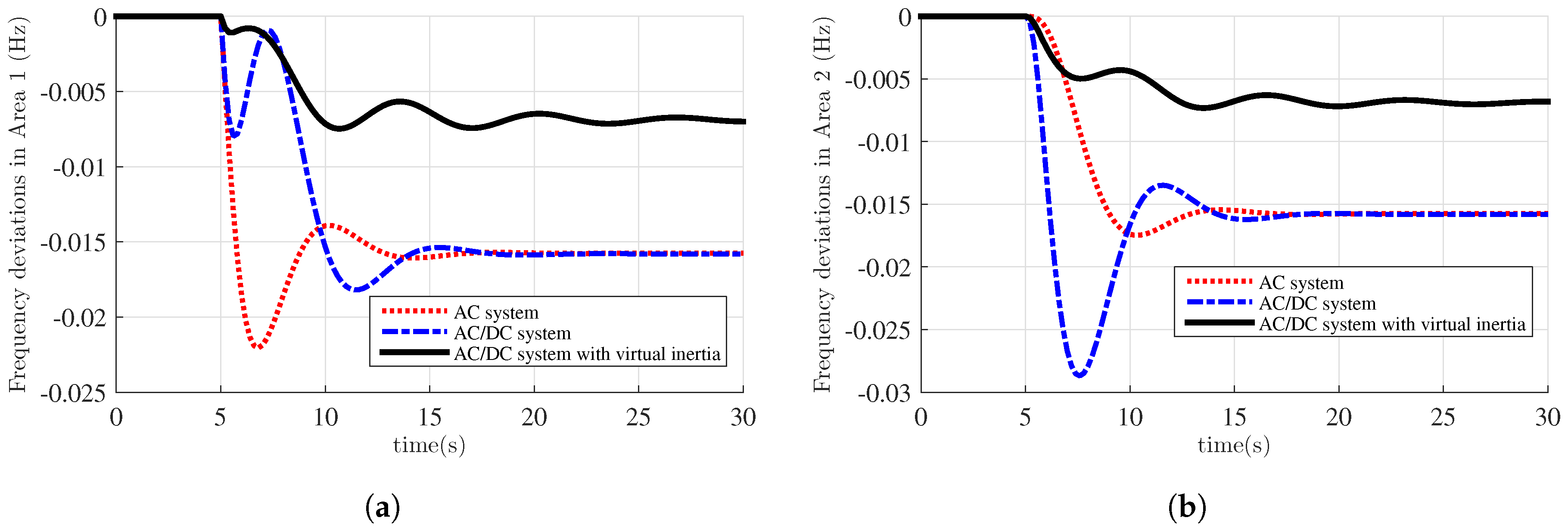
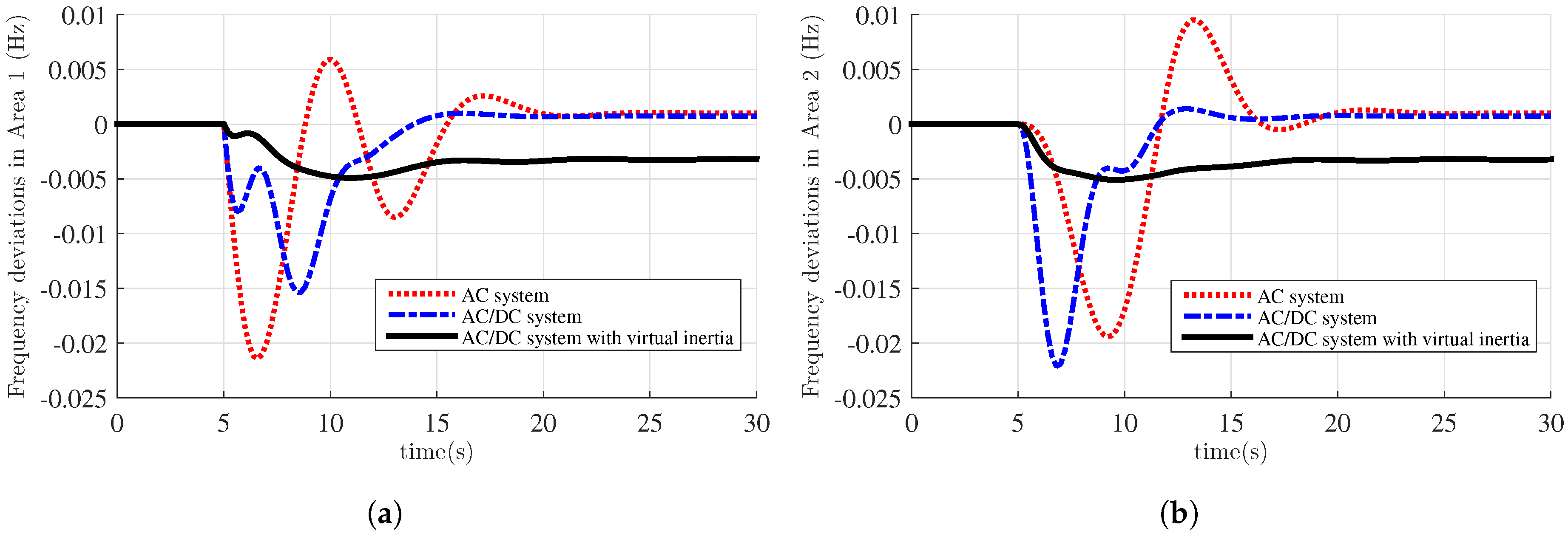
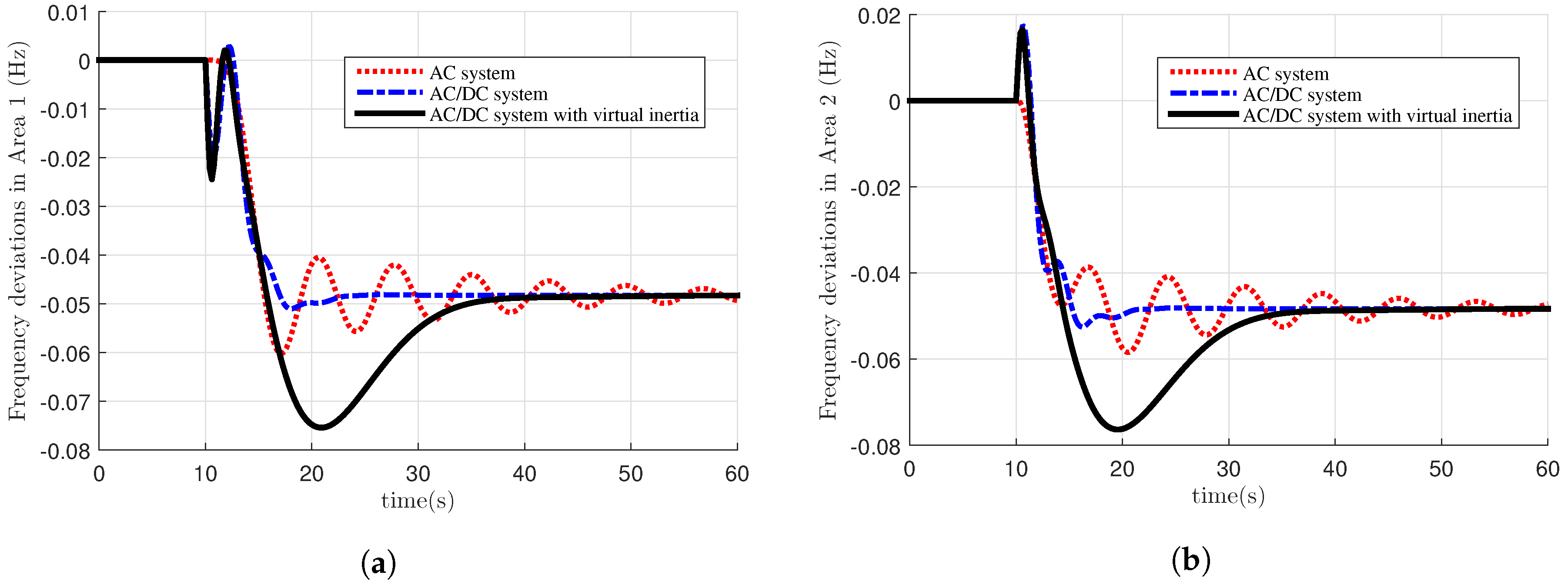
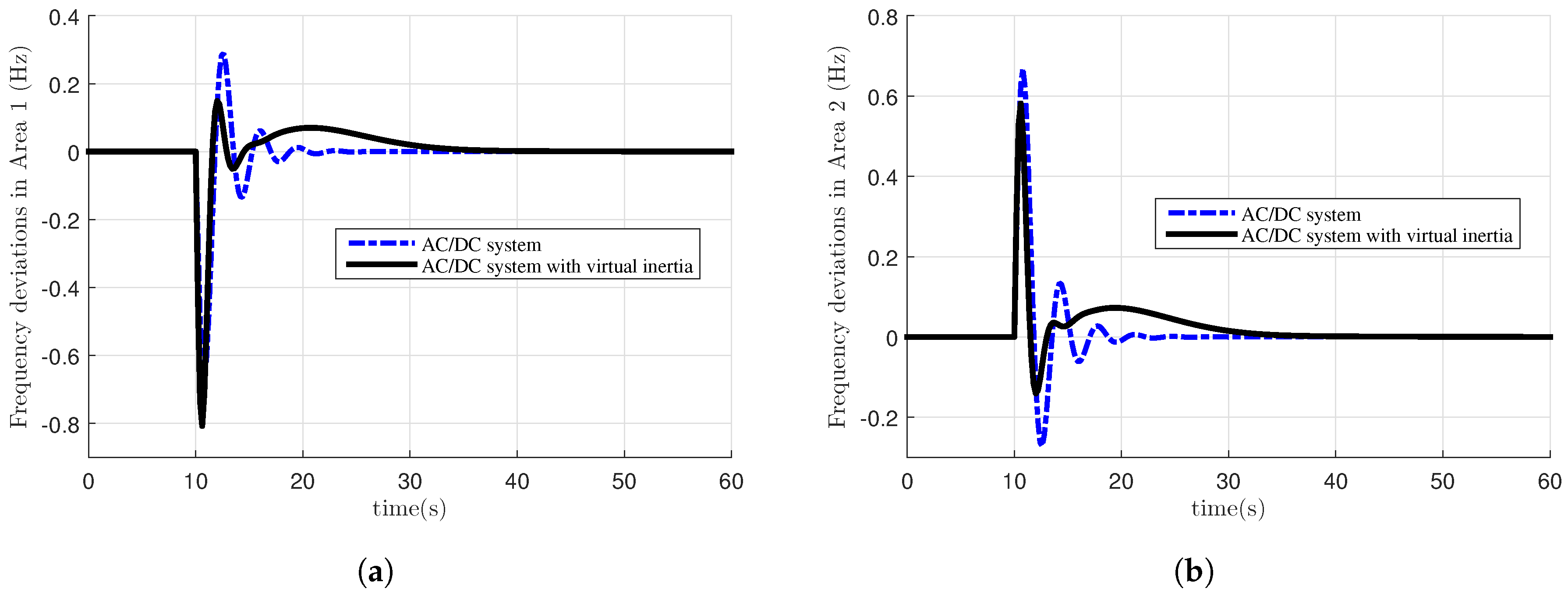
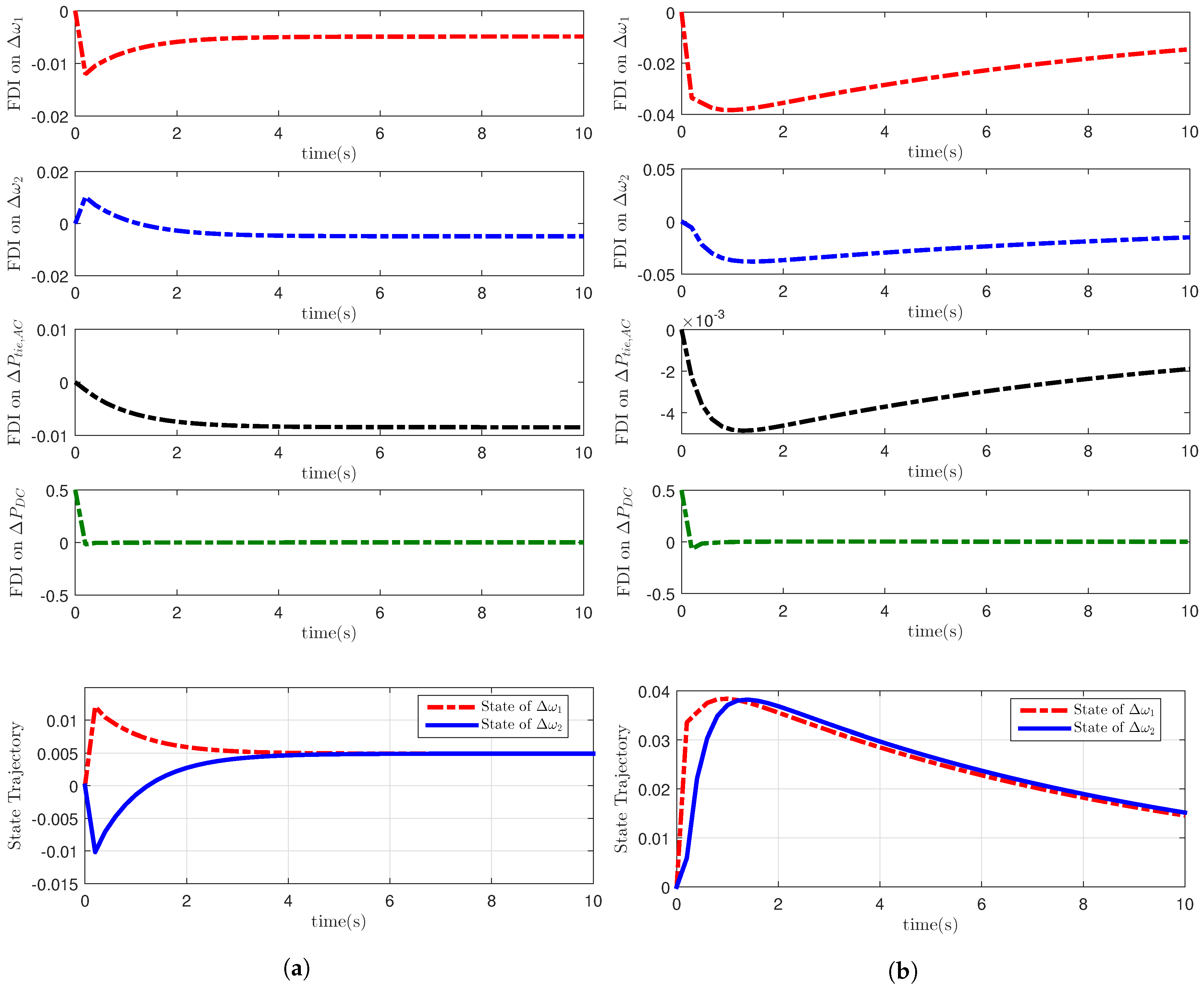
5. Simulation Results
- Normal AC system.
- AC/DC interconnected system.
- AC/DC interconnected system with virtual inertia.
5.1. DoS Attack Results
5.2. FDI Attack Results
5.3. Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| LFC | Load frequency control |
| HVDC | High-voltage direct-current |
| AC | Alternating-current |
| DoS | Denial of service |
| FDI | False data injection |
| RES | Renewable energy resources |
| ESS | Energy storage systems |
| SCADA | Supervisory control and data acquisition |
| GEN | Generation unit |
| ACE | Area control error |
| AGC | Automatic generation control |
| SPMC | Supplementary power modulation controller |
| ROCOF | Rate of change of frequency |
| MITM | Man-in-the-middle |
| ZOH | Zero-order hold |
| MFD | Maximum frequency deviation |
| SSFD | Steady-state frequency deviation |
| MILP | Mixed integer linear program |
References
- Alipoor, J.; Miura, Y.; Ise, T. Power System Stabilization Using Virtual Synchronous Generator With Alternating Moment of Inertia. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 451–458. [Google Scholar] [CrossRef]
- Castro, L.M.; Acha, E. On the Provision of Frequency Regulation in Low Inertia AC Grids Using HVDC Systems. IEEE Trans. Smart Grid 2016, 7, 2680–2690. [Google Scholar] [CrossRef]
- Zhang, W.; Rouzbehi, K.; Luna, A.; Gharehpetian, G.B.; Rodriguez, P. Multi-terminal HVDC grids with inertia mimicry capability. IET Renew. Power Gener. 2016, 10, 752–760. [Google Scholar] [CrossRef]
- Ten, C.W.; Liu, C.C.; Manimaran, G. Vulnerability Assessment of Cybersecurity for SCADA Systems. IEEE Trans. Power Syst. 2008, 23, 1836–1846. [Google Scholar] [CrossRef]
- Vrakopoulou, M.; Esfahani, P.M.; Margellos, K.; Lygeros, J.; Andersson, G. Cyber-attacks in the automatic generation control. In Cyber Physical Systems Approach to Smart Electric Power Grid; Springer: New York, NY, USA, 2015; pp. 303–328. [Google Scholar] [CrossRef]
- Sridhar, S.; Hahn, A.; Govindarasu, M. Cyber-Physical System Security for the Electric Power Grid. Proc. IEEE 2012, 100, 210–224. [Google Scholar] [CrossRef]
- Sridhar, S.; Govindarasu, M. Model-Based Attack Detection and Mitigation for Automatic Generation Control. IEEE Trans. Smart Grid 2014, 5, 580–591. [Google Scholar] [CrossRef]
- Ashok, A.; Wang, P.; Brown, M.; Govindarasu, M. Experimental evaluation of cyber attacks on Automatic Generation Control using a CPS Security Testbed. In Proceedings of the IEEE Power Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Khalaf, M.; Youssef, A.; El-Saadany, E. Joint Detection and Mitigation of False Data Injection Attacks in AGC Systems. IEEE Trans. Smart Grid 2019, 10, 4985–4995. [Google Scholar] [CrossRef]
- Beitollahi, H.; Deconinck, G. Analyzing well-known countermeasures against distributed denial of service attacks. Comput. Commun. 2012, 35, 1312–1332. [Google Scholar] [CrossRef]
- Liang, G.; Weller, S.R.; Zhao, J.; Luo, F.; Dong, Z.Y. The 2015 Ukraine Blackout: Implications for False Data Injection Attacks. IEEE Trans. Power Syst. 2017, 32, 3317–3318. [Google Scholar] [CrossRef]
- Pan, K.; Palensky, P.; Esfahani, P.M. From Static to Dynamic Anomaly Detection With Application to Power System Cyber Security. IEEE Trans. Power Syst. 2020, 35, 1584–1596. [Google Scholar] [CrossRef]
- Sridhar, S.; Manimaran, G. Data integrity attacks and their impacts on SCADA control system. In Proceedings of the IEEE Power Energy Society General Meeting, Providence, RI, USA, 25–29 July 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Esfahani, P.M.; Vrakopoulou, M.; Margellos, K.; Lygeros, J.; Andersson, G. Cyber attack in a two-area power system: Impact identification using reachability. In Proceedings of the American Control Conference (ACC), Baltimore, MD, USA, 30 June–2 July 2010; pp. 962–967. [Google Scholar] [CrossRef]
- Pan, K.; Gusain, D.; Palensky, P. Modelica-Supported Attack Impact Evaluation in Cyber Physical Energy System. In Proceedings of the IEEE 19th International Symposium on High Assurance Systems Engineering (HASE), Hangzhou, China, 3–5 January 2019; pp. 228–233. [Google Scholar] [CrossRef]
- Liu, S.; Liu, X.P.; El Saddik, A. Denial-of-Service (dos) attacks on load frequency control in smart grids. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 24–27 February 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Rahimi, K.; Parchure, A.; Centeno, V.; Broadwater, R. Effect of communication Time-Delay attacks on the performance of Automatic Generation Control. In Proceedings of the North American Power Symposium (NAPS), Charlotte, NC, USA, 4–6 October 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, J.; Domínguez-García, A.D. On the impact of communication delays on power system automatic generation control performance. In Proceedings of the North American Power Symposium (NAPS), Pullman, WA, USA, 7–9 September 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Bevrani, H.; Hiyama, T. On Load–Frequency Regulation With Time Delays: Design and Real-Time Implementation. IEEE Trans. Energy Convers. 2009, 24, 292–300. [Google Scholar] [CrossRef]
- Jiang, L.; Yao, W.; Wu, Q.H.; Wen, J.Y.; Cheng, S.J. Delay-Dependent Stability for Load Frequency Control With Constant and Time-Varying Delays. IEEE Trans. Power Syst. 2012, 27, 932–941. [Google Scholar] [CrossRef]
- Liu, S.; Liu, P.X.; Saddik, A.E. Modeling and Stability Analysis of Automatic Generation Control Over Cognitive Radio Networks in Smart Grids. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 223–234. [Google Scholar] [CrossRef]
- Rakhshani, E.; Remon, D.; Rodriguez, P. Effects of PLL and frequency measurements on LFC problem in multi-area HVDC interconnected systems. Int. J. Electr. Power Energy Syst. 2016, 81, 140–152. [Google Scholar] [CrossRef]
- Vural, A.M. Contribution of high voltage direct current transmission systems to inter-area oscillation damping: A review. Renew. Sustain. Energy Rev. 2016, 57, 892–915. [Google Scholar] [CrossRef]
- Rouzbehi, K.; Zhang, W.; Ignacio Candela, J.; Luna, A.; Rodriguez, P. Unified reference controller for flexible primary control and inertia sharing in multi-terminal voltage source converter-HVDC grids. Transm. Distrib. IET Gener. 2017, 11, 750–758. [Google Scholar] [CrossRef]
- Bevrani, H.; Hiyama, T. Intelligent Automatic Generation Control; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Chamorro, H.R.; Sevilla, F.R.S.; Gonzalez-Longatt, F.; Rouzbehi, K.; Chavez, H.; Sood, V.K. Innovative primary frequency control in low-inertia power systems based on wide-area RoCoF sharing. IET Energy Syst. Integr. 2020, 2, 151–160. [Google Scholar] [CrossRef]
- Rakhshani, E.; Rodriguez, P. Inertia Emulation in AC/DC Interconnected Power Systems Using Derivative Technique Considering Frequency Measurement Effects. IEEE Trans. Power Syst. 2017, 32, 3338–3351. [Google Scholar] [CrossRef]
- Gholami, A.; Mousavi, M.; Srivastava, A.K.; Mehrizi-Sani, A. Cyber-Physical Vulnerability and Security Analysis of Power Grid with HVDC Line. In Proceedings of the North American Power Symposium (NAPS), Wichita, KS, USA, 13–15 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Fan, R.; Lian, J.; Kalsi, K.; Elizondo, M. Impact of Cyber Attacks on High Voltage DC Transmission Damping Control. Energies 2018, 11, 1046. [Google Scholar] [CrossRef]
- Brown, H.E.; Demarco, C.L. Risk of Cyber-Physical Attack via Load With Emulated Inertia Control. IEEE Trans. Smart Grid 2018, 9, 5854–5866. [Google Scholar] [CrossRef]
- Roy, S.D.; Debbarma, S. Detection and Mitigation of Cyber-Attacks on AGC Systems of Low Inertia Power Grid. IEEE Syst. J. 2019, 14, 1–9. [Google Scholar] [CrossRef]
- Pan, K.; Rakhshani, E.; Palensky, P. False Data Injection Attacks on Hybrid AC/HVDC Interconnected Systems With Virtual Inertia—Vulnerability, Impact and Detection. IEEE Access 2020, 8, 141932–141945. [Google Scholar] [CrossRef]
- Kundur, P.; Balu, N.; Lauby, M. Power System Stability and Control; Discussion Paper Series; McGraw-Hill Education: New York, NY, USA, 1994. [Google Scholar] [CrossRef]
- Rakhshani, E.; Remon, D.; Mir Cantarellas, A.; Rodriguez, P. Analysis of derivative control based virtual inertia in multi-area high-voltage direct current interconnected power systems. Transm. Distrib. IET Gener. 2016, 10, 1458–1469. [Google Scholar] [CrossRef]
- Dolk, V.S.; Tesi, P.; De Persis, C.; Heemels, W.P.M.H. Event-Triggered Control Systems under Denial-of-Service Attacks. IEEE Trans. Control Netw. Syst. 2017, 4, 93–105. [Google Scholar] [CrossRef]
- Amin, S.; Cárdenas, A.A.; Sastry, S.S. Safe and secure networked control systems under denial-of-service attacks. In International Workshop on Hybrid Systems: Computation and Control; Springer: New York, NY, USA, 2009; pp. 31–45. [Google Scholar]
- Pan, K.; Teixeira, A.; Cvetkovic, M.; Palensky, P. Cyber Risk Analysis of Combined Data Attacks Against Power System State Estimation. IEEE Trans. Smart Grid 2018, 10, 3044–3056. [Google Scholar] [CrossRef]
- Ogata, K. Discrete-time Control Systems, 2nd ed.; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Chen, C.; Zhang, K.; Yuan, K.; Zhu, L.; Qian, M. Novel Detection Scheme Design Considering Cyber Attacks on Load Frequency Control. IEEE Trans. Ind. Inform. 2018, 14, 1932–1941. [Google Scholar] [CrossRef]
- Lin, H.; Antsaklis, P.J. Stability and Stabilizability of Switched Linear Systems: A Survey of Recent Results. IEEE Trans. Autom. Control 2009, 54, 308–322. [Google Scholar] [CrossRef]
- Teixeira, A.; Sou, K.C.; Sandberg, H.; Johansson, K.H. Secure control systems: A quantitative risk management approach. IEEE Control Syst. 2015, 35, 24–45. [Google Scholar] [CrossRef]
- Teixeira, A.; Shames, I.; Sandberg, H.; Johansson, K.H. A secure control framework for resource-limited adversaries. Automatica 2015, 51, 135–148. [Google Scholar] [CrossRef]


| Parameters | Area 1 | Area 2 | ||
|---|---|---|---|---|
| GEN 1 | GEN 2 | GEN 3 | GEN 4 | |
| 0.38 | 0.38 | 0.36 | 0.39 | |
| 2.4 | 2.5 | 2.5 | 2.7 | |
| 0.5 | 0.5 | 0.5 | 0.5 | |
| 102 | 102 | |||
| 20 | 25 | |||
| 0.425 | 0.396 | |||
| 0.7 | 0.7 | |||
| 0.026 | 0.026 | |||
| 0.245 | ||||
| 0.3 | ||||
| 0.1 | ||||
| 4.7 | ||||
| 0.87 | ||||
| 0.093 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, K.; Dong, J.; Rakhshani, E.; Palensky, P. Effects of Cyber Attacks on AC and High-Voltage DC Interconnected Power Systems with Emulated Inertia. Energies 2020, 13, 5583. https://doi.org/10.3390/en13215583
Pan K, Dong J, Rakhshani E, Palensky P. Effects of Cyber Attacks on AC and High-Voltage DC Interconnected Power Systems with Emulated Inertia. Energies. 2020; 13(21):5583. https://doi.org/10.3390/en13215583
Chicago/Turabian StylePan, Kaikai, Jingwei Dong, Elyas Rakhshani, and Peter Palensky. 2020. "Effects of Cyber Attacks on AC and High-Voltage DC Interconnected Power Systems with Emulated Inertia" Energies 13, no. 21: 5583. https://doi.org/10.3390/en13215583
APA StylePan, K., Dong, J., Rakhshani, E., & Palensky, P. (2020). Effects of Cyber Attacks on AC and High-Voltage DC Interconnected Power Systems with Emulated Inertia. Energies, 13(21), 5583. https://doi.org/10.3390/en13215583







