Experimental Investigation and Mechanism Analysis on Rock Damage by High Voltage Spark Discharge in Water: Effect of Electrical Conductivity
Abstract
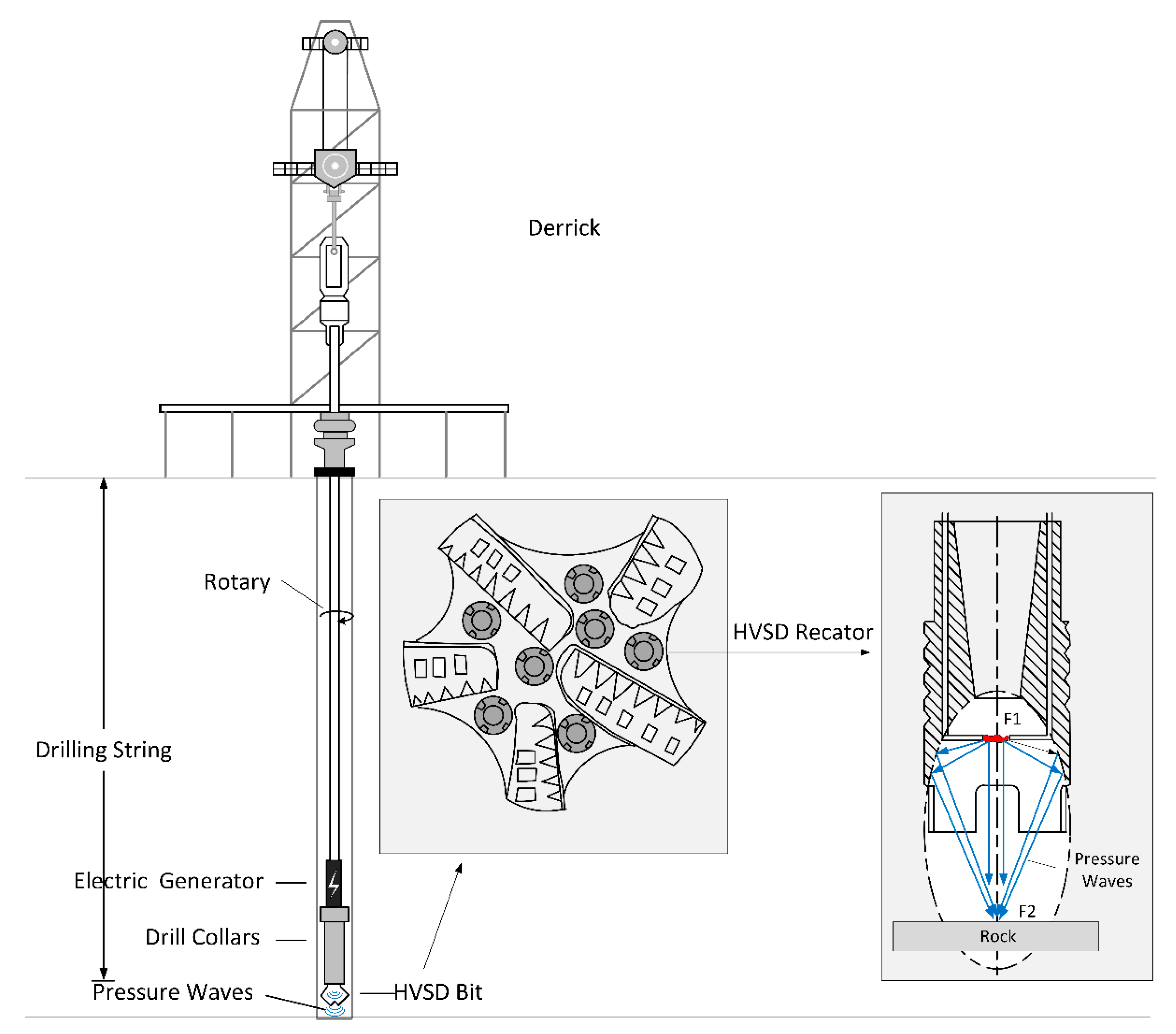
1. Introduction
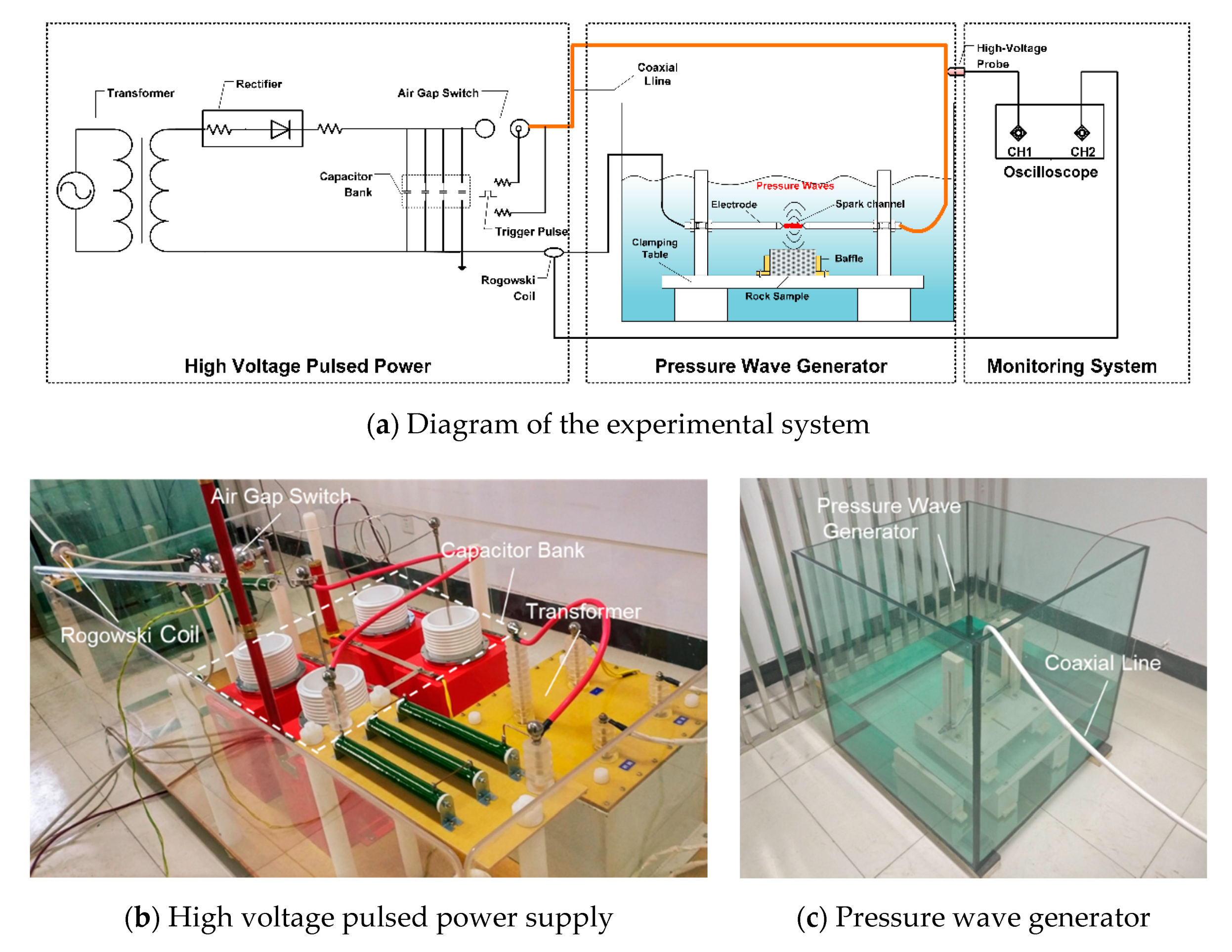
2. Experiment
2.1. Sample Preparation
2.2. Experimental Procedure
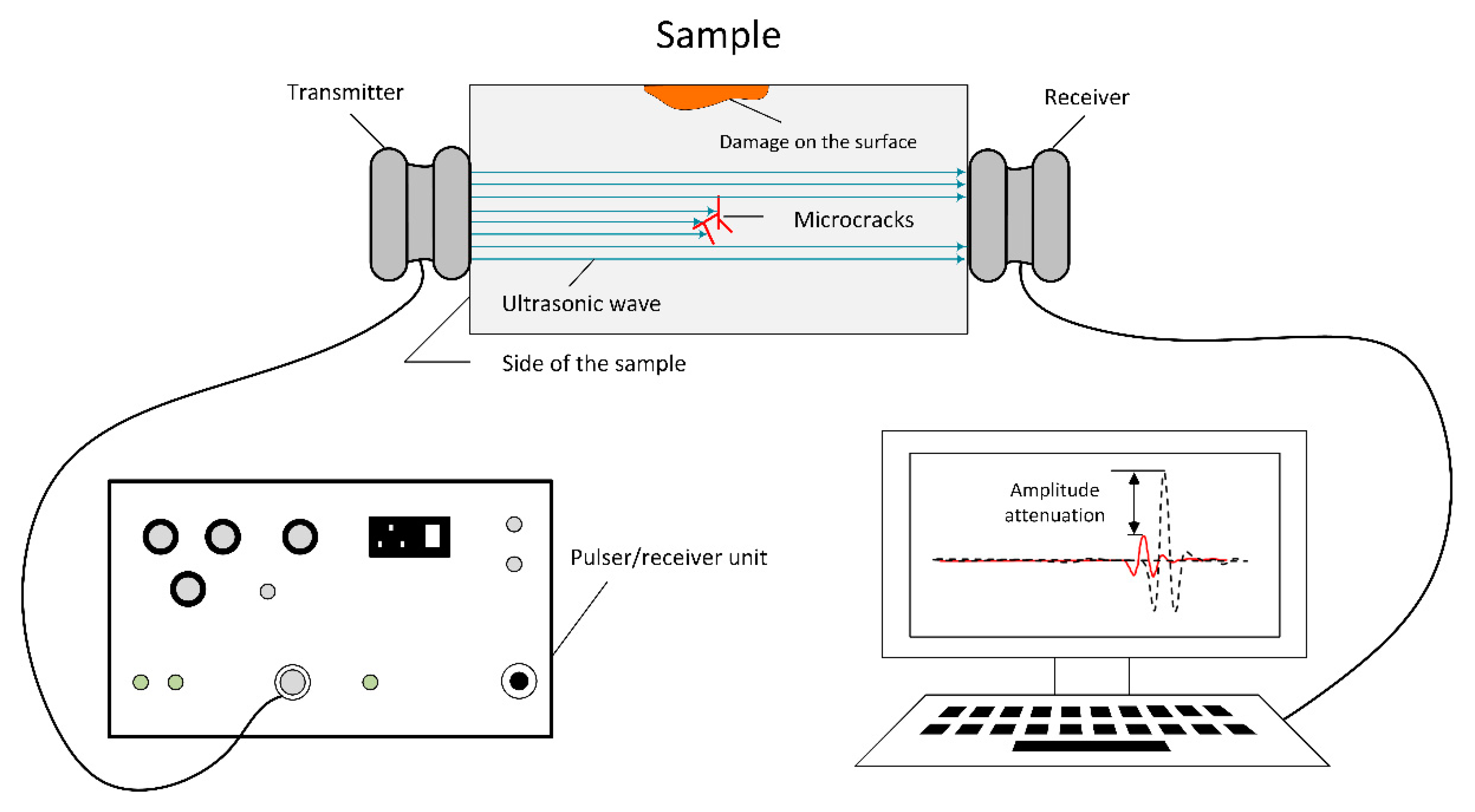
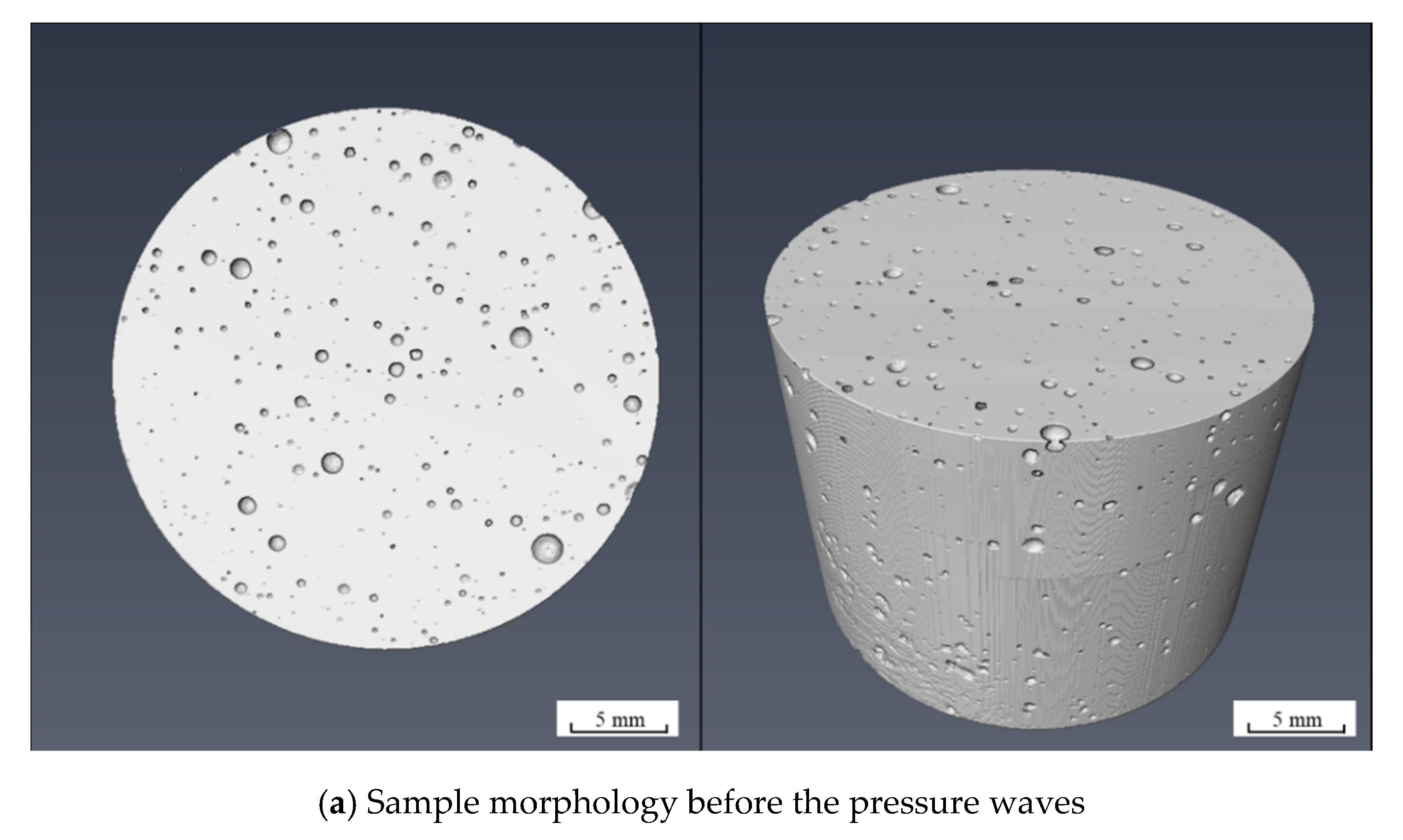
2.3. Analysis of Damage Characteristics
3. Results and Discussion
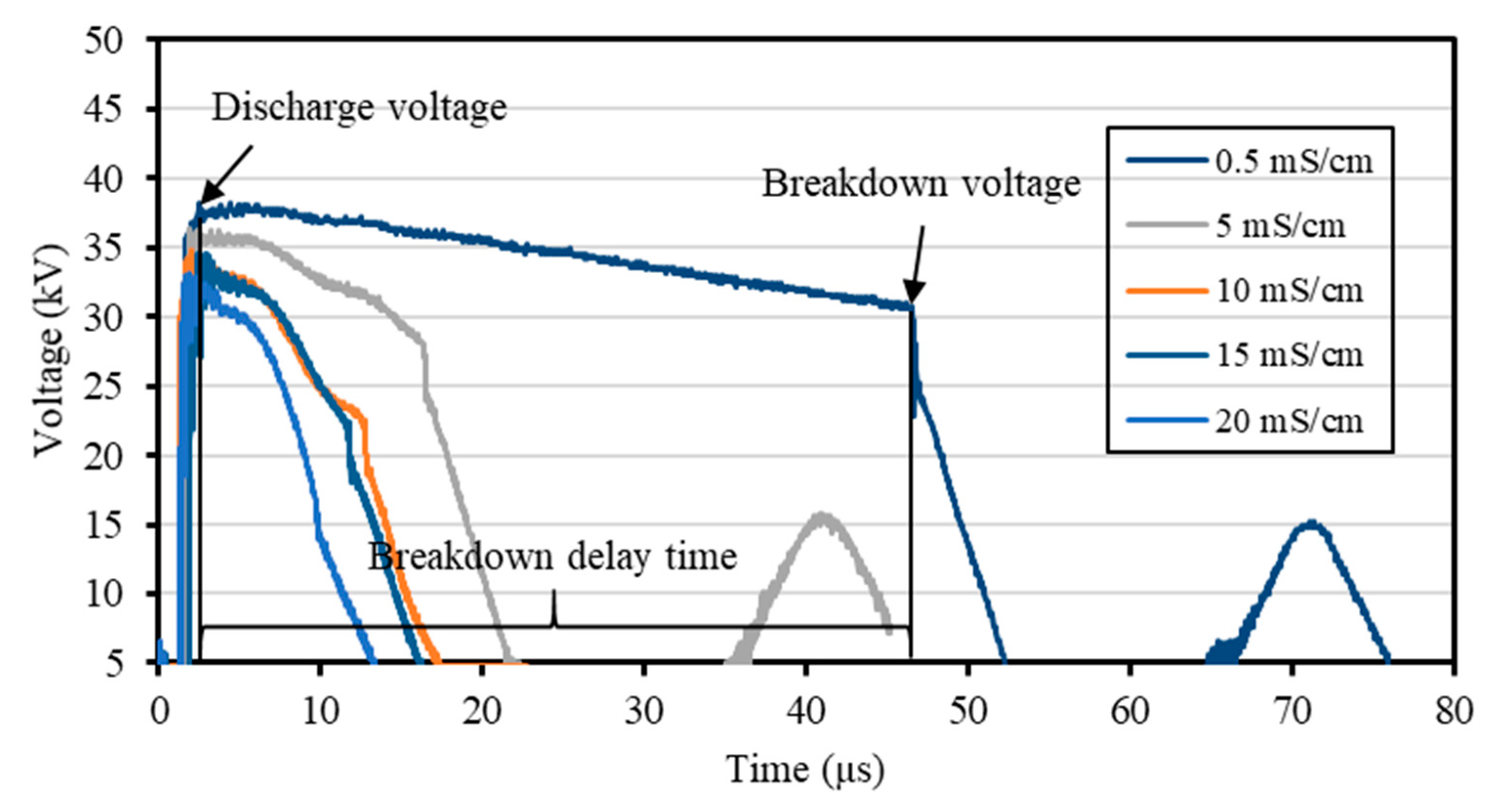
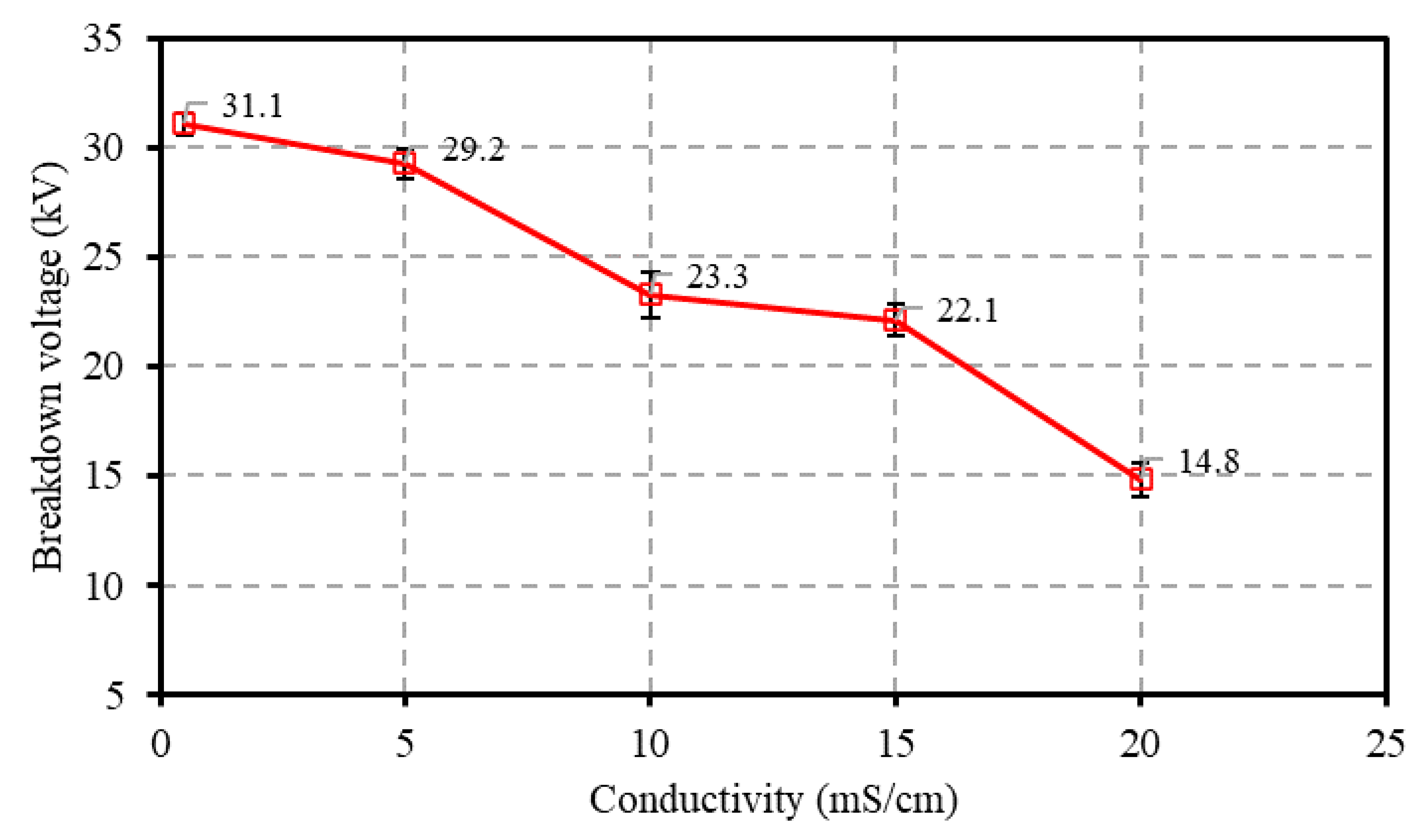
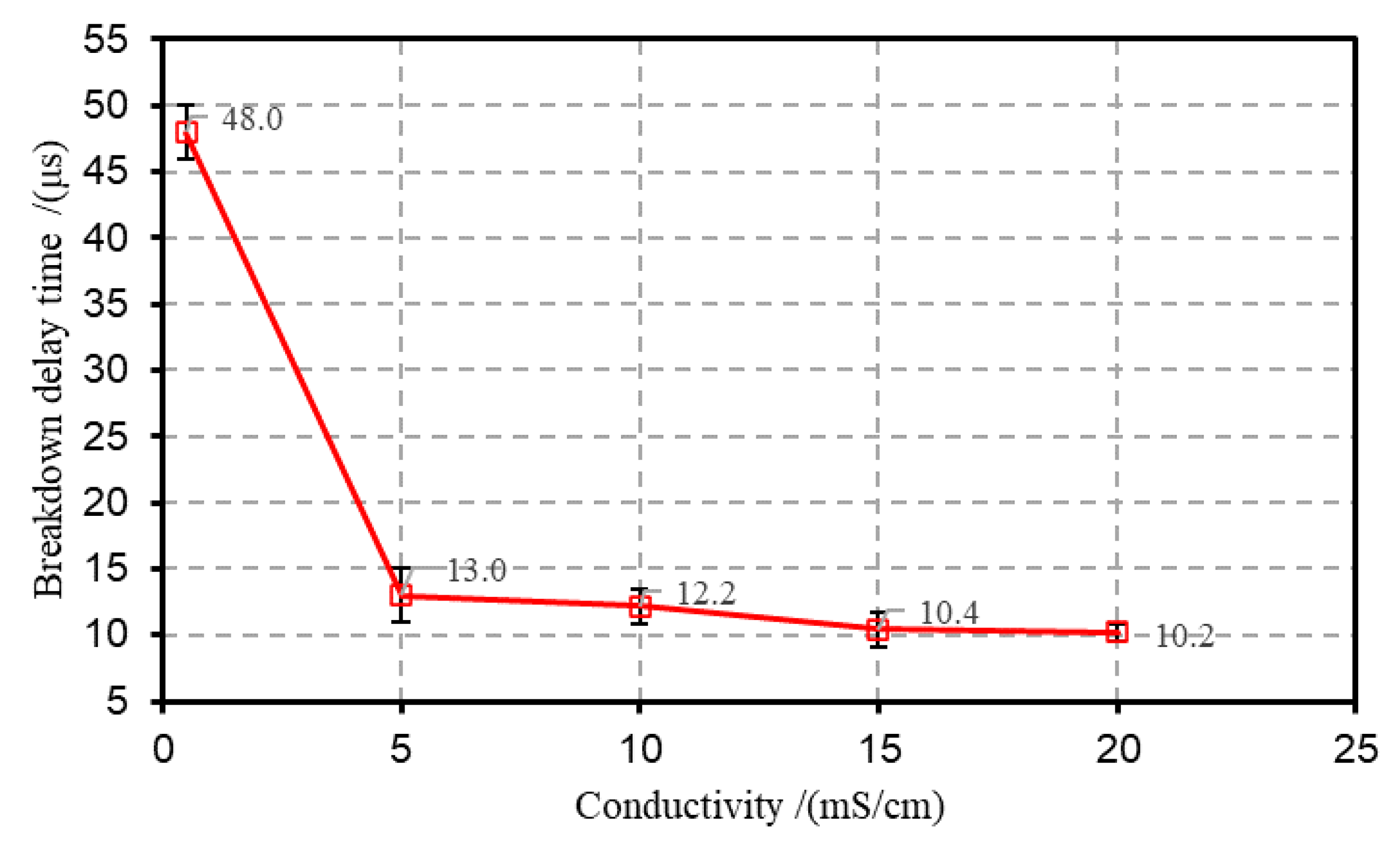
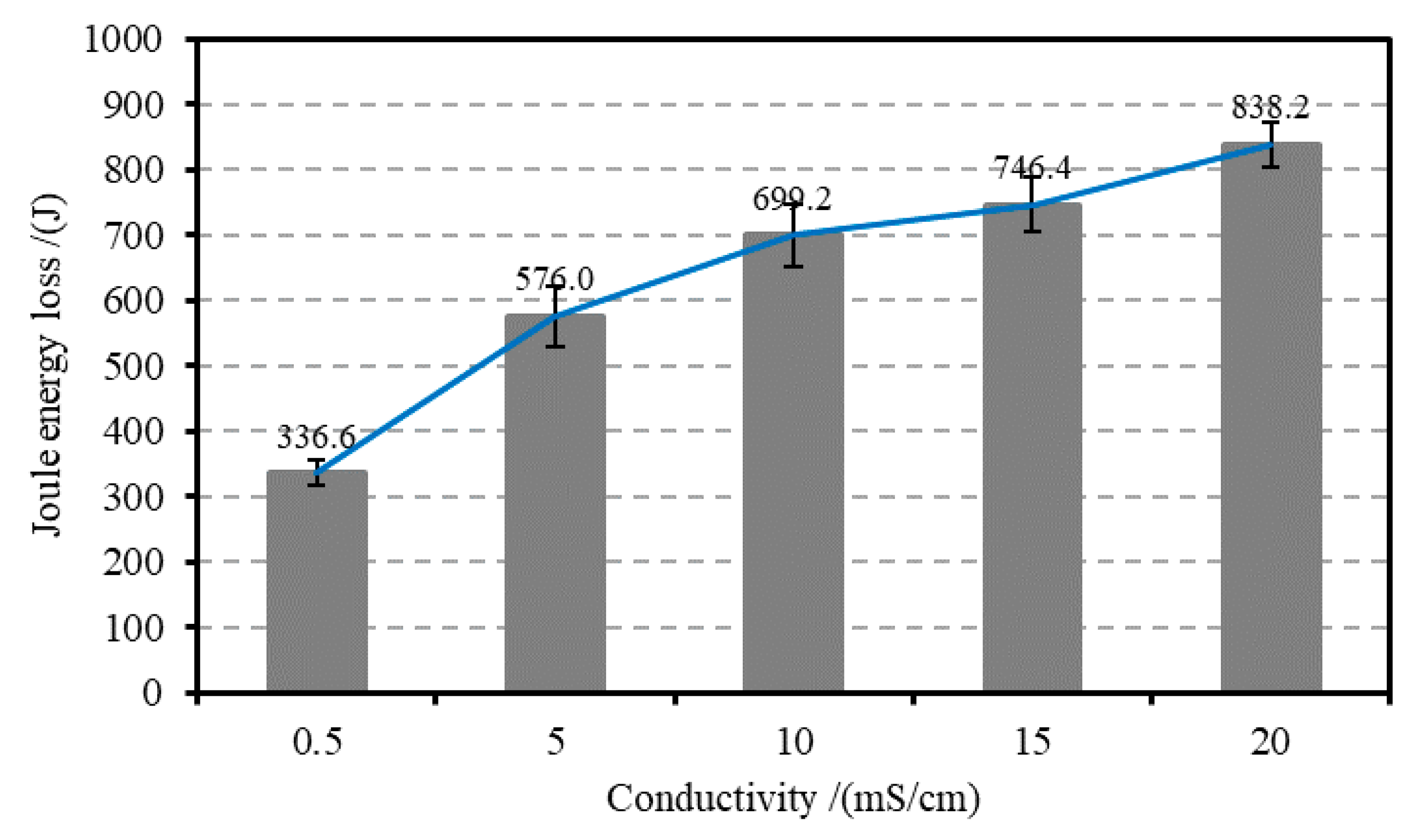
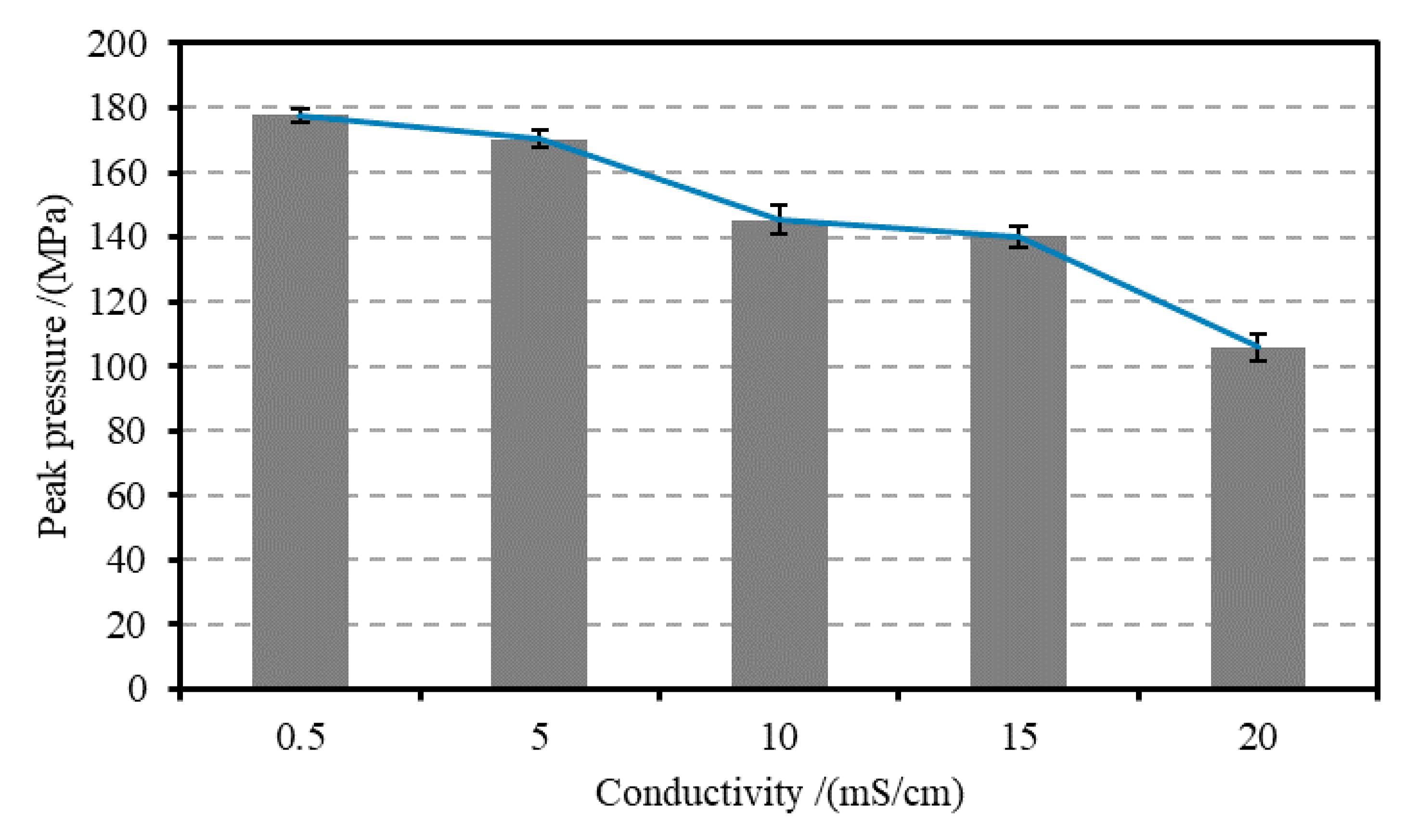
3.1. Electrical Characteristics of Underwater Discharge at Different Conductivity
3.2. Damage of Samples under Different Electrical Conductivity
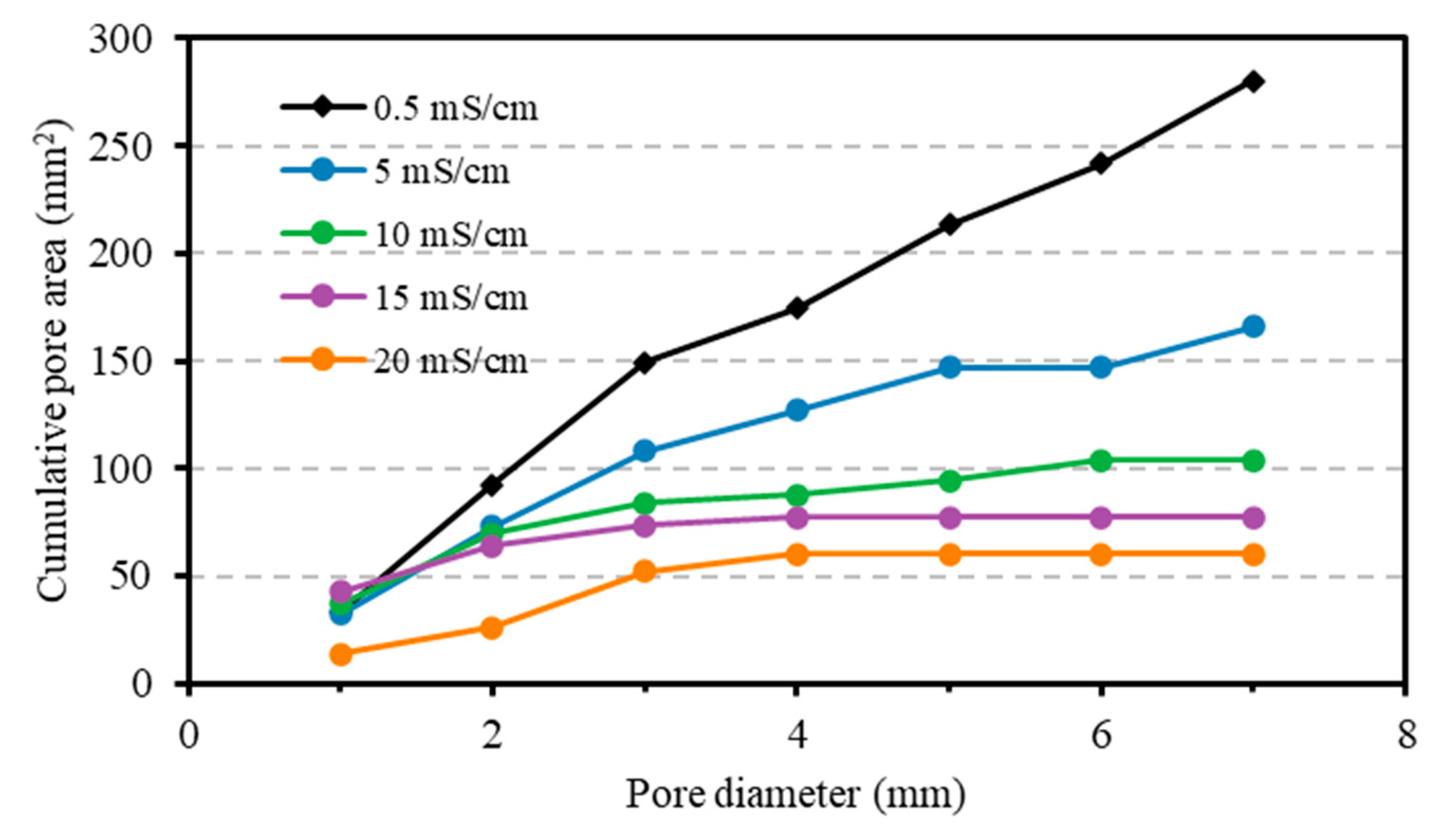
3.2.1. CT Results and Discussion
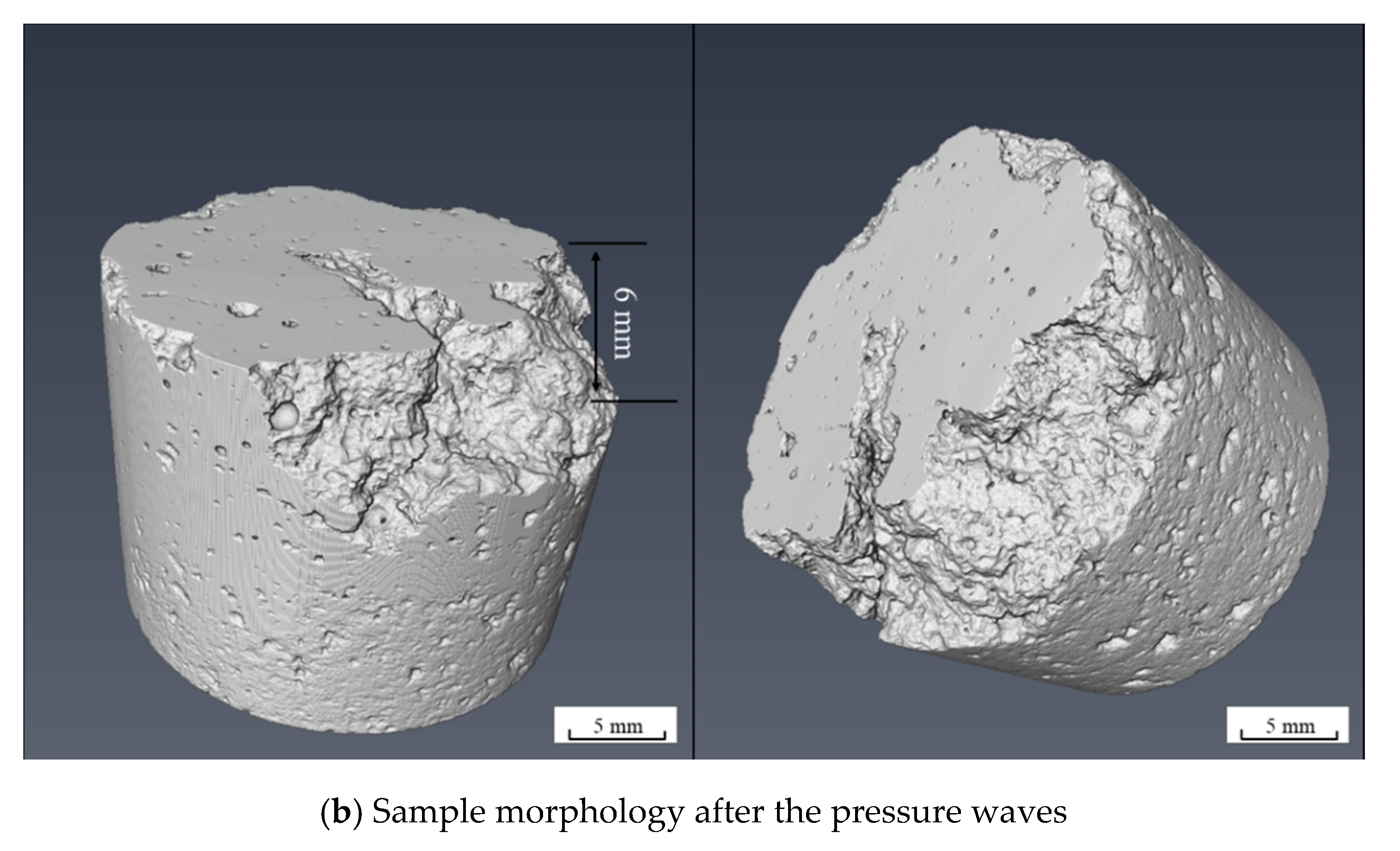
3.2.2. Surface Damage Results and Discussion
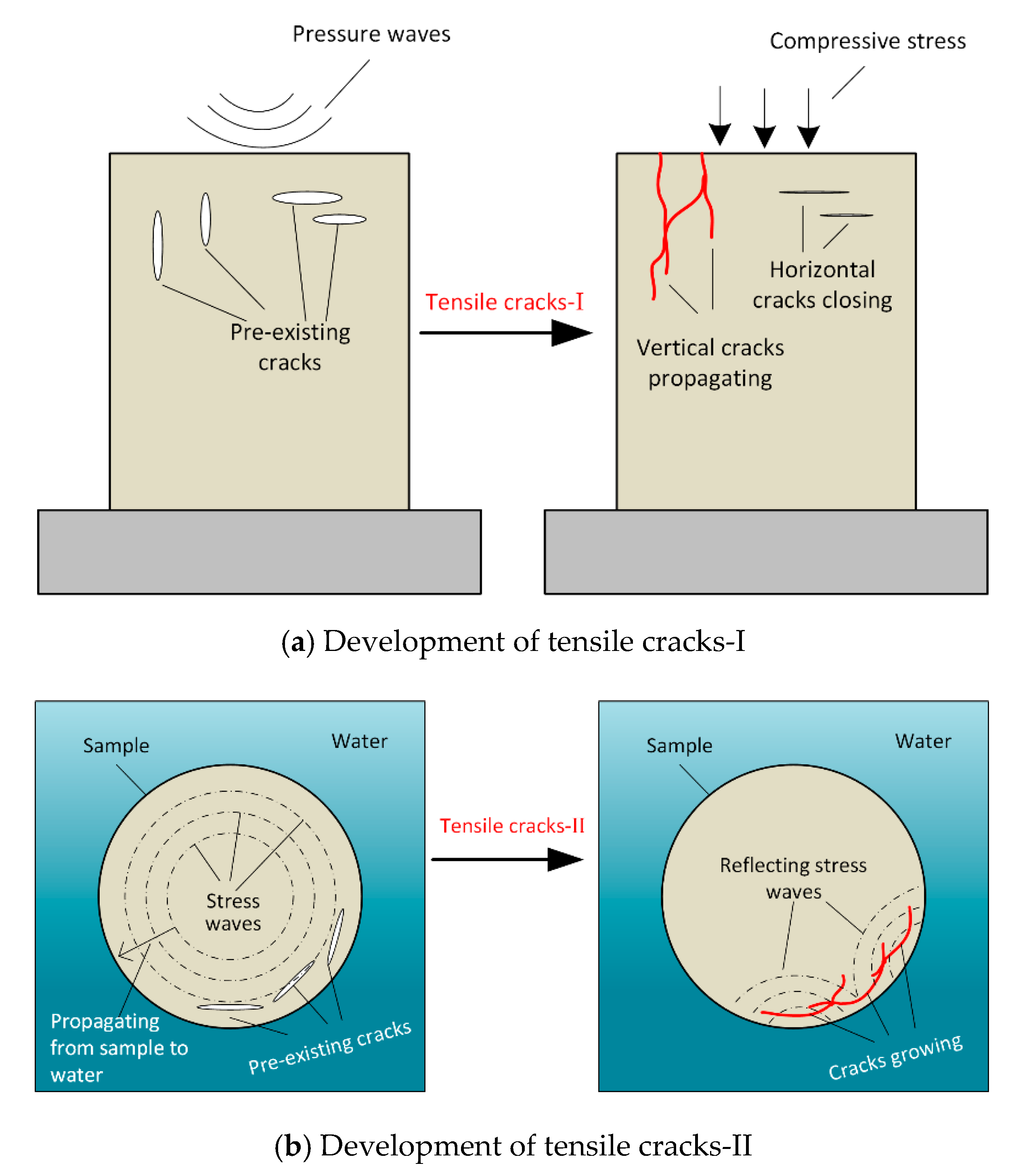
3.3. Internal Damage Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xu, Z.; Reed, C.B.; Konercki, G.; Parker, R.A.; Gahan, B.C.; Batarseh, S.; Graves, R.M.; Figueroa, H.; Skinner, N. Specific energy for pulsed laser rock drilling. J. Laser Appl. 2003, 15, 25–30. [Google Scholar] [CrossRef]
- Sinha, P.; Gour, A. Laser Drilling Research and Application: An Update. In Proceedings of the SPE/IADC Indian Drilling Technology Conference and Exhibition, Mumbai, India, 16–18 October 2006; Society of Petroleum Engineers: Richardson, TX, USA, 2006. [Google Scholar]
- Salehi, I.A.; Gahan, B.C.; Batarseh, S. Laser Drilling-Drilling with the Power of Light; Institute of Gas Technology: Des Plaines, IL, USA, 2007. [Google Scholar]
- Gajdos, M.; Kocis, I.; Kristofic, T.; Horvath, G.; Jankovic, S. Utilization of Electrical Plasma for Hard Rock Drilling and Casing Milling. In Proceedings of the SPE/IADC Drilling Conference and Exhibition, London, UK, 17–19 March 2015. [Google Scholar]
- Gajdos, M.; Kristofic, T.; Jankovic, S.; Horvath, G.; Kocis, I. Use of Plasma-Based Tool for Plug and Abandonment. In Proceedings of the SPE Offshore Europe Conference and Exhibition, Aberdeen, UK, 8–11 September 2015; Society of Petroleum Engineers: Richardson, TX, USA, 2015. [Google Scholar]
- Gravley, W. Review of downhole measurement-while-drilling systems. J. Pet. Technol. 1983, 35, 1439–1445. [Google Scholar] [CrossRef]
- Noureldin, A.; Irvine-Halliday, D.; Mintchev, M.P. Measurement-while-drilling surveying of highly inclined and horizontal well sections utilizing single-axis gyro sensing system. Meas. Sci. Technol. 2004, 15, 2426. [Google Scholar] [CrossRef]
- Yutkin, L.A. Electrohydraulic Effect. Available online: https://scholar.google.com.hk/scholar?hl=zh-CN&as_sdt=0%2C5&q=+8.%09Yutkin%2C+L.A.+Electrohydraulic+Effect%3B+Air+Force+Systems+Command+Wright-Patterson+Afb+oh+Foreign+Technology+Division%2C+1961.&btnG= (accessed on 14 October 2020).
- Chung, K.; Lee, S.; Hwang, Y.S.; Kim, C.Y. Modeling of pulsed spark discharge in water and its application to well cleaning. Curr. Appl. Phys. 2015, 15, 977–986. [Google Scholar] [CrossRef]
- Bodykov, D.U.; Abdikarimov, M.S.; Seitzhanova, M.A.; Nazhipkyzy, M.; Mansurov, Z.A.; Kabdoldina, A.O.; Ualiyev, Z.R. Processing of Oil Sludge with the Use of the Electrohydraulic Effect. J. Eng. Phys. Thermophys. 2017, 90, 1096–1101. [Google Scholar] [CrossRef]
- Xiong, L.; Liu, Y.; Yuan, W.; Huang, S.; Li, H.; Lin, F.; Pan, Y.; Ren, Y. Cyclic shock damage characteristics of electrohydraulic discharge shockwaves. J. Phys. D 2020, 53, 185502. [Google Scholar] [CrossRef]
- Chen, W.; Maurel, O.; Borderie, C.L.; Reess, T.; Ferron, A.D.; Matallah, M.; Pijaudier-Cabot, G.; Jacques, A.; Rey-Bethbeder, F. Experimental and numerical study of shock wave propagation in water generated by pulsed arc electrohydraulic discharges. Heat Mass Transf. 2014, 50, 673–684. [Google Scholar] [CrossRef]
- Chen, W.; La Borderie, C.; Maurel, O.; Pijaudier Cabot, G.; Rey Bethbeder, F. Simulation of damage–permeability coupling for mortar under dynamic loads. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 457–474. [Google Scholar] [CrossRef]
- Chen, W.; Maurel, O.; Reess, T.; De Ferron, A.S.; La Borderie, C.; Pijaudier-Cabot, G.; Rey-Bethbeder, F.; Jacques, A. Experimental study on an alternative oil stimulation technique for tight gas reservoirs based on dynamic shock waves generated by pulsed arc electrohydraulic discharges. J. Pet. Sci. Eng. 2012, 88, 67–74. [Google Scholar] [CrossRef]
- Li, C.; Duan, L.; Tan, S.; Chikhotkin, V. Influences on high-voltage electro pulse boring in granite. Energies 2018, 11, 2461. [Google Scholar] [CrossRef]
- Li, C.; Duan, L.; Tan, S.; Chikhotkin, V.; Fu, W. Damage model and numerical experiment of high-voltage electro pulse boring in granite. Energies 2019, 12, 727. [Google Scholar] [CrossRef]
- Cai, Z.; Zhang, H.; Li, J.; Zheng, J.; Yu, Q.; Liu, K.; Liu, Y. New Technology to Assist Drilling to Improve Drilling Rate in Unconventional Gas Resources: Pulsed Arc Plasma Shockwave Technology. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, UAE, 12–15 November 2018; Society of Petroleum Engineers: Richardson, TX, USA, 2018. [Google Scholar]
- Cai, Z.; Zhang, H.; Li, J.; Yang, M.; Yu, Q.; Zheng, J.; Liu, K. An Experimental Study of Using Plasma Shock Wave for Rock Damage. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2019. [Google Scholar]
- Hui, Z.; Zhixiang, C. Well Drilling System and Method. CN108533172B, 28 May 2019. [Google Scholar]
- Hui, Z.; Cai, Z. Plasma Generating Device, Fracturing System and Fracturing Method. CN111101915A, 5 May 2020. [Google Scholar]
- Cathignol, D.; Mestas, J.L.; Gomez, F.; Lenz, P. Influence of water conductivity on the efficiency and the reproducibility of electrohydraulic shock wave generation. Ultrasound Med. Biol. 1991, 17, 819–828. [Google Scholar] [CrossRef]
- Zhu, L.; He, Z.; Gao, Z.; Tan, F.; Yue, X.; Chang, J. Research on the influence of conductivity to pulsed arc electrohydraulic discharge in water. J. Electrostat. 2014, 72, 53–58. [Google Scholar] [CrossRef]
- Yaşar, E.; Ranjith, P.G.; Viete, D.R. An experimental investigation into the drilling and physico-mechanical properties of a rock-like brittle material. J. Pet. Sci. Eng. 2011, 76, 185–193. [Google Scholar] [CrossRef]
- Wang, H.; Wandell, R.J.; Tachibana, K.; Voráč, J.; Locke, B.R. The influence of liquid conductivity on electrical breakdown and hydrogen peroxide production in a nanosecond pulsed plasma discharge generated in a water-film plasma reactor. J. Phys. D 2018, 52, 75201. [Google Scholar] [CrossRef]
- Marinov, I.; Guaitella, O.; Rousseau, A.; Starikovskaia, S.M. Modes of underwater discharge propagation in a series of nanosecond successive pulses. J. Phys. D 2013, 46, 464013. [Google Scholar] [CrossRef]
- Fujita, H.; Kanazawa, S.; Ohtani, K.; Komiya, A.; Kaneko, T.; Sato, T. Initiation process and propagation mechanism of positive streamer discharge in water. J. Appl. Phys. 2014, 116, 213301. [Google Scholar] [CrossRef]
- Timoshkin, I.V.; Fouracre, R.A.; Given, M.J.; Macgregor, S.J. Hydrodynamic modeling of transient cavities in fluids generated by high voltage spark discharges. J. Phys. D 2006, 39, 4808. [Google Scholar] [CrossRef]
- Inglis, C.E. Stresses in a Plate Due to the Presence of Cracks and Sharp Corners. Trans. Inst. Naval Archit 1913, 55, 219–241. [Google Scholar]
- Fishman, Y.A. Features of compressive failure of brittle materials. Int. J. Rock Mech. Min. Sci. 2008, 45, 993–998. [Google Scholar] [CrossRef]
- Han, L.; He, Y.; Zhang, H. Study of rock splitting failure based on griffith strength theory. Int. J. Rock Mech. Min. Sci. 2016, 83, 116–121. [Google Scholar] [CrossRef]
- Wong, R.; Lin, P.; Tang, C.A. Experimental and numerical study on splitting failure of brittle solids containing single pore under uniaxial compression. Mech. Mater 2006, 38, 142–159. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.; Wang, J. Numerical analysis of blast-induced wave propagation and spalling damage in a rock plate. Int. J. Rock Mech. Min. Sci. 2008, 45, 600–608. [Google Scholar] [CrossRef]
- Cleveland, R.O.; Sapozhnikov, O.A. Modeling elastic wave propagation in kidney stones with application to shock wave lithotripsy. J. Acoust. Soc. Am. 2005, 118, 2667–2676. [Google Scholar] [CrossRef] [PubMed]
- Cao, S.; Zhang, Y.; Liao, D.; Zhong, P.; Wang, K.G. Shock-induced damage and dynamic fracture in cylindrical bodies submerged in liquid. Int. J. Solids Struct. 2019, 169, 55–71. [Google Scholar] [CrossRef]
- Touya, G.; Reess, T.; Pécastaing, L.; Gibert, A.; Domens, P. Development of subsonic electrical discharges in water and measurements of the associated pressure waves. J. Phys. D 2006, 39, 5236. [Google Scholar] [CrossRef]



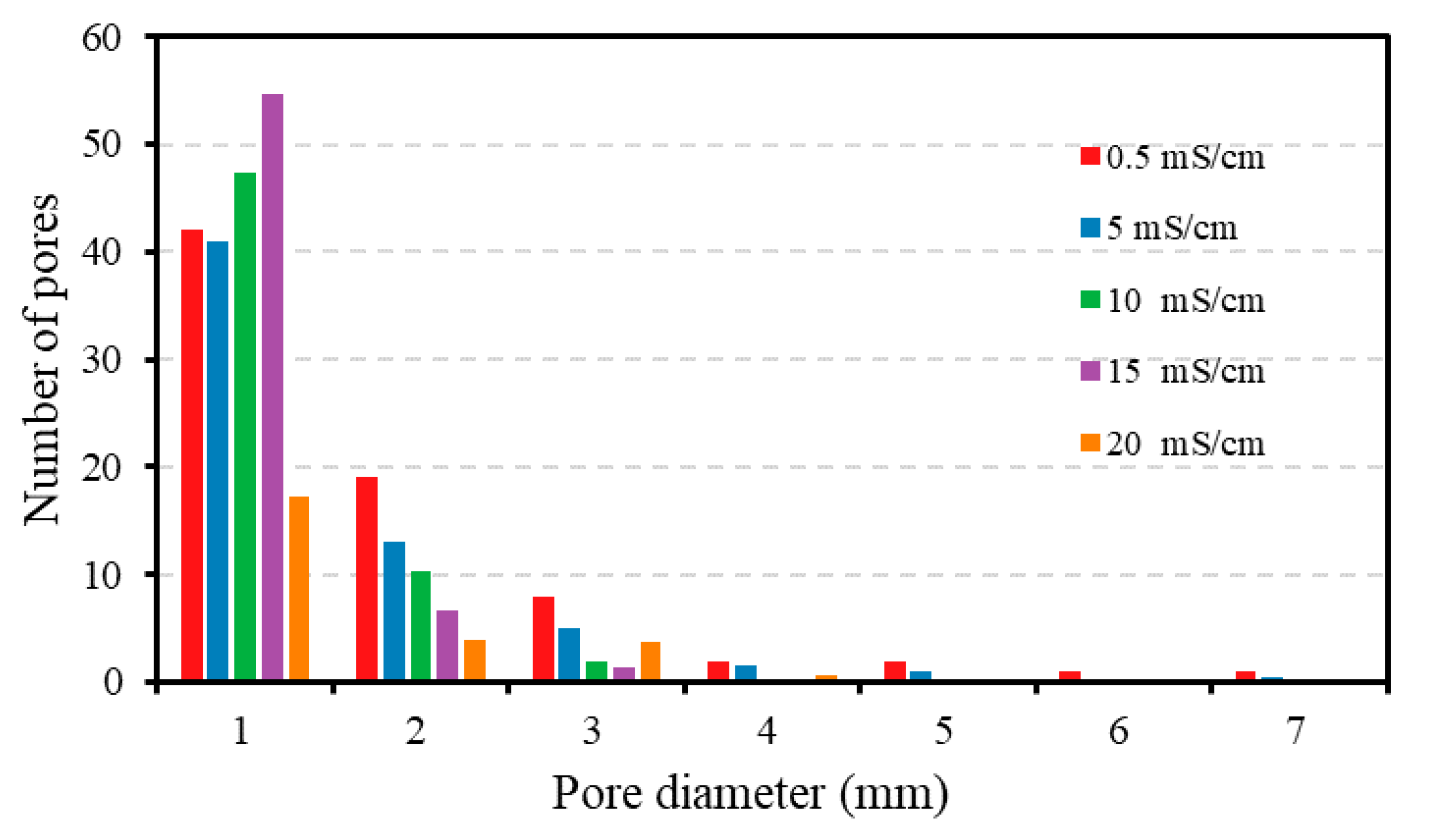
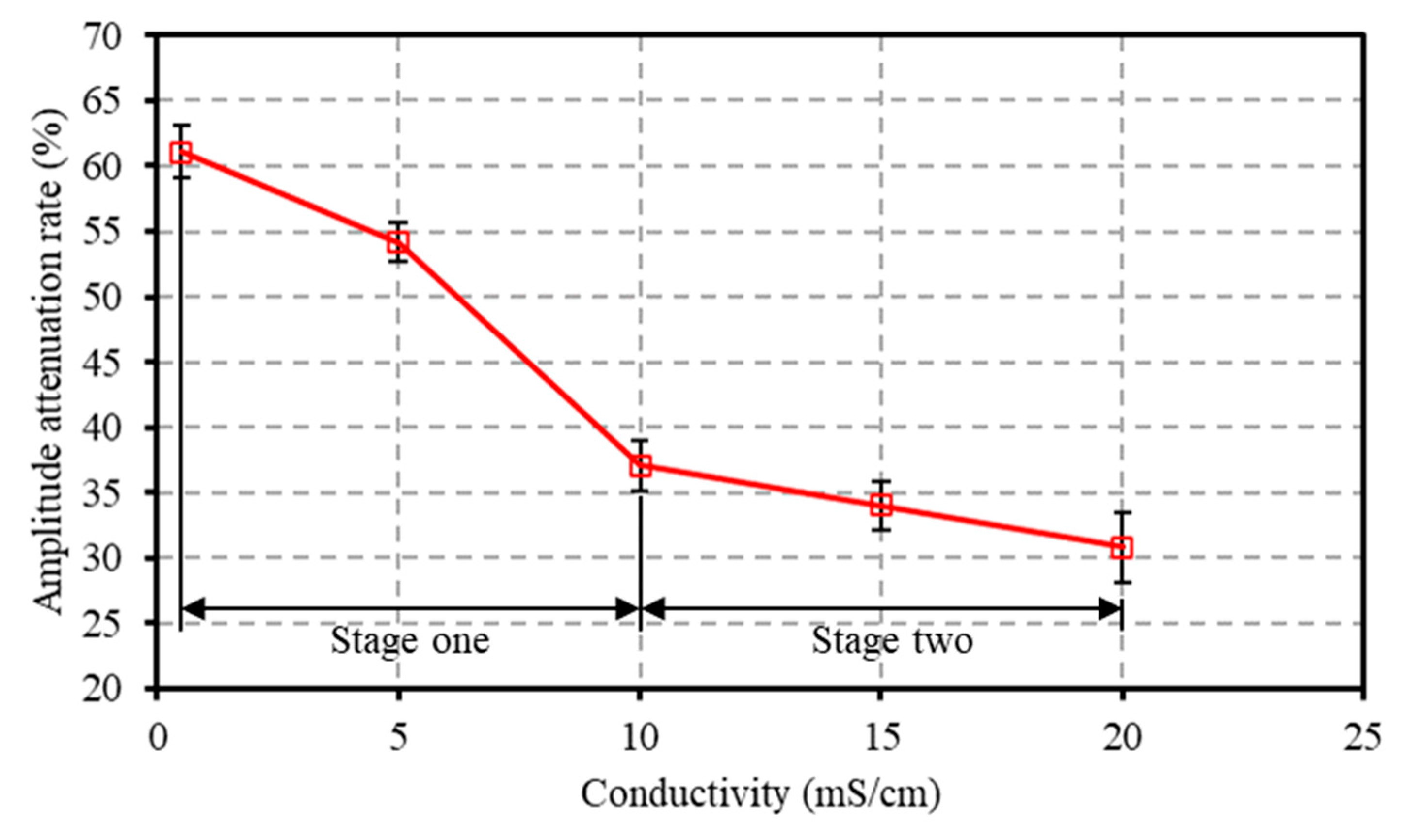
| Sample | Density (g/cm3) | Sound Velocity (m/s) | Acoustic Impedance (g/m2s) | Compressive Strength (MPa) | Tensile Strength (MPa) | Elastic Modulus (MPa) |
|---|---|---|---|---|---|---|
| Mortar | 2.44 | 4000 | 9.76 × 106 | 42 | 3.5 | 14,950 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Z.; Zhang, H.; Liu, K.; Chen, Y.; Yu, Q. Experimental Investigation and Mechanism Analysis on Rock Damage by High Voltage Spark Discharge in Water: Effect of Electrical Conductivity. Energies 2020, 13, 5432. https://doi.org/10.3390/en13205432
Cai Z, Zhang H, Liu K, Chen Y, Yu Q. Experimental Investigation and Mechanism Analysis on Rock Damage by High Voltage Spark Discharge in Water: Effect of Electrical Conductivity. Energies. 2020; 13(20):5432. https://doi.org/10.3390/en13205432
Chicago/Turabian StyleCai, Zhixiang, Hui Zhang, Kerou Liu, Yufei Chen, and Qing Yu. 2020. "Experimental Investigation and Mechanism Analysis on Rock Damage by High Voltage Spark Discharge in Water: Effect of Electrical Conductivity" Energies 13, no. 20: 5432. https://doi.org/10.3390/en13205432
APA StyleCai, Z., Zhang, H., Liu, K., Chen, Y., & Yu, Q. (2020). Experimental Investigation and Mechanism Analysis on Rock Damage by High Voltage Spark Discharge in Water: Effect of Electrical Conductivity. Energies, 13(20), 5432. https://doi.org/10.3390/en13205432





