Voltage Reduction in Medium Voltage Distribution Systems Using Constant Power Factor Control of PV PCS
Abstract
1. Introduction
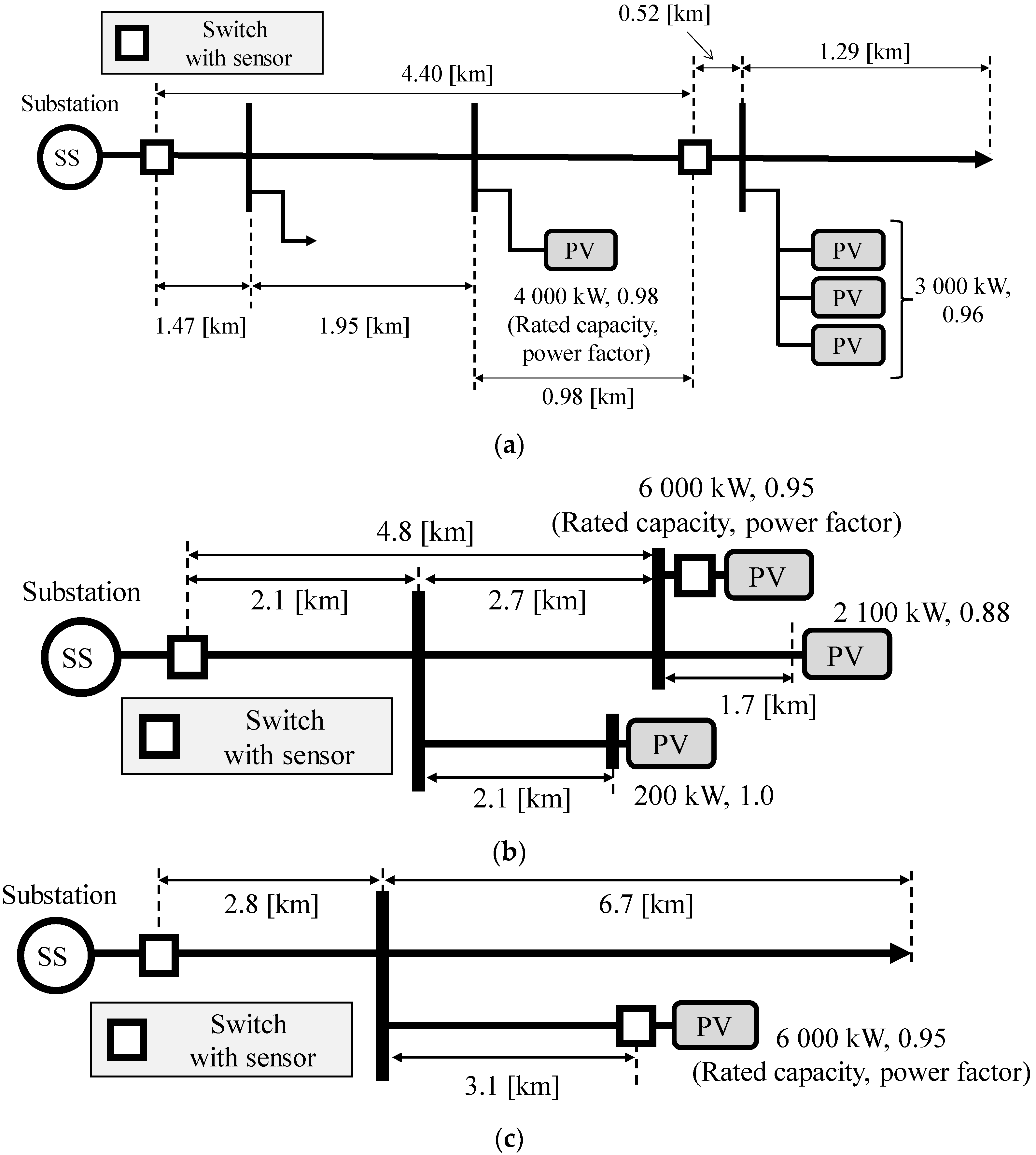
2. Measurement of Voltage Reduction Due to Reverse Power Flow
3. Medium and LV Distribution System Model
3.1. MV Distribution System Model
3.2. Low-Voltage Distribution System Model
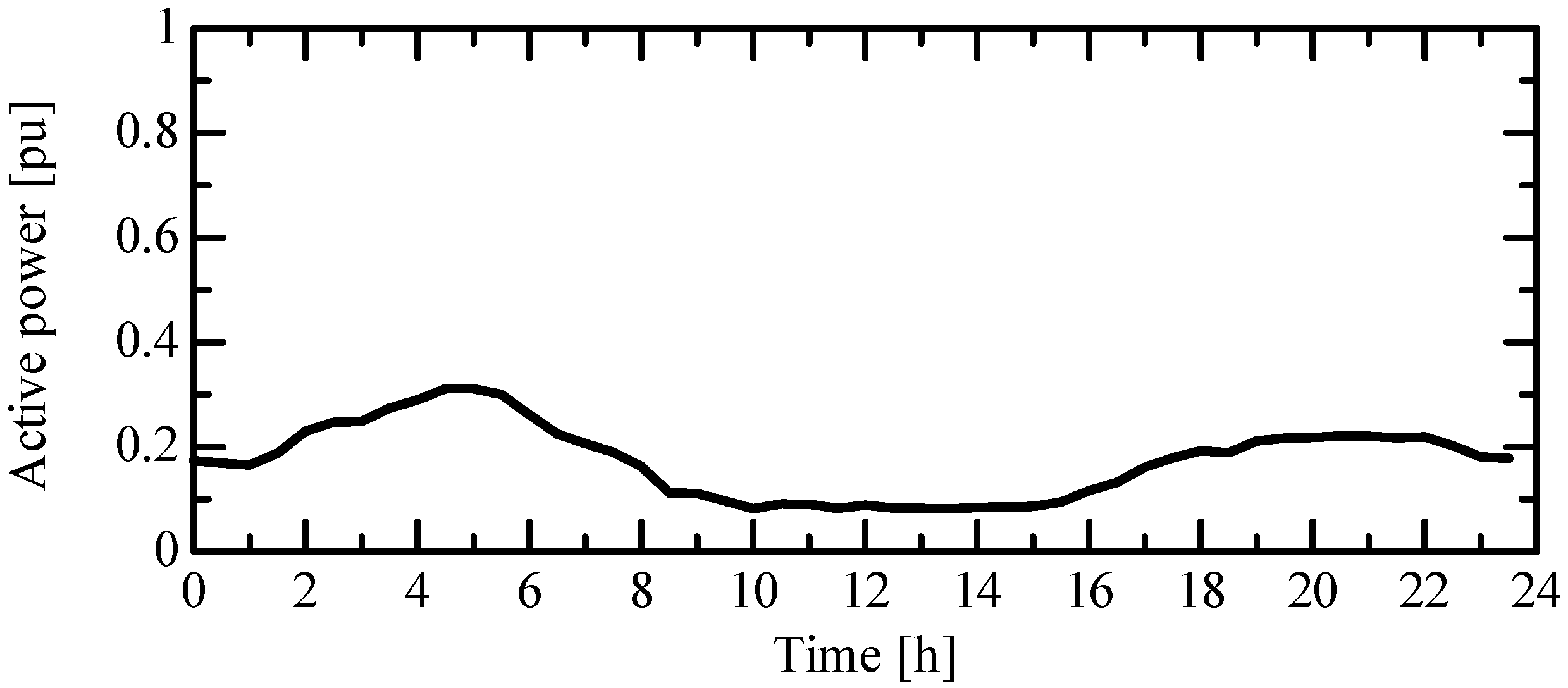
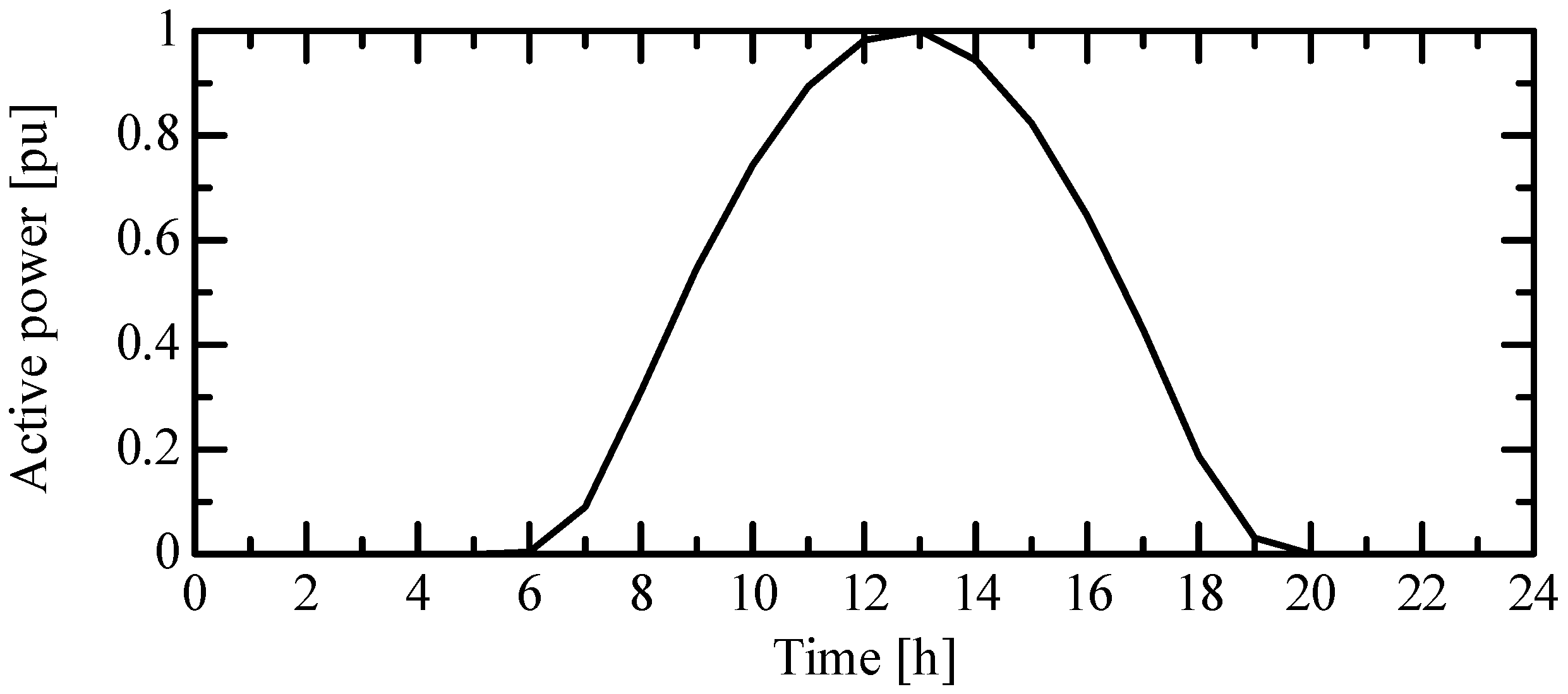
3.3. Load and PV Output Model
4. Effect of Constant Power Factor Control of PCS on Voltage in an MV Distribution System
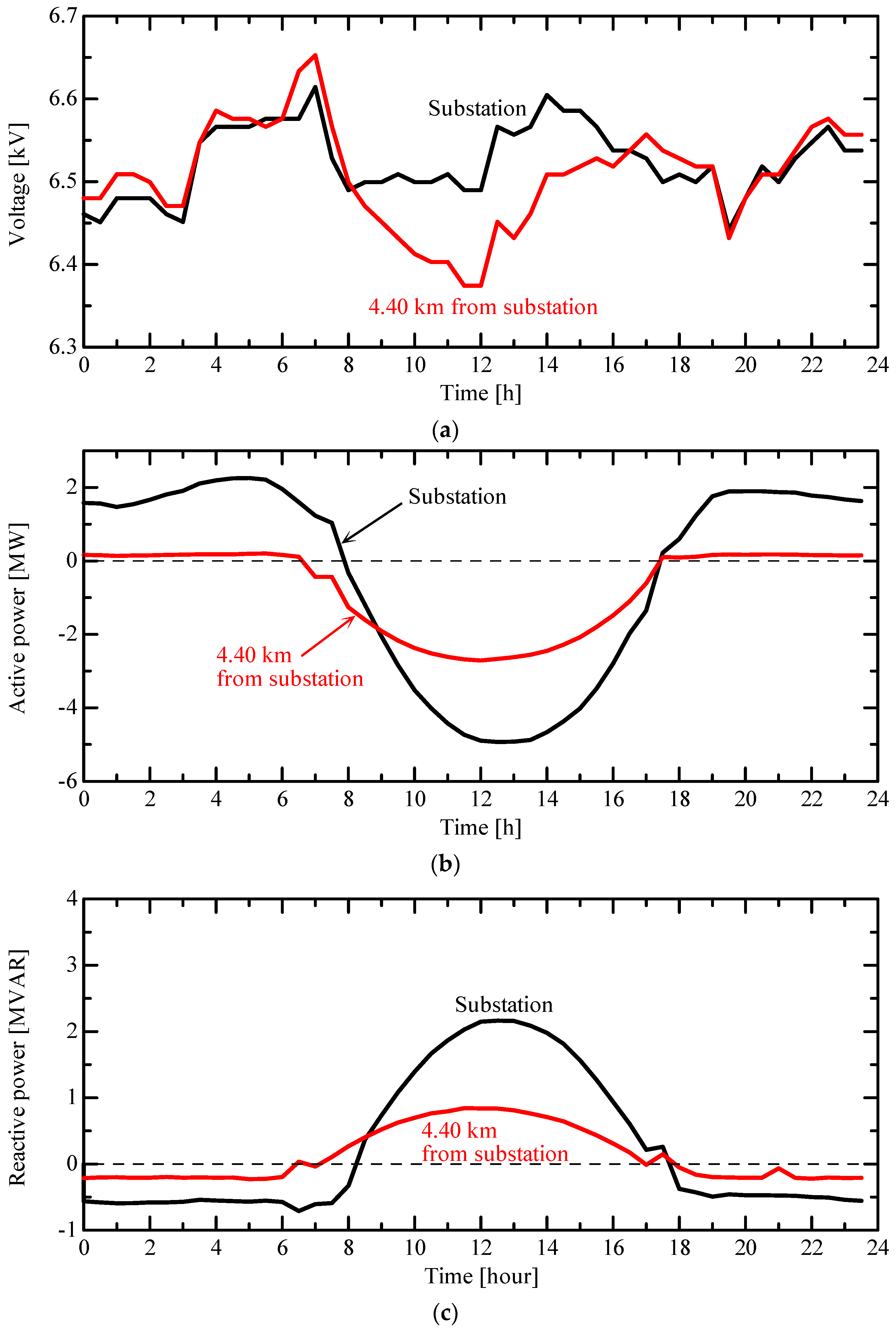
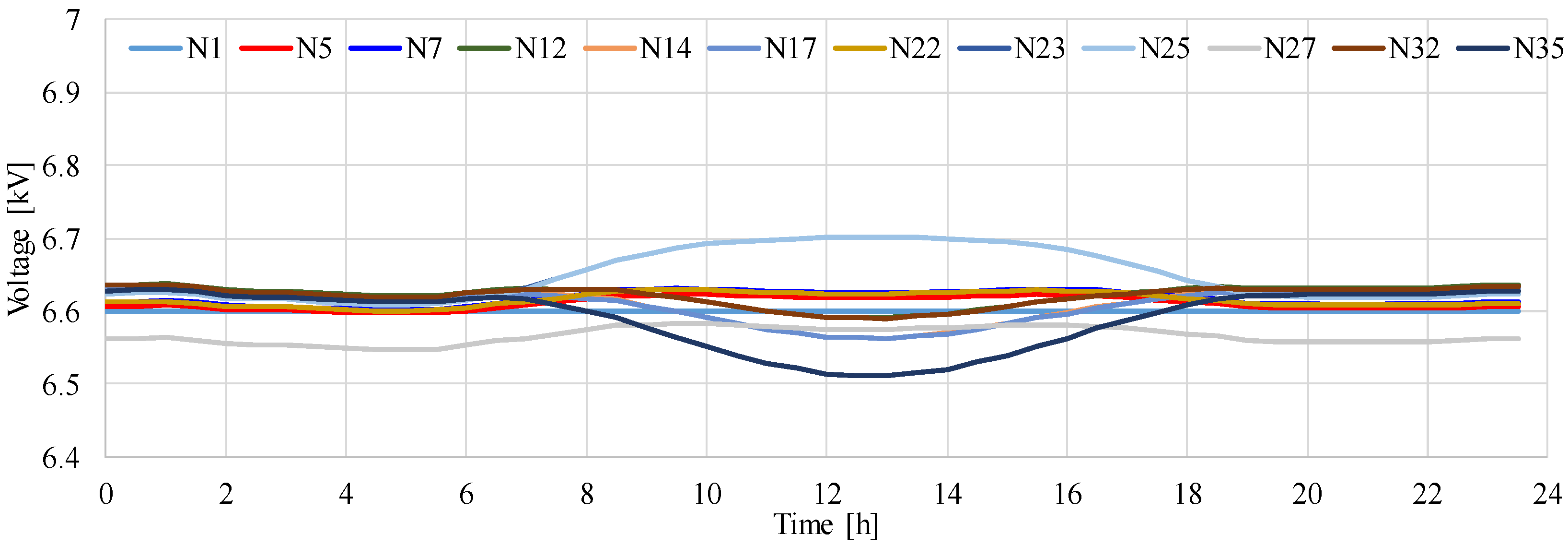
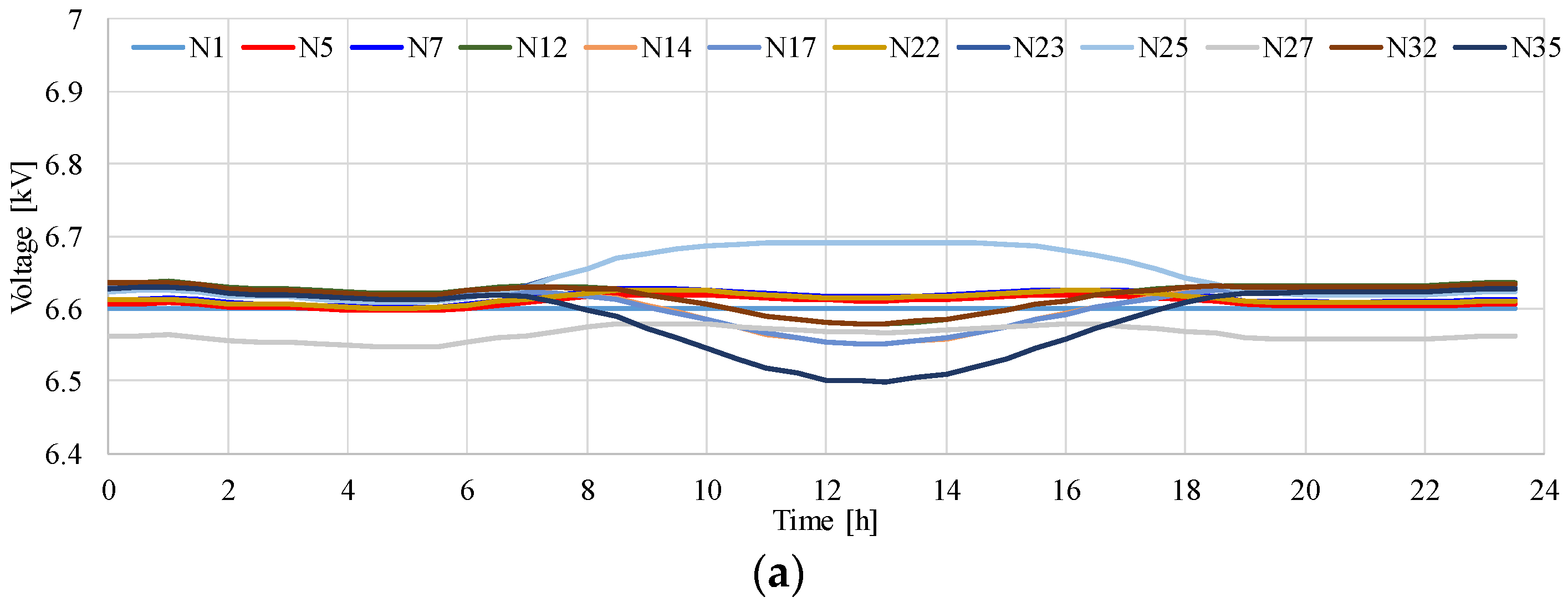
4.1. Voltage without LV PCS
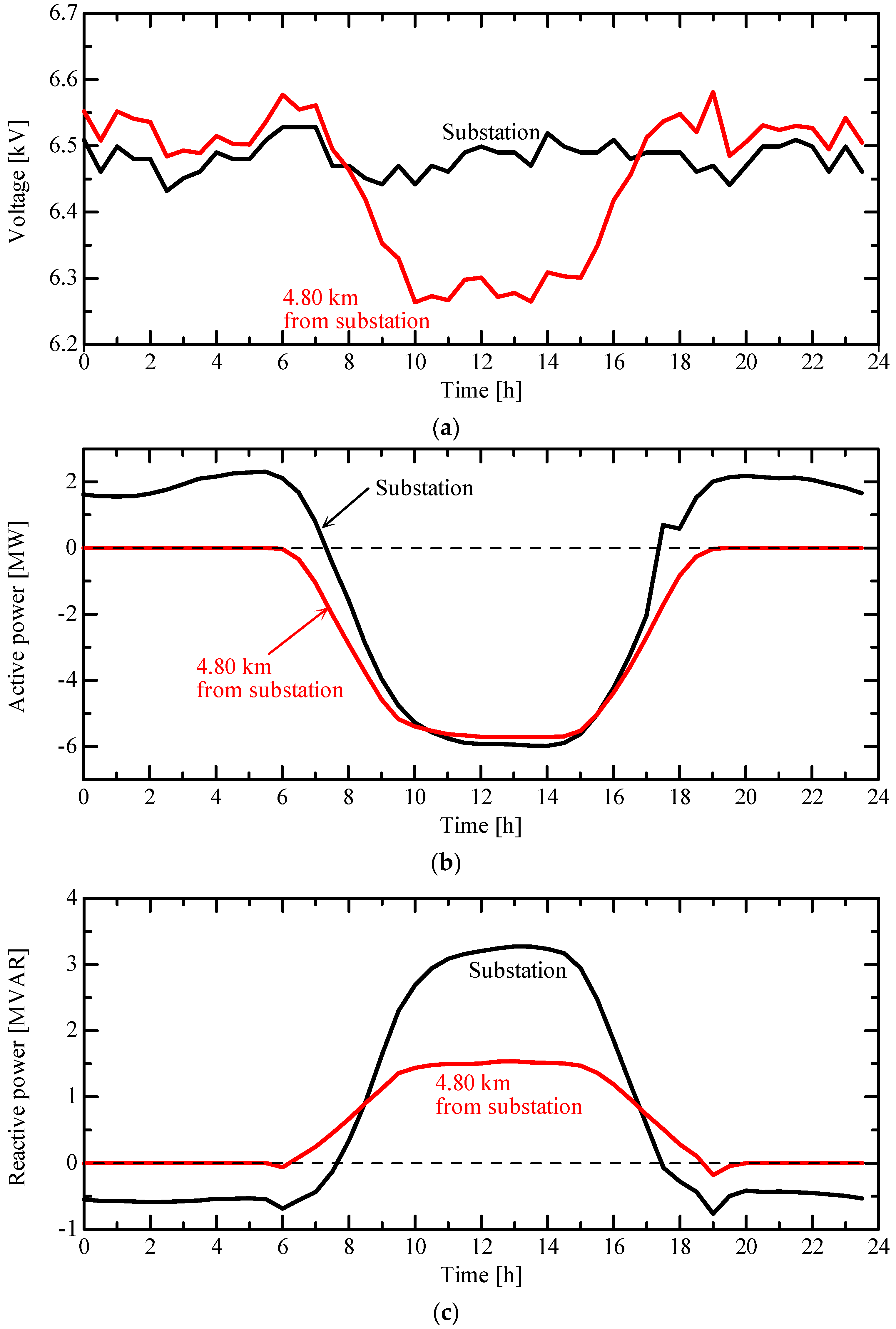
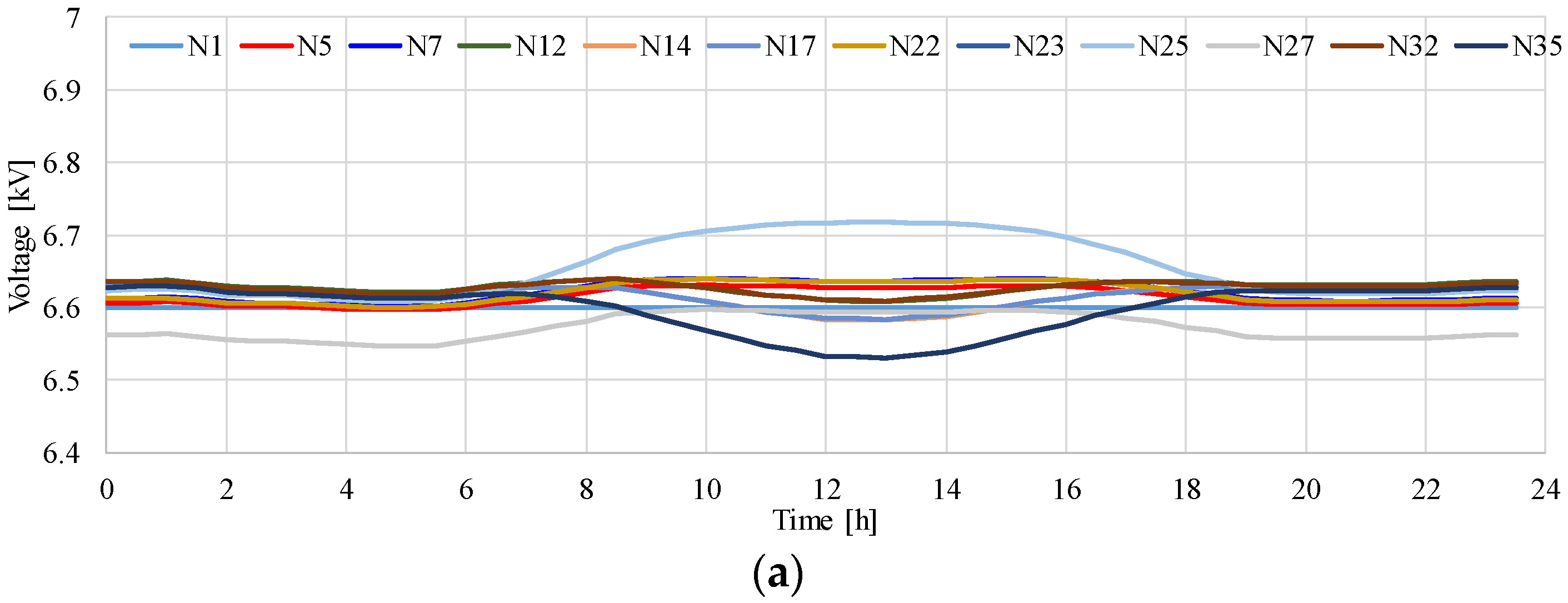
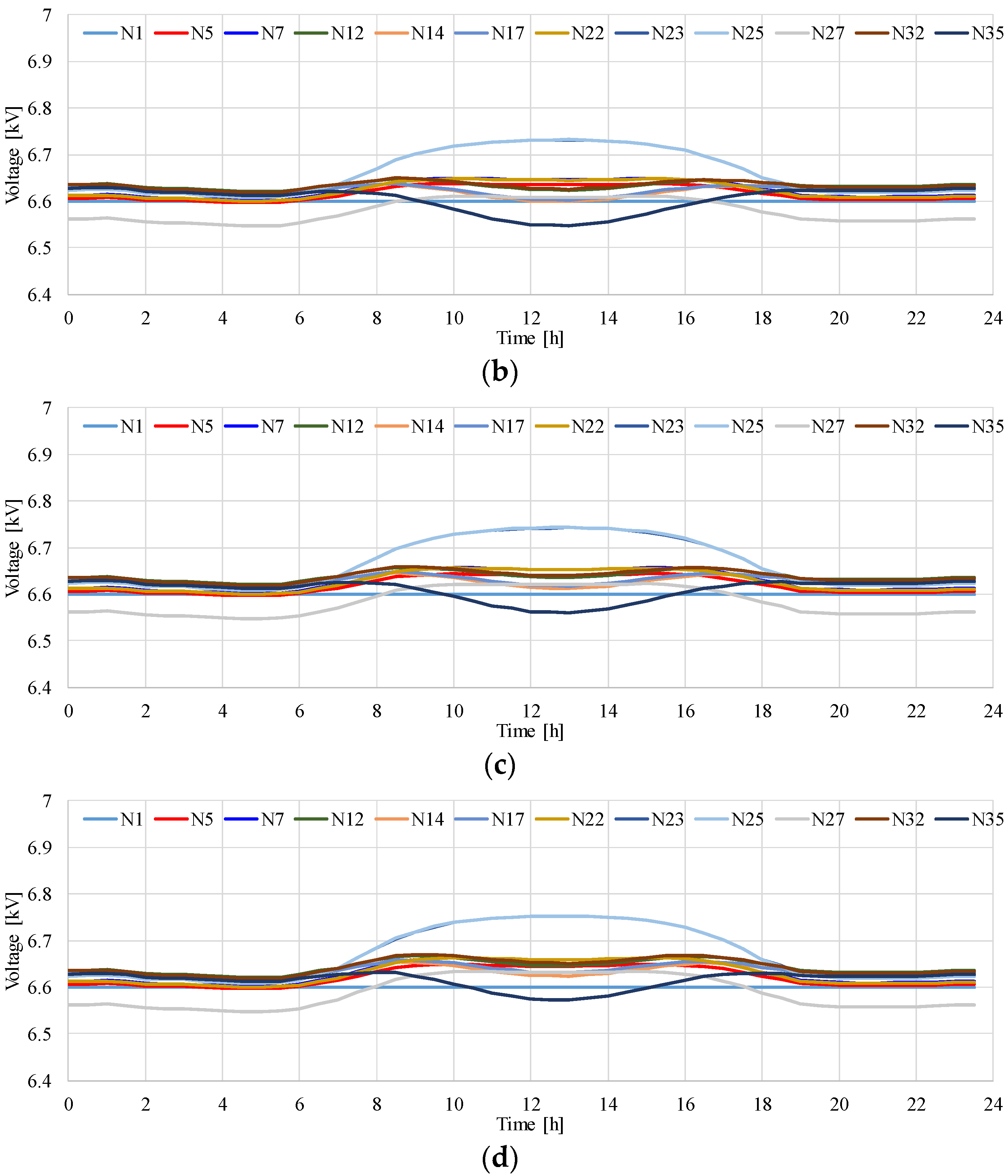
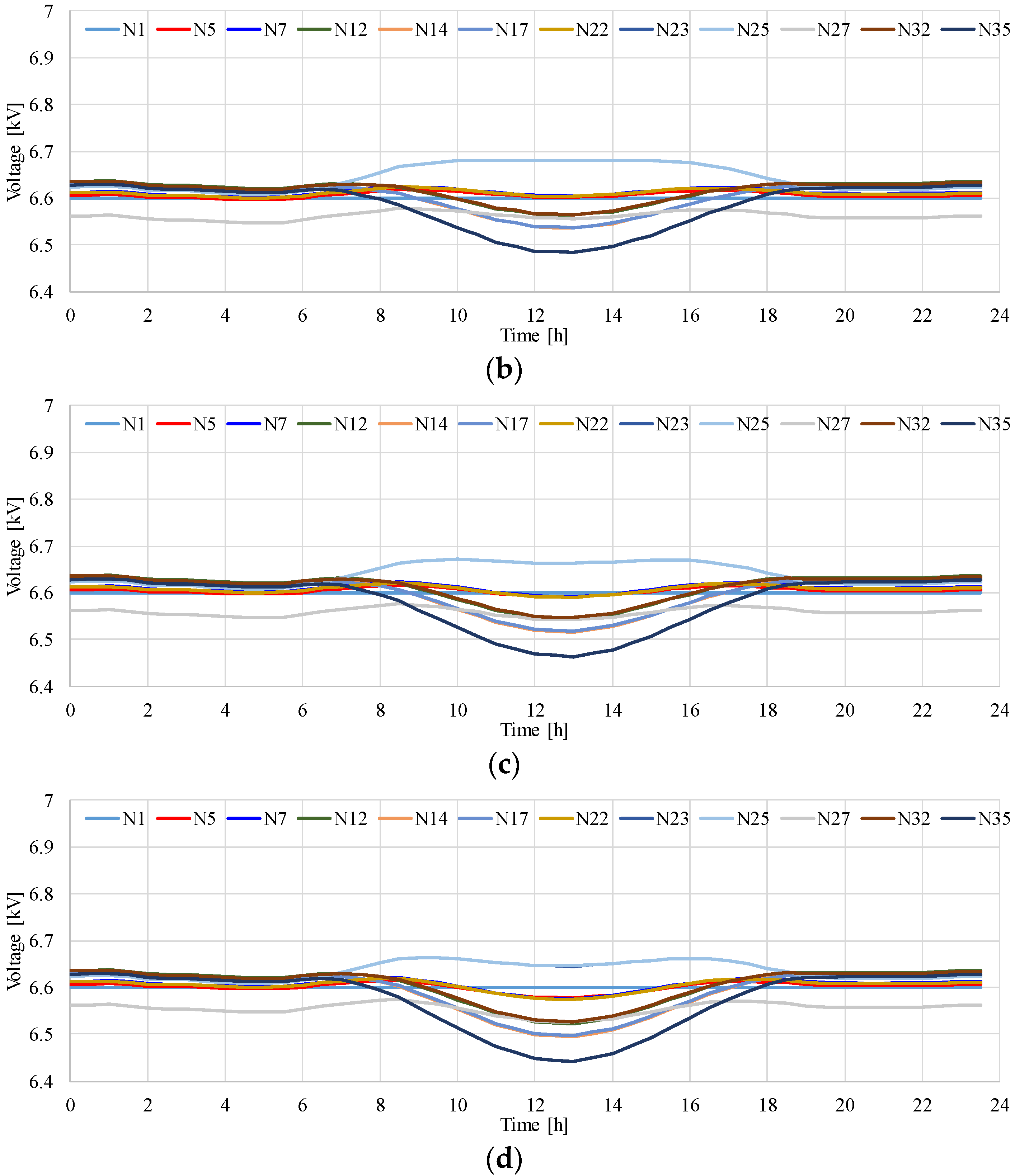
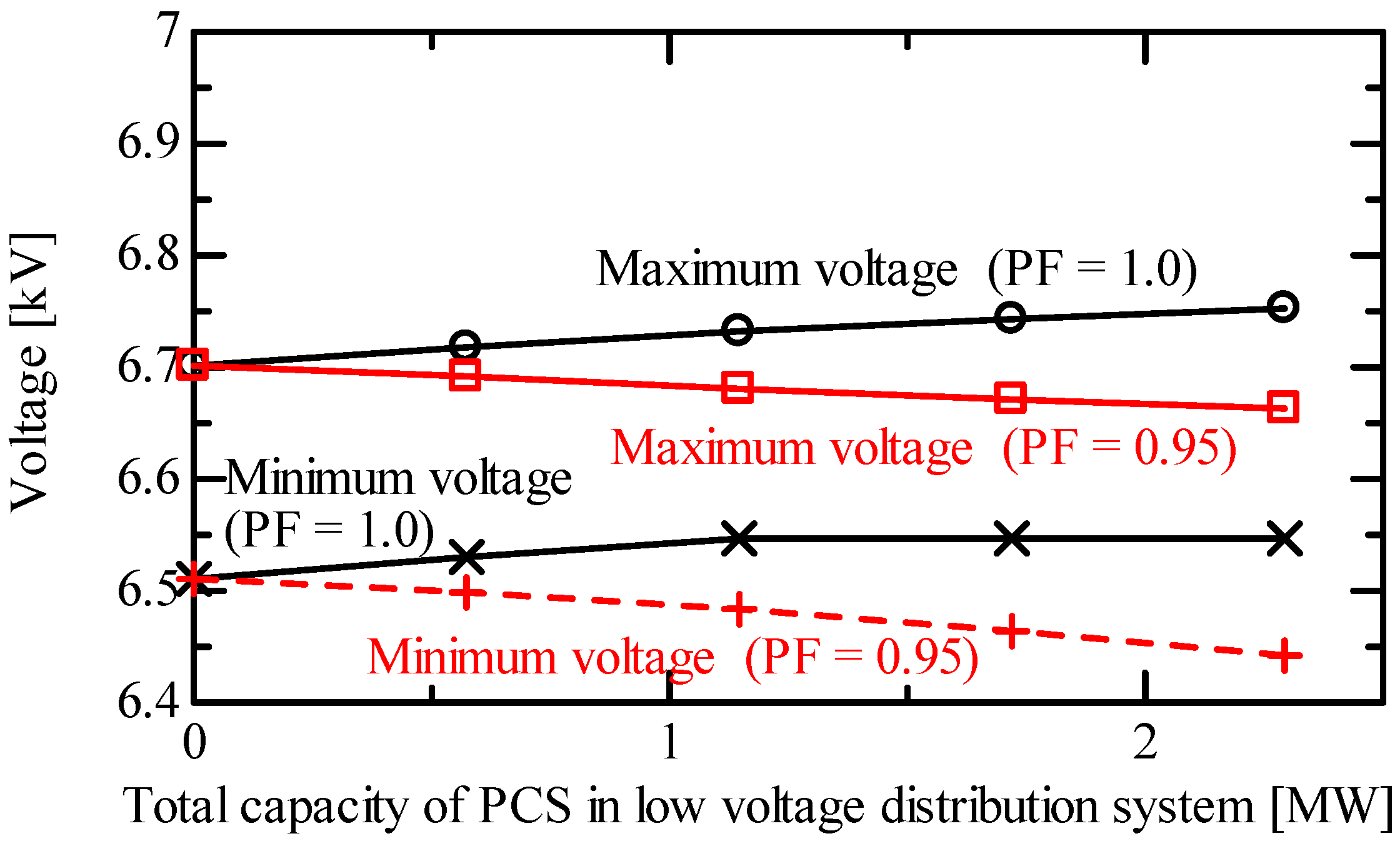
4.2. Effect of Constant Power Factor Control of PCS on Voltage at MV Distribution System
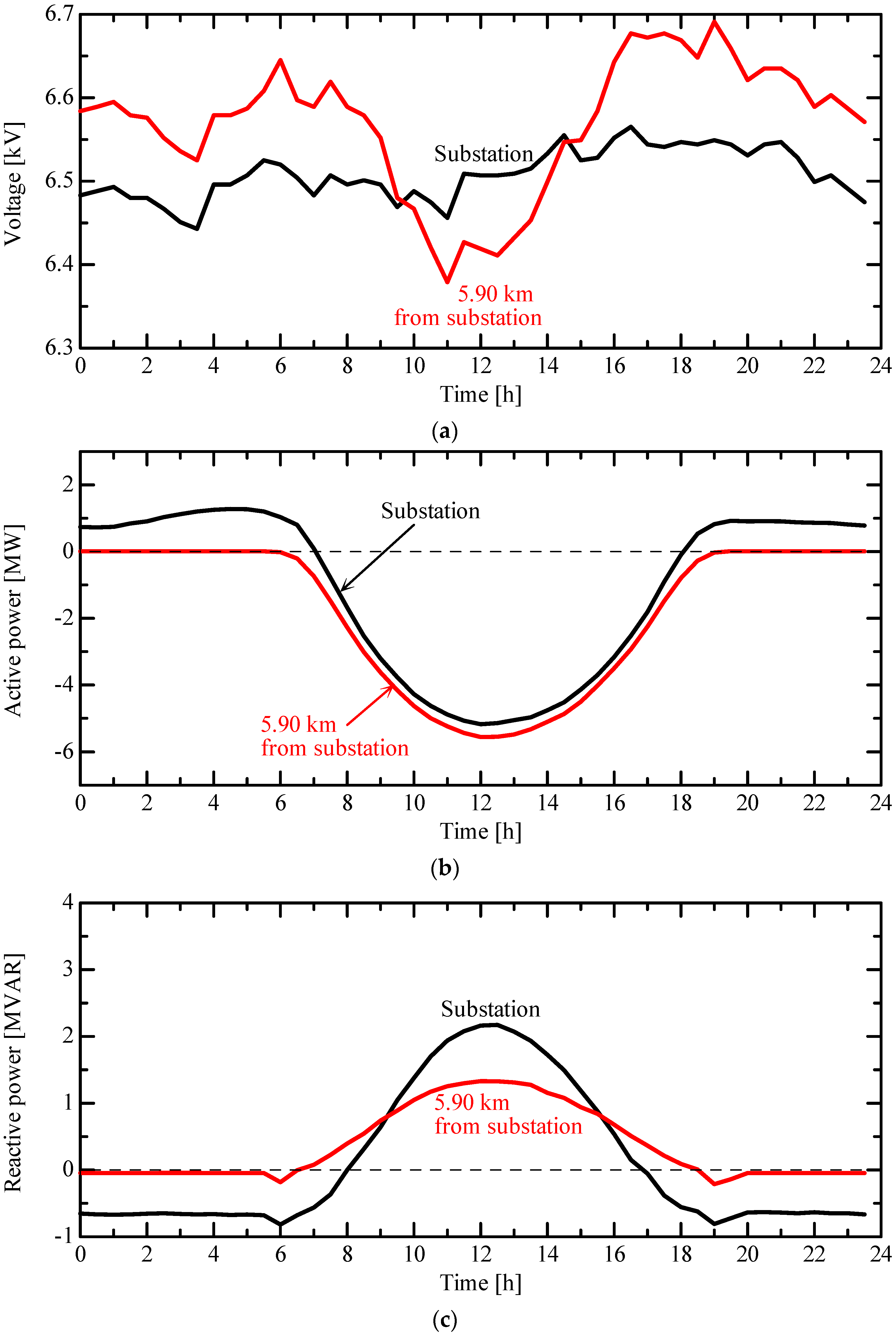
4.3. Comparison with Other MV Distribution System
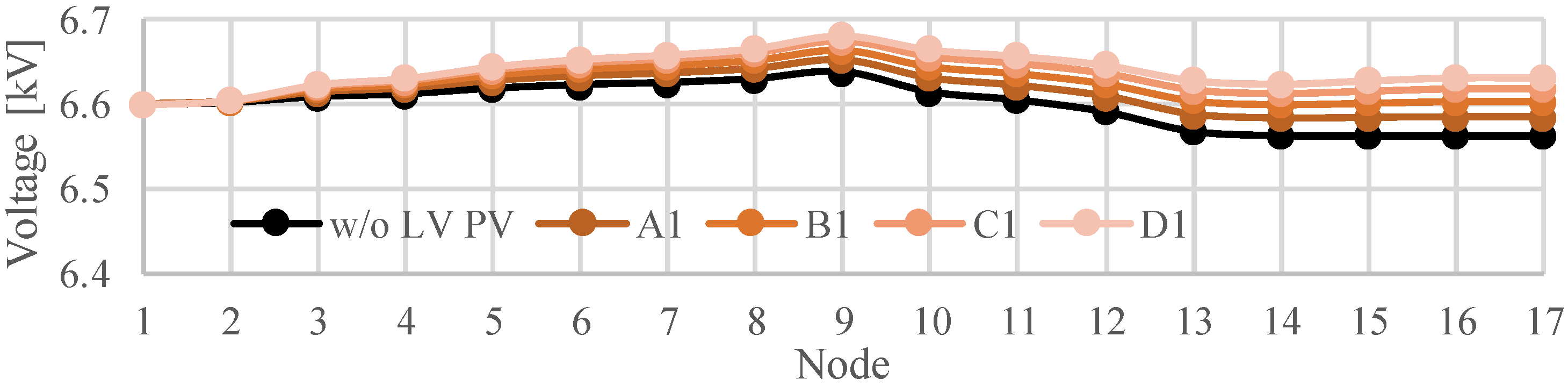
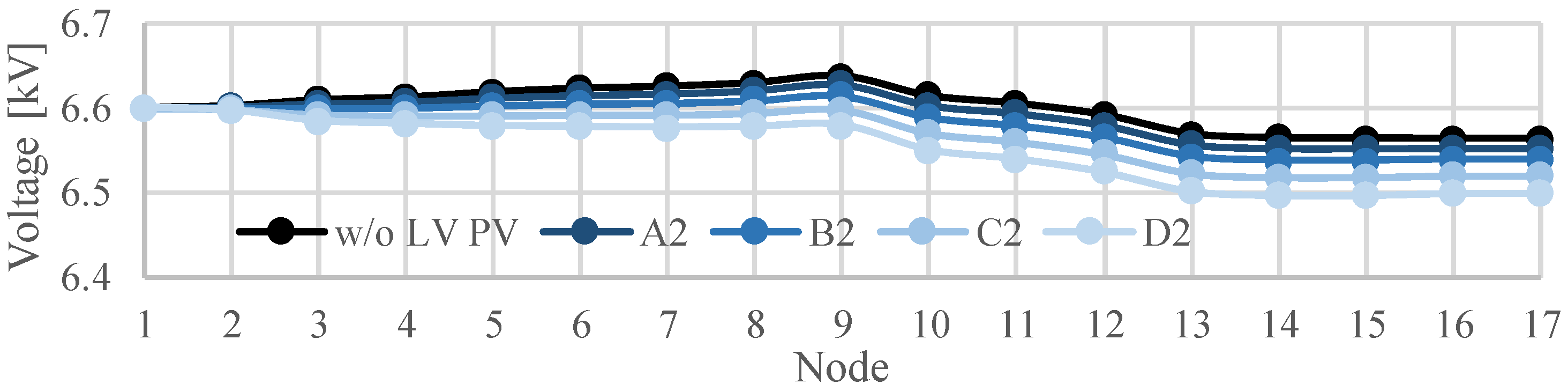
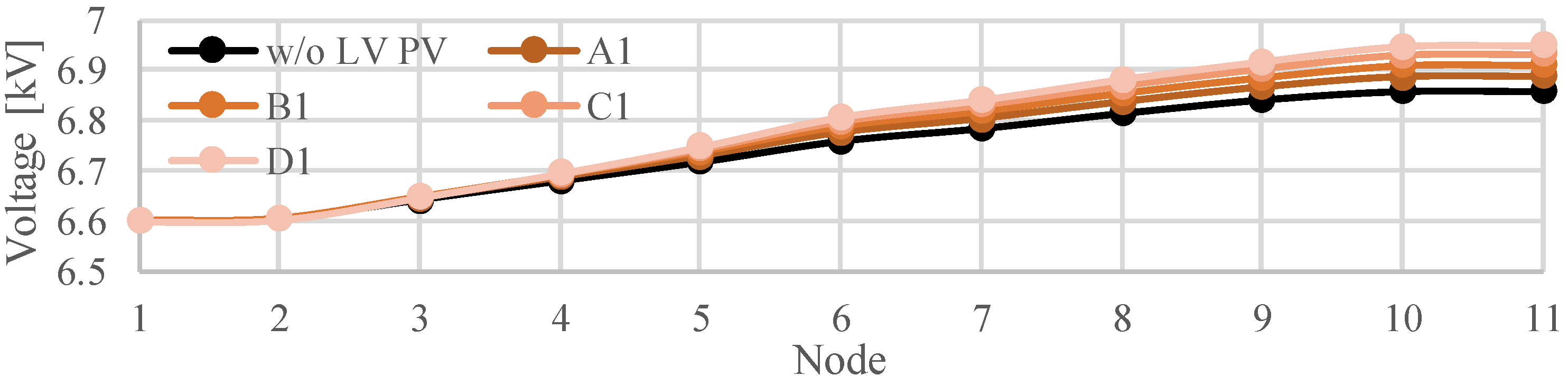
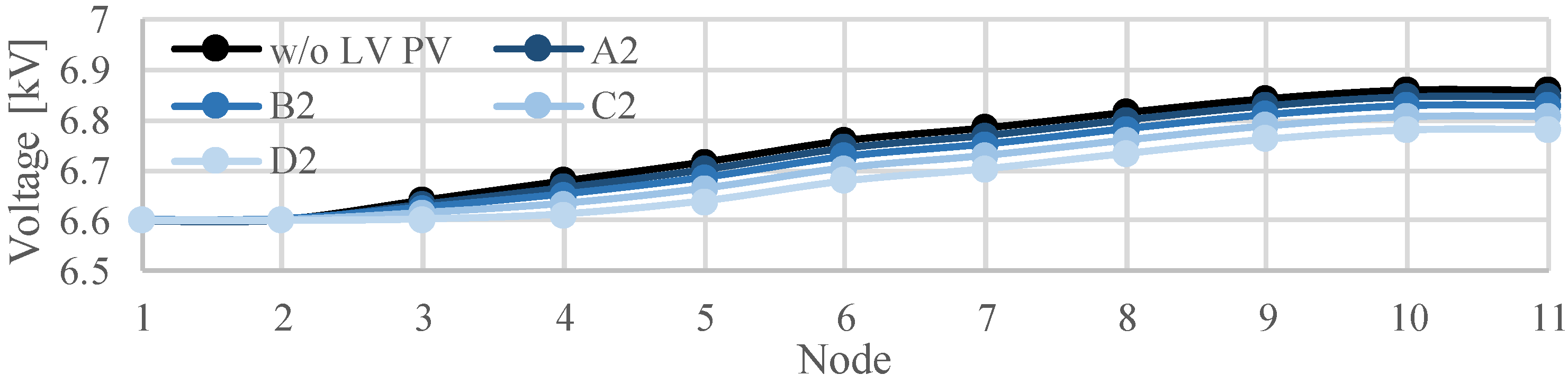
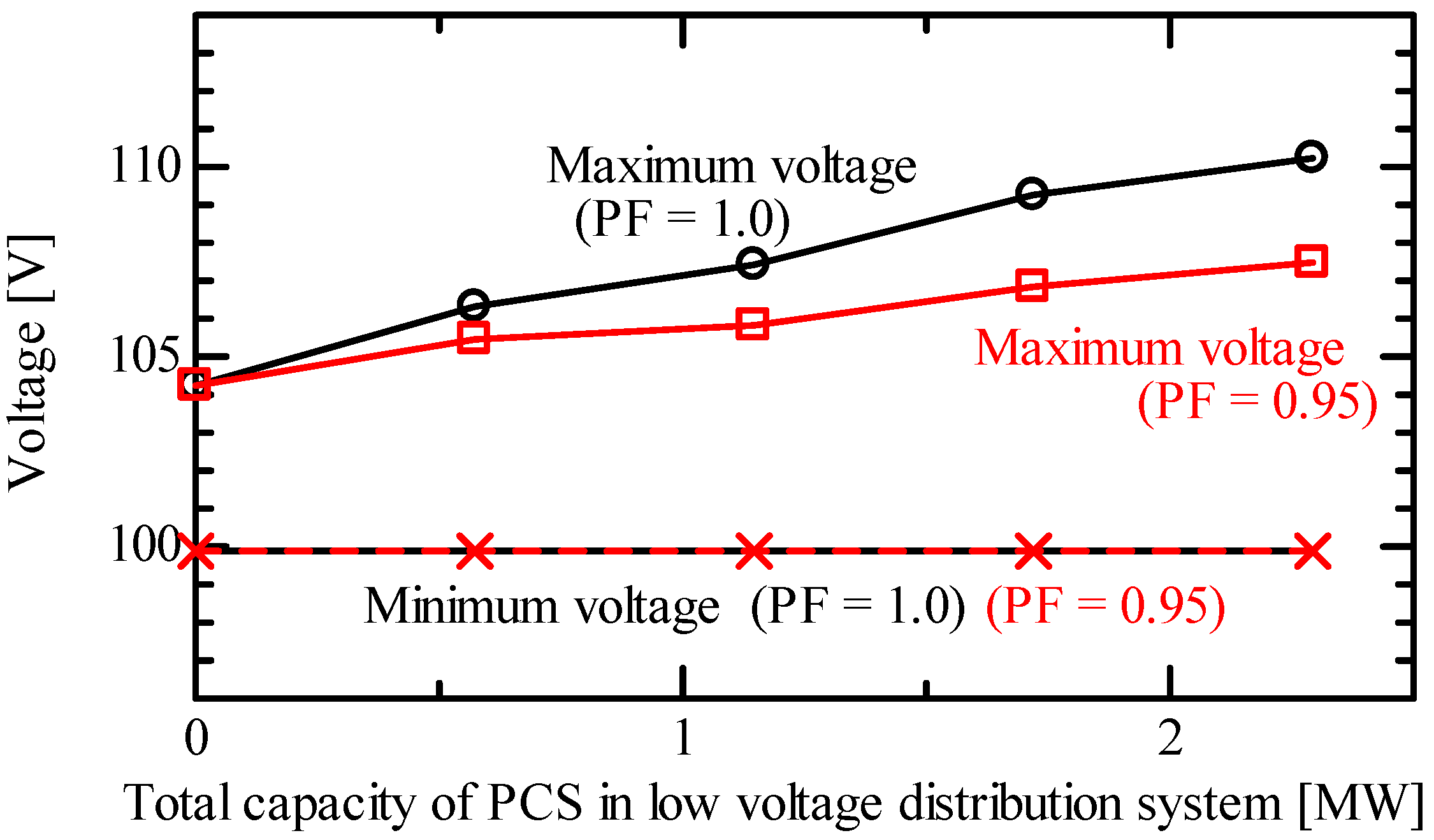
4.4. Effect of Constant Power Factor Control of PCS on Voltage in LV Distribution System
5. Conclusions
- Notably, the constant power factor control of PCS worsens voltage reduction in a MV distribution system. This can be explained by an increase in the reactive power loss in a MV distribution line due to reverse power flow. The decrease in the minimum voltage of the distribution system may affect the management of voltage regulation.
- The constant power factor control of PCS works effectively for mitigating the voltage rise in LV distribution systems and even in an MV distribution system with the characteristic of voltage reduction due to the reverse power flow.
- As described in many studies, it has been confirmed that the constant power factor control mitigates the voltage rise in a distribution system in which the voltage rises with the increase in the reverse power flow.
- Before the constant power factor control is applied to the PCS in the LV distribution system, the DSO should determine whether the voltage reduction due to reverse power flow may occur in the MV distribution line.
Author Contributions
Funding
Conflicts of Interest
References
- Masters, C.L. Voltage rise: The big issue when connecting embedded generation to long 11 kV overhead lines. Power Eng. J. 2002, 16, 5–12. [Google Scholar] [CrossRef]
- Choi, J.H.; Kim, J.C. Advanced voltage regulation method of power distribution systems interconnected with dispersed storage and generation systems. IEEE Trans. Power Deliv. 2001, 16, 329–334. [Google Scholar] [CrossRef]
- Iioka, D.; Sakakibara, K.; Yokomizu, Y.; Matsumura, T.; Izuhara, N. Distribution voltage rise at dense photovoltaic generation area and its suppression by SVC. Electr. Eng. Jpn. 2009, 166, 47–53. [Google Scholar] [CrossRef]
- Abdel-Rahman, M.H.; Youssef, F.M.H.; Saber, A.A. New static var compensator control strategy and coordination with under-load tap changer. IEEE Trans. Power Deliv. 2006, 21, 1630–1635. [Google Scholar] [CrossRef]
- Daratha, N.; Das, B.; Sharma, J. Coordination between OLTC and SVC for Voltage Regulation in Unbalanced Distribution System Distributed Generation. IEEE Trans. Power Syst. 2014, 29, 289–299. [Google Scholar] [CrossRef]
- Aryanezhad, M. Management and coordination of LTC, SVR, shunt capacitor and energy storage with high PV penetration in power distribution system for voltage regulation and power loss minimization. Int. J. Electr. Power Energy Syst. 2018, 100, 178–192. [Google Scholar] [CrossRef]
- Kraiczy, M.; Stetz, T.; Braun, M. Parallel Operation of Transformers with on Load Tap Changer and Photovoltaic Systems with Reactive Power Control. IEEE Trans. Smart Grid 2018, 9, 6419–6428. [Google Scholar] [CrossRef]
- Hassaine, L.; Olias, E.; Quintero, J.; Haddadi, M. Digital power factor control and reactive power regulation for grid-connected photovoltaic inverter. Renew. Energy 2009, 34, 315–321. [Google Scholar] [CrossRef]
- Chaudhary, P.; Rizwan, M. Voltage regulation mitigation techniques in distribution system with high PV penetration: A review. Renew. Sustain. Energy Rev. 2018, 82, 3279–3287. [Google Scholar] [CrossRef]
- Bolognani, S.; Carli, R.; Cavraro, G.; Zampieri, S. Distributed Reactive Power Feedback Control for Voltage Regulation and Loss Minimization. IEEE Trans. Autom. Control 2015, 60, 966–981. [Google Scholar] [CrossRef]
- Ghosh, S.; Rahman, S.; Pipattanasomporn, M. Distribution Voltage Regulation through Active Power Curtailment with PV Inverters and Solar Generation Forecasts. IEEE Trans. Sustain. Energy 2017, 8, 13–22. [Google Scholar] [CrossRef]
- Safayet, A.; Fajri, P.; Husain, I. Reactive Power Management for Overvoltage Prevention at High PV Penetration in a Low-Voltage Distribution System. IEEE Trans. Ind. Appl. 2017, 53, 5786–5794. [Google Scholar] [CrossRef]
- Dall’Anese, E.; Dhople, S.V.; Johnson, B.B.; Giannakis, G.B. Decentralized Optimal Dispatch of Photovoltaic Inverters in Residential Distribution Systems. IEEE Trans. Energy Convers. 2014, 29, 957–967. [Google Scholar] [CrossRef]
- Bello, M.; Montenegro, D.; York, B.; Smith, J. Optimal Settings for Multiple Groups of Smart Inverters on Secondary Systems Using Autonomous Control. In Proceedings of the 2017 IEEE Rural Electric Power Conference (REPC), Columbus, OH, USA, 23–26 April 2017; pp. 89–94. [Google Scholar] [CrossRef]
- Smith, J. Stochastic Analysis to Determine Feeder Hosting Capacity for Distributed Solar PV; EPRI Report; No. 1026640; EPRI: Palo Alto, CA, USA, 2012. [Google Scholar]
- Rylander, M.; Reno, M.J.; Quiroz, J.E.; Ding, F.; Li, H.; Broderick, R.J.; Mather, B.; Smith, J. Methods to determine recommended feeder-wide advanced inverter settings for improving distribution system performance. In Proceedings of the 2016 IEEE 43rd Photovoltaic Specialists Conference (PVSC), Portland, OR, USA, 5–10 June 2016; pp. 1393–1398. [Google Scholar] [CrossRef]
- Casavola, A.; Tedesco, F.; Vizza, M. Command Governor Strategies for the Online Management of Reactive Power in Smart Grids with Distributed Generation. IEEE Trans. Autom. Sci. Eng. 2017, 14, 449–460. [Google Scholar] [CrossRef]
- Iioka, D.; Fujii, T.; Orihara, D.; Tanaka, T.; Harimoto, T.; Shimada, A.; Goto, T.; Kubuki, T. Voltage reduction due to reverse power flow in distribution feeder with photovoltaic system. Int. J. Electr. Power Energy Syst. 2019, 113, 411–418. [Google Scholar] [CrossRef]
- Matsumura, T.; Tsukamoto, M.; Tsusaka, A.; Yukita, K.; Goto, Y.; Yokomizu, Y.; Tatewaki, K.; Iioka, D.; Shimizu, H.; Kanazawa, Y.; et al. Line-End Voltage and Voltage Profile along Power Distribution Line with Large-Power Photovoltaic Generation System. Int. J. Photoenergy 2019, 2019. [Google Scholar] [CrossRef]
- Iioka, D.; Miura, K.; Machida, M.; Kikuchi, S.; Imanaka, M.; Baba, J.; Takagi, M.; Asano, H. Hosting capacity of large scale PV power station in future distribution networks. In Proceedings of the 2017 IEEE Innovative Smart Grid Technologies-Asia (ISGT-Asia), Auckland, New Zealand, 4–7 December 2017. [Google Scholar] [CrossRef]
- Kikuchi, S.; Machida, M.; Tamura, J.; Imanaka, M.; Baba, J.; Iioka, D.; Miura, K.; Takagi, M.; Asano, H. Hosting capacity analysis of many distributed photovoltaic systems in future distribution networks. In Proceedings of the 2017 IEEE Innovative Smart Grid Technologies-Asia (ISGT-Asia), Auckland, New Zealand, 4–7 December 2017. [Google Scholar] [CrossRef]
- Takagi, M.; Bando, S.; Tagashira, N.; Nagata, Y.; Asano, H.; Ishihara, M.; Nogiwa, H.; Iioka, D.; Machida, M.; Kikuchi, S.; et al. Cost-effective analysis of countermeasures for solar photovoltaic systems in distribution networks. In Proceedings of the 2017 IEEE Innovative Smart Grid Technologies-Asia (ISGT-Asia), Auckland, New Zealand, 4–7 December 2017. [Google Scholar] [CrossRef]



| Node | Load Capacity [kW] | Node | Load Capacity [kW] |
|---|---|---|---|
| 5 | 130 | 19 | 224 |
| 6 | 46 | 22 | 95 |
| 7 | 195 | 23 | 341 |
| 8 | 47 | 24 | 138 |
| 9 | 92 | 25 | 1 |
| 12 | 92 | 27 | 63 |
| 13 | 113 | 28 | 117 |
| 14 | 139 | 30 | 56 |
| 15 | 138 | 31 | 25 |
| 16 | 144 | 32 | 26 |
| 17 | 1 | 33 | 70 |
| Node | Node | Impedance [Ω] |
|---|---|---|
| 1 | 2 | 0.0152 + j0.0195 |
| 2 | 3 | 0.0179 + j0.0160 |
| 2 | 4 | 0.0179 + j0.0160 |
| 2 | 6 | 0.0285 + j0.0013 |
| 2 | 7 | 0.0285 + j0.0013 |
| 3 | 8 | 0.0285 + j0.0013 |
| 3 | 9 | 0.0285 + j0.0013 |
| 4 | 5 | 0.0460 + j0.0160 |
| 4 | 10 | 0.0285 + j0.0013 |
| 4 | 11 | 0.0285 + j0.0013 |
| 5 | 12 | 0.0285 + j0.0013 |
| 5 | 13 | 0.0285 + j0.0013 |
| Case | Node w/PV System | Total Capacity of PCS in A LV Distribution System Shown in Figure 6 [kW] | Total Capacity of PCS in Distribution System Shown in Figure 5 [kW] | Power Factor of PCS |
|---|---|---|---|---|
| A1 | 8, 12 | 4 | 573 | 1.00 |
| A2 | 8, 12 | 4 | 573 | 0.95 |
| B1 | 6, 8, 10, 12 | 8 | 1 147 | 1.00 |
| B2 | 6, 8, 10, 12 | 8 | 1 147 | 0.95 |
| C1 | 6, 8, 9, 10, 12, 13 | 12 | 1 720 | 1.00 |
| C2 | 6, 8, 9, 10, 12, 13 | 12 | 1 720 | 0.95 |
| D1 | 6, 7, 8, 9, 10, 11, 12, 13 | 16 | 2 293 | 1.00 |
| D2 | 6, 7, 8, 9, 10, 11, 12, 13 | 16 | 2 293 | 0.95 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iioka, D.; Fujii, T.; Tanaka, T.; Harimoto, T.; Motoyama, J. Voltage Reduction in Medium Voltage Distribution Systems Using Constant Power Factor Control of PV PCS. Energies 2020, 13, 5430. https://doi.org/10.3390/en13205430
Iioka D, Fujii T, Tanaka T, Harimoto T, Motoyama J. Voltage Reduction in Medium Voltage Distribution Systems Using Constant Power Factor Control of PV PCS. Energies. 2020; 13(20):5430. https://doi.org/10.3390/en13205430
Chicago/Turabian StyleIioka, Daisuke, Takahiro Fujii, Toshio Tanaka, Tsuyoshi Harimoto, and Junpei Motoyama. 2020. "Voltage Reduction in Medium Voltage Distribution Systems Using Constant Power Factor Control of PV PCS" Energies 13, no. 20: 5430. https://doi.org/10.3390/en13205430
APA StyleIioka, D., Fujii, T., Tanaka, T., Harimoto, T., & Motoyama, J. (2020). Voltage Reduction in Medium Voltage Distribution Systems Using Constant Power Factor Control of PV PCS. Energies, 13(20), 5430. https://doi.org/10.3390/en13205430






