Adaptive Overhead Transmission Lines Auto-Reclosing Based on Hilbert–Huang Transform
Abstract
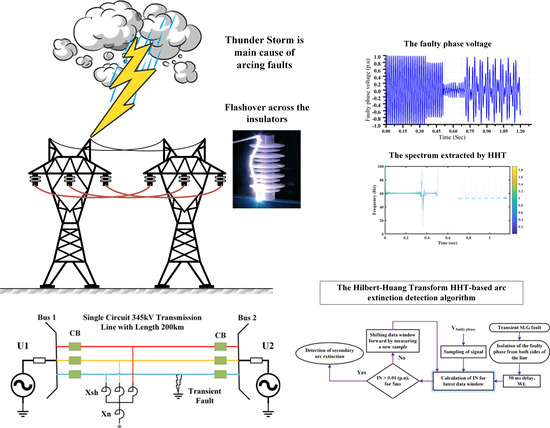
1. Introduction
- Improving power system marginal stability during faults;
- Improving in transient stability;
- Improving in system reliability and availability;
- Mitigating of switching over-voltages;
- Mitigating of shaft torsional oscillation of large thermal units;
- Minimizing unsuccessful reclosing; and
- Reducing system and equipment shocks.
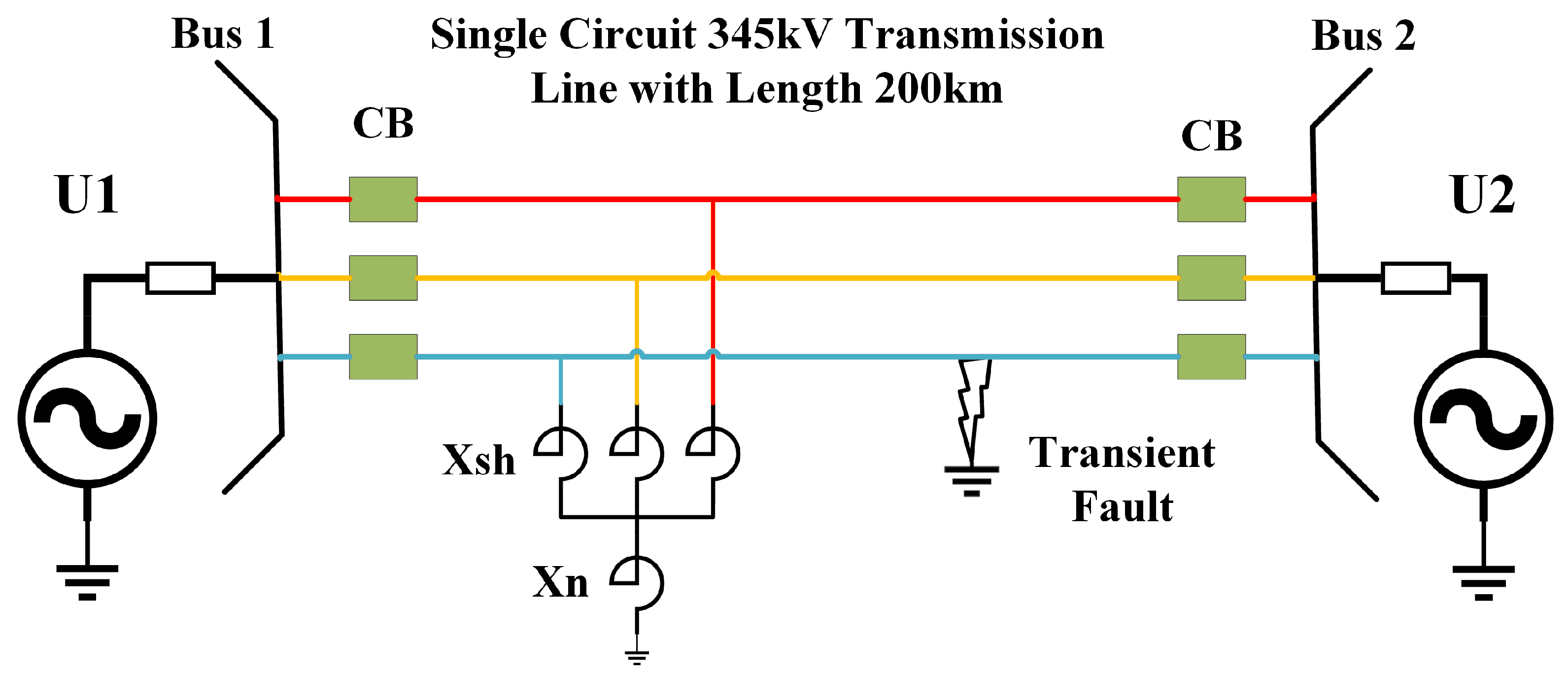
2. Modeling of Understudy System
Secondary Modeling
- Initial resistance (r0): 150 mΩ
- Voltage per unit of length (u0): 1.1 V/cm
- Initial time constant (τ0): 960 ms
- Initial length (l0) of arc: 3.5 m
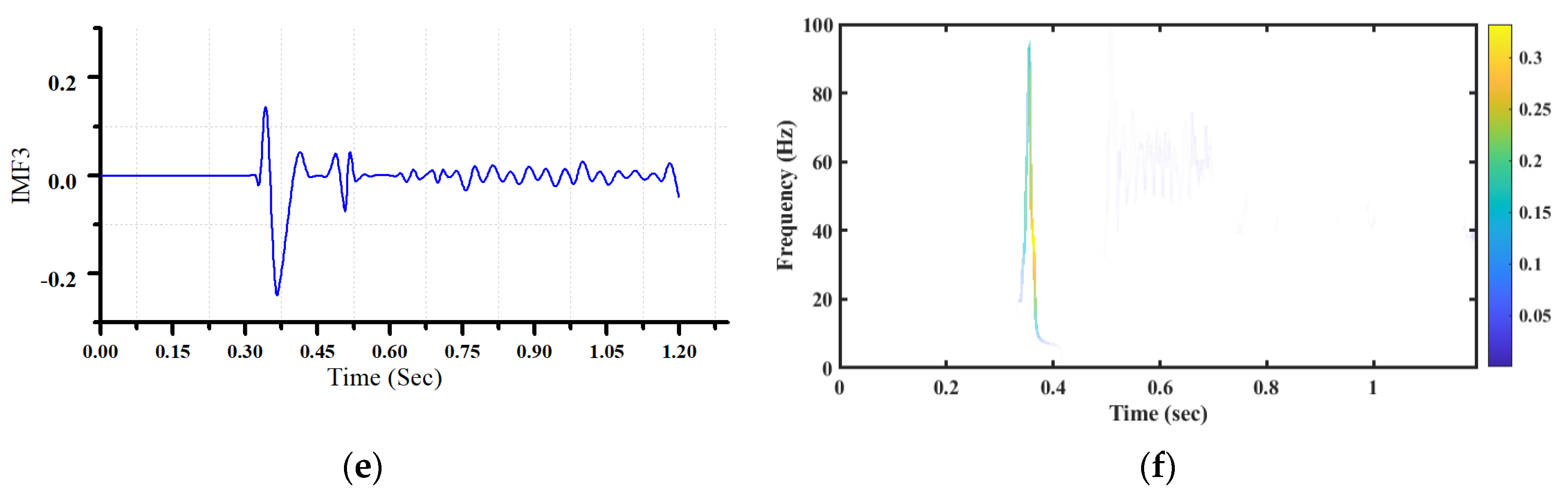
3. Hilbert–Huang Transform
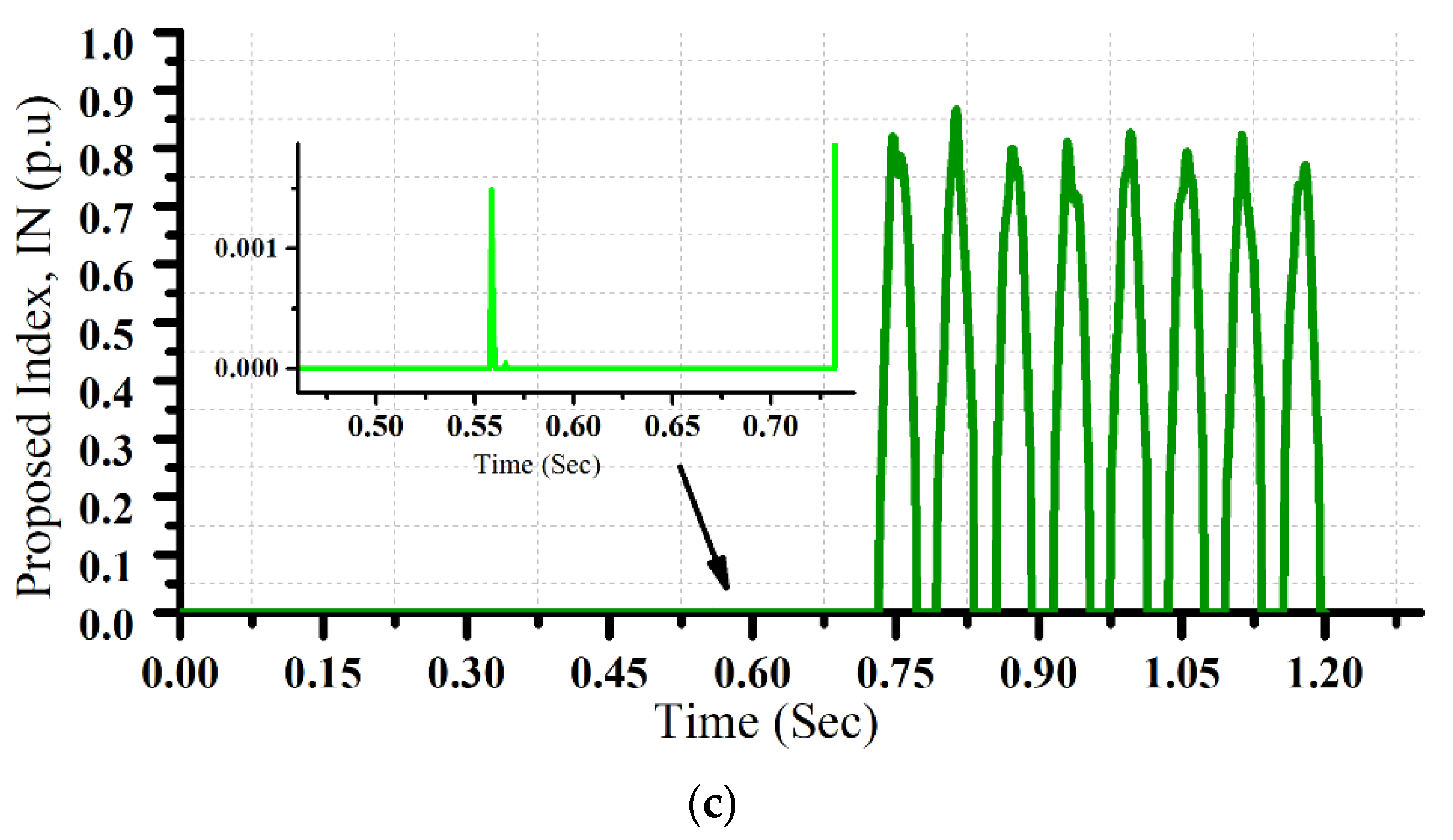
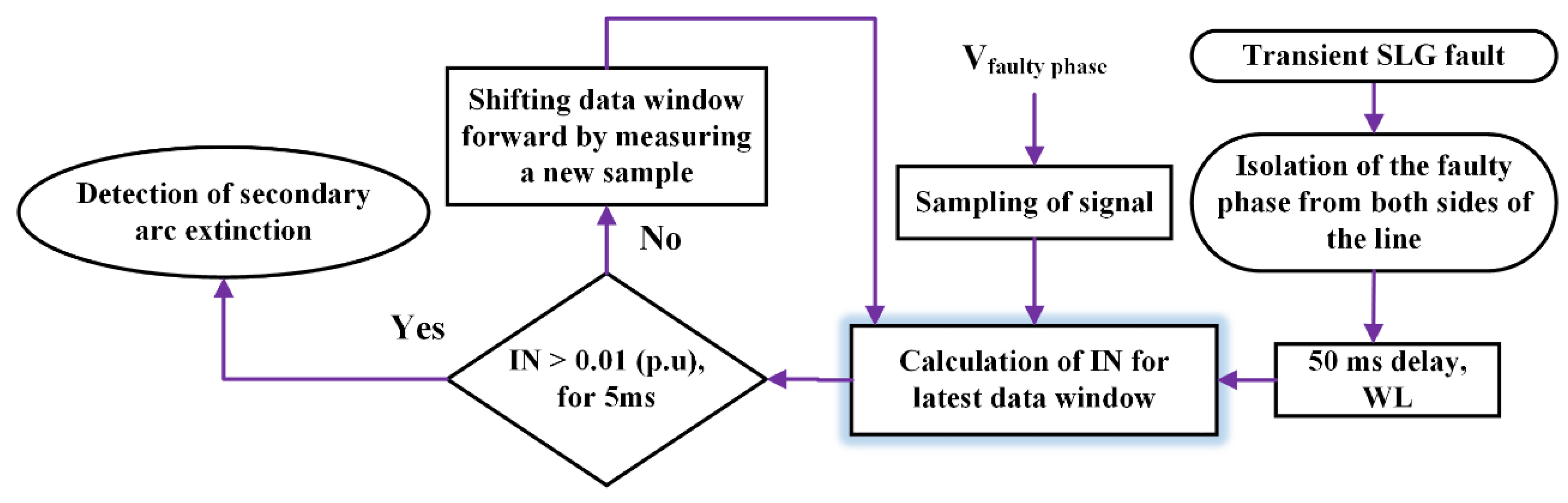
4. Proposed Method
- Extraction and monitoring of sub-synchronous voltage component using HHT, which is a powerful and suitable tool for this application.
- Proposing a criterion that is zero in most moments and cases during the secondary arc and takes a large amount immediately after the secondary arc is extinguished.
- The proposed criterion is very insensitive to voltage magnitude oscillations during the secondary arc, unlike many existing methods.
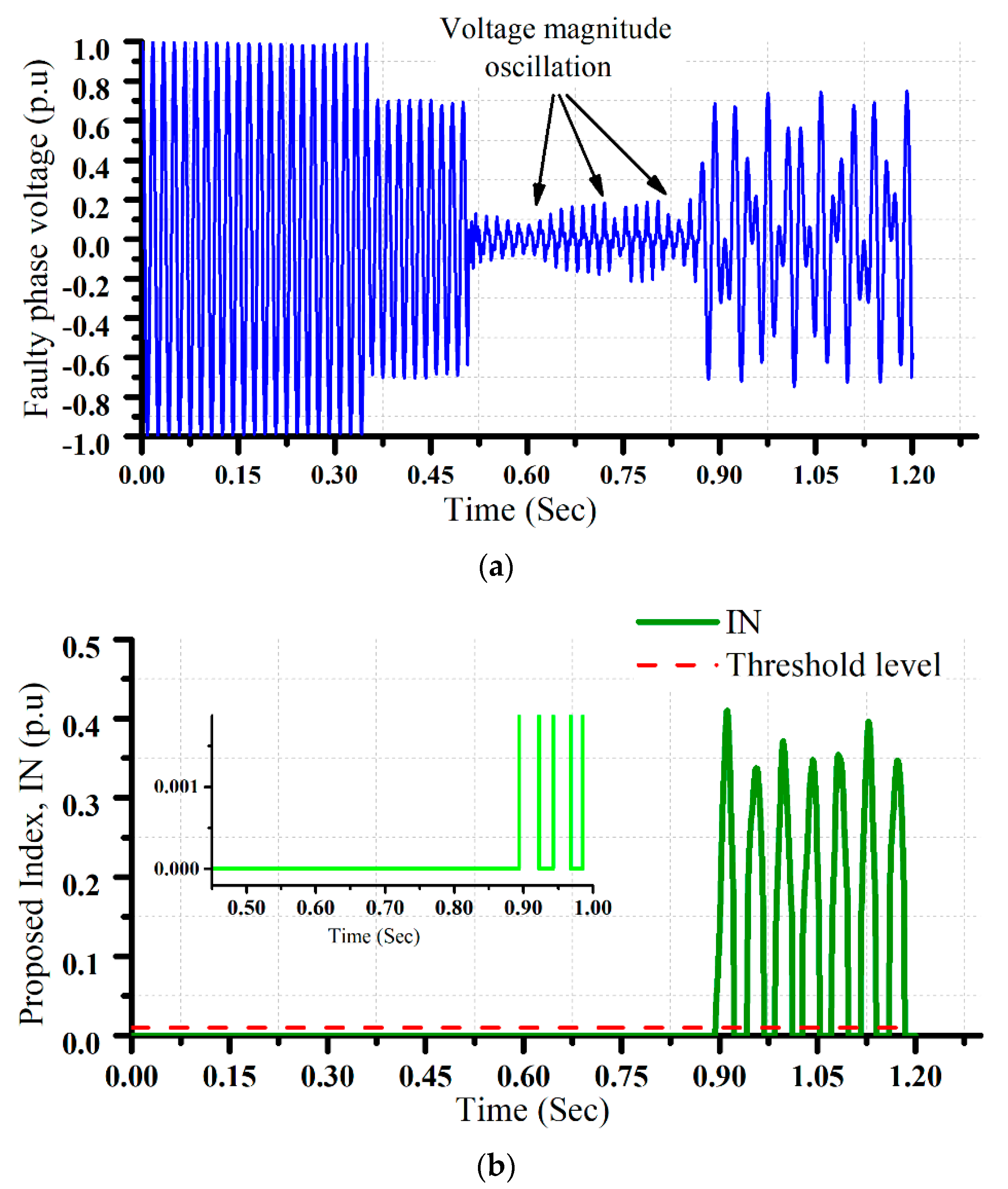
5. Simulations and Results
- Low starting time delay;
- Fast reclosing time delay (with average 32 ms);
- Medium sampling frequency (1.920 kHz);
- Very low sensitivity to voltage magnitude oscillation; and
- Global threshold.
6. Conclusions
- No adjustment is needed for different transmission systems, threshold is global.
- Fast operation time.
- Non-communication based (i.e., use of local measurements).
- Independent from voltage magnitude variation during dead-time.
- Using voltage phasor where it is more reliable rather than the current.
- Fast operation time; average reclosing time delay is 32 ms.
- Applicable for high penetration of renewable resources in the power system.
- Applicable for all types of shunt reactor configurations.
- Algorithm starting time delay is 50 ms, as a result, the algorithm can work properly. even when the fault clears very fast.
- Using the HHT, which is very powerful and practical in the analysis of nonstationary and nonlinear signals.
Author Contributions
Funding
Conflicts of Interest
References
- Bayati, N.; Hajizadeh, A.; Soltani, M. Protection in DC microgrids: A comparative review. IET Smart Grid 2018, 1, 66–75. [Google Scholar] [CrossRef]
- Bayati, N.; Baghaee, H.R.; Hajizadeh, A.; Soltani, M. A Fuse Saving Scheme for DC Microgrids with High Penetration of Renewable Energy Resources. IEEE Access 2020, 8, 137407–137417. [Google Scholar] [CrossRef]
- Bayati, N.; Baghaee, H.R.; Hajizadeh, A.; Soltani, M. Localized protection of radial DC microgrids with high penetration of constant power loads. IEEE Syst. J. 2020. [Google Scholar] [CrossRef]
- Nikoofekr, I.; Sadeh, J. Determining secondary arc extinction time for single-pole auto-reclosing based on harmonic signatures. Electr. Power Syst. Res. 2018, 163, 211–225. [Google Scholar] [CrossRef]
- Dias, O.; Tavares, M.C.; Magrin, F. Hardware implementation and performance evaluation of the fast adaptive single-phase auto reclosing algorithm. Electr. Power Syst. Res. 2019, 168, 169–183. [Google Scholar] [CrossRef]
- Jamali, S.; Ghaffarzadeh, N. Adaptive single-pole auto-reclosure for transmission lines using sound phases currents and wavelet packet transform. Electr. Power Compon. Syst. 2010, 38, 1558–1576. [Google Scholar] [CrossRef]
- Jannati, M.; Moshtagh, J. Hardware implementation of a real-time adaptive single-phase auto-reclosure for power transmission lines. Int. Trans. Electr. Energy Syst. 2020, 30, e12344. [Google Scholar] [CrossRef]
- Jamali, S.; Ghaffarzadeh, N. Adaptive single pole auto-reclosing using discrete wavelet transform. Eur. Trans. Electr. Power 2011, 21, 973–986. [Google Scholar] [CrossRef]
- Luo, X.; Huang, C.; Jiang, Y.; Guo, S. An adaptive three-phase reclosure scheme for shunt reactor-compensated transmission lines based on the change of current spectrum. Electr. Power Syst. Res. 2018, 158, 184–194. [Google Scholar] [CrossRef]
- Jannati, M.; Nazari, M.Y. Improving the stability of power transmission lines based on an adaptive single pole auto-reclosure using a two-step strategy. IET Gener. Transm. Distrib. 2020, 14, 873–882. [Google Scholar] [CrossRef]
- Jamali, S.; Parham, A. New approach to adaptive single pole auto-reclosing of power transmission lines. IET Gener. Transm. Distrib. 2010, 4, 115–122. [Google Scholar] [CrossRef]
- Zadeh, M.D.; Rubeena, R. Communication-aided high-speed adaptive single-phase reclosing. IEEE Trans. Power Deliv. 2012, 28, 499–506. [Google Scholar] [CrossRef]
- Vogelsang, J.; Romeis, C.; Jaeger, J. Real-time adaption of dead time for single-phase autoreclosing. IEEE Trans. Power Deliv. 2015, 31, 1882–1890. [Google Scholar] [CrossRef]
- Khodadadi, M.; Noori, M.R.; Shahrtash, S.M. A noncommunication adaptive single-pole autoreclosure scheme based on the ACUSUM algorithm. IEEE Trans. Power Deliv. 2013, 28, 2526–2533. [Google Scholar] [CrossRef]
- Jamali, S.; Baayeh, A.G. Detection of secondary arc extinction for adaptive single phase auto-reclosing based on local voltage behaviour. IET Gener. Transm. Distrib. 2017, 11, 952–958. [Google Scholar] [CrossRef]
- Baayeh, A.G.; Jamali, S. Detection of Secondary Arc Extinction for Adaptive Single Phase Auto-Reclosing. In Proceedings of the 11th International Conference on Protection and Automation in Power System IPAPC, Tehran, Iran, 17–18 January 2017. [Google Scholar]
- Baayeh, A.G.; Jamali, S. Adaptive Single Phase Auto-Reclosing Using Voltage Magnitude Pattern. In Proceedings of the 31th International Power System Conference, Tehran, Iran, 24–26 October 2016. [Google Scholar]
- Zhalefar, F.; Zadeh, M.R.; Sidhu, T.S. A high-speed adaptive single-phase reclosing technique based on local voltage phasors. IEEE Trans. Power Deliv. 2015, 32, 1203–1211. [Google Scholar] [CrossRef]
- Sohn, S.H.; Cho, G.J.; Kim, C.H. A Study on Application of Recloser Operation Algorithm for Mixed Transmission System Based on Travelling Wave Method. Energies 2020, 13, 2610. [Google Scholar] [CrossRef]
- Granizo Arrabe, R.; Platero Gaona, C.A.; Alvarez Gomez, F.; Rebollo Lopez, E. Novel Auto-Reclosing Blocking Method for Combined Overhead-Cable Lines in Power Networks. Energies 2016, 9, 964. [Google Scholar] [CrossRef]
- Cho, G.J.; Park, J.K.; Sohn, S.H.; Chung, S.J.; Gwon, G.H.; Oh, Y.S.; Kim, C.H. Development of a Leader-End Reclosing Algorithm Considering Turbine-Generator Shaft Torque. Energies 2017, 10, 622. [Google Scholar]
- Morales, J.; Muñoz, E.; Orduña, E.; Idarraga-Ospina, G. A novel approach to arcing faults characterization using multivariable analysis and support vector machine. Energies 2019, 12, 2126. [Google Scholar] [CrossRef]
- Khan, W.A.; Bi, T.; Jia, K. A review of single phase adaptive auto-reclosing schemes for EHV transmission lines. Prot. Control Mod. Power Syst. 2019, 4, 18. [Google Scholar] [CrossRef]
- Dantas, K.M.; Neves, W.L.; Fernandes, D. An approach for controlled reclosing of shunt-compensated transmission lines. IEEE Trans. Power Deliv. 2013, 29, 1203–1211. [Google Scholar] [CrossRef]
- Huang, X.; Song, G.; Wang, T.; Gu, Y. Three-phase adaptive reclosure for transmission lines with shunt reactors using mode current oscillation frequencies. J. Eng. 2018, 25, 1012–1017. [Google Scholar] [CrossRef]
- Jiaxing, N.; Baina, H.; Zhenzhen, W.; Jie, K. Algorithm for adaptive single-phase reclosure on shunt-reactor compensated extra high voltage transmission lines considering beat frequency oscillation. IET Gener. Transm. Distrib. 2018, 12, 3193–3200. [Google Scholar] [CrossRef]
- Xie, C.; Li, F.; Wang, B.; Fan, Y.; Jing, L.; Chen, W.; Wang, C. Anti-interference adaptive single-phase auto-reclosing schemes based on reactive power characteristics for transmission lines with shunt reactors. Electr. Power Syst. Res. 2019, 170, 176–183. [Google Scholar] [CrossRef]
- Xie, C.; Li, F.; Fan, Y.; Wang, C.; Wang, T. Faulty phase active power characteristics-based adaptive single-phase reclosing schemes for shunt reactors-compensated wind power outgoing line. Wind Energy 2019, 22, 1746–1759. [Google Scholar] [CrossRef]
- Xie, X.; Huang, C. A novel adaptive auto-reclosing scheme for transmission lines with shunt reactors. Electr. Power Syst. Res. 2019, 171, 47–53. [Google Scholar] [CrossRef]
- Khorashadi-Zadeh, H.; Li, Z. Design of a novel phasor measurement unit-based transmission line auto reclosing scheme. IET Gener. Transm. Distrib. 2011, 5, 806–813. [Google Scholar] [CrossRef]
- Kizilcay, M.; Pniok, T. Digital simulation of fault arcs in power systems. Eur. Trans. Electr. Power 1991, 1, 55–60. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Ge, Y.; Sui, F.; Xiao, Y. Prediction methods for preventing single-phase reclosing on permanent fault. IEEE Trans. Power Deliv. 1989, 4, 114–121. [Google Scholar]
- Jafarian, P.; Eskandari, H.; Sanaye-Pasand, M. Sizing Neutral Reactor Regardless of Line Length in Shunt Compensated Transmission Lines. In Proceedings of the 31th Power System Conference, Tehran, Iran, 24–26 October 2016. [Google Scholar]
- Jafarian, P.; Eskandari, H.; Sanaye-Pasand, M. Application of universal neutral reactor in shunt compensated transmission lines: Feasibility study. IET Gener. Transm. Distrib. 2018, 12, 2181–2189. [Google Scholar] [CrossRef]
- Zadeh, M.R.; Sanaye-Pasand, M.K. Investigation of neutral reactor performance in reducing secondary arc current. IEEE Trans. Power Deliv. 2008, 23, 2472–2479. [Google Scholar] [CrossRef]
- Al-Shetwi, A.Q.; Hannan, M.A.; Jern, K.P.; Alkahtani, A.A.; PG Abas, A.E. Power Quality Assessment of Grid-Connected PV System in Compliance with the Recent Integration Requirements. Electronics 2020, 9, 366. [Google Scholar] [CrossRef]
- Dias, O.; Magrin, F.; Tavares, M.C. Comparison of secondary arcs for reclosing applications. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1592–1599. [Google Scholar] [CrossRef]


| R (ohm) | L (H) | C (uF) | |
|---|---|---|---|
| Zero sequence | 2.8813 | 0.3647 | 1.4713 |
| Positive sequence | 0.0515 | 3.1572 | 2.3269 |
| Shunt Compensation Percentage | 50% | 75% | 95% | ||||
|---|---|---|---|---|---|---|---|
| Reactance (ohm) | |||||||
| Effectively grounded | Reactor at only one side | 2245.80 | - | 1506.60 | - | 1190.30 | - |
| Reactor at both ends | 4491.60 | - | 3013.20 | - | 2380.60 | - | |
| Grounded through neutral reactor, calculated based on [36] | Reactor at only one side | 2245.80 | 1967.10 | 1506.60 | 474.77 | 1190.30 | 247.23 |
| Reactor at both ends | 4491.60 | 3934.20 | 3013.20 | 949.55 | 2380.60 | 494.45 | |
| Grounded through neutral reactor, calculated based on [34,35] | Reactor at only one side | 2245.80 | 435.30 | 1506.60 | 292.04 | 1190.30 | 230.71 |
| Reactor at both ends | 4491.60 | 870.61 | 3013.20 | 584.08 | 2380.60 | 461.42 | |
| FCDD for ASPAR Relay at Substation1/Substation2 | Medium Loading, 50% of the Line SIL | High Loading, 100% of the Line SIL | ||||||
|---|---|---|---|---|---|---|---|---|
| fault location from Bus1 | 30% | 60% | 90% | 30% | 60% | 90% | ||
| Effectively grounded | Reactor at Bus1 | 50% | 32/34 | 29/34 | 34/30 | 35/32 | 32/36 | 31/31 |
| 75% | 35/32 | 32/31 | 30/32 | 33/30 | 30/34 | 32/29 | ||
| 95% | 28/32 | 31/33 | 28/29 | 31/31 | 32/34 | 33/32 | ||
| Reactor at Bus2 | 50% | 32/34 | 31/32 | 29/32 | 33/32 | 32/30 | 33/34 | |
| 75% | 30/33 | 30/34 | 33/31 | 32/35 | 33/33 | 31/32 | ||
| 95% | 38/33 | 31/33 | 33/36 | 30/30 | 32/31 | 32/31 | ||
| Reactor at both ends | 50% | 34/35 | 28/34 | 33/34 | 34/34 | 33/31 | 36/32 | |
| 75% | 35/34 | 34/32 | 32/27 | 32/33 | 33/31 | 28/30 | ||
| 95% | 30/33 | 34/32 | 33/33 | 32/32 | 30/30 | 37/31 | ||
| Grounded through neutral reactor, calculated based on [36] | Reactor at Bus1 | 50% | 31/31 | 32/34 | 31/29 | 33/30 | 31/30 | 33/32 |
| 75% | 32/31 | 32/28 | 34/32 | 32/32 | 31/32 | 34/32 | ||
| 95% | 34/35 | 31/31 | 29/32 | 30/32 | 32/29 | 29/32 | ||
| Reactor at Bus2 | 50% | 32/29 | 35/30 | 33/34 | 31/29 | 32/33 | 31/33 | |
| 75% | 34/32 | 32/31 | 30/31 | 31/33 | 33/32 | 32/32 | ||
| 95% | 28/28 | 31/34 | 31/35 | 31/31 | 26/33 | 33/36 | ||
| Reactor at both ends | 50% | 31/34 | 35/34 | 33/31 | 35/32 | 32/32 | 29/33 | |
| 75% | 30/34 | 32/30 | 34/33 | 30/33 | 35/33 | 33/36 | ||
| 95% | 29/32 | 31/31 | 30/33 | 31/30 | 30/29 | 30/31 | ||
| Grounded through neutral reactor, calculated based on [34,35] | Reactor at Bus1 | 50% | 33/32 | 32/32 | 35/32 | 30/32 | 34/30 | 32/33 |
| 75% | 33/27 | 31/32 | 33/34 | 29/33 | 33/31 | 33/32 | ||
| 95% | 32/33 | 30/33 | 32/33 | 31/29 | 32/32 | 33/33 | ||
| Reactor at Bus2 | 50% | 29/28 | 38/33 | 32/30 | 31/34 | 33/34 | 34/33 | |
| 75% | 34/28 | 36/30 | 32/28 | 35/37 | 29/31 | 34/28 | ||
| 95% | 33/32 | 33/32 | 32/36 | 31/34 | 32/34 | 31/29 | ||
| Reactor at both ends | 50% | 32/30 | 30/28 | 32/31 | 30/32 | 36/33 | 33/29 | |
| 75% | 32/33 | 31/34 | 32/32 | 35/33 | 33/34 | 30/33 | ||
| 95% | 32/34 | 32/31 | 34/33 | 34/30 | 33/32 | 29/35 | ||
| Method | Starting Time Delay, (ms) | Reclosing Time Delay (ms) | Communication-Based? | Sampling Frequency (Hz) | Threshold | Computation Burden | Sensitivity to Voltage Magnitude Oscillation |
|---|---|---|---|---|---|---|---|
| [4] | 80 | <15 | No | 3200 | Adaptive | Medium | Low |
| [5] | 200 | <76 | No | 1920 | Fixed | Medium | Low |
| [8] | 60 | <60 | No | 2500 | Fixed | High | Low |
| [10] | 120 | <10 | No | 5000 | Not used | Low | Very High |
| [11] | 60 | <9 | No | 1600 | Not used | Low | Low |
| [14] | 100 | <4 | No | 1000 | Fixed | Low | Very High |
| [16] | Adaptive, with average of 31 ms | <31 | No | 800 | Adaptive | Low | Medium |
| [18] | NM | <105 | No | 3840 | Fixed | Medium | Medium |
| [12] | NM | <67 | Yes | 3840 | Fixed | Medium | low |
| [30] | 40 | <14 | Yes | 720 | Fixed | Medium | low |
| Proposed method | 50 ms | <38 | No | 1920 | Global | Low | Very low |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baayeh, A.G.; Bayati, N. Adaptive Overhead Transmission Lines Auto-Reclosing Based on Hilbert–Huang Transform. Energies 2020, 13, 5416. https://doi.org/10.3390/en13205416
Baayeh AG, Bayati N. Adaptive Overhead Transmission Lines Auto-Reclosing Based on Hilbert–Huang Transform. Energies. 2020; 13(20):5416. https://doi.org/10.3390/en13205416
Chicago/Turabian StyleBaayeh, Arman Ghaderi, and Navid Bayati. 2020. "Adaptive Overhead Transmission Lines Auto-Reclosing Based on Hilbert–Huang Transform" Energies 13, no. 20: 5416. https://doi.org/10.3390/en13205416
APA StyleBaayeh, A. G., & Bayati, N. (2020). Adaptive Overhead Transmission Lines Auto-Reclosing Based on Hilbert–Huang Transform. Energies, 13(20), 5416. https://doi.org/10.3390/en13205416