The Ångström–Prescott Regression Coefficients for Six Climatic Zones in South Africa
Abstract
1. Introduction
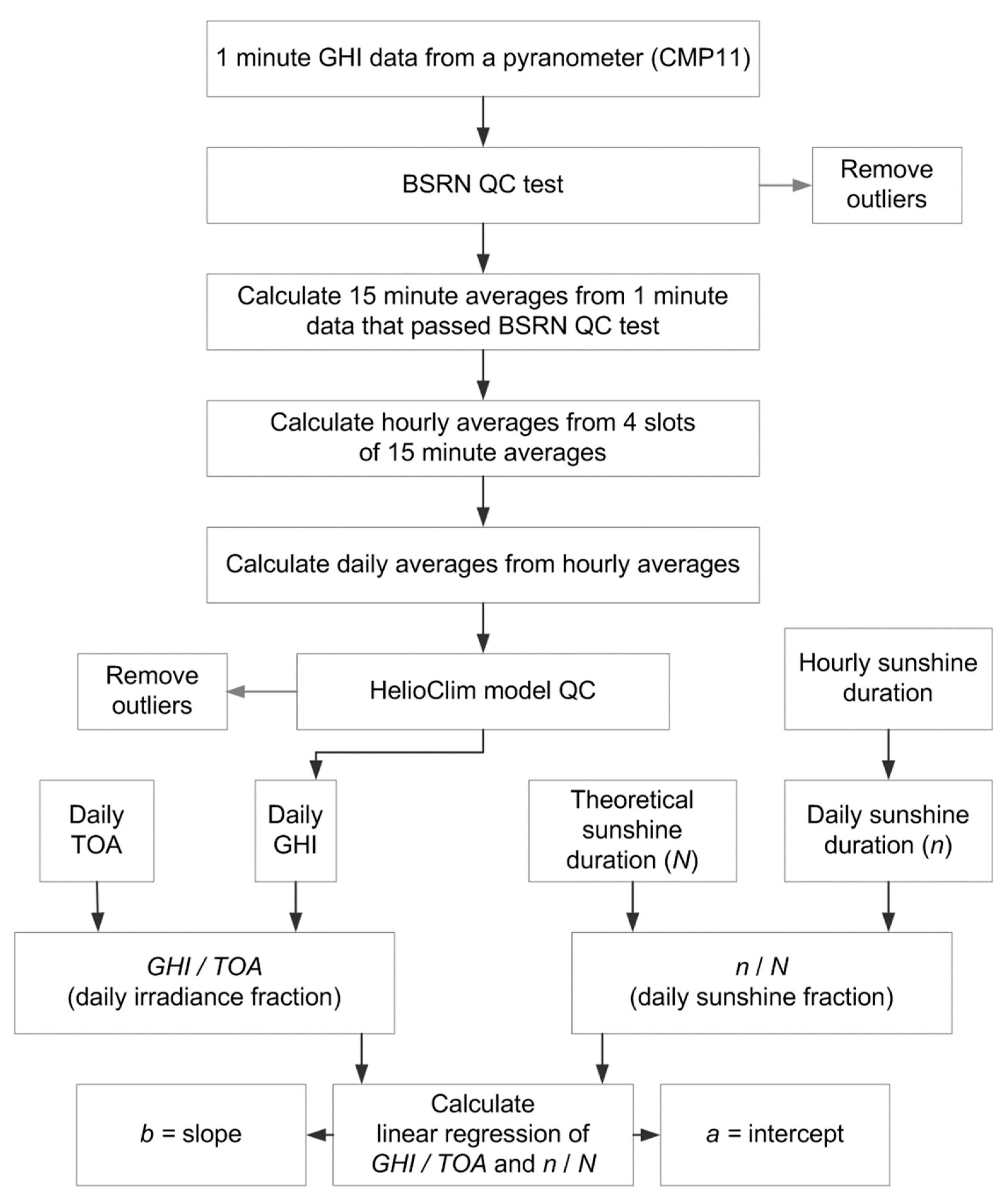
2. Materials and Methods
- Mean Bias Error (MBE), which estimates the average error in the prediction. A positive MBE indicates that the prediction is overestimated and vice versa; the lower values of MBE indicate a strong correlation between the prediction and observation. A relative Mean Bias Error (rMBE), which measures the size of the error in percentage terms, was also calculated. The metrices are expressed as:
- Mean Absolute Error (MAE), which measures the absolute value of the differences between the observed and the predicted values, gives a better idea of the prediction accuracy; relative Mean Absolute Error (rMAE), which measures the size of the error in percentage terms, was also calculated. The caution with MBE and rMBE is with the cancelling of positive and negative bias, which can lead to a false interpretation. The metrics are expressed as:
- Root Mean Square Error (RMSE), which compares the predicted and observed datasets, measures the statistical variability of the prediction accuracy and is expressed as shown in Equation (14), while Equation (15) shows the relative Root Mean Square Error (rRMSE), which measures the size error in percentage terms. The RMSE and rRMSE are also indifferent to the direction of the error. They are considered in this study since these put extra weight on large errors. The metrices are expressed as:
- Coefficient of Determination (R2), which is a statistical measure of the strength of the relationship between the movement of predicted and observed. R2 also measures how well the regression line represents the data. The value of R2 is such that . The closer R2 is to 1, the better the prediction. The metric is expressed as:where is the observation value, is the estimated value, is the average of the observation values, i is the time point, and n is the total number of points used.
3. Results and Discussion
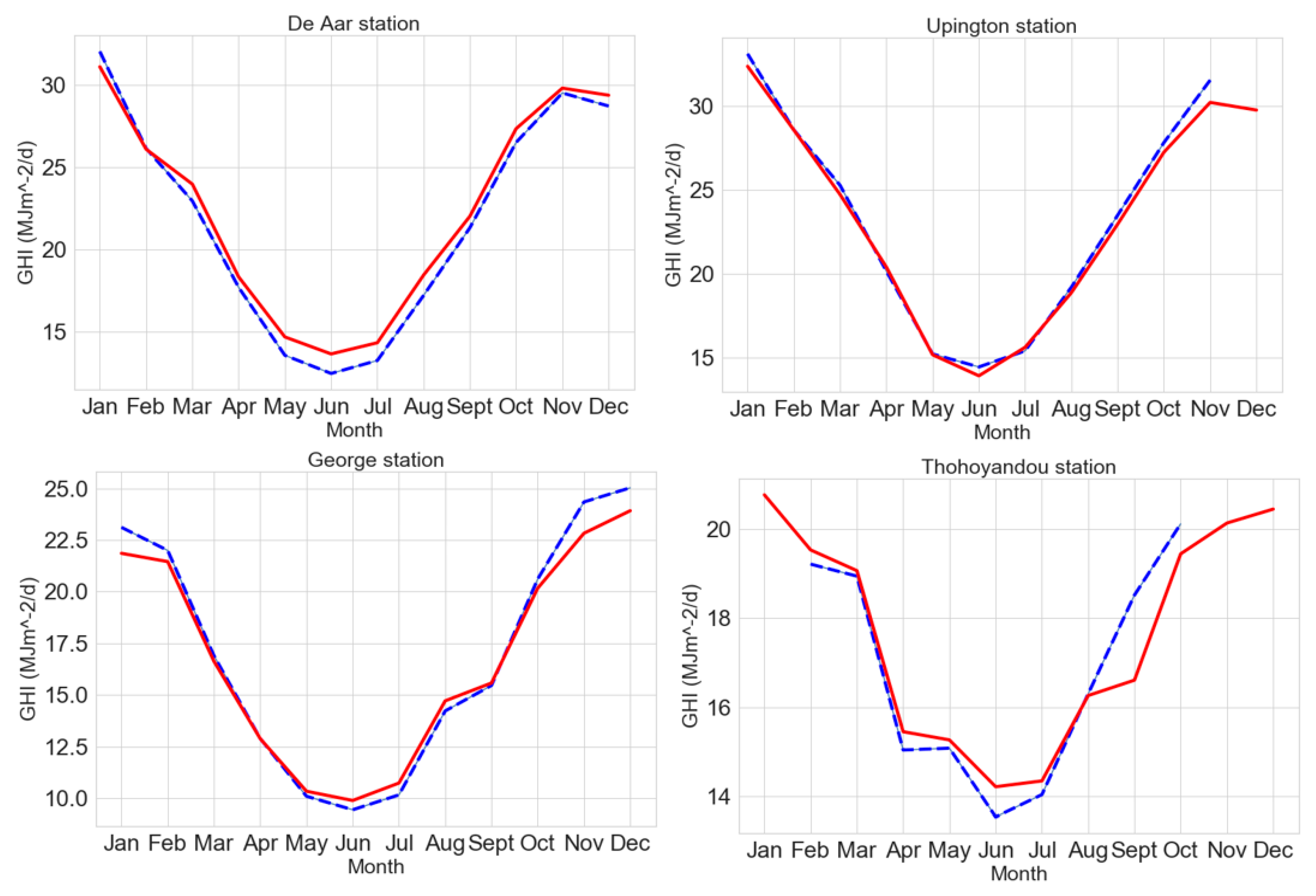
3.1. Annual AP Results
3.2. Validation Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviation | Full Description | Units |
| SAWS | South African Weather Service | |
| AP | Ångström–Prescott | |
| a | Ångström–Prescott regression coefficient | |
| b | Ångström–Prescott regression coefficient | |
| GHI | Global Horizontal Irradiance | W/m2 |
| Daily extraterrestrial or Top of the atmosphere global horizontal irradiance | W/m2 | |
| TOA | Top of the Atmosphere | W/m2 |
| N | Daily astronomical day length | Hours |
| n | Daily measured sunshine duration | Hours |
| BSRN | Baseline Solar Radiation Network | |
| QC | Quality control | |
| SPA | Solar Position Algorithm | |
| Solar constant | W/m2 | |
| Eccentricity factor | Degrees | |
| Sunset hour angle | Degrees | |
| Degrees of latitude | Degrees | |
| δ | Solar declination | Degrees |
| MBE | Mean Bias Error | MJ m−2d−1 |
| rMBE | relative Mean Bias Error | Percentage (%) |
| MAE | Mean Absolute Error | MJ m−2d−1 |
| rMAE | relative Mean Absolute Error | Percentage (%) |
| RMSE | Root Mean Square Error | MJ m−2d−1 |
| rRMSE | relative Root Mean Square Error | Percentage (%) |
| R2 | Correlation coefficient | |
| NaN | Not a Number | |
| D | Day of the year | |
| CMP11 | Secondary standard Kipp & Zonen pyranometers |
References
- Tang, W.; Yang, K.; He, J.; Qin, J. Quality control and estimation of global solar radiation in China. Sol. Energy 2010, 84, 466–475. [Google Scholar] [CrossRef]
- Adamala, S.; Reddy, Y.V.K. Evaluation of Different Solar Radiation Estimation Methods for Indian Locations. Water Resour. Environ. Eng. II 2018, 47–56. [Google Scholar] [CrossRef]
- Zhang, Q.; Cui, N.; Feng, Y.; Jia, Y.; Li, Z.; Gong, D. Comparative Analysis of Global Solar Radiation Models in Different Regions of China. Adv. Meteorol. 2018, 2018, 1–21. [Google Scholar] [CrossRef]
- De Medeiros, F.J.; Silva, C.M.; Bezerra, B.G. Calibration of Ångström-Prescott Equation to Estimate Daily Solar Radiation on Rio Grande do Norte State, Brazil. Rev. Bras. Meteorol. 2017, 32, 409–416. [Google Scholar] [CrossRef][Green Version]
- Almorox, J.; Benito, M.; Hontoria, C. Estimation of monthly Angström-Prescott equation coefficients from measured daily data in Toledo, Spain. Renew. Energy 2005, 30, 931–936. [Google Scholar] [CrossRef]
- Mabasa, M.B.; Botai, J.; Ntsangwane, M.L. Update on the Re-Establishment of the South African Weather Services (SAWS) Radiometric Network in All Six Climatological Regions and the Quality of the Data. In Proceedings of the South African Solar Energy Conference (SASEC), Blue Waters Hotel, KwaZulu-Natal, South Africa, 25–27 June 2018; Available online: https://www.sasec.org.za/full_papers/68.pdf (accessed on 20 January 2020).
- Mabasa, B.; Tazvinga, H.; Zwane, N.; Botai, J.; Ntsangwane, L. Assessment of Global Horizontal Irradiance in South Africa. In Proceedings of the South African Solar Energy Conference (SASEC), Mpekweni Beach Resort, Eastern Cape Province, South Africa, 25–27 November 2019; Available online: https://www.sasec.org.za/papers2019/47.pdf (accessed on 25 January 2020).
- Singh, J.; Kruger, A. Is the summer season losing potential for solar energy applications in South Africa? J. Energy South. Afr. 2017, 28, 52. [Google Scholar] [CrossRef]
- Wilbert, S.; Stoffel, T.; Myers, D.; Wilcox, S.; Habte, A.; Vignola, F.; Wood, J.; Pomares, L.M. Measuring Solar Radiation and Relevant Atmospheric Parameters. In Best Practices Handbook for the Collection and Use of Solar Resource Data for Solar Energy Applications; National Renewable Energy Laboratory: Golden, CO, USA, 2017; Available online: https://hal-mines-paristech.archives-ouvertes.fr/hal-01184753 (accessed on 12 March 2020).
- Garg, H.P.; Garg, S.N. Measurement of solar radiation—II. Calibration and standardization. Renew. Energy 1993, 3, 335–348. [Google Scholar] [CrossRef]
- Angstrom, A. Solar and terrestrial radiation: Report to the international commission for solar research on actinometric investigations of solar and atmospheric radiation. Quart. J. Roy. Meteorol. Soc. 1924, 50, 121–126. [Google Scholar] [CrossRef]
- Prescott, J.A. Evaporation from a water surface in relation to solar radiation. Trans. Roy. Soc. S. Aust. 1940, 46, 114–118. [Google Scholar]
- Iqbal, M. An Introduction to Solar Radiation; Academic Press: Toronto, ON, Canada, 1983. [Google Scholar]
- Martínez-Lozano, J.A.; Tena, F.; Onrubia, J.E.; De La Rubia, J. The historical evolution of the Angström formula and its modifications: A review and bibliography. Agric. For. Meteorol. 1984, 33, 109–128. [Google Scholar] [CrossRef]
- Tsung, K.Y.; Tan, R.; Ii, G.Y. Estimating the global solar radiation in Putrajaya using the Angstrom-Prescott model. IOP Conf. Series: Earth Environ. Sci. 2019, 268, 012056. [Google Scholar] [CrossRef]
- Besharat, F.; Dehghan, A.A.; Faghih, A.R. Empirical models for estimating global solar radiation: A review and case study. Renew. Sustain. Energy Rev. 2013, 21, 798–821. [Google Scholar] [CrossRef]
- Eberhard, A.A. A Solar Radiation Data Handbook for Southern Africa; Elan Press: Cape Town, South Africa, 1990. [Google Scholar]
- Malaudzi, S.T.; Sankaran, V.; Lysko, M.D. Solar radiation analysis and regression coefficients for the Vhembe Region, Limpopo Province, South Africa. J. Energy South. Afr. 2017, 24, 2–7. [Google Scholar] [CrossRef]
- Maupin, K.A.; Swiler, L.P.; Porter, N.W. Validation Metrics for Deterministic and Probabilistic Data. J. Verificat. Valid. Uncertain. Quantif. 2018, 3, 031002. [Google Scholar] [CrossRef]
- Paulescu, M.; Stefu, N.; Calinoiu, D.; Tulcan-Paulescu, E.; Pop, N.; Boata, R.; Mares, O. Ångström–Prescott equation: Physical basis, empirical models and sensitivity analysis. Renew. Sustain. Energy Rev. 2016, 62, 495–506. [Google Scholar] [CrossRef]
- Long, C.N.; Dutton, E.G. BSRN Global Network Recommended QC Tests, V2. 2010. Available online: https://epic.awi.de/30083/1/BSRN_recommended_QC_tests_V2.pdf (accessed on 11 December 2019).
- Thomas, C.; Wey, E.; Blanc, P.; Wald, L. Validation of three satellite-derived databases of surface solar radiation using measurements performed at 42 stations in Brazil. Adv. Sci. Res. 2016, 13, 81–86. [Google Scholar] [CrossRef]
- Urraca, R.; Gracia-Amillo, A.M.; Huld, T.; Martinez-De-Pison, F.J.; Trentmann, J.; Lindfors, A.V.; Riihelä, A.; Sanz-Garcia, A. Quality control of global solar radiation data with satellite-based products. Sol. Energy 2017, 158, 49–62. [Google Scholar] [CrossRef]
- Riihelä, A.; Kallio, V.; Devraj, S.; Sharma, A.; Lindfors, A.V. Validation of the SARAH-E Satellite-Based Surface Solar Radiation Estimates over India. Remote Sens. 2018, 10, 392. [Google Scholar] [CrossRef]
- Roesch, A.; Wild, M.; Ohmura, A.; Dutton, E.G.; Long, C.N.; Zhang, T. Assessment of BSRN radiation records for the computation of monthly means. Atmos. Meas. Tech. 2011, 4, 339–354. [Google Scholar] [CrossRef]
- Geiger, M.; Diabaté, L.; Ménard, L.; Wald, L. A web service for controlling the quality of measurements of global solar irradiation. Sol. Energy 2002, 73, 475–480. [Google Scholar] [CrossRef]
- Holmgren, W.F.; Hansen, C.; Mikofski, M. Pvlib python: A python package for modeling solar energy systems. J. Open Source Softw. 2018, 3. [Google Scholar] [CrossRef]
- Reda, I.; Andreas, A. Solar position algorithm for solar radiation applications. Sol. Energy 2004, 76, 577–589. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1980; pp. 6–13, 22. [Google Scholar]
- Gueymard, C.A. The sun’s total and spectral irradiance for solar energy applications and solar radiation models. Sol. Energy 2004, 76, 423–453. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Requirements-Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. 05109. Available online: https://appgeodb.nancy.inra.fr/biljou/pdf/Allen_FAO1998.pdf (accessed on 15 February 2020).
- CMP11 Pyranometer. Available online: https://www.campbellsci.eu/cmp11 (accessed on 17 March 2020).
- CMP11 Pyranometer. Available online: https://www.kippzonen.com/Product/13/CMP11-Pyranometer#.X1UGh-fivIV (accessed on 12 May 2020).
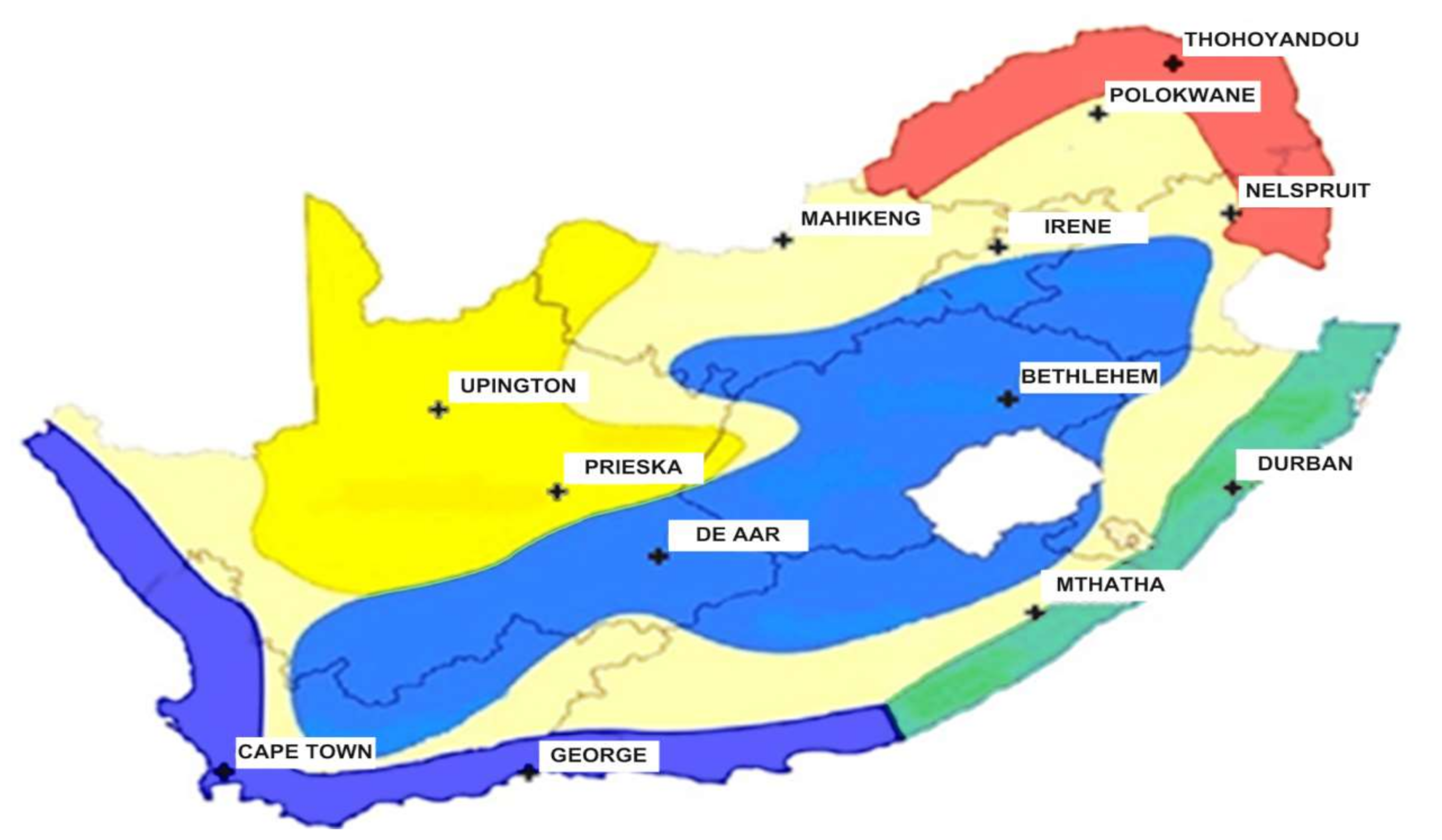


| Station | Latitude (°) | Longitude (°) | Altitude (m) | Period | Climatic Zone |
|---|---|---|---|---|---|
| Upington | −28.48 | 21.12 | 848 | 2014-02-01 to 2019-11-30 | Arid Interior |
| De Aar | −30.67 | 23.99 | 1284 | 2014-05-01 to 2019-12-31 | Cold Interior |
| Irene | −25.91 | 28.21 | 1524 | 2014-03-01 to 2019-12-31 | Temperate Interior |
| Mthatha | −31.55 | 28.67 | 744 | 2014-07-01 to 2019-12-31 | Subtropical Coastal |
| George | −34.01 | 22.38 | 192 | 2015-01-01 to 2019-12-31 | Temperate Coastal |
| Durban | −29.61 | 31.11 | 91 | 2015-03-01 to 2019-12-31 | Subtropical Coastal |
| Polokwane | −23.86 | 29.45 | 1233 | 2015-03-01 to 2019-12-31 | Temperate Interior |
| Thohoyandou | −23.08 | 30.38 | 619 | 2015-03-01 to 2017-10-31 | Hot Interior |
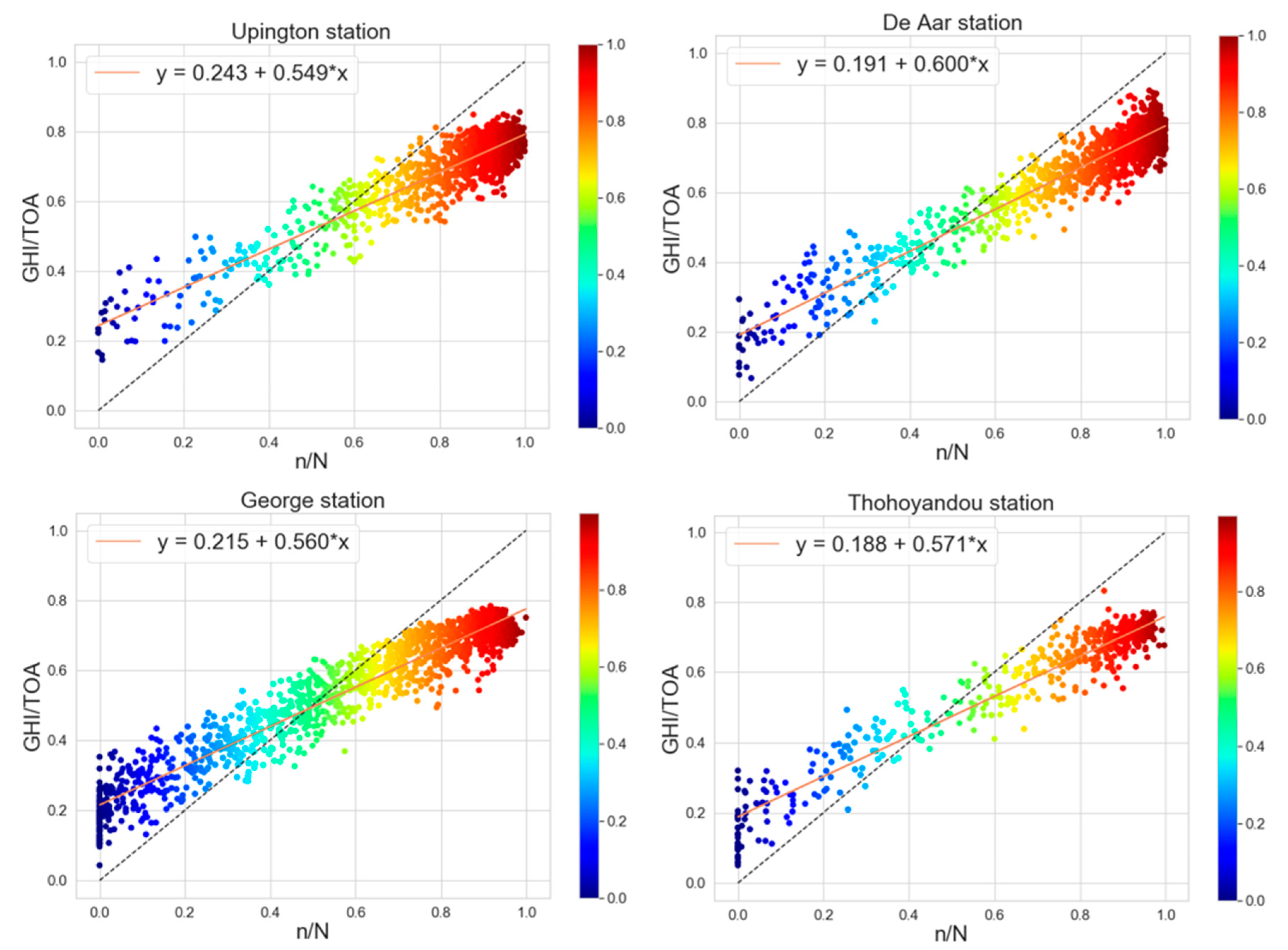
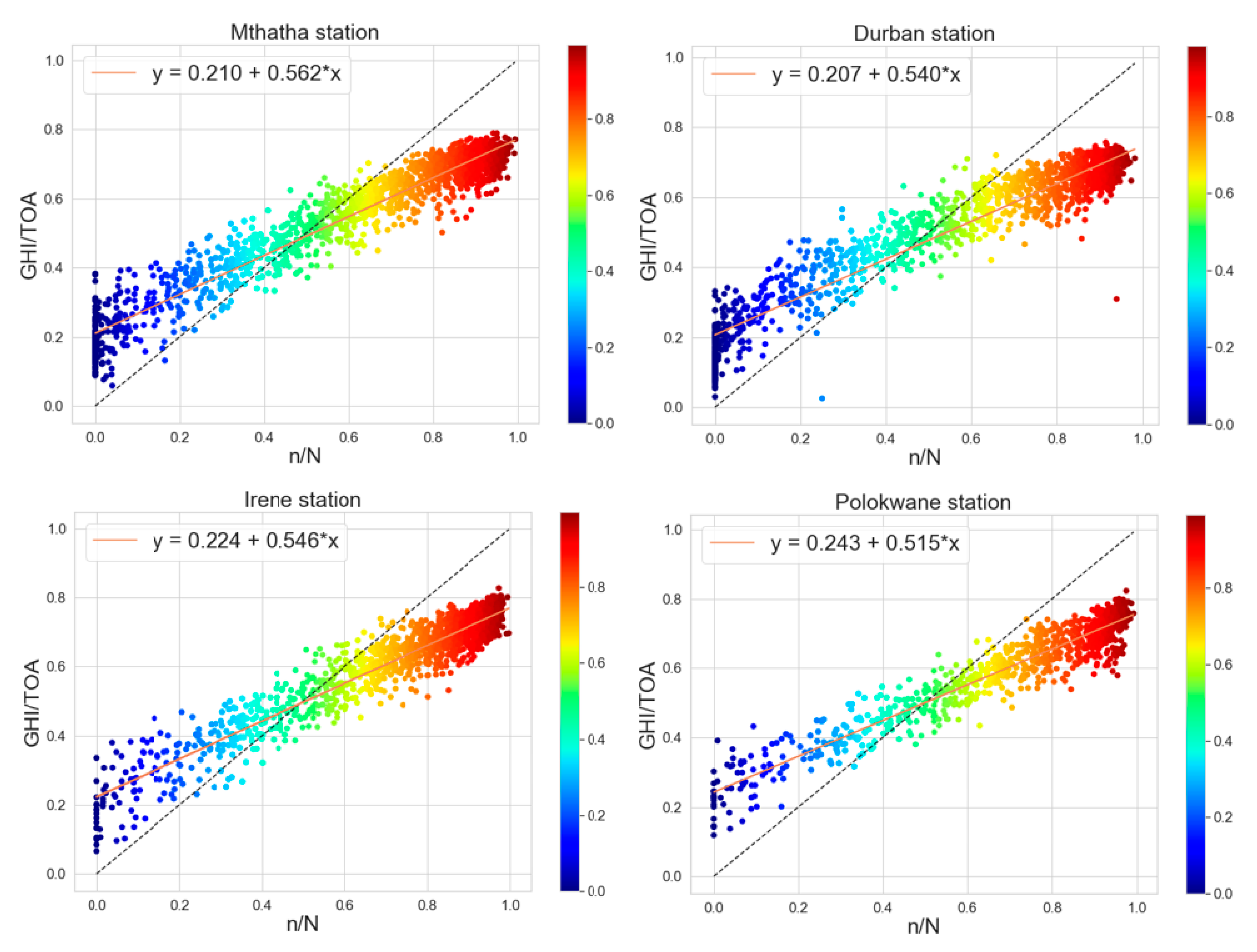
| Station | a | b | RMBE | rMBE (%) | MAE | rMAE (%) | RMSE | rRMSE (%) | R2 |
|---|---|---|---|---|---|---|---|---|---|
| Upington | 0.243 | 0.549 | −0.360 | −0.120 | 0.841 | 0.311 | 1.061 | 0.393 | 0.930 |
| De Aar | 0.191 | 0.600 | 0.733 | 0.371 | 1.136 | 0.506 | 1.375 | 0.598 | 0.930 |
| Irene | 0.224 | 0.546 | 0.689 | 0.353 | 1.328 | 0.608 | 1.618 | 0.729 | 0.912 |
| Mthatha | 0.210 | 0.562 | −0.104 | −0.013 | 1.168 | 0.582 | 1.474 | 0.735 | 0.951 |
| George | 0.215 | 0.560 | −0.270 | −0.036 | 1.261 | 0.636 | 1.520 | 0.769 | 0.948 |
| Durban | 0.207 | 0.540 | −0.322 | −0.106 | 1.425 | 0.745 | 1.741 | 0.910 | 0.915 |
| Polokwane | 0.243 | 0.515 | −0.286 | −0.085 | 1.272 | 0.488 | 1.572 | 0.606 | 0.910 |
| Thohoyandou | 0.188 | 0.571 | 0.286 | 0.168 | 1.071 | 0.550 | 1.433 | 0.746 | 0.937 |
| Almorox et al. | 0.287 | 0.452 | −0.002 | - | - | - | 1.260 | - | - |
| De Medeiros et al. | 0.39 | 0.29 | 1.040 | 6.29 | - | - | 1.94 | - | 0.58 |
| Tsung et al. | 0.5 | 0.11 | 0.85 | 3.4 | 1.8 | - | 1.9 | - | - |
| Zhang et al. | 0.214 | 0.552 | - | - | 2.249 | - | 0.214 | - | 0.875 |
| Adamala et al. | 0.28 | 0.52 | - | - | - | - | 7.04 | - | 0.74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mabasa, B.; Lysko, M.D.; Tazvinga, H.; Mulaudzi, S.T.; Zwane, N.; Moloi, S.J. The Ångström–Prescott Regression Coefficients for Six Climatic Zones in South Africa. Energies 2020, 13, 5418. https://doi.org/10.3390/en13205418
Mabasa B, Lysko MD, Tazvinga H, Mulaudzi ST, Zwane N, Moloi SJ. The Ångström–Prescott Regression Coefficients for Six Climatic Zones in South Africa. Energies. 2020; 13(20):5418. https://doi.org/10.3390/en13205418
Chicago/Turabian StyleMabasa, Brighton, Meena D. Lysko, Henerica Tazvinga, Sophie T. Mulaudzi, Nosipho Zwane, and Sabata J. Moloi. 2020. "The Ångström–Prescott Regression Coefficients for Six Climatic Zones in South Africa" Energies 13, no. 20: 5418. https://doi.org/10.3390/en13205418
APA StyleMabasa, B., Lysko, M. D., Tazvinga, H., Mulaudzi, S. T., Zwane, N., & Moloi, S. J. (2020). The Ångström–Prescott Regression Coefficients for Six Climatic Zones in South Africa. Energies, 13(20), 5418. https://doi.org/10.3390/en13205418






