A General Investigation on the Differential Leakage Factor for Symmetrical and Asymmetrical Multiphase Winding Design
Abstract
1. Introduction
2. Symmetry Conditions and Degree of Unbalance in m-Phase Machine Windings
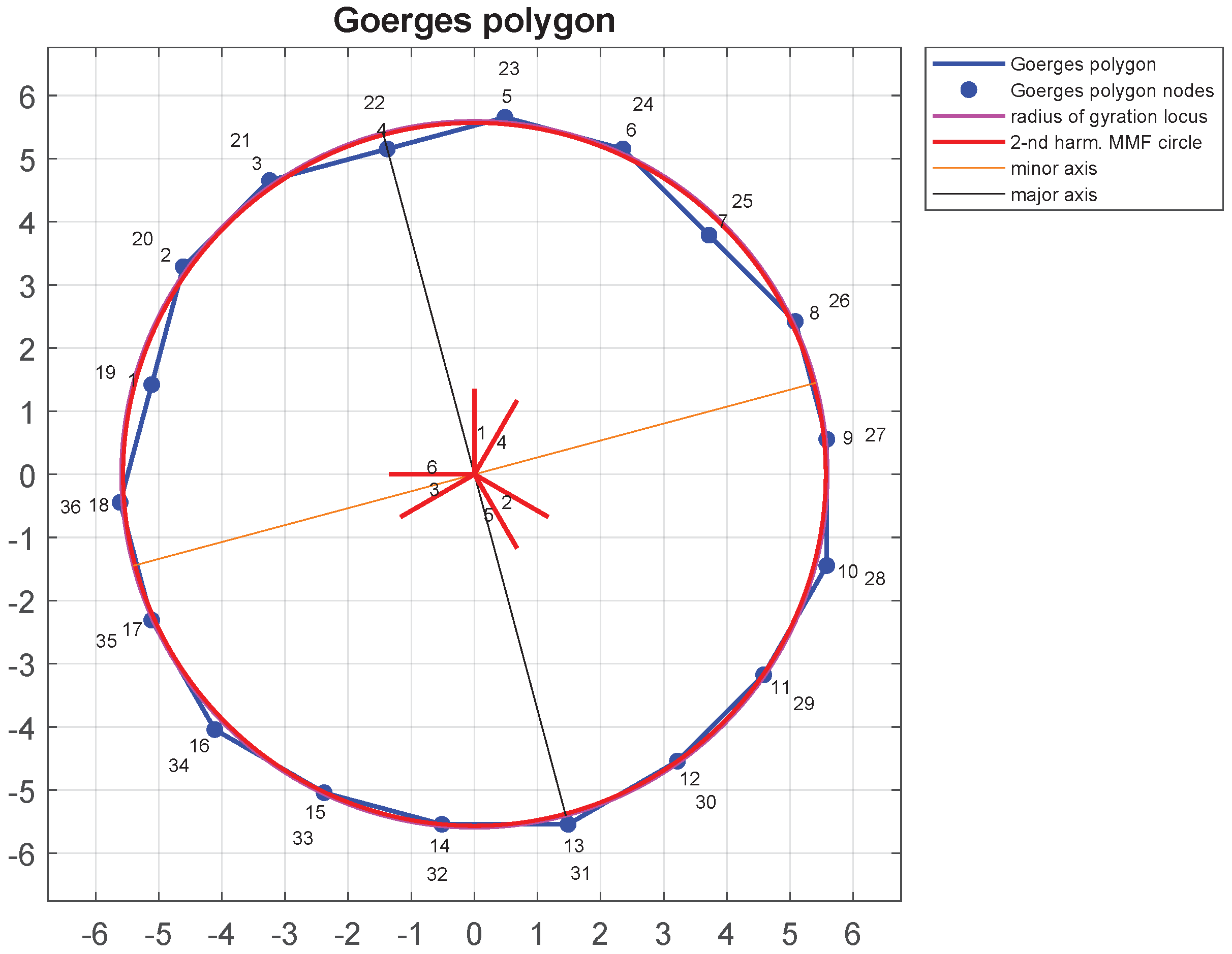
3. The Differential Leakage Factor in m-Phase Machine Windings
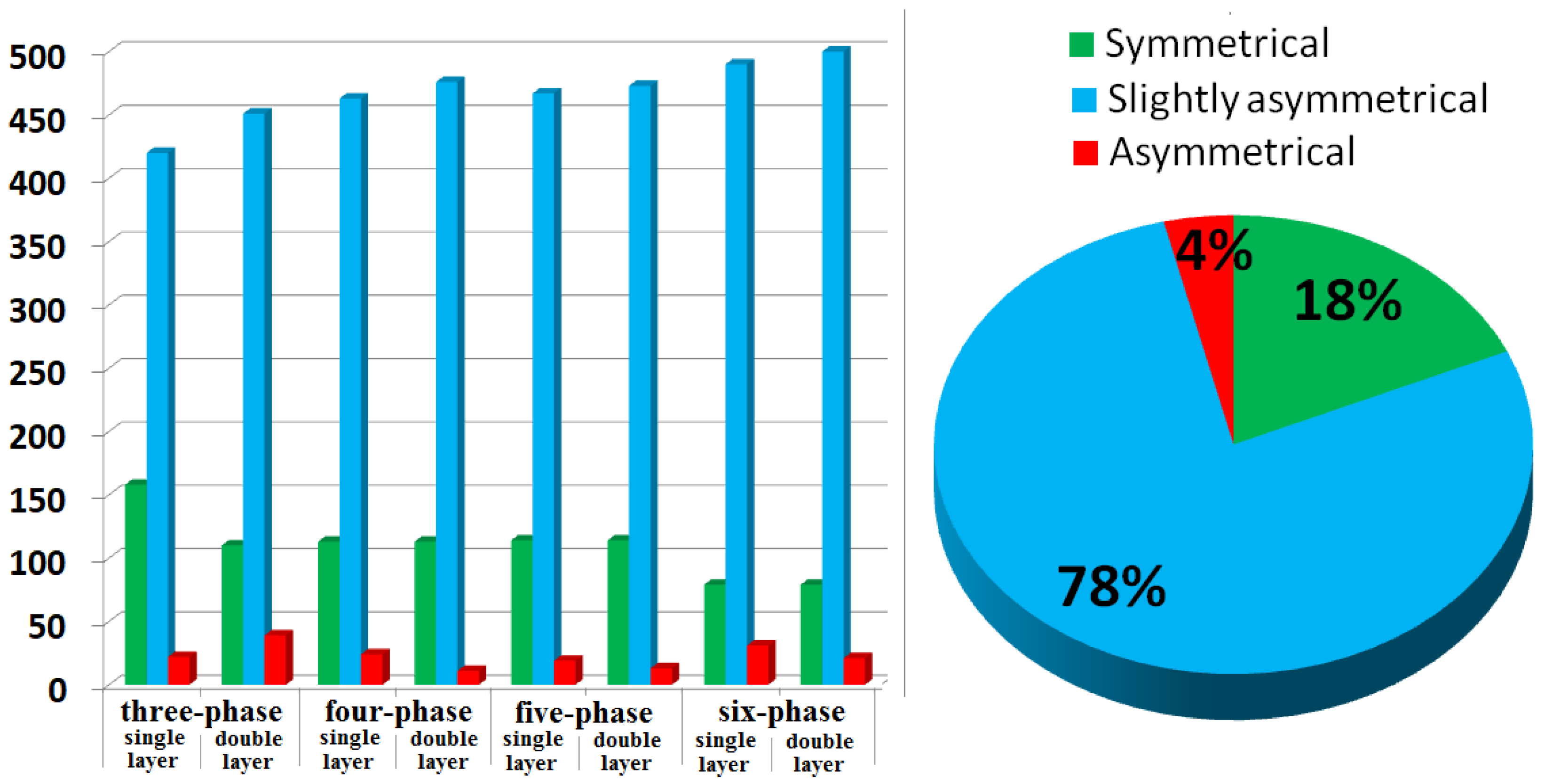
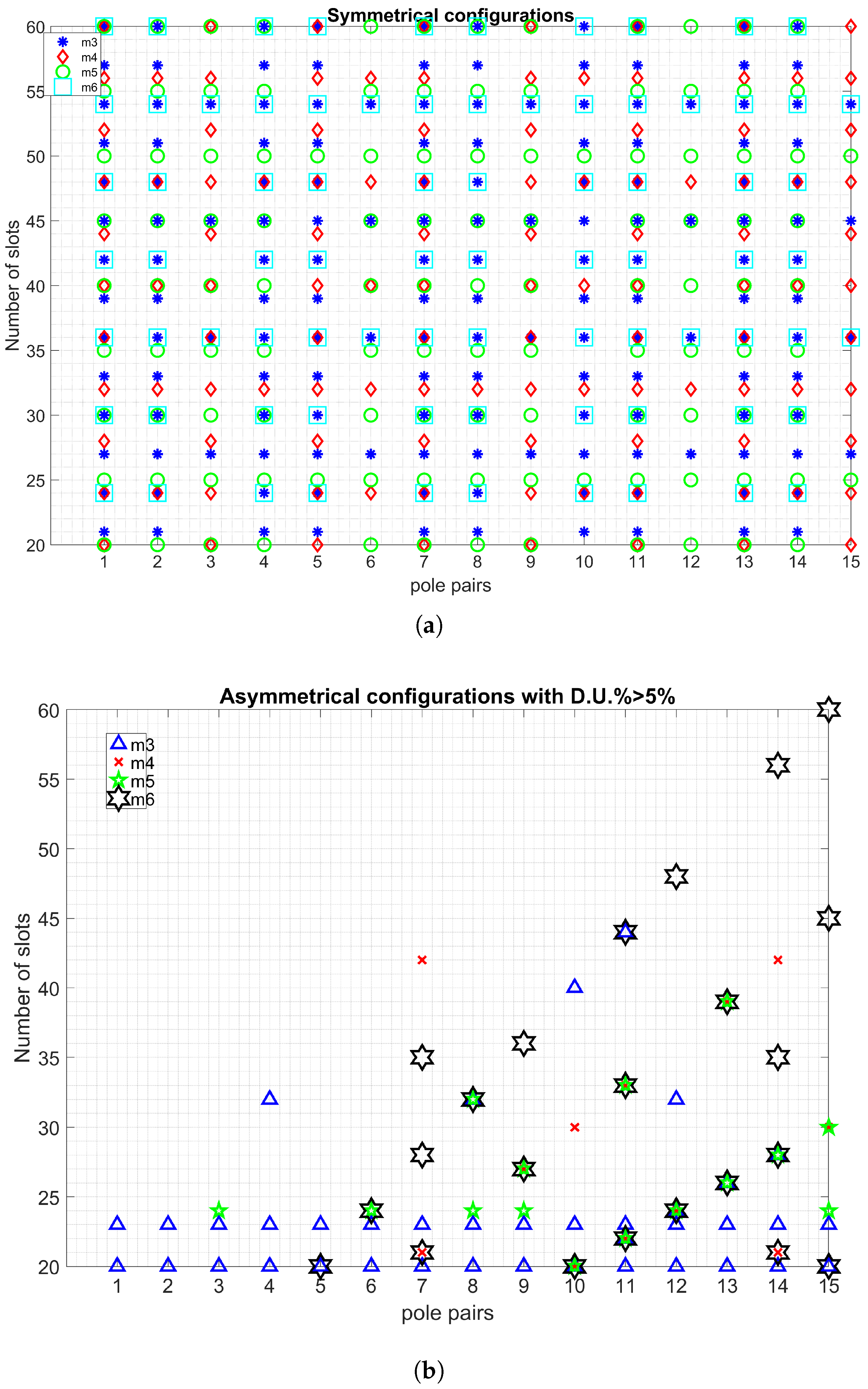
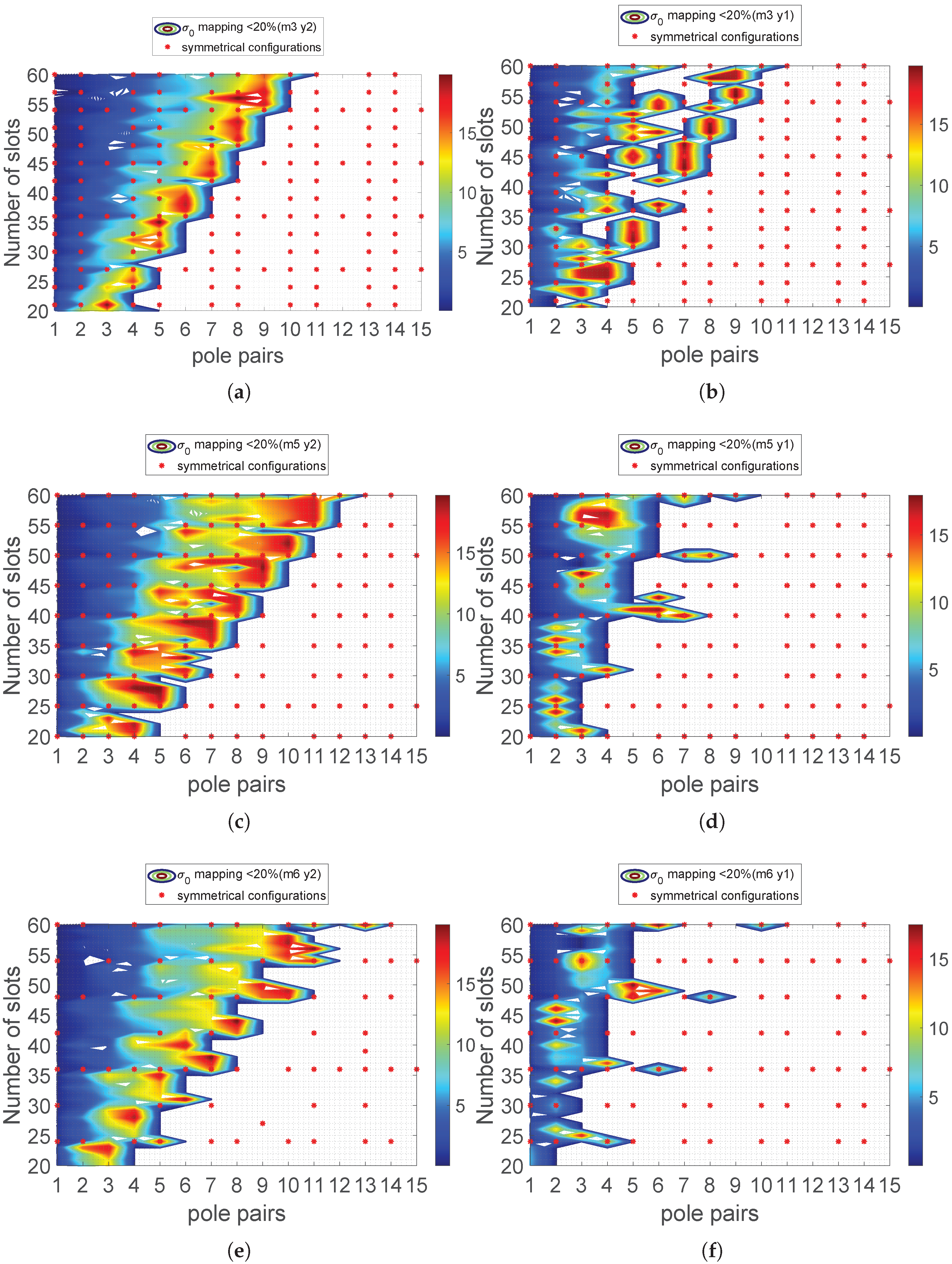
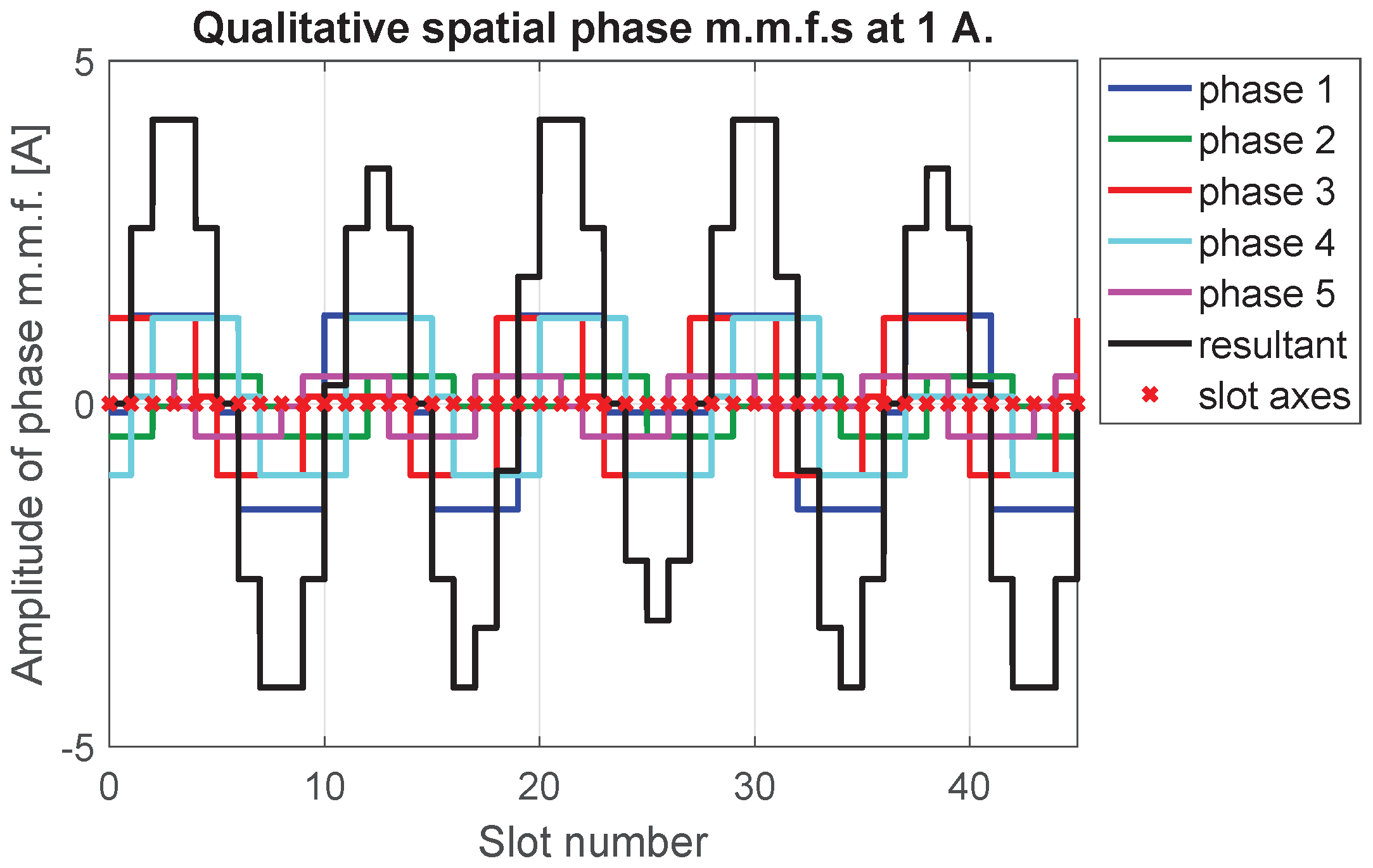
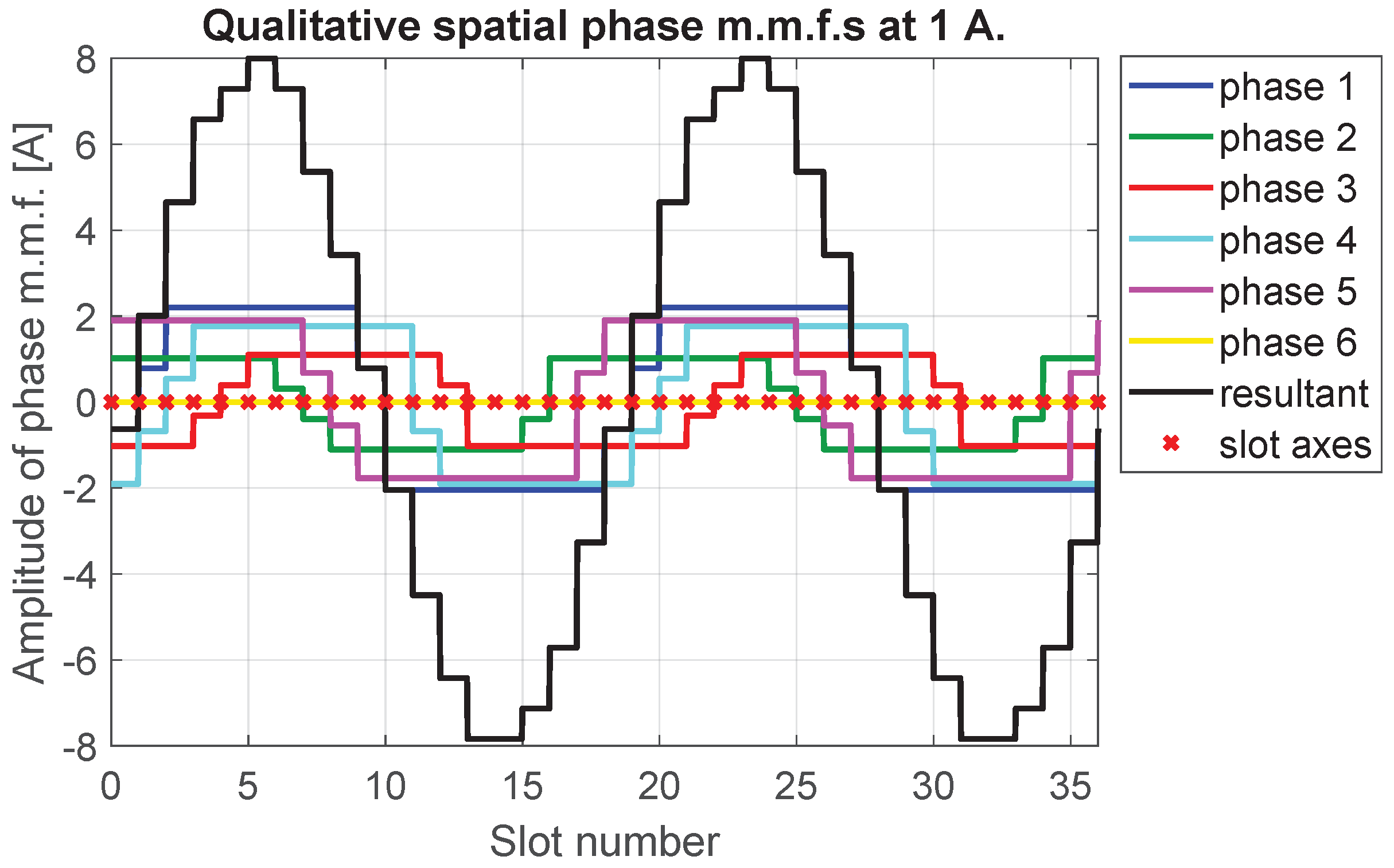
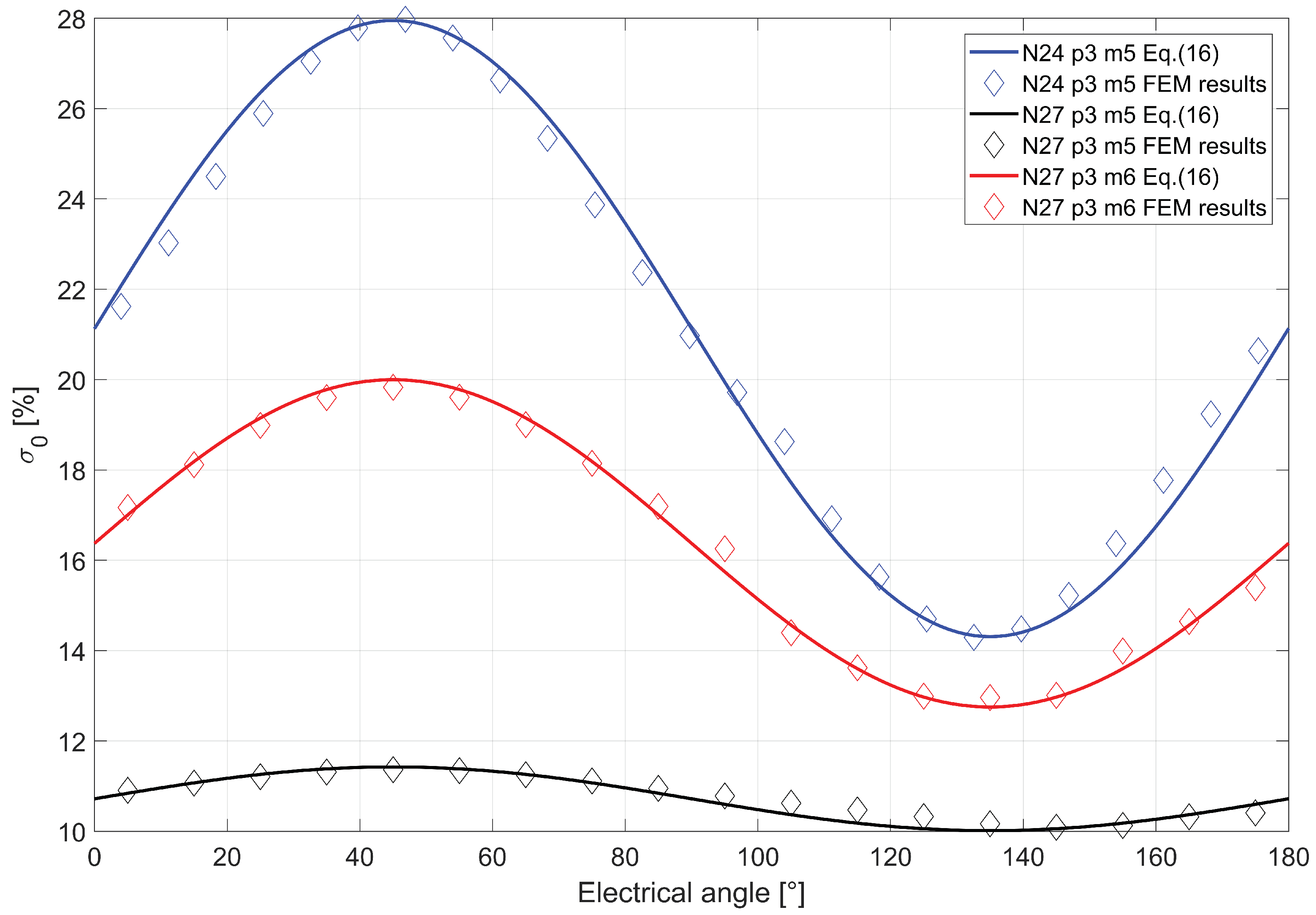
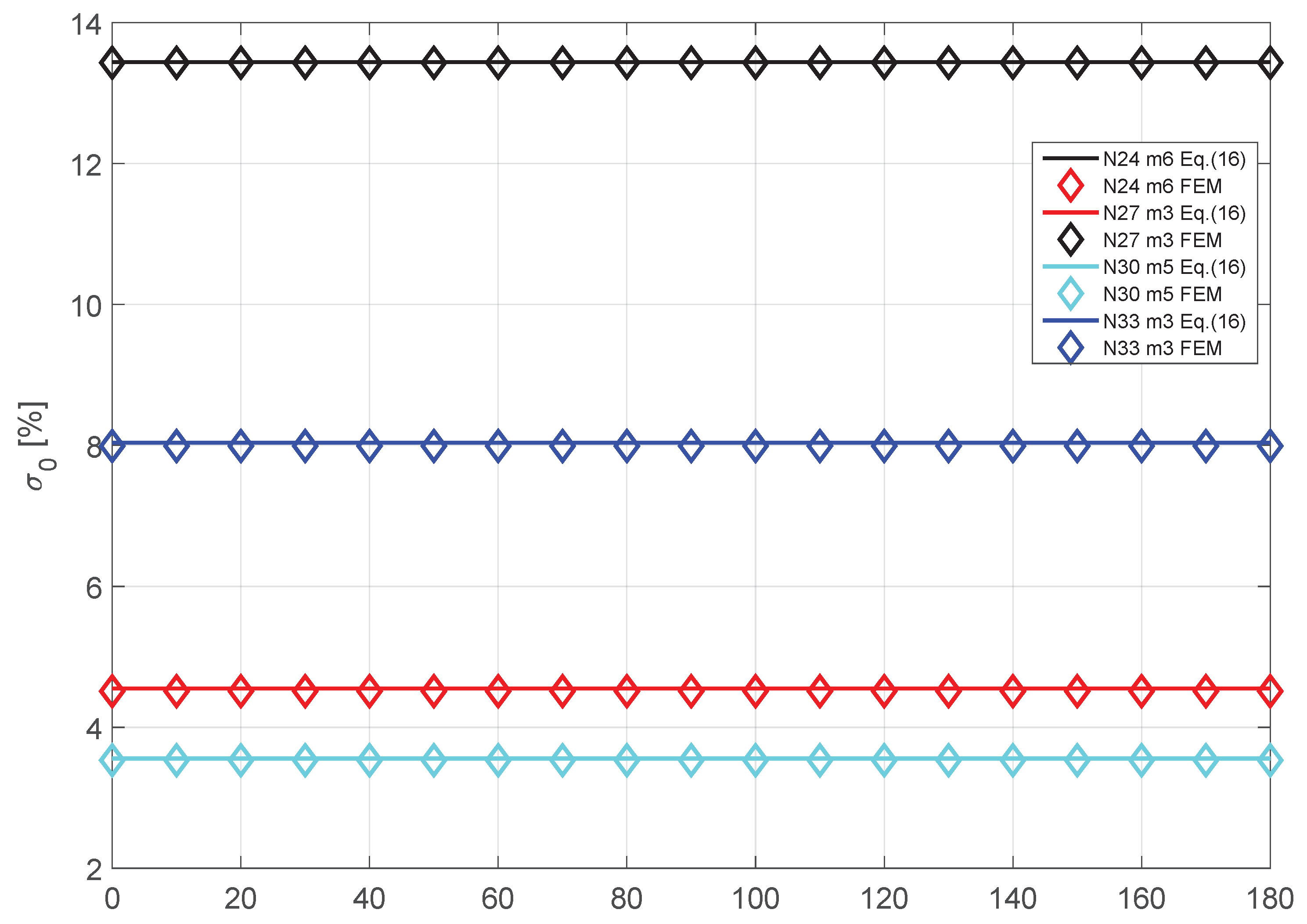
4. Results and Discussion
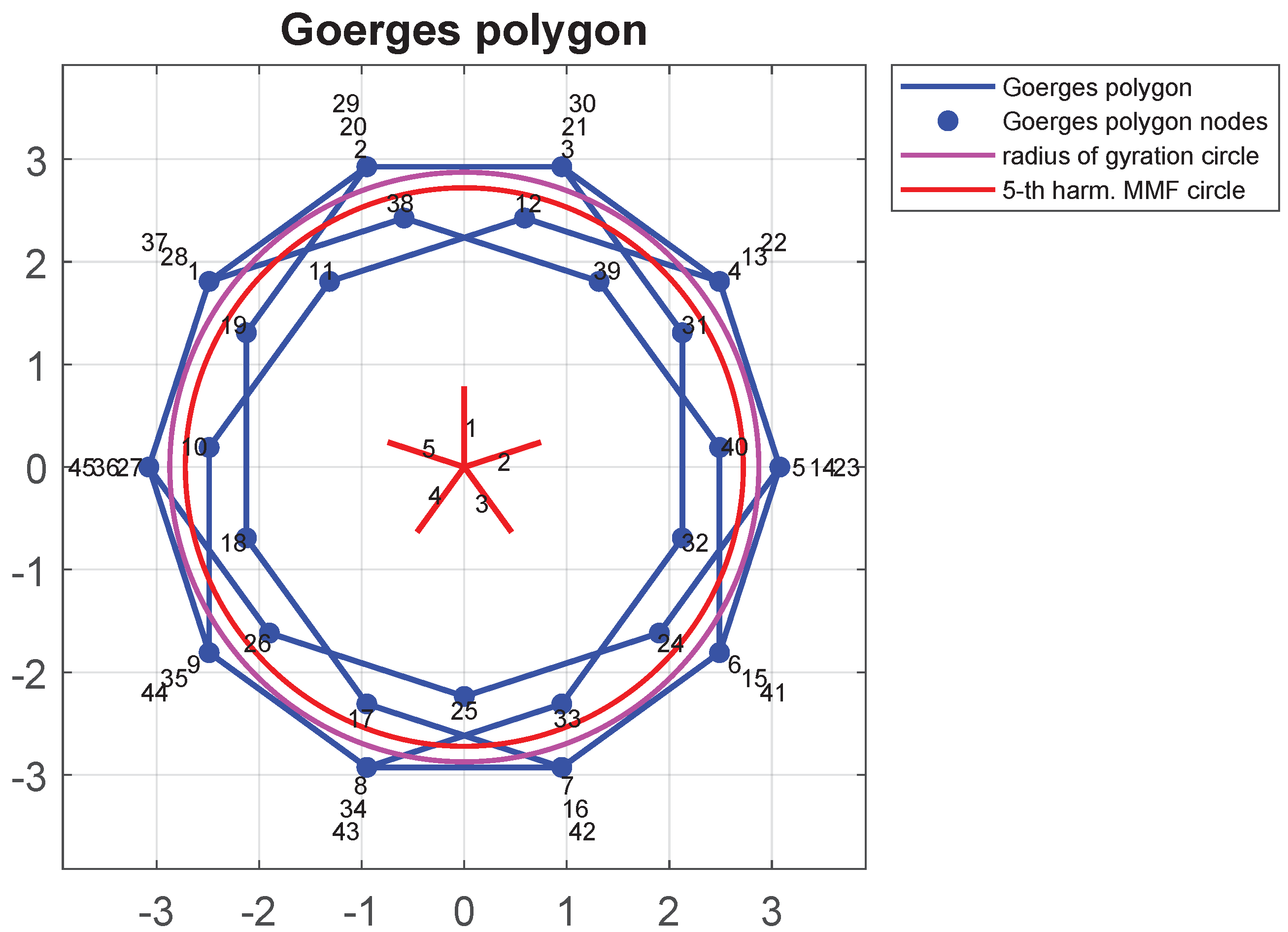
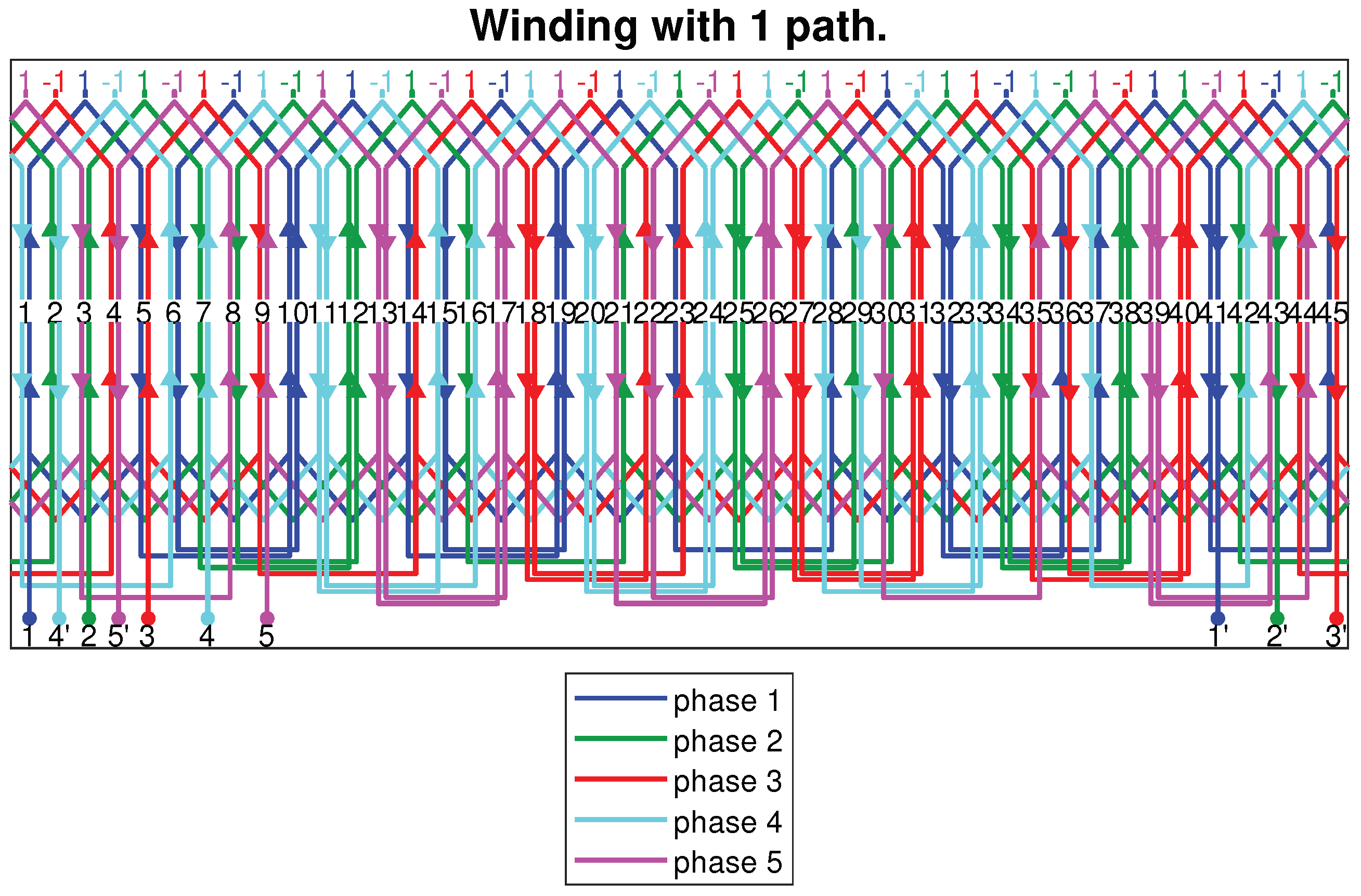
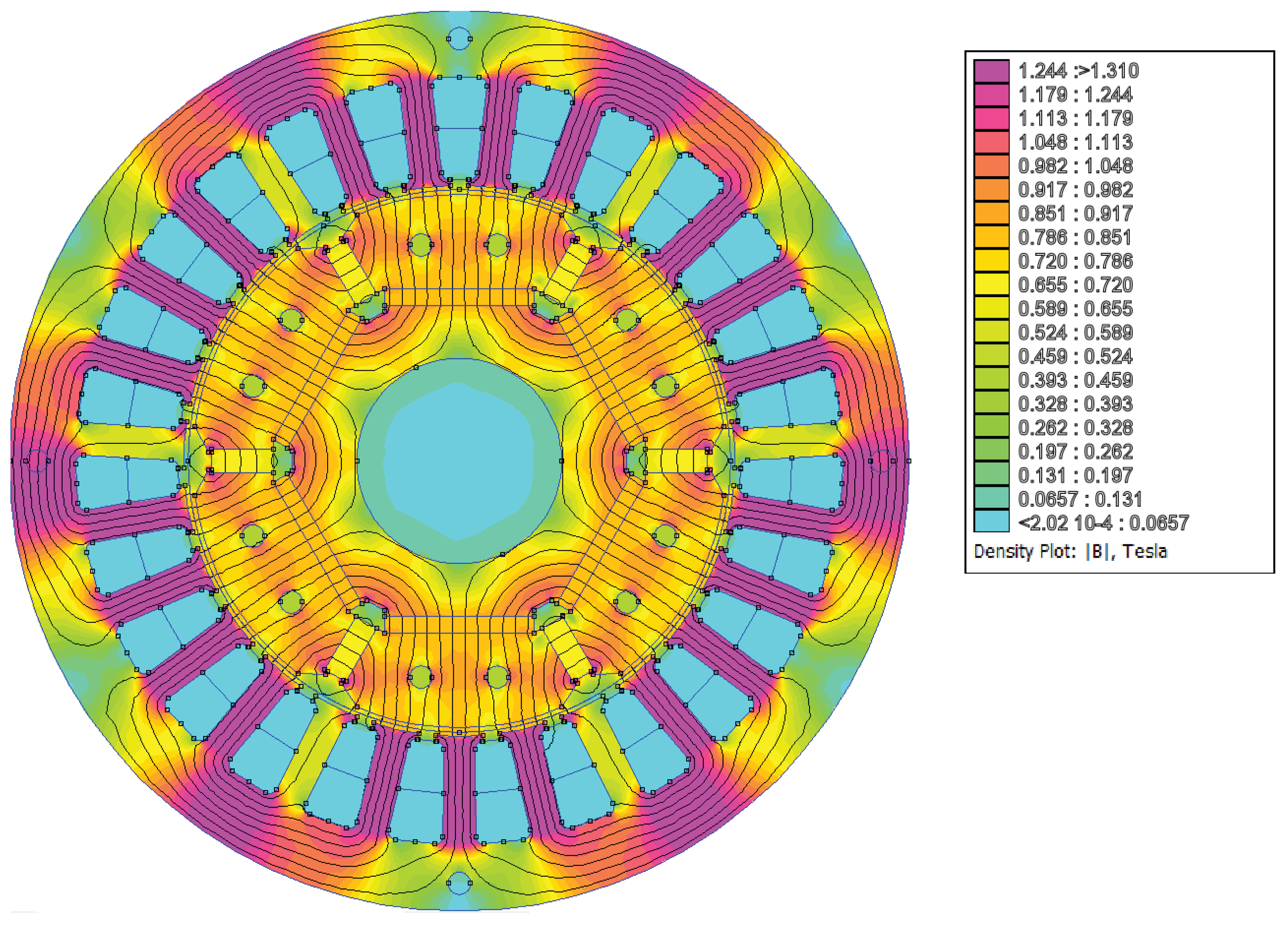
5. Finite-Element Validation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Barrero, F.; Duran, M.J. Recent Advances in the Design, Modeling, and Control of Multiphase Machines—Part I. IEEE Trans. Ind. Electron. 2016, 63, 449–458. [Google Scholar] [CrossRef]
- Duran, M.J.; Barrero, F. Recent Advances in the Design, Modeling, and Control of Multiphase Machines—Part II. IEEE Trans. Ind. Electron. 2016, 63, 459–468. [Google Scholar] [CrossRef]
- Liu, Y.; Niu, S.; Fu, W.N. A Novel Multiphase Brushless Power-Split Transmission System for Wind Power Generation. IEEE Trans. Magn. 2016, 52, 1–7. [Google Scholar] [CrossRef]
- Levi, E. Multiphase Electric Machines for Variable-Speed Applications. IEEE Trans. Ind. Electron. 2008, 55, 1893–1909. [Google Scholar] [CrossRef]
- Demir, Y.; Aydin, M. A Novel Asymmetric and Unconventional Stator Winding Configuration and Placement for a Dual Three-Phase Surface PM Motor. IEEE Trans. Magn. 2017, 53, 1–5. [Google Scholar] [CrossRef]
- Demir, Y.; Aydin, M. A Novel Dual Three-Phase Permanent Magnet Synchronous Motor With Asymmetric Stator Winding. IEEE Trans. Magn. 2016, 52, 1–5. [Google Scholar] [CrossRef]
- Caruso, M.; Di Tommaso, A.O.; Miceli, R.; Rizzo, R. The use of slightly asymmetrical windings for rotating electrical machines. Int. Trans. Electr. Energy Syst. 2018, 28, e2569. [Google Scholar] [CrossRef]
- Caruso, M.; Di Tommaso, A.O.; Ferraris, L.; Miceli, R.; Viola, F. Finite-element performance comparison of IPMSMs with unsymmetrical double-layer windings. In Proceedings of the 2017 Twelfth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 11–13 April 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Cistelecan, M.V.; Cosan, B.; Popescu, M.D. Analysis and Design Criteria for Fractional Unbalanced Windings of Three-phase Motors. In Proceedings of the 6th International Symposium on Advanced Electromechanical Motion Systems—ELECTROMOTION 2005, Lausanne, Switzerland, 27–29 September 2005; pp. 1–5. [Google Scholar] [CrossRef]
- Melcescu, L.; Cistelecan, M.; Craiu, O.; Cosan, H. A new 4/6 pole-changing double layer winding for three phase electrical machines. In Proceedings of the 2010 XIX International Conference on Electrical Machines (ICEM), Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Müller, G.; Vogt, K.; Ponick, B. Berechnung Elektrischer Maschinen, 6th ed.; Elektrische Maschinen, Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2008. [Google Scholar]
- Kouchih, D.; Boumalha, N.; Tadjine, M.; Boucherit, M.S. New approach for the modeling of induction machines operating under unbalanced power system. Int. Trans. Electr. Energy Syst. 2016, 26, 1832–1846. [Google Scholar] [CrossRef]
- Caruso, M.; Di Tommaso, A.O.; Marignetti, F.; Miceli, R.; Ricco Galluzzo, G. A General Mathematical Formulation for Winding Layout Arrangement of Electrical Machines. Energies 2018, 11, 446. [Google Scholar] [CrossRef]
- Caruso, M.; Tommaso, A.O.D.; Giangrasso, L.; Marignetti, F.; Miceli, R.; Rizzo, R. Differential Leakage Factor in Electrical Machines Equipped with Asymmetrical Multiphase Windings: A General Investigation. In Proceedings of the 2019 Fourteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 8–10 May 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Tommaso, A.O.D.; Genduso, F.; Miceli, R. A New Software Tool for Design, Optimization, and Complete Analysis of Rotating Electrical Machines Windings. IEEE Trans. Magn. 2015, 51, 1–10. [Google Scholar] [CrossRef]
- Caruso, M.; Di Tommaso, A.O.; Miceli, R.; Rizzo, R. Computer-aided analysis and design procedure for rotating induction machine magnetic circuits and windings. IET Electr. Power Appl. 2018, 12, 885–893. [Google Scholar] [CrossRef]
- Richter, R. Die Induktionsmaschinen, 2rd ed.; Elektrische Maschinen, Birkhäuser: Basel, Switzerland; Stuttgart, Germany, 1954; Volume 4, p. 691. [Google Scholar]
- Huang, X.; Du, Q.; Hu, M. A novel exact and universal approach for calculating the differential leakage related to harmonic waves in AC electric motors. IEEE Trans. Energy Convers. 2004, 19, 1–6. [Google Scholar] [CrossRef]
- Di Tommaso, A.O.; Genduso, F.; Miceli, R.; Ricco Galluzzo, G. An Exact Method for the Determination of Differential Leakage Factors in Electrical Machines with Non-Symmetrical Windings. IEEE Trans. Magn. 2016, 52, 1–9. [Google Scholar] [CrossRef]
- Caruso, M.; Di Tommaso, A.O.; Genduso, F.; Miceli, R.; Ricco Galluzzo, G. A General Mathematical Formulation for the Determination of Differential Leakage Factors in Electrical Machines with Symmetrical and Asymmetrical Full or Dead-Coil Multiphase Windings. IEEE Trans. Ind. Appl. 2018, 54, 5930–5940. [Google Scholar] [CrossRef]
- Müller, G.; Ponick, B. Theorie Elektrischer Maschinen, 6th ed.; Elektrische Maschinen, Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2009. [Google Scholar]
- Hruska, K.; Sokol, M. Advanced numeric tooth winding analyses. In Proceedings of the 2012 15th International Symposium Mechatronika, Prague, Czech Republic, 5–7 December 2012; pp. 1–7. [Google Scholar]
- Kron, A.W.; Bopp, K. Beitrag zur praktischen Berechnung des Koeffizienten der doppeltverketteten Streuung. Arch. Elektrotechnik 1953, 41, 136–142. [Google Scholar] [CrossRef]
- Cistelecan, M.; Melcescu, L.; Cosan, H.; Popescu, M. Induction motors with changeable pole windings in the ratio 1:4. In Proceedings of the 2011 International Aegean Conference on Electrical Machines and Power Electronics and 2011 Electromotion Joint Conference (ACEMP), Istanbul, Turkey, 8–10 September 2011; pp. 781–786. [Google Scholar] [CrossRef]
- Di Tommaso, A.O.; Genduso, F.; Miceli, R. A novel improved matlab-based software for the electric and magnetic analysis and design of rotating electrical machines. In Proceedings of the 2015 Tenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 31 March–2 April 2015; pp. 1–7. [Google Scholar]
- Caruso, M.; Di Tommaso, A.O.; Marignetti, F.; Miceli, R.; Galluzzo, G.R. A general procedure for the construction of Gorges polygons for multi-phase windings of electrical machines. In Proceedings of the 2018 Thirteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 10–12 April 2018; pp. 1–7. [Google Scholar]


| Parameter | Range of Variability |
|---|---|
| N | |
| p | |
| m | |
| y |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caruso, M.; Di Tommaso, A.O.; Marignetti, F.; Miceli, R. A General Investigation on the Differential Leakage Factor for Symmetrical and Asymmetrical Multiphase Winding Design. Energies 2020, 13, 5414. https://doi.org/10.3390/en13205414
Caruso M, Di Tommaso AO, Marignetti F, Miceli R. A General Investigation on the Differential Leakage Factor for Symmetrical and Asymmetrical Multiphase Winding Design. Energies. 2020; 13(20):5414. https://doi.org/10.3390/en13205414
Chicago/Turabian StyleCaruso, Massimo, Antonino Oscar Di Tommaso, Fabrizio Marignetti, and Rosario Miceli. 2020. "A General Investigation on the Differential Leakage Factor for Symmetrical and Asymmetrical Multiphase Winding Design" Energies 13, no. 20: 5414. https://doi.org/10.3390/en13205414
APA StyleCaruso, M., Di Tommaso, A. O., Marignetti, F., & Miceli, R. (2020). A General Investigation on the Differential Leakage Factor for Symmetrical and Asymmetrical Multiphase Winding Design. Energies, 13(20), 5414. https://doi.org/10.3390/en13205414







