Abstract
This article presents a novel passive fluid borne noise source reduction strategy, based on tandem axial-piston unit indexing with the usage of symmetric lines. The strategy consists of setting the phase between the two synchronous units to accomplish destructive interference in targeted unit harmonics. A strategy capable of achieving destructive interference in all odd harmonics is investigated first analytically and then confirmed by a simulation study. Experiments on the proposed strategy confirmed its effectiveness at the first and third pump fundamental harmonics, and pressure ripple reduction was accomplished. The fluid borne noise source reduction in the first and third harmonic is verified to be propagated to pipe vibration and sound power. Regarding the first harmonic, pressure ripple was reduced by up to 18 dB; while for third harmonic, pressure ripple was reduced by up to 11 dB. In the experiment, however, noise cancellation is not achieved for the higher odd harmonics, as is instead found in the simulation. Conversely, transfer functions form pressure ripple to pipe wall acceleration are obtained experimentally, and a critical vibration band from 2000 Hz to 3000 Hz is identified as being crucial for effective overall sound power reduction.
1. Introduction
The excessive noise emission of hydraulic systems is a detrimental aspect of many fluid power applications, such as construction, transportation, and manufacturing sectors. It also limits potential new applications, such as small and medium on-road vehicles, where hydraulic systems should achieve noise levels comparable to complementary technologies, such as electrical drives. Therefore, there is a demand for novel techniques that can reduce noise sources in hydraulic systems.
Noise is usually generated in the hydraulic supply unit, positive displacement machines. Due to the finite number of displacement chambers in positive displacement machines and force load in mechanical surfaces by the fluid pressure, respectively, both fluid and structure-borne noise will be generated and propagate through the hydraulic system, influencing the frequency response of the system’s impedance, affecting the mechanical response of the system and finally radiating it to the atmosphere in the form of audible air-borne noise. With the recent trend of the increasing power density of hydraulic systems, hydraulic components and systems become more compact, the mass and dampening of hydraulic systems have reduced, thus requiring better comprehension of the generation and propagation of undesired vibrations.
Structure-borne noise occurs when the fluid inside the displacement chamber and ports is rapidly pressurized, and this pressure variation loads the static and dynamic mechanical components of the unit in a periodic pattern generating vibrating forces. Fluid-borne noise happens when the oscillating flow meets the fluid inertia generating a pressure oscillation, thus a pressure ripple.
One strategy to reduce these sources, such as pressure ripple, generated by a pump, is to set the hydraulic system to specific frequency content to create destructive interference in the system. When the phase shift of both oscillations is fixed, and thus, the wave pattern is stationary (coherent interference), the waves will add up or subtract with the same phase all the time. Constructive interference is a wave combination to add up to a bigger amplitude than the original waves, having its maximum value at 0° phase shift, while destructive interference waves subtract each other to a smaller amplitude than the original waves yielding as low as zero amplitude at 180° phase shift.
To accomplish destructive interference, vibration control techniques are used. Vibration control techniques can be classified in passive, active, hybrid, and adaptive-passive vibration controls [1]. Active techniques usually require high implementation complexity, while being restricted to low frequencies, due to the actuator’s narrow area of working frequency [2]. Meanwhile, most passive techniques are hard to tune [3,4] and usually are only effective in a fixed frequency band unless adaptive-passive techniques, such as adaptive Helmholtz resonators [5,6], is implemented. This frequency band limitation can be considered as a drawback for multiple operation condition applications since hydraulic pumps and motors can operate at multiple pump shaft speeds, thus varying the frequency of the generated oscillations. Therefore, the critical frequency bands of the system’s mechanical response will vary depending on the displacement of machines operation conditions. Moreover, it is important to address that these pumps and motors generate a flow ripple at frequencies which are multiples of the unit speed; applying the principle of destructive interference requires a sophisticated technique that can effectively achieve destructive interference at a given set of frequency without compromising the others.
Most passive techniques involve using resistive or reactive devices, thus changing the acoustic impedance of a system that affects a wide range of frequencies. However, passive techniques also have the advantages of low cost and no need for feedback, supervisory system, or external energy. Avoiding the use of external energy can be understood as an advantage in the noise reduction strategy, since it does not increase the total oscillation energy of the system. Hydraulic circuits are systems with many subcomponents. Each subcomponent has specific multi-dimensional resonant modes, and a very deep understanding of the mechanical system response is required to accurately predict how new excitations will translate to audible noise. Thus, avoiding these new excitations, such as the ones generated by the active vibration control techniques, can be considered a good guideline for eliminating undesired vibrations.
Usually, fluid borne-noise reduction strategies are divided into reducing source flow ripple or introducing noise mitigation devices. Popular hydraulic circuit elements for limiting pressure ripple are closed-branch silencers [7], Helmholtz resonator [8,9,10], and adaptive Helmholtz resonators [5,6], Multi-element buffer bottles [11], vibration absorbing techniques [3,12]. Active load methods also had been tried, such as active variable chamber volume actuators, installed the delivery line [13]. There are also dampening focused devices developed commercially, such as the Pulsco liquid pulsation dampener [14], Hydropad [15], and Blacoh air-operated double-diaphragm (AODD) dampener [16]. However, when introducing a pressure ripple mitigation element in a hydraulic line, the pressure ripple will be affected differently in different positions of the line. This is because most of these devices reduce oscillation in a frequency band in a compromise of others [3], and each oscillation in a single frequency will vibrate as a standing wave in the whole length of the hydraulic path. Each standing wave will have maximum amplitude oscillation positions (antinodes) in particular line locations. Therefore, if the antinode of a given compromised frequency is placed in a spot with high mechanical resonance and/or high surface irradiance, then the circuit with the new element might yield more audible noise than its original configuration.
Thus, the alternative of neutralizing noise sources through reducing flow ripple by modifying the design of hydrostatic pumps has been the main industry and academia focus, since it ideally does not compromise vibrations of a given frequency while focusing on others.
Specifically, for the case of axial-piston displacement machines, ideal timing [17], filter volume introduction [18,19], and valve-plate design [20,21,22,23] have been the main focus of noise source reduction. Moreover, the swash-plate cross-angle, which is small fixed inclination perpendicular to the displacement direction, had been verified and selected in simulation by Johansson et al. [24,25] and later run experiments to verify audible noise reduction up to 4.5 dBA. As design solutions start narrowing, new axial-piston unit architectures had been elaborated. A new axial-piston unit architecture was conceptualized using the floating cup principle [26,27,28]. This architecture displays a centralized double-ring with back to back mirrored pistons, which allows a low tilt angle, a high number of displacement chambers, and cancelation of the forces. This architecture also showed great efficiency, due to the low friction compared with the slipper-type pumps [26] and high-speed operation because of barrel tipping torque reduction [27]. Experiments showed the high number of pistons, and the floating cup principle strongly reduces the pulsations [28]. This new architecture, however, is still not popular in the industry.
An alternative is to introduce vibration control techniques to the unit, which consists of using a second oscillation source to set the destructive interference pattern to the targeted oscillation. Active swash-plate vibration control techniques utilizing the pump control system have been documented in References [29,30,31]. However, the idea of passive vibration techniques in axial-piston unit techniques has rarely been tried for source flow ripple reduction. A related swash-plate vibration reduction was studied by Masuda and Ohuchi [32]. In their work, they used the displacement chamber pressure to reduce the swash-plate vibrations, and they achieved up to 6.5 dB of sound pressure reduction.
In vane units, Zanetti-Rocha et al. [33] accomplished first harmonic pressure ripple reduction by introducing properly designed discharge ports to achieve destructive interference. They reported up to 16 dB pressure ripple harmonic reduction in the best case. For gear units, secondary source flow ripple cancellation has been attempted by the Dowty 1P3000 series [34,35]. These units combined the concept of is pumping elements duplication with the destructive interference principle: anti-phasing. Anti-phasing is accomplished by displacing the two half-gear widths by a half tooth pitch creating a 180° phase shift at the fundamental first harmonic. Curiously, applying these principles has not been much studied in other hydraulic unit architectures, nor the anti-phasing practice has been standardized for axial-piston tandem-units.
This article aims to study and extend the concept based on secondary-source destructive interference strategy to axial-piston units. This strategy can be performed either by replacing a larger unit with a tandem unit or coupling two smaller units in the same shaft. This technique can be considered as a passive vibration control technique, since it does not add energy to the system. However, it is extremely adaptable because it is effective for all unit speeds and in multiple unit harmonics. This proposed technique tackles this problem by not altering the system impedance and relying on the symmetric unit design.
The paper first presents an analysis of the proposed solution following an analytical method, in Section 2. A numerical modeling strategy followed by simulation for evaluating such a solution is presented in Section 3. A properly designed experiment is described in Section 4, and finally, the results are summarized in Section 5 before conclusive remarks.
2. Proposed Solution Analysis
The proposed source design is exemplified in Figure 1. The secondary source noise source reduction solution implies replacing large hydraulic units by two smaller units joined by their axis. Anti-phasing will then be applied to the two individual units to achieve the desired interference pattern.
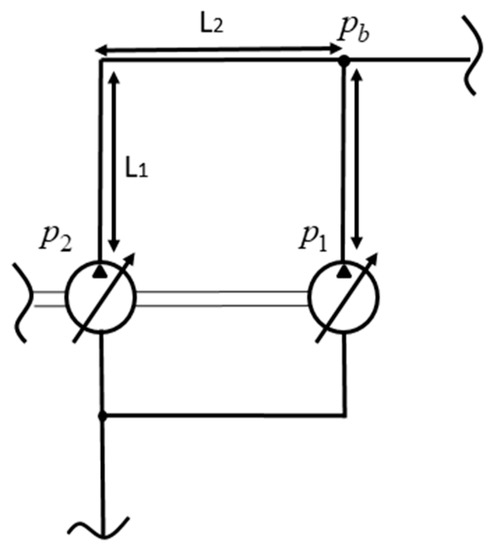
Figure 1.
Two coupled hydraulic pumps are supplying flow to the same line.
As shown in Figure 1, a given frequency pressure oscillation of both units will propagate through the hydraulic lines according to the general undamped wave Equation (1), given by Reference [36]:
As the pressure generated by the units reaches the branch, the translated distance value x is equal to the respective line segment length L1 for unit 1 and the sum of L1 and L2 for unit 2. This is also shown in Figure 1. The wavenumber k is dependent on the speed of sound c and angular frequency ω.
The constant terms B1 and B2 are a characteristic of the flow sources, and they depend on the unit speed and a given wave frequency. Generally, these constants are empirically calculated using consolidated techniques, such as the “Secondary Source method” [37] and “Two pressure two system method” [38]. However, assuming the ideal case of two units being identical, the constants are strongly determined by the unit geometry. These constants could be assumed to be equal in both units. Thus, the pressure oscillation generated by each unit at the branch is represented by Equations (2) and (3):
Evaluating the Equations (2) and (3), it can be noticed that the phase between these relations depends on four factors: The angular velocity ω, the speed of sound c, the difference in length of both lines L2, and the fixed phase shift ψ in between both units starting rotating point. Of these factors, the most critical is the speed of sound, which depends on several parameters, such as oil temperature, fluid pressure, the elastic properties of the duct material. This makes the phase too fickle to be controlled in different operating conditions unless there is no difference in length between the lines. In the specific case of perfectly symmetric lines, the phase difference between the waves is just the fixed phase shift, achieving the pattern of coherent interference. If the phase transformation is equivalent to 180°, the interference also becomes destructive, as shown by Equations (4) and (5). The elimination of the value L2 and attribution of the value to the phase shift makes the pressure wave generated by unit 2 has the negative value of the pressure wave generated by unit 1 on the branch. This property holds to every position after the branch as well.
3. Simulation
After analyzing the principle of anti-phasing, a simulation is developed for functional verification. The simulation of the interference pattern of pressure oscillations by two units is conducted to analyze the possible ways of canceling these oscillations. A larger unit (single flow source) simulation is also developed for comparison and evaluation of the isolated source duplication effects. The line diameter and dimensions are based on the test rig described in Section 4.
The simulation structure, which is displayed in Figure 2, comprises three main sub-blocks: A positive displacement machine model (Pmod) to simulate axial-piston units’ flow supply described in Section 3.1; a hydraulic line model (Line Model) capable of simulating the propagation of pressure ripple wave at a speed of sound which is shown in Section 3.2; and a branch model (Br. Model) able to calculate hydraulic branches interaction also explained in Section 3.2. The positive displacement machine model receives port pressure, swash-plate angle, and unit speed as input and calculates the intake and outtake flows of the unit while the line model obtains the upstream node and downstream node flows and computes the pressure and flow propagation through the line. Specifically, the proposed system simulation block in Figure 2 represents the high-pressure line of the circuit in Figure 1; Branch 1 is the spot where pb is present.
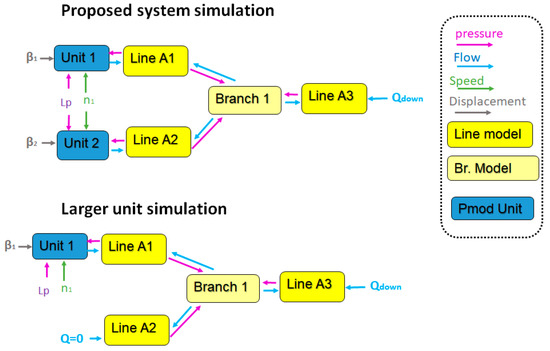
Figure 2.
A simulation model for testing unit oration kit indexation.
The model was implemented in Matlab/Simulink using inner loops in the Simulink functions for each block. The main Simulink simulation has a 50 µs fixed time step using the Euler method when the boundary conditions interfaces are updated. To achieve better numerically stability, the line model contains a 10 µs inner time step, while the unit model comprehends a 100 ns inner time step. The choice of the time steps (and thus, number of loop interactions) was based on verifying convergence for the units’ highest power operation condition (3400 rpm, 420 bar), and then a safety factor of 3 was considered. While stability would hold for even smaller time steps, it was not necessary to compromise the simulation speed further. This time steps are assured by the number of loop interactions each solver executes before updating the boundary conditions. The units update the displacement chamber pressures also using Euler method with Equation (7), described further in Section 3.1 to calculate the pressure build-up rate. After the pressure updating loop is repeated 500 times, the flows on the ports are calculated according to the summation of the flows entering and exiting each displacement chamber, as described by Equations (9) and (10). These total flows are then provided to the lines adjacent to the units. At the lines, as described in Section 3.2, the pressure at each node is calculated with the average of Equations (19) and (20), while the flow is updated according to Equation (21). After the hydraulic line model is completed five times, the pressures at the extremities are provided to the boundary conditions and updates to the units’ ports. Then, a loop of the main simulation is completed. The physical unit’s conversion is necessary at some sections of the simulation.
To accurately simulate the speed of sound in the simulation, a fixed time is used at all times, and the length of each node is calculated previously. This method can be used even in lines with variating parameters, such as line diameter and material. Further details on this strategy can be found in Reference [39].
3.1. Axial Piston Unit Model
The principle of positive displacement units is the displacement of fluid achieved with the volume variation of internal displacement chambers. As the volume in each displacement chamber varies, the working fluid is compressed, and as its pressure rises, it stimulates the output flow of the machine. Typically, the time evolution of the pressure in a control volume can be calculated assuming conservation of mass, control volume variation, and the fluid state equation as summarized by Equation (6). The mass transfers can be determined after the calculations of density and the volumetric flows discharging through the inlet and outlet ports are described by the orifice equation. This approach was successfully used for many types of positive displacement units [40,41,42,43].
In a swash-plate axial-piston unit, the drive shaft will revolve the rotating group, consisting of a cylinder block, slippers, pistons, and the shaft, as Figure 3 shows. Once the cylinder block rotates, the pistons are displaced increasing or decreasing the volume of the displacement chambers, thus, resulting in either flow displacement or pressure increase of the given fluid.
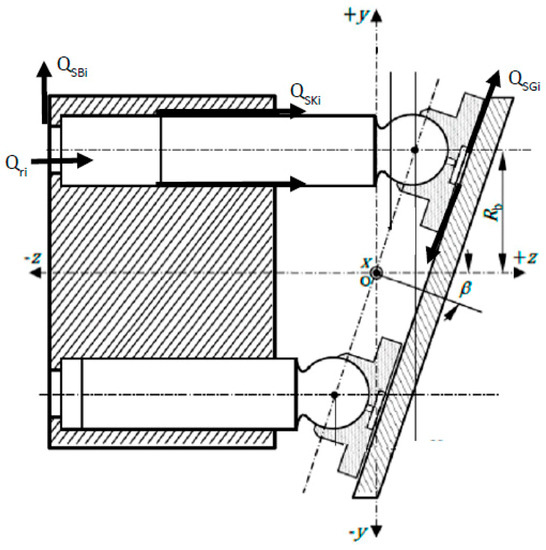
Figure 3.
Swash-plate axial-piston unit’s rotation group schematics.
Each displacement chamber of the unit, indexed by i, is delimited as a control volume. The pressure variation in the control volume is calculated by (7). Equation (7) applies the definition of Bulk Modulus on Equation (6) and evaluates the flows entering and exiting the displacement chamber. The leakage flows QSBi, QSKi and QSGi occur at their respective interfaces between the cylinder block and the valve-plate, between the piston and the cylinder block, and between the slipper and swash-plate.
The summation of flow going in and out each chamber Qri consists of the addition of flow between the given chamber and high-pressure port QrHPi and low-pressure port QrLPi (8). These flows are calculated by the orifice Equations (9) and (10), which are derived from Bernoulli’s equation by assuming an incompressible fluid. The respective orifices ArHPi, and ArLPi will be equivalent cross-sectional opening areas between the displacement chamber pressure ports and the unit valve-plate in a given moment of time. Since valve-plate design affects effective flow, cylinder pressure, and pressure pulsation, it had been studied extensively for noise reduction in axial-piston machines [20,21,22,23].
As the displacement chamber is filled with pressurized fluid, the pressure in each piston surface also generates resultant forces, the summation of which results in moments oscillations at all axis: x, y, and z, thus generating structure-borne noise. The reader interested in further details on the derivation of the swash-plate moments Equations (11)–(13) can refer to Reference [44]
In a tandem unit, two axial-piston units are connected by the same shaft and share the same case. Considering the torsional deformation of the shaft negligible, the phase between both rotating groups will remain constant; hence, the units will be synchronized, and coherent interference is possible. When connecting two units on the same axis, the rotating kits of both units are not necessarily aligned so that the center of each piston must be overlapped on the z-axis. Rotating on the z-axis, as represented by Figure 4, the angle between the centers of the piston from one unit to the center of the piston of another is the index of the rotation group.
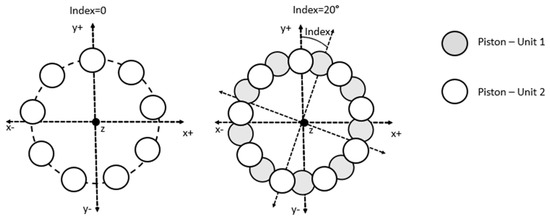
Figure 4.
Rotation kit index representation a tandem swash-plate axial-piston unit.
The rotating kit index in the unit will result in a constant delay between pressure waves generated by each unit, thus resulting in a given phase shift . Positive displacement units generate flow oscillations as multiples of the unit’s fundamental frequency given by . The phase shift index, given by I, will imply in a different phase shift for each wave harmonic frequency in a unit with m displacement chambers. This phase shift can be calculated equation by (14). For example, in a nine-piston unit, the index of rotation kit of 20° is equivalent to a 180° phase shift in the first harmonic, which achieves destructive interference. However, it is interesting to notice the 20° index will also analytically achieve destructive interference in all 1 + 2n harmonics (odd harmonics), thus becoming an interesting candidate index for achieving noise reductions in a broad frequency band. This happens because after removing the complete wave periods form the phase-shift, the remainder of the phase shift divided by 2π equals π/2 or 180° for all the other odd harmonics. A 10° phase shift will, in an analog manner, result in a destructive interference pattern for all 2 + 4n harmonics.
3.2. Line Model
To simulate the pressure excitations of the units propagating through the hydraulic line model, the developed model was developed using the method of characteristics (MOC) and had a fixed time-step. The MOC model is usually implemented for measuring water-hammer effect [45,46,47], but also has been successfully used for predicting fluid borne noise sources in hydraulic systems [39,48,49]. In this technique, the equations in which principles of conservation of fluid flow momentum (15) and continuity (16) are coupled together, and two characteristic curves are found. The characteristic curves C+ and C- are the pressure waves traveling at the speed of sound on positive and negative axial directions, respectively. From each curve, two ordinary differential Equations (17) and (18) can be deduced. Further details can found in References [44,45].
Boundary conditions are applied to these four equations using a fixed time step and discretizing the line into several nodes. This fixed-step must be synchronized to the hydraulic unit fixed time step. As a result, two speed of sound constants and two discrete characteristic equations are calculated. One characteristic equation describes the pressure traveling in the z-axis positive direction (19), while the other describes the propagation in the negative (20) direction. The variable BL is called the isothermal wave speed.
As both Equations (19) and (20) are added, the pressure in each node is updated to the next step. Finally, in the last step interaction of the model, the flow values in the inner nodes are calculated (21) by averaging two flow values traveling in the negative and positive directions. In the boundaries, the flows are the model inputs, and thus, are updated at every time step.
The branches of the line model are modeled based on Reference [34], which solves the pressure of the center of the branch based on the principle of mass conservation (22) for a branch with O segments, then calculates flows coming in and out each of segment o of the branch based on Equation (23), using the values of the characteristic equations C and isothermal wave speeds B of the adjacent nodes.
4. Experimental Setup
To test the proposed passive fluid-borne noise source reduction solution, the hydraulic circuit, shown in Figure 5, was assembled at the authors’ Maha Fluid Power Center (Figure 6). The tandem unit is connected to the driving electric motor, which has good speed control, and both units supply flow to a throttle valve, which is used to set up the pressure.
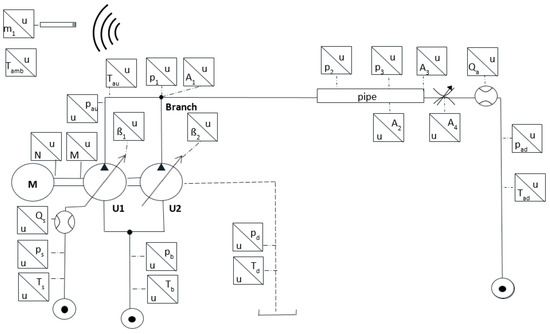
Figure 5.
Test rig hydraulic circuit.

Figure 6.
Hydraulic Test rig; (a) experimental circuit; (b) reference unit.
The sensors, listed in Table 1, are installed in the test rig to measure pressure ripple through the line, pipe vibrations, and to keep control of temperatures; thus, achieving steady-state conditions. Piezoelectric sensors p1, p2, and p3 are respectively positioned 55, 335, and 408 cm away from the pump outlet.

Table 1.
Assembled test rig installed sensors.
A G.R.A.S 40AO microphone, dynamic range from 20 dB to 163 dB, was installed 1.5 m above the center of the circuit. The microphone was installed to obtain sound pressure measurements. Although this measurement is not compliant, the ISO3744 standard (using the sound chamber available at the authors’ laboratory was not possible, due to packing limitations), single microphone measurements are still a common practice to assess noise emissions. A distance of the microphone from the pump greater than 0.5 m was chosen to avoid the field is being affected by near field intensity circulation [50], analog to the IS0 9614-l requirement.
To measure pipe surface acceleration close to the pressure ripple measurements, accelerometers 1, 2, and 3 are, respectively, installed close to piezoelectric sensors 1 and 3, as shown in Figure 7. Accelerometer 4 is installed in the throttle valve port to detect asymmetric excitation for structure-borne noise being propagated to the end of the pipeline. The selected unit, Rexroth A22, is a nine-piston tandem unit and the inner shaft of the cylinder block has exactly 18 splines, as shown in Figure 8. Due to this property, the rotation kit index can be shifted in 20° intervals, thus making possible to set the unit index 0° or 20° exact values and consequently achieving the set-ups in which all harmonics remain in full constructive interference or the to set destructive interference in specifically in all 1 + 2n harmonic, while keeping the even harmonics still in constructive interference.

Figure 7.
Accelerometer placement on the hydraulic circuit; (a) pump outlet; (b) pipe downstream.

Figure 8.
Selected tandem unit display; (a) closed case; (b) rotation kit.
5. Results
5.1. Simulation Results
The modeled unit inputs are based on the Rexroth A22 geometry, which also was the model used in experiments. The simulation model was firstly run neglecting leakages, and after the experiment was performed, the leakages of the unit were estimated and introduced as input to the model. The test rig dimensions were also included as inputs in the model.
Figure 9 shows the simulated test rig dimensions that were modeled with the simulation scheme, shown in Figure 2. A non-existing scaled unit with 90 cc per revolution unit twice the size of each Rexroth A22 single unit was also simulated. The reason for a scaled 90 cc unit is to pose a comparison of the proposed secondary source system to a system that actually will be default in an industry, which is a larger unit supplying flow to an application with a specific flow demand. Usually, tandem units are used to supply flow for different hydraulic lines, thus a comparison with a single 45 cc unit would not be appropriate. It is important to mention, however, that a larger unit will have considerable differences regarding structural borne noise forces and gap flows when compared to a tandem unit. For the simplification of this simulation, however, a fictitious inexistent 90 cc pump was considered to have similar leakages to the tandem unit.
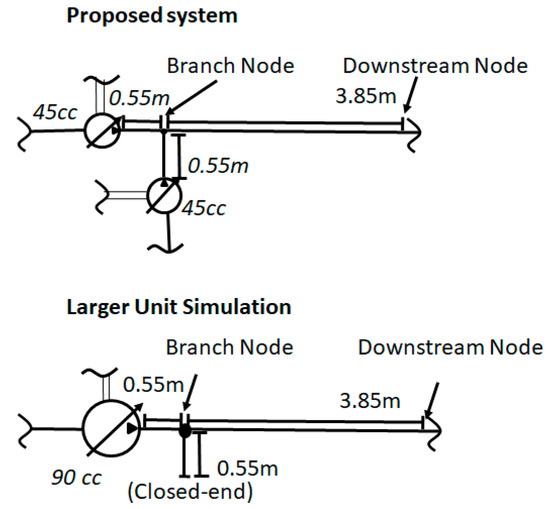
Figure 9.
Line model sizes.
The 90 cc unit is twice the size of each of two smaller units and had the geometry proportions of the original unit preserved by multiplying the original unit dimensions by ratios of 21/3 for measured geometric distances, 22/3 for geometric areas, and 2 for geometric volumes. The valve-plate area also was rescaled accordingly. To isolate the effects of the source generation, the larger unit simulation kept an extra branch with the close end in the simulation. The conduit diameter was kept constant as 25.6 mm through the whole line extension.
Figure 10 shows that the interference patterns deduced analytically are also verified in simulation on the branch, while Figure 11 shows the interference patterns are maintained at the discharge. Since simulation data does not contain any noise, each energy peak represents a multiple of the units’ fundamental harmonic. Compared to the 0° rotation indexed units and the larger unit, the 20° rotation index canceled the odd harmonics and maintained constructive interference in even harmonics unaltered. The 10° rotation rate canceled the harmonics 2 + 4n and maintained maximum constructive interference in harmonics 4n. This phenomenon happened in every simulated operating condition. Moreover, the larger unit has yielded significantly larger pressure ripple amplitudes for the first harmonic than the 0° rotation indexed units, implying benefits on pumping elements duplication even without anti-phasing.
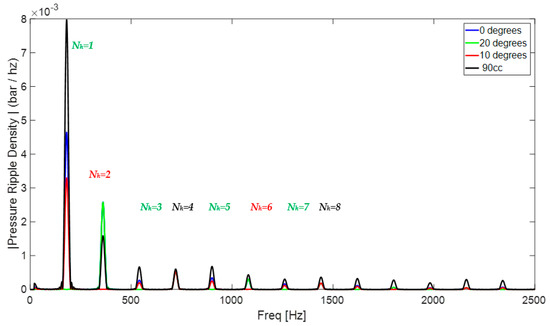
Figure 10.
Fast Fourier Transform of the pressure ripple in the branch.
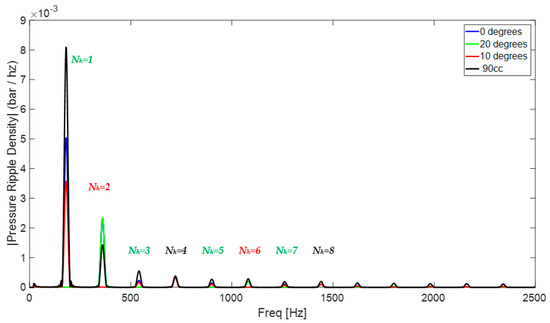
Figure 11.
Fast Fourier Transform of the pressure ripple in the discharge.
However, it is important to mention that in the simulation, a perfect symmetry of the units is possible—since both units are simulated by the same solver and have valve-plate symmetry and same leakages. Nonetheless, the simulation was considered a promising starting point for the solution. As Figure 12 shows, the tandem unit indexing also affects the moment in the z-axis, thus having effects in structure-borne noise.
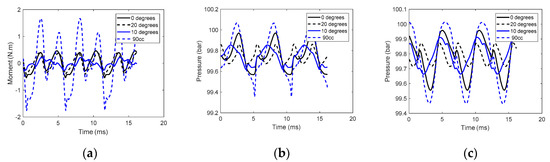
Figure 12.
Time-domain simulation results at 100 bar 1200 rpm; at (a) Mz-Torque ripple at the shaft and (b) pressure ripple at the branch, (c) pressure ripple at the discharge.
5.2. Experimental Results
Eight operating conditions, displayed in Table 2, were measured, and each operation condition was measured five times. Pump inlet pressure was set to 30 bar, and the inlet temperature was controlled to be between 52 °C and 53 °C, while all measurements were performed.

Table 2.
Measured operation conditions.
To represent power in the frequency domain and identify if different rotation kit indexes can lead to noise reduction, the power spectral density of the pressure sensors and accelerometers signals is used to represent power in the frequency domain. A transfer function is calculated for each operating speed, by averaging the power spectral density ratio of four operation conditions and five measurements per operation speed, totalizing m = 20 samples. The ratio is the normalization of the 20° index set up versus the 0° as a method to represent power conservation from one rotation kit index to another. For this study, the metric was called Spectral Power Ratio or SPR (24). This metric is analog to insertion loss, which is used for evaluating hydraulic line modifications; however, in this case, a noise source mitigation is rather a negative value than positive as in insertion loss.
Figure 13 shows the power ratio in the frequency domain for the unit running at 1200 rpm and 1660 rpm. The first two odd harmonics are represented in the figure by yellow dots. For a nine-piston unit, at 1200 rpm the first harmonic frequency is equal to 180 Hz, and the third harmonic frequency is equal to 540 Hz. At 1660 rpm the first and third harmonics frequencies are 249 Hz and 747 Hz, respectively. It is possible to verify pressure ripple in the branch was reduced in the first and third harmonics and that this reduction was propagated through the whole line to the end of the pipe where the piezoelectric sensor p3 is installed. At 1200 rpm and 1660 rpm, respectively, the first harmonic was reduced by 15.32 and 17.96 dB at p1 and by 16.87 and 15.87 dB at p3. Regarding the third harmonic, at 1200 rpm and 1660 rpm, respectively, the first harmonic was reduced by 10.31 and 9.55 dB at p1 and by 11.63 and 9.3 dB at p3.
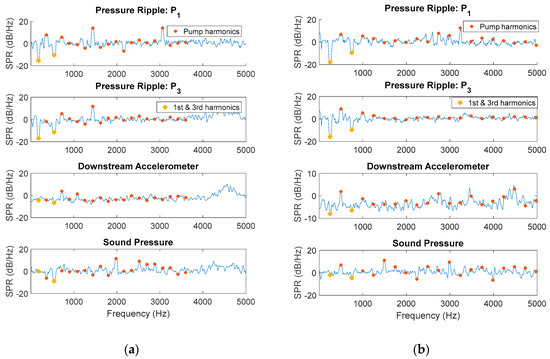
Figure 13.
Spectral power ratio frequency response function: 20° Index normalized over 0° index (a) n = 1200 rpm; (b) n = 1660 rpm.
Also, the reduction in the first and third harmonic influenced pipe wall vibrations and sound pressure measurements for both speeds. At 1200 rpm the sound pressure at the first and third harmonics, respectively, were reduced by 0 and 9 dB, while at 1660 rpm the first and third harmonics, respectively, were reduced by 2 and 4.66 dB. However, it is possible to verify that this noise source attenuation was conserved for all odd harmonics, as simulations suggested. The indexing strategy achieves a random pattern for the higher harmonics, increasing or decreasing the excitations at different frequencies.
Sound power is strongly affected by this higher harmonics amplification. To verify the reasons for this behavior, the transfer function from pressure ripple p1 and pipe acceleration A1 was calculated, just as the transfer function from pressure ripple p3 to pipe wall acceleration A2. To represent the transfer function from input to output for one given unit speed, the value of the four operation condition power spectral density is averaged. This transfer function is also calculated by using the average of 20 measurements dividing the power spectral density of the input by the power spectral density of the output (25). This metric was called the transfer function ratio.
Figure 14 shows the transfer function from inner pressure ripple to outer pipe wall acceleration for two positions in the line. As shown in Figure 10, in the position of p1, the conduit is a tee, while in the position of p3, the conduit is a thin-walled pipe. Regardless of shape differences, both positions transfer functions show a critical frequency band from 2000–3000 Hz where amplifications up to 40 dB higher than the lower frequencies, the region where strategy proved to be effective. This frequency range is also the region where measured sound power displayed in Figure 12 had large peaks.
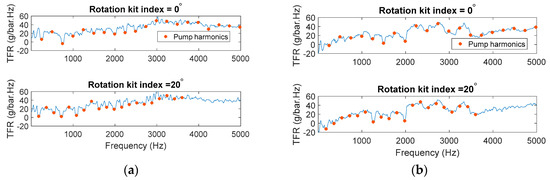
Figure 14.
Transfer Function Ratio of pressure ripple vs. pipe wall acceleration n = 1660 rpm at (a) branch; (b) pipe downstream.
Since the frequency bands from 2000 Hz to 3000 Hz contain the higher harmonics generated by the unit, and these harmonics are randomly affected by the strategy, the sound power reduction is highly dependent on speed. Table 3 shows the total measured sound power by the microphone. For each operation condition at full displacement with the lower measured sound pressure highlighted in blue. Since the strategy is not effective for higher frequencies and the measured sound pressure level is dominated by the 3000 Hz peak when the unit is at higher speed, the 0° index achieves smaller measured sound pressure for the unit running at 1660 rpm regardless of the pressure ripple cancelation in the first and third harmonic.

Table 3.
Total measured sound pressure.
6. Discussion
The indexing strategy proved to be effective for reducing partially pressure ripple generated by the hydraulic units. The first two odd harmonics of pressure ripple were reduced over 10 dB. There were reduction effects measured for acceleration and sound pressure also for these harmonics. However, the strategy was not effective in achieving this reduction for the higher odd harmonics. A possible reason for the higher harmonics noise source reduction ineffectiveness is the lack of enough symmetry either by the pipe or by the units. In the pipe, the speed of sound in the fluid is crucial, and it is influenced by factors, such as aeration and temperature. In the unit side, leakage differences and wear can lead to different constants B from equation 1 for the higher harmonics. The vibration and sound pressure measurements, showed that the higher frequency harmonics, such as the 2000–3000 Hz band, are very relevant. Pressure ripple reduction only in the first and third harmonics is not enough for always achieving overall sound pressure reduction. The operating conditions and resonant frequencies present in the hydraulic circuit must be taken into consideration.
7. Conclusions
The goal of this paper was to demonstrate source-flow duplication with anti-phasing can be applied for fluid-borne noise reduction in axial-piston units. A tandem-unit indexing strategy was conceptualized, modeled, and verified experimentally. A fixed-time step simulation based on the method of characteristic numerical solution was performed for demonstrating the propagation of destructive interference in the whole conduit length and the concept effectiveness for ideally symmetric units. The simulations suggested that, for perfect symmetric nine-piston units, a 20° rotation kit index could accomplish destructive interference for all odd multiples of the fundamental unit’s harmonic, while a 10° index obtains anti-phasing for 2 + 4n multiples of the first harmonic.
A test rig was assembled, and experiments were performed at eight different operation conditions. The experiments demonstrated the strategy was successful in reducing fluid borne-noise sources only for the first and third harmonics, and the reduction trend was maintained for line wall vibrations and sound power. Pressure ripple was reduced by up to 18 dB, while sound pressure was reduced up to 9 dB in for the first harmonic. Regarding the third harmonic, pressure ripple was reduced by up to 11 dB, while sound pressure was reduced up to 2 dB. These results suggest that passive source flow ripple control techniques are a good way of achieving reduction in vibrations and even hearable noise for targeted pump harmonics.
Since the destructive interference did not happen for higher harmonics, the strategy proved not to be enough to consistently achieve a reduction in hearable noise. However, as the strategy was successful for lower frequencies, there might still be opportunities to bundle the proposed technique with other strategies that are successful for higher frequency bands. Since the proposed solution eliminates the vibration on the source, there should be no drawbacks in combining the technique with other strategies.
Moreover, the proposed technique also may be successful for transitional operation conditions, which are known for generating loud noise—however, more study is needed to verify this statement.
Author Contributions
Conceptualization, L.D.; methodology, L.D.; software, A.V.; validation, L.D.; formal analysis, A.V.; investigation, L.D.; resources, A.V.; data curation, A.V.; writing—original draft preparation, L.D.; writing—review and editing, A.V.; visualization, L.D., and A.V.; supervision, A.V.; project administration, A.V.; All authors have read and agreed to the published version of the manuscript.
Funding
This paper acknowledges the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) for funding the work presented in this paper and Purdue University for providing support.
Conflicts of Interest
The authors declare no conflict of interest
Nomenclature
| Symbols | Description | Unit |
| AL | Area of the duct | [m2] |
| ArHPi | Valve plate area open to discharge port | [m2] |
| ArLPi | Valve plate area open to suction port | [m2] |
| B | Constant | [-] |
| BL | Isothermal wave speed | [kg/m4·s] |
| C | Characteristic equation (used in MOC line model) | [Pa] |
| c | Speed of sound | [m/s] |
| D | Line diameter | [m] |
| F | Force | [N][kg·m/s2] |
| Frki | Displacement chamber to piston force | [N][kg·m/s2] |
| fDW | Darcy–Weisbach friction coefficient | [m/s] |
| f | Frequency | [Hz] |
| I | Rotation kit index angle | [°] |
| i | Displacement Chamber number | [-] |
| j | Node | [-] |
| K | Fluid bulk modulus | [Pa][kg/m·s2] |
| k | Spatial frequency (wave number) | [-] |
| L | Line length | [m] |
| M | Torque | [N·m] |
| Mx | Swash plate moment about X axis | [Nm] |
| My | Swash plate moment about Y axis | [Nm] |
| Mz | Swash plate moment about Z axis | [Nm] |
| m | Unit’s piston number | [-] |
| Nh | Multiple of unit’s fundamental frequency | [-] |
| n | Rotational speed | [rpm] |
| O | Total number of branch segments | [-] |
| o | Total number of branch segments | [-] |
| p | Pressure | [Pa][kg/m·s2] |
| pi | ith displacement chamber pressure | [Pa][kg/m·s2] |
| pj | jth node pressure | [Pa][kg/m·s2] |
| pHP | High pressure port pressure | [bar] [Pa][kg/m·s2] |
| pLP | Low pressure port pressure | [bar] [Pa][kg/m·s2] |
| Q | Flow rate | [m3/s] |
| Qs | Volumetric loss flow rate | [m3/s] |
| QSBi | Gap flow through VP and CB | [m3/s] |
| QSGi | Gap flow through slipper and swash plate | [m3/s] |
| QSKBGi | Total flow from the gaps | [m3/s] |
| QSKi | Gap flow through piston and cylinder block | [m3/s] |
| QrHPi | Flow from HP port to DC | [m3/s] |
| QrLPi | Flow from LP port to DC | [m3/s] |
| Rb | Cylinder block pitch radius | [m] |
| S | Power Spectral Density | [bar/Hz] |
| T | temperature | [C°] |
| t | time | [s] |
| Vi | Derived displacement chamber volume | [m3] |
| z | Position | [m] |
| v | Fluid velocity | [m/s] |
| αD | Orifice coefficient of discharge | [-] |
| β | Unit displacement | [°] |
| λ | Wave length | [m] |
| Δp | Pressure ripple | [bar] [Pa][kg/m·s2] |
| τ | Shear Stress | [Pa][kg/m·s2] |
| ρ | Density | [kg/m3] |
| ω | Angular velocity | [rad/s] |
| ψ | fixed phase shift | [rad] |
| φi | Piston angular position | [rad] |
References
- Franchek, M.A.; Ryan, M.W.; Bernhard, R.J. Adaptive passive vibration control. J. Sound Vib. 1994, 189, 565–585. [Google Scholar] [CrossRef]
- Pingchao, O.; Zongxia, J.; Hongmei, L.; Shuli, L.; Yunhua, L. Active Control on Fluid Borne Pulsation Using Piezoelectric Valve as Absorber. In Proceedings of the IEEE Conference on Robotics, Automation and Mechatronics, Bangkok, Thailand, 1–3 June 2006; pp. 1–5. [Google Scholar] [CrossRef]
- Kartha, S.C. Active, Passive and Active/Passive Control Techniques for Reduction of Vibrational Power Flow in Fluid Filled Pipes. Master’s Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2000. [Google Scholar]
- Johnston, D.N.; Edge, K.A. Simulation of the pressure ripple characteristics of hydraulic circuits. Proc. Inst. Mech. Eng. 1989, 203, 275–282. [Google Scholar] [CrossRef]
- De Bedout, J.M.; Franchek, M.A.; Bernhardt, R.J.; Mongeau, L. Adaptive-passive noise control with self-tuning Helmholtz resonators. J. Sound Vib. 1997, 202, 109–123. [Google Scholar] [CrossRef]
- Makaryant, G.; Rodionov, L.; Radin, D.; Rekadze, P. Experimental investigation on adaptive Helmholtz resonator for hydraulic system. In Proceedings of the InterNoise 2019, Madrid, Spain, 16–19 June 2019; pp. 3891–3897. [Google Scholar]
- Dodson, J.M.; Dowling, D.R.; Grosh, K. Experimental investigation of quarter wavelength silencers in large scale hydraulic systems. Noise Control Eng. J. 1998, 46, 15–22. [Google Scholar] [CrossRef]
- Ichiyanagi, T.; Kuribayashi, T.; Nishiumi, T. Design criteria of a Helmholtz silencer with multiple degrees of freedom for hydraulic systems. J. Fluid Sci. Technol. 2013, 8, 277–293. [Google Scholar] [CrossRef][Green Version]
- Earnhart, N.E.; Cunefare, K.A. Compact Helmholtz resonators for hydraulic systems. Int. J. Fluid Power 2012, 13, 41–50. [Google Scholar] [CrossRef]
- Lechuga-Aranda, J.J.; Bader, S.; Oelmann, B. A space-coiling resonator for improved energy harvesting in fluid power systems. Sens. Actuators A Phys. 2019, 291, 58–67. [Google Scholar] [CrossRef]
- Li, L.; Lee, K.M.; Ouyang, X.; Yang, H. Attenuating characteristics of a multi-element buffer bottle an aircraft piston pump. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 1791–1803. [Google Scholar] [CrossRef]
- Mikota, G.; Haas, R.; Lukachev, E. Compensation of a hydraulic pipeline resonance by fluid–structure interaction. Int. J. Fluid Power 2018, 19, 14–26. [Google Scholar] [CrossRef]
- Pan, M.; Ding, B.; Yuan, C.; Zou, J.; Yang, H. Novel Integrated Control of Fluid-Borne Noise in Hydraulic Systems. In Proceedings of the BATH/ASME 2018 Symposium on Fluid Power and Motion Control FPMC2018, Bath, UK, 12–14 September 2018. [Google Scholar]
- Pulsco Aerospace Liquid Pulsation Dampener. Available online: https://www.pulsco.com/840 (accessed on 8 August 2020).
- Flexicraft Pulsation Dampener. Available online: http://www.flexicraft.com/Hydropad_Accumulator/Pulsation_Dampener (accessed on 8 August 2020).
- Blacoh. Introducing the AODDampener: All-New Dampner Designed Specifically Fot AAODD Pumps. Available online: https://www.blacoh.com/literature.aspx?l (accessed on 8 August 2020).
- Helgestad, B.O.; Foster, K.; Bannister, F.K. Pressure transients in an axial piston hydraulic pump. Proc. Inst. Mech. Eng. 1974, 188, 189–199. [Google Scholar] [CrossRef]
- Pettersson, M.; Weddfelt, K.; Palmberg, J.O. Methods of reducing flow ripple from fluid power piston pumps—A theoretical approach. In Proceedings of the SAE International Off-Highway and Powerplant Congress, Milwaukee, WI, USA, 1 September 1991. [Google Scholar]
- Frosina, E.; Marinaro, G.; Senatore, A.; Pavanetto, M. Effects of PCFV and Pre-Compression Groove on the Flow Ripple Reduction in Axial Piston Pumps. In Proceedings of the Global Fluid Power Society PhD Symposium (GFPS), Samara, Russia, 18–20 July 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Palmberg, J.O. Modelling of flow ripple from fluid power piston pumps. In 2nd Bath International Power Workshop; University of Bath: Bath, UK, 1989. [Google Scholar]
- Manring, N.D. Valve-Plate Design for an Axial Piston Pump Operating at Low Displacements ASME. J. Mech. Des. March 2003, 125, 200–205. [Google Scholar] [CrossRef]
- Kalbfleisch, P. Computational Valve Plate Design. Master’s Thesis, Purdue University, West Lafayette, IN, USA, 2015. [Google Scholar]
- Ye, S.; Zhang, J.; Xu, B. Noise Reduction of an Axial Piston Pump by Valve Plate Optimization. Chin. J. Mech. Eng. 2018, 31, 57. [Google Scholar] [CrossRef]
- Johansson, A. Design Principles for Noise Reduction in Hydraulic Piston Pumps—Simulation, Optimization and Experimental Verification. Ph.D. Thesis, Linkoping University, Linkoping, Sweden, 2005. [Google Scholar]
- Johansson, A.; Andersson, J.; Palmberg, J.O. Optimal Design of the Cross-Angle for Pulsation Reduction in Variable Displacement Pumps. In Proceedings of the Bath Workshop on Power Transmission and Motion Control, Bath, UK, 11–13 September 2002; pp. 11–13. [Google Scholar]
- Achten, P.; Schellekens, M.; Murrenhoff, H.; Deeken, M. Efficiency and Low Speed Behavior of the Floating Cup Pump. J. Commer. Veh. SAE Trans. 2004, 113, 366–376. [Google Scholar]
- Achten, P.; Eggenkamp, S. Barrel tipping in axial piston pumps and motors. In Proceedings of the 15th Scandinavian International Conference, SICFP2017, Linköping, Sweden, 7–9 June 2017. [Google Scholar]
- Platzer, T.; Van Malsen, R.A.H.; Achten, P.A.J. Floating Cup—Ein neues Konstruktionsprinzip für hydrostatische Maschinen. Ölhydraulik Pneum. 2004, 48, 375–378. [Google Scholar]
- Ohuchi, H.; Masuda, K.; Osada, T. Noise reduction of a variable displacement axial piston pump by compensating the exciting force. In Proceedings of the JFPS International Symposium on Fluid Power, Nara, Japan, 12–15 November 2002; Volume 33, pp. 76–81. [Google Scholar]
- Kim, T.; Ivantysynova, M. Active Vibration/Noise Control of Axial Piston Machine Using Swash Plate Control. In Proceedings of the ASME/BATH 2017 Symposium on Fluid Power and Motion Control, Sarasota, FL, USA, 16–19 October 2017. [Google Scholar]
- Casoli, P.; Pastori, M.; Scolari, F.; Rundo, M. Active Pressure Ripple Control in Axial Piston Pumps through High-Frequency Swash Plate Oscillations—A Theoretical Analisys. Energies 2019, 12, 1377. [Google Scholar] [CrossRef]
- Masuda, K.; Ohuchi, H. Noise reduction of a variable piston pump with even number of cylinders. In Proceedings of the JFPS International Symposium on Fluid Power, Atlanta, GA, USA, 17–22 November 1996; pp. 91–96. [Google Scholar]
- Zanetti-Rocha, L.; Gerges, S.N.Y.; Johnston, D.N.; Arenas, J.P. Rotating Group; Design for Vane Pump Flow Ripple Reduction. Int. J. Acoust. Vib. 2013, 18, 192–200. [Google Scholar] [CrossRef]
- Yudin, E.M. Gear Pumps Principal Parameters and Their Calculation; Translation of Russian book by Harris, E.; National Lending Library for Science and Technology: Yorkshire, UK, 1961. [Google Scholar]
- Lipscombe, B.R. The Reduction of Gear Pump Pressure Ripple by Source Flow Modification. Ph.D. Thesis, University of Bath, Bath, UK, 1987. [Google Scholar]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics; John Wiley & Sons: Hoboken, NJ, USA, 1982. [Google Scholar]
- Edge, K.A.; Johnston, D.N. The ‘Secondary Source’ Method for the Measurement of Pump Pressure Ripple Characteristics Part 1: Description of Method. Proc. Inst. Mech. Eng. Part A J. Power Energy 1990, 204, 33–40. [Google Scholar] [CrossRef]
- Kojima, E. A new method for the experimental determination of pump fluid borne noise characteristics. In Proceedings of the 5th Bath International Power Workshop, Bath, UK, 16–18 September 1992; pp. 111–137. [Google Scholar]
- Danes, L.; Vacca, A. The influence of line and fluid parameters on pressure ripple in hydraulic transmissions. SN Appl. Sci. 2020, 2, 1281. [Google Scholar] [CrossRef]
- Wieczorek, U.; Ivantysynova, M. Computer aided optimization of bearing and sealing gaps in hydrostatic machines—The simulation tool CASPAR. Int. J. Fluid Power 2002, 3, 7–20. [Google Scholar] [CrossRef]
- Borghi, M.; Milani, M.; Paltrinieri, F.; Zardin, B. Pressure transients in external gear pumps and motors meshing volumes, Rosemont, IL: T. Tech. Pap. SAE Int. 2005, SP-1989. [Google Scholar] [CrossRef]
- Klop, R.; Vacca, A.; Ivantysynova, M. A Method of Characteristics Based Coupled Pump/Line Model to Predict Noise Sources of Hydrostatic Transmissions. In Proceedings of the Bath ASME Symposium on Fluid Power and Motion Control, Hollywood, CA, USA, 12–14 October 2009. [Google Scholar]
- Wilhelm, S. Modeling, Analysis and Experimental Investigation of a Variable Displacement Linkage Pump. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2015. [Google Scholar]
- Ivantysyn, J.; Ivantysynova, M. Hydrostatic Pumps and Motors: Principles, Designs, Performance, Modelling, Analysis, Control and Testing; Tech Books International: New Delhi, India, 2003; ISBN 81-88305-08-1. [Google Scholar]
- Wylie, E.; Streeter, V. Fluid Transients; McGraw-Hill Inc.: New York, NY, USA, 1978; ISBN 0-07-072187-4. [Google Scholar]
- Vardy, A.E.; Hwang, K.L. A characteristics model of transient friction in pipes. J. Hydraul. Res. 1991, 29, 669–684. [Google Scholar] [CrossRef]
- Carlsson, J. Water Hammer Phenomenon Analysis using the Method of Characteristics and Direct Measurements Using a ”stripped” Electromagnetic Flow Meter. Master’s Thesis, Royal Institute of Technology, Stockholm, Sweden, 2016. [Google Scholar]
- Klop, R.J. Investigation of Hydraulic Transmission Noise Sources. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2010. [Google Scholar]
- Wang, L. Active Control of Fluid-Borne Noise. Ph.D. Thesis, University of Bath, Bath, UK, 2008. [Google Scholar]
- Fahy, F.J. Applied Acoustics, International Standards for the Determination of Sound Power Levels of Sources Using Sound Intensity Measurement: An Exposition. Appl. Acoust. 1997, 50, 97–109. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).