Review of Time and Space Harmonics in Multi-Phase Induction Machine
Abstract
1. Introduction
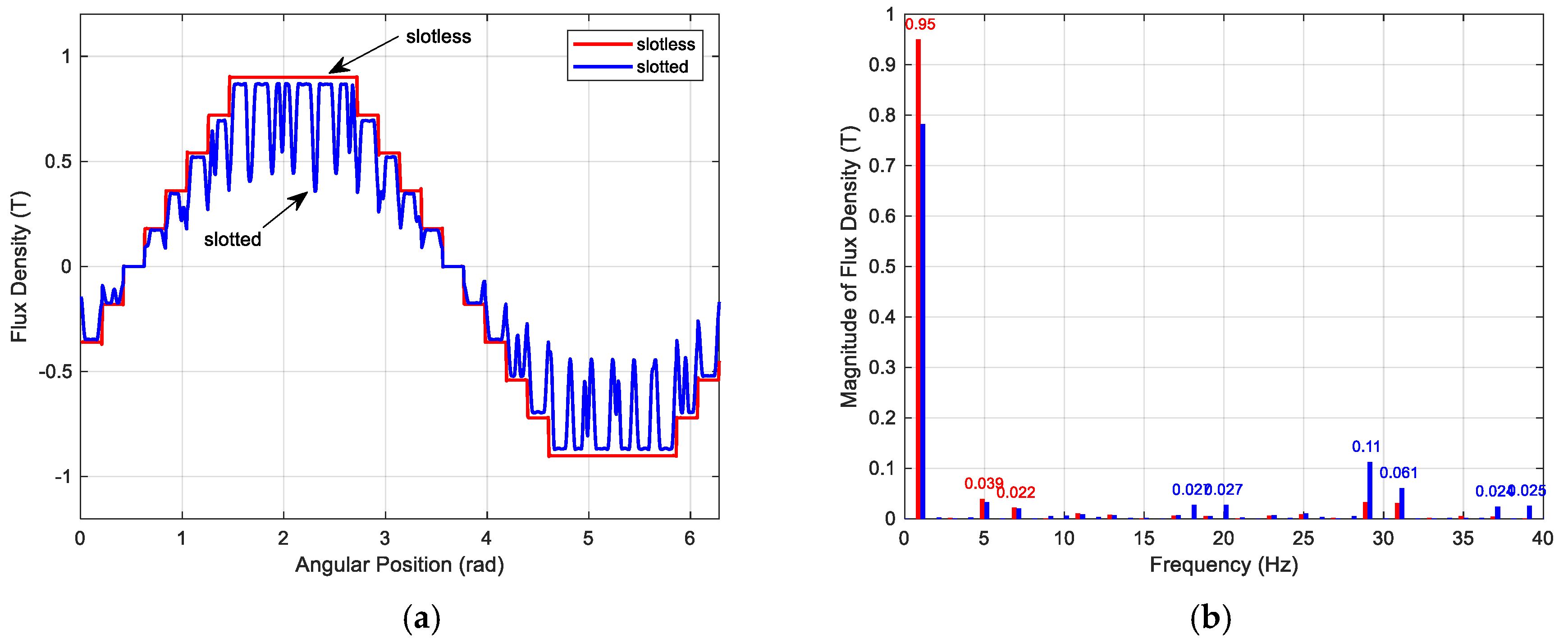
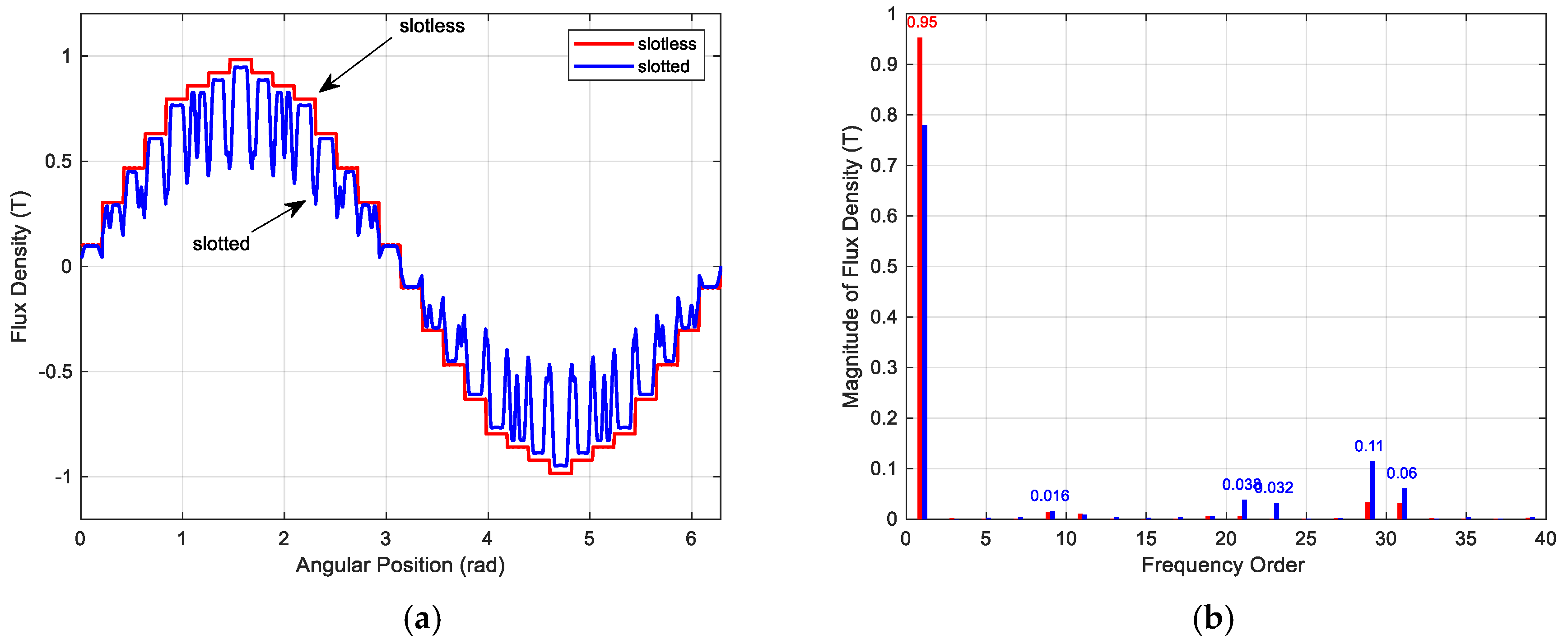
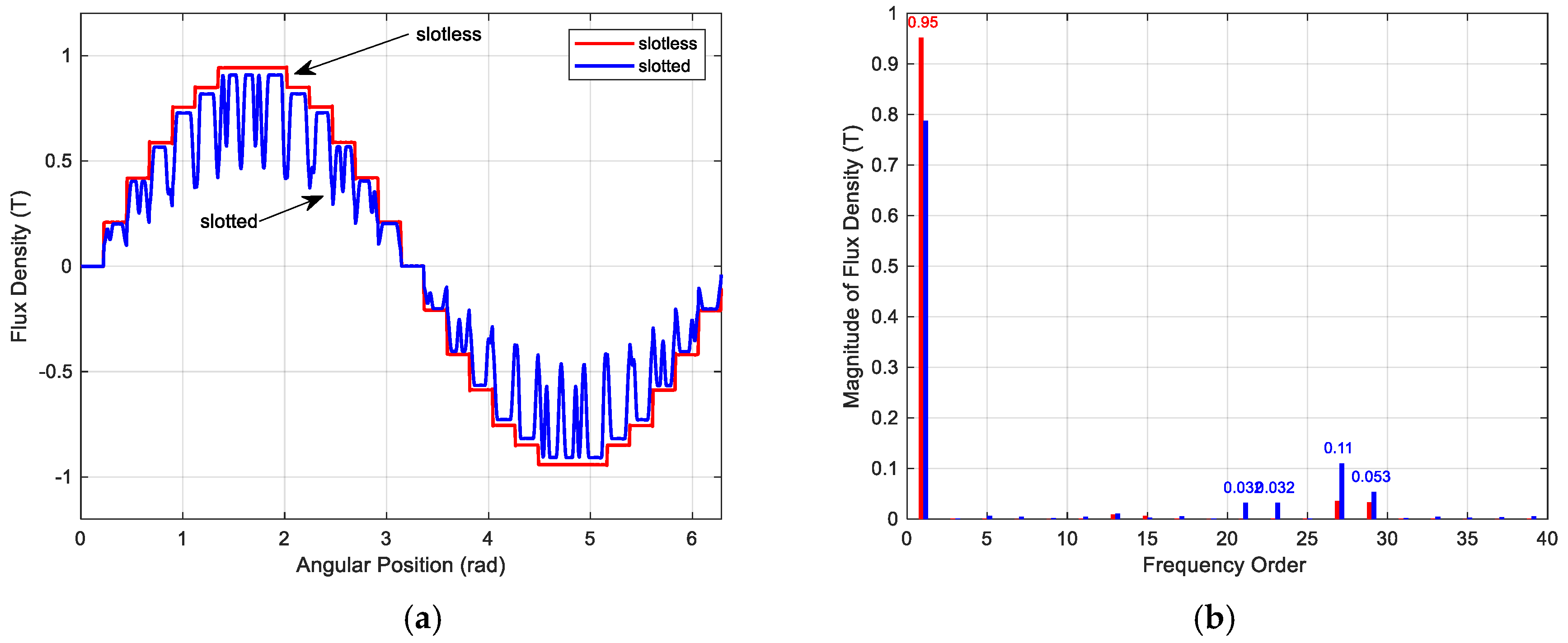
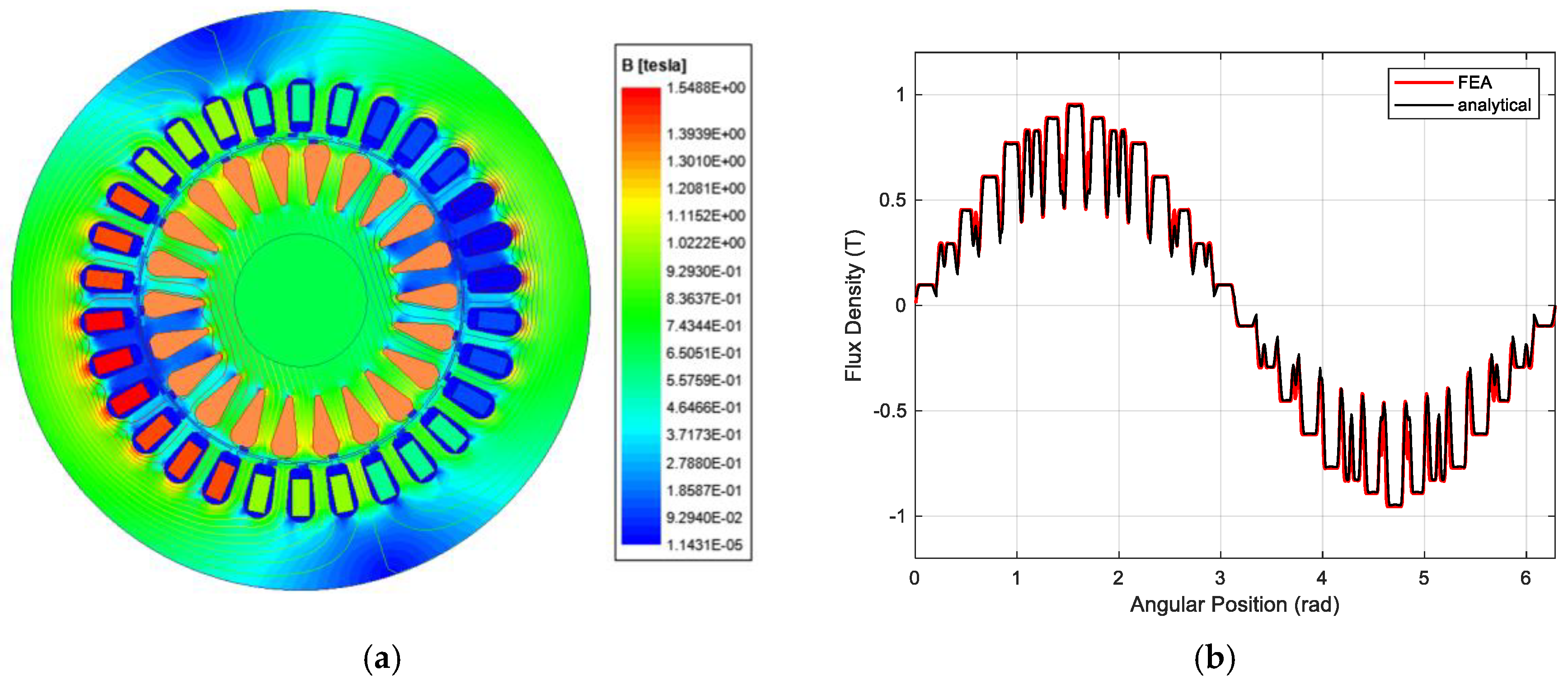
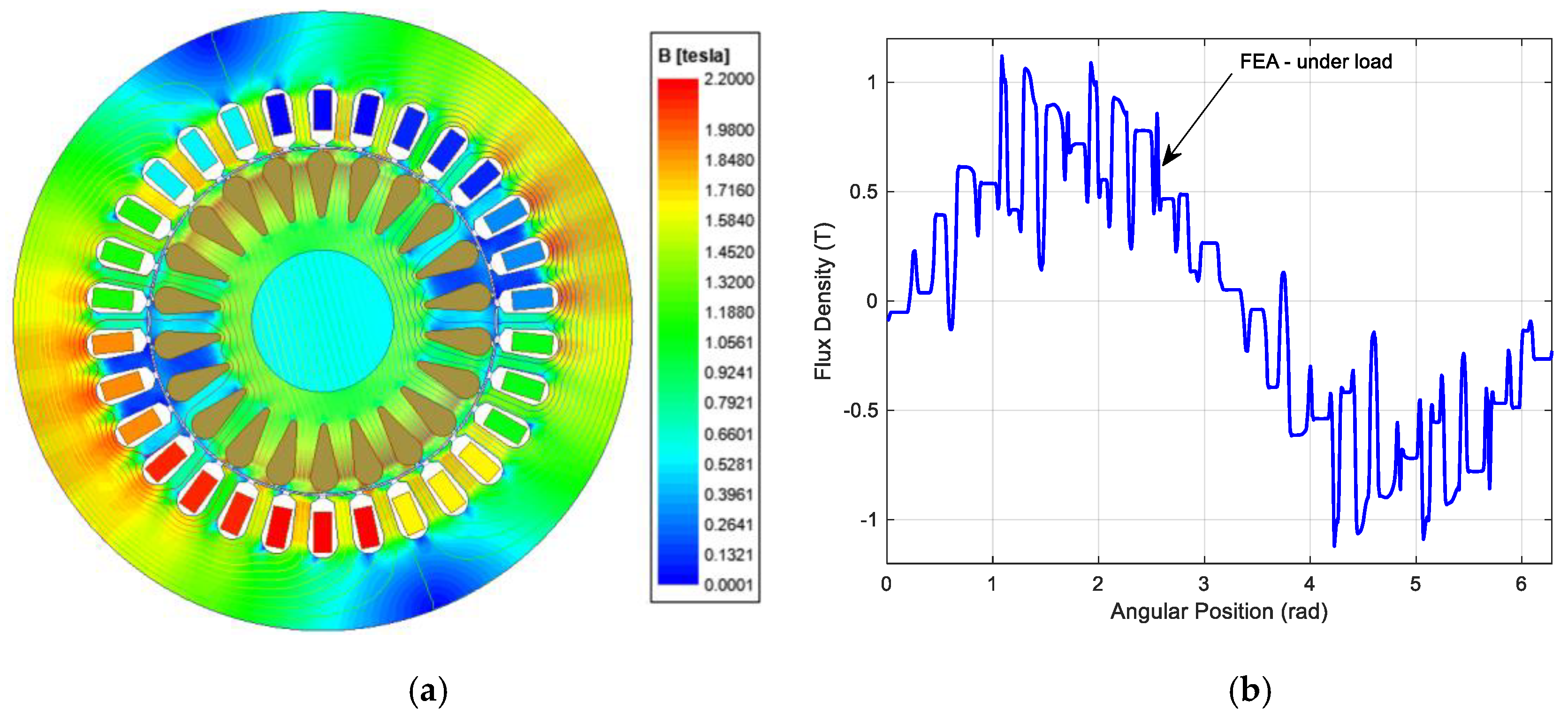
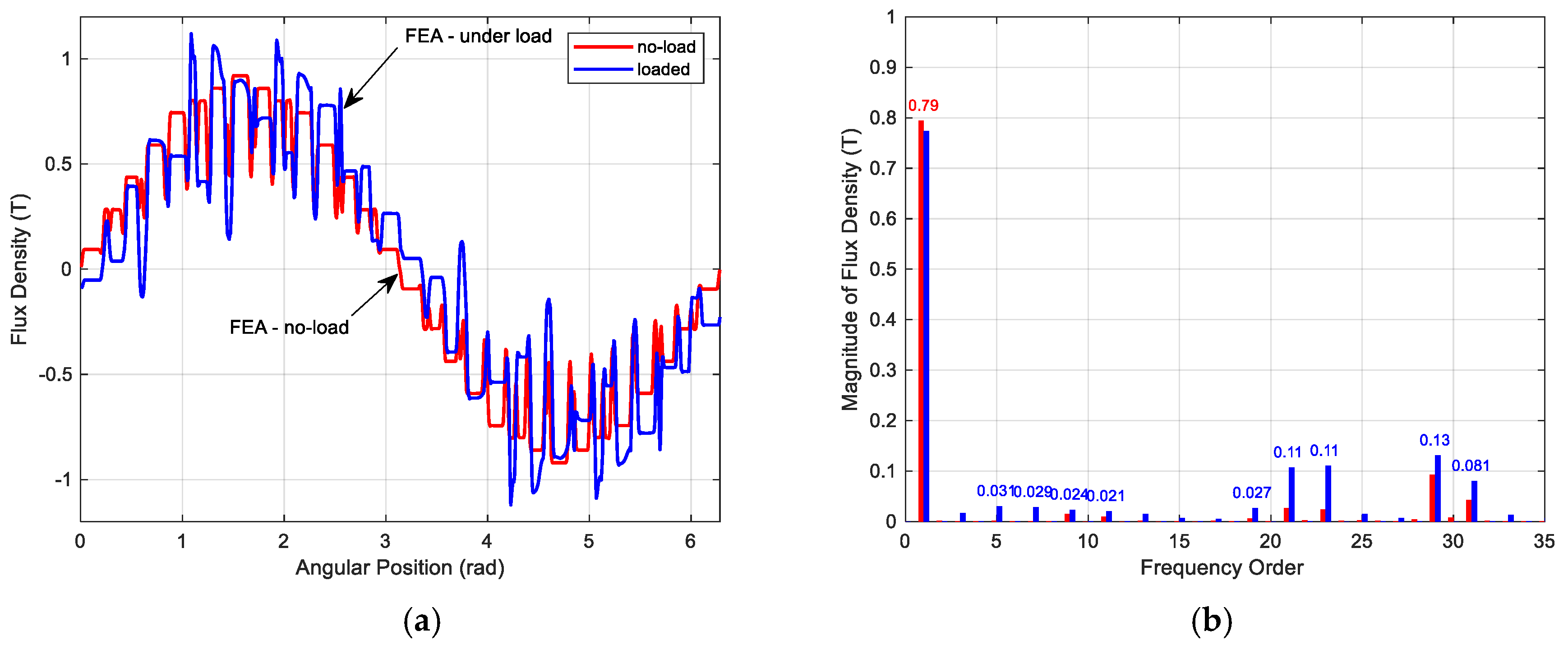
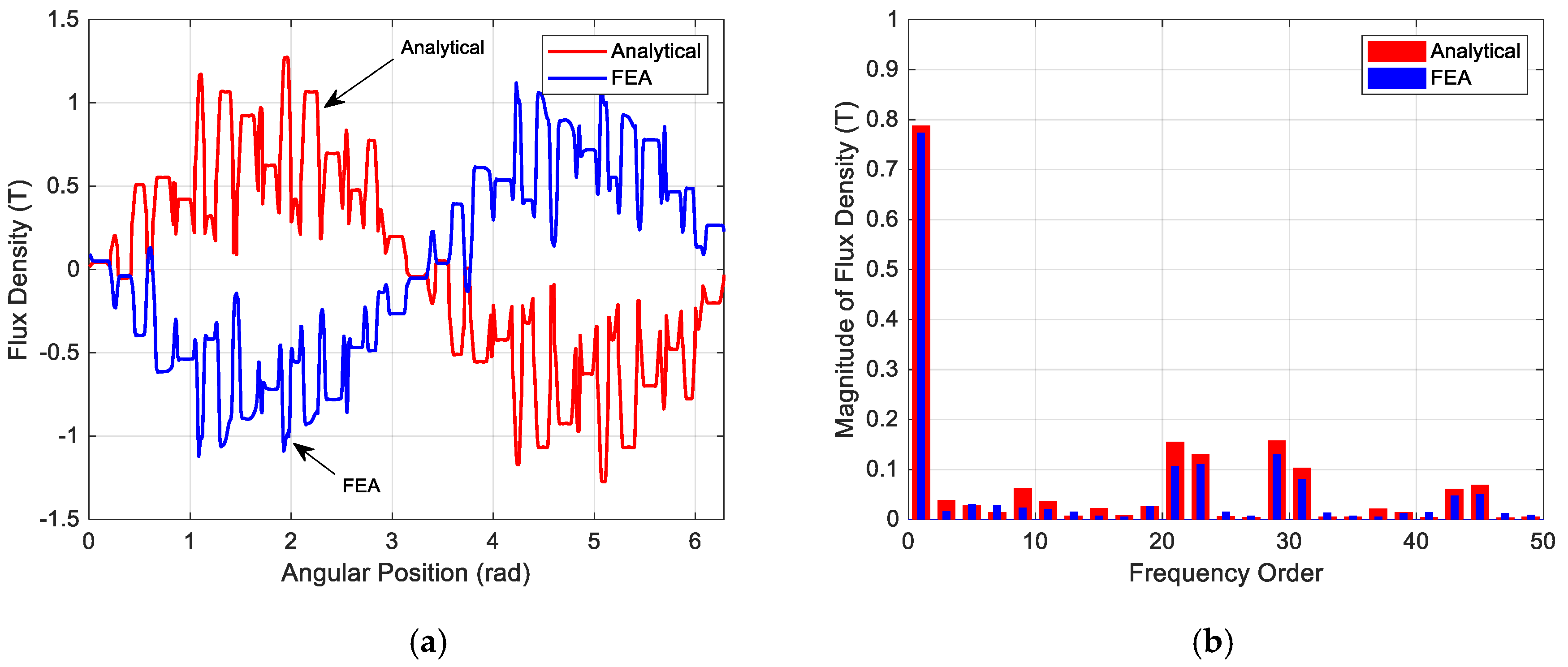
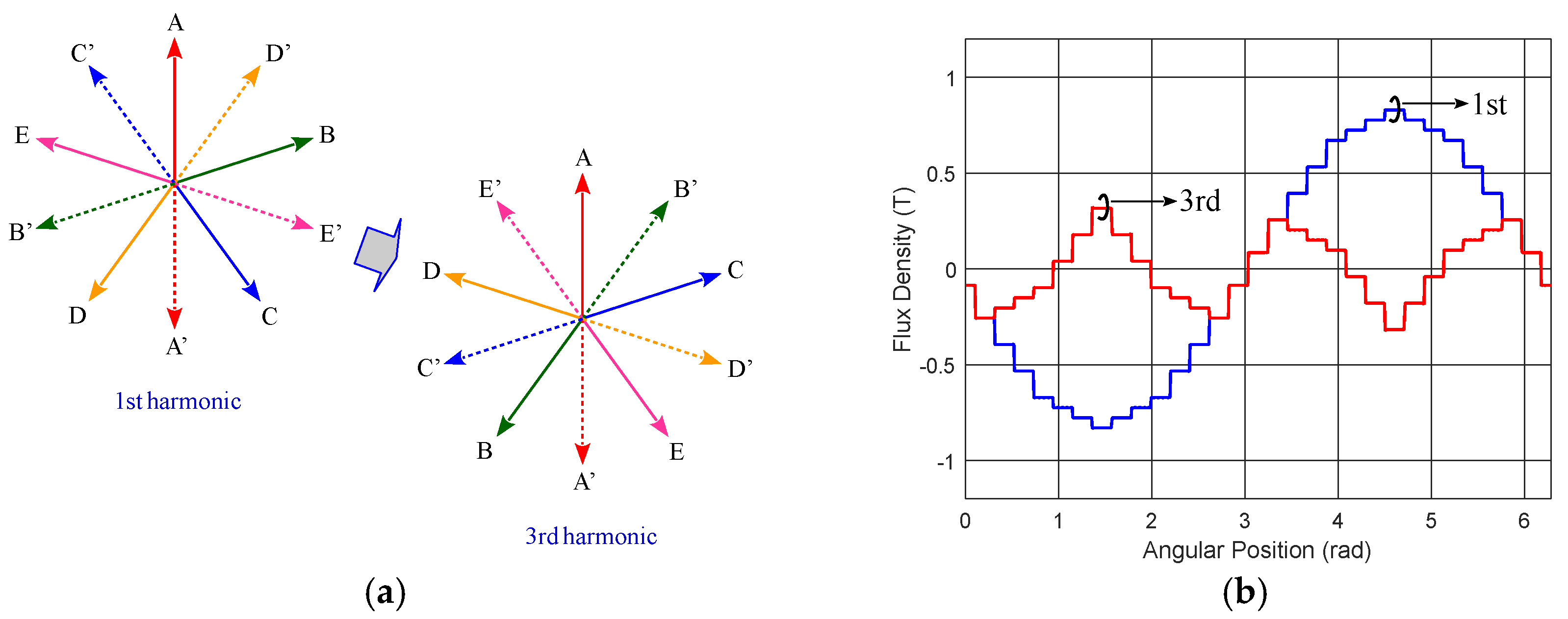
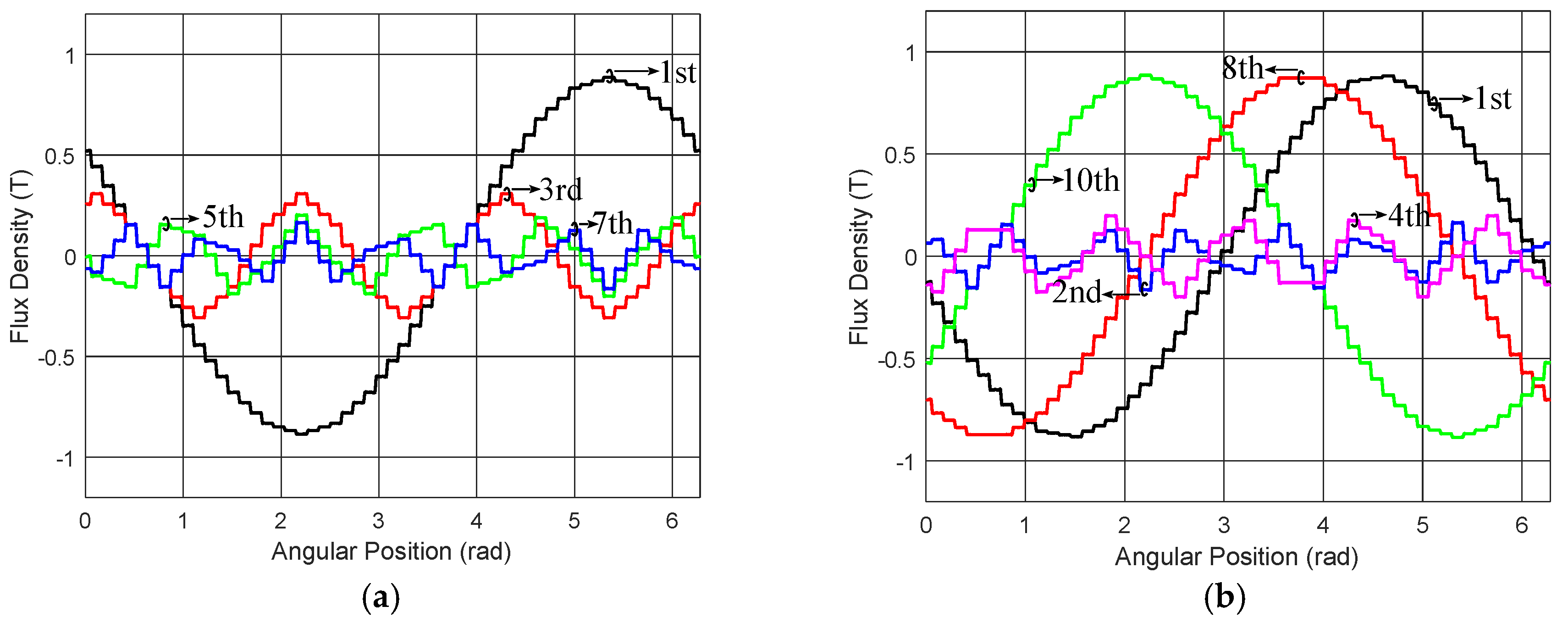
2. Space Harmonics in the Air Gap Magnetic Field
Synthesis of Air Gap Magnetic Field Formed by Symmetrically Distributed Windings
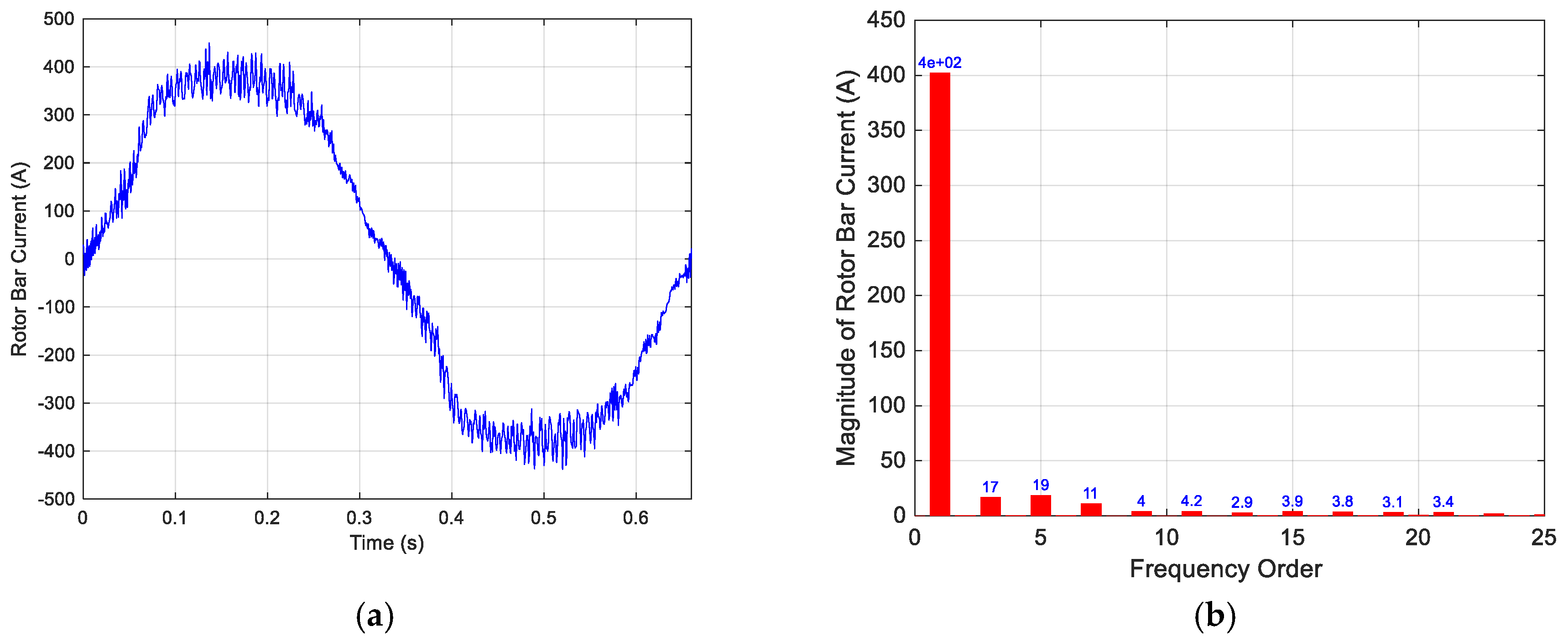
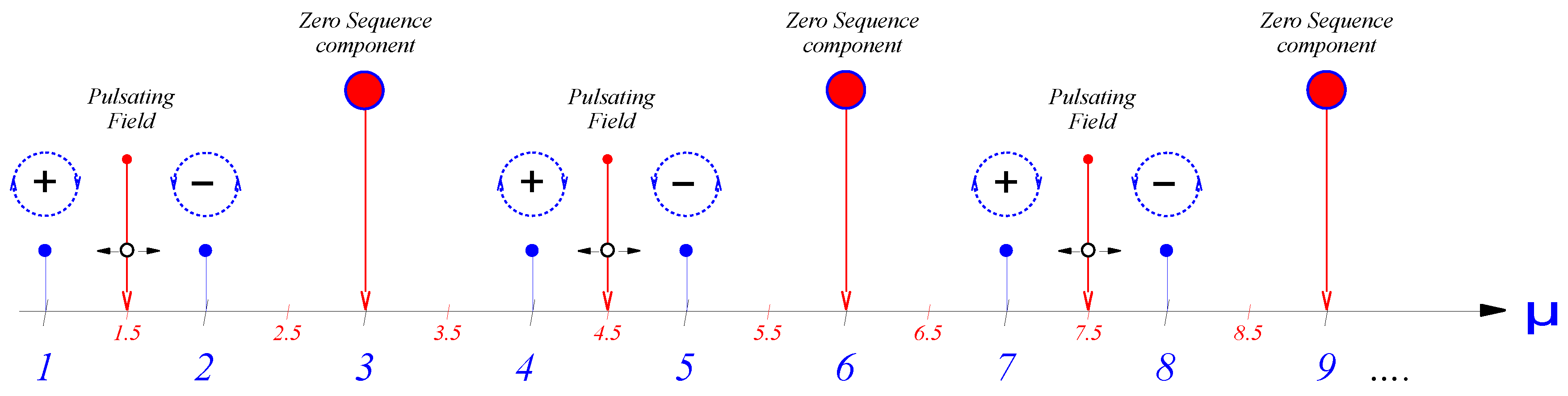
3. Time Harmonics in Multiphase Winding
3.1. Harmonics Creating 2p Number of Pole Pairs
3.2. Harmonics Creating Higher Number of Pole Pairs than 2p
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tie, S.F.; Tan, C.W. A review of energy sources and energy management system in electric vehicles. Renew. Sustain. Energy Rev. 2013, 20, 82–102. [Google Scholar] [CrossRef]
- Chau, K.T.; Wong, Y.S.; Chan, C.C. An overview of energy sources for electric vehicles. Energy Convers. Manag. 1999, 40, 1021–1039. [Google Scholar] [CrossRef]
- Su, W.; Eichi, H.; Zeng, W.; Chow, M.Y. A survey on the electrification of transportation in a smart grid environment. IEEE Trans. Ind. Inform. 2012, 8, 1–10. [Google Scholar] [CrossRef]
- Emadi, A.; Lee, Y.J.; Rajashekara, K. Power electronics and motor drives in electric, hybrid electric, and plug-in hybrid electric vehicles. IEEE Trans. Ind. Electron. 2008, 55, 2237–2245. [Google Scholar] [CrossRef]
- Rajashekara, K. Present status and future trends in electric vehicle propulsion technologies. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 3–10. [Google Scholar] [CrossRef]
- Chan, C.C. The state of the art of electric, hybrid, and fuel cell vehicles. Proc. IEEE 2007, 95, 704–718. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Howe, D. Electrical machines and drives for electric, hybrid, and fuel cell vehicles. Proc. IEEE 2007, 95, 746–765. [Google Scholar] [CrossRef]
- Pellegrino, G.; Vagati, A.; Boazzo, B.; Guglielmi, P. Comparison of induction and PM synchronous motor drives for EV application including design examples. IEEE Trans. Ind. Appl. 2012, 48, 2322–2332. [Google Scholar] [CrossRef]
- Popescu, M.; Goss, J.; Staton, D.A.; Hawkins, D.; Chong, Y.C.; Boglietti, A. Electrical vehicles—Practical solutions for power traction motor systems. IEEE Trans. Ind. Appl. 2018, 54, 2751–2762. [Google Scholar] [CrossRef]
- Yang, Z.; Shang, F.; Brown, I.P.; Krishnamurthy, M. Comparative study of interior permanent magnet, induction, and switched reluctance motor drives for EV and HEV applications. IEEE Trans. Transp. Electrif. 2015, 1, 245–254. [Google Scholar] [CrossRef]
- Boldea, I.; Tutelea, L.N.; Parsa, L.; Dorrell, D. Automotive electric propulsion systems with reduced or no permanent magnets: An overview. IEEE Trans. Ind. Electron. 2014, 61, 5696–5711. [Google Scholar] [CrossRef]
- Kowal, A.; Arahal, M.R.; Martin, C.; Barrero, F. Constraint satisfaction in current control of a five-phase drive with locally tuned predictive controllers. Energies 2019, 12, 2715. [Google Scholar] [CrossRef]
- Resa, J.; Cortes, D.; Marquez-Rubio, J.F.; Navarro, D. Reduction of induction motor energy consumption via variable velocity and flux references. Electronics 2019, 8, 740. [Google Scholar] [CrossRef]
- Zamani, J.S. Computer simulation of converter fed synchronous machine drives containing space harmonics. In Proceedings of the International Conference on Power Electronics, Drives and Energy Systems for Industrial Growth, New Delhi, India, 8–11 January 1996; pp. 944–950. [Google Scholar]
- Fu, J.-R.; Lipo, T.A. Disturbance-free operation of a multiphase current-regulated motor drive with an opened phase. IEEE Trans. Ind. Appl. 1994, 30, 1267–1274. [Google Scholar] [CrossRef]
- Zhao, Y.; Lipo, T.A. Modeling and control of a multi-phase induction machine with structural unbalance. IEEE Trans. Energy Convers. 1996, 11, 578–584. [Google Scholar] [CrossRef]
- Levi, E.; Bojoi, R.; Profumo, F.; Toliyat, H.A.; Williamson, S. Multiphase induction motor drives—A technology status review. IET Electr. Power Appl. 2007, 1, 489–516. [Google Scholar] [CrossRef]
- Toliyat, H.A.; Lipo, T.A. Analysis of concentrated winding induction machines for adjustable speed drive applications-experimental results. IEEE Trans. Energy Convers. 1994, 9, 695–700. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Masoud, M.I.; Williams, B.W. Improved flux pattern with third harmonic injection for multiphase induction machine. IEEE Trans. Power Electron. 2012, 27, 1563–1578. [Google Scholar] [CrossRef]
- Duran, M.J.; Salas, F.; Arahal, M.R. Bifurcation analysis of five-phase induction motor drives with third harmonic injection. IEEE Trans. Ind. Electron. 2008, 55, 2006–2014. [Google Scholar] [CrossRef]
- Lyra, R.O.C.; Lipo, T.A. Torque density improvement in a six-phase induction motor with third harmonic current injection. IEEE Trans. Ind. Appl. 2002, 38, 351–1360. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Masoud, M.I.; Ahmed, S.; Massoud, A.M. Effect of current harmonic injection on constant rotor multiphase induction machine stators: A comparative study. IEEE Trans. Ind. Appl. 2012, 48, 2002–2013. [Google Scholar] [CrossRef]
- Ferkova, Z.; Kindl, V. Influence of skewed squirrel cage rotor with intermediate ring on magnetic field of air gap in induction machine. Electr. Eng. 2017, 23, 26–30. [Google Scholar] [CrossRef][Green Version]
- Orság, O.; Rusnok, S.; Sobota, P.; Kačor, P. Influence of rotor slot shape on the parameters of induction motor. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and the 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–6. [Google Scholar]
- Bernat, P.; Kacor, P. Operational non-contact diagnostics of induction machine based on stray electromagnetic field. Commun. Sci. Lett. Univ. Zilina 2015, 17, 89–94. [Google Scholar]
- Alger, P.L. The Nature of Polyphaser Induction Machines; Wiley: Hoboken, NJ, USA, 1951. [Google Scholar]
- Neto, L.M.; Camacho, J.R.; Salerno, C.H.; Alvarenga, B.P. Analysis of a three-phase induction machine including time and space harmonic effects: The a, b, c reference frame. IEEE Trans. Energy Convers. 1999, 14, 80–85. [Google Scholar] [CrossRef]
- Stincescu, R.B.; Viarouge, P.; Cros, J.; Kamwa, I. A general approach of space and time harmonics interactions in induction motors. In Proceedings of the IEEE International Electric Machines and Drives Conference, Seattle, WA, USA, 3–12 May 1999; pp. 366–368. [Google Scholar] [CrossRef]
- Heller, B.; Hamata, V. Harmonic Field Effects in Induction Machines; Elsevier Science Ltd.: Amsterdam, The Netherlands, 1977; ISBN 9780444998569. [Google Scholar]
- Liao, Y.; Lipo, T.A. Effect of saturation third harmonic on the performance of squirrel-cage induction machines. Electr. Mach. Power Syst. 1994, 22, 155–171. [Google Scholar] [CrossRef]
- Lee, C.H. Saturation 597–harmonics of polyphase induction machines. Trans. Am. Inst. Electr. Eng. Part III Power Appar. Syst. 1961, 80, 603. [Google Scholar] [CrossRef]
- Pyrhönen, J.; Jokinen, T.; Hrabovcova, V. Design of Rotating Electrical Machines, 2nd ed.; John Wiley & Sons Ltd.: Chichester, UK, 2014; ISBN 978-1-118-58157-5. [Google Scholar]
- Laksar, J.; Sobra, J.; Veg, L. Numerical calculation of the effect of the induction machine load on the air gap magnetic flux density distribution. In Proceedings of the 2017 18th International Scientific Conference on Electric Power Engineering (EPE), Kouty nad Desnou, Czech Republic, 17–19 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
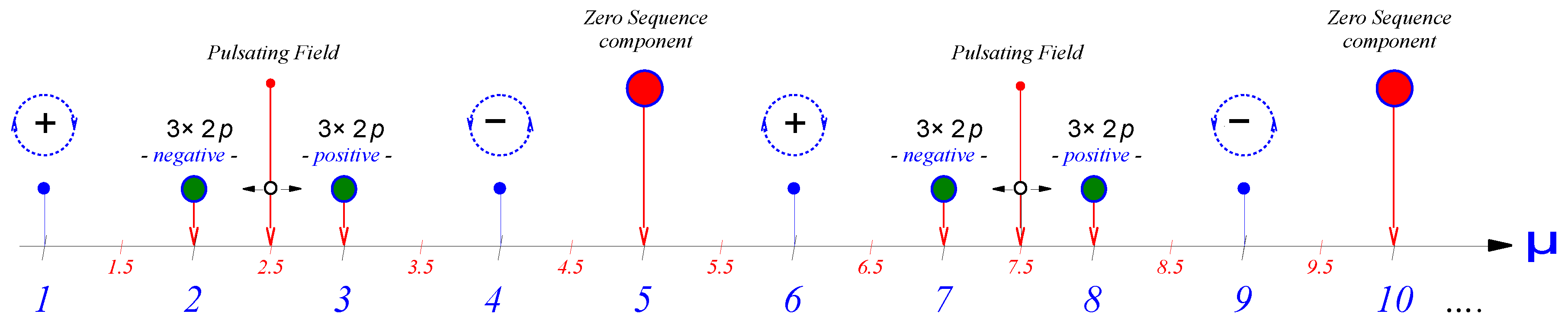

| Five-Phase Winding | Seven-Phase Winding | Nine-Phase Winding | |||||||
|---|---|---|---|---|---|---|---|---|---|
| μ | Poles | Sequence | Speed | Poles | Sequence | Speed | Poles | Sequence | Speed |
| 1 | 2p | + | 1 | 2p | + | 1 | 2p | + | 1 |
| 2 | 3 × 2p | − | 2/3 | 5 × 2p | − | 2/5 | 7 × 2p | − | 2/7 |
| 2.5 | 3 × 2p | puls. | 0 | ||||||
| 3 | 3 × 2p | + | 1 | 3 × 2p | + | 1 | 3 × 2p | + | 1 |
| 3.5 | 3 × 2p | puls. | 0 | ||||||
| 4 | 2p | − | 4 | 3 × 2p | − | 4/3 | 5 × 2p | − | 4/5 |
| 4.5 | 5 × 2p | puls. | 0 | ||||||
| 5 | 5 × 2p | zero | 0 | 5 × 2p | + | 1 | 5 × 2p | + | 1 |
| 6 | 2p | + | 6 | 2p | − | 6 | 3 × 2p | − | 6/3 |
| 7 | 3 × 2p | − | 7/3 | 7 × 2p | zero | 0 | 7 × 2p | + | 1 |
| 7.5 | 3 × 2p | puls. | 0 | ||||||
| 8 | 3 × 2p | + | 8/3 | 2p | + | 8 | 2p | − | 8 |
| 9 | 2p | − | 9 | 5 × 2p | − | 9/5 | 9 × 2p | zero | 0 |
| 10 | 5 × 2p | zero | 0 | 3 × 2p | + | 10/3 | 2p | + | 10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kindl, V.; Cermak, R.; Ferkova, Z.; Skala, B. Review of Time and Space Harmonics in Multi-Phase Induction Machine. Energies 2020, 13, 496. https://doi.org/10.3390/en13020496
Kindl V, Cermak R, Ferkova Z, Skala B. Review of Time and Space Harmonics in Multi-Phase Induction Machine. Energies. 2020; 13(2):496. https://doi.org/10.3390/en13020496
Chicago/Turabian StyleKindl, Vladimir, Radek Cermak, Zelmira Ferkova, and Bohumil Skala. 2020. "Review of Time and Space Harmonics in Multi-Phase Induction Machine" Energies 13, no. 2: 496. https://doi.org/10.3390/en13020496
APA StyleKindl, V., Cermak, R., Ferkova, Z., & Skala, B. (2020). Review of Time and Space Harmonics in Multi-Phase Induction Machine. Energies, 13(2), 496. https://doi.org/10.3390/en13020496