Real-Time Minimization Power Losses by Driven Primary Regulation in Islanded Microgrids
Abstract
1. Introduction
- The primary control is usually designed to use a droop-control method to stabilize voltage and frequency and regulate the power sharing between distributed generators in microgrids. This control level is also used to mitigate the circulating currents between paralleled three-phase generators’ converters that cause over-current phenomenon in the power electric devices and damage the capacitors in milliseconds.
- The secondary control is designed to compensate for the voltage and frequency deviation caused by the primary control. This control level has a slower dynamics response than the primary control level and is explicated in the range of seconds. In this way, the secondary control level can also be implemented to satisfy the power quality requirements.
- The tertiary control is the last and slower control level. It manages the power flows inside the MG and between the MG and the main grid providing the distributed energy resources the operating set-points. The tertiary control level also provides optimal operation setting by solving optimization problems for minimizing power losses and operating costs.
- A structure of an online driven droop regulation system is presented to decrease operating energy losses. The designed controller relies on the real-time measurements and online power flow optimization within microgrids by adjusting the droop coefficients of inverter interfaced units.
- Improving the real-time dynamic response of distributed energy resources and maintaining real-time stability for the microgrid. Indeed, the volumes of secondary and tertiary control taken over from primary control are relieved, thus getting a more reliable operation for microgrids.
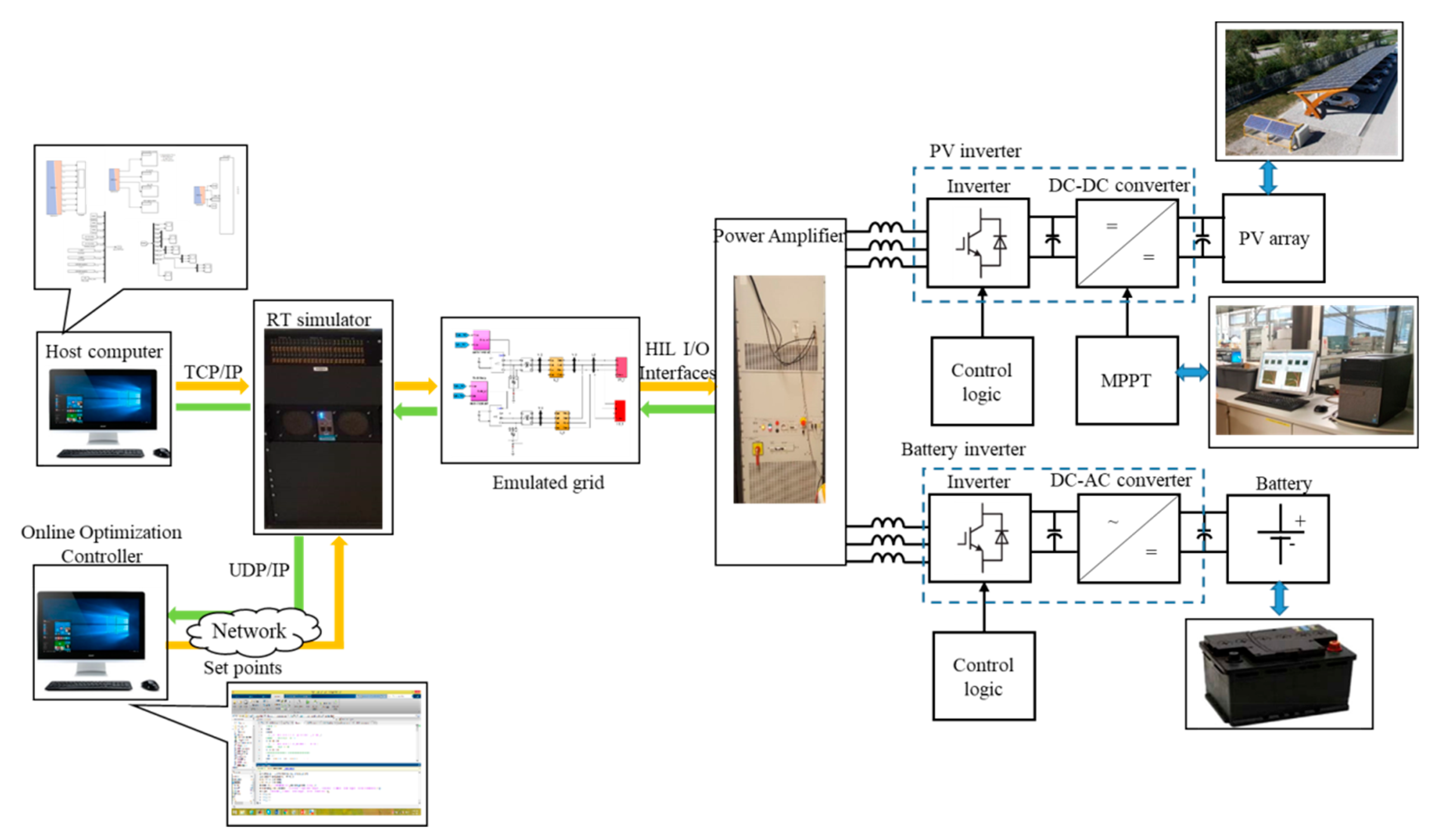
- In the application part of the work, experimental validation scenarios for a laboratory platform with optimization controllers and power-hardware-in-the-loop setups have been implemented to test the online operating characteristics of the system. During the experiments, the P-f droop coefficients have changed to adapt to load changing conditions. It is proved that the proposed architecture under realistic conditions achieves improved operation.
2. Optimization Program
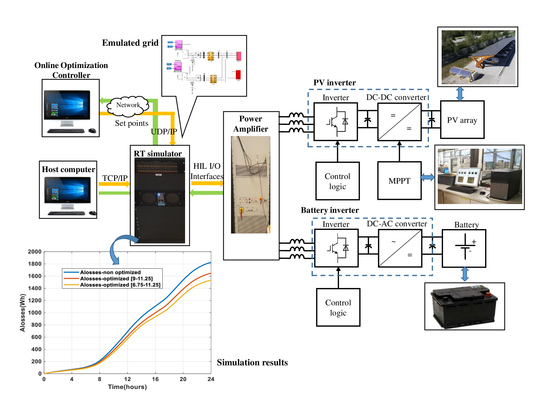
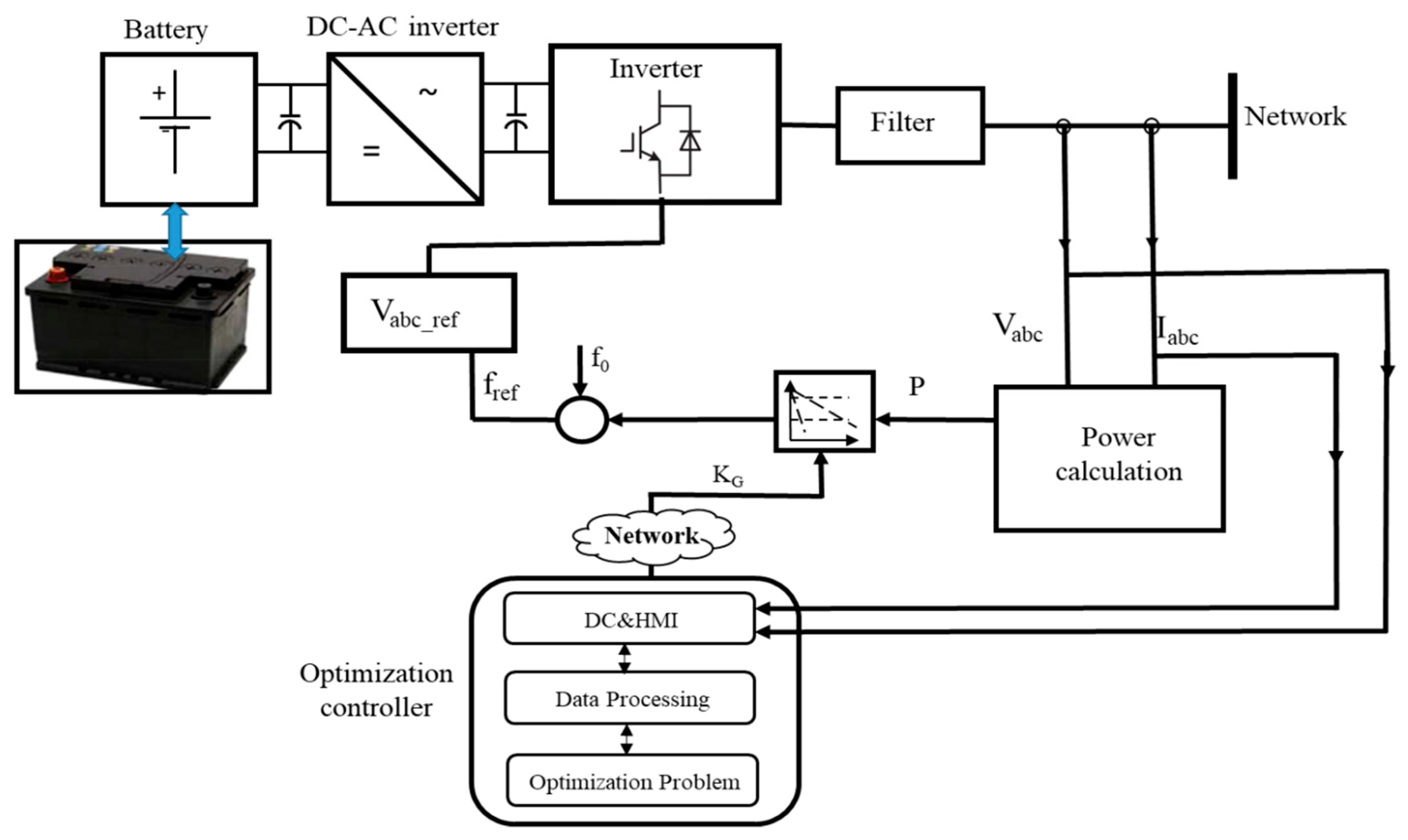
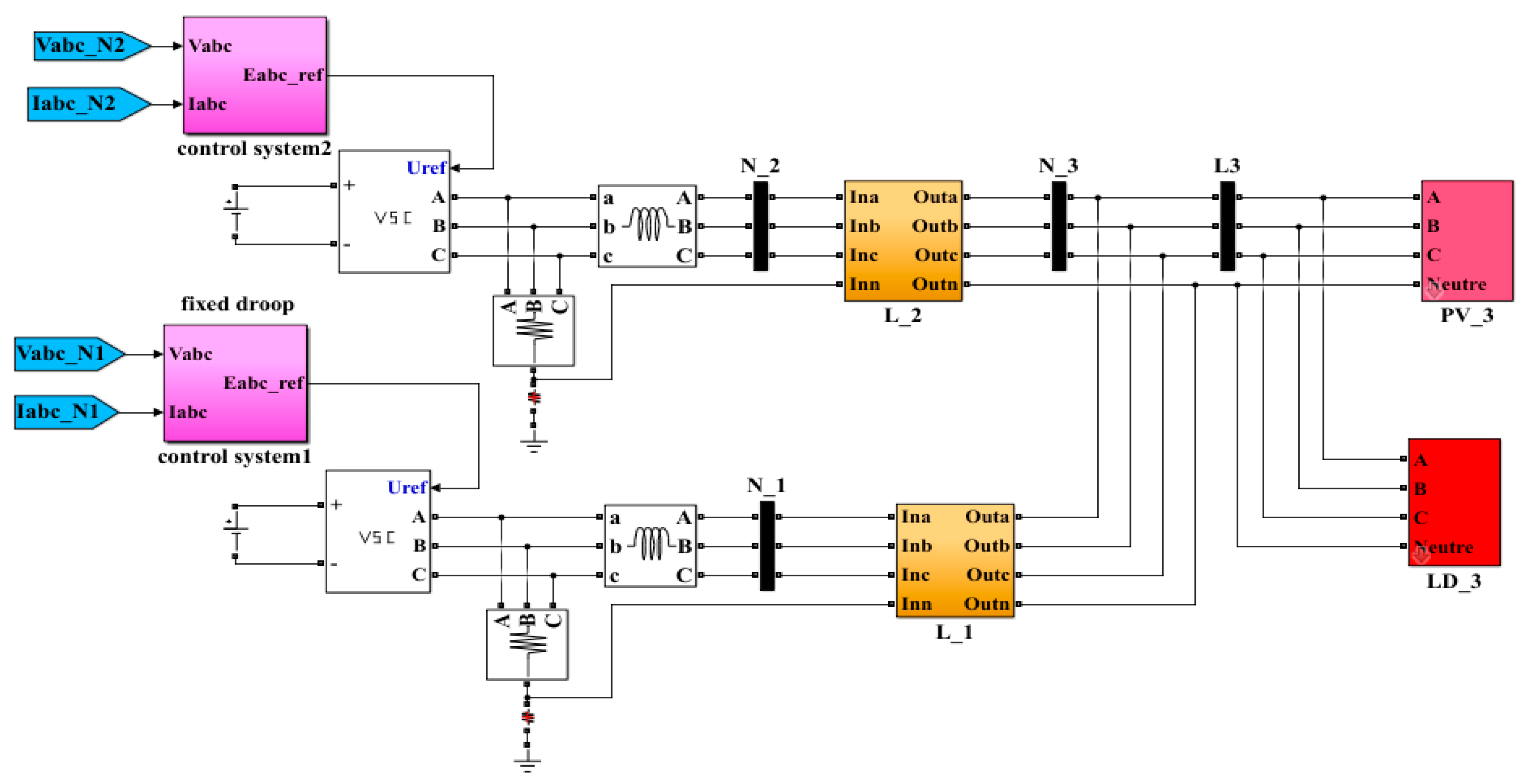
3. Structure of the Online Driven Droop Regulation for Minimum Power Losses Operation
4. Simulations and Results
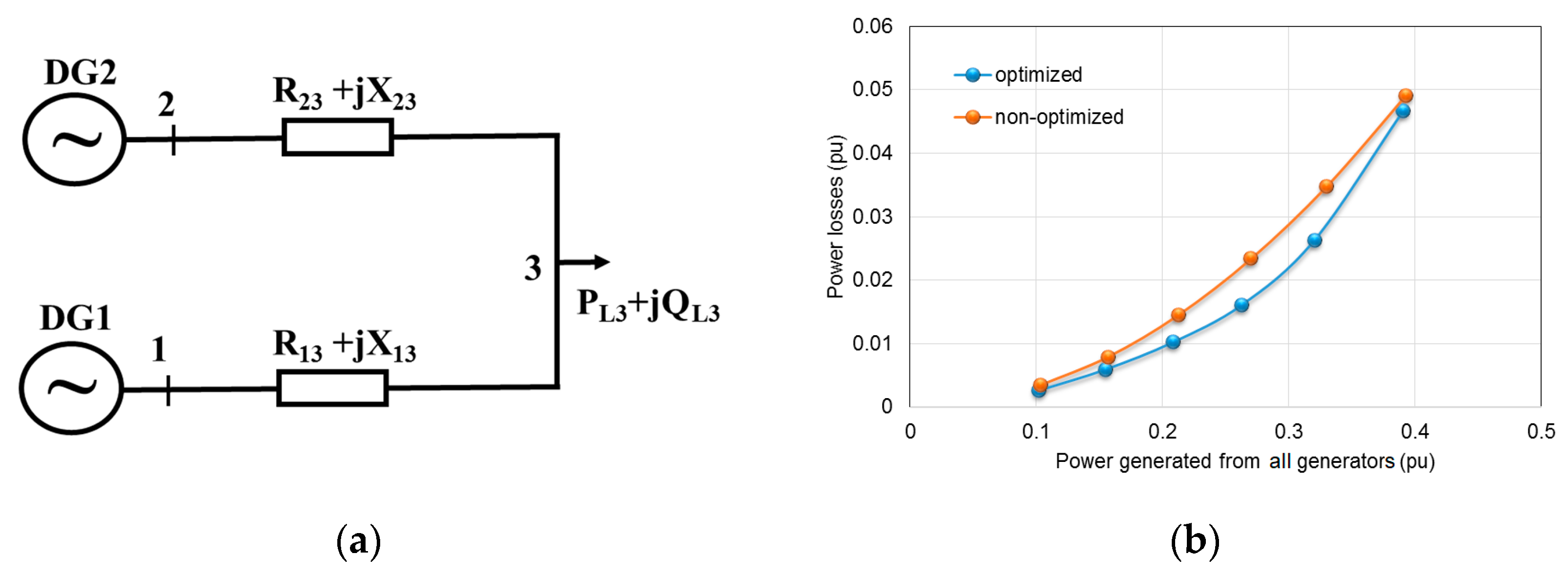
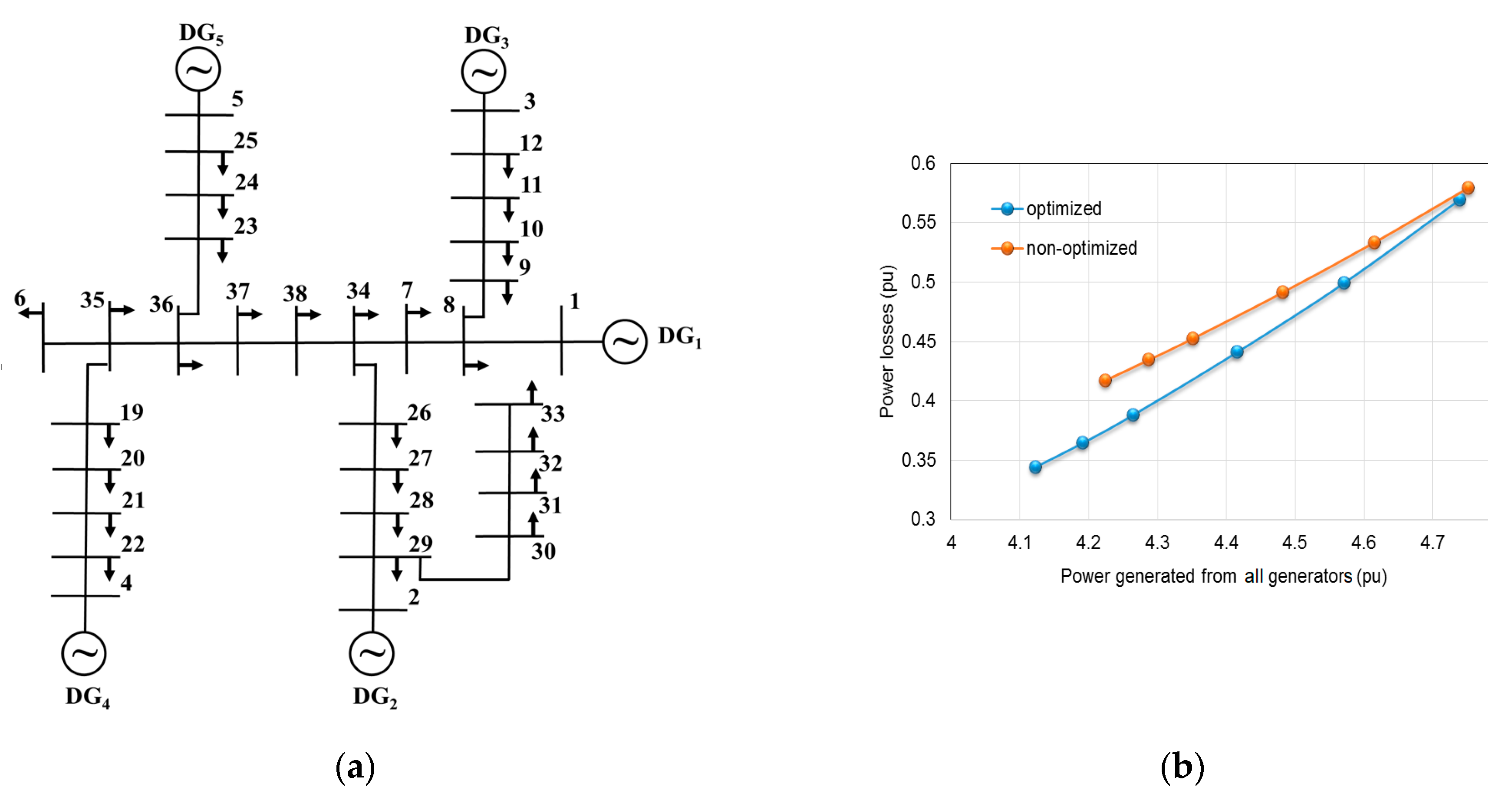
4.1. Simulation in an Optimization Program
4.2. Hardware in the Loop Simulation
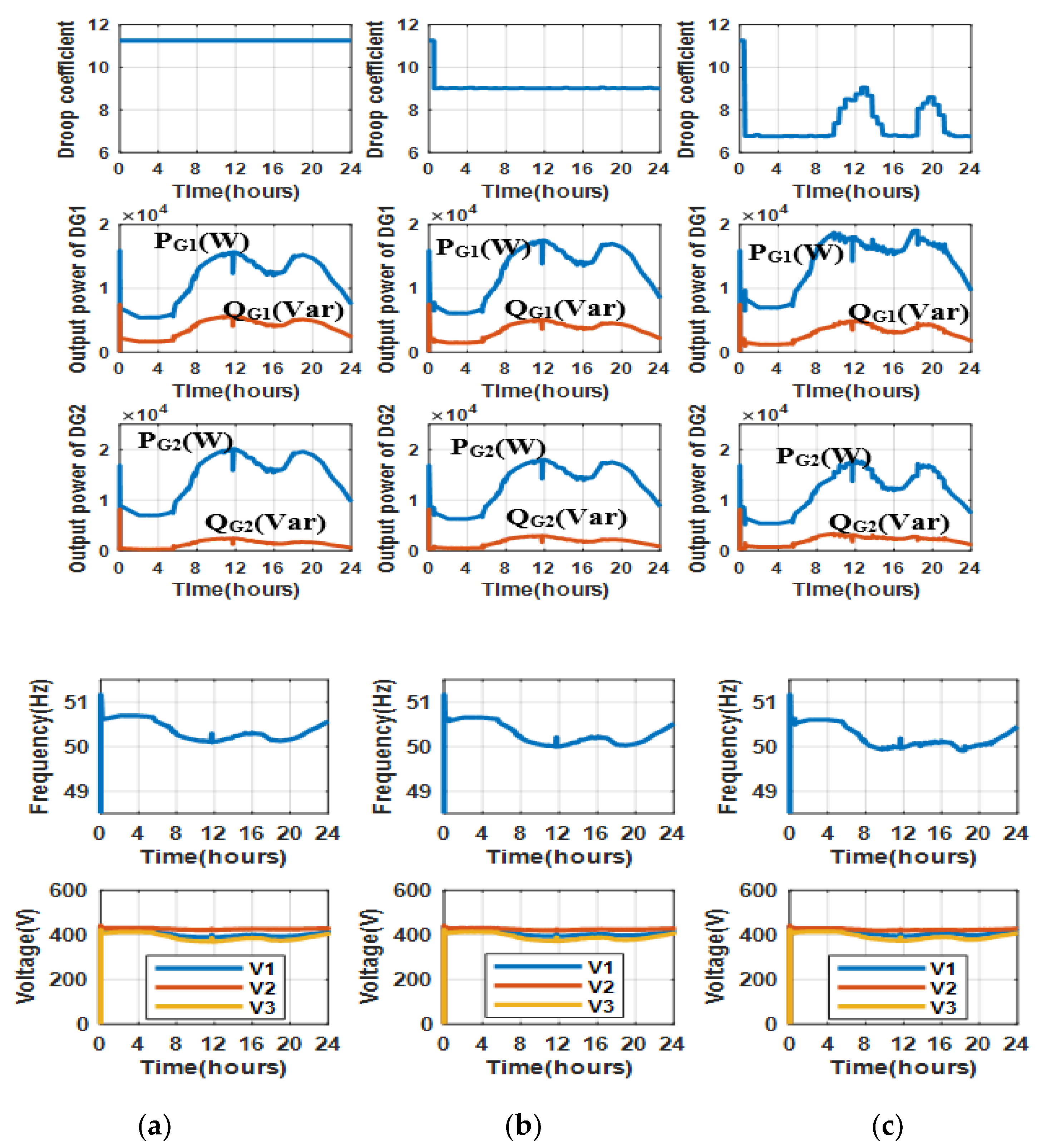
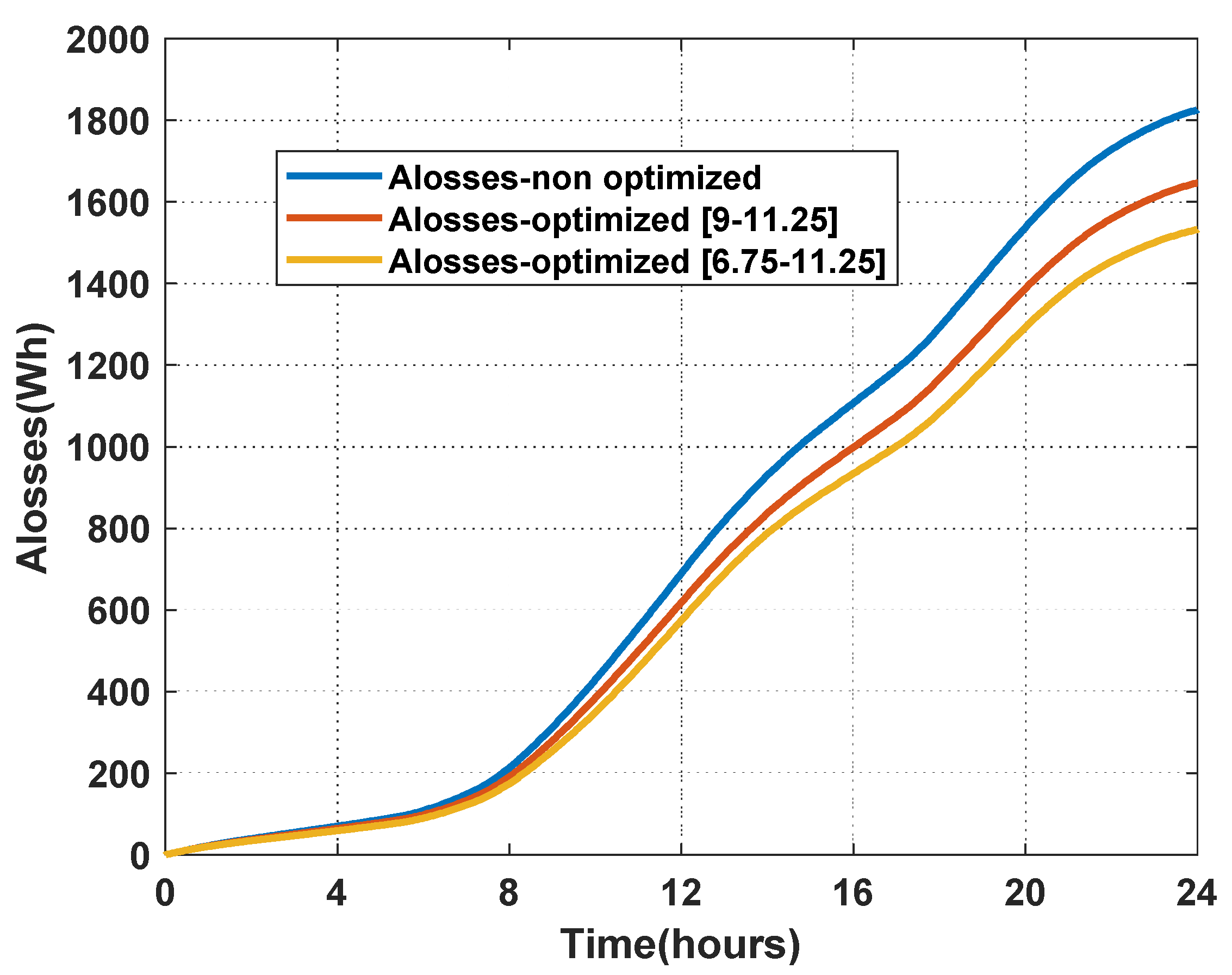
- Scenario 1: Test system is operated with the conventional droop control method;
- Scenario 2: Test system is operated with the proposed optimized droop control method to see how the system operates when KG2 is selected optimally in the range (9–11.25);
- Scenario 3: Test system is operated with the proposed optimized control method to see how the system operates when KG2 is selected optimally in a wider range (6.75–11.25).
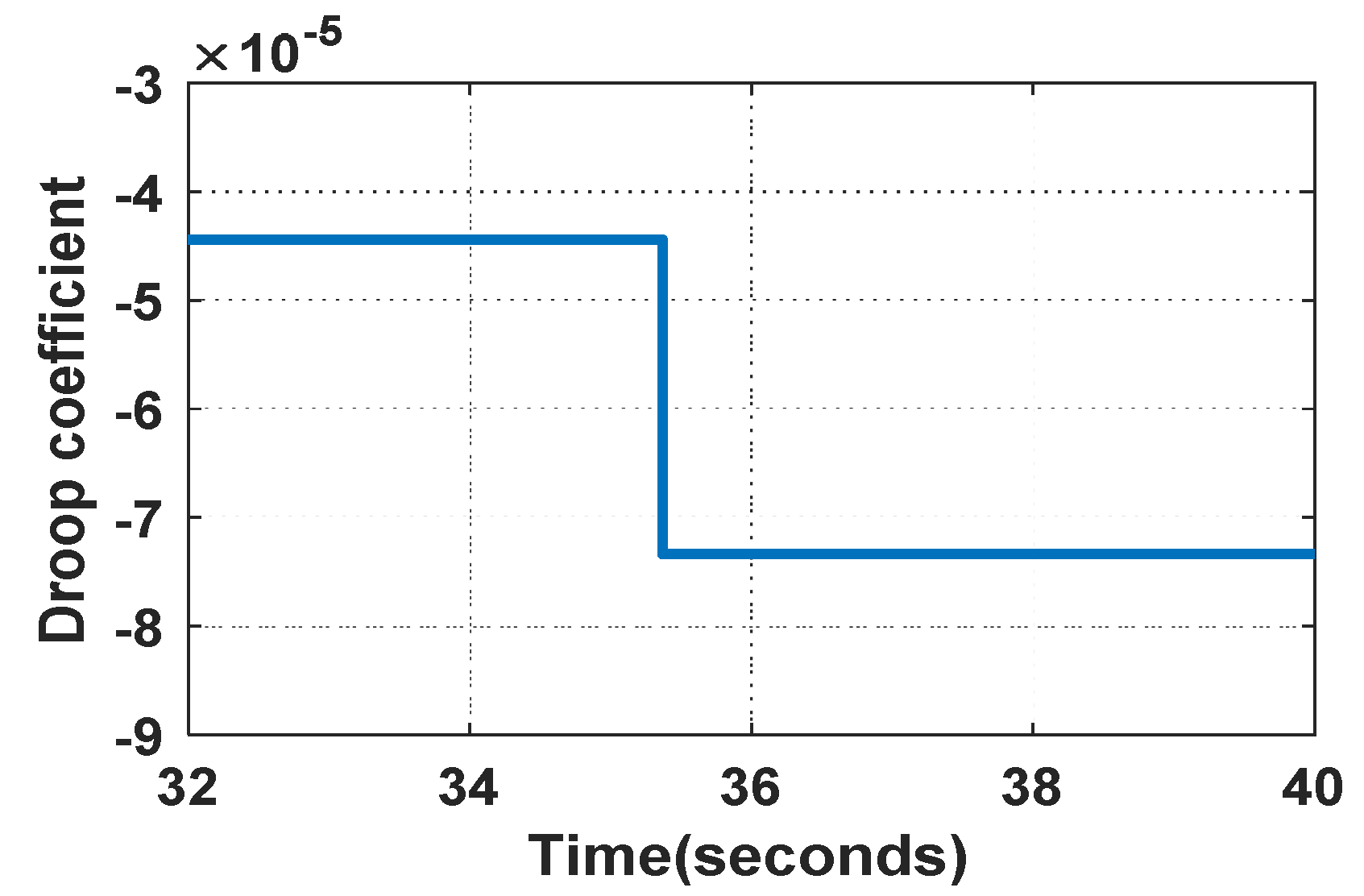
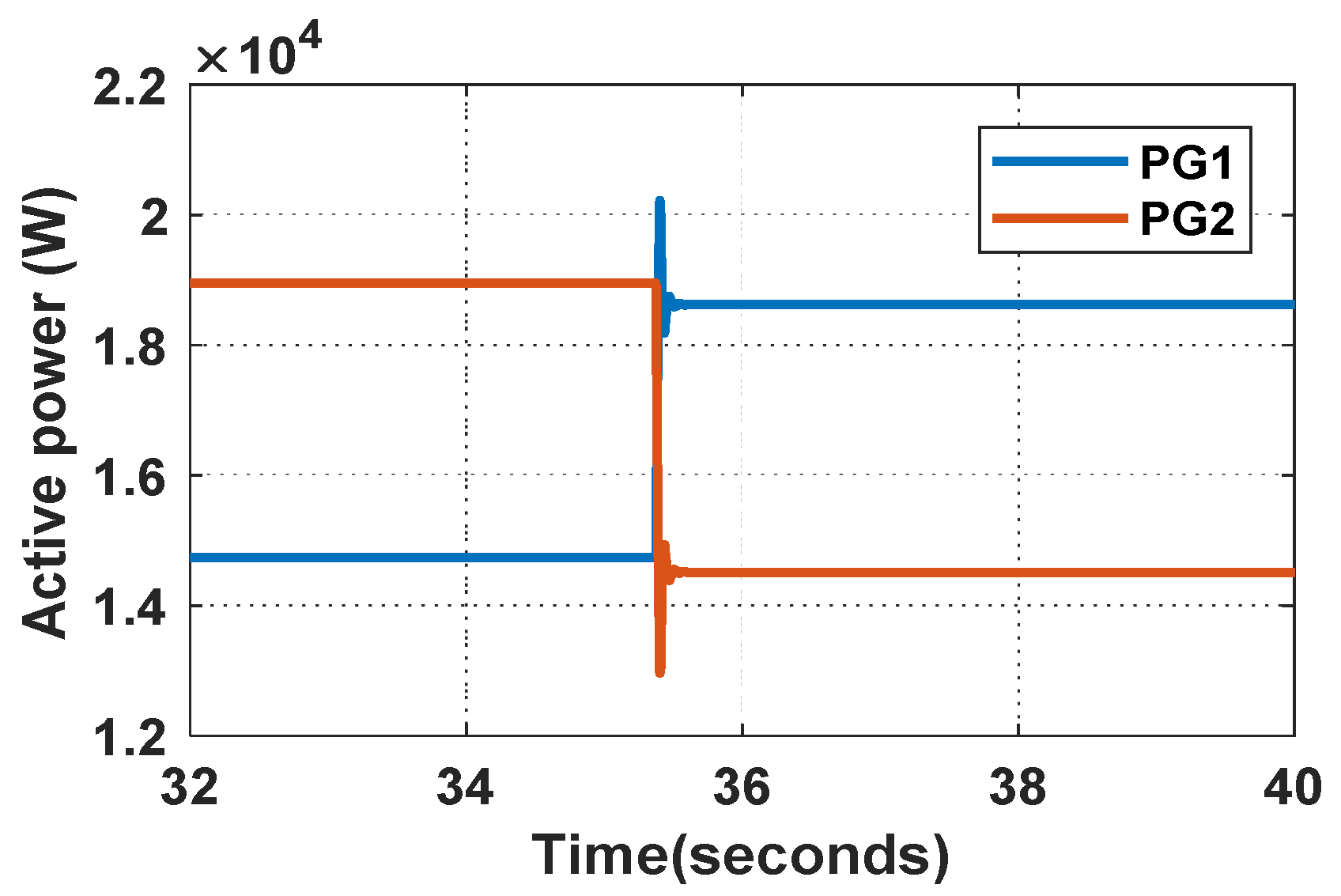
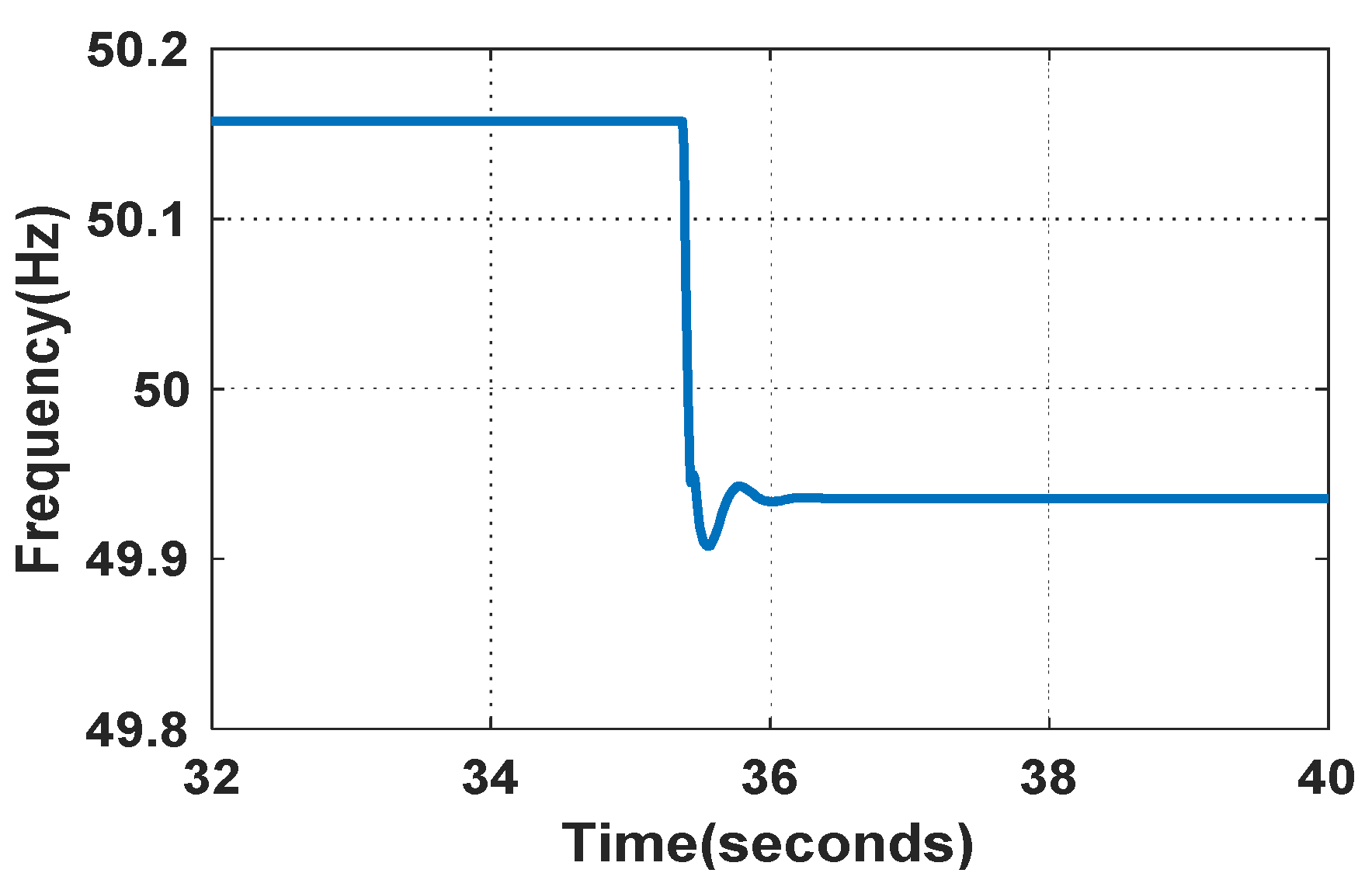
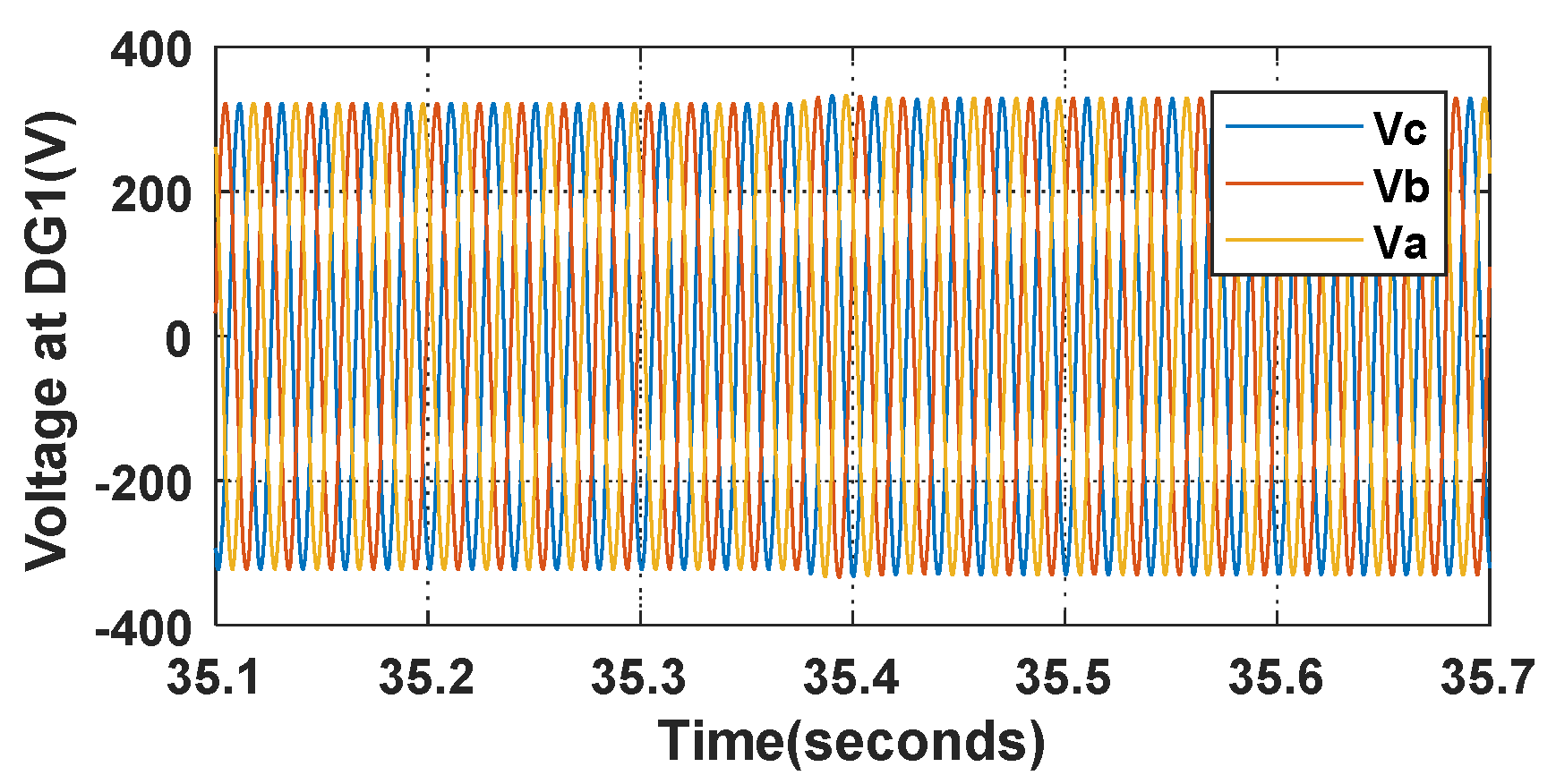
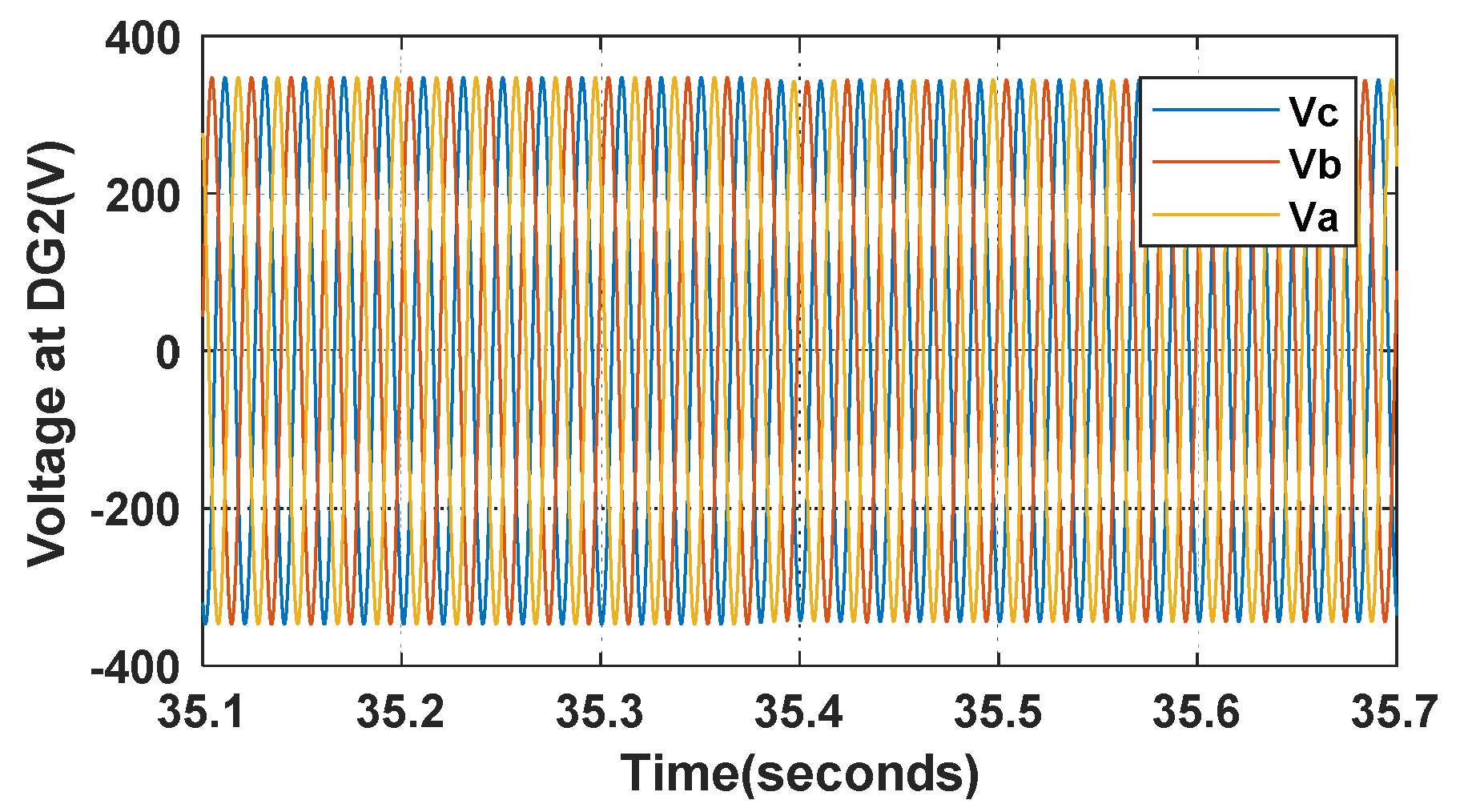
5. Experimental Results and Analysis
5.1. The Simulation Results of the Transient Responses
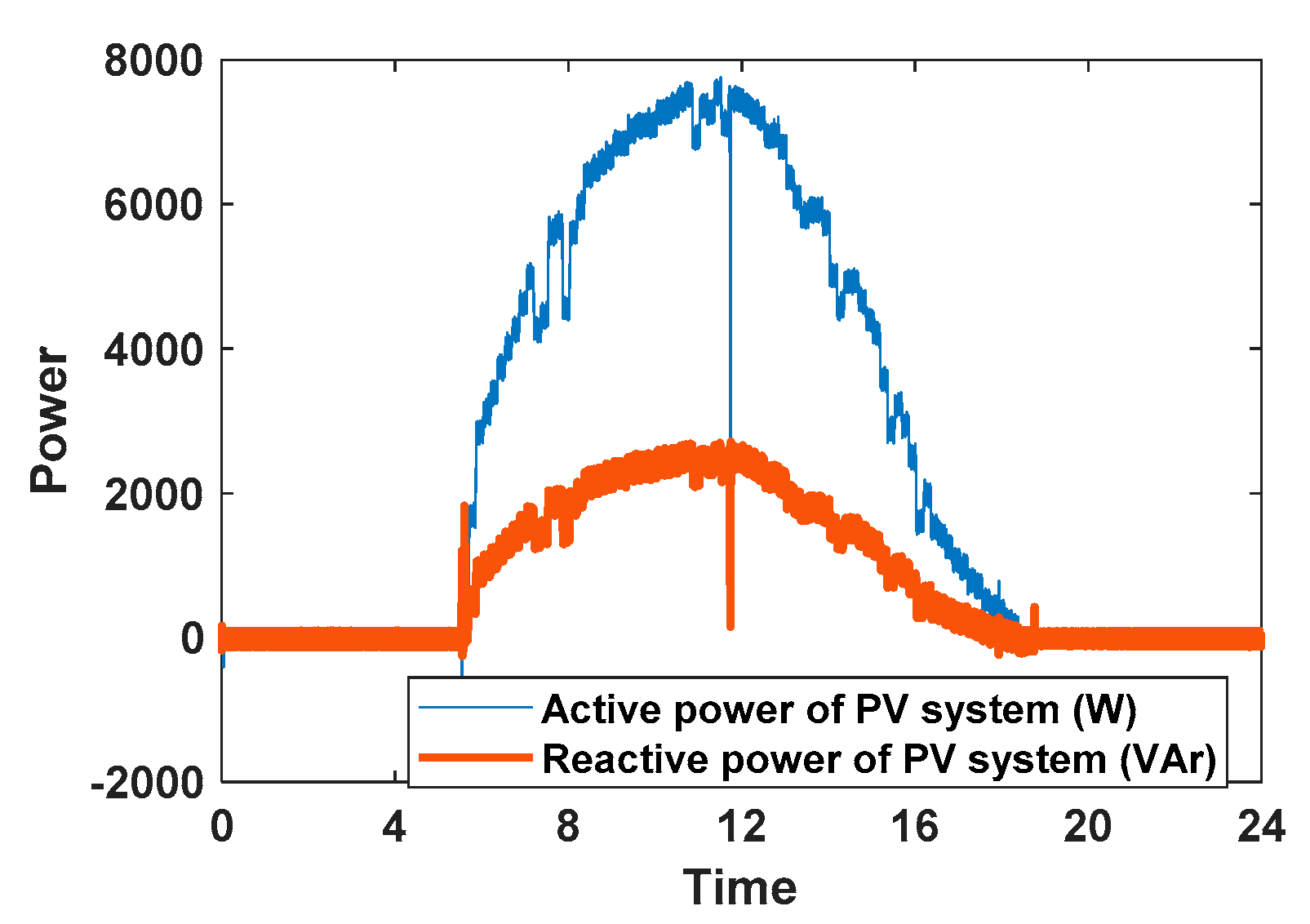
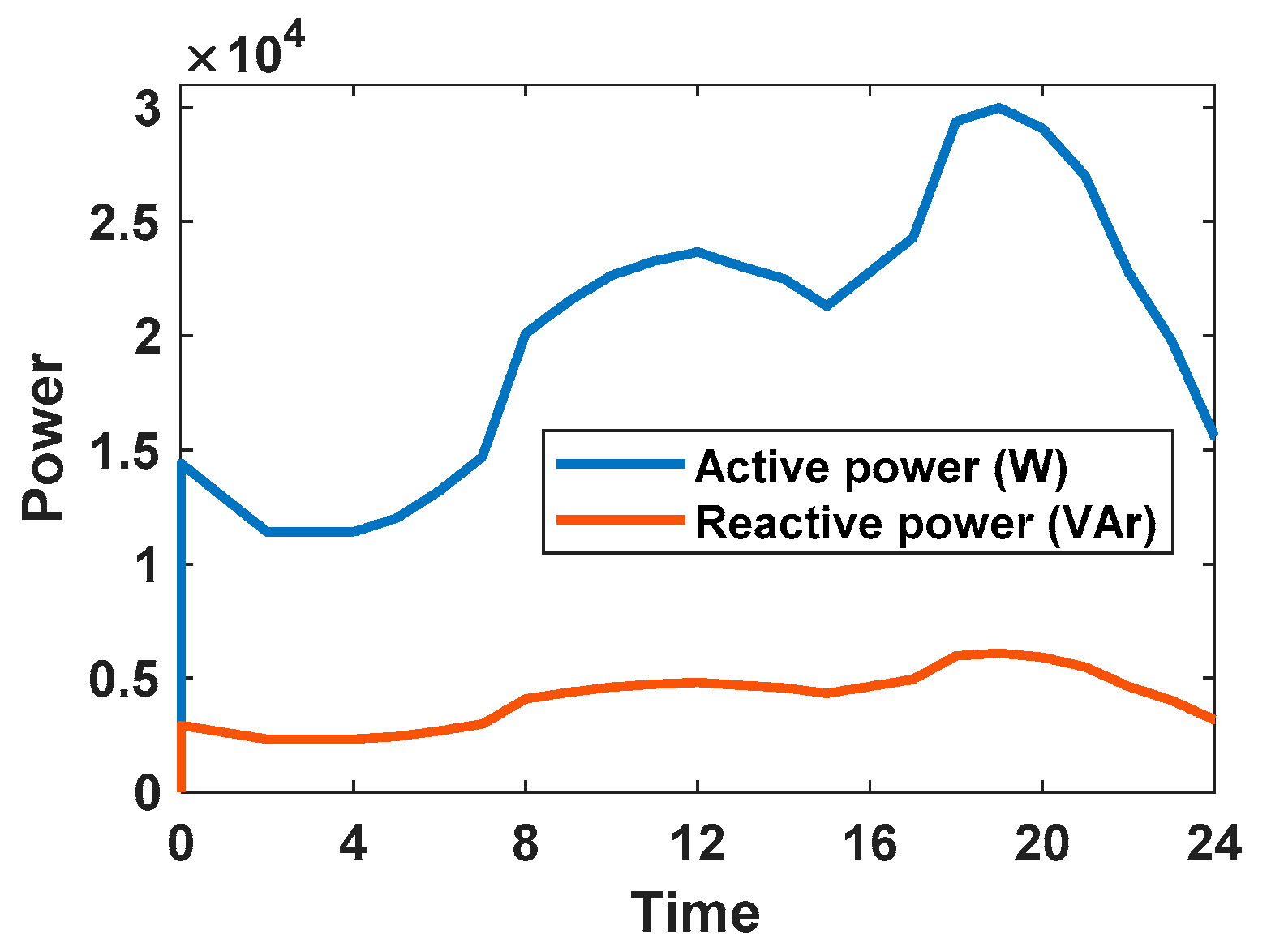
5.2. The Simulation Results in 24 H
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Soshinskaya, M.; Crijns-Graus, W.H.J.; Guerrero, J.M.; Vasquez, J.C. Microgrids: Experiences, barriers and success factors. Renew. Sustain. Energy Rev. 2014, 40, 659–672. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; Vicuna, L.G.D.; Castilla, M. Hierarchical Control of Droop-Controlled AC and DC Microgrids—A General Approach Toward Standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Karavas, C.-S.; Kyriakarakos, G.; Arvanitis, K.G.; Papadakis, G. A multi-agent decentralized energy management system based on distributed intelligence for the design and control of autonomous polygeneration microgrids. Energy Convers. Manag. 2015, 103, 166–179. [Google Scholar] [CrossRef]
- Atia, R.; Yamada, N. Sizing and Analysis of Renewable Energy and Battery Systems in Residential Microgrids. IEEE Trans. Smart Grid 2016, 7, 1204–1213. [Google Scholar] [CrossRef]
- Yunwei, L.; Vilathgamuwa, D.M.; Chiang, L.P. Design, analysis, and real-time testing of a controller for multibus microgrid system. IEEE Trans. Power Electron. 2004, 19, 1195–1204. [Google Scholar]
- Katiraei, F.; Iravani, M.R. Power Management Strategies for a Microgrid with Multiple Distributed Generation Units. IEEE Trans. Power Syst. 2006, 21, 1821–1831. [Google Scholar] [CrossRef]
- Hatziargyriou, N.; Asano, H.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energy Mag. 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Su, W.; Wang, J. Energy Management Systems in Microgrid Operations. Electr. J. 2012, 25, 45–60. [Google Scholar] [CrossRef]
- Salahi, S.; Bahramara, S. Modeling Operation Problem of Micro-grids Considering Economical, Technical and Environmental issues as Mixed-Integer Non-Linear Programming. Int. J. Renew. Energy Dev. 2016, 5, 139–149. [Google Scholar] [CrossRef]
- Silvente, J.; Kopanos, G.M.; Pistikopoulos, E.N.; Espuña, A. A rolling horizon optimization framework for the simultaneous energy supply and demand planning in microgrids. Appl. Energy 2015, 155, 485–501. [Google Scholar] [CrossRef]
- Wouters, C.; Fraga, E.S.; James, A.M. An energy integrated, multi-microgrid, MILP (mixed-integer linear programming) approach for residential distributed energy system planning—A South Australian case-study. Energy 2015, 85, 30–44. [Google Scholar] [CrossRef]
- Pan, X.; Niu, X.; Yang, X.; Chamollet, N.; Zheng, D. Robust scheduling for microgrid energy management optimization. In Proceedings of the 2016 China International Conference on Electricity Distribution (CICED), Xi’an, China, 10–13 August 2016; pp. 1–5. [Google Scholar]
- Luna, A.C.; Meng, L.; Diaz, N.L.; Graells, M.; Vasquez, J.C.; Guerrero, J.M. Online Energy Management Systems for Microgrids: Experimental Validation and Assessment Framework. IEEE Trans. Power Electron. 2018, 33, 2201–2215. [Google Scholar] [CrossRef]
- Pota, H.R. Droop control for islanded microgrids. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–4. [Google Scholar]
- Tayab, U.B.; Roslan, M.A.B.; Hwai, L.J.; Kashif, M. A review of droop control techniques for microgrid. Renew. Sustain. Energy Rev. 2017, 76, 717–727. [Google Scholar] [CrossRef]
- He, J.; Li, Y.W. Analysis, Design, and Implementation of Virtual Impedance for Power Electronics Interfaced Distributed Generation. IEEE Trans. Ind. Appl. 2011, 47, 2525–2538. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, C.; Dong, L.; Li, Y.; Zhao, J.; Nian, H.; Kong, L. An Enhanced Droop Control Strategy for Accurate Reactive Power Sharing in Islanded Microgrids. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 2352–2356. [Google Scholar]
- Xiao, J.; Setyawan, L.; Wang, P.; Jin, C. Power-Capacity-Based Bus-Voltage Region Partition and Online Droop Coefficient Tuning for Real-Time Operation of DC Microgrids. IEEE Trans. Energy Convers. 2015, 30, 1338–1347. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Berbel, N.; Vicuna, L.G.D.; Matas, J.; Miret, J.; Castilla, M. Droop control method for the parallel operation of online uninterruptible power systems using resistive output impedance. In Proceedings of the Twenty-First Annual IEEE Applied Power Electronics Conference and Exposition, APEC’06., Dallas, TX, USA, 19–23 March 2006; p. 7. [Google Scholar]
- Zhou, J.; Tsai, M.; Cheng, P. Consensus-Based Cooperative Droop Control for Accurate Reactive Power Sharing in Islanded AC Microgrid. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 5151–5157. [Google Scholar]
- Gai, B.; Pan, Z. Online transmission line impedance parameter identification for distributed generation. In Proceedings of the 2016 19th International Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan, 13–16 November 2016; pp. 1–5. [Google Scholar]
- Raghami, A.; Ameli, M.T.; Hamzeh, M. Online Droop Tuning of a Multi-DG Microgrid Using Cuckoo Search Algorithm. Electr. Power Compon. Syst. 2015, 43, 1583–1595. [Google Scholar] [CrossRef]
- Shokoohi, S.; Sabori, F.; Bevrani, H. Secondary voltage and frequency control in islanded microgrids: Online ANN tuning approach. In Proceedings of the 2014 Smart Grid Conference (SGC), Tehran, Iran, 9–10 December 2014; pp. 1–6. [Google Scholar]
- Habibi, F.; Shafiee, Q.; Bevrani, H. Online generalized droop-based demand response for frequency control in islanded microgrids. Electr. Eng. 2019, 101, 409–420. [Google Scholar] [CrossRef]
- Tran, Q.T.T.; di Silvestre, M.L.; Sanseverino, E.R.; Zizzo, G.; Pham, T. Driven Primary Regulation for Minimum Power Losses Operation in Islanded Microgrids. Energies 2018, 11, 2890. [Google Scholar] [CrossRef]
- Bacic, M. On hardware-in-the-loop simulation. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 15 December 2005; pp. 3194–3198. [Google Scholar]
- Riva Sanseverino, E.; Quynh, T.T.; Di Silvestre, M.L.; Zizzo, G.; Ninh, N.Q.; Luna, A.C.; Guerrero, J.M. Optimal power flow for technically feasible energy management systems in islanded microgrids. In Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016; pp. 1–6. [Google Scholar]
- Karegowda, A.G.; Prasad, M. A Survey of Applications of Glowworm Swarm Optimization Algorithm. In IJCA Proceedings on International Conference on Computing and information Technology 2013 IC2IT; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Kaipa, K.N.; Ghose, D. Glowworm Swarm Optimization: Theory, Algorithms, and Applications; Springer: Cham, Switzerland, 2017; Volume 698. [Google Scholar]
- Murty, P.S.R. Chapter 10—Power Flow Studies. In Power Systems Analysis, 2nd ed.; Murty, P.S.R., Ed.; Butterworth-Heinemann: Boston, MA, USA, 2017; pp. 205–276. [Google Scholar]
- The Multi Microgrid Platform PRISMES. Available online: http://www.ines-solaire.org/ (accessed on 5 December 2019).
- Sun, Y.; Huang, W.; Wang, G.; Wenjun, W.; Wang, D.; Li, Z. Study of control strategy of DG based on nonlinear droop characteristic. In Proceedings of the 2012 China International Conference on Electricity Distribution, Shanghai, China, 10–14 September 2012; pp. 1–4. [Google Scholar]
- Arani, A.A.K.; Gharehpetian, G.B. A new control method for improving transient response of parallel VSIs in islanded microgrids. In Proceedings of the 2014 Smart Grid Conference (SGC), Tehran, Iran, 9–10 December 2014; pp. 1–5. [Google Scholar]
- Rahimpour, H.; Mitchell, S.; Rahimpour, S. Online monitoring of power transformers using impulse frequency response analysis. In Proceedings of the 2017 Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 2–4 May 2017; pp. 1390–1394. [Google Scholar]
- Guerrero, J.M.; Chandorkar, M.; Lee, T.; Loh, P.C. Advanced Control Architectures for Intelligent Microgrids—Part I: Decentralized and Hierarchical Control. IEEE Trans. Ind. Electron. 2013, 60, 1254–1262. [Google Scholar] [CrossRef]




| Digital I/O | FPGA |
|---|---|
| Number of channels: 256 input/output configurable in 1- to 32-bit groups Compatibility: 3.3 V Power-on state: High impedance | Device: Xilinx Spartan 3 I/O Package: fg676 Embedded RAM available: 216 Kbytes Clock: 100 MHz Platform options: XC3S5000 Logic slices: 33,280 Equivalent logic cells: 74,880 Available I/O lines: 489 |
| Bus | |
| Dimensions (not including connectors): PCI-Express x1 Data transfer: 2.5 Gbit/s |
| From | To | R (Ohm/km) | X (Ohm/km) | L (km) |
|---|---|---|---|---|
| 1 | 3 | 0.43 | 0.14444 | 1 |
| 2 | 3 | 0.43 | 0.14444 | 2.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, Q.T.T.; Riva Sanseverino, E.; Zizzo, G.; Di Silvestre, M.L.; Nguyen, T.L.; Tran, Q.-T. Real-Time Minimization Power Losses by Driven Primary Regulation in Islanded Microgrids. Energies 2020, 13, 451. https://doi.org/10.3390/en13020451
Tran QTT, Riva Sanseverino E, Zizzo G, Di Silvestre ML, Nguyen TL, Tran Q-T. Real-Time Minimization Power Losses by Driven Primary Regulation in Islanded Microgrids. Energies. 2020; 13(2):451. https://doi.org/10.3390/en13020451
Chicago/Turabian StyleTran, Quynh T.T, Eleonora Riva Sanseverino, Gaetano Zizzo, Maria Luisa Di Silvestre, Tung Lam Nguyen, and Quoc-Tuan Tran. 2020. "Real-Time Minimization Power Losses by Driven Primary Regulation in Islanded Microgrids" Energies 13, no. 2: 451. https://doi.org/10.3390/en13020451
APA StyleTran, Q. T. T., Riva Sanseverino, E., Zizzo, G., Di Silvestre, M. L., Nguyen, T. L., & Tran, Q.-T. (2020). Real-Time Minimization Power Losses by Driven Primary Regulation in Islanded Microgrids. Energies, 13(2), 451. https://doi.org/10.3390/en13020451