SOH and RUL Prediction of Lithium-Ion Batteries Based on Gaussian Process Regression with Indirect Health Indicators
Abstract
1. Introduction
2. Extraction of Indirect Health Indicators
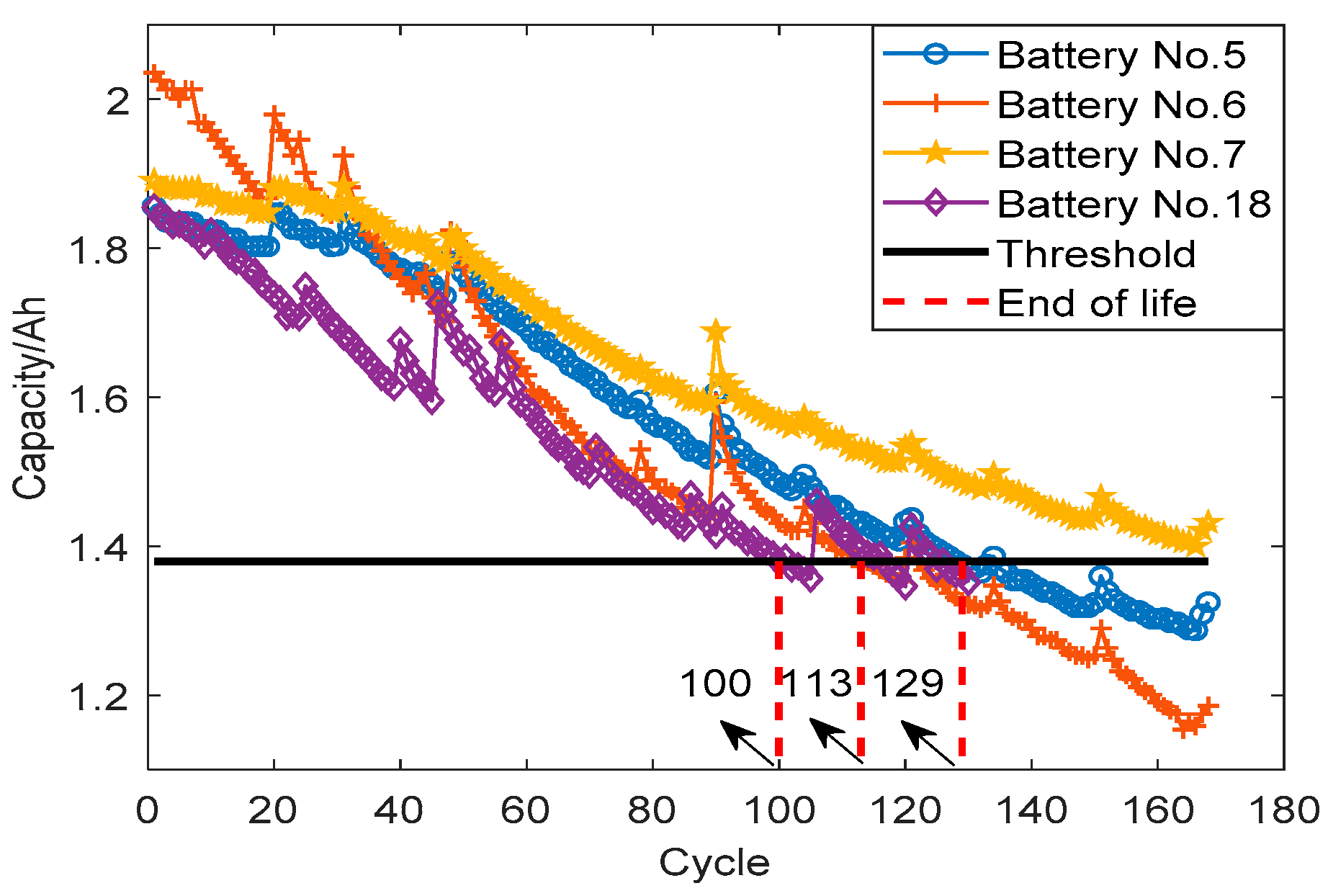
2.1. Experimental Data
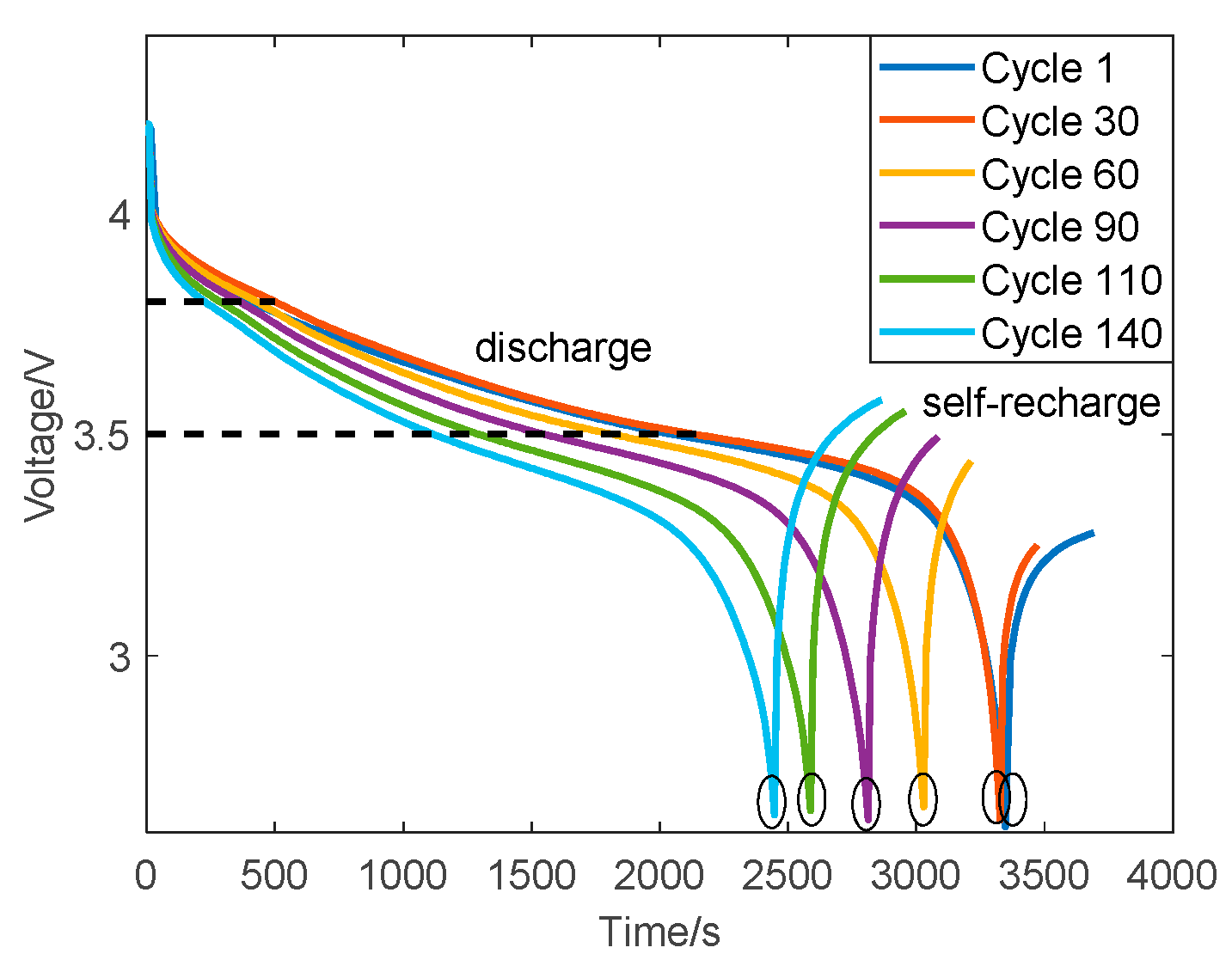
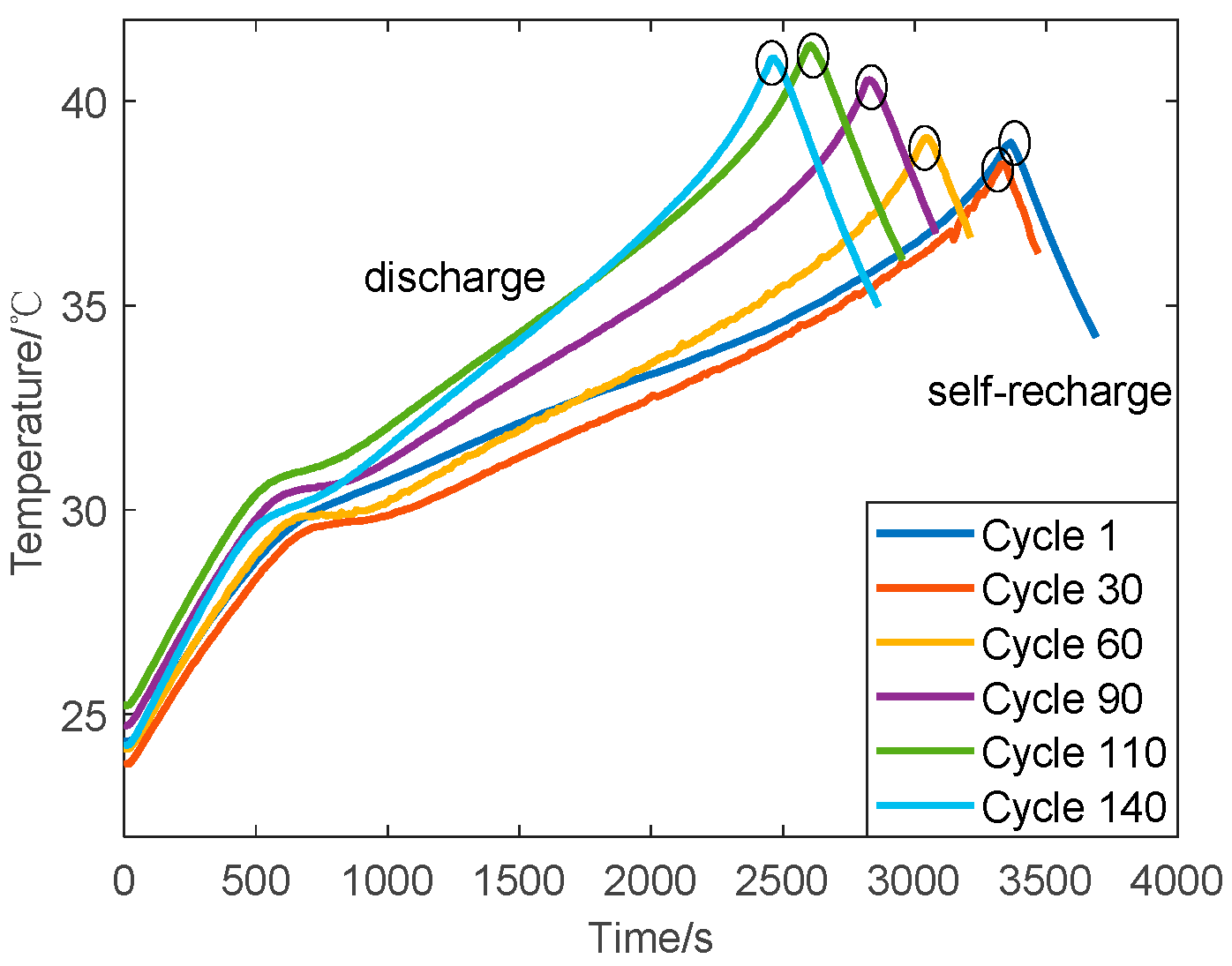
2.2. Extraction of Indirect Health Indicators
2.3. Grey Relational Analysis
3. Method
3.1. Gaussian Process Regression
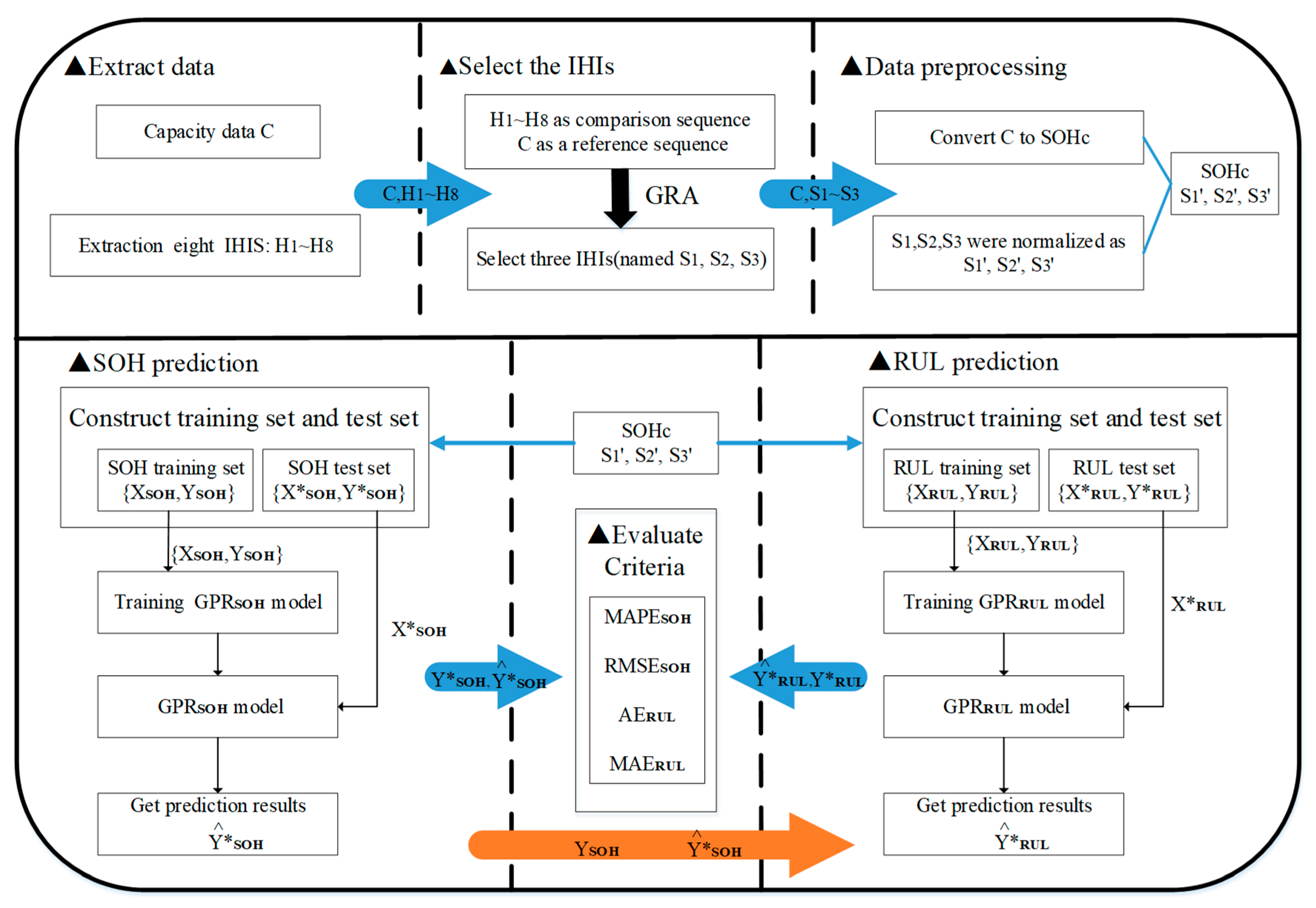
3.2. Overall Prediction Process
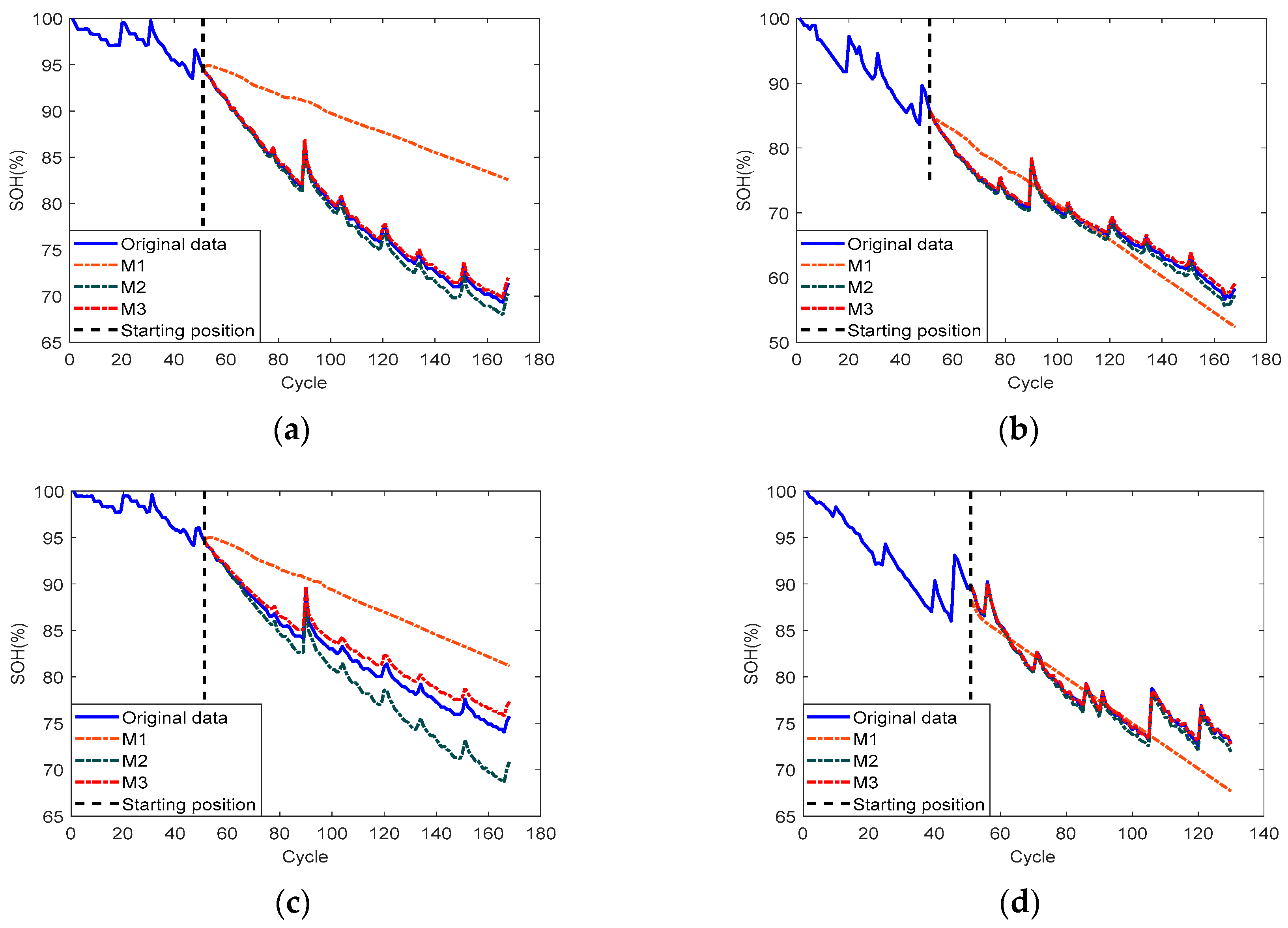
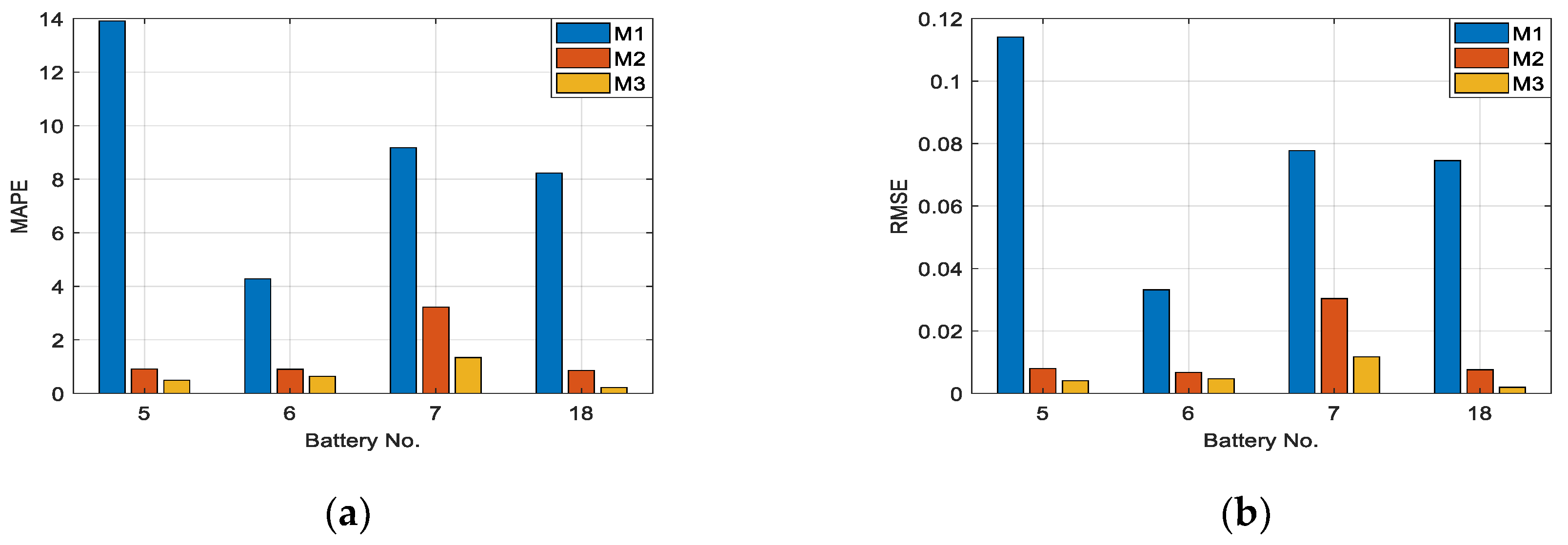
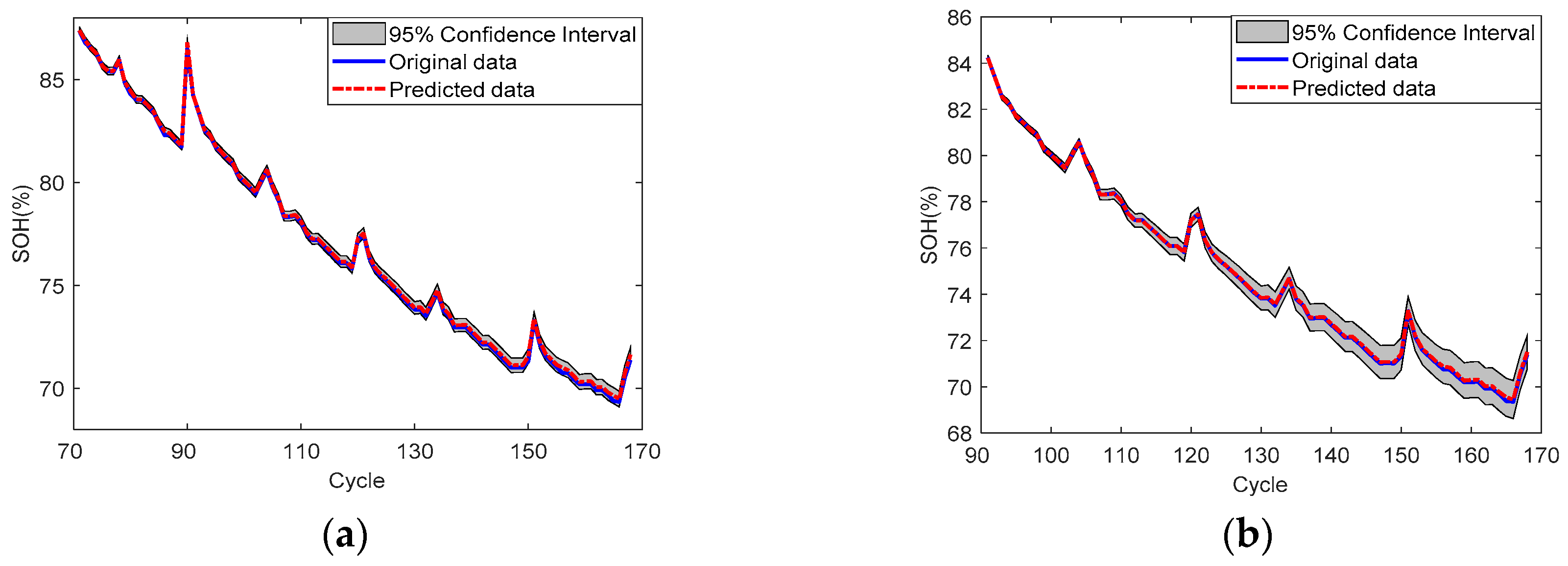
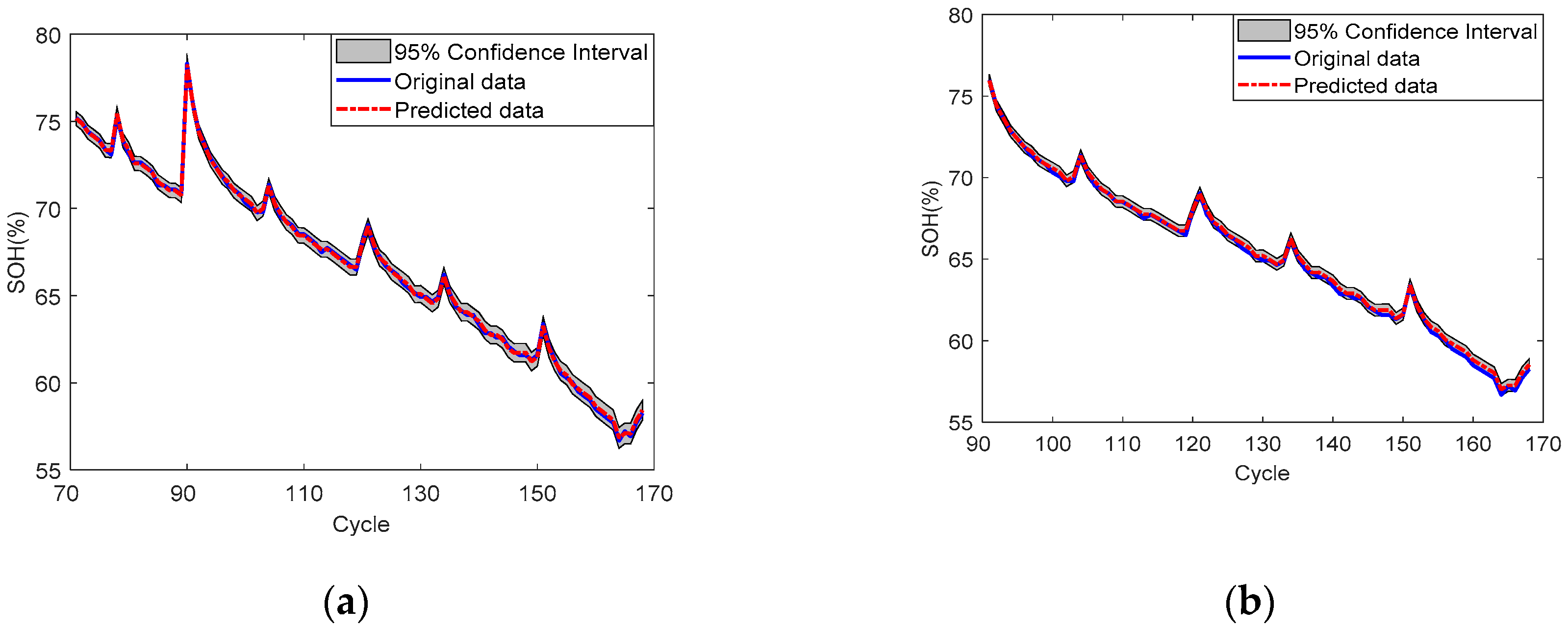
4. Experimental Analysis
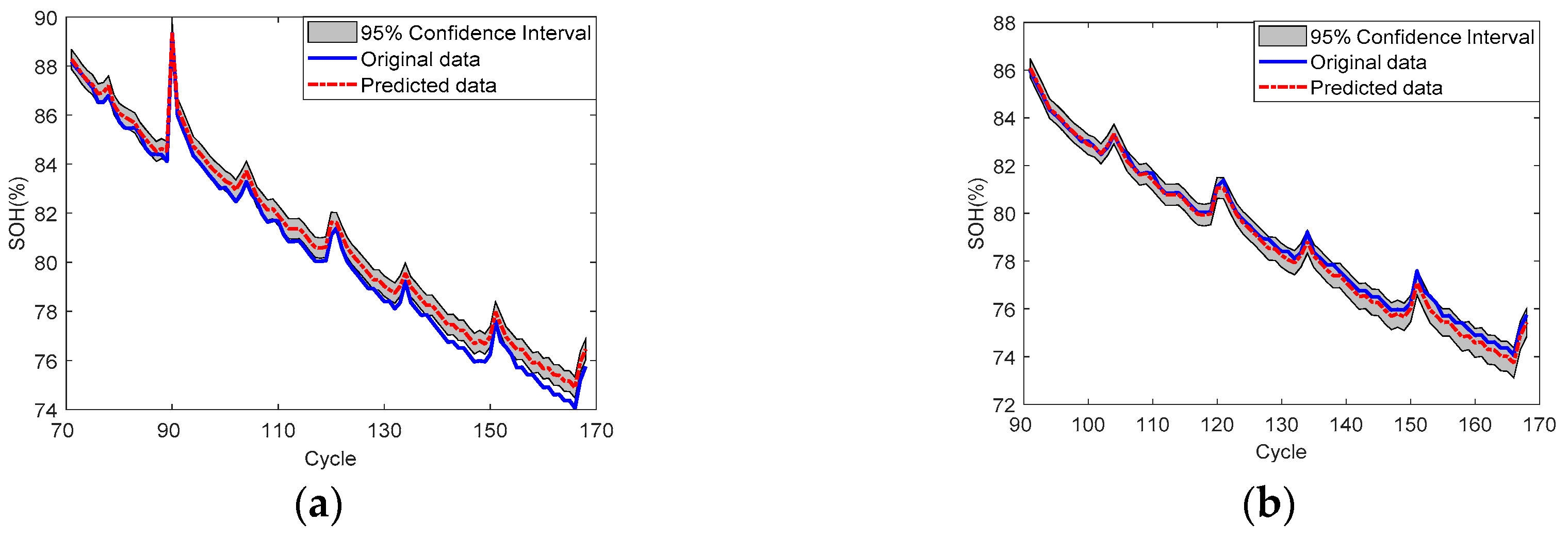
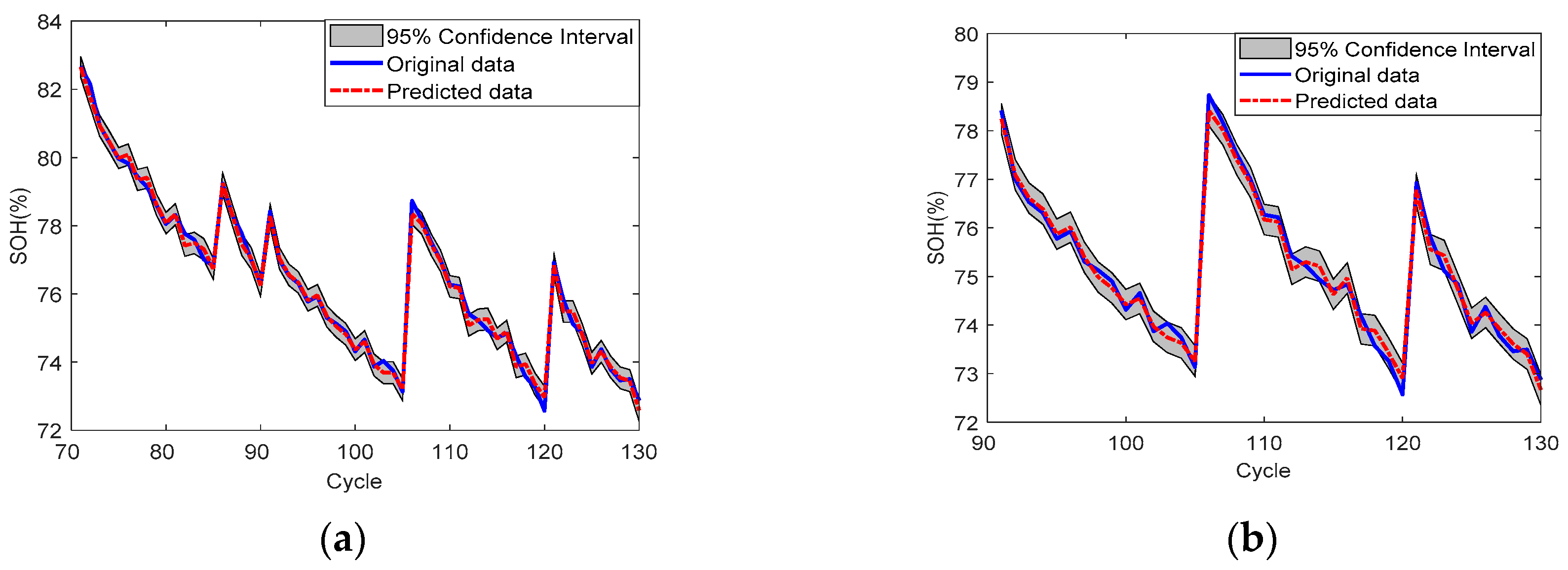
4.1. SOH Prediction
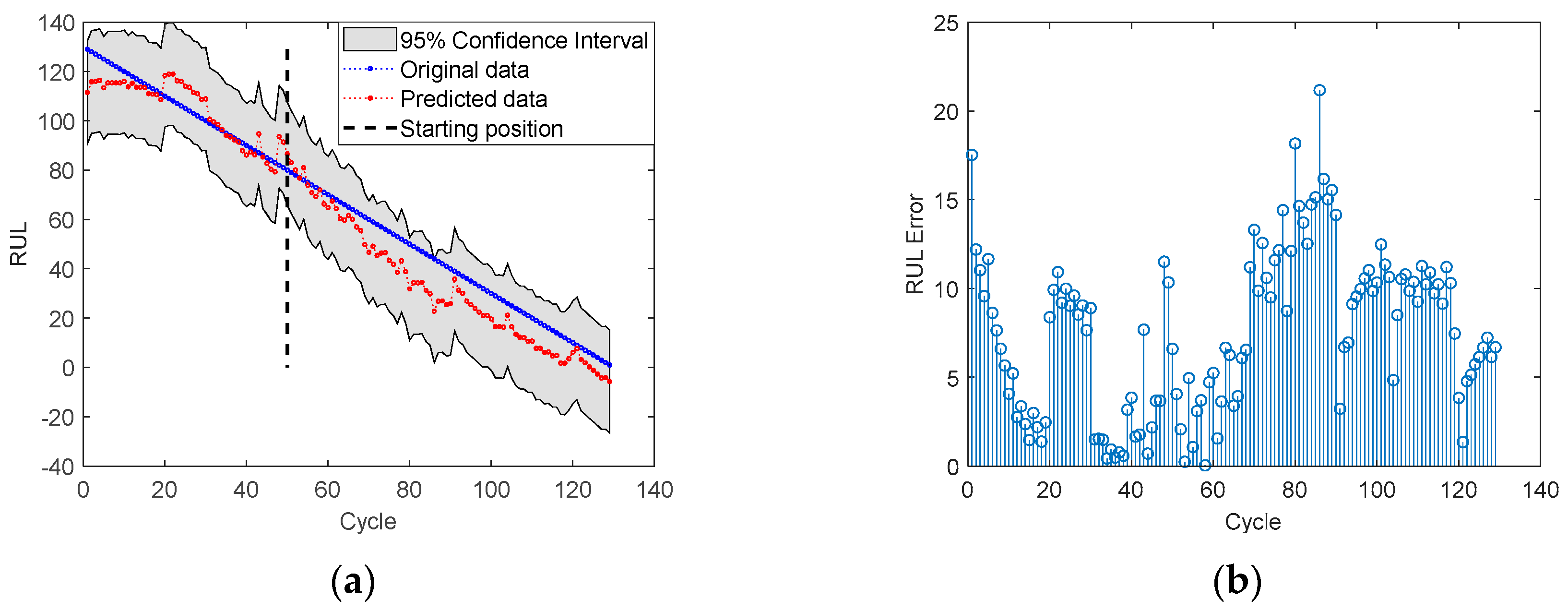
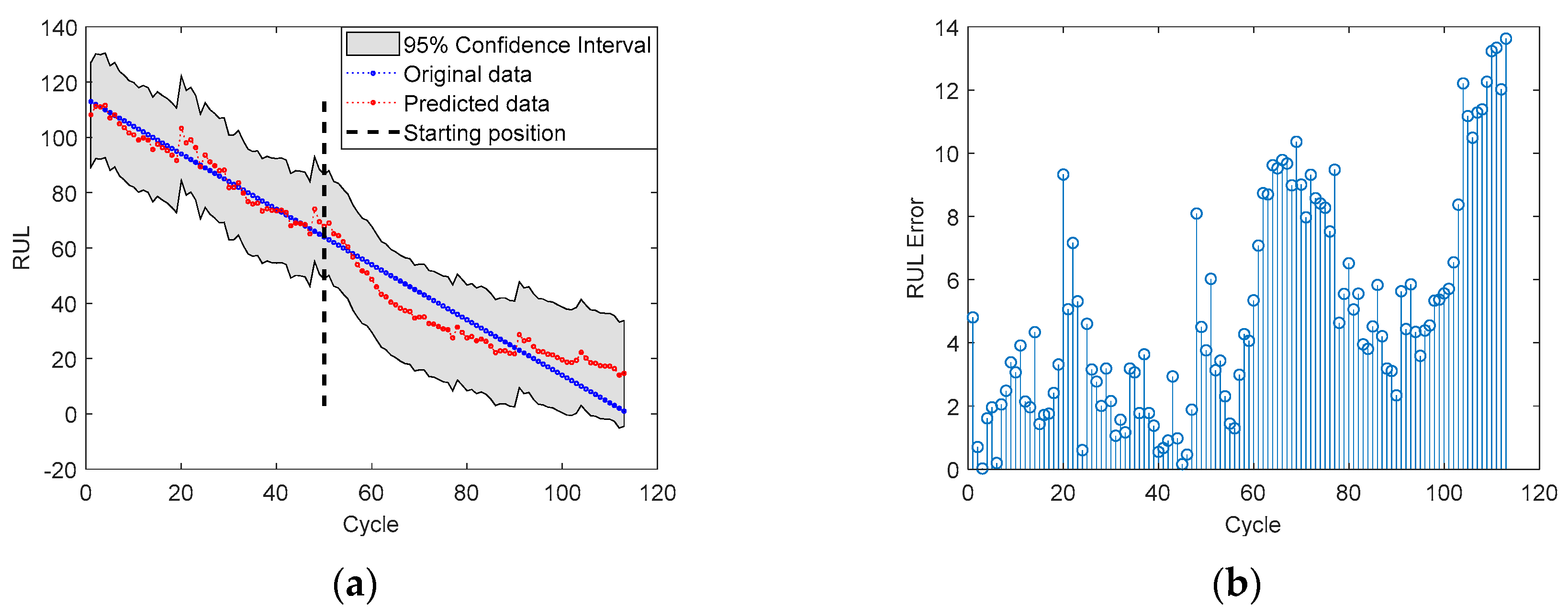
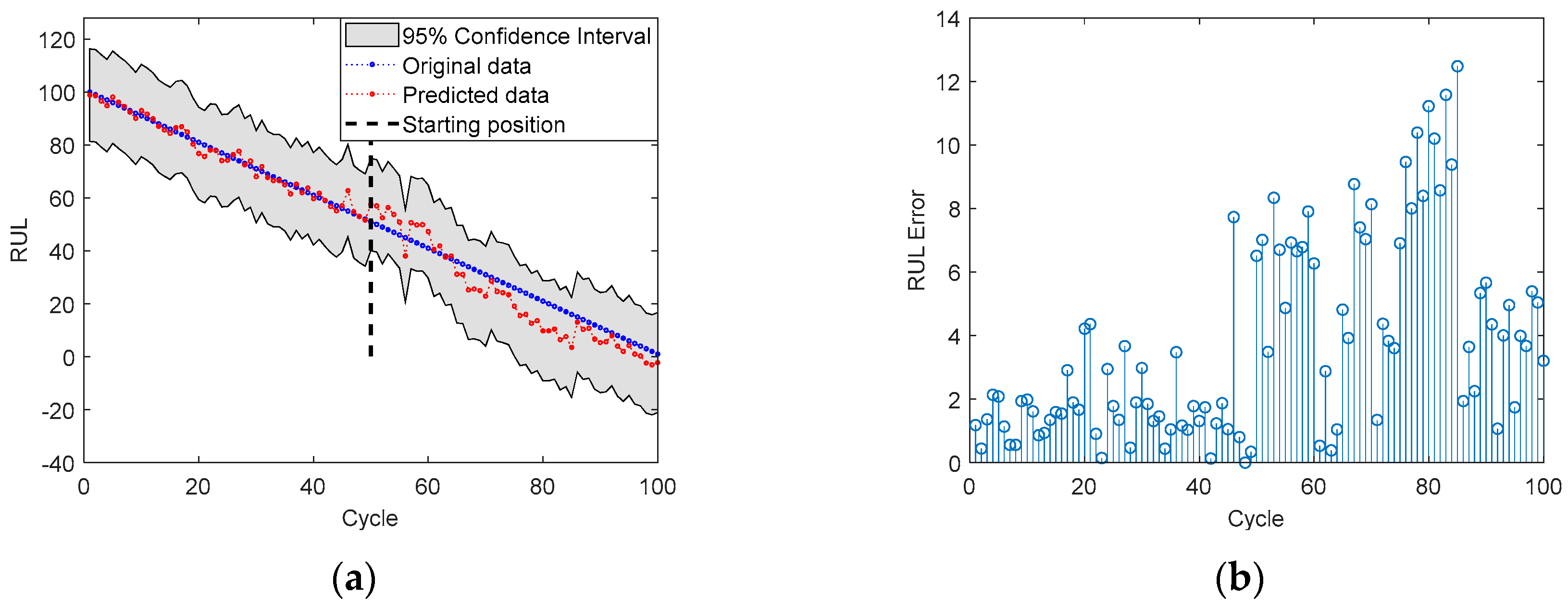
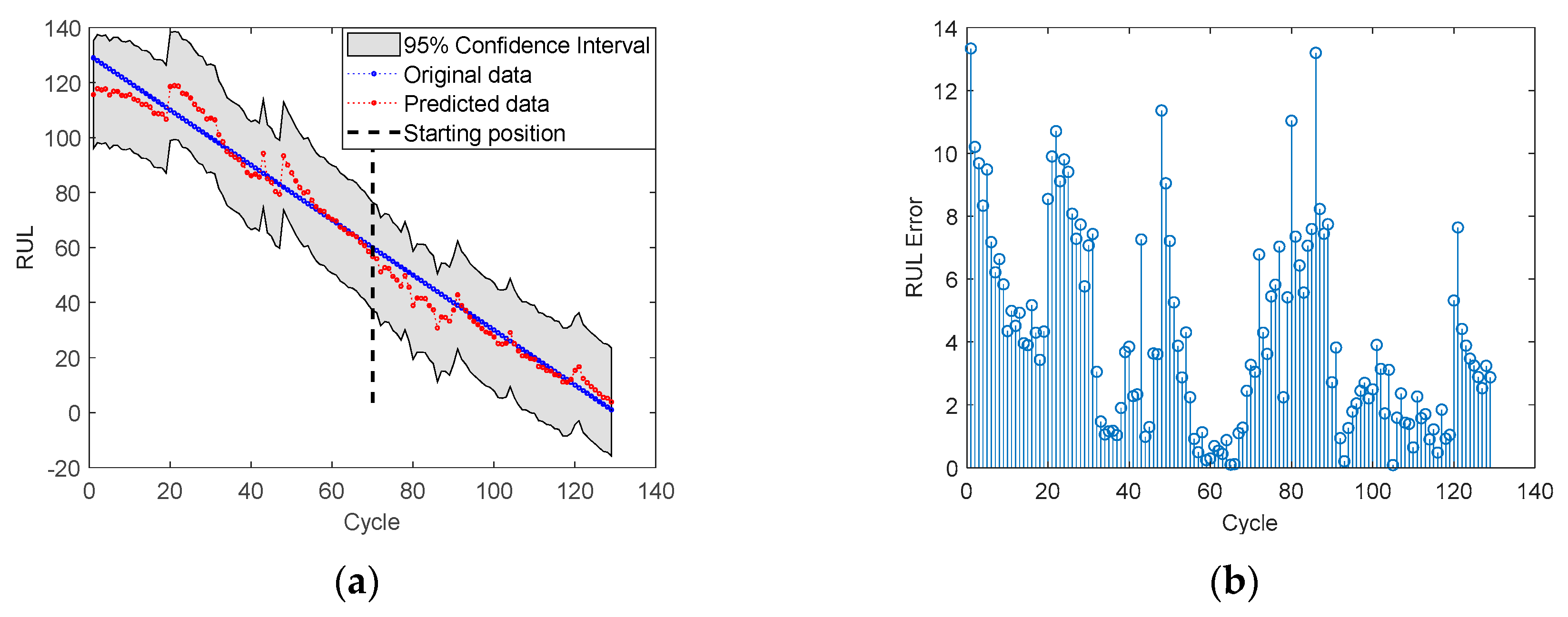
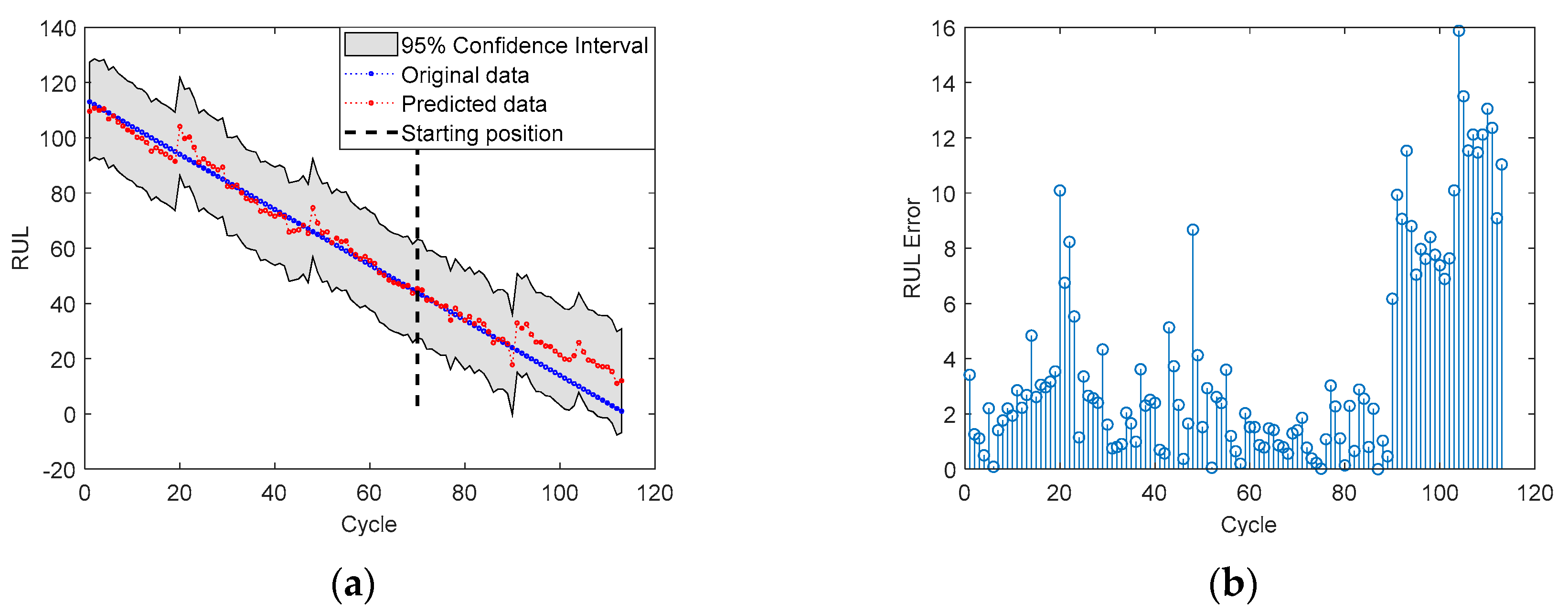
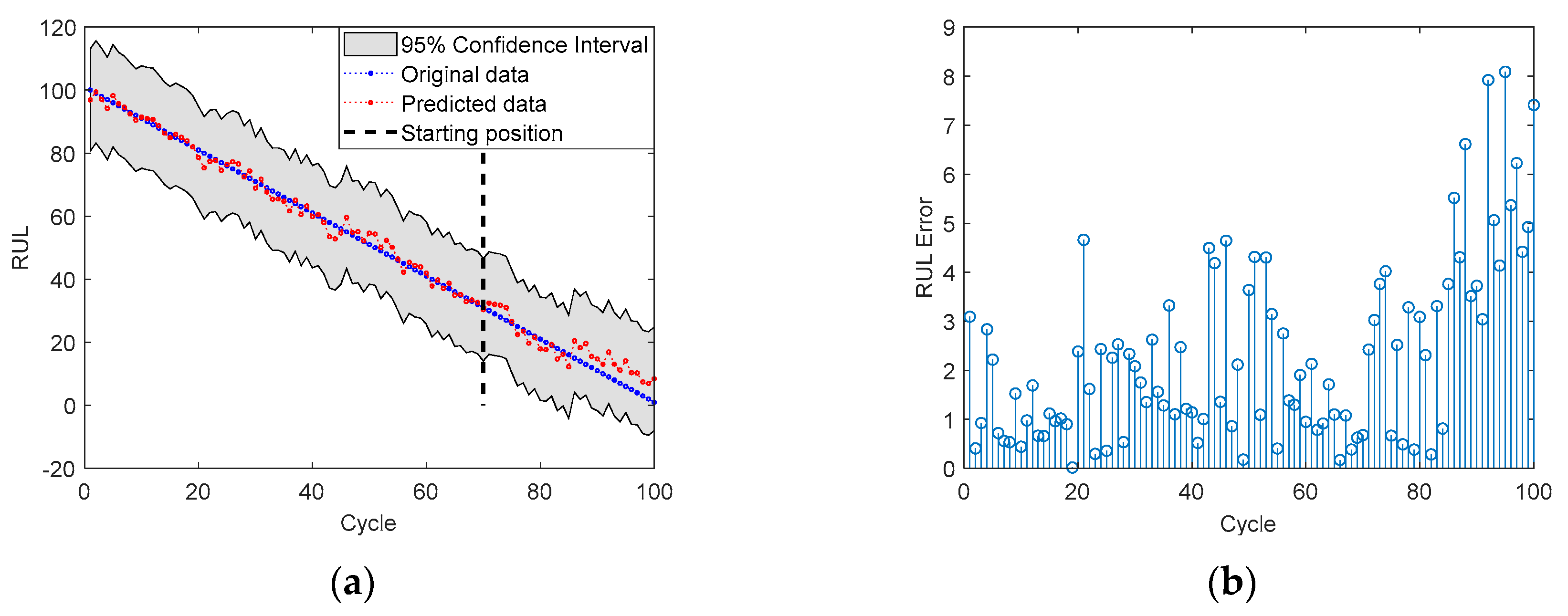
4.2. RUL Prediction
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Takami, N.; Inagaki, H.; Tatebayashi, Y.; Saruwatari, H.; Honda, K.; Egusa, S. High-power and long-life lithium-ion batteries using lithium titanium oxide anode for automotive and stationary power applications. J. Power Sources 2013, 244, 469–475. [Google Scholar] [CrossRef]
- Hu, X.; Zou, C.; Zhang, C.; Li, Y. Technological Developments in Batteries: A Survey of Principal Roles, Types, and Management Needs. IEEE Power Energy Mag. 2017, 15, 20–31. [Google Scholar] [CrossRef]
- Doughty, D.H.; Roth, E.P. A General Discussion of Li Ion Battery Safety. Interface Mag. 2012, 21, 37–44. [Google Scholar]
- Wang, Q.; Mao, B.; Stoliarov, S.I.; Sun, J. A review of lithium ion battery failure mechanisms and fire prevention strategies. Prog. Energy Combust. Sci. 2019, 73, 95–131. [Google Scholar] [CrossRef]
- Su, C.; Chen, H.J. A review on prognostics approaches for remaining useful life of lithium-ion battery. IOP Conf. Ser. Earth Environ. Sci. 2017, 93, 012040. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Doyle, M.; Newman, J. Modeling the performance of rechargeable lithium-based cells: Design correlations for limiting cases. J. Power Sources 1995, 54, 46–51. [Google Scholar] [CrossRef]
- Doyle, M.; Newman, J.; Gozdz, A.S.; Schmutz, C.N.; Tarascon, J.M. Comparison of Modeling Predictions with Experimental Data from Plastic Lithium Ion Cells. J. Electrochem. Soc. 1996, 143, 1890–1903. [Google Scholar] [CrossRef]
- Safari, M.; Morcrette, M.; Teyssot, A.; Delacourt, C. Multimodal Physics-Based Aging Model for Life Prediction of Li-Ion Batteries. J. Electrochem. Soc. 2009, 156, A145. [Google Scholar] [CrossRef]
- Abe, T.; Fukuda, H.; Iriyama, Y.; Ogumi, Z. Solvated Li-Ion Transfer at Interface Between Graphite and Electrolyte. J. Electrochem. Soc. 2004, 151, A1120. [Google Scholar] [CrossRef]
- Xu, K.; von Cresce, A.; Lee, U. Differentiating Contributions to “Ion Transfer” Barrier from Interphasial Resistance and Li + Desolvation at Electrolyte/Graphite Interface. Langmuir 2010, 26, 11538–11543. [Google Scholar] [CrossRef] [PubMed]
- Sankarasubramanian, S.; Krishnamurthy, B. A capacity fade model for lithium-ion batteries including diffusion and kinetics. Electrochim. Acta 2012, 70, 248–254. [Google Scholar] [CrossRef]
- Ramadesigan, V.; Chen, K.; Burns, N.A.; Boovaragavan, V.; Braatz, R.D.; Subramanian, V.R. Parameter Estimation and Capacity Fade Analysis of Lithium-Ion Batteries Using Reformulated Models. J. Electrochem. Soc. 2011, 158, A1048. [Google Scholar] [CrossRef]
- Ashwin, T.R.; Chung, Y.M.; Wang, J. Capacity fade modelling of lithium-ion battery under cyclic loading conditions. J. Power Sources 2016, 328, 586–598. [Google Scholar] [CrossRef]
- Johnson, V.H. Battery performance models in ADVISOR. J. Power Sources 2002, 110, 321–329. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Y.; Chen, Z. Degradation model and cycle life prediction for lithium-ion battery used in hybrid energy storage system. Energy 2019, 166, 796–806. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, D.; Zhang, X.; Chen, Z. Probability based remaining capacity estimation using data-driven and neural network model. J. Power Sources 2016, 315, 199–208. [Google Scholar] [CrossRef]
- Wang, D.; Miao, Q.; Pecht, M. Prognostics of lithium-ion batteries based on relevance vectors and a conditional three-parameter capacity degradation model. J. Power Sources 2013, 239, 253–264. [Google Scholar] [CrossRef]
- Li, Y.; Liu, K.; Foley, A.M.; Berecibar, M.; Nanini-Maury, E.; van Mierlo, J.; Hoster, H.E. Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review. Renew. Sustain. Energy Rev. 2019, 113, 109254. [Google Scholar] [CrossRef]
- Long, B.; Xian, W.; Jiang, L.; Liu, Z. An improved autoregressive model by particle swarm optimization for prognostics of lithium-ion batteries. Microelectron. Reliab. 2013, 53, 821–831. [Google Scholar] [CrossRef]
- Andre, D.; Nuhic, A.; Soczka-Guth, T.; Sauer, D.U. Comparative study of a structured neural network and an extended Kalman filter for state of health determination of lithium-ion batteries in hybrid electricvehicles. Eng. Appl. Artif. Intell. 2013, 26, 951–961. [Google Scholar] [CrossRef]
- Gao, D.; Huang, M. Prediction of Remaining Useful Life of Lithium-ion Battery based on Multi-kernel Support Vector Machine with Particle Swarm Optimization. J. Power Electron. 2017, 17, 1288–1297. [Google Scholar]
- He, Y.J.; Shen, J.N.; Shen, J.F.; Ma, Z.F. State of health estimation of lithium-ion batteries: A multiscale Gaussian process regression modeling approach. AIChE J. 2015, 61, 1589–1600. [Google Scholar] [CrossRef]
- Richardson, R.R.; Osborne, M.A.; Howey, D.A. Gaussian process regression for forecasting battery state of health. J. Power Sources 2017, 357, 209–219. [Google Scholar] [CrossRef]
- Liu, D.; Pang, J.; Zhou, J.; Pecht, M. Prognostics for state of health estimation of lithium-ion batteries based on combination Gaussian process functional regression. Microelectron. Reliab. 2013, 53, 832–839. [Google Scholar] [CrossRef]
- Peng, Y.; Hou, Y.; Song, Y.; Pang, J.; Liu, D. Lithium-Ion Battery Prognostics with Hybrid Gaussian Process Function Regression. Energies 2018, 11, 1420. [Google Scholar] [CrossRef]
- Yu, J. State of health prediction of lithium-ion batteries: Multiscale logic regression and Gaussian process regression ensemble. Reliab. Eng. Syst. Saf. 2018, 174, 82–95. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, X.; Pan, R.; Wang, Y.; Chen, Z. A novel Gaussian process regression model for state-of-health estimation of lithium-ion battery using charging curve. J. Power Sources 2018, 384, 387–395. [Google Scholar] [CrossRef]
- Saha, B.; Goebel, K. Battery Data Set. Available online: https://ti.arc.nasa.gov/tech/dash/groups/pcoe/prognostic-data-repository/ (accessed on 10 May 2019).
- Razavi-Far, R.; Chakrabarti, S.; Saif, M. Multi-step-ahead prediction techniques for Lithium-ion batteries condition prognosis. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, SMC 2016–Conference Proceedings, Budapest, Hungary, 9–12 October 2016; pp. 4675–4680. [Google Scholar]
- Coleman, M.; Kwan, L.C.; Chunbo, Z.; Hurley, W.G. State-of-Charge Determination From EMF Voltage Estimation: Using Impedance, Terminal Voltage, and Current for Lead-Acid and Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2007, 54, 2550–2557. [Google Scholar] [CrossRef]
- Sun, Y.H.; Jou, H.L.; Wu, J.C. Aging Estimation Method for Lead-Acid Battery. IEEE Trans. Energy Convers. 2011, 26, 264–271. [Google Scholar] [CrossRef]
- Liu, D.; Zhou, J.; Liao, H.; Peng, Y.; Peng, X. A Health Indicator Extraction and Optimization Framework for Lithium-Ion Battery Degradation Modeling and Prognostics. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 915–928. [Google Scholar]
- Li, X.; Wang, Z.; Zhang, L.; Zou, C.; Dorrell, D.D. State-of-health estimation for Li-ion batteries by combing the incremental capacity analysis method with grey relational analysis. J. Power Sources 2019, 410–411, 106–114. [Google Scholar] [CrossRef]
- Burnaev, E.V.; Panov, M.E.; Zaytsev, A.A. Regression on the basis of nonstationary Gaussian processes with Bayesian regularization. J. Commun. Technol. Electron. 2016, 61, 661–671. [Google Scholar] [CrossRef]
- Shi, J.Q.; Wang, B.; Murray-Smith, R.; Titterington, D.M. Gaussian process functional regression Modeling for batch data. Biometric 2007, 63, 714–723. [Google Scholar] [CrossRef]
- Pang, X.; Huang, R.; Wen, J.; Shi, Y.; Jia, J.; Zeng, J. A Lithium-ion Battery RUL Prediction Method Considering the Capacity Regeneration Phenomenon. Energies 2019, 12, 2247. [Google Scholar] [CrossRef]
| Indirect Health Indicators | The Mean Value of the Correlation Coefficients | |||
|---|---|---|---|---|
| No. 5 | No. 6 | No. 7 | No. 18 | |
| IHI1 | 0.9928 | 0.9908 | 0.9815 | 0.9879 |
| IHI2 | 0.9886 | 0.9920 | 0.9712 | 0.9828 |
| IHI3 | 0.9386 | 0.9101 | 0.9624 | 0.9598 |
| IHI4 | 0.8050 | 0.8819 | 0.7814 | 0.7426 |
| IHI5 | 0.7421 | 0.8205 | 0.6968 | 0.6554 |
| IHI6 | 0.5717 | 0.5909 | 0.5671 | 0.6192 |
| IHI7 | 0.5067 | 0.5251 | 0.5108 | 0.5753 |
| IHI8 | 0.5120 | 0.4998 | 0.5250 | 0.5618 |
| Model | Model Description |
|---|---|
| M1 | GPR direct prediction using a linear function as the mean function |
| M2 | GPR indirect prediction with the mean function of 0 |
| M3 | GPR indirect prediction using a linear function as the mean function |
| Battery | Prediction SP | MAPE | RMSE |
|---|---|---|---|
| No. 5 | 51 | 0.4890 | 0.0041 |
| 71 | 0.1187 | 0.0011 | |
| 91 | 0.0565 | 0.0005 | |
| No. 6 | 51 | 0.6413 | 0.0047 |
| 71 | 0.1642 | 0.0012 | |
| 91 | 0.2179 | 0.0019 | |
| No. 7 | 51 | 1.3367 | 0.0117 |
| 71 | 0.6310 | 0.0054 | |
| 91 | 0.2517 | 0.0024 | |
| No. 18 | 51 | 0.2067 | 0.0020 |
| 71 | 0.1685 | 0.0018 | |
| 91 | 0.1898 | 0.0019 |
| Evaluate Criteria | Model | Battery | ||
|---|---|---|---|---|
| No. 5 | No. 6 | No. 7 | ||
| RMSE | GPR-CF | 0.0095 | 0.0149 | 0.0078 |
| M3 | 0.0016 | 0.0017 | 0.0037 | |
| Battery | Prediction SP | MAE of RUL Prediction |
|---|---|---|
| No. 5 | 51 | 8.79 |
| 71 | 3.31 | |
| No. 6 | 51 | 6.89 |
| 71 | 6.09 | |
| No. 18 | 51 | 5.71 |
| 71 | 3.45 |
| Battery | Prediction SP | Model | |
|---|---|---|---|
| AE of MLR-GPR | AE of IHIs-GPR | ||
| No. 5 | 50 | 26 | 13 |
| 60 | 24 | 6 | |
| 70 | 18 | 9 | |
| 80 | 14 | 6 | |
| 90 | 13 | 4 | |
| No. 6 | 50 | 39 | 5 |
| 60 | 40 | 2 | |
| 70 | 23 | 1 | |
| 80 | 16 | 2 | |
| 90 | 14 | 3 | |
| No. 18 | 50 | 18 | 8 |
| 60 | 8 | 2 | |
| 70 | 7 | 1 | |
| 80 | 5 | 2 | |
| 90 | 4 | 3 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, J.; Liang, J.; Shi, Y.; Wen, J.; Pang, X.; Zeng, J. SOH and RUL Prediction of Lithium-Ion Batteries Based on Gaussian Process Regression with Indirect Health Indicators. Energies 2020, 13, 375. https://doi.org/10.3390/en13020375
Jia J, Liang J, Shi Y, Wen J, Pang X, Zeng J. SOH and RUL Prediction of Lithium-Ion Batteries Based on Gaussian Process Regression with Indirect Health Indicators. Energies. 2020; 13(2):375. https://doi.org/10.3390/en13020375
Chicago/Turabian StyleJia, Jianfang, Jianyu Liang, Yuanhao Shi, Jie Wen, Xiaoqiong Pang, and Jianchao Zeng. 2020. "SOH and RUL Prediction of Lithium-Ion Batteries Based on Gaussian Process Regression with Indirect Health Indicators" Energies 13, no. 2: 375. https://doi.org/10.3390/en13020375
APA StyleJia, J., Liang, J., Shi, Y., Wen, J., Pang, X., & Zeng, J. (2020). SOH and RUL Prediction of Lithium-Ion Batteries Based on Gaussian Process Regression with Indirect Health Indicators. Energies, 13(2), 375. https://doi.org/10.3390/en13020375






