A Novel State of Charge Estimating Scheme Based on an Air-Gap Fiber Interferometer Sensor for the Vanadium Redox Flow Battery
Abstract
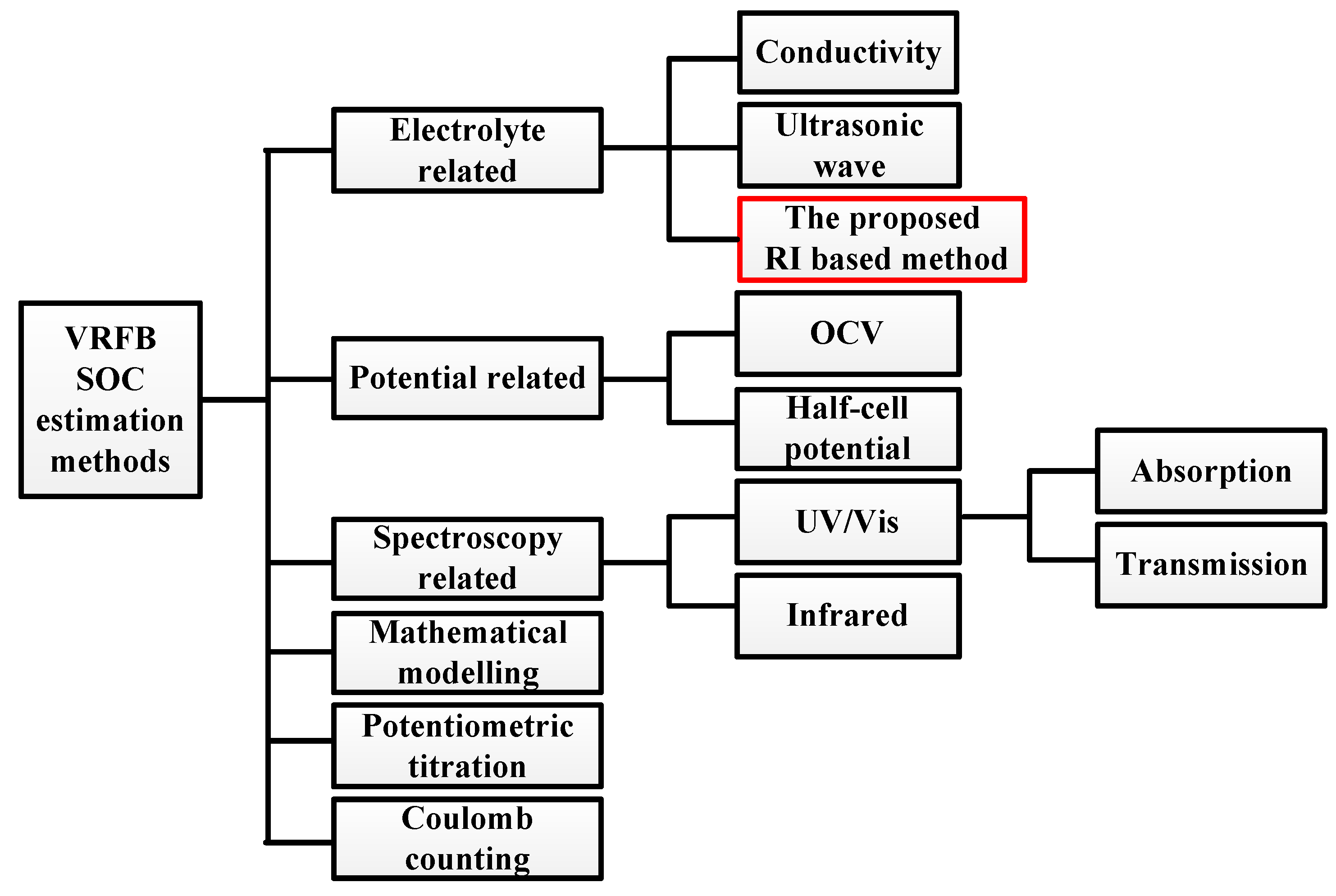
1. Introduction
2. Working Principle of VRFB and the Proposed SOC Detecting Method
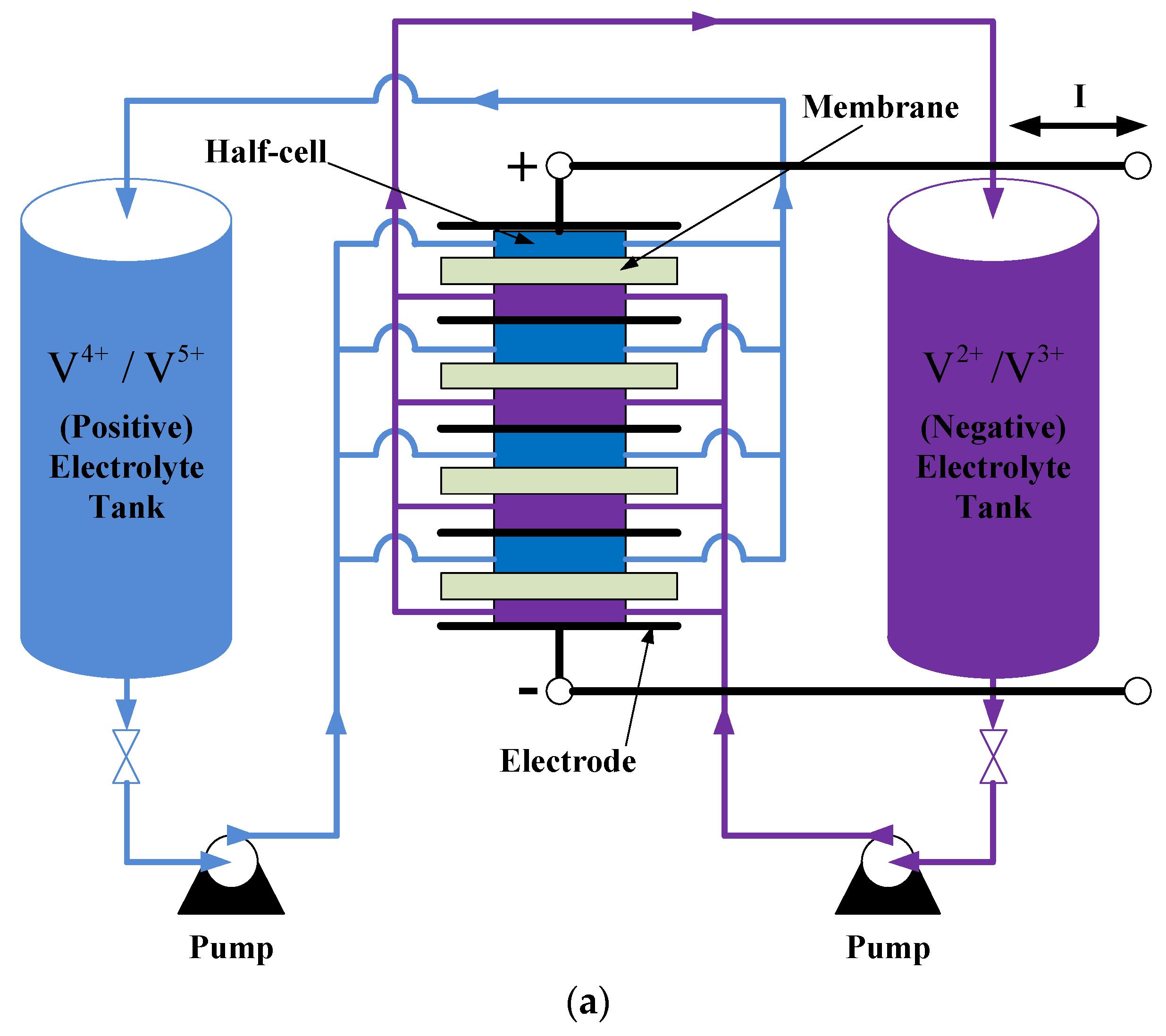
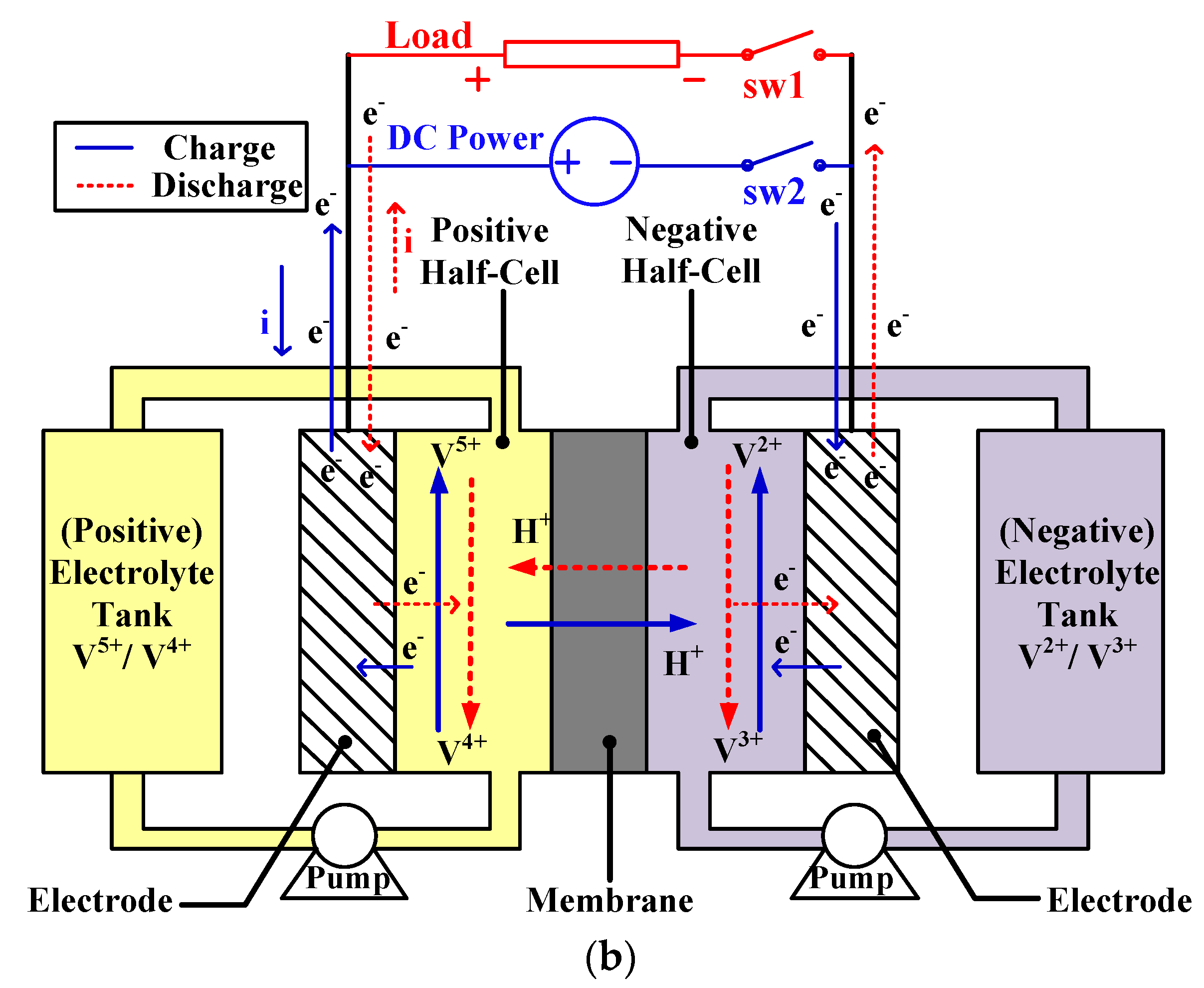
2.1. Working Principle of VRFB
2.2. Proposed SOC Detecting Method
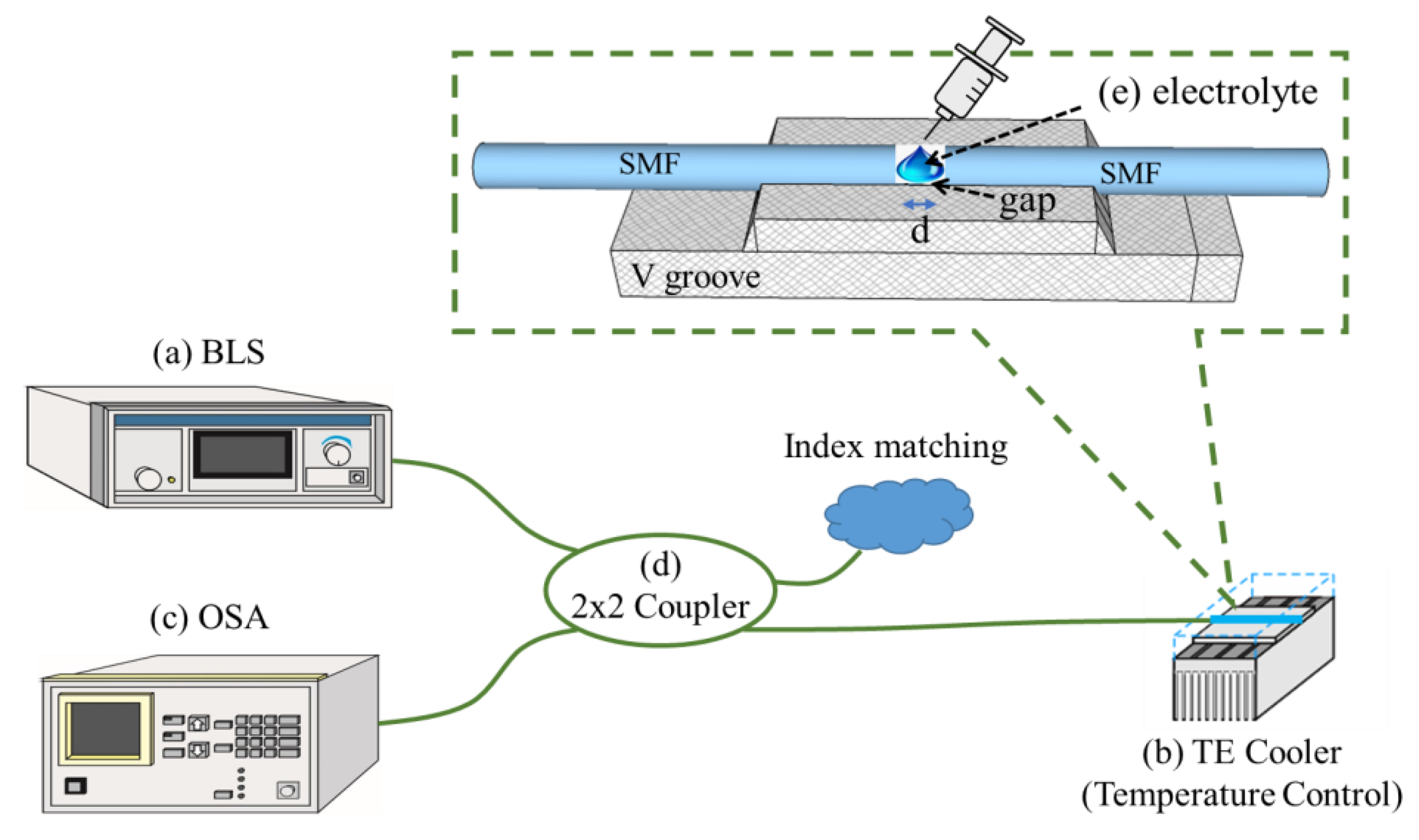
3. Fabrication of the Sensing Device and Experimental Setup
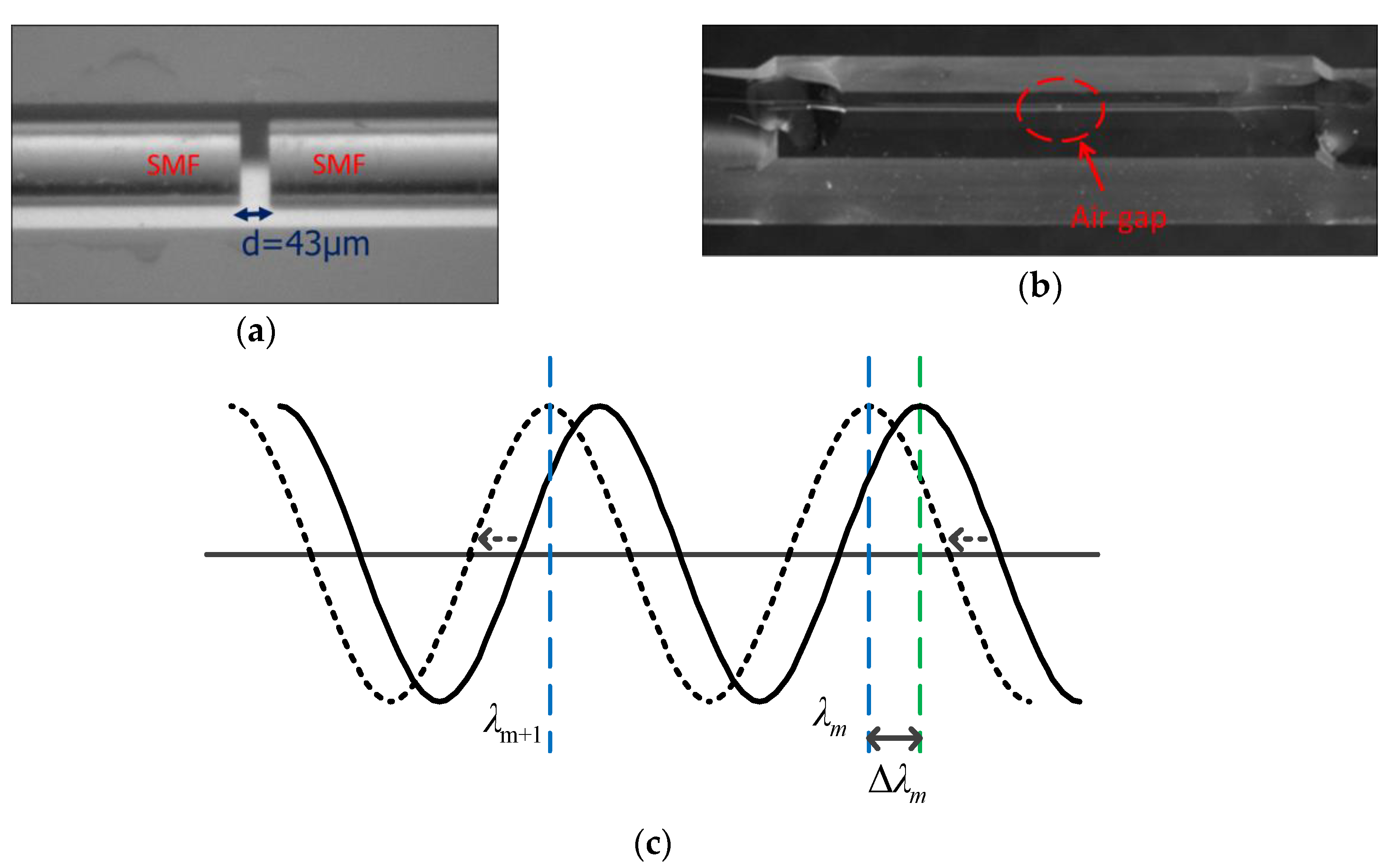
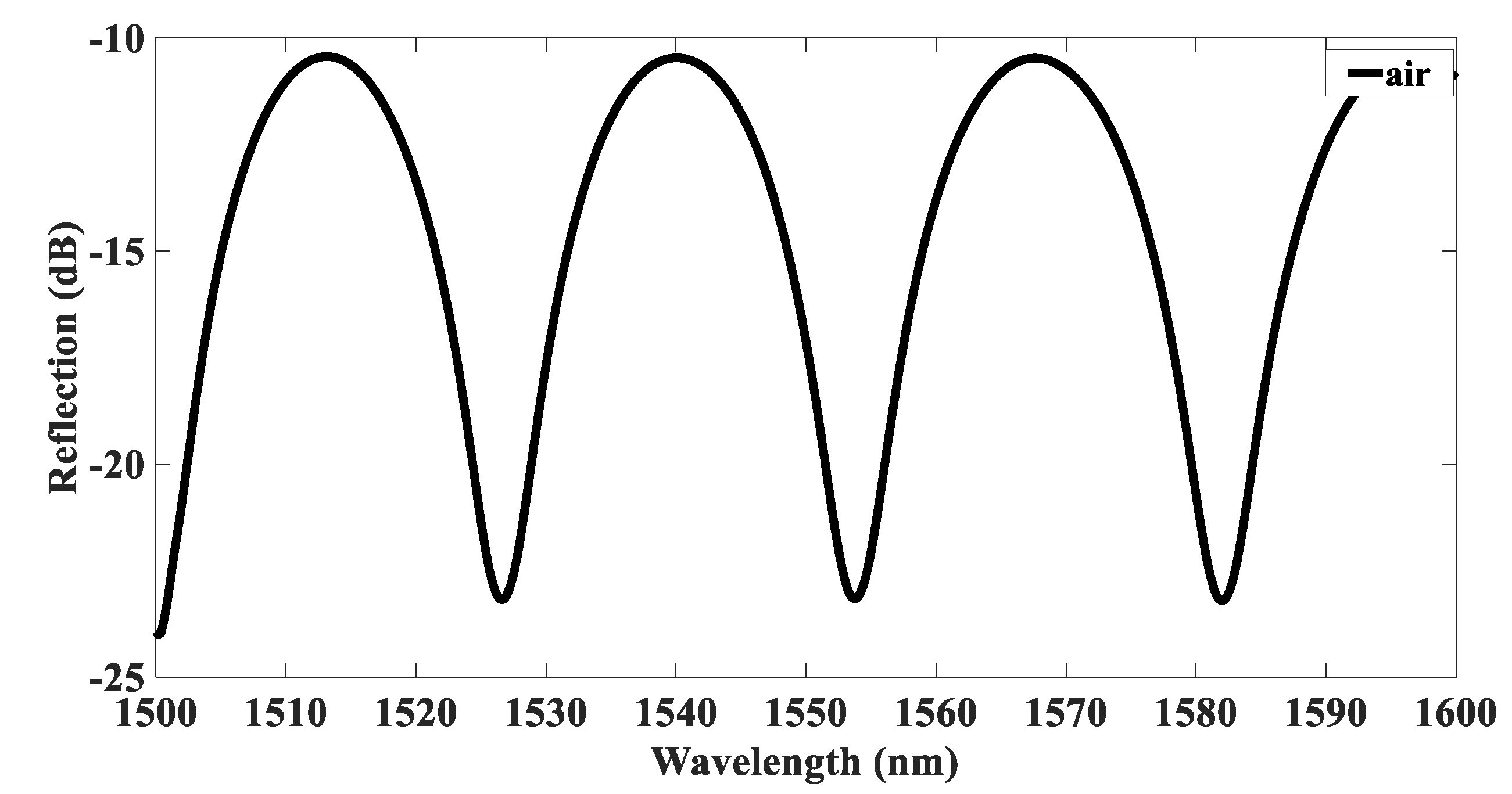
3.1. Fabrication and Characteristics of the Sensing Device
3.2. Experimental Setup
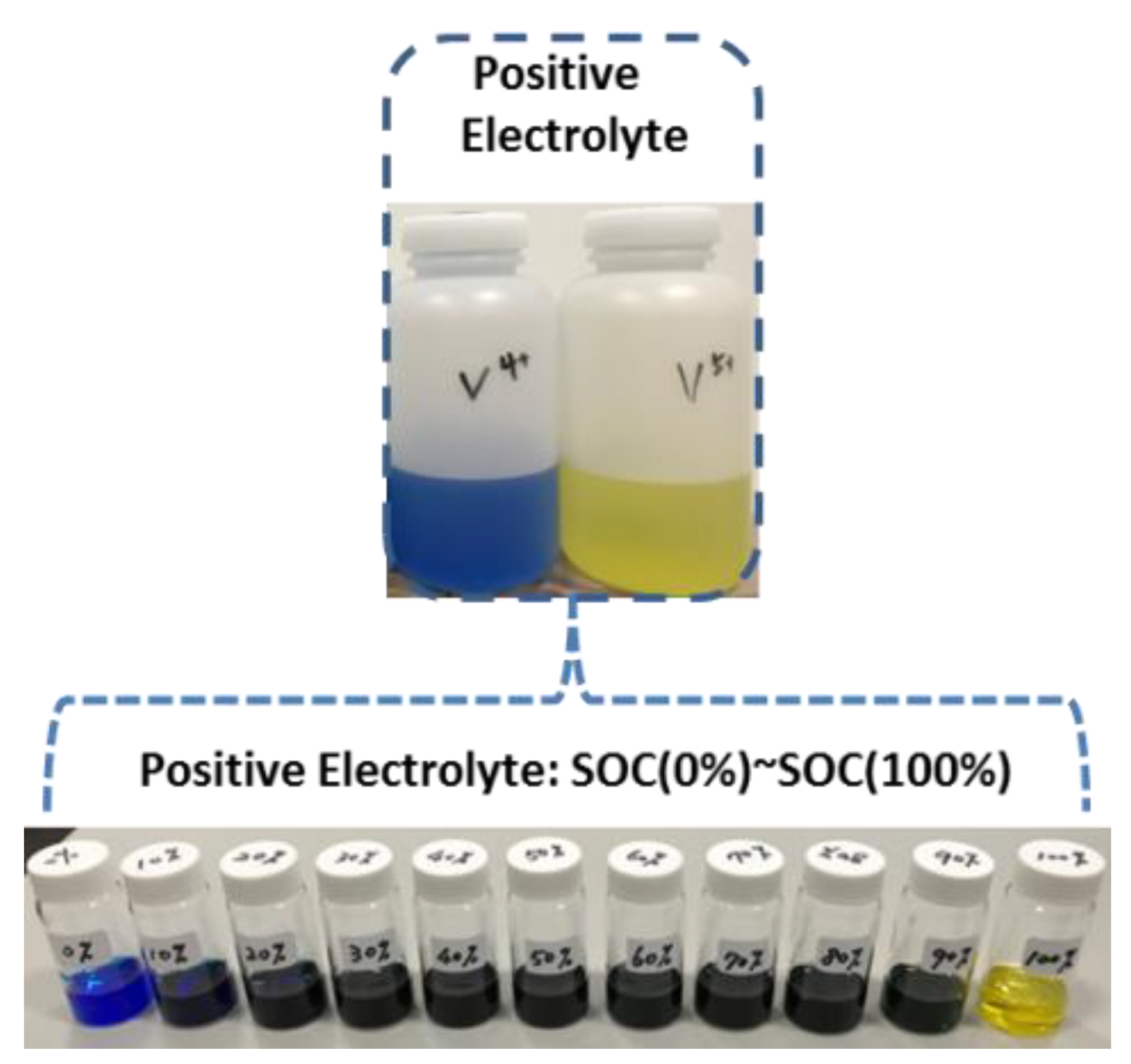
3.3. Preparation of Positive Electrolytes
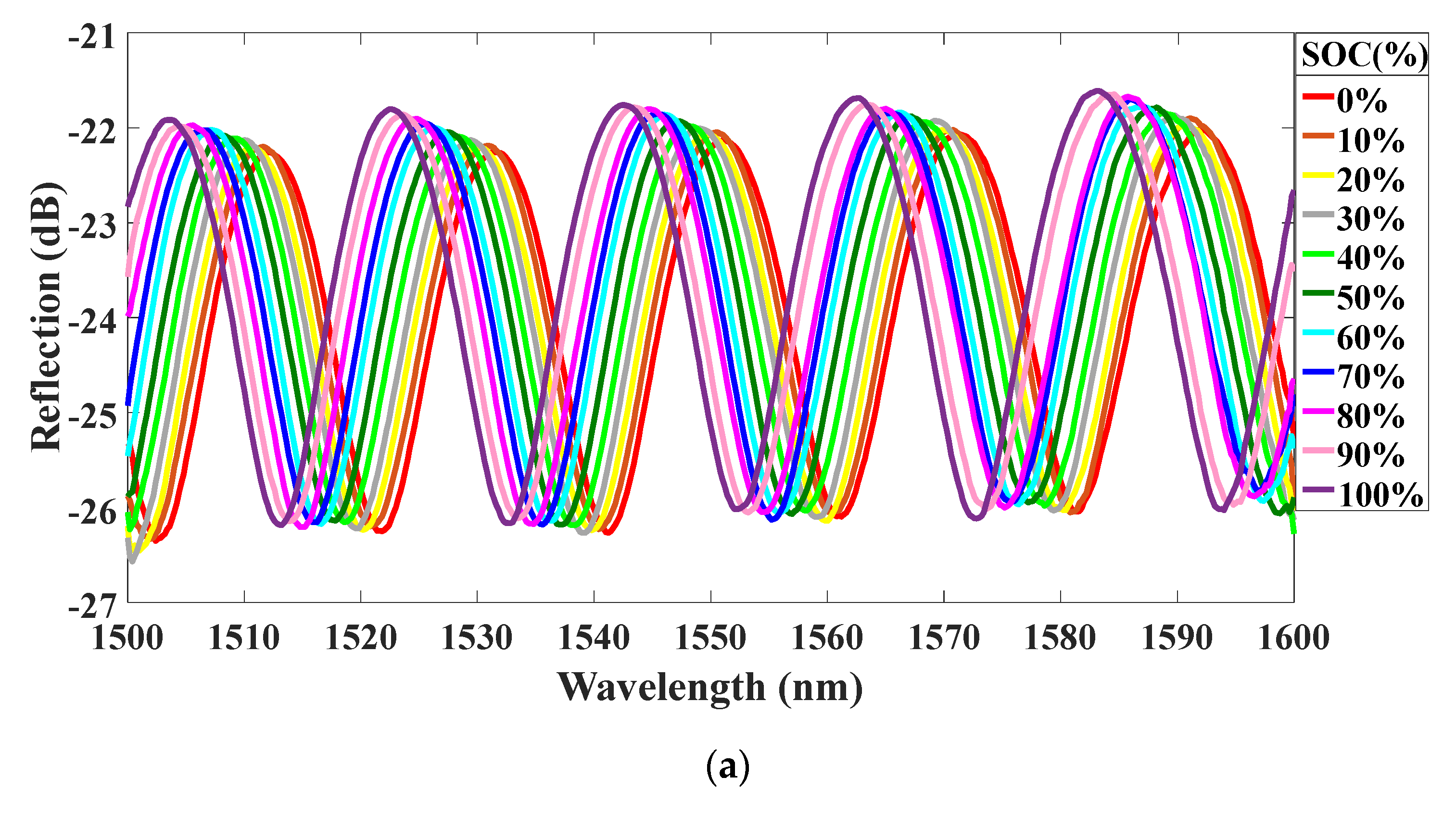
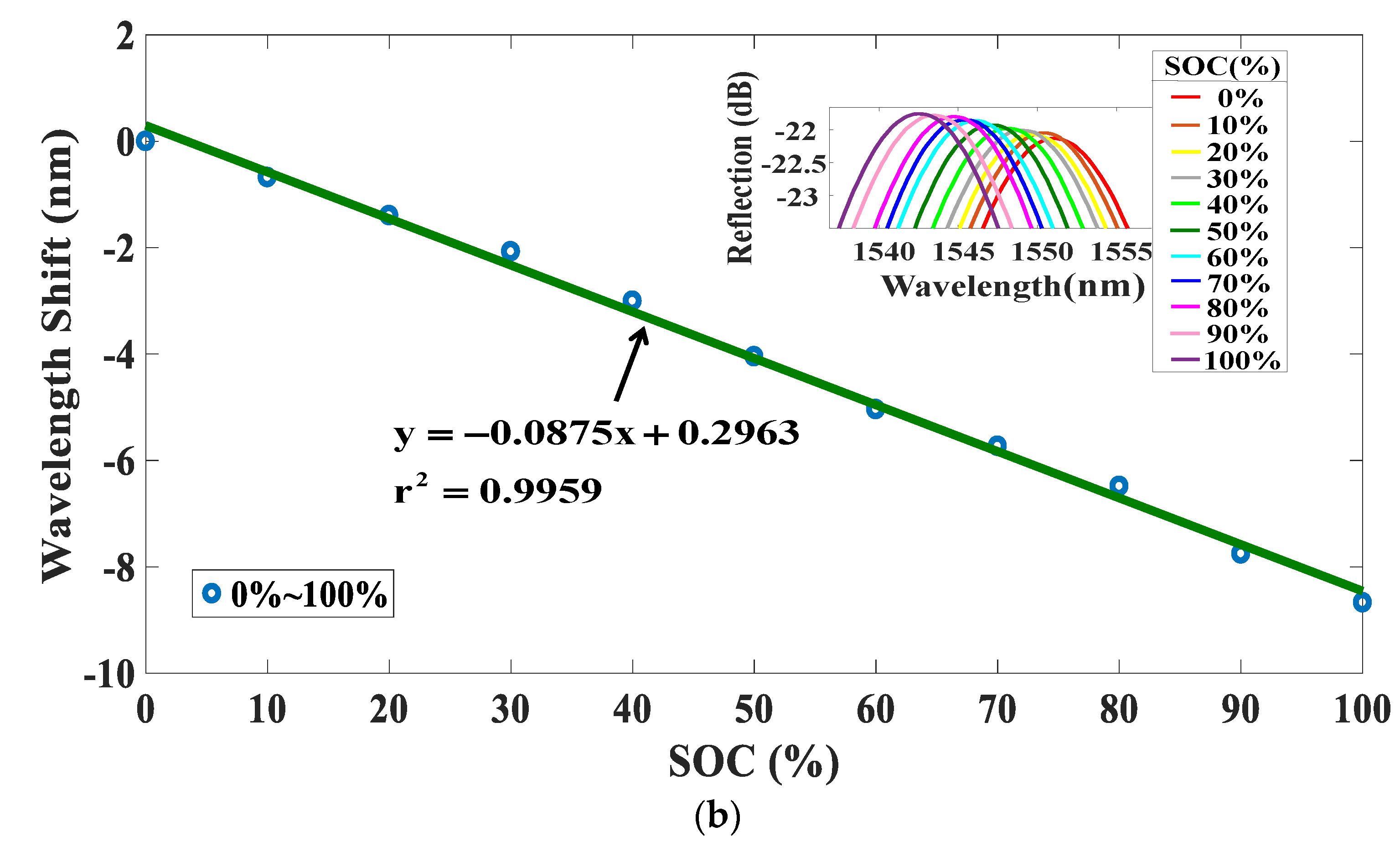
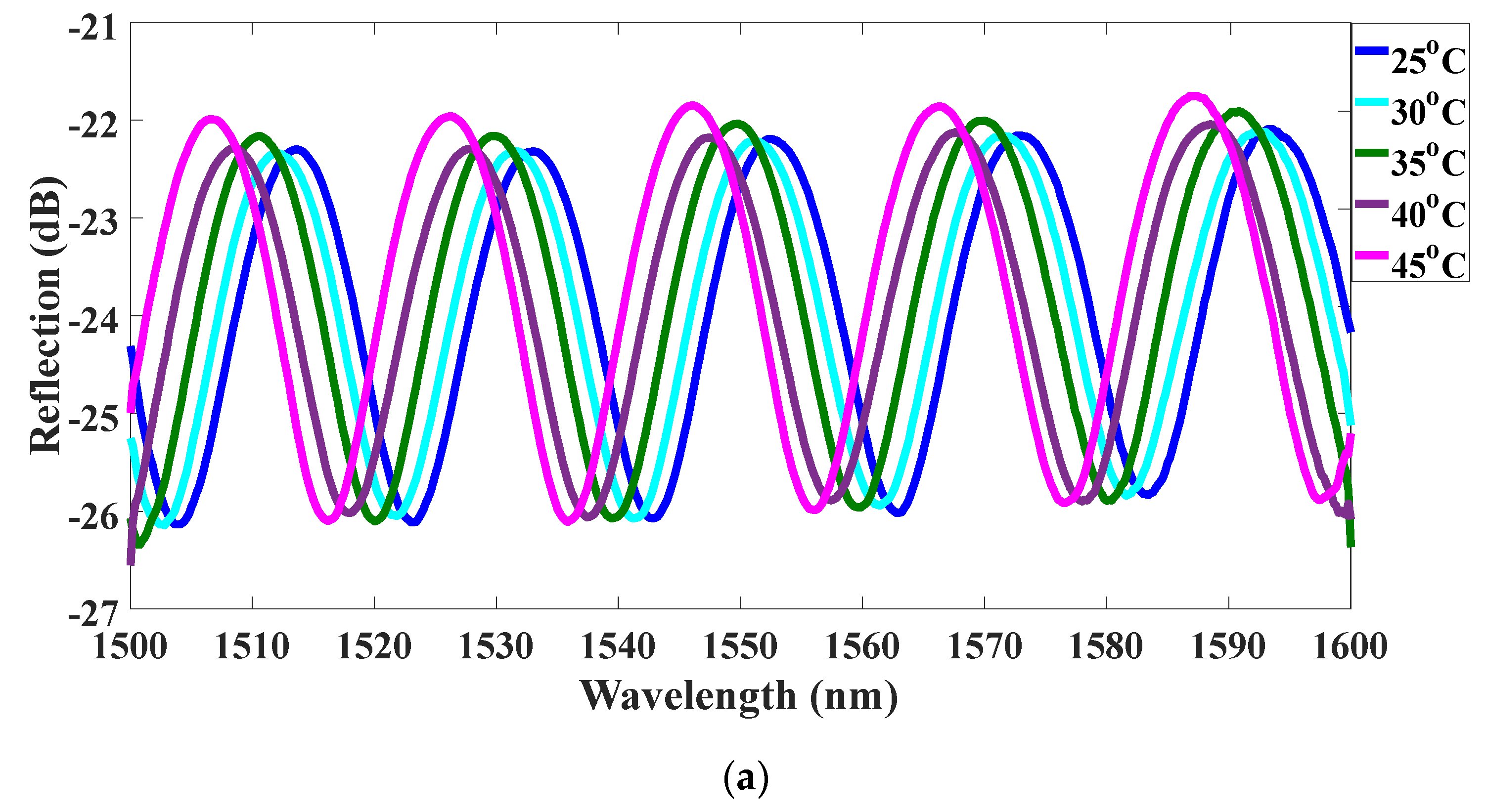
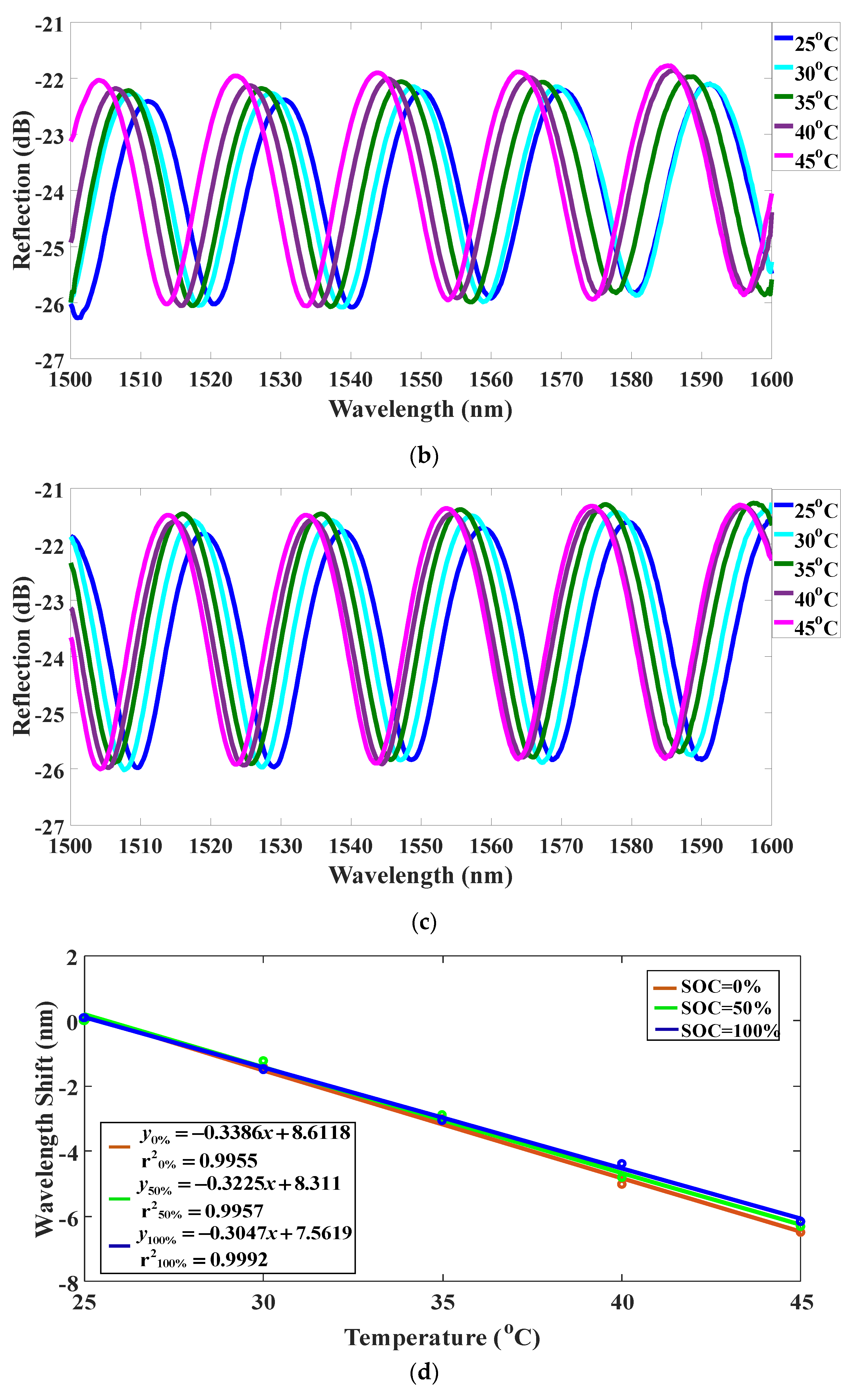
4. Experiments and Results
5. Discussions
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Mbungu, N.T.; Bansal, R.C.; Naidoo, R. Smart energy coordination of a hybrid wind/ PV with battery storage connected to grid. J. Eng. 2019, 2019, 5109–5113. [Google Scholar] [CrossRef]
- Yan, X.; Lin, X.; Qin, L.; Han, S.; Gao, L.; Yang, Y.; Zeng, B. Control strategy for wind power integration base on energy demand respond and distributed energy storage. J. Eng. 2017, 2017, 2374–2377. [Google Scholar] [CrossRef]
- Higashikawa, K.; Kiss, T. Novel Power System with Superconducting Cable with Energy Storage Function for Large-Scale Introduction of Renewable Energies. IEEE Trans. Appl. Supercond. 2019, 29, 5402204. [Google Scholar] [CrossRef]
- Alotto, P.; Guarnieri, M.; Moro, F. Redox flow batteries for the storage of renewable energy: A review. Renew. Sustain. Energy Rev. 2014, 29, 325–335. [Google Scholar] [CrossRef]
- Shirasakia, K.; Yamamura, T. Direct observation of vanadium ion permeation behavior through Nafion 117 using 48V radiotracer for all-vanadium redox flow battery. J. Membr. Sci. 2019, 592, 117367. [Google Scholar] [CrossRef]
- Jiang, B.; Fei, Y. Smart Home in Smart Microgrid: A Cost-Effective Energy Ecosystem with Intelligent Hierarchical Agents. IEEE Trans. Smart Grid 2015, 6, 3–13. [Google Scholar] [CrossRef]
- Ngamsai, K.; Arpornwichanop, A. Measuring the state of charge of the electrolyte solution in a vanadium redox flow battery using a four-pole cell device. J. Power Sources 2015, 298, 150–157. [Google Scholar] [CrossRef]
- Corcuera, S.; Skyllas-Kazacos, M. State-of-charge Monitoring and Electrolyte Rebalancing Methods for the Vanadium Redox Flow Battery. Eur. Chem. Bull. 2012, 1, 511–519. [Google Scholar]
- Skyllas-Kazacos, M.; Kazacos, M. State of charge monitoring methods for vanadium redox flow battery control. J. Power Sources 2011, 196, 8822–8827. [Google Scholar] [CrossRef]
- Chou, Y.S.; Hsu, N.Y.; Jeng, K.T.; Chen, K.H.; Yen, S.C. A novel ultrasonic velocity sensing approach to monitoring state of charge of vanadium redox flow battery. Appl. Energy 2016, 182, 253–259. [Google Scholar] [CrossRef]
- Davies, G.; Knehr, K.W.; Tassell, B.V.; Hodson, T.; Biswas, S.; Hsieh, A.G.; Steingarta, D.A. State of Charge and State of Health Estimation Using Electrochemical Acoustic Time of Flight Analysis. J. Electrochem. Soc. 2017, 164, A2746–A2755. [Google Scholar] [CrossRef]
- Tang, Z.; Aaron, D.S.; Papandrew, A.B.; Zawodzinski, T.A. Monitoring the State of Charge of Operating Vanadium Redox Flow Batteries. ECS Trans. 2012, 41, 1–9. [Google Scholar]
- Mohamed, M.R.; Ahmad, H.; Seman, M.N.A. Estimating the State-of-Charge of all-Vanadium Redox Flow Battery using a Divided, Open-circuit Potentiometric Cell. Elektron. Elektrotech. 2012, 19, 37–42. [Google Scholar] [CrossRef]
- Roznyatovskaya, N.; Herr, T.; Küttinger, M.; Fühl, M.; Noack, J.; Pinkwart, K.; Tübke, J. Detection of capacity imbalance in vanadium electrolyte and its electrochemical regeneration for all-vanadium redox-flow batteries. J. Power Sources 2016, 302, 79–83. [Google Scholar] [CrossRef]
- Petchsingh, C.; Quill, N.; Joyce, J.T.; Eidhin, D.N.; Oboroceanu, D.; Lenihan, C.; Gao, X.; Lynch, R.P.; Buckley, D.N. Spectroscopic Measurement of State of Charge in Vanadium Flow Batteries with an Analytical Model of VIV-VV Absorbance. J. Electrochem. Soc. 2016, 163, A5068–A5083. [Google Scholar] [CrossRef]
- Rudolph, S.; Schröder, U.; Bayanov, I.M.; Blenke, K.; Hage, D. High resolution state of charge monitoring of vanadium electrolytes with IR optical sensor. J. Electroanal. Chem. 2013, 694, 17–22. [Google Scholar] [CrossRef]
- Liu, L.; Xi, J.; Wu, Z.; Zhang, W.; Zhou, H.; Li, W.; He, Y. Online Spectroscopic Study on the Positive and the Negative Electrolytes in Vanadium Redox Flow Batteries. J. Spectrosc. 2013, 2013, 1–8. [Google Scholar] [CrossRef]
- Sun, G.; Lu, J.D.; Ye, Q.; Ren, L.; Shi, J.; Tang, Y.J. State of Charge Estimation Using EKF Method for VRB. Adv. Mater. Res. 2012, 512, 986–994. [Google Scholar] [CrossRef]
- Xiong, B.; Zhao, J.; Wei, Z.; Skyllas-Kazacos, M. Extended Kalman filter method for state of charge estimation of vanadium redox flow battery using thermal-dependent electrical model. J. Power Sources 2014, 262, 50–61. [Google Scholar] [CrossRef]
- Wei, Z.; Lim, T.M.; Skyllas-Kazacos, M.; Wai, N.; Tseng, K.J. Online state of charge and model parameter co-estimation based on a novel multi-timescale estimator for vanadium redox flow battery. Appl. Energy 2016, 172, 169–179. [Google Scholar] [CrossRef]
- Wei, Z.; Tseng, K.J.; Wai, N.; Skyllas-Kazacos, M. Adaptive estimation of state of charge and capacity with online identified battery model for vanadium redox flow battery. J. Power Sources 2016, 332, 389–398. [Google Scholar] [CrossRef]
- Xiong, B.; Zhao, J.; Su, Y.; Wei, Z.; Skyllas-Kazacos, M. State of Charge Estimation of Vanadium Redox Flow Battery Based on Sliding Mode Observer and Dynamic Model Including Capacity Fading Factor. IEEE Trans. Sustain. Energy 2017, 8, 1658–1667. [Google Scholar] [CrossRef]
- Wei, Z.; Bhattarai, A.; Zou, C.; Meng, S.; Lim, T.M.; Skyllas-Kazacos, M. Real-time monitoring of capacity loss for vanadium redox flow battery. J. Power Sources 2018, 390, 261–269. [Google Scholar] [CrossRef]
- Aaron, D.S.; Liu, Q.; Tang, Z.; Grim, G.M.; Papandrew, A.B.; Turhan, A.; Zawodzinski, T.A.; Mench, M.M. Dramatic performance gains in vanadium redox flow batteries through modified cell architecture. J. Power Sources 2012, 206, 450–453. [Google Scholar] [CrossRef]
- Becker, M.; Bredemeyer, N.; Tenhumberg, N.; Turek, T. Polarization curve measurements combined with potential probe sensing for determining current density distribution in vanadium redox-flow batteries. J. Power Sources 2016, 307, 826–833. [Google Scholar] [CrossRef]
- Li, X.; Warren-Smith, S.C.; Ebendorff-Heidepriem, H.; Zhang, Y.; Nguyen, L.V. Optical Fiber Refractive Index Sensor with Low Detection Limit and Large Dynamic Range Using a Hybrid Fiber Interferometer. J. Lightwave Technol. 2019, 37, 2954–2962. [Google Scholar] [CrossRef]
- Sun, L.P.; Huang, T.; Yuan, Z.; Yang, M.; Huang, Y.; Xiao, P.; Guan, B.O. Ultrasensitive Optofluidic Interferometer for Online Monitoring of Photocatalytic Reactions. J. Lightwave Technol. 2019, 37, 5435–5441. [Google Scholar] [CrossRef]
- Ma, C.T.; Chang, Y.W.; Yang, Y.J.; Lee, C.L. A Dual-Polymer Fiber Fizeau Interferometer for Simultaneous Measurement of Relative Humidity and Temperature. Sensors (Basel) 2017, 17, 2659. [Google Scholar] [CrossRef]
- Lee, C.L.; Hsuan, Y.H.; Gu, J.H.; Yeh, T.Y.; Tseng, C.H. Dual hollow core fiber-based Fabry–Perot interferometer for measuring the thermo-optic coefficients of liquids. Opt. Lett. 2015, 40, 459–462. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.-T. A Novel State of Charge Estimating Scheme Based on an Air-Gap Fiber Interferometer Sensor for the Vanadium Redox Flow Battery. Energies 2020, 13, 291. https://doi.org/10.3390/en13020291
Ma C-T. A Novel State of Charge Estimating Scheme Based on an Air-Gap Fiber Interferometer Sensor for the Vanadium Redox Flow Battery. Energies. 2020; 13(2):291. https://doi.org/10.3390/en13020291
Chicago/Turabian StyleMa, Chao-Tsung. 2020. "A Novel State of Charge Estimating Scheme Based on an Air-Gap Fiber Interferometer Sensor for the Vanadium Redox Flow Battery" Energies 13, no. 2: 291. https://doi.org/10.3390/en13020291
APA StyleMa, C.-T. (2020). A Novel State of Charge Estimating Scheme Based on an Air-Gap Fiber Interferometer Sensor for the Vanadium Redox Flow Battery. Energies, 13(2), 291. https://doi.org/10.3390/en13020291



