Abstract
Optimal scheduling is a requirement for microgrids to participate in current and future energy markets. Although the number of research articles on this subject is on the rise, there is a shortage of papers containing detailed mathematical modeling of the distributed energy resources available in a microgrid. To address this gap, this paper presents in detail how to mathematically model resources such as battery energy storage systems, solar generation systems, directly controllable loads, load shedding, scheduled intentional islanding, and generation curtailment in the microgrid optimal scheduling problem. The proposed modeling also includes a methodology to determine the availability cost of battery and solar systems assets. Simulations were carried out considering energy prices from an actual time-of-use tariff, costs based on real market data, and scenarios with scheduled islanding. Simulation results provide support to validate the proposed model. Data illustrate how energy arbitrage can reduce microgrid costs in a time-of-use tariff. Results also show how the microgrid’s self-sufficiency and the storage system’s capacity can impact the microgrid’s energy bill. The findings also bring out the need to consider the scheduled islanding event in the day-ahead optimization for microgrids.
1. Introduction
The introduction of distributed energy resources (DER) in the distribution system has brought several benefits to consumers, utilities, and society. These include increasing system reliability and resilience, reducing greenhouse gases, relieving distribution and transmission systems, reducing energy tariffs for consumers who also produce energy (referred to as prosumers in [1]), and the possibility of forming an energy market in which consumers and prosumers can participate actively. However, it also came with some challenges as the need to readapt distribution systems (infrastructure, automation, protection, control, operating systems, planning) to receive these new resources and to deploy modern energy tariffs to meet the equity criterion [1], finding a trade-off between encouraging renewable sources while avoiding cross-subsidization between consumers and prosumers. Microgrids (MG), as part of this new active distribution system, experience the same benefits and challenges; however, they have an additional purpose: being economically efficient, producing energy at the lowest possible cost while eliminating or minimizing waste.
A microgrid can contain loads and distributed energy resources such as distributed generators, storage devices, and controllable loads, and must be operated in a controlled way whether or not connected to the main grid [2]. With such resources, a microgrid can provide ancillary services to the distribution system operator (DSO), perform energy arbitrage (store energy when the price is low to sell it or use it when the price is high), actively participate in energy markets, in addition to participating in distribution systems with multiple microgrids. However, to make these activities feasible, a microgrid must optimize the use of its resources, seeking economic efficiency. Due to the renewable energy sources and load forecasting features, the time horizon for this optimization is the day-ahead. On the other hand, markets whose energy prices can vary hourly may require optimization with an equivalent time horizon. Thus, day-ahead and intra-day optimal schedulings are requirements for microgrids to participate in current and future energy markets.
The optimal scheduling of microgrids with battery energy storage system (BESS), solar and/or wind generation has been studied in [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. Although these works address the modeling of solar photovoltaic systems for microgrids, none of them discusses curtailment modeling in day-ahead scheduling. In addition, the costs related to the PV system can be modeled in the objective function by a fixed term, or by a term proportional to the power generated, or by a combination of them, depending on the methodology adopted to address such costs. The authors [7,14,17] model these costs through a term proportional to the power generated. In [18], these costs are modeled using a fixed term and another proportional to the power. Similar modeling is presented in [3] with a fixed term and two others which are proportional to the power and the square of the power. However, all of these works do not present a methodology for calculating costs related to the PV system. As a consequence, in the simulations presented in those works, the authors consider such costs as known values.
Regarding the modeling of battery energy storage systems, most authors present simplified modeling that considers only upper and lower limits for charging and discharging power and for the state of charge (SOC), as in [3,5,7,13,14]. Others present a recursive equation for the BESS state of charge but without clarifying how to transform such a recursive equation into a constraint of an optimization problem, as in [4,5,6,10,16,20]. The authors in [19] address the modeling of BESS costs considering the ratio between the cost of capital and the total number of cycles, however without considering the impacts of the depth of discharge and battery degradation. Finally, the authors in [18] address the modeling of BESS costs considering the cost of battery degradation, for a given depth of discharge, an exponential relationship that depends on a function fitting to the curve provided by the manufacturer. However, they do not address the method for obtaining the curve parameters.
Demand response programs in microgrids have been investigated through modeling of directly controlled loads (DCL) in [14,15,16,21]. Authors in [14,21] use a discrete DCL model with load blocks to analyze the problem of microgrids optimization with demand response, which is equivalent to a model of interruptible loads per block. Authors in [16] present a similar approach but considering the load to be interrupted as a continuous variable. However, these works do not address the modeling of shiftable loads as an option for DCLs. In [15], loads are classified as fixed and adjustable (DCL), including shiftable and curtailable (interruptible) loads. Both types of DCL are modeled only by an upper power limit. However, shiftable loads require more complete modeling due to their need for a continuous duty cycle, which was not addressed at that work.
Several studies address the problem of optimal day-ahead scheduling of microgrids by modeling uncertainties in load and generation forecasts. Authors in [6,10,16,17] divide the optimization problem into levels or stages to deal with uncertainties in load, generation, and price forecast. Thus, an intermediate stage of optimization has the role of finding, in a set of bounded uncertainties, the condition that maximizes the cost of the microgrid (the worst case). Once such a condition has been defined, the next stage seeks to minimize the cost of the microgrid. Authors refer to this technique as robust optimization. In [18], the authors model the uncertainties probabilistically, and in [19], the authors propose the interval mathematics technique to solve the same problem. However, considering uncertainties in the optimization problem comes at a price because, in addition to increasing the complexity of the problem, it leads to a sub-optimal solution compared to the deterministic solution. It is what the authors in [22,23] call the price of robustness in robust optimization. If on the one hand, there may be a mismatch between the forecasted and realized values as a deterministic solution is used, on the other hand, such a mismatch may even increase in solutions such as robust optimization. That is because in such a technique there is no correlation between the uncertainty considered in the day-ahead problem and that which should actually happen in the intra-day. These are the main reasons why the present study addresses this problem in a deterministic way, which has the advantage of simplicity and low implementation complexity.
Linear programming is the most used technique among the works consulted in the present literature review to solve the problem of day-ahead scheduling optimization for microgrids [6,10,13,15,16,21]. Furthermore, in an extensive literature review carried out in [24], it was found that mixed-integer linear programming (MILP) is the most appropriate approach for solving the scheduling problem for microgrids and virtual power plants. These works support the choice for linear programming in the present study, without prejudice to the mathematical modeling of the elements here presented.
The optimal dispatch of distributed energy resources in distribution systems and microgrids is of economic interest to the entities that operate these systems. Although there are some works published in the literature on the subject, there also are some gaps in the mathematical modeling that this work seeks to fill. For example, no previous work was found that formulated the day-ahead problem considering scheduled intentional islanding, as defined by the IEEE Std. 1547-2018 [25]. The same for the modeling of shiftable loads of continuous cycle and solar photovoltaic (PV) generation curtailment. Furthermore, there is no work in the present literature review that model in detail the BESS system and its cost of availability, maintaining the linearity of the problem.
Thus, this work presents detailed modeling of the optimal dispatch of microgrids with the distributed generation resources namely: a battery energy storage system; a PV system with the possibility of curtailment; demand response (DR) through directly controllable loads, such as the shiftable and interruptible ones; and the option of considering scheduled intentional islanding events with the possibility of performing load shedding (LS) when necessary.
The battery storage system is modeled according to the IEEE Std 2030.2.1-2019. Details of this modeling are presented, considering aspects such as the efficiency of the whole BESS, and state of charge as a non-recursive constraint. Furthermore, the ranges of some practical values for the model parameters are presented. In cost modeling, an exponential equation for the battery state of health (SOH) is presented in order to fit a possible BESS manufacturing data curve. The costs of BESS storage, charging, and discharging are then presented as a function of the SOH threshold, rated depth of discharge (DOD), cycle life, and the battery capacity.
In the cost modeling of the PV system, factors such as annual degradation of the photovoltaic panels, the lifespan of PV panels, and the solar generation capacity from the region of installation are considered. The methodology adopted in the modeling gave rise to a problem of mixed-integer linear programming, which was implemented in the MATLAB software. Simulation results seek to validate the mathematical model against all distributed energy resources of the microgrid. In addition, a case study based on the time-of-use tariff from the Brazilian energy market is presented considering actual tariff rates. Such a study examines the conditions for energy arbitrage performed by BESS in a microgrid.
The main contributions of this paper are:
- Presenting a practical methodology to compute the BESS availability cost in USD/kWh; modeling of BESS system considering battery, converter, and transformer useful values of efficiencies; modeling the BESS state of charge as a non-recursive constraint to the MILP problem;
- Modeling of scheduled intentional islanding in a microgrid with the possibility of curtailment and load shedding;
- Modeling of non-interruptible shiftable loads (continuous cycle) as washers and driers when participating in demand response programs;
- Presenting a practical methodology to compute the availability cost of PV systems.
The rest of this paper is organized as follows. Section 2 presents an overview of an energy management system (EMS) for microgrids considering the day-ahead and real-time modules. Section 3 presents the mathematical model of a microgrid regarding its dynamics of operation and costs. The simulation methodology is presented in Section 4, and simulation results in Section 5. A discussion of the main findings is presented in Section 6, and the main conclusions of the work in Section 7.
2. Microgrid Energy Management System
From a logical point of view, a microgrid EMS can be divided into day-ahead and real-time modules, as illustrated in Figure 1. Furthermore, the day-ahead EMS requires some input modules to update their data daily. The forecasting data input module is responsible for the daily forecast of the microgrid generation and load curves, which can be based on historical data and weather forecasting. The DSO inputs represent information passed on by the distribution system operator, as scheduled outages and distribution network operational limits, which can be established by a power flow analysis of the distribution network region in which the microgrid is located. The DR contracts data module has the role of updating technical information about consumers who participate in demand response programs. Finally, the energy price module is responsible for updating the energy market prices for the next day.
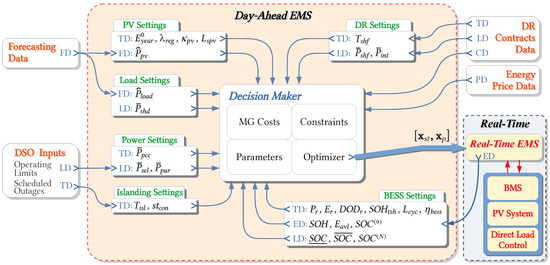
Figure 1.
Schematic diagram of the MG day-ahead EMS model addressed in the present work, showing its relationship with the input and output data and its interaction with the real-time EMS; CD, ED, FD, LD, PD, and TD stand for cost, estimated, forecasted, limit, price, and technical data, respectively.
The day-ahead EMS module must contain the microgrid settings data, the mathematical model of all the microgrid devices and the desired operating conditions, and an optimizer algorithm. The decision-maker block calculates costs that depend on settings data and sets up the optimization problem with constraints and parameters for the optimizer. The output of this module is the optimal solution, which is formed by the states and powers that will be the setup of operating for the real-time EMS module throughout the next day. Therefore, the day-ahead EMS module, as illustrated in Figure 1, defines and limits the scope of this work.
In addition to daily receiving the optimal operating condition from the day-ahead module, the real-time EMS module is updated with data from local and central controllers, electronic meters, and the battery management system (BMS) in real-time. This module has the role of a real-time decision-maker as it must correct the deviations between the forecasted load and generation and the real-time acquisition data. Such a correction can be made, for example, considering a one-hour horizon. These data are then passed on to lower-level controllers. In addition, this module has the role of deciding the microgrid’s operating strategy if the schedule received from the day-ahead module is broken, as can happen in the event of intentional unscheduled islanding [25]. Finally, this module can daily pass data estimated by the BMS to the day-ahead module, such as the current BESS capacity and state of health, as well as the state of charge expected to the end of the day. It will be the initial state of charge in the day-ahead module. Real-time EMS modeling is outside the scope of this work.
3. Modeling Methodology
3.1. Microgrid Modeling
Figure 2 illustrates a schematic diagram of the microgrid reference model for the MILP problem addressed in the present study. The model comprises integer (binary) and real decision variables. The former ( type) has the function of virtual disconnect switches, and the latter ( type) represents the active powers of each element of the model. Variables of type represent forecasted values, which are input variables for the model. Features of the model include: solar PV system, battery energy storage system, directly controllable loads, conventional loads, load shedding, energy transactions with the external grid, and the possibility of islanding. As this model requires a large number of decision variables, they are described in Table 1 and Table 2. Table 3 presents some input variables of the model in Figure 2.
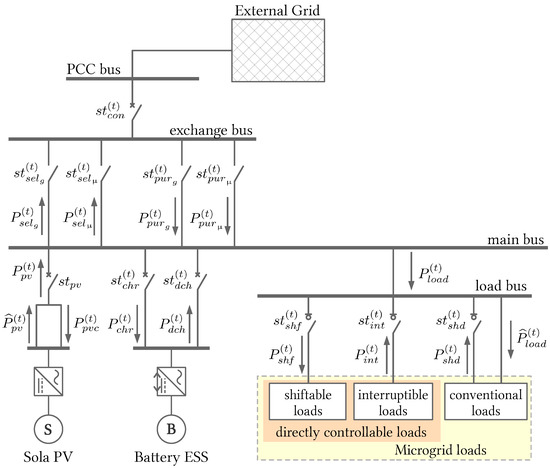
Figure 2.
Schematic diagram of the microgrid model used in the MILP problem of the present study. The model presents integer (binary) and real decision variables. The former ( type) work as virtual disconnectors and the latter ( type) represent the active powers of each element of the model. Type variables represent forecasted values.

Table 1.
State variables for the model, in which the value 1 means state enabled and 0 disabled.

Table 2.
Power variables for the model.

Table 3.
Input variables for the model.
Some elements in the model do not necessarily correspond to a real device present in the microgrid. The energy transacted with the external grid pass through virtual disconnectors (in practice, they are not required). Creating these branches connected to the exchange bus allows the model to identify the agents that are exchanging energy with the microgrid, in addition to quantifying that energy. In fact, such transaction can be a contractual obligation only, since all the energy that enters and leaves the microgrid through the point of common coupling (PCC) bus has a single source or destination: the external grid. Furthermore, in practical applications, the BESS is connected to the main bus through a single branch, and a battery management system is responsible for controlling the charge and discharge operations. On the other hand, without loss of generality, modeling charging and discharging by different branches (see Figure 2) may be more suitable for mathematical programming purposes.
In the MG model of Figure 2, DCL are loads in a demand response program that the MG operator can remotely disconnect or cycle upon contractual agreement and notification [26]. Furthermore called flexible loads, they can be interruptible or shiftable. The former are loads subject to curtailment or interruption under system contingencies, as air conditioners and water heaters [27]. The latter are continuous cycle loads that can be shifted in time as washers and dryers. On the other hand, when the microgrid operator needs to disconnect non-flexible loads, the conventional ones in Figure 2, due to a contingency or generation shortage, it must use the load shedding resource. As this type of load is not participating in a demand response program, there is a penalty associated with such a disconnection.
As a day-ahead scheduling is made up of a 24-hours time horizon, then the time slot for the model can be defined as,
where N represents the number of time slots. In addition, throughout this work, the independent variable represents the discrete-time of the model, where
The rate of change of the physical quantities handled by the model at each time slot should guide the choice of . It should be small enough to capture significant changes in the forecasted load and solar generation curves, for example. On the other hand, it must be large enough to the meet the time requirements of microgrid’s tertiary control. Typical values for are from h [9,10,12] to 1 h [6,16,28]. However, 1/4 h may be a more appropriate time slot when the problem involves controllable loads, as it can better adjust to load cycles.
3.1.1. Objective Function
Consider a daily MG energy bill () made up of the difference between daily costs and revenue, such that positive values indicate an amount to be paid, and negative, an amount to be received or converted into energy credits, i.e.,
where and are the purchase and sale prices of energy, respectively. Although it is usual in other studies to name a daily operating cost, Equation (2) shows its value does not always represent a cost. Therefore, optimizing the dispatch of a microgrid consists of minimizing its daily energy bill; and, the optimization problem can be formulated as
where , the vector of decision variables, is a feasible solution to the problem; and M is the number of external MGs with whom the microgrid carries out energy transactions.
The linear objective function in Equation (3) is a sum of products. Those of type , whose variables are shown in Table 1 and Table 4, represent fixed costs of energy transaction and operating DERs such as BESS, load shedding, and controllable loads. Products of type , whose variables are described in Table 2 and Table 5, represent the revenues and expenses with the amount of energy transacted and the costs to operate each kWh of the DERs.

Table 4.
State parameters.

Table 5.
Power parameters of the MILP problem.
3.1.2. Energy and Power Exchanges
Regarding the energy transaction, there must be a logical constraint to deny that the microgrid can buy and sell energy simultaneously, that is,
However, if energy market rules allow the purchase of energy from two or more entities simultaneously, then this constraint can be decomposed into constraints that consider each term individually. The same goes for a market logic of simultaneous selling.
According to Equation (4), to insert a condition of islanding into the schedule, it is enough to make during the desired period of islanding, , and , otherwise. In fact, means that the microgrid can be either indeed operating in island mode (the real disconnect switch is open, e.g., due to a scheduled maintenance outage planned by the DSO) or connected but without exchanging power with the grid (see Equation (5)). Furthermore, if the microgrid cannot sell energy to the main grid (e.g., due to contractual restrictions with the DSO), then it is enough to make, , where is the set of external microgrids.
Regarding the power exchange, some technical features as line capacity, PCC sizing, or contracted limits can restrain the power exchange ( and ) between the microgrid and the main grid or external microgrids [6]. Furthermore, if a state variable or is zero, then the respective power or must be zero, i.e.,
where and are individual upper limits imposed by external entities (index for MGs, and g for the main grid). Besides, a power flow analysis considering the MG exchange bus as a node in the external grid can result in a constraint of physical upper limit for the point of common coupling,
3.1.3. Power Balance
To satisfy the power balance at a given time t, the sum of the energy generated, imported and exported must equal the microgrid demand. Assuming the total load power is given by (see Figure 2)
then, the power balance equation is given by
where and are the forecasted load and PV output curves in kW.
3.1.4. Battery Energy Storage System
A battery energy storage system for power system applications can comprise a coupling transformer, a converter system, and a battery pack. The efficiency of each one (, , and , respectively) impacts the overall BESS efficiency as
which is valid for both charging and discharging operations, once in practical applications, it is usual to consider the charge and discharge efficiency () are the same. In this case, , where is the round trip efficiency. The storage efficiency () could also make up the value of ; however, batteries present high . The lead-acid technology, for example, can achieve a self-discharge of 2–5% per month, and lithium-ion 1% per month [29]. Therefore, the storage efficiency can be neglected in models with a time horizon of a day.
According to the authors in [30], higher technologies lithium-ion batteries can achieve an of 95%, which implies an of . On the other hand, authors in [31] stand lead-acid and lithium-ion technologies can achieve a round trip efficiency of 85% and 90%, respectively, which leads to the values of and for . In addition, according to data in [32], a battery manufactured with the LiFePO technology can achieve an of 0.9747. Regarding the efficiency of converters and transformers, manufacturing data [33] for systems from 500 kW to 5000 kW show that each can be greater than 97%. Table 6 presents a summary of these efficiency values for three battery technologies, and the respective calculated from Equation (9).

Table 6.
Values of energy storage system efficiency for three battery technologies.
The IEEE Std 2030.2.1™ [34] presents the main concepts related to BESS engineering. Some of them are illustrated in Figure 3. According to the standard, state of charge is “the degree to which a BESS is charged relative to the maximum possible amount of energy that can be stored by the system”, and depth of discharge is “the degree to which a BESS is discharged relative to the maximum possible amount of energy that can be discharged by the system”. Thus, let be the BESS available capacity (the maximum possible amount of energy..., kWh), then
and ; where is the stored energy.
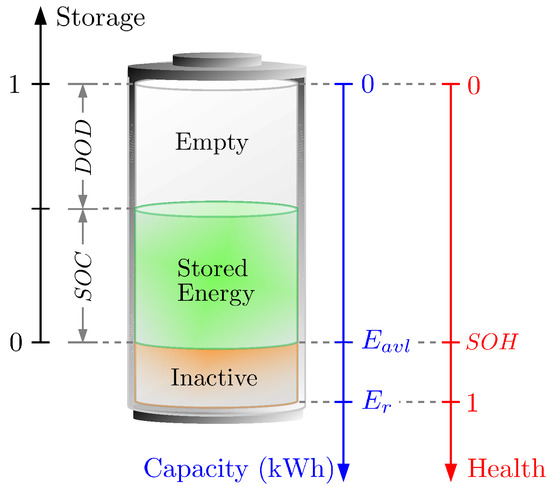
Figure 3.
Clarifying the nomenclature of BESS used throughout the present study. The definitions of SOC and DOD are following the IEEE Std 2030.2.1™ [34].
Furthermore, the ratio of available capacity to rated capacity () defines the battery state of health,
Therefore, the amount of stored energy during the BESS operation is . In real life systems, a battery management system can estimate the battery state of health at run time.
As the state of charge is a constraint in the optimization problem, Equation (10) needs to be rewritten to illustrate the dynamics of charging and discharging the battery. Adopting the main bus as the reference point, the next state of charge can be computed from the previous one as
Although Equation (12) is recursive, it can also be written directly, bringing up the initial state of charge , i.e.,
Furthermore, the SOC may vary within a limited range with maximal () and minimal () values,
As manufacturers usually define the battery cycle life () at a rated depth of discharge (), then it can be useful to consider , if the goal is to reach the amount of cycles.
Finally, the substitution of Equation (13) in (14) results in N MILP constraints for SOC, bringing out the decision variables and ,
Furthermore, by setting in Equation (13), it is possible to add an equality constraint to set the desired final state of charge , that is,
However, to make a more balanced economic analysis, at the end of an N period, the state of charge should return to its initial value, as in [10], which can be reached by setting in Equation (16).
The state variables for charging and discharging are binary, i.e., . As the system cannot perform charging and discharging operations at the same time, then
When a state variable disables operation of charging or discharging, naturally, the respective power decision variable must be forced to zero. Otherwise, the power is limited by the BESS rated power (). Then, for all ,
3.1.5. Directly Controllable Loads and Load Shedding
The state variable of load shedding is an integer of bounds , , and the amount of load shedding is bounded by ,
Typically, , as in [10], where is a factor of shedding.
Since the optimizer algorithm could schedule load shedding to avoid buying energy when it is more expensive, it may be of interest to refuse this type of operation. For example, it may be useful to allow disconnecting the load only during island condition, which requires that
In the model of directly controllable loads illustrated in Figure 2, the amount of interruptible loads , included in the forecasted daily load , is available for the optimizer algorithm to decide if it is necessary to disconnect it and when to do it. On the other hand, the amount of shiftable loads has different requirements, and the optimizer must connect this load block optimally throughout the day and ensure that it has a continuous cycle.
The state variables for interruptible and shiftable loads are integers such that and , , respectively. Now assuming that, according to the demand response program, the period of time that the MG operator can keep interruptible loads disconnected from the system is limited to , thus,
Furthermore, the amount of interruptible loads is bounded by , i.e.,
In fact, can vary throughout the day according to the characteristics of the interruptible load group available for the demand response program. Hence, in this work, interruptible loads are modeled as a fraction of the forecasted load, such that , where .
Assuming the block of shiftable loads has a cycle of period and magnitude , then Equations (23)–(25) are constraints required for power and time of connection,
However, to meet the continuous load cycle requirement, thus avoiding a sequence of turning the load on and off throughout the day, an additional restriction is required, which is
Algebraically, Equation (26) intents to ensure the time distance between any two enabled states is less than one period of load cycle . In this equation, a pseudocode technique was adopted as a mathematical resource to represent the inequality restrictions in a compact and readable way.
To add other blocks of shiftable loads with different magnitudes, periods, and states to the model, consider add to the problem the set of variables for the r-th load block, which must meet the constraints of Equations (23)–(26) for each r. However, the computational cost can be high, since the number of restrictions per load block is . For example, each block of two hours of shiftable loads requires 4013 constraints in the MILP problem ( h).
3.1.6. PV System
In a day-ahead schedule problem, the PV output power variable is usually equal to the forecasted value for the next day. However, there can be conditions in which the microgrid has surplus generation but is unable to transfer energy to the grid (technical restrictions or islanding condition) or to the battery (SOC is at the upper limit, or the battery is out of service for maintenance). In such a situation there must be generation curtailment to satisfy the power balance restriction. In addition, must be limited by the amount of generation expected for the next day. Such requirements result in the restriction of Equation (27) for the PV system.
The input variable must be set equal to zero if the PV system is out of service for maintenance; otherwise, it must be equal to 1. In fact, according to the modeling assumed in Equation (3), the daily cost of the PV System remains for all days of the year, even when the condition is valid (for some days of the year). According to the authors in [35], solar panels suffer degradation mainly due to climatic and environmental conditions. Therefore, in this modeling, the degradation of the PV system is assumed to be a continuous process that occurs even if it is turned off.
3.1.7. Matrix Formulation
Formulating the optimization problem in matrix notation may be more useful for performing it in computer algorithms. To this end, the solution vector can be split into a state vector and a power vector , i.e., , where,
Elements inside braces are row vectors; those with index are vectors, and with index , are vectors, i.e., a chain of vectors with index ; e.g., . Elements in the state vector are integers (binaries) and in the power vector, real numbers. Furthermore, as and the constraints are linear functions, the model fits a MILP problem. Furthermore, and are and vectors; therefore, the solution vector has variables. As an example, a scenario with one external MG and h ( and ) requires a MILP problem with 1825 decision variables, of which 865 are integers and 960 real numbers.
Similarly, the parameters presented in Table 4 and Table 5 can be grouped into a vector, i.e.,
where
where is a vector of ones; also, by definition and . The same notation rule for vectors used in can be applied to the elements in Equations (30a) and (30b).
Finally, the MILP problem written in matrix notation is
where and are the matrix and vector of linear inequality constraints, respectively; and are the matrix and vector of linear equality constraints, respectively; and and are the vectors of lower and upper bounds, respectively. Table 7 identifies the equations required to define and create the matrices and vectors of constraints.

Table 7.
Summary of the equations, organized by features, required to build the matrices and vectors of constraints of the MILP problem; is a vector of zeros.
3.2. Cost Estimation
3.2.1. BESS Costs
The calculation of the availability cost of a BESS () in $/kWh requires estimating the total charge and discharge energy of the battery over its lifetime (), and knowing its capital cost (), i.e.,
Theoretically, the battery life ends when it reaches the SOH threshold () for a given application. Thus, the curve SOH versus cycles can bring out the cycle life of the battery, since . Although it is possible to know the true only in time of operation from the BMS estimates, the curve provided by the BESS manufacturer can be used for cost estimation purposes.
The IEEE Std 2030.2.1™ [34] defines cycle as “the process of BESS discharging or charging from initial state of charge to the same state within a single discharge and charge”. A cycle can be full if it has , or partial if [36]. In a characterization testing, a battery manufacturer must determine how many full cycles (or partial cycles at a rated depth of discharge) the battery will achieve [36], and then build the curve. Therefore, the charge and discharge energy in a manufacturer’s test cycle is , or similarly, . As a consequence, a lower bound on the battery charge and discharge energy over its lifetime can be
as long as during the BESS operation, the condition is satisfied. Equation (33) is a lower limit because it considers that charging and discharging operations whose is less than , as it happens under real-world conditions, prolong battery life as pointed out by authors in [37]. In addition, calculating the integral of that equation requires knowing an analytical function that fits the empirical curve from the manufacturer. For lithium-ion batteries, an exponentially decreasing relationship between the state of health and the number of cycles can approximate a real . Thus, consider the base function . Applying the expansion technique on the x-axis, and compression and displacement on the y-axis, this function can be adjusted to the desired exponential , i.e.,
where , , , and , , is a factor of non-linearity. Note that , and .
It is possible to show (through limits calculation) that Equation (34) is a family of curves between a linear approximation for SOH and the line , for ranging from 0 to 1, respectively, as illustrated in Figure 4. In fact, the non-linearity factor allows a fine adjustment to the SOH curve of interest, as the one provided by the manufacturer. As an example, data in [38] show curve of a Lithium-ion BESS of 6000 cycle life, and of 0.8, which fits for .
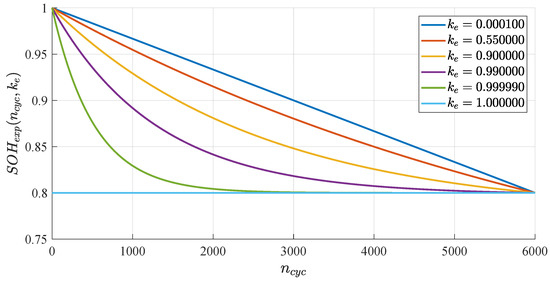
Figure 4.
Exponential approximation curves for state of health, where and .
As an example, consider a BESS of 140 kW/280 kWh, of 0.8, 6000 cycle life at of 0.90, of 0.92 (according to Table 6), where the cost of capital is 91,000 USD (real market data). Thus, using Equations (32) and (35), and assuming , the result is kWh, and USD/kWh, respectively.
As represents the cost of charging and discharging each kWh at the battery cells node, then the BESS powers in the objective function, whose reference is the main (bus) node, must be weighted by the efficiency of BESS, which is similar to consider
where is the portion of energy from that was stored.
Finally, in energy arbitrage applications, a microgrid can purchase energy during an off-peak period, at a price ($/kWh), and store it for use during an on-peak period, when the energy is more expensive (). Thus, the unit cost of energy after the storage process must be less than the on-peak price, i.e.,
If this relationship is not satisfied, the optimizer algorithm may decide not to use the storage system to perform energy arbitrage.
3.2.2. PV Costs
The capacity of solar photovoltaic generation can vary considerably according to the region where the solar panels are installed. For example, according to data in [39], the region of Curitiba (Brazil) has a generation capacity of about kWh/year per kW, at standard test conditions (STC), of solar panel (tilt , azimuth ), while the New York City has (tilt , azimuth ), considering system losses of 14% and inverter efficiency of 96% in both cases. As a consequence, given an annual amount of energy (kWh/year) to be generated by a PV system, its capital cost depends on the region of installation due to the local price and generation capacity, i.e.,
where ($/kW) is the local cost per kW of a installed PV system.
A PV system with an annual degradation rate of (%/year) should produce throughout its lifespan (years) an annual amount of energy of,
Similarly, the annual cost of generation can be proportional to the yearly energy generated, that is,
required that
Now, applying Equation (42) in Equation (39) to obtain the value of and then using the result in Equation (41), results in
For application in the day-ahead optimization model, the cost values must be daily. Thus, assuming an average daily cost of generation and an average daily capacity of generation in Equation (43) results in,
Authors in [40] summarized photovoltaic degradation rates using field tests reported in the literature. Results show an average degradation rate of %/year, which can be a practical value for . Furthermore, manufacturers usually offer a 25-year standard solar panel warranty, which can be a practical value for .
3.2.3. Other Costs
Costs in Table 4 are related to the operating states of the virtual disconnect switches, whereas those in Table 5 are related to the amount of energy for each operation. When participating in a free energy market, a microgrid may incur third-party service costs due to energy purchase and sale operations, which can be modeled by and . On the other hand, the market prices are covered in the model by and . Furthermore, in the present model, represents a penalty, imposed by the regulatory agency, for each operation of load disconnection performed by the microgrid, while it lasts. On the other hand, may represent a penalty due to the amount of disconnected load.
Finally, according to the modeling in the present study, if a cost does not apply to a given approach, it can be set zero.
4. Simulation Methodology
All results of the present paper were obtained through the implementation of the MG model, described in Section 3.1, in the MATLAB® software. The optimizer function intlinprog() was used to solve the MILP problem from Equation (31), subject to the constraints from Table 7. Furthermore, it was used a time resolution of 1/4 h, and time slots.
The BESS is a 140 kW/280 kWh LiFePO system with coupling transformer, where: (see Table 6), , , , , , , , and . Furthermore, according to the example from Section 3.2.1, USD/kWh, and from Equation (36), and are and USD/kWh respectively.
The solar PV system is the same from Section 3.2.2, for the city of Curitiba, with: kWh/year per kW, years, %, USD (market price). The average daily PV generation was defined according to the daily load , i.e., , where is the microgrid self-sufficiency, and is constant and equal to 2400 kWh. Thus, the daily cost of the PV system for the first year of use , calculated from Equation (44) and used in the simulations of this work is a function of the . USD, for , was used in the first three simulation cases. Furthermore, the PV generation curve was retrieved from [41], whose data are from a region in Africa and were collected on a sunny day of summer.
The load curve comes from field measurements of a group of middle-income residential consumers, which were collected during a business day [42].
The Brazilian time-of-use tariff, named White Tariff, was used to set the prices used in the simulations of this work. In the Brazilian captive energy market, customers can only buy electricity from an agent authorized to do the distribution service, typically the DSO. A regulatory agency (ANEEL) sets the price of energy, and the customer cannot negotiate it. However, the White Tariff allows customers to manage their consumption voluntarily according to the energy price. The regulated ToU time blocks are on-peak, off-peak, and pre and post-peak. Each energy distribution company can set its time blocks according to the load demand in its operation area. Table 8 shows the time blocks with their respective average periods [43]. Furthermore, it presents the weighted average of rates charged in Brazil for the conventional and ToU tariff. They were calculated considering data from 11 major energy distributors in Brazil [43], weighted by the number of customers of each company. In this table, ToU prices and time blocks define and (USD/kWh) used in this model. The conventional tariff was used as the reference price in Equation (45).

Table 8.
The Brazilian White Tariff; average time blocks were computed from 104 companies data; average prices were calculated from the 11 major energy distributors in Brazil, weighted by the number of customers of each company.
In load shedding simulations, it was adopted ($/kWh) as a penalty for the amount of disconnected load. Furthermore, in directly controllable loads simulations, it was adopted and , with (one hour) and (two hours and a half). All other costs whose values have not been mentioned have been set to zero.
Finally, although the model presented here is prepared to simulate external MGs supplying and acquiring energy from the microgrid, this feature was not explored in any simulation because it does not fit the adopted ToU tariff model.
4.1. Normalized Energy Bill
For results analysis purposes, it may be preferable to handle a normalized energy bill than to work with monetary values. To this end, consider a reference daily MG energy bill in which all distributed energy resources are turned off, that is,
where stands for a reference energy price. Therefore, the normalized energy bill is
can represent three distinct regions of operation for an MG: , , and , as Figure 5 shows. In the first, there was a relative increase in the energy bill; as an example, a microgrid could operate in this region when it is connected to the main grid with generation off, BESS in operation, and the purchase price of energy is constant throughout the day. Naturally, such a region should be avoided. In the second, there was a relative reduction in the energy bill; a microgrid can operate in this region when in the first mode of operation, however with energy prices favoring the practice of energy arbitrage. Finally, a microgrid can operate in the third region when in the previous operating modes, but with enough generation surplus to meet the load and still sell energy.
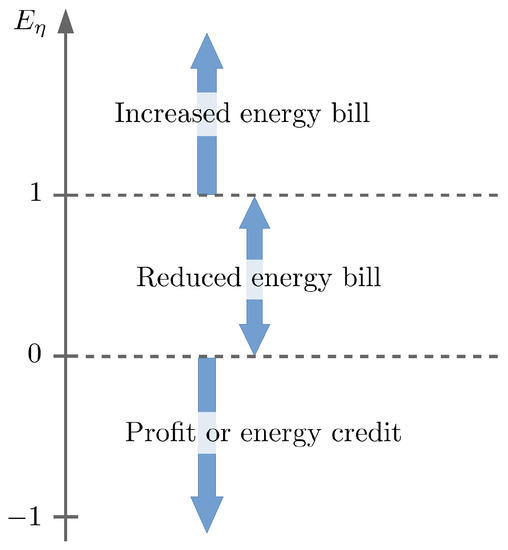
Figure 5.
Regions of MG operation represented by the normalized energy bill.
4.2. Simulation Cases
- Energy arbitrage as a result of the Brazilian White Tariff applied to a microgrid;
- MG scheduled intentional islanding using the resources of interruptible loads and PV output curtailment; two islanding periods: , from 02:00 to 05:15, and , from 10:30 to 12:30; .
- MG scheduled intentional islanding using the resources of interruptible loads, PV output curtailment, load shedding, and shiftable loads; two islanding periods: , from 02:00 to 06:00, and , from 10:30 to 12:30; .
- The impact of the microgrid self-sufficiency on the normalized energy bill; limit for energy import and export: kW; curves for , 16, 20, and 30% of .
5. Results
In power system buses with loads and generators connected, there is a convention in which the power generated is positive while the power consumed is negative [44]. Although in the modeling presented in this work all powers are positive, such a convention of signs was adopted in the figures throughout this section. This minimizes overlapping curves in the figures. Thus, the curves , , , and are shown with negative values. Furthermore, these quantities are included in parentheses in the legends of the figures. Figure 6 presents the main findings of simulation 1. The pre and pos-peak, and on-peak time blocks are represented by e , respectively. Figure 6a shows the curves that make up the balance of active powers in the microgrid. Figure 6b presents the BESS state of charge curve with its upper and lower bounds.
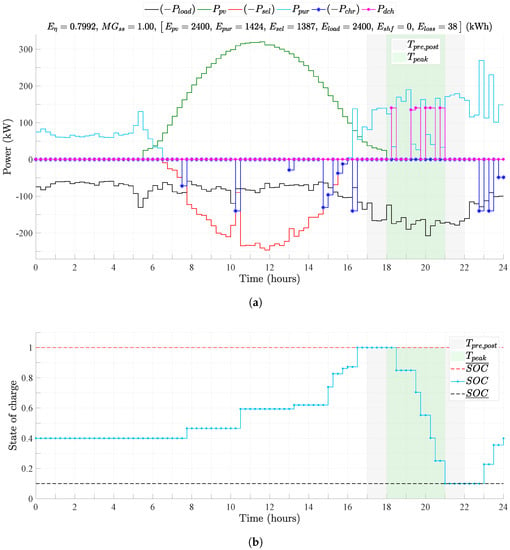
Figure 6.
Results of simulation 1. (a) Results of simulation 1 for the power balance curves; Ebill = 249.36 USD; Eloss represents energy losses throughout the day with BESS charging and discharging operations; Tpre,post stands for the pre and post-peak period; Tpeak is the on-peak period; (b) Results of simulation 1 for the BESS SOC.
Results show that, before solar generation begins, the microgrid has to import the energy necessary to supply its load. On the other hand, during the period of sunlight, the microgrid exports the PV generation surplus in addition to storing energy to use it during the on-peak period. As expected for the energy arbitrage simulation, the storage system reaches its maximum state of charge during the off-peak period and then performs a complete discharge to the lower limit during the on-peak. At the end of the day, the BESS is recharged to reach its final state of charge. Furthermore, the BESS performs a complete cycle throughout the day and presents an energy loss () of 38 kWh, which is the loss per full cycle of the storage system.
Figure 7 shows the results of simulation 2. Two islanding periods and were added to the simulation. The storage system has the role of avoiding load shedding in the first islanding, minimizing curtailment in the second, and performing energy arbitrage during the on-peak period. Although the results show that BESS reaches its maximum state of charge before the first islanding and performs a complete discharge during the same (Figure 7b), the stored energy is not sufficient to supply 100% of the microgrid load during that period. Thus, the interruptible load resource is required to complete the remaining energy and avoid load shedding, as illustrated in Figure 7a and expanded in Figure 7c; presents four pulses of 15 min long, at 02:45, 03:15, 04:00, and 04:15, during the first islanding, which contributes approximately 10 kWh to the energy balance for that period. In practice, each pulse can represent a temporary power reduction or even shutdown of interruptible load groups, such as air conditioners and water heaters.
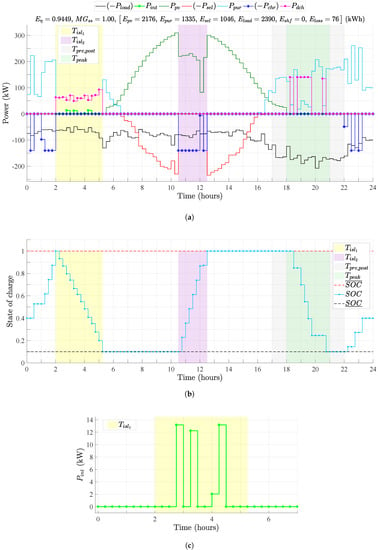
Figure 7.
Results of simulation 2. (a) Results of simulation 2 for the power balance curves; [Epvc = 223.85, Eint = 10.16] (kWh); Ebill = 294.82 USD; (b) Results of simulation 2 for the BESS SOC; (c) Expanding the curve of interruptible loads during the first period of islanding.
According to results, during the second islanding period, the BESS performs a full charge in response to the surplus of solar generation that cannot be injected into the main grid. Even so, a curtailment of kWh in the solar generation is expected for the next day. Besides, according to the optimal solution, all surplus energy produced outside the islanding must be exported to the main grid. Finally, BESS discharges during the on-peak period all energy stored during , performing the energy arbitrage, and then it returns to its initial state of charge.
Figure 8 illustrates the results of simulation 3, in which the first islanding period was increased by 45 min, and the shiftable load resource was added to the simulation. Results illustrated in Figure 8a show that although MG uses all its storage and interruptible loads resources (respecting the limit), it will be necessary to perform kWh of load shedding the next day, during the first islanding period.
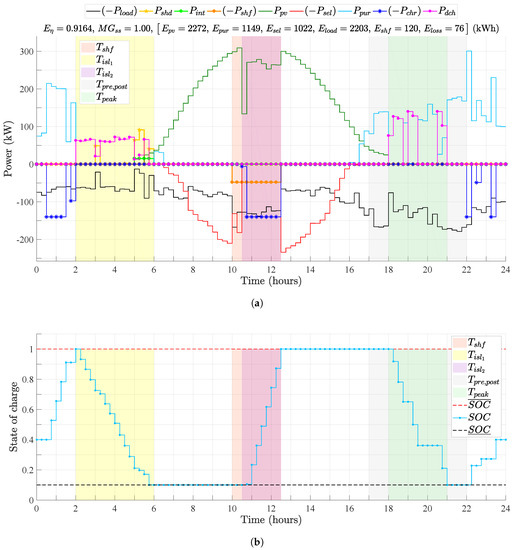
Figure 8.
Results of simulation 3. (a) Results of simulation 3 for the power balance curves; [Epvc = 127.85, Eshd = 61.98, Eint = 14.92] (kWh); Ebill = 285.92 USD; (b) Results of simulation 3 for the BESS SOC.
However, the use of shiftable loads allowed a drop in curtailment from 223.85 to 127.85 kWh during the second islanding. In the optimal solution, the optimizer reallocated 96 of the 120 kWh of shiftable loads taken from the on-peak period to the islanding period; the remaining 24 kWh were allocated in the half-hour before the second islanding. It is important to emphasize the optimizer performs the reallocation of shiftable loads in compliance with the continuous cycle requirement for this type of load. Finally, on this schedule (and the previous one), there should be a loss of 76 kWh due to the two full cycles to be performed by BESS the next day. In addition, the behavior of the BESS at the on-peak period is similar to simulations 1 and 2.
In the simulation 4, for a daily load of 2400 kWh (the same from previous simulations), the capacity of the PV system and the storage system were gradually increased. The storage system was configured as a percentage of the PV system capacity. Furthermore, the imported and exported energy at the microgrid PCC was limited by setting kW in the model. A simulation was performed for each setting, and an optimal solution was reached in each case. Figure 9 shows the curves obtained from simulations. No directly controllable load resources were used in those simulations.
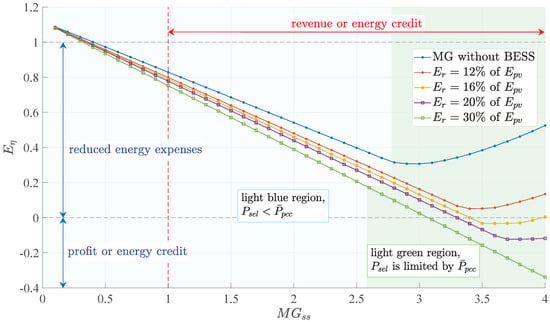
Figure 9.
Normalized energy bill for a sequence of simulations with increasing values of microgrid self-sufficiency; curves for BESS rated capacity () from 12% to 30% of the average daily PV system capacity (); kW; kWh; kWh.
All the curves start in the increased energy bill area where , because the microgrid does not have sufficient distributed energy resources to make economically attractive the participation in the White Tariff. From onwards, the curves enter the reduced energy expenses area where ; but only the curves of 16%, 20%, and 30% reach the profit or energy credit area (), for greater than or equal to 3.5, 3.3, and 3.1, respectively. In the light blue region (), the optimal use of the distributed energy resources is resulting in an energy export to the main grid whose power is less than the limit of 800 kW. On the other hand, the light green region contains the points for which this limit was reached. In that region, the generation surplus that cannot be exported must be stored by BESS. However, when the storage limit is reached, the curtailment process begins, which can be identified by the turning point of curves of 12%, 16%, and 20%. Similar reasoning can be applied to the MG without BESS curve. From the turning point onwards, the higher the capacity of the PV system, the more energy will be wasted, and by consequence, the more will be the cost of the microgrid, as can be seen in the figure for those curves. The turning point of the 30% curve is not shown in the figure as it must happen for .
Finally, although in this work, the MILP problem has thousands of variables and restrictions, the execution time in all simulations was less than 15 s on a personal computer of general use.
6. Discussion
Simulations presented in this work provide support to evaluate the proposed MG model. In general, results corroborate the consistency of the microgrid mathematical modeling proposed in this work. In practice, the MG used in the simulations can correspond to a medium to large industry, or to a residential area containing more than a hundred houses. Simulation 1 shows the Brazilian White Tariff can be economically attractive for a microgrid with solar generation and energy storage systems. In this example, a savings of 20% in the energy bill was observed. It is necessary to emphasize the energy arbitrage is directly related to the BESS costs. According to Equation (38), should be less than 0.0544 USD/kWh to enable energy arbitrage in the White Tariff; the value used in simulations, whose calculation is based on market data, was USD/kWh. Furthermore, the microgrid load profile used in this study presents an increase in consumption during peak hours, which helps to reduce the costs of a microgrid with BESS and to perform energy arbitrage.
The results of the second simulation highlight the role of the storage system when the microgrid is disconnected from the main system. In the first islanding, for more than three hours, the BESS can supply the microgrid load without requiring load shedding; in the second, the storage system can reduce the PV curtailment from 450.65 to 223.85 kWh (50.33%) in the next day.
Results also show directly controllable loads can play a complementary role to that of the storage system. In the second simulation, the optimizer algorithm makes use of interruptible loads during the first islanding to avoid load shedding. In the third, although it is not possible to prevent shedding, the results show the optimizer first exhausts the resource of interruptible loads and then uses the load shedding one; the cost to use the former is less than the penalty for using the latter. Regarding shiftable loads, the results of the third simulation show their use can also help to minimize the PV curtailment, which was reduced from 450.65 to 127.85 kWh (71.63%). Thus, even with the penalties of load shedding, the costs in the third simulation are lower than in the second.
Results of simulation 4 show that a BESS system can reduce the energy costs of a microgrid with operational limits (as in practice) at the PCC bus, in addition to the reduction achieved by the PV system. In this model, the energy balance of a full day of operation must be zero when the MG self-sufficiency is unitary, even when there is no BESS. This is because the microgrid uses the main grid as a battery of infinite capacity and power limited by to exchange energy with the grid both when it generates surplus energy and when it only demands energy. Thus, from onwards, the region in which there is an energy credit or revenue for the microgrid begins. However, making a profit from the generation of energy requires the revenue must exceed the costs of operating the microgrid. Thus, the results show that in practice reaching the profit region for this microgrid may require self-sufficiency as high as . Furthermore, the size of the storage system must be adequate for this purpose; otherwise, such a region may not be hit, as illustrated in Figure 9.
It is necessary to emphasize that in Brazil, the current captive energy market does not allow customers to sell the surplus energy, even in the White Tariff; however, it allows the accumulation of energy credits. In this market, a scenario with may not be economically attractive, since day after day there will be an accumulation of energy credits that cannot be traded. However, the model presented in this work has the purpose of being generic enough to be applied in other types of markets, including a free energy market and future markets that include microgrids and renewable energy resources.
Considering that load and solar generation forecasts can vary considerably over the year in a microgrid, then addressing the day-ahead scheduling problem for a single day may be a limitation of this work. A day-by-day analysis covering the four seasons as well as variations in load and solar generation forecasts could result in a richer set of simulation data. This type of analysis can be considered in future works. Furthermore, although in this work the decision variable for curtailment is continuous (a real number), in practice, it may be necessary to model this variable by ranges due to converter system technology limitations, which would make it an integer in the MILP problem. In addition, although the values used in this work are based on real market values, the results presented here must be interpreted with caution, as they are dependent on market prices for the PV system, the BESS, and the energy tariff.
7. Conclusions
This work aimed to model the optimal day-ahead scheduling problem in microgrids, filling some gaps found in mathematical modeling. Scheduled intentional islanding, shiftable loads of continuous cycle, the methodology for calculating the availability cost of PV and battery systems, and a comprehensive and detailed method for modeling battery energy storage systems are examples of gaps in modeling filled throughout this work. Although the microgrid resources have been modeled in detail, the linearity of the problem has been preserved, which contributes to simplifying its implementation in optimization software, and it helps to focus the work effort on modeling rather than optimization algorithms. Computational simulations validated the proposed model regarding all the modeled distributed energy resources and scheduled intentional islanding situations. A normalized energy bill approach was used as the variable to optimizing, and simulations were carried out to investigate how the microgrid self-sufficiency and the capacity of the storage system impact the normalized bill. Results showed a practical difficulty in reaching the region of profit operation.
The detailed mathematical modeling presented and validated in this work, covering the three types of distributed energy resources of a microgrid (renewables, storage, and controllable loads), can be relevant for microgrid operators and managers in the process of seeking economic efficiency through optimized use of their resources. Future works may examine the application of the model to an energy market with a framework of rules for free energy trading between entities, which can be multiple microgrids and as well as generation units distributed in an energy distribution network. Future work may also include an annual analysis of the optimal day-ahead scheduling problem. Finally, a study on the computational complexity and scalability of intra-day control of microgrids based on real-time data may also be a subject of future works.
Author Contributions
V.A.S. performed the literature review, conceptualization, methodology, software codification, simulations, validation, and writing. A.R.A. and G.L.-T. contributed to conceptualization, methodology, validation, and performed the review, corrections, supervision, advising, and funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Companhia Paranaense de Energia - COPEL research and technological development (RTD) program, through the PD-02866-0511/2019 project, regulated by ANEEL.
Acknowledgments
Alexandre Rasi Aoki thanks the grant for Technology Development of CNPq—National Council for Scientific and Technological Development within the Ministry of Science, Technology, Innovations, and Communications. Authors also thank the support of CAPES—Brazilian Federal Agency for Support and Evaluation of Graduate Education within the Ministry of Education of Brazil.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Faruqui, A.; Bourbonnais, C. The Tariffs of Tomorrow: Innovations in Rate Designs. IEEE Power Energy Mag. 2020, 18, 18–25. [Google Scholar] [CrossRef]
- Marnay, C.; Joos, G.; Iravani, R.; Mancarella, P.; Chatzivasileiadis, S. Microgrids 1, Engineering, Economics, & Experience—WG C6.22 Microgrids Evolution Roadmap; CIGRE: Paris, France, 2015. [Google Scholar]
- Ramli, M.A.; Bouchekara, H.; Alghamdi, A.S. Efficient Energy Management in a Microgrid with Intermittent Renewable Energy and Storage Sources. Sustainability 2019, 11, 3839. [Google Scholar] [CrossRef]
- Lee, G.H.; Park, J.Y.; Ham, S.J.; Kim, Y.J. Comparative Study on Optimization Solvers for Implementation of a Two-Stage Economic Dispatch Strategy in a Microgrid Energy Management System. Energies 2020, 13, 1096. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Crow, M.L. Stochastic Optimization of Renewable-Based Microgrid Operation Incorporating Battery Operating Cost. IEEE Trans. Power Syst. 2016, 31, 2289–2296. [Google Scholar] [CrossRef]
- Zhang, B.; Li, Q.; Wang, L.; Feng, W. Robust optimization for energy transactions in multi-microgrids under uncertainty. Appl. Energy 2018, 217, 346–360. [Google Scholar] [CrossRef]
- El-Hendawi, M.; Gabbar, H.; El-Saady, G.; Ibrahim, E.N. Control and EMS of a Grid-Connected Microgrid with Economical Analysis. Energies 2018, 11, 129. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, C.; Dong, Z. Interval Optimization Based Coordination of Demand Response and Battery Energy Storage System Considering SoC Management in A Microgrid. IEEE Trans. Sustain. Energy 2020, 1. [Google Scholar] [CrossRef]
- Kim, R.K.; Glick, M.B.; Olson, K.R.; Kim, Y.S. MILP-PSO Combined Optimization Algorithm for an Islanded Microgrid Scheduling with Detailed Battery ESS Efficiency Model and Policy Considerations. Energies 2020, 13, 1898. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, X.; Lin, D.; Calvin, M.M.; Morgan, J.C.; Qin, R.; Wang, C. Energy Management of Multiple Microgrids Based on a System of Systems Architecture. IEEE Trans. Power Syst. 2018, 33, 6410–6421. [Google Scholar] [CrossRef]
- Prudhviraj, D.; Kiran, P.B.S.; Pindoriya, N.M. Stochastic Energy Management of Microgrid with Nodal Pricing. J. Modern Power Syst. Clean Energy 2020, 8, 102–110. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J.; Wang, X. An improved charging/discharging strategy of lithium batteries considering depreciation cost in day-ahead microgrid scheduling. Energy Convers. Manag. 2015, 105, 675–684. [Google Scholar] [CrossRef]
- Liu, G.; Starke, M.; Xiao, B.; Zhang, X.; Tomsovic, K. Microgrid optimal scheduling with chance-constrained islanding capability. Electr. Power Syst. Res. 2017, 145, 197–206. [Google Scholar] [CrossRef]
- Kumar, K.P.; Saravanan, B. Day ahead scheduling of generation and storage in a microgrid considering demand Side management. J. Energy Stor. 2019, 21, 78–86. [Google Scholar] [CrossRef]
- Nguyen, A.D.; Bui, V.H.; Hussain, A.; Nguyen, D.H.; Kim, H.M. Impact of Demand Response Programs on Optimal Operation of Multi-Microgrid System. Energies 2018, 11, 1452. [Google Scholar] [CrossRef]
- Gao, H.; Liu, J.; Wang, L.; Wei, Z. Decentralized Energy Management for Networked Microgrids in Future Distribution Systems. IEEE Trans. Power Syst. 2018, 33, 3599–3610. [Google Scholar] [CrossRef]
- Ebrahimi, M.R.; Amjady, N. Adaptive robust optimization framework for day-ahead microgrid scheduling. Int. J. Electr. Power Energy Syst. 2019, 107, 213–223. [Google Scholar] [CrossRef]
- Esmaeili, S.; Anvari-Moghaddam, A.; Jadid, S. Optimal Operation Scheduling of a Microgrid Incorporating Battery Swapping Stations. IEEE Trans. Power Syst. 2019, 34, 5063–5072. [Google Scholar] [CrossRef]
- Huang, C.; Yue, D.; Deng, S.; Xie, J. Optimal Scheduling of Microgrid with Multiple Distributed Resources Using Interval Optimization. Energies 2017, 10, 339. [Google Scholar] [CrossRef]
- Baziar, A.; Kavoosi-Fard, A.; Zare, J. A Novel Self Adaptive Modification Approach Based on Bat Algorithm for Optimal Management of Renewable MG. J. Int. Learn. Syst. Appl. 2013, 5, 11–18. [Google Scholar] [CrossRef]
- Alqunun, K.; Guesmi, T.; Farah, A. Load shedding optimization for economic operation cost in a microgrid. Electr. Eng. 2020, 102, 779–791. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Goryashko, A.; Guslitzer, E.; Nemirovski, A. Adjustable robust solutions of uncertain linear programs. Math. Program. 2004, 99, 351–376. [Google Scholar] [CrossRef]
- Bertsimas, D.; Sim, M. The Price of Robustness. Oper. Res. 2004, 52, 35–53. [Google Scholar] [CrossRef]
- Nosratabadi, S.M.; Hooshmand, R.A.; Gholipour, E. A comprehensive review on microgrid and virtual power plant concepts employed for distributed energy resources scheduling in power systems. Renew. Sustain. Energy Rev. 2017, 67, 341–363. [Google Scholar] [CrossRef]
- IEEE. IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces: IEEE Std 1547-2018; IEEE: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Federal Energy Regulatory Commission—U.S. Department of Energy, Washington, DC. Assessment of Demand Response and Advanced Metering. 2012. Available online: https://www.ferc.gov/legal/staff-reports/12-20-12-demand-response.pdf (accessed on 1 April 2020).
- Deng, R.; Yang, Z.; Chow, M.Y.; Chen, J. A Survey on Demand Response in Smart Grids: Mathematical Models and Approaches. IEEE Trans. Ind. Inform. 2015, 11, 570–582. [Google Scholar] [CrossRef]
- Li, B.; Roche, R.; Miraoui, A. Microgrid sizing with combined evolutionary algorithm and MILP unit commitment. Appl. Energy 2017, 188, 547–562. [Google Scholar] [CrossRef]
- Divya, K.; Østergaard, J. Battery energy storage technology for power systems—An overview. Electr. Power Syst. Res. 2009, 79, 511–520. [Google Scholar] [CrossRef]
- Rodrigues, E.; Godina, R.; Santos, S.; Bizuayehu, A.; Contreras, J.; Catalão, J. Energy storage systems supporting increased penetration of renewables in islanded systems. Energy 2014, 75, 265–280. [Google Scholar] [CrossRef]
- Palizban, O.; Kauhaniemi, K. Energy storage systems in modern grids—Matrix of technologies and applications. J. Energy Stor. 2016, 6, 248–259. [Google Scholar] [CrossRef]
- Atlantic Clean Energy Supply LLC, Beijing. Customized ESS Solutions for Solar Farm & Micro Grid Application. 2019. Available online: https://www.atlanticces.com/wp-content/uploads/2019/11/100KW-with-350KWH.pdf (accessed on 29 March 2020).
- ABB. EssPro™ Energy Storage Power Conversion System (PCS). 2017. Available online: https://new.abb.com/power-converters-inverters/energy-storage-grid-stabilization/energy-storage-power-conversion-system-(pcs)/esspro-pcs (accessed on 22 February 2020).
- IEEE. IEEE Guide for Design, Operation, and Maintenance of Battery Energy Storage Systems, Both Stationary and Mobile, and Applications Integrated with Electric Power Systems: IEEE Std 2030.2.1-2019; IEEE: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Nehme, B.F.; Akiki, T.K.; Naamane, A.; M’Sirdi, N.K. Real-Time Thermoelectrical Model of PV Panels for Degradation Assessment. IEEE J. Photovolt. 2017, 7, 1362–1375. [Google Scholar] [CrossRef]
- Warner, J. Handbook of Lithium-Ion Battery Pack Design—Chemistry, Components, Types and Terminology; Elsevier Inc.: Amsterdam, The Netherlands, 2015; p. 239. [Google Scholar]
- Xu, B.; Oudalov, A.; Ulbig, A.; Andersson, G.; Kirschen, D.S. Modeling of Lithium-Ion Battery Degradation for Cell Life Assessment. IEEE Trans. Smart Grid 2018, 9, 1131–1140. [Google Scholar] [CrossRef]
- SAMSUNG SDI. Smart Battery Systems for Energy Storage: Lithium-ion. 2016. Available online: http://www.samsungsdi.com/upload/ess_brochure/Samsung%20SDI%20brochure_EN.pdf (accessed on 24 April 2020).
- PVWatts Calculator—NREL. Available online: https://pvwatts.nrel.gov/pvwatts.php (accessed on 17 April 2020).
- Jordan, D.C.; Kurtz, S.R. Photovoltaic Degradation Rates—An Analytical Review. 2012. Available online: https://www.nrel.gov/docs/fy12osti/51664.pdf (accessed on 17 April 2020).
- PVOUTPUT.ORG. 2020. Available online: https://pvoutput.org/ladder.jsp (accessed on 17 January 2020).
- Yamakawa, E.K. Sistema de Controle Nebuloso Para Bancos de Capacitores Automáticos Aplicados em Alimentadores de Distribuição de Energia Elétrica. Master’s Thesis, Federal University of Parana, Curitiba, Brazil, 2007. [Google Scholar]
- Agência Nacional de Energia Elétrica, Brasília. Postos Tarifários. 2020. Available online: https://www.aneel.gov.br/postos-tarifarios (accessed on 27 March 2020).
- Ponce, P.; Molina, A.; Mata, O.; Ibarra, L.; MacCleery, B. Power System Fundamentals, 1st ed.; CRC Press: Boka Raton, FL, USA, 2017; p. 445. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).