Energy Analysis and Exergy Optimization of Photovoltaic-Thermal Collector
Abstract
1. Introduction
2. Methodology
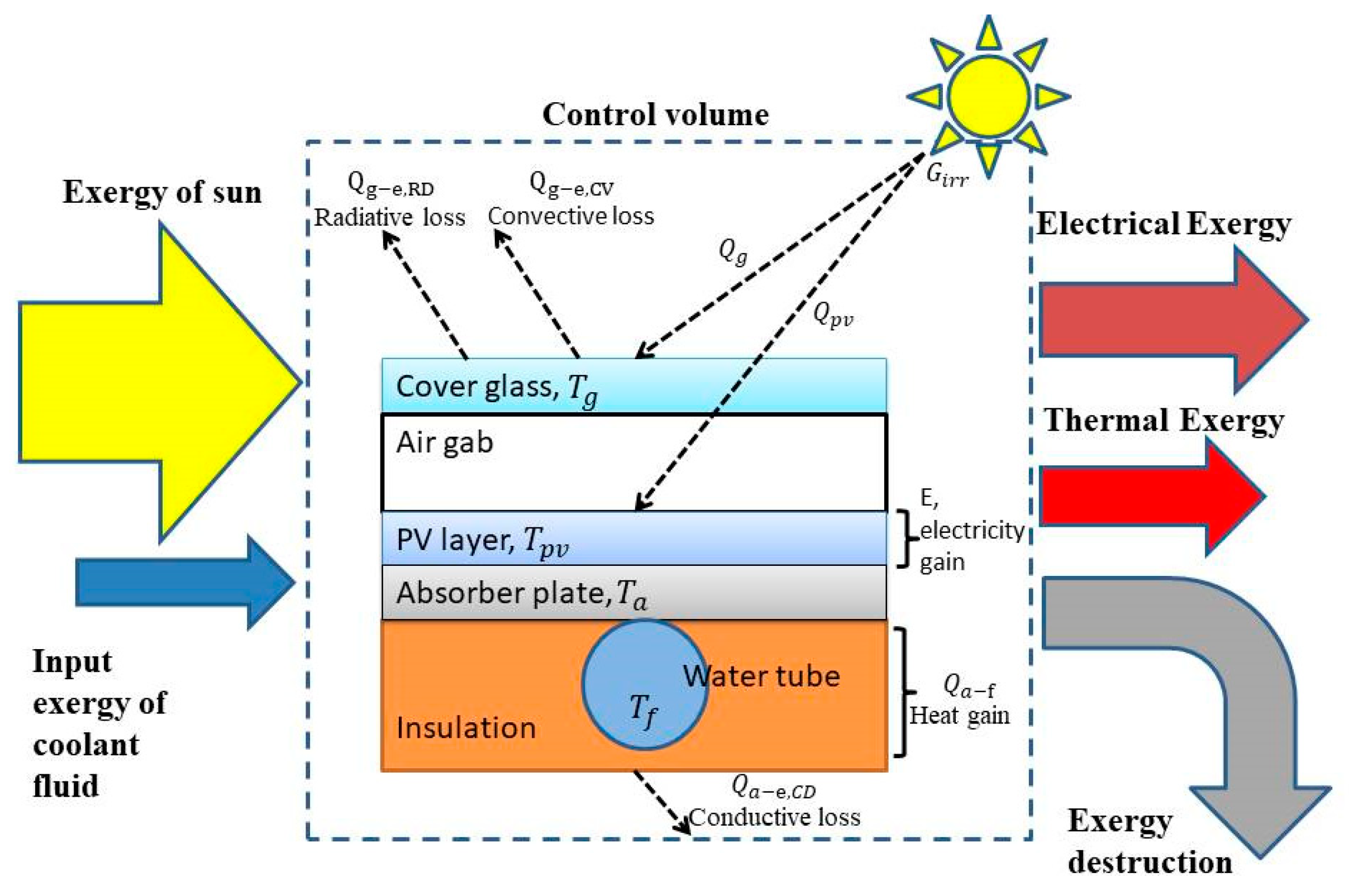
2.1. Description of Photovoltaic-Thermal (PVT) Collector
- The temperature distribution is uniform in the layers.
- It is assumed that there are no heat losses through the edges.
- The optical and thermal properties of the materials and fluids are constant.
- No surrounding shading or dust is taken into account.
- The thermal resistance between the layers is negligible.
- The ambient temperature is equal around the PVT collector.
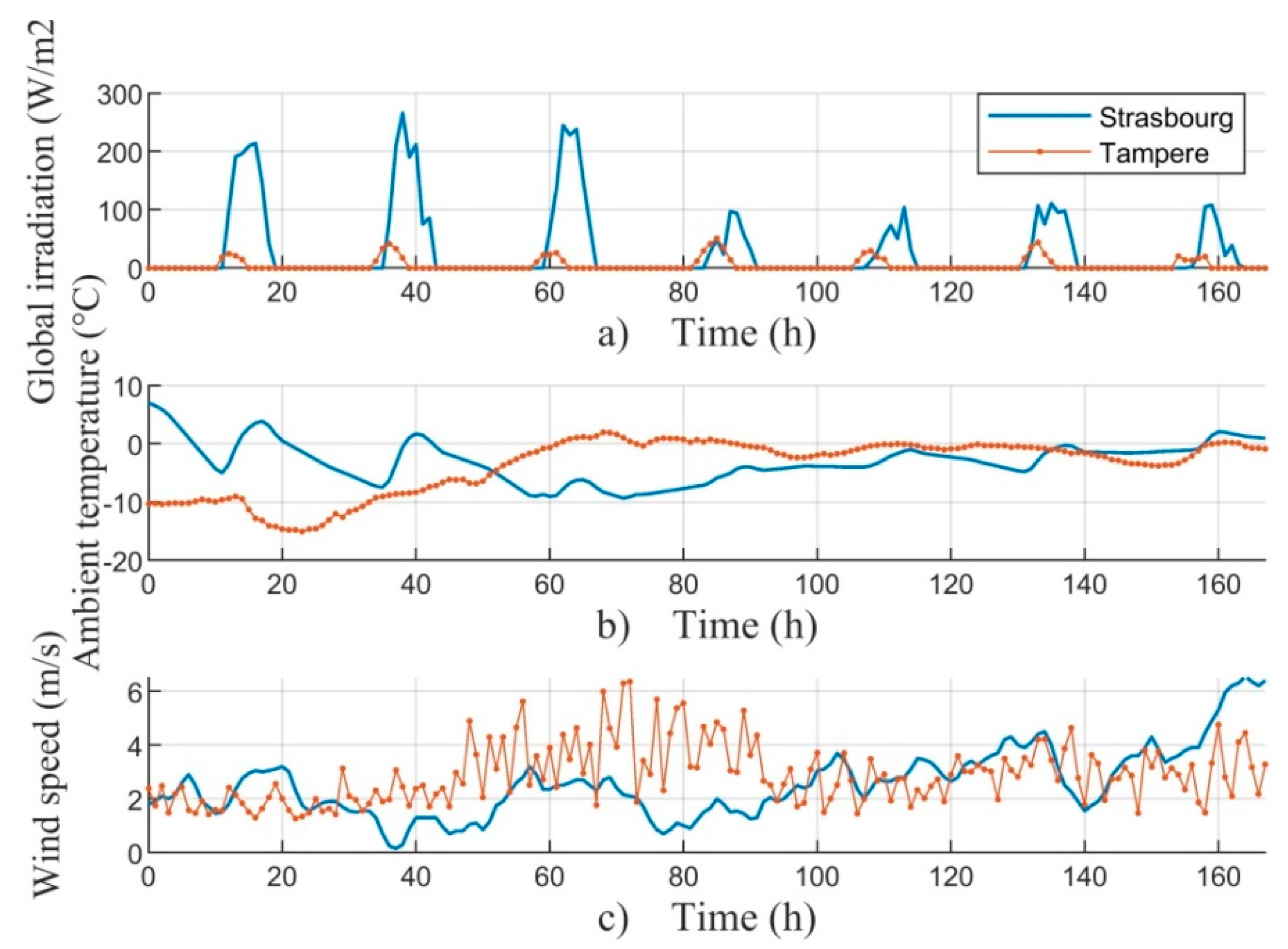
2.2. Meteorological Data
2.3. Mathematical Model
2.3.1. Numerical Model of PVT for Energy Analysis
2.3.2. Numerical Model for Exergy Analysis
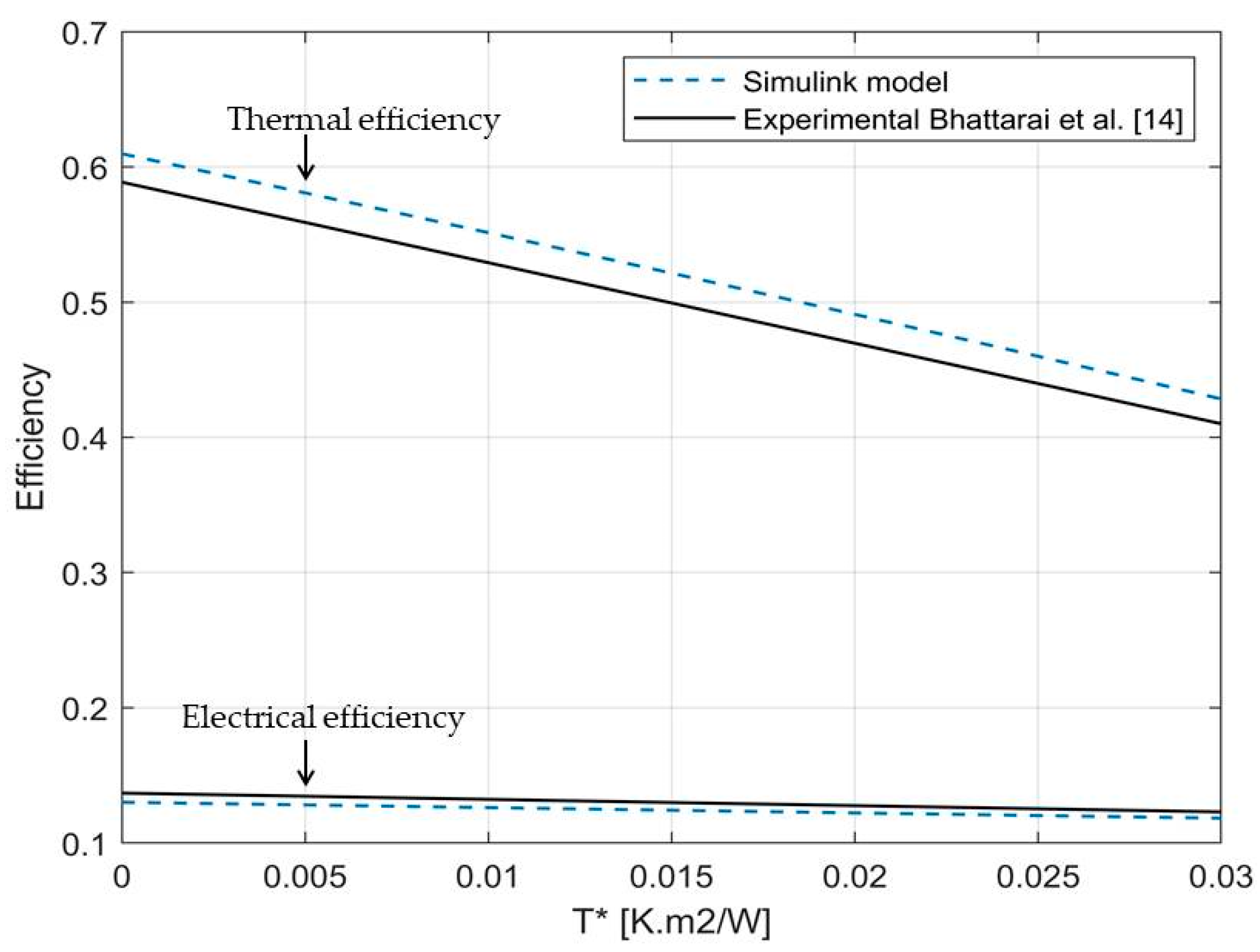
2.3.3. Model Validation
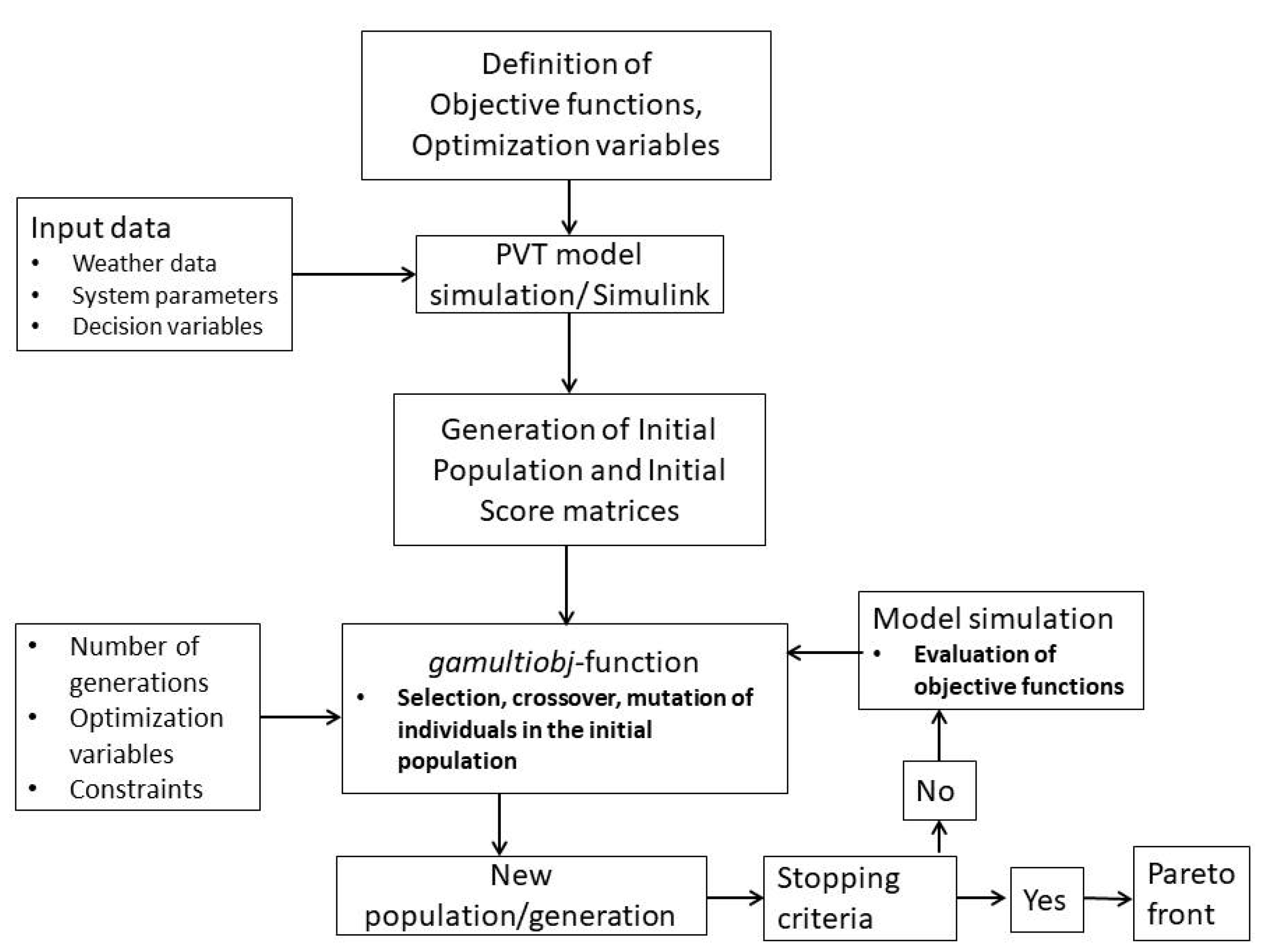
3. Multi-Objective Optimization of PVT Collector
Multi-Objective Optimization Using Gamultiobj Function
Subject to gj(x) ≥ 0, j = 1, 2, …, J;
hk(x) = 0, k = 1, 2, …, K;
xi(L) ≤ x ≤ xi(U), i = 1, 2, …, n;
4. Results and Discussion
4.1. Simulation Results
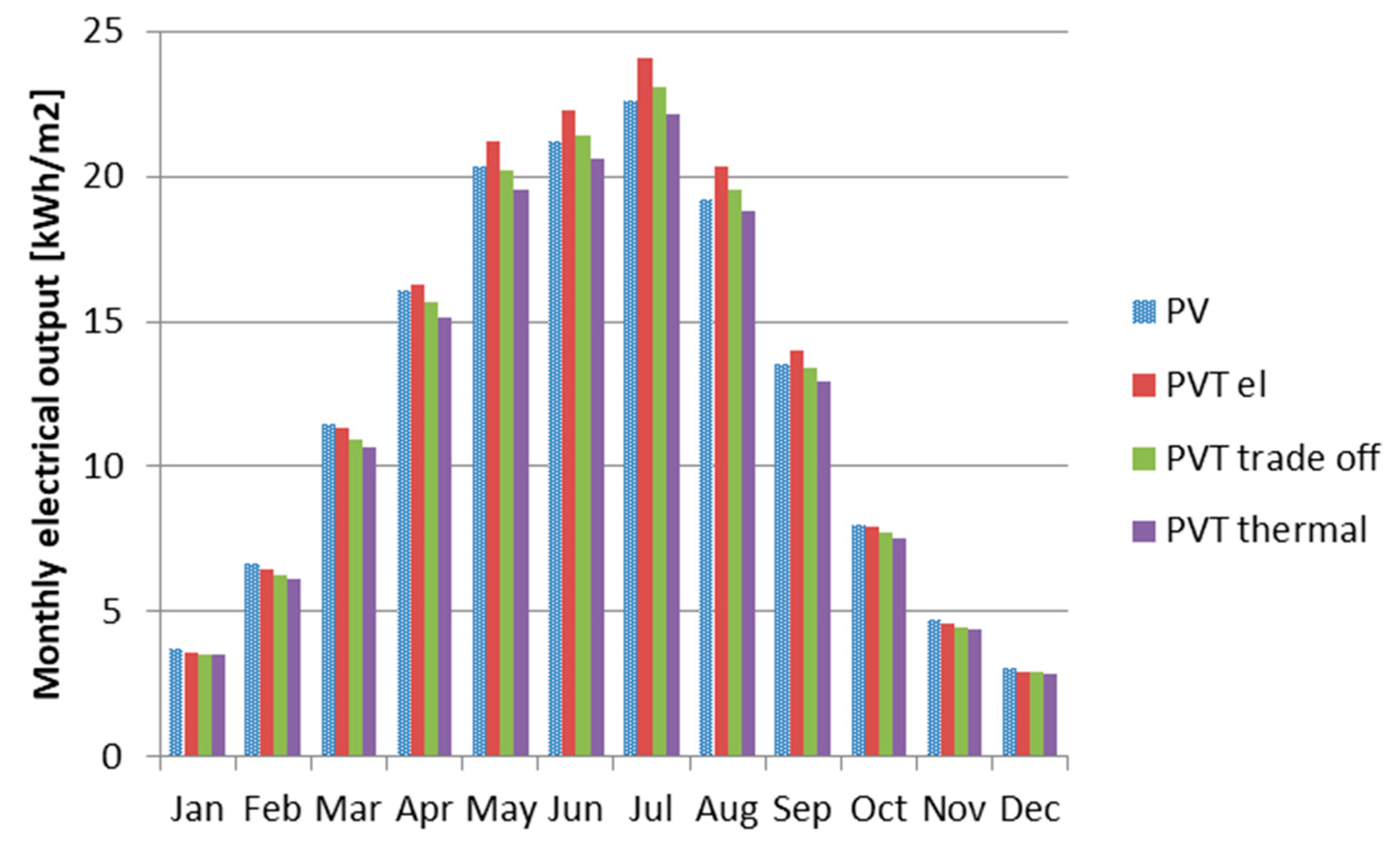
4.2. Comparison between PVT Collector and Photovoltaic (PV) Panel
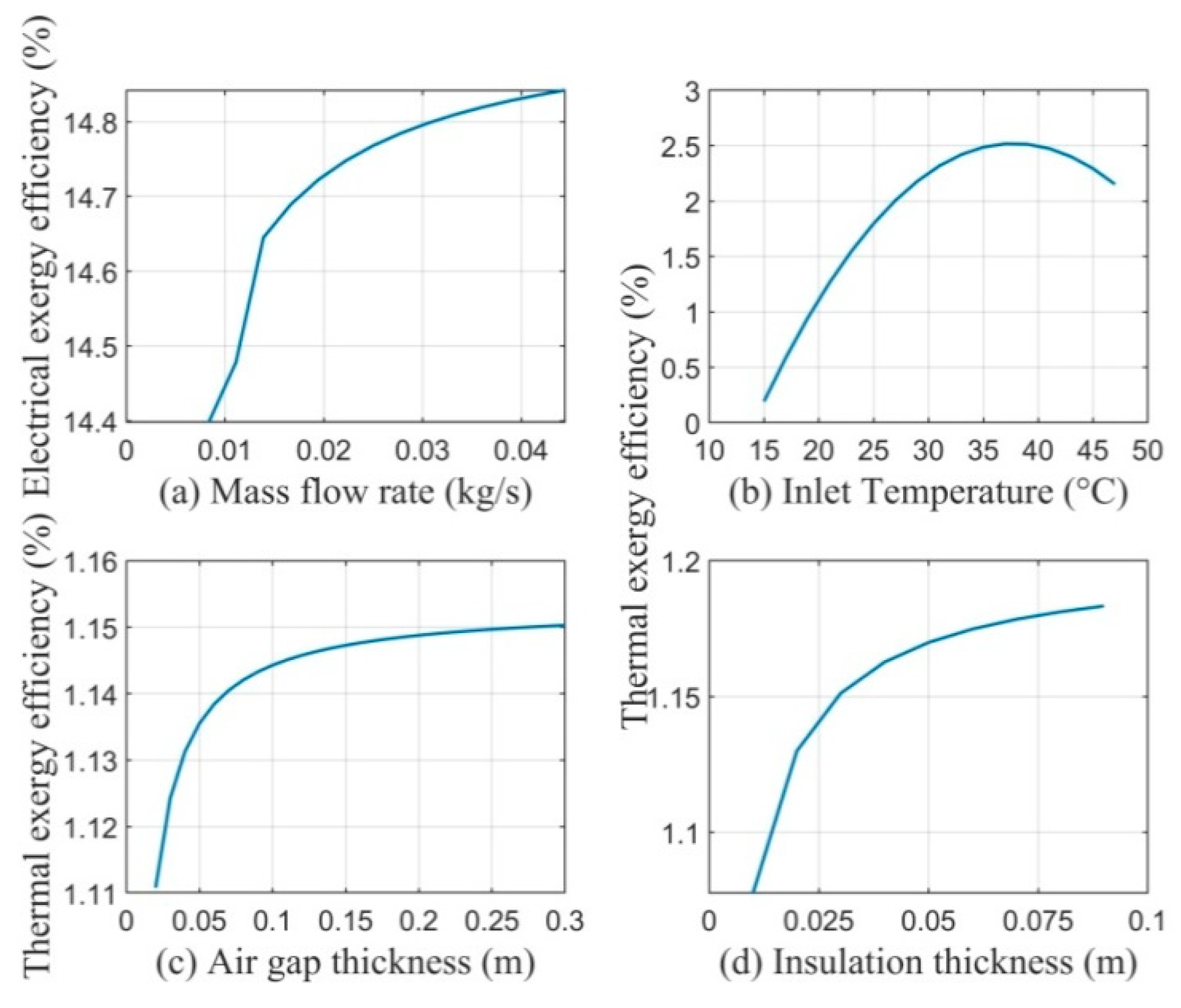
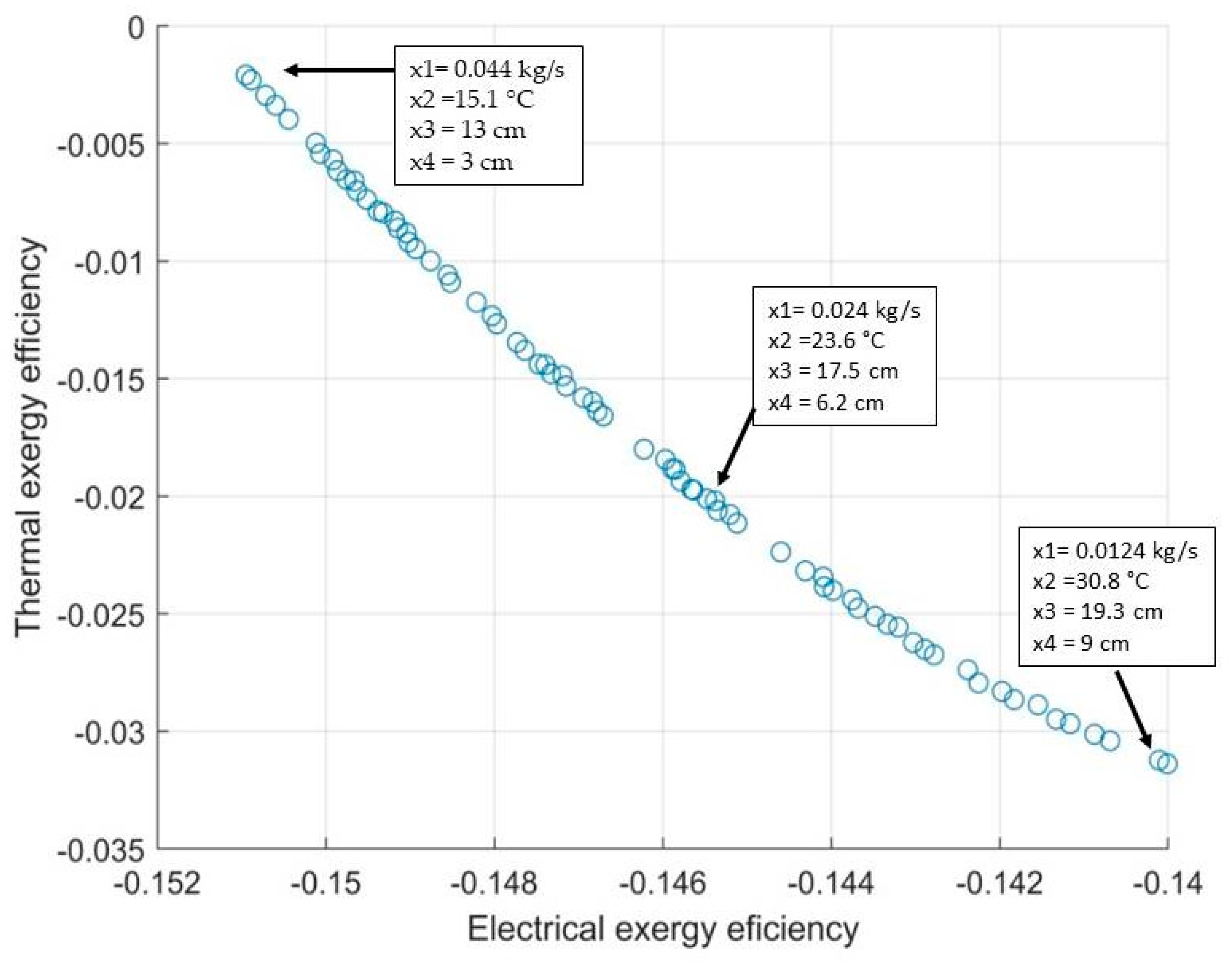
4.3. Multi-Objective Optimization
- Electric-driven: the priority is to maximize electricity production within the Pareto optimal;
- Thermal exergy-driven: the priority is to maximize thermal exergy production within the Pareto optimal;
- Trade-off solution: the priority is to produce optimally electricity and thermal exergy within the Pareto optimal front.
5. Conclusions
- Despite the northern location of Tampere, the similar electric power generation conditions were reached during the summer period than in Strasbourg.
- The monthly electrical efficiency reached 0.4–6.8% higher values in the northern location due to the cooler ambient conditions and lower PV cell operating temperature. However, during the summer months, the electrical efficiency was 13.8% in both locations.
- The annual thermal and electrical energy production and solar gain were 8.4%, 5.8% and 6.2%, respectively, higher in Strasbourg than Tampere. The total annual energy production was 7.7% higher in Strasbourg.
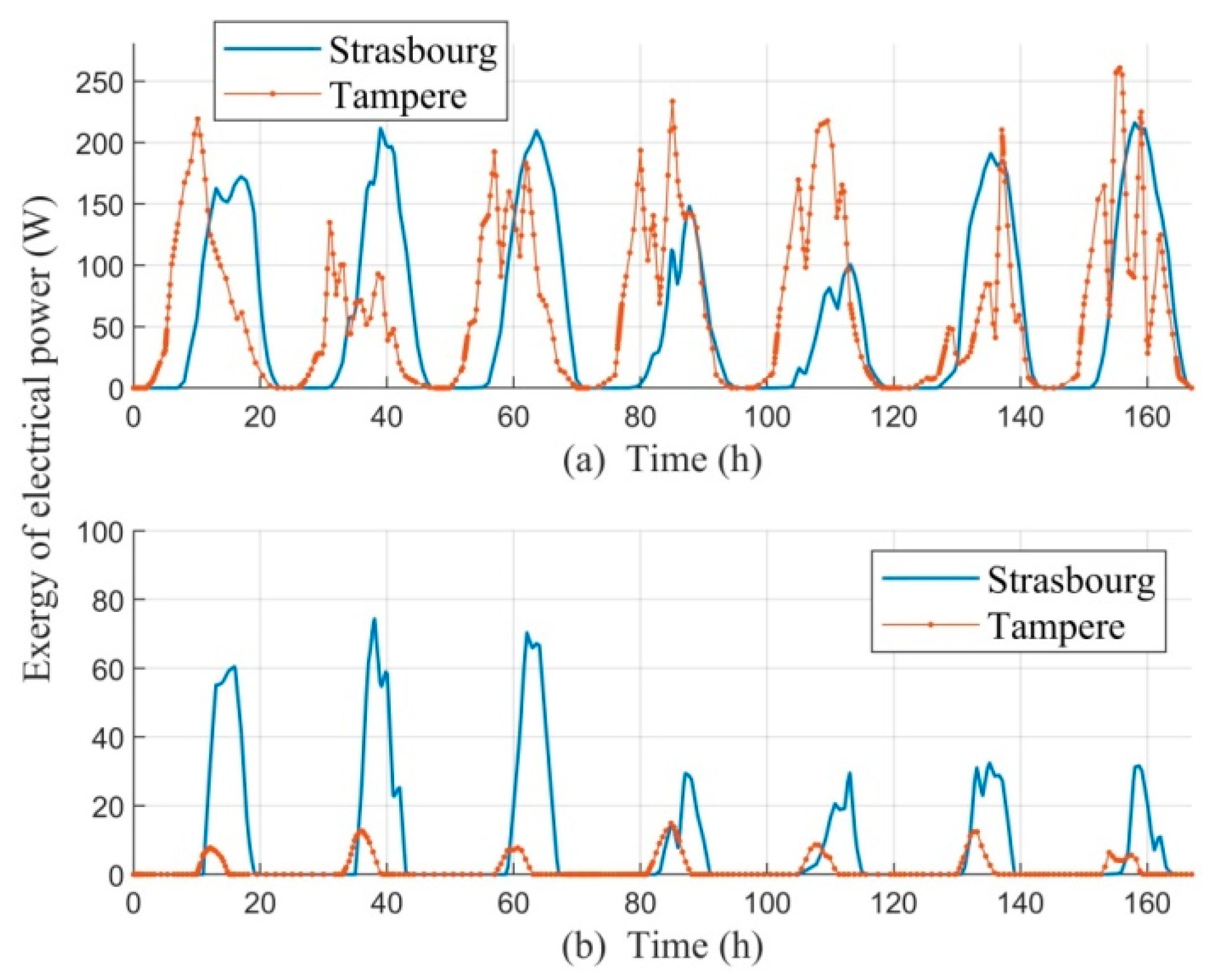
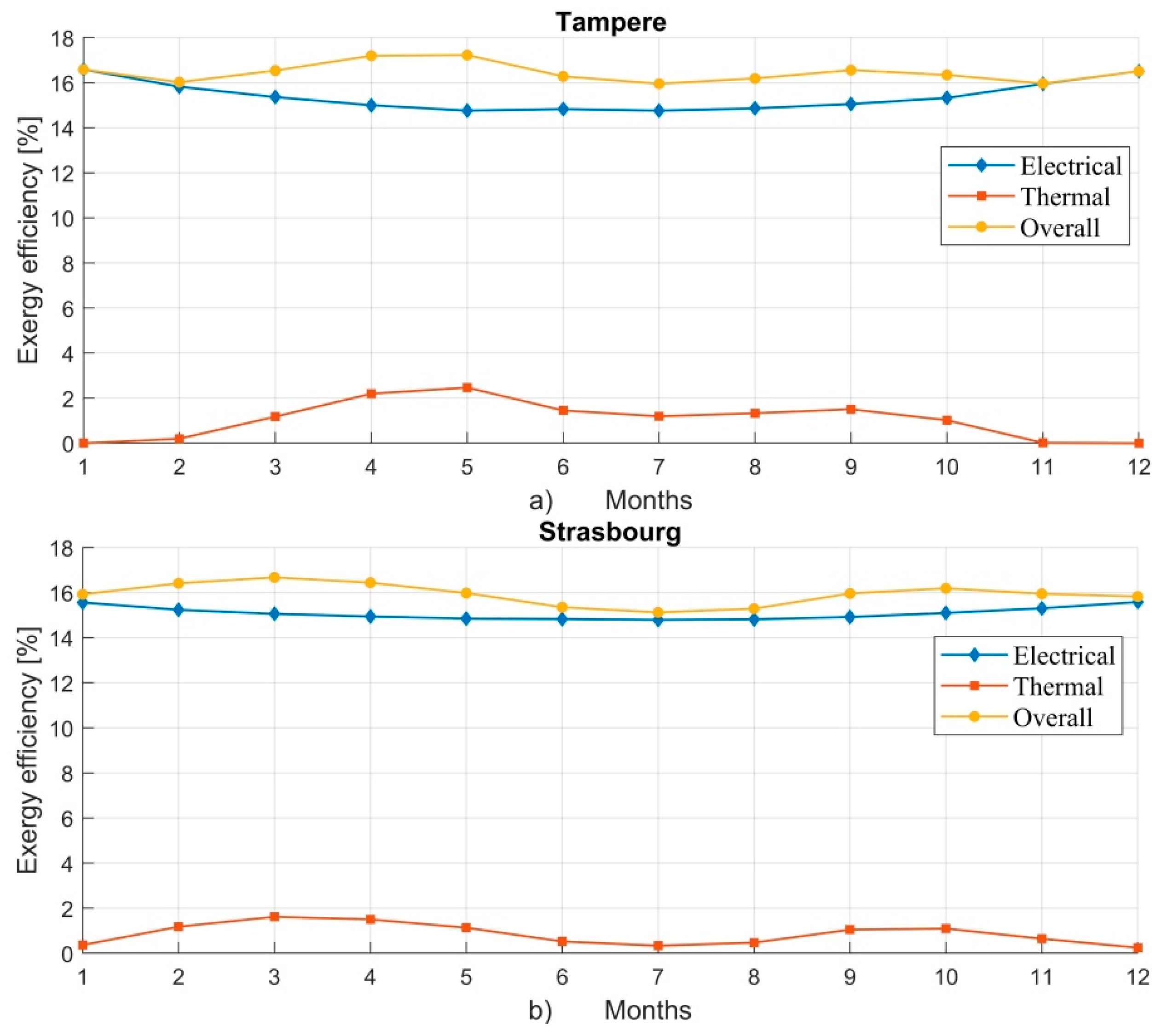
- Based on the exergy analysis, the thermal energy produced in the northern location of Tampere was of “higher quality” because the thermal exergy production in Tampere was 72.9% higher than Strasbourg. However, the total exergy production was 1.27% higher in Strasbourg than Tampere because of 5.8% higher electrical exergy production.
- The climate conditions with high solar irradiation but relatively low temperatures are favorable for thermal exergy production.
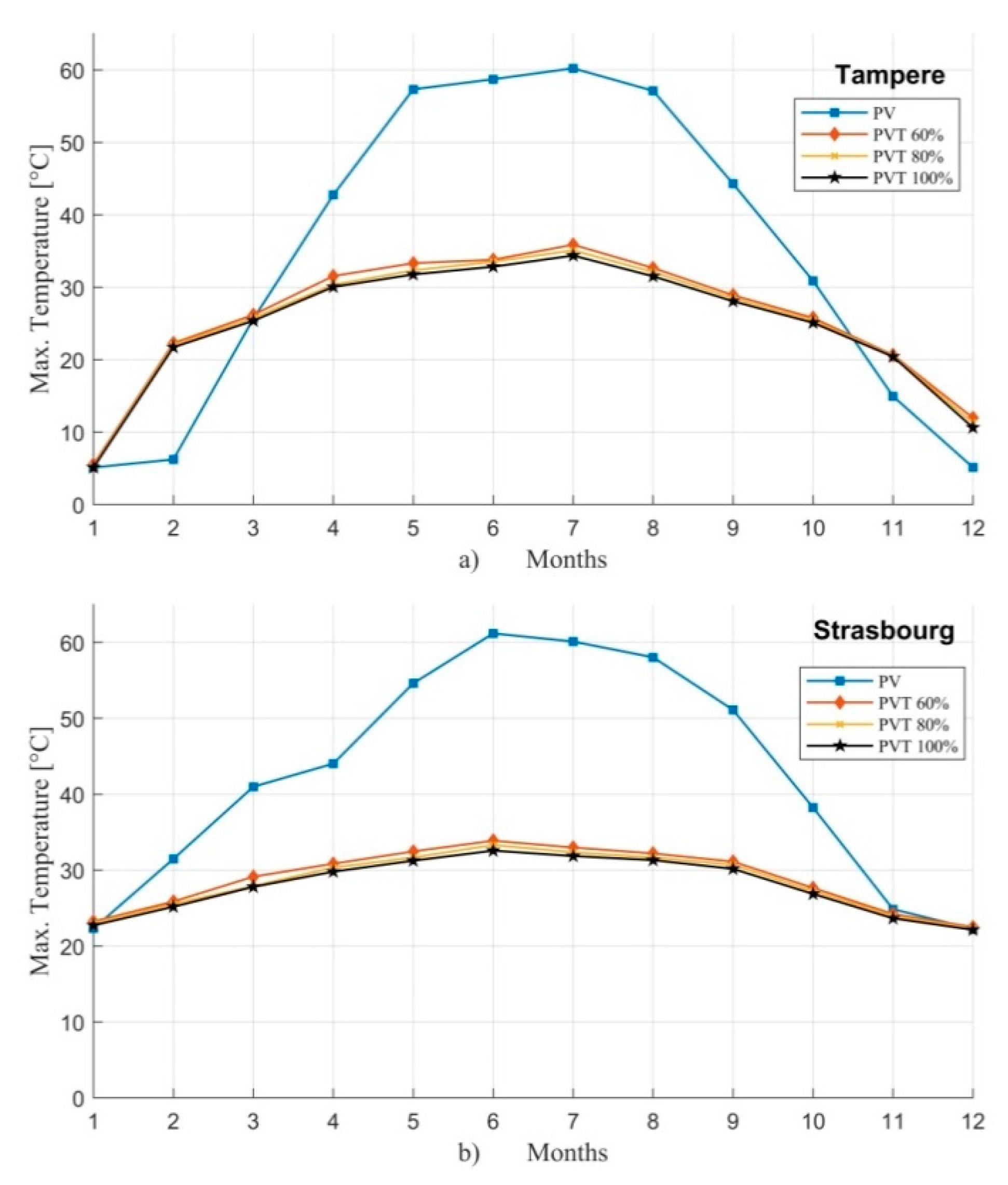
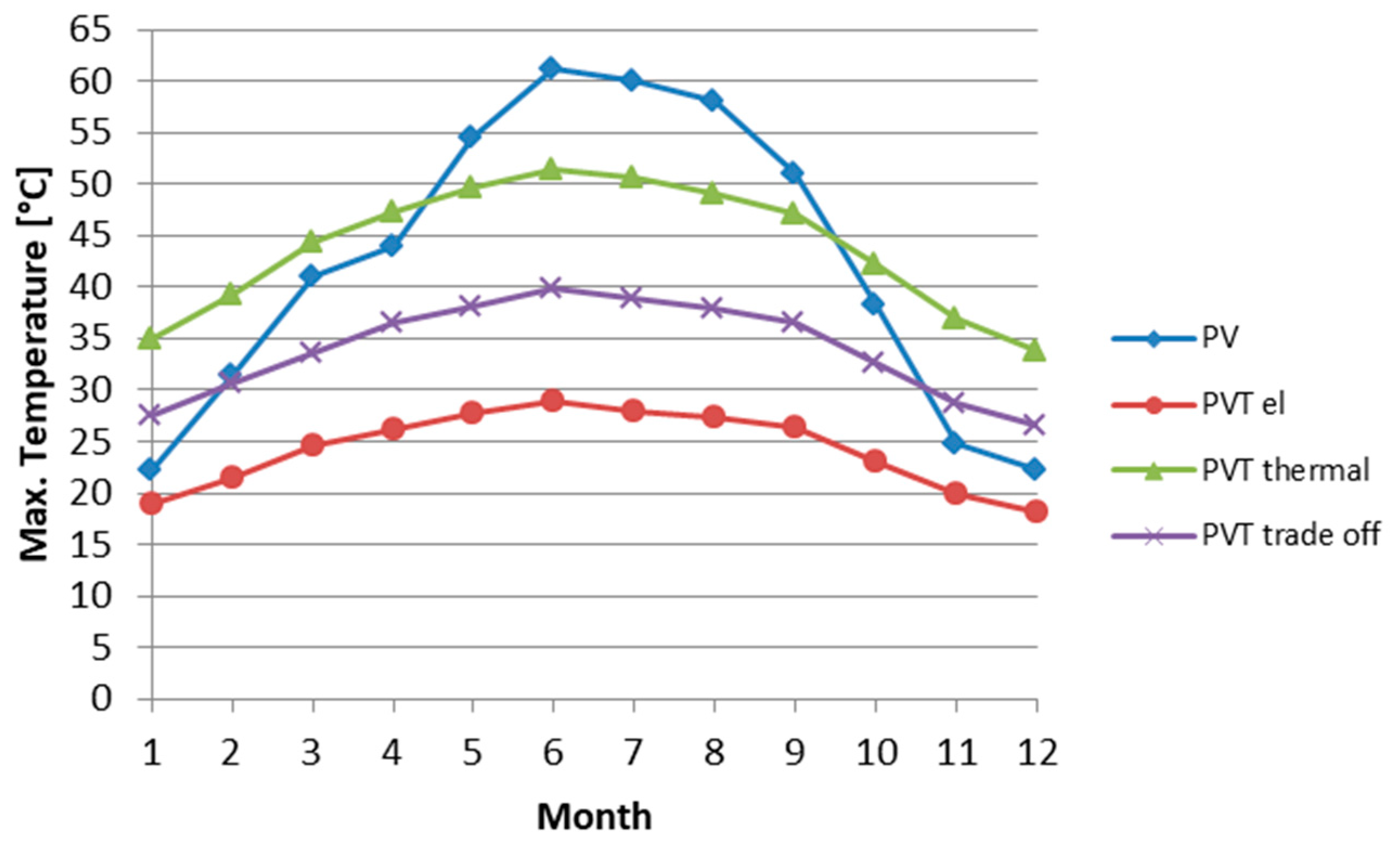
- In both locations, the monthly maximum PVT operating temperatures were lower than in the PV panel. The maximum operating temperature of the PVT was around 32–35 °C and of the PV 60–61 °C. The lower operating temperatures resulted in around 1%-unit higher cell efficiency in the PVT compared to the PV panel.
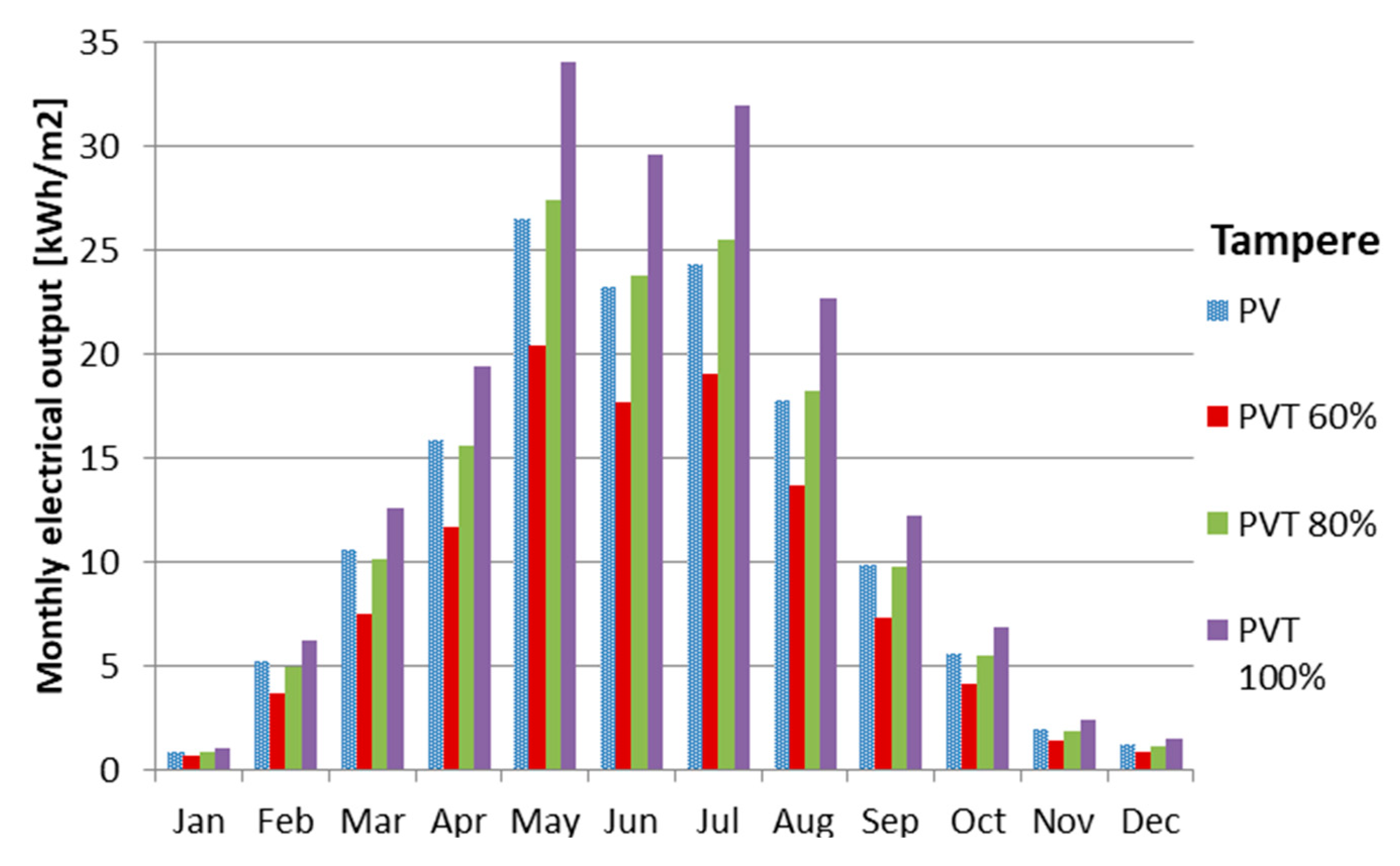
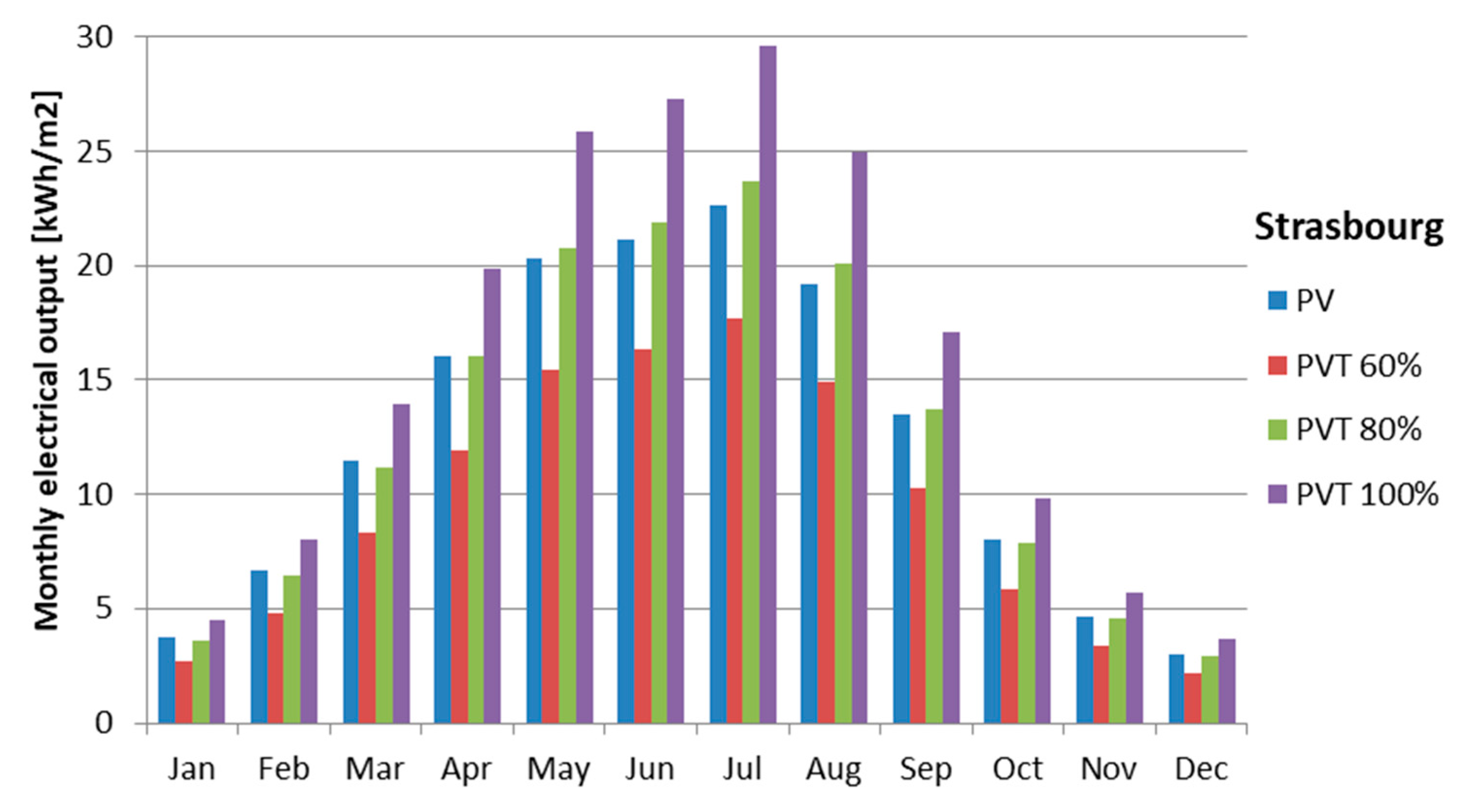
- The electrical output was significantly influenced by the PVT packing factor. The fully packed PVT collector resulted in the 26% higher annual electrical output than the PV panel.
- The PVT collector had a higher electrical output during the summer months compared to the PV panel.
- The annual PVT electrical output is competitive with the PV panel.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | area, m2 |
| c | specific heat, J/(kg K) |
| D | diameter, m |
| E | DC power, energy, W |
| Ex | exergy, W |
| G | solar irradiation density, W/m2 |
| H | thickness, m |
| h | heat transfer coefficient, W/(m2 K) |
| k | thermal conductivity, W/(mK) |
| L | length, m |
| M | number of objectives |
| m | mass, kg |
| mass flow rate, kg/s | |
| N | number of collectors |
| Nu | Nusselt number |
| P | power, W |
| Pr | Prandlt number |
| Q | heat flux, W |
| Re | Reynolds number |
| r | packing factor |
| T | temperature, °C, K |
| T* | reduced temperature, K m2/W |
| U | internal energy, J |
| v | wind speed, m/s |
| W | tube spacing, m |
| Greek symbols | |
| η | efficiency |
| α | absorbance |
| (ατ) | effective absorbance |
| β | temperature coefficient, %/K |
| ε | emissivity |
| ξ | exergy efficiency |
| τ | transmittance |
| ρ | density, kg/m3 |
| σ | Stefan–Boltzmann constant, W/m2/K4 |
| Subscripts | |
| a | absorber |
| adh | adhesive layer |
| c | collector |
| CD | conduction |
| CV | convection |
| d | destruction |
| e | environment |
| el | electrical |
| f | fluid |
| fin | fluid inlet |
| fout | fluid outlet |
| g | glass cover |
| gap | air gap |
| irr | irradiation |
| o | outer |
| pv | photovoltaic |
| PVg | photovoltaic glass |
| RD | radiation |
| sol | solar |
| ted | tedlar layer |
| th | thermal |
| tot | total |
| 0 | reference |
References
- Martinez, S.; Michaux, G.; Salagnac, P.; Faure, J. Numerical Investigation of Energy Potential and Performance of a Residential Building—Integrated Solar—Chp System. In Proceedings of the System Simulation in Buildings 2018: SSB20182018, Liège, Belgium, 10–12 December 2018; pp. 1–20. [Google Scholar]
- Vera, J.T.; Laukkanen, T.; Sirén, K. Performance evaluation and multi-objective optimization of hybrid photovoltaic-thermal collectors. Sol. Energy 2014, 102, 223–233. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, X.; Smith, S.; Xu, J.; Yu, X. Review of R&D progress and practical application of the solar photovoltaic/thermal (PV/T) technologies. Renew. Sustain. Energy Rev. 2012, 16, 599–617. [Google Scholar] [CrossRef]
- Lee, J.H.; Hwang, S.G.; Lee, G.H. Efficiency improvement of a photovoltaic thermal (PVT) system using nanofluids. Energies 2019, 12, 491. [Google Scholar] [CrossRef]
- Farzanehnia, A.; Sardarabadi, M. Exergy Its Application—Toward Green Energy Production and Sustainable Environment. In Exergy in Photovoltaic/Thermal Nanofluid-Based Collector Systems; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef]
- Han, X.; Chen, X.; Wang, Q.; Alelyani, S.M.; Qu, J. Investigation of CoSO4-based Ag nanofluids as spectral beam splitters for hybrid PV/T applications. Sol. Energy 2019, 177, 387–394. [Google Scholar] [CrossRef]
- Walshe, J.; Carron, P.M.; McLoughlin, C.; McCormack, S.; Doran, J.; Amarandei, G. Nanofluid Development Using Silver Nanoparticles and Organic-Luminescent Molecules for Solar-Thermal and Hybrid Photovoltaic-Thermal Applications. Nanomaterials 2020, 10, 1201. [Google Scholar] [CrossRef]
- Yazdanpanahi, J.; Sarhaddi, F.; Adeli, M.M. Experimental investigation of exergy efficiency of a solar photovoltaic thermal (PVT) water collector based on exergy losses. Sol. Energy 2015, 118, 197–208. [Google Scholar] [CrossRef]
- Feidt, M.; Costea, M. Energy and Exergy Analysis and Optimization of Combined Heat and Power Systems. Comparison of Various Systems. Energies 2012, 5, 3701–3722. [Google Scholar] [CrossRef]
- Feidt, M. Two examples of exergy optimization regarding the “thermo-frigopump” and combined heat and power systems. Entropy 2013, 15, 544–558. [Google Scholar] [CrossRef]
- Evola, G.; Marletta, L. Exergy and thermoeconomic optimization of a water-cooled glazed hybrid photovoltaic/thermal (PVT) collector. Sol. Energy 2014, 107, 12–25. [Google Scholar] [CrossRef]
- Calise, F.; Figaj, R.D.; Vanoli, L. Experimental and Numerical Analyses of a Flat Plate Photovoltaic/Thermal Solar Collector. Energies 2017, 10, 491. [Google Scholar] [CrossRef]
- Chow, T.T. Performance analysis of photovoltaic-thermal collector by explicit dynamic model. Sol. Energy 2003, 75, 143–152. [Google Scholar] [CrossRef]
- Bhattarai, S.; Oh, J.H.; Euh, S.H.; Kafle, G.K.; Kim, D.H. Simulation and model validation of sheet and tube type photovoltaic thermal solar system and conventional solar collecting system in transient states. Sol. Energy Mater. Sol. Cells 2012, 103, 184–193. [Google Scholar] [CrossRef]
- Da Silva, R.M.; Fernandes, J.L.M. Hybrid photovoltaic/thermal (PV/T) solar systems simulation with Simulink/Matlab. Sol. Energy 2010, 84, 1985–1996. [Google Scholar] [CrossRef]
- Barbu, M.; Darie, G.; Siroux, M. Analysis of a residential photovoltaic-thermal (PVT) system in two similar climate conditions. Energies 2019, 12, 3595. [Google Scholar] [CrossRef]
- Dubey, S.; Tiwari, G.N. Analysis of PV/T flat plate water collectors connected in series. Sol. Energy 2009, 83, 1485–1498. [Google Scholar] [CrossRef]
- Herrando, M.; Ramos, A.; Freeman, J.; Zabalza, I.; Markides, C.N. Technoeconomic modelling and optimisation of solar combined heat and power systems based on flat-box PVT collectors for domestic applications. Energy Convers. Manag. 2018, 175, 67–85. [Google Scholar] [CrossRef]
- Abdul-Ganiyu, S.; Quansah, D.A.; Ramde, E.W.; Seidu, R.; Adaramola, M.S. Investigation of solar photovoltaic-thermal (PVT) and solar photovoltaic (PV) performance: A case study in Ghana. Energies 2020, 13, 2701. [Google Scholar] [CrossRef]
- Vera, J.T.; Laukkanen, T.; Sirén, K. Multi-objective optimization of hybrid photovoltaic-thermal collectors integrated in a DHW heating system. Energy Build. 2014, 74, 78–90. [Google Scholar] [CrossRef]
- Ouhsiane, L.; Siroux, M.; El Ganaoui, M.; Mimet, A. Multi-Objective Optimization of Hybrid PVT Solar Panels. In Proceedings of the 2018 International Conference on the Industrial and Commercial Use of Energy (ICUE 2018), Cape Town, South Africa, 2–7 October 2018. [Google Scholar] [CrossRef]
- Conti, P.; Schito, E.; Testi, D. Cost-benefit analysis of hybrid photovoltaic/thermal collectors in a nearly zero-energy building. Energies 2019, 12, 1582. [Google Scholar] [CrossRef]
- Sobhnamayan, F.; Sarhaddi, F.; Alavi, M.A.; Farahat, S.; Yazdanpanahi, J. Optimization of a solar photovoltaic thermal (PV/T) water collector based on exergy concept. Renew. Energy 2014, 68, 356–365. [Google Scholar] [CrossRef]
- Wohlfeil, A. CARNOT Toolbox. FH Aachen. Available online: https://fh-aachen.sciebo.de/index.php/s/0hxub0iIJrui3ED (accessed on 12 August 2020).
- Aste, N.; Leonforte, F.; Del Pero, C. Design, modeling and performance monitoring of a photovoltaic-thermal (PVT) water collector. Sol. Energy 2015, 112, 85–99. [Google Scholar] [CrossRef]
- Ilmatieteen Laitos Kuukausitilastot—Ilmatieteen Laitos. Available online: https://www.ilmatieteenlaitos.fi/kuukausitilastot (accessed on 12 August 2020).
- Prevision-meteo.ch. Relevés Mensuels de Strasbourg pour L’année en Cours. Available online: https://www.prevision-meteo.ch/climat/mensuel/strasbourg (accessed on 12 August 2020).
- McAdams, W.H. Heat Transmission, 3rd ed.; McGraw-Hill: New York, NY, USA, 1954. [Google Scholar]
- Guarracino, I.; Mellor, A.; Ekins-Daukes, N.J.; Markides, C.N. Dynamic coupled thermal-and-electrical modelling of sheet-and-tube hybrid photovoltaic/thermal (PVT) collectors. Appl. Therm. Eng. 2016, 101, 778–795. [Google Scholar] [CrossRef]
- Touafek, K.; Khelifa, A.; Adouane, M. Theoretical and experimental study of sheet and tubes hybrid PVT collector. Energy Convers. Manag. 2014, 80, 71–77. [Google Scholar] [CrossRef]
- Hollands, K.G.T.; Unny, T.E.; Raithby, G.D.; Konicek, L. Free Convective Heat Transfer Across Inclined Air Layers. Am. Soc. Mech. Eng. 1975, 98, 189–193. [Google Scholar] [CrossRef]
- Incropera, F. Fundamentals of Heat and Mass Transfer; John Wiley and Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Kalyanmoy, D. Multi-Objective Optimization using Evolutionary Algorithms; John Wiley and Sons: Chichester, UK, 2001. [Google Scholar]






| Property | Glass | Air Gap | PV | Thermal Absorber | Fluid | Insulation | Unit |
|---|---|---|---|---|---|---|---|
| Emissivity (ε) | 0.88 | - | 0.96 | - | - | - | - |
| Absorbance (α) | 0.1 | - | 0.9 | - | - | - | - |
| Transmittance (τ) | 0.93 | - | - | - | - | - | - |
| Thickness (H) | 0.004 | 0.02 | 0.0002 | 0.0002 | - | 0.015 | m |
| Area (A) | 2 | 2 | 1.6 | 2 | - | 2 | m2 |
| Mass flow | - | - | - | - | 0.044 | - | kg/s |
| Density (ρ) | 2200 | - | 2330 | 2702 | 1050 | 20 | kg/m3 |
| Specific heat (c) | 670 | - | 900 | 800 | 3605 | 670 | J/(kgK) |
| Thermal conductivity (k) | 1.1 | - | 140 | 310 | 0.615 | 0.034 | W/(mK) |
| Month | Tampere, Average Temperature [°C] | Strasbourg, Average Temperature [°C] |
|---|---|---|
| January | −6.4 | 2.3 |
| February | −6.9 | 3.3 |
| March | −2.8 | 7.0 |
| April | 3.3 | 11.5 |
| May | 9.7 | 15.7 |
| June | 14.1 | 19.4 |
| July | 16.9 | 20.6 |
| August | 15 | 19.8 |
| September | 9.8 | 15.8 |
| October | 4.6 | 11.3 |
| November | −0.6 | 6.5 |
| December | −4.5 | 3.3 |
| Symbol | Decision Variable | Bounds | Unit |
|---|---|---|---|
| Fluid mass flow rate | 0.0083 ≤ x(1) ≤ 0.044 | kg/s | |
| Tin | Inlet temperature | 15 ≤ x(2) ≤ 45 | °C |
| Hgap | Air gap thickness | 0.02 ≤ x(3) ≤ 0.25 | m |
| Hi | Insulation thickness | 0.015 ≤ x(4) ≤ 0.09 | m |
| Production | Strasbourg [kWh/year] | Tampere [kWh/year] |
|---|---|---|
| Eth | 992.1 | 915.5 |
| Eel | 305.5 | 288.8 |
| Ein | 2191.8 | 2064.8 |
| Exth | 17.4 | 30.1 |
| Exel | 305.5 | 288.8 |
| Exin | 2046.2 | 1930 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kallio, S.; Siroux, M. Energy Analysis and Exergy Optimization of Photovoltaic-Thermal Collector. Energies 2020, 13, 5106. https://doi.org/10.3390/en13195106
Kallio S, Siroux M. Energy Analysis and Exergy Optimization of Photovoltaic-Thermal Collector. Energies. 2020; 13(19):5106. https://doi.org/10.3390/en13195106
Chicago/Turabian StyleKallio, Sonja, and Monica Siroux. 2020. "Energy Analysis and Exergy Optimization of Photovoltaic-Thermal Collector" Energies 13, no. 19: 5106. https://doi.org/10.3390/en13195106
APA StyleKallio, S., & Siroux, M. (2020). Energy Analysis and Exergy Optimization of Photovoltaic-Thermal Collector. Energies, 13(19), 5106. https://doi.org/10.3390/en13195106






