Design Optimization of a Composite Solar Wall Integrating a PCM in a Individual House: Heating Demand and Thermal Comfort Considerations
Abstract
1. Introduction
2. Methodology
2.1. Description of the House Model
2.2. Solar Trombe Wall Description and Climatic Regions
3. Parametric Study
4. Effect of Solar Wall Parameters on Heating Demand
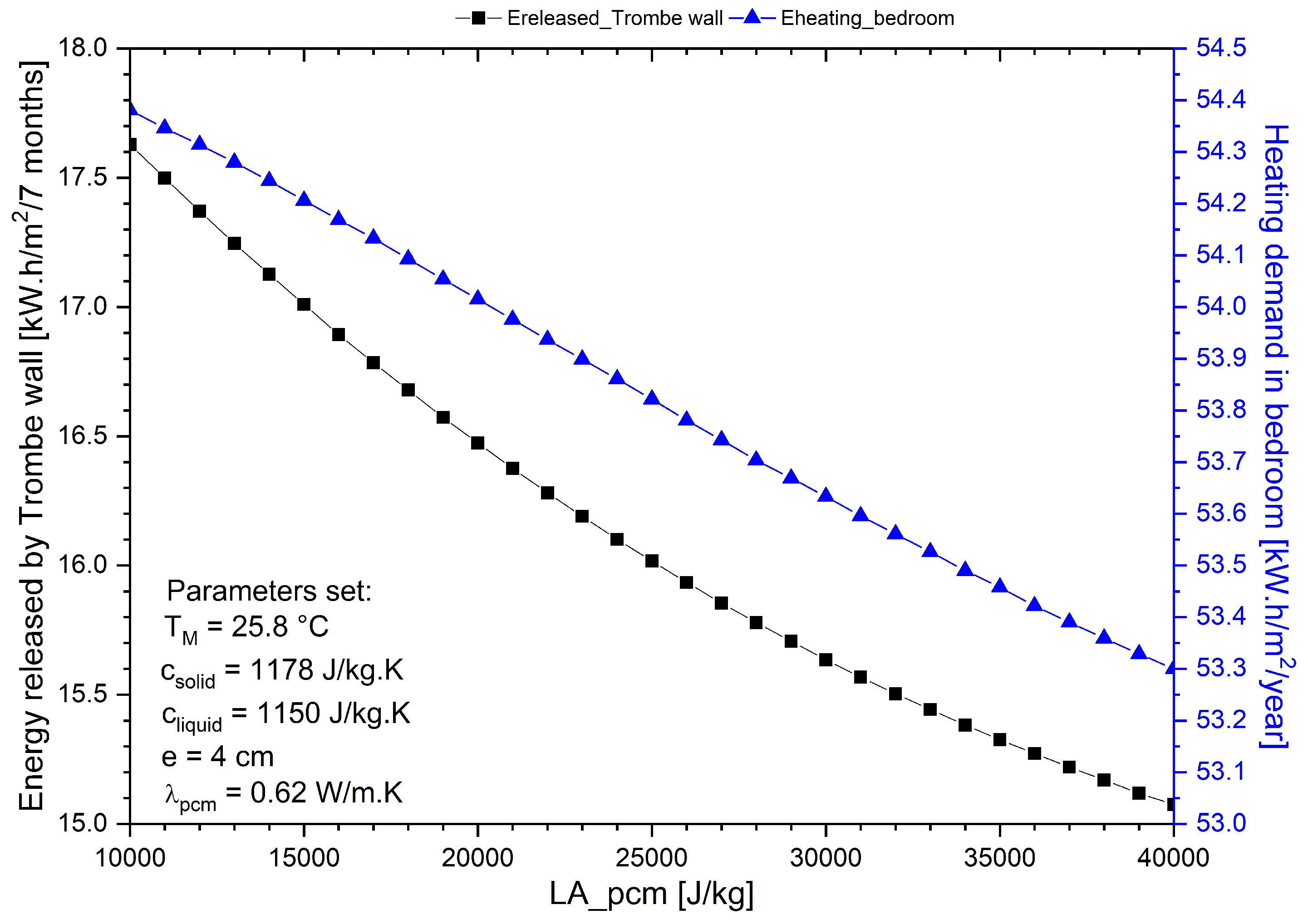
4.1. Variation in Latent Heat (LA_pcm)
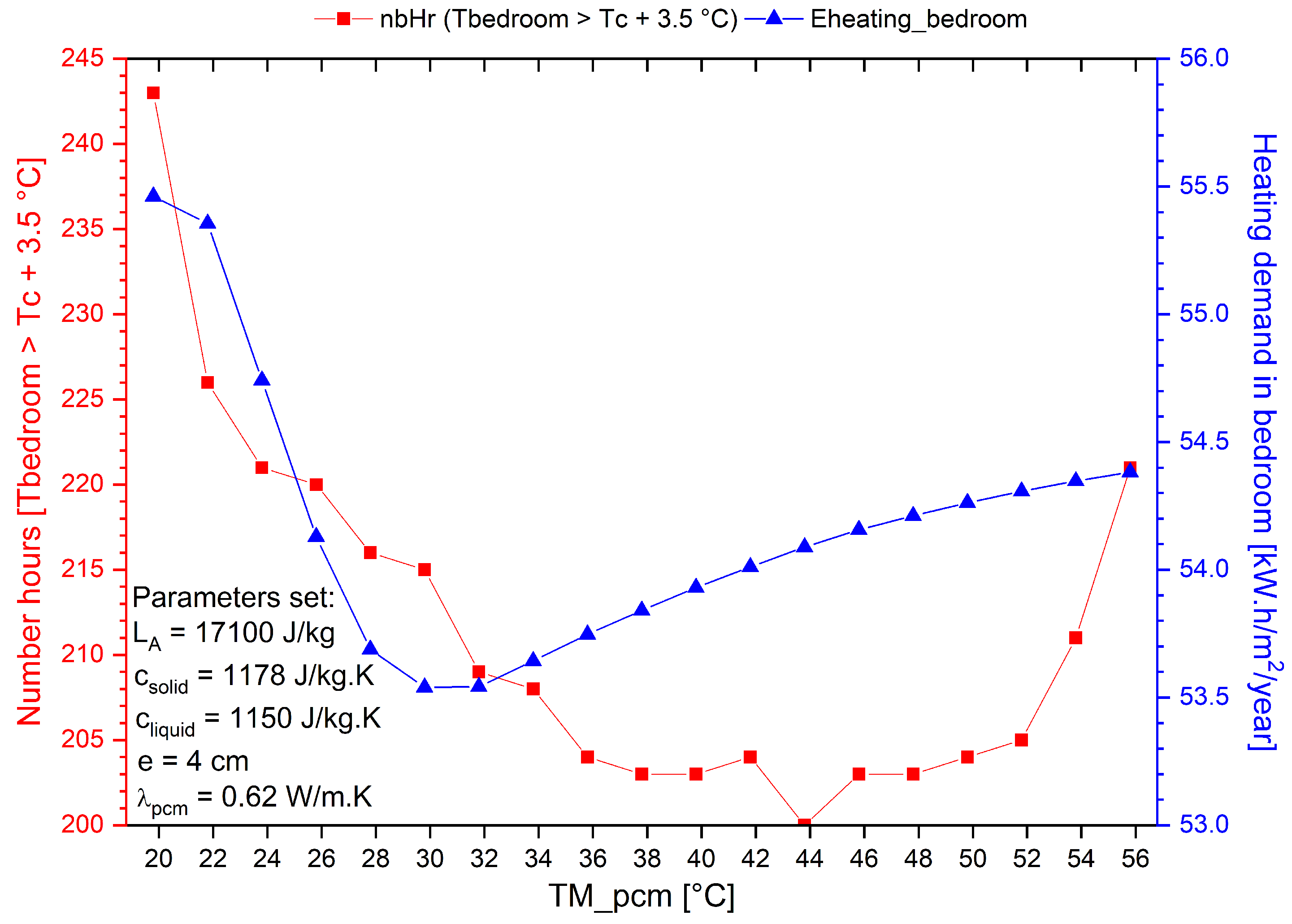
4.2. Variation in Melting Temperature (TM_pcm)
4.3. Variation in the PCM Storage Wall Thickness (e_pcm)
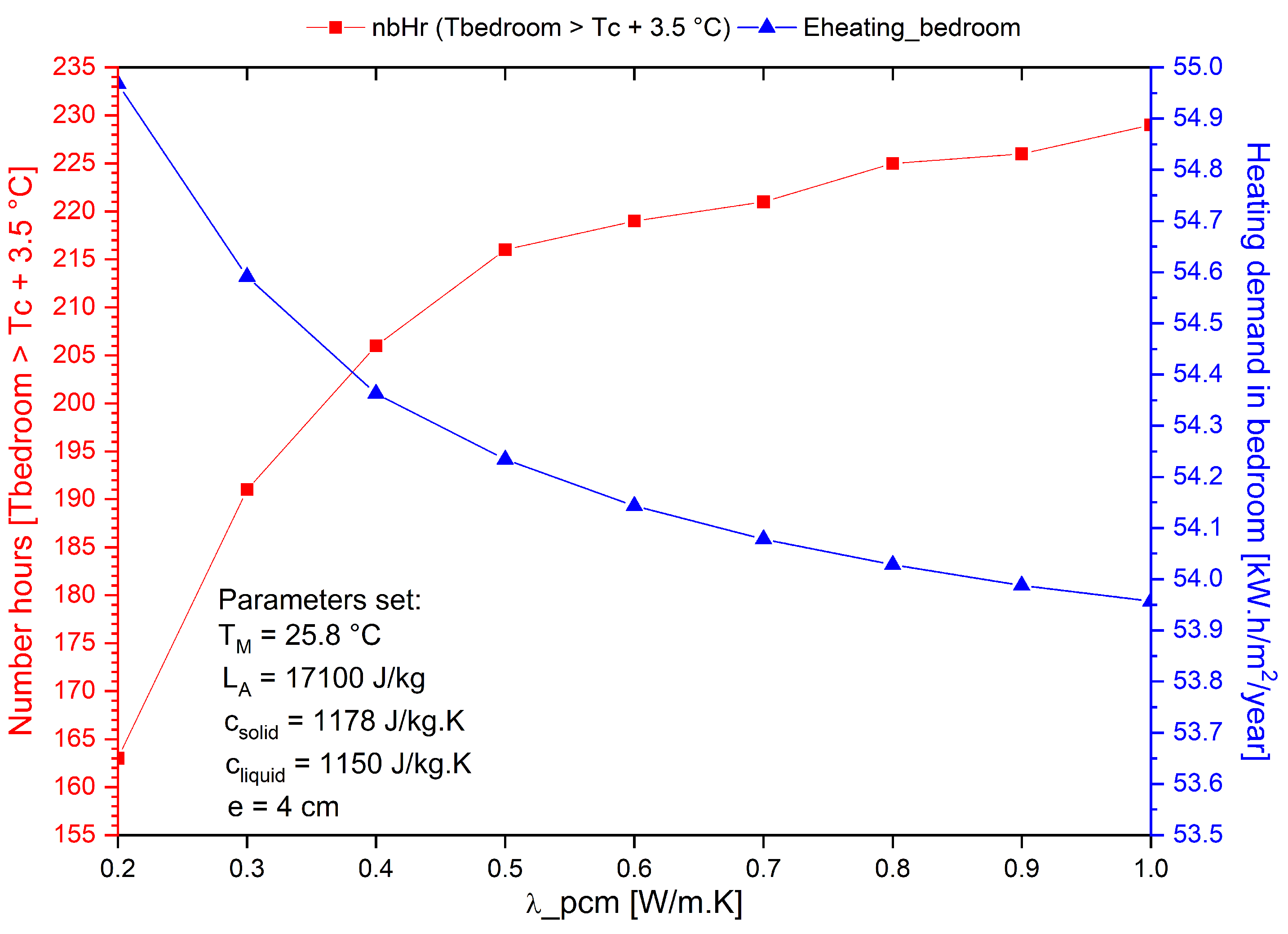
4.4. Variation in Thermal Conductivity (_pcm)
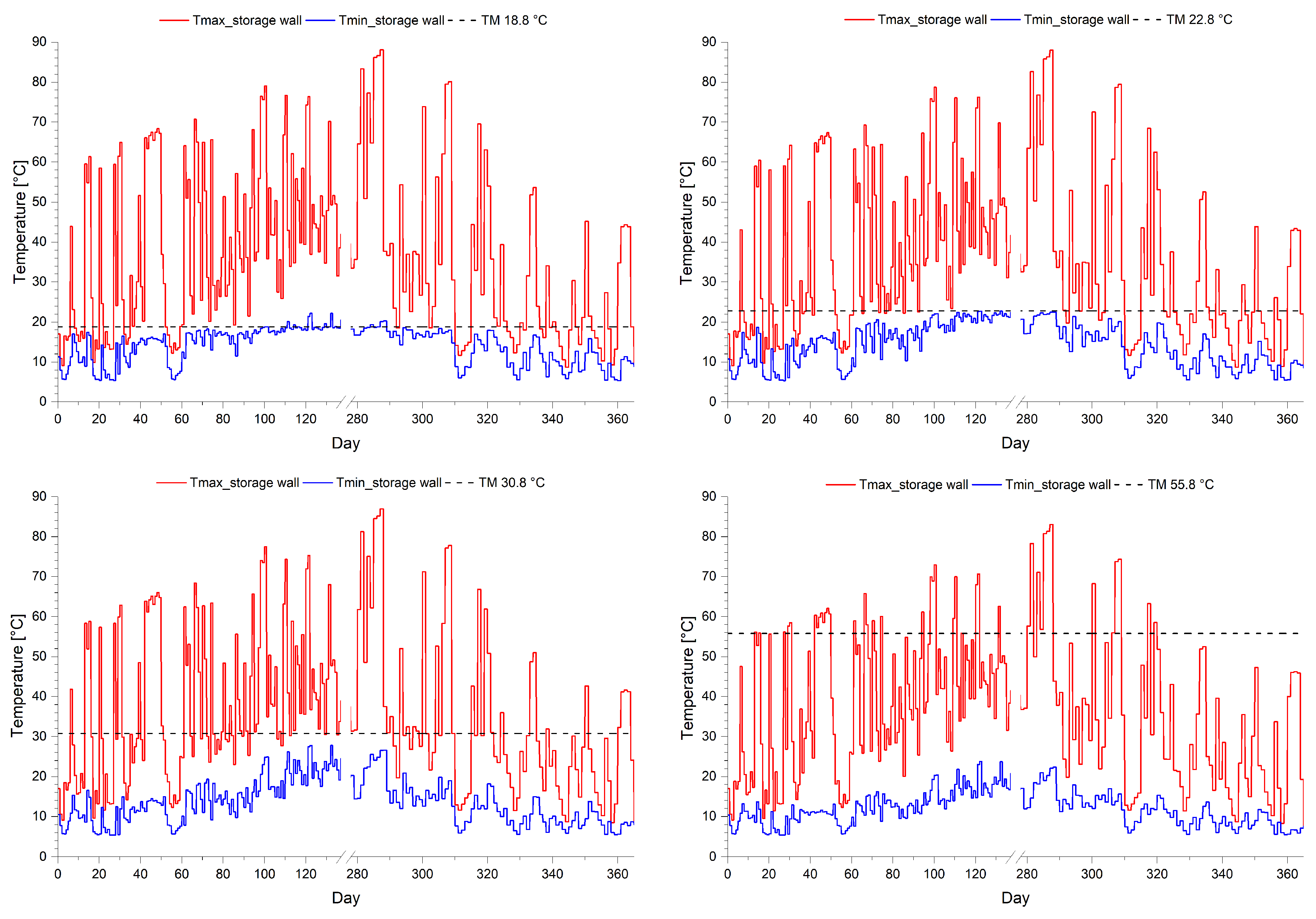
5. Effect of Solar Wall Parameters on Building Comfort during Winter
6. Optimization Process Methodology
6.1. Optimization Method
- Optimization of heating demand;
- Optimization of the number of hours of thermal discomfort;
- Simultaneous optimization of heating demand and number of hours of discomfort.
6.2. Optimization of Heating Demand
6.3. Optimization of the Number of Hours of Thermal Discomfort
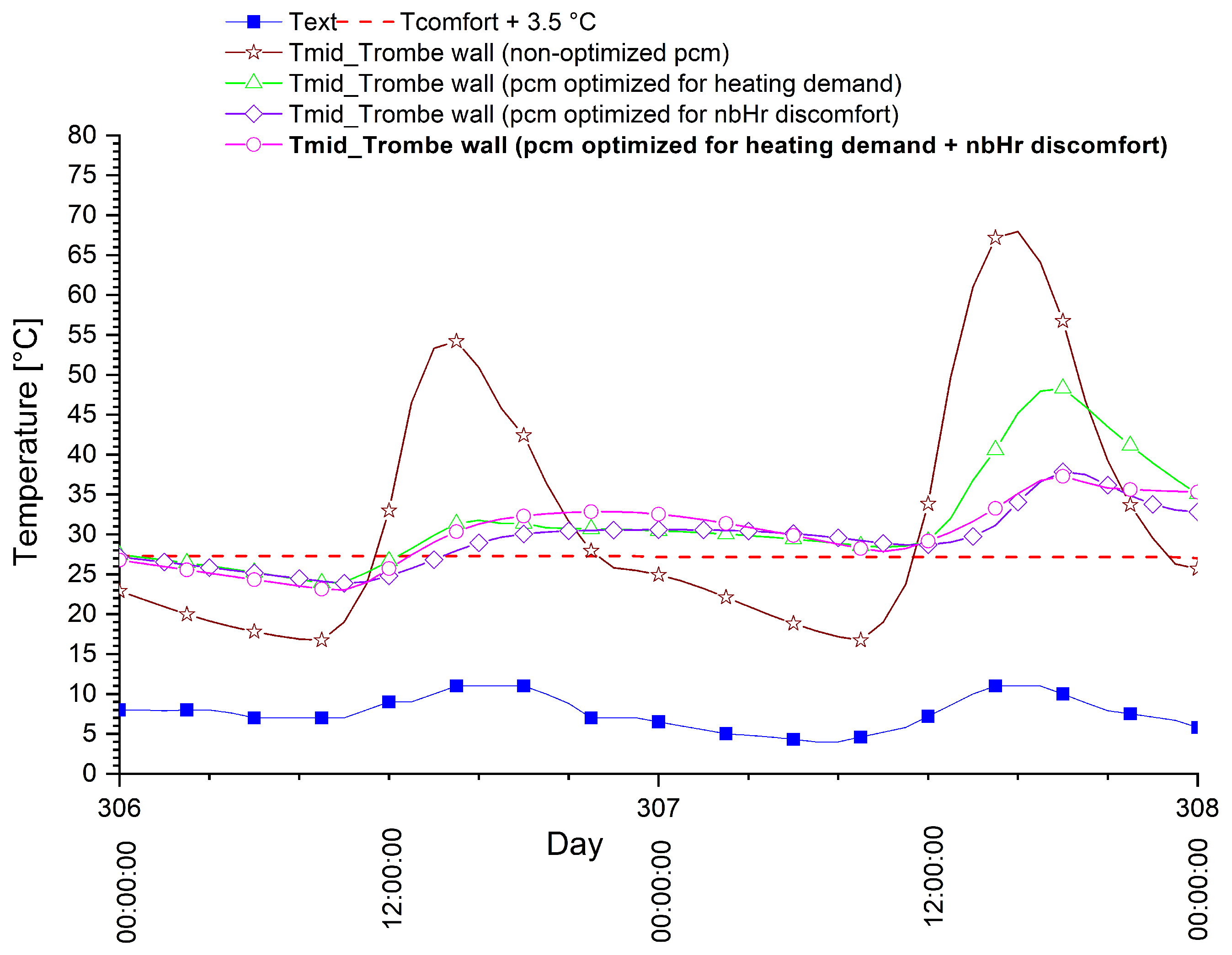
6.4. Simultaneous Optimization of Heating Demand and Number of Hours of Discomfort
7. Conclusions
- The higher the latent heat, the lower the heating demand and the better the thermal comfort in the bedroom, Figure 12;
- The optimal melting temperatures are approximately 31 for heating demand and 44 for number of hours of discomfort, Figure 13;
- The effect of storage wall thickness is small with respect to heating demand, whereas the higher the thickness, the lower the number of hours of discomfort and, thus, the better the thermal comfort, Figure 14;
- The higher the thermal conductivity, the lower the heating demand and the higher the number of hours of discomfort, Figure 15.
- Development of the mortar + PCM composition with higher latent heat, density and conductivity;
- Use of a macro-encapsulated PCM storage wall;
- Development of the solar wall relying on the same method, dimensions and location (e.g., living room, with a larger floor area to be heated);
- Use of a solar wall for preheating air within the entire house.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols: | |
| c | specific heat capacity, J/kg K |
| csolid | specific heat capacity when PCM is in the solid state, J/kg K |
| cliquid | specific heat capacity when PCM is in the liquid state, J/kg K |
| E | energy, kW·h |
| e | thickness, m |
| H | height, m |
| h | hour |
| LA | latent heat, J/kg |
| nbHr | number of hours |
| no | number |
| P | power supplied by the composite Trombe wall, W |
| T | temperature, C |
| TM | melting temperature, C |
| TC | comfort temperature, C |
| W | width, m |
| Greek symbols | |
| α | absorptivity |
| emissivity | |
| thermal conductivity, W/m K | |
| flux, W/m2 | |
| density, kg/m3 | |
| Subscripts | |
| bed | bedroom |
| c | comfort |
| ext | exterior |
| flc | floor concrete |
| fr | frame |
| glw | glass wool |
| hea | heating |
| lv | lower vent |
| liv | living room |
| max | maximum |
| mid | middle |
| nor | north-facing rooms |
| ref | reference |
| sal | salon |
| sup | supply |
| uv | upper vent |
| Abbreviations | |
| M_PCM | composite material: mortar + PCM |
| PCM | phase change material |
| U | frame window factor |
References
- European Commission. Focus: Energy Efficiency in Buildings. Available online: https://ec.europa.eu/info/news/focus-energy-efficiency-buildings-2020-feb-17_en (accessed on 23 April 2020).
- Parliament, E. Guidelines Accompanying Commission Delegated Regulation (EU) No 244/2012 of 16 January 2012. Off. J. Eur. Union 2012, 1–28. [Google Scholar]
- No, R. 244, Commission Delegated Regulation (EU) N. 244/2012 of 16 January 2012 supplementing Directive 2010/31/EU of the European Parliament and of the Council on the energy performance of buildings by establishing a comparative methodology framework for calculating cost-optimal levels of minimum energy performance requirements for buildings and building elements. Off. J. Eur. Union. L 2012, 81. [Google Scholar]
- Wetter, M. Simulation Research Group Building Technologies Department Environmental Energy Technologies Division Lawrence Berkeley National Laboratory Berkeley. In Proceedings of the IBPSA’s Building Simulation, 2001 Conference, Rio de Janeiro, Brazil, 13–15 August 2001; p. 109. [Google Scholar]
- Nguyen, A.T.; Reiter, S.; Rigo, P. A review on simulation-based optimization methods applied to building performance analysis. Appl. Energy 2014, 113, 1043–1058. [Google Scholar] [CrossRef]
- Baños, R.; Manzano-Agugliaro, F.; Montoya, F.G.; Gil, C.; Alcayde, A.; Gómez, J. Optimization methods applied to renewable and sustainable energy: A review. Renew. Sustain. Energy Rev. 2011, 15, 1753–1766. [Google Scholar] [CrossRef]
- Evins, R. A review of computational optimisation methods applied to sustainable building design. Renew. Sustain. Energy Rev. 2013, 22, 230–245. [Google Scholar] [CrossRef]
- Stevanović, S. Optimization of passive solar design strategies: A review. Renew. Sustain. Energy Rev. 2013, 25, 177–196. [Google Scholar] [CrossRef]
- Machairas, V.; Tsangrassoulis, A.; Axarli, K. Algorithms for optimization of building design: A review. Renew. Sustain. Energy Rev. 2014, 31, 101–112. [Google Scholar] [CrossRef]
- Boeck, L.D.; Verbeke, S.; Audenaert, A.; Mesmaeker, L.D. Improving the energy performance of residential buildings: A literature review. Renew. Sustain. Energy Rev. 2015, 52, 960–975. [Google Scholar] [CrossRef]
- Huang, Y.; Niu, J.l. Optimal building envelope design based on simulated performance: History, current status and new potentials. Energy Build. 2016, 117, 387–398. [Google Scholar] [CrossRef]
- Kheiri, F. A review on optimization methods applied in energy-efficient building geometry and envelope design. Renew. Sustain. Energy Rev. 2018, 92, 897–920. [Google Scholar] [CrossRef]
- Hashempour, N.; Taherkhani, R.; Mahdikhani, M. Energy performance optimization of existing buildings: A literature review. Sustain. Cities Soc. 2020, 54, 101967. [Google Scholar] [CrossRef]
- Dymola—Dassault Systèmes®. Library Catalog. Available online: www.3ds.com (accessed on 9 May 2020).
- Wetter, M.; Group, S.R. GenOpt–Generic Optimization Program, User Manual, V. 3.1.0; LBNL: Berkeley, CA, USA, 2011. [Google Scholar]
- Attia, S.; Hamdy, M.; O’Brien, W.; Carlucci, C. Computational Optimisation for Zero Energy Building Design, Interviews with Twenty Eight International Experts. In Proceedings of the 13th Conference of International Building Performance Simulation Association, Chambéry, France, 25–28 August 2013. [Google Scholar]
- EnergyPlus, L. Engineering Reference, the Reference to EnergyPlus Calculations; Ernest Orlando Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2013. [Google Scholar]
- Klein, S.A.; Beckman, W.A.; Mitchell, J.W.; Duffie, J.A.; Duffie, N.A.; Freeman, T.L.; Mitchell, J.C.; Braun, J.E.; Evans, B.L.; Kummer, J.P.; et al. TRNSYS 17—A TRaNsient SYstem Simulation Program, User Manual. Version 17.2.5; University of Wisconsin-Madison: Madison, WI, USA, 2014. [Google Scholar]
- Nguyen, A.T.; Reiter, S. Passive designs and strategies for low-cost housing using simulation-based optimization and different thermal comfort criteria. J. Build. Perform. Simul. 2014, 7, 68–81. [Google Scholar] [CrossRef]
- Nielsen, T.R. Optimization of Buildings with Respect to Energy and Indoor Environment; Technical University of Denmark (DTU): Kongens Lyngby, Denmark, 2003. [Google Scholar]
- Fesanghary, M.; Asadi, S.; Geem, Z.W. Design of low-emission and energy-efficient residential buildings using a multi-objective optimization algorithm. Build. Environ. 2012, 49, 245–250. [Google Scholar] [CrossRef]
- Hamdy, M.; Hasan, A.; Siren, K. Applying a multi-objective optimization approach for Design of low-emission cost-effective dwellings. Build. Environ. 2011, 46, 109–123. [Google Scholar] [CrossRef]
- Wright, J.A.; Loosemore, H.A.; Farmani, R. Optimization of building thermal design and control by multi-criterion genetic algorithm. Energy Build. 2002, 34, 959–972. [Google Scholar] [CrossRef]
- Leang, E.; Tittelein, P.; Zalewski, L.; Lassue, S. Impact of a Composite Trombe Wall Incorporating Phase Change Materials on the Thermal Behavior of an Individual House with Low Energy Consumption. Energies 2020, 13, 4872. [Google Scholar] [CrossRef]
- Bojić, M.; Johannes, K.; Kuznik, F. Optimizing energy and environmental performance of passive Trombe wall. Energy Build. 2014, 70, 279–286. [Google Scholar] [CrossRef]
- Stazi, F.; Mastrucci, A.; Munafò, P. Life cycle assessment approach for the optimization of sustainable building envelopes: An application on solar wall systems. Build. Environ. 2012, 58, 278–288. [Google Scholar] [CrossRef]
- Jaber, S.; Ajib, S. Optimum design of Trombe wall system in mediterranean region. Sol. Energy 2011, 85, 1891–1898. [Google Scholar] [CrossRef]
- Arıcı, M.; Bilgin, F.; Nižetić, S.; Karabay, H. PCM integrated to external building walls: An optimization study on maximum activation of latent heat. Appl. Therm. Eng. 2020, 165, 114560. [Google Scholar] [CrossRef]
- Cascone, Y.; Capozzoli, A.; Perino, M. Optimisation analysis of PCM-enhanced opaque building envelope components for the energy retrofitting of office buildings in Mediterranean climates. Appl. Energy 2018, 211, 929–953. [Google Scholar] [CrossRef]
- Xiao, W.; Wang, X.; Zhang, Y. Analytical optimization of interior PCM for energy storage in a lightweight passive solar room. Appl. Energy 2009, 86, 2013–2018. [Google Scholar] [CrossRef]
- Park, J.H.; Lee, J.; Wi, S.; Jeon, J.; Chang, S.J.; Chang, J.D.; Kim, S. Optimization of phase change materials to improve energy performance within thermal comfort range in the South Korean climate. Energy Build. 2019, 185, 12–25. [Google Scholar] [CrossRef]
- Saffari, M.; Gracia, A.d.; Fernández, C.; Cabeza, L.F. Simulation-based optimization of PCM melting temperature to improve the energy performance in buildings. Appl. Energy 2017, 202, 420–434. [Google Scholar] [CrossRef]
- Ascione, F.; Masi, R.F.D.; Rossi, F.d.; Ruggiero, S.; Vanoli, G.P. Optimization of building envelope design for nZEBs in Mediterranean climate: Performance analysis of residential case study. Appl. Energy 2016, 183, 938–957. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; Masi, R.F.D.; Rossi, F.d.; Vanoli, G.P. Energy refurbishment of existing buildings through the use of phase change materials: Energy savings and indoor comfort in the cooling season. Appl. Energy 2014, 113, 990–1007. [Google Scholar] [CrossRef]
- Ramakrishnan, S.; Wang, X.; Alam, M.; Sanjayan, J.; Wilson, J. Parametric analysis for performance enhancement of phase change materials in naturally ventilated buildings. Energy Build. 2016, 124, 35–45. [Google Scholar] [CrossRef]
- Soares, N.; Gaspar, A.R.; Santos, P.; Costa, J.J. Multi-dimensional optimization of the incorporation of PCM-drywalls in lightweight steel-framed residential buildings in different climates. Energy Build. 2014, 70, 411–421. [Google Scholar] [CrossRef]
- Oró, E.; Miró, L.; Farid, M.M.; Martin, V.; Cabeza, L.F. Energy management and CO2 mitigation using phase change materials (PCM) for thermal energy storage (TES) in cold storage and transport. Int. J. Refrig. 2014, 42, 26–35. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Miró, L.; Oró, E.; Gracia, A.D.; Martin, V.; Krönauer, A.; Rathgeber, C.; Farid, M.M.; Paksoy, H.O.; Martínez, M.; et al. CO2 mitigation accounting for Thermal Energy Storage (TES) case studies. Appl. Energy 2015, 155, 365–377. [Google Scholar] [CrossRef]
- de Gracia, A.; Barzin, R.; Fernández, C.; Farid, M.M.; Cabeza, L.F. Control strategies comparison of a ventilated facade with PCM—Energy savings, cost reduction and CO2 mitigation. Energy Build. 2016, 130, 821–828. [Google Scholar] [CrossRef]
- Asker, M.; Alptekin, E.; Tokuç, A.; Ezan, M.; Ganjehsarabi, H. The effect of phase change material incorporated building wall on the CO2 mitigation: A case study of Izmir, Turkey. Int. J. Glob. Warm. 2019. [Google Scholar] [CrossRef]
- Deng, T.; Li, X.; Zhang, L.; Lian, J.; Ma, T.; Wang, Q. Controlling effect of phase change material based heat exchanger on supercritical CO2 Brayton cycle. J. Clean. Prod. 2020, 277, 122994. [Google Scholar] [CrossRef]
- Ma, Q.; Fukuda, H.; Wei, X.; Hariyadi, A. Optimizing energy performance of a ventilated composite Trombe wall in an office building. Renew. Energy 2019, 134, 1285–1294. [Google Scholar] [CrossRef]
- Bajc, T.; Todorović, M.N.; Svorcan, J. CFD analyses for passive house with Trombe wall and impact to energy demand. Energy Build. 2015, 98, 39–44. [Google Scholar] [CrossRef]
- Leang, E.; Tittelein, P.; Zalewski, L.; Lassue, S. Numerical and Experimental Investigations of Composite Solar Walls Integrating Sensible or Latent Heat Thermal Storage. Appl. Sci. 2020, 10, 1854. [Google Scholar] [CrossRef]
- Wetter, M.; Bonvini, M.; Nouidui, T.S.; Tian, W.; Zuo, W. Modelica Buildings Library 3.0. In Proceedings of the 14th Conference of International Building Performance Simulation Association, Hyderabad, India, 7–9 December 2015. [Google Scholar]
- Ministry of Urban Planning and Housing. Arrêté du 24 Mars 1982 Relatives a L’aeration des Logements: Aeration Generale ou Permanente, Aeration Permanente Pouvant etre Limitee a Certaines Pieces; Legifrance: France, 1982; R119-2. [Google Scholar]
- Zalewski, L.; Franquet, E.; Gibout, S.; Tittelein, P.; Defer, D. Efficient Characterization of Macroscopic Composite Cement Mortars with Various Contents of Phase Change Material. Appl. Sci. 2019, 9, 1104. [Google Scholar] [CrossRef]
- Leang, E.; Tittelein, P.; Zalewski, L.; Lassue, S. Numerical study of a composite Trombe solar wall integrating microencapsulated PCM. Energy Procedia 2017, 122, 1009–1014. [Google Scholar] [CrossRef]
- Weather Data by Location|EnergyPlus. Available online: https://energyplus.net/weather (accessed on 14 July 2019).
- McCartney, K.J.; Nicol, J.F. Developing an adaptive control algorithm for Europe. Energy Build. 2002, 34, 623–635. [Google Scholar] [CrossRef]
- Stazi, F.; Mastrucci, A.; di Perna, C. The behaviour of solar walls in residential buildings with different insulation levels: An experimental and numerical study. Energy Build. 2012, 47, 217–229. [Google Scholar] [CrossRef]




















| Weather | Variable | January | February | March | April | May | June | July | August | September | October | November | December |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Paris | , (W/m) T, | 154 3.9 | 253 4.2 | 366 7 | 523 10 | 588 14.3 | 649 16.8 | 671 19.4 | 627 19.7 | 481 15.7 | 334 11.3 | 198 6.4 | 135 4.7 |
| Lyon | , (W/m) T, | 185 3.3 | 324 3.8 | 493 7.9 | 583 10.8 | 623 15.4 | 713 19 | 760 21.6 | 659 20.4 | 561 16.4 | 339 13 | 214 7.3 | 161 4 |
| Nice | , (W/m) T, | 314 9 | 432 8.8 | 541 11.5 | 675 13.1 | 724 17.5 | 779 20.6 | 841 23.9 | 793 24 | 636 20.8 | 439 16.2 | 327 11.8 | 273 9.2 |
| Parameter | Definition | Units | Minimum | Base | Maximum | Steps |
|---|---|---|---|---|---|---|
| latent heat | J/kg | 10,000 | 17,100 | 40,000 | 1000 | |
| melting temperature | 18.8 | 25.8 | 55.8 | 1 | ||
| storage wall thickness | m | 0.04 | 0.04 | 0.15 | 0.01 | |
| thermal conductivity | W/(m.K) | 0.2 | 0.62 | 1 | 0.05 |
| LApcm(J/kg) | E Supplied for 2 Whole Days | E Heating Demand for 2 Days |
|---|---|---|
| 10,000 | 2.60 kW·h | 0.35 kW·h |
| 25,000 | 2.26 kW·h | 0.52 kW·h |
| 40,000 | 1.89 kW·h | 0.58 kW·h |
| epcm(m) | E Supplied for 2 Whole Days | E Heating Demand for 2 Days |
|---|---|---|
| 4 | 6.791 kW·h | 0.282 kW·h |
| 12 | 4.251 kW·h | 0.837 kW·h |
| 15 | 3.393 kW·h | 0.818 kW·h |
| Calculation Number | TMpcm | LApcm J/kg | epcm cm | pcm W/m·K | Heating Demand kWh·m·4 months | |
|---|---|---|---|---|---|---|
| 1 | Initial value | 20.8 | 15,000 | 4 | 0.22 | 31.69 |
| Optimal value | 31.5 | 40,000 * | 9 | 1 * | 28.02 | |
| 2 | Initial value | 34.8 | 20,000 | 8 | 0.95 | 28.88 |
| Optimal value | 31.5 | 40,000 * | 9 | 1 * | 28.02 | |
| 3 | Initial value | 20.8 | 39,000 | 14 | 0.95 | 30.47 |
| Optimal value | 31.5 | 40,000 * | 9 | 1 * | 28.02 |
| Weather | TMpcm | LApcm J/kg | epcm cm | pcm W/m·K | Heating Demand kWh·m·4 months |
|---|---|---|---|---|---|
| Paris | 31.5 | 40,000 * | 9.0 | 1.00 * | 28.02 |
| Lyon | 32.9 | 40,000 * | 10 | 1.00 * | 24.10 |
| Nice | 32.8 | 40,000 * | 15 | 1.00 * | 2.23 |
| Weather Type | House Case Study | Number of Hours of Discomfort | Energy Supplied in the Cold Season (kWh·m−2·Year−1) | Heating Demand Energy (kWh·m−2·Year−1) |
|---|---|---|---|---|
| Paris-Orly | no Trombe wall | 0 | – | 66.07 |
| non-optimized PCM | 170 | 18.68 | 53.42 | |
| optimized PCM | 84 | 18.96 | 50.66 | |
| Lyon | no Trombe wall | 0 | – | 61.24 |
| non-optimized PCM | 362 | 26.73 | 48.99 | |
| optimized PCM | 150 | 23.03 | 46.46 | |
| Nice | no Trombe wall | 0 | – | 21.07 |
| non-optimized PCM | 1031 | 50.50 | 8.64 | |
| optimized PCM | 496 | 44.70 | 4.29 |
| Weather | TMpcm | LApcm J/kg | epcm cm | pcm W/m·K | Heating Demand kWh·m·4 Months | No. of Hours of Discomfort h/4 Months |
|---|---|---|---|---|---|---|
| Paris | 32.8 | 40,000 * | 15 * | 0.4 | 29.46 | 0 |
| Lyon | 35.2 | 39,889 ** | 15 * | 0.2 | 26.36 | 6.7 |
| Nice | 35.9 | 39,963 ** | 15 * | 0.2 | 3.44 | 11 |
| Weather | TMpcm | LApcm J/kg | epcm cm | pcm W/m·K | Heating Demand kWh·m·4 Months | No. Hours Discomfort h/4 Months |
|---|---|---|---|---|---|---|
| Paris | 35.8 | 40,000 * | 15 * | 0.733 | 28.57 | 0 |
| Lyon | 34.9 | 40,000 * | 14.9 ** | 0.2 | 26.33 | 7.2 |
| Nice | 36 | 39,963 ** | 15 * | 0.2 | 3.44 | 11.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leang, E.; Tittelein, P.; Zalewski, L.; Lassue, S. Design Optimization of a Composite Solar Wall Integrating a PCM in a Individual House: Heating Demand and Thermal Comfort Considerations. Energies 2020, 13, 5640. https://doi.org/10.3390/en13215640
Leang E, Tittelein P, Zalewski L, Lassue S. Design Optimization of a Composite Solar Wall Integrating a PCM in a Individual House: Heating Demand and Thermal Comfort Considerations. Energies. 2020; 13(21):5640. https://doi.org/10.3390/en13215640
Chicago/Turabian StyleLeang, Enghok, Pierre Tittelein, Laurent Zalewski, and Stéphane Lassue. 2020. "Design Optimization of a Composite Solar Wall Integrating a PCM in a Individual House: Heating Demand and Thermal Comfort Considerations" Energies 13, no. 21: 5640. https://doi.org/10.3390/en13215640
APA StyleLeang, E., Tittelein, P., Zalewski, L., & Lassue, S. (2020). Design Optimization of a Composite Solar Wall Integrating a PCM in a Individual House: Heating Demand and Thermal Comfort Considerations. Energies, 13(21), 5640. https://doi.org/10.3390/en13215640






