Abstract
This research work proposes a novel approach to estimate probabilities of availability states of the energy transfer network in marine energy conversion subsystems, using Bayesian Networks (BNs). The logical interrelationships between units at different level in this network can be understood through qualitative system analysis, which then can be modeled by the fault tree (FT). The FT can be mapped to a corresponding BN, and the condition probabilities of nodes can be determined based on the logic structure. A case study was performed to demonstrate how the mapping is implemented, and the probabilities of availability states were estimated. The results give the probability of each availability state as a function of time, which serves as a basis for choosing the optimal design solution.
1. Introduction
Marine energy, as a resource of clean energy, is expected to have a role in cutting global carbon emissions over the next few decades [1]. Over €600 million have been invested by the private sector over the last seven years, and this is set to increase further, provided that there are favorable conditions for the development of these devices [2]. Marine energy has seen the potential to compete with the traditional fossil fuels [3,4,5].
However, marine energy has not been commercialized due to design-stage and operation-stage challenges. A robust and reliable design has been a target of the marine energy industry. The study regarding the availability of marine energy systems has been a hot research topic over the past a few years. Availability is a measure of how long time a system/subsystem normally work. For the energy transfer subsystem, availability is directly linked to the power production. Higher mean availability indicates less maintenance-related costs in the lifetime, which is the final target of the owners. Time-based availability, defined as the ratio of the uptime to the design lifetime, was studied for this paper. See Section 2 for more details.
Marine energy systems are able to function with reduced energy transmission capacity, and only a complete system failure will terminate energy transmission altogether. However, the owner will lose revenue if the capacity of the system is reduced; thus, the owner is interested in the availability of the system.
The marine energy system can be divided into four subsystems, according to the primary design standard for marine energy system, IEC 62600-2 [6], as shown in Figure 1. The structural subsystem refers to the mooring lines and anchors. The mechanical subsystem is composed of the power take-offs and other accessories. The most critical subassembly in the mechanical subsystem refers to the power take-offs. The control subsystem generally refers to the circuits integrated into the undersea substations and the offshore substation. The electrical subsystem, called the energy transfer subsystem in this paper, is the target which availability is estimated for.
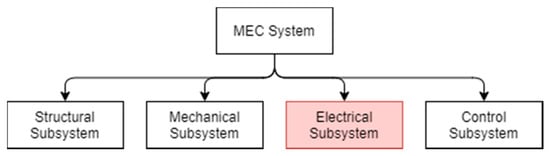
Figure 1.
Illustration of static Bayesian Network (BN).
With the aim to assess the system availability, a qualitative system analysis can be performed to clearly define the hierarchy based upon the domain knowledge. A fault tree (FT), as a traditional system failure analysis tool, can be further constructed based upon such a hierarchy. A FT is a straight forward approach to estimate the failure probabilities of the top event and the intermediate events. However, new information (e.g., observations) reflecting the system operation states can hardly be integrated into the FT to update failure probabilities. To address this inadequacy, Bayesian Network (BN) has been used as a substitute of FT over the past two decades. In nature, a BN can perform the same qualitative analysis as a FT. Besides, an advantage of a BN over a FT is that: new information can be easily integrated to the BN as observations (called evidences in some textbooks) to obtain the posterior failure probabilities. A BN model can be constructed through either the subjective experience or mapping from an existing FT. In this study, the latter approach will be used.
Compared to such industries as oil & gas, petroleum refinery, and wind energy, the marine energy is a new industry. There have been few research works regarding the availability of the marine energy conversion systems. Therefore, the following literature review only covers the research development in the aforementioned mature industries. The applications of BN models to availability assessment will be the focus in the literature review.
Bobbioa et al. [7] proposed an algorithm to convert a FT into a BN and it was shown that how the results obtained from a FT analysis can be cast in the BN setting and compared the two methodologies through some examples in order to show BN as a powerful candidate for dependency analyses. Khakzad et al. [8] used a very similar mapping algorithm and compared the two methodologies through a simple accident scenario in a gas process facility to show the advantages of BN over FT in terms of reasoning and uncertainty handling. Zakarya et al. [9] employed a hybrid of FT and BN converted from this FT based upon the same mapping algorithm to do the failure diagnosis of safety instrumented systems. FT analysis is used to identify all combinations of failure which can lead to dangerous failures. Wu et al. [10] attempted to use the BN techniques to address the potential uncertainty and randomness underlying the safety management in tunnel construction. In structural learning of BN, they converted the logic gates in FT to the corresponding directed edges in the BN model by using the mapping algorithm proposed by Bobbioa et al. [7]. Wang et al. [11] established the FT for the subsea Christmas tree and mapped it to the corresponding BN and assessed the reliability and availability of the subsea Christmas tree for two design solutions. Amin et al. [12] constructed a dynamic BN based upon a five-step safety assessment methodology and used this dynamic BN to assess the availability of both the fire alarm and steam generation systems. Jiang et al. [13] presented a systemic approach to evaluate the reliability and availability for the onboard system based on dynamic BN, with taking into account dynamic failure behaviors, imperfect coverage factors, and temporal effects in the operational phase.
The objective of this paper was to estimate the probability distribution of the availability as a function of time for the marine energy transfer subsystem. The methodology can be summarized as follows:
- Obtain the organization of the energy transfer subsystem and establish the logical interrelationship between the units at all levels in this subsystem, through a qualitative system analysis.
- A traditional FT is constructed based upon the hierarchical structure obtained from the system analysis and is mapped to the corresponding BN model; with consideration of the time-dependent state variations of basic components, the BN model should be extended to a dynamic BN model.
- Generally, the time of failure (TTF) of electrical components, e.g., cables, connectors, follows the exponential distribution. The TTF of basic components can be simulated based upon the fundamental assumptions that the failures of different basic components are statistically independent and the TTF follows the exponential distribution.
- The TTF of the energy transfer subsystem is estimated based upon the logic dependencies in the hierarchy and the TTFs of the basic components.
- The simulated TTFs, considered observations (evidences), can through a discretization of time be inserted into corresponding time slices (a time slice refers to a time interval considered in a dynamic BN, e.g., 1 day, 1 week, 1 month, 1 year, etc.). The probabilities of different states of the units at different level in the system can be calculated, with these observations taken into account. The information of these observations is kept or propagates from the time the failures occur to the time the failed components are replaced. See Section 7.5 for more details.
- Decision rules are defined according to the energy loss in the energy transfer subsystem. The mean availability corresponding to these decision rules are calculated and compared to choose the optimal one which gives the highest availability during the design lifetime.
This paper is outlined as follows. In Section 2, the way the availability is calculated for the energy transfer subsystem is presented. In Section 3, the fundamental theory of BN will be briefly reviewed. The mapping from a FT to a BN model will be detailed. In Section 4, the application of qualitative system analysis is presented. In Section 5, the approach of simulating failures of basic components is presented. In Section 6, the design rules are presented. In Section 7, a case study is performed, considering an actual design scenario. Section 7 concludes the analysis findings and recommends the promising research work in the future.
2. Availability of Energy Transfer Subsystem
The generic definition of availability is the probability that a system or component is performing its required function at a given point in time or over a stated period of time when operated and maintained in a prescribed manner [14]. The states of the energy transfer subsystem(referred to as subsystem in the following part of this section) highly depend upon the working conditions of the subassemblies and basic components. The influence of failures and repairs of basic components should be taken into account in calculating availability. For the sake of engineering application, this study proposes a concrete approach to define the availability. With no loss of generality, a subsystem is composed of N energy converters. The subsystem has a total of (N + 1) possible states, i.e., State 0, 1, …, N. State 0 represents the shut-down state, i.e., no electricity generated. State N represents that the subsystem works under a fully-rated condition (100% electricity exported). States 1~(N−1) represent (N − 1)/N, (N − 2)/N, …, 1/N loss of the full electricity export capacity. At a given time, the availability is an expectation of possible states of electricity export. The formula for calculating the availability is given in Equation (1).
where denotes the probability that the energy transfer subsystem is at state i. denotes the ratio of the actual electricity exported from the subsystem to the full electricity export capacity. Generally, the unit of availability should be converted to percentage.
In a dynamic BN model, the evolution of probabilities of the subsystem states between time slices can be simulated. Availability should be calculated in each time slice. With the temporal property considered, Equation (1) can be further extended, as expressed in Equation (2).
where t represents the temporal variable, i.e., time slice. (t) denotes the probability that the energy transfer subsystem is at state i in time slice t.
3. Mapping Fault Trees to Bayesian Networks
3.1. A Brief Review of Bayesian Network
A BN represents and reasons about an unknown domain in which the random variables are represented by nodes and the logic dependencies between these variables are represented by directed arcs [15,16]. There is a numerical model behind the graphic representation, which quantifies the dependencies through conditional probabilities.
Directed acyclic graph (DAG) and conditional probability table (CPT) are two important terminologies in BNs. A DAG represents the relationships of probabilistic dependence between the stochastic variables in a system in a qualitative manner. A CPT quantifies the probabilistic dependence between the parent node(s) and the child node(s) through conditional probabilities. Originally, BNs were introduced to only model the time-independent probabilistic dependency between nodes. Generally, this type of BNs is called static BNs, in which every nodes are graphically linked through arcs. However, the variables in a system, represented by nodes in BNs, can alternate significantly between time steps in engineering applications. This can be called the temporal dependency of nodes. Figure 2 shows a very simple static BN, in which an intermediate node represented by C is associated with 2 root nodes (each root node denoted by Ri, i = 1, 2).
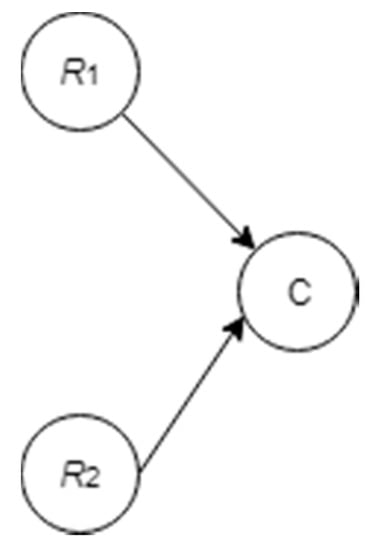
Figure 2.
Illustration of static BN.
There are two ways to construct a BN model, namely building it up from subjective engineering experience or mapping an existing FT to a BN model. The latter option will be used in this paper.
A FT is a traditional way representing failure events connected through logic gates. In the framework of FT, every element represents a failure event caused by a unit failure. ‘Unit’ is used because a unit may refer to a basic component, a subassembly, a subsystem or a system based upon the complexity degree of a system hierarchy. The principle behind the mapping algorithm graphically converts a FT to a BN model, including:
- the transformation of root, intermediate and top nodes in the FT into the corresponding counterparts in the BN model; and
- the logic gates in the FT interpreted as conditional probabilities in the CPT
The generic procedure for mapping a FT to a corresponding BN model is summarized as follows:
- identification of nodes;
- simulation of causal relations between nodes; and
- estimation of conditional probabilities
3.2. Identification of Nodes
Khakzad et al. [8] compared BNs and FTs and presented the graphical relation between them. Based upon their approach, each node in a BN model corresponds to a failure event in the FT.
The relation between nodes and failure events is given in Table 1. Basically, the failure events in a FT can be one-to-one mapped to the corresponding BN model.

Table 1.
Relation between nodes and failure events.
3.3. Simulation of Causal Relations between Nodes
3.3.1. General
The simple example shown in Figure 2 is also used to illustrate the way the causal relations between nodes can be simulated. A logic gate in a FT reflects the deterministic dependence between failure events at two consecutive levels.
In most engineering applications, the ‘gate’ can be either ‘OR’, ‘AND’, or ‘k/N’ (also called vote gate in some textbooks). With no loss of generality, the nodes underneath the gate are called input, and the node above it is called output. ‘OR’ means that any input to the gate fails, the output fails. ‘AND’ means that if all the inputs to the gate fail, the output fails. ‘k/N’ means that if either k out of N inputs fail, the output fails.
As mentioned in Section 3.2, the failure events are mapped to the corresponding nodes in the BN model, as shown in Figure 3 and the logic gate can be represented by a CPT in the mapped BN model.
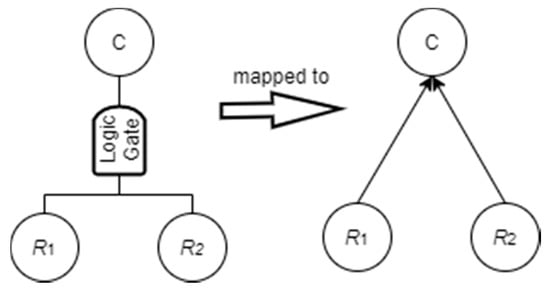
Figure 3.
Illustration of mapping a logic gate to BN model.
3.3.2. Simulation of Logic Gates
There is no sequential and functional dependencies between components in the energy transfer network to be analyzed. It is assumed that there are only two states for each node corresponding to basic components, namely ‘1’—healthy state; and ‘0’—failure state.
The prior conditional probabilities in CPTs can be estimated through the logic gates in the FT or in-field observations of failure events. Since there are no observations, the prior CPTs are defined based upon the logic gates. The logic gates are considered deterministic, without taking into account to the uncertainty of logic gates. The way CPTs can be estimated will be presented in detail in Case Study.
3.3.3. Simulation of Temporal Dependencies
Section 3.3.2 presents the way the CPTs of the units are estimated within one time slice. In a dynamic BN model, the temporal CPTs can formulate the transition probabilities of different states between time slices. In the following part of this subsection, a model for simulating the temporal CPTs will be proposed.
As mentioned in Section 1, the TTF of the basic component k is assumed to follow the exponential distribution, with a constant failure rate of . The temporal conditional probabilities can be defined in Table 2. denotes the time interval between two time slices. How to choose will be discussed further in Section 7.

Table 2.
A template of hierarchy.
It is assumed that no repair is done between two consecutive time slices. With no loss of generality, a single basic component, , is used to demonstrate how to define the temporal conditional probabilities. The conditional probabilities are given as follows:
These probabilities can be further explained. Apparently, if this basic component fails at (state 0), the probability of being at state 0 is unity at ; if this basic component fails at (state 0), the probability of being at state 1 is zero at . Let us keep the fundamental assumptions made in Section 1 in mind (the time to failure follows the exponential distribution). If the basic component is in state 1 at , the probability of failure (in state 0) should be at , and the probability of survival (in state 1) should be . at .
4. Qualitative System Analysis
The objective of qualitative system analysis is to understand the working philosophy of a system and to investigate into the logic interrelationship between the units (subsystems, subassemblies, or basic components) in the system. A hierarchy, as a result of qualitative system analysis [17], is a digital representation illustrating the working philosophy and the interrelationship of the units at different levels.
A hierarchy is constructed by means of the bottom-up technique, and the steps for defining such a hierarchy are briefly summarized as follows:
- Identification of nodes representing the basic components.
- Categorization of the basic components into groups; each group is a sub-assembly and stands for an intermediate-level node; according to the rules in the tree-like data structure, the basic components are considered as children of this intermediate-level node; a logic gate is inserted between the basic nodes (representing the basic components) and the intermediate-level node to reflect the logic dependencies between these nodes.
- These identified first-level subassemblies can be considered ‘basic’ components in order to identify the second-level subassemblies (a higher level) based upon the same method mentioned in the second bullet point; and this procedure can be repeated until the system to be analyzed is reached.
A template of hierarchy, showing the FT in Figure 3, is given in Table 2 to help readers understand the structure of a hierarchy. The first column, ‘Unit’, gives the names of units in a system. The second column, ‘Type’, defines the types of units, e.g., system, subsystem, subassembly, basic component. The third column, ‘Category’, defines which levels the units in the ‘Unit’ column belong to in the FT. The columns ‘Affiliated to’ and ‘Affiliated by’ define the dependencies of units at various levels. Each entry in ‘Affiliated to’ defines the label of the higher-level unit which the current unit in the column ‘Unit’ belongs to. Each entry in ‘Affiliated by’ defines the labels of lower-level units which belong to the current unit. Based upon the aforementioned descriptions, the units in the column ‘Affiliated by’ are connected through a specific logic gate to the higher-level unit. The logic gates are given in the column ‘Gate Type’. The logic gate in each entry of this column is used to connect the unit in the column ‘Unit’ and the units in the column ‘Affiliated by’.
The hierarchy includes all the basic information for constructing a FT and can be considered as a compact format of a FT. The simulation of time to failures depends upon the hierarchy, as mentioned in Section 5.
5. Simulation of Time to Failures
5.1. For Basic Components
This subsection is intended to elaborate on how to simulate the TTFs of basic components. The Monte Carlo simulation is the basic methodology used to randomly generate discrete failure events of basic components [18]. It is assumed that the TTFs of basic components are statistically independent. The procedure for simulating the TTFs of basic components is summarized as follows.
The probabilistic lifetime distribution of all basic components is assumed to follow the exponential distribution. The time to failure has the following probability distribution function. As mentioned in Section 1, the failure rates of basic components are constant.
where is the failure rate of a basic component.
5.2. For the System
The TTFs of basic components should be available before the TTF of the system can be estimated. An ID is assigned to each basic component to identify it in the system. The failed basic component ids are arranged in such a way that the corresponding TTFs of the basic component are arranged according to an ascending chronological order.
The TTFs of the units other than basic components can be simulated through a bottom-up approach. The state of an intermediate unit which is directly associated with the nodes representing the basic components can be determined according to the states of these basic components and the type of logic gate. Then, the state of a second-level intermediate unit can be determined according to the states of the 1st-level intermediate nodes and the type of logic gate. Such a recursive process can be repeated until the top node is reached. The process can be implemented in a computer code, with the flow chart illustrated in Figure 4.
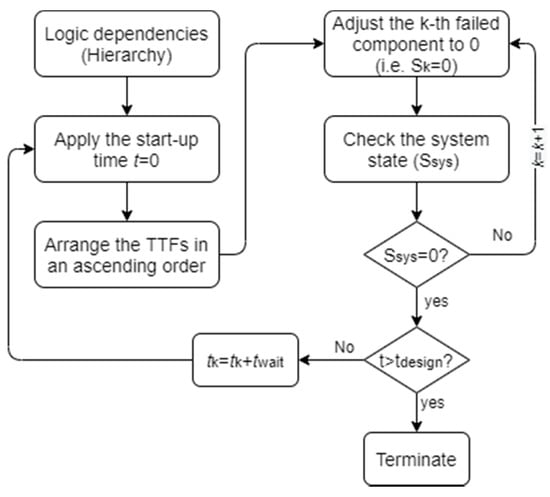
Figure 4.
Flowchart illustrating simulation of time of failures (TTFs).
6. Decision Rules
The terminology of decision rule first appeared in the decision-making theory [19]. Basically, a decision rule describes the action(s) to be taken, when a certain experiment outcome comes out.
For the energy transfer subsystem composed of M converters, the decision rules can be defined from the perspective of effective energy production. It is assumed that there is a threshold ratio of the full energy production, c. A maintenance team should be dispatched to repair the failed components, when the monitored energy productions is less than c% of the full energy export. See Table 3 for more details regarding the decision rules.

Table 3.
Descriptions of decision rules.
Failure of any component in the energy transfer subsystem can cause a certain amount of energy loss. The energy loss is a direct criterion for assessing the failure consequence. The decision rules are mainly developed from the perspective of energy loss.
7. Case Study
7.1. Background Information of Energy Transfer Networks
An energy transfer network [20], a subsystem in marine energy converter farm (referred to as subsystem in the following part of this section), serves to transport the generated power to the onshore terminal. The design lifetime is 20 years. Typical topologies of such an energy transfer network are shown in Figure 5. The white bubbles with dashed boundary lines represent the converters connected to the main cables represented by black bold lines, through the orange circles marked with numbers from 1 to 9 represent the connectors.
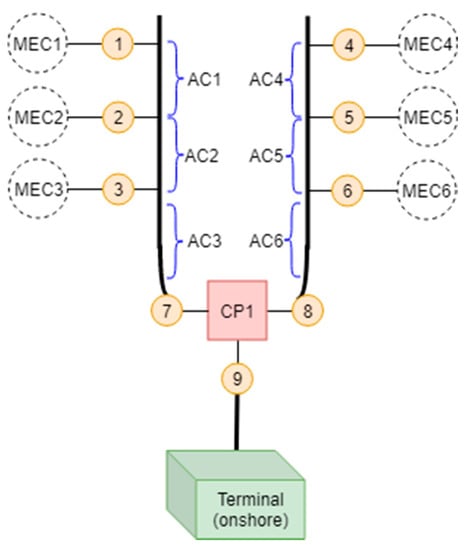
Figure 5.
Sketch of energy transfer network topology.
Due to no tailor-made reliability database for marine energy converters (MECs), the failure rates of the basic components can be referred to some generic database for electrical components in other industrial applications [21]. Ginaldi et al. [22] referred to the similar reliability database, took into account some influencing factors and proposed a simulation-based framework for assessing reliability, availability, and maintainability of the wave energy device components. These failure rates chosen for this case study, subject to engineering judgement, are given in Table 4. ‘AC’ denotes the cables. Cp1 denotes the on-shore substation (a special connector).

Table 4.
Interpretations of nodes in fault tree (FT) and BN Models.
7.2. Fault Tree
Several rounds of brain-storm workshops have been held to understand the working philosophy of the subsystem. Besides, research findings in Reference [23] have been referred to provide a better understanding of the application of FT in electrical subsystem. The hierarchy of subsystem has been clearly defined.
There are two independent energy transfer routes respectively connected to CP1 through the connectors 7 and 8 and two cables AC3 and AC6. The electricity is finally transmitted to the onshore terminal through the connector 9. Suppose that the two energy transfer routes are considered as a virtual unit denoted by T1. T1 is considered as a 1st-level sub-assembly. If either of CP1, X19 and T1 fails, the energy transfer system (T0) will be shut down (no electricity generated).
T1 is composed of two identical energy transfer routes respectively denoted by T2 and T3, which are the 2nd-level sub-assemblies. T1 fails, if both T2 and T3 fail.
T2 comprises X17, X3, a virtual unit T4, which comprises the other connectors directly connected to MECs and the other cables connecting these connectors. If either X17, X3, or T4 fails, this energy transfer route will be shut down. T2 can be considered a series system. T3 comprises X18, X6, a virtual unit T5, which comprises the other connectors directly connected to MECs and the other cables connecting these connectors. If either X18, X6, or T5 fails, this energy transfer route will be shut down. T3 can be considered a series system. Both T4 and T5 constitutes the 3rd-level sub-assembly.
T4 comprises X2, X13 and another virtual unit T6. If either two of X2, X13, and T6 fail, T4 fails. In a similar way, T5 comprises X6, X16 and another virtual unit T7. If either two of X6, X16, and T7 fail, T5 fails. Both T6 and T7 constitutes the 4th-level sub-assembly.
T6 comprises X12 and another virtual unit T8. If either X12 or T8 fails, T6 fails. T7 comprises X15 and another virtual unit T9. If either X15 or T9 fails, T7 fails. Both T8 and T9 constitutes the 5th-level sub-assembly.
T8 comprises X11 and X1. If either X11 or X1 fails, T8 fails. T9 comprises X14 and X4. If either X14 or X4 fails, T9 fails.
The hierarchy of the subsystem is given in Table 5.

Table 5.
Hierarchy of energy transfer system.
Based upon the qualitative system analysis, the FT can be constructed accordingly. The top event is denoted ‘Failure of ET system (T0)’. The intermediate failure events underneath the top event refer to ‘Failure of X19 (denoted X19 in the fault tree)’, ‘Failure of X20 (denoted X20 in the fault tree)’, and ‘Failure of T1’. An ‘OR’ gate is inserted according to the working philosophy. For simplicity, the label name is hereafter used to represent the failure event of this unit in the FT.
If ‘Failure of T1’ is considered the top failure event, the intermediate failure events refer to the two ‘Failure of T2’ or ‘Failure of T3’ events. An ‘AND’ gate is inserted according to the working philosophy.
If ‘Failure of T2’ is considered the top failure event, the intermediate failure events refer to ‘Failure of X17 (denoted X17 in the fault tree)’, ‘Failure of X3 (denoted X3 in the fault tree)’, and ‘Failure of T4’. An ‘OR’ gate is inserted according to the working philosophy. If ‘Failure of T3’ is considered the top failure event, the intermediate failure events refer to ‘Failure of X18 (denoted X18 in the fault tree)’, ‘Failure of X6 (denoted X6 in the fault tree)’, and ‘Failure of T5’. An ‘OR’ gate is inserted according to the working philosophy.
If ‘Failure of T4’ is considered the top failure event, the intermediate failure events refer to ‘Failure of X13 (denoted X13 in the fault tree)’, ‘Failure of X2 (denoted X2 in the fault tree)’, and ‘Failure of T6)’ A ‘2/3’ gate is inserted according to the working philosophy. If ‘Failure of T5’ is considered the top failure event, the intermediate failure events refer to ‘Failure of X16 (denoted X16 in the fault tree)’, ‘Failure of X5 (denoted X5 in the fault tree)’, and ‘Failure of T7’. A ‘2/3’ gate is inserted according to the working philosophy.
If ‘Failure of T6’ is considered the top failure event, the intermediate failure events refer to ‘Failure of X12 (denoted X12 in the fault tree)’ and ‘Failure of T8’. An ‘OR’ gate is inserted according to the working philosophy. If ‘Failure of T7’ is considered the top failure event, the intermediate failure events refer to ‘Failure of X15 (denoted X15 in the fault tree)’ and ‘Failure of T9’. An ‘OR’ gate is inserted according to the working philosophy.
If ‘Failure of T8’ is considered the top failure event, the bottom failure events refer to ‘Failure of X11 (denoted X11 in the fault tree)’ and ‘Failure of X1 (denoted X1 in the fault tree)’. An ‘OR’ gate is inserted according to the working philosophy. If ‘Failure of T9’ is considered the top failure event, the bottom failure events refer to ‘Failure of X14 (denoted X14 in the fault tree)’ and ‘Failure of X4 (denoted X4 in the fault tree)’. An ‘OR’ gate is inserted according to the working philosophy. The FT of the subsystem is shown in Figure 6.
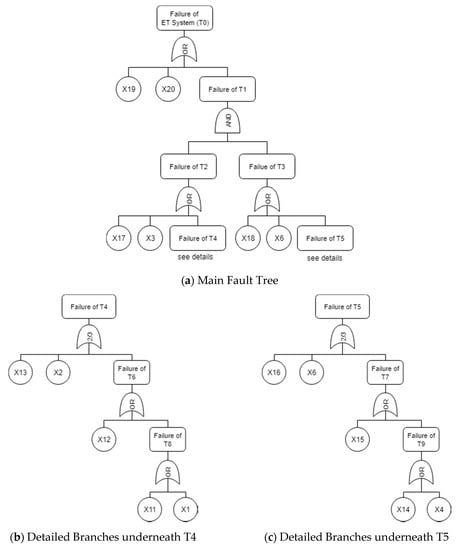
Figure 6.
Fault tree (FT) of energy transfer system.
7.3. Mapped Bayesian Network
Hugin Expert 8.9 is used to do the Bayesian inference. Hugin Expert [24] provides an independent interface for Python to construct the BN models, which is more efficient than manual operations of drawing BNs in the Hugin user interface are time-consuming. The BN model is shown in Figure 7. It should be noted that the arrows linking the same nodes in two time slices, schematically illustrating the temporal conditional transition probabilities, are not explicitly drawn to provide a high-resolution overview of the dynamic BN model.
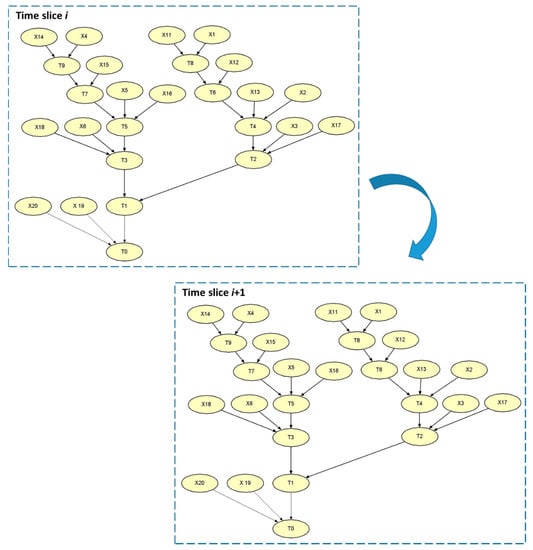
Figure 7.
BN of energy transfer system.
The dynamic Bayesian Network (BN) model describes the temporal probability evolution between time slices (a time slice refers to a time interval considered in a dynamic BN, e.g., 1 day, 1 week, 1 month, 1 year, etc.). The model in every time slice should be identical. In principle, the nodes representing the basic components in the current time slice should be linked through directed lines/arrows to the same nodes in the next time slice. If there are many nodes, e.g., in the case study, these lines/arrows will unfavorably affect the readability. The big blue arrow is used to approximately represent these arrows in Figure 7.
The criterion for choosing a time interval between slices should depend upon the actual maintenance interval adopted by the owners. As mentioned in Section 1, the marine energy industry is still at a pre-mature stage. So, the operating experience in wind industry can be borrowed. Generally, the wind turbine owners have both long-term of short-term maintenance plans. The short-term maintenance is usually planned on a monthly basis. Therefore, the time interval between slices is one month, namely , as mentioned in Section 3.3.3, is equal to 1 month. With consideration of 20-year design lifetime, there are 240 time slices in the dynamic BN model.
7.4. Estimation of CPTs
The states of nodes representing the units other than basic components depend upon the failure modes of these units and the logic gates. For the energy transfer network, the failure modes can be defined from the perspective of energy production. For the intermediate nodes, T8 and T9, there are two states of energy production, namely no energy production (denoted by 0) and one device under the healthy condition (denoted by 1). For the intermediate nodes, T6 and T7, there are three states of energy production, namely no energy production (denoted by 0), one device under the healthy condition (denoted by 1) and two devices under the healthy condition (denoted by 2). For the intermediate nodes, T2, T3, T4, and T5, there are four states of energy production, namely no energy production (denoted by 0), one device under the healthy condition (denoted by 1), two devices under the healthy condition (denoted by 2) and three devices under the healthy condition (denoted by 3). For the intermediate node T1 and the top node T0, there are seven states of energy production, namely no energy production (denoted by 0), one device under the healthy condition (denoted by 1), two devices under the healthy condition (denoted by 2), three devices under the healthy condition (denoted by 3), four device under the healthy condition (denoted by 4), five devices under the healthy condition (denoted by 5), and six devices under the healthy condition (denoted by 6). These energy production states correspond to the states of availability of the energy transfer system. See Appendix A for these CPTs.
7.5. Realizations of Time to Failure of Basic Components
In nature, the TTF of basic components is a stochastic variable. The Monte Carlo simulation is used to take into account of the uncertainty associated with the estimation of TTF. A total of N lifetime simulations (N = 1000) were performed. The TTF of basic components is simulated in parallel, based upon the fundamental assumption that the failures of basic components are statistically independent. The system TTF is determined by the logic dependencies in the hierarchy in Table 5.
The results of one realization are given in Table 6. The number of system failures simulated in this realization is listed in the first column. The second column includes the sequence of failure components until each system failure. The third column includes the time the components on the same row in the second column fail. For each system failure, the system failure time is just the last entry in the list. After the system failure, corrective maintenance should be done to replace the damaged basic components. The duration for corrective maintenance should take into account of the waiting time, the transportation time and the repair time, as twait shown in Figure 4. The accurate prediction of weather window is not the focus in this study. Therefore, an empirical estimation of twait is 24 h (e.g., in a benign sea), no matter which failed component is repaired.

Table 6.
Results of simulated TTFs and sequence of failure components in one realization.
Each of the component failures can be considered as an observation (evidence). The BN model takes into account of these observations, by setting the states of the failed components to 0. How these observations are taken into account in the BN model will be presented as follows.
The second system failure in Table 6 is used as an example to show the procedure, with the schematic shown in Figure 8. The boxes on the top represent the chronologic months. Green represents that no basic component fails in the specific month. Yellow represents the failure of a basic component in the specific month. Red represents the time the energy transfer subsystem fails. The arrows underneath both yellow and red boxes point to the names of the failed components. In Month 107 and 112, the basic components ‘X6’ and ‘X1’ fail, and such an information is stored as observations. The information, including the names of failed components and the failure time, is transferred to the BN model, through an interface function represented by the green container in Figure 9. The states of the nodes representing these two components are set to 0 and kept until they are replaced. The information is used to calculate the probabilities of different states of the units at all levels. In Month 113, the basic components ‘X20’ fails, which results in the energy transfer subsystem failure, based upon the logic interrelationship defined in Table 5. Such an observation can also be transferred to the BN model to calculate the probabilities of different states of the units at all levels. The failed components are replaced after M113, and the states of these components will be restored to 1. The current time is shifted to M113 + twait (twait is the waiting time as mentioned above). The time to failure of basic components will be simulated in parallel again. Repeat the same aforementioned procedure.
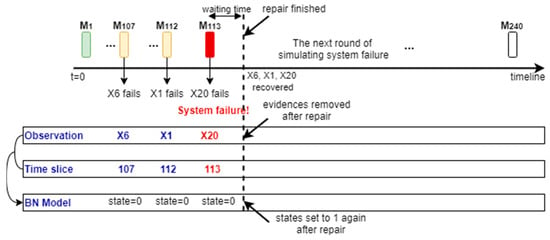
Figure 8.
Schematic illustrating how the evidences are considered in the BN model.
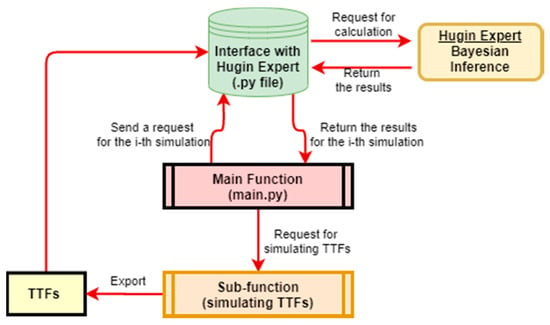
Figure 9.
Work flow of the reliability module in the modeling tool.
7.6. Calculation of Time-Dependent Availability
An analysis module for reliability assessment in a modeling tool has been developed to automatically implement the simulation of TTFs and link the module to Hugin Expert through the Python programming language, with the flowchart shown in Figure 9.
In each simulation, the simulated TTFs of basic components, considered observations (evidences), can be inserted to the corresponding time slices when the failures of the basic components occur and propagate for the rest of time slices. The probabilities of different states of the units at different levels in the subsystem can be calculated, with these observations (evidences) taken into account. For each simulation, the availability is calculated as a function of time. The base case corresponds to the case in which Decision rule 1 is used.
Based upon the N (N = 1000) simulations, the mean availability for the base case, as well as the 10% and 90% quantiles, will be finally obtained, as shown in Figure 10. The mean availability sees a significant decrease in the early period of the design lifetime (e.g., from the start-up of operation to Year 4) and stabilizes around a constant value since then. Because of a conservative decision rule (Decision rule 1) is used in the base case. The damaged component(s) can be repaired in time before more energy losses occur, which ensures the system availability keep around a constant value. Therefore, the application of Decision rule 1 can explain the constant mean availability over a long period of the design lifetime. The 90% quantile of availability shows a very similar tendency as the mean availability. The 10% quantile of availability shows a significant fluctuation after Year 6. This is due to the randomness of sampling the time to failure of basic components. The mean availability is converged to around 60%.
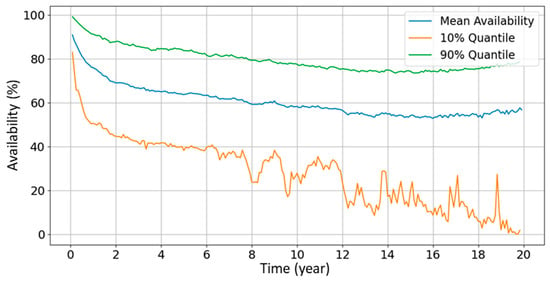
Figure 10.
Mean availability and 10% and 90% quantile.
7.7. Sensitivity Study
The purpose of sensitivity study is to verify how much different decision rules will influence the mean availability as a function of time.
The mean availability for the cases in which the decision rules other than Decision rule 1 (see Table 3 for more details) is calculated and compared to the availability for Decision rule 1, as shown in Figure 11. These curves indicate a tendency that more repairs are of help to significantly improve the availability, i.e., the base case gives the highest availability during the design lifetime. The cost-optimal decision rule can be determined by introducing a cost modeling, which is outside the scope of this paper.
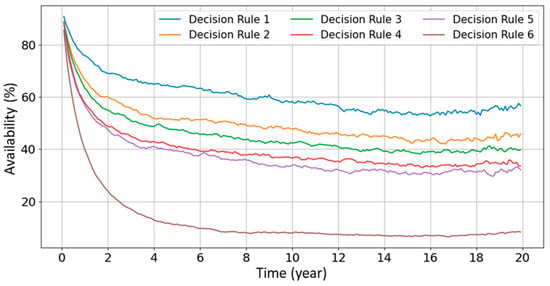
Figure 11.
Comparison of availability for different Decision rules.
8. Conclusions
The probabilistic analysis for availability of a marine energy transfer subsystem has been completed. The availability of the energy transfer subsystem was discretized to seven states from the perspective of energy production. The probabilities of these seven states were calculated using BN mapped from the FT, which was constructed through the qualitative system analysis. The simulation results indicated (as expected) that the highest availability can be maintained, if the decision rule is applied with the lowest number of accepted failed components.
For the time being, the approach proposed in this paper can help the owners and/or designers choose the optimal maintenance strategy, without taking into account of the maintenance costs. What can be improved in future work is to extend the modeling to integrate the cost modeling into the framework of the current methodology. Then, the cost-benefit optimal maintenance strategy can be chosen. Besides the energy transfer subsystem, the station keeping (mooring) and the energy transformation (PTOs) subsystems can be taken into account to achieve the actual system-level simulation.
Author Contributions
The methodology was proposed by Y.Y. and reviewed by J.D.S.; Y.Y. implemented the theoretical method in a computer code and developed the interface with Hugin Expert 8.9. All authors have read and agreed to the published version of the manuscript.
Funding
The research is financially supported by the DTOceanPlus project.
Acknowledgments
This work has been partially supported by European Union’s Horizon 2020 research and innovation programme under grant agreement No 785921, project DTOceanPlus (Advanced Design Tools for Ocean Energy Systems Innovation, Development and Deployment).
Conflicts of Interest
The authors declare that there is no conflict of interest.
Appendix A. Conditional Probability Table (CPTs) for the Intermediate and Top Nodes

Table A1.
CPT for T8 and T9.
Table A1.
CPT for T8 and T9.
| State | Probability | ||
|---|---|---|---|
| X1 or X4 | T11 or X14 | T8 or T9 | |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |

Table A2.
CPT for T6 and T7.
Table A2.
CPT for T6 and T7.
| State | Probability | ||
|---|---|---|---|
| X12 or X15 | T8 or T9 | T6 or T7 | |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 2 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 2 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 2 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 2 | 1 |

Table A3.
CPT for T4 and T5.
Table A3.
CPT for T4 and T5.
| State | Probability | |||
|---|---|---|---|---|
| X13 or X16 | X2 or X5 | T6 or T7 | T4 or T5 | |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 2 | 0 |
| 0 | 0 | 0 | 3 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 2 | 0 |
| 1 | 0 | 0 | 3 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 2 | 0 |
| 0 | 1 | 0 | 3 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 2 | 0 |
| 1 | 1 | 0 | 3 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 2 | 0 |
| 0 | 0 | 1 | 3 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 2 | 1 |
| 1 | 0 | 1 | 3 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 2 | 0 |
| 0 | 1 | 1 | 3 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 2 | 1 |
| 1 | 1 | 1 | 3 | 0 |
| 0 | 0 | 2 | 0 | 0 |
| 0 | 0 | 2 | 1 | 0 |
| 0 | 0 | 2 | 2 | 1 |
| 0 | 0 | 2 | 3 | 0 |
| 1 | 0 | 2 | 0 | 0 |
| 1 | 0 | 2 | 1 | 0 |
| 1 | 0 | 2 | 2 | 0 |
| 1 | 0 | 2 | 3 | 1 |
| 0 | 1 | 2 | 0 | 0 |
| 0 | 1 | 2 | 1 | 0 |
| 0 | 1 | 2 | 2 | 1 |
| 0 | 1 | 2 | 3 | 0 |
| 1 | 1 | 2 | 0 | 0 |
| 1 | 1 | 2 | 1 | 0 |
| 1 | 1 | 2 | 2 | 0 |
| 1 | 1 | 2 | 3 | 1 |

Table A4.
CPT for T2 and T3.
Table A4.
CPT for T2 and T3.
| State | Probability | |||
|---|---|---|---|---|
| X17 or X18 | X3 or X6 | T4 or T5 | T2 or T3 | |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 2 | 0 |
| 0 | 0 | 0 | 3 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 2 | 0 |
| 1 | 0 | 0 | 3 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 2 | 0 |
| 0 | 1 | 0 | 3 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 2 | 0 |
| 1 | 1 | 0 | 3 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 2 | 0 |
| 0 | 0 | 1 | 3 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 2 | 0 |
| 1 | 0 | 1 | 3 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 2 | 0 |
| 0 | 1 | 1 | 3 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 2 | 0 |
| 1 | 1 | 1 | 3 | 0 |
| 0 | 0 | 2 | 0 | 1 |
| 0 | 0 | 2 | 1 | 0 |
| 0 | 0 | 2 | 2 | 0 |
| 0 | 0 | 2 | 3 | 0 |
| 1 | 0 | 2 | 0 | 1 |
| 1 | 0 | 2 | 1 | 0 |
| 1 | 0 | 2 | 2 | 0 |
| 1 | 0 | 2 | 3 | 0 |
| 0 | 1 | 2 | 0 | 1 |
| 0 | 1 | 2 | 1 | 0 |
| 0 | 1 | 2 | 2 | 0 |
| 0 | 1 | 2 | 3 | 0 |
| 1 | 1 | 2 | 0 | 0 |
| 1 | 1 | 2 | 1 | 0 |
| 1 | 1 | 2 | 2 | 1 |
| 1 | 1 | 2 | 3 | 0 |
| 0 | 0 | 3 | 0 | 1 |
| 0 | 0 | 3 | 1 | 0 |
| 0 | 0 | 3 | 2 | 0 |
| 0 | 0 | 3 | 3 | 0 |
| 1 | 0 | 3 | 0 | 1 |
| 1 | 0 | 3 | 1 | 0 |
| 1 | 0 | 3 | 2 | 0 |
| 1 | 0 | 3 | 3 | 0 |
| 0 | 1 | 3 | 0 | 1 |
| 0 | 1 | 3 | 1 | 0 |
| 0 | 1 | 3 | 2 | 0 |
| 0 | 1 | 3 | 3 | 0 |
| 1 | 1 | 3 | 0 | 0 |
| 1 | 1 | 3 | 1 | 0 |
| 1 | 1 | 3 | 2 | 0 |
| 1 | 1 | 3 | 3 | 1 |

Table A5.
CPT for T1.
Table A5.
CPT for T1.
| State | Probability | ||
|---|---|---|---|
| T2 | T3 | T1 | |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 2 | 0 |
| 0 | 0 | 3 | 0 |
| 0 | 0 | 4 | 0 |
| 0 | 0 | 5 | 0 |
| 0 | 0 | 6 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 2 | 0 |
| 1 | 0 | 3 | 0 |
| 1 | 0 | 4 | 0 |
| 1 | 0 | 5 | 0 |
| 1 | 0 | 6 | 0 |
| 2 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 2 | 0 | 2 | 1 |
| 2 | 0 | 3 | 0 |
| 2 | 0 | 4 | 0 |
| 2 | 0 | 5 | 0 |
| 2 | 0 | 6 | 0 |
| 3 | 0 | 0 | 0 |
| 3 | 0 | 1 | 0 |
| 3 | 0 | 2 | 0 |
| 3 | 0 | 3 | 1 |
| 3 | 0 | 4 | 0 |
| 3 | 0 | 5 | 0 |
| 3 | 0 | 6 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 2 | 0 |
| 0 | 1 | 3 | 0 |
| 0 | 1 | 4 | 0 |
| 0 | 1 | 5 | 0 |
| 0 | 1 | 6 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 2 | 1 |
| 1 | 1 | 3 | 0 |
| 1 | 1 | 4 | 0 |
| 1 | 1 | 5 | 0 |
| 1 | 1 | 6 | 0 |
| 2 | 1 | 0 | 0 |
| 2 | 1 | 1 | 0 |
| 2 | 1 | 2 | 0 |
| 2 | 1 | 3 | 1 |
| 2 | 1 | 4 | 0 |
| 2 | 1 | 5 | 0 |
| 2 | 1 | 6 | 0 |
| 3 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 |
| 3 | 1 | 2 | 0 |
| 3 | 1 | 3 | 0 |
| 3 | 1 | 4 | 1 |
| 3 | 1 | 5 | 0 |
| 3 | 1 | 6 | 0 |
| 0 | 2 | 0 | 0 |
| 0 | 2 | 1 | 0 |
| 0 | 2 | 2 | 1 |
| 0 | 2 | 3 | 0 |
| 0 | 2 | 4 | 0 |
| 0 | 2 | 5 | 0 |
| 0 | 2 | 6 | 0 |
| 1 | 2 | 0 | 0 |
| 1 | 2 | 1 | 0 |
| 1 | 2 | 2 | 0 |
| 1 | 2 | 3 | 1 |
| 1 | 2 | 4 | 0 |
| 1 | 2 | 5 | 0 |
| 1 | 2 | 6 | 0 |
| 2 | 2 | 0 | 0 |
| 2 | 2 | 1 | 0 |
| 2 | 2 | 2 | 0 |
| 2 | 2 | 3 | 0 |
| 2 | 2 | 4 | 1 |
| 2 | 2 | 5 | 0 |
| 2 | 2 | 6 | 0 |
| 3 | 2 | 0 | 0 |
| 3 | 2 | 1 | 0 |
| 3 | 2 | 2 | 0 |
| 3 | 2 | 3 | 0 |
| 3 | 2 | 4 | 0 |
| 3 | 2 | 5 | 1 |
| 3 | 2 | 6 | 0 |
| 0 | 3 | 0 | 0 |
| 0 | 3 | 1 | 0 |
| 0 | 3 | 2 | 0 |
| 0 | 3 | 3 | 1 |
| 0 | 3 | 4 | 0 |
| 0 | 3 | 5 | 0 |
| 0 | 3 | 6 | 0 |
| 1 | 3 | 0 | 0 |
| 1 | 3 | 1 | 0 |
| 1 | 3 | 2 | 0 |
| 1 | 3 | 3 | 0 |
| 1 | 3 | 4 | 1 |
| 1 | 3 | 5 | 0 |
| 1 | 3 | 6 | 0 |
| 2 | 3 | 0 | 0 |
| 2 | 3 | 1 | 0 |
| 2 | 3 | 2 | 0 |
| 2 | 3 | 3 | 0 |
| 2 | 3 | 4 | 0 |
| 2 | 3 | 5 | 1 |
| 2 | 3 | 6 | 0 |
| 3 | 3 | 0 | 0 |
| 3 | 3 | 1 | 0 |
| 3 | 3 | 2 | 0 |
| 3 | 3 | 3 | 0 |
| 3 | 3 | 4 | 0 |
| 3 | 3 | 5 | 0 |
| 3 | 3 | 6 | 1 |

Table A6.
CPT for T0.
Table A6.
CPT for T0.
| State | Probability | |||
|---|---|---|---|---|
| X19 | X20 | T1 | T0 | |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 2 | 0 |
| 0 | 0 | 0 | 3 | 0 |
| 0 | 0 | 0 | 4 | 0 |
| 0 | 0 | 0 | 5 | 0 |
| 0 | 0 | 0 | 6 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 2 | 0 |
| 1 | 0 | 0 | 3 | 0 |
| 1 | 0 | 0 | 4 | 0 |
| 1 | 0 | 0 | 5 | 0 |
| 1 | 0 | 0 | 6 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 2 | 0 |
| 0 | 1 | 0 | 3 | 0 |
| 0 | 1 | 0 | 4 | 0 |
| 0 | 1 | 0 | 5 | 0 |
| 0 | 1 | 0 | 6 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 2 | 0 |
| 1 | 1 | 0 | 3 | 0 |
| 1 | 1 | 0 | 4 | 0 |
| 1 | 1 | 0 | 5 | 0 |
| 1 | 1 | 0 | 6 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 2 | 0 |
| 0 | 0 | 1 | 3 | 0 |
| 0 | 0 | 1 | 4 | 0 |
| 0 | 0 | 1 | 5 | 0 |
| 0 | 0 | 1 | 6 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 2 | 0 |
| 1 | 0 | 1 | 3 | 0 |
| 1 | 0 | 1 | 4 | 0 |
| 1 | 0 | 1 | 5 | 0 |
| 1 | 0 | 1 | 6 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 2 | 0 |
| 0 | 1 | 1 | 3 | 0 |
| 0 | 1 | 1 | 4 | 0 |
| 0 | 1 | 1 | 5 | 0 |
| 0 | 1 | 1 | 6 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 2 | 0 |
| 1 | 1 | 1 | 3 | 0 |
| 1 | 1 | 1 | 4 | 0 |
| 1 | 1 | 1 | 5 | 0 |
| 1 | 1 | 1 | 6 | 0 |
| 0 | 0 | 6 | 0 | 1 |
| 0 | 0 | 6 | 1 | 0 |
| 0 | 0 | 6 | 2 | 0 |
| 0 | 0 | 6 | 3 | 0 |
| 0 | 0 | 6 | 4 | 0 |
| 0 | 0 | 6 | 5 | 0 |
| 0 | 0 | 6 | 6 | 0 |
| 1 | 0 | 6 | 0 | 1 |
| 1 | 0 | 6 | 1 | 0 |
| 1 | 0 | 6 | 2 | 0 |
| 1 | 0 | 6 | 3 | 0 |
| 1 | 0 | 6 | 4 | 0 |
| 1 | 0 | 6 | 5 | 0 |
| 1 | 0 | 6 | 6 | 0 |
| 0 | 1 | 6 | 0 | 1 |
| 0 | 1 | 6 | 1 | 0 |
| 0 | 1 | 6 | 2 | 0 |
| 0 | 1 | 6 | 3 | 0 |
| 0 | 1 | 6 | 4 | 0 |
| 0 | 1 | 6 | 5 | 0 |
| 0 | 1 | 6 | 6 | 0 |
| 1 | 1 | 6 | 0 | 0 |
| 1 | 1 | 6 | 1 | 0 |
| 1 | 1 | 6 | 2 | 0 |
| 1 | 1 | 6 | 3 | 0 |
| 1 | 1 | 6 | 4 | 0 |
| 1 | 1 | 6 | 5 | 0 |
| 1 | 1 | 6 | 6 | 1 |
References
- The Economicst Group—World Ocean Initiative. 2018. Available online: https://www.woi.economist.com/could-the-future-of-marine-energy-be-onshore/ (accessed on 1 January 2018).
- European Commission—Maritime Affairs. 2014. Available online: https://www.atlanticstrategy.eu/sites/all/themes/clean_theme/doc/key-documents/ocean-energy-leaflet_en.pdf (accessed on 1 January 2014).
- Melikoglu, M. Current status and future of ocean energy sources: A global review. Ocean Eng. 2018, 148, 563–573. [Google Scholar] [CrossRef]
- Alamian, R.; Shafaghat, R.; Shadloo, M.S.; Bayani, R.; Amouei, A.H. An empirical evaluation of the sea depth effects for various wave characteristics on the performance of a point absorber wave energy converter. Ocean Eng. 2017, 137, 13–21. [Google Scholar] [CrossRef]
- Mustapa, M.; Yaakob, O.; Ahmed, Y.; Rheem, C.-K.; Koh, K.; Adnan, F.A. Wave energy device and breakwater integration: A review. Renew. Sustain. Energy Rev. 2017, 77, 43–58. [Google Scholar] [CrossRef]
- IEC. IEC TS 62600-2 ED2 Marine Energy—Wave, Tidal and Other Water Current Converters—Part 2: Design Requirements for Marine Energy Systems. Available online: https://webstore.iec.ch/publication/25634 (accessed on 12 January 2019).
- Bobbio, A.; Portinale, L.; Minichino, M.; Ciancamerla, E. Improving the analysis of dependable systems by mapping fault trees into Bayesian networks. Reliab. Eng. Syst. Saf. 2001, 71, 249–260. [Google Scholar] [CrossRef]
- Khakzad, N.; Khan, F.; Amyotte, P.R. Safety analysis in process facilities: Comparison of fault tree and Bayesian network approaches. Reliab. Eng. Syst. Saf. 2011, 96, 925–932. [Google Scholar] [CrossRef]
- Zakarya, C.; Nait, C.R.; Rachid, S. Probabilistic fault diagnosis of safety instrumented systems based on fault tree analysis and bayesian network. J. Fail. Anal. Prev. 2016, 16, 747–760. [Google Scholar]
- Wu, X.; Liu, H.; Zhang, L.; Skibniewski, M.J.; Deng, Q.; Teng, J. A dynamic Bayesian network based approach to safety decision support in tunnel construction. Reliab. Eng. Syst. Saf. 2015, 134, 157–168. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Y.; Hou, W.; Wang, G.; Zheng, Y. Reliability and availability modeling of Subsea Xmas tree system using Dynamic Bayesian network with different maintenance methods. J. Loss Prev. Process. Ind. 2020, 64, 104066. [Google Scholar] [CrossRef]
- Amin, T.; Khan, F.; Imtiaz, S.A. Dynamic availability assessment of safety critical systems using a dynamic Bayesian network. Reliab. Eng. Syst. Saf. 2018, 178, 108–117. [Google Scholar] [CrossRef]
- Cai, B.; Liu, Y.; Liu, Z.; Chang, Y.; Jiang, L. Operation-oriented reliability and availability evaluation for onboard high-speed train control system with dynamic bayesian network. Bayesian Netw. Reliab. Eng. 2019, 233, 109–133. [Google Scholar] [CrossRef]
- Ebeling, C.E. An Introduction to Reliability and Maintainability Engineering; McGraw, H., Ed.; McGraw Hill: New York, NY, USA, 1997. [Google Scholar]
- Pearl, J. Fusion, propagation, and structuring in bayesian netwotks. Artif. Intell. 1986, 29, 241–288. [Google Scholar] [CrossRef]
- Korb, K.B.; Nicholson, A.E. Bayesian Artificial Intelligence; Chapman & Hall/CRC Press: London, UK, 2004. [Google Scholar]
- Guess, F.M.; Hoyland, A.; Rausand, M. System reliability theory: Models and statistical methods. J. Am. Stat. Assoc. 1996, 91, 436. [Google Scholar] [CrossRef]
- Chang, K.P.; Chang, D.; Zio, E. Application of Monte Carlo simulation for the estimation of production availability in offshore installations. In Springer Series in Reliability Engineering; Springer Science and Business Media LLC: Cham, Switzerland, 2010; pp. 233–252. [Google Scholar]
- Raiffa, H.; Schlaifer, R. Applied Statistical Decision Theory; Harvard University Press; Cambridge University Press: Cambridge, UK, 1961. [Google Scholar]
- Yang, Y.; Nambiar, A.; Luxcey, N.; Fonseca, F.; Amarel, L. Advanced design tools for ocean energy systems innovation, development and deployment. In Deliverable D6.3—Reliability, Availability, Maintainability and Survivability Alpha Version; DTOcean+: Aalborg Øst, Denmark, 2020. [Google Scholar]
- Department of Defense Washington DC. Military Handbook—Reliability Prediction of Electronic Equipment; Department of Defense Washington DC: Washington, DC, USA, 1991; MIL-HDBK-217F. [Google Scholar]
- Rinaldi, G.; Portillo, J.; Khalid, F.; Henriques, J.; Thies, P.R.; Gato, L.; Johanning, L. Multivariate analysis of the reliability, availability, and maintainability characterizations of a Spar–Buoy wave energy converter farm. J. Ocean Eng. Mar. Energy 2018, 4, 199–215. [Google Scholar] [CrossRef]
- Chybowski, L. Importance Analysis of components of a multi-operational-state power system using fault tree models. Information 2020, 11, 29. [Google Scholar] [CrossRef]
- Hugin Expert A/S. Hugin API Reference Manual. 2019. Available online: http://download.hugin.com/webdocs/manuals/Python/ (accessed on 9 June 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).