Performance Assessment Based on the Relative Efficiency of Indian Opencast Coal Mines Using Data Envelopment Analysis and Malmquist Productivity Index
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Envelopment Analysis
2.2. Malmquist Productivity Index
2.3. Selection of Input and Output Variables for Performance Measurement
- Salary and wages expenditure (rupees/tonne): Salary and wages paid to the employee (salary of executive and staff; gratuity; regular and overtime duty; Sunday/holiday over time payment; fall back wages; leave travel concession; long leave travel concession and other perks)
- Administrative expenditure (rupees/tonne): Security/central industrial security force, head office expenditure, area office expenditure, etc.
- Store expenditure (rupees/tonne): Store expenditure contains different store items used for mines operation like POL (petroleum oil lubricant), explosive, spare parts of the machine, etc.
- Power expenditure (rupees/tonne): Power consumed by the individual mine per unit. The power is consumed through several sources like electricity, coal, and diesel, etc., based on the mine’s requirement.
- Depreciation expenditure (rupees/tonne): Depreciation costs involved in the capital items. Depreciation involves wear and tear occur to the mining asset per annum.
- Output per man-shift (tonne): Output in terms of coal production per total number of miners working in shift per annum.
- Capacity utilization (percentage): Percentage of the capacity of mines utilized. Here, capacity utilization considers the overall capacity utilization of the mines, considering man and machine utilization.
- Delivery performance (percentage): Percentage of the coal delivered by the mine.
2.4. Data Collection
3. Results
3.1. DEA Result for Opencast Mines
3.1.1. Efficiency Result from CCR and BCC Models
3.1.2. Target Values and Sources of Inefficiency
3.2. Evaluating Coal Mines Performance Using Malmquist Productive Index
4. Discussion
4.1. Strategies for the Reduction of Input Variables
4.1.1. Salary and Wages Cost and Performance
4.1.2. Administrative Cost and Performance
4.1.3. Store Cost and Performance
4.1.4. Depreciation Cost and Performance
4.1.5. Power Cost and Performance
4.2. Strategies for the Improvement of Output Variables
4.2.1. OMS and Performance
4.2.2. Capacity Utilization and Performance
4.2.3. Delivery Performance and Mine Performance
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| MINES | SWE | AE | SE | PE | DE | OMS | CU | DP |
|---|---|---|---|---|---|---|---|---|
| OC1 | 371 | 267 | 231 | 15 | 39 | 6.1 | 106.59 | 98.54 |
| OC2 | 1588 | 267 | 476 | 44 | 40 | 1.36 | 20.87 | 92 |
| OC3 | 1291 | 294 | 212 | 33 | 0 | 3.95 | 102.67 | 88.45 |
| OC4 | 1175 | 267 | 504 | 51 | 204 | 2.07 | 108.18 | 98.69 |
| OC5 | 1391 | 406 | 327 | 50 | 160 | 2.87 | 26.75 | 54.07 |
| OC6 | 1789 | 478 | 602 | 123 | 200 | 1.63 | 102.03 | 94.41 |
| OC7 | 1535 | 289 | 216 | 18 | 94 | 5.08 | 23.37 | 68.12 |
| OC8 | 462 | 113 | 234 | 22 | 59 | 9.14 | 50.92 | 52.03 |
| OC9 | 1489 | 203 | 421 | 74 | 73 | 2.34 | 104.51 | 89.24 |
| OC10 | 685 | 145 | 205 | 27 | 55 | 5.01 | 62.37 | 81.23 |
| OC11 | 1884 | 373 | 218 | 202 | 23 | 1.08 | 47.17 | 58.9 |
| OC12 | 1184 | 218 | 238 | 45 | 103 | 2.27 | 103.05 | 94.28 |
| OC13 | 865 | 292 | 242 | 36 | 67 | 3.21 | 57.19 | 72.54 |
| OC14 | 960 | 266 | 260 | 20 | 115 | 3.11 | 95.45 | 99.12 |
| OC15 | 835 | 280 | 473 | 44 | 506 | 3.53 | 45.95 | 82.54 |
| OC16 | 1986 | 246 | 247 | 47 | 90 | 3.09 | 79.39 | 72.18 |
| OC17 | 1518 | 420 | 420 | 119 | 202 | 1.64 | 57.8 | 78.39 |
| OC18 | 2526 | 280 | 252 | 228 | 50 | 1.22 | 101.67 | 94.29 |
| OC19 | 1134 | 150 | 14 | 103 | 25 | 2.53 | 65.44 | 69.15 |
| OC20 | 609 | 194 | 410 | 48 | 94 | 1.97 | 60.27 | 52.57 |
| OC21 | 705 | 217 | 125 | 45 | 142 | 7.7 | 45.45 | 47.69 |
| OC22 | 908 | 198 | 390 | 72 | 212 | 3.21 | 64.45 | 62.11 |
| OC23 | 179 | 134 | 141 | 28 | 112 | 9.11 | 79 | 87.5 |
| OC24 | 1045 | 323 | 280 | 98 | 131 | 4.23 | 78.71 | 87.65 |
| OC25 | 1215 | 465 | 389 | 121 | 144 | 4.78 | 82.3 | 88.1 |
| OC26 | 867 | 313 | 280 | 123 | 120 | 5.1 | 72.5 | 84 |
| OC27 | 1641 | 395 | 285 | 167 | 175 | 3.56 | 68.9 | 73.5 |
| OC28 | 1501 | 533 | 421 | 210 | 234 | 2.97 | 61.75 | 60.25 |
| MINES | SWE | AE | SE | PE | DE | OMS | CU | DP |
|---|---|---|---|---|---|---|---|---|
| OC1 | 246 | 194 | 87 | 9 | 33 | 8.44 | 185.38 | 94.86 |
| OC2 | 1126 | 229 | 306 | 28 | 34 | 2.1 | 115.89 | 92.57 |
| OC3 | 490 | 242 | 173 | 25 | 114 | 4.86 | 31.46 | 50.07 |
| OC4 | 438 | 229 | 158 | 20 | 10 | 4.52 | 32.03 | 54.34 |
| OC5 | 824.84 | 496 | 406 | 112 | 187 | 1.81 | 23.83 | 33.5 |
| OC6 | 542 | 318 | 195 | 20 | 83 | 4.17 | 90.86 | 98.34 |
| OC7 | 1220 | 281 | 602 | 143 | 199 | 1.24 | 28.8 | 47.21 |
| OC8 | 578 | 201 | 211 | 23 | 148 | 4.61 | 47.96 | 77.49 |
| OC9 | 1164 | 312 | 391 | 47 | 248 | 8.04 | 26.13 | 51.73 |
| OC10 | 432 | 121 | 167 | 32 | 64 | 4.49 | 86.76 | 88.38 |
| OC11 | 1040 | 311 | 225 | 56 | 14 | 2.46 | 76.12 | 91.31 |
| OC12 | 1191 | 290 | 232 | 49 | 79 | 2.1 | 126.89 | 98.45 |
| OC13 | 797.78 | 281 | 189 | 28 | 43 | 3.51 | 46 | 47.28 |
| OC14 | 719 | 267 | 198 | 19 | 102 | 3.71 | 49.61 | 71.43 |
| OC15 | 650 | 282 | 269 | 37 | 591 | 4.13 | 71.03 | 87.47 |
| OC16 | 860 | 234 | 581 | 147 | 427 | 0.67 | 189.75 | 97.21 |
| OC17 | 1111 | 394 | 349 | 82 | 156 | 2.12 | 37.21 | 49.05 |
| OC18 | 1586 | 207 | 240 | 193 | 203 | 1.73 | 66.32 | 72.5 |
| OC19 | 696 | 136 | 225 | 49 | 90.86 | 4.38 | 75.98 | 79.03 |
| OC20 | 392 | 271 | 164 | 34 | 144.73 | 7.65 | 119.17 | 98.34 |
| OC21 | 403 | 291 | 247 | 64 | 145.88 | 3.06 | 44.86 | 69.34 |
| OC22 | 893 | 174 | 374 | 67 | 198 | 3.15 | 62.5 | 63.5 |
| OC23 | 163 | 128 | 121 | 35 | 105 | 8.87 | 80.5 | 85.5 |
| OC24 | 987 | 310 | 255 | 103 | 127 | 4.21 | 72.23 | 74.5 |
| OC25 | 1111 | 423 | 347 | 123 | 136 | 4.89 | 87.11 | 85 |
| OC26 | 823 | 296 | 265 | 112 | 103 | 5.2 | 75.5 | 88.45 |
| OC27 | 1550 | 388 | 267 | 158 | 163 | 3.45 | 65.45 | 71.25 |
| OC28 | 1447 | 517 | 403 | 217 | 205 | 3.05 | 64 | 70.5 |
| MINES | SWE | AE | SE | PE | DE | OMS | CU | DP |
|---|---|---|---|---|---|---|---|---|
| OC1 | 272.62 | 103.56 | 109.67 | 12.77 | 20.84 | 6.25 | 189.99 | 94.5 |
| OC2 | 615.57 | 127.4 | 173.85 | 18.57 | 68.89 | 2.9 | 105.17 | 95 |
| OC3 | 328.58 | 188.11 | 146.81 | 17.27 | 83.87 | 5.22 | 56 | 61.25 |
| OC4 | 437.14 | 212.95 | 151.31 | 21.78 | 7.57 | 4.36 | 55.45 | 53.2 |
| OC5 | 790 | 201.4 | 289.59 | 61.13 | 232.41 | 2.49 | 35.89 | 45 |
| OC6 | 499.15 | 219.76 | 169.03 | 24.64 | 67.57 | 3.81 | 124.01 | 96.35 |
| OC7 | 1111.24 | 225.21 | 295.17 | 86.59 | 142.2 | 2.06 | 61.5 | 76 |
| OC8 | 582 | 117.64 | 187.85 | 29.87 | 74.22 | 3.51 | 50.53 | 51.11 |
| OC9 | 974.28 | 272.87 | 425.49 | 89.93 | 202.93 | 2.5 | 140.28 | 87 |
| OC10 | 425.28 | 112.6 | 120.51 | 26.96 | 51.92 | 4.65 | 92.22 | 93 |
| OC11 | 1085.57 | 343.88 | 314.31 | 243.29 | 156.39 | 1.84 | 38.1 | 47.75 |
| OC12 | 547.94 | 159.5 | 151.83 | 118.74 | 99.17 | 3.73 | 68.47 | 76.33 |
| OC13 | 694 | 213.94 | 155.25 | 36.14 | 71.37 | 3.03 | 94.88 | 91.35 |
| OC14 | 701.06 | 231.59 | 182.53 | 32.03 | 65.88 | 3.44 | 53.03 | 70 |
| OC15 | 610.05 | 275.31 | 176.79 | 25.82 | 219.97 | 3.51 | 37.54 | 41.45 |
| OC16 | 715.25 | 217.74 | 251.15 | 46.6 | 193.67 | 3.38 | 66.25 | 79.95 |
| OC17 | 980.67 | 338.91 | 150.4 | 104.14 | 111.59 | 0.08 | 173.29 | 94.35 |
| OC18 | 761.13 | 335.76 | 255.78 | 67.69 | 113.65 | 2.38 | 95.82 | 91.05 |
| OC19 | 571.49 | 112.36 | 199.66 | 43.22 | 37.41 | 3.14 | 68.34 | 78 |
| OC20 | 275.91 | 136.32 | 144.47 | 45.59 | 89.81 | 8.1 | 159.89 | 94 |
| OC21 | 402.79 | 142.92 | 209.68 | 46.9 | 87.49 | 5.69 | 102.83 | 93.25 |
| OC22 | 887 | 207 | 521 | 67 | 207 | 3.07 | 61.38 | 73.08 |
| OC23 | 158 | 128 | 155 | 17 | 78 | 9.07 | 54.23 | 81.93 |
| OC24 | 907 | 345 | 307 | 87 | 94 | 4.52 | 76.5 | 82.25 |
| OC25 | 1102 | 431 | 394 | 103 | 85 | 4.67 | 72.41 | 72.05 |
| OC26 | 756 | 290 | 321 | 130 | 112 | 4.85 | 68.15 | 74.2 |
| OC27 | 1411 | 370 | 310 | 124 | 141 | 3.21 | 61.25 | 63.5 |
| OC28 | 1225 | 415 | 387 | 146 | 189 | 3.07 | 63.3 | 67 |
Appendix B
| SLNO | DMUs | Actual SWE | Projected (SWE) | % Change | Actual AE | Projected (AE) | % Change | Actual SE | Projected (SE) | % Change | Actual PE | Projected (PE) | % CHANGE | Actual DE | Projected (DE) | % CHANGE |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | OC1 | 371 | 371.00 | 0% | 267 | 267.00 | 0.00% | 231 | 231.00 | 0% | 15 | 15.00 | 0% | 39 | 39.00 | 0% |
| 2 | OC2 | 1588 | 629.37 | 60.37% | 267 | 239.51 | 10.30% | 476 | 220.45 | 53.69% | 44 | 21.62 | 50.86% | 40 | 35.88 | 10.30% |
| 3 | OC3 | 1291 | 1291.00 | 0% | 294 | 294.00 | 0% | 212 | 212.00 | 0% | 33 | 33.00 | 0% | 0 | 0.00 | 0% |
| 4 | OC4 | 1175 | 1175.00 | 0% | 267 | 267.00 | 0% | 504 | 504.00 | 0% | 51 | 51.00 | 0% | 204 | 204.00 | 0% |
| 5 | OC5 | 1391 | 356.32 | 74.38% | 406 | 182.05 | 55.16% | 327 | 168.95 | 48.33% | 50 | 25.83 | 48.34% | 160 | 82.66 | 48.34% |
| 6 | OC6 | 1789 | 840.25 | 53.03% | 478 | 224.51 | 53.03% | 602 | 249.68 | 58.52% | 123 | 36.67 | 70.19% | 200 | 77.81 | 61.10% |
| 7 | OC7 | 1535 | 331.20 | 78.42% | 289 | 239.43 | 17.15% | 216 | 212.34 | 1.69% | 18 | 17.70 | 1.67% | 94 | 54.13 | 42.41% |
| 8 | OC8 | 462 | 462.00 | 0% | 113 | 113.00 | 0% | 234 | 234.00 | 0% | 22 | 22.00 | 0% | 59 | 59.00 | 0% |
| 9 | OC9 | 1489 | 1489.00 | 0% | 203 | 203.00 | 0% | 421 | 421.00 | 0% | 74 | 74.00 | 0% | 73 | 73.00 | 0% |
| 10 | OC10 | 685 | 685.00 | 0% | 145 | 145.00 | 0% | 205 | 205.00 | 0% | 27 | 27.00 | 0% | 55 | 55.00 | 0% |
| 11 | OC11 | 1884 | 1151.58 | 38.88% | 373 | 227.99 | 38.88% | 218 | 125.49 | 42.44% | 202 | 62.73 | 68.95% | 23 | 14.06 | 38.87% |
| 12 | OC12 | 1184 | 1184.00 | 0% | 218 | 218.00 | 0% | 238 | 238.00 | 0% | 45 | 45.00 | 0% | 103 | 103.00 | 0% |
| 13 | OC13 | 865 | 668.32 | 22.74% | 292 | 225.24 | 22.86% | 242 | 186.97 | 22.74% | 36 | 27.81 | 22.75% | 67 | 51.77 | 22.73% |
| 14 | OC14 | 960 | 960.00 | 0.00% | 266 | 266.00 | 0.00% | 260 | 260.00 | 0.00% | 20 | 20.00 | 0.00% | 115 | 115.00 | 0.00% |
| 15 | OC15 | 835 | 271.50 | 67.49% | 280 | 154.96 | 44.66% | 473 | 176.48 | 62.69% | 44 | 24.35 | 44.66% | 506 | 87.68 | 82.67% |
| 16 | OC16 | 1986 | 447.93 | 77.45% | 246 | 174.11 | 29.22% | 247 | 174.82 | 29.22% | 47 | 33.26 | 29.23% | 90 | 63.70 | 29.22% |
| 17 | OC17 | 1518 | 529.20 | 65.14% | 420 | 146.42 | 65.14% | 420 | 146.42 | 65.14% | 119 | 41.49 | 65.13% | 202 | 70.42 | 65.14% |
| 18 | OC18 | 2526 | 499.04 | 80.24% | 280 | 246.23 | 12.06% | 252 | 221.60 | 12.06% | 228 | 26.84 | 88.23% | 50 | 43.97 | 12.06% |
| 19 | OC19 | 1134 | 1134.00 | 0% | 150 | 150.00 | 0% | 14 | 14.00 | 0% | 103 | 103.00 | 0% | 25 | 25.00 | 0% |
| 20 | OC20 | 609 | 414.53 | 31.93% | 194 | 132.05 | 31.93% | 410 | 221.24 | 46.04% | 48 | 22.06 | 54.04% | 94 | 63.98 | 31.94% |
| 21 | OC21 | 705 | 359.05 | 49.07% | 217 | 137.02 | 36.86% | 125 | 117.06 | 6.35% | 45 | 42.14 | 6.36% | 142 | 95.60 | 32.68% |
| 22 | OC22 | 908 | 325.64 | 64.14% | 198 | 123.12 | 37.82% | 390 | 189.19 | 51.49% | 72 | 24.89 | 65.43% | 212 | 84.54 | 60.12% |
| 23 | OC23 | 179 | 179.00 | 0% | 134 | 134.00 | 0% | 141 | 141.00 | 0% | 28 | 28.00 | 0% | 112 | 112.00 | 0% |
| 24 | OC24 | 1045 | 419.89 | 59.82% | 323 | 178.03 | 44.88% | 280 | 154.33 | 44.88% | 98 | 35.22 | 64.06% | 131 | 72.20 | 44.89% |
| 25 | OC25 | 1215 | 485.17 | 60.07% | 465 | 193.40 | 58.41% | 389 | 161.79 | 58.41% | 121 | 36.19 | 70.09% | 144 | 59.89 | 58.41% |
| 26 | OC26 | 867 | 479.58 | 44.69% | 313 | 173.14 | 44.68% | 280 | 154.88 | 44.69% | 123 | 37.90 | 69.19% | 120 | 66.38 | 44.68% |
| 27 | OC27 | 1641 | 613.08 | 62.64% | 395 | 147.57 | 62.64% | 285 | 106.48 | 62.64% | 167 | 56.85 | 65.96% | 175 | 65.38 | 0% |
| 28 | OC28 | 1501 | 467.84 | 68.83% | 533 | 166.13 | 68.83% | 421 | 131.22 | 68.83% | 210 | 43.83 | 79.13% | 234 | 72.93 | 10.30% |
| NO | DMU | Actual OMS | Projected (OMS) | % Change | Actual CU | Projected (CU) | % Change | Actual DP | Projected (DP) | % Change |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | OC1 | 6.1 | 6.10 | 0% | 106.59 | 106.59 | 0% | 98.54 | 98.54 | 0% |
| 2 | OC2 | 1.36 | 5.40 | 297.06% | 20.87 | 94.03 | 350.55% | 92 | 92.00 | 0% |
| 3 | OC3 | 3.95 | 3.95 | 0% | 102.67 | 102.67 | 0% | 88.45 | 88.45 | 0% |
| 4 | OC4 | 2.07 | 2.07 | 0% | 108.18 | 108.18 | 0% | 98.69 | 98.69 | 0% |
| 5 | OC5 | 2.87 | 7.83 | 172.82% | 26.75 | 87.80 | 228.22% | 54.07 | 89.98 | 66.41% |
| 6 | OC6 | 1.63 | 4.30 | 163.80% | 102.03 | 102.03 | 0% | 94.41 | 94.41 | 0% |
| 7 | OC7 | 5.08 | 6.72 | 32.28% | 23.37 | 100.87 | 331.62% | 68.12 | 96.25 | 41.29% |
| 8 | OC8 | 9.14 | 9.14 | 0% | 50.92 | 50.92 | 0% | 52.03 | 52.03 | 0% |
| 9 | OC9 | 2.34 | 2.34 | 0% | 104.51 | 104.51 | 0% | 89.24 | 89.24 | 0% |
| 10 | OC10 | 5.01 | 5.01 | 0% | 62.37 | 62.37 | 0% | 81.23 | 81.23 | 0% |
| 11 | OC11 | 1.08 | 3.48 | 222.22% | 47.17 | 86.43 | 83.23% | 58.9 | 80.64 | 36.91% |
| 12 | OC12 | 2.27 | 2.27 | 0% | 103.05 | 103.05 | 0% | 94.28 | 94.28 | 0% |
| 13 | OC13 | 3.21 | 6.39 | 99.07% | 57.19 | 94.02 | 64.40% | 72.54 | 90.03 | 24.11% |
| 14 | OC14 | 3.11 | 3.11 | 0% | 95.45 | 95.45 | 0% | 99.12 | 99.12 | 0% |
| 15 | OC15 | 3.53 | 8.55 | 142.21% | 45.95 | 78.64 | 71.14% | 82.54 | 82.54 | 0% |
| 16 | OC16 | 3.09 | 7.19 | 132.69% | 79.39 | 79.39 | 0% | 72.18 | 80.08 | 10.94% |
| 17 | OC17 | 1.64 | 6.70 | 308.54% | 57.8 | 71.20 | 23.18% | 78.39 | 78.74 | 0.45% |
| 18 | OC18 | 1.22 | 5.71 | 368.03% | 101.67 | 101.67 | 0% | 94.29 | 94.95 | 0.70% |
| 19 | OC19 | 2.53 | 2.53 | 0% | 65.44 | 65.44 | 0% | 69.15 | 69.15 | 0% |
| 20 | OC20 | 1.97 | 8.82 | 347.72% | 60.27 | 60.55 | 0.46% | 52.57 | 61.68 | 17.33% |
| 21 | OC21 | 7.7 | 7.87 | 2.21% | 45.45 | 76.44 | 68.18% | 47.69 | 84.04 | 76.22% |
| 22 | OC22 | 3.21 | 9.13 | 184.42% | 64.45 | 64.45 | 0% | 62.11 | 69.12 | 11.29% |
| 23 | OC23 | 9.11 | 9.11 | 0% | 79 | 79.00 | 0% | 87.5 | 87.50 | 0% |
| 24 | OC24 | 4.23 | 6.89 | 62.88% | 78.71 | 84.16 | 6.92% | 87.65 | 87.65 | 0% |
| 25 | OC25 | 4.78 | 6.24 | 30.54% | 82.3 | 86.30 | 4.86% | 88.1 | 88.10 | 0% |
| 26 | OC26 | 5.1 | 6.65 | 30.39% | 72.5 | 80.44 | 10.95% | 84 | 84.00 | 0% |
| 27 | OC27 | 3.56 | 6.23 | 75.00% | 68.9 | 72.24 | 4.85% | 73.5 | 76.77 | 4.45% |
| 28 | OC28 | 2.97 | 6.81 | 129.29% | 61.75 | 80.76 | 30.79% | 60.25 | 84.28 | 39.88% |
References
- Energy Statistics. 2020. Available online: http://mospi.nic.in/sites/default/files/publication_reports/ES_2020_240420m.pdf (accessed on 11 June 2020).
- Coal Planning. Available online: www.coalcontroller.gov.in (accessed on 11 June 2020).
- Brignall, S.; Ballantine, J. Performance measurement in service business revisited. Int. J. Serv. Ind. Manag. 1996, 7, 6–31. [Google Scholar] [CrossRef]
- Purbey, S. Development of a Framework for Managing the Performance of Indian Healthcare Units. Ph.D. Thesis, Indian School of Mines, Dhanbad, India, 2008. [Google Scholar]
- Thompson, R.G.; Dharmapala, P.; Thrall, R.M. Linked-cone DEA profit ratios and technical efficiency with application to Illinois coal mines. Int. J. Prod. Econ. 1995, 39, 99–115. [Google Scholar] [CrossRef]
- Kulshreshtha, M.; Parikh, J.K. Study of efficiency and productivity growth in opencast and underground coal mining in India: A DEA analysis. Energy Econ. 2002, 24, 439–453. [Google Scholar] [CrossRef]
- Hosseinzadeh, A.; Smyth, R.; Valadkhani, A.; Le, V. Analyzing the efficiency performance of major Australian mining companies using bootstrap data envelopment analysis. Econ. Model. 2016, 57, 26–35. [Google Scholar] [CrossRef]
- Geisslera, B.; Mew, M.C.; Weber, O.; Steiner, G. Efficiency performance of the world’s leading corporations in phosphate rock mining. Resour. Conserv. Recycl. 2015, 105, 246–258. [Google Scholar] [CrossRef]
- Fang, H.; Wu, J.; Zeng, C. Comparative study on efficiency performance of listed coal mining companies in China and the U.S. Energy Policy 2009, 37, 5140–5148. [Google Scholar] [CrossRef]
- Lei, T.; Ding, R.J. Efficiency assessment of coal mine safety input by data envelopment analysis. J. China Univ. Min. Technol. 2008, 18, 88–92. [Google Scholar]
- Cui, Y.; Huang, G.; Yin, Z. Estimating regional coal resource efficiency in China using three-stage DEA and bootstrap DEA models. Int. J. Min. Sci. Technol. 2015, 25, 861–864. [Google Scholar] [CrossRef]
- Yang, H.; Pollitt, M.G. Incorporating both undesirable outputs and uncontrollable variables into DEA: The performance of Chinese coal-fired power plants. Eur. J. Oper. Res. 2009, 197, 1095–1105. [Google Scholar] [CrossRef]
- Wong, W.P.; Wong, K.Y. Supply chain performance measurement system using DEA modeling. Ind. Manag. Data Syst. 2007, 107, 361–381. [Google Scholar] [CrossRef]
- Singh, R.; Mahapatra, B.; Mukherjee, K.; Bhar, C. Application of DEA performance Evaluation of Indian Microfinance Institutions. Asian J. Manag. Res. 2014, 4, 597–605. [Google Scholar]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision-making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Fan, Y.; Bai, B.; Qiao, Q.; Kang, P.; Zhang, Y.; Guo, J. Study on eco-efficiency of industrial parks in China based on data envelopment analysis. J. Environ. Manag. 2017, 192, 107–115. [Google Scholar] [CrossRef] [PubMed]
- Malmquist, S. Index numbers and indifference curves. Trab. Estat. 1953, 4, 209–242. [Google Scholar] [CrossRef]
- Caves, D.W.; Christensen, L.R.; Diewart, W.E. The econometric theory of index numbers and the measurement of input, and output productivity. Econometrica 1982, 50, 1393–1414. [Google Scholar] [CrossRef]
- Fare, R.; Grosskopf, S.; Norris, M.; Zhang, Z. Productivity growth, technical progress, and efficiency change in industrialized countries. Am. Econ. Rev. 1994, 84, 66–83. [Google Scholar]
- Kao, C. Network Data Envelopment Analysis—Foundation and Extension; International Series in Operations Research & Management Science; Springer: Berlin/Heidelberg, Germany, 2017; Volume 240. [Google Scholar] [CrossRef]
- Vaninsky, A. Efficiency of electric power generation in the United States: Analysis and forecast based on data envelopment analysis. Energy Econ. 2006, 28, 326–338. [Google Scholar] [CrossRef]
- Barros, C.P. Efficiency analysis of hydroelectric generating plants: A case study for Portugal. Energy Econ. 2008, 30, 59–75. [Google Scholar] [CrossRef]
- Jamasb, T.; Pollitt, M.; Triebs, T. Productivity and efficiency of U.S. gas transmission companies: A European regulatory perspective. Energy Policy 2008, 36, 3398–3412. [Google Scholar] [CrossRef]

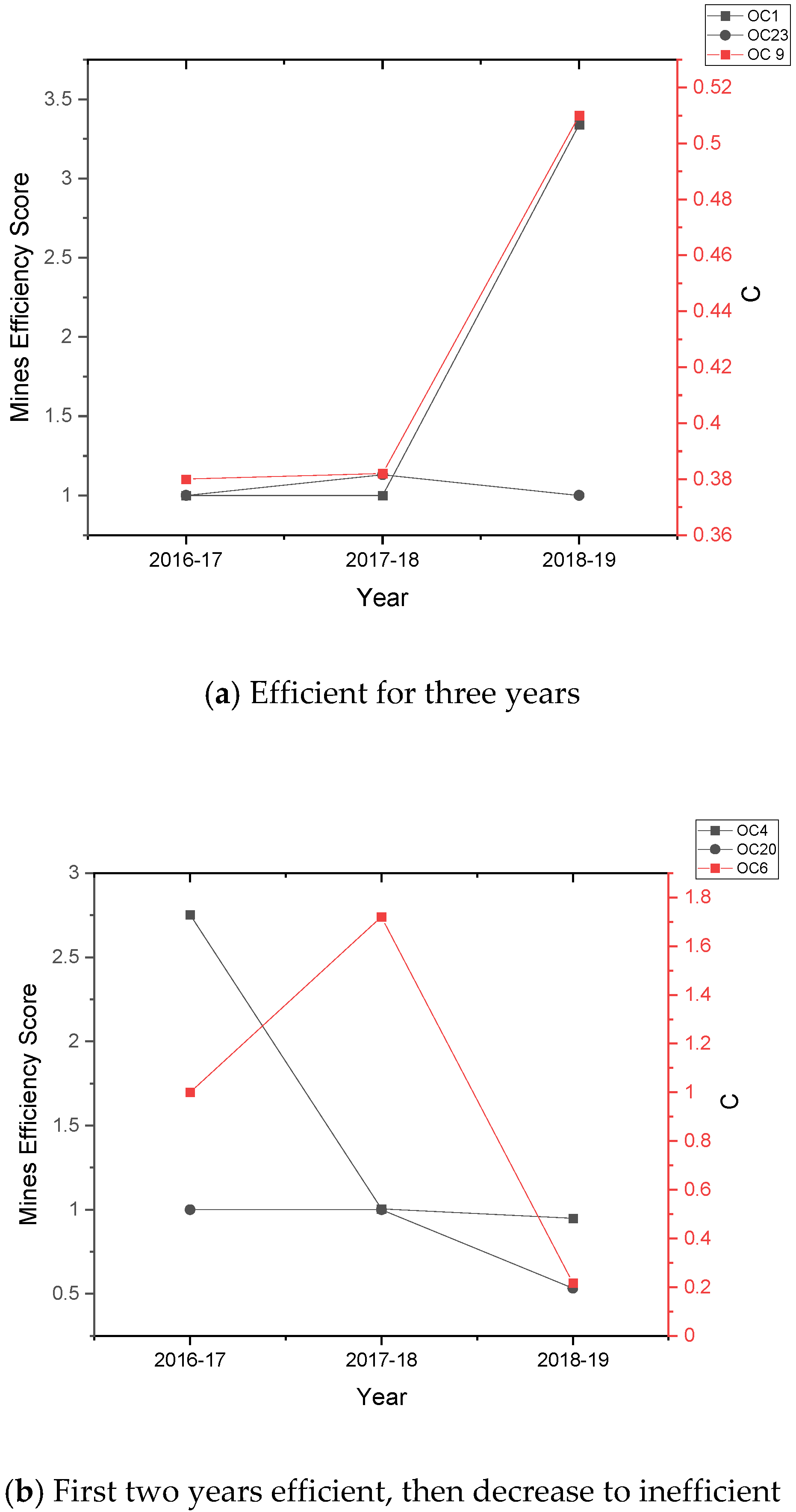
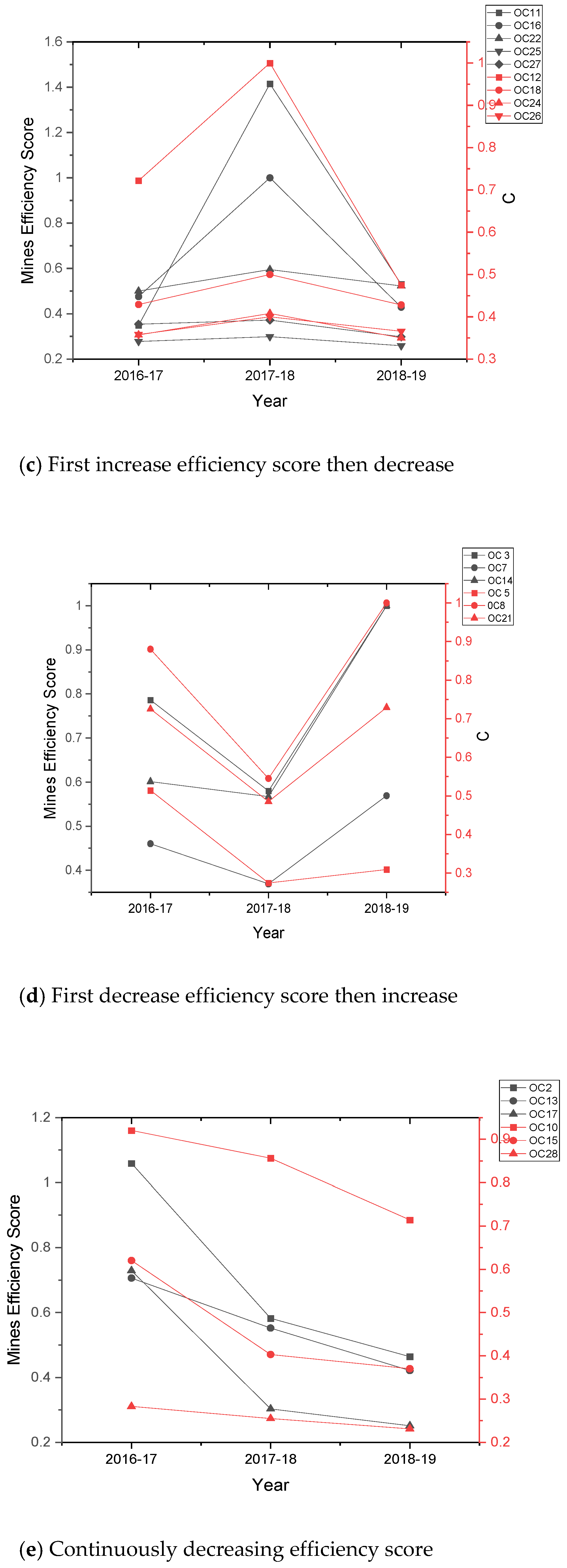
| S.L. No. | Input Variables | Notation | References | S.L. No. | Output Variables | Notation | References |
|---|---|---|---|---|---|---|---|
| 1 | Salary and Wages Expenditure | SWE | [7] | 1 | Output per Man-shift | OMS | Expert opinion |
| 2 | Administrative Expenditure | AE | [7] | 2 | Capacity Utilization | CU | [21,22] |
| 3 | Store Expenditure | SE | Expert opinion | 3 | Delivery Performance | DP | [23] |
| 4 | Power Expenditure | PE | Expert opinion | - | - | - | - |
| 5 | Depreciation Expenditure | DE | Expert opinion | - | - | - | - |
| No. | DMUs | Benchmark (Lambda) Based on an Input-Oriented Variable Return to Scale | Efficiency | Return to Scale | ||
|---|---|---|---|---|---|---|
| Pure Technical Efficiency | Technical Efficiency | Scale Efficiency | ||||
| 1 | OC1 | OC01(1.000000) | 1.00 | 1.00 | 1.00 | Constant |
| 2 | OC2 | OC01(0.543096); OC03(0.189614); OC10(0.267290) | 0.90 | 0.85 | 0.95 | Decreasing |
| 3 | OC3 | OC03(1.000000) | 1.00 | 1.00 | 1.00 | Constant |
| 4 | OC4 | OC04(1.000000) | 1.00 | 0.71 | 0.71 | Decreasing |
| 5 | OC5 | OC01(0.213842); OC03(0.122542); OC23(0.663616) | 0.52 | 0.31 | 0.60 | Increasing |
| 6 | OC6 | OC01(0.346575); OC09(0.130785); OC12(0.421276); OC23(0.101365) | 0.47 | 0.43 | 0.92 | Decreasing |
| 7 | OC7 | OC01(0.792683); OC23(0.207317) | 0.98 | 0.73 | 0.75 | Increasing |
| 8 | OC8 | OC08(1.000000) | 1.00 | 1.00 | 1.00 | Constant |
| 9 | OC9 | OC09(1.000000) | 1.00 | 1.00 | 1.00 | Constant |
| 10 | OC10 | OC10(1.000000) | 1.00 | 1.00 | 1.00 | Constant |
| 11 | OC11 | OC01(0.075745); OC03(0.480075); OC19(0.444180) | 0.61 | 0.45 | 0.73 | Increasing |
| 12 | OC12 | OC12(1.000000) | 1.00 | 0.95 | 0.95 | Decreasing |
| 13 | OC13 | OC01(0.205182); OC03(0.399035); OC19(0.006487); OC23(0.389297) | 0.77 | 0.61 | 0.78 | Increasing |
| 14 | OC14 | OC14(1.000000) | 1.00 | 0.92 | 0.92 | Decreasing |
| 15 | OC15 | OC01(0.188982); OC08(0.198657); OC23(0.612361) | 0.55 | 0.53 | 0.96 | Increasing |
| 16 | OC16 | OC01(0.319492); OC08(0.235384); OC09(0.004227); OC19(0.141816); OC23(0.299080) | 0.71 | 0.69 | 0.97 | Increasing |
| 17 | OC17 | OC01(0.071571); OC08(0.126618); OC10(0.207025); OC19(0.205100); OC23(0.389686) | 0.35 | 0.34 | 0.96 | Increasing |
| 18 | OC18 | OC01(0.798755); OC09(0.067988); OC19(0.081270); OC23(0.051988) | 0.88 | 0.82 | 0.94 | Decreasing |
| 19 | OC19 | OC19(1.000000) | 1.00 | 1.00 | 1.00 | Constant |
| 20 | OC20 | OC01(0.105459); OC08(0.760717); OC23(0.133824) | 0.68 | 0.61 | 0.90 | Increasing |
| 21 | OC21 | OC19(0.188535); OC23(0.811465) | 0.94 | 0.92 | 0.98 | Increasing |
| 22 | OC22 | OC08(0.518162); OC23(0.481838) | 0.62 | 0.55 | 0.89 | Increasing |
| 23 | OC23 | OC23(1.000000) | 1.00 | 1.00 | 1.00 | Constant |
| 24 | OC24 | OC01(0.306705); OC10(0.075647); OC19(0.150502); OC23(0.467145) | 0.55 | 0.53 | 0.96 | Decreasing |
| 25 | OC25 | OC01(0.416175); OC10(0.102251); OC19(0.182750); OC23(0.298824) | 0.42 | 0.41 | 1.00 | Decreasing |
| 26 | OC26 | OC01(0.274775); OC08(0.070309); OC10(0.098436); OC19(0.186510); OC23(0.369970) | 0.55 | 0.54 | 0.98 | Increasing |
| 27 | OC27 | OC01(0.071272); OC08(0.114583); OC19(0.406252); OC23(0.407894) | 0.37 | 0.35 | 0.94 | Increasing |
| 28 | OC28 | OC01(0.215875); OC08(0.028252); OC19(0.250679); OC23(0.505193) | 0.31 | 0.24 | 0.76 | Increasing |
| NO. | DMU | Efficiency (2016–2017) | Efficiency (2017–2018) | Efficiency (2018–2019) | Efficiency Change (2016–2017 to 2017–2018) | Efficiency Change (2017–2018 to 2018–2019) | Technological Change (2016–2017 to 2017–2018) | Technological Change (2017 to 2018) | Malmquist Index (2016–2017 to 2017–2018) | Malmquist Index (2017–2018 to 2018–2019) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | OC1 | 1.000 | 1.000 | 3.340 | 1.000 | 3.340 | 1.000 | 1.000 | 1.000 | 3.340 |
| 2 | OC2 | 1.059 | 0.582 | 0.464 | 0.550 | 0.797 | 1.041 | 1.070 | 0.572 | 0.853 |
| 3 | OC3 | 0.786 | 0.580 | 1.000 | 0.739 | 1.723 | 1.047 | 1.013 | 0.774 | 1.746 |
| 4 | OC4 | 2.753 | 1.005 | 0.949 | 0.365 | 0.944 | 2.201 | 1.000 | 0.803 | 0.944 |
| 5 | OC5 | 0.514 | 0.274 | 0.309 | 0.533 | 1.126 | 1.000 | 1.000 | 0.533 | 1.126 |
| 6 | OC6 | 1.000 | 1.720 | 0.217 | 1.720 | 0.126 | 0.706 | 1.644 | 1.214 | 0.207 |
| 7 | OC7 | 0.460 | 0.369 | 0.569 | 0.801 | 1.543 | 1.000 | 1.000 | 0.801 | 1.543 |
| 8 | OC8 | 0.880 | 0.545 | 1.000 | 0.619 | 1.836 | 1.000 | 1.000 | 0.619 | 1.836 |
| 9 | OC9 | 0.380 | 0.382 | 0.510 | 1.006 | 1.337 | 0.983 | 1.017 | 0.989 | 1.360 |
| 10 | OC10 | 0.920 | 0.856 | 0.714 | 0.931 | 0.834 | 1.000 | 1.000 | 0.931 | 0.834 |
| 11 | OC11 | 0.349 | 1.415 | 0.530 | 4.056 | 0.374 | 0.575 | 1.894 | 2.334 | 0.708 |
| 12 | OC12 | 0.722 | 1.000 | 0.475 | 1.384 | 0.475 | 2.835 | 0.379 | 3.924 | 0.180 |
| 13 | OC13 | 0.706 | 0.552 | 0.421 | 0.781 | 0.763 | 1.144 | 1.021 | 0.894 | 0.779 |
| 14 | OC14 | 0.601 | 0.567 | 1.000 | 0.944 | 1.763 | 1.107 | 1.000 | 1.045 | 1.763 |
| 15 | OC15 | 0.620 | 0.403 | 0.370 | 0.650 | 0.918 | 1.148 | 1.000 | 0.746 | 0.918 |
| 16 | OC16 | 0.476 | 1.000 | 0.429 | 2.103 | 0.429 | 1.000 | 1.000 | 2.103 | 0.429 |
| 17 | OC17 | 0.729 | 0.303 | 0.251 | 0.415 | 0.830 | 1.232 | 1.040 | 0.512 | 0.863 |
| 18 | OC18 | 0.429 | 0.500 | 0.428 | 1.167 | 0.855 | 1.100 | 1.000 | 1.283 | 0.855 |
| 19 | OC19 | 0.922 | 0.761 | 6.214 | 0.826 | 8.161 | 1.000 | 1.000 | 0.826 | 8.161 |
| 20 | OC20 | 1.000 | 1.000 | 0.534 | 1.000 | 0.534 | 0.799 | 1.000 | 0.799 | 0.534 |
| 21 | OC21 | 0.725 | 0.485 | 0.729 | 0.669 | 1.504 | 1.000 | 1.000 | 0.669 | 1.504 |
| 22 | OC22 | 0.500 | 0.595 | 0.523 | 1.190 | 0.879 | 1.000 | 1.000 | 1.190 | 0.879 |
| 23 | OC23 | 1.000 | 1.132 | 1.000 | 1.132 | 0.884 | 0.658 | 1.006 | 0.744 | 0.889 |
| 24 | OC24 | 0.357 | 0.408 | 0.350 | 1.141 | 0.859 | 0.985 | 1.080 | 1.124 | 0.927 |
| 25 | OC25 | 0.278 | 0.299 | 0.259 | 1.076 | 0.866 | 1.008 | 1.039 | 1.085 | 0.900 |
| 26 | OC26 | 0.358 | 0.400 | 0.366 | 1.116 | 0.914 | 0.966 | 1.035 | 1.078 | 0.947 |
| 27 | OC27 | 0.354 | 0.372 | 0.298 | 1.052 | 0.800 | 0.991 | 1.185 | 1.043 | 0.948 |
| 28 | OC28 | 0.283 | 0.255 | 0.231 | 0.899 | 0.906 | 1.006 | 1.061 | 0.904 | 0.961 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahapatra, B.; Bhar, C.; Mondal, S. Performance Assessment Based on the Relative Efficiency of Indian Opencast Coal Mines Using Data Envelopment Analysis and Malmquist Productivity Index. Energies 2020, 13, 4902. https://doi.org/10.3390/en13184902
Mahapatra B, Bhar C, Mondal S. Performance Assessment Based on the Relative Efficiency of Indian Opencast Coal Mines Using Data Envelopment Analysis and Malmquist Productivity Index. Energies. 2020; 13(18):4902. https://doi.org/10.3390/en13184902
Chicago/Turabian StyleMahapatra, Biswaranjita, Chandan Bhar, and Sandeep Mondal. 2020. "Performance Assessment Based on the Relative Efficiency of Indian Opencast Coal Mines Using Data Envelopment Analysis and Malmquist Productivity Index" Energies 13, no. 18: 4902. https://doi.org/10.3390/en13184902
APA StyleMahapatra, B., Bhar, C., & Mondal, S. (2020). Performance Assessment Based on the Relative Efficiency of Indian Opencast Coal Mines Using Data Envelopment Analysis and Malmquist Productivity Index. Energies, 13(18), 4902. https://doi.org/10.3390/en13184902





