Review of Steady-State Electric Power Distribution System Datasets
Abstract
1. Introduction
1.1. Related Literature and State of the Art
1.2. Contribution of the Paper and Structure
2. Available Grid Datasets
3. Compilation Process of Grid Datasets
3.1. Intended Use Case
3.2. Region
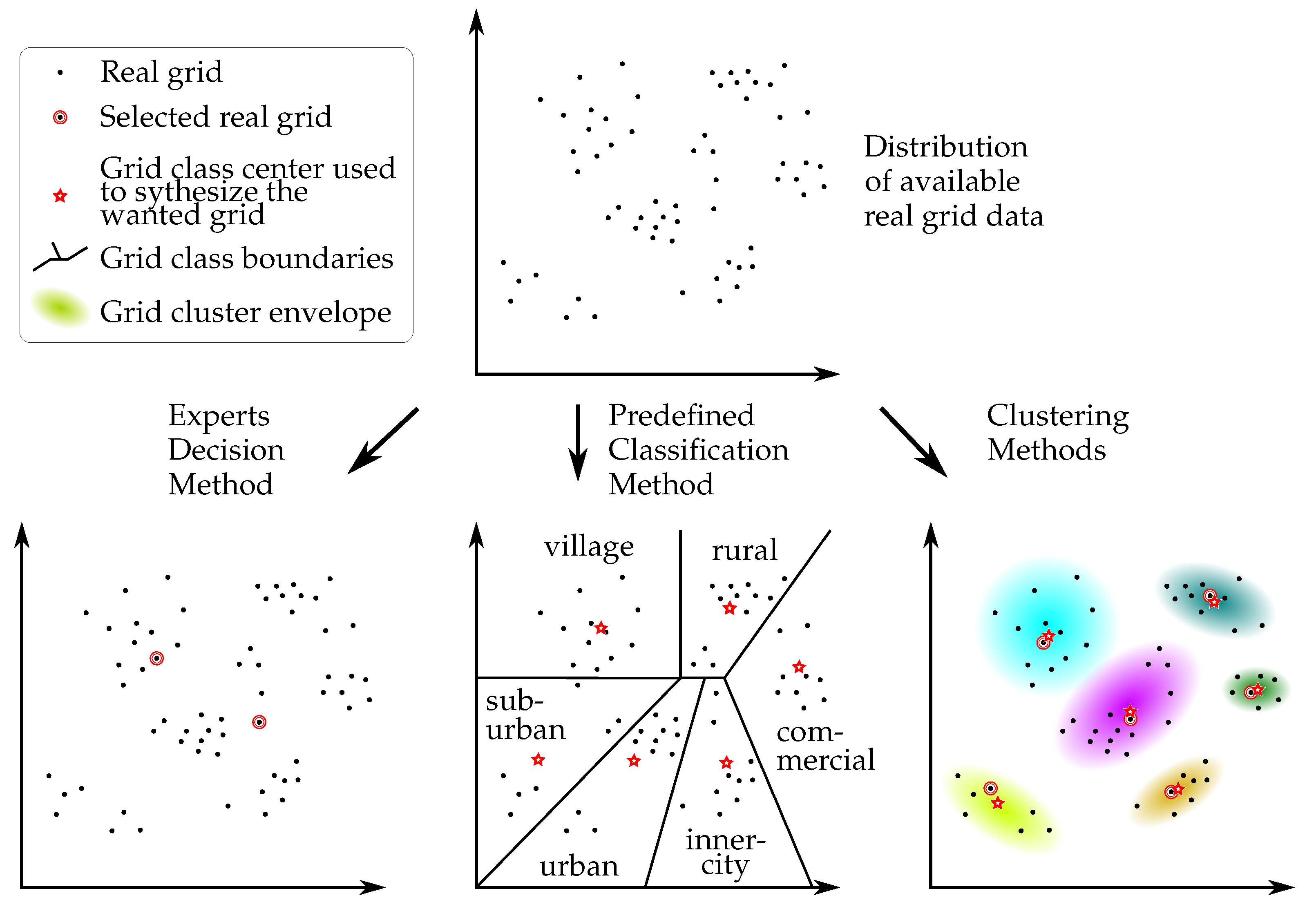
3.3. Grid Compilation Methodology
3.3.1. Introduction of Common Grid Compilation Methodologies
- (I)
- (II)
3.3.2. Comparison of Methodologies
- (i)
- What is the intended use case of the dataset?
- (ii)
- Which data base can be provided for the compilation process?
- (iii)
- May data from selected grids be published or must the data be kept confidential?
3.4. Methodic Origin of Data
4. Terminology to Characterize Distribution Grid Datasets
4.1. Review of Grid Term Nomenclature in Literature
4.1.1. Synthetic Grids
4.1.2. Example and Test Grids
4.1.3. Benchmark Grids
4.1.4. Representative Grids
4.1.5. Generic Grids
4.1.6. Typical Grids
4.1.7. Reference Grids
4.2. Recommended Terminology
5. Conclusions
Author Contributions
Funding

Conflicts of Interest
References
- Söder, L.; Pellinger, C.; Lopez-Botet Zulueta, M.; Milligan, M.; Kiviluoma, J.; Flynn, D.; Orths, A.; Silva, V.; O’Neill, B. Comparison of Integration Studies of 30–40 percent Energy Share from Variable Renewable Sources. In Proceedings of the 16th International Workshop on Large-Scale Integration of Wind Power into Power Systems as well as on Transmission Networks for Offshore Wind Power Plants, Berlin, Germany, 25–27 October 2017. [Google Scholar]
- Jain, A.K.; Horowitz, K.; Ding, F.; Gensollen, N.; Mather, B.; Palmintier, B. Quasi-Static Time-Series PV Hosting Capacity Methodology and Metrics. In Proceedings of the 2019 IEEE Power Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 18–21 February 2019; pp. 1–5. [Google Scholar]
- Gensollen, N.; Horowitz, K.; Palmintier, B.; Ding, F.; Mather, B. Beyond Hosting Capacity: Using Shortest-Path Methods to Minimize Upgrade Cost Pathways. IEEE J. Photovoltaics 2019, 9, 1051–1056. [Google Scholar] [CrossRef]
- Breker, S.; Rentmeister, J.; Sick, B.; Braun, M. Hosting capacity of low-voltage grids for distributed generation: Classification by means of machine learning techniques. Appl. Soft Comput. 2018, 70, 195–207. [Google Scholar] [CrossRef]
- Scheidler, A.; Thurner, L.; Braun, M. Heuristic Optimization for Automated Distribution System Planning in Network Integration Studies. IET Res. J. 2018, 12, 530–538. [Google Scholar]
- Thurner, L.; Scheidler, A.; Probst, A.; Braun, M. Heuristic optimisation for network restoration and expansion in compliance with the single-contingency policy. IET Gener. Transm. Distrib. 2017. [Google Scholar] [CrossRef]
- Menke, J.H.; Schaefer, F.; Braun, M. Performing a Virtual Field Test of a New Monitoring Method for Smart Power Grids. In Proceedings of the IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids, Aalborg, Denmark, 29–31 October 2018. [Google Scholar]
- Bell, K.R.W.; Tleis, A.N.D. Test system requirements for modelling future power systems. In Proceedings of the IEEE PES General Meeting, Providence, RI, USA, 25–29 July 2010; pp. 1–8. [Google Scholar]
- ARPA-E. Grid Data Program Overview—Generating Realistic Information for the Development of Distribution and Transmission Algorithms. 2016. Available online: https://arpa-e.energy.gov/?q=arpa-e-programs/grid-data (accessed on 26 August 2020).
- Marcos, P.; Fernando, E.; Mateo Domingo, C.; Gómez San Román, T.; Palmintier, B.; Hodge, B.M.; Krishnan, V.; De Cuadra García, F.; Mather, B. A review of power distribution test feeders in the United States and the need for synthetic representative networks. Energies 2017, 10, 1896. [Google Scholar] [CrossRef]
- Christie, R.D. Power Systems Test Case Archive; University of Washington: Seattle, WA, USA, 1999; Available online: http://www2.ee.washington.edu/research/pstca/ (accessed on 20 February 2020).
- Meinecke, S.; Drauz, S.R.; Pogacar, S. SimBench—Simulation Data Base for a Consistent Comparison of Innovative Solutions in the Field of Grid Analysis, Grid Planning and Grid Operation Management, 2016–2020. Available online: www.simbench.net (accessed on 13 March 2020).
- Fuller, J.; Dent, C.; Lima, L. Links to test cases. IEEE Power Energy Soc. 2017. Available online: http://sites.ieee.org/pes-tccwg/links-to-test-cases/ (accessed on 19 June 2020).
- Farid, A.M. LIINES Smart Power Grid Test Case Repository. Laboratory for Intelligent Integrated Networks of Engineering Systems. 2016. Available online: http://amfarid.scripts.mit.edu/Datasets/SPG-Data/index.php (accessed on 19 June 2020).
- Panumpabi, P. Power Cases. Illinois Center for a Smarter Electric Grid (ICSEG). 2017. Available online: http://icseg.iti.illinois.edu/power-cases/ (accessed on 19 June 2020).
- Weckesser, T. Power System Data and Test Cases. Available online: https://tweckesser.wordpress.com/power-system-data-and-test-cases/ (accessed on 19 June 2020).
- Birchfield, A. Electric Grid Test Cases. Engineering, Texas A&M University, 2016–2020. Available online: https://electricgrids.engr.tamu.edu/electric-grid-test-cases/ (accessed on 19 June 2020).
- Burkish, W.; McKinnon, K. Network Data of Real Transmission Networks; University of Edinburgh: Edinburgh, UK, 2013; Available online: http://www.maths.ed.ac.uk/optenergy/NetworkData/ (accessed on 19 June 2020).
- Kavasseri, R.; Ababei, C. REDS: REpository of Distribution Systems; Marquette Embedded SystemS Laboratory, ECE Marquette University: Milwaukee, WI, USA; Available online: http://www.dejazzer.com/reds.html (accessed on 19 June 2020).
- Zimmerman, R.D.; Murillo-Sanchez, C.E.; Thomas, R.J. MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef]
- Thurner, L.; Scheidler, A.; Schäfer, F.; Menke, J.; Dollichon, J.; Meier, F.; Meinecke, S.; Braun, M. Pandapower—An Open-Source Python Tool for Convenient Modeling, Analysis, and Optimization of Electric Power Systems. IEEE Trans. Power Syst. 2018, 33, 6510–6521. [Google Scholar] [CrossRef]
- Bialek, J.; Ciapessoni, E.; Cirio, D.; Cotilla-Sanchez, E.; Dent, C.; Dobson, I.; Henneaux, P.; Hines, P.; Jardim, J.; Miller, S.; et al. Benchmarking and validation of cascading failure analysis tools. IEEE Trans. Power Syst. 2016, 31, 4887–4900. [Google Scholar] [CrossRef]
- Schneider, K.P.; Mather, B.A.; Pal, B.C.; Ten, C.; Shirek, G.J.; Zhu, H.; Fuller, J.C.; Pereira, J.L.R.; Ochoa, L.F.; de Araujo, L.R.; et al. Analytic Considerations and Design Basis for the IEEE Distribution Test Feeders. IEEE Trans. Power Syst. 2018, 33, 3181–3188. [Google Scholar] [CrossRef]
- Tripathy, S.C.; Prasad, G.D.; Malik, O.P.; Hope, G.S. Load-Flow Solutions for Ill-Conditioned Power Systems by a Newton-Like Method. IEEE Trans. Power Appar. Syst. 1982, PAS-101, 3648–3657. [Google Scholar] [CrossRef]
- Zollenkopf, K. Load-flow calculation using loss-minimisation techniques. Proc. Inst. Electr. Eng. 1968, 115, 121–127. [Google Scholar] [CrossRef]
- Stott, B.; Alsac, O. Fast Decoupled Load Flow. IEEE Trans. Power Appar. Syst. 1974, PAS-93, 859–869. [Google Scholar] [CrossRef]
- Iwamoto, S.; Tamura, Y. A Load Flow Calculation Method for Ill-Conditioned Power Systems. IEEE Trans. Power Appar. Syst. 1981, PAS-100, 1736–1743. [Google Scholar] [CrossRef]
- Alsac, O.; Stott, B. Optimal load flow with steady-state security. IEEE Trans. Power Appar. Syst. 1974, 745–751. [Google Scholar] [CrossRef]
- Civanlar, S.; Grainger, J.J.; Yin, H.; Lee, S.S.H. Distribution feeder reconfiguration for loss reduction. IEEE Trans. Power Deliv. 1988, 3, 1217–1223. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- Kersting, W.H. Radial distribution test feeders. IEEE Trans. Power Syst. 1991, 6, 975–985. [Google Scholar] [CrossRef]
- Kersting, W.H. Radial distribution test feeders. In Proceedings of the Power Engineering Society Winter Meeting, Columbus, OH, USA, 28 January–1 February 2001; Volume 2, pp. 908–912. [Google Scholar] [CrossRef]
- Kersting, W.H. A comprehensive distribution test feeder. In Proceedings of the IEEE PES T & D 2010, New Orleans, LA, USA, 9–22 April 2010; pp. 1–4. [Google Scholar]
- Salama, M.M.A.; Chikhani, A.Y. A simplified network approach to the VAr control problem for radial distribution systems. IEEE Trans. Power Deliv. 1993, 8, 1529–1535. [Google Scholar] [CrossRef]
- Su, C.T.; Chang, C.F.; Chiou, J.P. Distribution network reconfiguration for loss reduction by ant colony search algorithm. Electr. Power Syst. Res. 2005, 75, 190–199. [Google Scholar] [CrossRef]
- Sunderman, W.G.; Dugan, R.C.; Dorr, D.S. The neutral-to-earth voltage (NEV) test case and distribution system analysis. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Penido, D.R.R.; Araujo, L.R.; Carneiro, S.; Pereira, J.L.R. Solving the NEV test case using the current injection full-newton power flow. In Proceedings of the 2008 IEEE/PES Transmission and Distribution Conference and Exposition, Bogota, Columbia, 13–15 August 2008; pp. 1–7. [Google Scholar] [CrossRef]
- Strunz, K.; Hatziargyriou, N.; Andrieu, C. Benchmark systems for network integration of renewable and distributed energy resources. Cigre Task Force C 2009, 6, 78. [Google Scholar]
- Arritt, R.F.; Dugan, R.C. The IEEE 8500-node test feeder. In Proceedings of the IEEE PES T & D 2010, New Orleans, LA, USA, 19–22 April 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Kerber, G. Aufnahmefähigkeit von Niederspannungsverteilnetzen für die Einspeisung aus Photovoltaikkleinanlagen (Hosting Capacity of Low-Voltage Distribution Grids for Small Scaled PV Systems). Ph.D. Thesis, Technische Universität München, München, Germany, 2011. [Google Scholar]
- Centre for Sustainable Electricity and Distributed Generation (SEDG). UKGDS: United Kingdom Generic Distribution System, April 29, 2015. Available online: https://github.com/sedg/ukgds (accessed on 15 February 2020).
- Kiaee, M.; Cruden, A.; Infield, D. Demand side management using alkaline electrolysers within the UKGDS simulation network. In Proceedings of the CIRED—21st International Conference on Electricity Distribution, Frankfurt, Germany, 6–9 June 2011. [Google Scholar]
- Pilo, F.; Pisano, G.; Scalari, S.; Canto, D.D.; Testa, A.; Langella, R.; Caldon, R.; Turri, R. ATLANTIDE—Digital archive of the Italian electric distribution reference networks. In Proceedings of the CIRED 2012 Workshop: Integration of Renewables into the Distribution Grid, Lisbon, Portugal, 29–30 May 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Celli, G.; Pilo, F.; Pisano, G.; Soma, G.G. Reference scenarios for Active Distribution System according to ATLANTIDE project planning models. In Proceedings of the 2014 IEEE International Energy Conference (ENERGYCON), Cavtat, Croatia, 13–16 May 2014; pp. 1190–1196. [Google Scholar]
- Bracale, A.; Caldon, R.; Celli, G.; Coppo, M.; Dal Canto, D.; Langella, R.; Petretto, G.; Pilo, F.; Pisano, G.; Proto, D.; et al. Analysis of the Italian distribution system evolution through reference networks. In Proceedings of the 2012 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Berlin, Germany, 14–17 October 2012; pp. 1–8. [Google Scholar]
- Dickert, J.; Domagk, M.; Schegner, P. Benchmark low voltage distribution networks based on cluster analysis of actual grid properties. In Proceedings of the PowerTech, 2013 IEEE Grenoble, Grenoble, France, 16–20 June 2013; pp. 1–6. [Google Scholar]
- Schneider, K.; Phanivong, P.; Lacroix, J. IEEE 342-node low voltage networked test system. In Proceedings of the 2014 IEEE PES General Meeting | Conference Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar] [CrossRef]
- IEEE PES AMPS DSAS Test Feeder Working Group. Test Feeders Resources. Available online: http://sites.ieee.org/pes-testfeeders/resources/ (accessed on 12 March 2020).
- Mateo, C.; Prettico, G.; Gómez, T.; Cossent, R.; Gangale, F.; Frías, P.; Fulli, G. European representative electricity distribution networks. Int. J. Electr. Power Energy Syst. 2018, 99, 273–280. [Google Scholar] [CrossRef]
- Meinecke, S.; Sarajlić, D.; Drauz, S.R.; Klettke, A.; Lauven, L.P.; Rehtanz, C.; Moser, A.; Braun, M. SimBench—A Benchmark Dataset of Electric Power Systems to Compare Innovative Solutions based on Power Flow Analysis. Energies 2020, 13, 3290. [Google Scholar] [CrossRef]
- Probability Methods Subcommittee. IEEE Reliability Test System. IEEE Trans. Power Appar. Syst. 1979, PAS-98, 2047–2054. [Google Scholar] [CrossRef]
- Anderson, P.M.; Fouad, A.A. Power System Control and Stability; Iowa State University Press: Iowa City, IA, USA, 1980. [Google Scholar]
- Uchida, N.; Kawata, K.; Egawa, M. Development of test case models for Japanese power systems. In Proceedings of the 2000 Power Engineering Society Summer Meeting (Cat. No.00CH37134), Seattle, WA, USA, 16–20 July 2000; Volume 3, pp. 1633–1638. [Google Scholar] [CrossRef]
- Josz, C.; Fliscounakis, S.; Maeght, J.; Panciatici, P. AC power flow data in MATPOWER and QCQP format: iTesla, RTE snapshots, and PEGASE. arXiv 2016, arXiv:1603.01533. [Google Scholar]
- Fliscounakis, S.; Panciatici, P.; Capitanescu, F.; Wehenkel, L. Contingency Ranking With Respect to Overloads in Very Large Power Systems Taking Into Account Uncertainty, Preventive, and Corrective Actions. IEEE Trans. Power Syst. 2013, 28, 4909–4917. [Google Scholar] [CrossRef]
- Porretta, B.; Kiguel, D.L.; Hamoud, G.A.; Neudorf, E.G. A comprehensive approach for adequacy and security evaluation of bulk power systems. IEEE Trans. Power Syst. 1991, 6, 433–441. [Google Scholar] [CrossRef]
- Grigg, C.; Wong, P.; Albrecht, P.; Allan, R.; Bhavaraju, M.; Billinton, R.; Chen, Q.; Fong, C.; Haddad, S.; Kuruganty, S.; et al. The IEEE Reliability Test System-1996. A report prepared by the Reliability Test System Task Force of the Application of Probability Methods Subcommittee. IEEE Trans. Power Syst. 1999, 14, 1010–1020. [Google Scholar] [CrossRef]
- Li, C.; Dong, Z.; Chen, G.; Luo, F.; Liu, J. Flexible transmission expansion planning associated with large-scale wind farms integration considering demand response. IET Gener. Transm. Distrib. 2015, 9, 2276–2283. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Z.; Jiang, Q. Optimal control method for wind farm to support temporary primary frequency control with minimised wind energy cost. IET Renew. Power Gener. 2015, 9, 350–359. [Google Scholar] [CrossRef]
- Pazouki, S.; Mohsenzadeh, A.; Ardalan, S.; Haghifam, M. Optimal place, size, and operation of combined heat and power in multi carrier energy networks considering network reliability, power loss, and voltage profile. IET Gener. Transm. Distrib. 2016, 10, 1615–1621. [Google Scholar] [CrossRef]
- Xing, H.; Cheng, H.; Zhang, Y.; Zeng, P. Active distribution network expansion planning integrating dispersed energy storage systems. IET Gener. Transm. Distrib. 2016, 10, 638–644. [Google Scholar] [CrossRef]
- Meinecke, S.; Bornhorst, N.; Braun, M. Power System Benchmark Generation Methodology. In Proceedings of the NEIS 2018, Conference on Sustainable Energy Supply and Energy Storage Systems, Hamburg, Germany, 20–21 September 2018. [Google Scholar]
- Kerber, G.; Witzmann, R. Statistische Analyse von NS-Verteilnetzen und Modellierung von Referenznetzen (Statistical Analsysis of Distribution Grid and Modelling of Reference Networks). eW, March 2008; 22–26. [Google Scholar]
- Scheffler, J.U. Bestimmung der Maximal Zulässigen Netzanschlussleistung Photovoltaischer Energiewandlungsanlagen in Wohnsiedlungsgebieten (Determination of the Maximum Permissible Power of Photovoltaic Power Plants in Residential Areas). Ph.D. Thesis, Technische Universität Chemnitz, Chemnitz, Germany, 2002. [Google Scholar]
- Schneider, K.P.; Chen, Y.; Engle, D.; Chassin, D. A Taxonomy of North American radial distribution feeders. In Proceedings of the 2009 IEEE Power Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Broderick, R.; Williams, J.; Munoz-Ramos, K. Clustering Method and Representative Feeder Selection for the California Solar Initiative; Technical Report; Sandia National Laboratories: Albuquerque, NM, USA, 2014. [Google Scholar]
- Walker, G.; Krauss, A.K.; Eilenberger, S.; Schweinfort, W.; Tenbohlen, S. Entwicklung eines standardisierten Ansatzes zur Klassifizierung von Verteilnetzen. In Proceedings of the VDE-Kongress, Frankfurt, Germany, 20–21 October 2014. [Google Scholar]
- Rigoni, V.; Ochoa, L.F.; Chicco, G.; Navarro-Espinosa, A.; Gozel, T. Representative residential LV feeders: A case study for the North West of England. IEEE Trans. Power Syst. 2016, 31, 348–360. [Google Scholar]
- Bhakar, R.; Padhy, N.P.; Gupta, H.O. Development of a flexible distribution reference network. In Proceedings of the IEEE PES General Meeting, Providence, RI, USA, 25–29 July 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Larscheid, P.; Maercks, M.; Dierkes, S.; Moser, A.; Patzack, S.; Vennegeerts, H.; Rolink, J.; Wieben, E. Increasing the hosting capacity of RES in distribution grids by active power control. In Proceedings of the International ETG Congress 2015, Die Energiewende—Blueprints for the New Energy Age, Bonn, Germany, 17–18 November 2015; pp. 1–7. [Google Scholar]
- Kays, J.; Seack, A.; Smirek, T.; Westkamp, F.; Rehtanz, C. The Generation of Distribution Grid Models on the Basis of Public Available Data. IEEE Trans. Power Syst. 2017, 32, 2346–2353. [Google Scholar] [CrossRef]
- Domingo, C.M.; Roman, T.G.S.; Sanchez-Miralles, A.; Gonzalez, J.P.P.; Martinez, A.C. A Reference Network Model for Large-Scale Distribution Planning With Automatic Street Map Generation. IEEE Trans. Power Syst. 2011, 26, 190–197. [Google Scholar] [CrossRef]
- Rui, H.; Arnold, M.; Wellssow, W.H. Synthetic medium voltage grids for the assessment of Smart Grid techniques. In Proceedings of the 2012 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Berlin, Germany, 14–17 October 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Han, X.; You, S.; Thordarson, F.; Victor Tackie, D.; Merete Ostberg, S.; Michael Pedersen, O.; Bindner, H.; Christian Nordentoft, N. Real-time measurements and their effects on state estimation of distribution power system. In Proceedings of the IEEE PES ISGT Europe 2013, Lyngby, Denmark, 6–9 October 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Bracale, A.; Caldon, R.; Celli, G.; Coppo, M.; Dal Canto, D.; Langella, R.; Petretto, G.; Pilo, F.; Pisano, G.; Ruggeri, S.; et al. Active Management of Distribution Networks with the ATLANTIDE models. In Proceedings of the 8th Mediterranean Conference on Power Generation, Transmission, Distribution and Energy Conversion (MEDPOWER 2012), Cagliari, Italy, 1–3 October 2012; pp. 1–7. [Google Scholar]
- Seack, A.; Kays, J.; Rehtanz, C. Generating Low Voltage Grids on the Basis of Public Available Map Data; CIRED Workshop: Rome, Italy, 2014; Volume 11. [Google Scholar]
- Zhou, Q.; Bialek, J.W. Approximate model of European interconnected system as a benchmark system to study effects of cross-border trades. IEEE Trans. Power Syst. 2005, 20, 782–788. [Google Scholar] [CrossRef]
- Fan, H.; Wang, M.; Ning, X.; Liu, Y. Transmission network expansion based on reference network concept. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; pp. 1405–1408. [Google Scholar] [CrossRef]
- Mayer, E. Benchmarking performance levels of distribution companies. In Proceedings of the 2001 Power Engineering Society Summer Meeting, Conference Proceedings (Cat. No.01CH37262), Vancouver, BC, Canada, 15–19 July 2001. [Google Scholar] [CrossRef]
- Scheidler, A.; Bolgaryn, R.; Ulffers, J.; Dasenbrock, J.; Horst, D.; Gauglitz, P.; Pape, C.; Becker, H.; Braun, M. DER Integration Study for the German State of Hesse—Methodology and Key Results. In Proceedings of the CIRED 2019 (25th International Conference on Electricity Distribution), Madrid, Spain, 3–6 June 2019. [Google Scholar]
- Garske, S.; Blaufuß, C.; Sarstedt, M.; Hofmann, L. Reactive power management analyses based on generic distribution grid models. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Torino, Italy, 26–29 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Adamczyk, A.; Altin, M.; Göksu, Ö.; Teodorescu, R.; Iov, F. Generic 12-bus test system for wind power integration studies. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Kraiczy, M.; Stetz, T.; Braun, M. Parallel operation of transformers with on-load tap changer and photovoltaic systems with reactive power control. IEEE Trans. Smart Grid 2017. [Google Scholar] [CrossRef]
- Hernando-Gil, I.; Shi, H.; Li, F.; Djokic, S.; Lehtonen, M. Evaluation of Fault Levels and Power Supply Network Impedances in 230/400 V 50 Hz Generic Distribution Systems. IEEE Trans. Power Deliv. 2017, 32, 768–777. [Google Scholar] [CrossRef]
- Shafiu, A.; Jenkins, N.; Strbac, G. Measurement location for state estimation of distribution networks with generation. IEE Proc. Gener. Transm. Distrib. 2005, 152, 240–246. [Google Scholar] [CrossRef]
- bin Ibrahim, K.A.; Au, M.T.; Gan, C.K. Generic characteristic of medium voltage reference network for the Malaysian power distribution system. In Proceedings of the 2015 IEEE Student Conference on Research and Development (SCOReD), Kuala Lumpur, Malaysia, 13–14 December 2015; pp. 204–209. [Google Scholar] [CrossRef]
- Chen, X.; Lin, J.; Wan, C.; Song, Y.; You, S.; Zong, Y.; Guo, W.; Li, Y. Optimal Meter Placement for Distribution Network State Estimation: A Circuit Representation Based MILP Approach. IEEE Trans. Power Syst. 2016, 31, 4357–4370. [Google Scholar] [CrossRef]
- Padhy, N.P.; Bhakar, R.; Nagendran, M. Smart reference networks. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Levi, V.; Strbac, G.; Allan, R. Assessment of performance-driven investment strategies of distribution systems using reference networks. IEE Proc. Gener. Transm. Distrib. 2005, 152, 1–10. [Google Scholar] [CrossRef]
| Grid Datasets | Year Published | Voltage Levels | Number of Buses | Switch Models | Dynamic Models | OPF Analysis | Reliability Analysis | State Estimation | Unbalanced Power Flow | Short Circuit Calculation | GIS Data | Time Series Data |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ICPSs [24,25,26,27] | 1968, 1974, 1981, 1982 | N/A | 11, 13, 43 | - | - | - | - | - | - | - | - | - |
| IEEE Case 30 [28] | 1974 | HV | 30 | - | - | ✓ | - | - | - | - | - | - |
| Cinvalar’s System [29] | 1988 | MV | 14 | (✓) | - | - | - | - | - | - | - | - |
| Baran’s System [30] | 1989 | MV | 33 | (✓) | - | - | - | - | - | - | - | - |
| IEEE DTFs [23,31,32,33] | 1991, 2002, 2010 | MV | 4–123 | - ,✓ | - | T | - | - | ✓ | - | - | - |
| Salama’s System [34] | 1993 | MV | 34 | - | - | (L) | - | - | - | - | - | - |
| Su’s TDG [35] | 2005 | MV | 84 | (✓) | - | - | - | - | - | - | - | - |
| IEEE NEV [23,36,37] | 2008 | MV | 21 | - | - | T, L | - | - | ✓ | ✓ | - | - |
| CIGRE Systems [38] | 2009 | LV, MV, EHV | 13–44 | (✓) | ✓ | G, EN, T, (L)-L | - | - | (✓) | (✓) | - | (✓) |
| IEEE 8500 NTF [23,39] | 2010 | LV, MV | 8500 | - | - | T, L | - | - | ✓ | - | ✓ | - |
| Kerber Grids [40] | 2011 | LV | 10–386 | - | - | V, T, L | - | - | - | - | - | (✓) |
| UKGDSs [41,42] | 2011 | MV, HV | 52–413 | - | - | ✓ | - | - | - | - | - | - |
| ATLANTIDE [43,44,45] | 2012 | MV | 97–103 | (✓) | ✓ | ✓ | ✓ | - | - | - | - | - |
| Dickert’s LVDNs [46] | 2013 | LV | 1–150 | - | - | L | - | - | - | - | - | - |
| IEEE LVNTS [23,47] | 2014 | LV, MV | 342 | - | - | T, (L) | - | - | ✓ | - | - | - |
| ELVTF [23,48] | 2015 | LV | 906 | - | - | T | - | - | ✓ | - | ✓ | ✓ |
| EREDNs [49] | 2016 | LV, MV | 13–6921 | - | - | V, T, L | - | - | - | - | - | - |
| SimBench [50] | 2019 | LV, MV, HV, EHV | 15–380 | ✓ | - | V, G, T, L | - | ✓ | - | - | (✓), ✓ | ✓ |
| IEEE RTS [51] | 1979 | HV, EHV | 24 | - | - | C, G, T, L | ✓ | - | - | - | - | ✓ |
| IEEE Case 9 [52] | 1980 | EHV | 9 | - | ✓ | G | - | - | - | - | - | - |
| IEEJs [53] | 2000 | HV EHV | 236–933 47–115 | ✓ - | - ✓ | T, L G, (L) | ✓ - | - | - | - ✓ | - | - (✓) |
| PEGASE Cases [54,55] | 2015 | HV, EHV | 89–13,659 | - | - | ✓ | - | - | - | - | - | - |
| RTE Cases [54] | 2016 | MV-EHV | 1888–6515 | - | - | ✓ | - | - | - | - | - | - |
| Grid Datasets | Intended Use Cases | Region | Information on Methodology | Methodic Origin of Data |
|---|---|---|---|---|
| ICPSs [24,25,26,27] | ill-conditioned sample systems for power flow methods | N/A | N/A | synthetic |
| IEEE Case 30 [28] | test case for optimal load flow with steady-state security | N/A | adaption of existing test case | N/A |
| Cinvalar’s System [29] | illustrating the problem of switch positioning for minimum distribution grid losses | North America | N/A | synthetic |
| Baran’s System [30] | test system for loss reduction and load balancing via network reconfiguration | North America | N/A | N/A |
| IEEE DTFs [23,31,32,33] | testing of new power flow solution methods for unbalanced systems | North America | N/A | N/A |
| Salama’s System [34] | application example for the VAr control problem | North America | N/A | N/A |
| Su’s TDG [35] | example grid for network reconfiguration | Taiwan | N/A | real |
| IEEE NEV [23,36,37] | examining the voltage rise on the neutral conductor | North America | N/A | N/A |
| CIGRE Systems [38] | benchmark system for issues of grid operation, planning, power quality, protection, stability | North America & Europe | use case driven approach based on experts decisions | derived from real grids |
| IEEE 8500 NTF [23,39] | representative of full-size distribution system with suitable complexity | North America | N/A | derived from real grid |
| Kerber Grids [40] | estimation of photovoltaic hosting capacity in low voltage grids | Germany | predefined classification method | synthetic |
| UKGDSs [41,42] | representative distribution grids to test and evaluate new concepts | United Kingdom | N/A | N/A |
| ATLANTIDE [43,44,45] | representative distribution grids to develop and simulate predictive scenarios | Italy | clustering method | real |
| Dickert’s LVDNs [46] | low voltage benchmark grids representative of German feeders | Germany | principal component analysis and clustering method | synthetic |
| IEEE LVNTS [23,47] | testing of solvers in highly meshed low voltage systems | North America | N/A | N/A |
| ELVTF [23,48] | typical test feeders | Europe | N/A | N/A |
| EREDNs [49] | large-scale distribution grids representative of European grids | Europe | greenfield reference network model | synthetic |
| SimBench [12,50] | benchmark dataset with multiple voltage levels and data of time series and study cases to compare innovative solutions of multiple use cases based on power flow analysis | Germany | use case driven approach deriving grids from avail- able data with validating against real grids [62] | synthetic |
| IEEE RTS [51] | test or compare methods for reliability analysis | North America | N/A | N/A |
| IEEE Case 9 [52] | small test system for stability studies | North America | N/A | synthetic |
| IEEJs [53] | testing of power supply restoration planning and reliability analysis algorithms bulk power systems for load flow and stability studies | Japan | N/A | N/A |
| PEGASE Cases [54,55] | development of new tools for control and operational planning of the pan-European transmission network | France Europe | N/A N/A | derived from real grids synthetic |
| RTE Cases [54] | validation of mathematical methods and tools | France | snapshots from SCADAs | real |
| Term | Recommended Usage |
|---|---|
| Synthetic Grid | Grid that either do not model a real grid or that is not obtained by simplifying or modifying models of a real grid. |
| Example and Test Grid | Grid that is simply created and used for basic testing, validation, or demonstration of only one issue. Transferring quantitative conclusions from this type of grid to conditions in real grids is doubtful. |
| Benchmark Grid | Grid that is used to compare the efficiency or validity of algorithms. When using a benchmark grid, the object of investigation is the algorithm rather than the grid itself. |
| Representative Grid | Grid that is created or selected to be considered instead of a number of grids. Since one grid can hardly be representative for all grids, there are usually multiple representative grids to cover different clusters of similar grids. |
| Generic Grid | Grid with variable parameters that allow to synthesize different grids through parametrization. While representative grids use multiple grids with fixed parameters to represent different states of grids, generic grids cover multiple states through parameter variation of one grid. |
| Typical Grid | Grid with common parameters. While representative grids intend to represent a wide range of possible grids, a typical grid claim solely to cover a common or normal grid type, so that outliers and extreme cases have little or no influence on a typical grid. |
| Reference Grid | Grid that is optimal with regard to a specific criterion, such as cost-optimality. |
| Grids | Synthetic | Example/Test | Benchmark | Representative | Generic | Typical | Reference |
|---|---|---|---|---|---|---|---|
| ICPSs [24,25,26,27] | ✓ | - | - | - | - | - | |
| IEEE Case 30 [28] | - | - | ✓ | - | - | - | - |
| Cinvalar’s System [29] | ✓ | - | - | - | - | - | |
| Baran’s System [30] | N/A | ✓ | - | - | - | - | - |
| IEEE DTFs [23,31,32,33] | N/A | (✓) | ✓ | - | - | - | - |
| Salama’s System [34] | N/A | ✓ | - | - | - | - | - |
| Su’s TDG [35] | - | (✓) | ✓ | - | - | - | - |
| IEEE NEV [23,36,37] | N/A | - | ✓ | - | - | - | - |
| CIGRE Systems [38] | - | - | ✓ | - | - | (✓) | - |
| IEEE 8500 NTF [23,39] | - | - | ✓ | - | - | - | - |
| Kerber Grids [40] | - | ✓ | - | ✓ | - | - | |
| UKGDSs [41,42] | N/A | - | ✓ | (✓) | - | - | - |
| ATLANTIDE [43,44,45] | - | - | (✓) | ✓ | - | - | - |
| Dickert’s LVDNs [46] | (✓) | - | ✓ | ✓ | (✓) | - | - |
| IEEE LVNTS [23,47] | N/A | - | ✓ | - | - | - | - |
| ELVTF [23,48] | N/A | - | ✓ | - | - | (✓) | - |
| EREDNs [49] | ✓ | - | - | (✓) | - | (✓) | ✓ |
| SimBench [50] | (✓) | - | ✓ | (✓) | - | - | - |
| IEEE RTS [51] | N/A | - | ✓ | - | - | - | - |
| IEEE Case 9 [52] | ✓ | - | - | - | - | - | |
| IEEJs [53] | N/A | - | ✓ | - | - | - | - |
| PEGASE Cases [54,55] | - | - | ✓ | - | - | - | - |
| RTE Cases [54] | - | - | ✓ | - | - | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meinecke, S.; Thurner, L.; Braun, M. Review of Steady-State Electric Power Distribution System Datasets. Energies 2020, 13, 4826. https://doi.org/10.3390/en13184826
Meinecke S, Thurner L, Braun M. Review of Steady-State Electric Power Distribution System Datasets. Energies. 2020; 13(18):4826. https://doi.org/10.3390/en13184826
Chicago/Turabian StyleMeinecke, Steffen, Leon Thurner, and Martin Braun. 2020. "Review of Steady-State Electric Power Distribution System Datasets" Energies 13, no. 18: 4826. https://doi.org/10.3390/en13184826
APA StyleMeinecke, S., Thurner, L., & Braun, M. (2020). Review of Steady-State Electric Power Distribution System Datasets. Energies, 13(18), 4826. https://doi.org/10.3390/en13184826





