Performance Evaluation of Analytical Methods for Parameters Extraction of Photovoltaic Generators
Abstract
1. Introduction
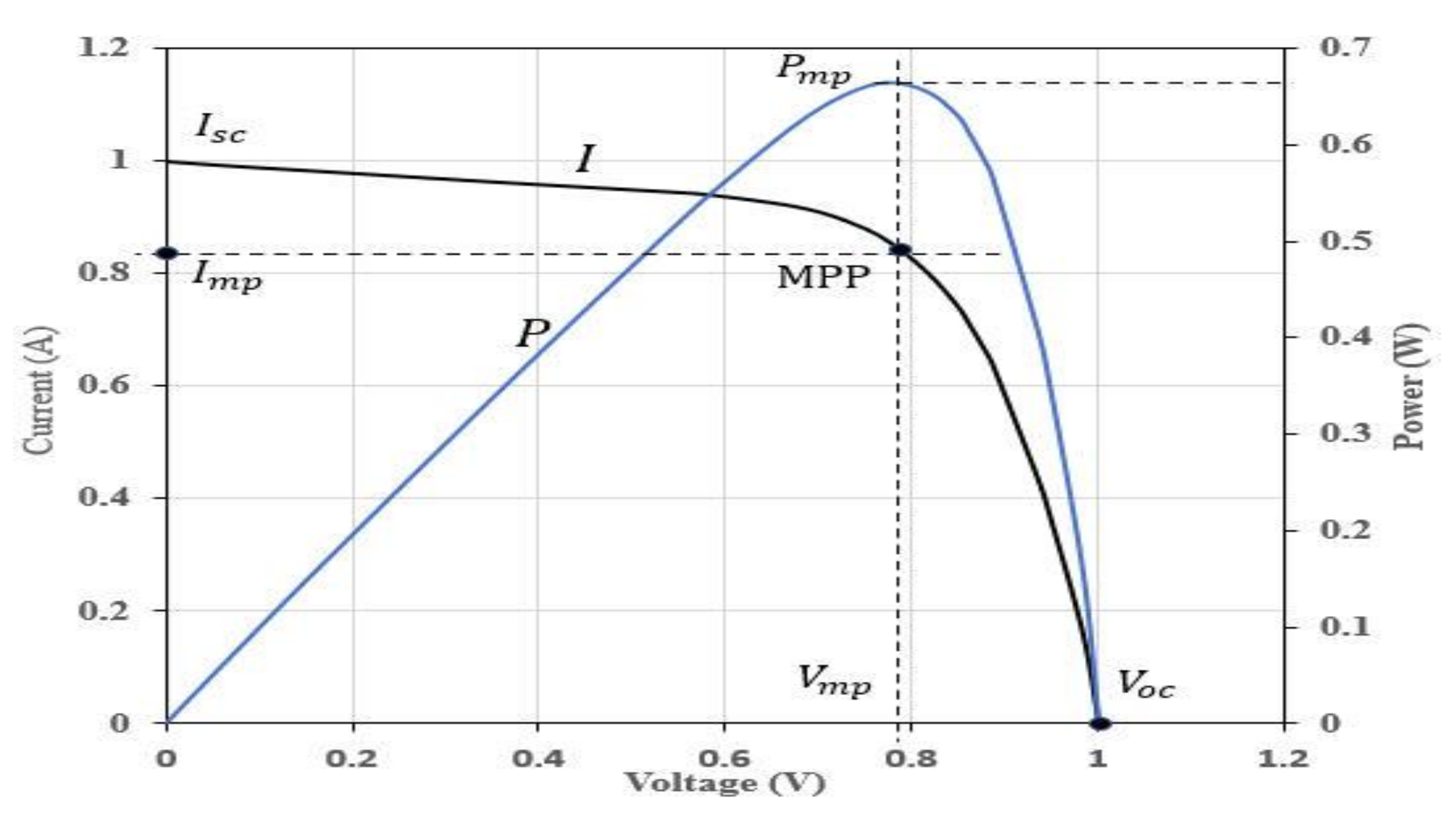
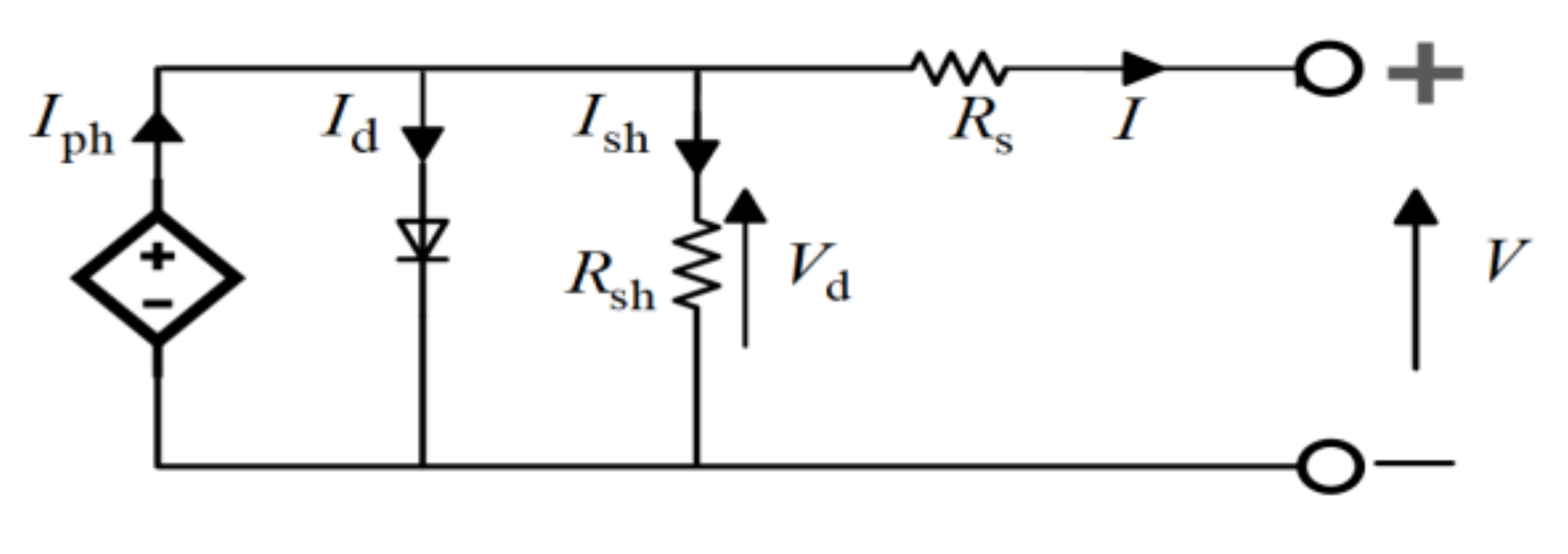
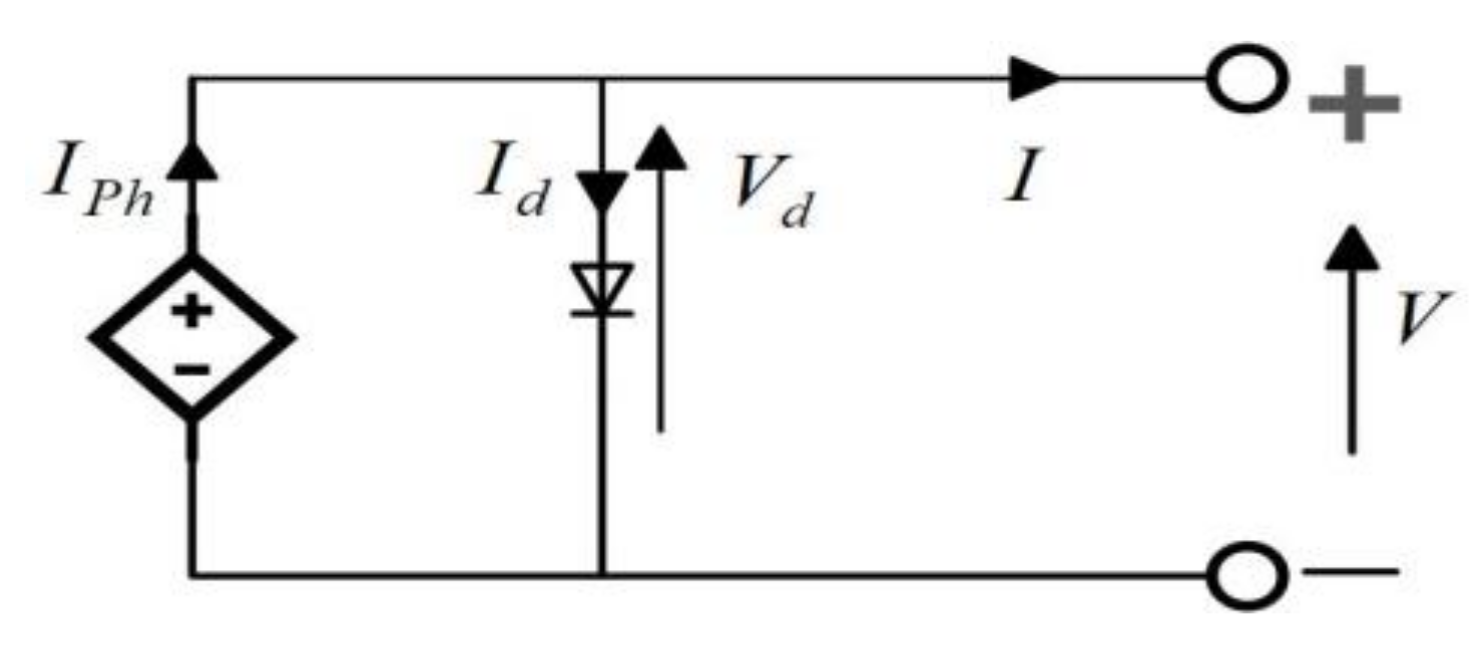
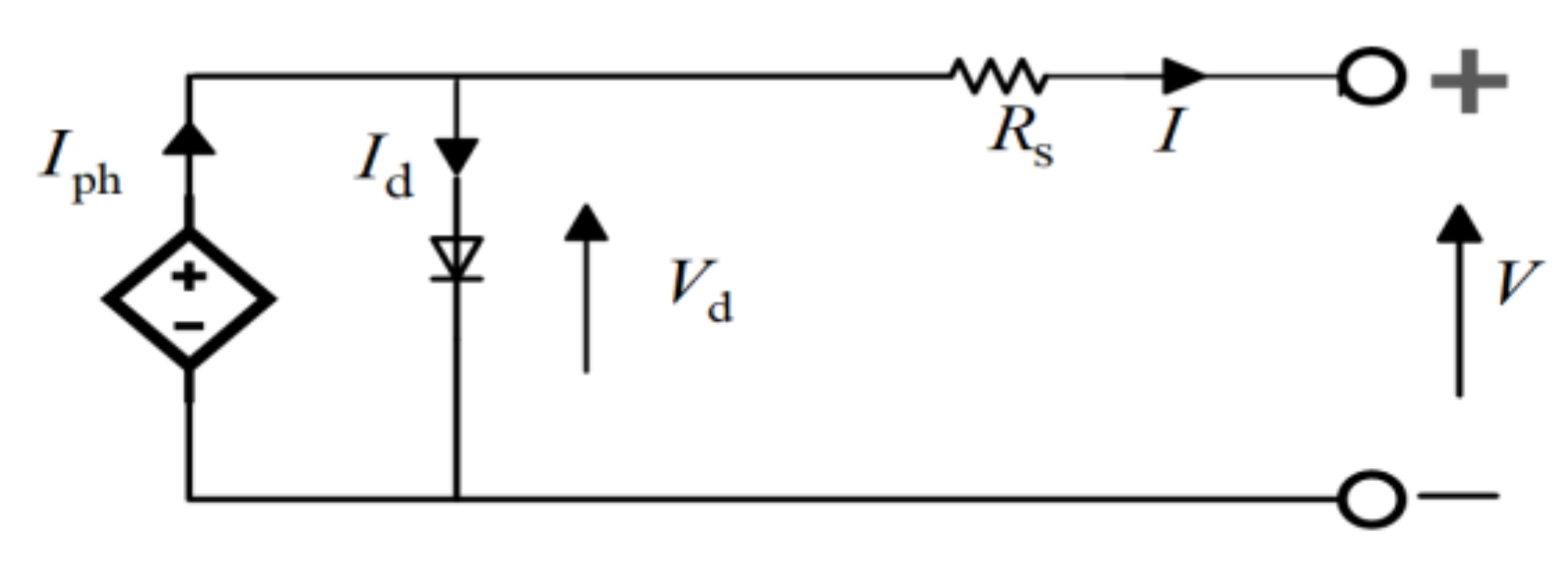
2. Mathematical Grounds for the Analytical Methods
3. Parameters Extraction Methods
3.1. Method One
3.1.1. Extraction of the Photocurrent
3.1.2. Extraction of the Shunt Resistance
3.1.3. Extraction of the Series Resistance
3.1.4. Extraction of the Reverse Saturation Current
3.1.5. Extraction of the Ideality Factor n
3.2. Method Two
3.3. Method Three
3.3.1. Extraction of the Photocurrent
3.3.2. Extraction of the Saturation Current
3.3.3. Extraction of the Series Resistance
3.3.4. Extraction of the Ideality Factor
3.4. Method Four
3.5. Method Five
3.6. Method Six
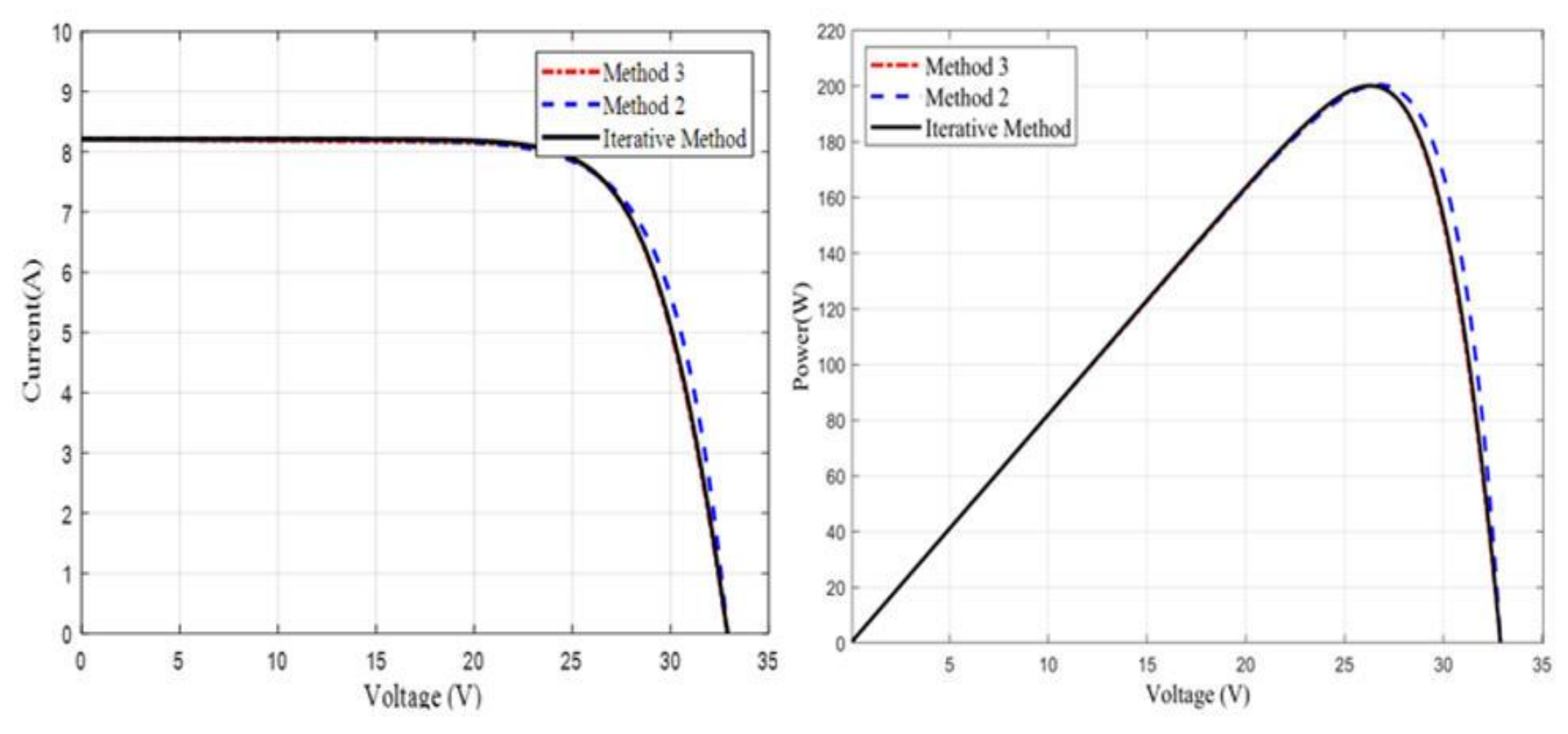
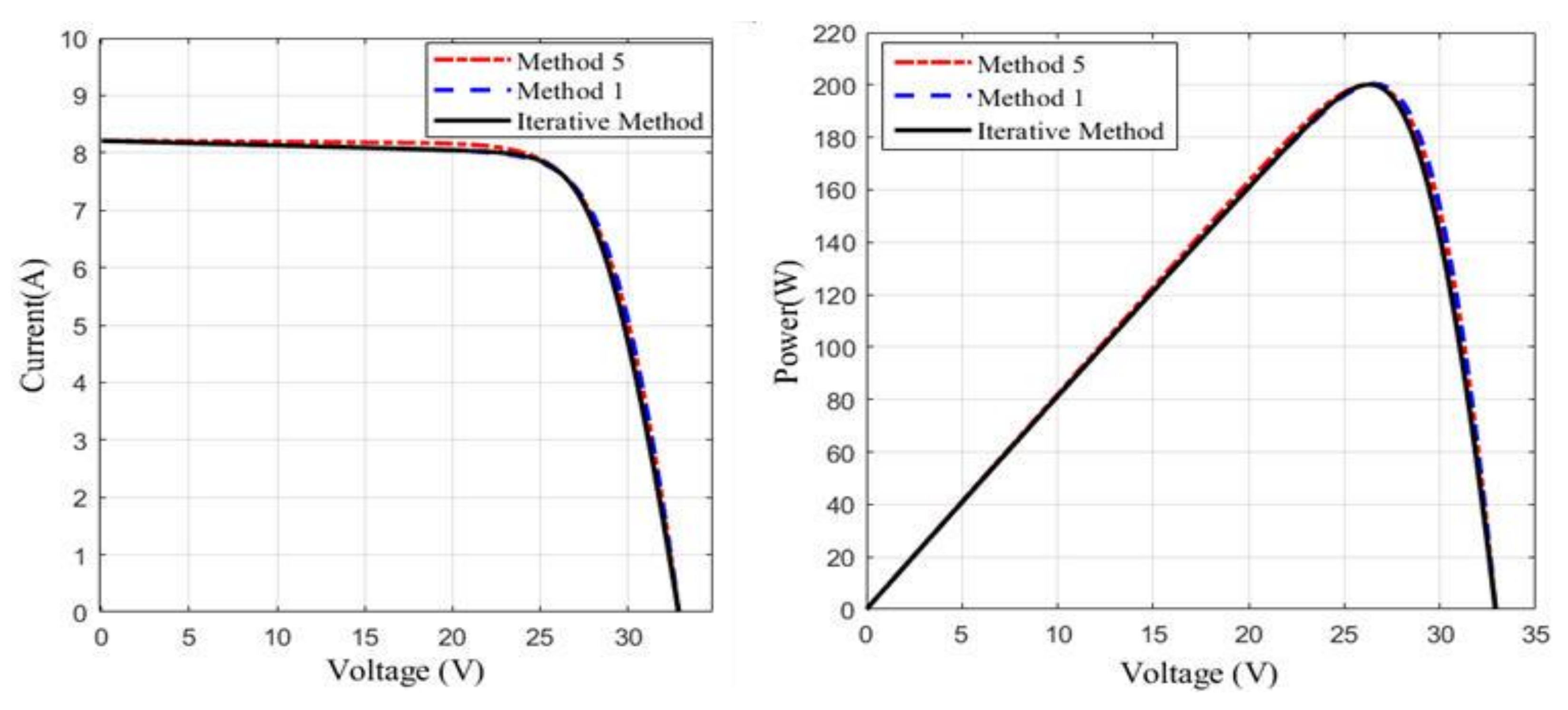
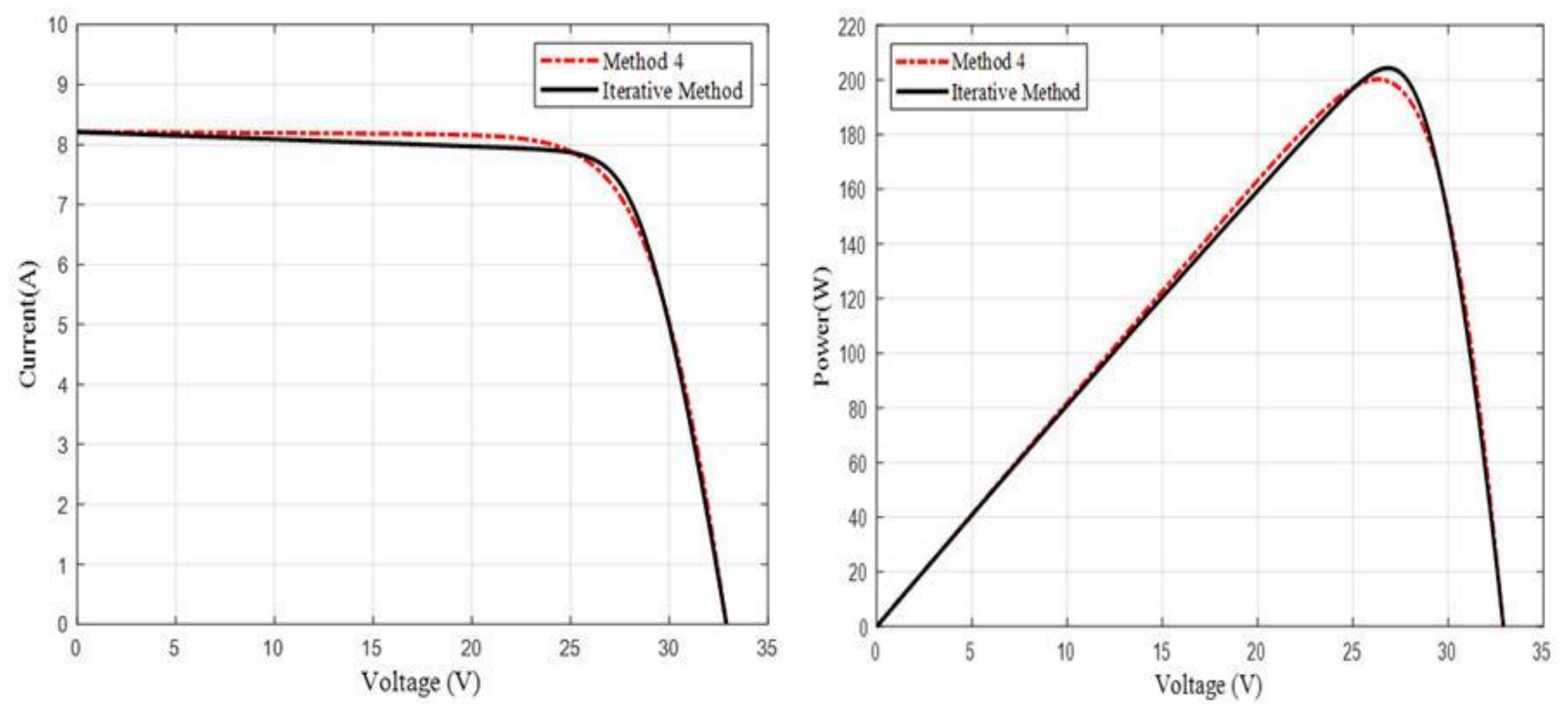
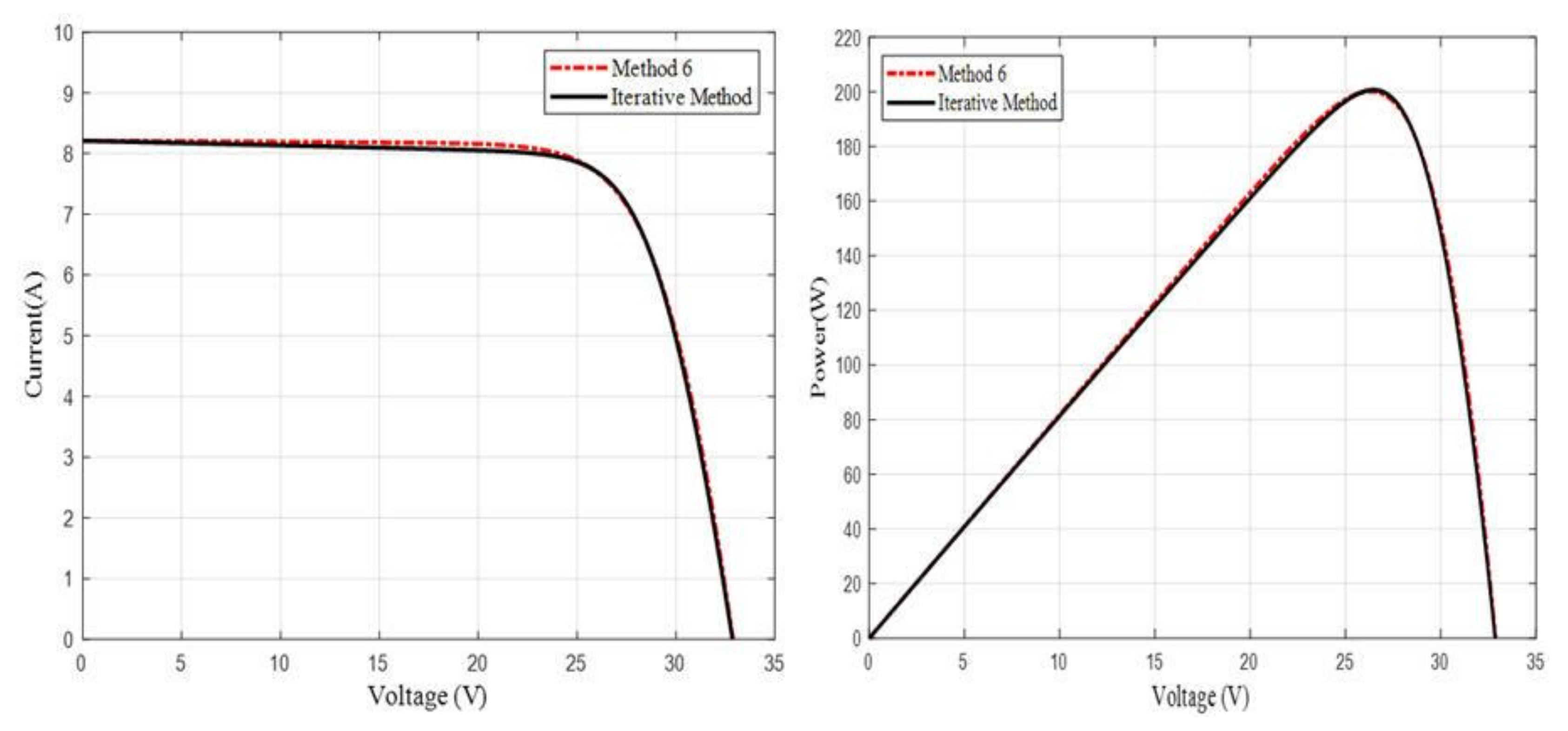
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Modified ideality factor () | |
| Temperature coefficient of the short-circuit current | |
| Temperature coefficient of the open-circuit voltage ( | |
| Coefficient for the single-diode model defined as . | |
| Insolation (W/m2) | |
| Insolation at standard test conditions () | |
| I | Terminal current of a photovoltaic cell or module (A) |
| Current at the maximum power point (A) | |
| Short-circuit current (A) | |
| Reverse saturation current (A) | |
| Photocurrent (A) | |
| Photocurrent at standard test conditions (A) | |
| k | Boltzmann’s constant () |
| MPP | Maximum power point |
| n | ideality factor of a PV cell/diode |
| Number of series-connected cells in a PV module | |
| P | Power (W) |
| Power at maximum power point (W) | |
| PV | Photovoltaic |
| q | Electronic charge 1.602 × 10−19 (C) |
| Series resistance of a photovoltaic module () | |
| The negative of the reciprocal of the slope of the I–V curve at the open-circuit voltage point | |
| Shunt resistance of a PV module () | |
| The negative of the reciprocal of the slope of the I–V curve at the short-circuit current point | |
| SDM | Single-diode model |
| STC | Standard test conditions (Insolation = 1000 , air mass AM = 1.5, T = 25 ) |
| T | Temperature (k) |
| Temperature at standard test conditions () | |
| V | Terminal voltage of a PV module (V) |
| Thermal voltage (V) | |
| Open-circuit voltage of a PV module (V) | |
| Voltage at maximum power point (V) | |
| Open-circuit voltage of a PV module at STC (V) | |
| Lambert-W function |
References
- Masters, G.M. Renewable and Efficient Electric Power Systems; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Femia, N.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Power Electronics and Control Techniques for Maximum Energy Harvesting in Photovoltaic Systems; Informa UK Limited: Colchester, UK, 2017. [Google Scholar]
- Cotfas, D.T.; Cotfas, P.A.; Machidon, O. Study of Temperature Coefficients for Parameters of Photovoltaic Cells. Int. J. Photoenergy 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Anani, N.; Ibrahim, H. Adjusting the Single-Diode Model Parameters of a Photovoltaic Module with Irradiance and Temperature. Energies 2020, 13, 3226. [Google Scholar] [CrossRef]
- Dhimish, M. Assessing MPPT Techniques on Hot-Spotted and Partially Shaded Photovoltaic Modules: Comprehensive Review Based on Experimental Data. IEEE Trans. Electron Devices 2019, 66, 1132–1144. [Google Scholar] [CrossRef]
- Esram, T.; Chapman, P.L. Comparison of Photovoltaic Array Maximum Power Point Tracking Techniques. IEEE Trans. Energy Convers. 2007, 22, 439–449. [Google Scholar] [CrossRef]
- Ma, J.; Pan, X.; Man, K.; Li, X.; Wen, H.; Ting, T. Detection and Assessment of Partial Shading Scenarios on Photovoltaic Strings. IEEE Trans. Ind. Appl. 2018, 54, 6279–6289. [Google Scholar] [CrossRef]
- Bi, Z.; Ma, J.; Wang, K.; Man, K.L.; Smith, J.S.; Yue, Y. Identification of Partial Shading Conditions for Photovoltaic Strings. IEEE Access 2020, 8, 75491–75502. [Google Scholar] [CrossRef]
- Mäki, A.; Valkealahti, S. Power Losses in Long String and Parallel-Connected Short Strings of Series-Connected Silicon-Based Photovoltaic Modules Due to Partial Shading Conditions. IEEE Trans. Energy Convers. 2012, 27, 173–183. [Google Scholar] [CrossRef]
- Ibrahim, H.; Anani, N. Variation of the performance of a PV panel with the number of bypass diodes and partial shading patterns. In Proceedings of the 2019 International Conference on Power Generation Systems and Renewable Energy Technologies (PGSRET), Istanbul, Turkey, 26–27 August 2019; Institute of Electrical and Electronics Engineers (IEEE): Piscataway Township, NJ, USA, 2019; pp. 1–4. [Google Scholar]
- Ibrahim, H.; Anani, N. Performance of Different PV Array Configurations under Different Partial Shading Conditions. In Advances in Wireless Communications and Applications; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2019; pp. 445–454. [Google Scholar]
- Ibrahim, H.; Anani, N. Study of the Effect of Different Configurations of Bypass Diodes on the Performance of a PV String. In Advances in Wireless Communications and Applications; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2019; pp. 593–600. [Google Scholar]
- Xiao, W.; Dunford, W.G.; Capel, A. A novel modeling method for photovoltaic cells. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; Institute of Electrical and Electronics Engineers (IEEE): Piscataway Township, NJ, USA, 2004. [Google Scholar]
- Villalva, M.; Gazoli, J.R.; Filho, E. Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Siddique, H.A.B.; Xu, P.; De Doncker, R.W. Parameter extraction algorithm for one-diode model of PV panels based on datasheet values. In Proceedings of the 2013 International Conference on Clean Electrical Power (ICCEP), Alghero, Italy, 11–13 June 2013; Institute of Electrical and Electronics Engineers (IEEE): Piscataway Township, NJ, USA, 2013; pp. 7–13. [Google Scholar]
- Tian, H.; Mancilla-David, F.; Ellis, K.; Muljadi, E.; Jenkins, P. A cell-to-module-to-array detailed model for photovoltaic panels. Sol. Energy 2012, 86, 2695–2706. [Google Scholar] [CrossRef]
- Ibrahim, H.; Anani, N. Variations of PV module parameters with irradiance and temperature. Energy Procedia 2017, 134, 276–285. [Google Scholar] [CrossRef]
- Cotfas, D.T.; Cotfas, P.; Kaplanis, S. Methods to determine the dc parameters of solar cells: A critical review. Renew. Sustain. Energy Rev. 2013, 28, 588–596. [Google Scholar] [CrossRef]
- De Soto, W.; Klein, S.; Beckman, W. Improvement and validation of a model for photovoltaic array performance. Sol. Energy 2006, 80, 78–88. [Google Scholar] [CrossRef]
- Phang, J.; Chan, D.; Phillips, J. Accurate analytical method for the extraction of solar cell model parameters. Electron. Lett. 1984, 20, 406. [Google Scholar] [CrossRef]
- Aldwane, B. Modeling, simulation and parameters estimation for Photovoltaic module. In Proceedings of the 2014 First International Conference on Green Energy ICGE 2014, Sfax, Tunisia, 25–27 March 2014; Institute of Electrical and Electronics Engineers (IEEE): Piscataway Township, NJ, USA, 2014; pp. 101–106. [Google Scholar]
- Saloux, E.; Teyssedou, A.; Sorin, M. Explicit model of photovoltaic panels to determine voltages and currents at the maximum power point. Sol. Energy 2011, 85, 713–722. [Google Scholar] [CrossRef]
- Louzazni, M.; Khouya, A.; Crăciunescu, A.; Amechnoue, K.; Mussetta, M. Modelling and Parameters Extraction of Flexible Amorphous Silicon Solar Cell a-Si:H. Appl. Sol. Energy 2020, 56, 1–12. [Google Scholar] [CrossRef]
- Luo, X.; Cao, L.; Wang, L.; Zhao, Z.; Huang, C. Parameter identification of the photovoltaic cell model with a hybrid Jaya-NM algorithm. Optik 2018, 171, 200–203. [Google Scholar] [CrossRef]
- AlRashidi, M.; Alhajri, M.; El-Naggar, K.; Al-Othman, A. A new estimation approach for determining the I–V characteristics of solar cells. Sol. Energy 2011, 85, 1543–1550. [Google Scholar] [CrossRef]
- Gude, S.; Jana, K.C. Parameter extraction of photovoltaic cell using an improved cuckoo search optimization. Sol. Energy 2020, 204, 280–293. [Google Scholar] [CrossRef]
- Gong, W.; Cai, Z. Parameter extraction of solar cell models using repaired adaptive differential evolution. Sol. Energy 2013, 94, 209–220. [Google Scholar] [CrossRef]
- Chan, D.; Phang, J. Analytical methods for the extraction of solar-cell single- and double-diode model parameters from I-V characteristics. IEEE Trans. Electron Devices 1987, 34, 286–293. [Google Scholar] [CrossRef]
- Hejri, M.; Mokhtari, H.; Azizian, M.R.; Ghandhari, M.; Söder, L. On the Parameter Extraction of a Five-Parameter Double-Diode Model of Photovoltaic Cells and Modules. IEEE J. Photovolt. 2014, 4, 915–923. [Google Scholar] [CrossRef]
- Sera, D.; Teodorescu, R.; Rodriguez, P. Photovoltaic module diagnostics by series resistance monitoring and temperature and rated power estimation. In Proceedings of the 2008 34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 10–13 November 2008; Institute of Electrical and Electronics Engineers (IEEE): Piscataway Township, NJ, USA, 2008; pp. 2195–2199. [Google Scholar]
- Haouari-Merbah, M.; Belhamel, M.; Tobias, I.; Ruiz, J. Extraction and analysis of solar cell parameters from the illuminated current–voltage curve. Sol. Energy Mater. Sol. Cells 2005, 87, 225–233. [Google Scholar] [CrossRef]
- Lim, L.H.I.; Ye, Z.; Ye, J.; Yang, D.; Du, H. A Linear Identification of Diode Models from Single II– VVCharacteristics of PV Panels. IEEE Trans. Ind. Electron. 2015, 62, 4181–4193. [Google Scholar] [CrossRef]
- Ortiz-Rivera, E.I.; Peng, F. Analytical Model for a Photovoltaic Module using the Electrical Characteristics provided by the Manufacturer Data Sheet. In Proceedings of the IEEE 36th Conference on Power Electronics Specialists, Recife, Brazil, 16 June 2005; Institute of Electrical and Electronics Engineers (IEEE): Piscataway Township, NJ, USA, 2006; pp. 2087–2091. [Google Scholar]
- Can, H.; Ickilli, D. Parameter Estimation in Modeling of Photovoltaic Panels Based on Datasheet Values. J. Sol. Energy Eng. 2013, 136, 021002. [Google Scholar] [CrossRef]
- Mahmoud, Y.; Xiao, W.; Zeineldin, H.H. A Parameterization Approach for Enhancing PV Model Accuracy. IEEE Trans. Ind. Electron. 2012, 60, 5708–5716. [Google Scholar] [CrossRef]
- Chatterjee, A.; Keyhani, A.; Kapoor, D. Identification of Photovoltaic Source Models. IEEE Trans. Energy Convers. 2011, 26, 883–889. [Google Scholar] [CrossRef]
- Batzelis, E.; Routsolias, I.A.; Papathanassiou, S.A. An Explicit PV String Model Based on the Lambert WW. Function and Simplified MPP Expressions for Operation Under Partial Shading. IEEE Trans. Sustain. Energy 2013, 5, 301–312. [Google Scholar] [CrossRef]
- De Blas, M.; Torres, J.; Prieto, E.; García, A. Selecting a suitable model for characterizing photovoltaic devices. Renew. Energy 2002, 25, 371–380. [Google Scholar] [CrossRef]
- Kennerud, K. Analysis of Performance Degradation in CdS Solar Cells. IEEE Trans. Aerosp. Electron. Syst. 1969, 5, 912–917. [Google Scholar] [CrossRef]
- Cubas, J.; Pindado, S.; Victoria, M. On the analytical approach for modeling photovoltaic systems behavior. J. Power Sources 2014, 247, 467–474. [Google Scholar] [CrossRef]
- Mahmoud, Y.; Xiao, W.; Zeineldin, H.H. A Simple Approach to Modeling and Simulation of Photovoltaic Modules. IEEE Trans. Sustain. Energy 2012, 3, 185–186. [Google Scholar] [CrossRef]
- Mahmoud, Y.; El-Saadany, E.F. Accuracy Improvement of the Ideal PV Model. IEEE Trans. Sustain. Energy 2015, 6, 1–3. [Google Scholar] [CrossRef]
- Wanger, A. Peak power and internal series resistance measurements under natural ambient conditions. In Proceedings of the EuroSun Conference, Dortmund, Denmark, 19–22 June 2000. [Google Scholar]
- Ishaque, K.; Salam, Z.; Taheri, H. Simple, fast and accurate two-diode model for photovoltaic modules. Sol. Energy Mater. Sol. Cells 2011, 95, 586–594. [Google Scholar] [CrossRef]
- Bai, J.; Liu, S.; Hao, Y.; Zhang, Z.; Jiang, M.; Zhang, Y. Development of a new compound method to extract the five parameters of PV modules. Energy Convers. Manag. 2014, 79, 294–303. [Google Scholar] [CrossRef]
- Orioli, A.; Di Gangi, A. A procedure to calculate the five-parameter model of crystalline silicon photovoltaic modules on the basis of the tabular performance data. Appl. Energy 2013, 102, 1160–1177. [Google Scholar] [CrossRef]
- Charles, J.; Abdelkrim, M.; Muoy, Y.; Mialhe, P. A practical method of analysis of the current-voltage characteristics of solar cells. Sol. Cells 1981, 4, 169–178. [Google Scholar] [CrossRef]
- Brano, V.L.; Orioli, A.; Ciulla, G.; Di Gangi, A. An improved five-parameter model for photovoltaic modules. Sol. Energy Mater. Sol. Cells 2010, 94, 1358–1370. [Google Scholar] [CrossRef]
- Batzelis, E.; Papathanassiou, S.A. A Method for the Analytical Extraction of the Single-Diode PV Model Parameters. IEEE Trans. Sustain. Energy 2015, 7, 504–512. [Google Scholar] [CrossRef]
- Batzelis, E.; Kampitsis, G.E.; Papathanassiou, S.A.; Manias, S. Direct MPP Calculation in Terms of the Single-Diode PV Model Parameters. IEEE Trans. Energy Convers. 2014, 30, 226–236. [Google Scholar] [CrossRef]
- Kyocera North America, “KC200GT solar module,” Kyocera Solar. Available online: https://www.kyocerasolar.com/dealers/product-center/archives/spec-sheets/KC200GT.pdf (accessed on 20 December 2019).
- Lorentz Solar Modules, “LC50-12M”. Available online: www.deparsolar.com/images/dosya/LC50_12M.pdf (accessed on 10 March 2020).
- Sanyo, “Sanyo 180BA19”. Available online: www.ecodirect.com/Sanyo-HIP-180BA19-180-Watt-p/sanyo-hip-180ba19.htm (accessed on 20 June 2019).
- Carrero, C.; Rodriguez, J.; Ramirez, D.; Platero, C. Simple estimation of PV modules loss resistances for low error modelling. Renew. Energy 2010, 35, 1103–1108. [Google Scholar] [CrossRef]
| Datasheet | KC200GT | LC50-12M | 180BA19 |
|---|---|---|---|
| Parameters | Multi-Crystalline | Mono-Crystalline | Thin Film |
| 8.21 A | 3.2 A | 3.65 A | |
| 32.9 V | 22.5 V | 66.4 V | |
| 7.61 A | 2.9 A | 3.33 A | |
| 26.3 V | 17.2 V | 54 V | |
| −1.23 × 10−1 | −7.88 × 10−2 | −173 × 10−3 | |
| 3.18 × 10−3 | 2.88 × 10−3 | 1.01 × 10−3 | |
| 54 | 36 | 96 |
| Method | Parameter | ||||
|---|---|---|---|---|---|
| n | |||||
| Method 1 | 1.08317 | 0.27077 | 124 | 2.4885 × 10−9 | 8.22793 |
| Method 2 | 1.81764 | 0 | infinite | 1.78074 × 10−5 | 8.21 |
| Method 3 | 1.40991 | 0.19455 | infinite | 4.09919 × 10−7 | 8.21 |
| Method 4 | 0.65008 | 0.39999 | 82.5508 | 1.14541 × 10−15 | 8.24978 |
| Method 5 | 0.88423 | 0.38033 | 123.62 | 1.81544 × 10−11 | 8.23526 |
| Method 6 | 1.00258 | 0.30567 | 130.466 | 4.43777 × 10−10 | 8.22924 |
| Iterative [14] | 1.3 | 0.2283 | 572.124 | 9.89443 × 10−8 | 8.21329 |
| Numerical [34] | 1.3405 | 0.2172 | 951.327 | 1.7097 × 10−7 | 8.2119 |
| Method | Parameter | ||||
|---|---|---|---|---|---|
| n | |||||
| Method 1 | 2.0361 | 0.10045 | 206 | 2.0109 × 10−5 | 3.20156 |
| Method 2 | 2.41979 | 0 | ∞ | 1.3832 × 10−4 | 3.2 |
| Method 3 | 1.76187 | 0.4969 | ∞ | 3.24464 × 10−6 | 3.2 |
| Method 4 | 0.79342 | 0.93255 | 105.70414 | 1.47618 × 10−13 | 3.22823 |
| Method 5 | 1.24254 | 0.77359 | 205.22641 | 9.82922 × 10−9 | 3.21206 |
| Method 6 | 0.99693 | 0.84024 | 125.53699 | 8.22168 × 10−11 | 3.22142 |
| Iterative method [14] | 1.2 | 0.784 | 186.40574 | 5.06574 × 10−9 | 3.21352 |
| Numerical method [19] | No convergence | ||||
| Method | Parameter | ||||
|---|---|---|---|---|---|
| n | |||||
| Method 1 | 0.55767 | 2.69004 | 2329 | 3.99938 × 10−21 | 3.65422 |
| Method 2 | 2.06455 | 0 | ∞ | 7.9701 × 10−6 | 3.65 |
| Method 3 | 2.11483 | −0.09068 | ∞ | 1.08651 × 10−5 | 3.65 |
| Method 4 | 0.95729 | 1.13544 | 313.85129 | 2.13594 × 10−12 | 3.6632 |
| Method 5 | 1.95145 | 0.10657 | 2328.8934 | 3.71538 × 10−6 | 3.65017 |
| Method 6 | 0.95589 | 1.41883 | 327.95525 | 2.1766 × 10−12 | 3.66579 |
| Iterative [14] | 1.8 | 0.27300 | 1181.56509 | 1.17348 × 10−12 | 3.65084 |
| Numerical method [19] | No convergence | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anani, N.; Ibrahim, H. Performance Evaluation of Analytical Methods for Parameters Extraction of Photovoltaic Generators. Energies 2020, 13, 4825. https://doi.org/10.3390/en13184825
Anani N, Ibrahim H. Performance Evaluation of Analytical Methods for Parameters Extraction of Photovoltaic Generators. Energies. 2020; 13(18):4825. https://doi.org/10.3390/en13184825
Chicago/Turabian StyleAnani, Nader, and Haider Ibrahim. 2020. "Performance Evaluation of Analytical Methods for Parameters Extraction of Photovoltaic Generators" Energies 13, no. 18: 4825. https://doi.org/10.3390/en13184825
APA StyleAnani, N., & Ibrahim, H. (2020). Performance Evaluation of Analytical Methods for Parameters Extraction of Photovoltaic Generators. Energies, 13(18), 4825. https://doi.org/10.3390/en13184825






