Abstract
The new generation of internal combustion engines is facing various research challenges which often include modern fuels and different operating modes. A robust modeling framework is essential for predicting the dynamic behavior of such complex phenomena. In this article, the implementation, verification, and validation of a Eulerian multi-fluid model for spray applications within the OpenFOAM toolbox are presented. Due to its open-source nature and broad-spectrum of available libraries and solvers, OpenFOAM is an ideal platform for academic research. The proposed work utilizes advanced interfacial momentum transfer models to capture the behavior of deforming droplets at a high phase fraction. Furthermore, the WAVE breakup model is employed for the transfer of mass from larger to smaller droplet classes. The work gives detailed instructions regarding the numerical implementation, with a dedicated section dealing with the implementation of the breakup model within the Eulerian multi-fluid formulation. During the verification analysis, the model proved to give stable and consistent results in terms of the selected number of droplet classes and the selected spatial and temporal resolution. In the validation section, the capability of the developed model to predict the dynamic behavior of non-evaporating sprays is presented. It was confirmed that the developed framework could be used as a stable foundation for future fuel spray modeling.
1. Introduction
To increase the efficiency of internal combustion (IC) engines, which is tightly coupled with the increase of the compression ratio, modern engines are being designed to operate in compression ignition mode [1]. Due to the high combustion temperatures (resulting from non-premixed combustion mode), conventional diesel engines suffer from high nitrogen oxides’ emissions. New strategies should lower the pollutant emissions while keeping the efficiencies as high as possible. One of the possible approaches is the partially premixed combustion [2], where the fuel spray is injected directly into the cylinder, but the timing and duration of the start of injection are varied to reach optimal combustion efficiencies at all working conditions. Optimization of fuel-air mixing significantly depends on the nozzle design, which controls the spray penetration length and droplet sizes. The characteristics of the in-nozzle flow affect the spray by causing velocity fluctuations, which enhance the mechanical breakup of the liquid jet, and consequently the formation and collapsing of cavitating bubbles [3,4]. Furthermore, the increase of injection pressure (up to 3000 bars) promotes effective breakup and atomization of liquid fuels [5,6]. Therefore, understanding these complex physical phenomena of spray dynamics at high pressures is crucial for improving the efficiency of IC technology.
Another critical task in the field of IC research is the development of engines which run on a wide variety of fuels and their blends. For instance, growing demand in the heavy-duty market introduced naphtha as an alternative fuel [7]. Solar energy can be utilized to produce synthetic chemical fuels such as methanol or ethanol, which suffer from long ignition delays. Therefore, they should be mixed with an appropriate amount of ignitable fuels (e.g., dimethyl/diethyl ether) [8] to obtain better properties. Surrogate fuels are formulated to reproduce the specific physical and chemical characteristics of the targeted real fuels [9,10]. The same research framework applies to the exploitation of unconventional low-grade fuels, e.g., heavy fuel oils which contain even more components with a broad spectrum of physical and chemical properties [11]. Another possibility is to take advantage of the high temperature and pressure conditions and utilize the spray/air mixture at supercritical states to promote diffusive mixing [12,13,14,15,16]. These advances in fuel development require a modeling framework capable of predicting the dynamic behavior of modern fuels.
Computational Fluid Dynamics (CFD) offers several approaches to describe such problems. The most common choice is the Lagrangian approach where the continuous gas phase is defined in the Eulerian frame of reference, and the droplet parcels are described in the Lagrangian frame of reference. This approach has numerous advantages, but it often experiences problems in the dense part of the spray, where the liquid phase fraction is very high [17,18]. Therefore, the Lagrangian solvers are often coupled with other models, which are used for the evaluation of the near-nozzle region. Another approach, which recently gained popularity due to constant improvement in available computational resources is the Direct Numerical Simulation (DNS) approach [18,19,20,21]. This approach does not require any sub-model to capture the complex spray physics, e.g., primary and secondary breakup. However, DNS is still not feasible for everyday engineering calculations. The third approach is the Eulerian approach, where both the gas and liquid phase are described in the Eulerian frame of reference. This approach can be employed for a wide range of different flow regimes, but due to averaging of the conservation equations [22,23], the results represent averaged quantities (small-scale phenomena are lost). The Eulerian approach has multiple formulations, and in this work, the Eulerian multi-fluid model is investigated in a detailed manner. Here, the gas and the liquid phase are treated as interpenetrating continua, and the liquid phase can be divided into an arbitrary number of droplet classes (to increase the precision of the model). The details of the employed model will be given in Section 2.
All of the mentioned approaches are still being actively researched [18,19,24,25,26,27,28,29,30,31], and the academic and engineering community is constantly re-evaluating which approach gives the best trade-off between the cost and accuracy for each problem. This work presents the development of a Eulerian multi-fluid framework for predicting dynamic spray behavior in OpenFOAM. To the authors’ knowledge, this is the first attempt to develop Eulerian multi-fluid simulation capability specialized for polydisperse spray behavior within a freely available and open-source library. For fuel spray applications, one of the critical modeling components is the description of the breakup process, and the presented work utilizes the WAVE breakup model [32,33,34] (which is coupled to a blob injection model). The paper gives a detailed description of the implementation procedure, which reduces the required effort for the implementation of other breakup models in the future.
The following sections present the employed mathematical model, which is followed by a detailed overview of the numerical implementation. Special attention was given to the implementation of the selected breakup model. The implemented model is verified by systematically varying the spatial and temporal resolution. Furthermore, to test the sensitivity to the selected number of classes, the same test case is calculated with a varying number of droplet classes. The implemented model is validated against available experimental measurements. The presented work is intended as a stable foundation for further development and upgrades with additional functionality.
2. Formulation of the Mathematical Model
This section presents a Eulerian multi-fluid model specialized for spray applications, which is generalized for an optional number of incompressible fluids. The first fluid is the continuous gas phase, and the remaining phases describe the liquid fuel phase. The liquid phase is sub-divided into an arbitrary number of fluids (using the classes method). The model equations are conditionally averaged using the procedures described by [23,35,36,37,38]. The proposed model is an upgrade of the work given in [39], which was developed for monodisperse bubbly flows. The model is enhanced with advance interfacial momentum transfer models specialized for deforming droplet flows at high phase fractions, which can reproduce thick spray effects in near nozzle regions. Furthermore, the proposed model now includes breakup functionality for high Weber number flows (We > 100) using the WAVE breakup model [32,33,34]. Within this work, the proposed model is tested for non-evaporating spray conditions. Therefore, the presented model does not contain an evaporation model.
Linking the population balance equation (PBE) [40] with the standard continuity and momentum equations enables the model to predict polydisperse flows. Moreover, the multi-fluid formulation (in comparison with the standard two-fluid formulation) allows the model to capture velocity and spatial variance because the interfacial momentum transfer models are strongly dependent on the droplet size. In this work, the PBE is discretized using the classes method, which means that droplets are divided into a finite number of droplet classes. This approach is similar to the Multiple Size Group (MUSIG) [41] or Inhomogeneous MUSIG [42,43] model, but it offers a higher resolution and precision (each droplet class has its momentum and phase continuity equation, i.e., there are no velocity groups).
The droplet diameters are discretized using the equal diameter distribution, i.e., the i-th droplet diameter is calculated from:
where and are the maximum and minimal droplet diameter and is the total number of droplet classes.
The solver employs the RANS approach using the single-phase k – turbulence model for the continuous gas phase [44]. The dispersed phase turbulence is evaluated using the turbulence response coefficient.
2.1. Phase-Intensive Momentum Equation
The conditionally averaged phase-intensive momentum equation for phase is given by the following expression:
where gives the averaged phase velocity, is the phase fraction, gives the joined viscous and turbulent stress, denotes the mixture pressure, is the phase density, is the gravitational acceleration, is the averaged interfacial momentum transfer term, and is the net momentum source term due to breakup, which is caused by the transfer of mass between the droplet classes.
The interfacial momentum transfer term reads:
where is the total number of fluids, and gives the momentum transferred between phases and i.
The presented work limits the model to droplet flows, where the gas is described by only one continuous phase, and the fuel phase is divided into an arbitrary number of classes depending on the droplet diameter. Therefore, , where is the total number of droplet classes. The momentum between the droplet phases and the continuous gas phase is exchanged via the turbulent dispersion force and drag (other forces such as virtual mass and lift can be neglected):
where the subscript indicates the dispersed phase, and the subscript signifies the continuous phase. The relative velocity term is calculated as . and are the drag and turbulent dispersion force coefficient of the i-th droplet phase. The term represents the turbulence kinetic energy of the continuous phase. The diameter of the i-th dispersed phase is given with .
In Equation (5), the turbulent dispersion force is implemented following the approach presented by Reeks [45] and Bertodano [46]. The coefficient can be treated as a constant value, but it can also be linked to the time scales associated with droplets, using the following expression:
where is the time constant of the particle, and is the effective time constant of the fluctuating force acting on the particle. is calculated as:
and is given by:
In Equation (7), indicates the kinematic viscosity of the gas (continuous) phase, and is the Reynolds number for the i-th droplet class given by:
and, in Equation (8), is the dissipation of turbulence energy of the continuous phase.
In Equation (5), the drag coefficient of i-th droplet class is implemented following the procedure described by Liu et al. [47]. Due to the large deformations of droplets in engine-like conditions (which also lead to droplet breakup), Liu et al. [47] suggested blending the drag coefficient between an ideal sphere and a disc (which is approx. 3.6 times greater):
where is the drag coefficient of ideally spherical particle with the diameter , and is the normalized distortion parameter (of the i-th droplet class) calculated with the Taylor–Analogy (TAB) model [48]. The TAB model assumes that the droplet distortion can be described as a one-dimensional mass spring system, where the droplet viscosity is the damping force and the surface tension is the restoring force, which leads to the following expression (when defined using the droplet diameter):
Integration of Equation (11) gives the time-dependent normalized distortion equation, which is used for the evaluation of the additional drag term.
The drag coefficient of an ideally spherical particle in Equation (5) can be calculated with the following relations:
which include the influence of the local phase fraction on the droplet drag presented by O’Rourke and Bracco [49].
The momentum transfer term for the gas phase is calculated as:
2.2. Phase Continuity Equation
For incompressible flows, the phase continuity equation (for phase ) can be written in the following form:
where denotes the net source term due to breakup mass transfer between droplet classes. In this work, the phase continuity equation is implemented following the formulation given by Weller [36], which contributes to the conservativeness and boundedness of the solution. The generalisation for the multi-fluid formulation is described in [50,51]. Consequently, the modified phase continuity equation for polydisperse flows can be written in the following form:
where denotes the mixture velocity, which is defined as:
The net source term is evaluated using the WAVE breakup model, which is presented in Section 2.3.
2.3. WAVE Breakup Model
The aerodynamic interaction between the high-speed droplets and the gas phase introduces the development and growth of disturbances on the droplet surface. The generated deformations of the droplets are practically the dominant cause of droplet breakup, especially in regions further away from the injector nozzle. Reitz and co-workers made a great effort in deriving [32,33,34] a continuous and unified breakup model, often referred to as the WAVE or the Kelvin-Helmholtz model, which was used for modeling of high-speed diesel jets [52,53].
The derived model assumes that a cylindrical liquid jet penetrates a stationary incompressible gas through a round opening. The surface of the liquid jet is subject to initial perturbations which are further increased by the liquid–gas interaction. It is also assumed that only the fastest growing disturbances (denoted with the growth rate , which matches the wavelength ) will cause the breakup. Furthermore, Reitz [53] simplified the problem by fitting the numerical results to analytical expressions which give the maximum growth rate (for i-th droplet class):
and its wavelength :
is the Taylor number:
is the liquid Weber number:
is the gas Weber number:
and (in Equation (19)) defines the liquid phase Reynolds number (defined using the droplet radius, and not the diameter as in previous models):
The size of droplets (stable radius ) which are formed by the breakup process is usually linearly coupled to the most unstable surface disturbance, i.e., to the wavelength :
where the proportionality coefficient is of order unity, and, in this work, the standard value of 0.61 is employed.
Due to the breakup process and the generation of new smaller droplets, the parent droplets lose mass, i.e., the radius of parent droplets is reduced with the following expression:
where the breakup time is calculated as:
In Equation (26), denotes a constant which describes the effects of the inner nozzle flow on the breakup time because those effects cannot be resolved directly with the model [52].
When using the Eulerian multi-fluid approach, the reduction of the parent droplet diameter needs to be converted into a phase sink term (in the parent phase continuity equation) and a corresponding source term (in the child phase continuity equation). Therefore, the net source term in Equation (15) is divided in the following manner:
where is the droplet birth rate due to breakup from larger droplets (into class i), and is the droplet death rate due to breakup (from class i) into smaller droplets.
Following the procedure described in [54], the rate of change of parent class radius, given in Equation (25), can be reformulated in mass loss per unit volume of phase i, i.e., it can be converted into :
More details about the numerical implementation of the model and details regarding the calculation of the droplet birth rate will be discussed in Section 3.1.
3. Numerical Model
This section gives an overview of the numerical procedures utilized for the implementation and solving of the previously described mathematical model. The collocated Finite Volume Method (FVM) is used for the solution of the previously given equations [55,56]. The proposed solution procedure uses the PISO algorithm [57] and the implemented procedure per each time step is given in Algorithm 1.
| Algorithm 1 Solution algorithm per each time step. |
|
3.1. Implementation of the WAVE Breakup Model and Phase Continuity Equations
This section gives details about the implementation of the phase continuity equations and the WAVE breakup model. As previously described, the presented model is limited to droplet flows, where the gas phase is represented with only one continuous phase, and the droplets of various sizes are described with an arbitrary number of droplet phases . The continuous gas phase does not undergo breakup, and since the model does not account for evaporation, the net source term in the phase continuity equation is equal to zero, i.e., . The phase continuity equation for the continuous phase is implemented as:
The dispersed phase continuity equations are implemented in the following form:
In this work, the droplet diameters are discretized using the equal diameter distribution using Equations (1) and (2). Consequently, the temporal change in the parent droplet radius is implemented as:
where the temporal change of the droplet radius and the droplet death rate are greater than zero only if the stable radius is smaller than the lower bound of the i-th droplet class. Therefore, the smallest droplet class does not undergo breakup.
The droplet death rate defined by Equation (28) can introduce negative solutions of the droplet phase continuity equation, especially when larger time steps are enforced. This work suggests a limiter, which keeps the solution bounded. The proposed limiter compares the local droplet death rate predicted by the model to the maximal allowed value:
where gives the time step value. However, the limiter requires implicit treatment (in terms of ) of the advection terms in the droplet phase continuity equation Equation (30). The corresponding droplet birth rate of phase j (from phase i) is implemented as:
where the mass is transferred from i-th to j-th class only if the stable radius of phase i is within the bounds of the droplet class j. Considering that the mass transfer due to breakup always goes from larger to smaller droplets, the total droplet birth rate of phase j is given by:
It is required that the implementation satisfies the conservation criterion, i.e., the total source needs to be zero when summed over all droplet classes:
3.2. Numerical Procedure
In this work, all presented calculations given in Section 4 used identical linear solver and discretization settings. Any differences in the case set-up are explicitly mentioned.
The turbulence model equations and the phase continuity equations were solved with a Bi-Conjugate Gradient Method preconditioned by DILU [58], and the pressure equation used the selection algebraic multigrid algorithm [59] with the Gauss–Seidel smoother [60]. All equations used the same absolute tolerance for the normalized residual value of . For a matrix system , the normalized residual r is evaluated as [61]:
and the normalization factor n is calculated as:
where is the current solution vector, and x denotes the average value of .
The phase fractions variables were advected using the linear upwind-biased approximation with a limiter for stronger bounding. The upwind scheme is used for the advection of the turbulence model variables. The momentum variables employed the Gamma scheme [62], which is a member of the normalized variable diagram family. All (first) time derivative terms were evaluated using the Crank–Nicholson scheme. Gradients, Laplacians, and cell-to-face interpolations were assessed using linear interpolation.
4. Results
In this section, a detailed verification study is presented, where the spatial and temporal resolution were systematically varied. Furthermore, the implemented model was tested with different numbers of droplet classes to examine the sensitivity of the model to the droplet class resolution. The last sub-section deals with the validation, where the results are compared with the available experimental measurements such as spray penetration, spray angle, and droplet size distribution.
The testing of the presented and implemented model is done for non-evaporating conditions, where the liquid fuel is injected into a pressurized (2.1 MPa) constant volume vessel filled with carbon dioxide. The diesel fuel is injected through a Mini-Sac nozzle with a diameter of 140 m and bore length of 0.8 mm. The experimental measurements are available in [63,64,65], where the data were used for testing of various numerical approaches for predicting spray behavior. The physical properties of the gas and liquid phase, which were employed in the following simulations are given in Table 1.

Table 1.
Physical properties employed in the simulation.
The given results utilize the blob injection model [53], i.e., through the duration of injection, large blobs (droplets which are the same size as the nozzle hole) are being added at the inlet boundary, and the inlet velocity is calculated from the corresponding fuel flow-rate. Immediately after the blobs enter the computational domain, the WAVE breakup model shears off smaller child droplets from the surface of the blobs.
The selected fuel injection flow-rate is shown in Figure 1, which was obtained by fitting the curve to the available experimental measurements available at [65].
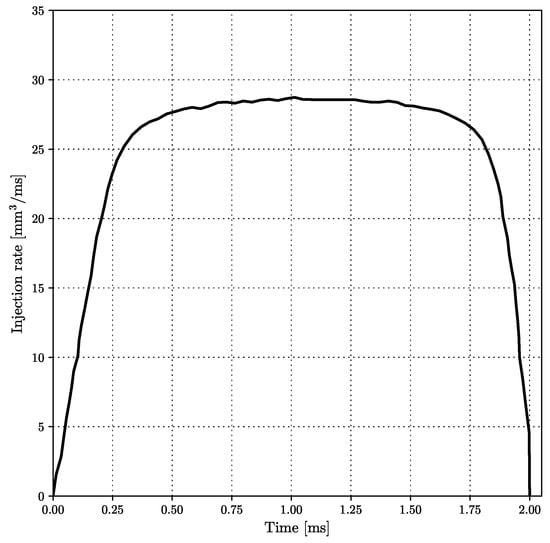
Figure 1.
Fuel injection flow-rate for the selected Mini-Sac nozzle.
4.1. Verification
The performed verification analysis follows the guidelines for unsteady flows given by [66]. The analysis was carried out by systematically varying spatial and temporal resolution, i.e., five structured grids with uniformly varied refinement levels and four different time step sizes were employed in the study. The grid density was increased towards the nozzle, both in the radial and axial direction. The initial coarse grid was constructed to have two cells per nozzle diameter, and for finer grids, the cell density was uniformly increased. The selected three-dimensional cylindrical computational domain is shown in Figure 2. The outer dimensions of the domain were quite large (the cylinder is 50 mm in radius and 80 mm in length) in comparison with the nozzle diameter, to minimize the influence of the boundary conditions on the solution.
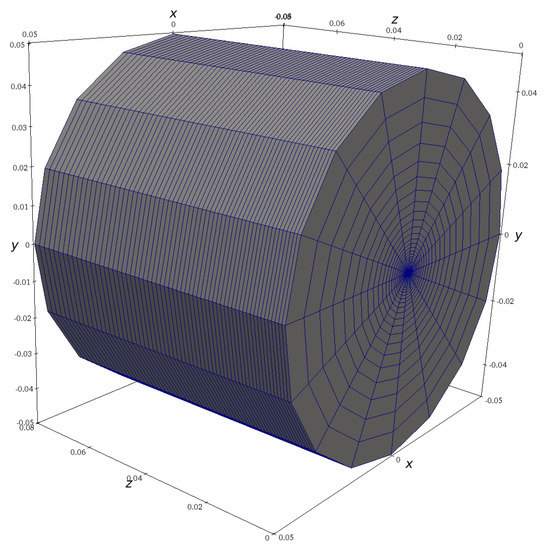
Figure 2.
Computational domain.
To reduce the computational load of the verification study, and, due to the too high Courant number, when using larger time steps for finer grids, only the smallest time step is used for all meshes. A visual representation of the employed computational grids (with a detailed view of the refinement area near the nozzle) and the corresponding number of cells are given in Figure 3 (sub-Figures 3a–e).
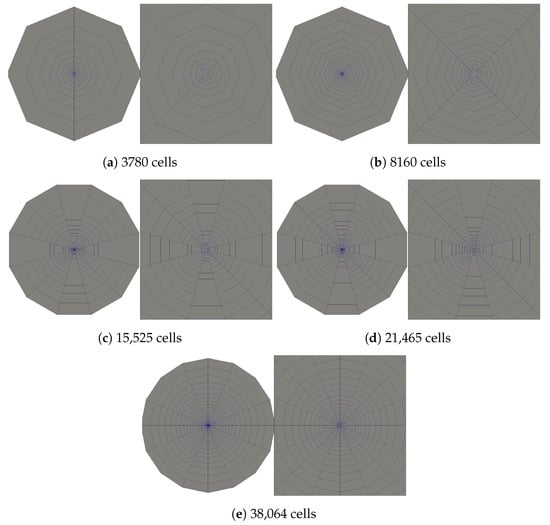
Figure 3.
Computational grids (and the corresponding number of cells) for the verification analysis.
The uncertainty and the achieved accuracy in space and time were estimated using the freely available ReFRESCO application [67]. The study is conducted for the spray tip penetration length after 0.5 ms (after the start of the fuel injection) with 14 droplet classes. The input values for the ReFRESCO application are given in Table 2.

Table 2.
Test matrix for the verification analysis. The values denote the spray tip penetration length (in mm) after 0.5 ms for various spatial and temporal resolutions.
The results of the estimator are given in Table 3, where is the extrapolated exact solution, is the finest level solution, is the uncertainty estimate, p is the achieved accuracy in space, and q is the achieved temporal accuracy.

Table 3.
Results of the uncertainty estimation.
The achieved second order accuracy (both in space and time) was expected, considering the employed numerical methods described in Section 3.
4.2. Sensitivity to the Selected Number of Droplet Classes
The sensitivity of the implemented model to the employed number of droplet classes is tested for the previously described flow conditions using the second finest computational grid with 21,465 cells. The sensitivity of the model is tested for the droplet size distribution and the spray tip penetration.
The droplets size distributions were calculated by integrating the fluxes of the individual droplet phases through time, i.e., counting the number of droplets, passing through the predefined circular sampling surface (1 mm in radius and located 62 mm downstream in the axial direction from the nozzle exit). The comparison of the droplet size distributions for 7, 14, and 28 classes is given in Figure 4. In Figure 4, the left sub-plots give the predefined droplet population at the inlet boundary, i.e., they present the employed blob population. The right sub-plots show the droplet population obtained with the previously described sampling surface. Figure 4 shows that the model behavior is consistent in terms of the selected number of droplet classes. However, as expected, the increase in the selected number of classes improves the resolution of the solution. The increased resolution predicts the distribution peak around 7.5 m, and not in the smallest droplet class, which is not visible from the lower resolution results. In Section 4.3, the presented droplet size distribution (obtained with 28 classes) is compared to available experimental measurements.
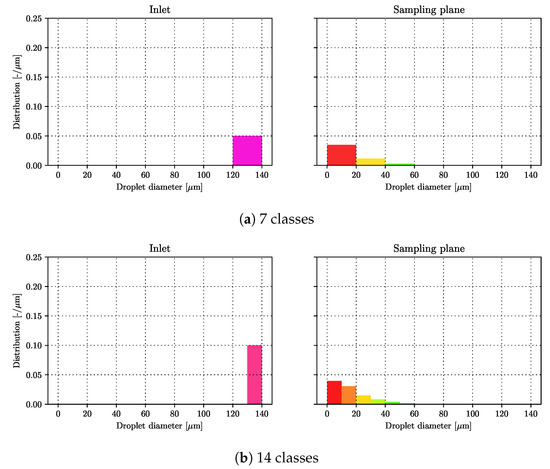
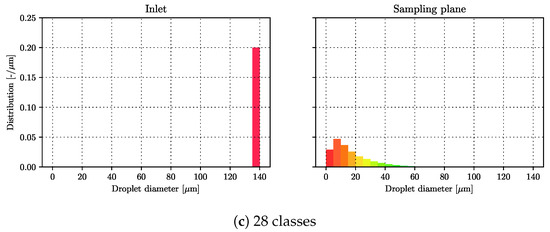
Figure 4.
Sensitivity of the droplet size distribution to the selected number of droplet classes.
Figure 5 gives a comparison of the spray penetration behavior over time. The presented results suggest that the spray penetration is not particularly sensitive to the selected number of classes.
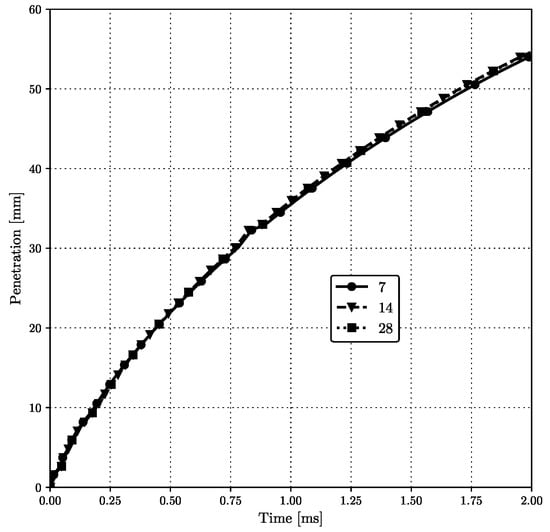
Figure 5.
Sensitivity of the spray penetration behavior to the selected number of droplet classes.
4.3. Validation
The validation of the model is performed using the results obtained with the second finest grid (21,465 cells) and using 28 droplet classes. The numerical results are compared to available experimental measurements [63,64,65]. The validation is performed in terms of spray angle, spray tip penetration, and droplet size distribution.
Figure 6 shows a comparison of the experimentally measured spray penetration curve (denoted by the dashed line) and the one obtained with the previously presented numerical model (indicated by the solid line). The numerical results capture the spray behavior quite well, but there is a significant lag in the penetration between 0.1 and 0.25 ms. The slowdown is a consequence of drag overprediction in the near-nozzle region. In the remaining time interval, the two curves are practically parallel, which suggest that the spray dynamics is captured adequately. The presented spray penetration curves indicate that the blob injection model should be replaced by a more advanced modeling approach, e.g., primary atomization modeling or initialization using the high-fidelity atomization simulations. In future work, the presented Eulerian multi-fluid model is planned to be initialized using the DNS results.
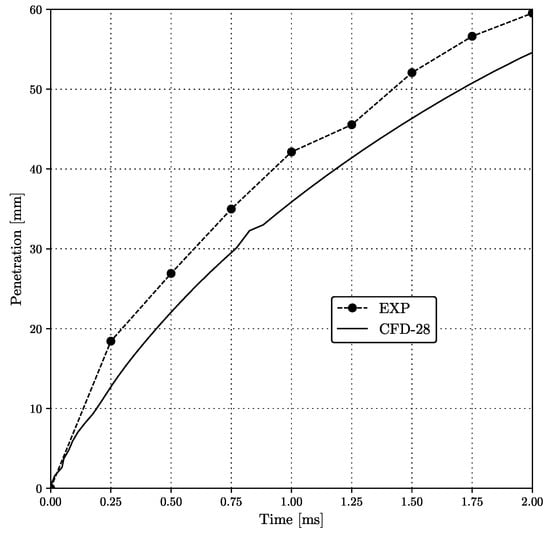
Figure 6.
Comparison of the spray tip penetration.
The comparison of the droplet size distributions is given in Figure 7. The left sub-plot presents the employed blob population in the numerical simulation, and the right one compares the droplet size distribution obtained with the experimental measurements (dashed line) and the numerical model (denoted by solid bars). The numerical simulation overpredicts the generation of smaller droplets in comparison with the measurements. The smallest droplets are generated immediately after the blobs enter the computational domain. In the near-nozzle region, the relative velocity between the blob droplet class and the gas phase is quite large, which results in tiny values of the stable radius. The numerical model correctly predicts the range of occurring droplets, but the distribution peak is shifted towards smaller droplets, due to the previously described issue. Therefore, the accuracy of the predicted droplet size distributions would benefit from a more advanced modeling approach in the nozzle exit region.
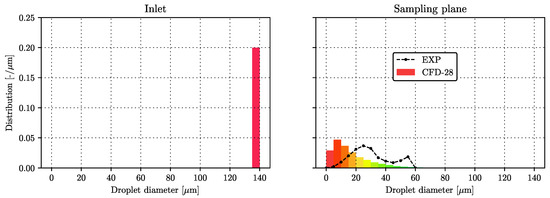
Figure 7.
Comparison of the droplet size distribution.
The spray angle is calculated as the droplet spreading angle at 70% of the spray penetration tip at the end of the fuel injection, i.e., after 2 ms [65]. The comparison of the experimentally measured spray angle and the numerical prediction is shown in Table 4.

Table 4.
Comparison of the spray angle.
The implemented model successfully predicts the cone shape of the spray for the given flow conditions.
Overall, the developed numerical model is capable of describing the dynamic spray behavior, but the employed initialization procedure coupled with the WAVE breakup model is not ideal for capturing all near-nozzle phenomena.
5. Conclusions
The objective of this work is to provide a new modeling approach to the publicly available simulation framework for fuel spray applications, which is vital for research and advancement in the internal combustion technology. This work presents a detailed description of the developed and implemented simulation framework for predicting the dynamic behavior of dense sprays using the Eulerian multi-fluid model. Special attention was given to the numerical implementation of the breakup model using the Eulerian approach. The presented work employs the WAVE breakup model and the blob injection approach. The implemented model was thoroughly tested to determine the achieved accuracy in space and time. Additional tests presented the sensitivity of the model to the chosen number of droplet classes. Furthermore, the numerical results were also compared to the available experimental data. The tests showed that the developed solver is giving stable and consistent results in terms of the selected number of droplet classes and employed computational grids. The validation section showed that the implemented model is capable of predicting the dynamic behavior of non-evaporating sprays in terms of the spray shape, penetration, and droplet size distribution, but with some limitations. The blob injection approach, coupled with the presented model, introduces some issues in the near-nozzle region. The numerical results overpredicted drag and generation of small droplets (due to breakup of blobs) in the vicinity of the nozzle exit. The calculation procedure is not taking into account the complex nozzle flow (e.g., cavitation and local turbulence) when injecting the blobs into the computational domain. Consequently, the droplet breakup is directly influenced only by aerodynamic forces, which undoubtedly reduces the accuracy of the solution. In future work, the Euler-Euler simulations will be initialized using the DNS results of the spray atomization [19] to test the impact on the solution accuracy. Furthermore, the model is planned to be expanded with evaporation functionality. The implementations presented within this work were done within foam-extend (a community-driven fork of OpenFOAM).
Author Contributions
Conceptualization, R.K. and M.B.; methodology, R.K. and M.B.; software, R.K. and H.J.; validation, R.K.; formal analysis, R.K., M.B. and A.C.; investigation, R.K.; resources, H.J., H.G.I. and A.C.; data curation, R.K. and A.C.; writing–original draft preparation, R.K.; writing–review and editing, R.K., A.C., M.B., H.G.I. and H.J.; visualization, R.K.; supervision, H.J.; project administration, H.G.I. and A.C.; funding acquisition, H.J. and H.G.I. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the King Abdullah University of Science and Technology within the OSR-2017-CRG6-3409.03 research grant, and the Croatian Science Foundation (project number DOK-01-2018).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kalghatgi, G.T. Developments in internal combustion engines and implications for combustion science and future transport fuels. Proc. Combust. Inst. 2015, 35, 101–115. [Google Scholar] [CrossRef]
- Manente, V.; Johansson, B.; Cannella, W. Gasoline partially premixed combustion, the future of internal combustion engines? Int. J. Engine Res. 2011, 12, 194–208. [Google Scholar] [CrossRef]
- Badock, C.; Wirth, R.; Fath, A.; Leipertz, A. Investigation of cavitation in real size diesel injection nozzles. Int. J. Heat Fluid Flow 1999, 20, 538–544. [Google Scholar] [CrossRef]
- Desantes, J.M.; Payri, R.; Salvador, F.J.; De La Morena, J. Influence of cavitation phenomenon on primary break-up and spray behavior at stationary conditions. Fuel 2010, 89, 3033–3041. [Google Scholar] [CrossRef]
- Weigand, A.; Atzler, F.; Kastner, O.; Rotondi, R.; Schwarte, A. The Effect of Closely Coupled Pilot Injections on Diesel Engine Emissions; Woodhead Publishing: Cambridge, UK, 2011; pp. 111–124. [Google Scholar] [CrossRef]
- Johnson, J.E.; Yoon, S.; Naber, J.; Lee, S.; Hunter, G.; Truemner, R.; Harcombe, T. Characteristics of 3000 bar Diesel Spray Injection under Non-Vaporizing and Vaporizing Conditions. In Proceedings of the ICLASS 2012, 12th Triennial International Conference on Liquid Atomization and Spray Systems, Heidelberg, Germany, 2–6 September 2012. [Google Scholar]
- Badra, J.A.; Sim, J.; Elwardany, A.; Jaasim, M.; Viollet, Y.; Chang, J.; Amer, A.; Im, H.G. Numerical Simulations of Hollow-Cone Injection and Gasoline Compression Ignition Combustion With Naphtha Fuels. J. Energy Resour. Technol. 2016, 138, 052202. [Google Scholar] [CrossRef]
- Sivasankaralingam, V.; Raman, V.; Mubarak Ali, M.J.; Alfazazi, A.; Lu, T.; Im, H.; Sarathy, S.M.; Dibble, R. Experimental and Numerical Investigation of Ethanol/Diethyl Ether Mixtures in a CI Engine; SAE International: Warren Dale, PA, USA, 2016; Volume 1. [Google Scholar] [CrossRef]
- Sarathy, S.M.; Kukkadapu, G.; Mehl, M.; Javed, T.; Ahmed, A.; Naser, N.; Tekawade, A.; Kosiba, G.; AlAbbad, M.; Singh, E.; et al. Compositional effects on the ignition of FACE gasolines. Combust. Flame 2016, 169, 171–193. [Google Scholar] [CrossRef]
- Elwardany, A.E.; Sazhin, S.S.; Im, H.G. A new formulation of physical surrogates of FACE A gasoline fuel based on heating and evaporation characteristics. Fuel 2016, 176, 56–62. [Google Scholar] [CrossRef]
- Elbaz, A.M.; Gani, A.; Hourani, N.; Emwas, A.H.; Sarathy, S.M.; Roberts, W.L. TG/DTG, FT-ICR Mass Spectrometry, and NMR Spectroscopy Study of Heavy Fuel Oil. Energy Fuels 2015, 29, 7825–7835. [Google Scholar] [CrossRef]
- Ningegowda, B.M.; Rahantamialisoa, F.; Zembi, J.; Pandal, A.; Im, H.G.; Battistoni, M. Large Eddy Simulations of Supercritical and Transcritical Jet Flows Using Real Fluid Thermophysical Properties; SAE International: Warren Dale, PA, USA, 2020. [Google Scholar] [CrossRef]
- Manin, J.; Bardi, M.; Pickett, L.M.; Dahms, R.N.; Oefelein, J.C. Microscopic investigation of the atomization and mixing processes of diesel sprays injected into high pressure and temperature environments. Fuel 2014, 134, 531–543. [Google Scholar] [CrossRef]
- Dahms, R.N.; Oefelein, J.C. Liquid jet breakup regimes at supercritical pressures. Combust. Flame 2014, 162. [Google Scholar] [CrossRef]
- Chehroudi, B. Recent experimental efforts on high-pressure supercritical injection for liquid rockets and their implications. Int. J. Aerosp. Eng. 2012. [Google Scholar] [CrossRef]
- Gopal, J.M.; Tretola, G.; Morgan, R.; de Sercey, G.; Atkins, A.; Vogiatzaki, K. Understanding Sub and Supercritical Cryogenic Fluid Dynamics in Conditions Relevant to Novel Ultra Low Emission Engines. Energies 2020, 13, 3038. [Google Scholar] [CrossRef]
- Hoyas, S.; Gil, A.; Margot, X.; Khuong-Anh, D.; Ravet, F. Evaluation of the Eulerian-Lagrangian Spray Atomization (ELSA) model in spray simulations: 2D cases. Math. Comput. Model. 2013, 57, 1686–1693. [Google Scholar] [CrossRef]
- Shinjo, J. Recent Advances in Computational Modeling of Primary Atomization of Liquid Fuel Sprays. Energies 2018, 11, 2971. [Google Scholar] [CrossRef]
- Vukcevic, V.; Keser, R.; Jasak, H.; Battistoni, M.; Im, H.; Roenby, J. Development of a CFD Solver for Primary Diesel Jet Atomization in FOAM-Extend; SAE International: Warren Dale, PA, USA, 2019. [Google Scholar] [CrossRef]
- Holz, S.; Braun, S.; Chaussonnet, G.; Koch, R.; Bauer, H.J. Close Nozzle Spray Characteristics of a Prefilming Airblast Atomizer. Energies 2019, 12, 2835. [Google Scholar] [CrossRef]
- Ries, F.; Li, Y.; Klingenberg, D.; Nishad, K.; Janicka, J.; Sadiki, A. Near-Wall Thermal Processes in an Inclined Impinging Jet: Analysis of Heat Transport and Entropy Generation Mechanisms. Energies 2018, 11, 1354. [Google Scholar] [CrossRef]
- Crowe, C.; Schwarzkopf, J.; Sommerfeld, M.; Tsuji, Y. Multiphase Flows with Droplets and Particles, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar] [CrossRef]
- Hill, D.P. The Computer Simulation of Dispersed Two-Phase Flows. Ph.D. Thesis, Imperial College London, London, UK, 1998. [Google Scholar]
- Zembi, J.; Battistoni, M.; Ranuzzi, F.; Cavina, N.; De Cesare, M. CFD Analysis of Port Water Injection in a GDI Engine under Incipient Knock Conditions. Energies 2019, 12, 3409. [Google Scholar] [CrossRef]
- Sparacino, S.; Berni, F.; D’Adamo, A.; Krastev, V.K.; Cavicchi, A.; Postrioti, L. Impact of the Primary Break-Up Strategy on the Morphology of GDI Sprays in 3D-CFD Simulations of Multi-Hole Injectors. Energies 2019, 12, 2890. [Google Scholar] [CrossRef]
- Gadalla, M.; Kannan, J.; Tekgül, B.; Karimkashi, S.; Kaario, O.; Vuorinen, V. Large-Eddy Simulation of ECN Spray A: Sensitivity Study on Modeling Assumptions. Energies 2020, 13, 3360. [Google Scholar] [CrossRef]
- Ishak, M.; Ismail, F.; Che Mat, S.; Abdullah, M.; Abdul Aziz, M.; Idroas, M. Numerical Analysis of Nozzle Flow and Spray Characteristics from Different Nozzles Using Diesel and Biofuel Blends. Energies 2019, 12, 281. [Google Scholar] [CrossRef]
- Petranović, Z.; Edelbauer, W.; Vujanović, M.; Duić, N. Modelling of spray and combustion processes by using the Eulerian multiphase approach and detailed chemical kinetics. Fuel 2017, 191, 25–35. [Google Scholar] [CrossRef]
- Vujanović, M.; Petranović, Z.; Edelbauer, W.; Baleta, J.; Duić, N. Numerical modeling of diesel spray using the Eulerian multiphase approach. Energy Convers. Manag. 2015, 104, 160–169. [Google Scholar] [CrossRef]
- Ganti, H.; Kamin, M.; Khare, P. Design Space Exploration of Turbulent Multiphase Flows Using Machine Learning-Based Surrogate Model. Energies 2020, 13, 4565. [Google Scholar] [CrossRef]
- Dauch, T.F.; Ates, C.; Rapp, T.; Keller, M.C.; Chaussonnet, G.; Kaden, J.; Okraschevski, M.; Koch, R.; Dachsbacher, C.; Bauer, H.J. Analyzing the Interaction of Vortex and Gas–Liquid Interface Dynamics in Fuel Spray Nozzles by Means of Lagrangian-Coherent Structures (2D). Energies 2019, 12, 2552. [Google Scholar] [CrossRef]
- Reitz, R.D. Atomization and Other Breakup Regimes of a Liquid Jet. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1978. [Google Scholar]
- Reitz, R.D.; Bracco, F.V. Mechanism of atomization of a liquid jet. Phys. Fluids 1982, 25, 1730–1742. [Google Scholar] [CrossRef]
- Reitz, R.D.; Bracco, F.V. Mechanisms of Breakup of Round Liquid Jets. In The Encyclopedia of Fluid Mechanics; Gulf Publishing Company: Houston, TX, USA, 1986; Volume 3, pp. 223–249. [Google Scholar]
- Rusche, H. Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions. Ph.D. Thesis, Imperial College London, London, UK, 2002. [Google Scholar]
- Weller, H.G. Derivation Modelling and Solution of the Conditionally Averaged Two-Phase Flow Equations; Technical Report Tech. Rep.; Nabla Ltd.: Bangkok, Thailand, 2002. [Google Scholar]
- Ishii, M.; Hibiki, T. Thermo-Fluid Dynamics of Two-Phase Flow; Springer: New York, NY, USA, 2006; pp. 1–462. [Google Scholar] [CrossRef]
- Drew, J.; Passman, S.L. Theory of Multicomponent Fluids; Springer: New York, NY, USA, 1998. [Google Scholar] [CrossRef]
- Keser, R.; Vukčević, V.; Battistoni, M.; Im, H.; Jasak, H. Implicitly coupled phase fraction equations for the Eulerian multi-fluid model. Comput. Fluids 2019. [Google Scholar] [CrossRef]
- Marchisio, D.L.; Fox, R.O. Computational Models for Polydisperse Particulate and Multiphase Systems; Cambridge University Press: Cambridge, UK, 2013; p. 498. [Google Scholar] [CrossRef]
- Lo, S. Application of Population Balance to CFD Modeling of Bubbly Flow Via the MUSIG Model; AEAT-1096; AEA Technology: Carlsbad, CA, USA, 1996. [Google Scholar]
- Moukalled, F.; Darwish, M. Mixing and evaporation of liquid droplets injected into an air stream flowing at all speeds. Phys. Fluids 2008, 20. [Google Scholar] [CrossRef]
- Duan, X.; Cheung, S.; Yeoh, G.; Tu, J.; Krepper, E.; Lucas, D. Gas–liquid flows in medium and large vertical pipes. Chem. Eng. Sci. 2011, 66, 872–883. [Google Scholar] [CrossRef]
- Gosman, A.D.; Lekakou, C.; Politis, S.; Issa, R.I.; Looney, M.K. Multidimensional modeling of turbulent two-phase flows in stirred vessels. AIChE J. 1992, 38, 1946–1956. [Google Scholar] [CrossRef]
- Reeks, M.W. On the continuum equations for dispersed particles in nonuniform flows. Phys. Fluids A Fluid Dyn. 1992, 4, 1290–1303. [Google Scholar] [CrossRef]
- Lopez de Bertodano, M.A. Two fluid model for two-phase turbulent jets. Nucl. Eng. Des. 1998, 179, 65–74. [Google Scholar] [CrossRef]
- Liu, A.B.; Mather, D.; Reitz, R.D. Modeling the Effects of Drop Drag and Breakup on Fuel Sprays; SAE Technical Paper; SAE International: Warren Dale, PA, USA, 1993. [Google Scholar] [CrossRef]
- O’Rourke, P.J.; Amsden, A.A. The Tab Method for Numerical Calculation of Spray Droplet Breakup; SAE International: Warren Dale, PA, USA, 1987. [Google Scholar] [CrossRef]
- O’Rourke, P.J.; Bracco, F.V. Modeling of drop interactions in thick sprays and a comparison with experiments. Proc. Inst. Mech. Eng. 1980, 404, 101–116. [Google Scholar] [CrossRef]
- Silva, L.F.; Lage, P.L. Development and implementation of a polydispersed multiphase flow model in OpenFOAM. Comput. Chem. Eng. 2011, 35, 2653–2666. [Google Scholar] [CrossRef]
- Kissling, K.; Springer, J.; Jasak, H.; Schütz, S.; Urban, K.; Piesche, M. A coupled pressure based solution algorithm based on the volume-of-fluid approach for two or more immiscible fluids. In Proceedings of the European Conference on Computational Fluid Dynamics 2010, Lisbon, Portugal, 14–17 June 2010; pp. 14–17. [Google Scholar]
- Stiesch, G. Modeling Engine Spray and Combustion Processes; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Reitz, R.D. Modeling atomization processes in high-pressure vaporizing sprays. At. Spray Technol. 1987, 3, 309–337. [Google Scholar]
- Vujanović, M. Numerical Modelling of Multiphase Flow in Combustion of Liquid Fuel. Ph.D. Thesis, Faculty of Mechanical Engineering and Naval Architecture, University of Zagreb, Zagreb, Croatia, 2010. [Google Scholar]
- Jasak, H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows. Ph.D. Thesis, Imperial College London, London, UK, 1996. [Google Scholar]
- Ferziger, J.H.; Peric, M.; Leonard, A. Computational Methods for Fluid Dynamics. Phys. Today 1997. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretized fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003. [Google Scholar]
- Uroić, T.; Jasak, H. Parallelisation of selective algebraic multigrid for block–pressure–velocity system in OpenFOAM. Comput. Phys. Commun. 2021, 258, 107529. [Google Scholar] [CrossRef]
- Uroić, T.; Jasak, H. Block-selective algebraic multigrid for implicitly coupled pressure-velocity system. Comput. Fluids 2018, 167, 100–110. [Google Scholar] [CrossRef]
- OpenCFD. OpenFOAM: User Guide v1906; OpenCFD: Bracknell, UK, 2019. [Google Scholar]
- Jasak, H.; Weller, H.G.; Gosman, A.D. High resolution NVD differencing scheme for arbitrarily unstructured meshes. Int. J. Numer. Methods Fluids 1999, 31, 431–449. [Google Scholar] [CrossRef]
- Petranović, Z. Numerical Modelling of Spray and Combustion Processes Using the Euler Eulerian Multiphase Approach. Ph.D. Thesis, Faculty of Mechanical Engineering and Naval Architecture, University of Zagreb, Zagreb, Croatia, 2016. [Google Scholar]
- Kadocsa, A. Modeling of Spray Formation in Diesel Engines. Ph.D. Thesis, Faculty of Mechanical Engineering, Budapest University of Technology and Economics, Budapest, Hungary, 2007. [Google Scholar]
- Nagaoka, M.; Ueda, R.; Masuda, R.; von Berg, E.; Tatschl, R. Modeling of diesel spray atomization linked with internal nozzle flow. In Proceedings of the 2008 Conference on Thermo- and Dynamic Processes in Diesel Engines, Valencia, Spain, 16–19 September 2008. [Google Scholar]
- Eça, L.; Hoekstra, M. A procedure for the estimation of the numerical uncertainty of CFD calculations based on grid refinement studies. J. Comput. Phys. 2014, 262, 104–130. [Google Scholar] [CrossRef]
- ReFRESCO. A Community Based Open-Usage and Open-Source CFD Code for the Maritime World; ReFRESCO: Rotterdam, The Netherlands, 2018. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).