Numerical Modeling of Transcritical and Supercritical Fuel Injections Using a Multi-Component Two-Phase Flow Model
Abstract
1. Introduction
2. Numerical Methodology
2.1. Governing Equations and Solution Algorithm
2.2. Real-Fluid EOS
2.3. Real-Fluid Chung Transport Model
2.4. Model Implementation Remarks and Property Verifications
3. Results and Discussion
3.1. Validation on Cryogenic Nitrogen Jet Data
3.2. Simulations of Cryogenic L-N2 Injections into G-N2
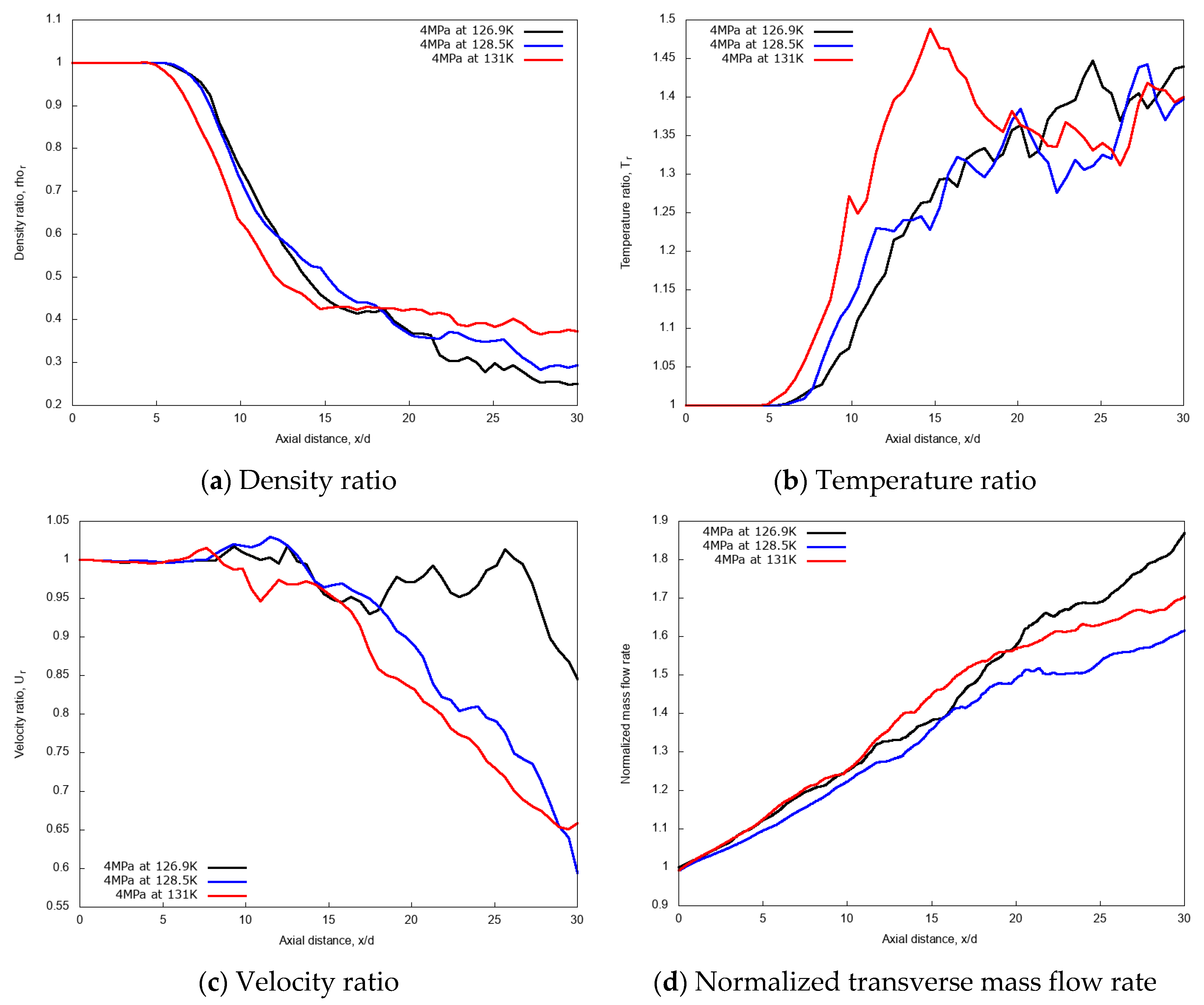
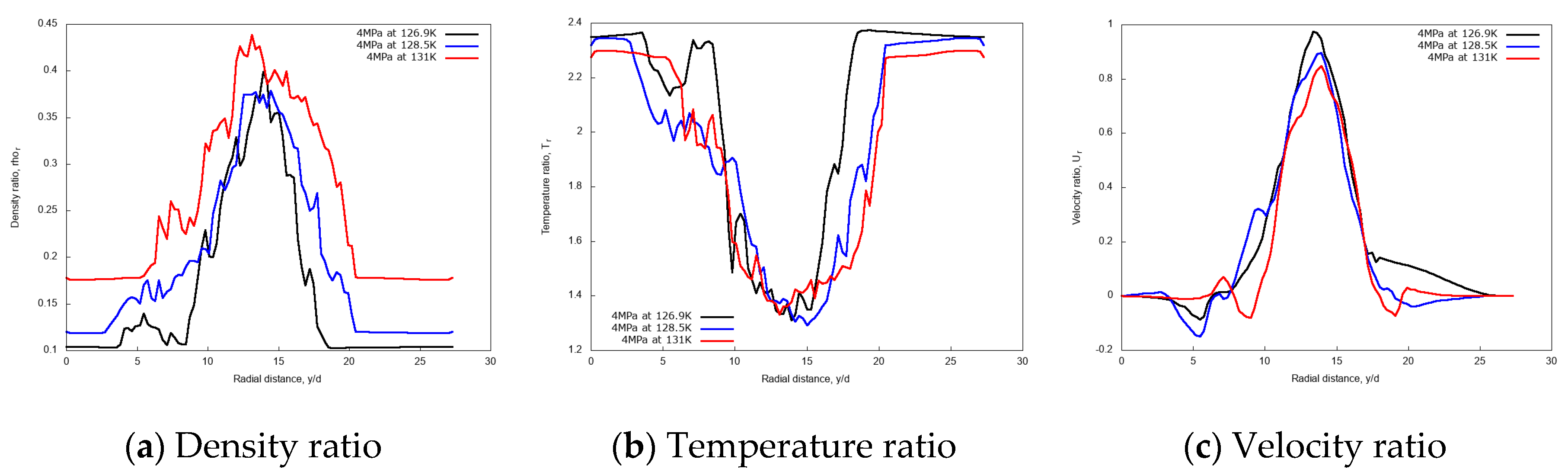
3.2.1. Effect of Injection Temperature
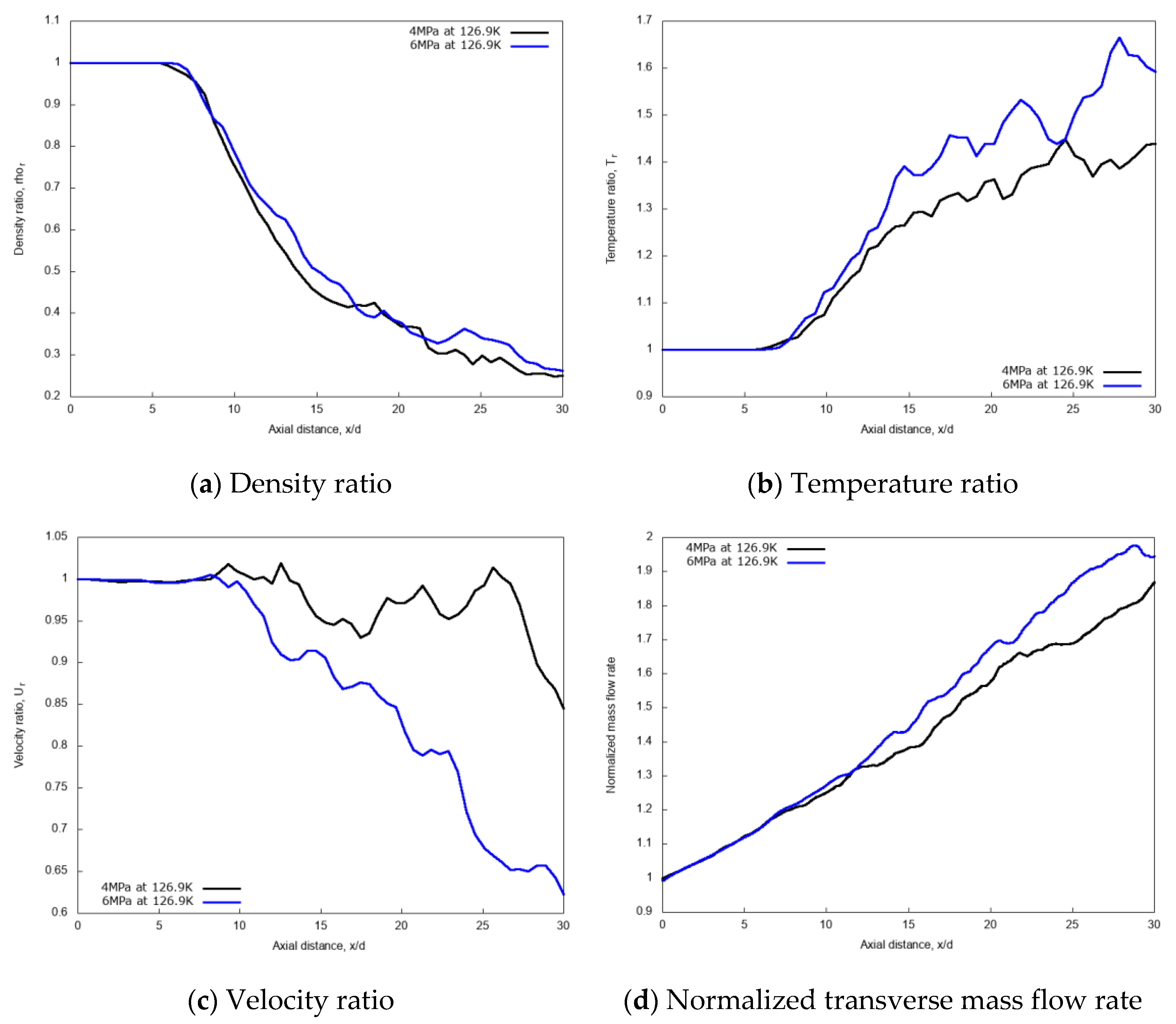
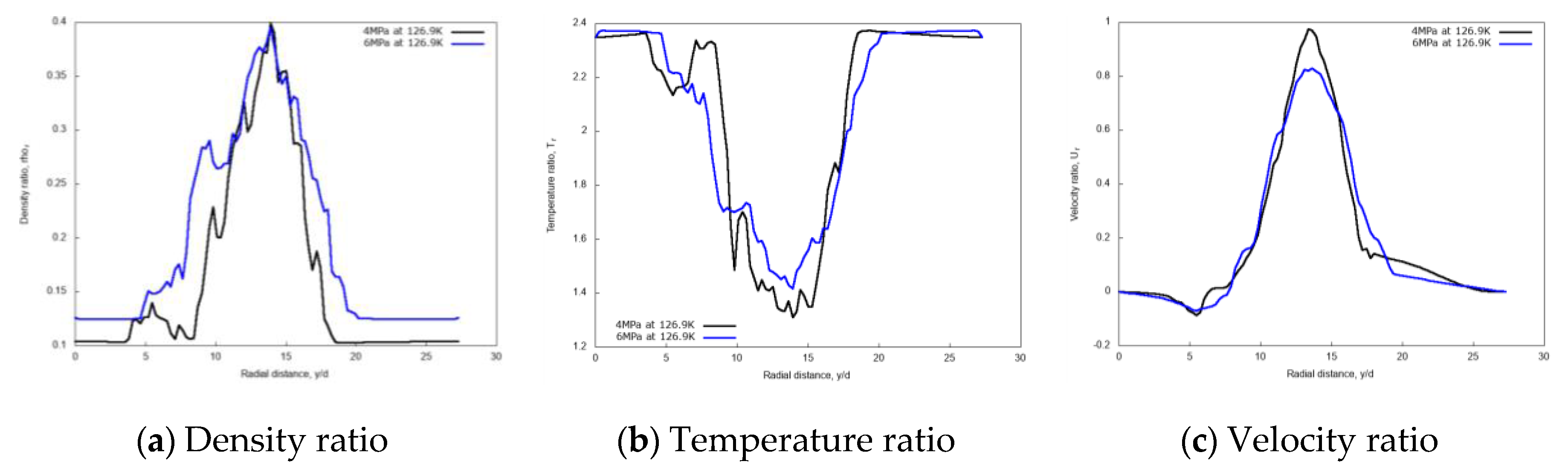
3.2.2. Effects of Chamber Pressure
3.2.3. Discussion
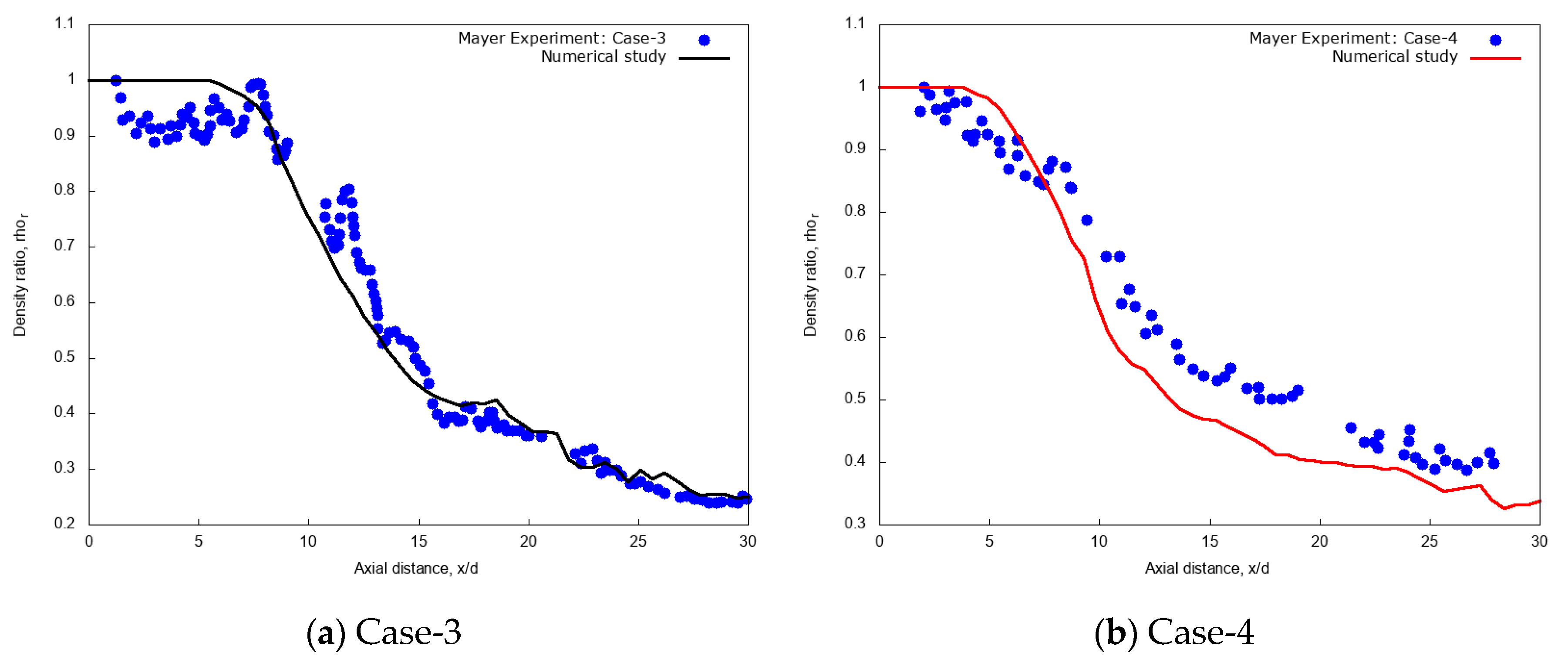
3.3. Simulations of N-Dodecane Injection into Hot Nitrogen Environment
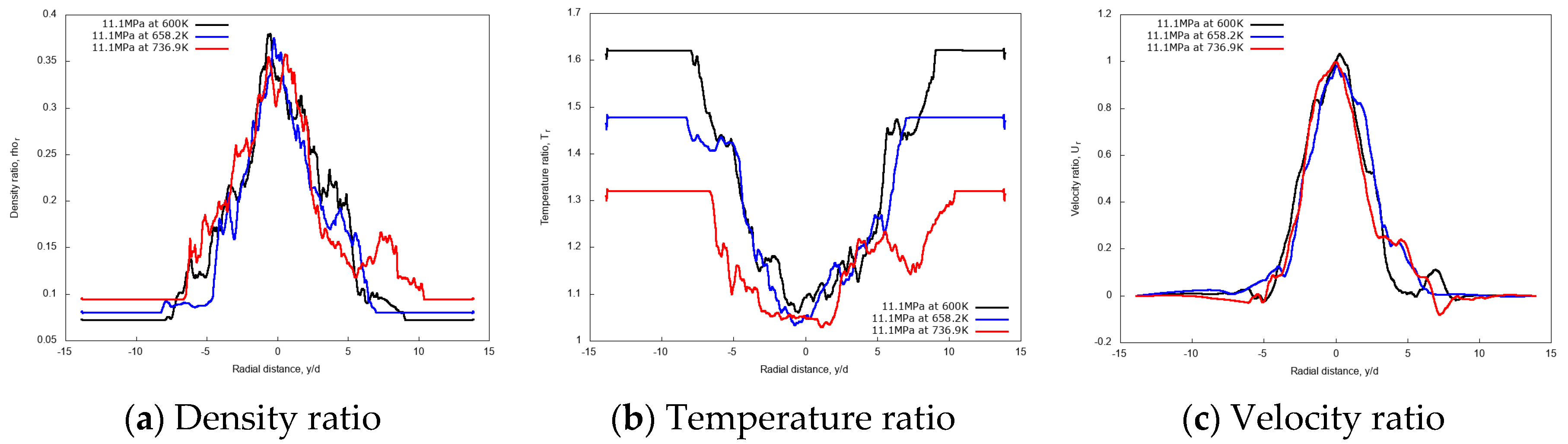
3.3.1. Effect of Injection Temperature
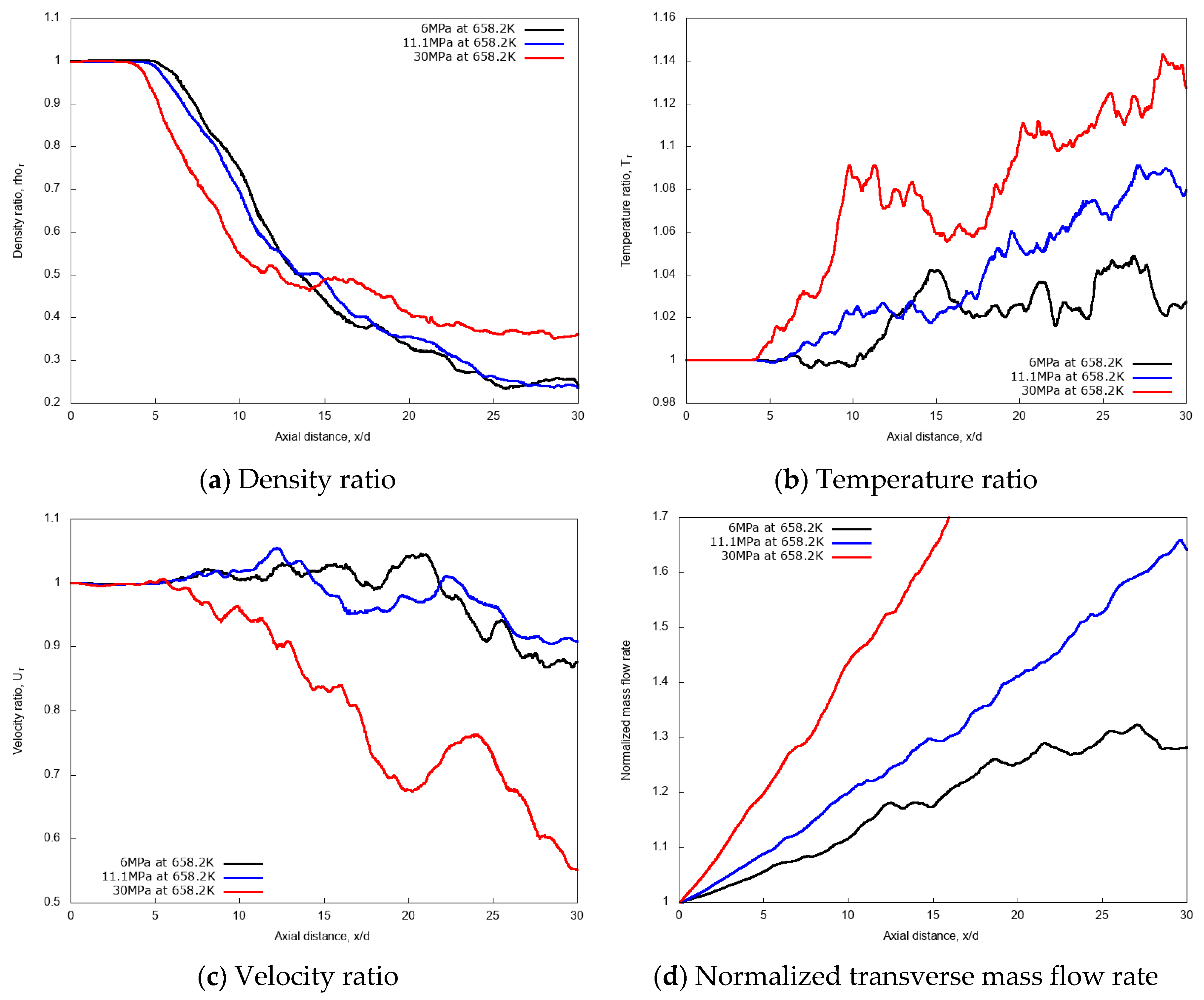
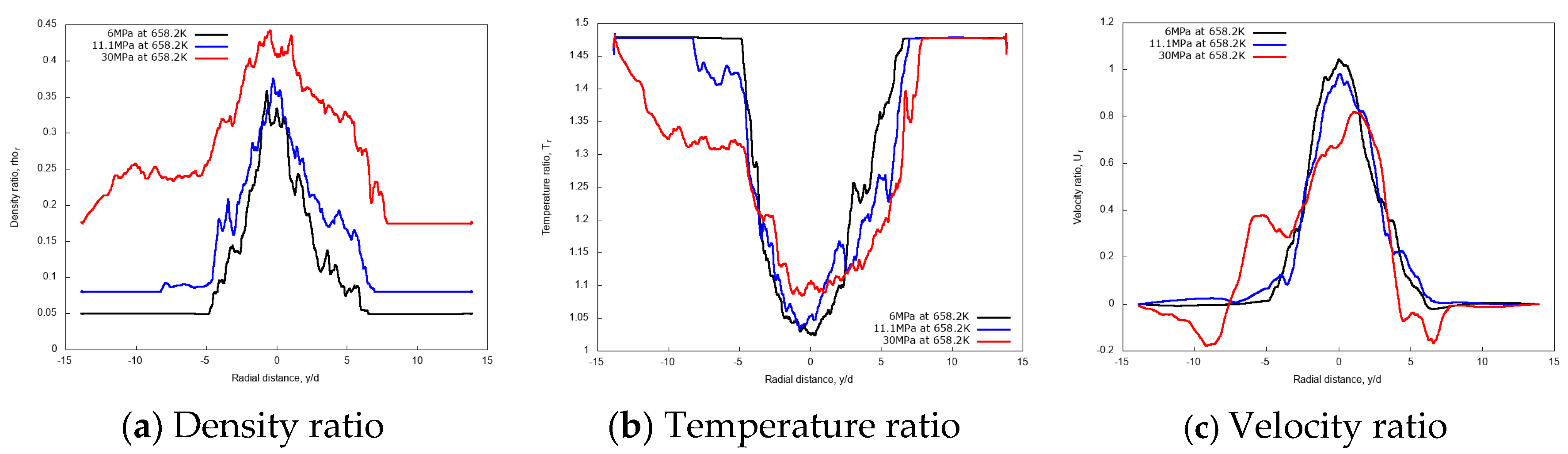
3.3.2. Effect of Chamber Pressure
3.3.3. Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dahms, R.N.; Oefelein, J.C. On the transition between two-phase and single-phase interface dynamics in multicomponent fluids at supercritical pressures. Phys. Fluids 2013, 25, 092103. [Google Scholar] [CrossRef]
- Jung, K.; Kim, Y.; Kim, N. Real-Fluid Modeling for Turbulent Mixing Processes of N-Dodecane Spray Jet Under Superciritical Pressure. Int. J. Automot. Technol. 2020, 21, 397–406. [Google Scholar] [CrossRef]
- Banuti, D.T. Crossing the Widom-line—Supercritical pseudo-boiling. J. Supercrit. Fluids 2015, 98, 12–16. [Google Scholar] [CrossRef]
- Ma, P.C.; Wu, H.; Banuti, D.T.; Ihme, M. Numerical analysis on mixing processes for transcritical real-fluid simulations. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Rodriguez, C.; Rokni, H.B.; Koukouvinis, P.; Gupta, A.; Gavaises, M. Complex multicomponent real-fluid thermodynamic model for high-pressure Diesel fuel injection. Fuel 2019, 257, 115888. [Google Scholar] [CrossRef]
- Taghizadeh, S.; Jarrahbashi, D. Proper orthogonal decomposition analysis of turbulent cryogenic liquid jet injection under transcritical and supercritical conditions. At. Sprays 2018, 28, 875–900. [Google Scholar] [CrossRef]
- Qiu, L.; Reitz, R.D. An investigation of thermodynamic states during high-pressure fuel injection using equilibrium thermodynamics. Int. J. Multiph. Flow 2015, 72, 24–38. [Google Scholar] [CrossRef]
- Branam, R.; Mayer, W. Length scales in cryogenic injection at supercritical pressure. Exp. Fluids 2002, 33, 422–428. [Google Scholar] [CrossRef]
- Chehroudi, B.; Talley, D.; Mayer, W.; Branam, R.; Smith, J.J.; Schik, A.; Oschwald, M.; Schick, A.; Oschwald, M. Understanding Injection into High Pressure Supercritical Environments. In Proceedings of the Fifth International Symposium on Space Propulsion, Chattanooga, TN, USA, 27–30 October 2003; pp. 1–37. [Google Scholar]
- Chehroudi, B.; Talley, D.; Coy, E. Visual characteristics and initial growth rates of round cryogenic jets at subcritical and supercritical pressures. Phys. Fluids 2002, 14, 850–861. [Google Scholar] [CrossRef]
- Ma, P.C.; Lv, Y.; Ihme, M. An entropy-stable hybrid scheme for simulations of transcritical real-fluid flows. J. Comput. Phys. 2017, 340, 330–357. [Google Scholar] [CrossRef]
- Müller, H.; Niedermeier, C.A.; Matheis, J.; Pfitzner, M.; Hickel, S. Large-eddy simulation of nitrogen injection at trans- and supercritical conditions. Phys. Fluids 2016, 28, 015102. [Google Scholar] [CrossRef]
- Rodriguez, C.; Vidal, A.; Koukouvinis, P.; Gavaises, M.; McHugh, M.A. Simulation of transcritical fluid jets using the PC-SAFT EoS. J. Comput. Phys. 2018, 374, 444–468. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Wang, T.; Hou, X. A numerical study on jet characteristics under different supercritical conditions for engine applications. Appl. Energy 2019, 252, 113428. [Google Scholar] [CrossRef]
- Ma, P.C.; Wu, H.; Jaravel, T.; Bravo, L.; Ihme, M. Large-eddy simulations of transcritical injection and auto-ignition using diffuse-interface method and finite-rate chemistry. Proc. Combust. Inst. 2019, 37, 3303–3310. [Google Scholar] [CrossRef]
- Ningegowda, B.M.; Rahantamialisoa, F.; Zembi, J.; Pandal, A.; Im, H.G.; Battistoni, M. Large Eddy Simulations of Supercritical and Transcritical Jet Flows Using Real Fluid Thermophysical Properties; SAE Technical Papers; SAE International: Warrendale, PA, USA, 2020; Volume 2020. [Google Scholar]
- Davis, D.W.; Chehroudi, B. Shear-coaxial jets from a rocket-like injector in a transverse acoustic field at high pressures. In Proceedings of the Collection of Technical Papers—44th AIAA Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 2006; Volume 13, pp. 9173–9190. [Google Scholar]
- Falgout, Z.; Rahm, M.; Sedarsky, D.; Linne, M. Gas/fuel jet interfaces under high pressures and temperatures. Fuel 2016, 168, 14–21. [Google Scholar] [CrossRef]
- Crua, C.; Manin, J.; Pickett, L.M. On the transcritical mixing of fuels at diesel engine conditions. Fuel 2017, 208, 535–548. [Google Scholar] [CrossRef]
- Segal, C.; Polikhov, S.A. Subcritical to supercritical mixing. Phys. Fluids 2008, 20, 052101. [Google Scholar] [CrossRef]
- Keser, R.; Ceschin, A.; Battistoni, M.; Im, H.G.; Jasak, H. Development of a Eulerian Multi-Fluid Solver for Dense Spray Applications in OpenFOAM. Energies 2020, 13, 4740. [Google Scholar] [CrossRef]
- Pandal, A.; García-Oliver, J.M.; Novella, R.; Pastor, J.M. A computational analysis of local flow for reacting Diesel sprays by means of an Eulerian CFD model. Int. J. Multiph. Flow 2018, 99, 257–272. [Google Scholar] [CrossRef]
- Desantes, J.M.; García-Oliver, J.M.; Pastor, J.M.; Olmeda, I.; Pandal, A.; Naud, B. LES Eulerian diffuse-interface modeling of fuel dense sprays near- and far-field. Int. J. Multiph. Flow 2020, 127, 103272. [Google Scholar] [CrossRef]
- Pandal, A.; Rahantamialisoa, F.; Ningegowda, B.M.; Battistoni, M. An Enhanced ς-Y Spray Atomization Model Accounting for Diffusion Due to Drift-Flux Velocities; SAE Technical Papers; SAE International: Warrendale, PA, USA, 2020; Volume 2020. [Google Scholar]
- Xue, Q.; Battistoni, M.; Powell, C.F.; Longman, D.E.; Quan, S.P.; Pomraning, E.; Senecal, P.K.; Schmidt, D.P.; Som, S. An Eulerian CFD model and X-ray radiography for coupled nozzle flow and spray in internal combustion engines. Int. J. Multiph. Flow 2015, 70, 77–88. [Google Scholar] [CrossRef]
- Battistoni, M.; Magnotti, G.M.; Genzale, C.L.; Arienti, M.; Matusik, K.E.; Duke, D.J.; Giraldo, J.; Ilavsky, J.; Kastengren, A.L.; Powell, C.F.; et al. Experimental and Computational Investigation of Subcritical Near-Nozzle Spray Structure and Primary Atomization in the Engine Combustion Network Spray D. SAE Int. J. Fuel Lubr. 2018, 11, 337–352. [Google Scholar] [CrossRef]
- Lebas, R.; Menard, T.; Beau, P.A.; Berlemont, A.; Demoulin, F.X. Numerical simulation of primary break-up and atomization: DNS and modelling study. Int. J. Multiph. Flow 2009, 35, 247–260. [Google Scholar] [CrossRef]
- Ménard, T.; Tanguy, S.; Berlemont, A. Coupling level set/VOF/ghost fluid methods: Validation and application to 3D simulation of the primary break-up of a liquid jet. Int. J. Multiph. Flow 2007, 33, 510–524. [Google Scholar] [CrossRef]
- Ningegowda, B.M.; Premachandran, B. A Coupled Level Set and Volume of Fluid method with multi-directional advection algorithms for two-phase flows with and without phase change. Int. J. Heat Mass Transf. 2014, 79, 532–550. [Google Scholar] [CrossRef]
- Ningegowda, B.M.; Premachandran, B. Numerical investigation of the pool film boiling of water and R134a over a horizontal surface at near-critical conditions. Numer. Heat Transf. Part A Appl. 2017, 71, 44–71. [Google Scholar] [CrossRef]
- Ningegowda, B.M.; Premachandran, B. Free convection film boiling over a discrete flat heater with different surface orientations. Numer. Heat Transf. Part A Appl. 2019, 76, 712–723. [Google Scholar] [CrossRef]
- Ningegowda, B.M.; Premachandran, B. Saturated film boiling of water over a finite size heater. Int. J. Therm. Sci. 2019, 135, 417–433. [Google Scholar] [CrossRef]
- Ningegowda, B.M.; Ge, Z.; Lupo, G.; Brandt, L.; Duwig, C. A mass-preserving interface-correction level set/ghost fluid method for modeling of three-dimensional boiling flows. Int. J. Heat Mass Transf. 2020, 162, 120382. [Google Scholar] [CrossRef]
- Jofre, L.; Urzay, J. Transcritical diffuse-interface hydrodynamics of propellants in high-pressure combustors of chemical propulsion systems. Prog. Energy Combust. Sci. 2021, 82, 100877. [Google Scholar] [CrossRef]
- Bellan, J. Direct numerical simulation of a high-pressure turbulent reacting temporal mixing layer. Combust. Flame 2017, 176, 245–262. [Google Scholar] [CrossRef]
- Yi, P.; Yang, S.; Habchi, C.; Lugo, R. A multicomponent real-fluid fully compressible four-equation model for two-phase flow with phase change. Phys. Fluids 2019, 31, 026102. [Google Scholar] [CrossRef]
- Yang, S.; Yi, P.; Habchi, C. Real-fluid injection modeling and LES simulation of the ECN Spray A injector using a fully compressible two-phase flow approach. Int. J. Multiph. Flow 2020, 122, 103145. [Google Scholar] [CrossRef]
- Yang, S.; Habchi, C. Real-fluid phase transition in cavitation modeling considering dissolved non-condensable gas. Phys. Fluids 2020, 32, 032102. [Google Scholar] [CrossRef]
- Zong, N.; Yang, V. Cryogenic fluid jets and mixing layers in transcritical and supercritical environments. Combust. Sci. Technol. 2006, 178, 193–227. [Google Scholar] [CrossRef]
- Gopal, J.M.; Tretola, G.; Morgan, R.; de Sercey, G.; Atkins, A.; Vogiatzaki, K. Understanding Sub and Supercritical Cryogenic Fluid Dynamics in Conditions Relevant to Novel Ultra Low Emission Engines. Energies 2020, 13, 3038. [Google Scholar] [CrossRef]
- Irannejad, A.; Banaeizadeh, A.; Jaberi, F. Large eddy simulation of turbulent spray combustion. Combust. Flame 2015, 162, 431–450. [Google Scholar] [CrossRef]
- Ghosh, S.; Hunt, J.C.R. Induced air velocity within droplet driven sprays. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1994, 444, 105–127. [Google Scholar] [CrossRef]
- Siebers, D.L. Liquid-Phase Fuel Penetration in Diesel Sprays. SAE Trans. 1998, 107, 1205–1227. [Google Scholar]
- Pickett, L.M.; Siebers, D.L. Orifice diameter effects on diesel fuel jet flame structure. J. Eng. Gas Turbines Power 2005, 127, 187–196. [Google Scholar] [CrossRef]
- Sepret, V.; Bazile, R.; Marchal, M.; Couteau, G. Effect of ambient density and orifice diameter on gas entrainment by a single-hole diesel spray. Exp. Fluids 2010, 49, 1293–1305. [Google Scholar] [CrossRef]
- Matheis, J.; Hickel, S. Multi-component vapor-liquid equilibrium model for LES of high-pressure fuel injection and application to ECN Spray A. Int. J. Multiph. Flow 2018, 99, 294–311. [Google Scholar] [CrossRef]
- Chungó Mohammad Ajlan, T.-H.; Lee, L.L.; Starling, K.E. Generalized Multiparameter Correlation for Nonpolar and Polar Fluid Transport Properties. Ind. Eng. Chem. Res. 1988, 27, 671–679. [Google Scholar]
- Jarczyk, M.; Pfitzner, M. Large eddy simulation of supercritical nitrogen jets. In Proceedings of the 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. [Google Scholar]
- Poling, B.E.; Prausnitz, J.M.; O’connell, J.P.; York, N.; San, C.; Lisbon, F.; Madrid, L.; City, M.; Delhi, M.N.; Juan, S. The Properties of Gases and Liquids, 5th ed.; McGraw Hill: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Petit, X.; Ribert, G.; Lartigue, G.; Domingo, P. Large-eddy simulation of supercritical fluid injection. J. Supercrit. Fluids 2013, 84, 61–73. [Google Scholar] [CrossRef]
- Banuti, D.T.; Ma, P.C.; Hickey, J.P.; Ihme, M. Thermodynamic structure of supercritical LOX-GH2 diffusion flames. Combust. Flame 2018, 196, 364–376. [Google Scholar] [CrossRef]
- NASA. Polynomials. Available online: http://combustion.berkeley.edu/gri-mech/data/nasa_plnm.html (accessed on 19 October 2020).
- Kim, T.; Kim, Y.; Kim, S.K. Numerical study of cryogenic liquid nitrogen jets at supercritical pressures. J. Supercrit. Fluids 2011, 56, 152–163. [Google Scholar] [CrossRef]
- Thermophysical Properties of Fluid Systems. Available online: https://webbook.nist.gov/chemistry/fluid/ (accessed on 18 October 2020).
- Mayer, W.; Telaar, J.; Branam, R.; Schneider, G.; Hussong, J. Raman measurements of cryogenic injection at supercritical pressure. Heat Mass Transf. und Stoffuebertragung 2003, 39, 709–719. [Google Scholar] [CrossRef]
- Engine Combustion Network|Engine Combustion Network Website. Available online: https://ecn.sandia.gov/ (accessed on 14 September 2020).
- Rodriguez, C.; Koukouvinis, P.; Gavaises, M. Simulation of supercritical diesel jets using the PC-SAFT EoS. J. Supercrit. Fluids 2019, 145, 48–65. [Google Scholar] [CrossRef]
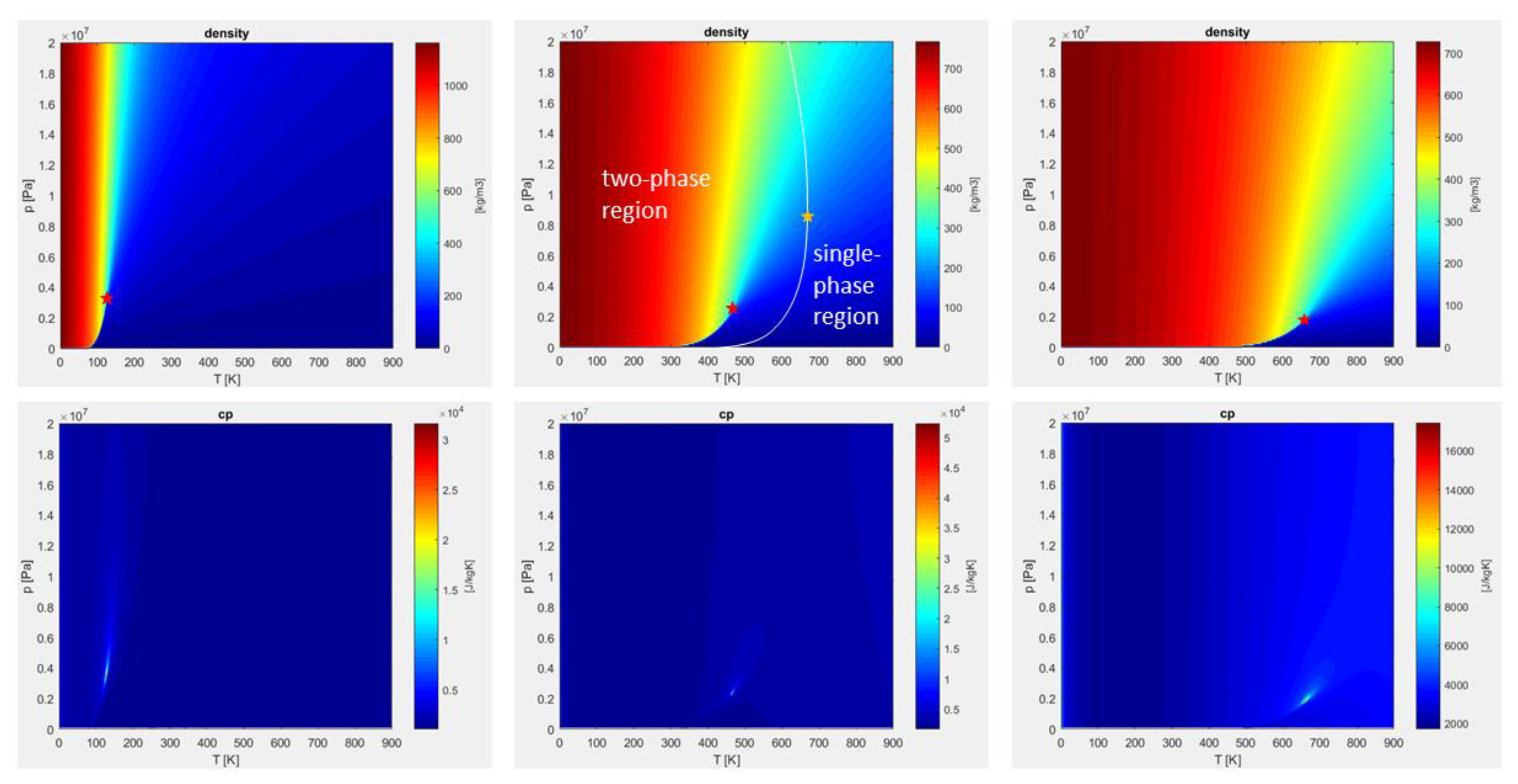
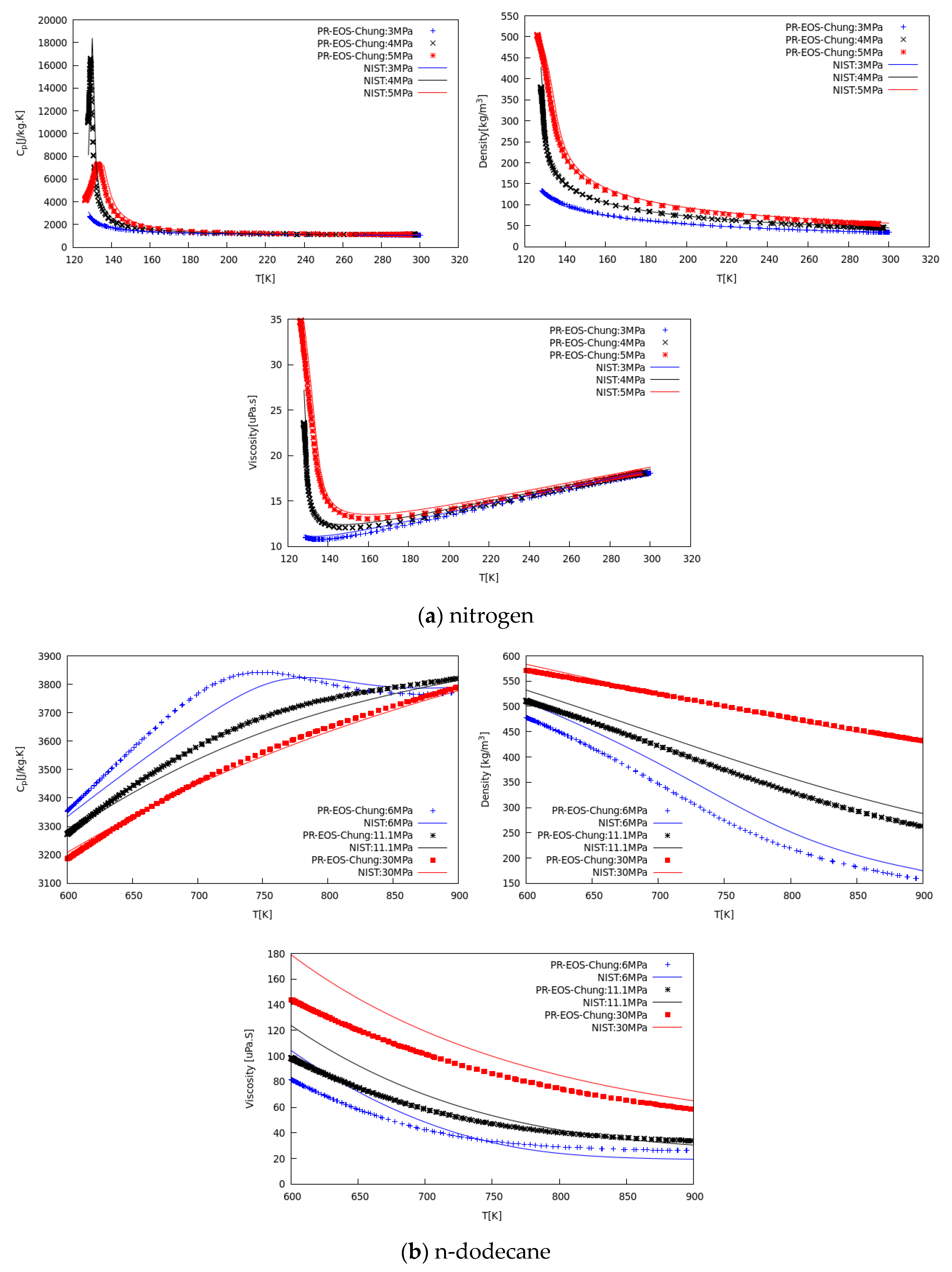





| Species | Tc [K] | pc [MPa] | vc [cm3/mol] | Acentric Factor, ω |
|---|---|---|---|---|
| N2 | 126.192 | 3.3958 | 89.41 | 0.0377 |
| C12H26 | 658.2 | 1.82 | 22.064 | 0.5764 |
| Input Parameters | Values |
|---|---|
| Injected Fluid | cryogenic nitrogen, N2 |
| Ambient chamber gas | nitrogen, N2 |
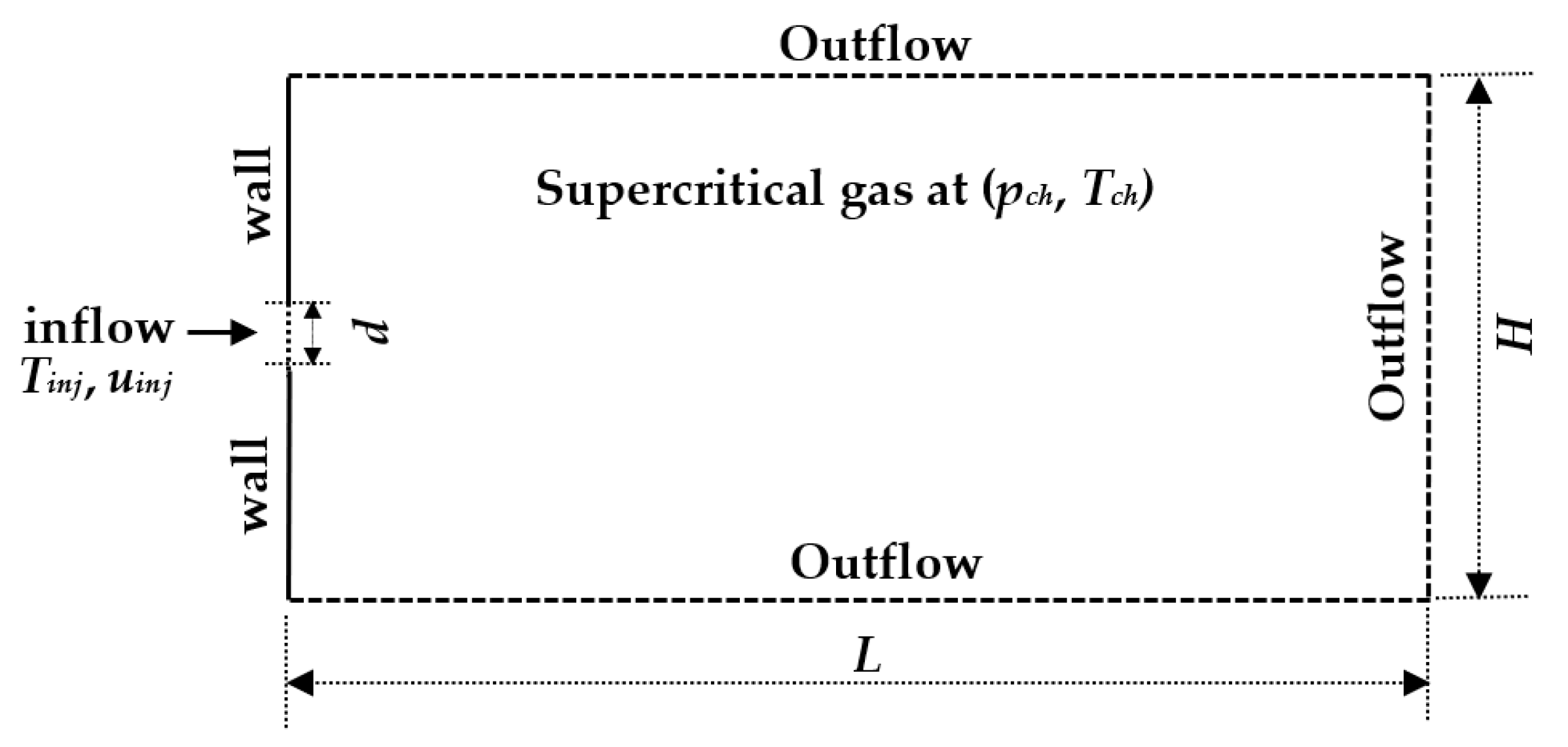
| Computational domain, L × H | 54 d × 27 d (~120 mm × 60 mm) |
| Total cell count (uniform grid) | 5.12 × 106 cells |
| Computational cells per jet diameter | 64 |
| Injection nozzle diameter, d | 2.2 mm |
| Inlet velocity (uniform profile), uinj | 4.9 m/s and 5.4 m/s |
| Chamber temperature, Tch | 298 K |
| Chamber pressure, pch | 4 MPa and 6 MPa |
| Injection temperature, Tinj | 126.9 K,128.5 K and 131 K |
| Input Parameters | Values |
|---|---|
| Injected Fluid | n-dodecane, C12H26 |
| Ambient chamber gas | nitrogen, N2 |
| Computational domain, L × H | 55 d × 28 d (~5 mm × 2.5 mm) |
| Total cell count (uniform grid) | 5.12 × 106 |
| Computational cells per jet diameter | 64 |
| Injection nozzle diameter, d | 90 μm (ECN Spray-A) |
| Inlet velocity, uinj | 200 m/s (uniform profile) |
| Chamber temperature, Tch | 972.9 K |
| Chamber pressure, pch | 6 MPa, 11.1 MPa and 30 MPa |
| Injection temperature, Tinj | 600 K, 658.2 K and 736.9 K |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ningegowda, B.M.; Rahantamialisoa, F.N.Z.; Pandal, A.; Jasak, H.; Im, H.G.; Battistoni, M. Numerical Modeling of Transcritical and Supercritical Fuel Injections Using a Multi-Component Two-Phase Flow Model. Energies 2020, 13, 5676. https://doi.org/10.3390/en13215676
Ningegowda BM, Rahantamialisoa FNZ, Pandal A, Jasak H, Im HG, Battistoni M. Numerical Modeling of Transcritical and Supercritical Fuel Injections Using a Multi-Component Two-Phase Flow Model. Energies. 2020; 13(21):5676. https://doi.org/10.3390/en13215676
Chicago/Turabian StyleNingegowda, Bittagowdanahalli Manjegowda, Faniry Nadia Zazaravaka Rahantamialisoa, Adrian Pandal, Hrvoje Jasak, Hong Geun Im, and Michele Battistoni. 2020. "Numerical Modeling of Transcritical and Supercritical Fuel Injections Using a Multi-Component Two-Phase Flow Model" Energies 13, no. 21: 5676. https://doi.org/10.3390/en13215676
APA StyleNingegowda, B. M., Rahantamialisoa, F. N. Z., Pandal, A., Jasak, H., Im, H. G., & Battistoni, M. (2020). Numerical Modeling of Transcritical and Supercritical Fuel Injections Using a Multi-Component Two-Phase Flow Model. Energies, 13(21), 5676. https://doi.org/10.3390/en13215676








