Multi-Rate Real-Time Simulation Method Based on the Norton Equivalent
Abstract
1. Introduction
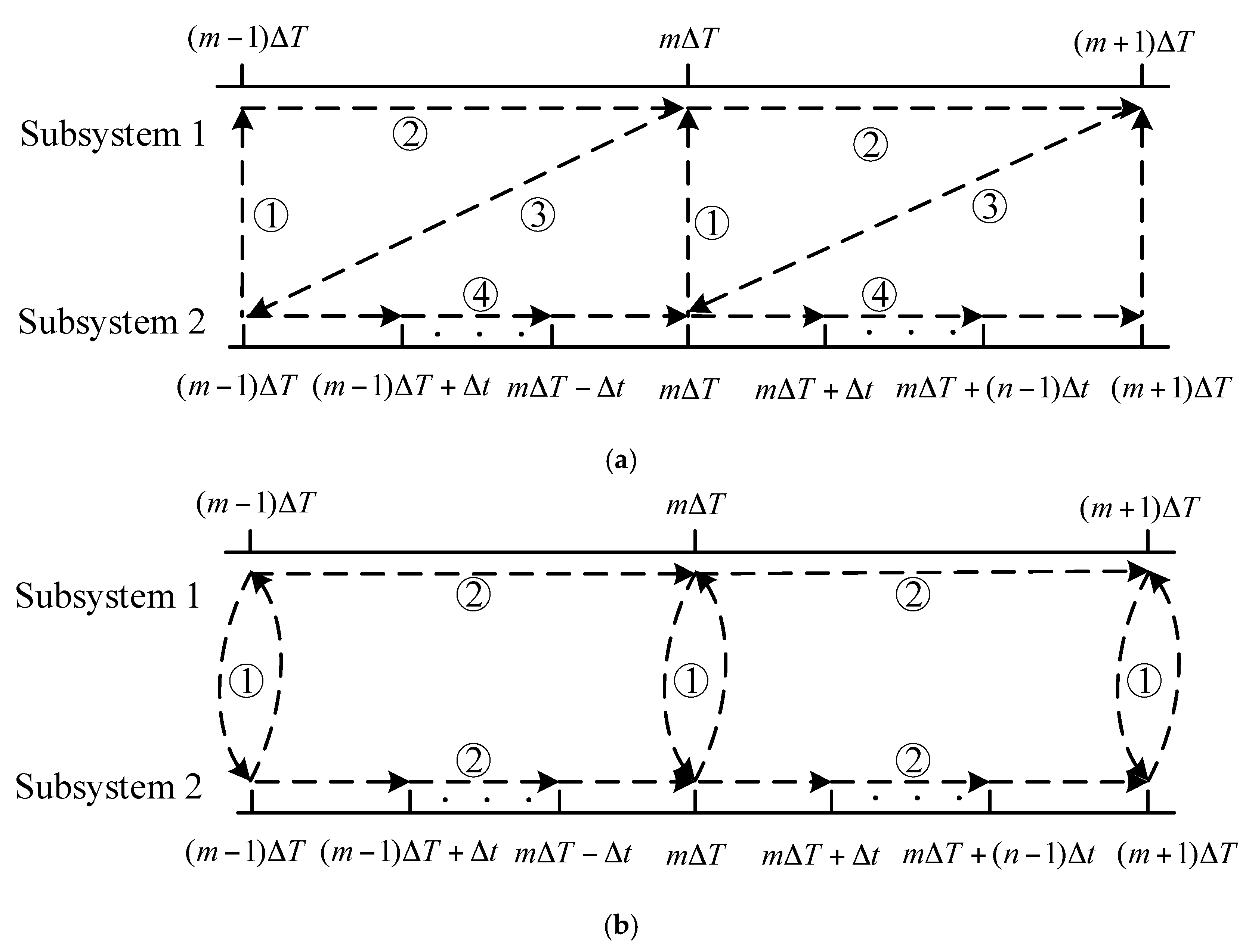
2. Multi-Rate Simulation Calculation Timing
3. Multi-Rate Real-Time Simulation Based on the Norton Equivalence
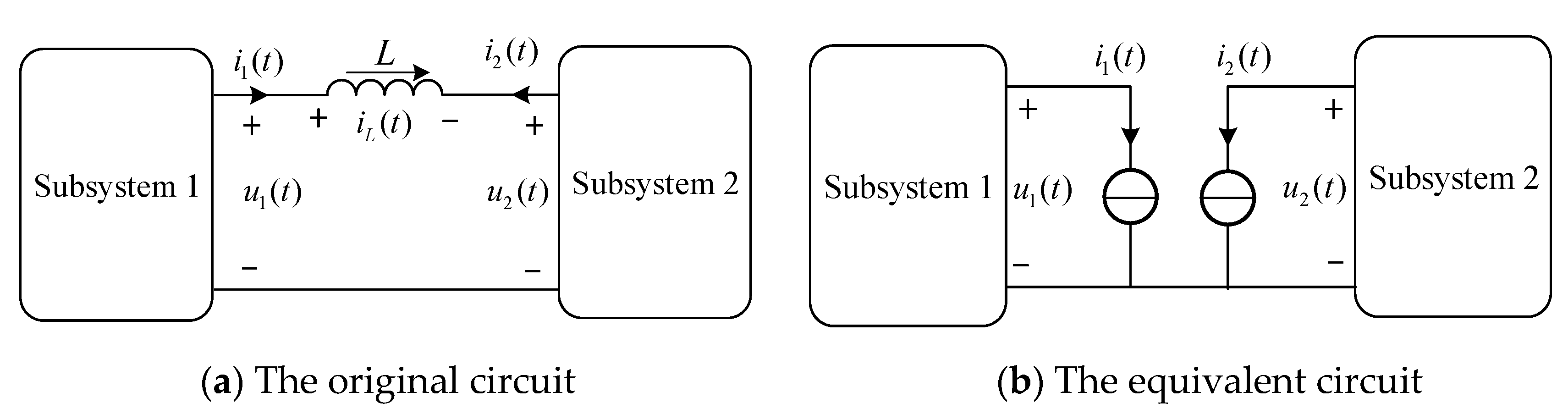
3.1. Multi-Rate Real-Time Simulation Method Based on the Ideal Source Equivalence
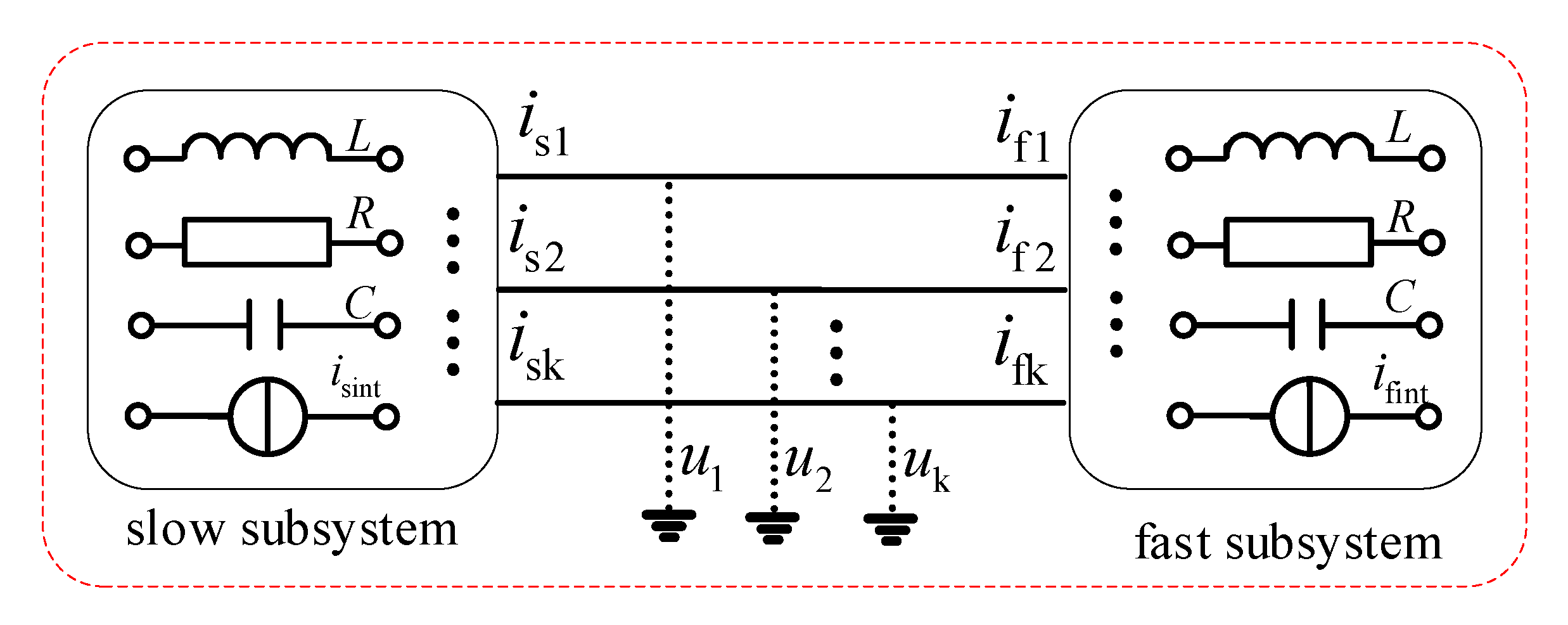
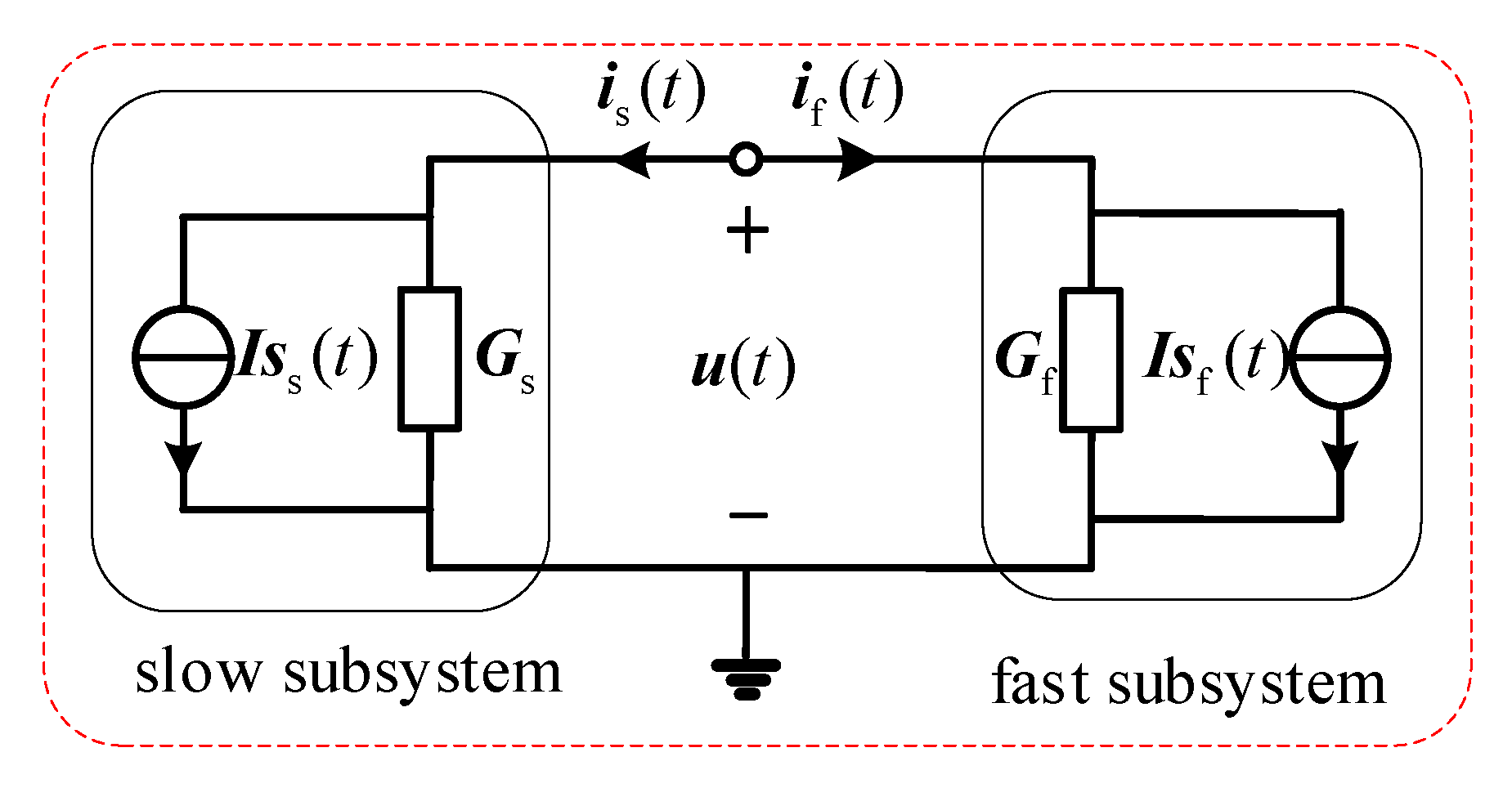
3.2. Multi-Rate Real-Time Simulation Method Based on the Norton Equivalence
- (1)
- Calculate the Norton equivalent circuit of the slow subsystem and the fast subsystem at the kth (k = 0, 1, 2, …, n − 1) period:
- (2)
- According to , , and , write the voltage equation of the interface nodes:
- (3)
- Solve the voltage equation of the interface nodes to get the voltage of the interface nodes
- (4)
- According to , the state variable xf(t + kΔt) of the fast subsystem can be obtained, and the state variable xs(t) of the slow subsystem can also be obtained.
3.3. The Data Interaction of Multi-Rate Real-Time Simulation
4. Case Study
4.1. Introduction to Real-Time Simulation Platform FRTDS
4.2. Introduction to the Simulation System
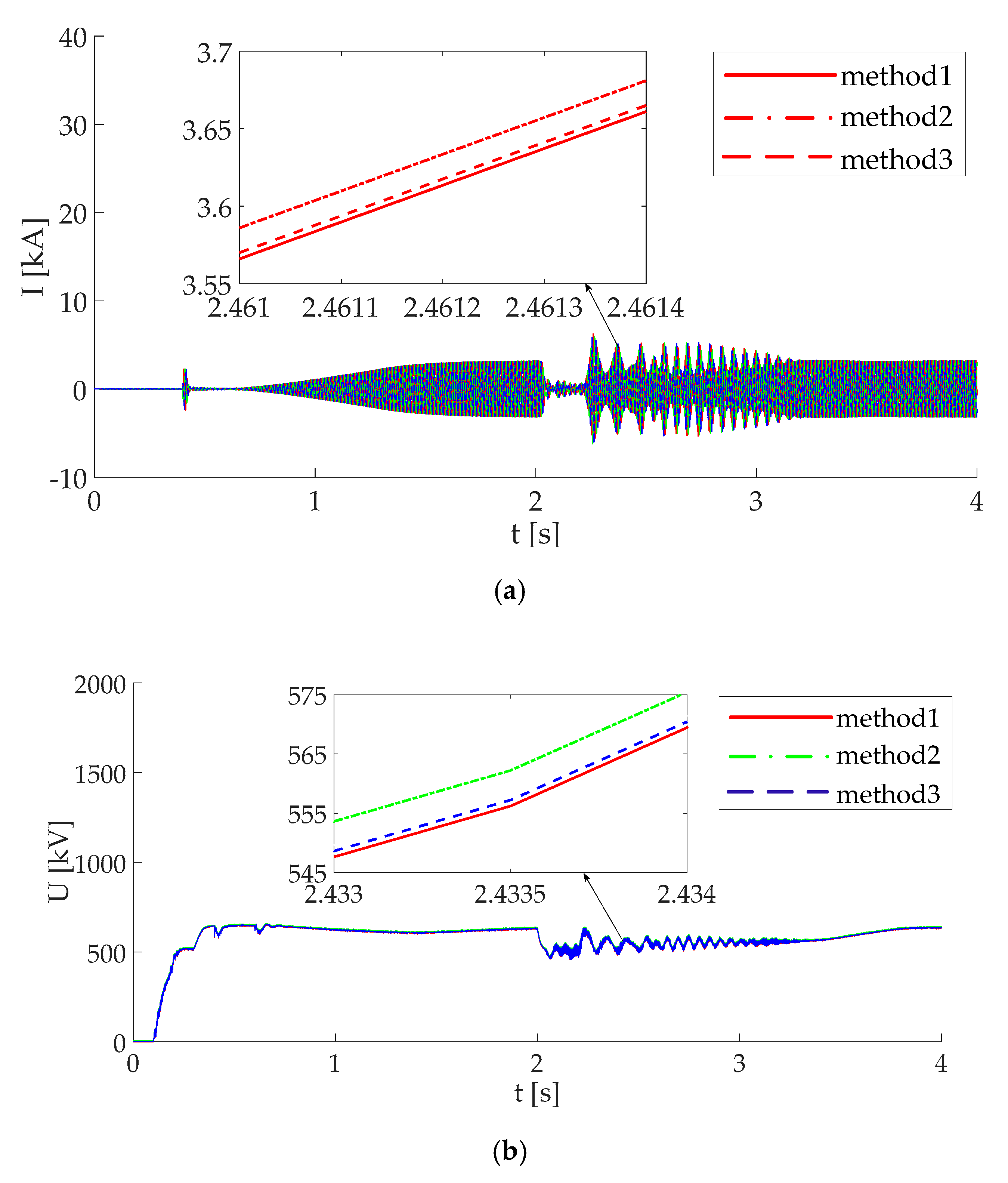
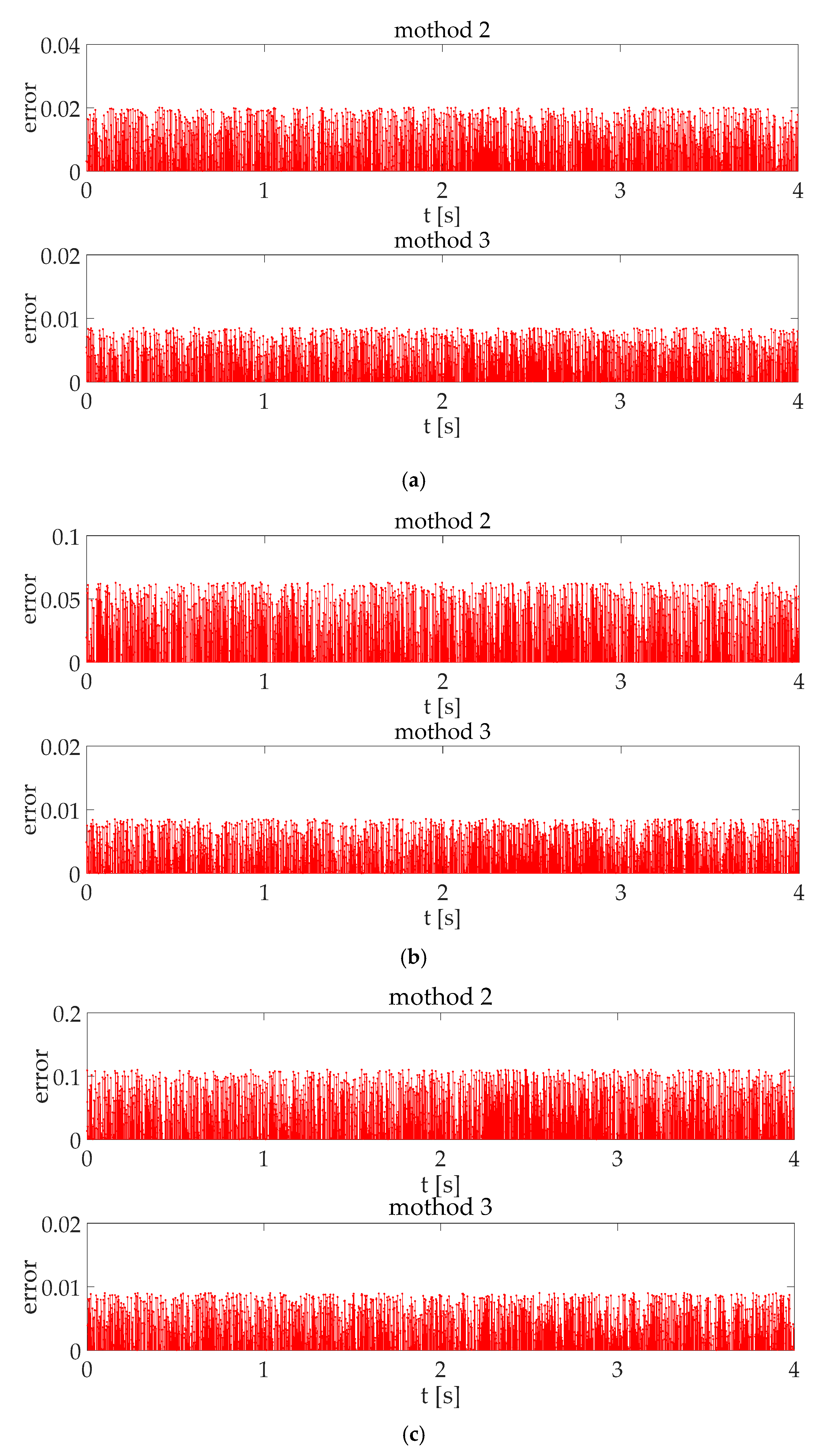
4.3. Simulation Result
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, H.B.; Bian, D.; Sun, L.; Yun, Z.J.; Li, Y. Research on Electromechanical-Electromagnetic Transient Hybrid Simulation of AC/DC Hybrid System. Power Syst. Prot. Control 2019, 47, 39–47. [Google Scholar]
- Li, Y.L.; Zhang, X.; Li, Y.J.; Chen, Z.J.; Wu, M.Q. Current Situation and Challenges of Simulation Technology for AC/DC Hybrid Power Grid. Electric Power Constr. 2015, 36, 1–8. [Google Scholar]
- He, Y.Y.; Zheng, X.D.; Tai, N.L.; Hou, J.X.; Xu, J.; Huang, W.T. Overview of Modeling Methods of LCC-HVDC Converter in AC-DC Hybrid Power Grid. Proc. CSEE 2019, 39, 3119–3128. [Google Scholar]
- Dong, X.Z.; Tang, Y.; Bu, G.Q. Confronting Problem and Challenge of Large Scale AC-DC Hybrid Power Grid Operation. Proc. CSEE 2019, 39, 3107–3119. [Google Scholar]
- Zhang, M.X. Research on Real Time Multi Rate Joint Simulation Technology for Power Electronic System. Master’s Thesis, Beijing Institute of Technology, Beijing, China, 2016. [Google Scholar]
- Jost, A.; Niklaus, F.; Min, L. High Fidelity Real-Time Simulation of Multi-Level Converters. In Proceedings of the 2018 International Power Electronics Conference, Niigata, Japan, 20–24 May 2018; pp. 2199–2203. [Google Scholar]
- Zhao, J.L.; Liu, J.T.; Li, P. GPU Based Parallel Matrix Exponential Algorithm for Large Scale Power System Electromagnetic Transient Simulation. In Proceedings of the 2016 IEEE Innovative Smart Grid Technologies-Asia, Melbourne, Australia, 28 November–1 December 2016; pp. 110–114. [Google Scholar]
- Lu, F.S.; Song, J.Q.; Yin, F.K.; Zhang, L.L. Overview of CPU/GPU collaborative parallel computing research. Comput. Sci. 2011, 38, 5–9. [Google Scholar]
- Han, J.; Dong, Y.F.; Miao, S.H.; Liu, Y.L.; Liu, Z.W. MATE-based multi-rate electromagnetic transient parallel simulation method for power system sub-network. High Volt. Eng. 2019, 45, 1857–1865. [Google Scholar]
- Crow, M.L.; Chen, J.G. The method for simulation of power system dynamics. IEEE Trans. Power Syst. 1994, 9, 1684–1890. [Google Scholar] [CrossRef]
- Chen, J.G.; Crow, M.L. A variable partitioning strategy for the multi-rate method in power system. IEEE Trans. Power Syst. 2008, 23, 259–266. [Google Scholar] [CrossRef]
- Tang, Y. New Development of Research on Simulation and Modeling of Multi-time Scale Whole Process of AC/DC Power System. Power Syst. Technol. 2009, 33, 1–8. [Google Scholar]
- Moreira, F.A.; Marti, J.R. Latency techniques for time-domain power system transients simulation. IEEE Trans. Power Syst. 2005, 20, 246–253. [Google Scholar] [CrossRef]
- Mu, Q.; Liang, J.; Zhou, X.X.; Li, G.; Zhang, X. A Node Splitting Interface Algorithm for Multi-rate Parallel Simulation of DC Grids. CSEE J. Power Energy Syst. 2018, 4, 388–397. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, B.D.; Chen, M. Multi-rate time Simulation Method Based on RTDS and FPGA Co-simulation Platform. Autom. Electr. Power Syst. 2016, 40, 144–150. [Google Scholar]
- Zhai, X.B.; Lin, C.; Gregoire, L.A. Multi-rate Real-time Simulation of Modular Multilevel Converter for HVDC Grids Application. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 1325–1330. [Google Scholar]
- Ou, K.J.; Li, P.F.; Guan, L.; Chai, Z.X.; Zhang, Y.J. Design and Research of Multi-time Scale Hybrid Real-Time Simulation System for AC and DC Power Grid. South. Power Syst. Technol. 2017, 11, 53–58, 64. [Google Scholar]
- Zhang, F.; Huang, W.C.; Li, C.D. MMC generalized fast simulation model suitable for multiple sub-module topologies. Electr. Power Autom. Equip. 2019, 39, 129–136, 143. [Google Scholar]
- Jost, A.; Niklaus, F. Sub-Cycle Average Models with Integrated Diodes for Real-Time Simulation of Power Converters. In Proceedings of the 2017 IEEE Southern Power Electronics Conference, Puerto Varas, Chile, 4–7 December 2017; pp. 6–11. [Google Scholar]
- Zhang, B.D.; Fu, S.W.; Jin, Z.; Hu, R.Z. A Novel FPGA Based Real-Time Simulator for Micro-Grids. Energies 2017, 8, 1239–1255. [Google Scholar] [CrossRef]
- Zhang, B.D.; Hu, R.Z.; Tu, S.J.; Zhang, J.; Jin, X.L.; Guan, Y.; Zhu, J.J. Modeling of Power System Simulation Based on FRTDS. Energies 2018, 11, 2749–2766. [Google Scholar] [CrossRef]
- Zhang, B.D.; Wang, Y.; Tu, S.J.; Jin, Z. FPGA-Based Real-Time Digital Solver for Electro-Mechanical Transient Simulation. Energies 2018, 11, 2650–2669. [Google Scholar] [CrossRef]
- Zhang, B.D.; Jin, X.L.; Tu, S.J.; Jin, Z.; Zhang, J. A new FPGA-based real-time digital solver for power system simulation. Energies 2019, 12, 4666. [Google Scholar] [CrossRef]

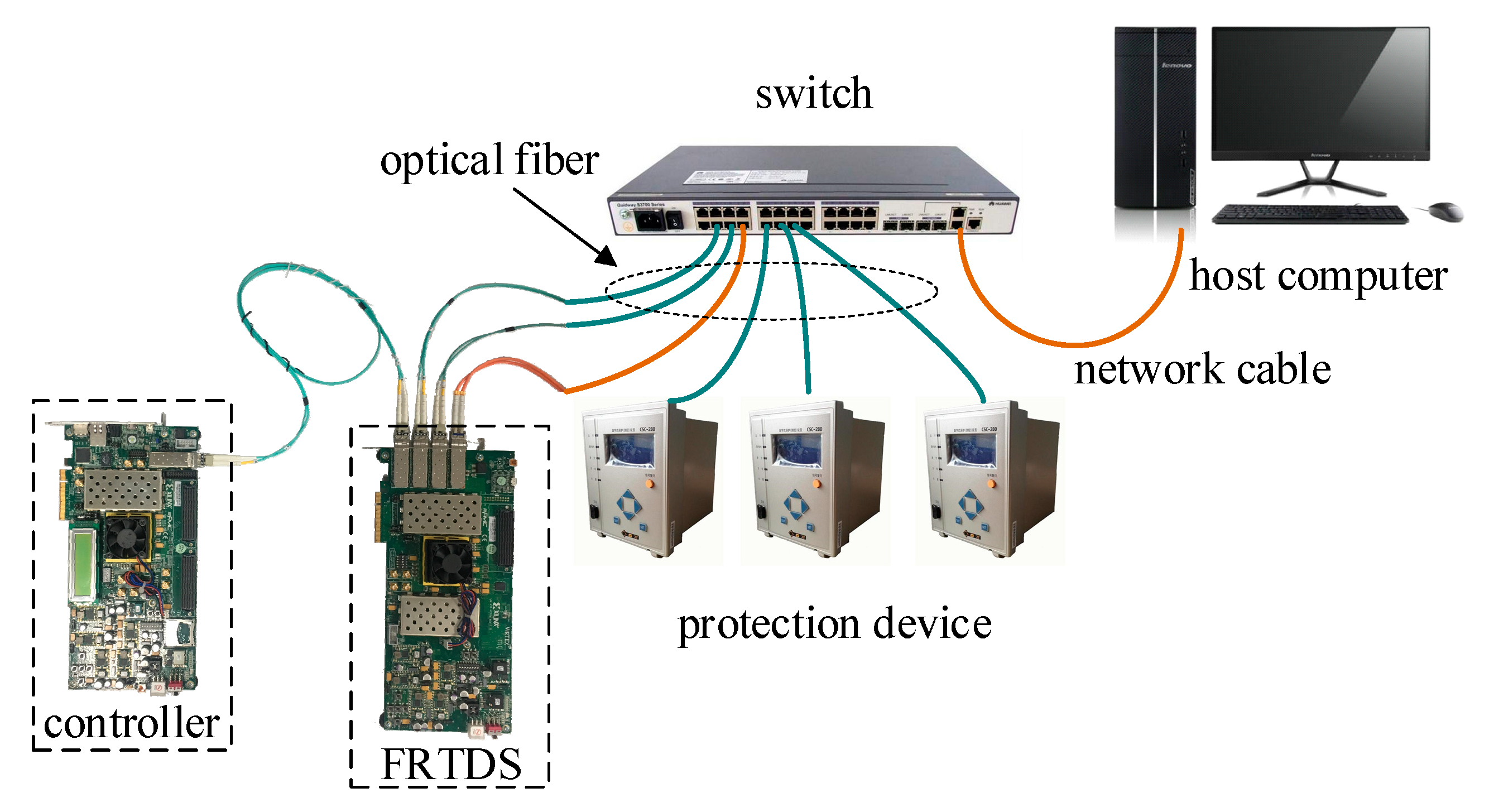


| Parameter | Parameter |
|---|---|
| The rated capacity of converter/MVA | 500 |
| The rated voltage of AC grid/kV | 230 |
| The rated capacity of converter transformer/MVA | 700 |
| The frequency of AC grid/Hz | 50 |
| The inductance of bridge legs/mH | 50 |
| The number of MMC sub-modules | 76 |
| The capacitance of MMC sub-modules/mF | 3 |
| The rated voltage of DC grid/kV | ±320 |
| The capacitance of DC line/μF | 1 |
| The Parameters of Line | ||||||||
| Line | Length (km) | |||||||
| L1 | 0.0502 | 1.0335 | 0.000227 | 10 | ||||
| L2 | 0.0502 | 1.0335 | 0.000227 | 10 | ||||
| L3 | 0.0502 | 1.0335 | 0.000227 | 30 | ||||
| L4 | 0.0502 | 1.0335 | 0.000227 | 20 | ||||
| L5 | 0.0502 | 1.0335 | 0.000227 | 15 | ||||
| L6 | 0.0502 | 1.0335 | 0.000227 | 20 | ||||
| The Parameters of Transformer | ||||||||
| transformer | ||||||||
| parameter | 720 | 14 | 0.1 | 1279.1 | 278.4 | |||
| The Parameters of Synchronous Generator | ||||||||
| generator | ||||||||
| parameter | 350 MVA | 2.27 p.u. | 0.3 p.u. | 0.22 p.u. | 2.21 p.u. | 0.45 p.u. | 0.22 p.u. | |
| generator | ||||||||
| parameter | 4.3 s | 0.05 s | 0.85 s | 0.07 s | 0.134 p.u. | 0.002 p.u. | ||
| The Number of Maximum Instruction Clocks | The Number of Task Instruction Clocks | |
|---|---|---|
| method 1 | 2000 | 2810 |
| method 2 | 10,000 | 9080 |
| method 3 | 10,000 | 9530 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Zhang, B. Multi-Rate Real-Time Simulation Method Based on the Norton Equivalent. Energies 2020, 13, 4562. https://doi.org/10.3390/en13174562
Zhu J, Zhang B. Multi-Rate Real-Time Simulation Method Based on the Norton Equivalent. Energies. 2020; 13(17):4562. https://doi.org/10.3390/en13174562
Chicago/Turabian StyleZhu, Junjie, and Bingda Zhang. 2020. "Multi-Rate Real-Time Simulation Method Based on the Norton Equivalent" Energies 13, no. 17: 4562. https://doi.org/10.3390/en13174562
APA StyleZhu, J., & Zhang, B. (2020). Multi-Rate Real-Time Simulation Method Based on the Norton Equivalent. Energies, 13(17), 4562. https://doi.org/10.3390/en13174562




