The Spectrum of Proactive, Resilient Multi-Microgrid Scheduling: A Systematic Literature Review
Abstract
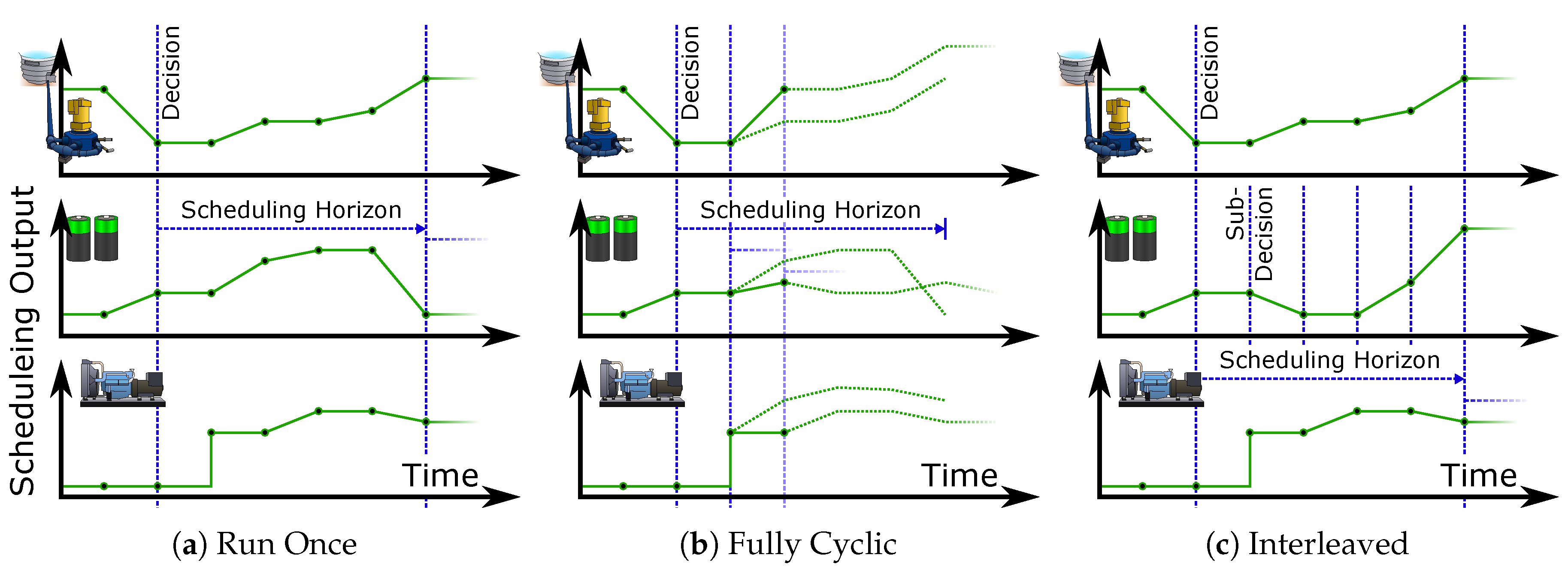
:1. Introduction
2. Work Related to a Resilient and Economic Multi-Microgrid Operation
2.1. Failure Modes and Resilience Metrics
2.2. Resilience-Aware Microgrid Scheduling
2.3. Multi-Microgrid Forming
2.4. Resilience-Aware Multi-Microgrid Scheduling
2.5. Related Reviews
2.6. Contributions of This Paper
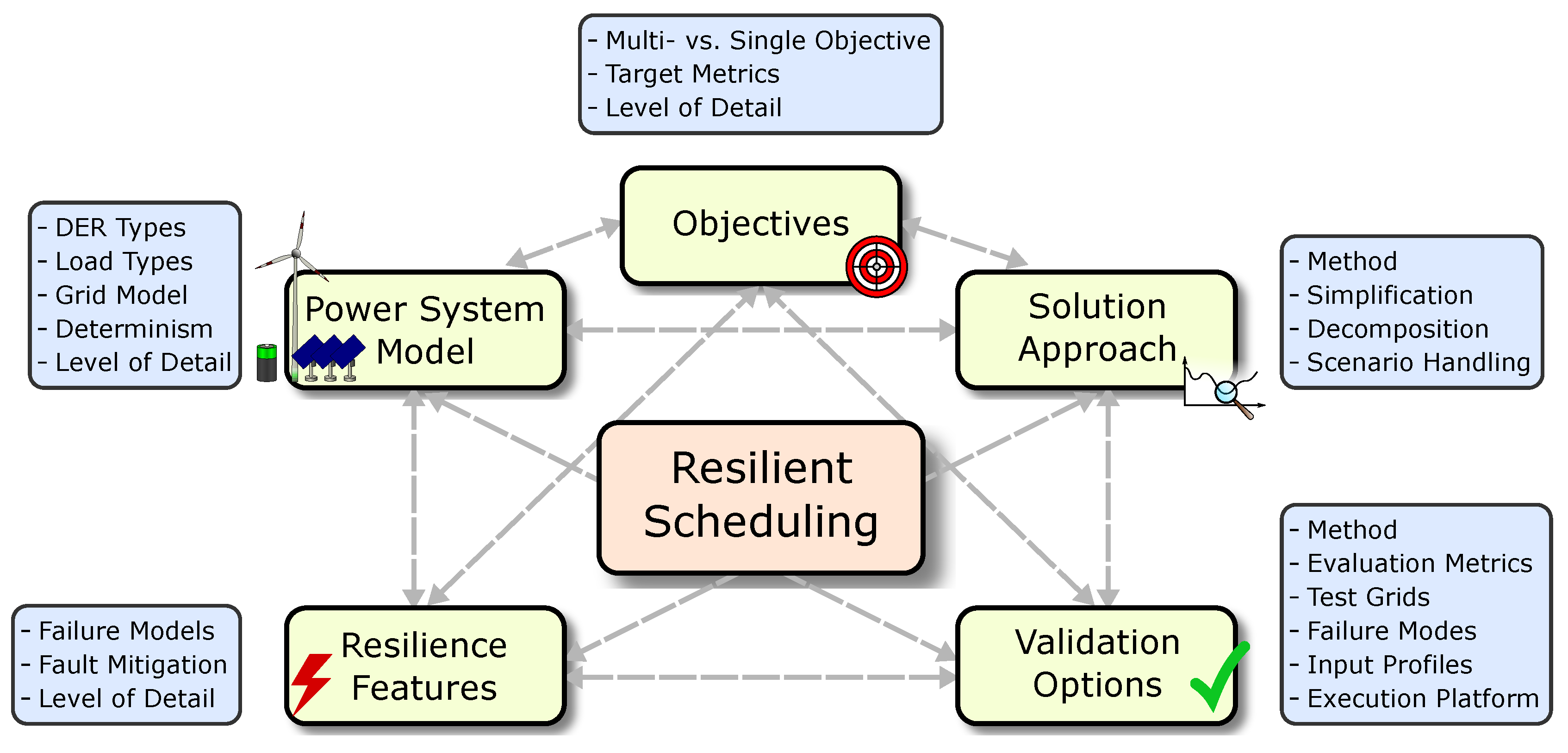
3. Systematic Review Method
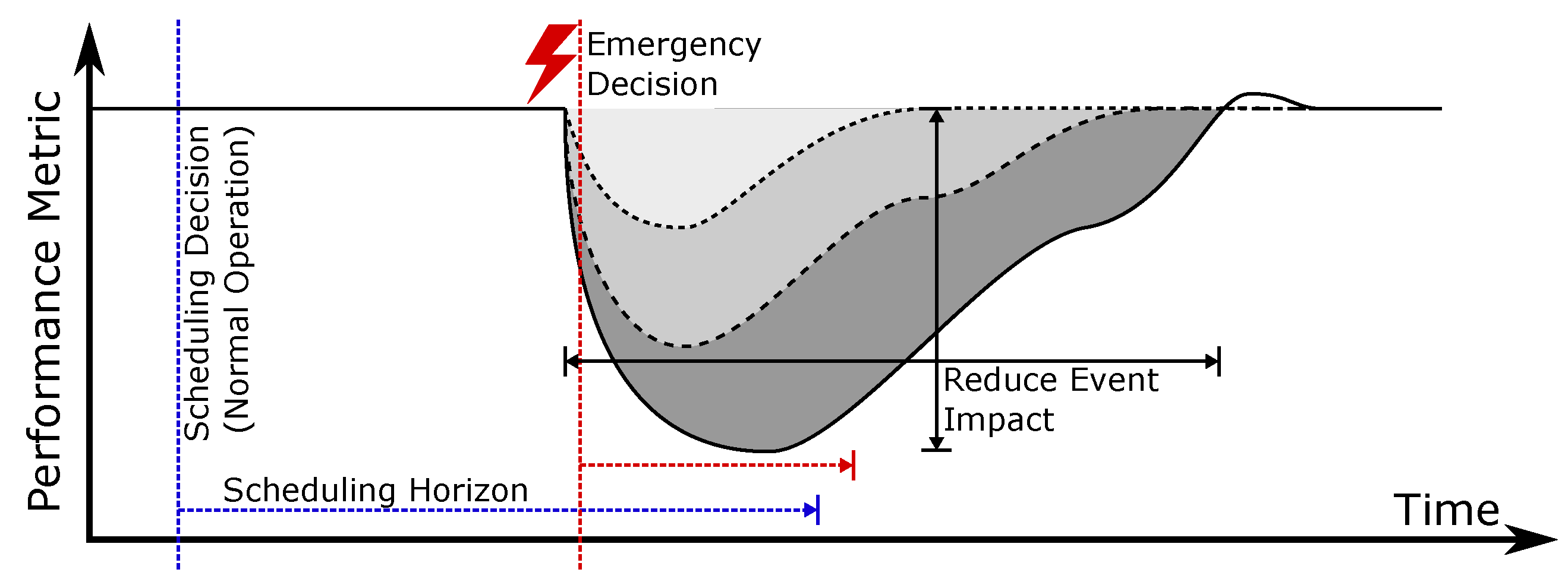
3.1. Definitions
3.2. Research Questions
Which types of resilience-oriented scheduling functions for multi-microgrids do exist and how do they differ from one another?
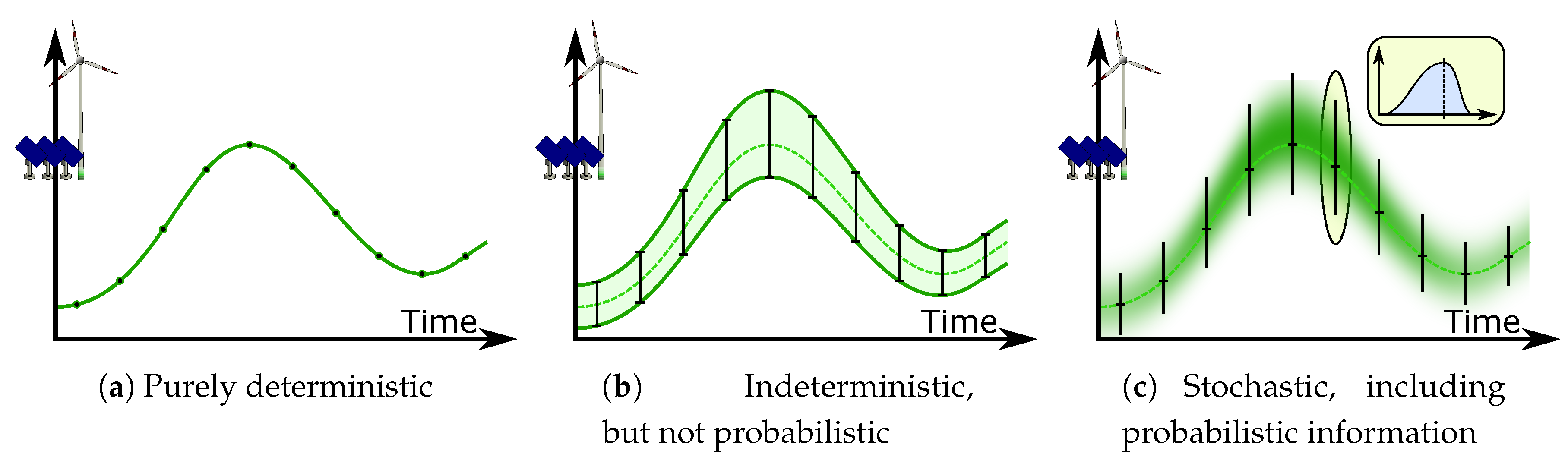
- Which aspects were modeled in SotA approaches? Such aspects include the type of DERs and their models, topological assumptions, failure modes, as well as the formulation of the objective functions. Additionally, sources and representations of uncertainty that are covered by presented models are addressed.
- Which type of proactive actions and fault mitigation techniques are considered to increase resilience and efficiency? For instance, shiftable loads and controllable generation may be scheduled such that certain types of faults can be tolerated. Other actions may include grid-reconfiguration measures and in case of post-fault actions various islanding schemes [3].
- How are these functions tested and evaluated? Which methodology is used to evaluate given approaches? Which input conditions (e.g., test networks, load and DER profiles) are used and do they differ in the degree of detail from the models used for optimization? Is there a common set of benchmarks? Which types of metrics are used to evaluate the performance of scheduling algorithms?
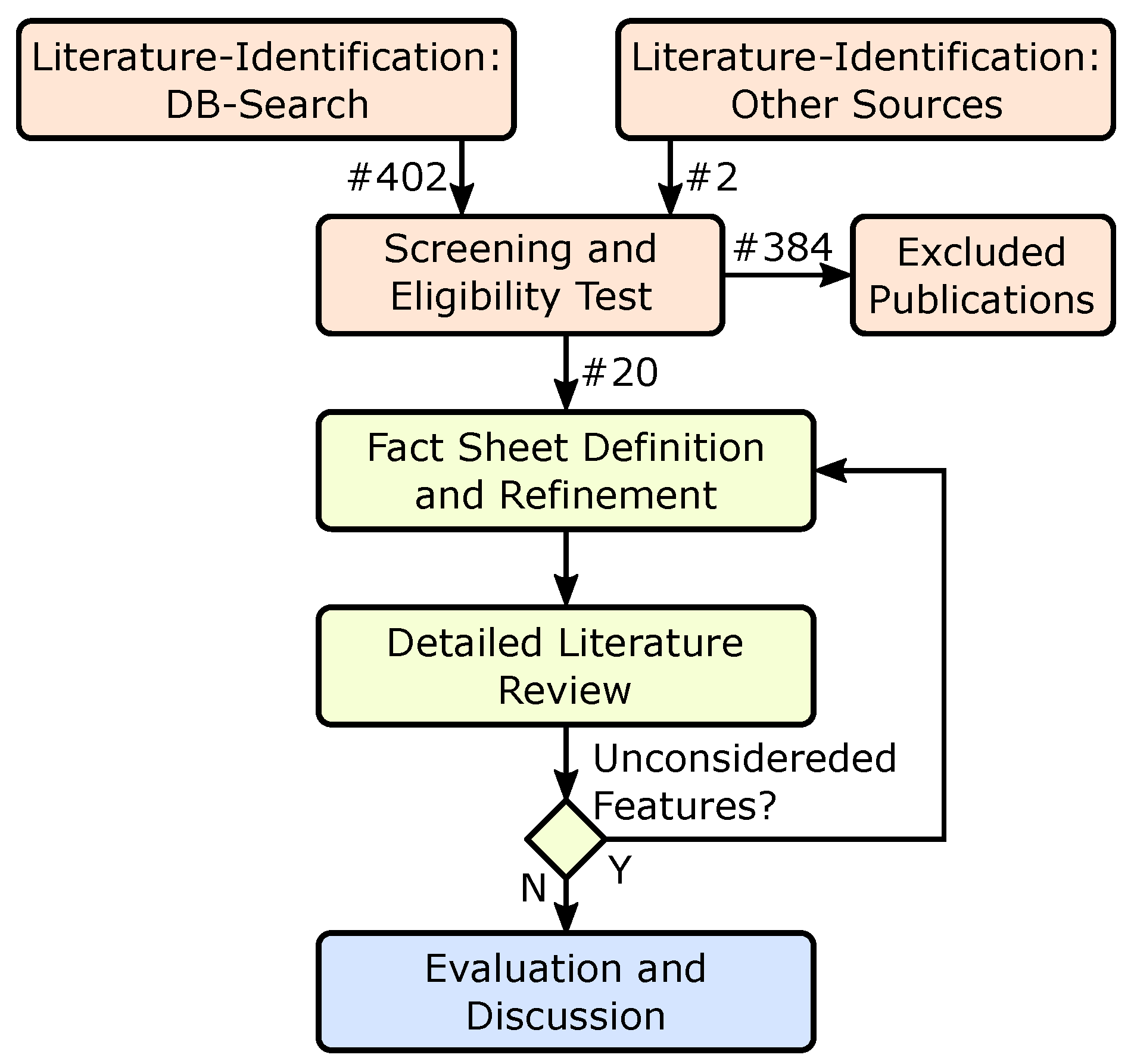
3.3. Literature Identification and Screening
- Full-Text Availability: One of the basic formal criteria for including the paper in the systematic study is its availability. A paper was included if and only if the full content is available in English or German language. Six papers out of 404 were excluded due to their availability.
- Scheduling Algorithm Available: For further evaluation, a scheduling algorithm which covers essential technical details must be given. Scheduling algorithm is thereby understood as an algorithm which computes the set-points of controllable assets such as gensets, battery storage, and controllable loads in advance. Algorithms and papers which focus on long-term resource planning or placement, e.g., for optimizing strategic investment, and therefore not only consider set-points but also asset variations are considered to be out of scope. In the screening step, 140 papers were excluded because they do not describe a scheduling algorithm.
- Focus on Normal Operation: By definition, a microgrid or multi-microgrid is considered to be in normal operation if it is connected to the main grid. Hence, algorithms which solely cover an islanded or emergency operation were rejected for review. Additionally, if an approach focuses on resilience parameters such as critical load supply only, without considering operation metrics such as costs relevant in normal operation, it is not considered for review. In total, 75 papers were excluded because they focus on emergency operation only.
- Resilience Aspects Covered: To answer the research question on resilient scheduling, only approaches which tackle resilience aspects need to be covered. Work is herein considered in case one failure mode during normal operation is taken into account in a way that tolerance of this failure mode is ensured (i.e., robustness) or the impact of these failures is minimized (i.e., resilience). Such failure modes include (main-)grid failures, communication failures, or generation faults. An approach is not considered to be resilient scheduling, in case it does not actively shape resilience and only operates on static security margins without deriving them form the microgrid properties or validating them in an independent simulation. Such static margins include spinning reserve requirements are not actively adapted to the microgrid state. While screening, 98 papers were found to neglect resilience aspects considerably.
- Covered Technology: To guarantee a broad applicability of the reviewed approaches and to be able to compare several detailed aspects, a minimum set of modeled assets is defined [30,31]. In particular, each approach must at least be able to handle a schedulable energy storage, non-schedulable, stochastic loads, stochastic generation, and in accordance with the microgrid definition, an interruptible connection to the main grid. In particular, non-schedulable generation covers a wide range of RES which can be subsumed under this term [2]. In total, 46 papers do not cover the required technology and are therefore not considered for further review.
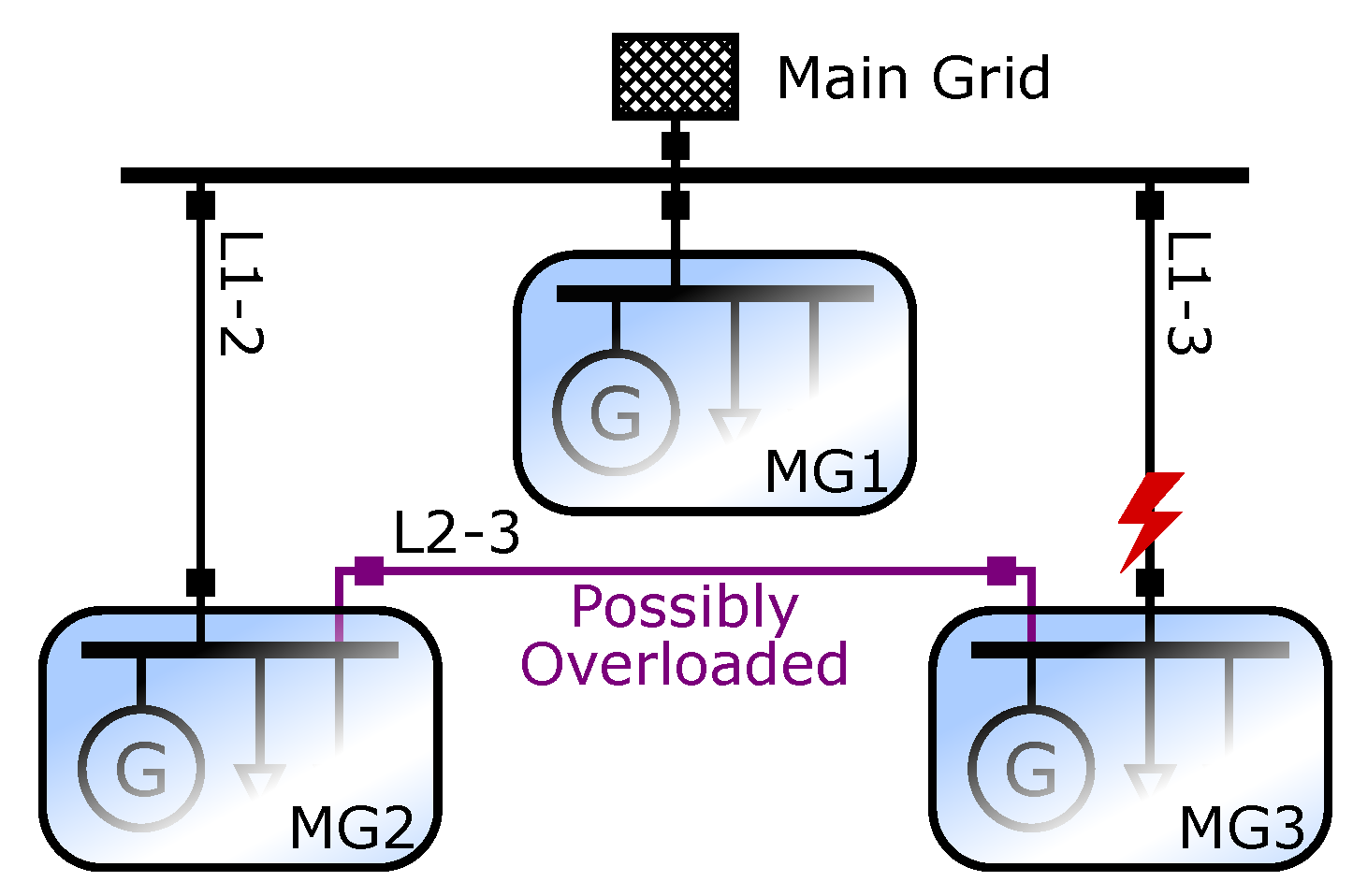
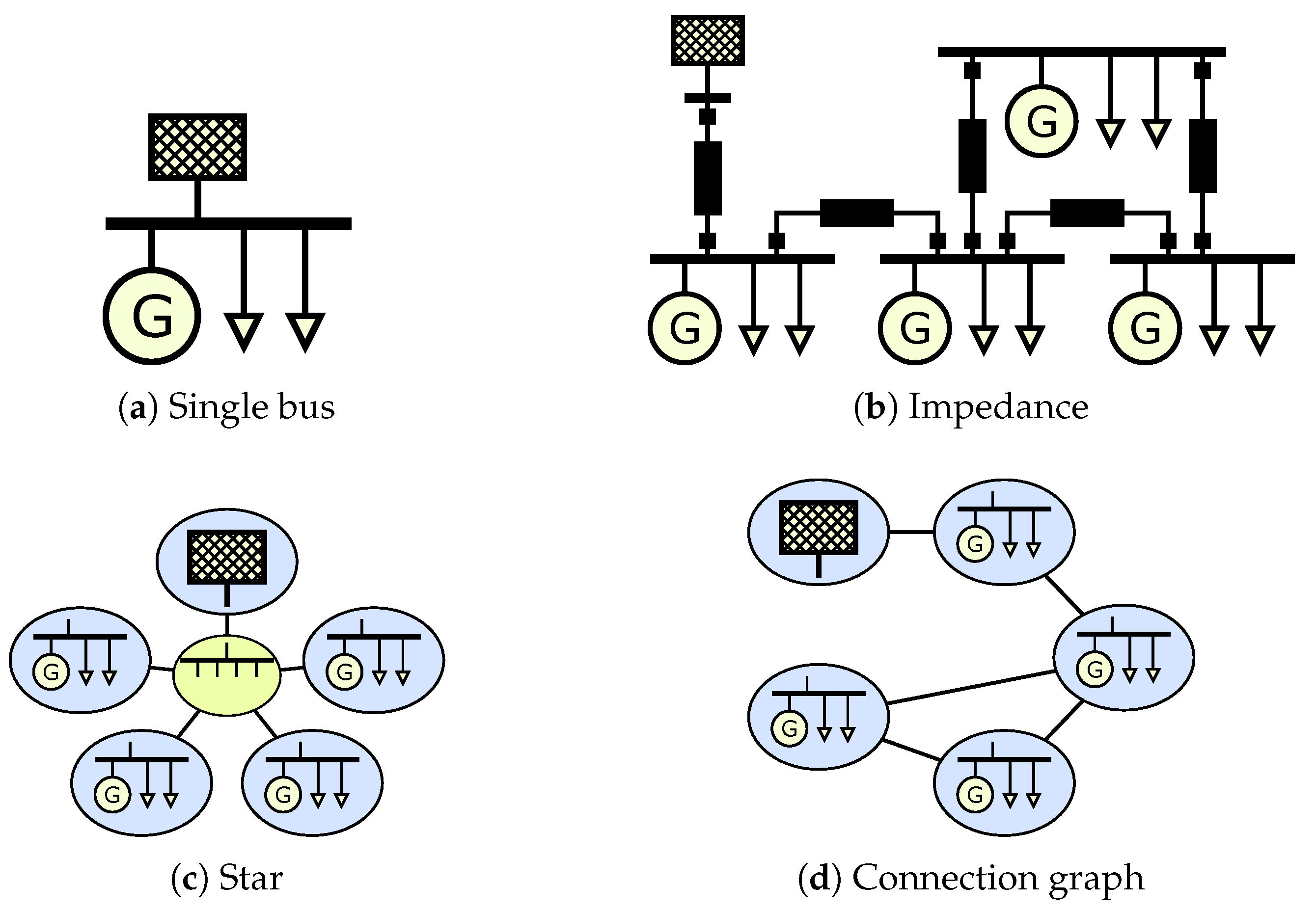
- MG Topology and Topological Constraints: A distribution system, which connects multiple, coordinated microgrids or which forms multiple, coordinated islands may not be able to handle every configuration without voltage and current violations [26]. It is, therefore, expected that network constraints such as topological constraints gain an increasing importance in multi-microgrids, compared to geographically contained single microgrids. Even if an algorithm does not actively alter the network topology, controls and scheduling decisions can have a considerable impact on a reliable operation [47].Since the study focuses on a resilient operation of multi-microgrids, it is decided that included work must take topological constraints into account. In particular, power-flow limits and the topology of the microgrid or multi-microgrid must be taken into account. An algorithm which assumes a single-bus microgrid is not considered to be multi-microgrid scheduling, even if power transfer constraints to the main grid are modeled. From the initial set of identified publications, 31 papers do not consider network constraints at all and 15 papers only model a single-bus microgrid with limited transfer capabilities to the main grid. Similarly, four papers were excluded because they only model Alternating Current (AC)/Direct Current (DC) converter assets without considering transmission constraints within the network.
3.4. Fact Sheet and Feature Extraction
4. Results and Discussion of the Systematic Review
4.1. Selected Literature
4.2. Modeling Approaches and Modeled Assets
4.3. Optimization Objective and Methods
4.4. Resilience Features
4.5. Validation Approaches
5. Future Perspectives
5.1. Modeling Approaches and Modeled Assets
- Level of Abstraction: Most assets such as loads, generation and grid facilities were modeled by different levels of abstraction. For instance, some papers consider a graph model and active power-flow constraints, only [54], while others include a detailed grid model [20] that considers reactive and apparent power flows, as well. Choosing the right level of abstraction may drastically influence the system performance [56], but few papers present the impact of simplification on a resilient schedule in detail.
- Hidden Aspects: To get a concise view on the required level of abstractions, several aspects, that are usually not modeled but that may impact an algorithm, should be considered. For instance, storage losses are commonly modeled via constant efficiencies. However, battery storage systems including their power electronics converters show various non-linear effects that strongly depend on the point of operation [89,90]. A more detailed model may cover system effects that potentially hamper supply security in critical part-load situations [3]. Similarly, few papers consider the effects and reserve requirements of low-level controls such as Q-of-U and P-of-f droop curves that may implement short-term power sharing and voltage control [17].
- Stochastic Effects: Following one of the eligibility criteria, all key contributions trivially consider stochastic effects such as volatile load and RESs. Some of these contributions directly use stochastic models of meteorological observables and forecasting deviations. On a common basis, errors and the observables themselves are assumed to be independently distributed as concerns points in time, i.e., one sample does not depend on previous samples. Such assumptions may be valid for yearly assessments, but may fail at short-term horizons [70] of scheduling problems. Work [91] studies forecasting errors and indicates that a commonly assumed normal distribution does not fit either. Some research is needed to quantify the effects on the performance of a resilient scheduling algorithm and to study alternative models.
- Robustness of the Asset Models: Asset models may be subject to parameter deviations and degradation. For RESs and loads, such phenomena are commonly considered, but for controlled assets, the effects of parameter deviations such as EES capacities are hardly covered. Future work may tackle the robustness of asset models by studying the effects of inevitable parameter deviations. A feedback mechanism may be included to assure a sufficient model quality [92] and further insights regarding the impact of inaccuracies may be gained.
- Covered Assets: Current scheduling algorithms focus on a specific set of assets such as generic DER, EES, and constant power loads. Other components such as transformers that are equipped with On-Load Tap Changers (OLTCs) are not included in the key contributions. However, these assets may impact the system performance and may even be actively controlled by the scheduling algorithms, e.g., to support voltage control via OLTCs [93]. In case specific plant types such as hydro turbines and hydrogen-based EES may be subsumed by generic models, the eligibility of these models needs to be assessed as well.
- Engineering Aspects: One open point that is beyond the scope of all key contributions is the efficient engineering of scheduling approaches. All approaches require a large amount of input information such as network and DER parameters that may not be easily available. Methods that inherently include a system and model identification process such as reinforcement learning [94], as well as common data sources and engineering support systems [95] may be used to assist practical implementation.
5.2. Optimization Objectives and Methods
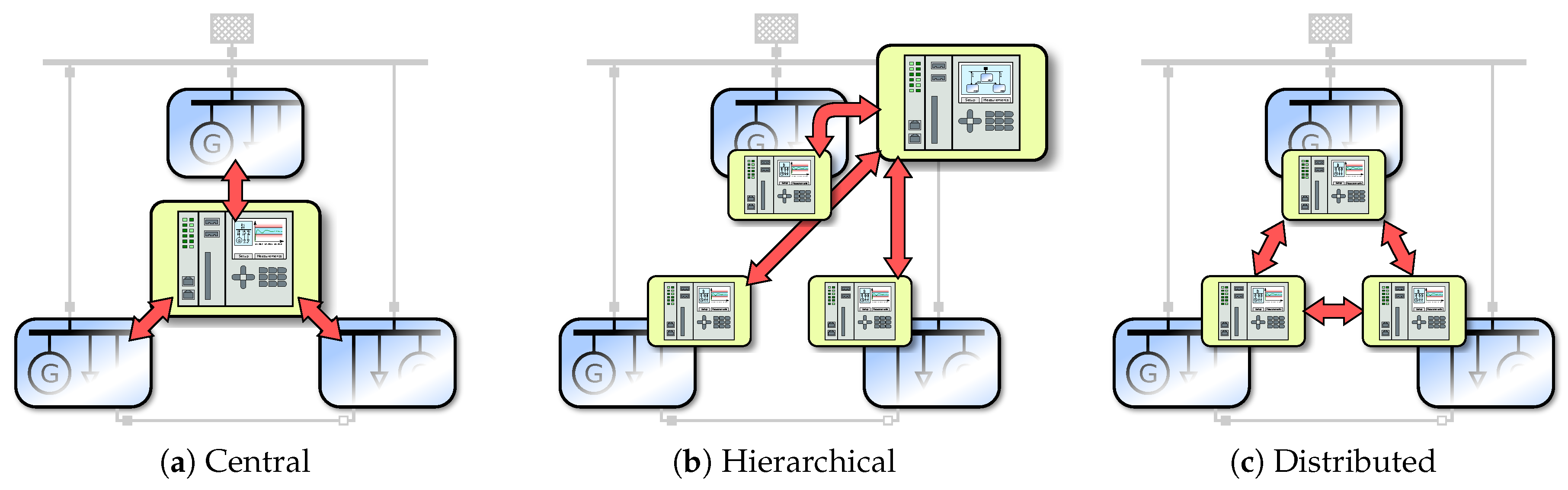
- Distributed Optimization: Out of 20 contributions, only a single one followed a fully distributed approach [63]. Most other publications implemented a centralized approach that requires extensive knowledge of the assets of various microgrids. Future work may include resilience aspects in distributed scheduling approaches more often [34] or may distribute centralized algorithms to tackle privacy, fault tolerance, and governance issues [35].
- Hybrid Optimization: Traditionally, optimization approaches either use mathematical programming or heuristics to obtain a feasible and possibly optimal solution [73]. However, there is a class of algorithms called hybrid optimization that tries to combine several complementary methods, for instance both mathematical programming and heuristic procedures. Some key contributions already successfully use hybrid approaches, e.g., for problem decomposition [27,53] or to interface external solvers [51,57]. Future work may improve the interaction between different solvers and study the application of hybrid optimization methods in detail. A particular focus may be put on the integration of detailed models that are solved by external tools.
- Scalability: Some papers such as [53] indicate that techniques to improve the performance are needed, but as listed in Table 9, few publications actually assess the execution time. Furthermore, no systematic scalability study is given that relates the execution time to the system size and complexity. It is still open to assess the scalability of scheduling approaches and to document the performance limits with respect to practical systems. A fine-grained evaluation may highlight performance trade-offs and assist future engineering work.
- Regulatory Frameworks: Although the key contributions include a wide variety of cost terms, including resilience and operating costs, few references to regulatory regimes that imply certain cost structures are given. Such frameworks may dictate when price information is available, how prices are determined and whether a market can be accessed [96]. Furthermore, energy transfer and trading within multi-microgrids or local energy communities may be restricted by various regulations that need to be considered in the design and operating phase. Some key contributions already consider regulatory measures by assuming certain market price structures [20,62], but a broad discussion is missing.
5.3. Resilience Features
- Extended Failure Modes: In most key contributions, only a few failure classes that must be withstood are considered. Typically, main-grid faults [27,52] and line tripping events [28,64] are tackled. Few papers also include other modes such as short-circuit failures [57] and no paper directly considers faulty DER set-points, invalid switching actions, or load disconnections. Open research includes the systematic identification of relevant failure modes that need to be considered in the scheduling problem. Additionally, the flexibility of algorithms in considering new and previously unknown failures may be assessed. Future work may further rely on the integration of external simulation tools to tackle both flexibility and the level of detail.
- Generic Failure Modes: Some failure modes may be subsumed by another class. For instance, main grid failures may be covered by a fault in the line that connects the point of common coupling [28,55]. However, a systematic study of prototypical failure modes in scheduling problems is still open. In particular when increasing the number of considered failure modes, a proper generalization may be needed to contain the computational effort of finding an optimal solution.
- Effects of Low-Level Controls: Low-level controls such as voltage and frequency control that are installed to provide immediate action in terms of disturbances [5] are commonly beyond the scope of key contributions. However, a high-level schedule may impact the feasibility of certain control actions, e.g., in case a generator is already close to a limit, and may hamper a successful mitigation action. Some emergency actions such as fault rerouting can also be implemented by a dedicated controller to guarantee a fast response. Future work may focus on the interaction of low-level controls and the scheduling algorithm to ensure a consistent behavior and a valid emergency response. Insights into the proper abstractions of low-level controls may decrease the complexity of the scheduler without impacting the resilience of the system.
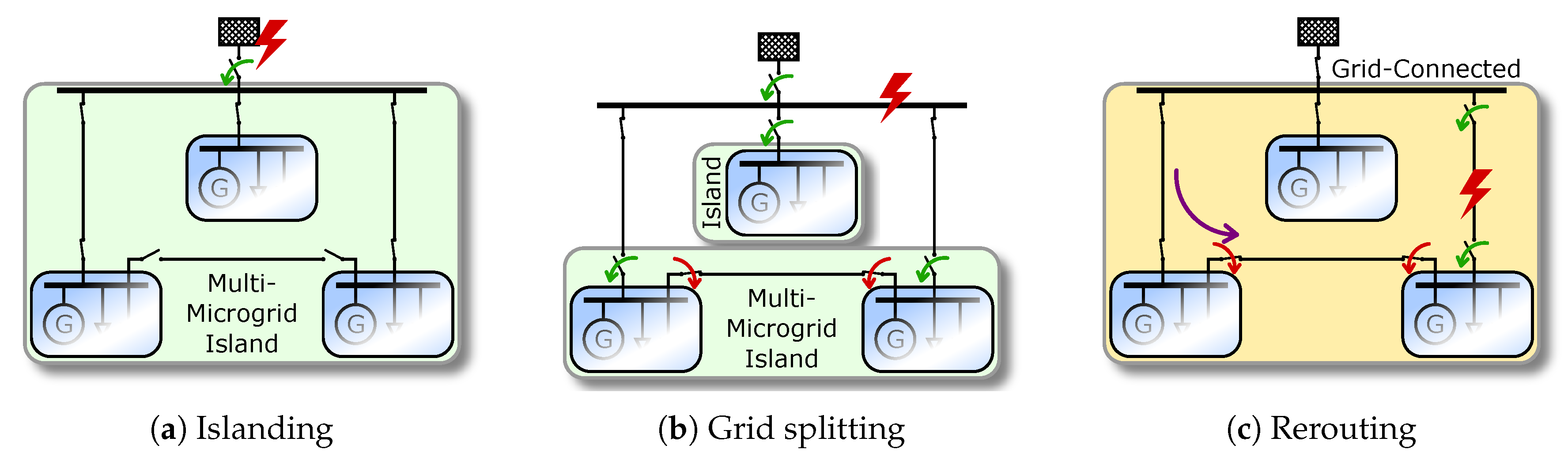
- Fault Mitigation Techniques: The key contributions deploy three different classes of fault mitigation techniques: Main-grid disconnection [27], rerouting [48], and grid splitting [28]. However, practical issues such as protection, inertia, grid-forming, and legal requirements [36] are hardly considered on assessing mitigation options. Some work may be conducted to increase the knowledge of feasibility aspects of mitigation techniques and to explore further options such as mobile generators and batteries that may quickly replace other units [97].
5.4. Validation Approaches
- Common Benchmark System: All key contributions include a simulation-based validation, but each of them uses different benchmark systems or diverging configurations to demonstrate their approaches. One of the most common test feeders is the Baran test feeder [77]. However, to demonstrate the algorithms, several independent modifications were introduced to account for DERs that were not considered in the original test feeder. Consequently, results from different papers cannot be directly compared. Existing benchmark systems [31] such as SimBench [98,99] and IEEE test feeders [100] may be evaluated and refined towards a unified multi-microgrid scheduling test bed. In addition to common typologies, a wide variety of assets, unified input profiles, and detailed DER parameters may reduce the need for custom modifications.
- Common Metrics: To be able to compare results from different studies, common metrics are required. While most papers provide operating costs, resilience-based metrics such as energy not supplied, are less common. Future work may profit from an increased focus on unified resilience metrics [48] and may intensify the discussion on their significance.
- Independent Validation: Rising from the need for comparable results, a fine-grained assessment of multiple algorithms may be conducted. In addition to common benchmark systems that are used by multiple authors, more detailed insights may be gained. A common execution platform may, for instance, enable detailed assessments on the computational performance. Some publications including [56,64] already compare their methods to a reference, but future implementations may profit from a more extensive study.
- Readiness and Practical Implementation: Although the first multi-microgrid test sites are already implemented [9], only one key contribution demonstrated the practical implementation of resilient scheduling [59] and no one went beyond laboratory experiments. Hence, considerable effort is needed until the approaches can demonstrate practical use in real-world situations [101]. Future testing and validation work may highly profit from previous experiences [9,31,102] and structured testing methodologies such as holistic testing [101,103].
- Resilience Assessment in the Field: One particular challenge towards a safe deployment is the resilience assessment in productive operation. Unlike in laboratory-based setups, testing the resilience may impact the overall performance of the grid. However, undiscovered failures in the control strategies may have fatal consequences as well [30]. Future work may include save strategies to verify resilience against low probability, high impact events in operation.
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AC | Alternating Current |
| CHP | Combined Heat and Power |
| CSA | Clonal Selection Algorithm |
| DC | Direct Current |
| DER | Distributed Energy Resource |
| DR | Demand Response |
| EES | Electrical Energy Storage |
| EMA | Exchange Market Algorithm |
| PaCcET | Pareto Concavity Elimination Transformation |
| EV | Electric Vehicle |
| FA | Firefly Algorithm |
| ICA | Imperialist Competitive Algorithm |
| MILP | Mixed Integer Linear Programming |
| MIP | Mixed Integer Programming |
| MT | Micro Turbine |
| OLTC | On-Load Tap Changer |
| PCC | Point of Common Coupling |
| PV | Photovoltaics |
| PRISMA | Preferred Reporting Items for Systematic Reviews and Meta-Analyses |
| PSO | Particle Swarm Optimization |
| RES | Renewable Energy Sources |
| SoC | State of Charge |
| SotA | State-of-the-Art |
| SRQ | Sub-Research Question |
| V2G | Vehicle to Grid |
| WT | Wind Turbine |
References
- Marnay, C.; Abbey, C.; Joos, G.; Ash, K.; Bando, S.; Braun, M.; Chatzivasileiadis, S.; Driesen, J.; Hatziargyriou, N.; Iravani, R.; et al. Microgrids 1 Engineering, Economics, & Experience–Capabilities, Benefits, Business Opportunities, and Examples; Technical report; WG C6.22; CIGRÉ: Paris, France, 2015. [Google Scholar]
- Parhizi, S.; Lotfi, H.; Khodaei, A.; Bahramirad, S. State of the Art in Research on Microgrids: A Review. IEEE Access 2015, 3, 890–925. [Google Scholar] [CrossRef]
- Hussain, A.; Bui, V.H.; Kim, H.M. Microgrids as a resilience resource and strategies used by microgrids for enhancing resilience. Appl. Energy 2019, 240, 56–72. [Google Scholar] [CrossRef]
- Gholami, A.; Aminifar, F.; Shahidehpour, M. Front Lines Against the Darkness: Enhancing the Resilience of the Electricity Grid Through Microgrid Facilities. IEEE Electrif. Mag. 2016, 4, 18–24. [Google Scholar] [CrossRef]
- Hatziargyriou, N. (Ed.) Microgrids: Architectures and Control; John Wiley & Sons: West Sussex, UK, 2014. [Google Scholar]
- Kariniotakis, G.; Martini, L.; Caerts, C.; Brunner, H.; Retiere, N. Challenges, innovative architectures and control strategies for future networks: The Web-of-Cells, fractal grids and other concepts. In Proceedings of the 24th International Conference & Exhibition on Electricity Distribution (CIRED), Glasgow, UK, 12–15 June 2017. [Google Scholar]
- Bullich-Massagué, E.; Díaz-González, F.; Aragüés-Peñalba, M.; Girbau-Llistuella, F.; Olivella-Rosell, P.; Sumper, A. Microgrid clustering architectures. Appl. Energy 2018, 212, 340–361. [Google Scholar] [CrossRef]
- Shirzadi, S.; Nair, N.K.C. Power system resilience through microgrids: A comprehensive review. In Proceedings of the 2018 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Kota Kinabalu, Malaysia, 7–10 October 2018. [Google Scholar]
- Xu, Z.; Yang, P.; Zheng, C.; Zhang, Y.; Peng, J.; Zeng, Z. Analysis on the organization and Development of multi-microgrids. Renew. Sustain. Energy Rev. 2018, 81, 2204–2216. [Google Scholar] [CrossRef]
- Khan, A.A.; Naeem, M.; Iqbal, M.; Qaisar, S.; Anpalagan, A. A compendium of optimization objectives, constraints, tools and algorithms for energy management in microgrids. Renew. Sustain. Energy Rev. 2016, 58, 1664–1683. [Google Scholar] [CrossRef]
- Arghandeh, R.; von Meier, A.; Mehrmanesh, L.; Mili, L. On the definition of cyber-physical resilience in power systems. Renew. Sustain. Energy Rev. 2016, 58, 1060–1069. [Google Scholar] [CrossRef] [Green Version]
- Gholami, A.; Shekari, T.; Amirioun, M.H.; Aminifar, F.; Amini, M.H.; Sargolzaei, A. Toward a consensus on the definition and taxonomy of power system resilience. IEEE Access 2018, 6, 32035–32053. [Google Scholar] [CrossRef]
- Henry, D.; Ramirez-Marquez, J.E. Generic metrics and quantitative approaches for system resilience as a function of time. Reliab. Eng. Syst. Saf. 2012, 99, 114–122. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, Y.; Li, F. Evaluating the reliability of islanded microgrid in an emergency mode. In Proceedings of the 2010 45th International Universities Power Engineering Conference (UPEC), Wales, UK, 31 August–3 September 2010. [Google Scholar]
- Falahati, B.; Kargarian, A.; Fu, Y. Timeframe capacity factor reliability model for isolated microgrids with renewable energy resources. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Bie, Z.; Zhang, P.; Li, G.; Hua, B.; Meehan, M.; Wang, X. Reliability evaluation of active distribution systems including microgrids. IEEE Trans. Power Syst. 2012, 27, 2342–2350. [Google Scholar] [CrossRef]
- Ahn, S.J.; Nam, S.R.; Choi, J.H.; Moon, S.I. Power scheduling of distributed generators for economic and stable operation of a microgrid. IEEE Trans. Smart Grid 2013, 4, 398–405. [Google Scholar] [CrossRef]
- Khodaei, A. Resiliency-oriented microgrid optimal scheduling. IEEE Trans. Smart Grid 2014, 5, 1584–1591. [Google Scholar] [CrossRef]
- Hussain, A.; Bui, V.H.; Kim, H.M. Robust optimization-based scheduling of multi-microgrids considering uncertainties. Energies 2016, 9, 278. [Google Scholar] [CrossRef] [Green Version]
- Gholami, A.; Shekari, T.; Aminifar, F.; Shahidehpour, M. Microgrid Scheduling With Uncertainty: The Quest for Resilience. IEEE Trans. Smart Grid 2016, 7, 2849–2858. [Google Scholar] [CrossRef]
- Zakariazadeh, A.; Jadid, S.; Siano, P. Smart microgrid energy and reserve scheduling with demand response using stochastic optimization. Int. J. Electr. Power Energy Syst. 2014, 63, 523–533. [Google Scholar] [CrossRef]
- Jayantilal, A.; McCarthy, C.A. Reducing Customer Outages–Smart Distribution through Layered Intelligence. NEMA Electroind. Mag. 2012, 3, 1170–1180. [Google Scholar]
- Che, L.; Khodayar, M.; Shahidehpour, M. Only connect: Microgrids for distribution system restoration. IEEE Power Energy Mag. 2014, 12, 70–81. [Google Scholar]
- Gao, H.; Chen, Y.; Xu, Y.; Liu, C.C. Resilience-oriented critical load restoration using microgrids in distribution systems. IEEE Trans. Smart Grid 2016, 7, 2837–2848. [Google Scholar] [CrossRef]
- Chen, C.; Wang, J.; Qiu, F.; Zhao, D. Resilient distribution system by microgrids formation after natural disasters. IEEE Trans. Smart Grid 2016, 7, 958–966. [Google Scholar] [CrossRef]
- Kimble, S.J.; Vedullapalli, D.T.; Makram, E.B. Optimal Partitioning of Distribution Networks for Micro-Grid Operation. J. Power Energy Eng. 2017, 5, 104–120. [Google Scholar] [CrossRef] [Green Version]
- Khodaei, A. Provisional microgrids. IEEE Trans. Smart Grid 2015, 6, 1107–1115. [Google Scholar] [CrossRef]
- Gazijahani, F.S.; Ravadanegh, S.N.; Salehi, J. Stochastic multi-objective model for optimal energy exchange optimization of networked microgrids with presence of renewable generation under risk-based strategies. ISA Trans. 2018, 73, 100–111. [Google Scholar] [CrossRef] [PubMed]
- Hatziargyriou, N.; Asano, H.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energy Mag. 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Kroposki, B.; Lasseter, R.; Ise, T.; Morozumi, S.; Papathanassiou, S.; Hatziargyriou, N. Making microgrids work. IEEE Power Energy Mag. 2008, 6, 40–53. [Google Scholar] [CrossRef]
- Lidula, N.; Rajapakse, A. Microgrids research: A review of experimental microgrids and test systems. Renew. Sustain. Energy Rev. 2011, 15, 186–202. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Cañizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in Microgrid Control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Nosratabadi, S.M.; Hooshmand, R.A.; Gholipour, E. A comprehensive review on microgrid and virtual power plant concepts employed for distributed energy resources scheduling in power systems. Renew. Sustain. Energy Rev. 2017, 67, 341–363. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, K.; Li, H.; Coelho, E.A.A.; Guerrero, J.M. MAS-based distributed coordinated control and optimization in microgrid and microgrid clusters: A comprehensive overview. IEEE Trans. Power Electron. 2017, 33, 6488–6508. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Z.; Duan, J.; Chow, M.Y. To centralize or to distribute: That is the question: A comparison of advanced microgrid management systems. IEEE Ind. Electron. Mag. 2018, 12, 6–24. [Google Scholar] [CrossRef]
- Hirsch, A.; Parag, Y.; Guerrero, J. Microgrids: A review of technologies, key drivers, and outstanding issues. Renew. Sustain. Energy Rev. 2018, 90, 402–411. [Google Scholar] [CrossRef]
- Zia, M.F.; Elbouchikhi, E.; Benbouzid, M. Microgrids energy management systems: A critical review on methods, solutions, and prospects. Appl. Energy 2018, 222, 1033–1055. [Google Scholar] [CrossRef]
- Chi, Y.; Xu, Y. Resilience-oriented microgrids: A comprehensive literature review. In Proceedings of the 2017 IEEE Innovative Smart Grid Technologies-Asia (ISGT-Asia), Auckland, New Zealand, 4–7 December 2017. [Google Scholar]
- Feng, W.; Jin, M.; Liu, X.; Bao, Y.; Marnay, C.; Yao, C.; Yu, J. A review of microgrid development in the United States–A decade of progress on policies, demonstrations, controls, and software tools. Appl. Energy 2018, 228, 1656–1668. [Google Scholar] [CrossRef]
- Alam, M.N.; Chakrabarti, S.; Ghosh, A. Networked microgrids: State-of-the-art and future perspectives. IEEE Trans. Ind. Informatics 2018, 15, 1238–1250. [Google Scholar] [CrossRef]
- Boqtob, O.; El Moussaoui, H.; El Markhi, H.; Lamhamdi, T. Microgrid energy management system: A state-of-the-art review. J. Electr. Syst. 2019, 15, 53–67. [Google Scholar]
- Wang, Y.; Chen, C.; Wang, J.; Baldick, R. Research on resilience of power systems under natural disasters–A review. IEEE Trans. Power Syst. 2015, 31, 1604–1613. [Google Scholar]
- Lin, Y.; Bie, Z.; Qiu, A. A review of key strategies in realizing power system resilience. Glob. Energy Interconnect. 2018, 1, 70–78. [Google Scholar]
- Anderson, A.A.; Suryanarayanan, S. Review of Energy Management and Planning of Islanded Microgrids. CSEE J. Power Energy Syst. 2019, 6, 329–343. [Google Scholar]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G.; Group, T.P. Preferred Reporting Items for Systematic Reviews and Meta-Analyses: The PRISMA Statement. PLoS Med. 2009, 6, e1000097. [Google Scholar] [CrossRef] [Green Version]
- Spiegel, M.H. Poster Abstract: Towards Advanced Resiliency-Oriented Multi-Microgrid Scheduling. In Proceedings of the Abstr. 8th DACH+ Conf. Energy Informatics, Salzburg, Austria, 26–27 September 2019; Volume 2. [Google Scholar]
- Farag, H.E.; Abdelaziz, M.M.A.; El-Saadany, E.F. Voltage and reactive power impacts on successful operation of islanded microgrids. IEEE Trans. Power Syst. 2013, 28, 1716–1727. [Google Scholar]
- Khodayar, M.E.; Barati, M.; Shahidehpour, M. Integration of high reliability distribution system in microgrid operation. IEEE Trans. Smart Grid 2012, 3, 1997–2006. [Google Scholar] [CrossRef]
- Bashiri, M. Optimal scheduling of distributed energy resources in a distribution system based on imperialist competitive algorithm considering reliability worth. Neural Comput. Appl. 2014, 25, 967–974. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Khodaei, A. Efficient integration of plug-in electric vehicles via reconfigurable microgrids. Energy 2016, 111, 653–663. [Google Scholar] [CrossRef]
- Farzin, H.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M. A stochastic multi-objective framework for optimal scheduling of energy storage systems in microgrids. IEEE Trans. Smart Grid 2017, 8, 117–127. [Google Scholar] [CrossRef]
- Hosseinnezhad, V.; Rafiee, M.; Ahmadian, M.; Siano, P. Optimal day-ahead operational planning of microgrids. Energy Convers. Manag. 2016, 126, 142–157. [Google Scholar] [CrossRef]
- Gholami, A.; Shekari, T.; Grijalva, S. Proactive management of microgrids for resiliency enhancement: An adaptive robust approach. IEEE Trans. Sustain. Energy 2017, 10, 470–480. [Google Scholar] [CrossRef]
- Qiu, H.; Zhao, B.; Gu, W.; Bo, R. Bi-level two-stage robust optimal scheduling for AC/DC hybrid multi-microgrids. IEEE Trans. Smart Grid 2018, 9, 5455–5466. [Google Scholar] [CrossRef]
- Gazijahani, F.S.; Salehi, J. Integrated DR and reconfiguration scheduling for optimal operation of microgrids using Hong’s point estimate method. Int. J. Electr. Power Energy Syst. 2018, 99, 481–492. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Zare, A.; Khodaei, A. Effective dynamic scheduling of reconfigurable microgrids. IEEE Trans. Power Syst. 2018, 33, 5519–5530. [Google Scholar] [CrossRef]
- Sarfi, V.; Livani, H. An economic-reliability security-constrained optimal dispatch for microgrids. IEEE Trans. Power Syst. 2018, 33, 6777–6786. [Google Scholar]
- Salyani, P.; Ravadanegh, S.N.; Tabatabaei, N.M. Optimal Scheduling of Networked-Microgrids to Resiliency Enhancement Under Uncertainty. In Power Systems Resilience; Mahdavi Tabatabaei, N., Najafi Ravadanegh, S., Bizon, N., Eds.; Springer: Cham, Switzerland, 2019; Chapter 6. [Google Scholar]
- Gan, L.K.; Hussain, A.; Howey, D.A.; Kim, H.M. Limitations in Energy Management Systems: A Case Study for Resilient Interconnected Microgrids. IEEE Trans. Smart Grid 2018, 10, 5675–5685. [Google Scholar] [CrossRef]
- Yang, F.; Feng, X.; Li, Z. Advanced microgrid energy management system for future sustainable and resilient power grid. IEEE Trans. Ind. Appl. 2019, 55, 7251–7260. [Google Scholar] [CrossRef]
- Teimourzadeh, S.; Tor, O.B.; Cebeci, M.E.; Adela, B.; Oprea, S.V. A three-stage approach for resilience-constrained scheduling of networked microgrids. J. Mod. Power Syst. Clean Energy 2019, 7, 705–715. [Google Scholar] [CrossRef] [Green Version]
- Liang, Z.; Alsafasfeh, Q.; Su, W. Proactive Resilient Scheduling for Networked Microgrids With Extreme Events. IEEE Access 2019, 7, 112639–112652. [Google Scholar] [CrossRef]
- Ananduta, W.; Maestre, J.M.; Ocampo-Martinez, C.; Ishii, H. Resilient distributed model predictive control for energy management of interconnected microgrids. Optim. Control Appl. Methods 2020, 41, 146–169. [Google Scholar] [CrossRef] [Green Version]
- Zadsar, M.; Sebtahmadi, S.S.; Kazemi, M.; Larimi, S.; Haghifam, M. Two stage risk based decision making for operation of smart grid by optimal dynamic multi-microgrid. Int. J. Electr. Power Energy Syst. 2020, 118, 105791. [Google Scholar] [CrossRef]
- Liu, N.; Chen, Q.; Liu, J.; Lu, X.; Li, P.; Lei, J.; Zhang, J. A heuristic operation strategy for commercial building microgrids containing EVs and PV system. IEEE Trans. Ind. Electron. 2014, 62, 2560–2570. [Google Scholar] [CrossRef]
- Hussain, A.; Bui, V.H.; Kim, H.M. A proactive and survivability-constrained operation strategy for enhancing resilience of microgrids using energy storage system. IEEE Access 2018, 6, 75495–75507. [Google Scholar] [CrossRef]
- Hussain, A.; Bui, V.H.; Kim, H.M. Resilience-oriented optimal operation of networked hybrid microgrids. IEEE Trans. Smart Grid 2019, 10, 204–215. [Google Scholar] [CrossRef]
- Bornapour, M.; Hooshmand, R.A.; Khodabakhshian, A.; Parastegari, M. Optimal stochastic scheduling of CHP-PEMFC, WT, PV units and hydrogen storage in reconfigurable micro grids considering reliability enhancement. Energy Convers. Manag. 2017, 150, 725–741. [Google Scholar] [CrossRef]
- Cardoso, G.; Stadler, M.; Siddiqui, A.; Marnay, C.; DeForest, N.; Barbosa-Póvoa, A.; Ferrão, P. Microgrid reliability modeling and battery scheduling using stochastic linear programming. Electr. Power Syst. Res. 2013, 103, 61–69. [Google Scholar] [CrossRef] [Green Version]
- Conradsen, K.; Nielsen, L.; Prahm, L. Review of Weibull statistics for estimation of wind speed distributions. J. Clim. Appl. Meteorol. 1984, 23, 1173–1183. [Google Scholar] [CrossRef]
- Emeis, S. Wind Energy Meteorology: Atmospheric Physics for Wind Power Generation; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Salameh, Z.M.; Borowy, B.S.; Amin, A.R. Photovoltaic module-site matching based on the capacity factors. IEEE Trans. Energy Convers. 1995, 10, 326–332. [Google Scholar] [CrossRef]
- Blum, C.; Puchinger, J.; Raidl, G.R.; Roli, A. Hybrid metaheuristics in combinatorial optimization: A survey. Appl. Soft Comput. 2011, 11, 4135–4151. [Google Scholar] [CrossRef] [Green Version]
- Gazijahani, F.S.; Salehi, J. Stochastic multi-objective framework for optimal dynamic planning of interconnected microgrids. IET Renew. Power Gener. 2017, 11, 1749–1759. [Google Scholar] [CrossRef]
- Chis, M.; Salama, M.; Jayaram, S. Capacitor placement in distribution systems using heuristic search strategies. IEE Proc.-Gener. Transm. Distrib. 1997, 144, 225–230. [Google Scholar] [CrossRef]
- Conti, S.; Nicolosi, R.; Rizzo, S.; Zeineldin, H. Optimal dispatching of distributed generators and storage systems for MV islanded microgrids. IEEE Trans. Power Deliv. 2012, 27, 1243–1251. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 101–102. [Google Scholar] [CrossRef]
- New York Independent System Operator. Available online: https://www.nyiso.com/ (accessed on 14 October 2019).
- Zolfaghari, S.; Riahy, G.H.; Abedi, M. A new method to adequate assessment of wind farms’ power output. Energy Convers. Manag. 2015, 103, 585–604. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Le, L.B. Optimal bidding strategy for microgrids considering renewable energy and building thermal dynamics. IEEE Trans. Smart Grid 2014, 5, 1608–1620. [Google Scholar] [CrossRef]
- Khodaei, A. Microgrid optimal scheduling with multi-period islanding constraints. IEEE Trans. Power Syst. 2014, 29, 1383–1392. [Google Scholar]
- McKenna, E.; Thomson, M. High-resolution stochastic integrated thermal–electrical domestic demand model. Appl. Energy 2016, 165, 445–461. [Google Scholar] [CrossRef] [Green Version]
- NREL Measurement and Instrumentation Data Center. Available online: https://midcdmz.nrel.gov/ (accessed on 12 May 2020).
- Turkish Energy Exchange Platform (EXIST). Available online: https://seffaflik.epias.com.tr/transparency/ (accessed on 16 April 2020).
- Wang, J.; Shahidehpour, M.; Li, Z. Security-constrained unit commitment with volatile wind power generation. IEEE Trans. Power Syst. 2008, 23, 1319–1327. [Google Scholar] [CrossRef]
- PJM Interconnection-Markets and Operation. Available online: https://www.pjm.com/markets-and-operations.aspx (accessed on 12 May 2020).
- Jager, D.; Andreas, A. NREL National Wind Technology Center (NWTC): M2 Tower; Boulder, Colorado (Data); Technical Report NREL/DA-5500-56489; National Renewable Energy Lab. (NREL): Golden, CO, USA, 1996.
- Liang, Z.; Bian, D.; Zhang, X.; Shi, D.; Diao, R.; Wang, Z. Optimal energy management for commercial buildings considering comprehensive comfort levels in a retail electricity market. Appl. Energy 2019, 236, 916–926. [Google Scholar] [CrossRef] [Green Version]
- Weniger, J.; Maier, S.; Orth, N.; Quaschning, V. Stromspeicher-Inspektion 2020; Technical report; Hochschule für Technik und Wirtschaft: Berlin, Germany, 2020. [Google Scholar]
- Schimpe, M.; Naumann, M.; Truong, N.; Hesse, H.C.; Santhanagopalan, S.; Saxon, A.; Jossen, A. Energy efficiency evaluation of a stationary lithium-ion battery container storage system via electro-thermal modeling and detailed component analysis. Appl. Energy 2018, 210, 211–229. [Google Scholar] [CrossRef]
- Bludszuweit, H.; Domínguez-Navarro, J.A.; Llombart, A. Statistical analysis of wind power forecast error. IEEE Trans. Power Syst. 2008, 23, 983–991. [Google Scholar] [CrossRef]
- Clarke, D.; Gawthrop, P. Self-tuning control. In Proceedings of the Institution of Electrical Engineers; IET: London, UK, 1979. [Google Scholar]
- Dou, X.; Xu, P.; Hu, Q.; Sheng, W.; Quan, X.; Wu, Z.; Xu, B. A distributed voltage control strategy for multi-microgrid active distribution networks considering economy and response speed. IEEE Access 2018, 6, 31259–31268. [Google Scholar] [CrossRef]
- Russell, S.J.; Norvig, P.V. Artificial Intelligence, 4th ed.; Pearson: Boston, MA, USA, 2019. [Google Scholar]
- Andrén, F.P.; Strasser, T.I.; Kastner, W. Engineering smart grids: Applying model-driven development from use case design to deployment. Energies 2017, 10, 374. [Google Scholar] [CrossRef] [Green Version]
- Parag, Y.; Sovacool, B.K. Electricity market design for the prosumer era. Nat. Energy 2016, 1, 1–6. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Wang, M.; Su, W. Stochastic resilient post-hurricane power system recovery based on mobile emergency resources and reconfigurable networked microgrids. IEEE Access 2018, 6, 72311–72326. [Google Scholar] [CrossRef]
- Spalthoff, C.; Sarajlić, D.; Kittl, C.; Drauz, S.; Kneiske, T.; Rehtanz, C.; Braun, M. SimBench: Open source time series of power load, storage and generation for the simulation of electrical distribution grids. In Proceedings of the Internationaler ETG-Kongress, Esslingen, Germany, 8–9 May 2019. Preprint. [Google Scholar]
- Meinecke, S.; Bornhorst, N.; Braun, M. Power system benchmark generation methodology. In Proceedings of the NEIS 2018, Conference on Sustainable Energy Supply and Energy Storage Systems, Hamburg, Germany, 20–21 September 2018. [Google Scholar]
- Schneider, K.; Mather, B.; Pal, B.; Ten, C.W.; Shirek, G.; Zhu, H.; Fuller, J.; Pereira, J.; Ochoa, L.; De Araujo, L.; et al. Analytic considerations and design basis for the IEEE distribution test feeders. IEEE Trans. Power Syst. 2017, 33, 3181–3188. [Google Scholar] [CrossRef]
- Heussen, K.; Steinbrink, C.; Abdulhadi, I.F.; Nguyen, V.H.; Degefa, M.Z.; Merino, J.; Jensen, T.V.; Guo, H.; Gehrke, O.; Bondy, D.E.M.; et al. ERIGrid holistic test description for validating cyber-physical energy systems. Energies 2019, 12, 2722. [Google Scholar] [CrossRef] [Green Version]
- Ebe, F.; Idlbi, B.; Casel, M.; Kondzialka, C.; Heilscher, G.; Seitl, C.; Bruendlinger, R.; Strasser, T. An approach for validating and testing micro grid and cell-based control concepts. In Proceedings of the CIRED 2018 Ljubljana Workshop on Microgrids and Local Energy Communities, Ljubljana, Slovenia, 7–8 June 2018. [Google Scholar]
- Strasser, T.I.; de Jong, E.C.; Sosnina, M. (Eds.) European Guide to Power System Testing; Springer: Cham, Switzerland, 2020. [Google Scholar]
| Ref. | Publication Date | Main Topic |
|---|---|---|
| [29] | 2007-06-02 | Microgrid-related research, development and demonstration effort |
| [30] | 2008-05-02 | Testing experiences in experimental microgrids |
| [31] | 2010-10-01 | Experimental and simulation-based microgrid test installations |
| [32] | 2014-04-20 | Microgrid control strategies |
| [42] | 2015-05-12 | Power system resilience |
| [2] | 2015-06-10 | Broad review of microgrid-related topics |
| [10] | 2016-02-02 | Optimization-based energy management in microgrids |
| [33] | 2016-09-16 | DERs scheduling for microgrids and virtual power plants |
| [9] | 2017-06-30 | Overview of multi-microgrids and available demonstration platforms |
| [34] | 2017-10-09 | Distributed control and optimization of microgrids and multi-microgrids |
| [7] | 2017-12-22 | Multi-microgrid architectures |
| [35] | 2018-03-22 | Microgrid management system architectures |
| [36] | 2018-04-03 | Recent microgrid-related developments and regulations |
| [37] | 2018-04-05 | Microgrid energy management systems |
| [38] | 2018-06-11 | Resilience of microgrids and multi-microgrids |
| [39] | 2018-06-18 | Microgrid achievements in the United States |
| [40] | 2018-11-15 | Networked microgrids |
| [8] | 2018-12-10 | Impact of microgrids on power system resilience |
| [43] | 2018-12-13 | Power system resilience |
| [3] | 2019-02-13 | Resilience aspects in microgrids |
| [41] | 2019-03 | Energy management in microgrids |
| [44] | 2019-12-09 | Optimal planning and operation of islanded microgrids |
| Ref. | Publication Date | Main Topic |
|---|---|---|
| [48] | 2012-09-28 | Integration of dynamic topology option into economic microgrid operation |
| [49] | 2014-04-09 | Optimal scheduling of DER considering the risk of outages |
| [27] | 2014-09-26 | Interaction of microgrids with and without independent islanding capabilities |
| [50] | 2016-06-13 | Value of reconfigurable microgrids in integrating Electric Vehicle (EVs) |
| [20] | 2016-08-10 | Resilient scheduling of microgrids affected by uncertainty |
| [51] | 2016-08-26 | Multi-objective scheduling of microgrids considering normal operation costs and the risk of load curtailment |
| [52] | 2016-10-15 | Microgrid scheduling considering operating costs, emissions, and reserve requirements |
| [53] | 2017-08-17 | Robust formulation of the optimal proactive scheduling problem for microgrids |
| [28] | 2017-12-13 | Risk-based strategies for multi-microgrid scheduling considering stochastic RESs |
| [54] | 2018-02-16 | Optimal scheduling for hybrid AC/DC multi-microgrids |
| [55] | 2018-02-20 | Integration of Demand Response (DR) programs and grid reconfiguration into microgrid asset scheduling |
| [56] | 2018-03-26 | Resilient asset scheduling in reconfigurable microgrids |
| [57] | 2018-05-11 | Security-constrained dispatch for microgrids using multi-objective optimization |
| [58] | 2018-08-17 | Resiliency enhancements by optional scheduling of networked microgrids |
| [59] | 2018-12-28 | Impact of scheduling discrepancies on interconnected microgrids |
| [60] | 2019-04-18 | Microgrid scheduling combining flexible time frame DER scheduling and single time interval-based optimal dispatch |
| [61] | 2019-07-02 | Resilient scheduling of networked multi-microgrids using a three-stage approach |
| [62] | 2019-08-07 | Proactive, resilient scheduling of interconnected microgrids |
| [63] | 2019-08-16 | Distributed energy management of interconnected microgrids considering adversarial actions |
| [64] | 2020-01-06 | Optimal, resilient operation of dynamic multi-microgrids |
| DER Types | DER Parameters | Load Types | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WT | PV | CHP | Thermal | EVs | MTs | EESs | Generic Unscheduled DERs | Generic Schedulable DERs | DER Ramp-Up/Down Constraints | DER Up/Down-Time Constraints | DER Operating P Constraints | DER Operating Q Constraints | DER Operating S Constraints | EV Charging Curve | Storage Capacity Constraints | Minimum Charge/Discharge Time | Constant Storage Efficiency | P(Q)-Loads | Z-Loads | Price-based DR Loads | Sheddable (Interruptible) Loads | Shiftable Loads | |
| Ref. | |||||||||||||||||||||||
| [48] | ✓(D) | ✓(St) | ✓(D) | ✓ | ✓ | ✓ | ✓ | ✓(St) | ✓(D) | ||||||||||||||
| [49] | ✓(D) | ✓(D) | ✓(D) | ✓(D) | ✓(D) | ✓ | ? | ✓(D) | ✓(D) | ||||||||||||||
| [27] | ✓(D) | ✓(ID) | ✓(D) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓(ID) | ✓(D) | ✓(D) | |||||||||||
| [50] | ✓(St) | ✓(St) | ✓(D) | ✓ | ✓ | ✓ | ✓(St) | ||||||||||||||||
| [20] | ✓(St) | ✓(St) | ✓(D) | ✓(D) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓(ID) | ✓(ID) | ✓(D) | |||||||||||
| [51] | ✓(D) | ✓(St) | ✓(D) | ✓ | ✓ | ✓ | ✓ | ✓(St) | ✓(D) | ||||||||||||||
| [52] | ✓(D) | ✓(St) | ✓(D) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓(St) | ||||||||||||
| [53] | ✓(D) | ✓(ID) | ✓(D) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓(ID) | ✓(ID) | ||||||||||||
| [28] | ✓(St) | ✓(St) | ✓(D) | ✓(D) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓(St) | |||||||||||||
| [54] | ✓(D) | ✓(ID) | ✓(D) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓(ID) | ✓(D) | ✓(D) | ||||||||||||
| [55] | ✓(St) | ✓(St) | ✓(D) | ✓(D) | ✓ | ✓ | ✓ | ✓(D) | ✓(D) | ||||||||||||||
| [56] | ✓(D) | ✓(St) | ✓(D) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓(St) | ✓(D) | ✓(D) | ||||||||||
| [57] | ✓(D) | ✓(D) | ✓(D) | ✓ | ✓ | ✓ | ✓(D) | ? | ✓(D) | ||||||||||||||
| [58] | ✓(St) | ✓(St) | ✓(D) | ✓(St) | ✓(D) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓(St) | ✓(D) | ✓(D) | ||||||||||
| [59] | ✓(D) | ✓(D) | ✓(D) | ✓ | ✓ | ✓ | ✓(St) | ✓(D) | |||||||||||||||
| [60] | ✓(D) | ✓(D) | ✓(D) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓(D) | ✓(D) | ||||||||||||
| [61] | ✓(St) | ✓(D) | ✓(D) | ✓ | ✓ | ✓ | ✓(St) | ✓(St) | |||||||||||||||
| [62] | ✓(ID) | ✓(D) | ✓(D) | ✓(ID) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓(ID) | ✓(D) | ||||||||||||
| [63] | ✓(D) | ✓(St) | ✓(D) | ✓ | ✓ | ✓ | ✓(St) | ||||||||||||||||
| [64] | ✓(D) | ✓(St) | ✓(D) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓(St) | ✓(St) | |||||||||||||
| Line Model | AC Links | DC Links | Bus-Voltage Model | Bus-Voltage Constraints | Bus-Voltage Transient Constraints | Voltage Angle Constraint (Bus or Line) | Frequency Constraints | Line-Active Power-Flow Constraints | Line-Reactive Power-Flow Constraints | Line-Apparent Power-Flow Constraints | Line-Current Constraints | Line/Main Grid-P/Q/S Fluctuation Constraints | Main Grid P (Min/Max) Constraints | Main Grid Q (Min/Max) Constraints | Main Grid S (Min/Max) Constraints | Single Main Grid Point of Common Coupling (PCC) | Static Transformer | VAR Compensator (Q) | Dynamic AC/DC or DC/DC or AC/AC Converter | Constant Converter Efficiency | Remote Switches | Switching Operation Constraints | Radial Topology Constraint | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ref. | ||||||||||||||||||||||||
| [48] | Res./Admittance | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||
| [49] | ? | ✓ | ? | ✓ | ✓ | ? | ✓ | |||||||||||||||||
| [27] | Single Bus | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||||
| [50] | Res./Admittance | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||
| [20] | Res./Admittance | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||
| [51] | Res./Admittance | ✓ | ✓ | ✓ | ? | ? | ✓ | ? | ✓ | |||||||||||||||
| [52] | Res./Admittance | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||
| [53] | Res./Admittance | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||
| [28] | Res./Admittance | ✓ | ✓ | ✓ | ✓ | ? | ||||||||||||||||||
| [54] | Connection Graph | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||||
| [55] | Res./Admittance | ✓ | ✓ | ✓ | ✓ | ? | ✓ | ✓ | ✓ | |||||||||||||||
| [56] | Res./Admittance | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||||
| [57] | Res./Admittance | ✓ | ? | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ? | ? | ? | ||||||||||
| [58] | Connection Graph | ? | ? | ✓ | ||||||||||||||||||||
| [59] | Line Efficiencies | ? | ? | ✓ | ✓ | ? | ||||||||||||||||||
| [60] | Res./Admittance | ✓ | ? | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ? | ? | |||||||||||||
| [61] | MMG Star | ? | ? | ✓ | ✓ | |||||||||||||||||||
| [62] | Res./Admittance | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||||
| [63] | Connection Graph | ? | ? | ✓ | ✓ | |||||||||||||||||||
| [64] | Res./Admittance | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Method | Location | Formulation | Model Type | Linearization | Convexification | Problem Decomposition | Independent Sampling | Correlated Sampling | Scenario Reduction | |
|---|---|---|---|---|---|---|---|---|---|---|
| Ref. | ||||||||||
| [48] | Mathematical | Central | Stochastic | MIP | ✓ | ✓ | ✓ | |||
| [49] | ICA | Central | Stochastic | Unconstrained | ||||||
| [27] | Mathematical | Central | Deterministic | MIP | ✓ | |||||
| [50] | CSA | Central | Stochastic | Unconstrained | ✓ | ✓ | ||||
| [20] | Mathematical | Central | Stochastic | Unconstrained | ✓ | ? | ? | ✓ | ||
| [51] | Genetic+Mat. | Central | Stochastic | MILP | ✓ | ✓ | ✓ | |||
| [52] | PSO+Mat. | Central | Stochastic | Unconstrained | ✓ | |||||
| [53] | Mathematical | Central | Deterministic | Quadratic | ✓ | ✓ | ||||
| [28] | Genetic | Central | Stochastic | MIP | ✓ | ✓ | ||||
| [54] | Mathematical | Hierarchical | Deterministic | Unconstrained | ✓ | ✓ | ||||
| [55] | EMA | Central | Stochastic | MIP | ✓ | |||||
| [56] | Mathematical | Central | Stochastic | Unconstrained | ✓ | ✓ | ✓ | ✓ | ||
| [57] | PaCcET | Central | Stochastic | Unconstrained | ||||||
| [58] | Mathematical | Central | Stochastic | MIP | ? | ? | ||||
| [59] | Mathematical | Central | Deterministic | MILP | ||||||
| [60] | Mathematical | Central | Deterministic | Unconstrained | ✓ | ✓ | ||||
| [61] | Mathematical | Central | Stochastic | MILP | ✓ | |||||
| [62] | Mathematical | Central | Deterministic | MILP | ✓ | ✓ | ||||
| [63] | Mathematical | Distributed | Stochastic | Quadratic | ✓ | ✓ | ||||
| [64] | PSO | Central | Stochastic | Unconstrained | ✓ | ✓ | ✓ | ✓ |
| Multi-Objective Formulation | Fuzzy Decision Making | Cost - DER Production Cost (Linear) | Cost - DER Production Cost (Non-Linear) | Cost - Start-up | Cost - Shut-down | Cost - Main-Grid Transfer | Cost - Energy Trading (Transfer) to Adjacent Microgrids | Cost - Maintenance | Cost - EES or V2G Operation | Cost (Income) - Energy Sold to Customers | Cost - Power Losses | Cost - Value of Lost Load/Energy not Supplied | Cost - Scheduling of Additional Load | Cost - Demand-Response Reserve Commitment | Cost - Generation Reserve Commitment | Cost - EES Capacity Reserve | Cost - Grid Capacity Reserve | Cost - Switching (Topology Changes) | Cost - Deviation from a (High-Level) Schedule | Cost - Uncertainty or Security Margins | Emissions (Directly) | Lost Load/Energy not Supplied (Directly) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ref. | |||||||||||||||||||||||
| [48] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||||
| [49] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||
| [27] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||
| [50] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||||
| [20] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||||
| [51] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||
| [52] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||
| [53] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||||
| [28] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||
| [54] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||
| [55] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||
| [56] | ✓ | ✓ | ✓ | ||||||||||||||||||||
| [57] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||||
| [58] | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||||
| [59] | ✓ | ✓ | ✓ | ||||||||||||||||||||
| [60] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||
| [61] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||
| [62] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||
| [63] | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||||
| [64] | ✓ | ✓ | ✓ |
| Failure Modes | Mitigation | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Main-Grid Failure | Generator Tripping | Line Tripping | Bus Fault or Disconnection | Short-Circuit Fault (Detailed Model) | Deviated Schedule (Generic) | Main-Grid Disconnection | Fault Isolation and Rerouting | Grid Splitting | |
| Ref. | |||||||||
| [48] | ✓(St) | ✓(St) | ✓(St) | ✓ | ✓ | ||||
| [49] | ✓(ID) | ✓(St) | ✓ | ||||||
| [27] | ✓(ID) | ✓ | |||||||
| [50] | ✓(St) | ✓ | |||||||
| [20] | ✓(St) | ✓ | |||||||
| [51] | ✓(St) | ✓ | |||||||
| [52] | ✓(ID) | ✓ | |||||||
| [53] | ✓(ID) | ✓ | |||||||
| [28] | ✓(St) | ✓(St) | ✓ | ? | ✓ | ||||
| [54] | ✓(ID) | ✓(ID) | ✓ | ✓ | |||||
| [55] | ✓(St) | ✓(St) | ✓(St) | ✓ | ✓ | ||||
| [56] | ✓(ID) | ✓ | ✓ | ✓ | |||||
| [57] | ✓(ID) | ✓(St) | ✓ | ||||||
| [58] | ✓(ID) | ✓ | |||||||
| [59] | ✓(ID) | ✓ | |||||||
| [60] | ✓(ID) | ✓ | |||||||
| [61] | ✓(St) | ✓(St) | ✓ | ✓ | |||||
| [62] | ✓(ID) | ✓(ID) | ✓(ID) | ✓ | ✓ | ||||
| [63] | ✓(St) | ✓ | ✓ | ||||||
| [64] | ✓(St) | ✓ | ✓ | ✓ | |||||
| Type | Failure Modes | Test-Grid | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Test Case ID | Numerical Simulation | Laboratory Test | Main-Grid Failure | Generator Tripping | Line Tripping | Deviated Schedule (Generic) | Parameter or Forecasting Deviations | Specification | No. of Buses | No. of DER (total) | No. of Schedulable DER | |
| Ref. | ||||||||||||
| [48] | Standard | ✓ | ✓ | ✓ | ✓ | IIT Standard MG | 10 | 2 | 2 | |||
| [48] | HRDS | ✓ | ✓ | ✓ | ✓ | IIT HRDS MG | 12 | 2 | 2 | |||
| [49] | ✓ | CIGRE | 12 | 6 | 3 | |||||||
| [27] | Base Case | ✓ | ✓ | - | 1 | 2 | 1 | |||||
| [27] | Extension | ✓ | ✓ | - | 1 | 3 | 2 | |||||
| [50] | ✓ | IEEE 33-bus | 32 | 8 | 5 | |||||||
| [20] | ✓ | ✓ | IEEE 33-bus | 33 | 11 | 6 | ||||||
| [51] | ✓ | ✓ | Listed in [75] | 34 | 5 | 3 | ||||||
| [52] | ✓ | Listed in [76] | 38 | 19 | 9 | |||||||
| [53] | ✓ | ✓ | IEEE 33-bus | 33 | 14 | 6 | ||||||
| [28] | ✓ | ✓ | ✓ | IEEE 33-bus | 33 | 10 | 5 | |||||
| [54] | ✓ | ✓ | ✓ | - | 4 | 4 | 1 | |||||
| [55] | ✓ | PG&E 69-bus | 69 | 11 | 5 | |||||||
| [56] | Case 0 | ✓ | IEEE 33-bus | 33 | 0 | 0 | ||||||
| [56] | Case 0 | ✓ | IEEE 69-bus | 69 | 0 | 0 | ||||||
| [56] | Case 1-3 | ✓ | ✓ | ? | 32 | 7 | 5 | |||||
| [57] | ✓ | - | 6 | 4 | 3 | |||||||
| [58] | ✓ | ✓ | - | 3 | 17 | 12 | ||||||
| [59] | ✓ | ✓ | ✓ | ✓ | - | 3 | 6 | 3 | ||||
| [60] | Case 1 | ✓ | IEEE 34-bus | 34 | 7 | 7 | ||||||
| [60] | Case 2 | ✓ | IEEE 123-bus | 123 | 15 | 15 | ||||||
| [61] | ✓ | ✓ | ✓ | - | 3 | 4 | 2 | |||||
| [62] | ✓ | ✓ | ✓ | ✓ | ✓ | IEEE 13-bus + 34-bus | 47 | 12 | 10 | |||
| [63] | ✓ | ✓ | PG&E 69-bus | 69 | 24 | 16 | ||||||
| [64] | ✓ | ✓ | ✓ | IEEE 33-bus | 33 | ? | 9 | |||||
| Execution Parameters | ||||||
|---|---|---|---|---|---|---|
| Test Case ID | Time Horizion [h] | Step-Size [min] | Scheduling Scheme | Execution Time [s] | Reported Execution Platform | |
| Ref. | ||||||
| [48] | Standard | 8760 (?) | 60 | Run-Once | ||
| [48] | HRDS | 8760 (?) | 60 | Run-Once | ||
| [49] | 24 | Run-Once | MATLAB implementation | |||
| [27] | Base Case | 24 | 60 | Run-Once | CPLEX 11.0, 2.4GHz PC | |
| [27] | Extension | 24 | 60 | Run-Once | CPLEX 11.0, 2.4GHz PC | |
| [50] | 24 | 60 | Run-Once | |||
| [20] | 24 | 60 | Run-Once | 22.59 | Intel Core i7 CPU, 3.20 GHz, 4GB RAM, IBM ILOG CPLEX 12.4, GAMS IDE | |
| [51] | 24 | 60 | Run-Once | MATPOWER | ||
| [52] | 24 | 60 | Run-Once | MATPOWER (MINOPF) | ||
| [53] | 24 | 60 | Run-Once | Intel Core i7 CPU, 3.20 GHz, 4GB RAM, IBM ILOG CPLEX 12.4, GAMS IDE | ||
| [28] | 24 | 60 | Run-Once | MINLP model, NSGAII algorithm, MATLAB 2016a | ||
| [54] | 24 | 15 | Run-Once | 124.37 | MATLAB, YALMIP toolbox, CPLEX 12.4, 32-bit PC, 2.10GHz CPU, 2GB RAM | |
| [55] | 24 | 60 | Run-Once | |||
| [56] | Case 0 | - | - | Run-Once | CPLEX 11.0, 2.4-GHz PC | |
| [56] | Case 1-3 | 24 | 60 | Run-Once | CPLEX 11.0, 2.4-GHz PC | |
| [57] | 5 | 60 | Run-Once | Win7, E5420 CPU, 2 Cores, 2.5 GHz, 16 GB RAM | ||
| [58] | 24 | 60 | Run-Once | GAMS, BARON | ||
| [59] | 24 | 1 | Run-Once | IBM CPLEX | ||
| [60] | Case 1 | 24 | 30 | Interleaved | 9.8 | OpenDSS + OPTI Toolbox + MATLAB, Windows, Intel Core i5-4300M, 2.60GHz, 8 GB RAM |
| [60] | Case 2 | 24 | 30 | Interleaved | 36.9 | OpenDSS + OPTI Toolbox + MATLAB, Windows, Intel Core i5-4300M, 2.60GHz, 8 GB RAM |
| [61] | 24 | 60 | Run-Once | 0.06 | GAMS DIE, CPLEX 12.4, Intel Core i7 CPU, 3GHz, 12 GB RAM | |
| [62] | 6 | 15 | Run-Once | Python 2.7, GUROBI 8.0.0, Intel Core i7-7700, 4.2 GHz, 16GB RAM | ||
| [63] | 1 | 15 | Fully Cyclic | MATLAB with YALMIP, Intel Core i7, 2.6 GHz, 16GB RAM | ||
| [64] | 24 | 60 | Run-Once | |||
| Load | Main-Grid Energy Prices | PV/Irradiation | Wind | EV Charging | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Type | Source | Type | Source | Type | Source | Type | Source | Type | Source | |
| Ref. | ||||||||||
| [48] | Det. | - | Det. | UnAv. | N.A. | - | N.A. | - | N.A. | - |
| [49] | Det. | - | Det. | UnAv. | Det. | - | Det. | - | N.A. | - |
| [27] | Det. + TI Dist. | - | Det. + TI Dist. | - | N.A. | - | N.A. | - | N.A. | - |
| [50] | Det. + TI Dist. | - | Det. + TI Dist. | - | Det. + TI Dist. | - | Det. + TI Dist. | - | Det. + TI Dist. | - |
| [20] | Dist. | [78] | Dist. | [78] | N.A. | - | TI Dist. | [79] | TI Dist. | - |
| [51] | Det. + TI Dist. | [80] | Det. | - | Det. + TI Dist. | [80] | Det. + TI Dist. | [80] | N.A. | - |
| [52] | Det. + TI Dist. | - | Det. | [81] | Det. + TI Dist. | - | Det. + TI Dist. | - | N.A. | - |
| [53] | Det. + Det. Dev. | [20] | Det. + ID Int. | [20] | N.A. | - | N.A. | - | N.A. | - |
| [28] | Det. + TI Dist. | - | Constant | - | TI Dist. | - | TI Dist. | - | N.A. | - |
| [54] | Det. + ID Int. | - | Det. | - | Det. + ID Int. | - | Det. + ID Int. | - | N.A. | - |
| [55] | Det. | - | Det. | - | Dist. | - | Dist. | - | N.A. | - |
| [56] | Det. + Dist. | - | Det. + Dist. | - | N.A. | - | Det. + Dist. | - | N.A. | - |
| [57] | Det. | - | Det. | - | Det. | - | N.A. | - | N.A. | - |
| [58] | Det. + TI Dist. | - | Det. | - | Det. + TI Dist. | - | Det. + TI Dist. | - | N.A. | - |
| [59] | Det. + Det. Dev. | [82] | Det. | - | Det. + Det. Dev. | [83] | N.A. | - | N.A. | - |
| [60] | Det. | - | Det. | - | Det. | - | Det. | - | N.A. | - |
| [61] | Dist. | [84] | Dist. | [84] | N.A. | - | Dist. | [84] | N.A. | - |
| [62] | Det. + ID Int. | [85] | Det. | [86] | N.A. | - | Det. + ID Int. | [87] | Constant | [88] |
| [63] | Det. + TI Dist. | UnAv. | Constant | - | Det. + TI Dist. | UnAv. | N.A. | - | N.A. | - |
| [64] | Det. + TI Dist. | - | Det. + TI Dist. | - | Det. + TI Dist. | - | Det. + TI Dist. | - | N.A. | - |
| Test Case ID | (Expected) Energy Not Supplied | System Average Interruption Frequency Index | System Average Interruption Duration Index | Customer Average Interruption Frequency Index | Customer Average Interruption Duration Index | Loss of Load Expectation | (Expected) Operating Cost | Emission (e.g., CO2) | (Expected) Energy Transfer or Trading (Main Grid, Intra-MG) | Power factor (Single line or min/max) | Network Losses (Single line, cumulative) | Voltage (Single Bus or min/max) | Current (Single Line or min/max) | Voltage Angle (Single Bus or min/max) | Frequency | Accumulated Reserve Capacities | Countermeasure Success/Failure Rate | Deviation to Expected Case | Value at Risk | Conditional Value at Risk | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ref. | |||||||||||||||||||||
| [48] | Standard | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [48] | HRDS | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [49] | ✓ | ✓ | |||||||||||||||||||
| [27] | Base Case | ✓ | ✓ | ||||||||||||||||||
| [27] | Extension | ✓ | ✓ | ||||||||||||||||||
| [50] | ✓ | ✓ | ✓ | ||||||||||||||||||
| [20] | ✓ | ✓ | |||||||||||||||||||
| [51] | ✓ | ✓ | ✓ | ||||||||||||||||||
| [52] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||||
| [53] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||
| [28] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| [54] | ✓ | ✓ | ✓ | ||||||||||||||||||
| [55] | ✓ | ✓ | ✓ | ||||||||||||||||||
| [56] | Case 0 | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||
| [56] | Case 1-3 | ✓ | ✓ | ||||||||||||||||||
| [57] | ✓ | ✓ | ✓ | ||||||||||||||||||
| [58] | ✓ | ✓ | ✓ | ||||||||||||||||||
| [59] | ✓ | ✓ | ✓ | ||||||||||||||||||
| [60] | Case 1 | ✓ | ✓ | ✓ | |||||||||||||||||
| [60] | Case 2 | ✓ | |||||||||||||||||||
| [61] | ✓ | ✓ | ✓ | ||||||||||||||||||
| [62] | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||
| [63] | ✓ | ✓ | |||||||||||||||||||
| [64] | ✓ | ✓ | ✓ | ✓ |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spiegel, M.H.; Veith, E.M.S.P.; Strasser, T.I. The Spectrum of Proactive, Resilient Multi-Microgrid Scheduling: A Systematic Literature Review. Energies 2020, 13, 4543. https://doi.org/10.3390/en13174543
Spiegel MH, Veith EMSP, Strasser TI. The Spectrum of Proactive, Resilient Multi-Microgrid Scheduling: A Systematic Literature Review. Energies. 2020; 13(17):4543. https://doi.org/10.3390/en13174543
Chicago/Turabian StyleSpiegel, Michael H., Eric M. S. P. Veith, and Thomas I. Strasser. 2020. "The Spectrum of Proactive, Resilient Multi-Microgrid Scheduling: A Systematic Literature Review" Energies 13, no. 17: 4543. https://doi.org/10.3390/en13174543
APA StyleSpiegel, M. H., Veith, E. M. S. P., & Strasser, T. I. (2020). The Spectrum of Proactive, Resilient Multi-Microgrid Scheduling: A Systematic Literature Review. Energies, 13(17), 4543. https://doi.org/10.3390/en13174543