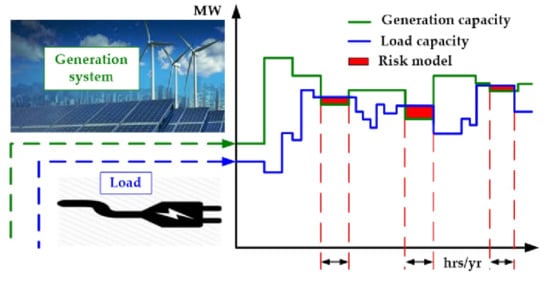
Predictive Reliability Assessment of Generation System
Abstract
:1. Introduction
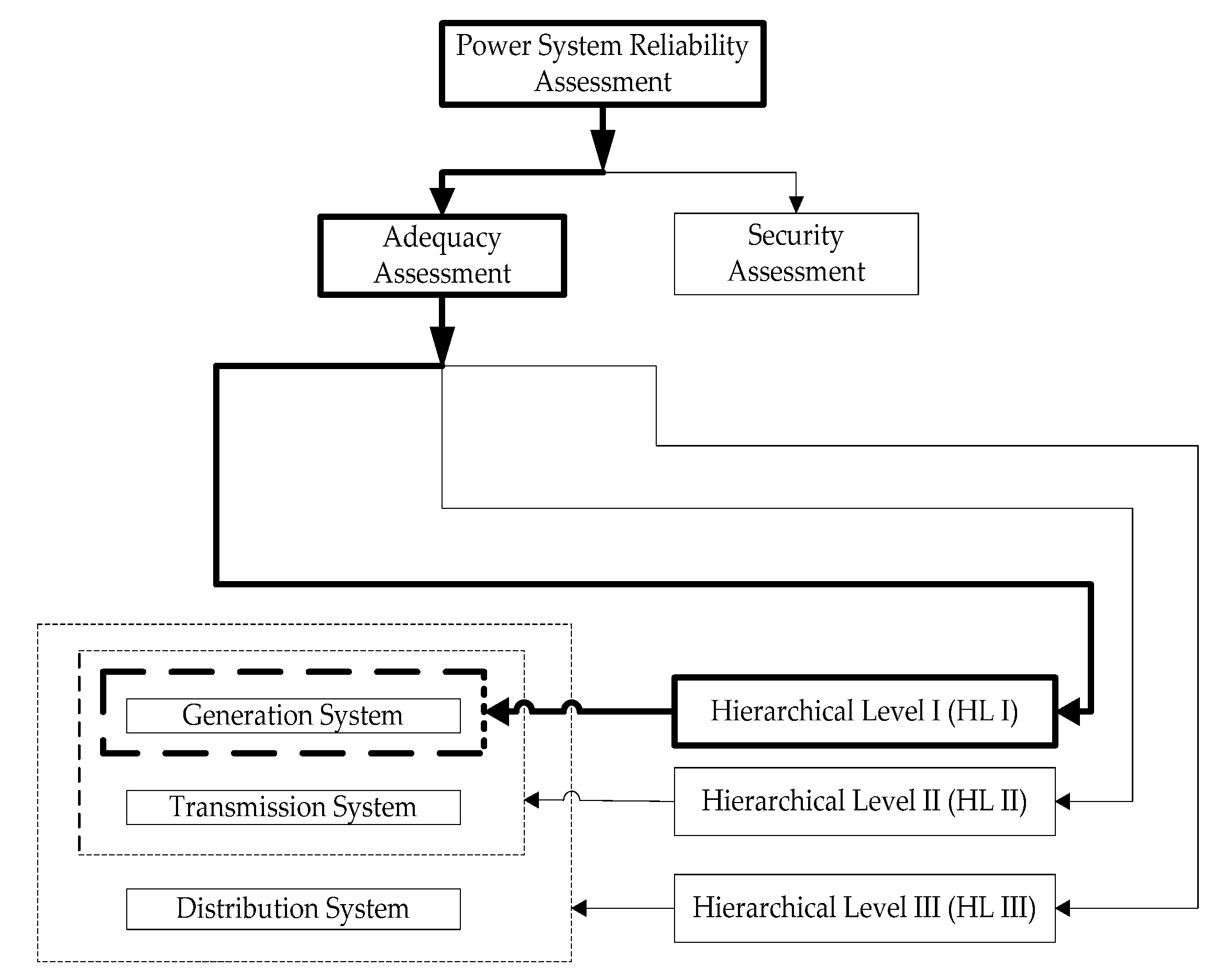
2. Power System Reliability Assessment
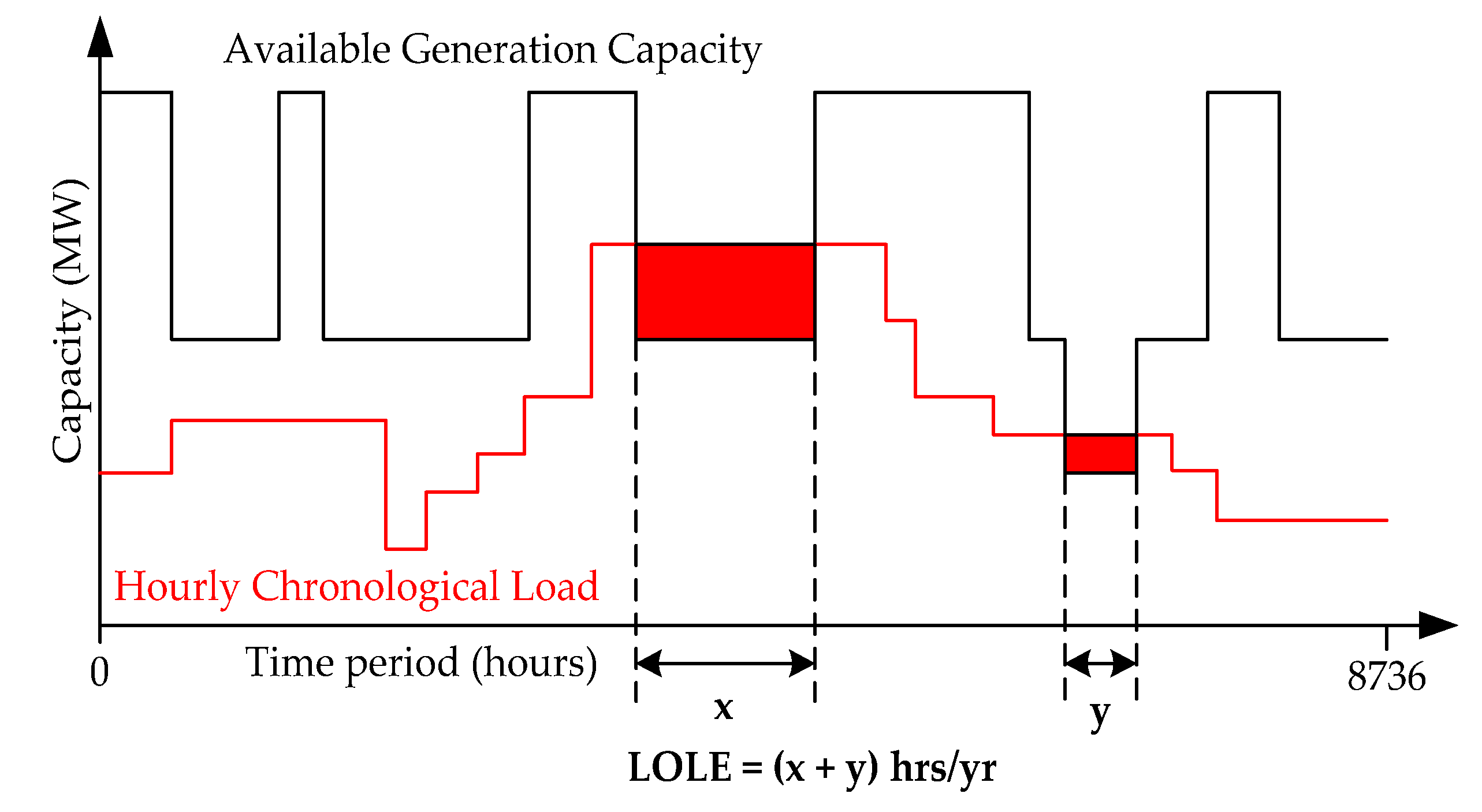
2.1. The Generation System Reliability Index
2.2. The Generation Model, Load Model and the Risk Model
- (1)
- For each of the random numbers generated in U1, the TTF is calculated using (2);
- (2)
- For each of the random numbers generated in U2, the TTR is calculated using (3);
- (3)
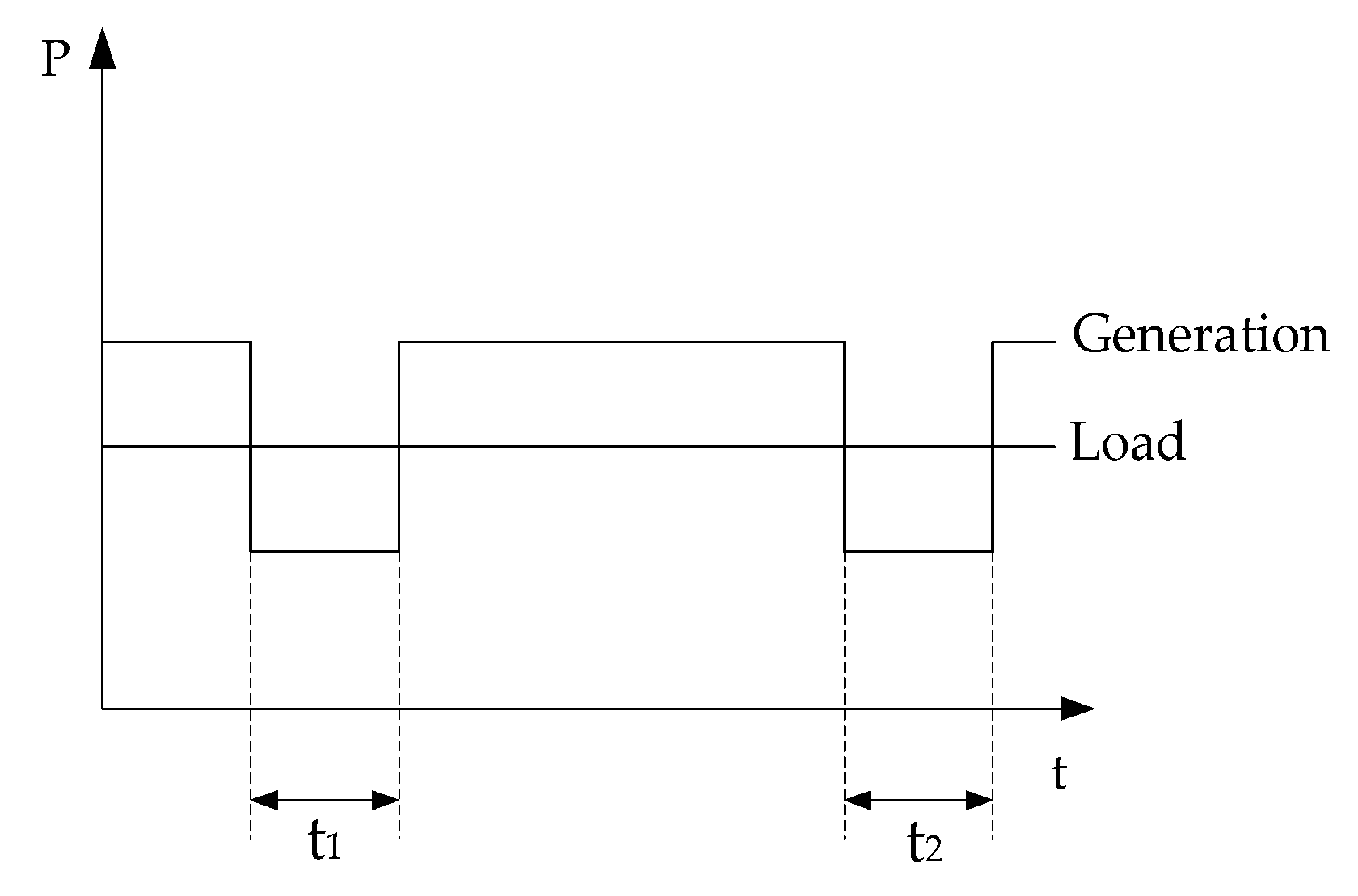
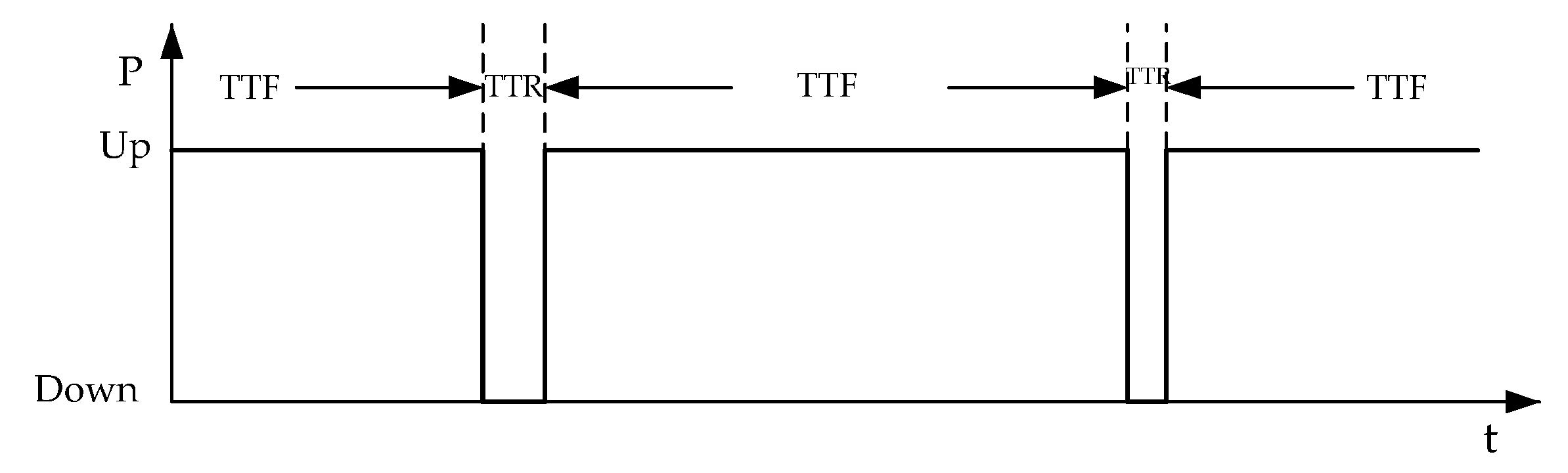
- The resultant series of TTF and TTR are thereafter graphically and sequentially joined (one after the other) (i.e., TTF, then TTR, then TTF, and so on) as shown in Figure 5. This is continued until the total value reaches 8736 representing the total number of hours of a year. This is performed for each of the entire generating units. In the end, they are combined by a superimposition method to obtain a single resultant system capacity as shown in Figure 4. This is the annual duration of the generation capacity states, otherwise known as the generation model.
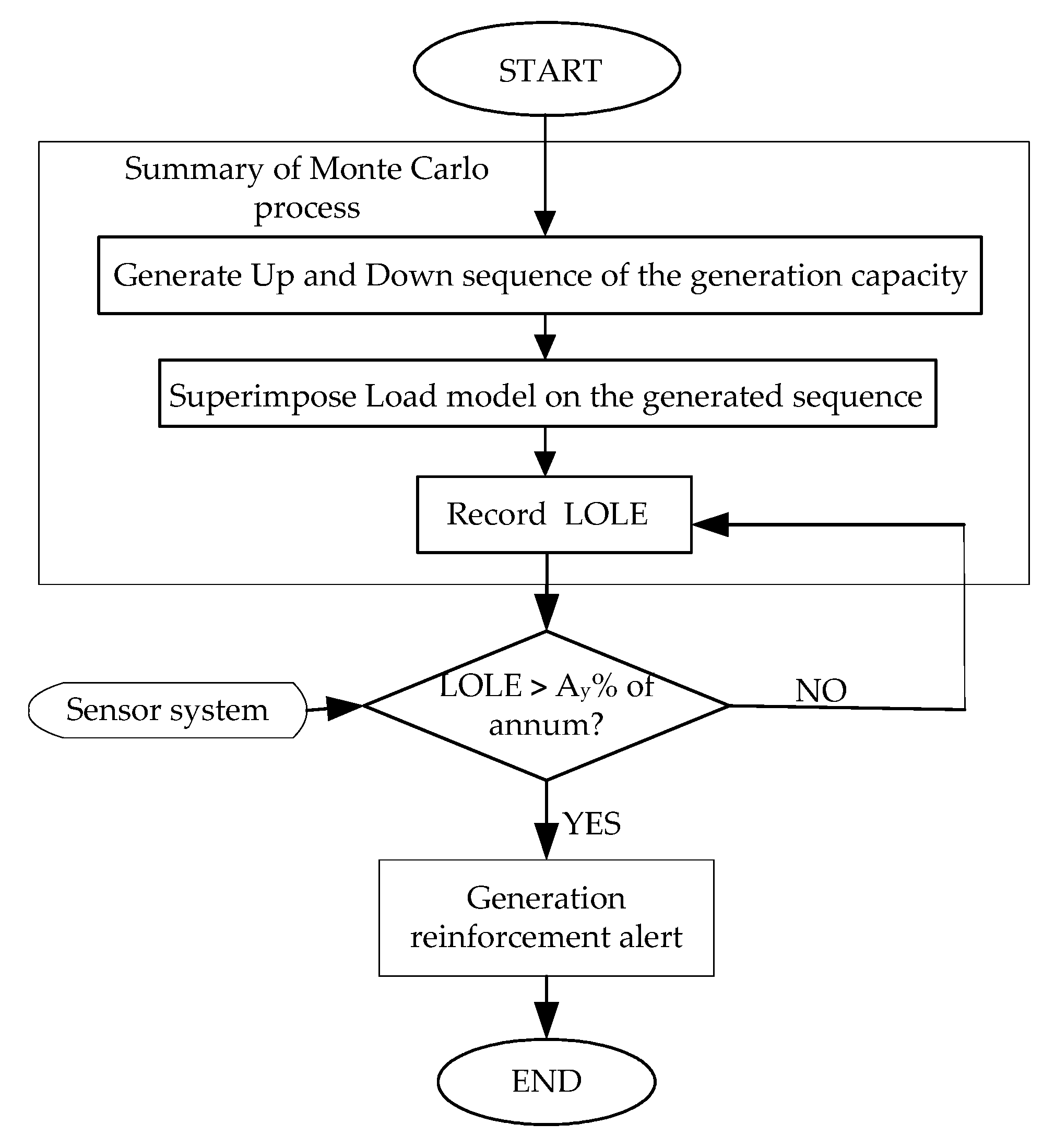
3. The Reliability Assessment and the Monte Carlo System
- A.
- Total generation capacity [Appendix A—Table A1] of 3405 MW ranging from 12 MW to 400 MW. This consists of 32 generating units and their individual forced outage rates, mean time to fail (MTTF) and mean time to repair (MTTR). The entire individual units are superimposed with one another to obtain a single unit known as the generation model. The generation model is further superimposed with the load model to calculate the assessment index (LOLE) [29].
- B.
- The load is made up of the following [Appendix B]:
- (1)
- The annual peak load of 2850 MW;
- (2)
- Weekly peak load presented in percent of the annual peak load. This comprises of 52 percentage values that represent the 52 weeks of a year (Table A2);
- (3)
- Daily peak load presented in percent of the weekly peak load. This comprises of 7 percentage values that represent the 7 days of a week (Table A3);
- (4)
- Hourly peak load presented in percent of the daily peak load. This comprises of 24 percentage values that represent the 24 h of a day (Table A4).
Modeling the Generation Capacity and the Load
- A% < Ay%, generation system is reliable,
- A% = Ay%, generation system is reliable, and
- A% > Ay%, generation system is unreliable.
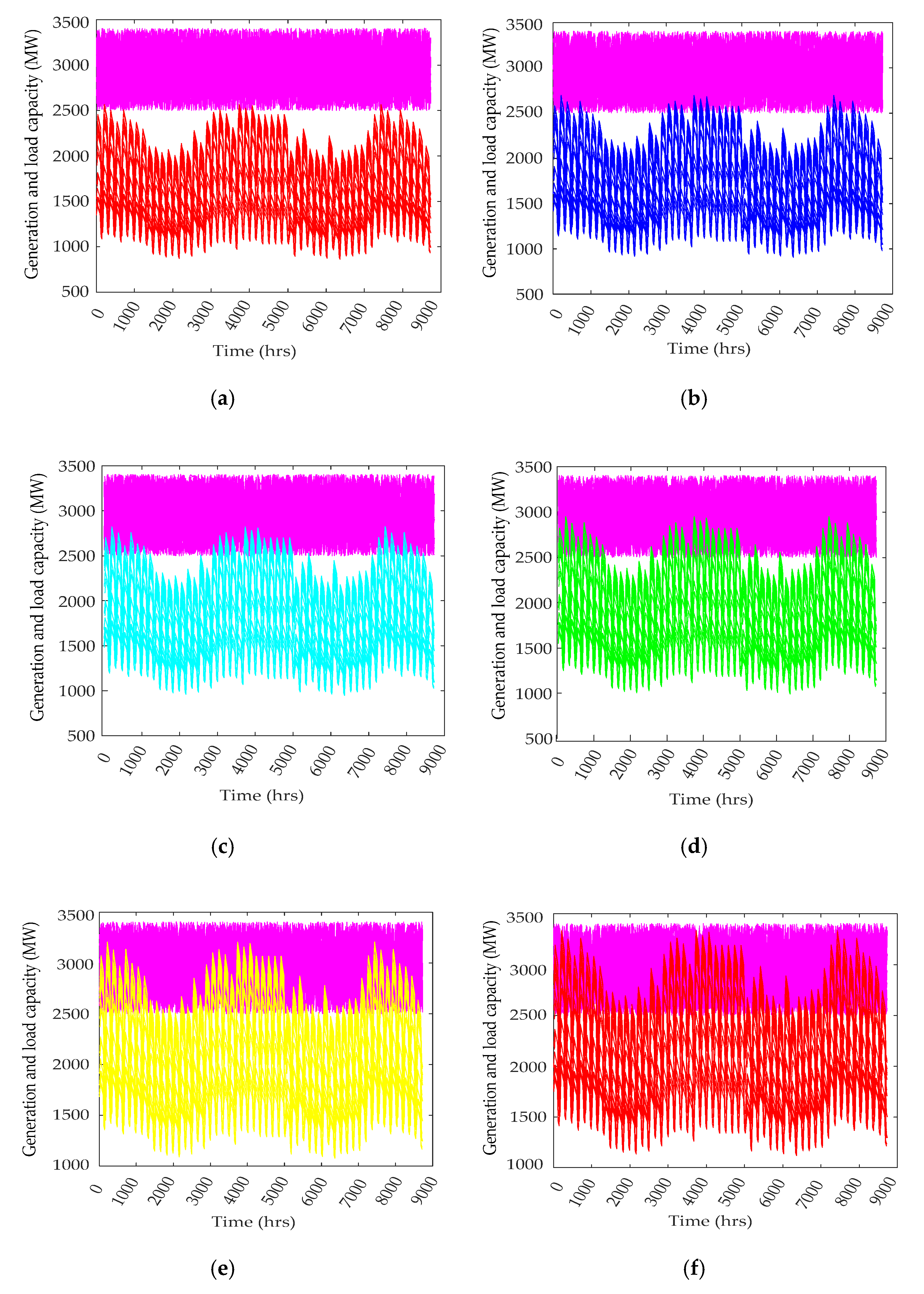
4. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Unit Size (MW) | Number of Units | Forced Outage Rate | Mean Time To Fail (MTTF) (Hours) | Mean Time To Repair (MTTR) (Hours) |
|---|---|---|---|---|
| 12 | 5 | 0.02 | 2940 | 60 |
| 20 | 4 | 0.10 | 450 | 50 |
| 50 | 6 | 0.01 | 1980 | 20 |
| 76 | 4 | 0.02 | 1960 | 40 |
| 100 | 3 | 0.04 | 1200 | 50 |
| 155 | 4 | 0.04 | 960 | 40 |
| 197 | 3 | 0.05 | 950 | 50 |
| 350 | 1 | 0.08 | 1150 | 100 |
| 400 | 2 | 0.12 | 1100 | 150 |
Appendix B
| Week | Peak Load (%) | Week | Peak Load (%) | Week | Peak Load (%) | Week | Peak Load (%) | Week | Peak Load (%) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 86.2 | 12 | 72.7 | 23 | 90.0 | 34 | 72.9 | 45 | 88.5 |
| 2 | 90.0 | 13 | 70.4 | 24 | 88.7 | 35 | 72.6 | 46 | 90.9 |
| 3 | 87.8 | 14 | 75.0 | 25 | 89.6 | 36 | 70.5 | 47 | 94.0 |
| 4 | 83.4 | 15 | 72.1 | 26 | 86.1 | 37 | 78.0 | 48 | 89.0 |
| 5 | 88.0 | 16 | 80.0 | 27 | 75.5 | 38 | 69.5 | 49 | 94.2 |
| 6 | 84.1 | 17 | 75.4 | 28 | 81.6 | 39 | 72.4 | 50 | 97.0 |
| 7 | 83.2 | 18 | 83.7 | 29 | 80.1 | 40 | 72.4 | 51 | 100.0 |
| 8 | 80.6 | 19 | 87.0 | 30 | 88.0 | 41 | 74.3 | 52 | 95.2 |
| 9 | 74.0 | 20 | 88.0 | 31 | 72.2 | 42 | 74.4 | – | – |
| 10 | 73.7 | 21 | 86.5 | 32 | 77.6 | 43 | 80.0 | – | – |
| 11 | 71.5 | 22 | 81.1 | 33 | 80.6 | 44 | 88.1 | – | – |
| Day | Peak Load (%) |
|---|---|
| Monday | 93 |
| Tuesday | 100 |
| Wednesday | 98 |
| Thursday | 96 |
| Friday | 94 |
| Saturday | 77 |
| Sunday | 75 |
| Winter Weeks 1–8 and 44–52 | Summer Weeks 18–30 | Spring/Fall Weeks 9–17 and 31–43 | ||||
|---|---|---|---|---|---|---|
| Hour | Weekday | Weekend | Weekday | Weekend | Weekday | Weekend |
| 12–1 a.m. | 67 | 78 | 64 | 74 | 63 | 75 |
| 1–2 | 63 | 72 | 60 | 70 | 62 | 79 |
| 2–3 | 60 | 68 | 58 | 66 | 60 | 69 |
| 3–4 | 59 | 66 | 56 | 65 | 58 | 66 |
| 4–5 | 59 | 64 | 56 | 64 | 59 | 65 |
| 5–6 | 60 | 65 | 58 | 62 | 65 | 65 |
| 6–7 | 74 | 66 | 64 | 62 | 72 | 68 |
| 7–8 | 86 | 70 | 76 | 66 | 85 | 74 |
| 8–9 | 95 | 80 | 87 | 81 | 95 | 83 |
| 9–10 | 96 | 88 | 95 | 86 | 99 | 89 |
| 10–11 | 96 | 90 | 99 | 91 | 100 | 92 |
| 11–Noon | 95 | 91 | 100 | 93 | 99 | 94 |
| Noon–1 p.m. | 95 | 90 | 99 | 93 | 93 | 91 |
| 1–2 | 95 | 88 | 100 | 92 | 92 | 90 |
| 2–3 | 93 | 87 | 100 | 91 | 90 | 90 |
| 3–4 | 94 | 87 | 97 | 91 | 88 | 86 |
| 4–5 | 99 | 91 | 96 | 92 | 90 | 85 |
| 5–6 | 100 | 100 | 96 | 94 | 92 | 88 |
| 6–7 | 100 | 99 | 93 | 95 | 96 | 92 |
| 7–8 | 96 | 97 | 92 | 95 | 98 | 100 |
| 8–9 | 91 | 94 | 92 | 100 | 96 | 97 |
| 9–10 | 83 | 92 | 93 | 93 | 90 | 95 |
| 10–11 | 73 | 87 | 87 | 88 | 80 | 90 |
| 11–12 | 63 | 81 | 72 | 80 | 70 | 85 |
References
- Alferidi, A.; Karki, R. Development of probabilistic reliability models of photovoltaic system topologies for system adequacy evaluation. Appl. Sci. 2017, 7, 176. [Google Scholar] [CrossRef] [Green Version]
- Singh, C.; Jirutitijaroen, P.; Mitra, J. Generation adequacy evaluation using discrete convolution. In Electric Power Grid Reliability Evaluation: Models and Methods, 1st ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2019; pp. 193–213. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, Y. A frequency and duration method for adequacy assessment of generation systems with wind farms. IEEE Trans. Power Syst. 2019, 34, 1151–1160. [Google Scholar] [CrossRef]
- Qi, X.; Ji, Z.; Wu, H.; Zhang, J.; Wang, L. Short-term reliability assessment of generating systems considering demand response reliability. IEEE Access 2020, 8, 74371–74384. [Google Scholar] [CrossRef]
- Micky, R.R.; Lakshmi, R.; Sunitha, R.; Ashok, S. Generation adequacy assessment for microgrid with ESS. In Proceedings of the IEEE 7th Power India International Conference (PIICON), Bikaner, India, 25–27 November 2016. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L.; Xiang, Y.; Ten, C.W. Power system reliability evaluation with scada cybersecurity considerations. IEEE Trans. Smart Grid 2015, 6, 1707–1721. [Google Scholar] [CrossRef]
- Jia, H.; Ding, Y.; Song, Y.; Singh, C.; Li, M. Operating reliability evaluation of power systems considering flexible reserve provider in demand side. IEEE Trans. Smart Grid 2019, 10, 3452–3464. [Google Scholar] [CrossRef] [Green Version]
- Gunduz, H.; Khan, Z.A.; Altamimi, A.; Jayaweera, D. An innovative methodology for load and generation modelling in a reliability assessment with PV and smart meter readings. In Proceedings of the IEEE Power and Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018. [Google Scholar] [CrossRef]
- Yan, C.; Bie, Z.; Ling, Y.; Li, G.; Xiong, F.; Wen, J. A comprehensive reliability assessment index system for regional grid with a large renewable energy penetration. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016. [Google Scholar] [CrossRef]
- Guo, J.; Liu, W.; Syed, F.R.; Zhang, J. Reliability assessment of a cyber physical microgrid system in island mode. CSEE J. Power Energy Syst. 2019, 5, 46–55. [Google Scholar] [CrossRef]
- Allan, R.N.; Billinton, R. Reliability Evaluation of Power Systems, 2nd ed.; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Singh, C.; Jirutitijaroen, P.; Mitra, J. Introduction to power system reliability. In Electric Power Grid Reliability Evaluation, 1st ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2019; pp. 185–191. [Google Scholar] [CrossRef]
- Bagchi, A.; Goel, L.; Wang, P. Generation adequacy evaluation incorporating an aggregated probabilistic model of active distribution network components and features. IEEE Trans. Smart Grid 2018, 9, 2667–2680. [Google Scholar] [CrossRef]
- He, J.; Yuan, Z.; Yang, X.; Huang, W.; Tu, Y.; Li, Y. Reliability modeling and evaluation of urban multi-energy systems: A review of the state of the art and future challenges. IEEE Access 2020, 8, 98887–98909. [Google Scholar] [CrossRef]
- Bagchi, A.; Goel, L.; Wang, P. Adequacy assessment of generating systems incorporating storage integrated virtual power plants. IEEE Trans. Smart Grid 2019, 10, 3440–3451. [Google Scholar] [CrossRef]
- Su, S.; Hu, Y.; He, L.; Yamashita, K.; Wang, S. An assessment procedure of distribution network reliability considering photovoltaic power integration. IEEE Access 2019, 7, 60171–60185. [Google Scholar] [CrossRef]
- Qi, X.; Cheng, Q. Imprecise reliability assessment of generating systems involving interval probability. IET Gener. Transm. Distrib. 2017, 11, 4332–4337. [Google Scholar] [CrossRef]
- Kadhem, A.A.; Wahab, N.I.A.; Aris, I.; Jasni, J.; Abdalla, A.N. Reliability assessment of power generation systems using intelligent search based on disparity theory. Energies 2017, 10, 343. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Yu, Y.; Qin, C. Unified two-stage reconfiguration method for resilience enhancement of distribution systems. IET Gener. Transm. Distrib. 2019, 13, 1734–1745. [Google Scholar] [CrossRef]
- Zamani-Gargari, M.; Kalavani, F.; Abapour, M.; Mohammadi-Ivatloo, B. Reliability assessment of generating systems containing wind power and air separation unit with cryogenic energy storage. J. Energy Storage 2018, 16, 116–124. [Google Scholar] [CrossRef]
- Peng, L.; Hu, B.; Xie, K.; Tai, H.M.; Ashenayi, K. Analytical model for fast reliability evaluation of composite generation and transmission system based on sequential Monte Carlo simulation. Int. J. Electr. Power Energy Syst. 2019, 109, 548–557. [Google Scholar] [CrossRef]
- Dunkelberg, H.; Sondermann, M.; Meschede, H.; Hesselbach, J. Assessment of flexibilisation potential by changing energy sources using Monte Carlo simulation. Energies 2019, 12, 711. [Google Scholar] [CrossRef] [Green Version]
- Ansari, O.A.; Chung, C.Y. A hybrid framework for short-term risk assessment of wind-integrated composite power systems. IEEE Trans. Power Syst. 2019, 34, 2334–2344. [Google Scholar] [CrossRef]
- Wang, Y. An enhanced Markov chain Monte Carlo-integrated cross-entropy method with a partially collapsed Gibbs sampler for probabilistic spinning reserve adequacy evaluation of generating systems. Electr. Power Compon. Syst. 2017, 45, 1617–1628. [Google Scholar] [CrossRef]
- Zhao, Y.; Tang, Y.; Li, W.; Yu, J. Composite power system reliability evaluation based on enhanced sequential cross-entropy Monte Carlo simulation. IEEE Trans. Power Syst. 2019, 34, 3891–3901. [Google Scholar] [CrossRef]
- Singh, S.S.; Fernandez, E. Reliability assessment of a remote hybrid renewable energy system using Monte Carlo simulation. Int. J. Renew. Energy Technol. 2018, 9, 368. [Google Scholar] [CrossRef]
- Dagoumas, A. Assessing the impact of cybersecurity attacks on power systems. Energies 2019, 12, 725. [Google Scholar] [CrossRef] [Green Version]
- Tchórzewski, J.; Pytel, M. Neural modeling of the electrical power system development based on IEEE RTS test data. In Proceedings of the Modern Electric Power Systems (MEPS), Wroclaw, Poland, 6–9 July 2015. [Google Scholar] [CrossRef]
- Rathore, A.; Patidar, N.P. Reliability assessment using probabilistic modelling of pumped storage hydro plant with PV-Wind based standalone microgrid. Int. J. Electr. Power Energy Syst. 2019, 106, 17–32. [Google Scholar] [CrossRef]
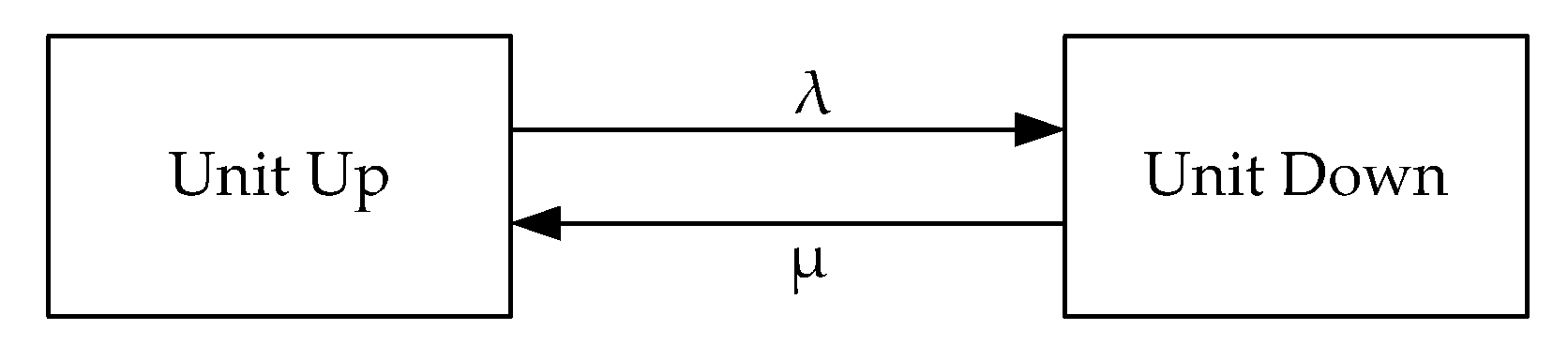


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Okoye, M.O.; Yang, J.; Lei, Z.; Yuan, J.; Ji, H.; Wang, H.; Feng, J.; Otitoju, T.A.; Li, W. Predictive Reliability Assessment of Generation System. Energies 2020, 13, 4350. https://doi.org/10.3390/en13174350
Okoye MO, Yang J, Lei Z, Yuan J, Ji H, Wang H, Feng J, Otitoju TA, Li W. Predictive Reliability Assessment of Generation System. Energies. 2020; 13(17):4350. https://doi.org/10.3390/en13174350
Chicago/Turabian StyleOkoye, Martin Onyeka, Junyou Yang, Zhenjiang Lei, Jingwei Yuan, Huichao Ji, Haixin Wang, Jiawei Feng, Tunmise Ayode Otitoju, and Weidong Li. 2020. "Predictive Reliability Assessment of Generation System" Energies 13, no. 17: 4350. https://doi.org/10.3390/en13174350
APA StyleOkoye, M. O., Yang, J., Lei, Z., Yuan, J., Ji, H., Wang, H., Feng, J., Otitoju, T. A., & Li, W. (2020). Predictive Reliability Assessment of Generation System. Energies, 13(17), 4350. https://doi.org/10.3390/en13174350