A Comprehensive Review on Grid Connected Photovoltaic Inverters, Their Modulation Techniques, and Control Strategies
Abstract
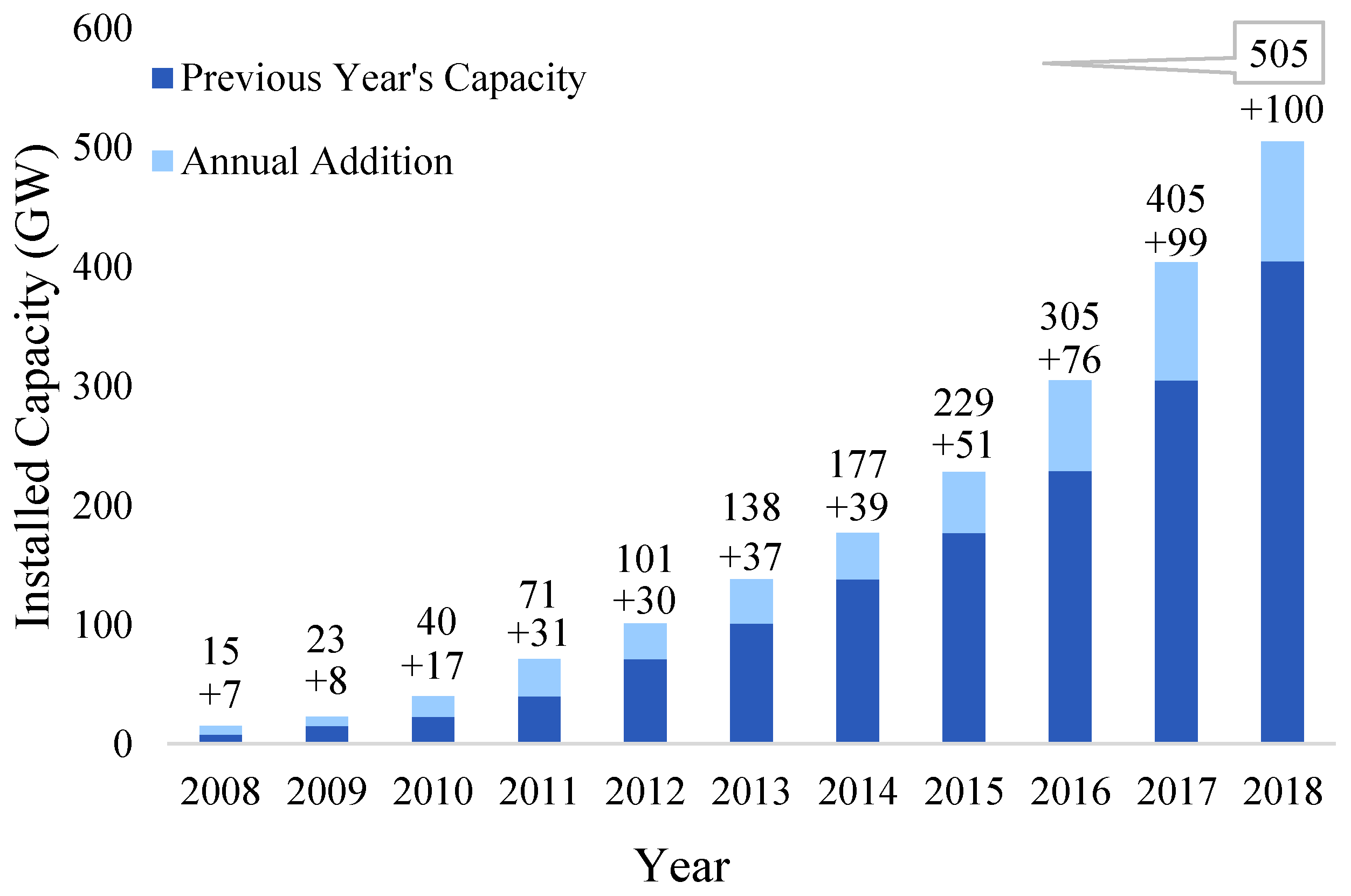
1. Introduction
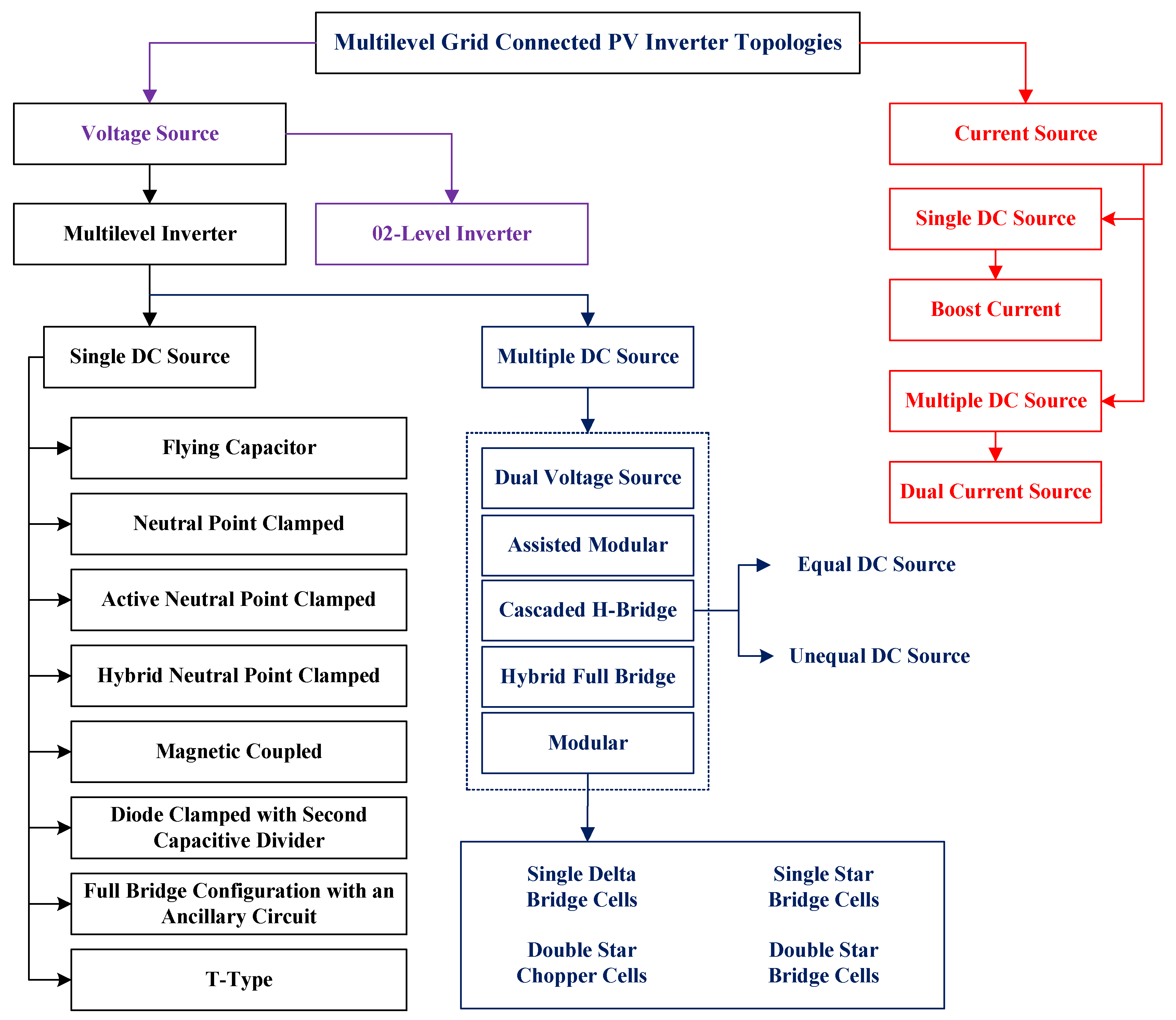
2. Classification of Inverters
2.1. Line Commutated Inverter
2.2. Self Commutated Inverter
2.2.1. Current Source Inverter
2.2.2. Voltage Source Inverter
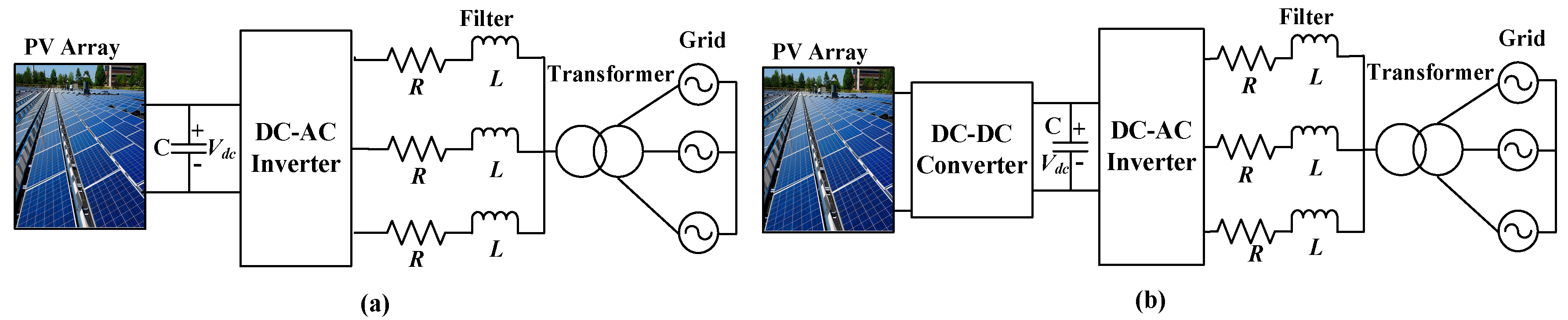
3. Configuration of PV Inverters
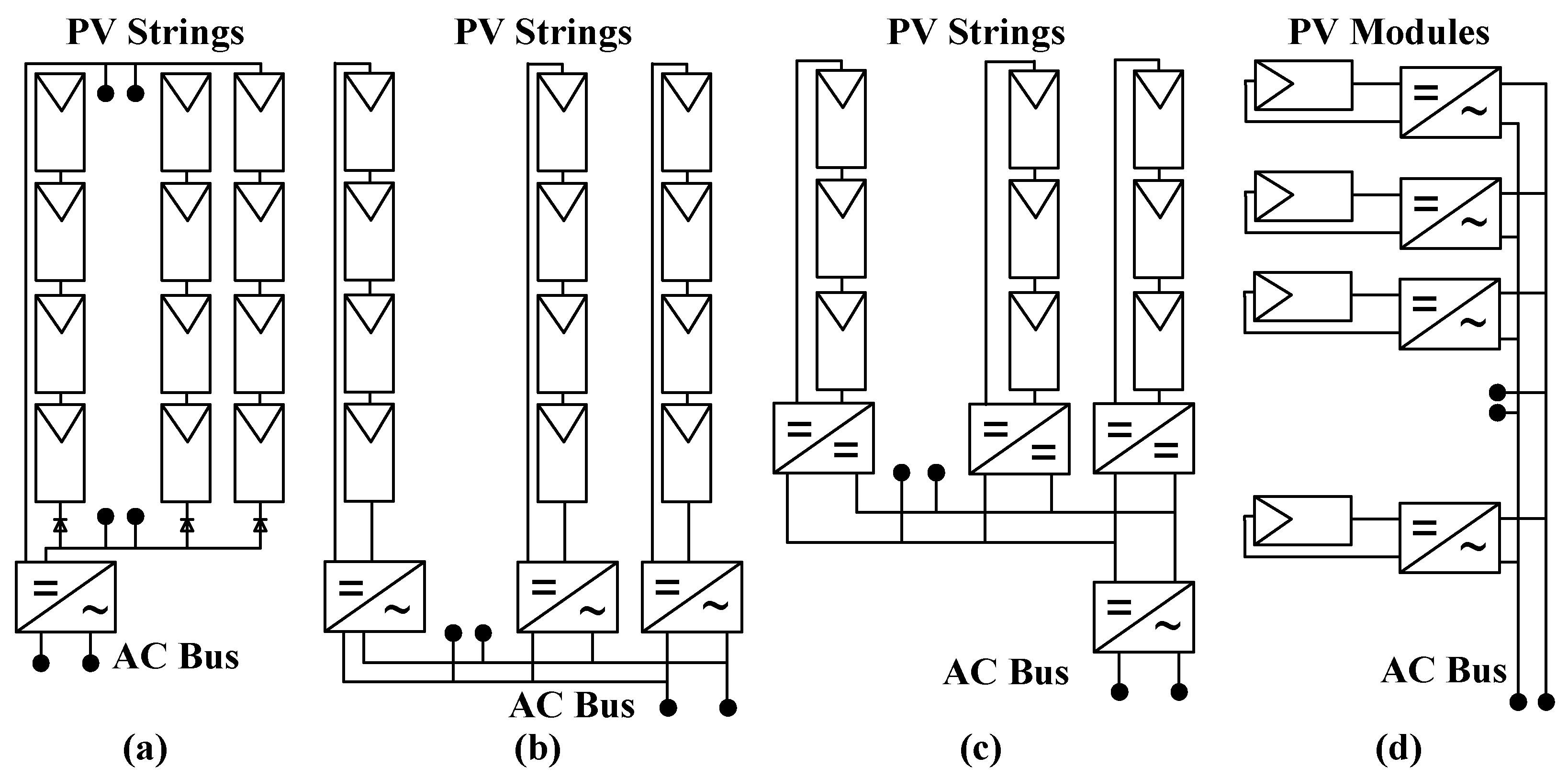
3.1. Central Inverter
3.2. String Inverter
3.3. Multi-String Inverter
3.4. Module Integrated or AC Module
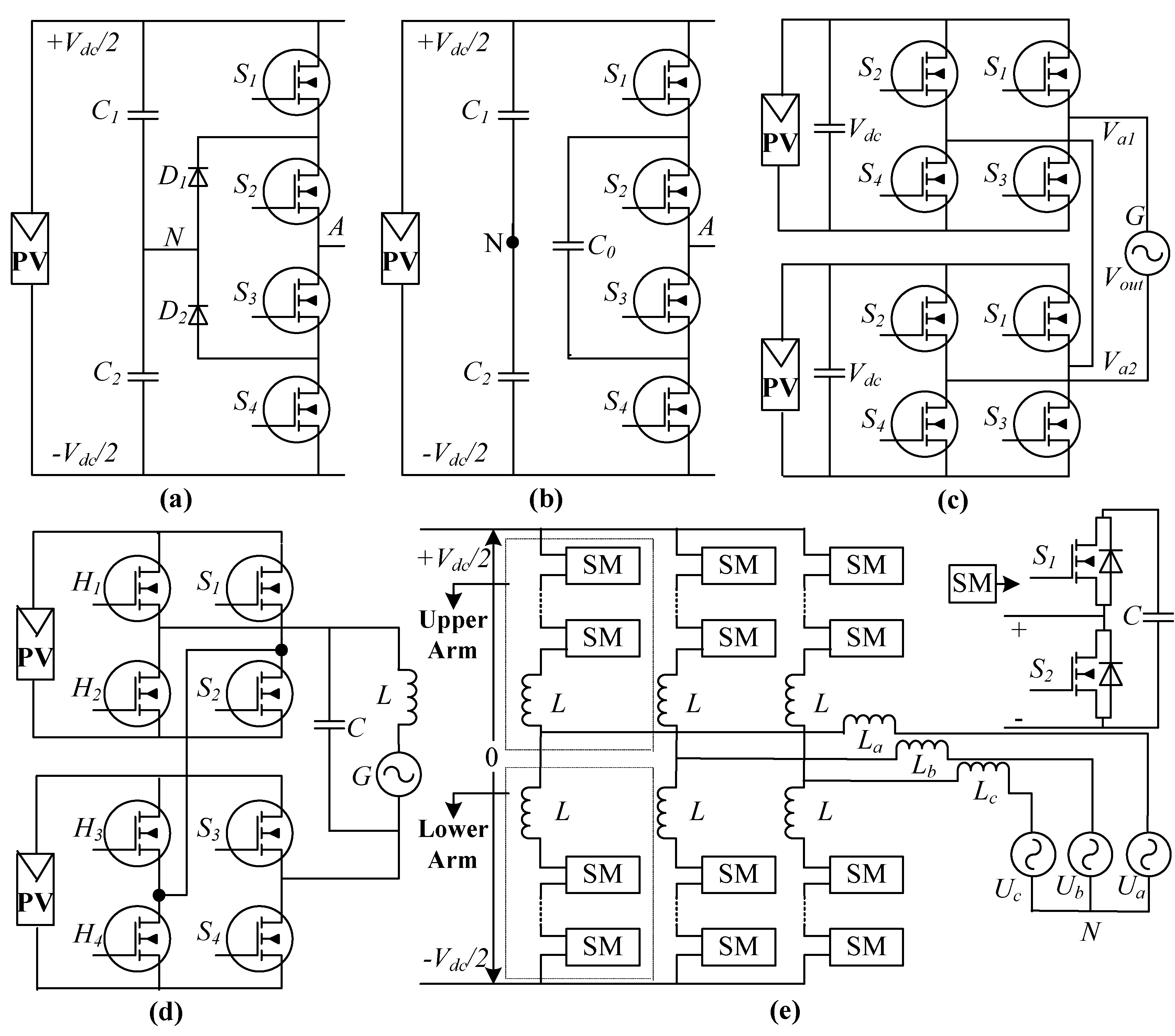
4. Multi-Level Inverter Topologies
4.1. Neutral Point Clamped GCMLI (NPC-GCMLI)
4.2. Flying Capacitor GCMLI (FC-GCMLI)
4.3. Cascaded H-Bridge GCMLI (CHB-GCMLI)
4.4. Modular GCMLI (M-GCMLI)
- Auxiliary Functionalities: The inverter must have the ability to provide the auxiliary functionalities when demanded from the grid operator. Moreover, the voltage compensation mostly focused on voltage interruption, swell, and sag. While the current compensation mostly focused on active and reactive components. However, unbalance and harmonic compensation require further research.
- Efficiency: The selection of a grid-connected PV inverter is mainly based on its efficiency. The inverter must be capable to attain a high efficiency over a wide range of loads. Due to the technological advancement in the last few decades, the power losses of the inverter are greatly reduced, and high efficiency is achieved.
- Anti-Islanding Detection: A GCPVI must have the capability to detect the islanding situation and disconnect it from the grid for safety purposes, while supplying power to the local load. In these conditions, the function of the inverter is usually referred to as anti-islanding.
- Cost: The selection of an inverter mainly depends on the manufacturing and installation cost. There is a tradeoff between the manufacturing cost and the performance and power quality of the inverter. On the contrary, the installation cost mainly depends on land acquisition, labor, and local factors that vary from region to region.
- Leakage Current: In transformer-based inverters the leakage current is interrupted by the galvanic isolation. However, in transformer-less MLIs the leakage current is a major issue as it increases the losses, harmonics in the grid injected current, and electromagnetic interference. Therefore, for a grid-connected system those MLIs are needed to be selected that are capable is to reduce the leakage current according to the international regulations.
- Power Density and Capacity: Generally, most of the experimental prototypes of GCMLIs are of low power density and capacity. Therefore, high power rated prototypes should be focused and enabled their integration with medium and high voltage grid connection.
- DC-Link Capacitor: The DC-link capacitor plays an important role in supplying the AC component of input current the inverter. The control and design of the DC-link capacitor is not an easy task and become more complex if their number rises.
- Switching Frequency: The switching frequency of small capacity GCMLIs is usually higher as compared to the large capacity inverters.
- Semiconductor Devices: The cost of GCPVIs mainly depends on the number and power ratings of the switches. Therefore, those topologies should be focused that have less number of switches with low voltage ratings.
- Galvanic Isolation: It is one of the most important requirements for safety purpose. In transformer-based inverter the galvanic isolation is provided by the transformer. However, in transformer-less inverter topologies, the isolation is achieved by using switches. Hence, the inverter should be selected according to the requirement of galvanic isolation.
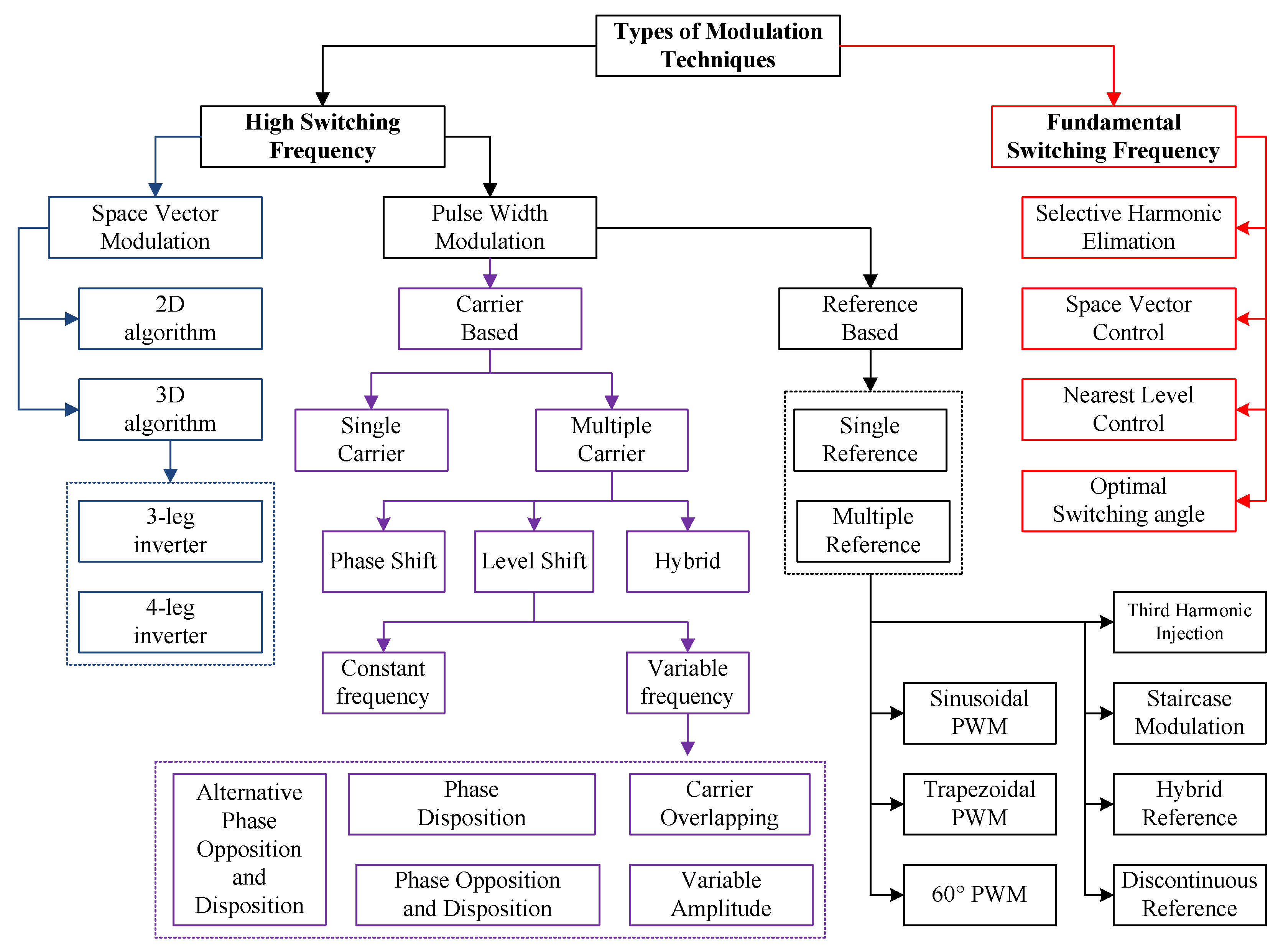
5. Modulation Techniques for Multi-Level Inverters
5.1. High Switching Frequency (HSF)
5.1.1. PWM
Carrier-Based PWM (MCB)
Reference-Based PWM
5.1.2. SVM
5.2. Fundamental Switching Frequency (FSF)
5.2.1. Selective Harmonic Elimination (SHE)
5.2.2. Switching Angle Calculation (SAC)
5.2.3. Space Vector Control (SVC)
5.2.4. Nearest Level Control (NLC)
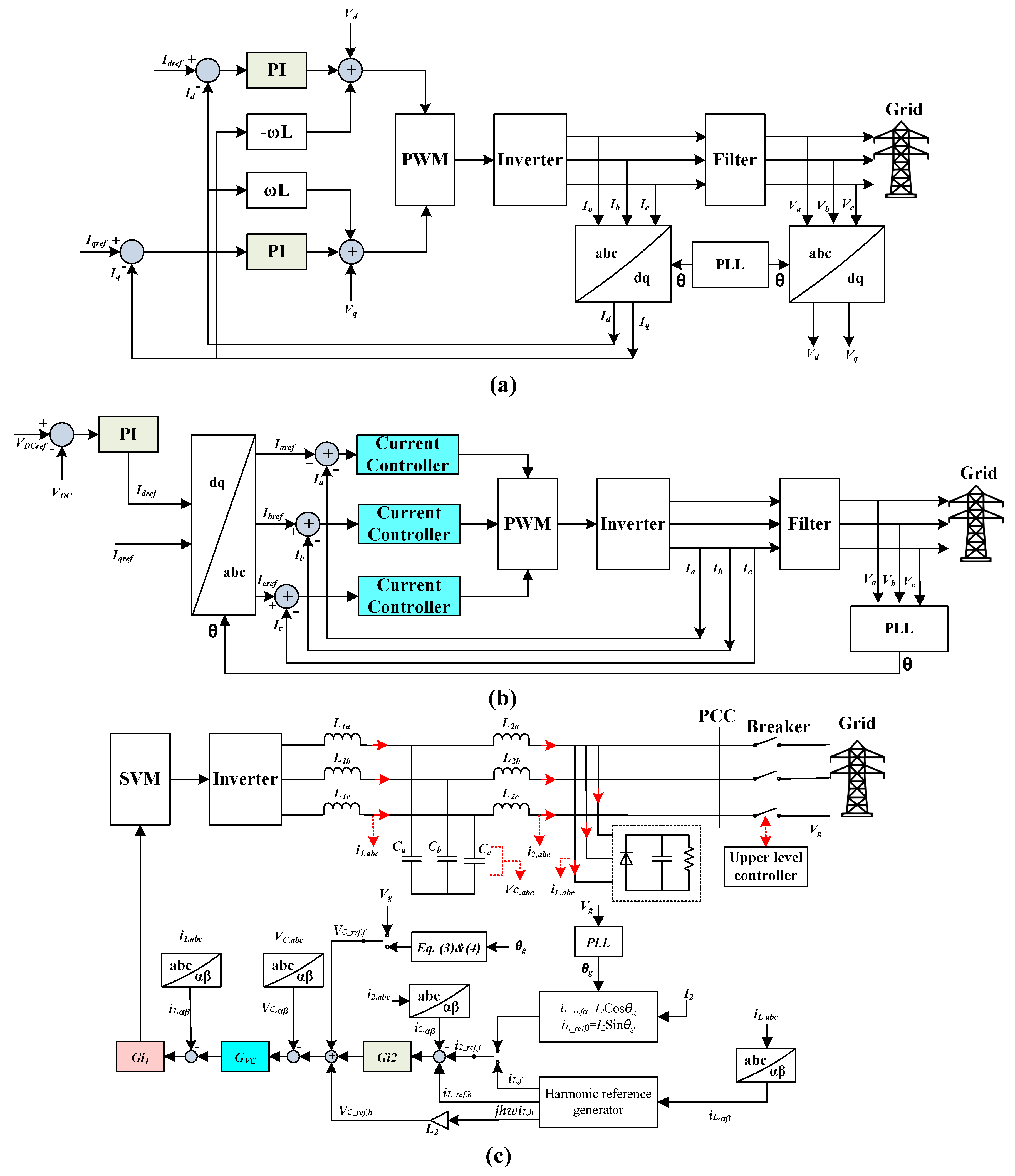
6. Controllers Reference Frames
6.1. dq Reference Frame
6.2. abc Reference Frame
6.3. αβ Reference Frame
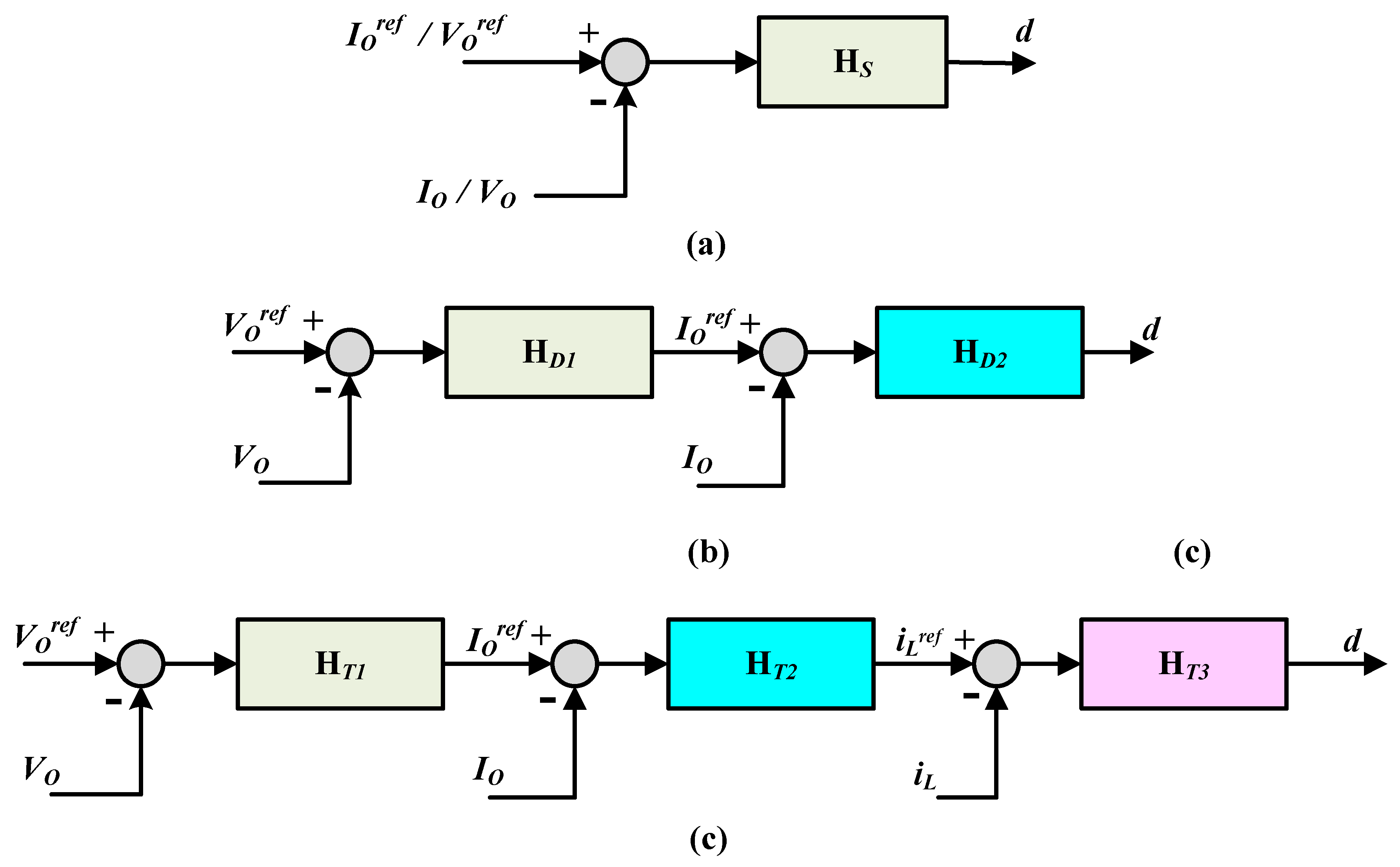
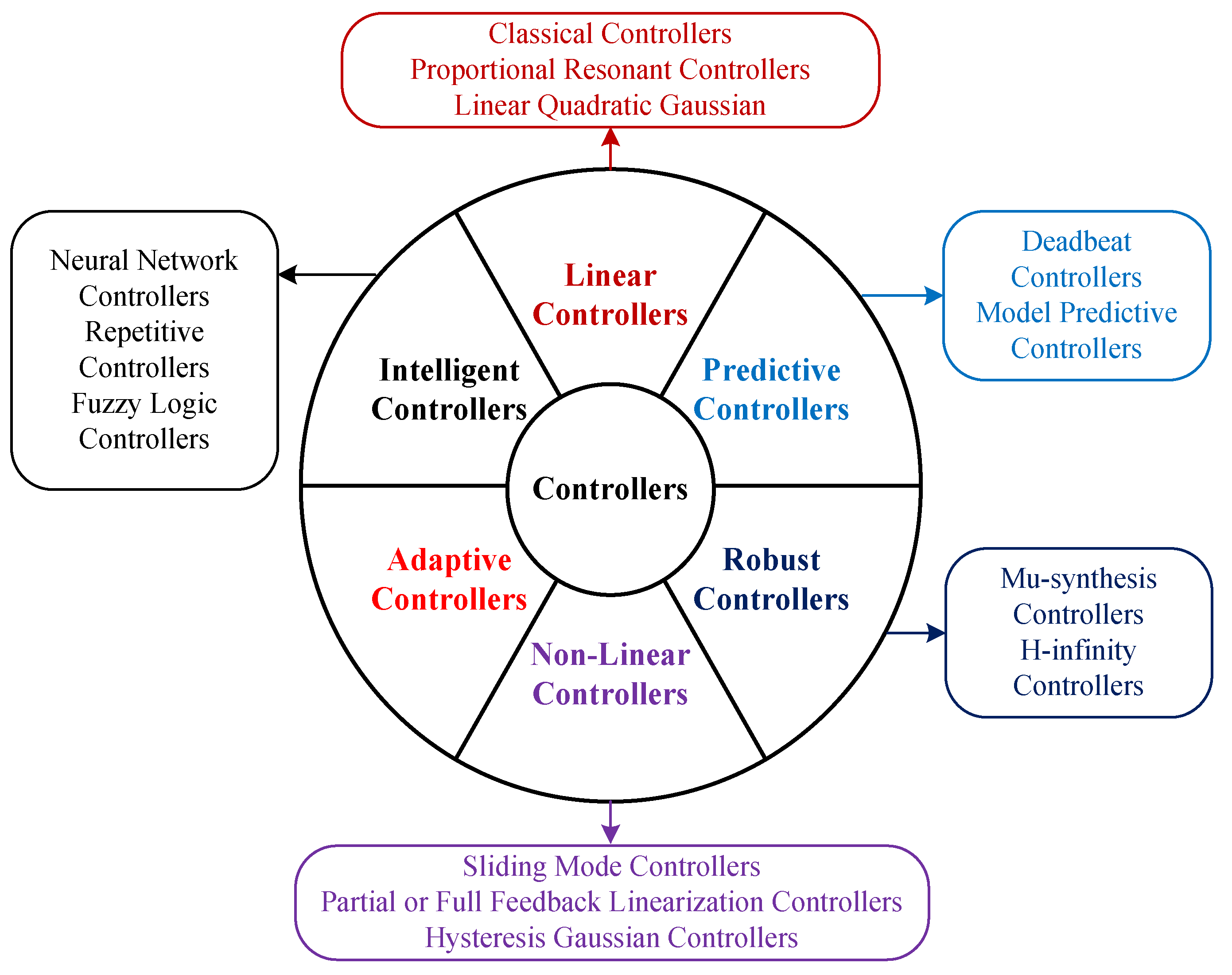
7. Control Strategies for Grid-Connected PV Systems
7.1. Linear Controllers
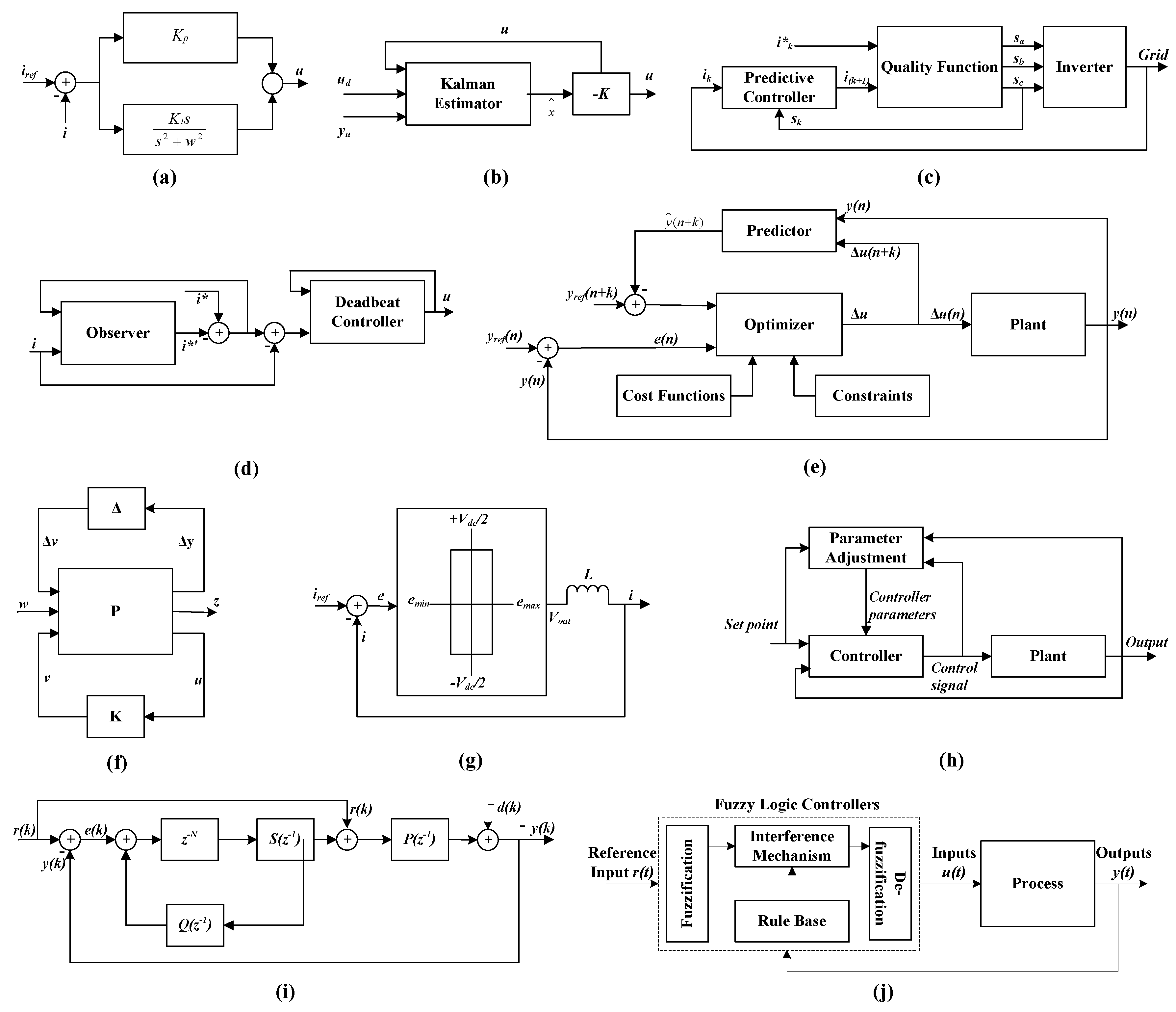
7.1.1. Classic Controllers
7.1.2. Proportional Resonant (PR) Controllers
7.1.3. Linear Quadratic Gaussian (LQG) Controllers
7.2. Predictive Controllers (PC)
7.2.1. Deadbeat Controllers
7.2.2. Model Predictive Controller (MPC)
7.3. Robust Controllers
7.3.1. Mu-Synthesis Controllers
7.3.2. H-Infinity Controllers
7.4. Non-Linear Controllers
7.4.1. Sliding Mode Controllers (SMC)
7.4.2. Partial or Full Feedback Linearization (PFL or FFL) Controllers
7.4.3. Hysteresis Controllers (HC)
7.5. Adaptive Controllers
7.6. Intelligent Controllers
7.6.1. Neural Network (NN) Controllers (NNC)
7.6.2. Repetitive Controllers (RC)
7.6.3. Fuzzy Logic Controllers (FLC)
8. Future Scope of Research
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- O’Shaughnessy, E.; Cutler, D.; Ardani, K.; Margolis, R. Solar plus: A review of the end-user economics of solar PV integration with storage and load control in residential buildings. Appl. Energy 2018, 228, 2165–2175. [Google Scholar] [CrossRef]
- Shah, R.; Mithulananthan, N.; Bansal, R.C.; Ramachandaramurthy, V.K. A review of key power system stability challenges for large-scale PV integration. Renew. Sustain. Energy Rev. 2015, 41, 1423–1436. [Google Scholar] [CrossRef]
- Renewables 2018 Global Status Report. Available online: https://www.ren21.net/wp-content/uploads/2019/08/Full-Report-2018.pdf (accessed on 15 March 2020).
- Zhu, Y.; Yao, J.; Wu, D. Comparative study of two stages and single stage topologies for grid-tie photovoltaic generation by PSCAD/EMTDC. In Proceedings of the 2011 International Conference on Advanced Power System Automation and Protection, Beijing, China, 16–20 October 2011; pp. 1304–1309. [Google Scholar]
- Daher, S.; Schmid, J.; Antunes, F.L.M. Multilevel Inverter Topologies for Stand-Alone PV Systems. IEEE Trans. Ind. Electron. 2008, 55, 2703–2712. [Google Scholar] [CrossRef]
- Villanueva, E.; Correa, P.; Rodriguez, J.; Pacas, M. Control of a Single-Phase Cascaded H-Bridge Multilevel Inverter for Grid-Connected Photovoltaic Systems. IEEE Trans. Ind. Electron. 2009, 56, 4399–4406. [Google Scholar] [CrossRef]
- Abu-Rub, H.; Holtz, J.; Rodriguez, J.; Ge, B. Medium-Voltage Multilevel Converters—State of the Art, Challenges, and Requirements in Industrial Applications. IEEE Trans. Ind. Electron. 2010, 57, 2581–2596. [Google Scholar] [CrossRef]
- Mehta, P.; Kunapara, A.; Karelia, N. Improvement in Switching Strategy Used for Even Loss Distribution in ANPC Multilevel Inverter. Procedia Technol. 2015, 21, 386–392. [Google Scholar] [CrossRef]
- Metri, J.I.; Vahedi, H.; Kanaan, H.Y.; Al-Haddad, K. Real-Time Implementation of Model-Predictive Control on Seven-Level Packed U-Cell Inverter. IEEE Trans. Ind. Electron. 2016, 63, 4180–4186. [Google Scholar] [CrossRef]
- Wu, H.; Zhu, L.; Yang, F.; Mu, T.; Ge, H. Dual-DC-Port Asymmetrical Multilevel Inverters With Reduced Conversion Stages and Enhanced Conversion Efficiency. IEEE Trans. Ind. Electron. 2017, 64, 2081–2091. [Google Scholar] [CrossRef]
- Chattopadhyay, S.K.; Chakraborty, C. A New Asymmetric Multilevel Inverter Topology Suitable for Solar PV Applications With Varying Irradiance. IEEE Trans. Sustain. Energy 2017, 8, 1496–1506. [Google Scholar] [CrossRef]
- Khodaparast, A.; Azimi, E.; Azimi, A.; Adabi, M.E.; Adabi, J.; Pouresmaeil, E. A New Modular Multilevel Inverter Based on Step-Up Switched-Capacitor Modules. Energies 2019, 12, 524. [Google Scholar] [CrossRef]
- Sandeep, N.; Yaragatti, U.R. Operation and Control of a Nine-Level Modified ANPC Inverter Topology With Reduced Part Count for Grid-Connected Applications. IEEE Trans. Ind. Electron. 2018, 65, 4810–4818. [Google Scholar] [CrossRef]
- Bassi, H.M.; Salam, Z. A new hybrid multilevel inverter topology with reduced switch count and dc voltage sources. Energies 2019, 12, 977. [Google Scholar] [CrossRef]
- Alexander, S.A. Development of solar photovoltaic inverter with reduced harmonic distortions suitable for Indian sub-continent. Renew. Sustain. Energy Rev. 2016, 56, 694–704. [Google Scholar] [CrossRef]
- Abdel-Rahim, O.; Alamir, N.; Abdelrahem, M.; Orabi, M.; Kennel, R.; Ismeil, M.A. A Phase-Shift-Modulated LLC-Resonant Micro-Inverter Based on Fixed Frequency Predictive-MPPT. Energies 2020, 13, 1460. [Google Scholar] [CrossRef]
- Steczek, M.; Chudzik, P.; Szelag, A. Combination of SHE- and SHM-PWM Techniques for VSI DC-Link Current Harmonics Control in Railway Applications. IEEE Trans. Ind. Electron. 2017, 64, 7666–7678. [Google Scholar] [CrossRef]
- Hernández-Callejo, L.; Gallardo-Saavedra, S.; Alonso-Gómez, V. A review of photovoltaic systems: Design, operation and maintenance. Sol. Energy 2019, 188, 426–440. [Google Scholar] [CrossRef]
- Athari, H.; Niroomand, M.; Ataei, M. Review and Classification of Control Systems in Grid-tied Inverters. Renew. Sustain. Energy Rev. 2017, 72, 1167–1176. [Google Scholar] [CrossRef]
- Zeb, K.; Uddin, W.; Khan, M.A.; Ali, Z.; Ali, M.U.; Christofides, N.; Kim, H.J. A comprehensive review on inverter topologies and control strategies for grid-connected photovoltaic system. Renew. Sustain. Energy Rev. 2018, 94, 1120–1141. [Google Scholar] [CrossRef]
- Sinha, A.; Chandra Jana, K.; Kumar Das, M. An inclusive review on different multi-level inverter topologies, their modulation and control strategies for a grid-connected photo-voltaic system. Sol. Energy 2018, 170, 633–657. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of Control and Grid Synchronization for Distributed Power Generation Systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Zeb, K.; Khan, I.; Uddin, W.; Khan, M.A.; Sathishkumar, P.; Busarello, T.D.C.; Ahmad, I.; Kim, H. A review on recent advances and future trends of transformerless inverter structures for single-phase grid-connected photovoltaic systems. Energies 2018, 11, 1968. [Google Scholar] [CrossRef]
- Hassaine, L.; Olias, E.; Quintero, J.; Salas, V. Overview of power inverter topologies and control structures for grid-connected photovoltaic systems. Renew. Sustain. Energy Rev. 2014, 30, 796–807. [Google Scholar] [CrossRef]
- Barghi Latran, M.; Teke, A. Investigation of multilevel multifunctional grid-connected inverter topologies and control strategies used in photovoltaic systems. Renew. Sustain. Energy Rev. 2015, 42, 361–376. [Google Scholar] [CrossRef]
- Islam, M.; Mekhilef, S.; Hasan, M. Single phase transformerless inverter topologies for grid-tied photovoltaic system: A review. Renew. Sustain. Energy Rev. 2015, 45, 69–86. [Google Scholar] [CrossRef]
- Obi, M.; Bass, R. Trends and challenges of grid-connected photovoltaic systems—A review. Renew. Sustain. Energy Rev. 2016, 58, 1082–1094. [Google Scholar] [CrossRef]
- Mahela, O.P.; Shaik, A.G. Comprehensive overview of grid interfaced solar photovoltaic systems. Renew. Sustain. Energy Rev. 2017, 68, 316–332. [Google Scholar] [CrossRef]
- Hasan, N.S.; Rosmin, N.; Osman, D.A.A.; Musta’amal, A.H. Reviews on multilevel converter and modulation techniques. Renew. Sustain. Energy Rev. 2017, 80, 163–174. [Google Scholar] [CrossRef]
- Mahlooji, M.H.; Mohammadi, H.R.; Rahimi, M. A review on modeling and control of grid-connected photovoltaic inverters with LCL filter. Renew Sustain. Energy Rev. 2018, 81, 563–578. [Google Scholar] [CrossRef]
- Kavya Santhoshi, B.; Mohana Sundaram, K.; Padmanaban, S.; Holm-Nielsen, J.B.; Prabhakaran, K.K. Critical Review of PV Grid-Tied Inverters. Energies 2019, 12, 1921. [Google Scholar] [CrossRef]
- Dogga, R.; Pathak, M.K. Recent trends in solar PV inverter topologies. Sol. Energy 2019, 183, 57–73. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Moghassemi, A.; Olamaei, J. PV Inverters and Modulation Strategies: A Review and A Proposed Control Strategy for Frequency and Voltage Regulation. Signal Proc. Renew. Energy 2020, 4, 1–21. [Google Scholar]
- Parvez, M.; Elias, M.F.M.; Rahim, N.A.; Osman, N. Current control techniques for three-phase grid interconnection of renewable power generation systems: A review. Sol. Energy 2016, 135, 29–42. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, B.; Li, Y.; Chen, J.; Loh, P.C. High-Efficiency T-Source Inverter With Low Voltage Spikes Across the Switch Bridge. IEEE Trans. Power Electron. 2020, 35, 10554–10566. [Google Scholar] [CrossRef]
- Al-Shetwi, A.Q.; Sujod, M.Z.; Blaabjerg, F.; Yang, Y. Fault ride-through control of grid-connected photovoltaic power plants: A review. Sol. Energy 2019, 180, 340–350. [Google Scholar] [CrossRef]
- Ishikawa, T. Grid-Connected Photovoltaic Power Systems: Survey of Inverter and Related Protection Equipments; IEA-PVPS-T5-05: Paris, France, 2002; p. 64. [Google Scholar]
- Calais, M.; Agelidis, V.G.; Meinhardt, M. Multilevel converters for single-phase grid-connected photovoltaic systems: An overview. Sol. Energy 1999, 66, 325–335. [Google Scholar] [CrossRef]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics, 3rd ed.; Springer Science & Business Media: Berlin, Germany, 2007; ISBN 978-1-4757-0559-1. [Google Scholar]
- Azmi, S.A.; Ahmed, K.H.; Finney, S.J.; Williams, B.W. Comparative analysis between voltage and current source inverters in grid-connected application. In Proceedings of the IET Conference on Renewable Power Generation (RPG 2011), Edinburgh, UK, 6–8 September 2011; p. 101. [Google Scholar]
- Hojabri, M.; Soheilirad, M.S. Harmonic Distortion in an Off-Grid Renewable Energy System with Different Loads. In Proceedings of the International MultiConference of Engineers and Computer Scientists 2014, Hong Kong, China, 12–14 March 2014; pp. 1–6. [Google Scholar]
- Wang, Y.-J.; Hsu, P.C. An investigation on partial shading of PV modules with different connection configurations of PV cells. Energy 2011, 36, 3069–3078. [Google Scholar] [CrossRef]
- Kouro, S.; Leon, J.I.; Vinnikov, D.; Franquelo, L.G. Grid-Connected Photovoltaic Systems: An Overview of Recent Research and Emerging PV Converter Technology. IEEE Ind. Electron. Mag. 2015, 9, 47–61. [Google Scholar] [CrossRef]
- Kjaer, S.B.; Pedersen, J.K.; Blaabjerg, F. A Review of Single-Phase Grid-Connected Inverters for Photovoltaic Modules. IEEE Trans. Ind. Appl. 2005, 41, 1292–1306. [Google Scholar] [CrossRef]
- Mohd.Ali, J.S.; Krishnaswamy, V. An assessment of recent multilevel inverter topologies with reduced power electronics components for renewable applications. Renew. Sustain. Energy Rev. 2018, 82, 3379–3399. [Google Scholar] [CrossRef]
- Kjaer, S.B.; Pedersen, J.K.; Blaabjerg, F. Power inverter topologies for photovoltaic modules-a review. In Proceedings of the Conference Record of the 2002. IEEE Industry Applications Conference. 37th IAS Annual Meeting (Cat. No.02CH37344), Pittsburgh, PA, USA, 13–19 October 2002. [Google Scholar]
- Myrzik, J.M.; Calais, M. String and module integrated inverters for single-phase grid connected photovoltaic systems-a review. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; p. 8. [Google Scholar]
- Meinhardt, M.; Cramer, G. Past, present and future of grid-connected photovoltaic- and hybrid-power-systems. In Proceedings of the 2000 Power Engineering Society Summer Meeting (Cat. No.00CH37134), Seattle, WA, USA, 6 August 2000; pp. 1–6. [Google Scholar]
- Calais, M.; Myrzik, J.; Spooner, T.; Agelidis, V.G. Inverters for single-phase grid-connected photovoltaic systems-an overview. In Proceedings of the 2002 IEEE 33rd Annual IEEE Power Electronics Specialists Conference. Proceedings (Cat. No.02CH37289), Cairns, Qld, Australia, 23–27 June 2002; pp. 1995–2000. [Google Scholar]
- Verhoeven, B. Utility Aspects of Grid Connected Photovoltaic Power Systems; International Energy Agency: Paris, France, 1998. [Google Scholar]
- Elrayyah, A.; Sozer, Y.; Elbuluk, M. Microgrid-Connected PV-Based Sources: A Novel Autonomous Control Method for Maintaining Maximum Power. IEEE Ind. Appl. Mag. 2015, 21, 19–29. [Google Scholar] [CrossRef]
- Khomfoi, S.; Tolbert, L.M. Multilevel power converters. In Power Electronics Handbook; Elsevier: Amsterdam, The Netherlands, 2011; pp. 455–486. [Google Scholar]
- Nabae, A.; Takahashi, I.; Akagi, H. A New Neutral-Point-Clamped PWM Inverter. IEEE Trans. Ind. Appl. 1981, 5, 518–523. [Google Scholar] [CrossRef]
- Rodriguez, J.; Franquelo, L.G.; Kouro, S.; Leon, J.I.; Portillo, R.C.; Prats, M.A.M.; Perez, M.A. Multilevel converters: An enabling technology for high-power applications. Proc. IEEE 2009, 97, 1786–1817. [Google Scholar] [CrossRef]
- Rodriguez, J.; Jih-Sheng, L.; Fang Zheng, P. Multilevel inverters: A survey of topologies, controls, and applications. IEEE Trans. Ind. Electron. 2002, 49, 724–738. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, K.; Feng, L.; Wu, H.; Xing, Y. A Family of Neutral Point Clamped Full-Bridge Topologies for Transformerless Photovoltaic Grid-Tied Inverters. IEEE Trans. Power Electron. 2013, 28, 730–739. [Google Scholar] [CrossRef]
- Meynard, T.; Foch, H. Multi-level conversion: High voltage choppers and voltage-source inverters. In Proceedings of the PESC’92 Record. 23rd Annual IEEE Power Electronics Specialists Conference, Toledo, Spain, 29 June–3 July 1992; pp. 397–403. [Google Scholar]
- Adam, G.P.; Anaya-Lara, O.; Burt, G.M.; Finney, S.J.; Williams, B.W.; McDonald, J.R. Comparison between flying capacitor and modular multilevel inverter. In Proceedings of the IECON 2009, the 35th Annual Conference of the IEEE Industrial Electronics Society and ICELIE 2009, the 3rd IEEE International Conference on E-Learning in Industrial Electronics, Porto, Portugal, 3–5 November 2009; pp. 1–6. [Google Scholar]
- Sowjanya, T.; Veerendranath, K. Cascaded H-Bridge with Single DC Source and Regulated Capacitor Voltage. Int. J. Adv. Sci. Technol. 2014, 73, 89–102. [Google Scholar] [CrossRef]
- Sumithira, T.R.; Nirmal Kumar, A. Elimination of Harmonics in Multilevel Inverters Connected to Solar Photovoltaic Systems Using ANFIS: An Experimental Case Study. J. Appl. Res. Technol. 2013, 1, 124–132. [Google Scholar] [CrossRef]
- Jana, J.; Saha, H.; Das Bhattacharya, K. A review of inverter topologies for single-phase grid-connected photovoltaic systems. Renew. Sustain. Energy Rev. 2017, 72, 1256–1270. [Google Scholar] [CrossRef]
- Mahato, B.; Raushan, R.; Jana, K.C. Modulation and control of multilevel inverter for an open-end winding induction motor with constant voltage levels and harmonics. IET Power Electron. 2017, 10, 71–79. [Google Scholar] [CrossRef]
- Babaei, E.; Dehqan, A.; Sabahi, M. Improvement of the Performance of the Cascaded Multilevel Inverters Using Power Cells with Two Series Legs. J. Power Electron. 2013, 13, 223–231. [Google Scholar] [CrossRef]
- Perez, M.A.; Bernet, S.; Rodriguez, J.; Kouro, S.; Lizana, R. Circuit Topologies, Modeling, Control Schemes, and Applications of Modular Multilevel Converters. IEEE Trans. Power Electron. 2015, 30, 4–17. [Google Scholar] [CrossRef]
- Wang, T.; Hussain, K.S.T.; Song, G.; Han, W.; Liu, C. Adaptive single-phase/three-phase reclosing scheme for transmission lines in passive network supplied by MMC-HVDC. Int. J. Electr. Power Energy Syst. 2019, 113, 597–606. [Google Scholar] [CrossRef]
- Kharade, J.M.; Thorat, A.R. Simulation of an Alternate Arm Modular Multilevel Converter with overlap angle control for capacitor voltage balancing. In Proceedings of the 2015 International Conference on Industrial Instrumentation and Control (ICIC), Pune, India, 28–30 May 2015; pp. 502–506. [Google Scholar]
- Valan Rajkumar, M.; Manoharan, P.S. FPGA based multilevel cascaded inverters with SVPWM algorithm for photovoltaic system. Sol. Energy 2013, 87, 229–245. [Google Scholar] [CrossRef]
- Ahmed, T.A.; Mohamed, E.E.; Youssef, A.-R.; Ibrahim, A.; Saeed, M.S.; Ali, A.I. Three phase modular multilevel inverter-based multi-terminal asymmetrical DC inputs for renewable energy applications. Eng. Sci. Technol. Int. J. 2020, 23, 831–839. [Google Scholar] [CrossRef]
- Singh, D.; Kumar, V.; Saxena, A.; Gupta, S.K.; Singh, A.K. A Single Phase Level Shifted PWM Asymmetrical Multilevel Inverter for 7-Level. In Proceedings of the International Conference on Advances in Electronics, Electrical & Computational Intelligence (ICAEEC) 2019, IIIT Allahabad, India, 17 April 2020; pp. 1–8. [Google Scholar]
- Di Benedetto, M.; Lidozzi, A.; Solero, L.; Crescimbini, F.; Grbović, P.J. Symmetrical Three-Phase 7-Level E-Type Inverter for PV Applications. In Proceedings of the 2019 International Conference on Clean Electrical Power (ICCEP), Otranto, Italy, 2–4 July 2019; pp. 419–426. [Google Scholar]
- Prabaharan, N.; Palanisamy, K. Analysis and integration of multilevel inverter configuration with boost converters in a photovoltaic system. Energy Convers. Manag. 2016, 128, 327–342. [Google Scholar] [CrossRef]
- Dasari, M.S.; Mani, V. Simulation and analysis of three-phase parallel inverter using multicarrier PWM control schemes. SN Appl. Sci. 2020, 2, 1–10. [Google Scholar] [CrossRef]
- Matalata, H.; Yusiana, V. New Topology Multilevel Inverter Type Diode Clamped Five Level Single Phase. MSE 2020, 807, 012039. [Google Scholar] [CrossRef]
- Joshi, N.R.; Sant, A.V. Analysis of a New Symmetic Multilevel Inverter Topology with Reduced Component Count. In Proceedings of the 2020 International Conference on Emerging Trends in Information Technology and Engineering (ic-ETITE), Nellore, India, 24–25 February 2020; pp. 1–6. [Google Scholar]
- Silva, J.L.; Matias, R.R.; de Carvalho Alves, M.D.; e Silva, R.N.A.L.; Monteiro, A.T.S.; dos Santos, K.P. FSC-MPC Current Control of a 5-level Half-Bridge/ANPC Hybrid Three-phase Inverter. In Proceedings of the 2019 IEEE 15th Brazilian Power Electronics Conference and 5th IEEE Southern Power Electronics Conference (COBEP/SPEC), Santos, Brazil, 1–4 December 2019; pp. 1–6. [Google Scholar]
- Calle-Prado, A.; Alepuz, S.; Bordonau, J.; Cortes, P.; Rodriguez, J. Predictive Control of a Back-to-Back NPC Converter-Based Wind Power System. IEEE Trans. Ind. Electron. 2016, 63, 4615–4627. [Google Scholar] [CrossRef]
- Kumar, V.A.; Mouttou, A.A. Improved performance with fractional order control for asymmetrical cascaded H-bridge multilevel inverter. Bull. Electr. Eng. Inform. 2020, 9, 1335–1344. [Google Scholar]
- Chitra, S.; Valluvan, K. Design And Implementation Of Cascaded H-Bridge Multilevel Inverter Using Fpga With Multiple Carrier Phase Disposition Modulation Scheme. Microprocess. Microsyst. 2020, 76, 103108. [Google Scholar] [CrossRef]
- Kartick, J.C.; Suparna, K.; Sujit, B.K. Dual reference phase shifted pulse width modulation technique for a N-level inverter based grid-connected solar photovoltaic system. IET Renew. Power Gener. 2016, 10, 928–935. [Google Scholar] [CrossRef]
- Sun, J.; Liu, H. Sequence Impedance Modeling of Modular Multilevel Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1427–1443. [Google Scholar] [CrossRef]
- Mortezaei, A.; Simoes, M.G.; Bubshait, A.S.; Busarello, T.D.C.; Marafao, F.P.; Al-Durra, A. Multifunctional Control Strategy for Asymmetrical Cascaded H-Bridge Inverter in Microgrid Applications. IEEE Trans. Ind. Appl. 2017, 53, 1538–1551. [Google Scholar] [CrossRef]
- Manoharan, M.S.; Ahmed, A.; Park, J.-H. A PV Power Conditioning System Using Nonregenerative Single-Sourced Trinary Asymmetric Multilevel Inverter with Hybrid Control Scheme and Reduced Leakage Current. IEEE Trans. Power Electron. 2017, 32, 7602–7614. [Google Scholar] [CrossRef]
- Panda, K.P.; Bana, P.R.; Panda, G. Design and Control of an Asymmetrical Cascaded Compact Module Multilevel Inverter for PV System. In Proceedings of the TENCON 2019—2019 IEEE Region 10 Conference (TENCON), Kochi, India, 17–20 October 2019; pp. 2616–2621. [Google Scholar]
- Das, C.K.; Kirubakaran, A.; Somasekhar, V.T. A Five-Level Quasi Z-Source Based NPC Inverter for PV Applications. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC / I&CPS Europe), Genova, Italy, 11–14 June 2019; pp. 1–5. [Google Scholar]
- Pilli, N.K.; Singh, S.K. Comparative analysis of CB-PWM techniques in modified multilevel DC link inverter for PV applications. IET Power Electron. 2019, 12, 3802–3809. [Google Scholar] [CrossRef]
- Abronzini, U.; Attaianese, C.; D’Arpino, M.; Monaco, M.D.; Tomasso, G. Induction Motor Drives Fed by an NPC Inverter with Unbalanced DC-Link. Electronics 2019, 8, 1379. [Google Scholar] [CrossRef]
- El-Naggar, K.; Abdelhamid, T.H. Selective harmonic elimination of new family of multilevel inverters using genetic algorithms. Energy Convers. Manag. 2008, 49, 89–95. [Google Scholar] [CrossRef]
- Jing, Z.; Xiangning, H.; Rongxiang, Z. A Novel PWM Control Method for Hybrid-Clamped Multilevel Inverters. IEEE Trans. Ind. Electron. 2010, 57, 2365–2373. [Google Scholar] [CrossRef]
- Holmes, D.G.; Lipo, T.A. Pulse Width Modulation for Power Converters: Principles and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2003; Chapter 5; Volume 18, ISBN 9780470546284. [Google Scholar]
- Carrara, G.; Gardella, S.; Marchesoni, M.; Salutari, R.; Sciutto, G. A new multilevel PWM method: A theoretical analysis. IEEE Trans. Power Electron. 1992, 7, 497–505. [Google Scholar] [CrossRef]
- Floricau, D.; Floricau, E.; Gateau, G. Three-level active NPC converter: PWM strategies and loss distribution. In Proceedings of the 34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 10–13 November 2008; pp. 3333–3338. [Google Scholar]
- Hosseini, S.H.; Sadeghi, M. Reduced diode clamped multilevel converter with a modified control method. In Proceedings of the 2011 7th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 1–4 December 2011; pp. I-302–I-306. [Google Scholar]
- Miao, C.-X.; Shi, L.-P.; Wang, T.-X.; Cui, C.-B. Flying capacitor multilevel inverters with novel PWM method. Procedia Earth Planet. Sci. 2009, 1, 1554–1560. [Google Scholar]
- Rando, G.; Dannier, A.; Del Pizzo, A.; Rizzo, R. Power quality problems in unbalanced operations of fault tolerant H-bridge multilevel active front-ends. In Proceedings of the 9th International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 9–11 October 2007; pp. 1–6. [Google Scholar]
- Yan, G.; Liu, J.; Gang, M.U.; Liu, Y.; Liu, Y.; Song, W. Research on Modular Multilevel Converter Suitable for Direct-drive Wind Power System. Energy Procedia 2012, 17, 1497–1506. [Google Scholar]
- António-Ferreira, A.; Collados-Rodríguez, C.; Gomis-Bellmunt, O. Modulation techniques applied to medium voltage modular multilevel converters for renewable energy integration: A review. Electr. Power Syst. Res. 2018, 155, 21–39. [Google Scholar] [CrossRef]
- Gandomi, A.A.; Babaei, E.; Sabahi, M.; Saeidabadi, S.; Hosseini, S.H. Transformer-based inverter with reduced number of switches for renewable energy applications. IET Power Electron. 2015, 8, 1875–1884. [Google Scholar] [CrossRef]
- Naderi, R.; Rahmati, A. Phase-Shifted Carrier PWM Technique for General Cascaded Inverters. IEEE Trans. Power Electron. 2008, 23, 1257–1269. [Google Scholar] [CrossRef]
- Ayob, S.M.; Salam, Z.; Jusoh, A. Trapezoidal PWM scheme for cascaded multilevel inverter. In Proceedings of the 2006 IEEE International Power and Energy Conference, Putra Jaya, Malaysia, 28–29 November 2006; pp. 368–372. [Google Scholar]
- Pérez, M.; Rodríguez, J.; Pontt, J.; Kouro, S. Power distribution in hybrid multi-cell converter with nearest level modulation. In Proceedings of the 2007 IEEE International Symposium on Industrial Electronics, Vigo, Spain, 4–7 June 2007; pp. 736–741. [Google Scholar]
- Thorborg, K. Staircase PWM an uncomplicated and efficient modulation technique for ac motor drives. In Proceedings of the 1986 17th Annual IEEE Power Electronics Specialists Conference, Vancouver, BC, Canada, 23–27 June 1986; pp. 593–602. [Google Scholar]
- Rashid, M.H. Power Electronic Circuits, Devices, and Applications; Pearson Publishing: Florida, FL, USA, 2004; ISBN 0-12-581650-2. [Google Scholar]
- Boost, M.A.; Ziogas, P.D. State-of-the-art carrier PWM techniques: A critical evaluation. IEEE Trans. Ind. Appl. 1988, 24, 271–280. [Google Scholar] [CrossRef]
- Nho-Van, N.; Bac-Xuan, N.; Hong-Hee, L. An Optimized Discontinuous PWM Method to Minimize Switching Loss for Multilevel Inverters. IEEE Trans. Ind. Electron. 2011, 58, 3958–3966. [Google Scholar] [CrossRef]
- Silva, C.A.; Cordova, L.A.; Lezana, P.; Empringham, L. Implementation and Control of a Hybrid Multilevel Converter With Floating DC Links for Current Waveform Improvement. IEEE Trans. Ind. Electron. 2011, 58, 2304–2312. [Google Scholar] [CrossRef]
- Ahmed, I.; Borghate, V.B.; Matsa, A.; Meshram, P.M.; Suryawanshi, H.M.; Chaudhari, M.A. Simplified Space Vector Modulation Techniques for Multilevel Inverters. IEEE Trans. Power Electron. 2016, 31, 8483–8499. [Google Scholar] [CrossRef]
- Massoud, A.M.; Finney, S.J.; Williams, B.W. Mapped hybrid spaced vector modulation for multilevel cascaded-type voltage source inverters. IET Power Electron. 2008, 1, 318–335. [Google Scholar] [CrossRef]
- Tan, C.; Xiao, D.; Fletcher, J.E. An improved space vector modulation strategy for three-level five-phase neutral-point-clamped inverters. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–10. [Google Scholar]
- Choi, S.; Saeedifard, M. Capacitor Voltage Balancing of Flying Capacitor Multilevel Converters by Space Vector PWM. IEEE Trans. Power Deliv. 2012, 27, 1154–1161. [Google Scholar] [CrossRef]
- Morya, A.K.; Shukla, A.; Doolla, S. Control of grid-connected cascaded H-bridge multilevel converter during grid voltage unbalance for photovoltaic application. In Proceedings of the IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 7990–7995. [Google Scholar]
- Dekka, A.; Wu, B.; Zargari, N.R.; Fuentes, R.L. A Space-Vector PWM-Based Voltage-Balancing Approach With Reduced Current Sensors for Modular Multilevel Converter. IEEE Trans. Ind. Electron. 2016, 63, 2734–2745. [Google Scholar] [CrossRef]
- Turnbull, F.G. Selected harmonic reduction in static D-C—A-C inverters. IEEE Trans. Commun. Electron. 1964, 83, 374–378. [Google Scholar] [CrossRef]
- Moeed Amjad, A.; Salam, Z. A review of soft computing methods for harmonics elimination PWM for inverters in renewable energy conversion systems. Renew. Sustain. Energy Rev. 2014, 33, 141–153. [Google Scholar] [CrossRef]
- Kavousi, A.; Vahidi, B.; Salehi, R.; Bakhshizadeh, M.K.; Farokhnia, N.; Fathi, S.H. Application of the Bee Algorithm for Selective Harmonic Elimination Strategy in Multilevel Inverters. IEEE Trans. Power Electron. 2012, 27, 1689–1696. [Google Scholar] [CrossRef]
- Taghizadeh, H.; Tarafdar Hagh, M. Harmonic Elimination of Cascade Multilevel Inverters with Nonequal DC Sources Using Particle Swarm Optimization. IEEE Trans. Ind. Electron. 2010, 57, 3678–3684. [Google Scholar] [CrossRef]
- Luo, F.L. Investigation on best switching angles to obtain lowest THD for multilevel DC/AC inverters. In Proceedings of the 2013 IEEE 8th Conference on Industrial Electronics and Applications (ICIEA), Melbourne, VIC, Australia, 19–21 June 2013; pp. 1814–1818. [Google Scholar]
- Babaei, E.; Gowgani, S.S. Hybrid Multilevel Inverter Using Switched Capacitor Units. IEEE Trans. Ind. Electron. 2014, 61, 4614–4621. [Google Scholar] [CrossRef]
- Rodriguez, J.; Moran, L.; Correa, P.; Silva, C. A vector control technique for medium-voltage multilevel inverters. IEEE Trans. Ind. Electron. 2002, 49, 882–888. [Google Scholar] [CrossRef]
- Deng, Y.; Harley, R.G. Space-Vector Versus Nearest-Level Pulse Width Modulation for Multilevel Converters. IEEE Trans. Power Electron. 2015, 30, 2962–2974. [Google Scholar] [CrossRef]
- Choudhury, A.; Pillay, P.; Williamson, S.S. DC-Bus Voltage Balancing Algorithm for Three-Level Neutral-Point-Clamped (NPC) Traction Inverter Drive With Modified Virtual Space Vector. IEEE Trans. Ind. Appl. 2016, 52, 3958–3967. [Google Scholar] [CrossRef]
- Kouro, S.; Bernal, R.; Miranda, H.; Silva, C.A.; Rodriguez, J. High-Performance Torque and Flux Control for Multilevel Inverter Fed Induction Motors. IEEE Trans. Power Electron. 2007, 22, 2116–2123. [Google Scholar] [CrossRef]
- Moranchel, M.; Bueno, E.J.; Rodriguez, F.J.; Sanz, I. Implementation of nearest level modulation for Modular Multilevel Converter. In Proceedings of the 2015 IEEE 6th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aachen, Germany, 22–25 June 2015; pp. 1–5. [Google Scholar]
- Franquelo, L.; Rodriguez, J.; Leon, J.; Kouro, S.; Portillo, R.; Prats, M. The age of multilevel converters arrives. IEEE Ind. Electron. Mag. 2008, 2, 28–39. [Google Scholar] [CrossRef]
- Xin, Z.; Mattavelli, P.; Yao, W.; Yang, Y.; Blaabjerg, F.; Loh, P.C. Mitigation of grid-current distortion for LCL-filtered voltage-source inverter with inverter-current feedback control. IEEE Trans. Power Electron. 2017, 33, 6248–6261. [Google Scholar] [CrossRef]
- Wang, X.; Loh, P.C.; Blaabjerg, F. Stability analysis and controller synthesis for single-loop voltage-controlled VSIs. IEEE Trans. Power Electron. 2017, 32, 7394–7404. [Google Scholar] [CrossRef]
- Ciobotaru, M.; Teodorescu, R.; Blaabjerg, F. Control of single-stage single-phase PV inverter. EPE J. 2006, 16, 20–26. [Google Scholar] [CrossRef]
- Buso, S.; Caldognetto, T.; Brandao, D.I. Dead-beat current controller for voltage-source converters with improved large-signal response. IEEE Trans. Ind. Appl. 2015, 52, 1588–1596. [Google Scholar] [CrossRef]
- Yang, D.; Ruan, X.; Wu, H. A Real-Time Computation Method with Dual Sampling Mode to Improve the Current Control Performance of the $ LCL $-Type Grid-Connected Inverter. IEEE Trans. Ind. Electron. 2014, 62, 4563–4572. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, K.; Xing, Y.; Feng, L.; Ge, H. A Modular Grid-Connected Photovoltaic Generation System Based on DC Bus. IEEE Trans. Power Electron. 2011, 26, 523–531. [Google Scholar] [CrossRef]
- Tang, Y.; Loh, P.C.; Wang, P.; Choo, F.H.; Gao, F. Exploring inherent damping characteristic of LCL-filters for three-phase grid-connected voltage source inverters. IEEE Trans. Power Electron. 2011, 27, 1433–1443. [Google Scholar] [CrossRef]
- Tzou, Y.-Y. DSP-based fully digital control of a PWM DC-AC converter for AC voltage regulation. In Proceedings of the PESC ’95—Power Electronics Specialist Conference, Atlanta, GA, USA, 18–22 June 1995; pp. 1218–1226. [Google Scholar]
- Guo, X.; Liu, W.; Lu, Z. Flexible power regulation and current-limited control of the grid-connected inverter under unbalanced grid voltage faults. IEEE Trans. Ind. Electron. 2017, 64, 7425–7432. [Google Scholar] [CrossRef]
- Sathiyanarayanan, T.; Mishra, S. Synchronous reference frame theory based model predictive control for grid connected photovoltaic systems. IFAC PapersOnLine 2016, 49, 766–771. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Chen, Z.; Wu, W. Resonance analysis in parallel voltage-controlled Distributed Generation inverters. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 2977–2983. [Google Scholar]
- He, J.; Li, Y.W. Analysis, design, and implementation of virtual impedance for power electronics interfaced distributed generation. IEEE Trans. Ind. Appl. 2011, 47, 2525–2538. [Google Scholar] [CrossRef]
- Gonçalves, A.F.Q.; Aguiar, C.R.; Bastos, R.F.; Pozzebon, G.G.; Machado, R.Q. Voltage and power control used to stabilise the distributed generation system for stand-alone or grid-connected operation. IET Power Electron. 2016, 9, 491–501. [Google Scholar] [CrossRef]
- Papavasiliou, A.; Papathanassiou, S.; Manias, S.; Demetriadis, G. Current control of a voltage source inverter connected to the grid via LCL filter. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 2379–2384. [Google Scholar]
- Komurcugil, H.; Bayhan, S.; Abu-Rub, H. Variable-and fixed-switching-frequency-based HCC methods for grid-connected VSI with active damping and zero steady-state error. IEEE Trans. Ind. Electron. 2017, 64, 7009–7018. [Google Scholar] [CrossRef]
- Buso, S.; Caldognetto, T.; Liu, Q. Analysis and experimental characterization of a large-bandwidth triple-loop controller for grid-tied inverters. IEEE Trans. Power Electron. 2018, 34, 1936–1949. [Google Scholar] [CrossRef]
- Tenti, P.; Caldognetto, T.; Buso, S.; Costabeber, A. Control of utility interfaces in low voltage microgrids. In Proceedings of the 2014 IEEE 5th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Galway, Ireland, 24–27 June 2014; pp. 1–8. [Google Scholar]
- Yao, Z.; Xiao, L.; Yan, Y. Seamless transfer of single-phase grid-interactive inverters between grid-connected and stand-alone modes. IEEE Trans. Power Electron. 2009, 25, 1597–1603. [Google Scholar]
- Huang, Q.; Rajashekara, K. A unified selective harmonic compensation strategy using DG-interfacing inverter in both grid-connected and islanded microgrid. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 1588–1593. [Google Scholar]
- Armstrong, M.; Elgendy, M.A.; Mulolani, F. Three-phase grid-connected PV inverters using the proportional resonance controller. In Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016; pp. 1–6. [Google Scholar]
- Zeng, Z.; Yang, H.; Zhao, R.; Cheng, C. Topologies and control strategies of multi-functional grid-connected inverters for power quality enhancement: A comprehensive review. Renew. Sustain. Energy Rev. 2013, 24, 223–270. [Google Scholar] [CrossRef]
- Teodorescu, R.; Blaabjerg, F.; Liserre, M.; Loh, P.C. Proportional-resonant controllers and filters for grid-connected voltage-source converters. IEE Proc. Electr. Power Appl. 2006, 153, 750–762. [Google Scholar] [CrossRef]
- Huerta, F.; Pizarro, D.; Cobreces, S.; Rodriguez, F.J.; Giron, C.; Rodriguez, A. LQG Servo Controller for the Current Control of $LCL$ Grid-Connected Voltage-Source Converters. IEEE Trans. Ind. Electron. 2012, 59, 4272–4284. [Google Scholar] [CrossRef]
- Cortes, P.; Kazmierkowski, M.P.; Kennel, R.M.; Quevedo, D.E.; Rodriguez, J. Predictive Control in Power Electronics and Drives. IEEE Trans. Ind. Electron. 2008, 55, 4312–4324. [Google Scholar] [CrossRef]
- Mattavelli, P.; Spiazzi, G.; Tenti, P. Predictive Digital Control of Power Factor Preregulators With Input Voltage Estimation Using Disturbance Observers. IEEE Trans. Power Electron. 2005, 20, 140–147. [Google Scholar] [CrossRef]
- Trabelsi, M.; Ghazi, K.A.; Al-Emadi, N.; Ben-Brahim, L. An original controller design for a grid-connected PV system. In Proceedings of the IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 924–929. [Google Scholar]
- Falkowski, P.; Sikorski, A. Finite control set model predictive control for grid-connected AC–DC converters with LCL filter. IEEE Trans. Ind. Electron. 2017, 65, 2844–2852. [Google Scholar] [CrossRef]
- Xia, C.; Liu, T.; Shi, T.; Song, Z. A simplified finite-control-set model-predictive control for power converters. IEEE Trans. Ind. Inf. 2013, 10, 991–1002. [Google Scholar]
- Yaramasu, V.; Rivera, M.; Wu, B.; Rodriguez, J. Model predictive current control of two-level four-leg inverters—Part I: Concept, algorithm, and simulation analysis. IEEE Trans. Power Electron. 2012, 28, 3459–3468. [Google Scholar] [CrossRef]
- Weiland, A.D. Robust Control, draft version; Eindhoven University of Technology, Measurement and Control Group Department of Electrical Engineering: Eindhoven, The Netherlands, 2002. [Google Scholar]
- Chhabra, M.; Barnes, F. Robust current controller design using mu-synthesis for grid-connected three phase inverter. In Proceedings of the 2014 IEEE 40th Photovoltaic Specialist Conference (PVSC), Denver, CO, USA, 8–13 June 2014; pp. 1413–1418. [Google Scholar]
- Bahrampour, E.; Asemani, M.H.; Badfar, F.; Vafamand, N. High-Performance Robust Grid-Connected Power Systems. In Proceedings of the 2019 6th International Conference on Control, Instrumentation and Automation (ICCIA), Sanandaj, Iran, 30–31 October 2019; pp. 1–6. [Google Scholar]
- Bevrani, H.; Feizi, M.R.; Ataee, S. Robust Frequency Control in an Islanded Microgrid: H∞ and μ-synthesis Approaches. IEEE Trans. Smart Grid 2015, 7, 706–717. [Google Scholar] [CrossRef]
- Hornik, T.; Zhong, Q.C. A Current-Control Strategy for Voltage-Source Inverters in Microgrids Based on H∞ and Repetitive Control. IEEE Trans. Power Electron. 2011, 26, 943–952. [Google Scholar] [CrossRef]
- Yang, S.; Lei, Q.; Peng, F.Z.; Qian, Z. A robust control scheme for grid-connected voltage-source inverters. IEEE Transa. Ind. Electron. 2010, 58, 202–212. [Google Scholar] [CrossRef]
- Hong, Q.C.; Hornik, T. Cascaded current–voltage control to improve the power quality for a grid-connected inverter with a local load. IEEE Trans. Ind. Electron. 2012, 60, 1344–1355. [Google Scholar]
- Kumar, N.; Saha, T.K.; Dey, J. Sliding-Mode Control of PWM Dual Inverter-Based Grid-Connected PV System: Modeling and Performance Analysis. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 435–444. [Google Scholar] [CrossRef]
- Jeong, H.-G.; Kim, W.-S.; Lee, K.-B.; Jeong, B.-C.; Song, S.-H. A sliding-mode approach to control the active and reactive powers for a DFIG in wind turbines. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 120–125. [Google Scholar]
- Özbay, H.; Öncü, S.; Kesler, M. SMC-DPC based active and reactive power control of grid-tied three phase inverter for PV systems. Int. J. Hydrog. Energy 2017, 42, 17713–17722. [Google Scholar] [CrossRef]
- Fei, J.; Zhu, Y. Adaptive fuzzy sliding control of single-phase PV grid-connected inverter. PLoS ONE 2017, 12, e0182916. [Google Scholar] [CrossRef]
- Zhu, Y.; Fei, J. Adaptive global fast terminal sliding mode control of grid-connected photovoltaic system using fuzzy neural network approach. IEEE Access 2017, 5, 9476–9484. [Google Scholar] [CrossRef]
- Zué, A.O.; Chandra, A. State feedback linearization control of a grid connected photovoltaic interface with MPPT. In Proceedings of the 2009 IEEE Electrical Power & Energy Conference (EPEC), Montreal, QC, Canada, 22–23 October 2009; pp. 1–6. [Google Scholar]
- Lalili, D.; Mellit, A.; Lourci, N.; Medjahed, B.; Berkouk, E. Input output feedback linearization control and variable step size MPPT algorithm of a grid-connected photovoltaic inverter. Renew. Energy 2011, 36, 3282–3291. [Google Scholar] [CrossRef]
- Begh, M.A.W.; Liegmann, E.; Mahajan, A.; Palanisamy, A.; Siwakoti, Y.P.; Karamanakos, P.; Abdelrahem, M.; Kennel, R. Design of State-Feedback Controller for a Single-Phase Grid-Connected Siwakoti-H Inverter with LCL filter. In Proceedings of the PCIM Europe 2019; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 7–9 May 2019; pp. 1–8. [Google Scholar]
- Mahmud, M.A.; Pota, H.R.; Hossain, M.J. Nonlinear controller design for single-phase grid-connected photovoltaic systems using partial feedback linearization. In Proceedings of the 2012 2nd Australian Control Conference, Sydney, NSW, Australia, 15–16 November 2012; pp. 30–35. [Google Scholar]
- Wu, F.; Feng, F.; Luo, L.; Duan, J.; Sun, L. Sampling period online adjusting-based hysteresis current control without band with constant switching frequency. IEEE Trans. Ind. Electron. 2014, 62, 270–277. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, L.; Wu, Q. Simple unipolar maximum switching frequency limited hysteresis current control for grid-connected inverter. IET Power Electron. 2013, 7, 933–945. [Google Scholar] [CrossRef]
- Holmes, D.G.; Davoodnezhad, R.; McGrath, B.P. An improved three-phase variable-band hysteresis current regulator. IEEE Trans. Power Electr. 2012, 28, 441–450. [Google Scholar] [CrossRef]
- Alarcón-Gallo, E.; de Vicuña, L.G.; Castilla, M.; Miret, J.; Matas, J.; Camacho, A. Decoupled sliding mode control for three-phase LCL VSI operating at fixed switching frequency. In Proceedings of the 2012 IEEE International Symposium on Industrial Electronics, Hangzhou, China, 28–31 May 2012; pp. 1572–1578. [Google Scholar]
- Li, Y.; Hao, X.; Yang, X.; Xie, R.; Liu, T. A variable-band hysteresis modulated multi-resonant sliding-mode controller for three-phase grid-connected VSI with an LCL-filter. In Proceedings of the 2013 IEEE ECCE Asia Downunder, Melbourne, VIC, Australia, 3–6 June 2013; pp. 670–676. [Google Scholar]
- Do, T.D.; Leu, V.Q.; Choi, Y.-S.; Choi, H.H.; Jung, J.-W. An Adaptive Voltage Control Strategy of Three-Phase Inverter for Stand-Alone Distributed Generation Systems. IEEE Trans. Ind. Electron. 2013, 60, 5660–5672. [Google Scholar] [CrossRef]
- Espi, J.M.; Castello, J.; García-Gil, R.; Garcera, G.; Figueres, E. An Adaptive Robust Predictive Current Control for Three-Phase Grid-Connected Inverters. IEEE Trans. Ind. Electron. 2011, 58, 3537–3546. [Google Scholar] [CrossRef]
- Escobar, G.; Mattavelli, P.; Stankovic, A.M.; Valdez, A.A.; Leyva-Ramos, J. An adaptive control for UPS to compensate unbalance and harmonic distortion using a combined capacitor/load current sensing. IEEE Trans. Ind. Electron. 2007, 54, 839–847. [Google Scholar] [CrossRef]
- Roy, T.; Pervej, M.; Tumpa, F. Adaptive controller Design for grid current regulation of a CSI based PV system. In Proceedings of the 2016 2nd International Conference on Electrical, Computer & Telecommunication Engineering (ICECTE), Rajshahi, Bangladesh, 8–10 December 2016; pp. 1–4. [Google Scholar]
- Lin, W.-M.; Hong, C.-M. A new Elman neural network-based control algorithm for adjustable-pitch variable-speed wind-energy conversion systems. IEEE Trans. Power Electr. 2010, 26, 473–481. [Google Scholar] [CrossRef]
- Davanipoor, M.; Zekri, M.; Sheikholeslam, F. Fuzzy wavelet neural network with an accelerated hybrid learning algorithm. IEEE Trans. Fuzzy Syst. 2011, 20, 463–470. [Google Scholar] [CrossRef]
- Sozhamadevi, N.; Delcause, R.S.L.; Sathiyamoorthy, S. Design and implementation of probabilistic fuzzy logic control system. In Proceedings of the 2012 International Conference on Emerging Trends in Science, Engineering and Technology (INCOSET), Tiruchirappalli, India, 13–14 December 2012; pp. 523–531. [Google Scholar]
- Lin, F.-J.; Lu, K.-C.; Ke, T.H. Probabilistic Wavelet Fuzzy Neural Network based reactive power control for grid-connected three-phase PV system during grid faults. Renew. Energy 2016, 92, 437–449. [Google Scholar] [CrossRef]
- Mahmud, N.; Zahedi, A.; Mahmud, A. A Cooperative Operation of Novel PV Inverter Control Scheme and Storage Energy Management System Based on ANFIS for Voltage Regulation of Grid-Tied PV System. IEEE Trans. Ind. Inf. 2017, 13, 2657–2668. [Google Scholar] [CrossRef]
- Mohamed, I.S.; Rovetta, S.; Do, T.D.; Dragicević, T.; Diab, A.A.Z. A neural-network-based model predictive control of three-phase inverter with an output $ LC $ filter. IEEE Access 2019, 7, 124737–124749. [Google Scholar] [CrossRef]
- De Almeida, P.M.; Barbosa, P.G.; Ribeiro, P.F.; Duarte, J.L. Repetitive controller for improving grid-connected photovoltaic systems. IET Power Electron. 2014, 7, 1466–1474. [Google Scholar] [CrossRef]
- Li, S.; Chen, W.; Fang, B.; Zhang, D. A strategy of PI+ repetitive control for LCL-type photovoltaic inverters. Soft Comput. 2020. [Google Scholar] [CrossRef]
- Tariq, S. Intelligent Control: An Overview of Techniques. In Perspectives in Control Engineering Technologies, Applications, and New Directions; Wiley-IEEE Press: Hoboken, NJ, USA, 2001; ISBN 9780470545485. [Google Scholar]
- Gupta, N.; Garg, R. Tuning of asymmetrical fuzzy logic control algorithm for SPV system connected to grid. Int. J. Hydrog. Energy 2017, 42, 16375–16385. [Google Scholar] [CrossRef]
- Yatak, M.O.; Bay, O.F. Fuzzy control of a grid connected three phase two stage photovoltaic system. In Proceedings of the 2011 International Conference on Power Engineering, Energy and Electrical Drives, Malaga, Spain, 11–13 May 2011; pp. 1–6. [Google Scholar]
- Hannan, M.; Ghani, Z.A.; Mohamed, A.; Uddin, M.N. Real-time testing of a fuzzy-logic-controller-based grid-connected photovoltaic inverter system. IEEE Trans. Ind. Appl. 2015, 51, 4775–4784. [Google Scholar] [CrossRef]
- Thao, N.G.M.; Uchida, K. Control the photovoltaic grid-connected system using fuzzy logic and backstepping approach. In Proceedings of the 2013 9th Asian Control Conference (ASCC), Istanbul, Turkey, 23–26 June 2013; pp. 1–8. [Google Scholar]
- Thao, N.G.M.; Uchida, K. A two-level control strategy with fuzzy logic for large-scale photovoltaic farms to support grid frequency regulation. Control Eng. Pract. 2017, 59, 77–99. [Google Scholar] [CrossRef]
- Zeng, L.; Jinjun, L.; Yalin, Z. A Unified Control Strategy for Three-Phase Inverter in Distributed Generation. IEEE Trans. Power Electron. 2014, 29, 1176–1191. [Google Scholar] [CrossRef]
- Zarei, S.F.; Mokhtari, H.; Ghasemi, M.A.; Peyghami, S.; Davari, P.; Blaabjerg, F. Control of Grid-Following Inverters Under Unbalanced Grid Conditions. IEEE Trans. Energy Convers. 2020, 35, 184–192. [Google Scholar] [CrossRef]
- Samui, A.; Samantaray, S.R. New active islanding detection scheme for constant power and constant current controlled inverter-based distributed generation. IET Gener. Transm. Distrib. 2013, 7, 779–789. [Google Scholar] [CrossRef]
- Chilipi, R.; Beig, A.R.; Al Hosani, K.; Al Sayari, N. Control scheme for grid-tied distributed generation inverter under unbalanced and distorted utility conditions with power quality ancillary services. IET Renew. Power Gener. 2016, 10, 140–149. [Google Scholar] [CrossRef]
- Radwan, A.A.A.; Mohamed, Y.A.R.I. Power Synchronization Control for Grid-Connected Current-Source Inverter-Based Photovoltaic Systems. IEEE Trans. Energy Convers. 2016, 31, 1023–1036. [Google Scholar] [CrossRef]
- Xu, J.; Xie, S.; Tang, T. Active Damping-Based Control for Grid-Connected $LCL$ -Filtered Inverter With Injected Grid Current Feedback Only. IEEE Trans. Ind. Electron. 2014, 61, 4746–4758. [Google Scholar] [CrossRef]
- Bao, C.; Ruan, X.; Wang, X.; Li, W.; Pan, D.; Weng, K. Step-by-Step Controller Design for LCL-Type Grid-Connected Inverter with Capacitor–Current-Feedback Active-Damping. IEEE Trans. Power Electron. 2014, 29, 1239–1253. [Google Scholar]
- Yao, Z.; Xiao, L. Control of Single-Phase Grid-Connected Inverters With Nonlinear Loads. IEEE Trans. Ind. Electron. 2013, 60, 1384–1389. [Google Scholar] [CrossRef]
- Camacho, A.; Castilla, M.; Miret, J.; Vasquez, J.C.; Alarcon-Gallo, E. Flexible Voltage Support Control for Three-Phase Distributed Generation Inverters Under Grid Fault. IEEE Trans. Ind. Electron. 2013, 60, 1429–1441. [Google Scholar] [CrossRef]
- Eren, S.; Pahlevani, M.; Bakhshai, A.; Jain, P. An Adaptive Droop DC-Bus Voltage Controller for a Grid-Connected Voltage Source Inverter With LCL Filter. IEEE Trans. Power Electron. 2015, 30, 547–560. [Google Scholar] [CrossRef]
- Jung, J.-W.; Vu, N.T.-T.; Dang, D.Q.; Do, T.D.; Choi, Y.-S.; Choi, H.H. A Three-Phase Inverter for a Standalone Distributed Generation System: Adaptive Voltage Control Design and Stability Analysis. IEEE Trans. Energy Convers. 2014, 29, 46–56. [Google Scholar] [CrossRef]
- Bonala, A.K.; Sandepudi, S.R. Centralised model-predictive decoupled active–reactive power control for three-level neutral point clamped photovoltaic inverter with preference selective index-based objective prioritisation. IET Power Electron. 2019, 12, 840–851. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Yu, C.; Guo, L.; Cao, R. Hysteresis Model Predictive Control for High-Power Grid-Connected Inverters With Output LCL Filter. IEEE Trans. Ind. Electron. 2016, 63, 246–256. [Google Scholar] [CrossRef]
- Ouchen, S.; Betka, A.; Abdeddaim, S.; Menadi, A. Fuzzy-predictive direct power control implementation of a grid-connected photovoltaic system, associated with an active power filter. Energy Convers. Manag. 2016, 122, 515–525. [Google Scholar] [CrossRef]
- Chen, X.; Wu, W.; Gao, N.; Liu, J.; Chung, H.S.-H.; Blaabjerg, F. Finite Control Set Model Predictive Control for an LCL-Filtered Grid-Tied Inverter with Full Status Estimations under Unbalanced Grid Voltage. Energies 2019, 12, 2691. [Google Scholar] [CrossRef]
- Priyadarshi, N.; Bhoi, A.K.; Sharma, A.K.; Mallick, P.K.; Chakrabarti, P. An Efficient Fuzzy Logic Control-Based Soft Computing Technique for Grid-Tied Photovoltaic System. In Proceedings of the Cognitive Informatics and Soft Computing, Singapore, 15 January 2020; pp. 131–139. [Google Scholar]
- F Fallah Ardashir, J.; Mohammadpour Shotorbani, A.; khoun-Jahan, H.; Sabahi, M. Fractional PR Control of a Grid-tied Flying Capacitor Inverter for PV Applications. J. Energy Manag. Technol. 2019, 3, 58–64. [Google Scholar]
- Lakshmi, M.; Hemamalini, S. Decoupled control of grid-connected photovoltaic system using fractional order controller. Ain Shams Eng. J. 2018, 9, 927–937. [Google Scholar] [CrossRef]
- Hamrouni, N.; Younsi, S.; Jraidi, M. A Flexible Active and Reactive Power Control Strategy of a LV Grid-connected PV System. Energy Procedia 2019, 162, 325–338. [Google Scholar] [CrossRef]
- Islam, S.U.; Zeb, K.; Din, W.U.; Khan, I.; Ishfaq, M.; Busarello, T.D.C.; Kim, H.J. Design of a proportional resonant controller with resonant harmonic compensator and fault ride trough strategies for a grid-connected photovoltaic system. Electronics 2018, 7, 451. [Google Scholar] [CrossRef]
- Zhu, Y.; Fei, J. Disturbance Observer Based Fuzzy Sliding Mode Control of PV Grid-connected Inverter. IEEE Access 2018, 6, 21202–21211. [Google Scholar] [CrossRef]
- Sun, X.; Chen, Z.; Tian, Y. Adaptive decoupled power control method for inverter connected DG. IET Renew. Power Gener. 2014, 8, 171–182. [Google Scholar] [CrossRef]
- Katkamwar, S.S.; Doifode, V.R. Cascaded H-bridge multilevel PV inverter with MPPT for grid-connected application. In Proceedings of the 2016 International Conference on Energy Efficient Technologies for Sustainability (ICEETS), Nagercoil, India, 7–8 April 2016; pp. 641–646. [Google Scholar]
- Xiao, B.; Hang, L.; Mei, J.; Riley, C.; Tolbert, L.M.; Ozpineci, B. Modular Cascaded H-Bridge Multilevel PV Inverter With Distributed MPPT for Grid-Connected Applications. IEEE Trans. Ind. Appl. 2015, 51, 1722–1731. [Google Scholar] [CrossRef]
- Yan, X.; Li, J.; Wang, L.; Zhao, S.; Li, T.; Lv, Z.; Wu, M. Adaptive-MPPT-Based Control of Improved Photovoltaic Virtual Synchronous Generators. Energies 2018, 11, 1834. [Google Scholar] [CrossRef]
- Ma, M.; Liu, X.; Lee, K.Y. Maximum Power Point Tracking and Voltage Regulation of Two-Stage Grid-Tied PV System Based on Model Predictive Control. Energies 2020, 13, 1304. [Google Scholar] [CrossRef]
- Rey-Boué, A.B.; Guerrero-Rodríguez, N.F.; Stöckl, J.; Strasser, T.I. Modeling and Design of the Vector Control for a Three-Phase Single-Stage Grid-Connected PV System with LVRT Capability according to the Spanish Grid Code. Energies 2019, 12, 2899. [Google Scholar] [CrossRef]
- Zeng, F.; Shu, H.; Zhu, T.; Swe, T.; Yang, B. Fractional-order Feedback Linearization Sliding-mode Control Design for Grid-connected PV Inverters. In Proceedings of the 2019 IEEE 3rd International Electrical and Energy Conference (CIEEC), Beijing, China, 7–9 September 2019; pp. 874–878. [Google Scholar]
- Ebadi, M.; Joorabian, M.; Moghani, J.S. Voltage look-up table method to control multilevel cascaded transformerless inverters with unequal DC rail voltages. IET Power Electron. 2014, 7, 2300–2309. [Google Scholar] [CrossRef]
- Koch, G.G.; Pinheiro, H.; Oliveira, R.C.; Montagner, V.F. Experimental evaluation of robust and nonrobust H∞ controllers for three-phase grid-connected converters. In Proceedings of the 2017 Brazilian Power Electronics Conference (COBEP), Juiz de Fora, Brazil, 19–22 November 2017; pp. 1–6. [Google Scholar]
- Chen, X.; Wu, W.; Gao, N.; Chung, H.S.; Liserre, M.; Blaabjerg, F. Finite Control Set Model Predictive Control for LCL-Filtered Grid-Tied Inverter with Minimum Sensors. IEEE Trans. Ind. Electron. 2020. [Google Scholar] [CrossRef]
- Zhao, Q.; Ye, Y.; Xu, G.; Zhu, M. Improved repetitive control scheme for grid-connected inverter with frequency adaptation. IET Power Electron. 2016, 9, 883–889. [Google Scholar] [CrossRef]

| Ref. | GS PV | PV CS | CI | IT | MT | CRF | CT | FS |
|---|---|---|---|---|---|---|---|---|
| [23] | ✓ | ✗ | ✓ | ✓ | ✗ | ✓ | ✗ | ✓ |
| [24] | ✓ | ✗ | ✗ | ✓ | ✗ | ✓ | ✗ | ✗ |
| [25] | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | ✗ |
| [26] | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✓ |
| [27] | ✓ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✓ |
| [19] | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ |
| [28] | ✗ | ✓ | ✓ | ✓ | ✗ | ✓ | ✗ | ✓ |
| [29] | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ |
| [30] | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ |
| [21] | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ |
| [31] | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | ✓ | ✓ |
| [32] | ✗ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✓ |
| [33] | ✗ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ |
| [34] | ✓ | ✗ | ✓ | ✗ | ✗ | ✓ | ✓ | ✗ |
| [OS] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Performance | Central | String | Multi-String | AC Module |
|---|---|---|---|---|
| Very High | Variation of DC input voltage | ------ | ------ | Maintenance Installation cost MPPT efficiency Flexibility Reliability |
| High | Cables cost Voltage balancing DC power loss Switching loss Panels mismatching Robustness | Installation cost MPPT efficiency Flexibility Reliability | Variation of DC input voltage | AC Cables cost AC Power loss |
| Medium | Installation cost | DC Cables cost DC voltage variation AC Power loss Voltage balancing | Maintenance MPPT efficiency Flexibility Reliability Robustness DC and AC power loss Switching loss Installation and cables cost | ------ |
| Low | MPPT efficiency Flexibility Reliability Maintenance AC Power loss | Robustness Cables cost DC Power loss Switching loss Panels mismatching | Voltage balancing Panels mismatching | Voltage balancing |
| Very low | ------ | ------ | ------ | Robustness Cables cost DC voltage variation DC Power loss Switching loss Panels mismatching |
| Power rating | 1–50 MW | 1–5 kW/string | 1–50 kW | 500–600 W |
| Cost | Lowest cost | Costly than centralized inverter | Costly than centralized inverter | Highest cost |
| Type of GCMLI | Pros | Cons |
|---|---|---|
| NPC-GCMLI | Simple design Fast dynamic response Low voltage rating switches are needed High efficiency | As level increases the clamping diode count increases As level increases the complexity to balance the DC-link increases DC-link voltage regulation is required |
| FC-GCMLI | During power outage it has the capability to provide an extra ride through facility Phase redundant Low component count Low stress on components Low THD and have high modularity | As level increases the capacitor count increases As level increases the control system become more complicated High installation cost Less efficient due to low switching efficiency |
| CHB-GCMLI | Provide modular solution to achieve high voltage level Good fault tolerance Highly reliable | The inverter faces the problem of voltage misbalancing among the different phases Separate DC sources are used |
| M-GCMLI | Suitable for all voltage levels High modularity Low component count As the level increase the power switches count not increases Simpler structure Low THD and have compact size | High thermal losses High conduction losses High voltage ripples through SMs capacitors Current flows within inverter Large quantity of DC voltage sources (isolated) are required |
| Ref. | MLI Topology | NOL | NOP | MT | C | SF (kHz) | CP (kW) |
|---|---|---|---|---|---|---|---|
| [67] | CHB | 05 | 3-Φ | SV-PWM | PI | 10 | --- |
| [68] | M | 7 | 3-Φ | MC-PWM | PI | 10 | 0.4 |
| [69] | Reduced switch | 7 | 1-Φ | MC-PWM | --- | --- | --- |
| [70] | E-Type | 7 | 3-Φ | PWM | --- | 20 | 4 |
| [71] | CHB | 13 | 1-Φ | PWM | --- | 5 | --- |
| [72] | Three phase | 5 | 3-Φ | MC-PWM | --- | 20 | 1 |
| [73] | Diode Clamped | 5 | 1-Φ | PWM | --- | --- | --- |
| [74] | symmetrical | 7 | 3-Φ | PWM | --- | --- | --- |
| [75] | Hybrid | 5 | 3-Φ | PWM | Finite Control Set-MPC | 6 | 7.5 |
| [76] | NPC Back to Back | --- | 3-Φ | PWM | MPC | 10 | 0.28 |
| [77] | CHB | 5 | 1-Φ | LS-PWM | FO-PID | 2 | --- |
| [78] | CHB | 7, 15 | 1-Φ | MC-PWM | --- | --- | --- |
| [79] | CHB with T type | m | 3-Φ | PS-PWM | PI | 3 | 1 |
| [80] | Modular | m | 3-Φ | LS-PWM | PR | 1 | --- |
| [81] | CHB | 7, 9 | 1-Φ | LS-PWM | CPT | 12 | 2 |
| [82] | Cascaded Full-bridge with FC | 9 | 1-Φ | PWM | Hysteresis | 20 | --- |
| [83] | Asymmetrical Cascaded | 17 | 1-Φ | SHE-PWM | --- | --- | --- |
| [84] | Quasi Z-Source Based NPC | 5 | 1-Φ | LS-PWM | PI | 10 | 0.5 |
| [85] | Modified DC link | 7 | 1-Φ | MC-PWM | --- | 6 | --- |
| [86] | NPC | 3 | 3-Φ | SV-PWM | --- | 2 | 1.1 |
| α Calculation Methods | α, for i = 1, 2,…(n − 1)/2 | THD in Output Voltage | Nature of α | Remarks |
|---|---|---|---|---|
| Feed Forward | sin−1((i − 0.5)/n) | Small | High | Feasible for any voltage level |
| Half Equal Phase | 180°/(n + 1) | High | Low | Feasible for low voltage level |
| Equal Phase | 180°/n | High | Very Low | Feasible for low voltage level |
| Half Height | sin−1((2i − 1)/(n − 1)) | Medium | Moderate | Feasible for medium and low voltage levels |
| Ref. | NOP, CRF | CC | DLC | FL | CP | F | MT | A |
|---|---|---|---|---|---|---|---|---|
| [133] | 3-Φ, (dq) | MPC | --- | S-L | C | L | SVM | PV |
| [139] | 3-Φ, (abc) | DB, PI | DB | M-L | C, V | LCL | DPWM | G |
| [152] | 1-Φ | FSC-MPC | --- | S-L | C | L | PWM | G |
| [154] | 3-Φ, (dq) | μ-synthesis | PI | M-L | C, V | LC | PWM | PV |
| [158] | 3-Φ, (dq) | H-infinity | PI | M-L | C, V | LC | PWM | RE |
| [137] | 3-Φ, (dq) | SMC | --- | S-L | C | L | PWM | PV |
| [162] | 3-Φ, (αβ) | SMC-DPC | SMC-DPC | M-L | V, P | L | SVPWM | PV |
| [166] | 3-Φ, (dq) | FFL | LC | M-L | C, V | L | SVPWM | PV |
| [168] | 1-Φ | PFL | PFL | M-L | V, C | L | PWM | PV |
| [181] | 3-Φ, (abc) | Fuzzy Neural Network | Fuzzy Neural Network | M-L | V, P | L | PWM | PV |
| [182] | 3-Φ, (dq) | ANFISPID | ANFISPID | M-L | V, C | L | PWM | PV |
| [184] | 3-Φ, (dq) | Repetitive | --- | S-L | C | L | SVM | PV |
| [192] | 3-Φ, (dq) | PI | PI | M-L | V, C | LC | SVM | DG |
| [193] | 3-Φ, (dq) | Instantaneous Active Reactive Control | PI, PR | M-L | V, P | L | PWM | G |
| [194] | 3-Φ, (dq) | PI | PI | M-L | V, C | L | PWM | DG |
| [195] | 3-Φ, (αβ) | I | --- | S-L | C | L | PWM | DG |
| [196] | 3-Φ, (dq) | Reactive Power Control | PI | M-L | V, P | LC | PWM | PV |
| [197] | 1-Φ | PR | PI | M-L | V, C | LCL | PWM | G |
| [198] | 1-Φ | PI, PR | --- | S-L | C | LCL | SPWM | G |
| [199] | 1-Φ | PI, Hysteresis | PI | M-L | V, C | LC | PWM | G |
| [200] | 3-Φ, (αβ) | PR | PI | M-L | V, P | LCL | PWM | DG |
| [201] | 1-Φ | --- | Adaptive droop | M-L | V | LCL | PWM | G |
| [202] | 3-Φ, (dq) | Adaptive | PI | M-L | V, C | LC | SVPWM | DG |
| [203] | 3-Φ, (αβ) | MPC | --- | S-L | V, C | L | PWM | PV |
| [204] | 3-Φ, (αβ) | Hysteresis MPC | --- | S-L | C | LCL | PWM | G |
| [205] | 3-Φ, (αβ) | Predictive DPC | PI | M-L | V, P | L | PWM | PV |
| [206] | 3-Φ, (αβ) | MPC | --- | S-L | C | LCL | PWM | G |
| [207] | 3-Φ, (αβ) | Fuzzy | PI | M-L | V, C | L | SVPWM | PV |
| [208] | 1-Φ | Fractional order PR | --- | M-L | C, P | L | SPWM | PV |
| [209] | 3-Φ, (dq) | Fractional order PI | Fractional order PI | M-L | V, C | LCL | PWM | PV |
| [210] | 3-Φ, (dq) | PI | PI | M-L | V, C | LCL | PWM | PV |
| [211] | 3-Φ, (dq) | PR | PI | M-L | V, C | LCL | PWM | PV |
| [212] | 1-Φ | Fuzzy SMC | --- | S-L | V | L | PWM | PV |
| [213] | 3-Φ, (dq) | Droop | --- | M-L | V, C | LC | PWM | DG |
| [214] | 3-Φ, (dq) | PI | PI | M-L | V, C | L | PWM | PV |
| [215] | 3-Φ, (dq) | PI | PI | M-L | V, C | L | SPWM | PV |
| [216] | 3-Φ, (dq) | PI | PI | M-L | V, C | L | SVPWM | PV |
| [217] | 1-Φ | PI, MPC | PI, MPC | M-L | V, C | L | PWM | PV |
| [218] | 3-Φ, (dq) | PI, Vector control | PI | M-L | V, C | L | PWM | PV |
| [219] | 3-Φ, (dq) | Fractional order SMC | --- | S-L | C | L | PWM | PV |
| [220] | 3-Φ, (dq) | Voltage look-up table method | Voltage look-up table method | M-L | V, C | L | VLUT | DG |
| [221] | 3-Φ, (αβ) | H-infinity | --- | S-L | C | LCL | SVM | G |
| [222] | 3-Φ, (αβ) | MPC | --- | S-L | C | LCL | PWM | G |
| [223] | 1-Φ | Fractional order RC | --- | S-L | C | LCL | PWM | G |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali Khan, M.Y.; Liu, H.; Yang, Z.; Yuan, X. A Comprehensive Review on Grid Connected Photovoltaic Inverters, Their Modulation Techniques, and Control Strategies. Energies 2020, 13, 4185. https://doi.org/10.3390/en13164185
Ali Khan MY, Liu H, Yang Z, Yuan X. A Comprehensive Review on Grid Connected Photovoltaic Inverters, Their Modulation Techniques, and Control Strategies. Energies. 2020; 13(16):4185. https://doi.org/10.3390/en13164185
Chicago/Turabian StyleAli Khan, Muhammad Yasir, Haoming Liu, Zhihao Yang, and Xiaoling Yuan. 2020. "A Comprehensive Review on Grid Connected Photovoltaic Inverters, Their Modulation Techniques, and Control Strategies" Energies 13, no. 16: 4185. https://doi.org/10.3390/en13164185
APA StyleAli Khan, M. Y., Liu, H., Yang, Z., & Yuan, X. (2020). A Comprehensive Review on Grid Connected Photovoltaic Inverters, Their Modulation Techniques, and Control Strategies. Energies, 13(16), 4185. https://doi.org/10.3390/en13164185






