1. Introduction
The strong development of electric vehicles (EVs) moves the research actions on new solutions for the automotive field. First, batteries and storage systems represent the burning issues of this sector. Among them, lithium ion batteries represent the main technology that is catching on for different purposes. These kinds of batteries are used for both stationary and mobile applications because of their high-energy density and high-power density. Great performances and innovative designs are asked for by the electric transportation market [
1]; for this reason, accurate and reliable models are needed. Knowing SoC (State of Charge) [
2,
3], SoH (State of Health) [
4], OCV (Open Circuit Voltage) [
5], currents, and voltages is absolutely necessary in order to have well designed and efficient energy storage systems, because nonlinear physical effects in batteries strongly influence battery lifetime [
6]. An accurate battery model allows, in the design phase, to consider several factors such as charging strategies or extreme operating conditions [
7]. The main difficulty in modeling is related to the need to make models as simple as possible [
8]. Actually, in most cases, accurate models need complex solutions. In literature, a lot of different modeling methods are available and these can be mainly classified into three categories: electrochemical, mathematical or electrical [
9,
10,
11].
Electrochemical models are the more accurate but also more complex. They consider the chemical reactions happening through the electrodes to estimate the external parameters and are useful specially to describe thermodynamic and kinetic phenomena occurring in the cell. The first models were introduced by Fuller, Doyle and Newman [
12,
13,
14], developing the porous electrode theory. They provide insight into batteries’ internal dynamics such as electrochemical reactions, mass transportation, diffusion, concentration distribution, and ion distribution. They can relate the constructive parameters (material used for electrode, thickness of separator, dimensions of the cell) to the electrical parameters (voltage, current, capacity) and thermal behavior. An electrochemical model is made of a system of coupled time-variant spatial partial differential equations. To solve these models, high computational efforts are needed and, in addition, several parameters that are difficult to measure or obtain, are needed. In [
15], Kandler et al. considered a 1-dimensional model, in which the
x coordinate is used to define the thickness of each component of the cell (current collectors, electrodes, separator). Many parameters are needed to fully parametrize the model, and most of them require a deep knowledge of the cell chemistry, production process, etc. The complexity and difficulty of finding all the necessary parameters make these models suitable only in the battery design phases. In order to decrease the electrochemical model complexity, Model Order Reduction (MOR) techniques can be applied. In [
16,
17], the reduced order model equations and the model parameters identification for a lithium-iron phosphate battery is presented. The maximum Root Mean Square Error (RMSE) between the measured voltage and the electrochemical reduced order model output is within 55 mV for a single cell. In [
18], a reduced order model based on a Galerkin projection method is developed for Lithium-Iron-Phosphate (LFP) and Nickel-Manganese-Cobalt (NMC) batteries, achieving a maximum RMSE equal to 15.5 mV.
Mathematical models can be further divided into two categories: empirical and stochastic [
19]. The first ones are used to describe a specific behaviour of the battery using simple equations. These models can only be used for specific applications, making errors of the order of 5–20%. The advantages of the empirical models are the low complexity and the possibility to achieve real-time parameter identification. The second category of mathematical models, the stochastic models, are based on the principle of the discrete-time Markov chain. They can achieve higher accuracy with respect to the empirical model while keeping low complexity and fast simulation. In [
20], a mathematical method based on the least square algorithm is used for the dynamic parameters identification by modifying the Shepherd battery model. Hybrid method can be also applied, such as that used in [
21] in which both static and dynamic parameters are estimated thanks the an extended Kalman Filtering Algorithm-based method.
Equivalent circuit battery models are developed by using resistors, capacitors and voltage sources in various combinations [
22,
23,
24,
25]. In [
26], three equivalent circuital models, the
Rint model, the
Thevenin model and the
Double Polarization (DP) model, are compared. The DP model gives the best results, with a maximum RMSE of 10 mV, but requires a more complex procedure for the parameter estimation.
Most of the battery models proposed in the previously cited literature require time-consuming experimental tests and costly equipment for their parametrization [
27]. In the first design phase of a battery powered application, it is important to quickly evaluate the performances considering different kinds of batteries, different configurations, etc. [
28]. The possibility to easily obtain battery models parameters from the technical datasheets and to readily implement the model becomes of great importance [
29].
The aim of this article is to compare three different parameter identifications and the modeling approaches. In particular, the modified
Shepherd model, the
Rint model and the
Thevenin model are considered. The first two models are parametrized using just the datasheet information. For the
Thevenin model, a pulse discharge test is executed for parametrization. The models are then validated at steady state, comparing the simulation results with the datasheet discharge curves, and in transient operation, comparing the simulation results with experimental results. The test-bench used for the parametrization and validation of the models is extensively described, considering the accuracy of each employed instrument. The three modeling and parametrization approaches are systematically applied to the LG 18650HG2 lithium-ion cell, and the results are presented, compared and discussed.
Section 2 presents the three different battery models.
Section 3 describes the test-bench.
Section 4 faces the validation of models, and
Section 5 presents the discussion. Finally, conclusions arrive.
2. Battery Modeling and Parametrization
In this section, the three considered battery models are analyzed, considering the governing equations. Then, the parametrization procedures are explained in detail and applied to the LG 18650HG2 cell.
2.1. Shepherd Model
One of the best-known mathematical models for constant-current discharge is the
Shepherd model [
30,
31]:
where:
represents the open circuit voltage of a battery at full capacity (V);
is the polarization resistance coefficient ;
is the battery capacity ;
is the battery current ;
is the internal resistance ;
is the removed charge ;
are empirical constants (V), (1/Ah).
Several mathematical models take the
Shepherd model and try to improve it, adding or modifying some terms. In [
32], a term to consider the polarization voltage is added to the discharge model and the polarization resistance effect is slightly modified, resulting in the following equation
where:
is the filtered current.
Furthermore, a different equation is given for the battery charging:
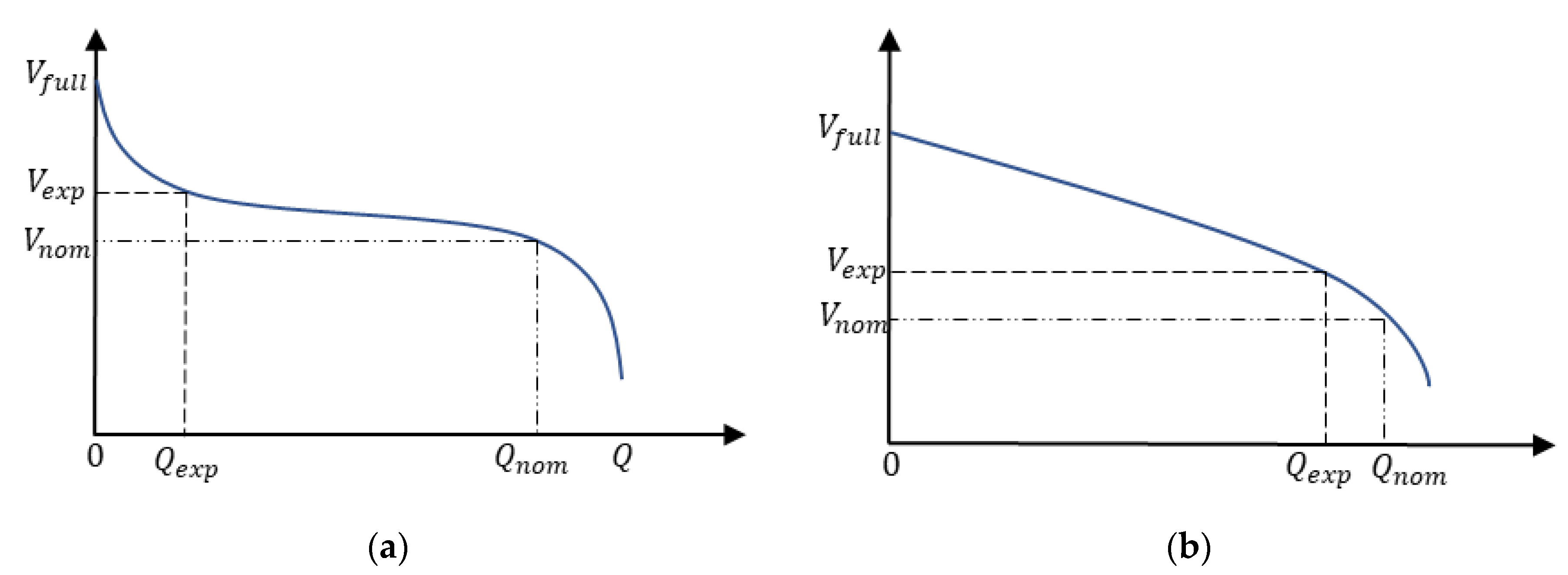
An important feature of this model is the possibility to easily find all the model parameters without the need of experimental tests. Starting from a typical discharge curve given in the manufacturer’s datasheet, four points are identified:
fully charged voltage , first point of the characteristic;
end of the exponential zone ;
end of the nominal zone (when the voltage starts to decrease quickly);
maximum capacity , last point of the characteristic.
Depending on the cell’s chemistry, the discharge curves can be slightly different and the points are shifted accordingly, as can be seen in
Figure 1a,b.
In addition, the cell internal resistance is needed, which is generally given in the datasheet. It should be noted that the discharge curves are obtained with a constant current discharge. Once all the data has been obtained, Equation (2) can be rewritten for each of the identified points to write a set of three equations with three unknowns .
At the start of the characteristic
, the supplied charge is
, the filtered current is
, and the cell current is
. Equation (2) gives:
The parameter
, which represents the time constant of the exponential term, depends on the shape of the discharge curve. For the discharge curve of
Figure 1a, it can be noticed that the exponential term energy is almost zero and can be approximated to 4
. For the discharge curve of
Figure 1b, the exponential term is still predominant and the parameter
can be approximated to
. For the exponential point, the voltage is
, the supplied charge is
, and the filtered current is
because it is assumed that steady state has been reached. With the previous assumption, Equation (2) gives:
For the end of the nominal zone, the voltage is
, the supplied charge is
and Equation (2) gives:
Solving the set of Equations (4)–(6) gives the models parameters, which can be expressed as
where:
;
;
;
;
The parameter estimation procedure described above is now applied to the LG 18650HG2 cell.
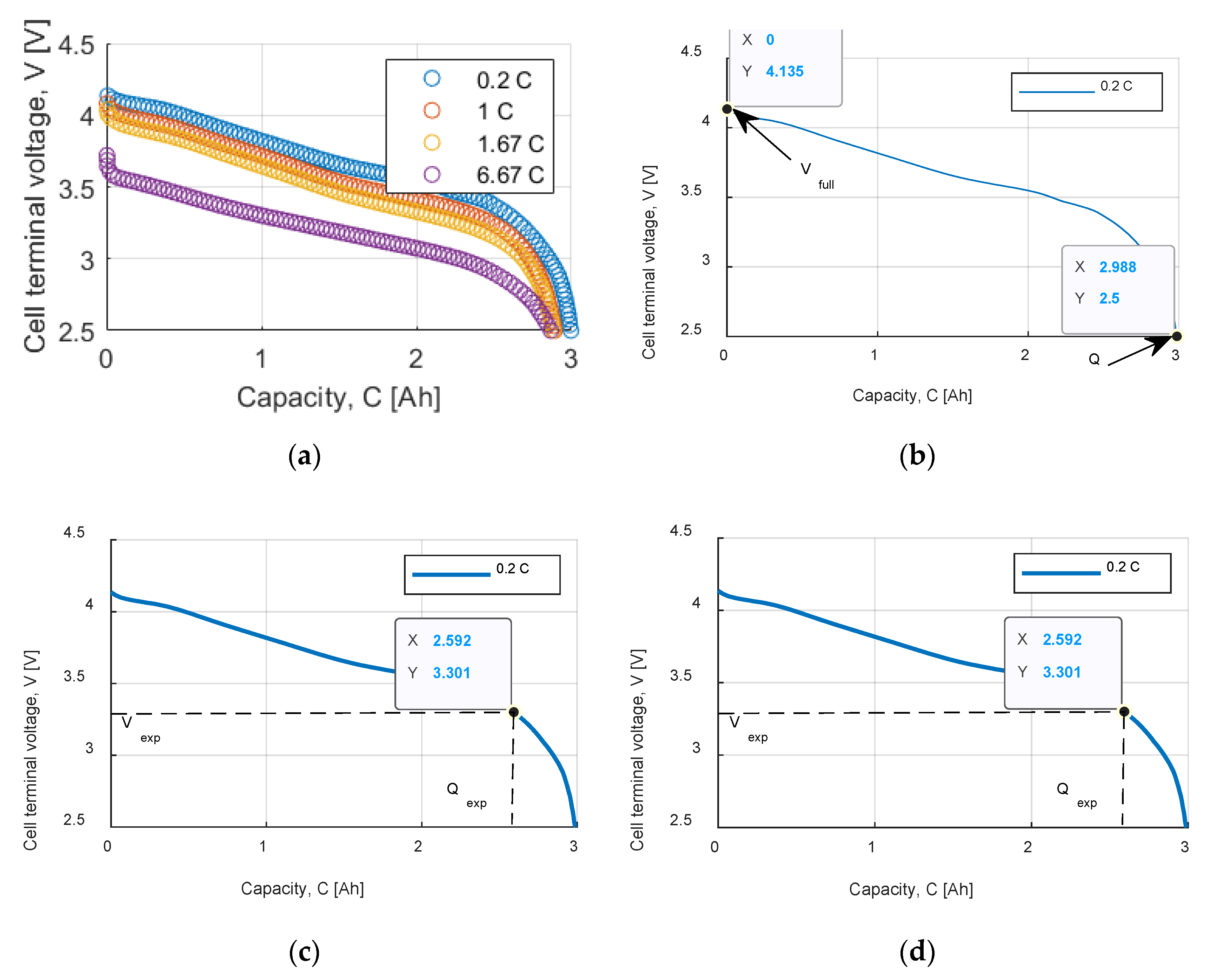
Figure 2a shows the extracted points from the datasheet discharge curves. Among the four characteristics, the one at 0.2 C was chosen for the parameter estimation procedure.
Figure 2b–d shows the point identification on the 0.2 C discharge curves.
Figure 2a depicts the maximum charge voltage
and the maximum capacity
Figure 2b,c represent respectively the exponential zone and the nominal zone detection.
Table 1 summarizes the identified points and the cell internal resistance
given in the manufacturer’s datasheet. To estimate the other parameters, first a value for
must be chosen looking at the shape of the discharge curve, as described in
Section 2.1. In this case,
was chosen. Using the data from
Table 1 and the Equations (7)–(10), the model parameters, summarized in
Table 2, were obtained.
2.2. Rint Model
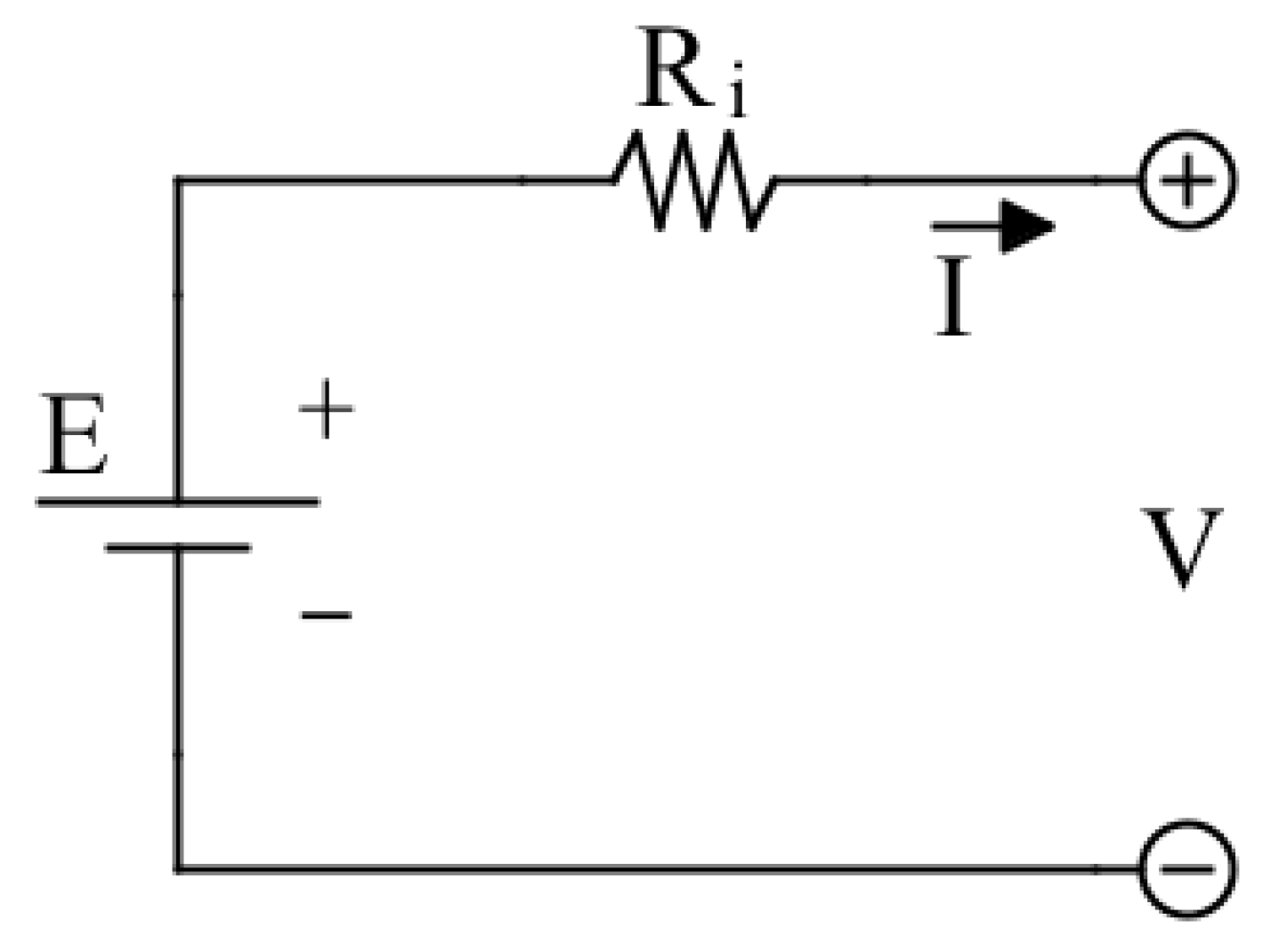
A basic equivalent circuit battery model is shown
Figure 3, and it is known as
Internal Resistance Model or
Rint model. This model describes the battery behavior using an ideal voltage source
, whose purpose is to simulate the battery open circuit voltage, and a resistor
that takes into account the battery internal resistance due to the electrodes [
33]. The battery terminal voltage can be expressed as:
In this model, and are considered constant and the battery capacity is considered infinite. It can be used in simulation where the variation of the SoC is negligible.
Higher accuracy can be achieved by adding the
SoC dependence for the open circuit voltage and the internal resistance.
To fully parametrize the model, and are needed. One of the advantages of this model is the possibility to parametrize it taking only the information from a typical cell manufacturer’s datasheet. Moreover, to consider the dependency of the battery capacity with the discharge current, the Peukert equation is used.
Normalization
The first step to parametrize the model is the extraction of the discharge curves from the datasheet. The discharge curves give the cell terminal voltage as a function of the supplied capacity, expressed in Ah, for different values of the discharge current. The discharge curves are then normalized and interpolated to have datasets with equally spaced grids. To achieve normalization, the capacity values are divided by their maximum values:
where the subscript
is the considered discharge curve C-rate, and
is the maximum capacity of the considered discharge curve. In this way, the discharge curves are represented as function of the Depth of Discharge (
DoD).
Internal Resistance
The internal resistance as function of
DoD can be derived from the normalized discharge curves, considering two different characteristics
If the internal resistance
does not depend on the discharge current, it can be calculated as
Since usually
N discharge curves are available in the datasheets, Equation (15) can be applied to all the curves combination. The internal resistance used in the model is finally calculated as the average value
where
J is the number of possible combinations, given by
Open circuit voltage
The open circuit voltage as a function of
DoD can be estimated as
Applying Equation (18) to all the discharge curves available in the datasheet, the average open circuit voltage as a function of the
DoD is derived as
Capacity
The cell capacity depends on the discharge current, and to consider this phenomenon, the Peukert Capacity is considered [
34,
35]. If the battery supplies a current
to the load, from the point of view of the battery capacity, it is as if a current equal to
was supplied. If the battery is recharged, the phenomenon is negligible, therefore
Accordingly, an equivalent battery capacity, defined as Peukert capacity, can be calculated as
where:
is the Peukert Capacity (Ah);
is the Peukert coefficient (-);
is the discharge current (A);
is the discharge time for discharge current (h).
To estimate the Peukert coefficient for a given cell, the discharge times at two different discharge currents are needed. From the manufacturer datasheet, the actual supplied capacity and the discharge current can be extrapolated, and the discharge time can be calculated as
And the Peukert coefficient is given by
From (22), the Peukert coefficient can be derived for any different discharge curves included in the datasheet. Usually,
is chosen equal to the minimum discharge current while
is varied to consider all the discharge profiles. The Peukert coefficient used for the simulation is then given by the average value as
The parameter estimation procedure described above is now applied to the LG18650HG2 cell.
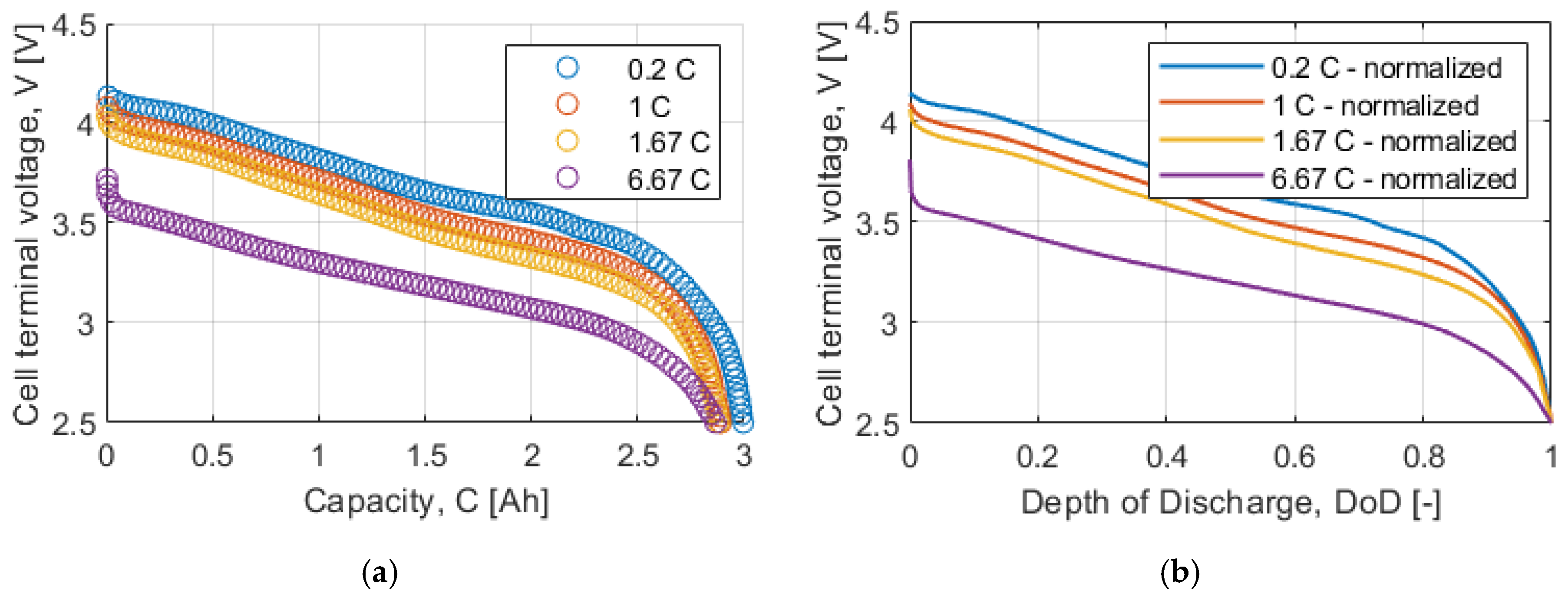
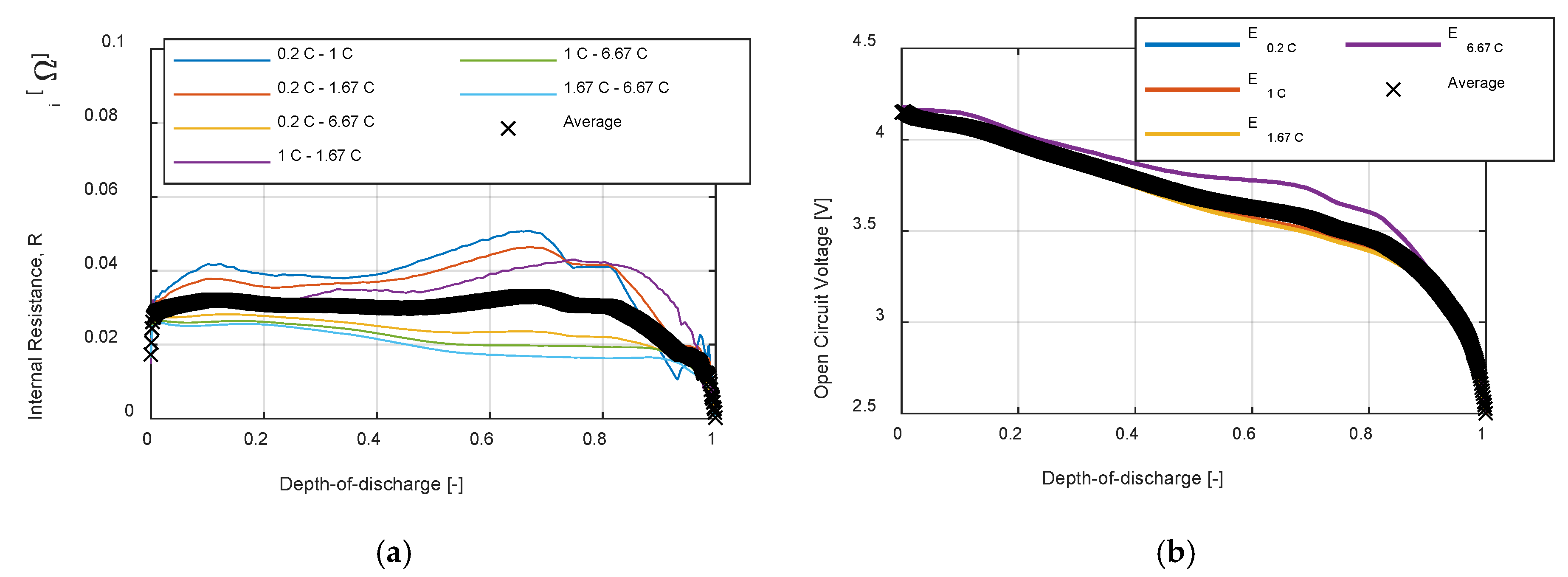
Figure 4a shows the datasheet discharge curve, which is given as a function of the supplied capacity. The curves are then normalized, using Equation (13), and interpolated as shown in
Figure 4b. The internal resistance is estimated for each possible curve combination using Equation (15), obtaining the solid curves represented in
Figure 5a. Finally, using Equation (16), the average internal resistance, represented in
Figure 5b with the crossed line, is obtained.
The open circuit voltage is calculated for each discharge curve using Equation (18), represented in
Figure 5b with the solid lines. The average open circuit voltage, shown in
Figure 5b with the crossed line, is then obtained with Equation (19).
Table 3 summarizes the
Rint model parameters.
2.3. Thevenin Model
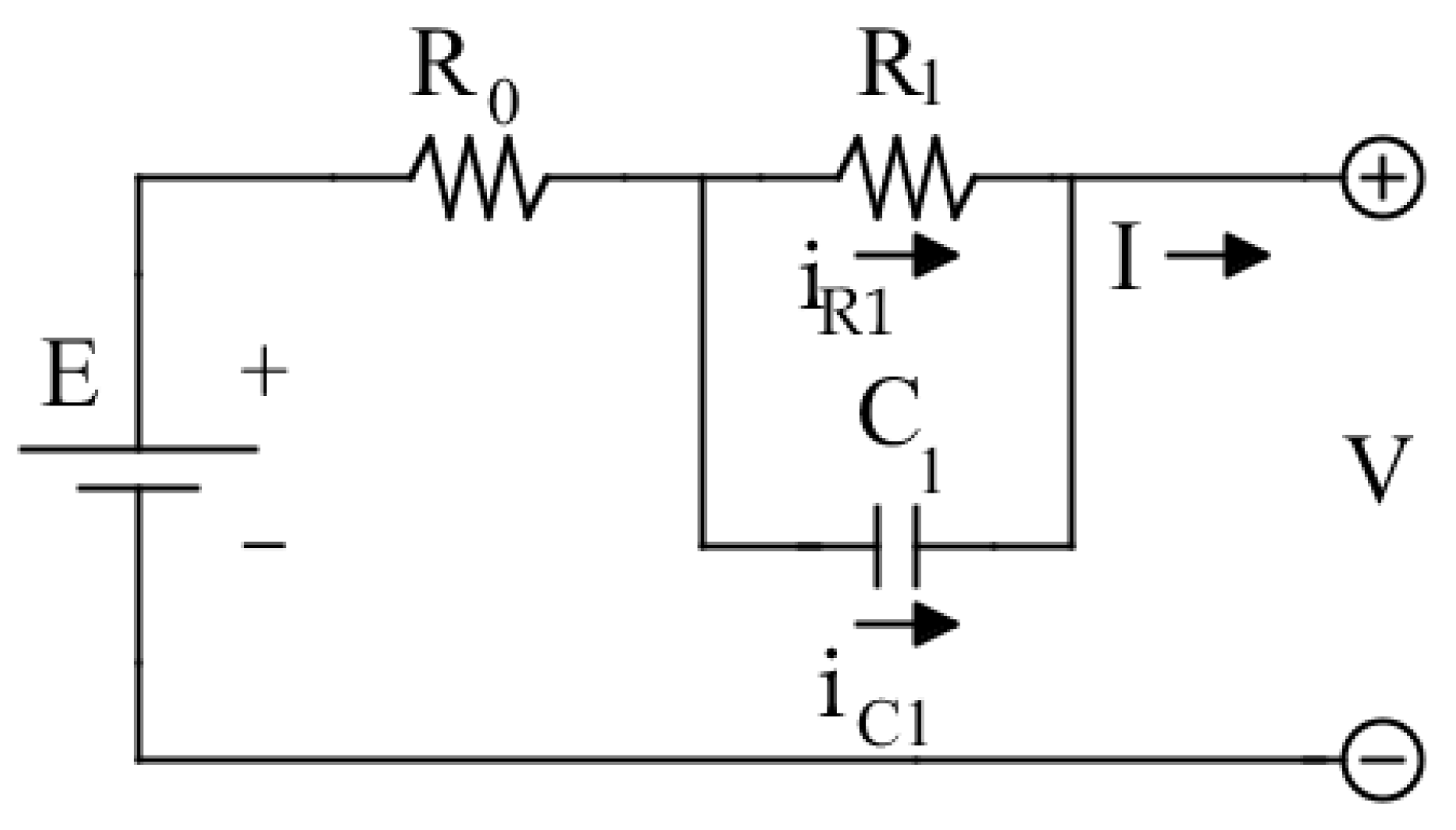
The
Rint model does not consider the transient behavior of the battery. The insertion of a parallel Resistor-Capacitor (RC) branch, as shown in
Figure 6, allows considering the short-term transient due to the electrolyte polarization. Similarly to
Rint model,
E and
represent respectively the battery open circuit voltage and the electrode resistance,
represents the polarization resistance and
represents the polarization capacitance [
33]. To enhance the model accuracy and consider transient phenomenon with different time constants, other RC branches can be included in series with
Thevenin’s model. However, the parameterization process of the model becomes even more complicated. If the model is employed to simulate the battery behavior in one operating condition at a given
SoC, the model’s parameters can be counted as constants. Otherwise, if wide
SoC operating range has to be simulated, the parameters can be considered dependent on temperature and
SoC. The model is defined by the next equations:
To fully parametrize the model, four parameters are needed:
and they are all
SoC dependent. For this model, the manufacturer’s specifications do not provide enough information to proceed with the parametrization procedure. Thus, some experimental tests must be performed, in particular a Pulse Discharge Test (PDT) [
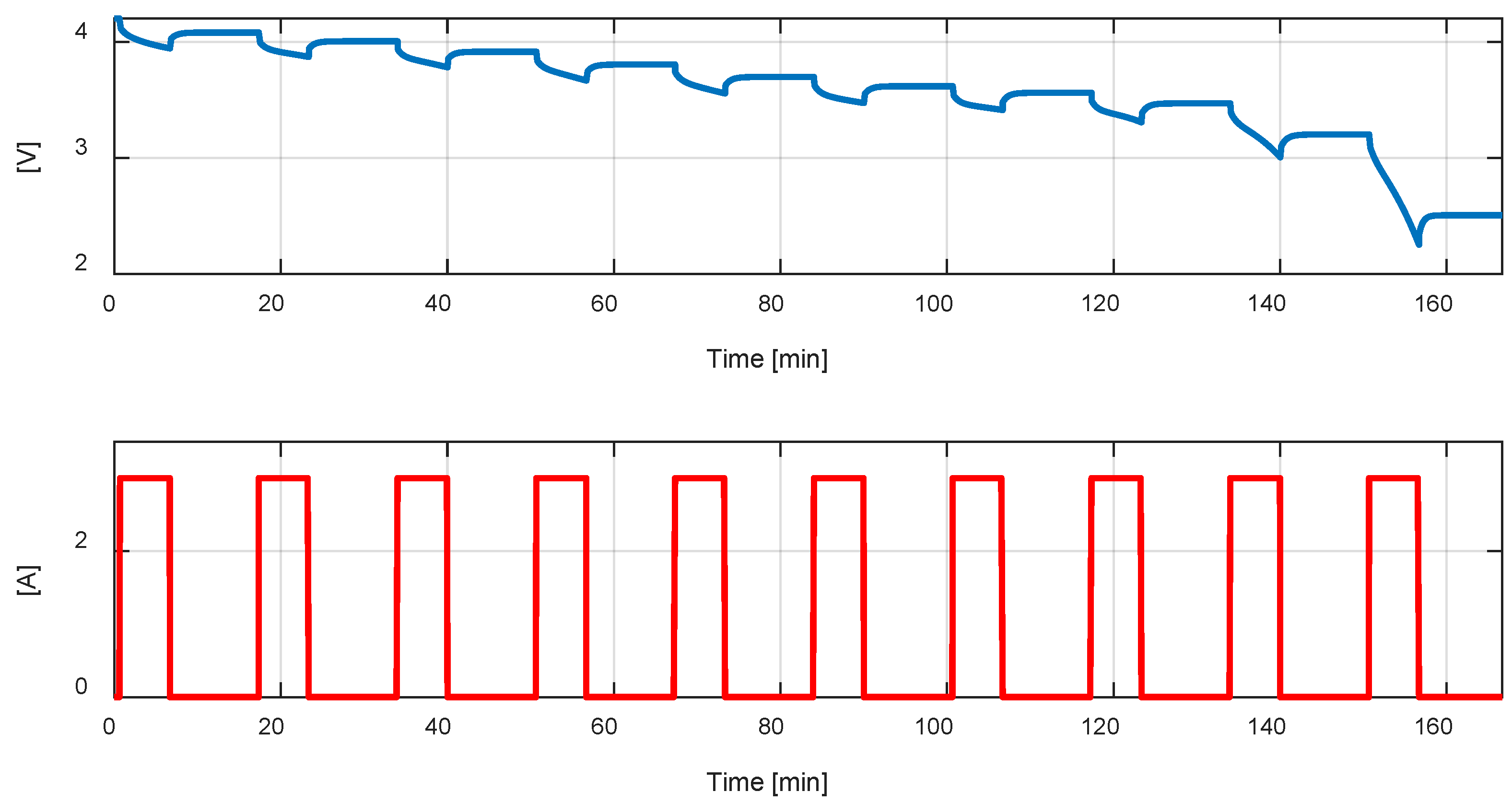
36]. The PDT consists in discharging a fully charged cell with a current pulse of specified amplitude and duration. At the end of the pulse, the cell is left in open circuit to stay at rest. At the end of the rest period, another current pulse is applied, and the procedure is repeated until the cell reaches the cut-off voltage.
The test starts charging the cell to its maximum voltage using the Constant Current/Constant Voltage procedure. After a rest period, the Pulse Discharge test is performed. The cell voltage is continuously acquired, and a pre-defined current pulse is applied. The removed charge in Ah can be calculated as:
Figure 7 illustrates the current pulse and the cell voltage, with all the equations used for the parameter estimation. At the start of the test, the acquired voltage corresponds to the cell open circuit voltage at 0% Depth of Discharge, due to the rest period after the full charge. The acquired voltage at the end of the rest period of the first current pulse, corresponds to the cell open circuit voltage at
Depth of Discharge, where
is the nominal capacity of the cell.
The immediate voltage reduction after the start of the current pulse is
And the internal resistance can be estimated as
Then, the cell is left open circuit for as long as it takes for the electrolyte polarization phenomenon to complete. The voltage rise, from end of the current pulse to the end of the rest period, is:
From the Equations (27) and (28),
can be computed as:
Finally, the polarization capacitance is estimated considering that, after approximately five time constants, the cell terminal voltage is equal to
, thus
And
can be estimated as:
The parameter estimation procedure described above is now applied to the LG 18650HG2 cell. First, the characteristics of the current pulse are chosen. The pulse starts after 40 s from the beginning of the test, with an amplitude
for
. The removed charge is therefore
Corresponding to approximately 10% of the nominal capacity of the battery.
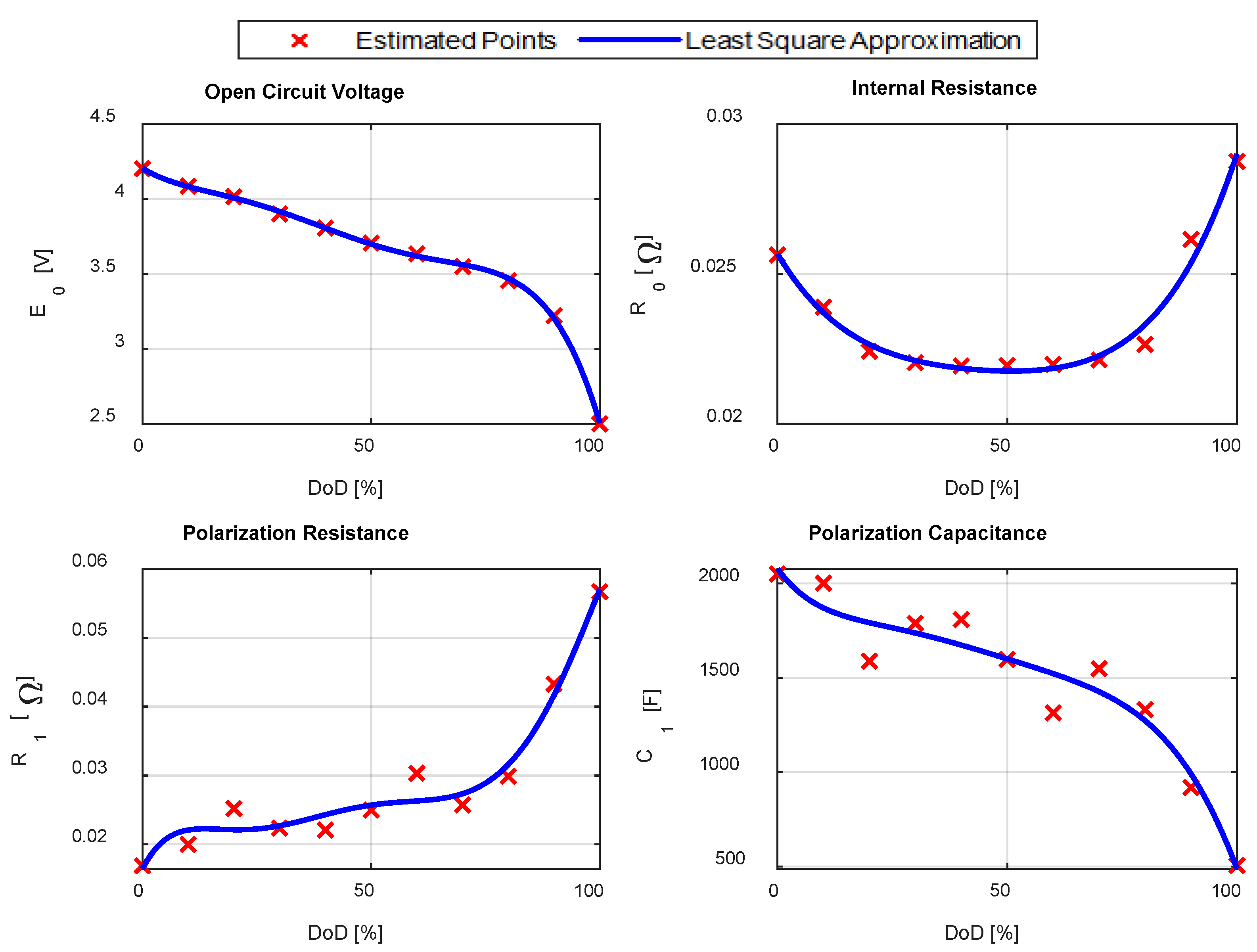
Figure 8 shows the experimental cell terminal voltage, acquired during the PDT, and used for the parameter estimation procedure. A MATLAB application was created to programmatically estimate all the parameters. The application considers each pulse individually and applies Equations (25)–(32) to calculate
The results are reported in
Figure 9, in which the red crosses are the estimated points and the blue solid line is a polynomial function, obtained with a least square approximation procedure.
Table 4 summarizes the
Thevenin model parameters.
3. Test-Bench Description
With the aim to validate experimentally the described models, a test bench (
Figure 10) was implemented, composed of:
a LG18650HG2 cell, whose characteristics are reported in
Table 5;
a Fluke PM2812 Programmable Power Supply, whose characteristics are reported in
Table 6, used to charge the cells;
an Agilent 6060B Single Input Electronic Load, whose characteristics are reported in
Table 7, used on the discharge phase of the cell;
a NI 9215 16-Bit Data Acquisition Board (placed in a NI cDAQ 9172 chassis), whose characteristics are reported in
Table 8, used to acquire the cell voltage signal;
a SRD05VDCSl-C 4-Channels Optical Isolated Relay;
a NI 9401 Digital Module (placed in the NI cDAQ 9172 chassis), used to control the relay.
All the instrumentation is controlled by a PC connected to the power supply and the electronic load via GPIB and to the NI chassis via USB.
The cell voltage signal is acquired at a 10 kS/s sampling frequency and then scaled at a 10 S/s sampling frequency calculating the average value in a 0.1 s time window. All the acquisitions were carried out after the calibration of the board.
The battery current is not directly measured and its values are taken from the values settled in the power supply (during the charge phase) or in the electronic load (during the discharge phase).
The battery capacity is estimated using the Coulomb Counting method, as:
where
is the battery current, and
is the sampling period.
Measurement Uncertainty Evaluation
In order to assess the accuracy of the parameters estimation for the
Thevenin model, the uncertainty evaluation was performed, strictly following the rules prescribed by [
37], for the measurements of the four parameters
,
,
and
.
The acquired voltage is affected by three main error sources, namely offset error, gain error and noise. The first step is to evaluate the uncertainty associated with each error source starting from the data acquisition board specifications:
considering a recutangular distribution for the offset error;
considering a rectangular distribution for the gain error and considering the worst case that corresponds to the maximum measured value (4.2 V);
considering a gaussian distribution for the noise and considering that each measured values is the mean of 1000 acquired samples.
Therefore, the voltage standard uncertainty is
And the expanded uncertainty with a 99% confidence level (coverage factor k = 2.58) is, therefore, equal to 2.6 mV.
Actually, for the estimation of
,
and
, only the differential voltage value
is needed. In this case, the offset errors do not generate uncertainty, and, therefore:
And the expanded uncertainty is therefore equal to 1.3 mV.
With regard to the current measurement, starting from the electronic load specifications, three error sources have to be considered:
considering a rectangular distribution for the offset error;
considering a rectangular distribution for the gain error and considering the worst case that corresponds to the maximum measured value (5 A);
the noise error is expressed as rms value.
Therefore, the current standard uncertainty is
The expanded uncertainty with a 99% confidence level is, therefore, equal to 91 mA.
Regarding the
measurement, applying the uncertainty propagation low to Equation (27) and considering that the current during the parametrization process is set at 3 A, and the worst case, which corresponds to the maximum observed
(
)
The expanded uncertainty with a 99% confidence level is, therefore, equal to .
About the
measurement, applying the uncertainty propagation low to Equation (29)
And the expanded uncertainty is therefore equal to .
Regarding the
measurement, applying the uncertainty propagation low to Equation (31)
However, considering the low value of time jitter of the data acquisition board, the uncertainty of the
measurement can be safely neglected. Therefore:
And the expanded uncertainty is therefore equal to .
With regard to the
SoC measurement, referring to Equation (33)
That, neglecting the
uncertainty and considering that the
are constant (0.1 s) and considering
steps, becomes
5. Discussion
This article carried out a comparison study of battery modeling and parameter identification techniques. Three models were considered: the Shepherd, the Rint and the Thevenin battery models. The Shepherd model belongs to the category of mathematical models. It can simulate the battery behavior both in static and transient operations thanks to the filtered current term. The parametrization procedure is quite simple, because all the necessary information can be found in the battery datasheet. The parametrization was carried out considering the 0.2 C discharge curve characteristic and considering the parameters current-independent.
The Rint model belongs to the category of equivalent circuit models and it does not consider the short-term battery dynamics. The parametrization procedure is a bit more complex than the Shepherd model one, but all the information can still be found in the manufacturer’s datasheet. The parametrization procedure considers different discharge curves, thus obtaining parameters that are somehow current dependent.
The Thevenin model belongs to the category of equivalent circuit models and, thanks to the RC branch, it can simulate the short-term battery dynamics. To parametrize the model, costly and time-consuming tests are required.
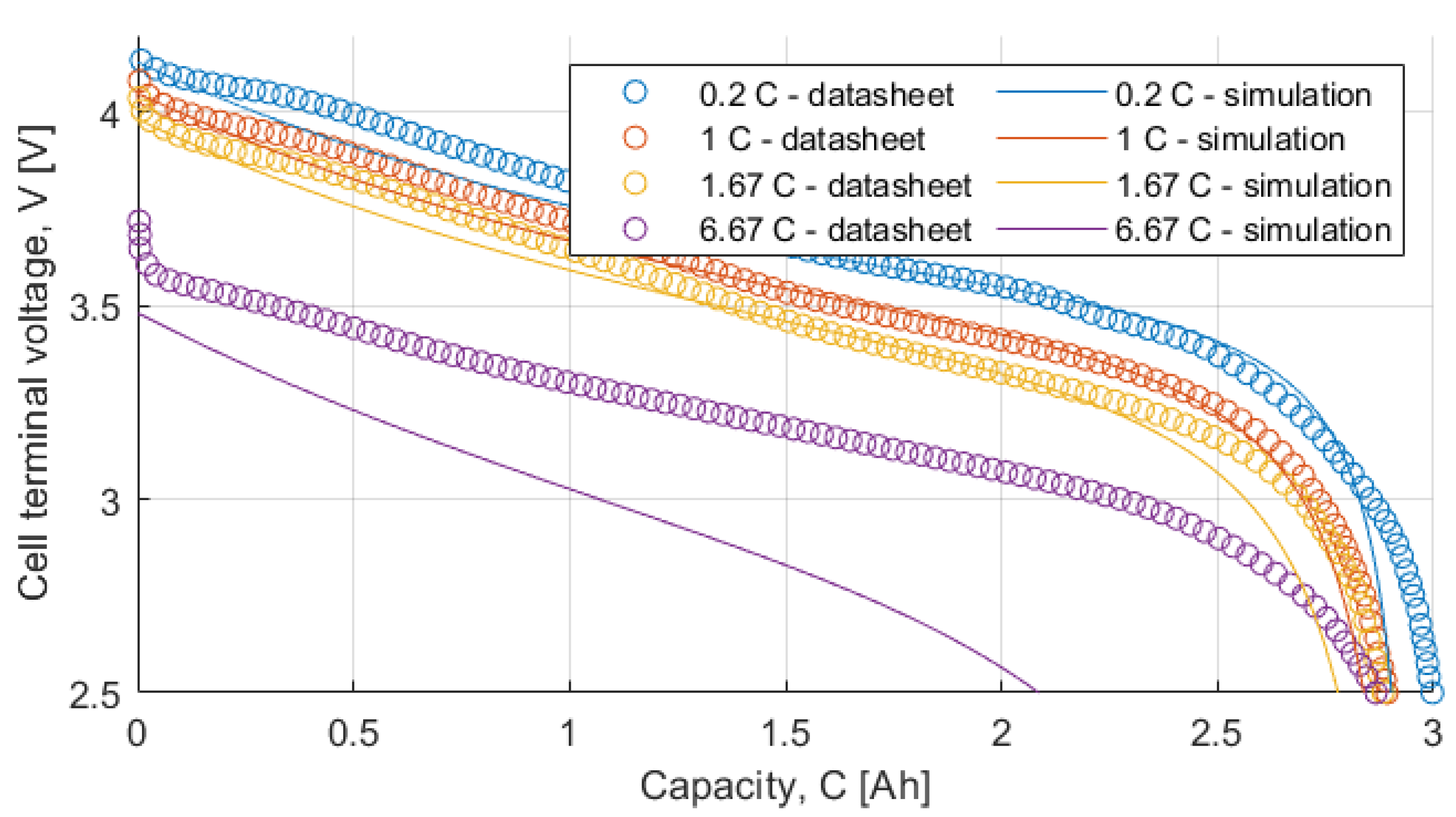
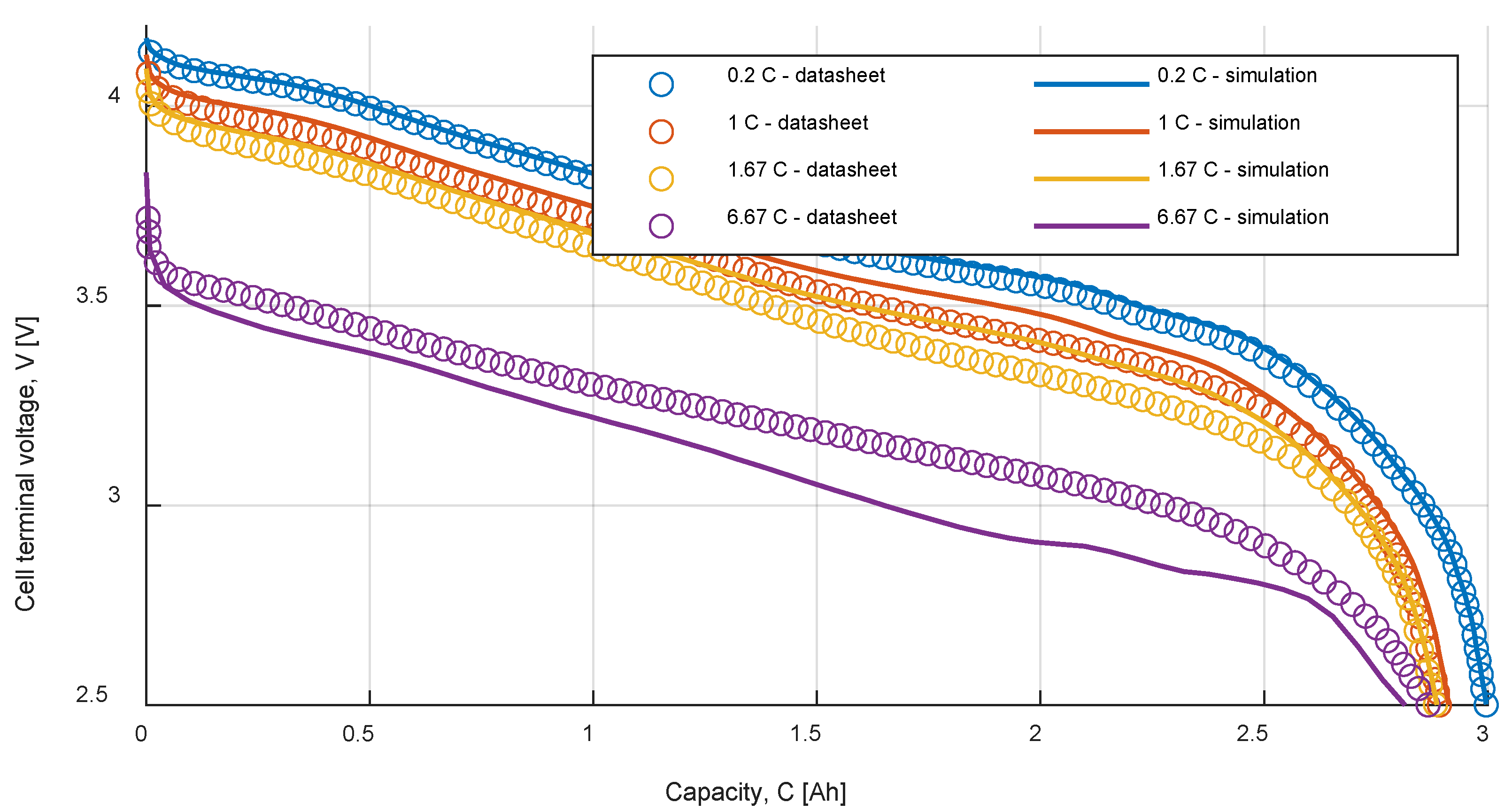
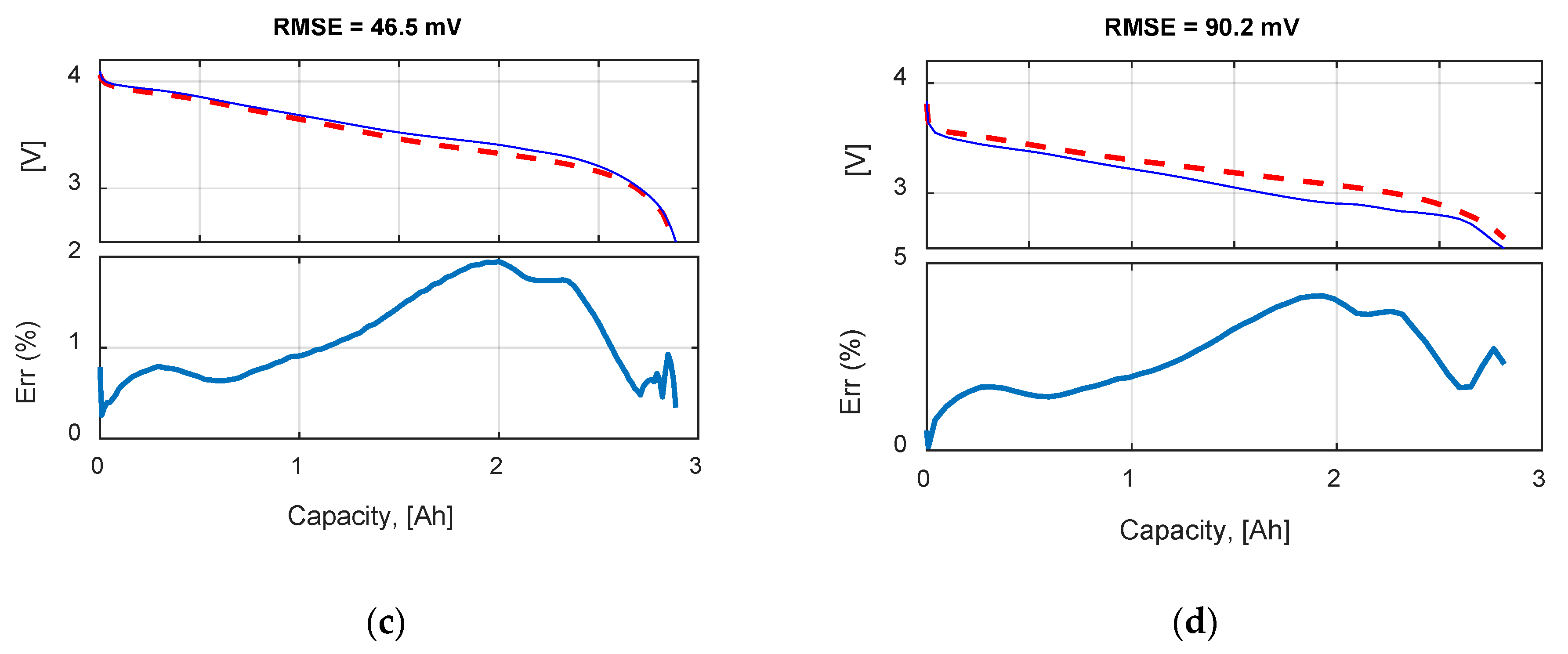
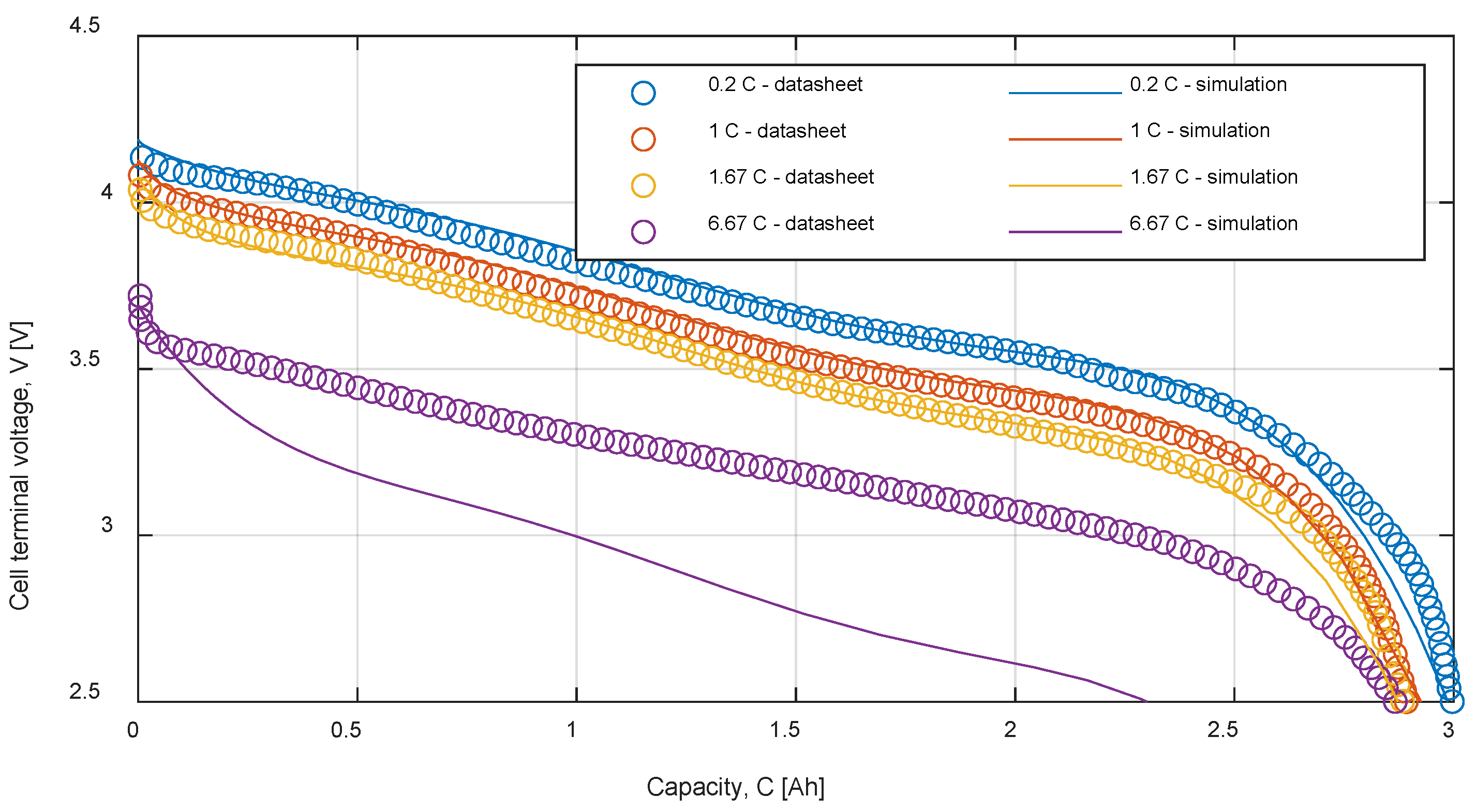
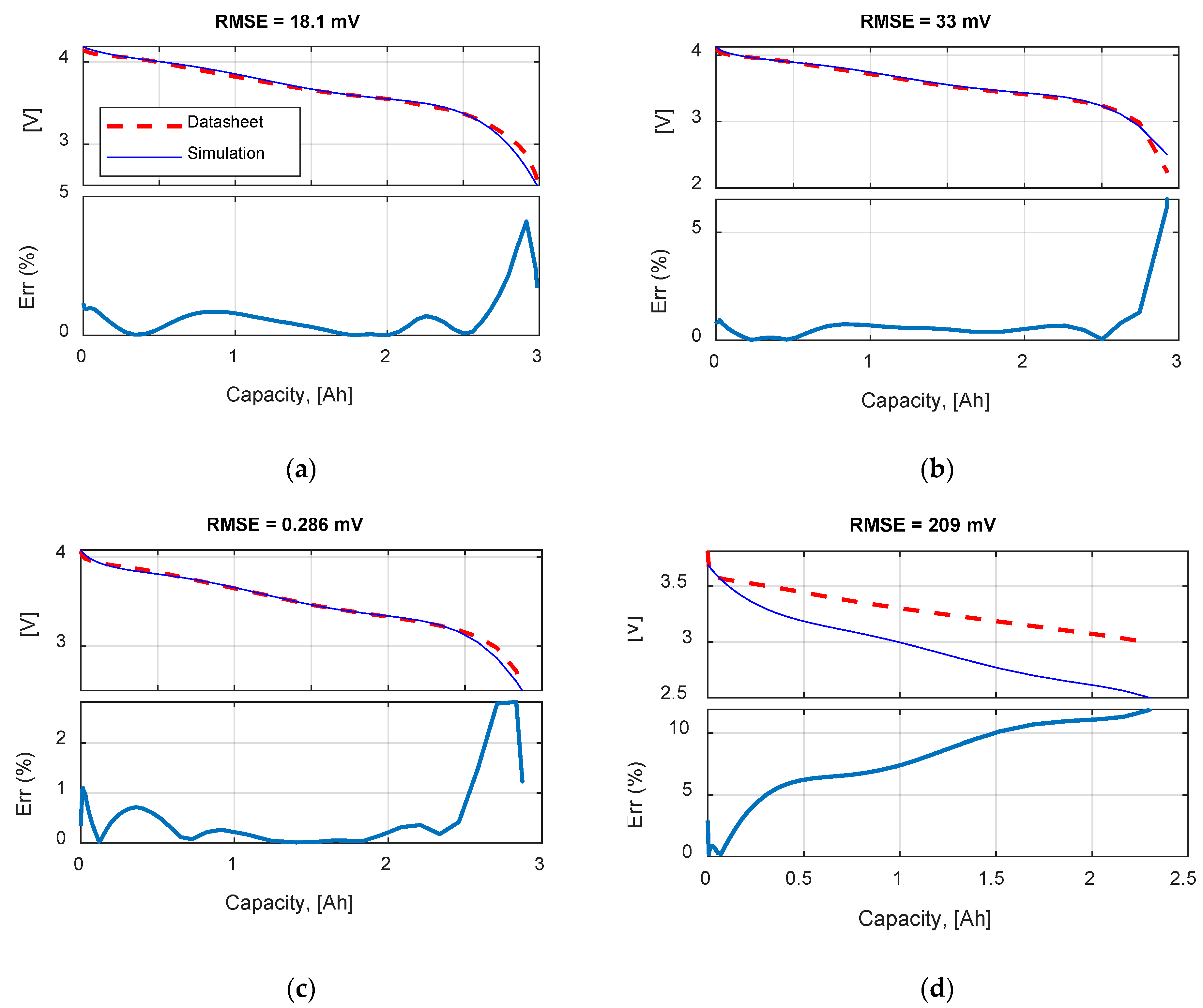
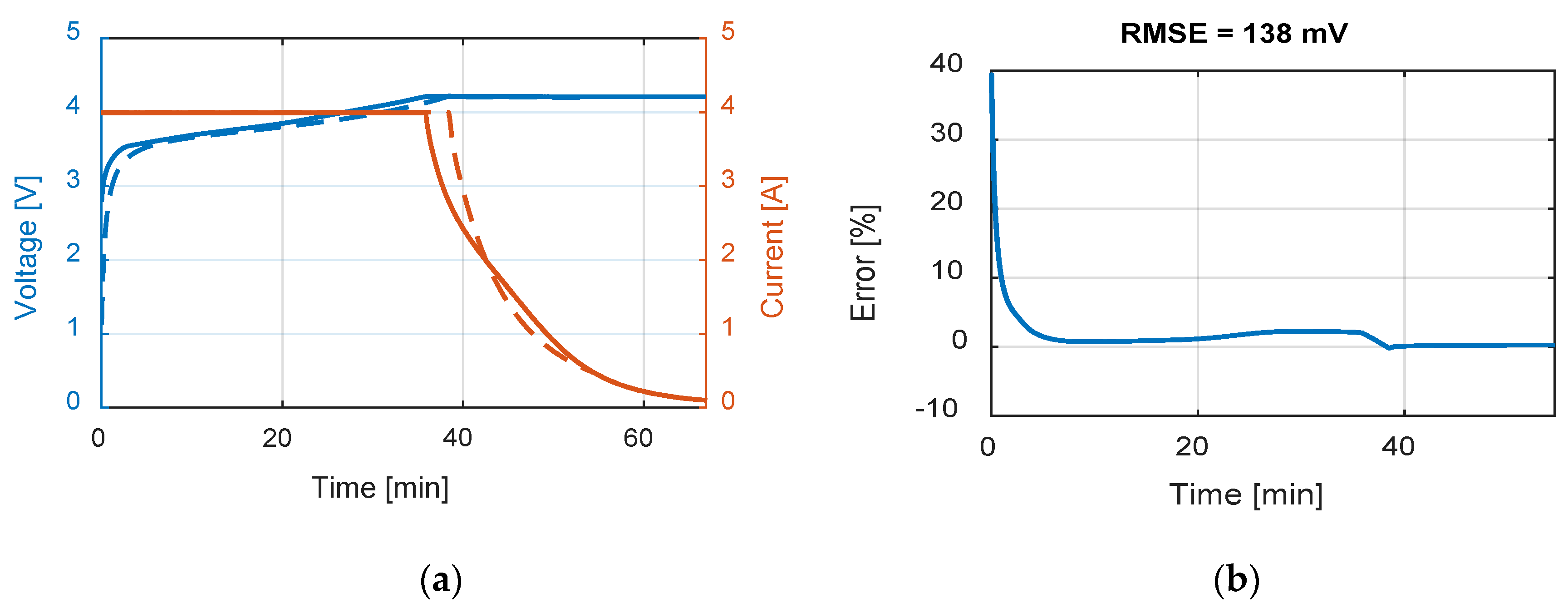
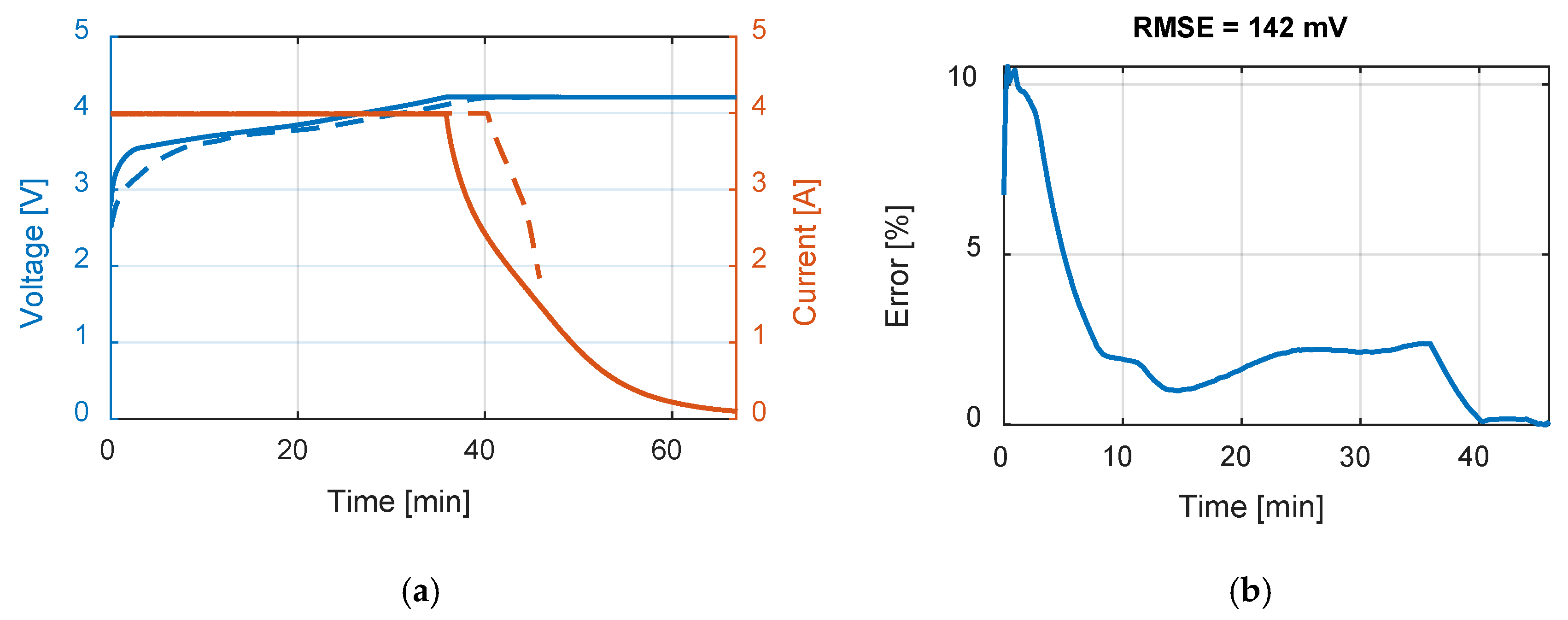
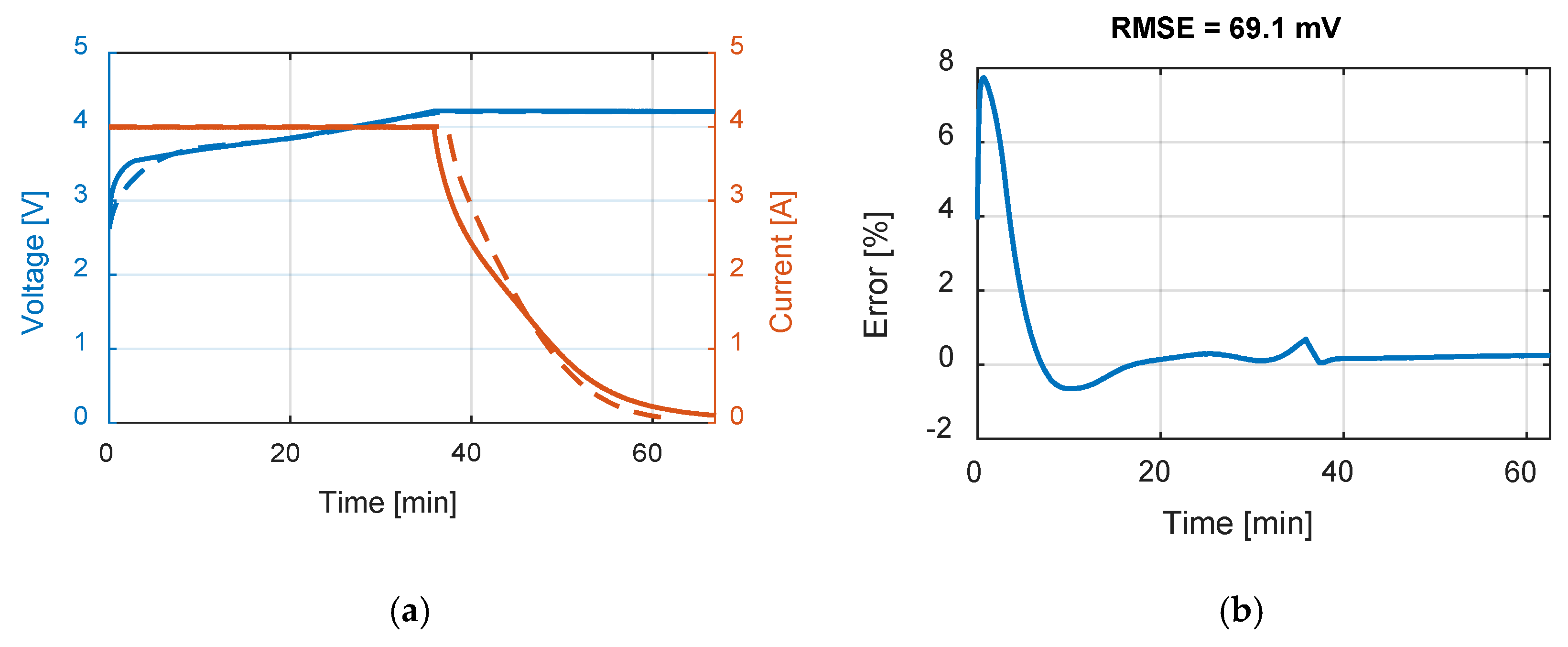
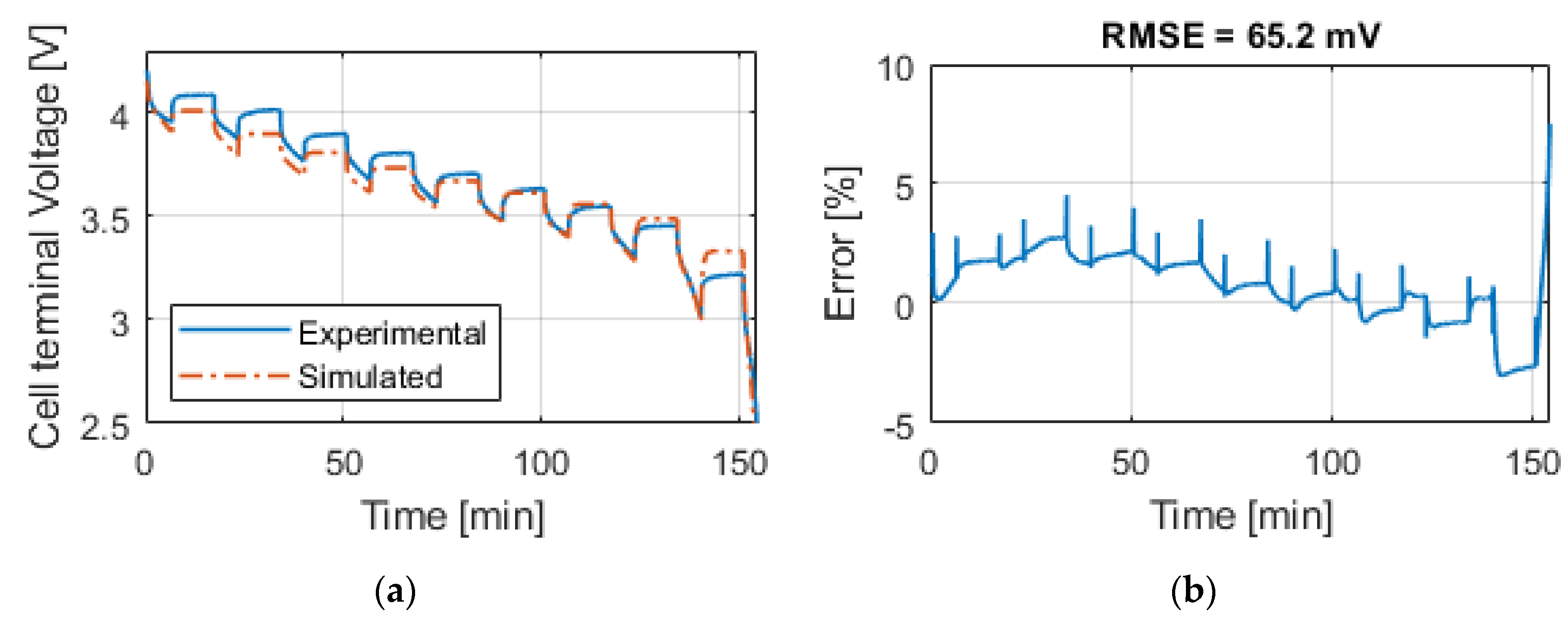
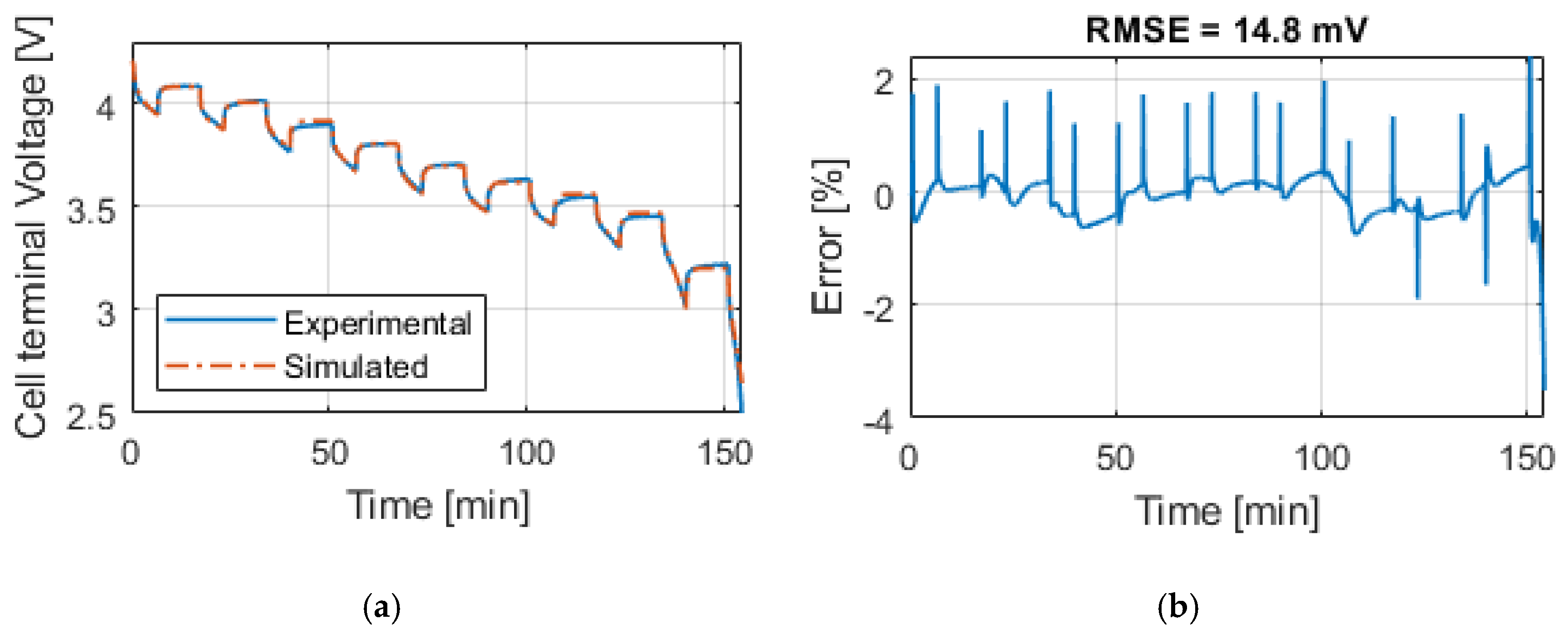
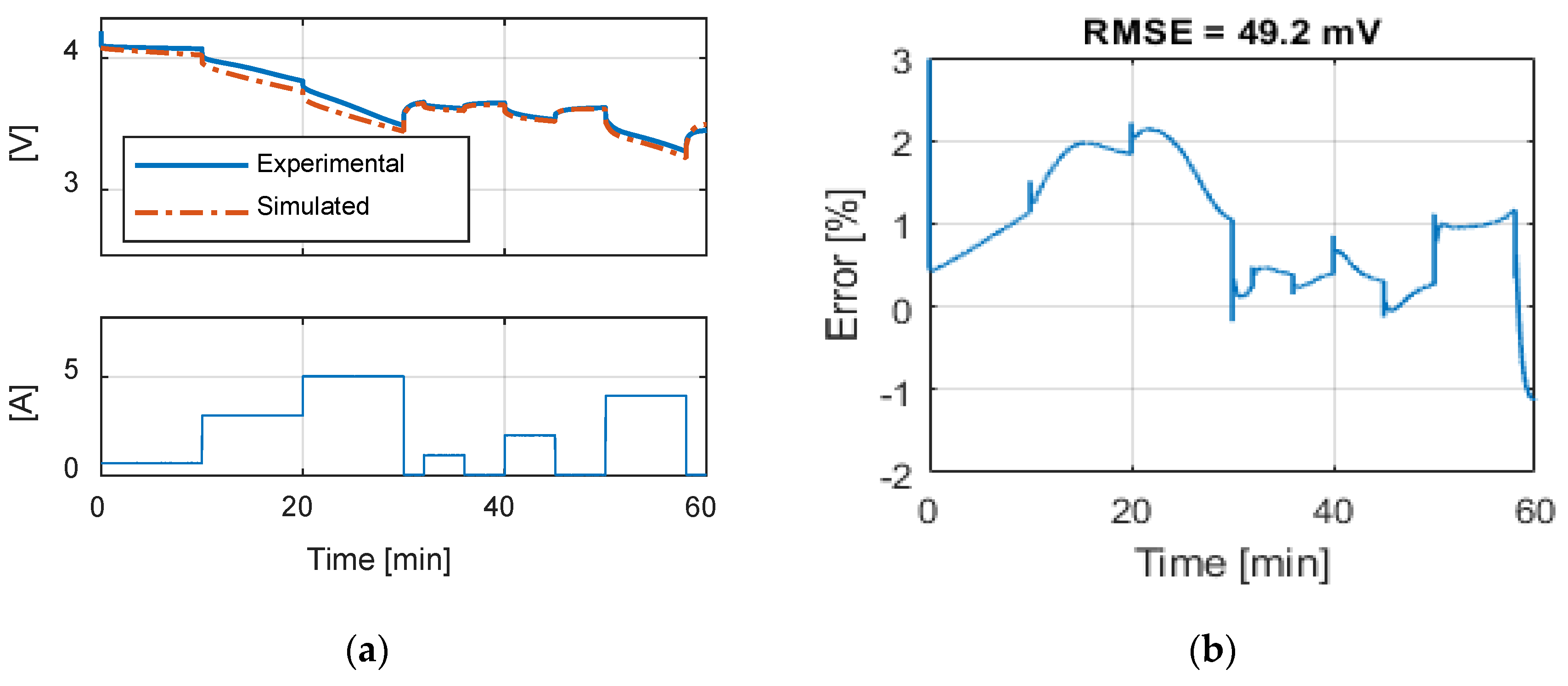
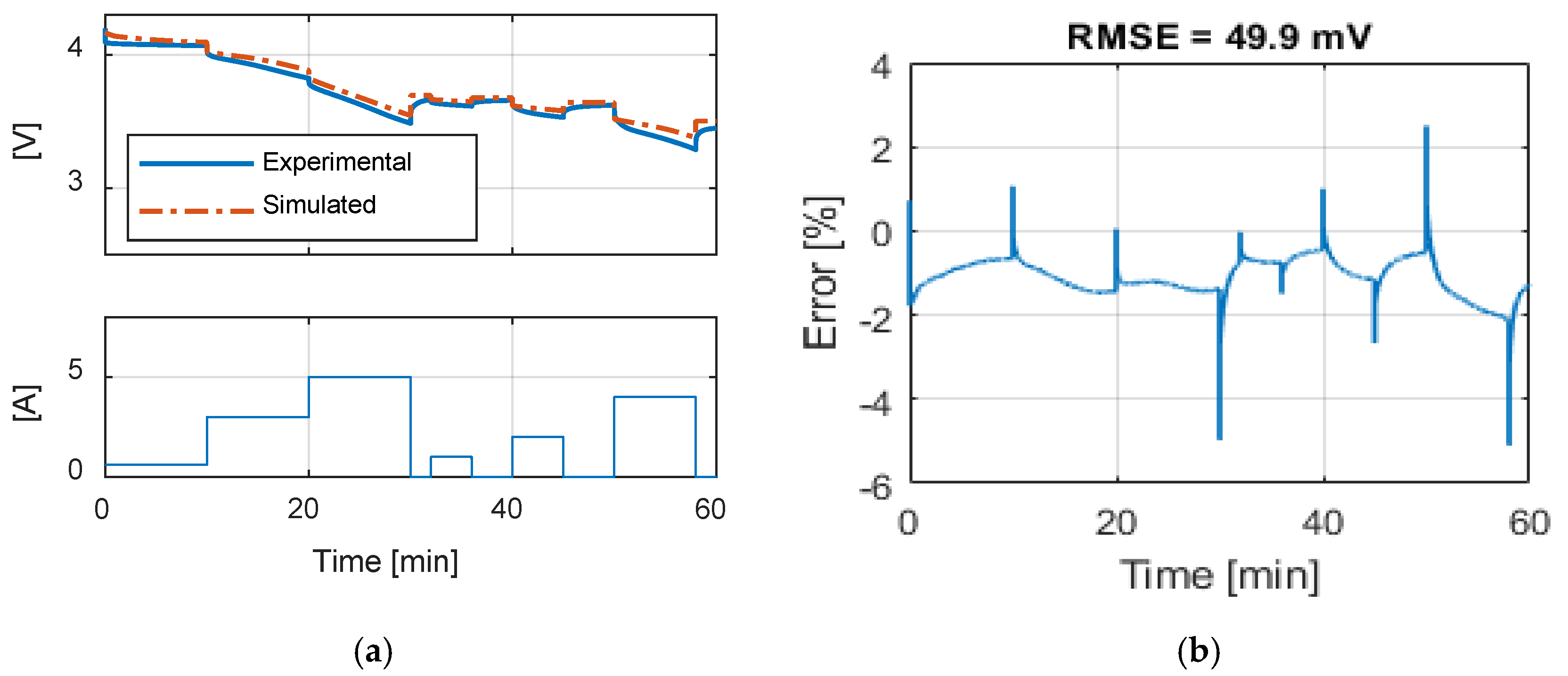
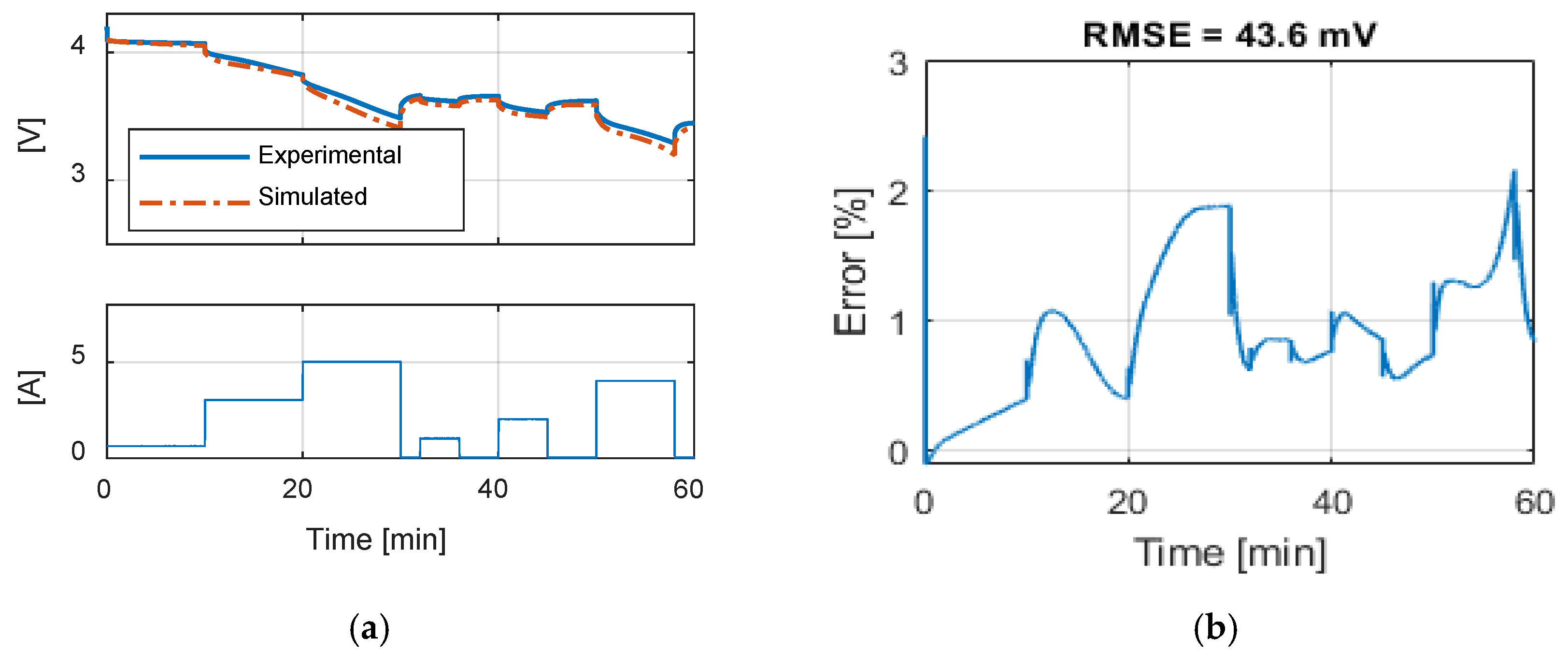
Table 9 summarizes the RMSE, expressed in mV, for all the model and test combinations. The bold numbers highlight the minimum obtained RMSE. It can be noticed that, considering the datasheet curves, the models can describe well the behavior of the battery for 0.2, 1 and 1.67 C. For 6.67 C (20 A), the best results were obtained with the
Rint model. The
Thevenin model gives the best results in all the experimental tests in terms of RMSE, but both the
Sheperd and
Rint models give adequate simulation results.
The Sheperd and Rint models can be therefore used in early design phase, for example for a rough comparison between different types of cells, considering nominal voltage, weight, cost, overall dimensions, and quickly evaluating the performance of the battery pack. Once the cell type for the application is defined, the PDT can be performed to obtain the parameters for the Thevenin model, which gives better results in terms of accuracy. Moreover, the accuracy of the Thevenin model can be further improved by considering the parameters variable with current, temperature, age etc. by performing appropriate tests.
6. Conclusions
In this article, three battery equivalent circuit models (Shepherd, Rint, Thevenin) selected from the literature were presented and the parameters estimation procedures for each model were described. The parameters estimation procedures were systematically applied to the LG 18650HG2 battery cell. It should be noted that, for the Shepherd and Rint models, the parametrization can be carried out using just the information on manufacturer’s datasheets. However, their accuracy is limited by the veracity and precision of the curves and parameters in the datasheets. On the other hand, the Thevenin model requires a costly test-bench and time-consuming experimental test for its parametrization. The advantage, in this case, is the possibility to have a perfect knowledge of measurements and parameters estimation uncertainties. The comparison of the three models showed that Thevenin model, whose parameters were obtained from experimental tests, gave the best results as expected. However, the Shepherd and Rint models gave adequate simulation results, proving to be suitable for the early design stages of a battery-powered system. In this work, the temperature, battery current and ageing effect on the parameters were not considered, as this information would require expensive equipment and extensive testing. The aim of the work was to identify three easy-to-implement battery models, suitable for the early stages simulation and design of a battery-powered system. In the optimization phase of such systems, more accurate models should be used instead.