Operational Performance of Electric Power Firms: Comparison between Japan and South Korea by Non-Radial Measures

Abstract

This study compares the electric power sectors between Japan and South (S) Korea. Both nations have been under a global trend of deregulation. To assess their progress due to industrial change and technology development, we use Data Envelopment Analysis (DEA) as an assessment tool that enables us to evaluate the level of simultaneous achievements on economic and technological measures, so assessing the degree of holistic development. DEA has been widely applied for performance assessment in the past decades. In this study, the method compares electric power firms by their operational efficiencies. To compare their achievements, it is necessary to develop a new type of DEA application for performance measurement. The proposed approach adds two analytical capabilities. First, the approach needs to handle “zero” in a data set and then restrict multipliers (i.e., weights among inputs and outputs) without any prior information to increase our empirical reliability. No study has simultaneously explored the two capabilities in DEA. Using the proposed method, our empirical study identifies two findings. One of the two is that the electric power industry of S. Korea outperformed that of the Japanese industry in the observed periods (2014–2018) because the Japanese power sector still suffered from an occurrence of the Fukushima Daiichi nuclear plant disaster which occurred on 1 March 2011. However, the difference has been gradually diminishing because the Japanese electricity industry has been gradually recovering from the huge disaster. The other is that the S. Korean power industry has been in a descending trend because the nation has shown technical regress as a result of inconsistent technology development (e.g., shifting its R&D: Research and Development) focus from electrical engineering to chemistry). The former R&D area is essential in maintaining the technical level of S. Korea′s electric power industry.

1. Introduction

In regulated markets, electricity firms often hold control over a complete process, from generation all the way down to end-users. Electricity deregulation takes some of the ownership/operation away from the electric power process under vertically-integrated structures. In contrast, in deregulated markets, they may control part of the generation, distribution, maintenance of wires and poles, and invoicing of consumers for those services. Some expected benefits of the deregulation include (a) improved energy technologies, (b) lower rates, (c) additional energy options, (d) advanced customer service, and (e) economic growth. The deregulation in the electric power industry is a world-wide trend, because we may expect many benefits due to the deregulation. Both Japan and South (S) Korea belong to the global trend of deregulation.

A difficulty in assessing such a competitive and deregulated industry is that we do not have a practical method to assess firms from both their economic and technological developments on multiple production factors. To partly deal with the methodological difficulty, this research proposes a new use of Data Envelopment Analysis (DEA) that we have previously utilized as a practical approach for performance assessment on various organizations in private and public sectors [1].

In the previous studies [2] on DEA, we observed that the assessment had a wide range of applications, because it could avoid specifying a functional form that connects among multiple components of X (inputs) and G (outputs) in the assessment. The method can relatively evaluate an efficiency level of many organizations, often referred to as Decision-Making Units (DMUs: electric power firms in this research), by a percentile expression (so, measuring operational efficiency). Such unique features indicate the practicality of DEA in the area of energy.

However, the practicality is still limited in the scope of this study. For example, in the comparison of two electric power sectors, we find two methodological difficulties. One of them is that the proposed approach needs to handle “zero” in our data set. This study uses the amount of R&D expenditure (as an input) and the number of patents (as an output) to measure technology progress in the power sectors. The number of patents contains zero in our data set. The conventional DEA usually assumes strict positivity on all observations so that a straight forward use of DEA does not function in this study. To handle the zero in a data set, we select a “non-radial model” as a tool for our performance assessment. The other difficulty is that we need to consider multiplier restriction, in which multipliers are weights among inputs and outputs, without any prior information to attain empirical reliability. In conventional use, DEA usually produces many efficient DMUs as a result of not using multiplier restriction. For example, the conventional DEA result shows that 90% of DMUS are efficient and the remaining 10% are inefficient. Such a result is mathematically acceptable but practically not ideal. To reduce the number of efficient DMUs in DEA, scholars have developed many multiplier restriction techniques, such as assurance region analysis [3] and cone ration [4], based upon prior information (e.g., experimental results and common sense). A problem is that this study cannot assess such prior information. Thus, it is necessary for us to develop an approach for multiplier restriction without prior information.

Research motivation: In addition to the two methodological difficulties identified in this study, we need to mention two research motivations. One of the two is that for our international comparison, the Japanese power sector has suffered from the occurrence of the Fukushima Daiichi nuclear plant′s disaster on 11 March 2011. The use of nuclear energy has been limited and it is almost impossible to resume the nuclear power plants in Japan [5]. The nation needs other energy sources, such as liquid natural gas and renewable energies. In contrast, S. Korea did not have such a nuclear problem in the operation of electric power plants. Even so, some previous administrations have implemented pro-nuclear policies. Due to the difference in their fuel mixes, we expect that S. Korea may operate more efficiently than Japan in terms of their operational efficiencies. The other concern is that the two nations may have different industrial structures. So, it is important for us to examine the performance of the electric power firms by considering whether their industrial structures influence their operational efficiencies. No study has explored this type of research issue.

This article is organized as follows. Section 2 summarizes a literature review. Section 3 compares Japan and S. Korea in terms of their industrial restructures. Section 4 describes the methodological features of DEA and explains why we use the method for this research. We also explain the extensions in the proposed approach. Section 5 summarizes the DEA-based empirical results. Section 6 concludes this study, along with future research tasks. Appendix A compares differences in the fuel mixes and industrial structures between the two nations.

All abbreviations used in this study are summarized as follows: CNIPA: China National Intellectual Property Administration, DEA: Data Envelopment Analysis, DMU: Decision-Making Unit, EPO: European Patent Office, EPSIS: Electric Power Statistics Information System, FTE: Full Time Equivalent, GDP: Gross Domestic Product. GHG: Greenhouse Gas, GWh: Gigawatt hours, IPC: International Patent Classification, JPO: Japan Patent Office, KEPCO: Korea Electric Power Corporation, KIPO: Korean Intellectual Property Office, KPX: Korea Power Exchange, METI: Ministry of Economy, Trade and Industry, OCCT: Organization for Cross-regional Coordination Transmission, OE: Operational Efficiency, OECD: Organization for Economic Co-operation and Development, PV: Photovoltaic, R&D: Research and Development, RTS: Returns to Scale, URS: Unrestricted, US: United States, USPTO: U.S. Patent and Trademark Office and WIPO: World Intellectual Property Organization.

2. Literature Review

In reviewing previous efforts on DEA, the works [1,2] have provided their historical review on the developments from the contribution of Professor W.W. Cooper, who was the first inventor. The research [1] has examined a research trend on the DEA applications from the 1980s to 2010s. Many researchers have paid serious attention to the environmental issues regarding how to combat various difficulties in the areas of energy and environment. As a result, the number of articles that used DEA environmental assessment has dramatically increased, particularly after the 2000s. The book [2] extended the previous work [1] by adding previous studies on conventional DEA. The work listed more than 800 peer-reviewed articles on DEA and these applications in performance assessment. Since the two previous efforts [1,2] have summarized most of previous works on DEA environmental assessment, this research does not provide a detailed description on previous research efforts here.

Considering its significant contribution to reduce carbon emissions as well as industrial base (particularly manufacturing base), the electric power sector has attracted attention among DEA researchers. While there is a great body of DEA applications in many countries (e.g., [6] in Australia and [7] in China), this study focuses on comparing Japanese with S. Korean electric power sectors.

Table 1. Data Envelopment Analysis (DEA) Applications to Japanese and Korean Electric Power Sectors.

Author(s)	Country	Level	Summary	Input	Output
Park and Lesourd [18]	Korea	Power plant	This study assessed the operating efficiencies of 64 Korean conventional fuel power plants using radial model with variable RTS	Fuel consumed; power installed; manpower	Net electricity output
Nemoto and Goto [19]	Japan	Company	This study analyzed the dynamic efficiencies of 9 Japanese electric power companies over the period of 1981–1995 using quasi-fixed inputs	Inputs: fuel; laborQuasi-fixed inputs: generation plants; transmission facilities; distribution facilities	Electricity for commercial and industrial use; electricity for residential use
Nakano and Managi [20]	Japan	Company	This study examined the efficiency of 10 Japanese electric power companies over the period of 1978–2003 using the Malmquist productivity index	Number of employees; fuel used; capital stock	Electricity generated
Sueyoshi and Goto [21]	Japan	Company	This study shed light on the operational and environmental performance of 9 Japanese electric power companies over the period of 2004–2008 using the unified efficiency concept	Generation capacity; number of employees; amount of coal, oil and LNG	Power generated; CO2 emissions
Han [22]	Korea	Company	This study measured the eco-efficiency scores of 6 Korean electric power companies over the period of 2002–2008 using radial models	Operating expense; water; CO2; NOx	Power generated; sales
Zhang and Choi [23]	Korea	Company	This study compared the CO2 emission performance of state-owned fossil fuel power plants in China and Korea over the period of 2005–2010 using a series of non-radial DEA models	Capital; fossil fuel; labor	Electricity; CO2 emissions
Matsushita and Asano [24]	Japan	Company	This study explored the thermal power generation efficiency of 10 Japanese electric power companies over the period of 1990–2011 using DODF.	Capacity of thermal plants; capital of generation facility; labor; energy	Electricity generated; CO2 emissions
Sueyoshi and Goto [25]	OECD	Country	This study looked into Japanese fuel mix strategy based on the DEA performance evaluations of 33 OECD countries	Combustible generation; hydro generation; nuclear generation; pumped hydro generation; other renewable generations (geothermal, solar, tide, and wind)	Electricity generated; CO2 emissions
Patrick et al. [26]	World	Country	This study evaluated the electricity supply resilience of 140 countries using a radial model and LP- and MCS-based robust efficiency analysis	System Average Interruption Duration Index (SAIDI); accident risks; import dependence; average outage time	Control of corruption; political stability and absence of violence/terrorism; mix diversity; equivalent availability factor; GDP per capita; insurance penetration; government effectiveness; ease of doing business

Note: RTS: Returns to Scale, DODF: Directional Output Distance Function, LNG: liquid Natural Gas, LP: linear programming, and MCS: Monte Carlo Simulation.

summarizes major literature in the area. While they contributed to closing gaps in the pre-existing literature by (a) assessing efficiencies of electric power sector at multiple levels (power plant, company, and country) and (b) incorporating the emissions of CO₂ or other air pollutants to reflect the importance of environmental sustainability, there is still room for new studies from the perspective of deregulation and technology development.

Note that Japan and S. Korea have some similarities in deregulation. Both countries started the liberalization efforts in the late 1990s. S. Korea implemented actual policy programs (particularly divesting one state-owned, vertically-integrated company of power generation part) in the early 2000s [8]. With globalization, both nations accepted the liberalization of the electric power industry as a global standard and sought to take advantage of (through competition) lowering the price of electricity, which was critical for maintaining their industrial competitiveness (particularly in electricity-intensive industries such as information and communications technology and automobile manufacturing). On the other hand, both nations were concerned about the unintended consequences of rapid liberalization shown in California, U.S.A. and the United Kingdom (e.g., the price of electricity dropped right after the deregulation but it went up again after a while in the U.S.A. [9]; and a power pool market in the U.K. did not function as well as expected [10]). Thus, they adopted an incremental reform rather than a revolutionary one.

However, there are also differences between the two nations, particularly in the speed of liberalization. Although both nations sought a gradual transition from the generation competition to the wholesale competition and further to the retail competition market, Japan reached the last stage through a series of reforms whereas S. Korea stagnates in the first stage [11]. Japan already opened its wholesale and retail market to the private sector, but S. Korea remains in the competitive generation market, which is still not completely privatized yet. Six major power generation companies are subsidiaries of Korea Electric Power Company (KEPCO), which monopolizes the transmission, distribution, and retail of electric power. Also, more than 50% of KEPCO′s shares are owned by the government [12].

The two countries have also faced different challenges. While Japan has improved the efficiency, independence, and transparency of its electric power industry over time, the nation was confronted with an unforeseen event, the Fukushima Daiichi disaster, which disrupted its electricity market [13,14]. On the other hand, S. Korea has experienced deteriorating productivity issues primarily because of technical regress stemming from increasing generation cost [15]. One of the potential reasons was increased peak-load generation, rather than base-load generation, which is related to the expansion of power plant facilities. Another reason was the inefficiency of technological innovation activities. There may be a lack of R&D investment or insufficient technology development in the Korean electricity industry.

Position of this study: To the best of our knowledge, no DEA study has explored the comparison between Japanese and Korean electric power industries, although both countries have a strong manufacturing focus and similar industrial base (particularly in information and communications technology, as well as automobile manufacturing). In addition to their energy-intensive industries, they also share some other similarities. Both nations are highly reliant on imported energy sources, given their scarce fossil energy reserves. They have also embraced the global trend of deregulation in the electric power sector (particularly in the power generation area) in a relatively similar timeframe.

Another concern to be noted is the issue of data and period length used in the DEA literature. While there are some non-DEA studies that show more recent datasets related to the electric power sector, existing DEA literature unveiled the Japanese or Korean electric power sector relatively long time ago. In the former, for instance, [16] employed the negative binomial panel regression model but used Japanese electric power companies′ 1999–2018 data, although the data focused on the R&D activities. The work [17] investigated the efficiency issue of Korean electric power companies by employing cost function (rather than production function) and used 1982–2016 data. In the latter, however, they used 2005–2010 and 1990–2010 data, respectively, to study Japanese and S. Korean cases. This study may be a timely effort to update the performance of the current electric power sector in both countries. Additionally, with the emergence of electronic government initiatives (e.g., Open Government Data Projects in Japan and Public Data Portal such as data.go.kr in S. Korea), both nations have tended to open more data to the public and have become more transparent. In S. Korea, for instance, the ALIO (All Public Information In-One) system offers various types of management information of public agencies, including utility companies since 2015. This study takes advantage of using more reliable and consistent datasets containing more recent information.

In addition, the existing literature tends to belittle the role of technological development and does not include any relevant measures. Japan and S. Korea have both invested enormous amount of money in R&D (Japan: US$185.5 billion (3.21% of GDP) and S. Korea: US$69.7 billion (4.55% of GDP) in 2017) and belong to the top five global R&D spenders. This is also true for the electric power sector. Both countries have actively invested in the R&D of not only power generation, distribution, and transmission technologies, but also green technologies.

The two countries are also strongly interested in protecting their R&D outcomes via intellectual property rights. This is evidenced by their affiliations with IP5 (Intellectual Property 5: five major patent offices including the U.S. Patent and Trademark Office (USPTO), the European Patent Office (EPO), the Japan Patent Office (JPO), the Korean Intellectual Property Office (KIPO), and the National Intellectual Property Administration in China (CNIPA)).

In this regard, this study seeks to add value to the existing DEA applications to the Japanese and S. Korean electric power sectors by (a) comparing the performance of electric power companies in the two industrialized countries with similar performance base, (b) looking into more recent data after game-changing events (including financial crisis, deregulation, Fukushima Daiichi Accident, and global race for technological innovation), and (c) incorporating technological development-related measure (e.g., patents) and shedding light on the technological trajectories and portfolios of electric power companies in both countries.

3. Electric Power Industry in Japan and South Korea

3.1. Deregulation in Japan

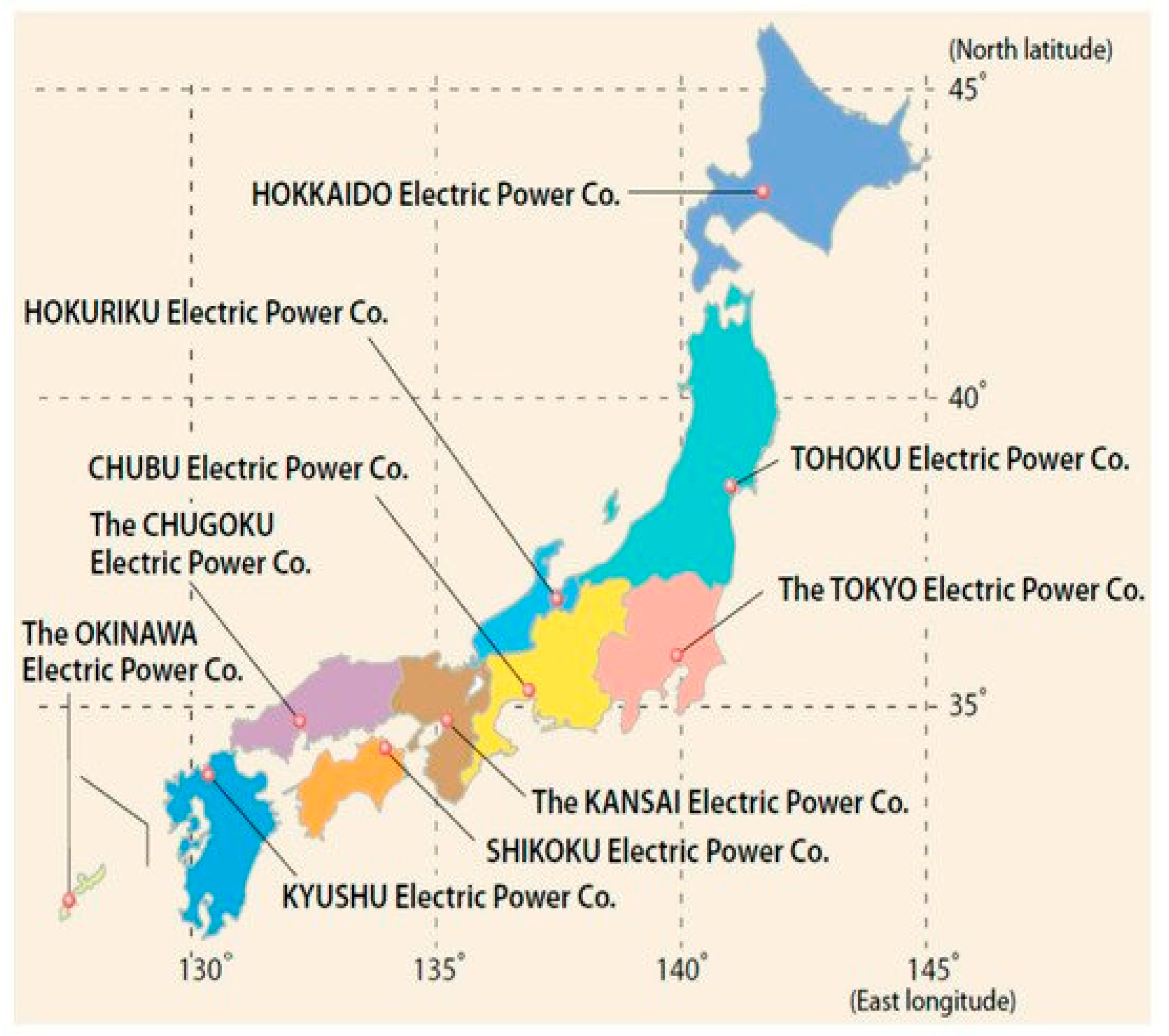
In Japan, nine electric power companies have provided their utility services as a regional monopoly. Figure 1 lists the nine companies from north to south. They include: (a) Hokkaido Electric Power, (b) Tohoku Electric Power, (c) Chubu Electric Power, (d) Hokuriku Electric Power, (e) Kansai Electric Power, (f) Chugoku Electric Power, (g) Shikoku Electric Power, and (h) Kyushu Electric Power. We know that there is Okinawa Electric Power Company, but its business scale is much smaller than the other nine firms to be examined, so this research does not include the firm for our international comparison.

Japan has been gradually deregulating the electric power market since 1995. Although the Japanese government tried to facilitate institutional reforms, the challenge belonged to a slow process of market restructuring. The situation has advanced after the Great East Japan Earthquake on 1 March 2011. The Fukushima Daiichi nuclear disaster occurred with the earthquake. After the disaster, a major reform started the following three plans [27].

First, Japan established the Organization for Cross-regional Coordination of Transmission Operators (OCCTO) in 2015, whose missions were to promote the development of transmission and distribution networks, both of which were necessary for cross-regional electricity uses. The organization also enhanced the nationwide function of maintaining a supply and demand balance of electricity in normal or emergency conditions.

Second, Japan implemented the full deregulation of the retail market in 2016, which gave regulated residential users eligibility to choose an electricity supplier from incumbent and new entrant firms. Licensing unbundling was also introduced in 2016, under which the electricity supply had different licenses on generation, transmission, distribution, and retail. Currently, any firm can enter the power generation by just notifying the government. Entrants into the retail sector need to register for starting their businesses. The transmission and distribution have remained in regional monopoly. The power businesses are still constrained under governmental regulation.

Finally, in 2020, the nation implemented legal unbundling between transmission and distribution from generation and retail sectors. The purpose of the separation is to secure a high level of fairness for all players in electricity generation and retail markets and to facilitate a high level of competition among players, because incumbent companies have an advantage in transmission and distribution.

Note that [16] has recently discussed a marginal effect of R&D on the deregulation of the Japanese electric power industry. The research used an econometric approach (i.e., negative binomial panel data regression) to assess the influence of R&D on the Japanese market from 1999 to 2018. Meanwhile, the purpose of this study is to compare the Japanese electric power sector with that of S. Korea. The DEA is a non-parametric approach to measure the level of operational efficiency, so different from the econometric approach utilized in [16]. The research has considered neither international comparison nor efficiency measurement. We borrow the Japanese data set from the research in [16], but we obtain the S. Korean data set by our research effort. The observed annual periods are from 2014 to 2018. The observed periods are less than those of [16], because we have difficulty in accessing a data set prior to 2014 on the S. Korean electric power industry.

3.2. Deregulation/Liberalization in South Korea

Different from Japan, to start the deregulation/liberalization process of an electric power sector that was originally monopolized by a state-owned giant, the S. Korean government has changed it by partially opening the electricity generation market. The government privatized companies for improving efficiency, cutting debt, and improved transparency. See research [29,30] that describes the process for deregulation and liberalization in S. Korea.

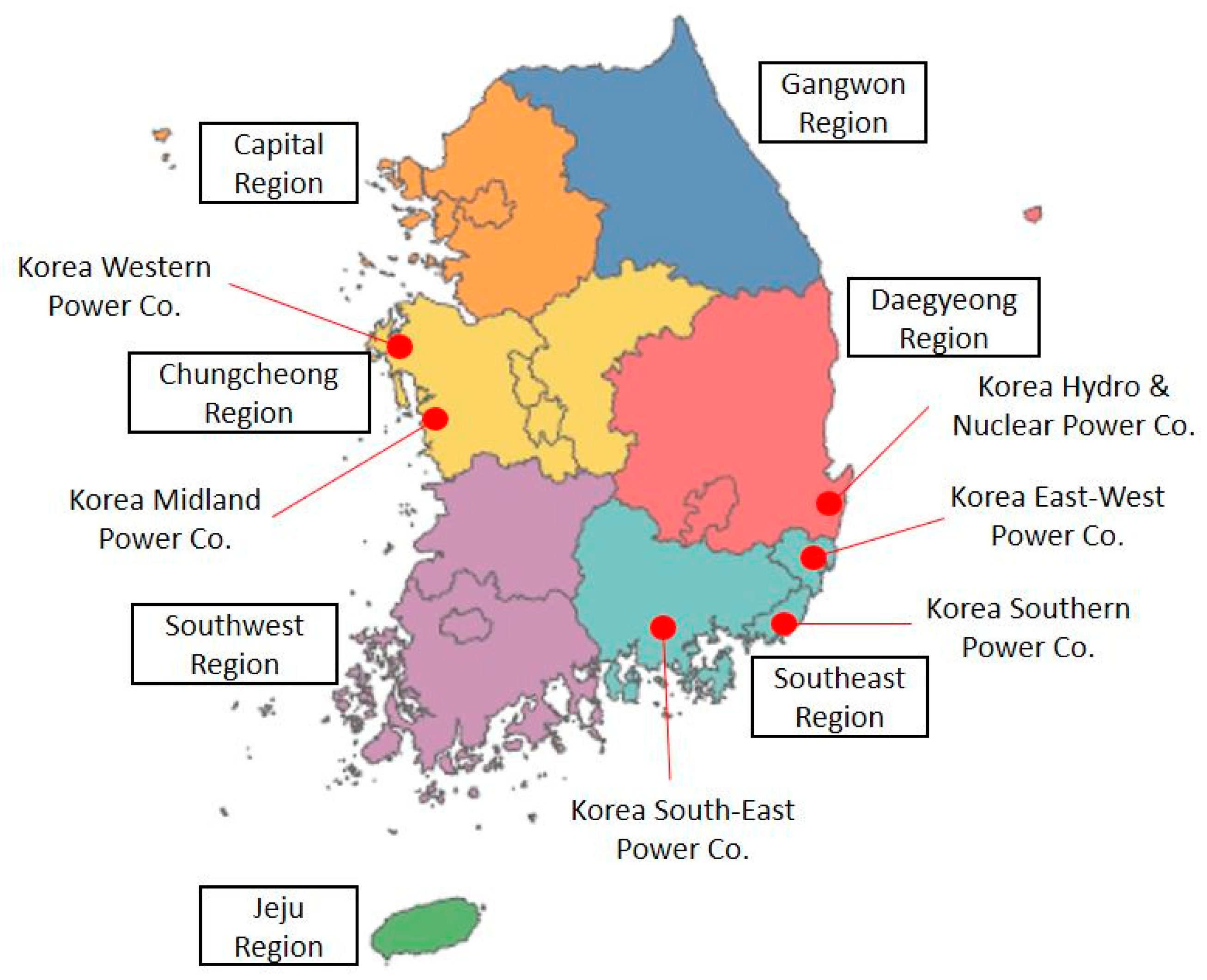
The process of S. Korea started from the liberalization, implying that the state-owned KEPCO has separated its power generation part into five subsidiaries: (a) Korea South-East Power, (b) Korea Midland Power, (c) Korea Western Power, (d) Korea Southern Power, and (e) Korea East-West Power. It also includes (f) Korea Hydro and Nuclear Power, which is KEPCO′s wholly-owned subsidiary. The company owns and operates the nation′s 21 nuclear power plants and produces a third of the country′s power. While there are several independent power producers, their portion is minimal when compared to the six power generation companies. In addition, the Korea Power Exchange (KPX) plays as an independent power system operator. Figure 2 visually describes the six firms in S. Korea.

In privatizing KEPCO after the financial crisis in 1997, the government attempted to increase private holdings of the company′s 40% shares, drawing on the basic plan for the restructuring of the Korean power industry in 1999, whose purposes were (a) to increase the efficiency of the power industry through competition, (b) to ensure the long-term viability of electricity supply, and (c) to promote consumer convenience and choice. However, the privatization did not prove easy, owing to the company′s size and the low price of power. Since then, the government has been discouraged from continuing its electricity market restructuring process by anti-nuclear activists, as well as labor unions and environmental issues. Today, transmission and retail services are still monopolized by KEPCO. The S. Korean government holds about 51% of the company′s shares. This aspect of shareholding is very different from Japan, where electric power companies do not have such public ownership, of course being under governmental regulation.

The government has reported that it could cap the private sector′s stake in KEPCO entities at 20% to 30% to preserve the government′s majority share. However, it may also allow renewable energy companies to sell power directly to consumers. Currently, private companies and individuals must trade and distribute power through the KEPCO.

3.3. Technology Differences between Japan and S. Korea

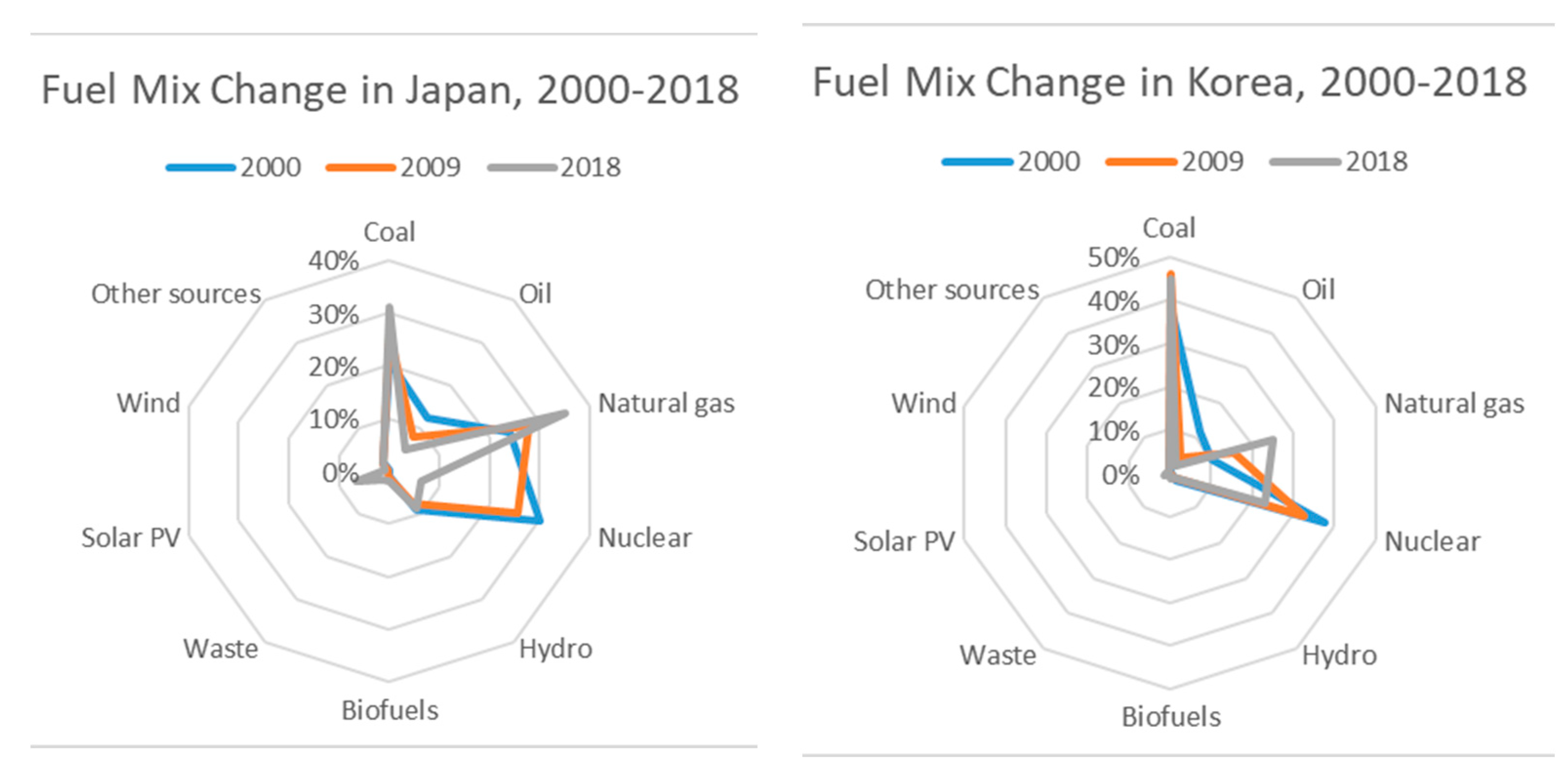
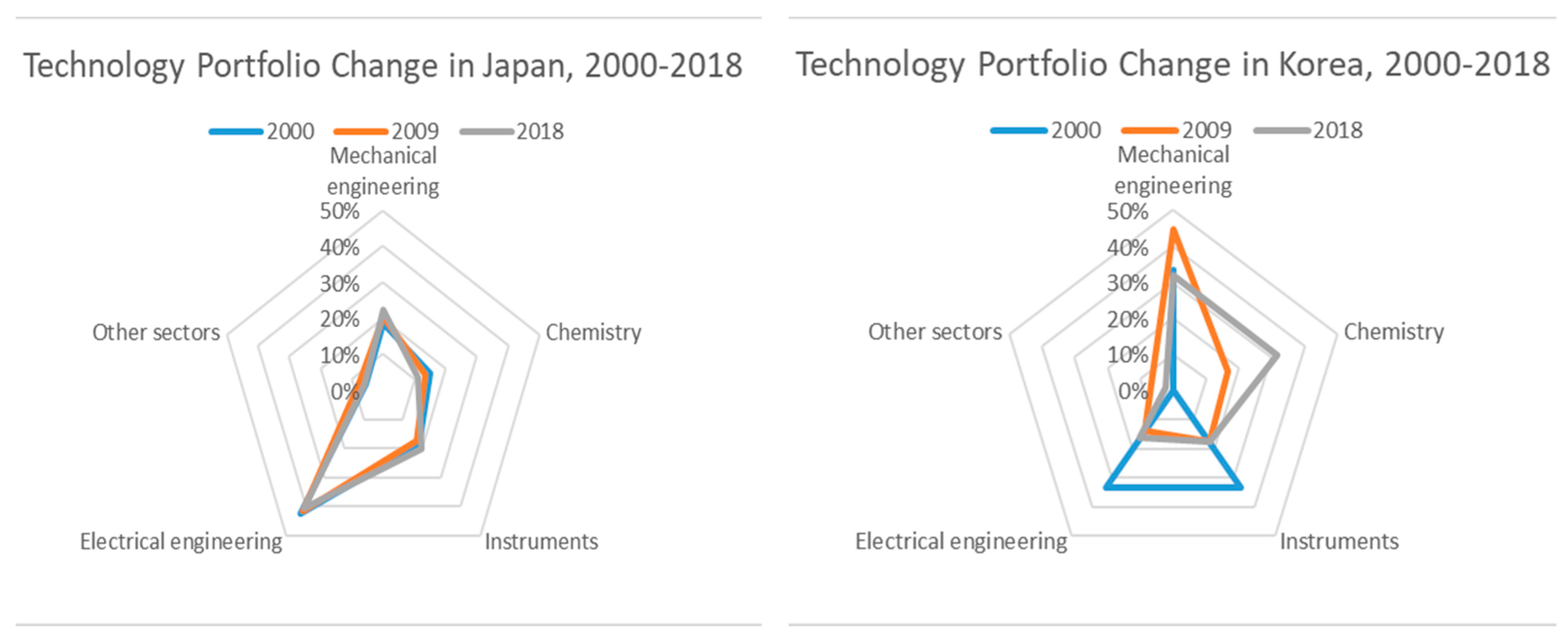
Appendix A of this article discusses differences in fuel mixes and industrial structures in the two nations. The discussion implies that a dwarfed portion of nuclear-based power generation may negatively influence the performance of Japanese electric power generation companies. Meanwhile, S. Korea shows a similar trajectory in the fuel mix but not in the technology portfolio (e.g., a shift from electricity to chemistry). S. Korea′s inconsistent technological innovations activities may lead to its technical regress in maintaining power generation technology. See Appendix A, which summarizes numerical analysis on the concern.

4. Methodology

4.1. Primary

Nomenclatures used in this study are summarized as follows: $x_{ijt}$ is the observed ith input of the jth DMU (i = 1, …, m & j = 1, …, n) at the tth period, $g_{rjt}$ is the observed rth output of the jth DMU (r = 1, …, s & j = 1, …, n) at the tth period, $\xi$ is a measure of inefficiency, $d_{it}^x$ is an unknown slack variable of the ith input at the tth period, $d_{rt}^g$ is an unknown slack variable of the rth output at the tth period, ${\lambda }_{jt}$ is an unknown intensity (or structural) variable of the jth DMU at the tth period, ${\epsilon }_s$ is a prescribed small number.

Before applying the proposed DEA models, we need to specify the following data ranges on X and G:

$R_i^x$ is a data range on the ith input, which is specified as:

$$R_i^x={(m+s)}^{-1}\left\{{\mathit{max}}_{jt}(x_{ijt}|allj\&\mathit{all}t)-{\mathit{min}}_{jt}(x_{ijt}|allj\&\mathit{all}t)\right\}.$$

(1)

$R_r^g$ is a data range on the rth desirable output, which is specified as:

$$R_r^g={(m+s)}^{-1}\left\{{\mathit{max}}_{jt}(g_{rjt}|allj\&\mathit{all}t)-{\mathit{min}}_{jt}(g_{rjt}|allj\&\mathit{all}t)\right\}.$$

(2)

The data ranges are applied to the all DMUs (j = 1, …, n) in all periods (t = 1, …, T) in the proposed performance assessment. We use the data ranges to avoid an occurrence of zero in dual variables (i.e., multipliers). Such an occurrence implies that corresponding production factors (X and G) are not utilized in our DEA applications. However, the data restriction does not function for reducing the number of efficient DMUs.

Here, it is important to note that this study uses a DEA non-radial approach that determines the level of Operational Efficiency (OE) on the specific kth DMU at the tth period. The proposed approach has two differences from the conventional use. One of the two is that we evaluate the performance of the kth DMU to be examined. The DMU is one of all (J_t) at the tth period. The subscription (j) is used to express each DMU (j = 1, …, n) in the total set (J). Even if a DMU(s) has negative or zero in its value, the proposed approach can handle the data set. See Section 4.3 that explains our mathematical rationale. The other DEA models (i.e., radial and intermediate) do not have such a desirable property. The other difference is that the proposed approach measures the level of inefficiency in OE and then it determines the degree of efficiency by subtracting it from unity. The analytical feature cannot be found in the conventional DEA.

4.2. Operational Efficiency under Variable RTS

Using the data ranges (1) and (2), this study proposes the following formulation to measure the degree of Operational Efficiency ($O{E}_{kt}^v$) on the kth DMU at the tth period:

$$\begin{array}{ccc}\mathit{Maximize}& {\displaystyle \sum _{t=1}^T}({\displaystyle \sum _{i=1}^m}{R}_i^x{d}_{it}^x+{\displaystyle \sum _{r=1}^s}{R}_r^g{d}_{rt}^g)\hfill & \\ s.t.& {\displaystyle \sum _{j=1}^n}{x}_{ijt}{\lambda }_{jt}+d_{it}^x=x_{ikt}\hfill & (i=1,\dots ,m\&t=1,\dots ,T),\hfill \\ & {\displaystyle \sum _{j=1}^n}{g}_{rjt}{\lambda }_{\mathit{jt}}-d_{rt}^g=g_{\mathit{rkt}}\hfill & (r=1,\dots ,s\&t=1,\dots ,T),\hfill \\ & {\displaystyle \sum _{j=1}^n}{\lambda }_{jt}=1(t=1,\dots ,T),{\lambda }_{\mathit{jt}}\ge 0\hfill & (j=1,\dots ,n\&t=1,\dots ,T),\hfill \\ & d_{\mathit{it}}^x\ge 0(i=1,\dots ,m\&t=1,\dots ,T)\hfill & {\&d}_{\mathit{rt}}^g\ge 0(r=1,\dots ,s\&t=1,\dots ,T).\hfill \end{array}$$

(3)

The superscript (v) of $O{E}_{kt}^v$ indicates variable RTS in the scale treatment.

We measure the degree of the kth DMU at the tth period by:

$$O{E}_{kt}^v=1-{\epsilon }_s({\displaystyle \sum _{i=1}^m}{R}_i^x{d}_{it}^{x*}+{\displaystyle \sum _{r=1}^s}{R}_r^g{d}_{rt}^{g*}),$$

(4)

where the inefficiency score and all slack variables are determined on the optimality of Model (3). Thus, the equation within the parenthesis is obtained from the optimality of Model (3).

Here, it is important to note that the conventional use of an output-oriented DEA model, for example, is different from that of Model (3). The major difference is that the former maximizes $\tau +{\epsilon }_n\left({\sum }_{i=1}^m{d}_{it}^x+{\sum }_{r=1}^s{d}_{rt}^g\right)$ in the objective function, where ${\epsilon }_n$ is a non-Archimedean small number. We use the very small number, but not non-Archimedean, to control the magnitude of the degree of operational efficiency. Assuming all slacks are zero, the efficiency measure is determined by 1/$\tau *$ on optimality in the conventional use. Thus, the measurement of Model (3) is different from the previous models. Accordingly, the constraints of Model (3) need to incorporate the direction ($g_{\mathit{rkt}}$) for maximization, given the observed $g_{\mathit{rkt}}$. The conventional DEA does not have such a direction for optimal projection. As a result, it often suffers from an occurrence of multiple projections.

Next, Model (3) has the following dual formulation:

$$\begin{array}{ccc}\mathit{Minimize}& {\displaystyle \sum _{t=1}^T}({\displaystyle \sum _{i=1}^m}{v}_{it}{x}_{ikt}-{\displaystyle \sum _{r=1}^s}{u}_{rt}{g}_{rkt}+{\sigma }_t)\hfill & \\ s.t.& {\displaystyle \sum _{i=1}^m}{v}_{it}{x}_{ijt}-{\displaystyle \sum _{r=1}^s}{u}_{rt}{g}_{rjt}+{\sigma }_t\ge 0\hfill & (j=1,\dots ,n\&t=1,\dots ,T),\hfill \\ & v_{\mathit{it}}\ge {\epsilon }_s{R}_i^x\hfill & (i=1,\dots ,m\&t=1,\dots ,T),\hfill \\ & u_{\mathit{rt}}\ge {\epsilon }_s{R}_r^g\hfill & (r=1,\dots ,s\&t=1,\dots ,T).\hfill \\ & \hfill {\sigma }_t:\mathit{URS}.& \end{array}$$

(5)

where $v_{it}$ (i = 1, …, m) and $u_{rt}$ (r = 1, …, s) are all positive dual variables (i.e., multipliers, implying weights among production factors) related to the first and second groups of constraints in Model (3). The dual variable (${\sigma }_t$), representing a constant, is unrestricted (URS) in the sign.

The comparison between Models (3) and (5) provides the following three concerns: First, the objective value of Model (3) equals that of Model (5) on optimality. So, we have the following relationship:

$${\displaystyle \sum _{i=1}^m}{R}_i^x{d}_{it}^{x*}+{\displaystyle \sum _{r=1}^s}{R}_r^g{d}_{rt}^{g*}={\displaystyle \sum _{t=1}^T}({\displaystyle \sum _{i=1}^m}{v}_{it}^{*}{x}_{ikt}-{\displaystyle \sum _{r=1}^s}{u}_{rt}^{*}{g}_{rkt}+{\sigma }_t^{*}),$$

(6)

on optimality. We measure the operational efficiency ($O{E}_{kt}^v$) of the kth DMU by the following equation:

$$O{E}_{kt}^v=1-{\epsilon }_s({\displaystyle \sum _{i=1}^m}{v}_{it}^{*}{x}_{ikt}-{\displaystyle \sum _{r=1}^s}{u}_{rt}^{*}{g}_{rkt}+{\sigma }_t^{*}).$$

(7)

Second, an important feature of Model (5) is that all the dual variables, except ${\sigma }_t^{*}$, are positive as, formulated in (5). Thus, the information on all production factors is fully utilized as specified in the last three constraints of Model (5). Finally, each dual variable indicates an amount of change in operational inefficiency (1-$O{E}_{kt}^v$) due to a unit change in each production factor.

4.3. Translation Invariance: Handling Zero in A Data Set

To handle zero and/or negative values in a data set, we use the property of “translation invariance”. The proposed approach has the property. This study starts with a description of specifying the following data shift on all DMUs (j = 1, …, n):

$${\overline{x}}_{ijt}=x_{ijt}+{\alpha }_{it}(i=1,\dots ,m)\mathrm{and}{\overline{g}}_{rjt}=g_{rjt}+{\beta }_{rt}(r=1,\dots ,s).$$

(8)

The two Greek symbols are specific positive numbers (e.g., 1 and 100) that can be subjectively selected by a user(s). As a result of the data shifts, all production factors of the jth DMU become ${\overline{x}}_{ijt}>0$ (i = 1,…, m) and ${\overline{g}}_{rjt}>0$, where the inequality implies strict positivity in sign.

To examine the property of translation invariance, let us return to Model (3) and modify the two groups of constraints as follows:

$${\sum }_{j=1}^n(x_{ijt}+{\alpha }_{it}){\lambda }_{jt}+d_{it}^x=x_{ikt}+{\alpha }_{it}(i=1,\dots ,m)\mathrm{and}{\sum }_{j=1}^n(g_{rjt}+{\beta }_{rt}){\lambda }_{jt}-d_{rt}^g=g_{rkt}+{\beta }_{rt}(r=1,\dots ,s).$$

(9)

Equation (9) maintains the following conditions:${\sum }_{j=1}^n{\alpha }_{it}{\lambda }_{jt}={\alpha }_{it}$ and ${\sum }_{j=1}^n{\beta }_{rt}{\lambda }_{jt}={\beta }_{rt}$ because of ${\sum }_{j=1}^n{\lambda }_{jt}=1$. Consequently, the two constraints of Equations (9) become:

$${\sum }_{j=1}^n{x}_{ijt}{\lambda }_{jt}+d_{it}^x=x_{ikt}(i=1,\dots ,m)\mathrm{and}{\sum }_{j=1}^n{g}_{rjt}{\lambda }_{jt}-d_{rt}^g=g_{rkt}(r=1,\dots ,s).$$

(10)

The above two groups of constraints are the same as Model (3). Thus, the proposed data shifts do not influence the constraints of Model (3).

Next, paying attention to the objective function of Model (3), the data shifts change the two types of slacks as follows:

$$\begin{array}{c}{\sum }_{i=1}^m{R}_i^x[(x_{ikt}+{\alpha }_{it})-{\sum }_{j=1}^n(x_{ijt}+{\alpha }_{it}){\lambda }_{jt}]={\sum }_{j=1}^m{R}_i^x(x_{ikt}-{\sum }_{j=1}^n{x}_{ijt}{\lambda }_{jt})={\sum }_{j=1}^m{R}_i^x{d}_{it}^x\\ \mathrm{and}\\ {\sum }_{r=1}^s{R}_r^g[{\sum }_{j=1}^n(g_{rjt}+{\beta }_{rt}){\lambda }_{jt}-(g_{rkt}+{\beta }_{rt})]={\sum }_{r=1}^s{R}_r^g({\sum }_{j=1}^n{g}_{rjt}{\lambda }_{jt}-g_{rkt})={\sum }_{r=1}^s{R}_r^g{d}_{rt}^g.\end{array}$$

(11)

Equation (11) indicates the translation invariance on the objective value of (3). Thus, the proposed data shifts from zero or negative to positive do not influence the objective value of Model (3). The proposed model (3) can solve a data set with zero for our international comparison.

4.4. Multiplier Restriction

To extend Model (3) further into rank analysis and a statistical test on null hypotheses, we need to consider multiple (weights among inputs and outputs) restrictions for our empirical results. To conduct the restriction, we start describing a supporting hyperplane(s) of the kth DMU at the specific tth period that becomes as follows:

$${\sum }_{i=1}^m{v}_{it}{x}_{it}-{\sum }_{r=1}^s{u}_{rt}{g}_{rt}+{\sigma }_t=0,$$

(12)

where dual variables, $v_{it}$ (i = 1,…, m) and $u_{rt}$ (r = 1,…, s) are unknown parameters for indicating the direction of the supporting hyperplane (s), and ${\sigma }_t$ indicates an intercept of the supporting hyperplane. The following equations determine these parameters:

$${\sum }_{i=1}^m{v}_{it}{x}_{ijt}-{\sum }_{r=1}^s{u}_{rt}{g}_{rjt}+{\sigma }_t=0,j\in R{S}_{kt},$$

(13)

where $R{S}_{kt}$ stands for “a reference set” of the kth DMU at the tth period. Model (3) determines $R{S}_{kt}$ that is part of efficient DMUs.

If the supporting hyperplane is in a simple case (i.e., a single component of each production factor), Equation (12) becomes $v_t{x}_t-u_t{g}_t+{\sigma }_t=0$ at the tth period. The ratio between factors becomes $\partial g_t/\partial x_t=v_t/u_t$. Since these factors have lower and upper bounds, the ratios are expressed by the following conditions: $g_t^L/x_t^U\le v_t/u_t\le g_t^U/x_t^L$. The superscripts (L and U) indicate Lower and Upper bounds of each production factor. Note that we determine these values on the observed production factors (x and g) at the tth period.

The extension to multiple components of X and G produces the following conditions:

$$g_{rt}^L/x_{it}^U\le v_{it}/u_{rt}\le g_{rt}^U/x_{it}^L(i=1,\dots ,m,r=1,\dots s\&t=1,\dots ,T).$$

(14)

After incorporating (14), Model (5) becomes:

$$\begin{array}{ccc}\mathit{Minimize}& {\displaystyle \sum _{t=1}^T}({\displaystyle \sum _{i=1}^m}{v}_{it}{x}_{ikt}-{\displaystyle \sum _{r=1}^s}{u}_{rt}{g}_{rkt}+{\sigma }_t)\hfill & \\ s.t.& {\displaystyle \sum _{i=1}^m}{v}_{it}{x}_{ijt}-{\displaystyle \sum _{r=1}^s}{u}_{rt}{g}_{rjt}+{\sigma }_t\ge 0\hfill & (j=1,\dots ,n\&t=1,\dots ,T),\hfill \\ & g_{rt}^L/x_{it}^U\le v_{it}/u_{rt}\le g_{rt}^U/x_{it}^L\hfill & (i=1,\dots ,m,r=1,\dots s\&t=1,\dots ,T).\hfill \\ & v_{\mathit{it}}\ge {\epsilon }_s{R}_i^x\hfill & (i=1,\dots ,m\&t=1,\dots ,T),\hfill \\ & u_{\mathit{rt}}\ge {\epsilon }_s{R}_r^g\hfill & (r=1,\dots ,s\&t=1,\dots ,T).\hfill \\ & \hfill {\sigma }_t:\mathit{URS}.& \end{array}$$

(15)

The level of OE on the kth DMU at the tth period is measured by:

$$O{E}_{kt}^v=1-{\epsilon }_s({\displaystyle \sum _{i=1}^m}{v}_{it}^{*}{x}_{ikt}-{\displaystyle \sum _{r=1}^s}{u}_{rt}^{*}{g}_{rkt}+{\sigma }_t^{*}).$$

(16)

where all dual variables (i.e., multipliers) are determined by Model (15).

Methodological contribution: For our international comparison between Japanese and S. Korean electric power industries, we used the new model (15) because it has two unique features. First, the proposed approach can handle “zero” in a dataset, as found in Model (3). The capability is important because our data set contained zero in an output (i.e., the number of patents). The proposed approach, structured by Model (3), has the property of “translation invariance” that allows us to handle zero or negative values by shifting them to positive. The data shift does not change the degree of OE. Second, we extended Model (3) to Model (15). The model incorporates an analytical capability to restrict multipliers without any prior information. The multiplier restriction has been long used as assurance region analysis [3] and cone ration [4] in the conventional DEA. However, these techniques need prior information. In contrast, Model (15) is structured by the dual formulation so that it can mathematically express a range of supporting hyperplane(s). The importance of the proposed approach is that we restrict multiplier(s) by the upper and lower bounds of the supporting hyperplane(s). As a result, multipliers are all positive in a required range. Here, the positivity of multipliers implies that all data are fully used in the proposed DEA assessment so that it reduces the number of efficient DMUs.

5. Empirical Results

5.1. Data

This study kept track of nine electric power companies in Japan and six in South Korea over five annual periods (from 2014–2018). The data set on Japanese companies was obtained from [16] and this study newly sampled the data set on Korean companies. For the comparative analysis in the framework of multiple inputs and outputs, we collected data from two common sources: (a) firms′ demographic and financial data from their annual financial reports and (b) patent publication data from PATENTSCOPE offered by the World Intellectual Property Organization (WIPO). For the amount of electricity sold in South Korea, additionally, we referred to the Electric Power Statistics Information System (EPSIS) provided by the Korea Power Exchange (KPX).

In this research, there were four inputs: the amount of total assets, the number of employees, the amount of operating expenses, and the amount of R&D expenditure. They were measured in US$ million dollars that were converted from Japanese Yen and Korean Won based on each year′s exchange rate. Here, the number of employees was measured in Full Time Equivalent (FTE). There were three outputs: the amount of sales, electricity sold, and patents. Sales were measured in US$ Million (M). The amount of electricity sold was measured in gigawatt hours (GWh). The number of patents was based on the publication date.

Table 2. Data of Japanese Power Companies in 2018: An Illustrative Example.

Production Factors	Input				Output
Company	Total Asset	Employees	Operating Expenses	R&D Expenses	Sales	Electricity Sold	Patent Publications
	(US$ M)	(FTE)	(US$ M)	(US$ M)	(US$ M)	(GWh)	(No.)
Hokkaido Electric Power	19,178	10,937	6965	23.03	7379	22,774	10
Tohoku Electric Power	41,776	25,032	21,196	85.77	22,016	85,096	28
Tokyo Electric Power	125,147	41,086	59,115	183.15	62,179	230,306	222
Chubu Electric Power	58,736	30,321	28,538	97.36	29,773	123,602	39
Hokuriku Electric Power	15,432	8498	5985	16.09	6111	26,060	6
Kansai Electric Power	71,192	32,597	30,438	117.72	32,447	132,722	45
Chugoku Electric Power	31,996	13,418	13,316	110.85	13,508	52,944	426
Shikoku Electric Power	13,282	8207	6980	36.54	7232	3296	0
Kyushu Electric Power	47,028	21,103	18,939	53.55	19,788	72,219	7
Average	47,085	21,244	21,275	80.45	22,270	85,447	87

and

Table 3. Data of Korean Power Companies in 2018: An Illustrative Example.

Production Factors	Inputs				Outputs
Company	Total Asset	Employees	Operating Expenses	R&D Expenses	Sales	Electricity Sold	Patent Publications
	(US$ M)	(FTE)	(US$ M)	(US$ M)	(US$ M)	(GWh)	(No.)
Korea South-East Power	10,181	2418	5375	47.12	5531	64,219	16
Korea Midland Power	11,237	2694	4427	30.24	4449	45,628	11
Korea Western Power	9851	2486	4719	32.56	4859	49,290	32
Korea East-West Power	8794	2569	4904	30.23	4963	50,767	7
Korea Southern Power	10,187	2322	5775	25.50	5961	55,607	0
Korea Hydro & Nuclear Power	55,920	12,317	7726	477.83	8840	132,135	61
Average	17,695	4134	5488	107.25	5767	66,274	21

Note: M stands million, FTE indicates Full Time Equivalent, GWh is Gigawatt Hours, and No. stands for the number.

show illustrative data sets regarding Japanese and Korean electric power companies, respectively, in 2018. The data set included four inputs and three outputs of companies in each country. Tokyo electric power company in Table 2 and Korea hydro and nuclear power firm in Table 3 are relatively larger than others in each country.

As of 2018, on average, Japanese companies sold 85,447 GWh of electricity, made US$22,270 million of sales, and created 87 patents using 21,244 employees, US$47,085 million, 21,244 million, and 80 million of assets, operation expenses, and R&D expenses, respectively (Table 2). On the other hand, Korean companies sold 66,274 GWh of electricity, made US$5767 million in sales, and created 21 patents using 4134 employees, US$17,695 million, 5488 million, and 107 million in assets, operation expenses, and R&D expenses, respectively (Table 3). The gap between Japanese and Korean companies reflects differences in Gross Domestic Product (GDP; Japan: US$4,971,323 million and South Korea: US$1,619,424 million as of 2018).

Like Table 2 and Table 3, we collected data sets from 2014 to 2018.

Table 4. Descriptive Statistics of Japanese Power Companies′ Data.

Production Factors		Inputs				Outputs
Company	Variables	Total Asset	Employees	Operating Expenses	R&D Expenses	Sales	Electricity Sold	Patent Publications
(Units)		(US$ M)	(FTE)	(US$ M)	(US$ M)	(US$ M)	(GWh)	(No.)
Hokkaido Electric Power	Avg.	18,634	10,979	6893	23.07	7188	26,557	7
	Max.	20,045	11,027	7597	25.07	7650	29,810	11
	Min.	17,603	10,937	6534	21.78	6799	22,774	1
	S.D.	1027	33	432	1.22	334	2836	4
Tohoku Electric Power	Avg.	41,722	24,736	19,699	78.14	21,065	76,607	30
	Max.	45,608	25,058	22,216	85.77	24,090	85,096	36
	Min.	40,027	24,285	17,600	66.00	18,862	72,000	22
	S.D.	2290	330	1942	9.60	2030	5030	5
Tokyo Electric Power	Avg.	131,010	42,171	57,821	183.41	62,365	241,810	135
	Max.	156,907	43,330	71,604	192.79	73,211	257,046	222
	Min.	118,785	41,086	49,333	167.38	52,138	230,306	67
	S.D.	15,221	924	8452	10.45	7839	10,818	71
Chubu Electric Power	Avg.	56,091	30,603	27,338	97.17	29,289	122,586	37
	Max.	62,169	30,848	33,081	103.14	31,378	124,075	59
	Min.	52,356	30,321	23,869	91.19	27,613	121,431	23
	S.D.	4196	191	3670	4.32	1591	1174	14
Hokuriku Electric Power	Avg.	15,293	8363	5423	15.88	5659	27,646	8
	Max.	16,333	8498	5985	16.76	6111	28,663	14
	Min.	14,550	8239	4882	13.54	5249	26,060	5
	S.D.	716	104	430	1.33	390	979	4
Kansai Electric Power	Avg.	72,482	32,884	30,606	117.22	32,194	126,294	49
	Max.	85,487	33,539	38,470	132.94	37,602	134,490	95
	Min.	66,304	32,527	27,028	110.11	29,134	115,244	26
	S.D.	7588	427	4563	9.39	3255	7985	27
Chugoku Electric Power	Avg.	31,366	13,656	12,391	70.53	12,827	56,043	521
	Max.	34,293	14,149	13,560	110.85	14,348	57,868	670
	Min.	29,602	13,418	11,280	44.50	11,614	52,944	426
	S.D.	1879	290	1056	31.86	1136	1951	92
Shikoku Electric Power	Avg.	13,560	8233	6665	37.01	6923	25,252	5
	Max.	15,469	8382	7014	42.53	7334	26,392	9
	Min.	12,590	8156	6066	34.94	6304	23,296	0
	S.D.	1123	91	408	3.14	441	1182	3
Kyushu Electric Power	Avg.	47,168	20,928	18,241	61.71	18,985	77,620	9
	Max.	52,823	21,103	21,161	81.07	20,683	81,279	15
	Min.	44,384	20,753	16,495	53.55	17,681	72,219	5
	S.D.	3297	127	1936	11.37	1313	3420	4

and

Table 5. Descriptive Statistics of Korean Power Companies′ Data.

Production Factors		Inputs				Outputs
Company	Variables	Total Asset	Employees	Operating Expenses	R&D Expenses	Sales	Electricity Sold	Patent Publications
(Units)		(US$ M)	(FTE)	(US$ M)	(US$ M)	(US$ M)	(GWh)	(No.)
Korea South-East Power	Avg.	9169	2269	4313	36.91	4821	65,950	12
	Max.	10,181	2418	5375	47.12	5531	67,765	16
	Min.	8361	2103	3665	26.75	4154	63,923	6
	S.D.	703	125	746	8.35	514	1758	4
Korea Midland Power	Avg.	8771	2480	3847	22.54	4095	46,594	9
	Max.	11,237	2694	4585	30.24	4740	50,323	17
	Min.	6693	2252	3084	16.71	3571	42,925	5
	S.D.	1783	195	644	5.20	490	3493	5
Korea Western Power	Avg.	8831	2294	3888	26.84	4223	47,556	16
	Max.	9851	2486	4719	32.56	4859	49,290	32
	Min.	7622	2099	3360	24.00	3902	45,525	9
	S.D.	830	165	592	3.47	433	1630	9
Korea East-West Power	Avg.	8322	2392	3885	21.65	4269	48,795	7
	Max.	8794	2569	4904	30.23	4963	50,767	9
	Min.	7796	2232	3227	14.85	3800	46,960	3
	S.D.	366	139	667	7.36	447	1390	2
Korea Southern Power	Avg.	9127	2159	4487	21.62	4781	50,975	1
	Max.	10,187	2322	5775	25.50	5961	56,727	2
	Min.	8089	1969	3382	17.66	3947	46,819	0
	S.D.	819	146	1142	2.95	1005	4776	1
Korea Hydro & Nuclear Power	Avg.	50,089	11,710	6963	388.01	9326	150,771	76
	Max.	55,920	12,317	7726	477.83	10,448	161,466	159
	Min.	45,879	11,003	6334	289.70	8696	132,135	35
	S.D.	3941	620	643	80.17	776	11,869	49

summarize descriptive statistics on Japanese and Korean electric power companies during the observed periods. Note that these descriptive statistics in Table 4 and Table 5 are related to four inputs and three outputs, as summarized in Table 2 and Table 3. Note that the business scope of Japanese power companies is larger than that of the Korean. Moreover, the number of patents in Japanese companies (87) is larger than that of the Korean one (21).

5.2. Analysis and Discussion

Table 6. Efficiencies of Japanese and Korean Power Companies.

Country	Company	2014	2015	2016	2017	2018
Japan	Hokkaido Electric Power	0.925	0.944	0.930	0.934	0.938
	Tohoku Electric Power	1.000	0.911	0.868	0.886	0.930
	Tokyo Electric Power	1.000	1.000	1.000	1.000	1.000
	Chubu Electric Power	0.924	1.000	0.952	0.933	0.930
	Hokuriku Electric Power	0.987	1.000	0.962	0.972	0.992
	Kansai Electric Power	0.880	0.869	0.863	0.857	0.878
	Chugoku Electric Power	1.000	0.981	0.983	0.967	0.936
	Shikoku Electric Power	0.925	0.933	0.938	0.937	0.933
	Kyushu Electric Power	0.850	0.864	0.878	0.910	0.931
South Korea	Korea South-East Power	1.000	1.000	1.000	0.994	1.000
	Korea Midland Power	1.000	1.000	1.000	0.989	0.978
	Korea Western Power	1.000	1.000	0.995	0.988	0.987
	Korea East-West Power	1.000	1.000	1.000	0.986	0.986
	Korea Southern Power	1.000	1.000	1.000	0.988	0.992
	Korea Hydro & Nuclear Power	1.000	1.000	0.961	0.899	0.864

Note: (a) Model (3) computes these operational efficiency measures. (b) The number of efficient DMUs is 26 (35%) and that of inefficient DMUs is 49 (65%).

summarizes the efficiency measures of Japanese and S. Korea electric power companies from 2014 to 2018. We estimated the efficiency measures by Model (3). In Japan, Tokyo Electric Power Company showed the status of efficiency in OE in the observed five years. The other Japanese firms showed the status of inefficiency (except Chugoku in 2014). Meanwhile, in S. Korea, all electric power companies exhibited efficiency in 2014, but gradually decreased in status. Figure 3 visually describes such a difference in electric power industries between the two nations. The numbers listed in Figure 3 indicate average efficiencies of these firms. An important finding in Figure 3 is that the electric power companies in S. Korea outperformed the Japanese.

Table 7. Efficiencies of Japanese and Korean Power Companies with Multiplier Restriction.

Country	Company	2014	2015	2016	2017	2018
Japan	Hokkaido Electric Power	0.925	0.941	0.930	0.933	0.935
	Tohoku Electric Power	0.965	0.911	0.868	0.886	0.930
	Tokyo Electric Power	1.000	1.000	1.000	1.000	1.000
	Chubu Electric Power	0.924	1.000	0.952	0.933	0.930
	Hokuriku Electric Power	0.978	1.000	0.961	0.969	0.985
	Kansai Electric Power	0.880	0.869	0.863	0.857	0.878
	Chugoku Electric Power	1.000	0.981	0.983	0.967	0.936
	Shikoku Electric Power	0.925	0.933	0.938	0.937	0.933
	Kyushu Electric Power	0.850	0.864	0.878	0.909	0.930
South Korea	Korea South-East Power	1.000	1.000	0.998	0.994	0.995
	Korea Midland Power	1.000	1.000	1.000	0.989	0.978
	Korea Western Power	1.000	0.995	0.995	0.988	0.987
	Korea East-West Power	1.000	1.000	1.000	0.986	0.986
	Korea Southern Power	1.000	1.000	1.000	0.988	0.992
	Korea Hydro & Nuclear Power	1.000	1.000	0.961	0.899	0.864

Note: (a) Model (15) computes operational efficiency measures. (b) Four firms had status transition from efficiency to inefficiency. See Tohoku Electric Power in 2014, Korea South-East Power in 2016 and 2018, and Korea Western Power in 2015 as a result of multiplier restriction. (c) The number of efficient DMUs is 22 (29%) and that of inefficient DMUs is 53 (71%).

extends the computational results on OE summarized in Table 6 by incorporating multiple restrictions on dual variables. We used Model (15) to examine whether they produced difference results. This type of examination confirmed the reliability of our empirical result. As summarized in Table 7, we obtained similar results in Table 6. The Korean electric power companies outperformed the Japanese ones, as well. Figure 4 depicts such a difference in terms of their efficiency averages. As mentioned previously, the S. Korean firms have gradually decreased their average on OE measures, but the Japanese firms have not produced major changes in their measures.

Policy implication: It is necessary to note two rationales on the findings of Table 6 and Table 7 (i.e., the S. Korea companies outperformed the Japanese firms). One of the two is that the number of nuclear power plants is 60 in Japan, but only 9 plants are operating as of June 2020. After the Fukushima Daiichi disaster, almost no nuclear power plant has operated because of very strong resentment among people and local governments toward the nuclear operation. Meanwhile, 19 nuclear power plants have been operating now among 24 plants in S. Korea. It is widely known that electricity generated by nuclear energy can serve as a “base load” and is operationally efficient once the plant is established. See the research in [29] that gives a detailed description on the S. Korean operation. Thus, S. Korea has an advantage over Japan in terms of power generation, because it has had no nuclear disaster like Fukushima Daiichi. The other is that Tokyo Electric Power Company has showed the status of efficiency in its OE measurement even though the firm has suffered from the nuclear disaster. The firm became a public entity after the disaster and it has been financially supported by the Japanese government. The Fukushima Daiichi nuclear power plant, belonging to the Tokyo Electric Power Company, has produced a huge damage. The underlying policy rationale discussed by the Japanese government was “too big to make it bankrupt” at that time. The Japanese government asked the other eight electric firms to compensate Tokyo′s huge damage. As a result, the company has exhibited efficiency because of the governmental support. Such support is not given to the other utility firms in Japan. Meanwhile, the S. Korean firms do not have such a financial burden due to the nuclear operation.

6. Conclusions

This research compared the operational performance of Japanese and S. Korean electric power sectors. Both have different and similar industrial and organizational structures at the same time. For instance, they showed similar fuel mixes but it became heterogeneous after the Fukushima Daiichi Disaster. The Japanese companies have been under private ownership from the beginning, while the S. Korean ones started as public entities, but changed to public/private joint entities. To assess their operational progress, we used DEA as a measurement tool that allowed us to examine the level of simultaneous achievements on economic and technological factors. The method assessed the degree of their holistic development. The DEA-based OE measurement, including the amount of R&D expenditure (an input) and the number of patents (an output) served as a useful tool for the comparison because it can handle multiple production factors without any functional specification between multiple inputs and outputs.

The proposed approach first discussed how to handle zero in an observed data set (i.e., the number of patents) by using the property of “translation invariance”. Model (3) had the property. Then, we extended the model by restricting multipliers without any prior information so that we could reduce the number of efficient firms. Model (15) was the final model that addressed the two methodological issues (i.e., the existence of zeroes in a data set and too many efficient firms). Without addressing these issues, it was impossible for this study to conduct an empirical investigation on the comparison between Japan and S. Korea. Thus, the proposed approach documented the DEA practicality by comparing them in terms of their operational efficiencies.

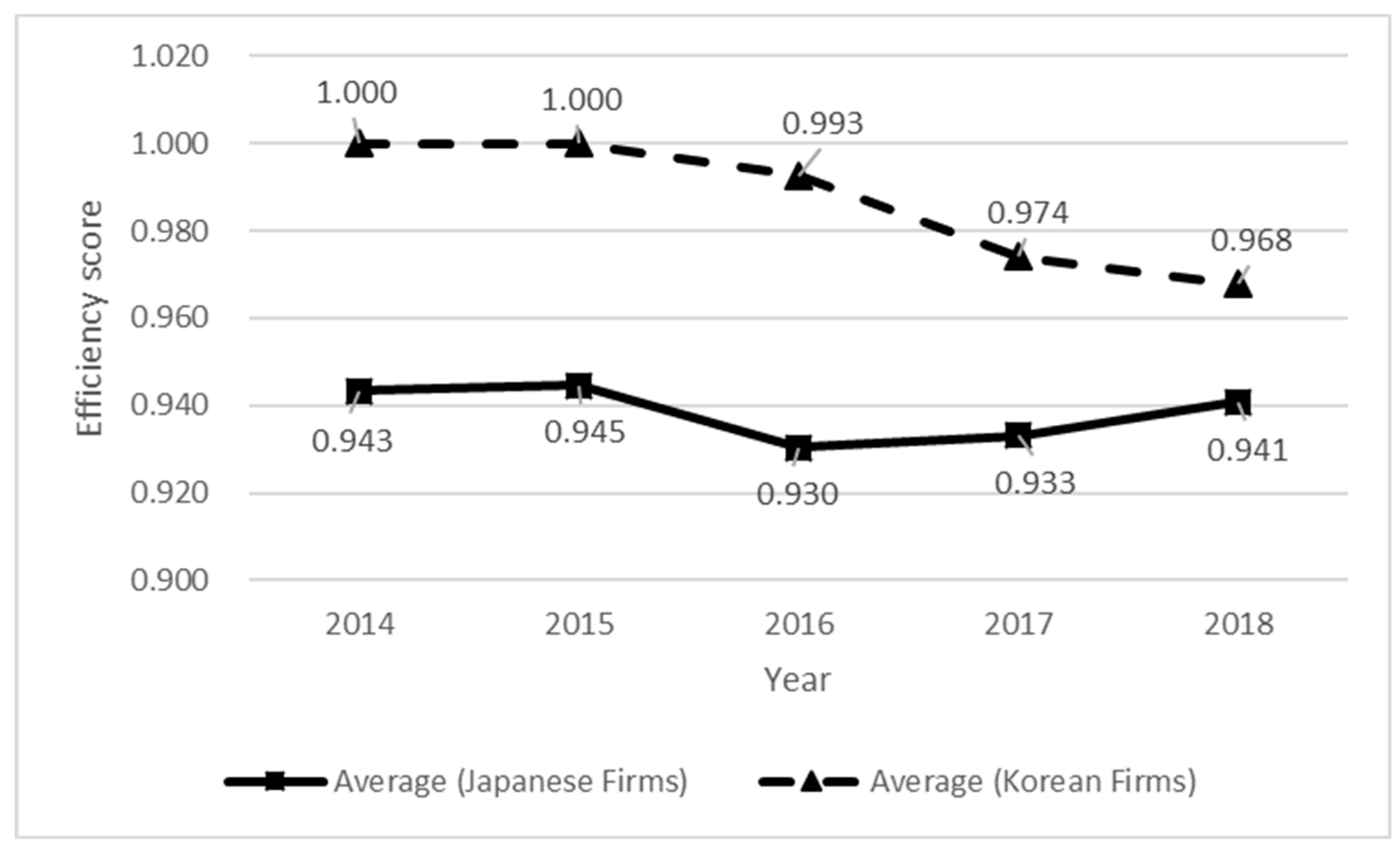
Our empirical study identified two important implications. One of them was that the electric power industry of S. Korean outperformed Japan in the observed period (2014–2018). For example, Figure 4 visually documented that the OE measures of S. Korea were 100% in 2014, 99.9% in 2015, 99.2% in 2016, 97.4% in 2017, and 96.7% in 2018, which were about 5% higher than the Japanese ones (i.e., 93.9%, 94.4%, 93.0%, 93.2%, and 94.0%, respectively). We conjecture the reason from the fact that the Japanese power sector has suffered from the occurrence of the Fukushima Daiichi nuclear disaster on 11 March 2011. A rationale is that despite nuclear energy′s significant contribution to the efficient power generation, its use has been limited and it has been almost impossible to resume the power plants in Japan. As a consequence, Japan needed other energy sources, such as liquid natural gas and renewable energies. See the previous work [31] that discussed a new direction on the Japanese electric power industry.

Another implication was that the difference in performance between the two nations has gradually diminished partly because the Japanese electric power sector has been gradually recovering from the disaster. Another explanation is partly possible from the structure of heterogeneous technology portfolios. For example, S. Korea′s inconsistent technological innovation activities may lead to its technical regress. Particularly, the technological shift (including R&D expenditure and patents) from electrical engineering and instruments, which are fundamental technologies for the electric power generation sector, to chemistry may interfere with maintaining the nation′s relatively higher performance in operational efficiency.

The proposed DEA approach evidences its usefulness in the application to the electric power industry. However, it is necessary for us to overcome five empirical difficulties in future extensions. First, technology development occurs between different periods. This study needs to incorporate the analytical structure (e.g., the measurement of a frontier shift) within a time horizon. This indicates a methodological limit to be fixed in the future. Second, examination at company level may provide more detailed insights than a national level. A future extension needs to examine the company or sector-based OE measures. Third, it is necessary to explore how innovation activities (e.g., R&D expenditure) may influence corporate performance in the industry. In this case, we may need to consider a time lag between R&D and technological innovations. Fourth, another future extension needs to include more industrialized nations, such as the United States and European nations, where the deregulation of electricity was implemented before Japan and S. Korea. Such a research extension is an important future task. Finally, we have not yet investigated operational progress due to technology development (not only patents discussed in this study) on electricity among other industries and other nations. The issue is an important research concern, as well.

In conclusion, it is hoped that this study can contribute to the advancement of the electric power industry. We look forward to seeing future development as discussed in this article.