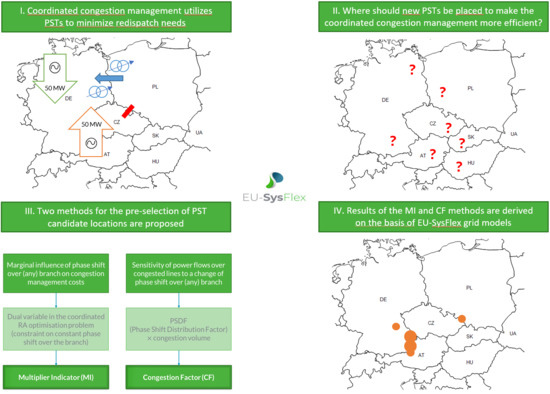
Pre-Selection of the Optimal Sitting of Phase-Shifting Transformers Based on an Optimization Problem Solved within a Coordinated Cross-Border Congestion Management Process
Abstract
1. Introduction
- costly actions—shifting the operating points of generating units located in affected areas, reducing demand with DSR (demand side response) or, if other means fail, shedding load (which results in non-zero Energy Not Served (ENS)),
- non-costly actions—switching taps of phase shifting transformers (PSTs) or topology switching (turning selected power system elements on or off by TSOs).
- redispatch—to characterize the shift in generation of thermal units,
- RES curtailment—to denote the reduction of the infeed of renewable energy sources.
2. Literature Review
3. Theoretical Description—Coordinated Cross-Border Congestion Management Model
3.1. Theoretical Description of the Congestion Management Model
- N-0 state—the case when no outage occurs in the system,
- N-1 state—the case representing the grid with an outage of one transmission line, which is referred to as the critical outage (CO).
- Candidate CBCOs were identified with COs selected out of the XB connections and their nearest neighbors—intra-zonal lines terminating at the border stations.
- The LODFs for all candidate CBCO pairs were calculated.
- The final CBCOs were identified as the ones for which the absolute value LODF was greater than the threshold selected as 5%.
- is the power shift up of thermal generator i;
- is the power shift down of thermal generator i;
- is the curtailed power of RES generator i;
- is the variable representing the energy curtailment of the demand or Energy Not Served per demand in bus i;
- is the variable representing the tap setting of PST i.
- is the number of thermal generators in the system;
- is the number of loads in the system;
- is the number of RES generators in the system;
- is the cost of regulating up thermal generator i;
- is the revenue from regulating down thermal generator i;
- is the penalty cost for curtailment of RES;
- is the penalty cost for the energy curtailment.
- is the power capacity limit for transmission line CB;
- is the initial power flow over line CB in outage state of CO;
- is the initial generation point in power of thermal generator i;
- , are, respectively, the maximal and minimal operating power limit of thermal generator i;
- is the initial generation point in power of RES generator i;
- is the number of PSTs in the system;
- is the initial tap setting of PST i;
- , are, respectively, the maximal and minimal tap setting of PST i;
- is a set of nodal balance equations;
- is the set of the flow equations.
3.2. Modified DC Power Flow Formulation
3.3. PSDF and PTDF Formulation
4. Theoretical Description—Methods for Pre-Selecting the Candidates of the PST Investments
4.1. Multiplier Indicator (MI)
- A possibility of changing the phase angle of each branch in the model was added—each branch is allowed to introduce a phase shift like a PST. In particular, the new power flow equations now take the following form:where:
- is the PSDF coefficient of flow over CBCO with respect to phase angle of branch i (acting like a PST),
- is the angle per tap sensitivity assigned to branch i—the change of the phase angle resulting from shifting one tap (a reference value of , based on the values for existing PSTs, is used for the “candidates”)
- is the number of branches in the grid,
- are the optimal tap settings of existing PSTs, obtained in the cross-border congestion management optimal solution for the given grid scenario,
- is the set of vector variables from Equation (2) with the optimal PST tap settings,
- is the modified set of vector variables.
- The new phase shift is set to a parameter , by additional constraints:When solving the optimization model, the extra constraints defined above with parameters all set to zero allow deriving the Lagrange multipliers associated with keeping the phase shift of each branch constant. Then, the multiplier for branch i can be interpreted as the cost-benefit from a marginal phase shift of candidate PST assigned to that branch.
- The variables are defined as continuous, which makes the optimization problem continuous (not MILP) and thus the Lagrange multipliers of each constraint can be obtained.
- and —assigned to constraints limiting power flows for CBCOs (in both directions),
- —assigned to constraints setting the phase angles equal to .
4.2. Congestion Factor (CF)
- is the so-called Tap-Shift Distribution Factor (TSDF) joining the PSDF and the angle per tap sensitivity of the branch i,
- is the congestion volume for a CBCO in grid scenario , which is the value of power flow over the CB line that exceeds its thermal limit, defined by Equation (20) with:
- –
- —the set of vector variables in the optimal point including zero-valued vectors,
- –
- —the vector of optimal tap settings of the existing PSTs for the scenario .
4.3. Combined Methodology for Pre-Selecting the PST Candidates
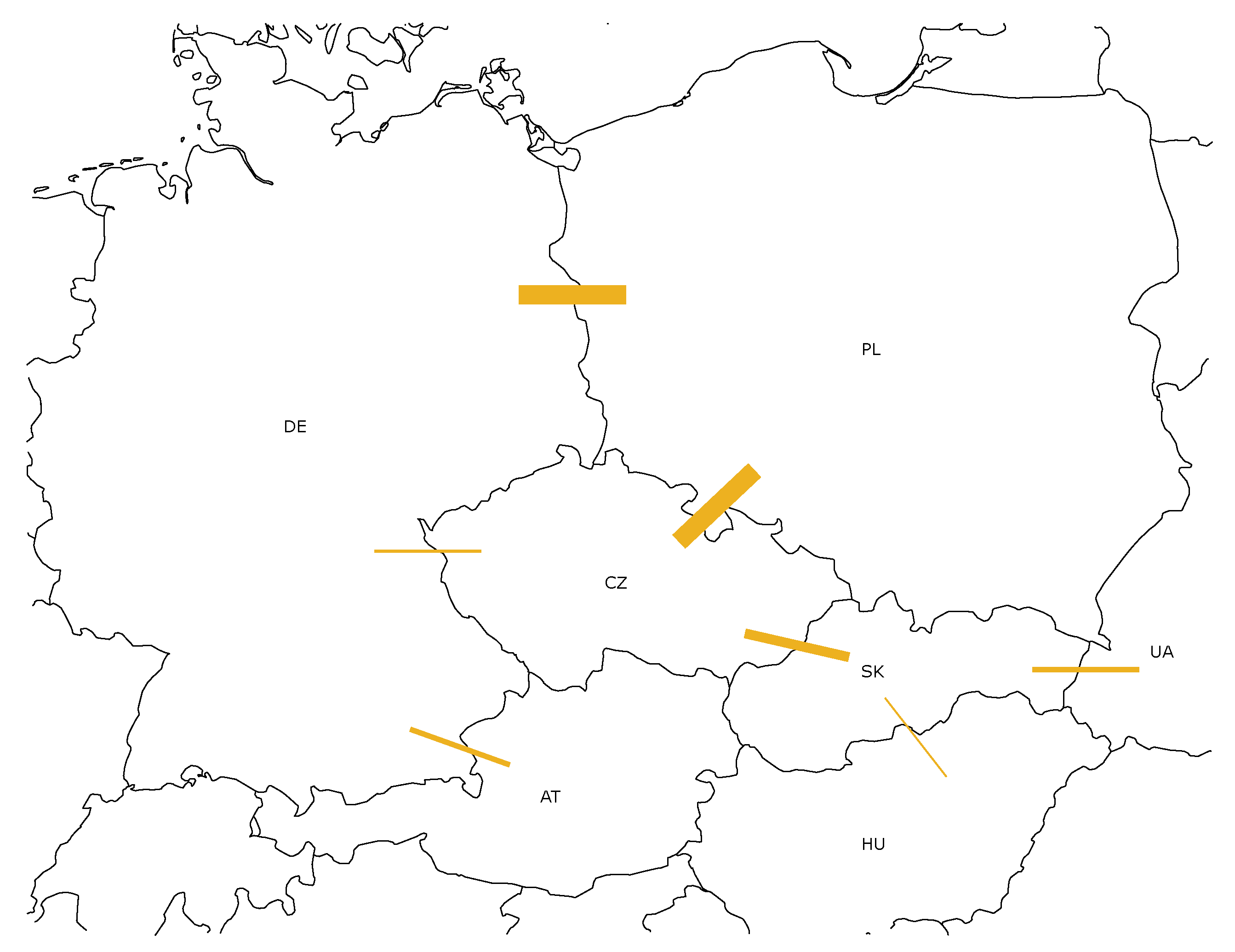
5. EU-SysFlex Scenarios
- with high detailed resolution: Poland, Germany, Czech Republic, Slovakia,
- with medium detailed resolution: Austria, Hungary, Ukraine,
- an equivalent representation of other European countries connected to the synchronous grid.
6. Results
6.1. Congestion Management Model
6.2. Long-Term Analysis—Candidate Selection for PST Investments
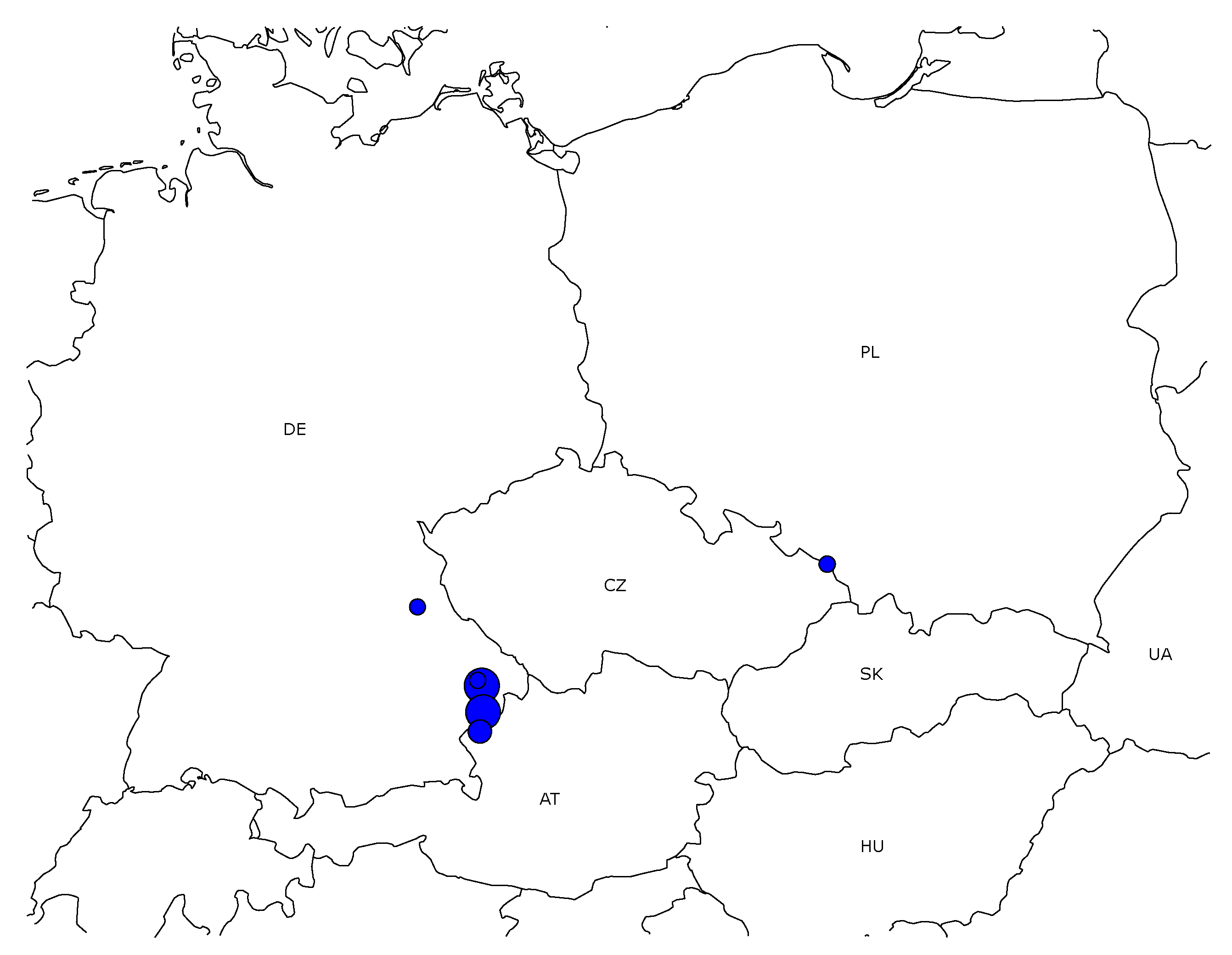
6.2.1. Multiplier Indicator Method
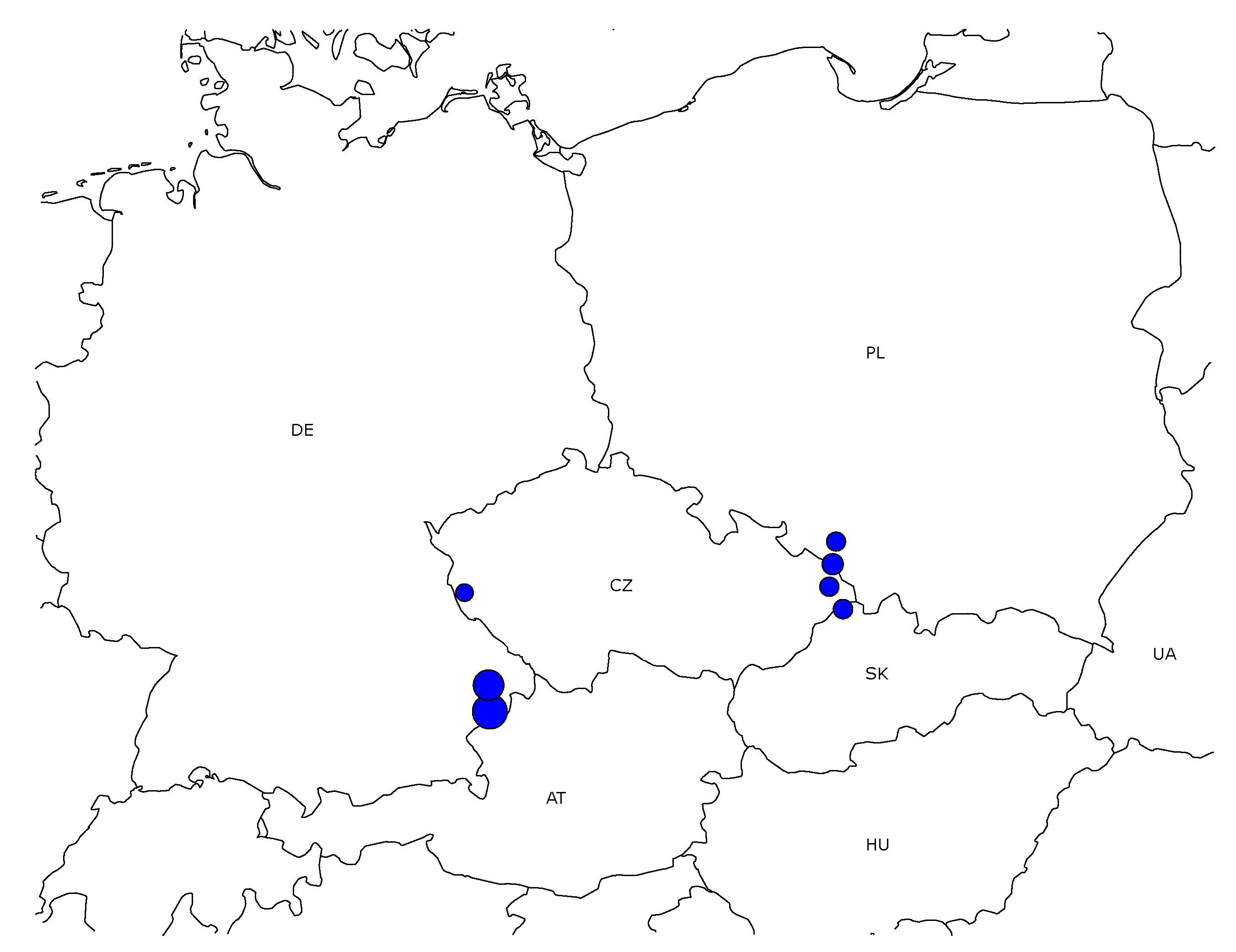
6.2.2. Congestion Factor Method
6.2.3. Summary of the Validation Results
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Data Consideration for the Generation Cost
Appendix B. Possible Extensions of the Multiplier INdicator
Appendix C. Possible Extensions of the Congestion Factor
Appendix D. Combination of PST Candidates—Horizontal Congestion Factor
References
- Regulation (EU) 2019/943 of the European Parliament and of the Council of 5 June 2019 on the internal market for electricity. Offic J. Eur. Union 2019, L 158, 54–124.
- Commission Regulation (EU) 2017/1485 of 2 August 2017 establishing a guideline on electricity transmission system operation. Offic. J. Eur. Union 2017, L 220, 1–120.
- Commission Regulation (EU) 2015/1222 of 24 July 2015 establishing a guideline on capacity allocation and congestion management. Offic. J. Eur. Union 2015, L 197, 24–72.
- Korab, R.; Owczarek, R. Impact of phase shifting transformers on cross-border power flows in the Central and Eastern Europe region. Bull. Pol. Acad. Sci. Tech. Sci. 2016, 64, 127–133. [Google Scholar] [CrossRef]
- Korab, R.; Owczarek, R.; Połomski, M. Coordinated Control of Phase Shifting Transformers in the Power System. Acta Energetica 2017, 3/32, 97–103. [Google Scholar]
- Commission for Electricity and Gas Regulation. Study on the Best Forecast of Remedial Actions to Mitigate Market Distortion; CREG Study (F)1987. Commission for Electricity and Gas Regulation: Bruxelles, Belgium, 2019. Available online: https://www.creg.be/sites/default/files/assets/Publications/Studies/F1987EN.pdf (accessed on 20 July 2020).
- Verboomen, J.; Van Hertem, D.; Schavemaker, P.H.; Kling, W.L.; Belmans, R. Analytical approach to grid operation with phase shifting transformers. IEEE Trans. Power Syst. 2008, 23, 41–46. [Google Scholar] [CrossRef]
- Jordehi, A.R. Optimal allocation of FACTS devices for static security enhancement in power systems via imperialistic competitive algorithm (ICA). Appl. Soft Comput. 2016, 48, 317–328. [Google Scholar] [CrossRef]
- Miranda, V.; Alves, R. PAR/PST location and sizing in power grids with wind power uncertainty. In Proceedings of the 2014 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Durham, NC, USA, 7–10 July 2014; pp. 1–6. [Google Scholar]
- Bekaert, D.; Meeus, L.; Van Hertem, D.; Delarue, E.; Delvaux, B.; Kupper, G.; Belmans, R.; D’Haeseleer, W.; Deketelaere, K.; Proost, S. How to increase cross border transmission capacity? A case study: Belgium. In Proceedings of the 2009 6th International Conference on the European Energy Market, Leuven, Belgium, 27–29 May 2009; pp. 1–6. [Google Scholar]
- Ippolito, L.; Siano, P. Selection of optimal number and location of thyristor-controlled phase shifters using genetic based algorithms. IEEE Proc. Gener. Transm. Distrib. 2004, 151, 630–637. [Google Scholar] [CrossRef]
- Hadzimuratovic, S.; Fickert, L. Determination of critical factors for optimal positioning of Phase-Shift Transformers in interconnected systems. In Proceedings of the 2018 19th International Scientific Conference on Electric Power Engineering (EPE), Brno, Czech Republic, 16–18 May 2018; pp. 1–6. [Google Scholar]
- Paterni, P.; Vitet, S.; Bena, M.; Yokoyama, A. Optimal location of phase shifters in the French network by genetic algorithm. IEEE Trans. Power Syst. 1999, 14, 37–42. [Google Scholar] [CrossRef]
- Lima, F.G.; Galiana, F.D.; Kockar, I.; Munoz, J. Phase shifter placement in large-scale systems via mixed integer linear programming. IEEE Trans. Power Syst. 2003, 18, 1029–1034. [Google Scholar] [CrossRef]
- Mekonnen, M.T.; Belmans, R. The influence of phase shifting transformers on the results of flow-based market coupling. In Proceedings of the 2012 9th International Conference on the European Energy Market, Florence, Italy, 10–12 May 2012; pp. 1–7. [Google Scholar]
- Baczynska, A.; Wierzbowski, M. Market coupling and the impact of cross border flows on the balancing of power demand. In Proceedings of the 2017 14th International Conference on the European Energy Market (EEM), Dresden, Germany, 6–9 June 2017; pp. 1–5. [Google Scholar]
- Zeraatzade, M.; Kockar, I.; Song, Y.H. Minimizing balancing market congestion re-dispatch costs by optimal placements of FACTS devices. In Proceedings of the 2007 IEEE Lausanne Power Tech, Lausanne, Switzerland, 1–5 July 2007; pp. 873–878. [Google Scholar]
- Gerbex, S.; Cherkaoui, R.; Germond, A.J. Optimal location of multi-type FACTS devices in a power system by means of genetic algorithms. IEEE Trans. Power Syst. 2001, 16, 537–544. [Google Scholar] [CrossRef]
- Ahmad, A.A.; Sirjani, R. Optimal placement and sizing of multi-type FACTS devices in power systems using metaheuristic optimisation techniques: An updated review. Ain Shams Eng. J. 2019. [Google Scholar] [CrossRef]
- Guo, J.; Fu, Y.; Li, Z.; Shahidehpour, M. Direct calculation of line outage distribution factors. IEEE Trans. Power Syst. 2009, 24, 1633–1634. [Google Scholar]
- Zimmerman, R.; Murillo-Sanchez, C. MATPOWER 5.1 User’s Manual; Power Systems Engineering Research Center (PSERC): Tempe, AZ, USA, 2015; Available online: https://matpower.org/docs/MATPOWERmanual-5.1.pdf (accessed on 20 July 2020).
- Han, Z.X. Phase Shifter and Power Flow Control. IEEE Trans. Power Appar. Syst. 1982, PAS-101, 3790–3795. [Google Scholar] [CrossRef]
- Verboomen, J. Optimisation of Transmission Systems by Use of Phase Shifting Transformers. Ph.D. Thesis, TU Delft, Delft, The Netherlands, 2008. [Google Scholar]
- D2.2. Models for Simulating Technical Scarcities on the European Power System with High Levels of Renewable Generation. Available online: http://eu-sysflex.com/wp-content/uploads/2018/12/D2.2_EU-SysFlex_Scenarios_and_Network_Sensitivities_v1.pdf (accessed on 20 July 2020).
- D2.3 EU-SysFlex Scenarios and Network Sensitivities. Available online: http://eu-sysflex.com/wp-content/uploads/2018/12/D2.3_Models_for_Simulating_Technical_Scarcities_v1.pdf (accessed on 20 July 2020).
- D2.4. Technical Shortfalls for Pan European Power System with High Levels of Renewable Generation. Available online: https://eu-sysflex.com/wp-content/uploads/2020/05/EU-SysFlex_D2.4_Scarcity_identification_for_pan_European_-System_V1.0_For-Submission.pdf (accessed on 20 July 2020).
- Zimmerman, R.D.; Murillo-Sanchez, C.E.; Thomas, R.J. MATPOWER: Steady-state operations, planning and analysis tools for power systems research and education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef]
| Border | Average Congestion [MW] | Number of Congestions |
|---|---|---|
| DE-AT | 35.61 | 25 |
| PL-CZ | 129.16 | 26 |
| CZ-SK | 48.48 | 35 |
| SK-UA | 75.26 | 12 |
| PL-DE | 140.06 | 24 |
| DE-CZ | 99.14 | 5 |
| SK-HU | 42.71 | 6 |
| PST Usage | Total Congestion Management Cost [EUR] | Maximal Congestion Management Cost [EUR] | Total Volume of Redispatching [MW] |
|---|---|---|---|
| Used | 12,579.28 | 2561.32 | 3573.09 |
| Not used | 134,023.58 | 58,598.78 | 16,435.82 |
| Branch Location | MI | Congestion Management Costs [EUR] |
|---|---|---|
| line (A) on DE-AT border | 3045.15 | 394 |
| DE station (B) next to DE-AT border | 1285.90 | 808 |
| DE transformer (C) next to DE-AT border | 916.84 | 490 |
| DE transformer (D) next to DE-AT border | 866.77 | 641 |
| line (E) on DE-AT border | 695.62 | 5391 |
| line (F) on DE-AT border | 690.63 | 5422 |
| DE line (G) next to DE-AT border | 651.30 | 2007 |
| line (H) on PL-CZ border | 629.70 | 9407 |
| DE line (I) next to DE-AT border | 610.58 | 2335 |
| Branch Location | CF | Congestion Management Costs [EUR] |
|---|---|---|
| line (A) on DE-AT border | 21,441.05 | 394 |
| DE station (B) next to DE-AT border | 11,078.74 | 808 |
| line (H) on PL-CZ border | 7436.30 | 9407 |
| line (J) on CZ-SK border | 6343.77 | 9569 |
| CZ station (K) next to PL-CZ border | 6142.07 | 10,474 |
| PL station (L) next to PL-CZ border | 5908.53 | 9454 |
| DE transformer (C) next to DE-AT border | 5319.99 | 490 |
| line (M) on DE-CZ border | 5163.14 | 3546 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urresti-Padrón, E.; Jakubek, M.; Jaworski, W.; Kłos, M. Pre-Selection of the Optimal Sitting of Phase-Shifting Transformers Based on an Optimization Problem Solved within a Coordinated Cross-Border Congestion Management Process. Energies 2020, 13, 3748. https://doi.org/10.3390/en13143748
Urresti-Padrón E, Jakubek M, Jaworski W, Kłos M. Pre-Selection of the Optimal Sitting of Phase-Shifting Transformers Based on an Optimization Problem Solved within a Coordinated Cross-Border Congestion Management Process. Energies. 2020; 13(14):3748. https://doi.org/10.3390/en13143748
Chicago/Turabian StyleUrresti-Padrón, Endika, Marcin Jakubek, Wojciech Jaworski, and Michał Kłos. 2020. "Pre-Selection of the Optimal Sitting of Phase-Shifting Transformers Based on an Optimization Problem Solved within a Coordinated Cross-Border Congestion Management Process" Energies 13, no. 14: 3748. https://doi.org/10.3390/en13143748
APA StyleUrresti-Padrón, E., Jakubek, M., Jaworski, W., & Kłos, M. (2020). Pre-Selection of the Optimal Sitting of Phase-Shifting Transformers Based on an Optimization Problem Solved within a Coordinated Cross-Border Congestion Management Process. Energies, 13(14), 3748. https://doi.org/10.3390/en13143748